1. Introduction
Fiber-reinforced polymer composites (FRCs) are widely employed due to their high specific stiffness and strength. With the growing demand for sustainable materials, the attention of both the scientific community and the petrochemical industry is drawn towards FRCs composed of a recyclable, thermoplastic matrix, e.g., isotactic polypropylene [
1,
2,
3,
4] or biodegradable alternatives, such as polylactic acid [
5,
6]. The semi-crystalline microstructure of these matrices makes the mechanical performance of FRCs strongly dependent on the processing conditions [
7]. Despite the extensive literature on the crystallization of iPP/fiber composites, a detailed understanding of fiber-induced nucleation is still lacking. Both fiber surface chemistry [
8,
9,
10] and topography, i.e., roughness [
5,
11,
12,
13], are thought to be important, but the exact roles of the two parameters are far from being elucidated [
14]. In addition, the heterogeneous nucleation process is believed to be controlled by the number of chain ends and, thus, the molecular weight of the material considered [
15]. Under relevant processing conditions, the application of pressure and flow induces shear stresses at the fiber–polymer interface, which strongly enhance the nucleation ability of the fiber surface with respect to quiescent conditions [
16]. These stresses, in turn, give rise to a special crystal morphology, the so-called cylindritic morphology, which is often referred to as a transcrystalline layer (TCL). The subtle difference between these conventions was explained in detail by Varga et al. [
17], but in this work, the latter is adopted for the structure that forms in both quiescent and shear flow conditions. Moreover, the mechanical performance of the fiber-reinforced polymer material is governed by the bonding between this TCL and the fiber [
1,
2,
18,
19]. In order to improve the adhesion between the two components, typically, the fiber surface and/or the matrix component are functionalized [
8,
9,
10,
20,
21,
22]. Hence, a comprehensive understanding of the effects of these compatibilization techniques on the developed morphology is indispensable for the design of long-, short-, and continuous-fiber composites.
The quantification of orientation around such interfaces is, however, rather limited when using optical microscopy techniques. While in quiescent conditions, the determination of the nucleation ability of the surface is well established [
11,
23,
24,
25], the vast number of nuclei that develop in shear flow conditions make the exact determination of structure practically impossible. As a result, the controversial data on the effect of interphase morphology on the mechanical properties of polymer composites may originate from the often ill-defined structure of the TCL. To fully characterize the microstructure that is probed when performing a mechanical test, quantitative data on the degree of chain orientation in the transcrystalline morphology with micrometer spatial resolution are essential. A wide variety of characterization techniques aiming to quantify this orientation have been developed over the years, e.g., birefringence measurements [
26], vibrational linear dichroism (infrared and Raman based) [
27,
28,
29,
30], and X-ray scattering and diffraction [
7], of which the latter can be considered the most mature. However, recently, Zhao et al. showed that linear dichroism measured with Fourier-transform infrared (FTIR) spectroscopy can quantitatively capture the decrease in orientation with increasing crystallization temperature when considering a TCL around a carbon fiber in an iPP melt [
31]. At the same time, polarization-modulated synchrotron infrared microspectroscopy (PM-SIRMS) has emerged as a powerful tool for providing precise spatial information on variations in polymer chain orientation and, hence, the alignment of crystal axes in lamellar structures [
32]. Contrary to conventional optical techniques, with PM-SIRMS, it is possible to quantitatively distinguish highly oriented transcrystalline morphologies. In the recent past, the technique has been successfully applied to study transcrystallinity in iPP/fiber composites [
29,
33,
34].
In the present work, this versatile technique is adopted to study transcrystallization in iPP matrices of different molecular weights around both neat and surface-modified glass fibers, as well as aramid fibers. The obtained measure from the PM-SIRMS resembling the fiber surface nucleation ability corresponds well with the nucleation density that is deduced from quiescent crystallization studies of different fibers. Hence, the morphological development during processing of these systems still depends to a large extent on the chemical and topological compatibility of the two phases and is not solely determined by the shear flow. In order to verify that small variations in experimental conditions do not contribute to the significant differences measured in the nucleation density at the fiber–matrix interphase, numerical simulations were performed. Using a finite element method (FEM) framework, the effect of a deviation in fiber velocity, fiber displacement, shear time, and sample height on the wall shear stress (responsible for molecular alignment and, thus, TCL formation) was investigated. Within reasonable limits, an inconsistency in either of these aforementioned parameters cannot cause the wall shear stress to vary more than a factor of two, i.e., it does not explain the significant differences in the degree of lamellar orientation measured using PM-SIRMS.
3. Results and Discussion
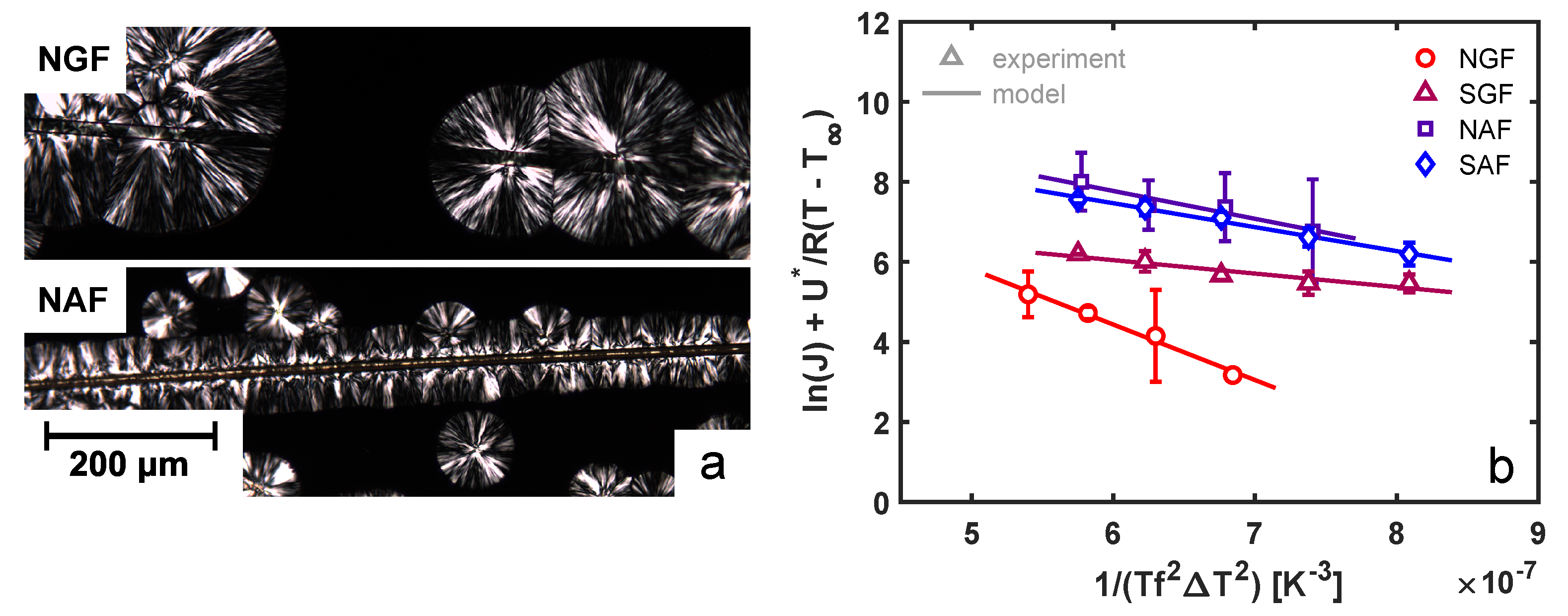
To study the effect of fiber surface chemistry on the nucleation ability towards an iPP melt, samples were isothermally crystallized at various temperatures under quiescent conditions. An example that highlights the difference in the nucleation ability of various substrates is presented in
Figure 5a, where a glass fiber (top panel) is compared to an aramid fiber (bottom panel). Whereas the glass fiber shows no interaction with the matrix material surrounding it, the aramid fiber clearly shows an enhanced nucleation efficiency at the fiber surface. By capturing optical microscopy images between two cross-polarizers in time, the nucleation rate was quantified by simply counting the number density of nuclei in time. The obtained nucleation rates per unit surface area are shown in
Figure 5b as a function of temperature for the various fibers. With the lowest surface roughness and no chemical compatibility with the matrix, the neat glass fiber shows the lowest nucleation ability, followed by the functionalized glass fiber and, subsequently, the aramid fibers. These local differences between the various fibers in terms of the bulk and interphase morphology may lead to substantial variations in mechanical performance. Due to the development of an oriented transcrystalline layer perpendicular to the fiber direction, the modulus and strength in the direction parallel to the fiber orientation may have been increased, while the ultimate tensile strain was drastically decreased.
To quantitatively describe these differences in fiber–matrix affinity, classical heterogeneous nucleation theory was used; the nucleation ability of a given substrate towards a polymer matrix is proven to be effectively captured by a parameter
that is directly proportional to the free-energy barrier for nucleation. The temperature-dependent nucleation rate is then given by [
40]:
where
is a pre-factor that is independent of temperature,
represents the energy barrier for diffusion of chain segments over the phase boundary,
R is the universal gas constant,
is a fictive temperature at which all viscous flow is assumed to cease, typically 30 °C below the glass-transition temperature,
and
are the free energies of the lateral and fold surface, respectively, under the conditions that they are fully in contact with the undercooled amorphous melt,
is the equilibrium melting temperature,
k is Boltzmann’s constant,
f is a correction factor (
), and
is the specific enthalpy of fusion for a perfect crystal at its equilibrium melting point.
The parameters for the equilibrium melting point
K, the fictive temperature
K, the energy barrier
J mol
, and the enthalpy of fusion
J m
were adopted from the classical works of Clark and Hoffman [
41] and Cheng et al. [
42]. The product of
and
was deduced from the work of Wang et al. [
43] to be 732 mJ
2 m
. Fitting Equation (
7) to the experimental data presented in
Figure 5b yields the parameters for the pre-factor
and the energy barrier for nucleation
; see
Table 1. When considering the neat (NGF) and sized glass fiber (SGF), it is clear that the application of a surface coating effectively lowers the free-energy barrier for nucleation, resulting in a high nucleation density at the surface. However, comparing the aramid fibers to the glass fibers, an energy barrier that is between that of the NGF and SGF is found (based on the above-described model). This suggests that the chemical compatibility of both the NAF and SAF with the iPP matrix is worse than that of the SGF, yet the number of nuclei that are observed at the fiber surface is higher than in the case of the SGF for all temperatures assessed. In fact, the
values found for the aramid fibers are close to those reported for bulk heterogeneous nucleation of polypropylene, i.e.,
mJ m
[
43]. It may be evident that the difference in pre-exponential factor
is the determining figure here; due to the manufacturing process of the aramid fibers, a slight surface texture and heterogeneity were present, which may have enhanced the nucleation process [
12]. Scanning electron microscopy (SEM) images of the different fibers are shown in the
Supplementary Material. The Twaron fibers possess significantly greater amounts of heterogeneities at the surface in comparison with the findings of Wang et al. [
25] on Kevlar 49 fibers. This difference is ascribed to the different manufacturing techniques used by the aramid producers and can explain the significant difference in the
values obtained when comparing our work to the literature.
Under shear flow conditions, on the other hand, this strong influence of the fiber surface characteristics seemingly vanishes. The alignment of polymer chains close to the fiber surface leads to the formation of a so-called columnar morphology, as a vast amount of
-phase nuclei can form on highly oriented
-phase crystals. Visually, it becomes extremely difficult to observe structural differences in such highly oriented systems, as can be seen from the cross-polarized micrographs presented in
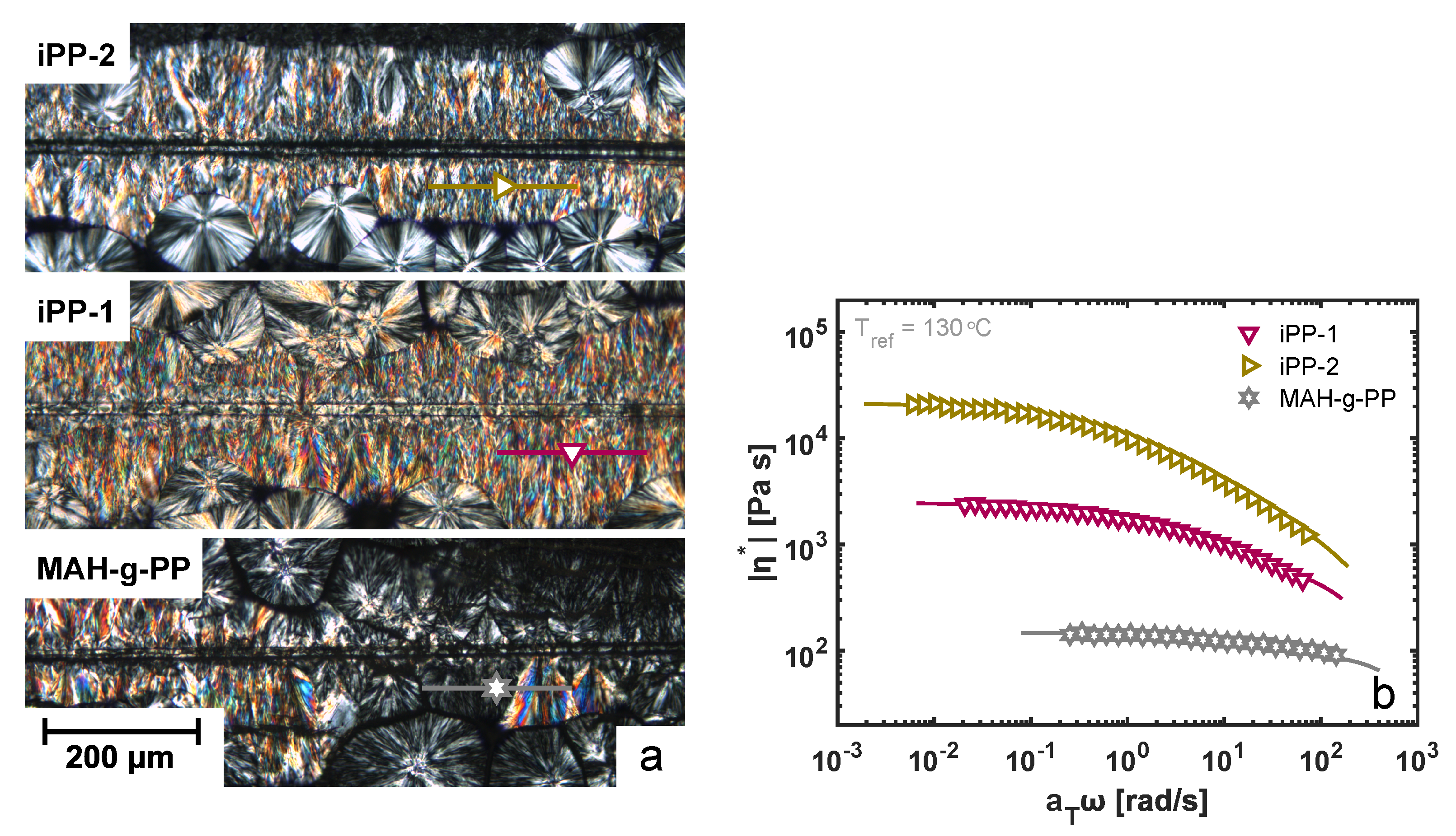
Figure 6a. Whereas an intuitive distinction between the structures formed around a glass fiber for matrix materials of different molecular weights may be still possible, a quantitative measure of the nucleation density is rather unachievable. By means of polarization-modulated infrared spectroscopy, a technique increasingly applied in the field of polymer science [
33,
34], we were able to detect lamellar orientation in transcrystalline and columnar morphologies, as was recently demonstrated [
29]. Combining this technique with a highly brilliant synchrotron light source, a spatial resolution down to the diffraction limit is achieved, and hence, the degree of orientation in the single fiber systems can be determined down to a length scale of approximately 10 × 10 μm
2. Polarization-modulated synchrotron infrared microscopy (PM-SIRMS) line scans with a length of 200 μm were traced parallel to the fiber surface at a distance of 50 μm from the surface and a step size of 5 μm at the locations indicated in
Figure 6a. The degree of alignment was calculated from the differential absorbance spectrum, as defined by Equation (
1), at a wavelength of 1169 cm
, which corresponds to the carbon–carbon symmetrical stretch vibrational band and may, thus, be considered a measure for the backbone stretch of the polypropylene main chain.
Three different molecular weights of the matrix material are considered in this work. The complex viscosity was measured as a function of frequency using small-amplitude oscillatory shear (SAOS), and the resulting master curves at a shifted temperature of 130 °C are presented in
Figure 6b. The variation in zero-shear viscosity between the three materials is roughly a factor of 10, and hence, under comparable shear flow conditions, the flow field and resulting crystalline morphology is very different, as deduced from
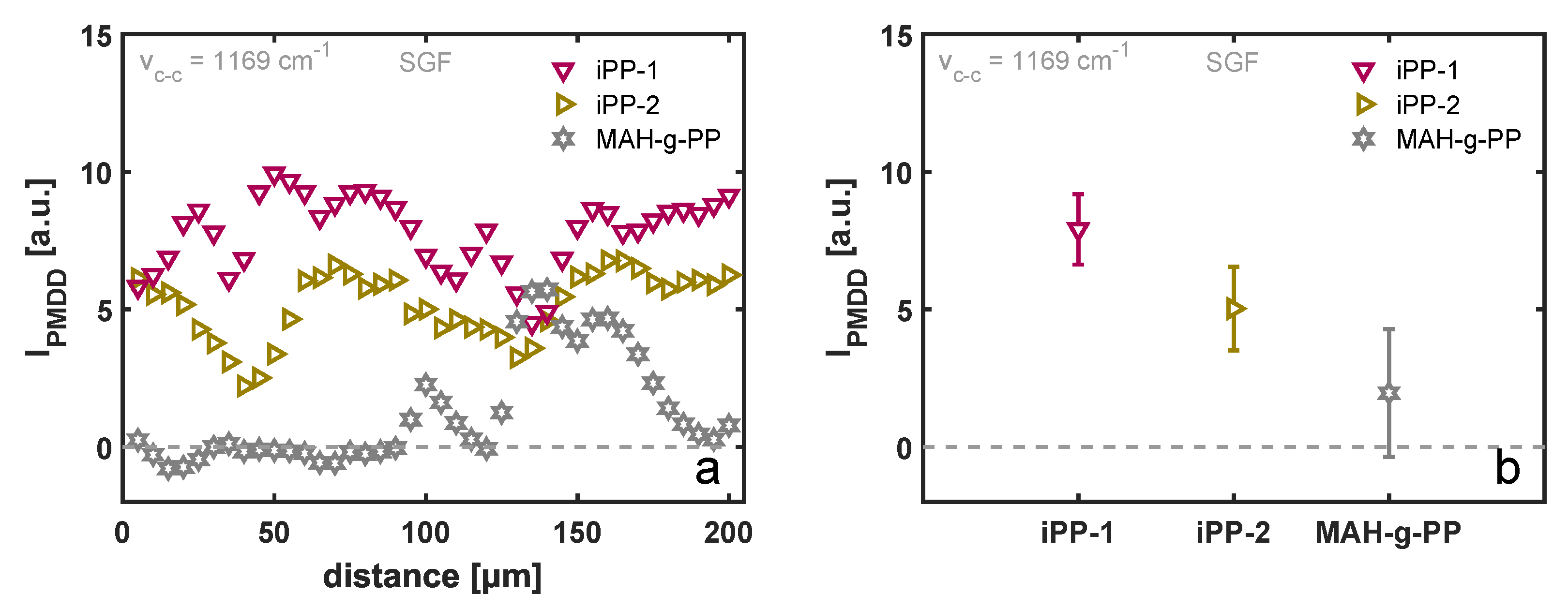
Figure 6a. The results of the PM-SIRMS line scans are presented in
Figure 7a as a function of the scan distance. For the iPP-1 and iPP-2 samples, which showed the most homogeneous TCL morphology in POM, the polarization-modulated dichroic ratio is fairly constant, yet due to the small spot size of the IR beam, local differences are detected. These variations could arise from local differences in the arrangement of the lamellae, as well as the twisting of the β-phase lamellae [
44]. For the MAH-g-PP sample, however, where due to the fast relaxation of the polymer chains after application of shear flow a distorted interphase layer was formed, that dichroic ratio is close to zero in the region where no TCL was observed and increases when the scan position reached the partially oriented β-phase crystals. This implies that the above-described characterization technique is capable of detecting these structural changes, although it is not particularly useful for the characterization of weakly oriented morphologies. The average PMDD ratio is presented in
Figure 7b, where the markers correspond to the mean values measured over a distance of 200 μm, while the error bars indicate the standard deviation of the individual measurement points. Contrary to what may be expected, yet in line with earlier findings by Folkes and Hardwick [
15], a substantially lower degree of chain alignment was measured for the material with the highest molecular weight, i.e., iPP-2, as compared to the lower-molecular-weight material, iPP-1. Typically, the high-molecular-weight fraction of a polymer material leads to a stronger alignment of chains, and thus, a greater orientation of the TCL can be anticipated. Taking into account the larger resistance of the iPP-2 material against flow, presented by the master curves of the complex viscosity in
Figure 6b, it is likely that the smooth and stiff fiber slipped through the soft melt when being pulled rather than deforming the polymer chains at the interphase. This hypothesis is substantiated by the results of the FEM simulations, but this is outside the scope of this work and is not elaborated upon further.
Polarized optical micrographs of the morphology around four different fibers sheared through an iPP-1 matrix are shown in
Figure 8. It may be clear that for these systems, it is practically impossible to rank or quantify the degree of lamellar alignment based solely on such images, and that when these morphologies are observed, one jumps to the conclusion that adhesive parameters at the fiber–matrix interphase become irrelevant, and crystal structure formation is governed by the applied flow. Therefore, to verify whether that assumption was valid, for both iPP-1 and iPP-2, PM-SIRMS scans of 200 μm at a distance of 50 μm from the fiber interface were collected, the locations of which are indicated in
Figure 8. The average peak intensity of the backbone stretching, i.e., the vibrational band at 1169 cm
, is shown in
Figure 9 for the different fibers. The horizontal dotted line represents a PMDD intensity of zero, indicating an isotropic microstructure at the length scale of the IR light. For both matrix materials, a similar trend was observed when comparing the fiber types; the neat glass fiber showed the lowest degree of lamellar alignment, followed by the sized glass fiber and aramid fibers, respectively. For the iPP-1 samples, the average PMDD intensity is higher for all fiber types compared to the iPP-2 (higher molecular weight) sample, which can be attributed to slippage between fiber and matrix during pulling, as discussed before. The degree of orientation measured in the TCL correlates well with the nucleation rate observed in quiescent conditions. As the nucleation density at the fiber surface increases, the steric hindrance of neighboring lamellae prevents a nucleus from growing in the lateral direction as a spherulite, and growth solely takes place from the fiber surface outward, creating a columnar morphology around the fiber. Hence, the vibration corresponding to the stretching of the backbone of the chain is directly related to the nucleation density at the fiber surface. This result demonstrates that the TCL structure formation upon shear flow is not solely determined by the flow field and flow strength, nor by the chemical interaction between fiber and matrix alone, but rather by a synergistic combination of the two.
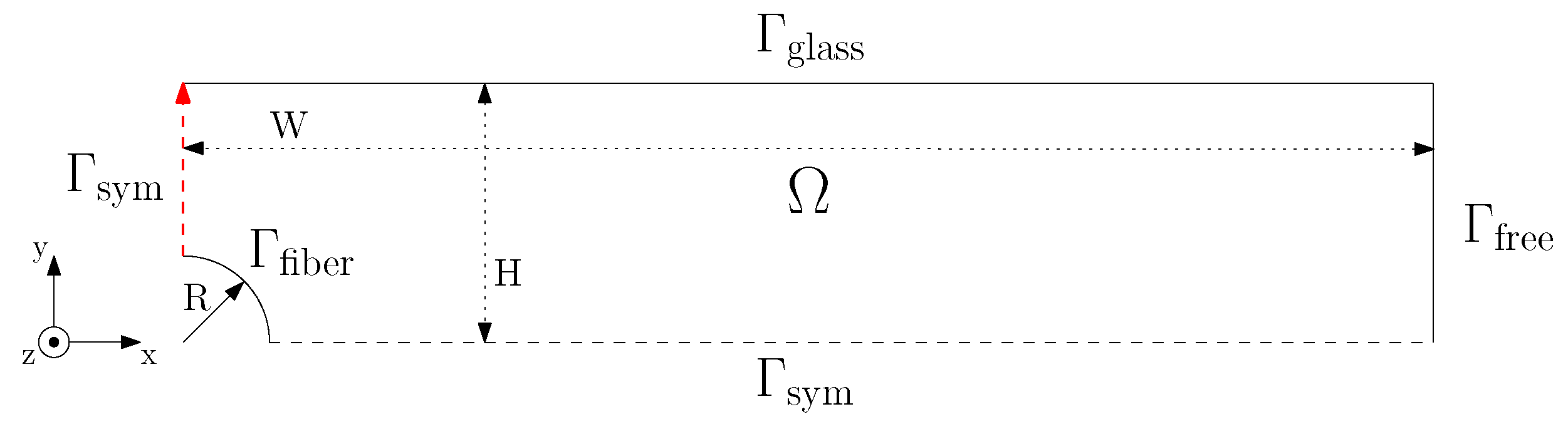
During the sample preparation of these TCL morphologies, parameters such as sample thickness, shear rate, shear time, and isothermal crystallization temperature were kept constant. However, given the high sensitivity of the PM-SIRMS measurement and the resolution of the equipment used to prepare the morphology, small deviations in the flow field upon pulling may have emerged. In order to verify that the observed differences in crystal alignment resulted solely from a difference in fiber surface chemistry rather than a variation in the applied flow field due to experimental inconsistencies, FEM simulations of the fiber-pulling experiment were performed. The incompressible mass and momentum balance were solved on the domain shown in
Figure 3 using a nonlinear viscoelastic (Giesekus) constitutive model [
38,
39]. The nonlinear parameter
represents the decrease in viscosity with increasing deformation rate and was fitted to the complex viscosity data under the assumption that for these linear polymer systems, the Cox–Merz rule [
45] is applicable; for both iPP-1 and iPP-2, this parameter is set equal to 0.49. The deformation profile and viscoelastic stress state are evaluated for the two highest matrix molecular weights, i.e., iPP-1 and iPP-2, for varying sample thicknesses, pulling distances, -rates, and -times. Here, solely the results regarding an inconsistency in the maximum velocity and sample thickness for the iPP-1 sample are discussed, while the influence of time lag and displacement amplitude, as well as all results for the iPP-2 sample, can be found in the
Supplementary Material.
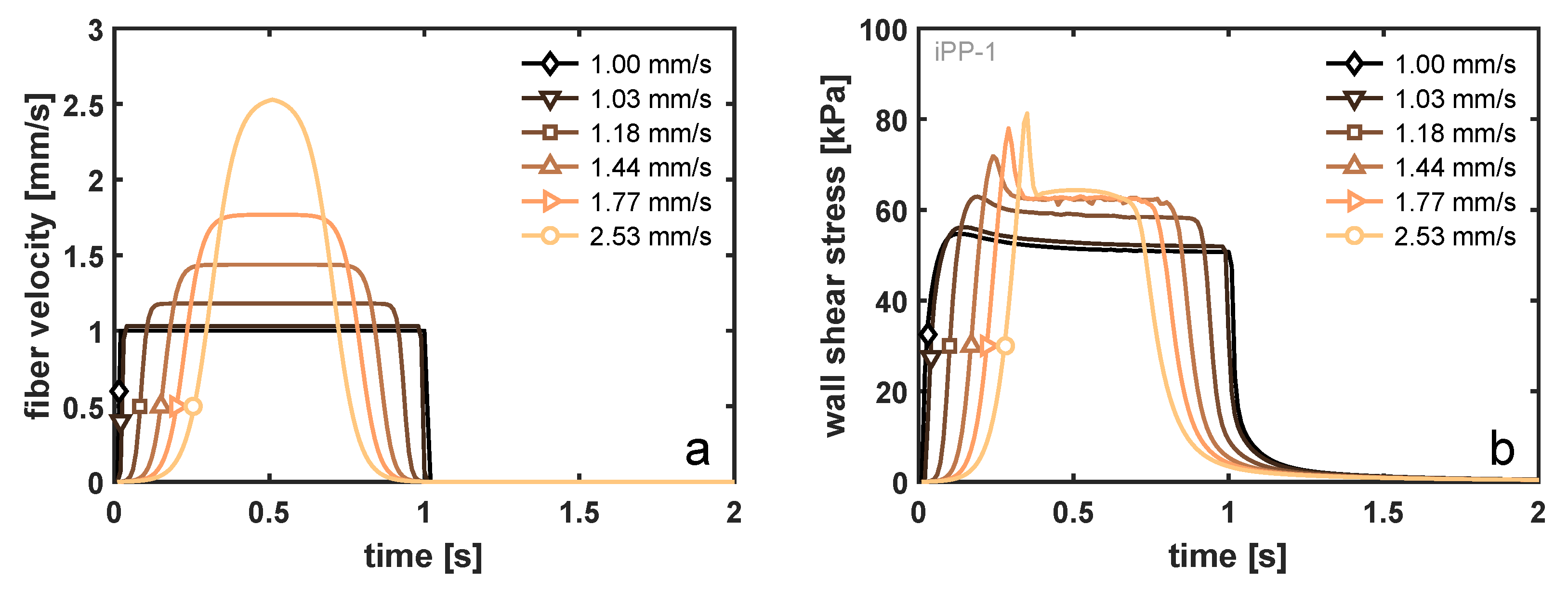
The fiber-pulling experiment was set up such that the total displacement of the fiber and the time to reach that displacement are fixed. It is assumed that the mass of the fiber is sufficiently low that its acceleration is infinitely fast, and hence, a step velocity profile is applied to the fiber. The fact that, in reality, the acceleration of the fiber is finite may influence the imposed velocity profile in the vicinity of the interface, as well as the local stress state, due to the simultaneous stress build-up from the increase in deformation (rate) and stress decrease because of viscoelastic relaxation. In the simulations, the gradual increase in fiber velocity was modeled using an arctangent velocity profile, as illustrated in
Figure 10a, while keeping the total displacement of the fiber equal to 1.00 mm and the total shear time equal to 1 s. As a result, the maximum velocity at the fiber wall increases, and that effect on the viscoelastic shear stress at the wall is examined and is shown in
Figure 10a. Comparing the velocity profile with a maximum velocity of 2.53 mm/s with that of a step-velocity profile (1.00 mm/s), the lag in acceleration reduces the initial increase in wall shear stress due to a competition between stress build-up and relaxation. In fact, due to the relatively low relaxation times of the iPP-1 sample (
Table S1 of the Supplementary Material), a decrease in wall shear stress was already observed prior to the fiber reaching its maximum velocity. Pronounced shear thinning of this material leads to a peak stress that is only 45% increased at a fiber velocity of 2.53 mm/s, as compared to the 1.00 mm/s reference (increase of 153% in velocity), and an increase of only 20% of the steady-state plateau stress. For the iPP-2 material, where shear thinning is present at already lower deformation rates, this increase in wall shear stress is even less pronounced. It should be noted that the lag in acceleration described here is highly exaggerated in relation to the possible experimental error, and that, even in this extreme case, a marginal increase in the stress was observed.
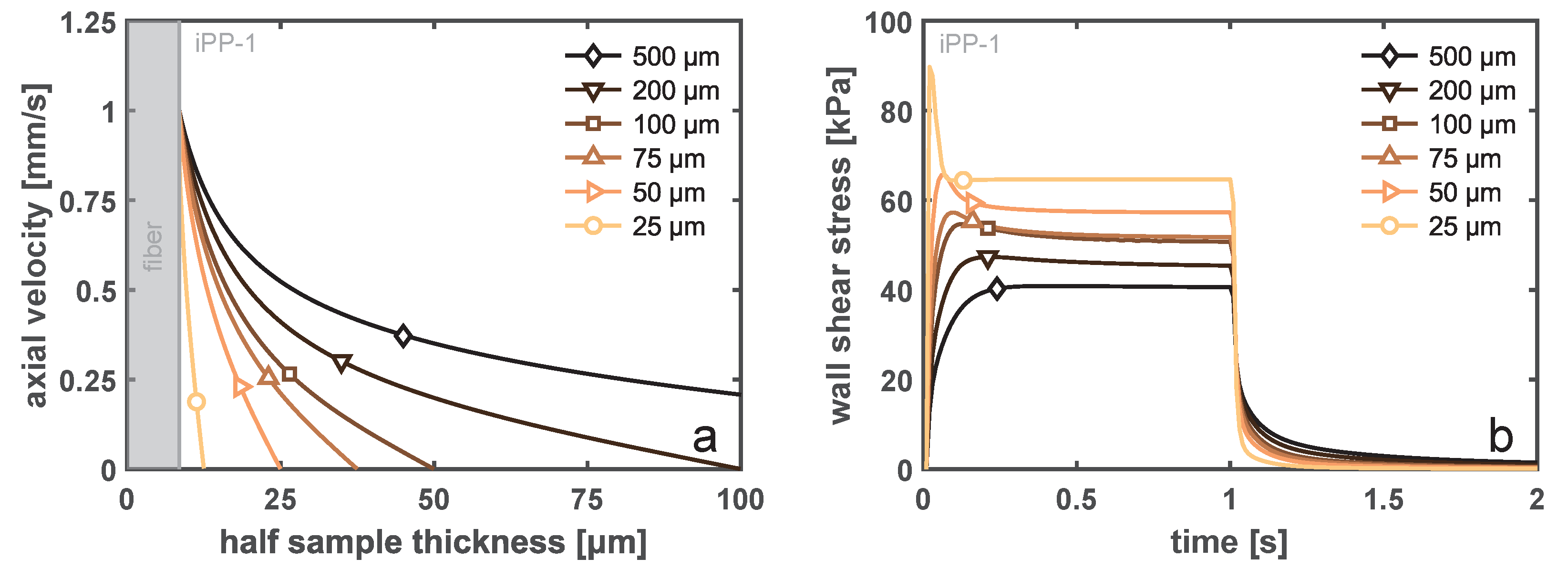
A similar conclusion may be drawn from the FEM results describing a step-velocity experiment at 1 mm/s for 1 s for varying sample thicknesses.
Figure 11a displays the steady-state velocity profile over the sample height, where the sample width was always 500 μm and the fiber diameter was 17 μm. With decreasing sample thickness, the shear rate at the fiber surface increases in order to fulfill the imposed boundary conditions at both ends (no slip). This effect was historically modeled using the theory of Monasse [
46], who took the effect of shear thinning into account for a viscous fluid. In the
Supplementary Material, we present the velocity profiles around a fiber for iPP-1 and iPP-2. These two homopolymer grades have the same power-law exponent for the model of Monasse, which implies that the velocity profile should look identical. From the viscoelastic simulations, it becomes clear that this can not be true, and a more pronounced boundary layer starts to form when the resistance against flow increases, i.e., the viscosity increases and mobility becomes dominated by relaxation. The low molecular weight of the iPP-1 material leads to a fast relaxation and, hence, a nonlinear shear profile, even for thin samples. However, although the wall shear rates may be very different with changing sample thickness, due to the fact that the imposed deformation mostly occurs at rates that are in the shear thinning region of the material, the net increase in the wall shear stress is minute, as can be deduced from
Figure 11b. When the thickness was reduced from 500 to 50 μm, i.e., a factor of 10, the wall shear stress increases solely by
. In the case in which the sample thickness was decreased to be approximately equal to the fiber diameter, confinement effects and fiber–wall interactions start to be significant, which increases the local stress substantially. Again, this is an extreme condition that was not encountered experimentally.
Taking all FEM simulation results into consideration, it becomes evident that variations in the molecular weight (distribution), i.e., the relaxation time spectrum of the material, contribute far more to the local shear stress at the fiber surface than any experimental variable that we impose. Hence, the substantial differences in crystal orientation measured by PM-SIRMS must have originated from the intrinsic interplay between the matrix and fiber and were only negligibly influenced by the imposed experimental conditions. The influence of temperature was outside of the scope of this numerical study, as the control of the Linkam heating stage was far more precise than the temperature dependence of the relaxation times, i.e., even with a (large) deviation of 1 °C in shear temperature, the difference in viscoelastic properties was negligible. In addition, the temperature was always checked using the growth rate of the spherulites, which was well established for iPP, as an “intrinsic thermocouple”.
These insights into structural development and characterization will aid in the quantitative understanding of the mechanical performance and provide processing guidelines for fiber-reinforced polymer (FRP) constructs. The single-fiber flow experiments resulted in a detailed understanding of the semi-crystalline morphology that developed at the matrix–fiber interface, be it a short, long, or continuous FRP. The combination of fiber length, orientation distribution, and interface structure determines the eventual mechanical properties of a multi-fiber product.