Abstract
An accurate calculation of the flexural capacity of flexural members is vital for the safe and economical design of FRP reinforced structures. The existing empirical models are not accurately calculating the flexural capacity of beams and columns. This study investigated the estimation of the flexural capacity of beams using non-linear capabilities of two Artificial Intelligence (AI) models, namely Artificial neural network (ANN) and Random Forest (RF) Regression. The models were trained using optimized hyperparameters obtained from the trial-and-error method. The coefficient of correlation (R), Mean Absolute Error, and Root Mean Square Error (RMSE) were observed as 0.99, 5.67 kN-m, and 7.37 kN-m, for ANN, while 0.97, 7.63 kN-m, and 8.02 kN-m for RF regression model, respectively. Both models showed close agreement between experimental and predicted results; however, the ANN model showed superior accuracy and flexural strength performance. The parametric and sensitivity analysis of the ANN models showed that an increase in bottom reinforcement, width and depth of the beam, and increase in compressive strength increased the bending moment capacity of the beam, which shows the predictions by the model are corroborated with the literature. The sensitivity analysis showed that variation in bottom flexural reinforcement is the most influential parameter in yielding flexural capacity, followed by the overall depth and width of the beam. The change in elastic modulus and ultimate strength of FRP manifested the least importance in contributing flexural capacity.
1. Introduction
Concrete is the principal construction material for the building industry used in the construction of buildings and infrastructure because of its excellent construction properties considering an additional advantage of adding rebars in reinforced concrete structures. Although rebars improve the properties of concrete without modifying the cementitious properties of the matrix [1]. But susceptibility to corrosion of the rebars embedded in concrete has been recognized as one of the major durability problems associated with reinforced concrete (RC) structures. Corrosion infiltrates chloride ions into the concrete mix, which decomposes the protective layer formed on the steel surface [2,3,4]. The corrosion may not only induce an expansion pressure but may also result in cracking, crack widening, and spalling of concrete clear cover, which not only reduces the service life of RC structures but also causes a reduction in the cross-section of the rebars and weakens the load-carrying capacity of RC structures. The statistical evaluation indicates that a significant percentage of infrastructure failure globally has occurred due to corrosion of mild steel reinforcement embedded in concrete [5,6,7,8]. Also, marine infrastructure, including offshores, seaports, and subsea structures, is very important for the overall development of a country. To control the continuous deflation of natural resources and avoid transportation of natural resources to construct marine structures, sea sand and seawater may be a suitable replacement t [9]. However, its use may be hindered due to its high alkalinity and chloride content which may cause corrosion of steel reinforcement [10].
To avoid the critical problem of the high corrosion rate of mild steel, fiber-reinforced polymers (FRPs) are proposed as a potential alternative material due to their superior corrosion resistance and competent mechanical properties. Fiber-reinforced concrete also can resist corrosion and allow the direct utilization of sea sand and seawater as efficient and economical construction materials for marine structures [9,11,12,13,14,15,16,17]. FRP materials exhibit several properties, such as lightweight, and high tensile strength, making them suitable for structural reinforcement [18]. Different types of FRP, such as Carbon FRPs, Aramid FRPs, Glass FRPs, and Basalt FRPs, are available as common replacements for conventional steel reinforcement. FRPs have been subjected to experimental investigation for decades for their durability assessment. FRPs are reported to have the highest retention of tensile strength subjected to the highly alkaline solution [19,20,21,22,23,24,25]. Several factors shall be considered, including the performance advantage, materials cost, and application field, before using FRP. For instance, CFRP has better mechanical properties, and fatigue/creep/corrosion resistance. However, its high material price and low elongation at break are the main disadvantages. In contrast, GFRP and BFRP have a higher elongation at break and lower price, but their mechanical, corrosive, and creep properties are relatively poor, especially exposed to an alkaline environment [26,27,28]. Moreover, CFRP is highly recommended for higher flexure strength of RC beams, improved confinement, and lower deflection compared to GFRP and BFRP [17,29]. The performance of GFRP beams improves with the addition of steel bars. Crack width and mid-span deflection decreased by increasing the reinforcement ratio, whereas the load-carrying capacity was increased [30,31]. GFRP and CFRP showed superior effects on the load-carrying capacity, stiffness, and energy absorption of RC structural elements compared with conventional steel reinforcement [32].
The previous researchers recommended the use of a variety of AI models for solving engineering problems [33,34,35,36,37,38,39,40,41]. Modern engineering values numerical [42,43,44] and artificial intelligence (AI) models for solving complex and nonlinear problems. Earlier studies have employed AI models for estimating the flexural strength of FRP reinforced beams. Murad et al. [45] developed the GEP model and evaluated a high value of R equalling 0.977 compared to the one obtained from the ACI model (R= 0.974). It is noteworthy to mention that Murad et al. [45] based the accuracy of the model based on the value of R only. In the recent study conducted by Amin et al. [46], it was evaluated that the accuracy of the GEP model developed by Murad et al. [45] was smaller compared to the ACI models in terms of error indices. The ensemble tree-based models developed for the same problem also showed the superiority of ACI equations compared to the gradient boosting tree and decision tree models [46]. However, it was suggested that new AI models that can accurately predict flexural strength should be investigated.
Naderpour et al. [47] proposed an AI model for predicting shear resistance of FRP-reinforced concrete beams using an Artificial Neural Network (ANN). The accuracy of the proposed ANN model was more than ACI 440.1R-06, ISIS-M03-07, BISE, JSCE, and CNR DT 203. Lee et al. [48] developed an ANN model that resulted in improved statistical parameters with better accuracy than the other existing models. Random Forest (RF) was evaluated more robust model in comparison to ANN, GEP, and decision tree (DT) model [49] while investigating the compressive strength of high strength concrete. Similarly, Khan et al. [50] also evaluated the superiority of RF in comparison to the GEP model in estimating the compressive strength of geopolymer concrete. Therefore, ANN and Random Forest (RF) models, which are modern Artificial intelligence (AI) techniques, are explored in this research work to develop a simple and more accurate model that can predict the flexural capacity of concrete beams reinforced with FRP bars. The ANN model developed in this study showed higher accuracy in comparison to the previously developed AI models, therefore leading to study optimization of the ANN model in the future work.
2. ACI Approach towards Calculating Flexural Capacity
Numerous analytical and numerical models are available in the literature for the prediction of the flexure behavior of FRP reinforced beams [51]. ACI-440-17 [52] and the CSA S806-12 [53] have also developed guidelines for designing FRP reinforced beams. The formulation shown in Equations (1)–(5) presents the ACI model for calculating the flexural capacity of FRP reinforced beams, where, cb is the distance from extreme compression fiber to the neutral axis of the member at balanced strain condition (mm) and c is the distance from extreme compression fiber to the neutral axis of the member (mm). is a balanced reinforcement ratio. ff is tensile stress of FRP rebar at failure, is the elastic modulus of longitudinal FRP bars, is ultimate concrete strain = 0.003, is the ultimate tensile strength of FRP rabars. is the FRP reinforcement ratio, is the area of longitudinal flexural reinforcement (mm2), b is the width of the beam (mm), and d is the depth of the beam (mm). is the compressive stress block parameter, and is the concrete compressive strength.
3. Experimental Database
Table 1 lists the experiments that were used to construct the experimental database, collected from a wide range of literature, also reported by Murad, Y., A. Tarawneh, F. Arar, A. Al-Zu’bi, A. Al-Ghwairi, A. Al-Jaafreh and M. Tarawneh [45] and Amin et al. [46]. As depicted from Equation (6), flexural strength, i.e., the moment, is governed by six input factors: beam depth (D), beam width (W), concrete compression strength (fc′), area of bottom flexural reinforcement (As), Elastic modulus of the FRP rebar (EM), and the ultimate tensile strength of rebar upon failure (Tf). The data collected in terms of attributes is corroborated with the ACI formulations for flexural strength capacity [54].

Table 1.
Summary of input and output characteristics utilized in the model formulation using ANN and RF regression.
Such that M refers to the total flexural capacity. ACI formulas demonstrate the importance of various input factors in contributing to the bending capacity. In addition, Figure 1 and Table 2 illustrate the distribution histogram and the descriptive statistics for the variables utilized here, respectively. From the histograms (Figure 1) it can be seen that the most of the samples (exceeding approximately 80%) tested in a variety of experimental works exhibit width between 130–205 mm, depth ranging from 152 to 302 mm, fc’ having values between 24–54 MPa, As of 57–657 mm2, EM of 35,630–51,260 MPa, whereas Tf ranges from 552 to 1152 MPa. The standard deviation values in Table 2 show that the models are constructed using a wider range of variable values.
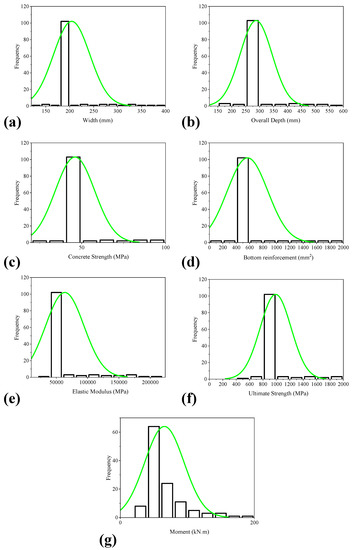
Figure 1.
Histograms of the input and output parameters used in the current study; (a) Width, (b) Overall depth, (c) Concrete strength, (d) Bottom reinforcement, (e) Elastic modulus, (f) Ultimate strength, and (g) Moment.

Table 2.
Descriptive statistics of input and output variables used in the current study.
4. Machine Learning Approaches
4.1. Artificial Neural Network (ANN)
As a bioneural network model, an artificial neural network (ANN) comes with immense sophistication to handle many complexities within any data. As an ML technique, ANN aims to mimic the knowledge accumulation and interpretation process that transpires in the human brain [73]. ANN has been extensively employed to solve nonlinear regression analysis issues [74]. The backpropagation neural network, a common ANN training approach, is often utilized in regression analysis and practical applications. In a backpropagation neural network, there are three layers: the input layer, the output layer, and a hidden (intermediate) layer linked to both input and output layers. A gradient descent algorithm, such as Widrow–Hoff arithmetic, is commonly used in backpropagation networks. Weights are modified or shifted along with the negative value of the running function’s gradient in this network. The word “backpropagation” is used to describe how nonlinear multilayer neural networks do progressive computing [75]. Despite the excellent predictive performance of the backpropagation approach, its drawback is its slow convergence speed [76]. The problem has been addressed using many optimization algorithms using simple gradient descent algorithms. Among the tested algorithms, the conjugate gradient algorithm has proven to be better than most algorithms in improving the learning time, leading to a quick convergence rate of the neural network.
The search direction for all conjugate gradient algorithms is periodically reset to the gradient’s negative [77]. The usual reset point happens when the number of repetitions equals the number of network parameters, mainly weights, and bias. In addition, to reset procedures, other methods have been used to enhance training efficiency. Concerning those approaches, it was argued by [78] relying on Beale’s version [79] that there will always be a restart in the technique process if there is a slight orthogonality change between the current and previous gradient. The following inequality demonstrates this:
where is the kth iteration’s gradient. The search direction is reset to the negative of the gradient if this condition in Equation (7) is met.
The number of neurons in the hidden layer is crucial in designing the network. Fewer neurons often lead to incomplete signal recognition or underfitting in complex datasets [80]. When the neurons are more than needed for the network, the lattice time increases, leading to overfitting because the network receives too much information or the training sub-dataset does not need enough specific information to train the network. Factors like the number of network’s input and output layers, target data noise, number of sample set cases, error function complexity, the network’s architecture, and the network’s training algorithm affect the number of hidden layers. As there is no method to quickly determine the optimal number of neurons in the hidden layers without prior training of the network [81], the trial-and-error approach is still widely adopted.
4.2. Random Forest Regression (RFR)
Random forest trees (RFT) employ the concept of ensemble learning, contain several decision classification trees, gather the findings by randomly picking characteristics from each decision tree, and then utilize the majority voting or averages approach to conclude. On a general note, statistical evaluation indices like correlation coefficient and error metrics (MAE, MSE, RMSE, etc.) attained by the current RF model are equivalent to those produced by other ML models like ANFIS and GEP. However, the simplicity with which RF may be used to represent categorical variables makes it a popular technique for prediction. The benefit of using a decision tree is that it can quickly model enormous datasets [82]. It can also handle both numeric and category data. According to the tree’s leaf, the base of the decision tree reflects a collection of ordered circumstances [83,84]. At the start, samples required for bootstrapping are obtained at random by replacing the existing datasets for training. RF then receives the values of various empirical characteristics, i.e., the (x) input vector. Following that, RF constructs a set of K regression trees and averages the findings. The RF equation for prediction presented in Equation (8) is arrived at after
As a result of the bagging process, trees become more diverse as they grow from multiple training data subsets selected to avoid tree correlation. The Out-of-Bag (OOB) samples were not selected for the training of the kth tree during the bagging process. Performance evaluation can be carried out by the kth tree on these OOB elements. RF can obtain a precise generalization error estimate without using an external subset of text data [85].
The model’s capacity to generalize [75,86] can be used to assess the predictive power of the proposed model. The better the generalization ability and the lower the generalization error, the better the results from the proposed model. Numerous tree predictors are randomly selected and trained for data X and prediction set Y. hence, the mean square error (generalization) of one tree predictor V(X) is .
As the number of trees continues to increase until it gets to infinity, then the generalization error, thus becomes,
where is the average value, is the value of a random variable, is the expected function, and represents the generalization error of the RF proposed model.
where represents the average generalization error of the RF. Assuming that for any , then;
where is the weighted correlation between and
5. Results and Discussion
5.1. Linear Correlation Matrix
The data used in this study were examined for linear Pearson’s correlation in order to assess the correlation between the variables. It can be observed that the flexural capacity of beams has a significant positive association with As and D equaling 0.70 and 0.85, respectively. The fundamental ACI equation for beam flexural strength shows a similar trend in the flexural capacity with rise in As and D. The width of the beam (W) and fc’ have a moderately positive relationship with M. Small linear correlations are depicted by the remaining properties EM and Tf, indicating the presence of non-linear correlations between the inputs and the target variable. The detailed coefficient matrix provided can be seen in Table 3.

Table 3.
Correlation matrix among variables used in the development of models.
5.2. Prediction Performance of the Developed Models
The results predicted by the proposed models (ANN and RFR) are cross-plotted against the experimental data, as shown in Figure 2a,c. The estimated results from the two proposed models are strongly correlated with the experimental data, with the slope of the regression lines for the training data being 0.98 and 0.94 for ANN and RFR, respectively. As shown in Figure 2a,c, the validation datasets also reveal a strong correlation in terms of the regression line slope compared with the slope of the ideal fit (1:1). The validation dataset yields a regression line slope of 0.93 and 0.80 for the ANN and RFR models. The effectiveness and efficiency of the ML models are revealed by the closeness of their data points to the regression line (1:1). In addition, error analysis plots for the training and validation datasets Figure 2b,d have been plotted to show the range of residual errors while prediction of moment (kN.m) in contrast to the actual experimental dataset. For the ANN model, the error values range from −15 to 22 kN.m for the training data and from −32 to 23 kN.m for validation data, as depicted in Figure 2b. In contrast, for the RFR model, the error values range from −51 to 41 kN.m for the training data and −20 to 54 kN.m for validation data as shown in Figure 2d. The statistical evaluation of the generated models is illustrated in Figure 2e using four main performance indices, i.e., RSE, RMSE, MAE, and correlation coefficient. This is performed to evaluate the robustness, efficacy, as well as the relative examination of the formulated ANN and RFR models in order to predict the flexural strength of FRP, reinforced concrete beams. For robust performance and strongly linked models, the distribution of sample points has to be closer to the standard line, having a slope larger than 0.8, minimum error indices (MAE and RMSE), and R greater than 0.8 [87,88,89,90,91,92]. The values of Rtraining dataset of ANN and RFR models are 0.99 and 0.97, respectively. Similarly, the Rvalidation dataset equals 0.98 each for both the models thus suggesting that both models are strongly correlated in case of both the datasets. Since the values of both the training and validation stages are almost the same, therefore, there are no problems with overfitting in the ANN and the RFR models. It is important to note that a greater R-value is not necessarily the only tool to evaluate the AI model’s reliability [90]. As a result, we have deployed several error indices such as RSE, RMSE, and MAE in the current study. The optimization procedure primarily focuses on minimizing MAE while training the model with greater correlation metrics. The values of MAE are recorded to be 5.67 MPa and 7.63 MPa during the training stage of ANN and RFR models, respectively. The validation dataset witnessed 7.37 and 8.72 MPa for ANN and RFR models. The RSE and RMSE equals (0.06 and 8.02) and (0.03 and 7.37) in the training stage; (0.10 and 10.01) and (0.05 and 9.14) in the validation phase, respectively, for ANN and RFR models.
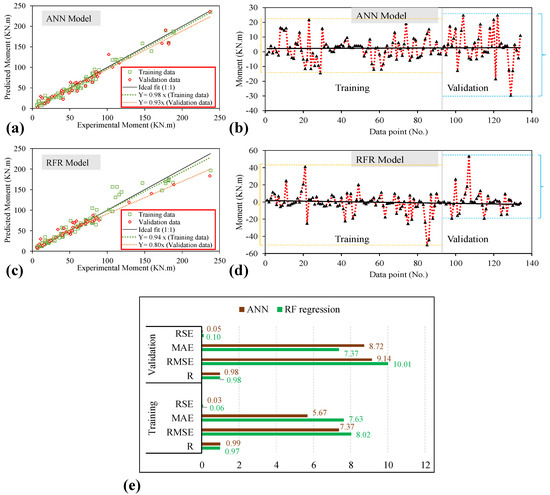
Figure 2.
(a,c) Comparison of experimental and predicted results, (b,d) Error Analysis of the proposed models, and (e) Performance indices values for training and validation datasets, in case of ANN and RFR modeling.
Figure 3 shows the tracing of experimental results by the prediction models for ANN and RFR models. It can be observed that the ANN model traces the experimental results more closely compared to the RFR model. The ANN model outperforms the RFR model owing to a higher R-value for both training and validation datasets and other statistical measures. Thus, the ANN model proves to be more robust in performance in contrast to the RFR model. As a result, in addition to having a greater correlation and lower error statistics, the proposed models may be utilized to predict the flexural strength of FRP reinforced beams, allowing designers as well as practitioners to prevent extensive testing and thus save money and effort.
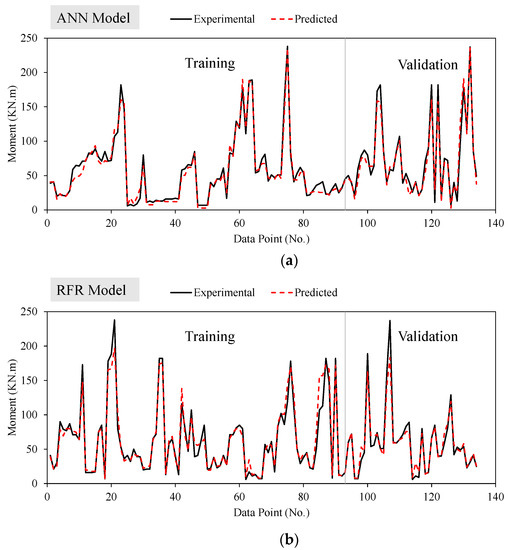
Figure 3.
Tracing of experimental results by the prediction models (a) ANN and (b) RFR.
5.3. Sensitivity and Parametric Analysis
Due to the high accuracy of the ANN model compared to the RF regression model, ANN was used to see the effect of contributing parameters in yielding flexural capacity. In order to validate the developed model, it is necessary to investigate the importance of each variable and compare its results with the existing literature. A simulated data set was therefore created, with one input variable being altered equally between its extremes while the other input variables remained fixed at their mean values (Table 4). To determine the parametric effect of a variable, the variation in the target variable was plotted versus the variable input. In the same way, the simulated dataset was used to perform the sensitivity analysis. The relative proportion of each contributing variable was calculated by normalizing the difference in the values of the target variable with regard to every input variable.

Table 4.
Simulated data set used for Parametric and Sensitivity Analysis.
Figure 4 depicts the results of the sensitivity analysis. It can be observed that the results obtained in the sensitivity analysis are corroborated with the Pearson’s correlation obtained in Table 3. The variation in bottom flexural reinforcement is the most influential parameter, followed by the depth of beam among the attributes considered in this study. The width of the beam and compressive strength of concrete is the next important attributes in yielding flexural capacity of FRP reinforced beams. The ultimate tensile strength of FRP and elastic modulus are the least important parameters, which is evident from the Pearson correlation as well. Suppose we see the formulations of ACI regarding flexural capacity based on the principles of mechanics, shown in Equation (1), As is directly related to the nominal capacity. The effective depth is another important term, followed by the compression block depth, which depends on the width of the beam. Thus, the results of the developed model are corroborated with the literature; therefore, the prediction model is considered reliable for estimating the flexural capacity of beams for unseen data.
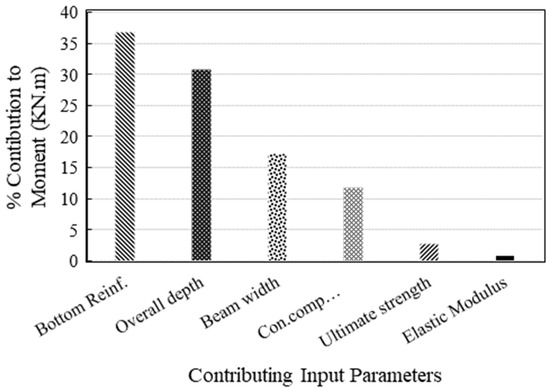
Figure 4.
Importance of the variables reflected from the ANN model.
Figure 5 illustrates the parametric analysis based on the ANN model. It can be noted that an increase in bottom reinforcement from 0 to 2000 mm2 increases the flexural capacity from 20 kN.m to 190 kN.m (170 kN.m change). The change in beam depth from 152–550 mm increased the capacity of bending from 20 to 150 kN.m (130 kN.m change). The width of the beam from 130–381 mm increased the flexural capacity by 70 kN.m. The variation in bending capacity due to elastic modulus of FRP rebar and concrete compressive strength depicted a two-degree polynomial variation. The results obtained corroborate the sensitivity and Pearson’s correlation; thus, the developed ANN model can be relied upon for future predictions. Actually, the parametric study is conducted in order to validate the trained model. The purpose was to see that the trend achieved from the trained ANN model and literature are the same. Moreover, increasing parameters like width and depth of beam, and flexural reinforcement generally increases the flexural capacity; however, optimum values depend upon many other factors like availability of clear space, aesthetics, and economy.
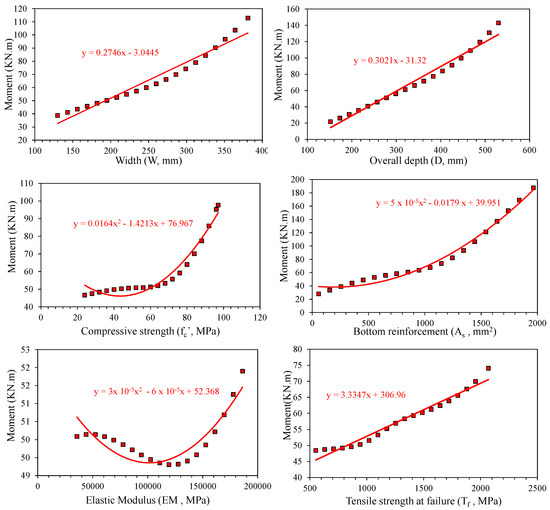
Figure 5.
Parametric Analysis of ANN model.
5.4. Comparison of ANN Model with ACI Formulations
The statistical results obtained previously by Amin et al. [46] and Murad et al. [45] revealed that the training data of the GEP and ACI model for the same dataset depicted a value of R, MAE, and RMSE equaling (0.977, 15.23, and 19.57), and (0.974, 4, 11.91), respectively. The Gradient Boosting Tree (GBT) model yielded R, MAE, and RMSE as 0.974, 10.7, and 17.2, respectively. It can be noticed that the GEP and GBT predicted reliably in terms of R only; however, R shall not be solely used for the evaluation of AI models. It can be noticed that error evaluation reflects the results from ACI formations as more robust compared to the GEP and GBT models. If we compare the results of the current ANN model, R (0.99), for the training set surpassed all other models; however, error evaluation depicts MAE and RMSE equal to 5.67 and 7.37, which shows that RMSE for ANN is smaller compared to the ACI formulations whereas, MAE for the ACI is smaller. The accuracy of the ANN model is more comparable to the ACI model rather than GEP, GBT, and RF regression models. This compassion suggests that hybrid ANN models optimized by a variety of Algorithms are capable of further minimizing this prediction error [38].
6. Conclusions
The existing ACI formulations for the flexural capacity of FRP reinforced beams, based on the principles of mechanics, are based on several assumptions that cause a difference in experimental and calculated values. Due to the availability of robust AI models, an attempt has been made in this study to estimate the flexural capacity of beams using ANN and RF regression models. Following conclusions can be drawn from this study.
- The accuracy of the existing ACI guidelines was measured using R, MAE, and RMSE with the experimental data, which yielded values equaling 0.974, 4, and 11.91, respectively. This shows that more robust models are required that can predict flexural capacity more accurately.
- The linear Pearson’s correlation obtained for the experimental data showed that bottom flexural reinforcement and depth of the beam are strong positive correlated with the bending capacity of the beam. The results from the parametric and sensitivity analysis also reflected similar interpretations of these variables. According to the ACI guidelines, bottom flexural reinforcement and depth are critical parameters in enhancing flexural capacity. Thus, the results of Pearson’s correlation, sensitivity ad parametric study, and the literature are highly matching with each other, making the developed models more reliable for future use.
- An ANN model yielded R, MAE, and RMSE of 0.99, 5.67, and 7.37, respectively whereas the RF regression model manifested 0.97, 7.63, and 8.02, respectively, for the training data. The ANN model surpassed the accuracy in comparison to the RF models as well as previously developed GEP and GBT models in the literature.
- The accuracy analysis of the ANN model is comparable to the ACI formulations, and it is expected that ANN hybrid models optimized by various algorithms may increase the performance of the ANN model. Therefore, future study is needed on the basis of hybrid ANN models to increase the prediction accuracy to a more robust level.
Author Contributions
Conceptualization, K.K., M.I., B.A.S., M.N.A. and F.E.J.; methodology, M.I. and F.E.J.; software, A.A.A., F.E.J. and M.I.; validation, A.A.A., M.I. and F.E.J.; formal analysis, A.A.A.; investigation, K.K. and B.A.S.; resources, K.K.; data curation, M.N.A. and M.I.; writing—original draft preparation, K.K., M.I., I.A., B.A.S. and F.E.J.; writing—review and editing, A.M.A.A., M.I., I.A., B.A.S. and F.E.J.; visualization, A.M.A.A., M.I. and F.E.J.; supervision, K.K.; project administration, K.K. and M.I.; funding acquisition, K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. GRANT649].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this research has been properly cited and reported in the main text.
Acknowledgments
The authors acknowledge the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. GRANT649].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, W.; Lin, X.; Bao, D.W.; Xie, Y.M. A Review of Formwork Systems for Modern Concrete Construction; Presented at Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 38, pp. 52–63. [Google Scholar]
- Ahmad, S. Reinforcement corrosion in concrete structures, its monitoring and service life prediction––A review. Cem. Concr. Compos. 2003, 25, 459–471. [Google Scholar] [CrossRef]
- Polder, R.B.; Peelen, W.H.A.; Courage, W.M.G. Non-traditional assessment and maintenance methods for aging concrete structures–technical and non-technical issues. Mater. Corros. 2012, 63, 1147–1153. [Google Scholar] [CrossRef]
- Angst, U.M. Challenges and opportunities in corrosion of steel in concrete. Mater. Struct. 2018, 51, 4. [Google Scholar] [CrossRef] [Green Version]
- Reou, J.; Ann, K. Electrochemical assessment on the corrosion risk of steel embedment in opc concrete depending on the corrosion detection techniques. Mater. Chem. Phys. 2009, 113, 78–84. [Google Scholar] [CrossRef]
- Vedalakshmi, R.; Dolli, H.; Palaniswamy, N. Embeddable corrosion rate-measuring sensor for assessing the corrosion risk of steel in concrete structures. Struct. Control. Health Monit. Off. J. Int. Assoc. Struct. Control. Monit. Eur. Assoc. Control Struct. 2009, 16, 441–459. [Google Scholar] [CrossRef]
- Morris, W.; Vico, A.; Vazquez, M.; De Sanchez, S. Corrosion of reinforcing steel evaluated by means of concrete resistivity measurements. Corros. Sci. 2002, 44, 81–99. [Google Scholar] [CrossRef]
- Lee, G.C.; Mohan, S.; Huang, C.; Fard, B.N. A Study of us Bridge Failures (1980–2012); MCEER: Buffalo, NY, USA, 2013. [Google Scholar]
- Xiao, J.; Qiang, C.; Nanni, A.; Zhang, K. Use of sea-sand and seawater in concrete construction: Current status and future opportunities. Constr. Build. Mater. 2017, 155, 1101–1111. [Google Scholar] [CrossRef]
- Iqbal, M.; Zhao, Q.; Zhang, D.; Jalal, F.E.; Jamal, A. Evaluation of tensile strength degradation of gfrp rebars in harsh alkaline conditions using non-linear genetic-based models. Mater. Struct. 2021, 54, 190. [Google Scholar] [CrossRef]
- Mousavi, T.; Shafei, E. Impact Response of Hybrid Frp-Steel Reinforced Concrete Slabs; Presented at Structures; Elsevier: Amsterdam, The Netherlands, 2019; Volume 19, pp. 436–448. [Google Scholar]
- Hassan, A.; Khairallah, F.; Mamdouh, H.; Kamal, M. Evaluation of Self-Compacting Concrete Columns Reinforced with Steel and Frp Bars with Different Strengthening Techniques; Presented at Structures; 2018. Elsevier: Amsterdam, The Netherlands, 2018; Volume 15, pp. 82–93. [Google Scholar]
- Li, Y.; Wang, Y.; Ou, J. Mechanical behavior of bfrp-steel composite plate under axial tension. Polymers 2014, 6, 1862–1876. [Google Scholar] [CrossRef]
- Iqbal, M.; Zhang, D.; Jalal, F.E. Durability evaluation of gfrp rebars in harsh alkaline environment using optimized tree-based random forest model. J. Ocean. Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Iqbal, M.; Zhang, D.; Jalal, F.E.; Javed, M.F. Computational ai Prediction Models for Residual Tensile Strength of Gfrp Bars aged in the Alkaline Concrete Environment. Ocean. Eng. 2021, 232, 109134. Available online: https://www.sciencedirect.com/science/article/pii/S0029801821005680 (accessed on 15 April 2022). [CrossRef]
- Nie, R.; Huang, Y.; Li, X.; Sun, H.; Li, D.; Ying, J. Bond of epoxy-coated reinforcement to seawater coral aggregate concrete. Ocean. Eng. 2020, 208, 107350. [Google Scholar] [CrossRef]
- Guo, F.; Al-Saadi, S.; Raman, R.S.; Zhao, X. Durability of fiber reinforced polymer (frp) in simulated seawater sea sand concrete (swssc) environment. Corros. Sci. 2018, 141, 1–13. [Google Scholar] [CrossRef]
- 440, A.C.I. Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (Frp) Bars; American Concrete Institute: Farmington Hills, MI, USA, 2015; Available online: https://basalt-fibers.com/wp-content/uploads/2021/05/Standart_ACI-4401R15.pdf (accessed on 30 April 2022).
- Wu, G.; Dong, Z.-Q.; Wang, X.; Zhu, Y.; Wu, Z.-S. Prediction of long-term performance and durability of bfrp bars under the combined effect of sustained load and corrosive solutions. J. Compos. Constr. 2015, 19, 04014058. [Google Scholar] [CrossRef]
- Micelli, F.; Nanni, A. Durability of frp rods for concrete structures. Constr. Build. Mater. 2004, 18, 491–503. [Google Scholar] [CrossRef]
- Kim, H.-Y.; Park, Y.-H.; You, Y.-J.; Moon, C.-K. Short-term durability test for gfrp rods under various environmental conditions. Compos. Struct. 2008, 83, 37–47. [Google Scholar] [CrossRef]
- Chen, Y.; Davalos, J.F.; Ray, I.; Kim, H.-Y. Accelerated aging tests for evaluations of durability performance of frp reinforcing bars for concrete structures. Compos. Struct. 2007, 78, 101–111. [Google Scholar] [CrossRef]
- Chen, Y.; Davalos, J.F.; Ray, I. Durability prediction for gfrp reinforcing bars using short-term data of accelerated aging tests. J. Compos. Constr. 2006, 10, 279–286. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A.; El-Gamal, S.; Almusallam, T.; Alsayed, S.; Aqel, M. Effect of harsh environmental conditions on the tensile properties of gfrp bars. Comps. Part B Eng. 2013, 45, 835–844. [Google Scholar] [CrossRef]
- Wu, G.; Wang, X.; Wu, Z.; Dong, Z.; Zhang, G. Durability of basalt fibers and composites in corrosive environments. J. Compos. Mater. 2015, 49, 873–887. [Google Scholar] [CrossRef]
- Guo, R.; Xian, G.; Li, F.; Li, C.; Hong, B. Hygrothermal resistance of pultruded carbon, glass and carbon/glass hybrid fiber reinforced epoxy composites. Constr. Build. Mater. 2022, 315, 125710. [Google Scholar] [CrossRef]
- Attia, K.; Alnahhal, W.; Elrefai, A.; Rihan, Y. Flexural behavior of basalt fiber-reinforced concrete slab strips reinforced with bfrp and gfrp bars. Compos. Struct. 2019, 211, 1–12. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C.; Wang, Y. Mechanical performance evolution and life prediction of prestressed cfrp plate exposed to hygrothermal and freeze-thaw environments. Compos. Struct. 2022, 293, 115719. [Google Scholar] [CrossRef]
- Durgadevi, S.; Karthikeyan, S.; Lavanya, N.; Kavitha, C. A review on retrofitting of reinforced concrete elements using FRP. Mater. Today: Proc. 2020, 45, 1050–1054. [Google Scholar] [CrossRef]
- Almahmood, H.; Ashour, A.; Sheehan, T. Flexural behaviour of hybrid steel-GFRP reinforced concrete continuous T-beams. Compos. Struct. 2020, 254, 112802. [Google Scholar] [CrossRef]
- Vickers, N.J. Animal communication: When i’m calling you, will you answer too? Curr. Biol. 2017, 27, R713–R715. [Google Scholar] [CrossRef]
- Al-Rousan, R.Z.; Alhassan, M.; Al-Wadi, R. Nonlinear Finite Element Analysis of Full-Scale Concrete Bridge Deck Slabs Reinforced with Frp Bars; Presented at Structures; Elsevier: Amsterdam, The Netherlands, 2020; Volume 27, pp. 1820–1831. [Google Scholar]
- Imam, A.; Salami, B.A.; Oyehan, T.A. Predicting the compressive strength of a quaternary blend concrete using bayesian regularized neural network. J. Struct. Integr. Maint. 2021, 6, 237–246. [Google Scholar] [CrossRef]
- Salami, B.A.; Olayiwola, T.; Oyehan, T.A.; Raji, I.A. Data-Driven Model for Ternary-Blend Concrete Compressive Strength Prediction Using Machine Learning Approach. Constr. Build. Mater. 2021, 301, 124152. Available online: https://www.sciencedirect.com/science/article/pii/S0950061821019127 (accessed on 20 April 2022). [CrossRef]
- Algaifi, H.A.; Bakar, S.A.; Alyousef, R.; Sam, A.R.M.; Alqarni, A.S.; Ibrahim, M.; Shahidan, S.; Ibrahim, M.; Salami, B.A. Machine learning and rsm models for prediction of compressive strength of smart bio-concrete. Smart Struct. Syst. 2021, 28, 535–551. [Google Scholar]
- Biswas, R.; Rai, B. Effect of cementing efficiency factor on the mechanical properties of concrete incorporating silica fume. J. Struct. Integr. Maint. 2020, 5, 190–203. [Google Scholar] [CrossRef]
- Biswas, R.; Bardhan, A.; Samui, P.; Rai, B.; Nayak, S.; Armaghani, D.J. Efficient soft computing techniques for the prediction of compressive strength of geopolymer concrete. Comput. Concr. 2021, 28, 221–232. [Google Scholar]
- Bardhan, A.; Biswas, R.; Kardani, N.; Iqbal, M.; Samui, P.; Singh, M.; Asteris, P.G. A novel integrated approach of augmented grey wolf optimizer and ann for estimating axial load carrying-capacity of concrete-filled steel tube columns. Constr. Build. Mater. 2022, 337, 127454. Available online: https://www.sciencedirect.com/science/article/pii/S095006182201131X (accessed on 25 April 2022). [CrossRef]
- Khan, K.; Salami, B.A.; Iqbal, M.; Amin, M.N.; Ahmed, F.; Jalal, F.E. Compressive Strength Estimation of Fly Ash/Slag Based Green Concrete by Deploying Artificial Intelligence Models. Materials. 2022, 15, 3722. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Rai, B.; Biswas, R.; Samui, P.; Kim, D. Prediction of rapid chloride permeability of self-compacting concrete using multivariate adaptive regression spline and minimax probability machine regression. J. Build. Eng. 2020, 32, 101490. [Google Scholar] [CrossRef]
- Khan, S.; Horoub, M.M.; Shafiq, S.; Ali, S.; Bhatti, U.N. Optimization of vehicle suspension system using genetic algorithm. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Belgium, Brussels, 22–25 July 2019; pp. 203–207. [Google Scholar]
- Ali, S.; Kamran, M.A.; Khan, S. Effect of baffle size and orientation on lateral sloshing of partially filled containers: A numerical study. Eur. J. Comput. Mech. 2017, 26, 584–608. [Google Scholar] [CrossRef]
- Jamal, A.; Al-Ahmadi, H.M.; Butt, F.M.; Iqbal, M.; Almoshaogeh, M.; Ali, S. Metaheuristics for Traffic Control and Optimization: Current Challenges and Prospects; IntechOpen: London, UK, 2021. [Google Scholar]
- Bhatti, U.N.; Khan, S.; Ali, S.; Horoub, M.M. A numerical modeling study of the effects of various joint boundary conditions on stiffness behavior of 6dof platform’s top plate. In Proceedings of the 2018 9th International Conference on Mechanical and Aerospace Engineering (ICMAE), Hungary, Budapest, 10–13 July 2018; pp. 243–248. [Google Scholar]
- Murad, Y.; Tarawneh, A.; Arar, F.; Al-Zu’Bi, A.; Al-Ghwairi, A.; Al-Jaafreh, A.; Tarawneh, M. Flexural Strength Prediction for Concrete Beams Reinforced with Frp Bars Using Gene Expression Programming; Presented at Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 33, pp. 3163–3172. [Google Scholar]
- Amin, M.N.; Iqbal, M.; Khan, K.; Qadir, M.G.; Shalabi, F.I.; Jamal, A. Ensemble tree-based approach towards flexural strength prediction of frp reinforced concrete beams. Polymers 2022, 14, 1303. [Google Scholar] [CrossRef]
- Naderpour, H.; Poursaeidi, O.; Ahmadi, M. Shear resistance prediction of concrete beams reinforced by frp bars using artificial neural networks. Measurement 2018, 126, 299–308. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C. Prediction of shear strength of frp-reinforced concrete flexural members without stirrups using artificial neural networks. Eng. Struct. 2014, 61, 99–112. [Google Scholar] [CrossRef]
- Farooq, F.; Nasir Amin, M.; Khan, K.; Rehan Sadiq, M.; Faisal Javed, M.; Aslam, F.; Alyousef, R. A comparative study of random forest and genetic engineering programming for the prediction of compressive strength of high strength concrete (hsc). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Khan, M.A.; Memon, S.A.; Farooq, F.; Javed, M.F.; Aslam, F.; Alyousef, R. Compressive strength of fly-ash-based geopolymer concrete by gene expression programming and random forest. Adv. Civ. Eng. 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Silva, L.C.; Mendes, N.; Lourenço, P.B.; Ingham, J. Seismic Structural Assessment of the Christchurch Catholic Basilica, New Zealand; Presented at Structures; Elsevier: Amsterdam, The Netherlands, 2018; Volume 15, pp. 115–130. [Google Scholar]
- Soudki, K.; Alkhrdaji, T. Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures (ACI 440.2 R-02). In Structures Congress 2005: Metropolis and Beyond; American Society of Civil Engineers: Reston, VA, USA, 2005; pp. 1–8. [Google Scholar]
- R2017, C.S.A. Design and Construction of Building Structures with Fibre-Reinforced Polymers; Canadian Standards Association: Toronto, ON, Canada, 2017; Available online: https://www.csagroup.org/store/product/S806-12/ (accessed on 2 May 2022).
- Junaid, M.T.; Elbana, A.; Altoubat, S.; Al-Sadoon, Z. Experimental study on the effect of matrix on the flexural behavior of beams reinforced with Glass Fiber Reinforced Polymer (GFRP) bars. Compos. Struct. 2019, 222, 110930. [Google Scholar] [CrossRef]
- Faza, S.S. Bending and Bond Behavior and Design of Concrete Beams Reinforced with Fiber-Reinforced Plastic Rebars; West Virginia University: Morgantown, WV, USA, 1991. [Google Scholar]
- Brown, V.L.; Bartholomew, C.L. Frp reinforcing bars in reinforced concrete members. Mater. J. 1993, 90, 34–39. [Google Scholar]
- El-Nemr, B.A.; Ahmed, E.A.; Benmokrane, B. Flexural behavior and serviceability of normal-and high-strength concrete beams reinforced with glass fiber-reinforced polymer bars. ACI Struct. J. 2013, 110, 1077–1087. [Google Scholar]
- Benmokrane, B.; Masmoudi, R. Flexural response of concrete beams reinforced with frp reinforcing bars. Struct. J. 1996, 93, s46–s55. [Google Scholar]
- Almusallam, T.; Al-Salloum, Y.; Alsayed, S.; Amjad, M. Behavior of concrete beams doubly reinforced by frp bars. In Proceedings of the third international symposium on non-metallic (FRP) reinforcement for concrete structures (FRPRCS-3), Sapporo, Japan, 14–16 October 1997; Volume 2, pp. 471–478. [Google Scholar]
- Duranovic, N.; Pilakoutas, K.; Waldron, P. Tests on concrete beams reinforced with glass fibre reinforced plastic bars. Non-Met. (FRP) Reinf. Concr. Struct. 1997, 2, 479–486. [Google Scholar]
- Kassem, C.; Farghaly, A.S.; Benmokrane, B. Evaluation of flexural behavior and serviceability performance of concrete beams reinforced with frp bars. J. Compos. Constr. 2011, 15, 682–695. [Google Scholar] [CrossRef]
- Thériault, M.; Benmokrane, B. Effects of frp reinforcement ratio and concrete strength on flexural behavior of concrete beams. J. Compos. Constr. 1998, 2, 7–16. [Google Scholar] [CrossRef]
- Ashour, A. Flexural and shear capacities of concrete beams reinforced with gfrp bars. Constr. Build. Mater. 2006, 20, 1005–1015. [Google Scholar] [CrossRef]
- Yost, J.R.; Goodspeed, C.H.; Schmeckpeper, E.R. Flexural performance of concrete beams reinforced with frp grids. J. Compos. Constr. 2001, 5, 18–25. [Google Scholar] [CrossRef]
- Masmoudi, R.; Theriault, M.; Benmokrane, B. Flexural behavior of concrete beams reinforced with deformed fiber reinforced plastic reinforcing rods. Struct. J. 1998, 95, 665–676. [Google Scholar]
- Toutanji, H.A.; Saafi, M. Flexural behavior of concrete beams reinforced with glass fiber-reinforced polymer (gfrp) bars. Struct. J. 2000, 97, 712–719. [Google Scholar]
- Alsayed, S.; Al-Salloum, Y.; Almusallam, T. Performance of glass fiber reinforced plastic bars as a reinforcing material for concrete structures. Compos. Part B Eng. 2000, 31, 555–567. [Google Scholar] [CrossRef]
- Gao, D.; Benmokrane, B. Calculation Method of Flexural Capacity of Gfrp-Reinforced Concrete Beam. J. Hydraul. Eng. 2001, 73–80. [Google Scholar]
- Wang, H.; Belarbi, A. Flexural behavior of fiber-reinforced-concrete beams reinforced with frp rebars. ACI Struct. J. SP230 2005, 51, 895–914. [Google Scholar]
- Bischoff, P.H. Reevaluation of deflection prediction for concrete beams reinforced with steel and fiber reinforced polymer bars. J. Struct. Eng. 2005, 131, 752–767. [Google Scholar] [CrossRef]
- Lau, D.; Pam, H.J. Experimental study of hybrid frp reinforced concrete beams. Eng. Struct. 2010, 32, 3857–3865. [Google Scholar] [CrossRef]
- El Refai, A.; Abed, F.; Al-Rahmani, A. Structural performance and serviceability of concrete beams reinforced with hybrid (gfrp and steel) bars. Constr. Build. Mater. 2015, 96, 518–529. [Google Scholar] [CrossRef]
- Montavon, G. Introduction to neural networks. In Machine Learning Meets Quantum Physics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 37–62. [Google Scholar]
- Lippmann, R. An introduction to computing with neural nets. IEEE Assp Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]
- Mai, H.-V.T.; Nguyen, T.-A.; Ly, H.-B.; Tran, V.Q. Investigation of ann model containing one hidden layer for predicting compressive strength of concrete with blast-furnace slag and fly ash. Adv. Mater. Sci. Eng. 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Zweiri, Y.; Whidborne, J.; Seneviratne, L. A three-term backpropagation algorithm. Neurocomputing 2003, 50, 305–318. [Google Scholar] [CrossRef]
- Sandhu, P.S.; Chhabra, S. A comparative analysis of conjugate gradient algorithms & pso based neural network approaches for reusability evaluation of procedure based software systems. Chiang Mai J. Sci. 2011, 38, 123–135. [Google Scholar]
- Zounemat-Kermani, M.; Stephan, D.; Barjenbruch, M.; Hinkelmann, R. Ensemble data mining modeling in corrosion of concrete sewer: A comparative study of network-based (MLPNN & RBFNN) and tree-based (RF, CHAID, & CART) models. Adv. Eng. Inform. 2020, 43, 101030. [Google Scholar]
- Beale, E.; A deviation of conjugate gradients. In Numerical Methods for Nonlinear Optimization; 1972; pp. 39–43. Available online: https://ci.nii.ac.jp/naid/10008947012/ (accessed on 3 May 2022).
- Sheela, K.; Deepa, S. Selection of Number of Hidden Neurons in Neural Networks in Renewable Energy Systems. 2014. Available online: http://nopr.niscair.res.in/handle/123456789/29456 (accessed on 3 May 2022).
- Šipoš, T.K.; Miličević, I.; Siddique, R. Model for mix design of brick aggregate concrete based on neural network modelling. Constr. Build. Mater. 2017, 148, 757–769. [Google Scholar] [CrossRef]
- Deng, B. Machine learning on density and elastic property of oxide glasses driven by large dataset. J. Non-Cryst. Solids 2020, 529, 119768. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression t Rees (Monterey, California: Wadsworth); Taylor & Francis Group: Newyork, USA, 1984. [Google Scholar]
- Rodriguez-Galiano, V.; Mendes, M.P.; Garcia-Soldado, M.J.; Olmo, M.C.; Ribeiro, L. Predictive modeling of groundwater nitrate pollution using random forest and multisource variables related to intrinsic and specific vulnerability: A case study in an agricultural setting (southern spain). Sci. Total Environ. 2014, 476, 189–206. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Lin, J.; Lei, X.; Wei, T. Compressive strength prediction of basalt fiber reinforced concrete via random forest algorithm. Mater. Today Commun. 2022, 30, 103117. [Google Scholar] [CrossRef]
- Khan, M.A.; Zafar, A.; Akbar, A.; Javed, M.; Mosavi, A. Application of gene expression programming (gep) for the prediction of compressive strength of geopolymer concrete. Materials 2021, 14, 1106. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Iqbal, M.F.; Javed, M.F.; Nazar, S.; Wang, F.; Liu, Q.-F. Semi-Analytical Model for Compressive Arch Action Capacity of rc Frame Structures; Presented at Structures; Elsevier: Amsterdam, The Netherlands, 2020; Volume 27, pp. 1231–1245. [Google Scholar]
- Onyelowe, K.C.; Iqbal, M.; Jalal, F.E.; Onyia, M.E.; Onuoha, I.C. Application of 3-algorithm ann programming to predict the strength performance of hydrated-lime activated rice husk ash treated soil. Multiscale Multidiscip. Modeling Exp. Des. 2021, 4, 259–274. [Google Scholar] [CrossRef]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Jamhiri, B.; Javed, M.F. Predicting the Compaction Characteristics of Expansive Soils Using Two Genetic Programming-Based Algorithms. Transp. Geotech. 2021, 30, 100608. Available online: https://www.sciencedirect.com/science/article/pii/S2214391221000982 (accessed on 3 May 2022). [CrossRef]
- Kaloop, M.R.; Samui, P.; Iqbal, M.; Hu, J.W. Soft computing approaches towards tensile strength estimation of GFRP rebars subjected to alkaline-concrete environment. Case Stud. Constr. Mater. 2022, 16, p.e00955. [Google Scholar] [CrossRef]
- qbal, M.; Onyelowe, K.C.; Jalal, F.E. Smart computing models of california bearing ratio, unconfined compressive strength, and resistance value of activated ash-modified soft clay soil with adaptive neuro-fuzzy inference system and ensemble random forest regression techniques. Multiscale Multidiscip. Modeling Exp. Des. 2021, 4, 207–225. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).