A Review on Modeling Cure Kinetics and Mechanisms of Photopolymerization
Abstract
1. Introduction
2. Materials and Curing Chemistry
2.1. Radical Polymerizations
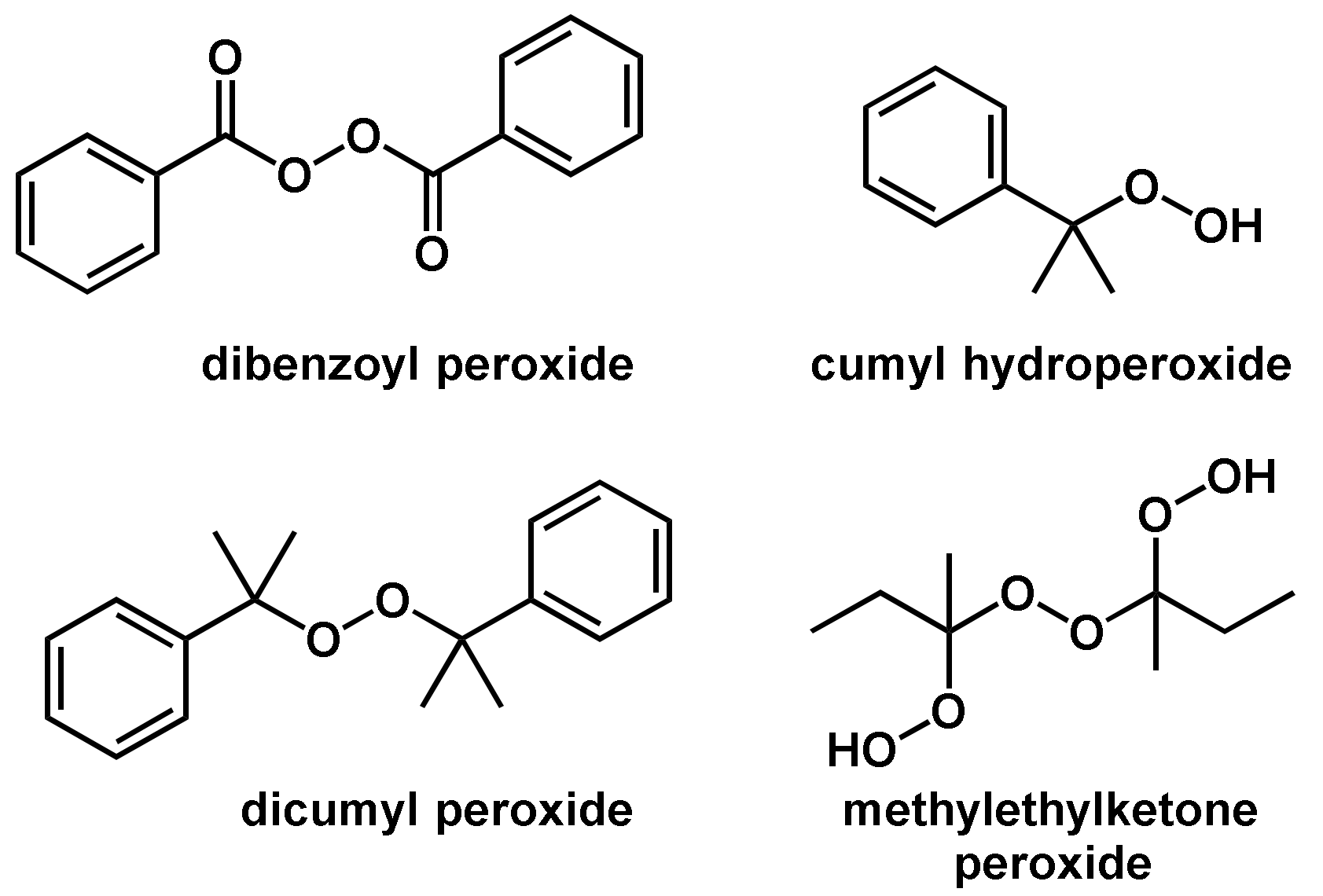
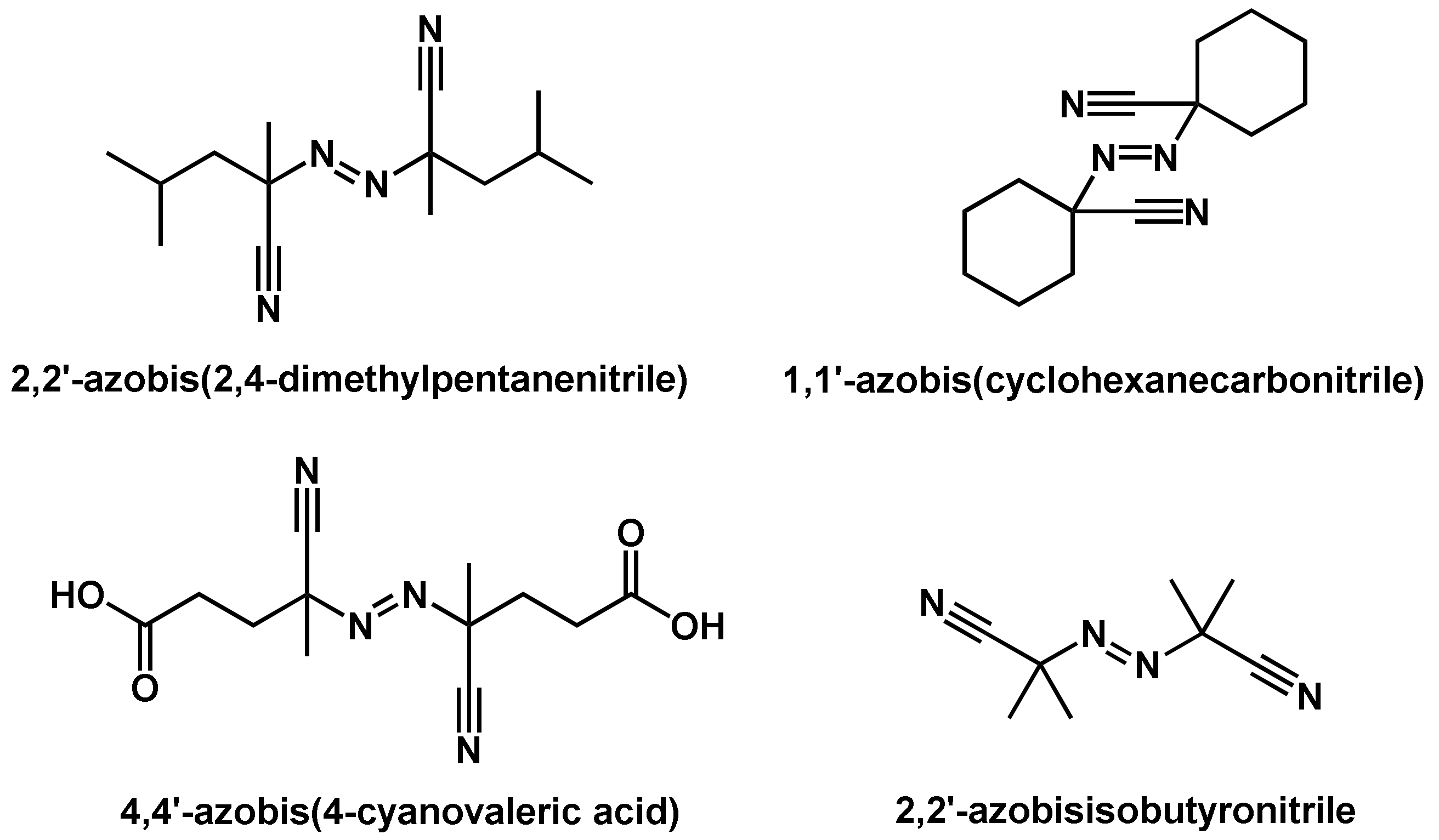
2.1.1. Thermally-Initiated Radical Polymerizations
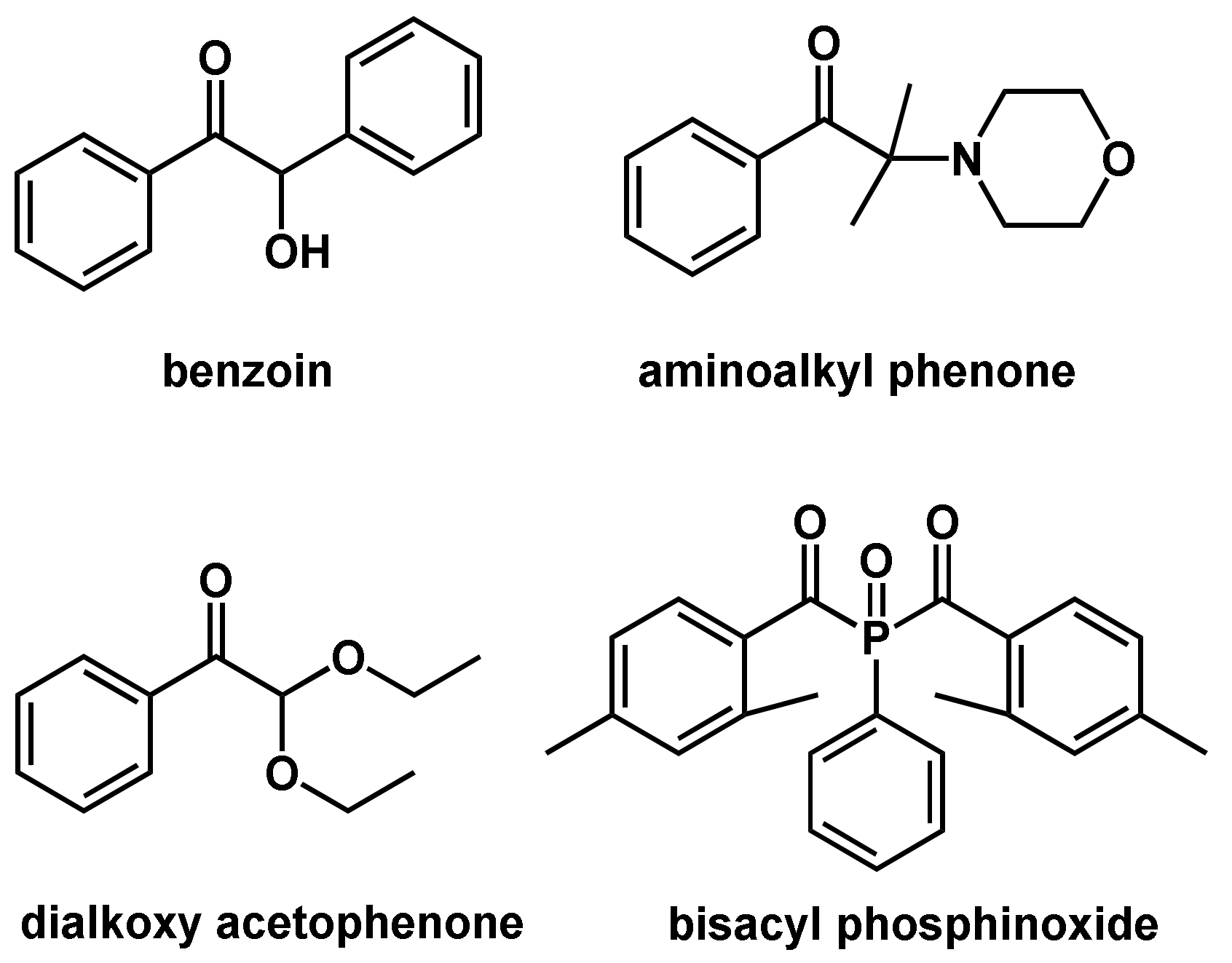
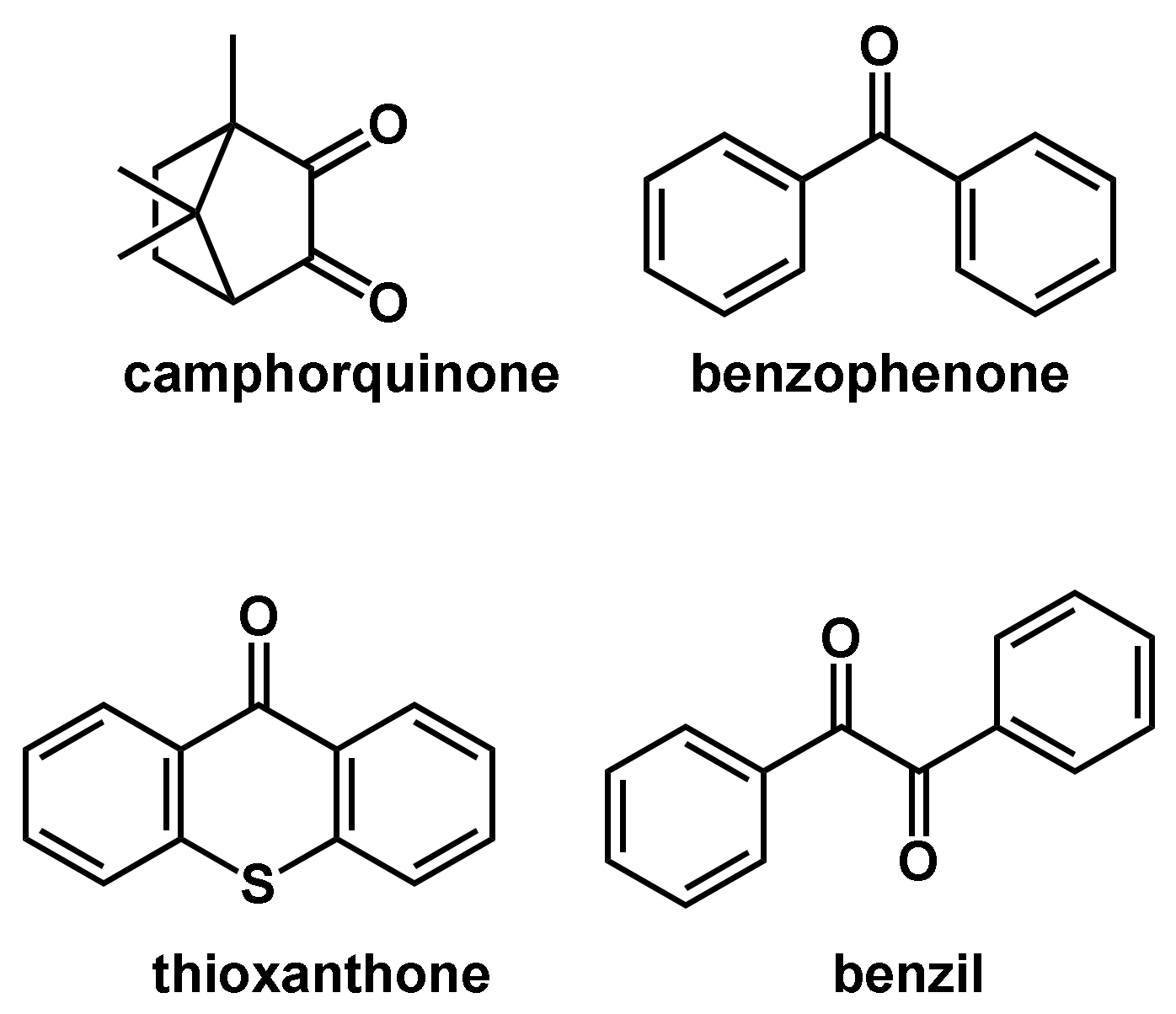
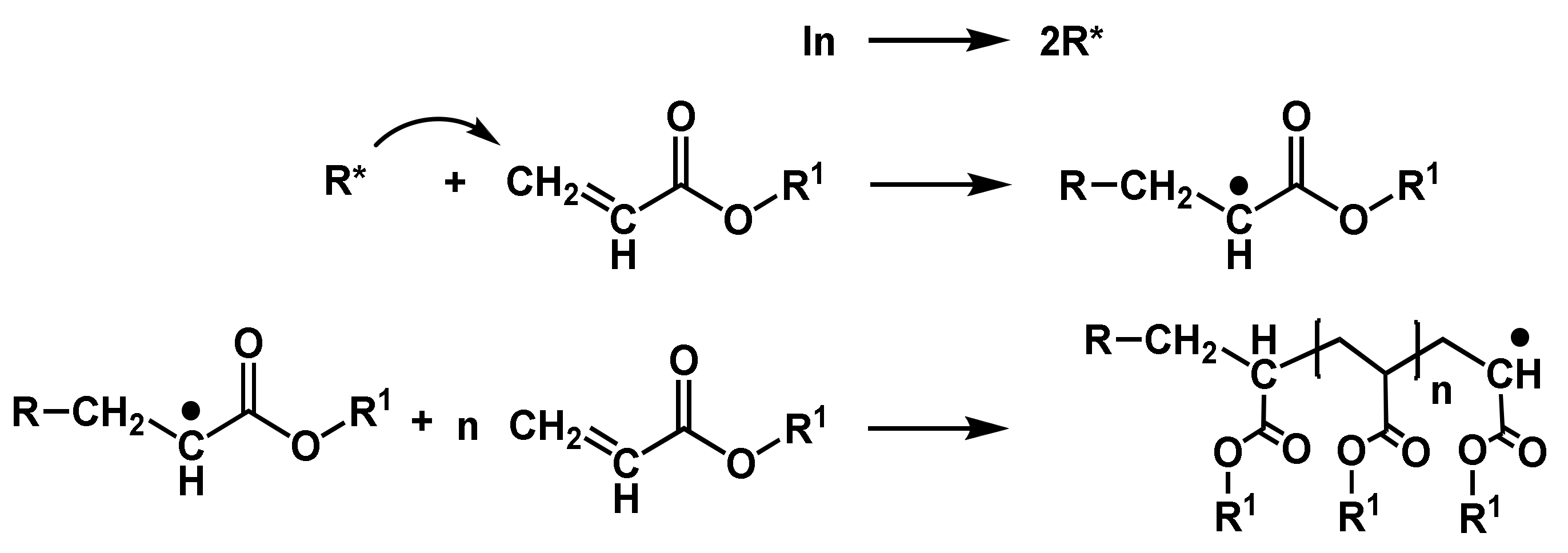
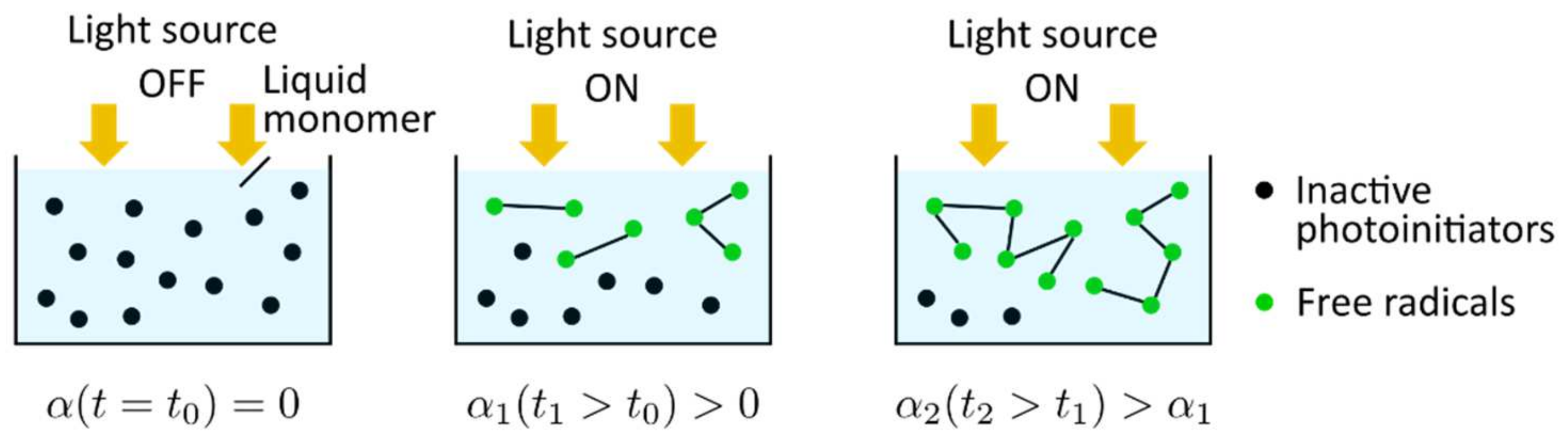
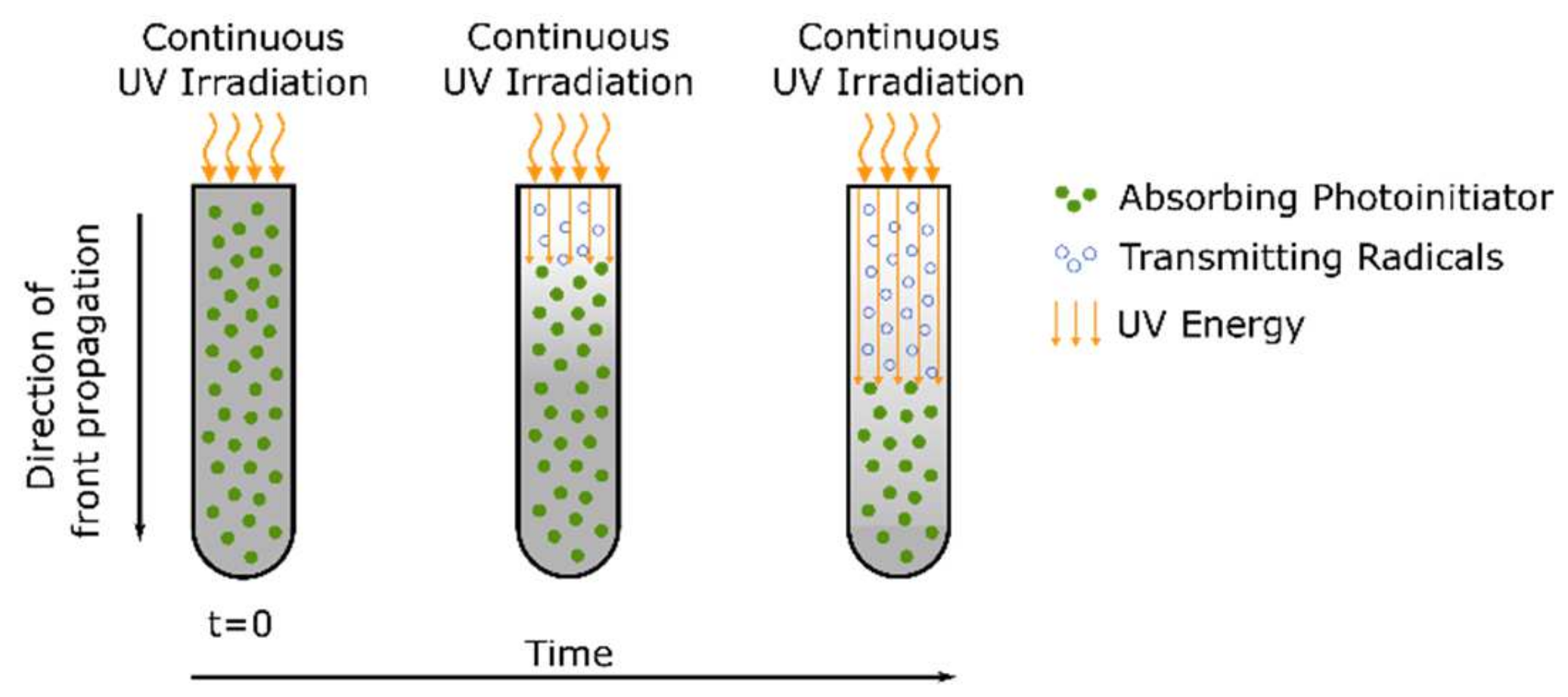
2.1.2. Photoinitiated Radical Polymerizations
2.2. Cationic Polymerizations
2.2.1. Cationic Polymerizations Initiated by Carbonium Ions, BrØnsted Acids, or Lewis Acids
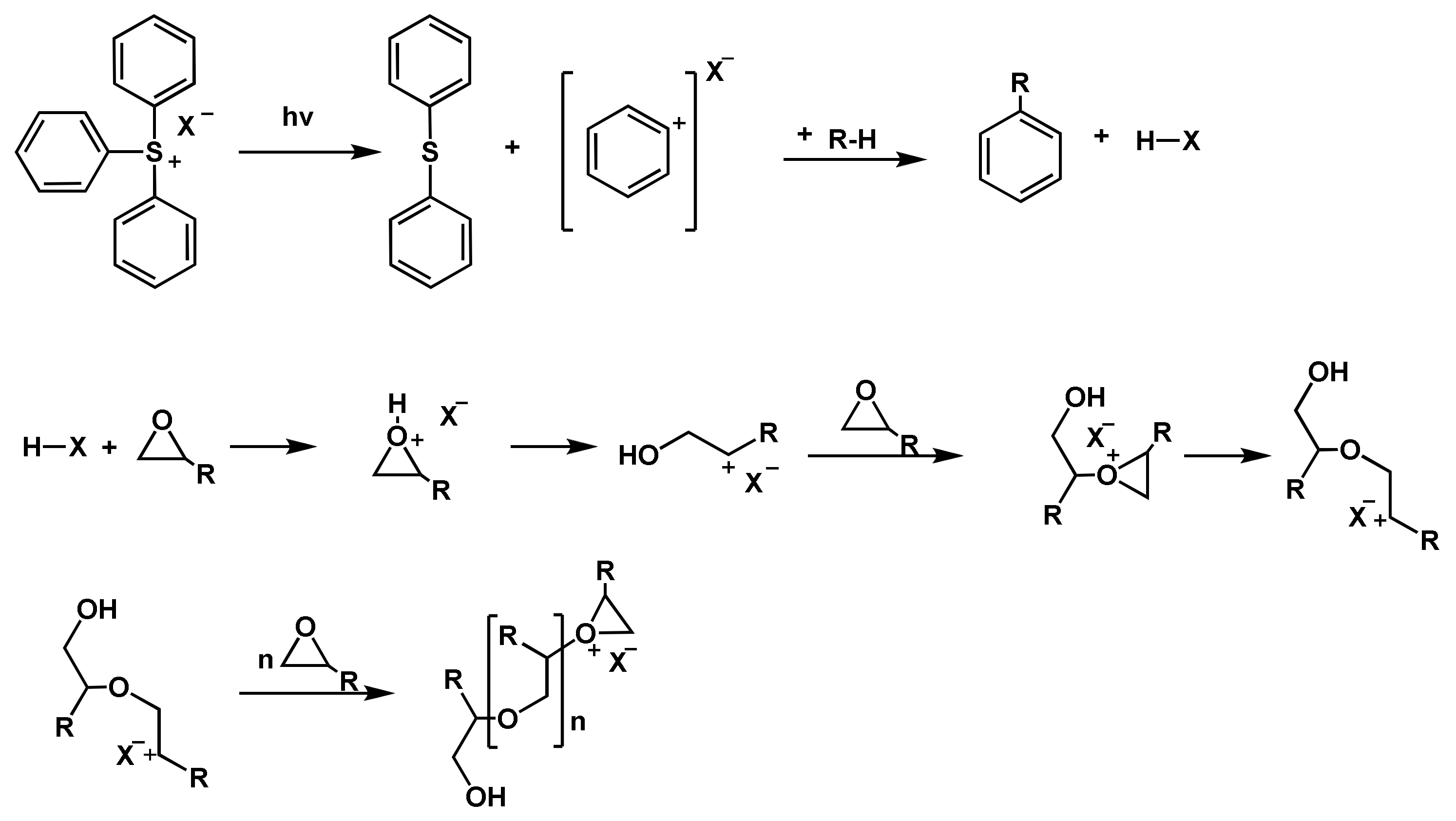
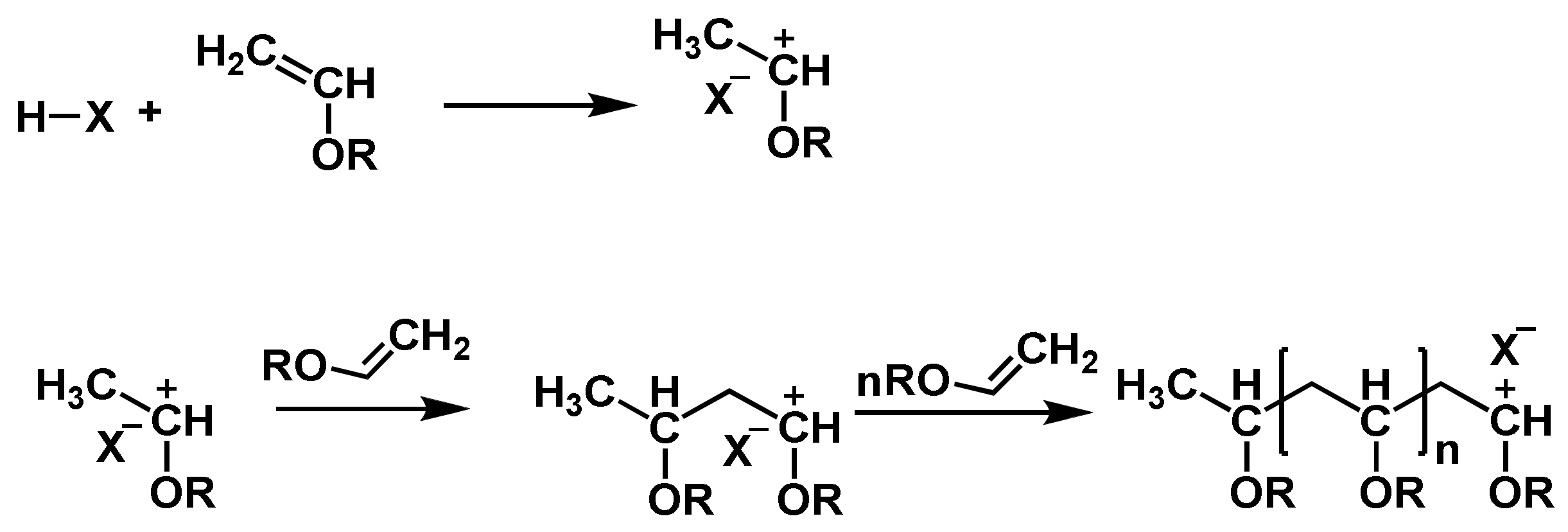
2.2.2. Photoinitiated Cationic Polymerizations
2.3. Radical and Cationic Polymerizations Highlighted in This Review
2.3.1. Radical Polymerization of Acrylates
2.3.2. Cationic Polymerization of Epoxides and Vinyl Ethers
3. Models of Cure Kinetics
3.1. Free-Radical Photopolymerization
3.1.1. Mechanistic Models for Free-Radical Photopolymerizations
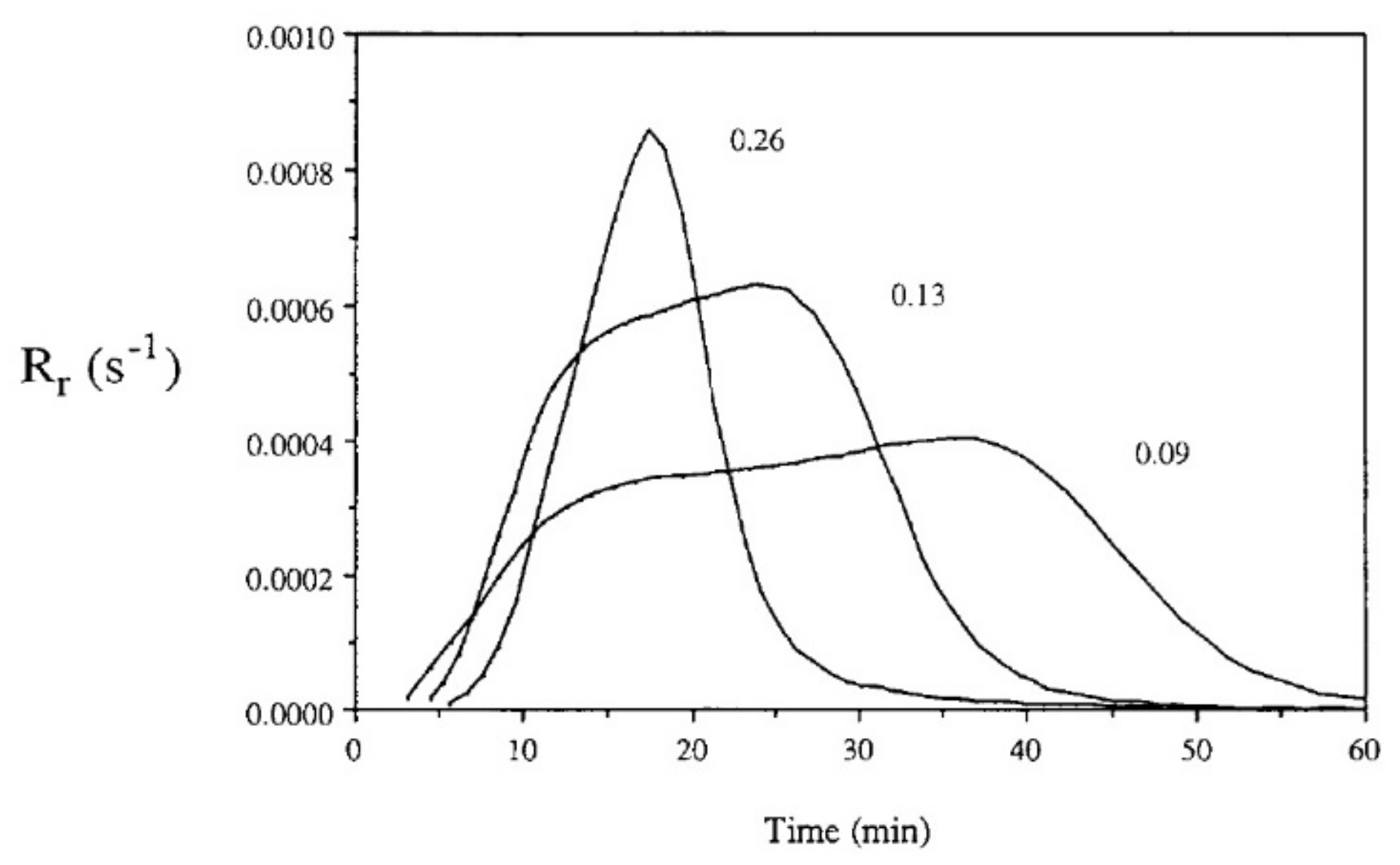
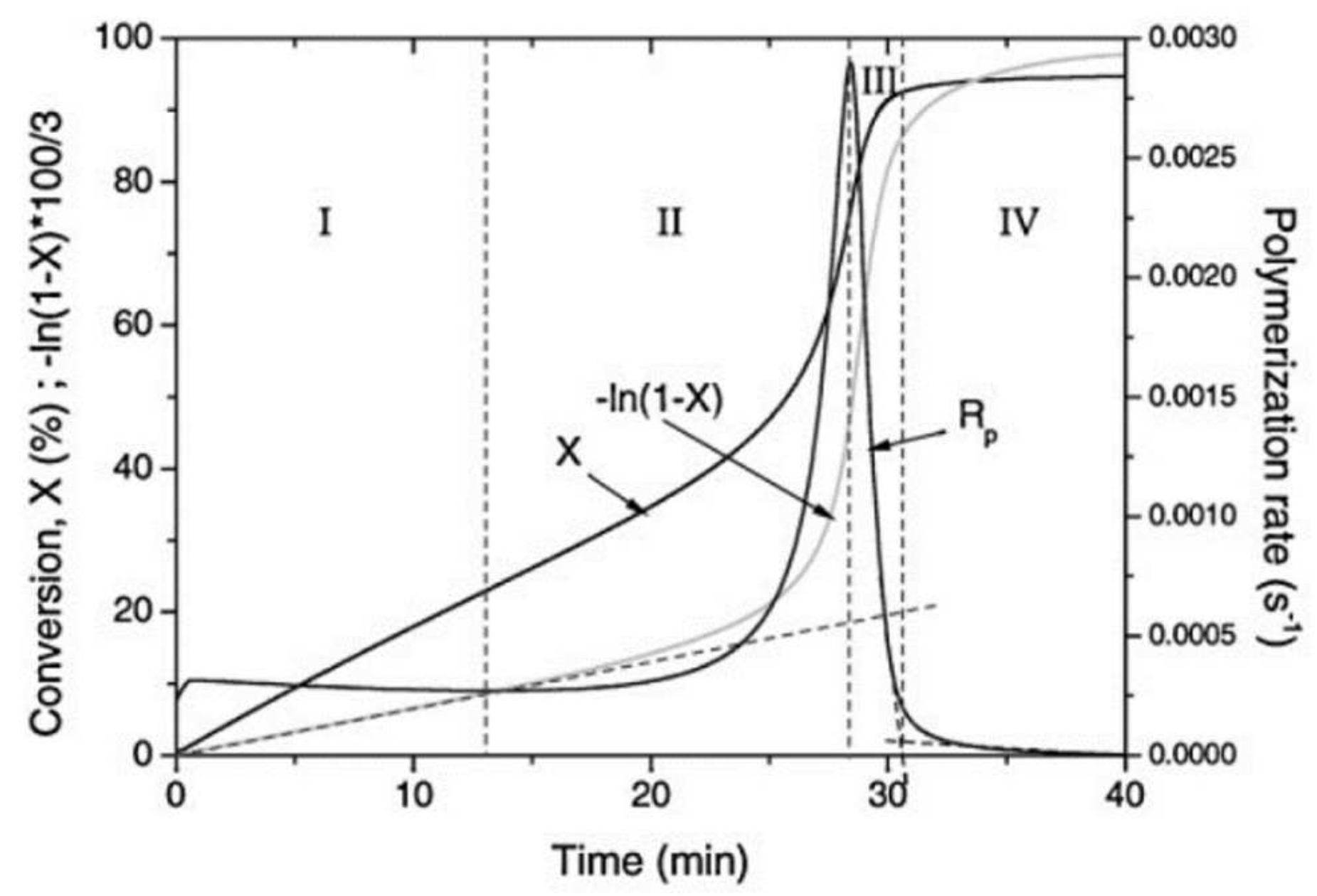
3.1.2. Phenomenological Models for Free-Radical Photopolymerizations
3.2. Cationic Photopolymerizations
3.2.1. Mechanistic Models for Cationic Photopolymerizations
3.2.2. Phenomenological Models for Cationic Photopolymerization
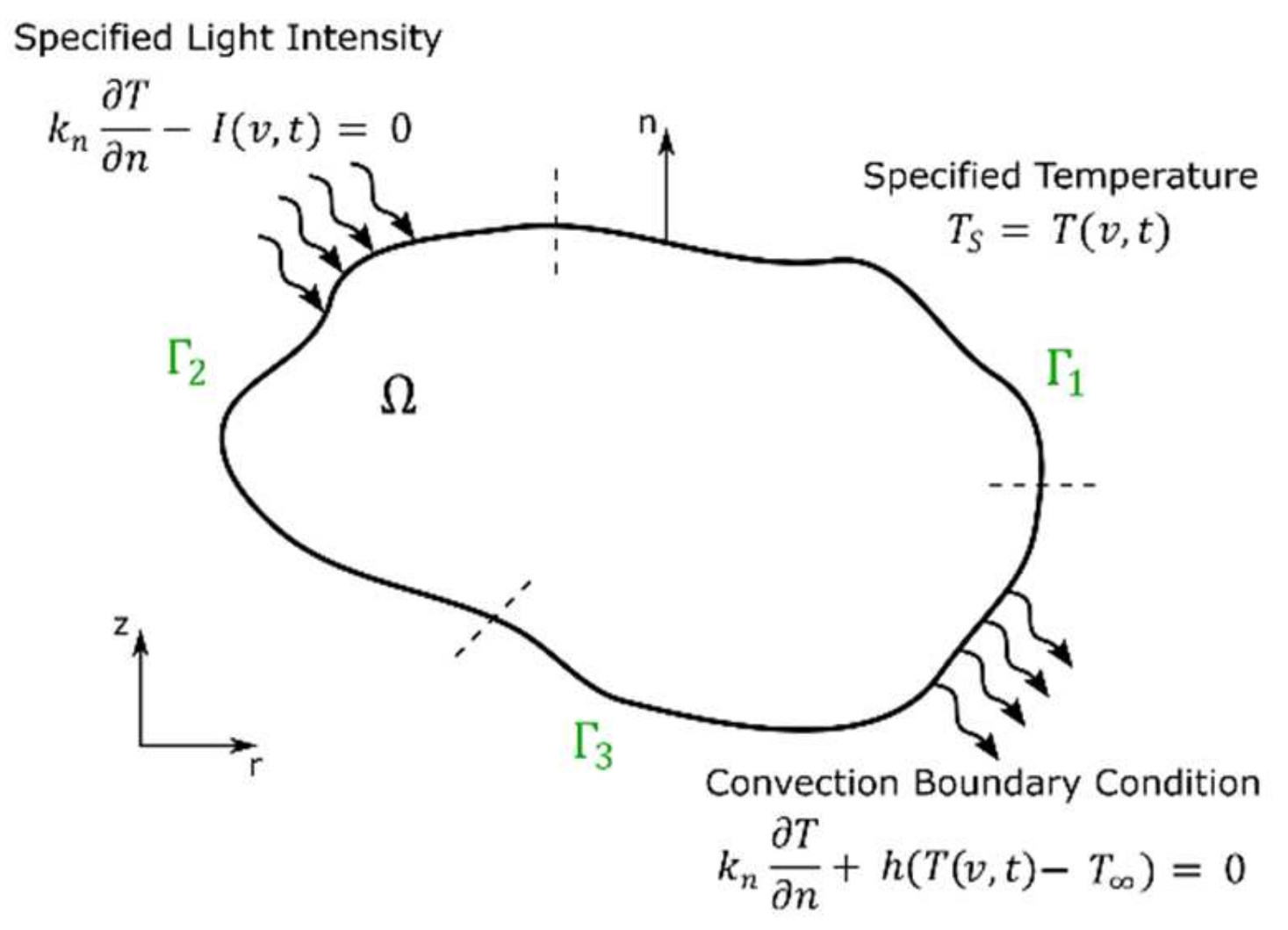
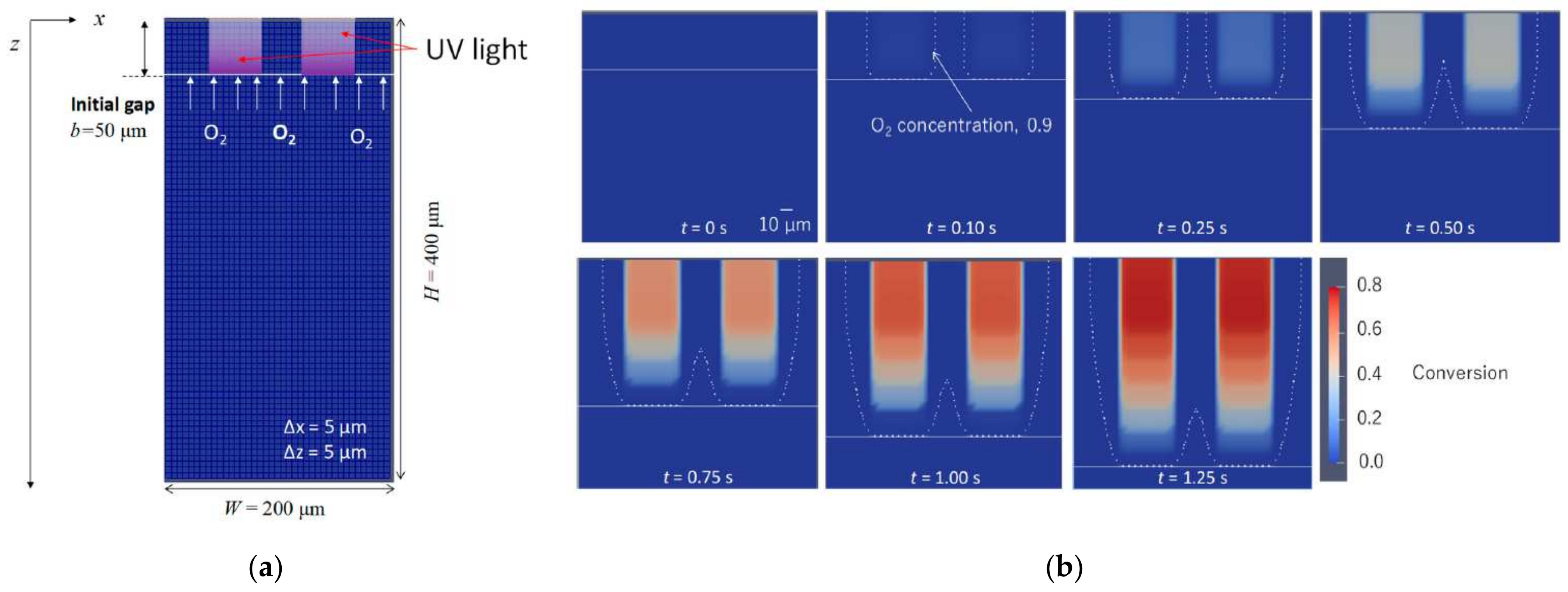
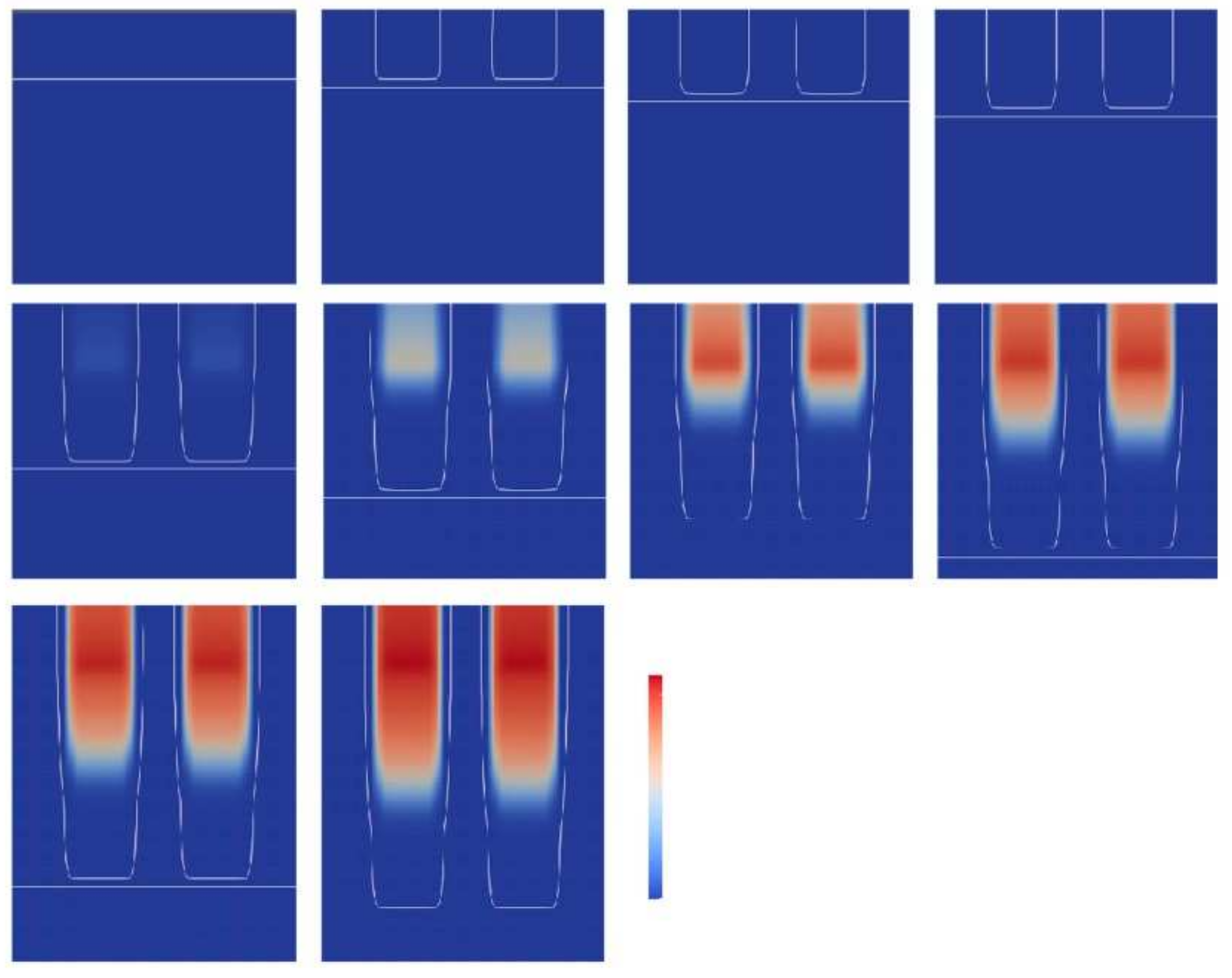
4. Implementation of Photopolymerization in Numerical Simulations
5. Photopolymerization Composites
5.1. Fiber-Reinforced Polymers
5.2. Nanodielectrics
5.3. Electromagnetic Shielding Materials
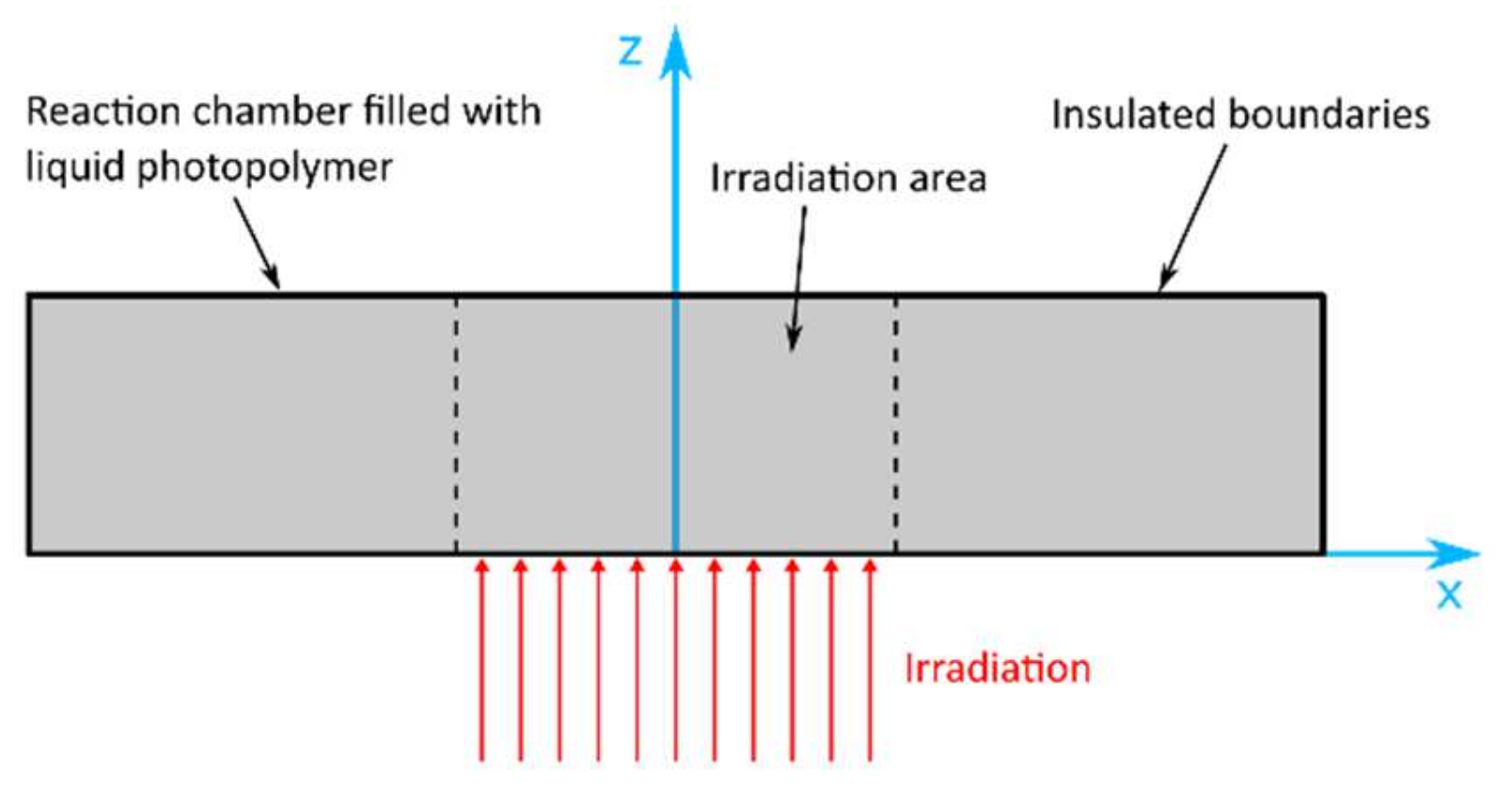
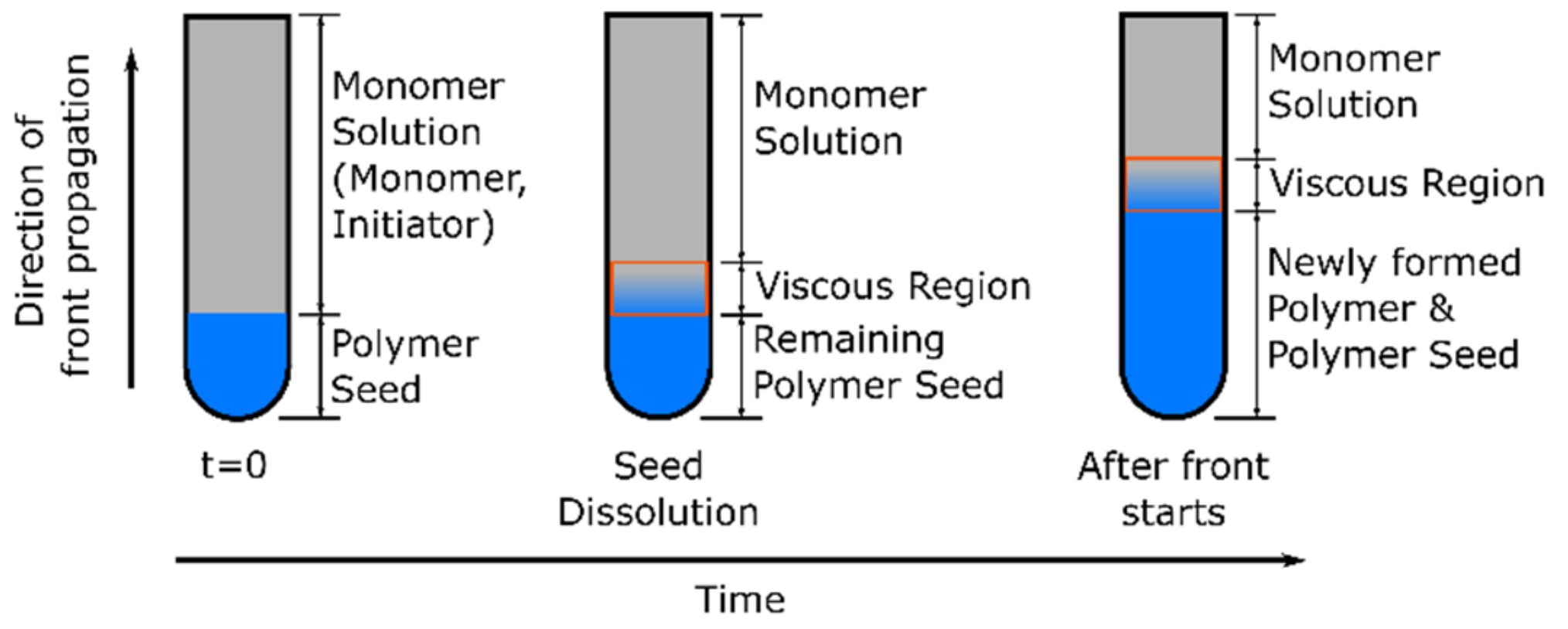
6. Frontal Polymerization
7. Discussion
8. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIBN | Azobisisbutyronitrile |
| CADE | Cycloaliphatic Diepoxide |
| CLDT | Chain Length Dependent Termination |
| CLIP | Continuous Liquid Interface Production |
| DCPD | Dicyclopentadiene |
| DEGDMA | Diethylene Glycol Dimethacrylate |
| DGEBA | Diglycidyl Ether of Bisphenol A |
| DGEBF | Diglycidyl Ether of Bisphenol F |
| DLP | Digital Light Processing |
| DMPA | Dimethoxy Phenylacetophenone |
| DSC | Differential Scanning Calorimetry |
| ECH | Epichlorohydrin |
| ECPL | Exposure Controlled Projection Lithography |
| EVE | Ethyl Vinyl Ether |
| FE | Finite Elements |
| FEA | Finite Element Analysis |
| FP | Frontal Polymerization |
| FPP | Frontal Photo Polymerization |
| FROMP | Frontal Ring-Opening Metathesis Polymerization |
| FTIR | Fourier-Transformed Infrared |
| IBVE | Iso-Butyl Vinyl Ether |
| IFP | Isothermal Frontal Polymerization |
| HBVE | Hydroxylbutyl Vinyl Ether |
| MMA | Methyl Methacrylate |
| PAG | Photoacid Generator |
| PEGDA | Poly(ethylene glycol) Diacrylate |
| PRT | Primary Radical Termination |
| RICFP | Radical-Induced Frontal Polymerization |
| RT-FTIR | Real-Time Fourier-Transformed Infrared |
| TFP | Thermal Frontal Polymerization |
| TPO | Trimethylbenzoyl diphenylphosphine oxide |
| UV | Ultraviolet |
| SLA | Stereolithography Applications |
| WLF | Williams-Lendel-Ferry |
References
- Decker, C. The use of UV irradiation in polymerization. Polym. Int. 1998, 45, 133–141. [Google Scholar] [CrossRef]
- Peiffer, R.W. Applications of Photopolymer Technology; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1997; pp. 1–14. ISBN 0097-6156. [Google Scholar]
- Bednarczyk, P.; Nowak, M.; Mozelewska, K.; Czech, Z. Photocurable Coatings Based on Bio-Renewable Oligomers and Monomers. Materials 2021, 14, 7731. [Google Scholar] [CrossRef] [PubMed]
- Tytgat, L.; Markovic, M.; Qazi, T.H.; Vagenende, M.; Bray, F.; Martins, J.C.; Rolando, C.; Thienpont, H.; Ottevaere, H.; Ovsianikov, A.; et al. Photo-crosslinkable recombinant collagen mimics for tissue engineering applications. J. Mater. Chem. B 2019, 7, 3100–3108. [Google Scholar] [CrossRef] [PubMed]
- Pereira, R.F.; Bártolo, P.J. 3D Photo-Fabrication for Tissue Engineering and Drug Delivery. Engineering 2015, 1, 90–112. [Google Scholar] [CrossRef]
- Hutchison, J.B.; Haraldsson, K.T.; Good, B.T.; Sebra, R.P.; Luo, N.; Anseth, K.S.; Bowman, C.N. Robust polymer microfluidic device fabrication via contact liquid photolithographic polymerization (CLiPP). Lab Chip 2004, 4, 658–662. [Google Scholar] [CrossRef]
- Grant Willson, C.; Trinque, B.C. The Evolution of Materials for the Photolithographic Process. J. Photopol. Sci. Technol. 2003, 16, 621–627. [Google Scholar] [CrossRef][Green Version]
- Rogers, J.A.; Nuzzo, R.G. Recent progress in soft lithography. Mater. Today 2005, 8, 50–56. [Google Scholar] [CrossRef]
- Del Barrio, J.; Sánchez-Somolinos, C. Light to Shape the Future: From Photolithography to 4D Printing. Adv. Opt. Mater. 2019, 7, 1900598. [Google Scholar] [CrossRef]
- Haraldsson, K.T.; Hutchison, J.B.; Sebra, R.P.; Good, B.T.; Anseth, K.S.; Bowman, C.N. 3D polymeric microfluidic device fabrication via contact liquid photolithographic polymerization (CLiPP). Sens. Actuators B Chem. 2006, 113, 454–460. [Google Scholar] [CrossRef]
- Xu, Y.; Qi, F.; Mao, H.; Li, S.; Zhu, Y.; Gong, J.; Wang, L.; Malmstadt, N.; Chen, Y. In-situ transfer vat photopolymerization for transparent microfluidic device fabrication. Nat. Commun. 2022, 13, 918. [Google Scholar] [CrossRef]
- Liska, R.; Schuster, M.; Inführ, R.; Turecek, C.; Fritscher, C.; Seidl, B.; Schmidt, V.; Kuna, L.; Haase, A.; Varga, F.; et al. Photopolymers for rapid prototyping. J. Coat. Technol. Res. 2007, 4, 505–510. [Google Scholar] [CrossRef]
- Rocheva, V.V.; Koroleva, A.V.; Savelyev, A.G.; Khaydukov, K.V.; Generalova, A.N.; Nechaev, A.V.; Guller, A.E.; Semchishen, V.A.; Chichkov, B.N.; Khaydukov, E.V. High-resolution 3D photopolymerization assisted by upconversion nanoparticles for rapid prototyping applications. Sci. Rep. 2018, 8, 3663. [Google Scholar] [CrossRef] [PubMed]
- Klikovits, N.; Sinawehl, L.; Knaack, P.; Koch, T.; Stampfl, J.; Gorsche, C.; Liska, R. UV-Induced Cationic Ring-Opening Polymerization of 2-Oxazolines for Hot Lithography. ACS Macro Lett. 2020, 9, 546–551. [Google Scholar] [CrossRef]
- Pagac, M.; Hajnys, J.; Ma, Q.-P.; Jancar, L.; Jansa, J.; Stefek, P.; Mesicek, J. A Review of Vat Photopolymerization Technology: Materials, Applications, Challenges, and Future Trends of 3D Printing. Polymers 2021, 13, 598. [Google Scholar] [CrossRef] [PubMed]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mülhaupt, R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef] [PubMed]
- Shusteff, M.; Browar, A.E.M.; Kelly, B.E.; Henriksson, J.; Weisgraber, T.H.; Panas, R.M.; Fang, N.X.; Spadaccini, C.M. One-step volumetric additive manufacturing of complex polymer structures. Sci. Adv. 2017, 3, eaao5496. [Google Scholar] [CrossRef]
- Hayki, N.; Lecamp, L.; Désilles, N.; Lebaudy, P. Kinetic Study of Photoinitiated Frontal Polymerization. Influence of UV Light Intensity Variations on the Conversion Profiles. Macromolecules 2010, 43, 177–184. [Google Scholar] [CrossRef]
- Bowman, C.N.; Kloxin, C.J. Toward an enhanced understanding and implementation of photopolymerization reactions. AIChE J. 2008, 54, 2775–2795. [Google Scholar] [CrossRef]
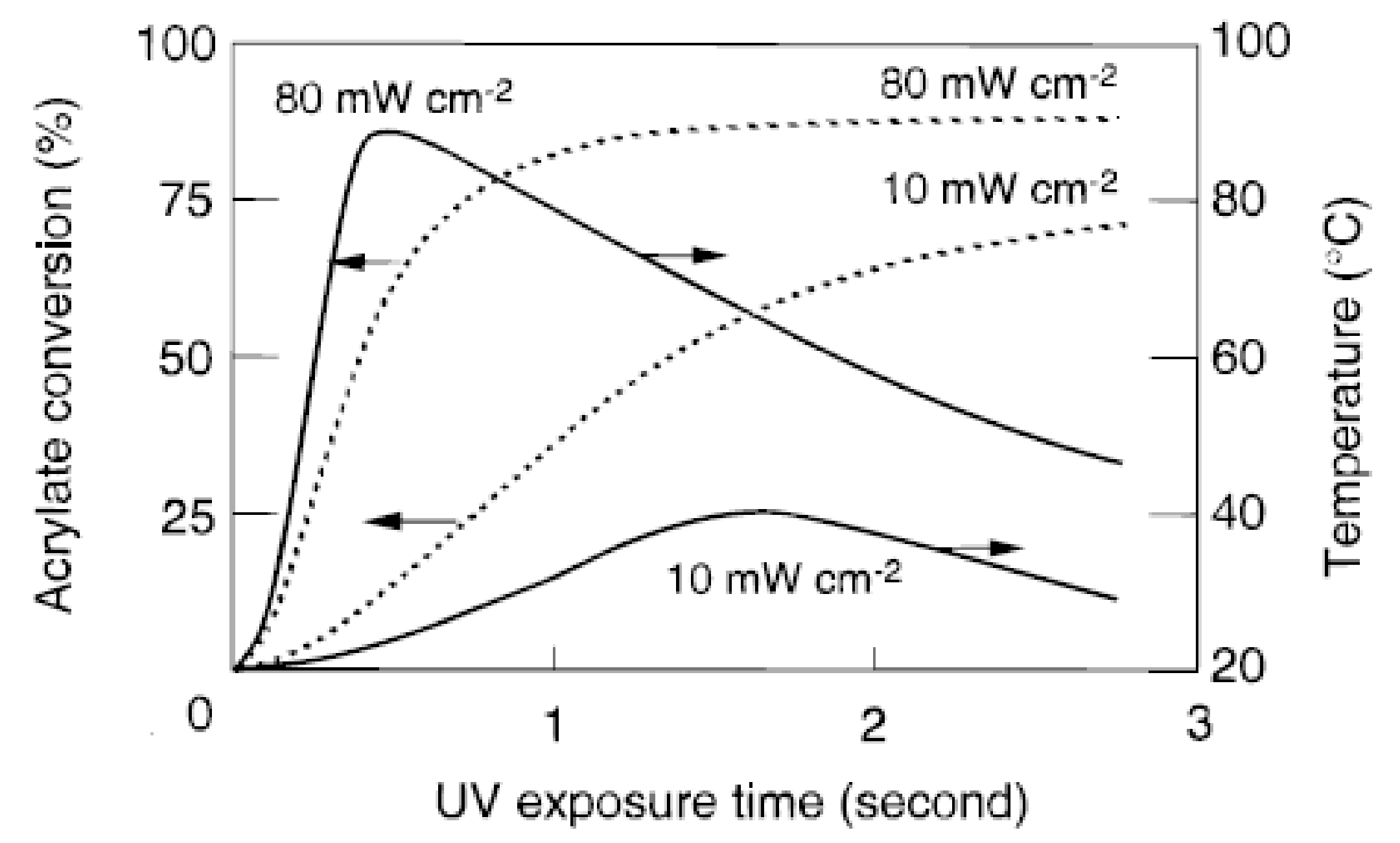
- Rusu, M.C.; Block, C.; van Assche, G.; van Mele, B. Influence of temperature and UV intensity on photo-polymerization reaction studied by photo-DSC. J. Therm. Anal. Calorim. 2012, 110, 287–294. [Google Scholar] [CrossRef]
- Kaur, M.; Srivastava, A.K. PHOTOPOLYMERIZATION: A REVIEW. J. Macromol. Sci. Part C Polym. Rev. 2002, 42, 481–512. [Google Scholar] [CrossRef]
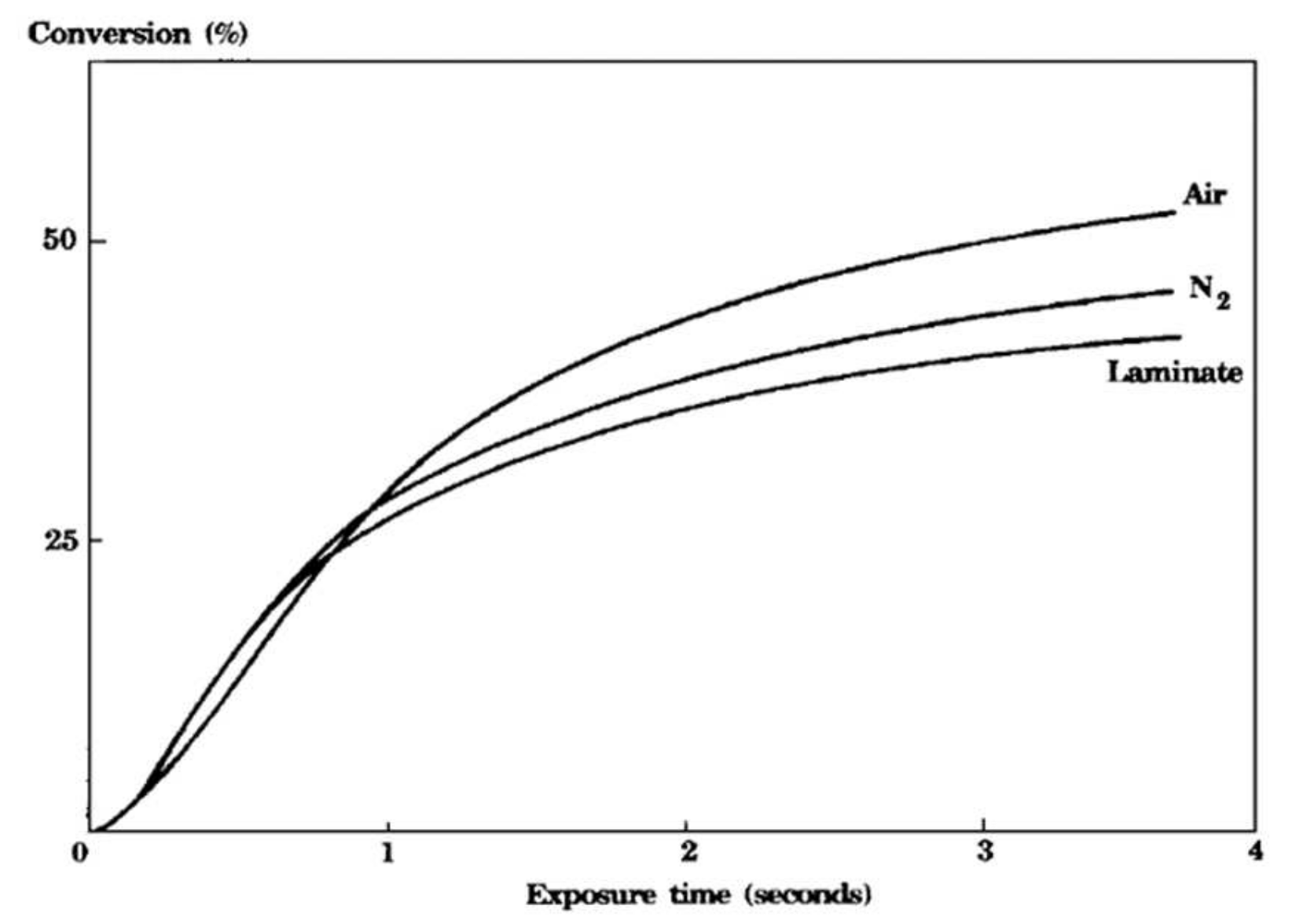
- Decker, C.; Jenkins, A.D. Kinetic approach of oxygen inhibition in ultraviolet- and laser-induced polymerizations. Macromolecules 1985, 18, 1241–1244. [Google Scholar] [CrossRef]
- Lovestead, T.M.; O’Brien, A.K.; Bowman, C.N. Models of multivinyl free radical photopolymerization kinetics. J. Photochem. Photobiol. A Chem. 2003, 159, 135–143. [Google Scholar] [CrossRef]
- Studer, K.; Decker, C.; Beck, E.; Schwalm, R. Overcoming oxygen inhibition in UV-curing of acrylate coatings by carbon dioxide inerting, Part I. Prog. Org. Coat. 2003, 48, 92–100. [Google Scholar] [CrossRef]
- Decker, C.; Moussa, K. Kinetic study of the cationic photopolymerization of epoxy monomers. J. Polym. Sci. Part A Polym. Chem. 1990, 28, 3429–3443. [Google Scholar] [CrossRef]
- Ficek, B.A. The Potential of Cationic Photopolymerization’s Long Lived Active Centers. Master’s Thesis, University of Iowa, Iowa, IA, USA, 2008. [Google Scholar]
- Malik, M.S.; Schlögl, S.; Wolfahrt, M.; Sangermano, M. Review on UV-Induced Cationic Frontal Polymerization of Epoxy Monomers. Polymers 2020, 12, 2146. [Google Scholar] [CrossRef] [PubMed]
- Esposito Corcione, C.; Greco, A.; Maffezzoli, A. Photopolymerization Kinetics of an Epoxy Based Resin for Stereolithography—Calorimetric Analysis. J. Therm. Anal. Calorim. 2003, 72, 687–693. [Google Scholar] [CrossRef]
- Kim, Y.-M.; Kostanski, L.K.; MacGregor, J.F. Kinetic studies of cationic photopolymerizations of cycloaliphatic epoxide, triethyleneglycol methyl vinyl ether, and cyclohexene oxide. Polym. Eng. Sci. 2005, 45, 1546–1555. [Google Scholar] [CrossRef]
- Lin, J.T.; Lalevee, J.; Cheng, D.C. A Critical Review for Synergic Kinetics and Strategies for Enhanced Photopolymerizations for 3D-Printing and Additive Manufacturing. Polymers 2021, 13, 2325. [Google Scholar] [CrossRef]
- De Beer, M.P.; Van Der Laan, H.L.; Cole, M.A.; Whelan, R.J.; Burns, M.A.; Scott, T.F. Rapid, continuous additive manufacturing by volumetric polymerization inhibition patterning. Sci. Adv. 2019, 5, eaau8723. [Google Scholar] [CrossRef]
- Van Der Laan, H.L.; Burns, M.A.; Scott, T.F. Volumetric Photopolymerization Confinement through Dual-Wavelength Photoinitiation and Photoinhibition. ACS Macro Lett. 2019, 8, 899–904. [Google Scholar] [CrossRef]
- Andrzejewska, E.; Lindén, L.-Å.; Rabek, J.F. Modelling the Kinetics of Photoinitiated Polymerization of Di(meth)acrylates. Polym. Int. 1997, 42, 179–187. [Google Scholar] [CrossRef]
- Decker, C.; Moussa, K. Kinetic investigation of photopolymerizations induced by laser beams. Die Makromol. Chem. 1990, 191, 963–979. [Google Scholar] [CrossRef]
- Decker, C. Ultra-fast polymerization of epoxy-acrylate resins by pulsed laser irradiation. J. Polym. Sci. Polym. Chem. Ed. 1983, 21, 2451–2461. [Google Scholar] [CrossRef]
- Lin, Y.; Stansbury, J.W. Kinetics studies of hybrid structure formation by controlled photopolymerization. Polymer 2003, 44, 4781–4789. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Yu, J. Autoacceleration in free radical polymerization. Phys. Rev. Lett. 1994, 73, 1723–1726. [Google Scholar] [CrossRef] [PubMed]
- Anseth, K.S.; Bowman, C.N. Reaction Diffusion Enhanced Termination in Polymerizations of Multifunctional Monomers. Polym. React. Eng. 1993, 1, 499–520. [Google Scholar] [CrossRef]
- Brighenti, R.; Cosma, M.P.; Marsavina, L.; Spagnoli, A.; Terzano, M. Laser-based additively manufactured polymers: A review on processes and mechanical models. J. Mater. Sci. 2021, 56, 961–998. [Google Scholar] [CrossRef]
- Davtyan, S.P.; Berlin, A.A.; Tonoyan, A.O. Advances and problems of frontal polymerization processes. Ref. J. Chem. 2011, 1, 56–92. [Google Scholar] [CrossRef]
- Davtyan, S.P.; Avetisyan, A.S.; Berlin, A.A.; Tonoyan, A.O. Synthesis and properties of particle-filled and intercalated polymer nanocomposites. Ref. J. Chem. 2013, 3, 1–51. [Google Scholar] [CrossRef]
- Cui, Y.; Yang, J.; Zhan, Y.; Zeng, Z.; Chen, Y. In situ fabrication of polyacrylate/nanozirconia hybrid material via frontal photopolymerization. Colloid Polym. Sci. 2008, 286, 97–106. [Google Scholar] [CrossRef]
- Pojman, J.A. Mathematical modeling of frontal polymerization. Math. Model. Nat. Phenom. 2019, 14, 604. [Google Scholar] [CrossRef]
- Garra, P.; Dietlin, C.; Morlet-Savary, F.; Dumur, F.; Gigmes, D.; Fouassier, J.-P.; Lalevée, J. Photopolymerization processes of thick films and in shadow areas: A review for the access to composites. Polym. Chem. 2017, 8, 7088–7101. [Google Scholar] [CrossRef]
- Ebner, C.; Mitterer, J.; Eigruber, P.; Stieger, S.; Riess, G.; Kern, W. Ultra-High Through-Cure of (Meth)Acrylate Copolymers via Photofrontal Polymerization. Polymers 2020, 12, 1291. [Google Scholar] [CrossRef] [PubMed]
- Carion, P.; Ibrahim, A.; Allonas, X.; Croutxé-Barghorn, C.; L’Hostis, G. Frontal free-radical photopolymerization of thick samples: Applications to LED-induced fiber-reinforced polymers. J. Polym. Sci. Part A Polym. Chem. 2019, 57, 898–906. [Google Scholar] [CrossRef]
- Moad, G.; Solomon, D.H. The Chemistry of Radical Polymerization, 2nd ed.; Elsevier: Boston, MA, USA, 2006; ISBN 9780080442884. [Google Scholar]
- Matyjaszewski, K.; Davis, T.P. Handbook of Radical Polymerization; Wiley-Interscience: Hoboken, NJ, USA, 2003; ISBN 9780471461579. [Google Scholar]
- Guerrero-Santos, R.; Saldívar-Guerra, E.; Bonilla-Cruz, J. Free Radical Polymerization. In Handbook of Polymer Synthesis, Characterization, and Processing; Saldívar-Guerra, E., Vivaldo-Lima, E., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 65–83. ISBN 9781118480793. [Google Scholar]
- Elias, H.-G. Makromoleküle: Chemische Struktur und Synthesen-Sechste; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 3-527-29872-X. [Google Scholar]
- Odian, G.G. Principles of Polymerization, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 0-471-27400-3. [Google Scholar]
- Fouassier, J.; Allonas, X.; Burget, D. Photopolymerization reactions under visible lights: Principle, mechanisms and examples of applications. Prog. Org. Coat. 2003, 47, 16–36. [Google Scholar] [CrossRef]
- Elian, C.; Brezová, V.; Sautrot-Ba, P.; Breza, M.; Versace, D.-L. Lawsone Derivatives as Efficient Photopolymerizable Initiators for Free-Radical, Cationic Photopolymerizations, and Thiol-Ene Reactions. Polymers 2021, 13, 2015. [Google Scholar] [CrossRef]
- Daglen, B.C.; Tyler, D.R. Photodegradable plastics: End-of-life design principles. Green Chem. Lett. Rev. 2010, 3, 69–82. [Google Scholar] [CrossRef]
- Yagci, Y.; Jockusch, S.; Turro, N.J. Photoinitiated Polymerization: Advances, Challenges, and Opportunities. Macromolecules 2010, 43, 6245–6260. [Google Scholar] [CrossRef]
- Ibrahim, A.; Stefano, L.; Tarzi, O.; Tar, H.; Ley, C.; Allonas, X. High-performance photoinitiating systems for free radical photopolymerization. Application to holographic recording. Photochem. Photobiol. 2013, 89, 1283–1290. [Google Scholar] [CrossRef]
- Schlüter, A.-D. Synthesis of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1998; ISBN 9783527294497. [Google Scholar]
- Sangermano, M. Advances in cationic photopolymerization. Pure Appl. Chem. 2012, 84, 2089–2101. [Google Scholar] [CrossRef]
- Crivello, J.V. Design of Photoacid Generating Systems. J. Photopol. Sci. Technol. 2009, 22, 575–582. [Google Scholar] [CrossRef]
- Crivello, J.V.; Lee, J.L. Alkoxy-substituted diaryliodonium salt cationic photoinitiators. J. Polym. Sci. Part A Polym. Chem. 1989, 27, 3951–3968. [Google Scholar] [CrossRef]
- Akhtar, S.R.; Crivello, J.V.; Lee, J.L. Synthesis of aryl-substituted sulfonium salts by the phosphorus pentoxide-methanesulfonic acid promoted condensation of sulfoxides with aromatic compounds. J. Org. Chem. 1990, 55, 4222–4225. [Google Scholar] [CrossRef]
- Vitale, A.; Sangermano, M.; Bongiovanni, R.; Burtscher, P.; Moszner, N. Visible Light Curable Restorative Composites for Dental Applications Based on Epoxy Monomer. Materials 2014, 7, 554–562. [Google Scholar] [CrossRef]
- Barner-Kowollik, C. Acrylate free radical polymerization: From mechanism to polymer design. Macromol. Rapid Commun. 2009, 30, 1961–1963. [Google Scholar] [CrossRef]
- Tripathy, R.; Crivello, J.V.; Faust, R. Photoinitiated polymerization of acrylate, methacrylate, and vinyl ether end-functional polyisobutylene macromonomers. J. Polym. Sci. Part A Polym. Chem. 2013, 51, 305–317. [Google Scholar] [CrossRef]
- Chen, J.; Chu, N.; Zhao, M.; Jin, F.-L.; Park, S.-J. Synthesis and application of thermal latent initiators of epoxy resins: A review. J. Appl. Polym. Sci. 2020, 137, 49592. [Google Scholar] [CrossRef]
- Brydson, J.A. Epoxide Resins. In Plastics Materials; Elsevier: Amsterdam, The Netherlands, 1999; pp. 744–777. ISBN 9780750641326. [Google Scholar]
- McGrath, J.E. Ring-Opening Polymerization: Introduction. In Ring-Opening Polymerization; McGrath, J.E., Ed.; American Chemical Society: Washington, DC, USA, 1985; pp. 1–22. ISBN 9780841209268. [Google Scholar]
- Sanda, F.; Endo, T. Radical ring-opening polymerization. J. Polym. Sci. Part A Polym. Chem. 2001, 39, 265–276. [Google Scholar] [CrossRef]
- Higashimura, T.; Sawamoto, M. Carbocationic Polymerization: Vinyl Ethers. In Comprehensive Polymer Science and Supplements; Elsevier: Amsterdam, The Netherlands, 1989; pp. 673–696. ISBN 9780080967011. [Google Scholar]
- Kammiyada, H.; Ouchi, M.; Sawamoto, M. A Study on Physical Properties of Cyclic Poly(vinyl ether)s Synthesized via Ring-Expansion Cationic Polymerization. Macromolecules 2017, 50, 841–848. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Nakamoto, T. Micro Fabrication by UV Laser Photopolymerization; Nagoya University: Nagoya, Japan, 1998. [Google Scholar]
- Tomeckova, V.; Halloran, J.W. Predictive models for the photopolymerization of ceramic suspensions. J. Eur. Ceram. Soc. 2010, 30, 2833–2840. [Google Scholar] [CrossRef]
- Blanco, M.; Corcuera, M.A.; Riccardi, C.C.; Mondragon, I. Mechanistic kinetic model of an epoxy resin cured with a mixture of amines of different functionalities. Polymer 2005, 46, 7989–8000. [Google Scholar] [CrossRef]
- Matias, J.M.; Bartolo, P.J.; Pontes, A.V. Modeling and simulation of photofabrication processes using unsaturated polyester resins. J. Appl. Polym. Sci. 2009, 114, 3673–3685. [Google Scholar] [CrossRef]
- Da Silva Bartolo, P.J. Photo-curing modelling: Direct irradiation. Int. J. Adv. Manuf. Technol. 2007, 32, 480–491. [Google Scholar] [CrossRef]
- Han, C.D.; Lee, D.-S. Analysis of the curing behavior of unsaturated polyester resins using the approach of free radical polymerization. J. Appl. Polym. Sci. 1987, 33, 2859–2876. [Google Scholar] [CrossRef]
- Nogueira, T.R.; Goncalves, M.C.; Ferrareso Lona, L.M.; Vivaldo-Lima, E.; McManus, N.; Penlidis, A. Effect of initiator type and concentration on polymerization rate and molecular weight in the bimolecular nitroxide-mediated radical polymerization of styrene. Adv. Polym. Technol. J. Polym. Processing Inst. 2010, 29, 11–19. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Altun-Çiftçioğlu, G.A.; Ersoy-Meriçboyu, A.; Henderson, C.L. Stochastic modeling and simulation of photopolymerization process. Polym. Eng. Sci. 2011, 51, 1710–1719. [Google Scholar] [CrossRef]
- Boddapati, A. Modeling Cure Depth during Photopolymerization of Multifunctional Acrylates. Ph.D Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2010. [Google Scholar]
- Goodner, M.D.; Bowman, C.N. Modeling Primary Radical Termination and Its Effects on Autoacceleration in Photopolymerization Kinetics. Macromolecules 1999, 32, 6552–6559. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, Z.; Hamel, C.M.; Mu, X.; Kuang, X.; Guo, Z.; Qi, H.J. Evolution of material properties during free radical photopolymerization. J. Mech. Phys. Solids 2018, 112, 25–49. [Google Scholar] [CrossRef]
- Zhang, Y.; Kranbuehl, D.E.; Sautereau, H.; Seytre, G.; Dupuy, J. Modeling and Measuring UV Cure Kinetics of Thick Dimethacrylate Samples. Macromolecules 2009, 42, 203–210. [Google Scholar] [CrossRef]
- Achilias, D.S. A Review of Modeling of Diffusion Controlled Polymerization Reactions. Macromol. Theory Simul. 2007, 16, 319–347. [Google Scholar] [CrossRef]
- Batch, G.L.; Macosko, C.W. Kinetic model for crosslinking free radical polymerization including diffusion limitations. J. Appl. Polym. Sci. 1992, 44, 1711–1729. [Google Scholar] [CrossRef]
- Anastasio, R.; Peerbooms, W.; Cardinaels, R.; van Breemen, L.C.A. Characterization of Ultraviolet-Cured Methacrylate Networks: From Photopolymerization to Ultimate Mechanical Properties. Macromolecules 2019, 52, 9220–9231. [Google Scholar] [CrossRef]
- Long, K.N.; Scott, T.F.; Jerry Qi, H.; Bowman, C.N.; Dunn, M.L. Photomechanics of light-activated polymers. J. Mech. Phys. Solids 2009, 57, 1103–1121. [Google Scholar] [CrossRef]
- O’Brien, A.K.; Bowman, C.N. Modeling the Effect of Oxygen on Photopolymerization Kinetics. Macromol. Theory Simul. 2006, 15, 176–182. [Google Scholar] [CrossRef]
- Brighenti, R.; Cosma, M.P.; Marsavina, L.; Spagnoli, A.; Terzano, M. Multiphysics modelling of the mechanical properties in polymers obtained via photo-induced polymerization. Int. J. Adv. Manuf. Technol. 2021, 117, 481–499. [Google Scholar] [CrossRef]
- Buback, M.; Huckestein, B.; Russell, G.T. Modeling of termination in intermediate and high conversion free radical polymerizations. Macromol. Chem. Phys. 1994, 195, 539–554. [Google Scholar] [CrossRef]
- Buback, M.; Hesse, P.; Hutchinson, R.A.; Kasák, P.; Lacík, I.; Stach, M.; Utz, I. Kinetics and Modeling of Free-Radical Batch Polymerization of Nonionized Methacrylic Acid in Aqueous Solution. Ind. Eng. Chem. Res. 2008, 47, 8197–8204. [Google Scholar] [CrossRef]
- Buback, M. Free-radical polymerization up to high conversion. A general kinetic treatment. Die Makromol. Chem. 1990, 191, 1575–1587. [Google Scholar] [CrossRef]
- Dickey, M.D.; Willson, C.G. Kinetic parameters for step and flash imprint lithography photopolymerization. AIChE J. 2006, 52, 777–784. [Google Scholar] [CrossRef]
- Gan, S.; Seferis, J.C.; Prime, R.B. A viscoelastic description of the glass transition-conversion relationship for reactive polymers. J. Therm. Anal. Calorim. 1991, 37, 463–478. [Google Scholar] [CrossRef]
- Goodner, M.D.; Bowman, C.N. Development of a comprehensive free radical photopolymerization model incorporating heat and mass transfer effects in thick films. Chem. Eng. Sci. 2002, 57, 887–900. [Google Scholar] [CrossRef]
- Goodner, M.D.; Lee, H.R.; Bowman, C.N. Method for Determining the Kinetic Parameters in Diffusion-Controlled Free-Radical Homopolymerizations. Ind. Eng. Chem. Res. 1997, 36, 1247–1252. [Google Scholar] [CrossRef]
- O’Brien, A.K.; Bowman, C.N. Modeling Thermal and Optical Effects on Photopolymerization Systems. Macromolecules 2003, 36, 7777–7782. [Google Scholar] [CrossRef]
- Lovestead, T.M.; Berchtold, K.A.; Bowman, C.N. Modeling the Effects of Chain Length on the Termination Kinetics in Multivinyl Photopolymerizations. Macromol. Theory Simul. 2002, 11, 729–738. [Google Scholar] [CrossRef]
- Bowman, C.N.; Peppas, N.A. Coupling of kinetics and volume relaxation during polymerizations of multiacrylates and multimethacrylates. Macromolecules 1991, 24, 1914–1920. [Google Scholar] [CrossRef]
- Zhu, S.; Tian, Y.; Hamielec, A.E.; Eaton, D.R. Radical trapping and termination in free-radical polymerization of methyl methacrylate. Macromolecules 1990, 23, 1144–1150. [Google Scholar] [CrossRef]
- Anseth, K.S.; Wang, C.M.; Bowman, C.N. Kinetic evidence of reaction diffusion during the polymerization of multi(meth)acrylate monomers. Macromolecules 1994, 27, 650–655. [Google Scholar] [CrossRef]
- Christmann, J.; Ley, C.; Allonas, X.; Ibrahim, A.; Croutxé-Barghorn, C. Experimental and theoretical investigations of free radical photopolymerization: Inhibition and termination reactions. Polymer 2019, 160, 254–264. [Google Scholar] [CrossRef]
- Ibrahim, A.; Maurin, V.; Ley, C.; Allonas, X.; Croutxe-Barghorn, C.; Jasinski, F. Investigation of termination reactions in free radical photopolymerization of UV powder formulations. Eur. Polym. J. 2012, 48, 1475–1484. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, L.; Zhao, Y.; You, Z.; Guan, Q. 3D printing preview for stereo-lithography based on photopolymerization kinetic models. Bioact. Mater. 2020, 5, 798–807. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhao, C.; Zhang, Y.; Jariwala, A.; Rosen, D. (Eds.) Process Modeling and In-Situ Monitoring of Polymerization for Exposure Controlled Projection Lithography (ECPL). In Proceedings of the 28th Annual International Solid Free Form Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 7–9 August 2017. [Google Scholar]
- Lee, J.H.; Prud’homme, R.K.; Aksay, I.A. Cure depth in photopolymerization: Experiments and theory. J. Mater. Res. 2001, 16, 3536–3544. [Google Scholar] [CrossRef]
- Dickey, M.D.; Burns, R.L.; Kim, E.K.; Johnson, S.C.; Stacey, N.A.; Willson, C.G. Study of the kinetics of step and flash imprint lithography photopolymerization. AIChE J. 2005, 51, 2547–2555. [Google Scholar] [CrossRef]
- Perry, M.F.; Young, G.W. A Mathematical Model for Photopolymerization From a Stationary Laser Light Source. Macromol. Theory Simul. 2005, 14, 26–39. [Google Scholar] [CrossRef]
- Wenand, M.; McCormick, A.V. A Kinetic Model for Radical Trapping in Photopolymerization of Multifunctional Monomers. Macromolecules 2000, 33, 9247–9254. [Google Scholar] [CrossRef]
- Anseth, K.S.; Anderson, K.J.; Bowman, C.N. Radical concentrations, environments, and reactivities during crosslinking polymerizations. Macromol. Chem. Phys. 1996, 197, 833–848. [Google Scholar] [CrossRef]
- Bueche, F. Physical Properties of Polymers; Interscience: New York, NY, USA, 1962. [Google Scholar]
- Lin, J.-T.; Wang, K.-C. Analytic formulas and numerical simulations for the dynamics of thick and non-uniform polymerization by a UV light. J. Polym. Res. 2016, 23, 53. [Google Scholar] [CrossRef]
- Lin, J.-T.; Cheng, D.-C. Modeling the efficacy profiles of UV-light activated corneal collagen crosslinking. PLoS ONE 2017, 12, e0175002. [Google Scholar] [CrossRef]
- Lin, J.-T.; Liu, H.-W.; Chen, K.-T.; Cheng, D.-C. Modeling the Optimal Conditions for Improved Efficacy and Crosslink Depth of Photo-Initiated Polymerization. Polymers 2019, 11, 217. [Google Scholar] [CrossRef]
- Lin, J.-T.; Liu, H.-W.; Chen, K.-T.; Cheng, D.-C. Modeling the Kinetics, Curing Depth, and Efficacy of Radical-Mediated Photopolymerization: The Role of Oxygen Inhibition, Viscosity, and Dynamic Light Intensity. Front. Chem. 2019, 7, 760. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.-T.; Cheng, D.-C.; Chen, K.-T.; Chiu, Y.-C.; Liu, H.-W. Enhancing UV Photopolymerization by a Red-light Preirradiation: Kinetics and Modeling Strategies for Reduced Oxygen Inhibition. J. Polym. Sci. 2020, 58, 683–691. [Google Scholar] [CrossRef]
- Lin, J.-T.; Lee, Y.-Z.; Lalevee, J.; Kao, C.-H.; Lin, K.-H.; Cheng, D.-C. Modeling the Enhanced Efficacy and Curing Depth of Photo-Thermal Dual Polymerization in Metal (Fe) Polymer Composites for 3D Printing. Polymers 2022, 14, 1158. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, V.V.; Decker, C. Kinetic study of photoinitiated frontal polymerization. Polym. Int. 2001, 50, 113–118. [Google Scholar] [CrossRef]
- Childress, K.K.; Kim, K.; Glugla, D.J.; Musgrave, C.B.; Bowman, C.N.; Stansbury, J.W. Independent Control of Singlet Oxygen and Radical Generation via Irradiation of a Two-Color Photosensitive Molecule. Macromolecules 2019, 52, 4968–4978. [Google Scholar] [CrossRef]
- Kamal, M.R.; Sourour, S. Kinetics and thermal characterization of thermoset cure. Polym. Eng. Sci. 1973, 13, 59–64. [Google Scholar] [CrossRef]
- Sourour, S.; Kamal, M.R. Differential scanning calorimetry of epoxy cure: Isothermal cure kinetics. Thermochim. Acta 1976, 14, 41–59. [Google Scholar] [CrossRef]
- Harikrishna, R.; Ponrathnam, S.; Tambe, S.S. Reaction kinetics and modeling of photoinitiated cationic polymerization of an alicyclic based diglycidyl ether. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2014, 318, 263–268. [Google Scholar] [CrossRef]
- Atai, M.; Watts, D.C. A new kinetic model for the photopolymerization shrinkage-strain of dental composites and resin-monomers. Dent. Mater. 2006, 22, 785–791. [Google Scholar] [CrossRef]
- Khudyakov, I.V.; Legg, J.C.; Purvis, M.B.; Overton, B.J. Kinetics of Photopolymerization of Acrylates with Functionality of 1−6. Ind. Eng. Chem. Res. 1999, 38, 3353–3359. [Google Scholar] [CrossRef]
- Cook, W.D. Photopolymerization kinetics of dimethacrylates using the camphorquinone/amine initiator system. Polymer 1992, 33, 600–609. [Google Scholar] [CrossRef]
- Ganglani, M.; Carr, S.H.; Torkelson, J.M. Influence of cure via network structure on mechanical properties of a free-radical polymerizing thermoset. Polymer 2002, 43, 2747–2760. [Google Scholar] [CrossRef]
- Maffezzoli, A.; Terzi, R. Effect of irradiation intensity on the isothermal photopolymerization kinetics of acrylic resins for stereolithography. Thermochim. Acta 1998, 321, 111–121. [Google Scholar] [CrossRef]
- Rehbein, T.; Lion, A.; Johlitz, M.; Constantinescu, A. Experimental investigation and modelling of the curing behaviour of photopolymers. Polym. Test. 2020, 83, 106356. [Google Scholar] [CrossRef]
- Bartolo, P.J.d.S. Optical Approaches to Macroscopic and Microscopic Engineering. Ph.D. Thesis, University of Reading, Reading, UK, 2001. [Google Scholar]
- Yang, Y.; Li, L.; Zhao, J. Mechanical property modeling of photosensitive liquid resin in stereolithography additive manufacturing: Bridging degree of cure with tensile strength and hardness. Mater. Des. 2019, 162, 418–428. [Google Scholar] [CrossRef]
- Kenny, J.M.; Trivisano, A. Isothermal and dynamic reaction kinetics of high performance epoxy matrices. Polym. Eng. Sci. 1991, 31, 1426–1433. [Google Scholar] [CrossRef]
- Park, I.-K.; Lee, D.-S.; Nam, J.-D. Equivalent processing time analysis of glass transition development in epoxy/carbon fiber composite systems. J. Appl. Polym. Sci. 2002, 84, 144–154. [Google Scholar] [CrossRef]
- Kim, Y.C.; Hong, S.; Sun, H.; Kim, M.G.; Choi, K.; Cho, J.; Choi, H.R.; Koo, J.C.; Moon, H.; Byun, D.; et al. UV-curing kinetics and performance development of in situ curable 3D printing materials. Eur. Polym. J. 2017, 93, 140–147. [Google Scholar] [CrossRef]
- Nelson, E.W.; Jacobs, J.L.; Scranton, A.B.; Anseth, K.S.; Bowman, C.N. Photo-differential scanning calorimetry studies of cationic polymerizations of divinyl ethers. Polymer 1995, 36, 4651–4656. [Google Scholar] [CrossRef]
- Nelson, E.W.; Scranton, A.B. Kinetics of cationic photopolymerizations of divinyl ethers characterized usingin situ Raman spectroscopy. J. Polym. Sci. Part A Polym. Chem. 1996, 34, 403–411. [Google Scholar] [CrossRef]
- Nelson, E.W.; Carter, T.P.; Scranton, A.B. The role of the triplet state in the photosensitization of cationic polymerizations by anthracene. J. Polym. Sci. Part A Polym. Chem. 1995, 33, 247–256. [Google Scholar] [CrossRef]
- Corcione, C.E.; Greco, A.; Maffezzoli, A. Time–temperature and time-irradiation intensity superposition for photopolymerization of an epoxy based resin. Polymer 2005, 46, 8018–8027. [Google Scholar] [CrossRef]
- Pantiru, M.; Vuluga, D.M.; Vasilescu, D.S.; Abadie, M.J.M. Study of the cationic photopolymerization kinetics of cyclic acetals. Polym. Bull. 2002, 47, 485–492. [Google Scholar] [CrossRef]
- Van Assche, G.; Swier, S.; van Mele, B. Modeling and experimental verification of the kinetics of reacting polymer systems. Thermochim. Acta 2002, 388, 327–341. [Google Scholar] [CrossRef]
- Kamal, M.R. Thermoset characterization for moldability analysis. Polym. Eng. Sci. 1974, 14, 231–239. [Google Scholar] [CrossRef]
- Rabinowitch, E. Collision, co-ordination, diffusion and reaction velocity in condensed systems. Trans. Faraday Soc. 1937, 33, 1225. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Wisanrakkit, G.; Gillham, J.K. The glass transition temperature (Tg) as an index of chemical conversion for a high-Tg amine/epoxy system: Chemical and diffusion-controlled reaction kinetics. J. Appl. Polym. Sci. 1990, 41, 2885–2929. [Google Scholar] [CrossRef]
- Cho, J.-D.; Hong, J.-W. Photo-curing kinetics for the UV-initiated cationic polymerization of a cycloaliphatic diepoxide system photosensitized by thioxanthone. Eur. Polym. J. 2005, 41, 367–374. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Boey, F.; Qiang, W. Experimental modeling of the cure kinetics of an epoxy-hexaanhydro-4-methylphthalicanhydride (MHHPA) system. Polymer 2000, 41, 2081–2094. [Google Scholar] [CrossRef]
- Abadie, M.J.M.; Chia, N.K.; Boey, F. Cure kinetics for the ultraviolet cationic polymerization of cycloliphatic and diglycidyl ether of bisphenol-A (DGEBA) epoxy systems with sulfonium salt using an auto catalytic model. J. Appl. Polym. Sci. 2002, 86, 1587–1591. [Google Scholar] [CrossRef]
- Macan, J.; Ivanković, H.; Ivanković, M.; Mencer, H.J. Study of cure kinetics of epoxy-silica organic–inorganic hybrid materials. Thermochim. Acta 2004, 414, 219–225. [Google Scholar] [CrossRef]
- Golaz, B.; Michaud, V.; Leterrier, Y.; Månson, J.-A. UV intensity, temperature and dark-curing effects in cationic photo-polymerization of a cycloaliphatic epoxy resin. Polymer 2012, 53, 2038–2048. [Google Scholar] [CrossRef]
- Šesták, J.; Berggren, G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures. Thermochim. Acta 1971, 3, 1–12. [Google Scholar] [CrossRef]
- Voytekunas, V.Y.; Ng, F.L.; Abadie, M.J. Kinetics study of the UV-initiated cationic polymerization of cycloaliphatic diepoxide resins. Eur. Polym. J. 2008, 44, 3640–3649. [Google Scholar] [CrossRef]
- Jiang, F.; Drummer, D. Curing Kinetic Analysis of Acrylate Photopolymer for Additive Manufacturing by Photo-DSC. Polymers 2020, 12, 1080. [Google Scholar] [CrossRef]
- Xu, W.; Bao, S.; Shen, S.; Wang, W.; Hang, G.; He, P. Differential scanning calorimetric study on the curing behavior of epoxy resin/diethylenetriamine/organic montmorillonite nanocomposite. J. Polym. Sci. B Polym. Phys. 2003, 41, 378–386. [Google Scholar] [CrossRef]
- Chen, D.Z.; He, P.S.; Pan, L.J. Cure kinetics of epoxy-based nanocomposites analyzed by Avrami theory of phase change. Polym. Test. 2003, 22, 689–697. [Google Scholar] [CrossRef]
- Murias, P.; Byczyński, Ł.; Maciejewski, H.; Galina, H. A quantitative approach to dynamic and isothermal curing of an epoxy resin modified with oligomeric siloxanes. J. Therm. Anal. Calorim. 2015, 122, 215–226. [Google Scholar] [CrossRef][Green Version]
- Pollard, M.; Kardos, J.L. Analysis of epoxy resin curing kinetics using the Avrami theory of phase change. Polym. Eng. Sci. 1987, 27, 829–836. [Google Scholar] [CrossRef]
- Marschik, C.; Roland, W.; Löw-Baselli, B.; Steinbichler, G. Application of Hybrid Modeling in Polymer Processing. In Proceedings of the Annual Technical Conference for Plastic Professionals (SPE ANTEC), Online, 30 March–5 May 2020. [Google Scholar]
- Taki, K. A Simplified 2D Numerical Simulation of Photopolymerization Kinetics and Oxygen Diffusion-Reaction for the Continuous Liquid Interface Production (CLIP) System. Polymers 2020, 12, 875. [Google Scholar] [CrossRef] [PubMed]
- Taki, K.; Watanabe, Y.; Ito, H.; Ohshima, M. Effect of Oxygen Inhibition on the Kinetic Constants of the UV-Radical Photopolymerization of Diurethane Dimethacrylate/Photoinitiator Systems. Macromolecules 2014, 47, 1906–1913. [Google Scholar] [CrossRef]
- Taki, K.; Watanabe, Y.; Tanabe, T.; Ito, H.; Ohshima, M. Oxygen concentration and conversion distributions in a layer-by-layer UV-cured film used as a simplified model of a 3D UV inkjet printing system. Chem. Eng. Sci. 2017, 158, 569–579. [Google Scholar] [CrossRef]
- Gao, K.; Ingenhut, B.L.J.; van de Ven, A.P.A.; Valega Mackenzie, F.O.; ten Cate, A.T. (Eds.) Multiphysics Modeling of Photo-Polymerization in Stereolithography Printing Process and Validation. In Proceedings of the 2018 COMSOL Conference in Lausanne, Lausanne, Switzerland, 22–24 October 2018. [Google Scholar]
- Mizukami, Y.; Rajniak, D.; Rajniak, A.; Nishimura, M. A novel microchip for capillary electrophoresis with acrylic microchannel fabricated on photosensor array. Sens. Actuators B Chem. 2002, 81, 202–209. [Google Scholar] [CrossRef]
- Erdmann, L. MOEMS-based lithography for the fabrication of micro-optical components. J. Micro/Nanolithography MEMS MOEMS 2005, 4, 41601. [Google Scholar] [CrossRef]
- Jariwala, A.S.; Ding, F.; Zhao, X.; Rosen, D.W. A Film Fabrication Process on Transparent Substrate Using Mask Projection Micro-Stereolithography; The University of Texas at Austin: Austin, TX, USA, 2008. [Google Scholar]
- Jariwala, A.S.; Ding, F.; Boddapati, A.; Breedveld, V.; Grover, M.A.; Henderson, C.L.; Rosen, D.W. Modeling effects of oxygen inhibition in mask-based stereolithography. Rapid Prototyp. J. 2011, 17, 168–175. [Google Scholar] [CrossRef]
- Huang, Y.; Kormakov, S.; He, X.; Gao, X.; Zheng, X.; Liu, Y.; Sun, J.; Wu, D. Conductive polymer composites from renewable resources: An overview of preparation, properties, and applications. Polymers 2019, 11, 187. [Google Scholar] [CrossRef]
- Zhang, X.; Fujiwara, S.; Fujii, M. Measurements of Thermal Conductivity and Electrical Conductivity of a Single Carbon Fiber. Int. J. Thermophys. 2000, 21, 965–980. [Google Scholar] [CrossRef]
- Morak, M.; Marx, P.; Gschwandl, M.; Fuchs, P.F.; Pfost, M.; Wiesbrock, F. Heat Dissipation in Epoxy/Amine-Based Gradient Composites with Alumina Particles: A Critical Evaluation of Thermal Conductivity Measurements. Polymers 2018, 10, 1131. [Google Scholar] [CrossRef] [PubMed]
- Moradi, S.; Calventus, Y.; Román, F.; Hutchinson, J.M. Achieving High Thermal Conductivity in Epoxy Composites: Effect of Boron Nitride Particle Size and Matrix-Filler Interface. Polymers 2019, 11, 1156. [Google Scholar] [CrossRef] [PubMed]
- Plesa, I.; Notingher, P.V.; Schlögl, S.; Sumereder, C.; Muhr, M. Properties of Polymer Composites Used in High-Voltage Applications. Polymers 2016, 8, 173. [Google Scholar] [CrossRef] [PubMed]
- Kochetov, R.; Andritsch, T.; Lafont, U.; Morshuis, P.; Smit, J.J. Thermal Conductivity of Nano-Filled Epoxy Systems. In 2009 Annual Report, Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena, CEIDP 2009: Virginia Beach, VA, USA, 18–21 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 658–661. ISBN 978-1-4244-4557-8. [Google Scholar]
- Huang, X.; Jiang, P.; Tanaka, T. A review of dielectric polymer composites with high thermal conductivity. IEEE Elects. Insul. Mag. 2011, 27, 8–16. [Google Scholar] [CrossRef]
- Windberger, M.S.; Dimitriou, E.; Rendl, S.; Wewerka, K.; Wiesbrock, F. Temperature-Triggered/Switchable Thermal Conductivity of Epoxy Resins. Polymers 2020, 13, 65. [Google Scholar] [CrossRef]
- Ma, H.; Gao, B.; Wang, M.; Yuan, Z.; Shen, J.; Zhao, J.; Feng, Y. Strategies for enhancing thermal conductivity of polymer-based thermal interface materials: A review. J. Mater. Sci. 2021, 56, 1064–1086. [Google Scholar] [CrossRef]
- Friedrich, K.; Breuer, U. Multifunctionality of Polymer Composites: Challenges and New Solutions; Elsevier: Kidlington, UK, 2015; ISBN 9780323265034. [Google Scholar]
- Unterweger, C.; Brüggemann, O.; Fürst, C. Synthetic fibers and thermoplastic short-fiber-reinforced polymers: Properties and characterization. Polym. Compos. 2014, 35, 227–236. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber-Reinforced Polymer Composites: Manufacturing, Properties, and Applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef]
- Holbery, J.; Houston, D. Natural-fiber-reinforced polymer composites in automotive applications. JOM 2006, 58, 80–86. [Google Scholar] [CrossRef]
- Tan, D.; Irwin, P.; Sikalidis, C. Polymer Based Nanodielectric Composites. In Advances in Ceramics: Electric and Magnetic Ceramics, Bioceramics, Ceramics and Environment; InTech: London, UK, 2011; p. 115. ISBN 978-953-307-350-7. [Google Scholar]
- Song, W.; Han, B.; Zhang, D.; Sun, Z.; Wang, X.; Lei, Q. Preparation and properties of BiFeO3/LDPE nanocomposite. In Proceedings of the 2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials (ICPADM 2015), Sydney, Australia, 19–22 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 800–803, ISBN 978-1-4799-8903-4. [Google Scholar]
- Keith Nelson, J. Overview of Nanodielectrics: Insulating Materials of the Future. In Proceedings of the 2007 Electrical Insulation Conference and Electrical Manufacturing Expo (EIC/EME), Nashville, TN, USA, 22–24 October 2007; IEEE Service Center: Piscataway, NJ, USA, 2007; pp. 229–235, ISBN 978-1-4244-0446-9. [Google Scholar]
- Qiao, Y.; Islam, M.S.; Wang, L.; Yan, Y.; Zhang, J.; Benicewicz, B.C.; Ploehn, H.J.; Tang, C. Thiophene Polymer-Grafted Barium Titanate Nanoparticles toward Nanodielectric Composites. Chem. Mater. 2014, 26, 5319–5326. [Google Scholar] [CrossRef]
- King, R.W.P. Electric currents and fields induced in cells in the human brain by radiation from hand-held cellular telephones. J. Appl. Phys. 2000, 87, 893–900. [Google Scholar] [CrossRef]
- Gandhi, O.P. Electromagnetic fields: Human safety issues. Annu. Rev. Biomed. Eng. 2002, 4, 211–234. [Google Scholar] [CrossRef] [PubMed]
- Roh, J.-S.; Chi, Y.-S.; Kang, T.J.; Nam, S. Electromagnetic Shielding Effectiveness of Multifunctional Metal Composite Fabrics. Text. Res. J. 2008, 78, 825–835. [Google Scholar] [CrossRef]
- Sathish Kumar, K.; Rengaraj, R.; Venkatakrishnan, G.R.; Chandramohan, A. Polymeric materials for electromagnetic shielding—A review. Mater. Today Proc. 2021, 47, 4925–4928. [Google Scholar] [CrossRef]
- Pojman, J.A. Frontal Polymerization. In Polymer Science, 2nd ed.; Moeller, M., Matyjaszewski, K., Eds.; Elsevier Science: Burlington, NJ, USA, 2012; pp. 957–980. ISBN 9780080878621. [Google Scholar]
- Lewis, L.L.; DeBisschop, C.S.; Pojman, J.A.; Volpert, V.A. Isothermal frontal polymerization: Confirmation of the mechanism and determination of factors affecting the front velocity, front shape, and propagation distance with comparison to mathematical modeling. J. Polym. Sci. Part A Polym. Chem. 2005, 43, 5774–5786. [Google Scholar] [CrossRef]
- Warren, J.A.; Cabral, J.T.; Douglas, J.F. Solution of a field theory model of frontal photopolymerization. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005, 72, 21801. [Google Scholar] [CrossRef]
- Pojman, J.A.; Ilyashenko, V.M.; Khan, A.M. Free-radical frontal polymerization: Self-propagating thermal reaction waves. J. Chem. Soc. Faraday Trans. 1996, 92, 2825. [Google Scholar] [CrossRef]
- Khan, A.M.; Pojman, J.A. The Use of Frontal Polymerization in Polymer Synthesis. Trends Polym. Sci. 1996, 8, 253–257. [Google Scholar]
- Cabral, J.T.; Douglas, J.F. Propagating waves of network formation induced by light. Polymer 2005, 46, 4230–4241. [Google Scholar] [CrossRef]
- Rytov, B.L.; Ivanov, V.B.; Ivanov, V.V.; Anisimov, V.M. Mechanisms of front propagation of photochemical reactions in polymer containing media: 1. Frontal regimes of photochemical reactions in polymer matrices with bleaching of specimen behind the front. Polymer 1996, 37, 5695–5698. [Google Scholar] [CrossRef]
- Miller, G.A.; Gou, L.; Narayanan, V.; Scranton, A.B. Modeling of photobleaching for the photoinitiation of thick polymerization systems. J. Polym. Sci. Part A Polym. Chem. 2002, 40, 793–808. [Google Scholar] [CrossRef]
- Petko, F.; Świeży, A.; Ortyl, J. Photoinitiating systems and kinetics of frontal photopolymerization processes—The prospects for efficient preparation of composites and thick 3D structures. Polym. Chem. 2021, 12, 4593–4612. [Google Scholar] [CrossRef]
- Frulloni, E.; Salinas, M.M.; Torre, L.; Mariani, A.; Kenny, J.M. Numerical modeling and experimental study of the frontal polymerization of the diglycidyl ether of bisphenol A/diethylenetriamine epoxy system. J. Appl. Polym. Sci. 2005, 96, 1756–1766. [Google Scholar] [CrossRef]
- Robertson, I.D.; Yourdkhani, M.; Centellas, P.J.; Aw, J.E.; Ivanoff, D.G.; Goli, E.; Lloyd, E.M.; Dean, L.M.; Sottos, N.R.; Geubelle, P.H.; et al. Rapid energy-efficient manufacturing of polymers and composites via frontal polymerization. Nature 2018, 557, 223–227. [Google Scholar] [CrossRef]
- Slugovc, C.; Trimmel, G. Polymer Meeting 14—Book of Abstracts; Verlag der Technischen Universität Graz: Graz, Austria, 2021. [Google Scholar]
- Ghosh, A.K.; Dwivedi, M. Advantages and Applications of Polymeric Composites. In Processability of Polymeric Composites; Springer: New Delhi, India, 2020; pp. 29–57. [Google Scholar]




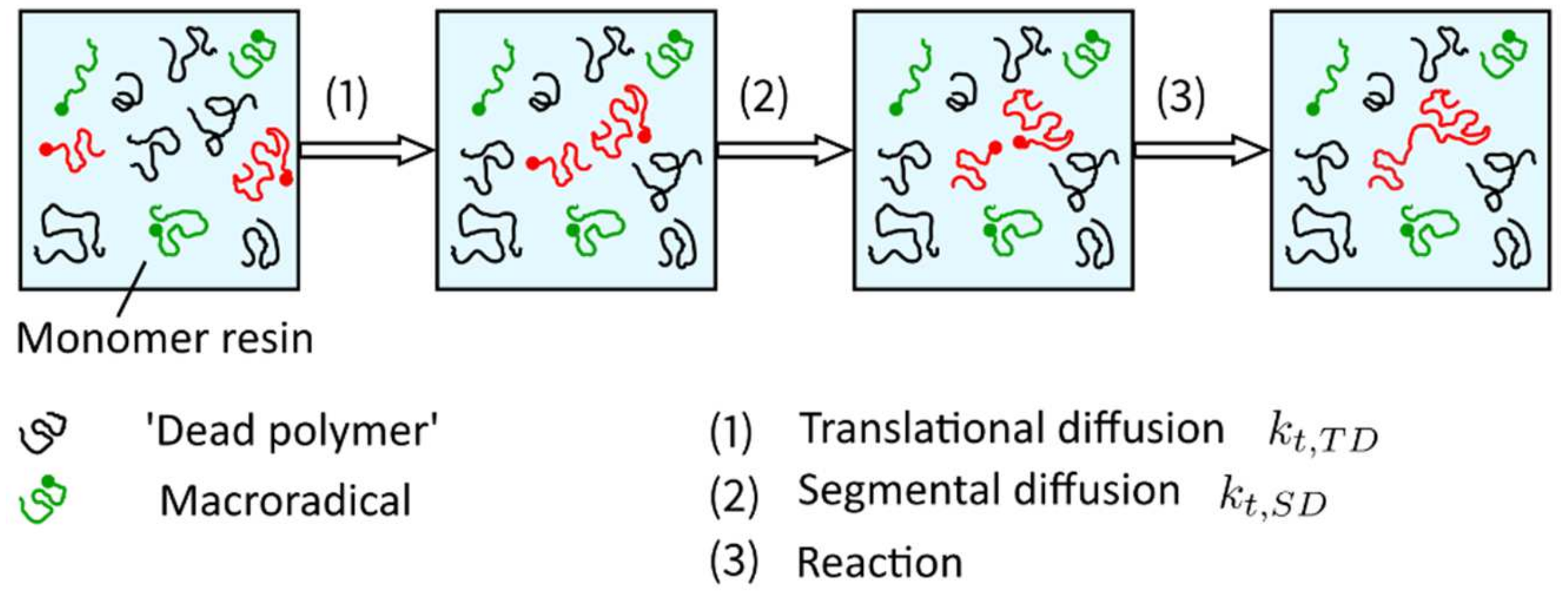


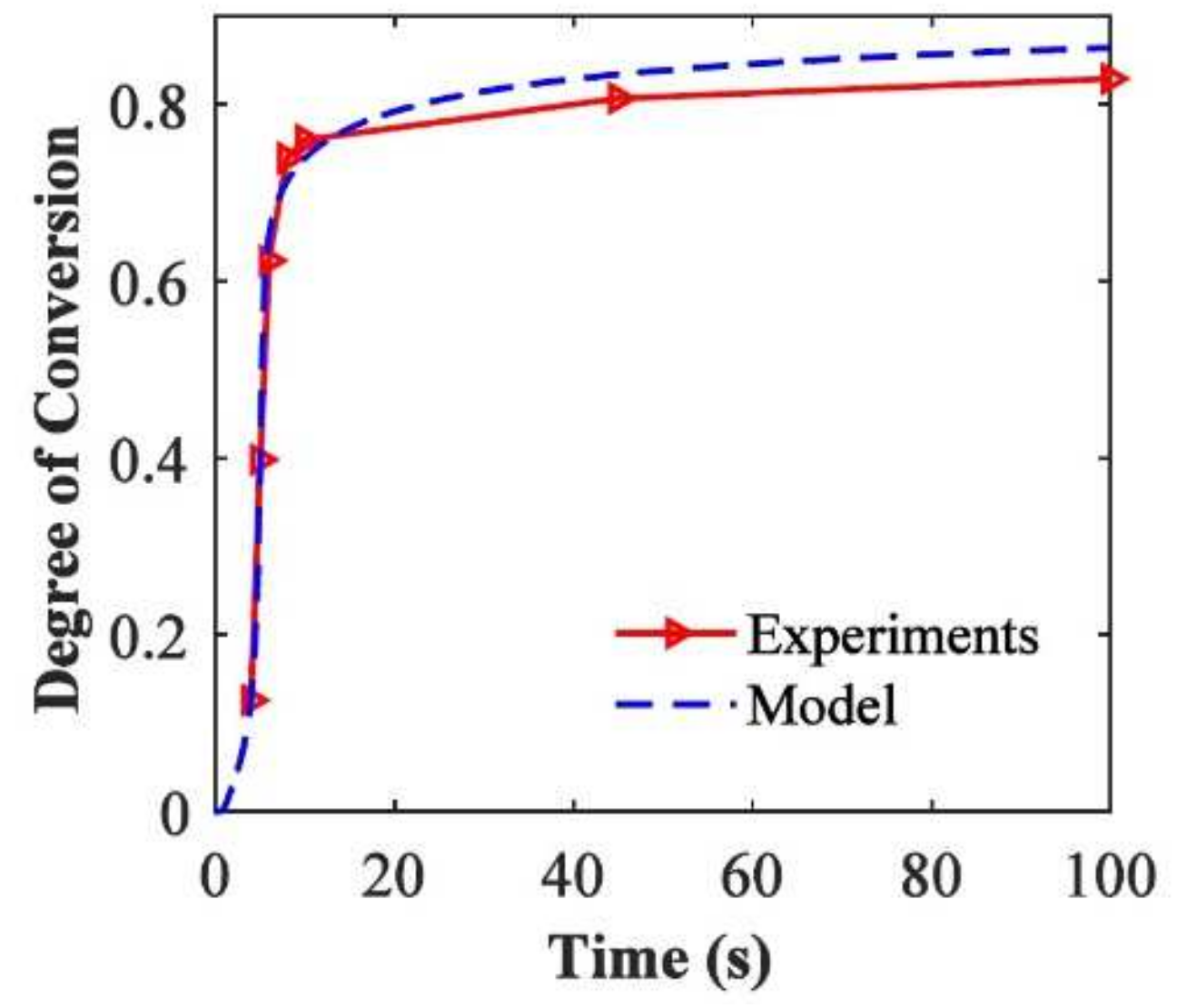
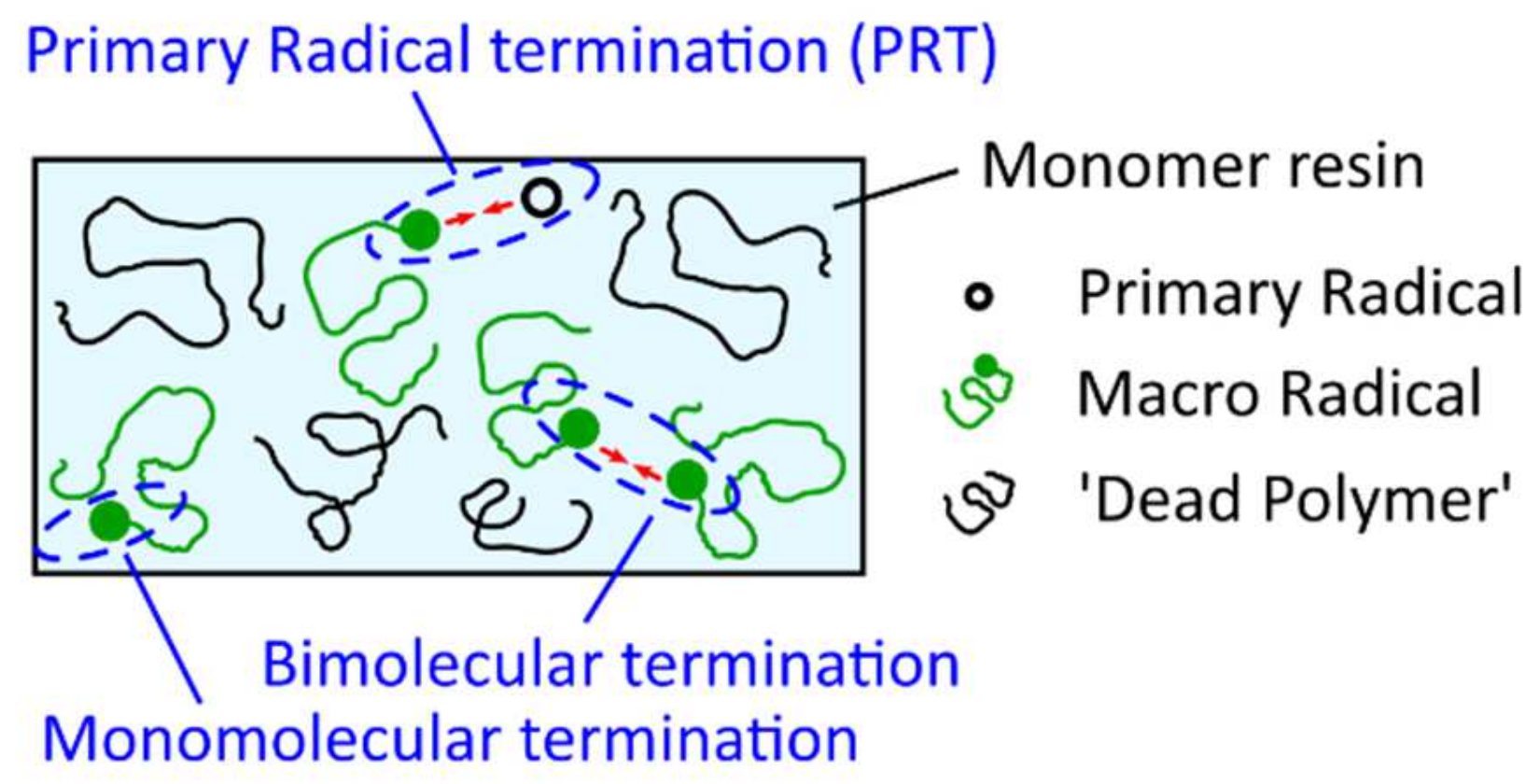


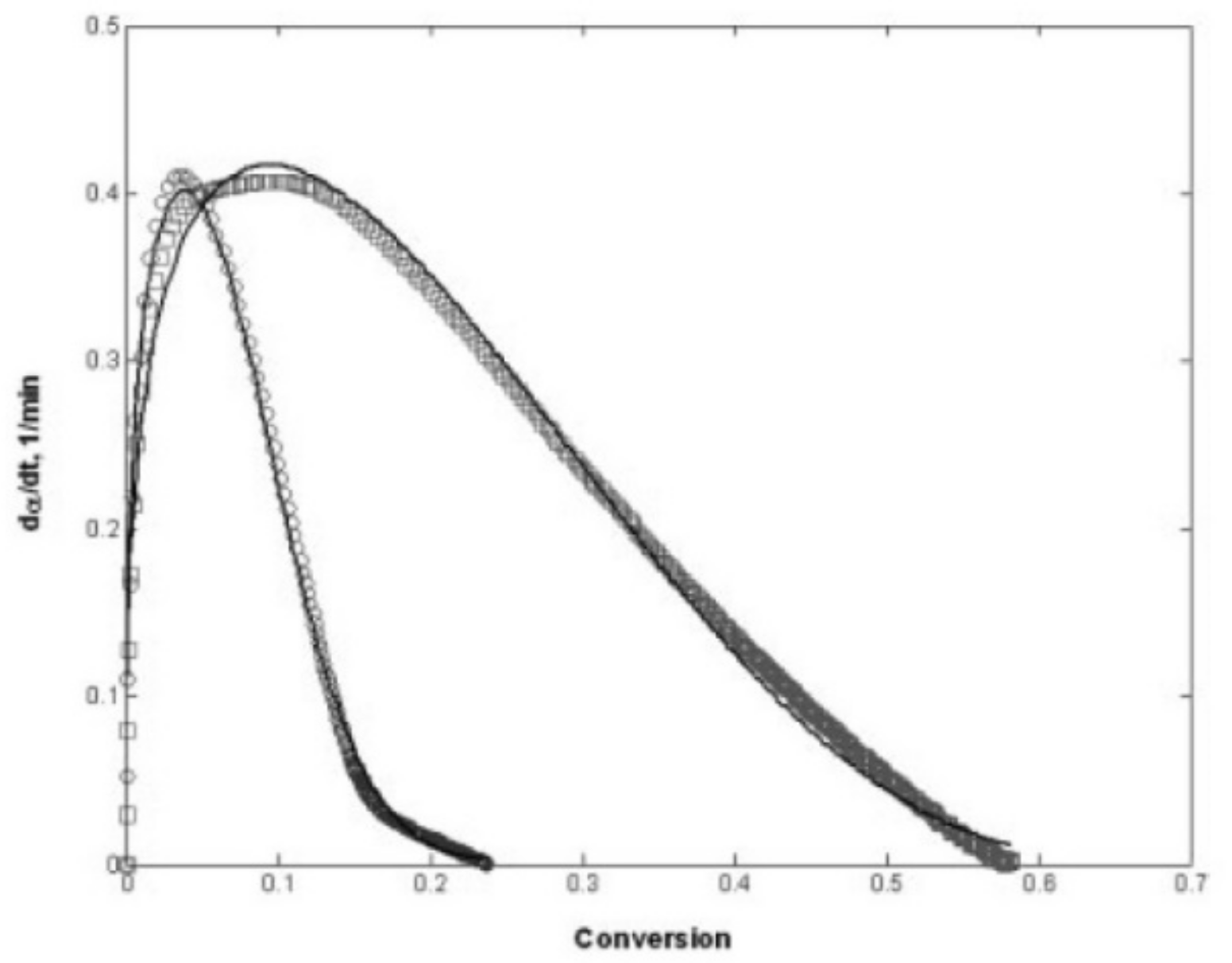



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, M.; Hirner, S.; Wiesbrock, F.; Fuchs, P. A Review on Modeling Cure Kinetics and Mechanisms of Photopolymerization. Polymers 2022, 14, 2074. https://doi.org/10.3390/polym14102074
Lang M, Hirner S, Wiesbrock F, Fuchs P. A Review on Modeling Cure Kinetics and Mechanisms of Photopolymerization. Polymers. 2022; 14(10):2074. https://doi.org/10.3390/polym14102074
Chicago/Turabian StyleLang, Margit, Stefan Hirner, Frank Wiesbrock, and Peter Fuchs. 2022. "A Review on Modeling Cure Kinetics and Mechanisms of Photopolymerization" Polymers 14, no. 10: 2074. https://doi.org/10.3390/polym14102074
APA StyleLang, M., Hirner, S., Wiesbrock, F., & Fuchs, P. (2022). A Review on Modeling Cure Kinetics and Mechanisms of Photopolymerization. Polymers, 14(10), 2074. https://doi.org/10.3390/polym14102074






