Modelling of Environmental Ageing of Polymers and Polymer Composites—Modular and Multiscale Methods
Abstract
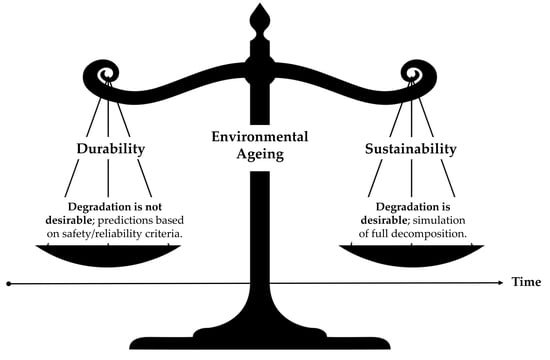
1. Introduction
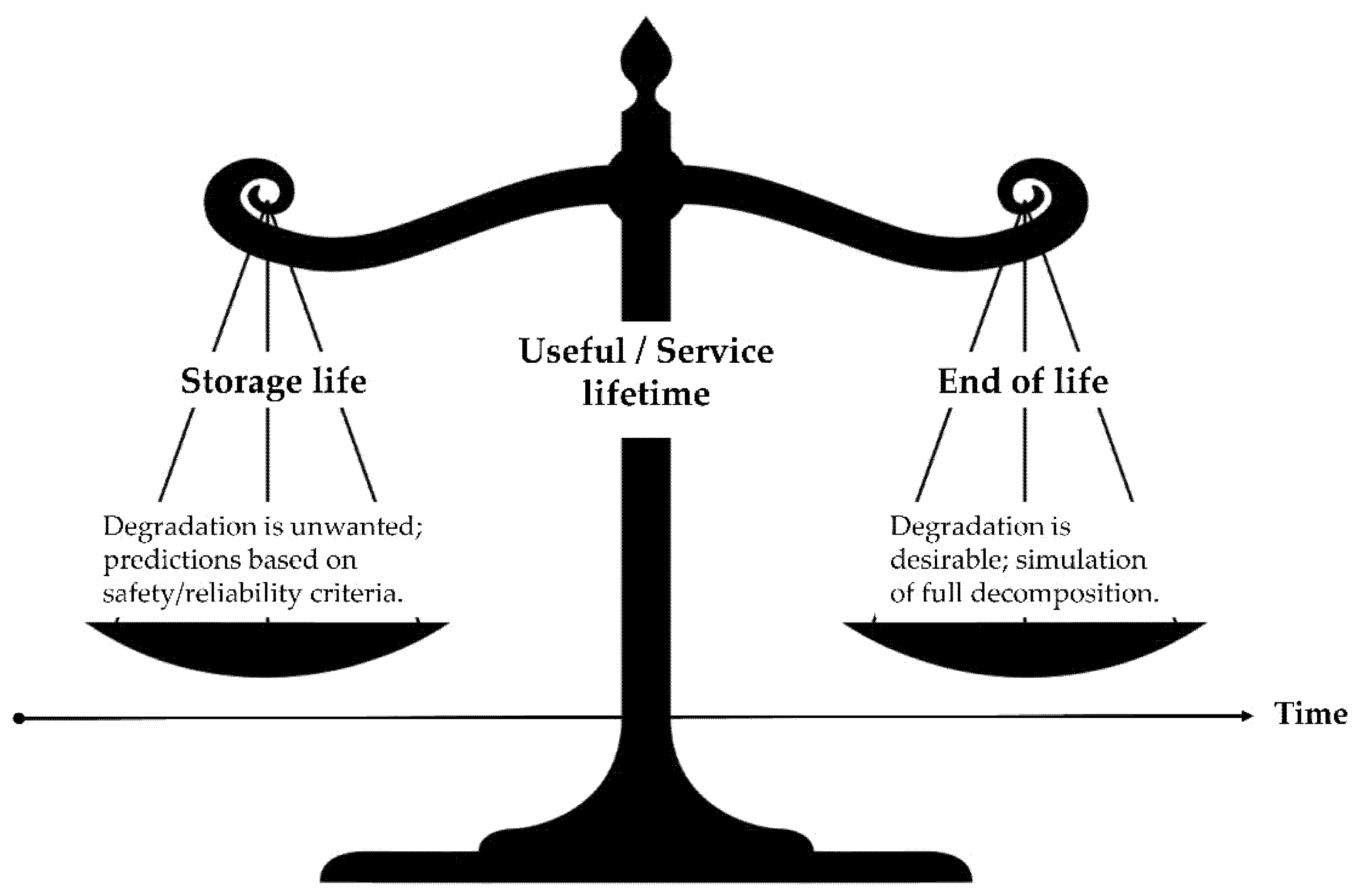
Terminology
2. Ageing and Degradation Modelling of Composite Microconstituents
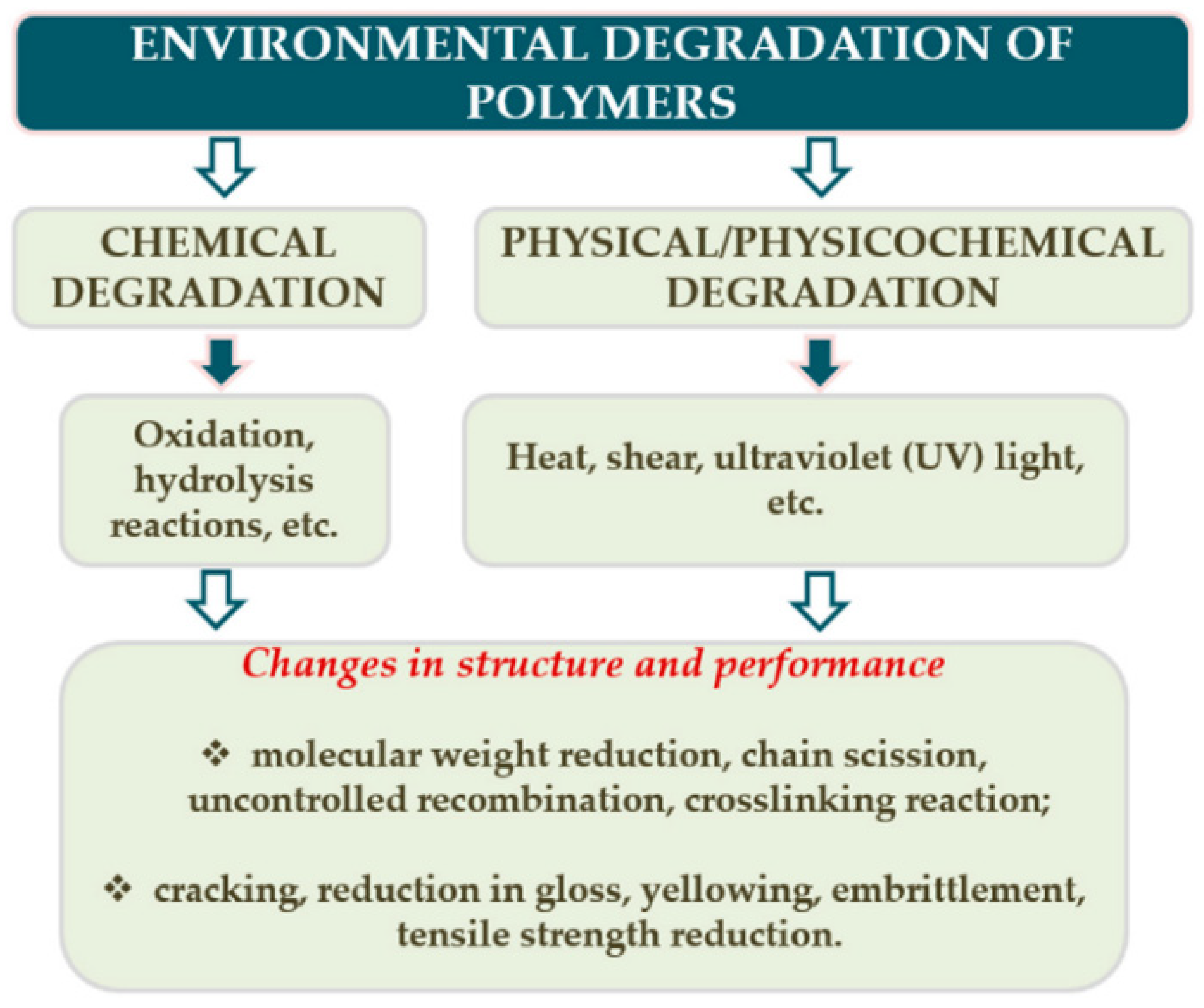
2.1. Polymer Degradation Models
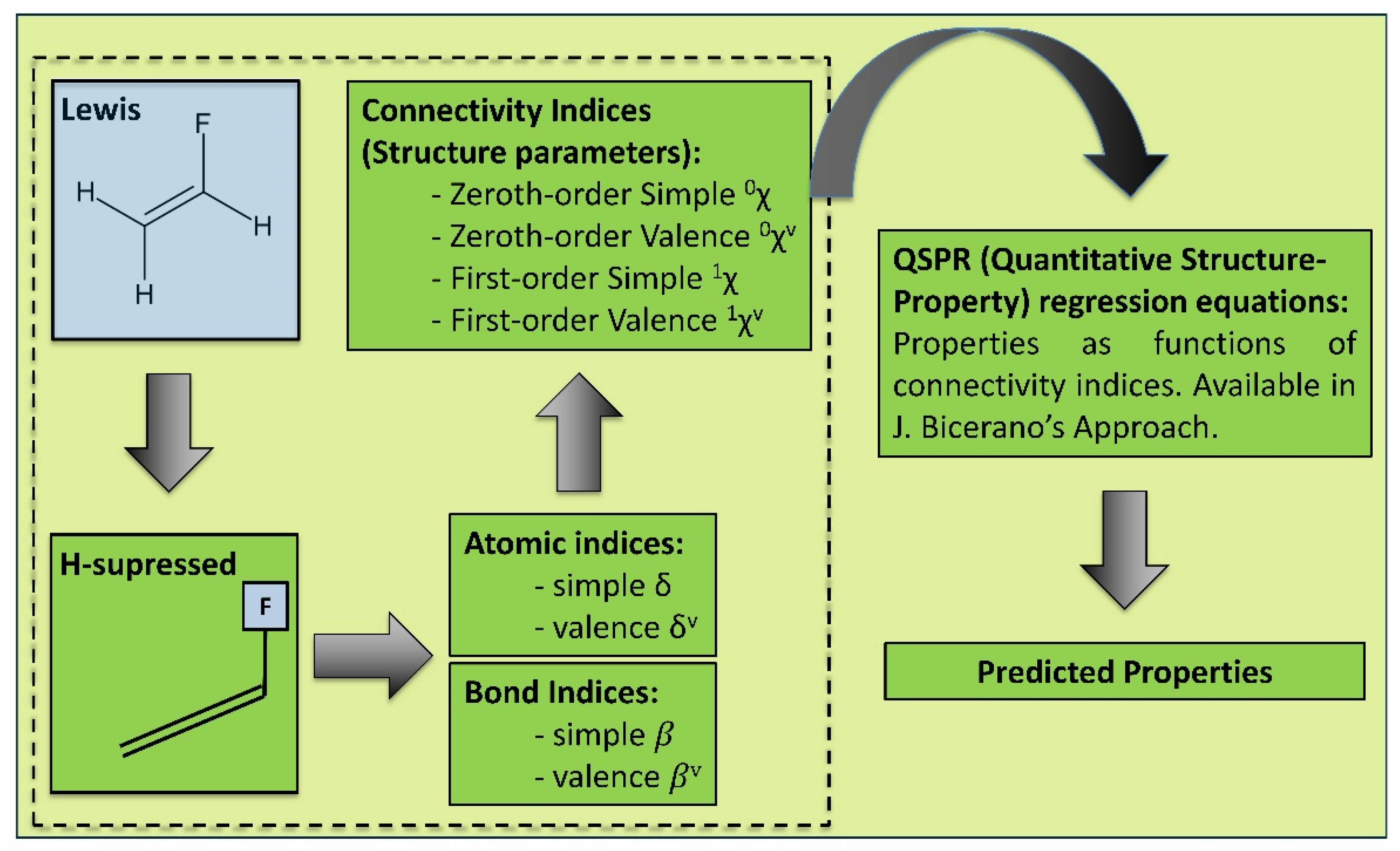
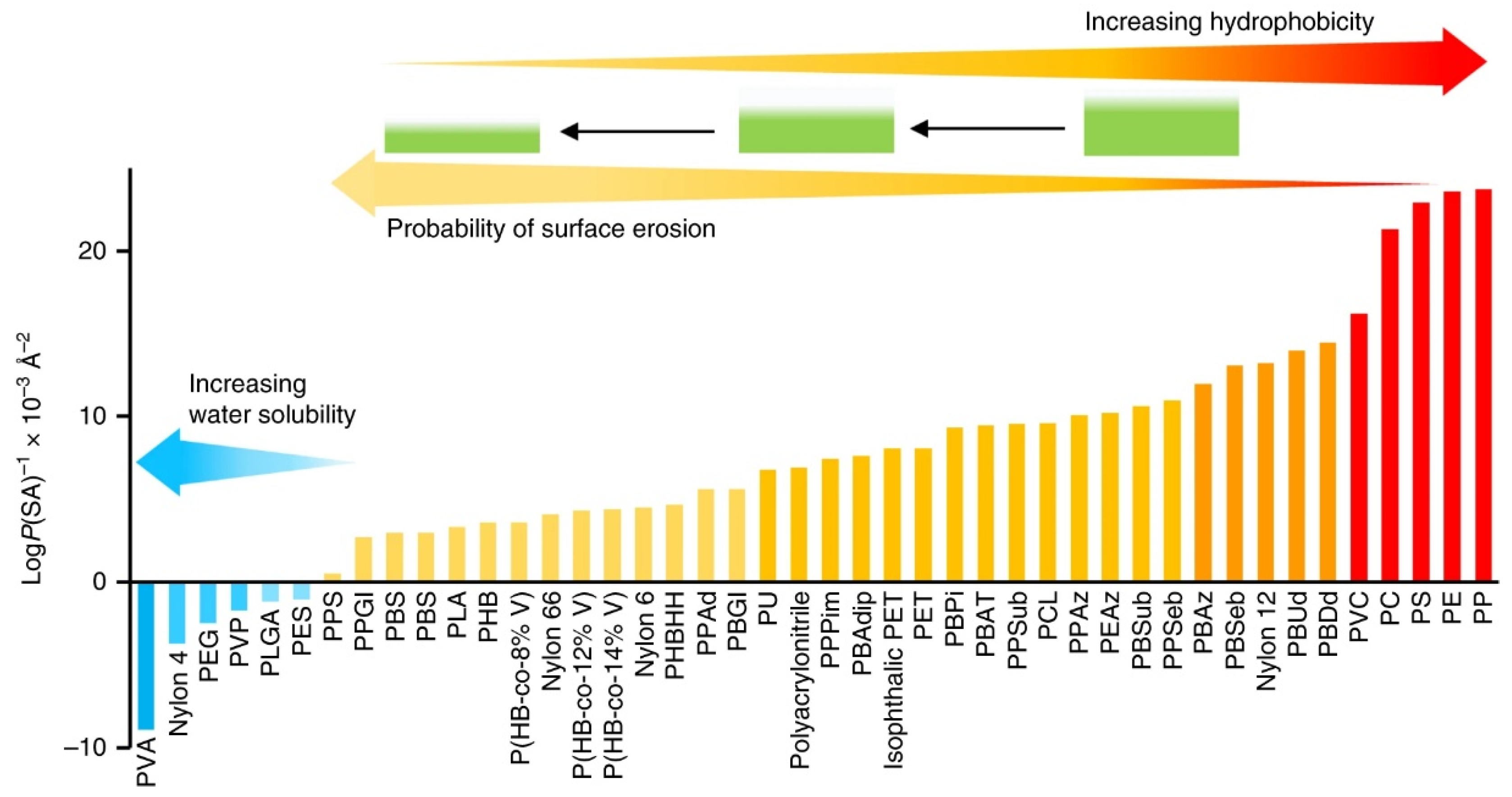
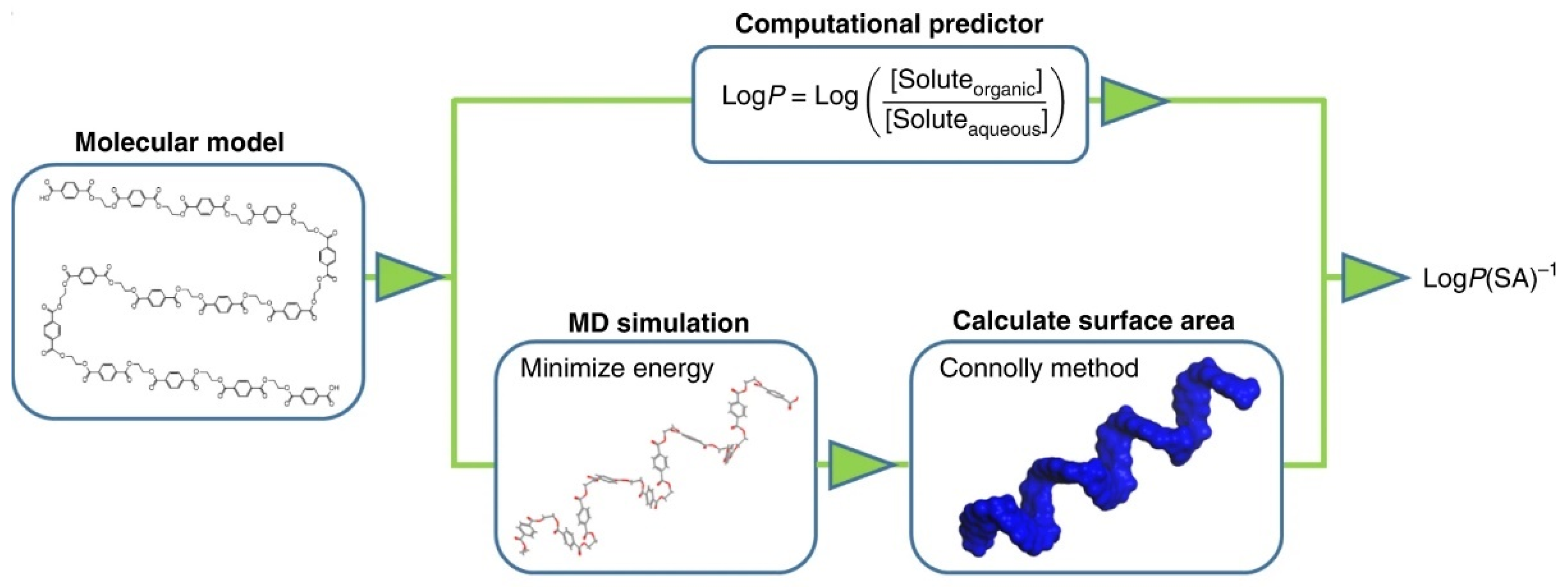
2.1.1. Predicting Polymer Properties from Chemical Structure
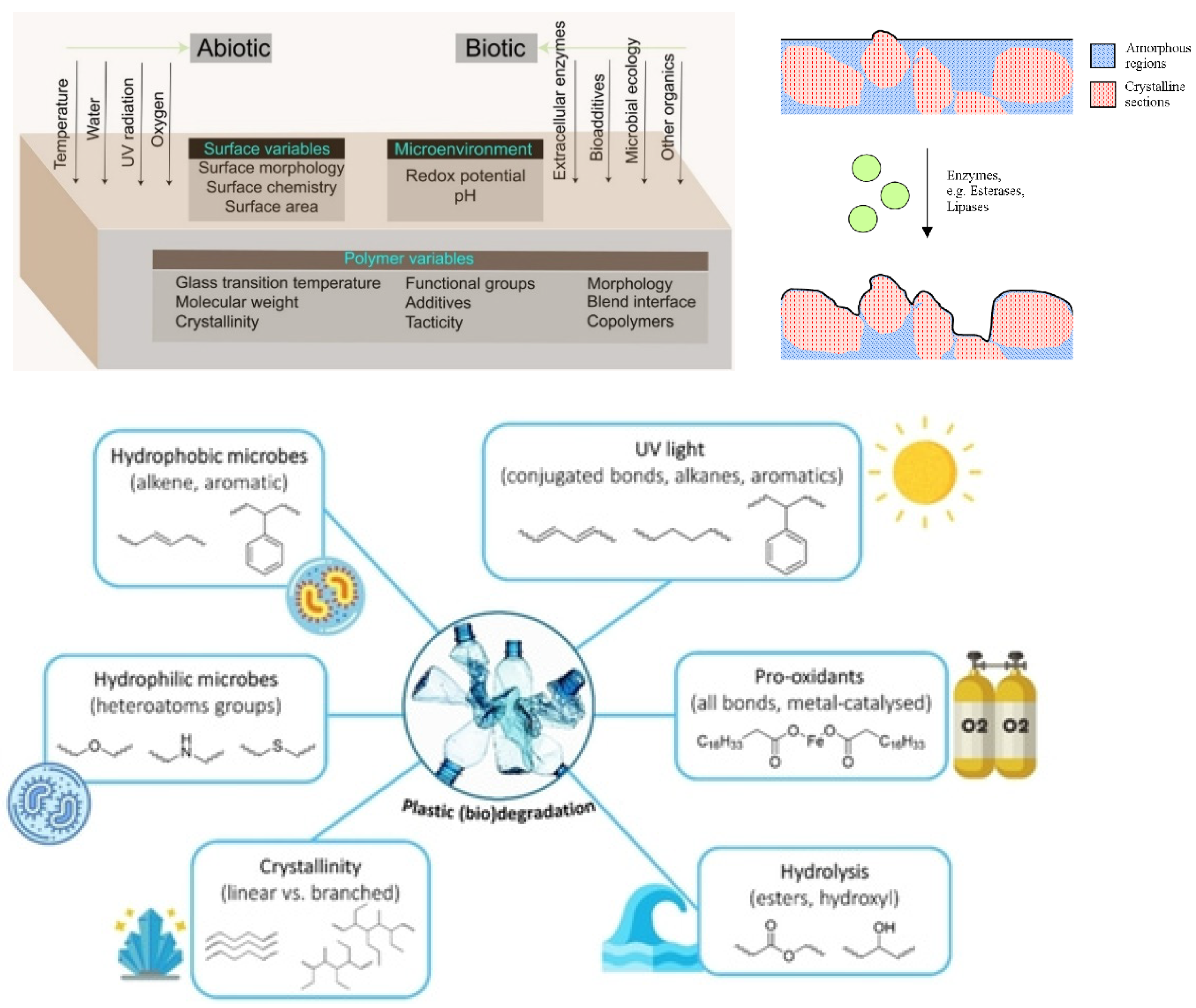
2.1.2. Degradation Mechanisms
2.1.3. Diffusion and Leaching
2.1.4. Swelling and Plasticization
2.1.5. Hydrolysis
2.2. Fibre Degradation Models
2.2.1. An Introduction to Glass Fibre Degradation
2.2.2. Chemical Reactions during Hydrolytic Degradation of Glass Fibres
2.2.3. Molecular Mechanism and Kinetics of Degradation
2.2.4. Modelling of Mass Loss and Radius Reduction of Glass Fibres
2.2.5. Modelling Crack Growth and Strength Loss of Glass Fibres
2.2.6. Carbon Fibre Degradation
2.2.7. Aramid Fibre Degradation
2.2.8. Basalt Fibre Degradation
2.2.9. Natural Fibre Degradation
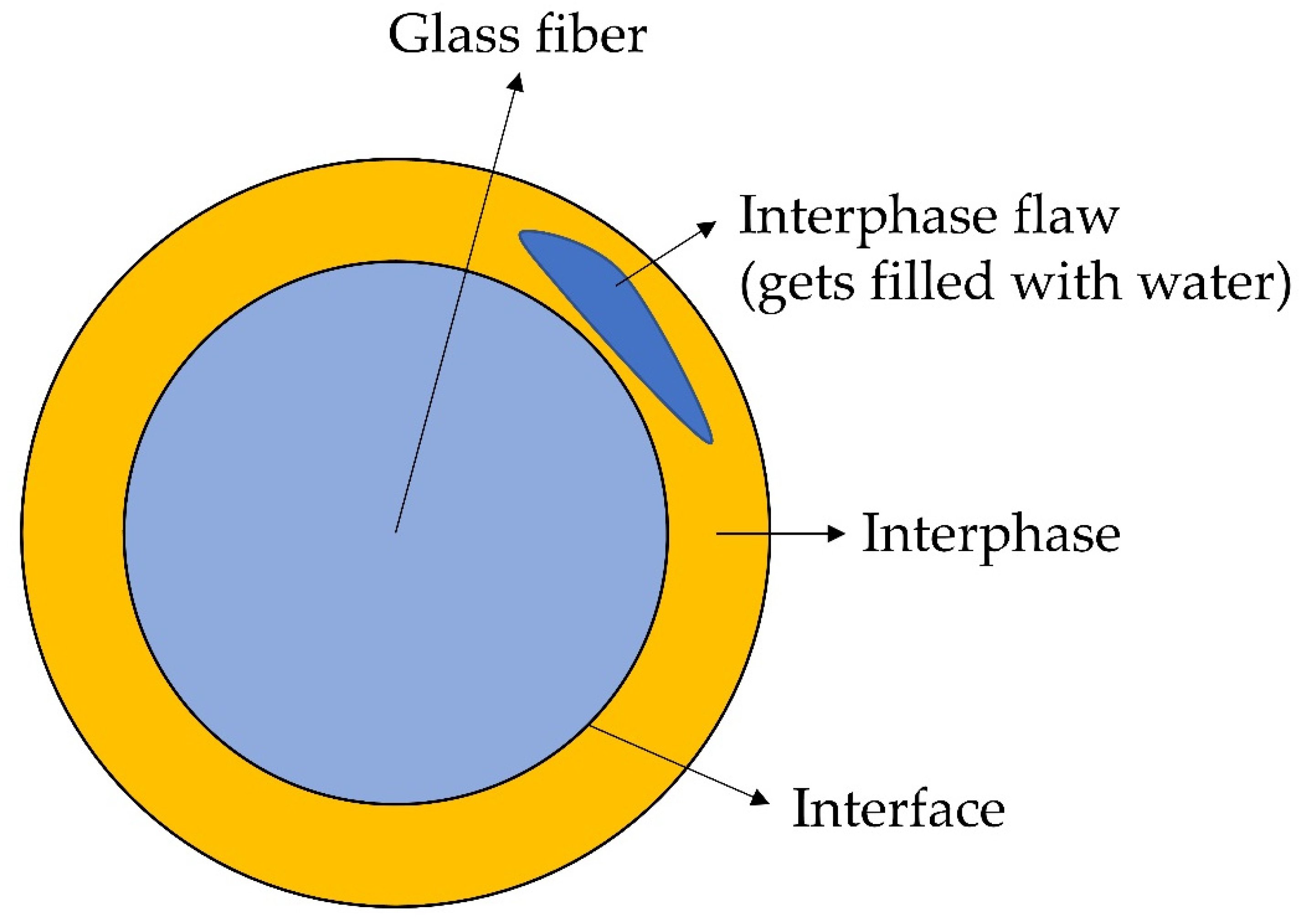
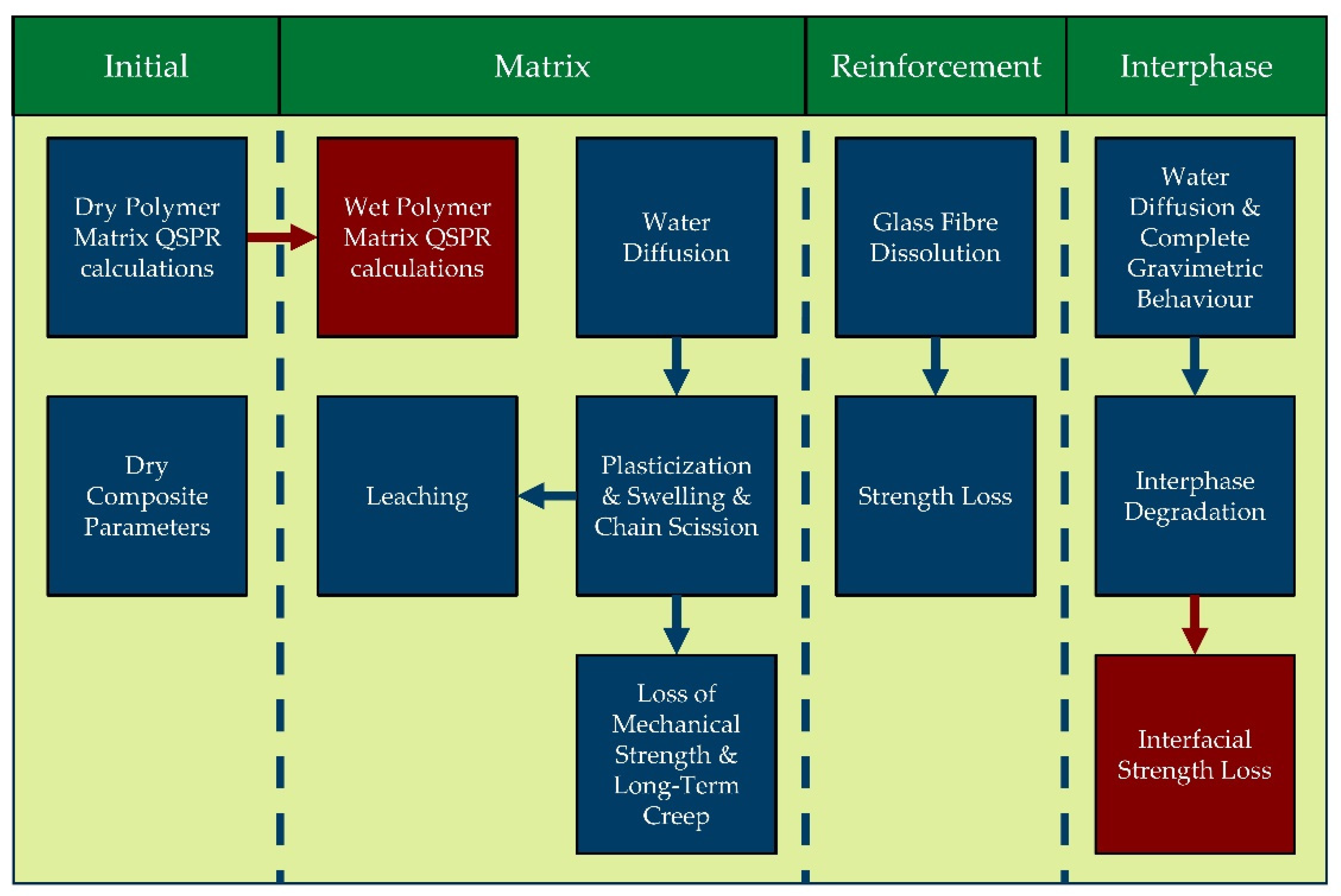
2.3. Interphase Degradation Models
3. Modular and Multiscale Approaches
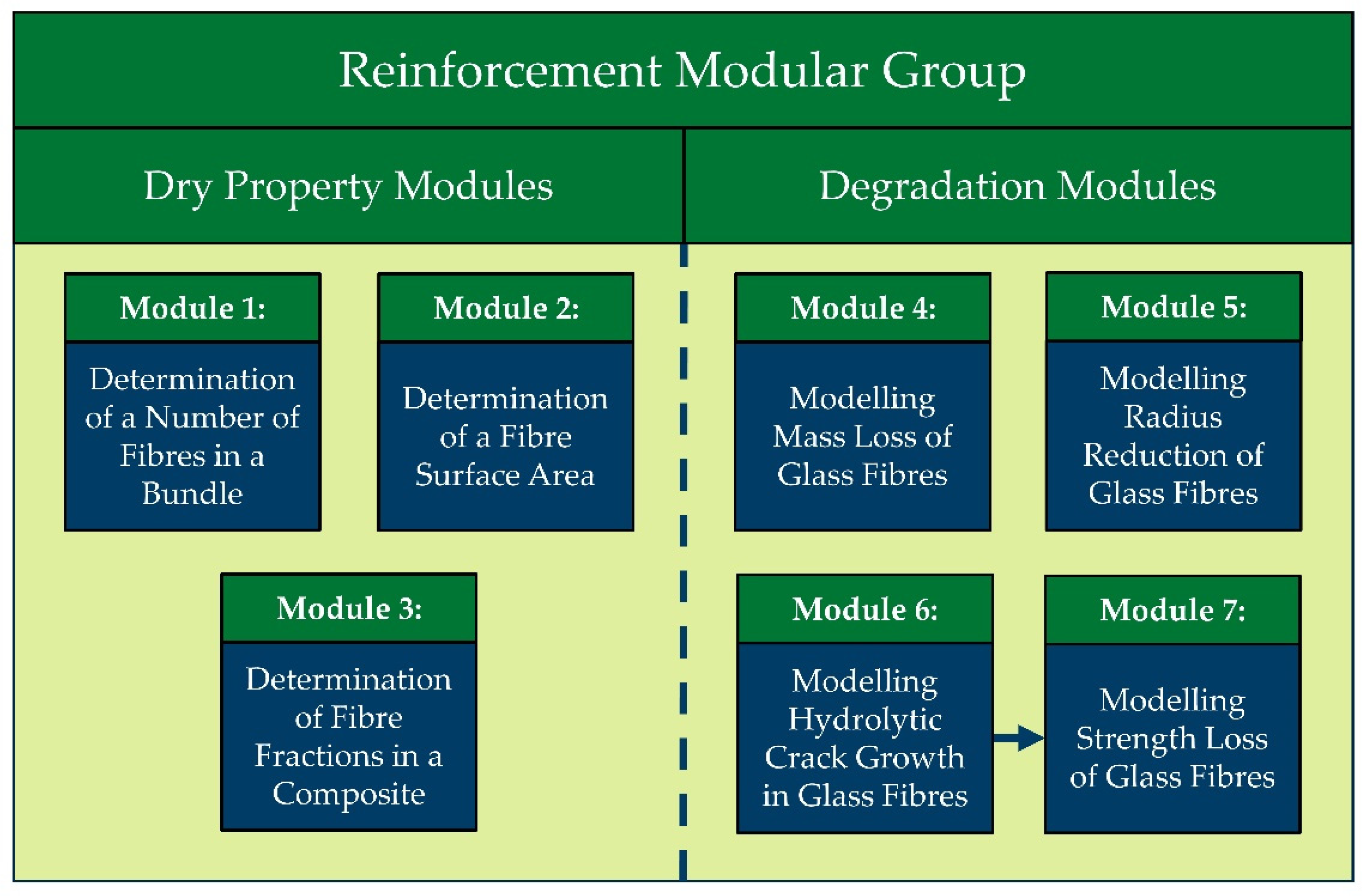
3.1. Modular Approach
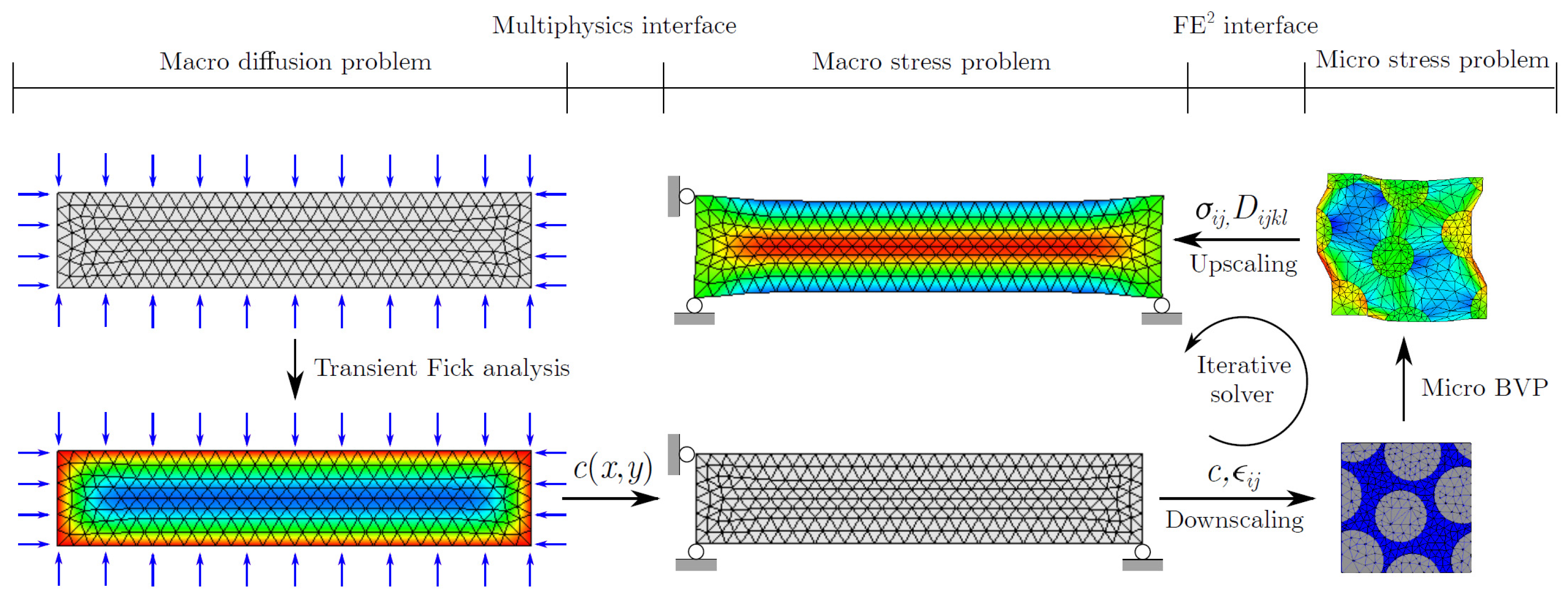
3.2. Multiscale Simulation Frameworks
3.3. Direct Numerical Simulation (DNS)
3.4. Analytical Homogenization (AH)
3.5. Numerical Homogenization (NH)
3.6. Computational Homogenization (CH)
3.7. Multiple Time Scales and Other Approaches
3.8. Accelerating Multiscale Simulations
- When performing long-term predictions of material degradation under cyclic environmental exposure, with transient simulations requiring a large number of time steps;
- As part of many-query applications such as design optimization, in which evaluating each trial design requires a complete set of high-fidelity simulations to be run;
- When employing models as part of Structural Health Monitoring (SHM) frameworks requiring inverse problems to be solved on the fly as new sensor measurements are obtained.
3.9. Model Order Reduction (MOR)
3.10. Machine Learning (ML) Approaches
4. Emerging Trends in Degradation Modelling of Biodegradable Polymers
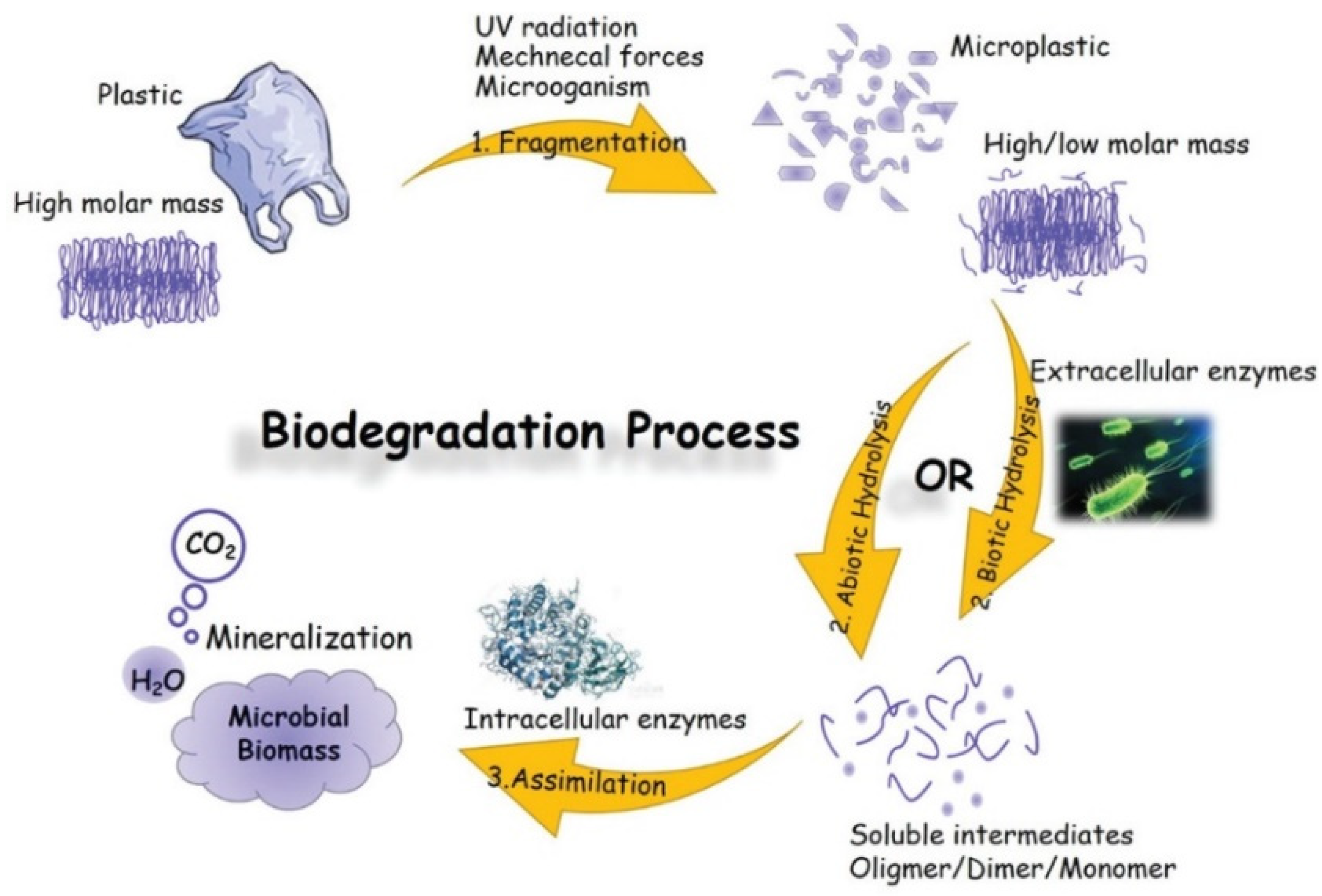
4.1. Biodegradation—An Introduction to Terms and Definitions
4.2. Data-Driven Approach to Elucidate Degradation Trends
4.3. Laboratory vs. Field Experiments: Outlook
5. Economic Role of Degradation Modelling
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Weitsman, Y.; Elahi, M. Effects of Fluids on the Deformation, Strength and Durability of Polymeric Composites—An Overview. Mech. Time Depend. Mater. 2000, 4, 107–126. [Google Scholar] [CrossRef]
- Echtermeyer, A.T.; Gagani, A.; Krauklis, A.; Mazan, T. Multiscale Modelling of Environmental Degradation—First Steps. In Durability of Composites in a Marine Environment 2. Solid Mechanics and Its Applications; Davies, P., Rajapakse, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 135–149. [Google Scholar]
- McGeorge, D.; Echtermeyer, A.; Leong, K.; Melve, B.; Robinson, M.; Fischer, K. Repair of floating offshore units using bonded fibre composite materials. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1364–1380. [Google Scholar] [CrossRef]
- Krauklis, A.E. Environmental Durability of Composite Materials: Analytical Modelling Toolbox. In Proceedings of the Aachen Reinforced, Symposium, Aachen, Germany, 11–13 May 2021. [Google Scholar]
- Siemens (Munich, Germany). Siemens case study. Personal communication, 2021. [Google Scholar]
- Lee, H.-S.; Rhee, S.Y.; Yoon, J.-H.; Yoo, J.-T.; Min, K.J. Establishment of Aerospace Composite Materials Data Center for Qualification. Compos. Res. 2015, 28, 402–407. [Google Scholar] [CrossRef][Green Version]
- Schafrik, R. Technology Transition in Aerospace Industry. In Proceedings of the Workshop on Accelerating Technology Transition, National Research Council, Washington, DC, USA, November 2003. [Google Scholar]
- Hagnell, M.; Kumaraswamy, S.; Nyman, T.; Åkermo, M. From aviation to automotive—A study on material selection and its implication on cost and weight efficient structural composite and sandwich designs. Heliyon 2020, 6, e03716. [Google Scholar] [CrossRef]
- Offshore Energy. DNV GL: Two New JIPs Have Potential to Save Over $10M in Costs. Available online: https://www.offshore-energy.biz/dnv-gl-two-new-jips-have-potential-to-save-over-10m-in-costs/ (accessed on 10 November 2021).
- Bortolotti, P.; Berry, D.S.; Murray, R.; Gaertner, E.; Jenne, D.S.; Damiani, R.R.; EBarter, G.; Dykes, K.L. A Detailed Wind Turbine Blade Cost Model; Technical Report for National Renewable Energy Laboratory: Golden, CO, USA, 2019.
- Krauklis, A.E. Environmental Aging of Constituent Materials in Fiber-Reinforced Polymer Composites. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2019. [Google Scholar]
- Starkova, O.; Gagani, A.I.; Karl, C.W.; Rocha, I.B.C.M.; Burlakovs, J.; Krauklis, A.E. Modelling of Environmental Ageing of Polymers and Polymer Composites—Durability Prediction Methods. Polymers, 2021; to be submitted. [Google Scholar]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Long-Term Hydrolytic Degradation of the Sizing-Rich Composite Interphase. Coatings 2019, 9, 263. [Google Scholar] [CrossRef]
- ASTM. D883—Standard Terminology Relating to Plastics; ASTM International: Conshohocken, PA, USA, 2020. [Google Scholar]
- Chamas, A.; Moon, H.; Zheng, J.; Qiu, Y.; Tabassum, T.; Jang, J.H.; Abu-Omar, M.M.; Scott, S.L.; Suh, S. Degradation Rates of Plastics in the Environment. ACS Sustain. Chem. Eng. 2020, 8, 3494–3511. [Google Scholar] [CrossRef]
- Plota, A.; Masek, A. Lifetime Prediction Methods for Degradable Polymeric Materials—A Short Review. Materials 2020, 13, 4507. [Google Scholar] [CrossRef]
- Göpferich, A. Mechanisms of polymer degradation and erosion. Biomaterials 1996, 17, 103–114. [Google Scholar] [CrossRef]
- Wang, G.-X.; Huang, D.; Ji, J.-H.; Völker, C.; Wurm, F.R. Seawater-Degradable Polymers—Fighting the Marine Plastic Pollution. Adv. Sci. 2020, 8, 2001121. [Google Scholar] [CrossRef]
- Ogawa, R. Marine-Degradable Plastics Progressing for Popularization under New International Standards Backdrop to the Publication of the New International Standard for Evaluation of Marine Degradability of Plastics; Mitsui & Co. Global Strategic Studies Institute: Tokyo, Japan, 2020; pp. 1–9. [Google Scholar]
- ISO 22766:2020; Plastics—Determination of the Degree of Disintegration of Plastic Materials in Marine Habitats under Real Field Conditions. ISO: Geneva, Switzerland, 2020.
- ISO 22403:2020; Plastics—Assessment of the Intrinsic Biodegradability of Materials Exposed to Marine Inocula under Meso-Philic Aerobic Laboratory Conditions—Test Methods and Requirements. ISO: Geneva, Switzerland, 2020.
- SAPEA Report, Biodegradability of Plastics in the Open Environment. Available online: https://www.sapea.info/topics/biodegradability-of-plastics (accessed on 15 December 2020).
- Lott, C.; Eich, A.; Makarow, D.; Unger, B.; van Eekert, M.; Schuman, E.; Reinach, M.S.; Lasut, M.T.; Weber, M. Half-Life of Biodegradable Plastics in the Marine Environment Depends on Material, Habitat, and Climate Zone. Front. Mar. Sci. 2021, 8, 426. [Google Scholar] [CrossRef]
- Ghosh, K.; Jones, B.H. Roadmap to Biodegradable Plastics—Current State and Research Needs. ACS Sustain. Chem. Eng. 2021, 9, 6170–6187. [Google Scholar] [CrossRef]
- ISO 14855-1:2012; Determination of the Ultimate Aerobic Biodegradability of Plastic Materials under Controlled Composting Conditions—Method by Analysis of Evolved Carbon Dioxide—Part 1: General Method and Part 2: Gravimetric Measurement of Carbon Dioxide Evolved in a Laboratory-Scale Test. ISO: Geneva, Switzerland, 2012.
- Dřímal, P.; Hoffmann, J.; Družbík, M. Evaluating the aerobic biodegradability of plastics in soil environments through GC and IR analysis of gaseous phase. Polym. Test. 2007, 26, 729–741. [Google Scholar] [CrossRef]
- Kunioka, M.; Ninomiya, F.; Funabashi, M. Novel evaluation method of biodegradabilities for oil-based polycaprolactone by naturally occurring radiocarbon-14 concentration using accelerator mass spectrometry based on ISO 14855-2 in controlled compost. Polym. Degrad. Stab. 2007, 92, 1279–1288. [Google Scholar] [CrossRef]
- Di Bartolo, A.; Infurna, G.; Dintcheva, N. A Review of Bioplastics and Their Adoption in the Circular Economy. Polymers 2021, 13, 1229. [Google Scholar] [CrossRef] [PubMed]
- Degli Innocenti, F.; Breton, T. Intrinsic Biodegradability of Plastics and Ecological Risk in the Case of Leakage. ACS Sustain. Chem. Eng. 2020, 8, 9239–9249. [Google Scholar] [CrossRef]
- Ncube, L.; Ude, A.; Ogunmuyiwa, E.; Zulkifli, R.; Beas, I. An Overview of Plastic Waste Generation and Management in Food Packaging Industries. Recycling 2021, 6, 12. [Google Scholar] [CrossRef]
- Grimaldo, E.; Herrmann, B.; Jacques, N.; Kubowicz, S.; Cerbule, K.; Su, B.; Larsen, R.; Vollstad, J. The effect of long-term use on the catch efficiency of biodegradable gillnets. Mar. Pollut. Bull. 2020, 161, 111823. [Google Scholar] [CrossRef] [PubMed]
- Deroiné, M.; Pillin, I.; Le Maguer, G.; Chauvel, M.; Grohens, Y. Development of new generation fishing gear: A resistant and biodegradable monofilament. Polym. Test. 2018, 74, 163–169. [Google Scholar] [CrossRef]
- ISO 8930:2021; General Principles on Reliability for Structures—Vocabulary. ISO: Geneva, Switzerland, 2021.
- ISO 1986:2021; Test Conditions for Surface Grinding Machines with Horizontal Grinding Wheel Spindle and Reciprocating Table —Testing of the Accuracy—Part 1: Machines with a Table Length of Up to 1600 mm. ISO: Geneva, Switzerland, 2021.
- White, J.R. Polymer ageing: Physics, chemistry, or engineering? Time to reflect. Comptes Rendus Chim. 2006, 9, 1396–1408. [Google Scholar] [CrossRef]
- Badia, J.; Gil-Castell, O.; Ribes-Greus, A. Long-term properties and end-of-life of polymers from renewable resources. Polym. Degrad. Stab. 2017, 137, 35–57. [Google Scholar] [CrossRef]
- Miyano, Y.; Nakada, M.; Cai, H. Formulation of Long-term Creep and Fatigue Strengths of Polymer Composites Based on Accelerated Testing Methodology. J. Compos. Mater. 2008, 42, 1897–1919. [Google Scholar] [CrossRef]
- Bicerano, J. Prediction of Polymer Properties; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Porter, D. Group Theory Book Group Interaction Modelling of Polymer Properties; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Van Krevelen, D.W.; Te Nijenhuis, K. Properties of Polymers: Their Correlation with Chemical Structure, Their Numerical Estimation and Prediction from Additive Group Contributions, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Bartók, A.P.; Kondor, R.; Csányi, G. On representing chemical environments. Phys. Rev. B 2013, 87, 184115. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Sild, S.; Lobanov, V.; Karelson, M. Quantitative Structure−Property Relationship (QSPR) Correlation of Glass Transition Temperatures of High Molecular Weight Polymers. J. Chem. Inf. Comput. Sci. 1998, 38, 300–304. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Akulichev, A.G.; Gagani, A.; Echtermeyer, A.T. Time—Temperature—Plasticization Superposition Principle: Predicting Creep of a Plasticized Epoxy. Polymers 2019, 11, 1848. [Google Scholar] [CrossRef]
- Wang, M.; Xu, X.; Ji, J.; Yang, Y.; Shen, J.; Ye, M. The hygrothermal aging process and mechanism of the novolac epoxy resin. Compos. Part B Eng. 2016, 107, 1–8. [Google Scholar] [CrossRef]
- Clancy, T.; Frankland, S.; Hinkley, J.; Gates, T. Molecular modeling for calculation of mechanical properties of epoxies with moisture ingress. Polymer 2009, 50, 2736–2742. [Google Scholar] [CrossRef]
- Krauklis, A.; Gagani, A.I.; Echtermeyer, A.T. Hygrothermal Aging of Amine Epoxy: Reversible Static and Fatigue Properties. Open Eng. 2018, 8, 447–454. [Google Scholar] [CrossRef]
- Xiao, G.; Shanahan, M. Swelling of DGEBA/DDA epoxy resin during hygrothermal ageing. Polymer 1998, 39, 3253–3260. [Google Scholar] [CrossRef]
- Rocha, I.; Raijmaekers, S.; Nijssen, R.; van der Meer, F.; Sluys, B. Hygrothermal ageing behaviour of a glass/epoxy composite used in wind turbine blades. Compos. Struct. 2017, 174, 110–122. [Google Scholar] [CrossRef]
- Coutinho, I.; Lima, A.M.; Fernandes, F.B.; Ramos, A. Studies on Degradation of Epoxy Resins Used for Conservation of Glass. In Proceedings of the Holding It All Together, Ancient and Modern Approaches to Joining, Repair and Consolidation; Archetype Publications Ltd.: London, UK, 2008; pp. 21–22. [Google Scholar]
- Krauklis, A.E.; Echtermeyer, A.T. Mechanism of Yellowing: Carbonyl Formation during Hygrothermal Aging in a Common Amine Epoxy. Polymers 2018, 10, 1017. [Google Scholar] [CrossRef]
- Starkova, O.; Gaidukovs, S.; Platnieks, O.; Barkane, A.; Garkusina, K.; Palitis, E.; Grase, L. Water absorption and hydrothermal ageing of epoxy adhesives reinforced with amino-functionalized graphene oxide nanoparticles. Polym. Degrad. Stab. 2021, 191, 109670. [Google Scholar] [CrossRef]
- Celina, M.C.; Dayile, A.R.; Quintana, A. A perspective on the inherent oxidation sensitivity of epoxy materials. Polymer 2013, 54, 3290–3296. [Google Scholar] [CrossRef]
- Down, J.L. The Yellowing of Epoxy Resin Adhesives: Report on High-Intensity Light Aging. Stud. Conserv. 1986, 31, 159. [Google Scholar] [CrossRef]
- Ernault, E.; Richaud, E.; Fayolle, B. Thermal-oxidation of epoxy/amine followed by glass transition temperature changes. Polym. Degrad. Stab. 2017, 138, 82–90. [Google Scholar] [CrossRef]
- Gilev, V.G.; Rusakov, S.V.; Chudinov, V.S.; Rakhmanov, A.Y.; Kondyurin, A.V. Modeling the Curing Kinetics of an Epoxy Binder with Disturbed Stoichiometry for a Composite Material of Aerospace Purpose. Mech. Compos. Mater. 2021, 57, 361–372. [Google Scholar] [CrossRef]
- Gagani, A.; Fan, Y.; Muliana, A.H.; Echtermeyer, A.T. Micromechanical modeling of anisotropic water diffusion in glass fiber epoxy reinforced composites. J. Compos. Mater. 2017, 52, 2321–2335. [Google Scholar] [CrossRef]
- Gagani, A.I.; Krauklis, A.E.; Echtermeyer, A.T. Orthotropic fluid diffusion in composite marine structures. Experimental procedure, analytical and numerical modelling of plates, rods, and pipes. Compos. Part A Appl. Sci. Manuf. 2018, 115, 196–205. [Google Scholar] [CrossRef]
- Bonniau, P.; Bunsell, A.R. Water Absorption by Glass Fibre Reinforced Epoxy Resin. In Composite Structures; Marshall, I.H., Ed.; Springer: Dordrecht, The Netherlands, 1981; pp. 92–105. [Google Scholar]
- Augl, J.M.; Berger, A.E. The Effect of Moisture on Carbon Fiber Reinforced Epoxy Composites. 1. Diffusion; Technical Report NSWC/WOL/TR–76–7; White Oak Laboratory: Silver Spring, MD, USA, 1976. [Google Scholar]
- Toscano, A.; Pitarresi, G.; Scafidi, M.; Di Filippo, M.; Spadaro, G.; Alessi, S. Water diffusion and swelling stresses in highly crosslinked epoxy matrices. Polym. Degrad. Stab. 2016, 133, 255–263. [Google Scholar] [CrossRef]
- Maggana, C.; Pissis, P. Water sorption and diffusion studies in an epoxy resin system. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 1165–1182. [Google Scholar] [CrossRef]
- Min, K.; Cuiffi, J.D.; Mathers, R.T. Ranking environmental degradation trends of plastic marine debris based on physical properties and molecular structure. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef]
- Morel, E.; Bellenger, V.; Verdu, J. Structure-water absorption relationships for amine-cured epoxy resins. Polymer 1985, 26, 1719–1724. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1956. [Google Scholar]
- Dana, H.R.; Perronnet, A.; Freour, S.; Casari, P.; Jacquemin, F. Identification of moisture diffusion parameters in organic matrix composites. J. Compos. Mater. 2013, 47, 1081–1092. [Google Scholar] [CrossRef]
- Starkova, O.; Aniskevich, K.; Sevcenko, J. Long-term moisture absorption and durability of FRP pultruded rebars. Mater. Today Proc. 2020, 34, 36–40. [Google Scholar] [CrossRef]
- Yin, X.; Liu, Y.; Miao, Y.; Xian, G. Water Absorption, Hydrothermal Expansion, and Thermomechanical Properties of a Vinylester Resin for Fiber-Reinforced Polymer Composites Subjected to Water or Alkaline Solution Immersion. Polymers 2019, 11, 505. [Google Scholar] [CrossRef] [PubMed]
- Tsai, Y.; Bosze, E.; Barjasteh, E.; Nutt, S. Influence of hygrothermal environment on thermal and mechanical properties of carbon fiber/fiberglass hybrid composites. Compos. Sci. Technol. 2009, 69, 432–437. [Google Scholar] [CrossRef]
- Arnold, J.; Alston, S.; Korkees, F. An assessment of methods to determine the directional moisture diffusion coefficients of composite materials. Compos. Part A Appl. Sci. Manuf. 2013, 55, 120–128. [Google Scholar] [CrossRef]
- Korkees, F.; Alston, S.; Arnold, C. Directional diffusion of moisture into unidirectional carbon fiber/epoxy Composites: Experiments and modeling. Polym. Compos. 2017, 39, E2305–E2315. [Google Scholar] [CrossRef]
- Shen, C.-H.; Springer, G.S. Moisture Absorption and Desorption of Composite Materials. J. Compos. Mater. 1976, 10, 2–20. [Google Scholar] [CrossRef]
- Pan, Y.; Xian, G.; Li, H. Numerical modeling of moisture diffusion in a unidirectional fiber-reinforced polymer composite. Polym. Compos. 2017, 40, 401–413. [Google Scholar] [CrossRef]
- Aiello, M.A.; Leone, M.; Aniskevich, A.N.; Starkova, O.A. Moisture Effects on Elastic and Viscoelastic Properties of CFRP Rebars and Vinylester Binder. J. Mater. Civ. Eng. 2006, 18, 686–691. [Google Scholar] [CrossRef]
- Loos, A.C.; Springer, G.S. Environmental Effects on Composite Materials; Technomic Pub. Co.: Lancaster, UK, 1988. [Google Scholar]
- Di Filippo, M.; Alessi, S.; Pitarresi, G.; Sabatino, M.A.; Zucchelli, A.; Dispenza, C. Hydrothermal aging of carbon reinforced epoxy laminates with nanofibrous mats as toughening interlayers. Polym. Degrad. Stab. 2016, 126, 188–195. [Google Scholar] [CrossRef]
- Starkova, O.; Chandrasekaran, S.; Schnoor, T.; Sevcenko, J.; Schulte, K. Anomalous water diffusion in epoxy/carbon nano-particle composites. Polym. Degrad. Stab. 2019, 164, 127–135. [Google Scholar] [CrossRef]
- Guloglu, G.E.; Altan, M.C. Moisture Absorption of Carbon/Epoxy Nanocomposites. J. Compos. Sci. 2020, 4, 21. [Google Scholar] [CrossRef]
- Guloglu, G.E.; Hamidi, Y.K.; Altan, M.C. Moisture absorption of composites with interfacial storage. Compos. Part A Appl. Sci. Manuf. 2020, 134, 105908. [Google Scholar] [CrossRef]
- De Brito, M.K.T.; Dos Santos, W.R.G.; Correia, B.R.D.B.; De Queiroz, R.A.; Tavares, F.V.D.S.; Neto, G.L.D.O.; De Lima, A.G.B. Moisture Absorption in Polymer Composites Reinforced with Vegetable Fiber: A Three-Dimensional Investigation via Langmuir Model. Polymers 2019, 11, 1847. [Google Scholar] [CrossRef] [PubMed]
- Starkova, O.; Buschhorn, S.; Mannov, E.; Schulte, K.; Aniskevich, A. Water transport in epoxy/MWCNT composites. Eur. Polym. J. 2013, 49, 2138–2148. [Google Scholar] [CrossRef]
- Carter, H.G.; Kibler, K.G. Langmuir-type model for anomalous moisture diffusion in composite resins. J. Compos. Mater. 1978, 12, 118–130. [Google Scholar] [CrossRef]
- Jacobs, P.M.; Jones, F.R. Diffusion of moisture into two-phase polymers. Part 1: The development of an analytical model and its application to styrene-ethylene/ butylene-styrene block copolymer. J. Mater. Sci. 1989, 24, 2331–2336. [Google Scholar] [CrossRef]
- Zhou, J.; Lucas, J.P. Hygrothermal effects of epoxy resin. Part I: The nature of water in epoxy. Polymer 1999, 40, 5505–5512. [Google Scholar] [CrossRef]
- Weitsman, Y. Diffusion with Time-Varying Diffusivity, with Application to Moisture-Sorption in Composites. J. Compos. Mater. 1976, 10, 193–204. [Google Scholar] [CrossRef]
- Glaskova, T.I.; Guedes, R.M.; Morais, J.J.; Aniskevich, A.N. A comparative analysis of moisture transport models as applied to an epoxy binder. Mech. Compos. Mater. 2007, 43, 377–388. [Google Scholar] [CrossRef]
- Berens, A.; Hopfenberg, H. Diffusion and relaxation in glassy polymer powders: 2. Separation of diffusion and relaxation parameters. Polymer 1978, 19, 489–496. [Google Scholar] [CrossRef]
- Bao, L.R.; Yee, A.F.; Lee, C.Y.C. Moisture absorption and hygrothermal aging in a bismaleimide resin. Polymer 2001, 42, 7327–7333. [Google Scholar] [CrossRef]
- Gagani, A. Environmental Effects on Fiber Reinforced Polymer Composites—Fluid and Temperature Effects on Mechanical Performance. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2019. [Google Scholar]
- Gagani, A.I.; Krauklis, A.E.; Sæter, E.; Vedvik, N.P.; Echtermeyer, A.T. A novel method for testing and determining ILSS for marine and offshore composites. Compos. Struct. 2019, 220, 431–440. [Google Scholar] [CrossRef]
- Gagani, A.I.; Monsås, A.B.; Krauklis, A.E.; Echtermeyer, A.T. The effect of temperature and water immersion on the interlaminar shear fatigue of glass fiber epoxy composites using the I-beam method. Compos. Sci. Technol. 2019, 181, 107703. [Google Scholar] [CrossRef]
- ASTM D5229/D5229M-14; Standard Test Method for Moisture Absorption Properties and Equilibrium Conditioning of Polymer Matrix Composite Materials. ASTM International: Conshohocken, PA, USA, 2014.
- Perreux, D.; Choqueuse, D.; Davies, P. Anomalies in moisture absorption of glass fibre reinforced epoxy tubes. Compos. Part A Appl. Sci. Manuf. 2002, 33, 147–154. [Google Scholar] [CrossRef]
- Shirangi, M.H.; Michel, B. Mechanism of Moisture Diffusion, Hygroscopic Swelling, and Adhesion Degradation in Epoxy Molding Compounds. In Moisture Sensitivity of Plastic Packages of IC Devices; Fan, X.J., Suhir, E., Eds.; Springer: New York, NY, USA, 2010; pp. 29–69. [Google Scholar]
- Ibarra, L.; Chamorro, C. Short fiber–elastomer composites. Effects of matrix and fiber level on swelling and mechanical and dynamic properties. J. Appl. Polym. Sci. 1991, 43, 1805–1819. [Google Scholar] [CrossRef]
- Halpin, J.C. Effects of Environmental Factors on Composite Materials; Technical Report AFML-TR-67–423; Air Force Materials Laboratory: Dayton, OH, USA, 1969. [Google Scholar]
- Hahn, H.T.; Kim, R.Y. Swelling of Composite Laminates in Advanced Composite Materials: Environmental Effects; ASTM STP 658; American Society for Testing and Materials: Philadelphia, PA, USA, 1978; pp. 98–120. [Google Scholar]
- Cairns, D.S.; Adams, D.F. Moisture and Thermal Expansion Properties of Unidirectional Composite Materials and the Epoxy Matrix. J. Reinf. Plast. Compos. 1983, 2, 239–255. [Google Scholar] [CrossRef]
- Ashton, J.E.; Halpin, J.C.; Petit, P.H. Primer on Composite Materials Analysis; Technomic Pub. Co.: Stamford, CT, USA, 1969. [Google Scholar]
- Schapery, R.A. Thermal Expansion Coefficients of Composite Materials Based on Energy Principles. J. Compos. Mater. 1968, 2, 380–404. [Google Scholar] [CrossRef]
- Coran, A.Y.; Boustany, K.; Hamed, P. Unidirectional fiber–polymer composites: Swelling and modulus anisotropy. J. Appl. Polym. Sci. 1971, 15, 2471–2485. [Google Scholar] [CrossRef]
- Daniels, B.K. Orthotropic swelling, and simplified elasticity laws with special reference to cord-reinforced rubber. J. Appl. Polym. Sci. 1973, 17, 2847–2853. [Google Scholar] [CrossRef]
- Fan, Y.; Gomez, A.; Ferraro, S.; Pinto, B.; Muliana, A.; La Saponara, V. Diffusion of water in glass fiber reinforced polymer composites at different temperatures. J. Compos. Mater. 2018, 53, 1097–1110. [Google Scholar] [CrossRef]
- Jacquemin, F.; Freour, S.; Guillén, R. Analytical modeling of transient hygro-elastic stress concentration—Application to embedded optical fiber in a non-uniform transient strain field. Compos. Sci. Technol. 2006, 66, 397–406. [Google Scholar] [CrossRef]
- Meng, M.; Rizvi, J.; Le, H.; Grove, S. Multi-scale modelling of moisture diffusion coupled with stress distribution in CFRP laminated composites. Compos. Struct. 2015, 138, 295–304. [Google Scholar] [CrossRef]
- Sinchuk, Y.; Pannier, Y.; Gueguen, M.; Tandiang, D.; Gigliotti, M. Computed tomography-based modeling and simulation of moisture diffusion and induced swelling in textile composite materials. Int. J. Solids Struct. 2018, 154, 88–96. [Google Scholar] [CrossRef]
- Sinchuk, Y.; Pannier, Y.; Gueguen, M.; Gigliotti, M. Image-based modeling of moisture-induced swelling and stress in 2D textile composite materials using a global-local approach. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 1505–1519. [Google Scholar] [CrossRef]
- Weitsman, Y.J. Fluid Effects in Polymers and Polymeric Composites; Springer: New York, NY, USA, 2012. [Google Scholar]
- Obeid, H.; Clément, A.; Fréour, S.; Jacquemin, F.; Casari, P. On the identification of the coefficient of moisture expansion of polyamide-6: Accounting differential swelling strains and plasticization. Mech. Mater. 2018, 118, 1–10. [Google Scholar] [CrossRef]
- Sar, B.; Fréour, S.; Davies, P.; Jacquemin, F. Accounting for differential swelling in the multi-physics modelling of the diffusive behaviour of polymers. ZAMM 2013, 94, 452–460. [Google Scholar] [CrossRef]
- Fan, Y.; Gomez, A.; Ferraro, S.; Pinto, B.; Muliana, A.; La Saponara, V. The effects of temperatures and volumetric expansion on the diffusion of fluids through solid polymers. J. Appl. Polym. Sci. 2017, 134, 45151. [Google Scholar] [CrossRef]
- Kappert, E.J.; Raaijmakers, M.J.; Tempelman, K.; Cuperus, F.P.; Ogieglo, W.; Benes, N.E. Swelling of 9 polymers commonly employed for solvent-resistant nanofiltration membranes: A comprehensive dataset. J. Membr. Sci. 2018, 569, 177–199. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Prediction of Orthotropic Hygroscopic Swelling of Fiber-Reinforced Composites from Isotropic Swelling of Matrix Polymer. J. Compos. Sci. 2019, 3, 10. [Google Scholar] [CrossRef]
- Wu, C.F.; Xu, W.J. Atomistic simulation study of absorbed water influence on structure and properties of crosslinked epoxy resin. Polymer 2007, 48, 5440–5448. [Google Scholar] [CrossRef]
- Shtarkman, B.P.; Razinskaya, I.N. Plasticization mechanism and structure of polymers. Acta Polym. 1983, 34, 514–520. [Google Scholar] [CrossRef]
- Chen, Y.; Davalos, J.F.; Ray, I.; Kim, H.-Y. Accelerated aging tests for evaluations of durability performance of FRP reinforcing bars for concrete structures. Compos. Struct. 2007, 78, 101–111. [Google Scholar] [CrossRef]
- Yiu, C.K.Y.; King, N.M.; Pashley, D.H.; Suh, B.I.; Carvalho, R.M.; Carrilho, M.R.O.; Tay, F.R. Effect of resin hydrophilicity and water storage on resin strength. Biomaterials 2004, 25, 5789–5796. [Google Scholar] [CrossRef] [PubMed]
- Mazan, T.; Jørgensen, J.K.; Echtermeyer, A. Aging of polyamide 11. Part 2: General multiscale model of the hydrolytic degradation applied to predict the morphology evolution. J. Appl. Polym. Sci. 2015, 132, 42630. [Google Scholar] [CrossRef]
- Mazan, T.; Berggren, R.; Jørgensen, J.K.; Echtermeyer, A. Aging of polyamide 11. Part 1: Evaluating degradation by thermal, mechanical, and viscometric analysis. J. Appl. Polym. Sci. 2015, 132, 41971. [Google Scholar] [CrossRef]
- Mazan, T.; Jørgensen, J.K.; Echtermeyer, A. Aging of polyamide 11. Part 3: Multiscale model predicting the mechanical properties after hydrolytic degradation. J. Appl. Polym. Sci. 2015, 132, 42792. [Google Scholar] [CrossRef]
- Jacques, B.; Werth, M.; Merdas, I.; Thominette, F.; Verdu, J. Hydrolytic ageing of polyamide 11. 1. Hydrolysis kinetics in water. Polymer 2002, 43, 6439. [Google Scholar] [CrossRef]
- Vieira, A.C.; Vieira, J.C.; Ferra, J.M.; Magalhães, F.; Guedes, R.M.; Marques, A.T. Mechanical study of PLA–PCL fibers during in vitro degradation. J. Mech. Behav. Biomed. Mater. 2011, 4, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Vieira, A.; Guedes, R.; Tita, V. Constitutive modeling of biodegradable polymers: Hydrolytic degradation and time-dependent behavior. Int. J. Solids Struct. 2014, 51, 1164–1174. [Google Scholar] [CrossRef]
- Glaskova-Kuzmina, T.; Starkova, O.; Gaidukovs, S.; Platnieks, O.; Gaidukova, G. Durability of Biodegradable Polymer Nanocomposites. Polymers 2021, 13, 3375. [Google Scholar] [CrossRef] [PubMed]
- Krauklis, A.E.; Karl, C.W.; Gagani, A.I.; Jørgensen, J.K. Composite Material Recycling Technology—State-of-the-Art and Sustainable Development for the 2020s. J. Compos. Sci. 2021, 5, 28. [Google Scholar] [CrossRef]
- Fakhrul, T.; Islam, M. Degradation Behavior of Natural Fiber Reinforced Polymer Matrix Composites. Procedia Eng. 2013, 56, 795–800. [Google Scholar] [CrossRef]
- Abdullah, M.Z.; Dan-Mallam, Y.; Yusoff, P.S.M.M. Effect of Environmental Degradation on Mechanical Properties of Kenaf/Polyethylene Terephthalate Fiber Reinforced Polyoxymethylene Hybrid Composite. Adv. Mater. Sci. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- WindEurope—Cefic—EuCIA. Accelerating Wind Turbine Blade Circularity. White Paper. May 2020. Available online: https://windeurope.org/wp-content/uploads/files/about-wind/reports/WindEurope-Accelerating-wind-turbine-blade-circularity.pdf (accessed on 11 November 2020).
- Van der Woude, J. (EuCIA) Recycling, Status and Developments in Europe. In Proceedings of the International Glass Fiber Symposium, Aachen, Germany, 29–30 October 2018. [Google Scholar]
- Tournie, A.; Ricciardi, P.; Colomban, P. Glass corrosion mechanisms: A multiscale analysis. Solid State Ion. 2008, 179, 2142–2154. [Google Scholar] [CrossRef]
- Bledzki, A.; Spaude, R.; Ehrenstein, G. Corrosion phenomena in glass fibers and glass fibers reinforced thermosetting resins. Compos. Sci. Technol. 1985, 23, 263–285. [Google Scholar] [CrossRef]
- Iler, R.K. The Chemistry of Silica: Solubility, Polymerization, Colloid and Surface Properties and Biochemistry of Silica; Wiley: New York, NY, USA, 1979; p. 896. [Google Scholar]
- Wiederhorn, S.M.; Bolz, L.H. Stress Corrosion and Static Fatigue of Glass. J. Am. Ceram. Soc. 1970, 53, 543–548. [Google Scholar] [CrossRef]
- Brown, E.; Davis, A.; Jonnalagadda, K.; Sottos, N. Effect of surface treatment on the hydrolytic stability of E-glass fiber bundle tensile strength. Compos. Sci. Technol. 2004, 65, 129–136. [Google Scholar] [CrossRef]
- Agarwal, B.D.; Broutman, L.J. Analysis and Performance of Fiber Composites, 2nd ed.; Wiley: Hoboken, NJ, USA, 1990; pp. 339–359. [Google Scholar]
- Schutte, C.L. Environmental durability of glass-fiber composites. Mater. Sci. Eng. R Rep. 1994, 13, 265–323. [Google Scholar] [CrossRef]
- Renaud, C.M.; Greenwood, M.E. Effect of Glass Fibers and Environments on Long-Term Durability of GFRP Composites. In Proceedings of the 9th EFUC Meeting, Wroclaw, Poland, 9–11 July 2005. [Google Scholar]
- Krauklis, A.E.; Echtermeyer, A.T. Dissolving Cylinder Zero-Order Kinetic Model for Predicting Hygrothermal Aging of Glass Fiber Bundles and Fiber-Reinforced Composites. In Proceedings of the 4th International Glass Fiber Symposium, Aachen, Germany, 29–30 October 2018; pp. 66–72. [Google Scholar]
- Krauklis, A.E.; Gagani, A.I.; Vegere, K.; Kalnina, I.; Klavins, M.; Echtermeyer, A.T. Dissolution Kinetics of R-Glass Fibres: Influence of Water Acidity, Temperature, and Stress Corrosion. Fibers 2019, 7, 22. [Google Scholar] [CrossRef]
- Krauklis, A.E. Modular Paradigm for Composites: Modeling Hydrothermal Degradation of Glass Fibers. Fibers 2021, 9, 83. [Google Scholar] [CrossRef]
- Grambow, B.; Müller, R. First-order dissolution rate law and the role of surface layers in glass performance assessment. J. Nucl. Mater. 2001, 298, 112–124. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Echtermeyer, A.T. Long-Term Dissolution of Glass Fibers in Water Described by Dissolving Cylinder Zero-Order Kinetic Model: Mass Loss and Radius Reduction. Open Chem. 2018, 16, 1189–1199. [Google Scholar] [CrossRef]
- Hunter, F.M.I.; Hoch, A.R.; Heath, T.G.; Baston, G.M.N. Review of Glass Dis-Solution Models and Application to UK Glasses; Report RWM005105, AMEC/103498/02 Issue 2; AMEC: Oxfordshire, UK, 2015. [Google Scholar]
- Michalske, T.A.; Freiman, S.W. A Molecular Mechanism for Stress Corrosion in Vitreous Silica. J. Am. Ceram. Soc. 1983, 66, 284–288. [Google Scholar] [CrossRef]
- Putnis, C.V.; Ruiz-Agudo, E. The Mineral-Water Interface: Where Minerals React with the Environment. Elements 2013, 9, 177–182. [Google Scholar] [CrossRef]
- Echtermeyer, A.T.; Krauklis, A.E.; Gagani, A.I.; Sæter, E. Zero Stress Aging of Glass and Carbon Fibers in Water and Oil—Strength Reduction Explained by Dissolution Kinetics. Fibers 2019, 7, 107. [Google Scholar] [CrossRef]
- Delage, F.; Ghaleb, D.; Dussossoy, J.; Chevallier, O.; Vernaz, E. A mechanistic model for understanding nuclear waste glass dissolution. J. Nucl. Mater. 1992, 190, 191–197. [Google Scholar] [CrossRef]
- Geisler, T.; Nagel, T.; Kilburn, M.; Janssen, A.; Icenhower, J.P.; Fonseca, R.O.C.; Grange, M.; Nemchin, A. The mechanism of borosilicate glass corrosion revisited. Geochim. Cosmochim. Acta 2015, 158, 112–129. [Google Scholar] [CrossRef]
- Icenhower, J.P.; Steefel, C.I. Dissolution rate of borosilicate glass SON68: A method of quantification based upon interferometry and implications for experimental and natural weathering rates of glass. Geochim. Cosmochim. Acta 2015, 157, 147–163. [Google Scholar] [CrossRef]
- Ma, T.; Jivkov, A.; Li, W.; Liang, W.; Wang, Y.; Xu, H.; Han, X. A mechanistic model for long-term nuclear waste glass dissolution integrating chemical affinity and interfacial diffusion barrier. J. Nucl. Mater. 2017, 486, 70–85. [Google Scholar] [CrossRef]
- Geisler, T.; Dohmen, L.; Lenting, C.; Fritzsche, M.B.K. Real-time in situ observations of reaction and transport phenomena during silicate glass corrosion by fluid-cell Raman spectroscopy. Nat. Mater. 2019, 18, 342–348. [Google Scholar] [CrossRef] [PubMed]
- Grambow, B. A General Rate Equation for Nuclear Waste Glass Corrosion. MRS Proc. 1984, 44. [Google Scholar] [CrossRef]
- Mišíková, L.; Liška, M.; Galusková, D. Corrosion of E-Glass Fibers in Distilled Water. Ceram. Silik. 2007, 51, 131–135. [Google Scholar]
- Bashir, S.T.; Yang, L.; Liggat, J.J.; Thomason, J.L. Kinetics of dissolution of glass fiber in hot alkaline solution. J. Mater. Sci. 2018, 53, 1710–1722. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-State Kinetic Models: Basics and Mathematical Fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef]
- Sekine, H.; Beaumont, P.W. A physically based micromechanical theory of macroscopic stress-corrosion cracking in aligned continuous glass-fibre-reinforced polymer laminates. Compos. Sci. Technol. 1998, 58, 1659–1665. [Google Scholar] [CrossRef]
- Charles, R.J. Static Fatigue of Glass. II. J. Appl. Phys. 1958, 29, 1554–1560. [Google Scholar] [CrossRef]
- Inglis, C.E. Stresses in a plate due to the presence of cracks and sharp corners. Proc. Inst. Nav. Archit. 1913, 60, 219–241. [Google Scholar]
- Griffith, A.A. The Phenomena of Rupture and Flow in Solids. Philos. Trans. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1921, 221, 163–198. [Google Scholar]
- Orowan, E. Energy Criteria of Fracture. Weld. J. 1955, 34, 157–160. [Google Scholar]
- Charles, R.J. Static Fatigue of Glass. I. J. Appl. Phys. 1958, 29, 1549–1553. [Google Scholar] [CrossRef]
- Horstman, R.; Peters, K.; Enright, C.; Meltzer, R.; Vieth, M.B.; Bush, A. Stress Intensity Factors for Single-Edge-Crack Solid, and Hollow Round Bars Loaded in Tension. J. Test. Eval. 1981, 9, 216. [Google Scholar] [CrossRef]
- Vijayan, K. Effect of Environmental Exposures on the Aramid Fibre—Kevlar. Met. Mater. Process. 2000, 12, 259–268. [Google Scholar]
- Horta, A.; Coca, J.; Diez, F. Degradation mechanism and kinetics of a high thermally stable aromatic polyamide. Adv. Polym. Technol. 2000, 19, 120–131. [Google Scholar] [CrossRef]
- Horta, A.; Coca, J.; Diez, F.V. Degradation kinetics of meta- and para-aromatic polyamides. Adv. Polym. Technol. 2003, 22, 15–21. [Google Scholar] [CrossRef]
- Yang, H.H. Aromatic High-Strength Fibers; Wiley: Hoboken, NJ, USA, 1989. [Google Scholar]
- Shubha, M.; Parimala, H.V.; Vijayan, K. Moisture uptake by Keviar fibres. J. Mater. Sci. Lett. 1993, 12, 60–62. [Google Scholar]
- Connor, C.; Chadwick, M.M. Characterization of absorbed water in aramid fibre by nuclear magnetic resonance. J. Mater. Sci. 1996, 31, 3871–3877. [Google Scholar] [CrossRef]
- Perry, M.C. The Behavior of Kevlar Fibers under Environmental-Stress Conditions. Ph.D. Thesis, The University of Utah, Salt Lake City, UT, USA, 1997. [Google Scholar]
- Jain, A.; Vijayan, K. Effect of penetrants on the aramid Nomex. Bull. Mater. Sci. 2000, 23, 211–214. [Google Scholar] [CrossRef][Green Version]
- Lin, J.-S.; Chiu, H.-T. Hydrolysis of Kevlar Fibres. Polym. Polym. Compos. 2001, 9, 239–246. [Google Scholar] [CrossRef]
- Tanaka, K.; Minoshima, K.; Grela, W.; Komai, K. Characterization of the aramid/epoxy interfacial properties by means of pull-out test and influence of water absorption. Compos. Sci. Technol. 2002, 62, 2169–2177. [Google Scholar] [CrossRef]
- Menail, Y.; El Mahi, A.; Assarar, M.; Redjel, B.; Kondratas, A. The Effects of Water Aging on the Mechanical Properties of Glass-Fiber and Kevlar-Fiber Epoxy Composite Materials. Mechanika 2009, 76, 28–32. [Google Scholar]
- Ramesh, C.; Arumugam, V.; Stanley, J.; Kumar, V. Effects of Hydrolytic Aging on Glass/Epoxy, Kevlar/Epoxy, and Hybrid (Glass/ Kevlar/Epoxy) Composites. Int. J. Eng. Res. Technol. 2013, 2, 1589–1596. [Google Scholar]
- Menail, Y.; ElMahi, A.; Assarar, M.; Redjel, B. Acoustic emission monitoring of damage mechanisms an aramid-epoxy composite after tensile fatigue and aging seawater. Mechanics 2016, 22, 14–18. [Google Scholar] [CrossRef]
- Srivastav, P.A.; Wangikar, K.S.; Kale, A.D. Mechanical Characterization and Effects of Hydrolytic Aging on Glass Kevlar Hybrid Composites. Int. J. Mech. Prod. Eng. 2017, 5, 2320-2092. [Google Scholar]
- Engelbrecht-Wiggans, A.; Burni, F.; Guigues, E.; Jiang, S.; Huynh, T.; Tsinas, Z.; Jacobs, D.; Forster, A. Effects of temperature and humidity on high-strength p-aramid fibers used in body armor. Text. Res. J. 2020, 90, 2428–2440. [Google Scholar] [CrossRef]
- Oğuz, Z.A.; Erkliğ, A.; Bozkurt, Y. Effects of Hydrothermal Seawater Aging on the Mechanical Properties and Water Absorption of Glass/Aramid/Epoxy Hybrid Composites. Int. Polym. Process. 2021, 36, 79–93. [Google Scholar] [CrossRef]
- Thomason, J.; Jenkins, P.; Yang, L. Glass Fibre Strength—A Review with Relation to Composite Recycling. Fibers 2016, 4, 18. [Google Scholar] [CrossRef]
- Wei, B.; Cao, H.; Song, S. Degradation of basalt fibre and glass fibre/epoxy resin composites in seawater. Corros. Sci. 2011, 53, 426–431. [Google Scholar] [CrossRef]
- Sharma, S.; Zhang, D.; Zhao, Q. Degradation of basalt fiber–reinforced polymer bars in seawater and sea sand concrete environment. Adv. Mech. Eng. 2020, 12. [Google Scholar] [CrossRef]
- Li, G.; Hartmann, J.; Derry, L.A.; West, A.J.; You, C.-F.; Long, X.; Zhan, T.; Li, L.; Li, G.; Qiu, W.; et al. Temperature dependence of basalt weathering. Earth Planet. Sci. Lett. 2016, 443, 59–69. [Google Scholar] [CrossRef]
- Fan, Y.; Guo, J.; Wang, X.; Xia, Y.; Han, P.; Shangguan, L.; Zhang, M. Comparative Failure Study of Different Bonded Basalt Fiber-Reinforced Polymer (BFRP)-AL Joints in a Humid and Hot Environment. Polymers 2021, 13, 2593. [Google Scholar] [CrossRef] [PubMed]
- Glaskova-Kuzmina, T.; Zotti, A.; Borriello, A.; Zarrelli, M.; Aniskevich, A. Basalt Fibre Composite with Carbon Nanomodified Epoxy Matrix under Hydrothermal Ageing. Polymers 2021, 13, 532. [Google Scholar] [CrossRef] [PubMed]
- Thomason, J.L. Glass Fiber Sizing: A Review of the Scientific Literature; University of Strathclyde: Glasgow, UK, 2012. [Google Scholar]
- Piret, W.; Mason, N.; Luc, P. Glass Fibre Sizing Composition by 3B-Fibreglass SPRL. EP2540683A1, 28 June 2011. [Google Scholar]
- Thomason, J.L. Glass Fiber Sizing: A Review of Size Formulation Patents; Blurb Co.: Glasgow, UK, 2015. [Google Scholar]
- Thomason, J.; Adzima, L. Sizing up the interphase: An insider’s guide to the science of sizing. Compos. Part A Appl. Sci. Manuf. 2001, 32, 313–321. [Google Scholar] [CrossRef]
- Plueddemann, E.P. Nature of Adhesion Through Silane Coupling Agents. In Silane Coupling Agents; Springer: Boston, MA, USA, 1991; pp. 115–152. [Google Scholar]
- Plonka, R.; Mäder, E.; Gao, S.; Bellmann, C.; Dutschk, V.; Zhandarov, S. Adhesion of epoxy/glass fibre composites influenced by aging effects on sizings. Compos. Part A Appl. Sci. Manuf. 2004, 35, 1207–1216. [Google Scholar] [CrossRef]
- Feuillade, V.; Bergeret, A.; Quantin, J.-C.; Crespy, A. Characterisation of glass fibres used in automotive industry for SMC body panels. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1536–1544. [Google Scholar] [CrossRef]
- Riaño, L.; Belec, L.; Chailan, J.-F.; Joliff, Y. Effect of interphase region on the elastic behavior of unidirectional glass-fiber/epoxy composites. Compos. Struct. 2018, 198, 109–116. [Google Scholar] [CrossRef]
- Riaño, L.; Chailan, J.-F.; Joliff, Y. Evolution of effective mechanical and interphase properties during natural ageing of glass-fibre/epoxy composites using micromechanical approach. Compos. Struct. 2020, 258, 113399. [Google Scholar] [CrossRef]
- Gagani, A.; Krauklis, A.; Echtermeyer, A.T. Anisotropic fluid diffusion in carbon fiber reinforced composite rods: Experimental, analytical, and numerical study. Mar. Struct. 2018, 59, 47–59. [Google Scholar] [CrossRef]
- Joliff, Y.; Belec, L.; Heman, M.B.; Chailan, J.F. Experimental, Analytical and Numerical Study of Water Diffusion in Unidirec-tional Composite Materials—Interphase Impact. In Proceedings of the Computational Materials Science; Elsevier: Amsterdam, The Netherlands, 2012; pp. 141–145. [Google Scholar]
- Joliff, Y.; Belec, L.; Chailan, J. Modified water diffusion kinetics in a unidirectional glass/fibre composite due to the interphase area: Experimental, analytical and numerical approach. Compos. Struct. 2013, 97, 296–303. [Google Scholar] [CrossRef]
- Joliff, Y.; Rekik, W.; Belec, L.; Chailan, J.F. Study of the moisture/stress effects on glass fibre/epoxy composite and the impact of the interphase area. Compos. Struct. 2014, 108, 876–885. [Google Scholar] [CrossRef]
- Djellouli, B.; Zouari, W.; Assarar, M.; Ayad, R. Analysis of the hygroscopic and hygroelastic behaviours of water aged flax-epoxy composite. Compos. Struct. 2021, 265, 113692. [Google Scholar] [CrossRef]
- Heide-Jørgensen, S.; Ibsena, C.H.; Budzik, M.K. Effective through-the-thickness diffusivity of plain-woven composite from analytical homogenization. Compos. Sci. Technol. 2020, 202, 108552. [Google Scholar] [CrossRef]
- Kanerva, M.; Jokinen, J.; Sarlin, E.; Pärnänen, T.; Lindgren, M.; Järventausta, M.; Vuorinen, J. Lower stiffness of GFRP after sulfuric acid-solution aging is due to degradation of fibre-matrix interfaces? Compos. Struct. 2019, 212, 524–534. [Google Scholar] [CrossRef]
- van Soestbergen, M.; Herrmann, A.; Erich, S.; Adan, O. Effect of interfacial transport on the diffusivity of highly filled polymers. Colloid Interface Sci. Commun. 2021, 42, 100405. [Google Scholar] [CrossRef]
- Wang, J.; Dai, F.; Ma, L. A multi-scale moisture diffusion coupled with stress model for composite materials. Compos. Struct. 2017, 171, 345–359. [Google Scholar] [CrossRef]
- Rocha, I.B.C.M.; Raijmaekers, S.; van der Meer, F.P.; Nijssen, R.P.L.; Fischer, H.R.; Sluys, L.J. Combined experi-mental/numerical investigation of directional moisture diffusion in glass/epoxy composites. Compos. Sci. Technol. 2017, 151, 16–24. [Google Scholar] [CrossRef]
- Abhilash, A.; Joshi, S.P.; Mukherjee, A.; Mishnaevsky, L. Micromechanics of diffusion-induced damage evolution in reinforced polymers. Compos. Sci. Technol. 2011, 71, 333–342. [Google Scholar] [CrossRef]
- Tang, X.; Whitcomb, J.D.; Li, Y.; Sue, H.-J. Micromechanics modeling of moisture diffusion in woven composites. Compos. Sci. Technol. 2005, 65, 817–826. [Google Scholar] [CrossRef]
- Li, Z.; Furmanski, J.; Lepech, M.D. Micromechanics modeling and homogenization of glass fiber reinforced polymer composites subject to synergistic deterioration. Compos. Sci. Technol. 2020, 203, 108629. [Google Scholar] [CrossRef]
- Li, Z.; Lepech, M.D.; Furmanski, J. Development of a multiphysics model of synergistic effects between environmental exposure and damage in woven glass fiber reinforced polymeric composites. Compos. Struct. 2020, 258, 113230. [Google Scholar] [CrossRef]
- Terada, K.; Kurumatani, M. Two-scale diffusion-deformation coupling model for material deterioration involving micro-crack propagation. Int. J. Numer. Methods Eng. 2010, 83, 426–451. [Google Scholar] [CrossRef]
- Bailakanavar, M.; Fish, J.; Aitharaju, V.; Rodgers, W. Computational coupling of moisture diffusion and mechanical deformation in polymer matrix composites. Int. J. Numer. Methods Eng. 2014, 98, 859–880. [Google Scholar] [CrossRef]
- Rocha, I.B.C.M.; van der Meer, F.P.; Nijssen, R.P.L.; Sluys, L.J. A multiscale and multiphysics numerical framework for mod-elling of hygrothermal ageing in laminated composites. Int. J. Numer. Methods Eng. 2017, 112, 360–379. [Google Scholar] [CrossRef]
- Rocha, I.; van der Meer, F.; Raijmaekers, S.; Lahuerta, F.; Nijssen, R.; Mikkelsen, L.; Sluys, L. A combined experimental/numerical investigation on hygrothermal aging of fiber-reinforced composites. Eur. J. Mech. A Solids 2018, 73, 407–419. [Google Scholar] [CrossRef]
- Oskay, C. Variational multiscale enrichment for modeling coupled mechano-diffusion problems. Int. J. Numer. Methods Eng. 2011, 89, 686–705. [Google Scholar] [CrossRef]
- Shi, B.; Zhang, M.; Liu, S.; Sun, B.; Gu, B. Multi-scale ageing mechanisms of 3D four directional and five directional braided composites’ impact fracture behaviors under thermo-oxidative environment. Int. J. Mech. Sci. 2019, 155, 50–65. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Met. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Feyel, F. Multiscale FE2 elastoviscoplastic analysis of composite structures. Comput. Mater. Sci. 1999, 16, 344–354. [Google Scholar] [CrossRef]
- Geers, M.; Kouznetsova, V.; Brekelmans, W. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Lloberas-Valls, O.; Stroeven, M.; Sluys, L.J. Computational homogenization for multiscale crack modelling. Implementation and computational aspects. Int. J. Numer. Methods Eng. 2012, 89, 192–226. [Google Scholar] [CrossRef]
- Özdemir, I.; Brekelmans, W.A.M.; Geers, M.G.D. Computational homogenization for heat conduction in heterogeneous solids. Int. J. Numer. Methods Eng. 2007, 73, 185–204. [Google Scholar] [CrossRef]
- Sengupta, A.; Papadopoulos, P.; Taylor, R.L. A multiscale finite element method for modeling fully coupled thermomechanical problems in solids. Int. J. Numer. Methods Eng. 2012, 91, 1386–1405. [Google Scholar] [CrossRef]
- Berthelsen, R.; Denzer, R.; Oppermann, P.; Menzel, A. Computational homogenisation for thermoviscoplasticity: Application to thermally sprayed coatings. Comput. Mech. 2017, 60, 739–766. [Google Scholar] [CrossRef]
- Tikarrouchine, E.; Chatzigeorgiou, G.; Chemisky, Y.; Meraghni, F. Fully coupled thermo-viscoplastic analysis of composite structures by means of multi-scale three-dimensional finite element computations. Int. J. Solids Struct. 2019, 164, 120–140. [Google Scholar] [CrossRef]
- Yang, Z.; Guan, T.; Sun, Y. Chemo-mechanical coupling analysis of composites by second-order multiscale asymptotic expan-sion. Arch. Appl. Mech. 2019, 89, 769–788. [Google Scholar] [CrossRef]
- Yu, Q.; Fish, J. Multiscale asymptotic homogenization for multiphysics problems with multiple spatial and temporal scales: A coupled thermo-viscoelastic example problem. Int. J. Solids Struct. 2002, 39, 6429–6452. [Google Scholar] [CrossRef]
- Haouala, S.; Doghri, I. Two-scale Time Homogenization for Isotropic Viscoelastic- Viscoplastic Homogeneous Solids under Large Numbers of Cycles. Procedia Eng. 2013, 66, 598–607. [Google Scholar] [CrossRef][Green Version]
- Haouala, S.; Doghri, I. Modeling and algorithms for two-scale time homogenization of viscoelastic-viscoplastic solids under large numbers of cycles. Int. J. Plast. 2015, 70, 98–125. [Google Scholar] [CrossRef]
- Chu, C.; Bhattacharyya, M.; Dureisseix, D.; Faverjon, B. Weakly intrusive time homogenization technique to deal with pseu-docyclic coupled thermomechanical problems with uncertainties. Comput. Mech. 2020, 66, 669–682. [Google Scholar] [CrossRef]
- Passieux, J.-C.; Ladevèze, P.; Néron, D. A scalable time–space multiscale domain decomposition method: Adaptive time scale separation. Comput. Mech. 2010, 46, 621–633. [Google Scholar] [CrossRef]
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems: An Overview. In Proceedings of the IFAC Proceedings Volumes (IFAC-PapersOnline); IFAC Secretariat: Laxenburg, Austria, 2004; pp. 19–28. [Google Scholar]
- Chinesta, F.; Ammar, A.; Cueto, E. Recent Advances and New Challenges in the Use of the Proper Generalized Decomposition for Solving Multidimensional Models. Arch. Comput. Methods Eng. 2010, 17, 327–350. [Google Scholar] [CrossRef]
- Kerfriden, P.; Gosselet, P.; Adhikari, S.; Bordas, S. Bridging proper orthogonal decomposition methods and augmented Newton–Krylov algorithms: An adaptive model order reduction for highly nonlinear mechanical problems. Comput. Methods Appl. Mech. Eng. 2011, 200, 850–866. [Google Scholar] [CrossRef]
- Ryckelynck, D. Hyper-reduction of mechanical models involving internal variables. Int. J. Numer. Methods Eng. 2008, 77, 75–89. [Google Scholar] [CrossRef]
- Hernández, J.; Caicedo, M.; Ferrer, A. Dimensional hyper-reduction of nonlinear finite element models via empirical cubature. Comput. Methods Appl. Mech. Eng. 2017, 313, 687–722. [Google Scholar] [CrossRef]
- Ghavamian, F.; Tiso, P.; Simone, A. POD–DEIM model order reduction for strain-softening viscoplasticity. Comput. Methods Appl. Mech. Eng. 2016, 317, 458–479. [Google Scholar] [CrossRef]
- Oskay, C.; Fish, J. Eigendeformation-based reduced order homogenization for failure analysis of heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2007, 196, 1216–1243. [Google Scholar] [CrossRef]
- Yuan, Z.; Jiang, T.; Fish, J.; Morscher, G. Reduced-Order Multiscale-Multiphysics Model for Heterogeneous Materials. Int. J. Multiscale Comput. Eng. 2014, 12, 45–64. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Bessa, M.A.; Bostanabad, R.; Liu, Z.; Hu, A.; Apley, D.W.; Brinson, C.; Chen, W.; Liu, W.K. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 2017, 320, 633–667. [Google Scholar] [CrossRef]
- Ghavamian, F.; Simone, A. Accelerating multiscale finite element simulations of history-dependent materials using a recurrent neural network. Comput. Methods Appl. Mech. Eng. 2019, 357, 112594. [Google Scholar] [CrossRef]
- Rocha, I.; Kerfriden, P.; van der Meer, F. Micromechanics-based surrogate models for the response of composites: A critical comparison between a classical mesoscale constitutive model, hyper-reduction, and neural networks. Eur. J. Mech. A Solids 2020, 82, 103995. [Google Scholar] [CrossRef]
- Nash, W.; Drummond, T.; Birbilis, N. A review of deep learning in the study of materials degradation. NPJ Mater. Degrad. 2018, 2, 37. [Google Scholar] [CrossRef]
- Doblies, A.; Boll, B.; Fiedler, B. Prediction of Thermal Exposure and Mechanical Behavior of Epoxy Resin Using Artificial Neural Networks and Fourier Transform Infrared Spectroscopy. Polymers 2019, 11, 363. [Google Scholar] [CrossRef]
- Valenzuela, L.; Knight, D.D.; Kohn, J. Developing a Suitable Model for Water Uptake for Biodegradable Polymers Using Small Training Sets. Int. J. Biomater. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Nguyen, S.-N.; Truong-Quoc, C.; Han, J.-W.; Im, S.; Cho, M. Neural network-based prediction of the long-term time-dependent mechanical behavior of laminated composite plates with arbitrary hygrothermal effects. J. Mech. Sci. Technol. 2021, 35, 4643–4654. [Google Scholar] [CrossRef]
- Keprate, A.; Ratnayake, R.C. Use of Bayesian Network for Risk-Based Fatigue Integrity Assessment: Application for Topside Piping in an Arctic Environment. Int. J. Offshore Polar Eng. 2019, 29, 421–428. [Google Scholar] [CrossRef]
- Keprate, A.; Moslemian, R. Multiscale Damage Modelling of Composite Materials Using Bayesian Network. In Proceedings of 1st International Conference on Structural Damage Modelling and Assessment; Abdel Wahab, M., Ed.; Springer: Singapore, 2021; pp. 135–150. [Google Scholar]
- Shabouei, M.; Subber, W.; Williams, C.W.; Matouš, K.; Powers, J.M. Chemo-thermal model, and Gaussian process emulator for combustion synthesis of Ni/Al composites. Combust. Flame 2019, 207, 153–170. [Google Scholar] [CrossRef]
- Lackner, M. Bioplastics. In Kirk-Othmer Encyclopedia of Chemical Technology; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Chiellini, E.; Solaro, R. Biodegradable Polymeric Materials. Adv. Mater. 1996, 8, 305–313. [Google Scholar] [CrossRef]
- Laycock, B.; Nikolić, M.; Colwell, J.M.; Gauthier, E.; Halley, P.; Bottle, S.; George, G. Lifetime prediction of biodegradable polymers. Prog. Polym. Sci. 2017, 71, 144–189. [Google Scholar] [CrossRef]
- Rittié, L.; Perbal, B. Enzymes used in molecular biology: A useful guide. J. Cell Commun. Signal. 2008, 2, 25–45. [Google Scholar] [CrossRef] [PubMed]
- Lucas, N.; Bienaime, C.; Belloy, C.; Queneudec, M.; Silvestre, F.; Nava-Saucedo, J.-E. Polymer biodegradation: Mechanisms and estimation techniques—A review. Chemosphere 2008, 73, 429–442. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Fernandez, C.; Sialve, B.; Molinuevo-Salces, B. Anaerobic digestion of microalgal biomass: Challenges, opportunities, and research needs. Bioresour. Technol. 2015, 198, 896–906. [Google Scholar] [CrossRef]
- Mueller, R.-J. Biological degradation of synthetic polyesters—Enzymes as potential catalysts for polyester recycling. Process Biochem. 2006, 41, 2124–2128. [Google Scholar] [CrossRef]
- Filiciotto, L.; Rothenberg, G. Biodegradable Plastics: Standards, Policies, and Impacts. ChemSusChem 2020, 14, 56–72. [Google Scholar] [CrossRef] [PubMed]
- Krasowska, A.; Sigler, K. How microorganisms use hydrophobicity and what does this mean for human needs? Front. Cell. Infect. Microbiol. 2014, 4, 112. [Google Scholar] [CrossRef] [PubMed]
- Webb, H.K.; Arnott, J.; Crawford, R.J.; Ivanova, E.P. Plastic Degradation and Its Environmental Implications with Special Reference to Poly(ethylene terephthalate). Polymers 2013, 5, 1–18. [Google Scholar] [CrossRef]
- Dharmaratne, N.U.; Jouaneh, T.M.M.; Kiesewetter, M.K.; Mathers, R.T. Quantitative Measurements of Polymer Hydrophobicity Based on Functional Group Identity and Oligomer Length. Macromolecules 2018, 51, 8461–8468. [Google Scholar] [CrossRef]
- Ben Halima, N. Poly(vinyl alcohol): Review of its promising applications and insights into biodegradation. RSC Adv. 2016, 6, 39823–39832. [Google Scholar] [CrossRef]
- Avery-Gomm, S.; O’Hara, P.D.; Kleine, L.; Bowes, V.; Wilson, L.K.; Barry, K.L. Northern fulmars as biological monitors of trends of plastic pollution in the eastern North Pacific. Mar. Pollut. Bull. 2012, 64, 1776–1781. [Google Scholar] [CrossRef] [PubMed]
- Erni-Cassola, G.; Zadjelovic, V.; Gibson, M.I.; Christie-Oleza, J.A. Distribution of plastic polymer types in the marine environment; a metaanalysis. J. Hazard. Mat. 2019, 369, 691–698. [Google Scholar] [CrossRef]
- Haider, T.P.; Völker, C.; Kramm, J.; Landfester, K.; Wurm, F.R. Plastics of the Future? The Impact of Biodegradable Polymers on the Environment and on Society. Angew. Chem. Int. Ed. 2018, 58, 50–62. [Google Scholar] [CrossRef]
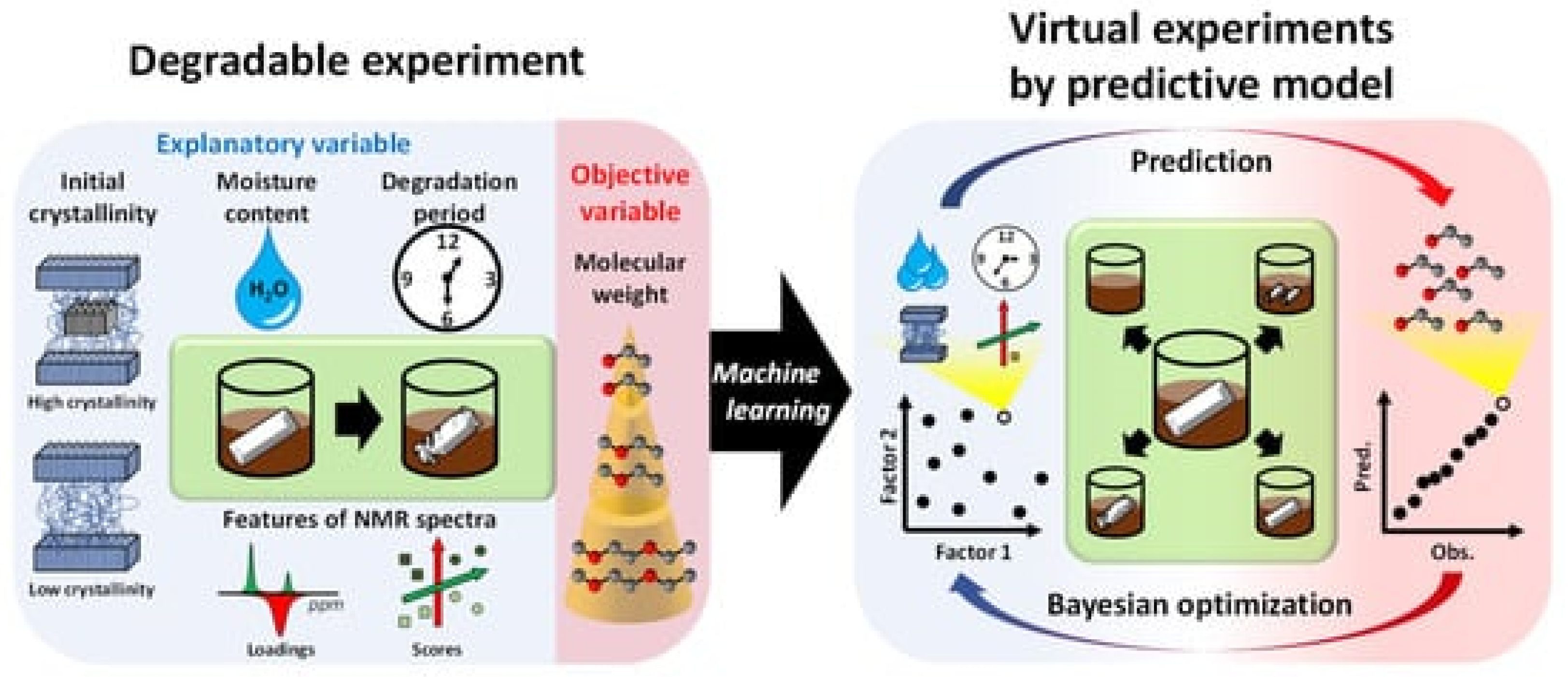
- Yamawaki, R.; Tei, A.; Ito, K.; Kikuchi, J. Decomposition Factor Analysis Based on Virtual Experiments throughout Bayesian Optimization for Compost-Degradable Polymers. Appl. Sci. 2021, 11, 2820. [Google Scholar] [CrossRef]
- Ollier, R.P.; Casado, U.; Nicolini, A.T.; Alvarez, V.A.; Pérez, C.J.; Ludueña, L.N. Improved creep performance of melt-extruded polycaprolactone/organo-bentonite nanocomposites. J. Appl. Polym. Sci. 2021, 138, 50961. [Google Scholar] [CrossRef]
- Nanni, A.; Messori, M. Effect of the wine lees wastes as cost-advantage and natural fillers on the thermal and mechanical properties of poly(3-hydroxybutyrate-co-hydroxyhexanoate) (PHBH) and poly(3-hydroxybutyrate-co-hydroxyvalerate) (PHBV). J. Appl. Polym. Sci. 2020, 137, 48869. [Google Scholar] [CrossRef]
- Amiri, A.; Yu, A.; Webster, D.; Ulven, C. Bio-Based Resin Reinforced with Flax Fiber as Thermorheologically Complex Materials. Polymers 2016, 8, 153. [Google Scholar] [CrossRef]
- Albertsson, A.-C.; Karlsson, S. The three stages in degradation of polymers—Polyethylene as a model substance. J. Appl. Polym. Sci. 1988, 35, 1289–1302. [Google Scholar] [CrossRef]
- Choe, S.; Kim, Y.; Won, Y.; Myung, J. Bridging Three Gaps in Biodegradable Plastics: Misconceptions and Truths About Biodegradation. Front. Chem. 2021, 9, 671750. [Google Scholar] [CrossRef]
- Karl, C.W.; Grimaldo, E.; Benjaminsen, C. Combating Marine Waste and Ghost Fishing with New Materials. Norwegian Science Tech News, May 2021. Available online: https://norwegianscitechnews.com/2021/06/combating-marine-waste-and-ghost-fishing-with-new-materials/ (accessed on 28 September 2021).
- Conversio. Global Plastics Flow; Conversio: Toronto, ON, Canada, 2018; Volume 49, p. 102. [Google Scholar]
- Broughton, W.R.; Maxwell, A.S. Measurement Good Practice Guide No. 103 Accelerated Environmental Ageing of Polymeric Materials; National Physical Laboratory: Teddington, UK, 2007. [Google Scholar]
- Shamsuyeva, M.; Endres, H.J. Plastics in the Context of the Circular Economy and Sustainable Plastics Recycling: Compre-hensive Review on Research Development, Standardization and Market. Compos. Part C 2021, 6, 100168. [Google Scholar] [CrossRef]
- Conversio. Plastics—The Facts; Conversio: Toronto, ON, Canada, 2019; p. 35. [Google Scholar]
- Burlakovs, J.; Kriipsalu, M.; Porshnov, D.; Jani, Y.; Ozols, V.; Pehme, K.-M.; Rudovica, V.; Grinfelde, I.; Pilecka, J.; Vincevica-Gaile, Z.; et al. Gateway of Landfilled Plastic Waste Towards Circular Economy in Europe. Separations 2019, 6, 25. [Google Scholar] [CrossRef]
- Witik, R.A.; Teuscher, R.; Michaud, V.; Ludwig, C.; Månson, J.-A.E. Carbon fibre reinforced composite waste: An environmental assessment of recycling, energy recovery and landfilling. Compos. Part A Appl. Sci. Manuf. 2013, 49, 89–99. [Google Scholar] [CrossRef]
- Conversio. Trucost Plastic and Sustainability; Conversio: Toronto, ON, Canada, 2016; pp. 1–86. [Google Scholar]
- Costanza, R.; Fisher, B.; Mulder, K.; Liu, S.; Christopher, T. Biodiversity, and ecosystem services: A multi-scale empirical study of the relationship between species richness and net primary production. Ecol. Econ. 2007, 61, 478–491. [Google Scholar] [CrossRef]
- Srubar, W.V.; Miller, S.A.; Lepech, M.D.; Billington, S.L. Incorporating spatiotemporal effects and moisture diffusivity into a multi-criteria materials selection methodology for wood–polymer composites. Constr. Build. Mater. 2014, 71, 589–601. [Google Scholar] [CrossRef]
- Duflou, J.R.; Yelin, D.; Van Acker, K.; Dewulf, W. Comparative impact assessment for flax fibre versus conventional glass fibre reinforced composites: Are bio-based reinforcement materials the way to go? CIRP Ann. 2014, 63, 45–48. [Google Scholar] [CrossRef]
- Gillen, K.T.; Celina, M. Predicting polymer degradation and mechanical property changes for combined radiation-thermal aging environments. Rubber Chem. Technol. 2018, 91, 27–63. [Google Scholar] [CrossRef]
- Ead, A.S.; Appel, R.; Alex, N.; Ayranci, C.; Carey, J.P. Life cycle analysis for green composites: A review of literature including considerations for local and global agricultural use. J. Eng. Fibers Fabr. 2021, 16. [Google Scholar] [CrossRef]
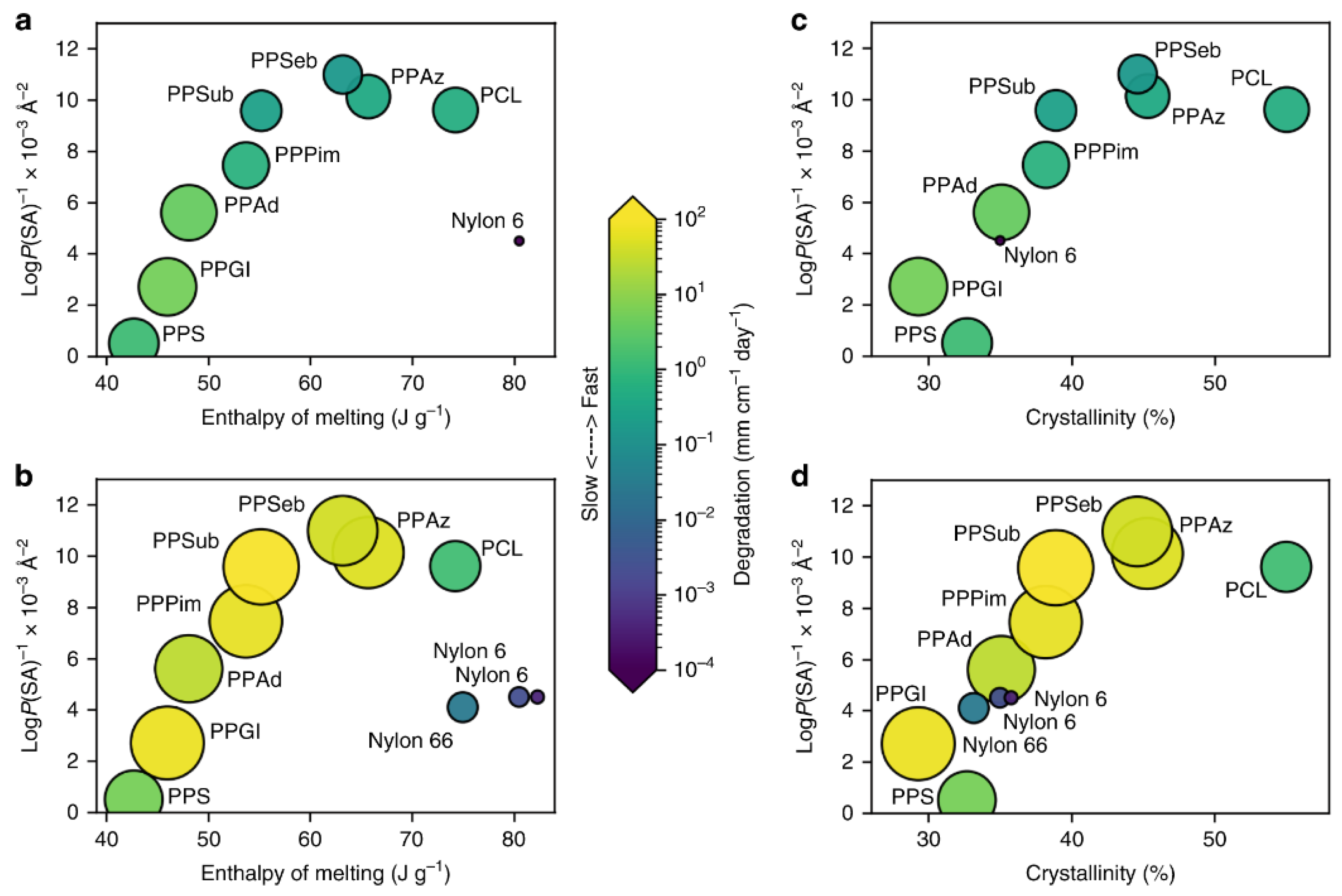
| Fibre Type 1 | Market Share [%] | Cost Range [$/kg] | Tensile Strength [GPa] | Young’s Modulus [GPa] |
|---|---|---|---|---|
| E-Glass | ~70% | 1.3–2.6 | 3.45–3.5 | 72.5–73.5 |
| E-CR-Glass | 1.2–3 | 2–3.625 | 72.5–83 | |
| AR-Glass | 2.5–3 | 1.7–3.5 | 72–175 | |
| C-Glass | 1–2.5 | 3.3 | 69 | |
| A-Glass | 2–3 | 3.3 | 72 | |
| S/S-2-Glass | 16–26 | 4.6–4.9 | 86–89 | |
| R-Glass | 16–26 | 4.4 | 86 | |
| PAN Type Carbon | ~12% | 15–120 | 1.8–7.0 | 230–540 |
| HS Carbon | 20–120 | 3.31–5 | 228–248 | |
| IM Carbon | 25–120 | 4.1–6 | 265–320 | |
| HM Carbon | 25–120 | 1.52–2.41 | 393–483 | |
| UHM Carbon | 30–120 | 2.24 | 724 | |
| Basalt | ~11% | 5 | 4.84 | 89 |
| Aramid/Kevlar | ~7% | 15–30 | 2.6–3.4 | 55–127 |
| Ref(s) | Material(s) | Model | Process(es) |
|---|---|---|---|
| [194,195,196] | GFRP | DNS | Diffusion, swelling |
| [104] | CFRP | DNS | Diffusion, swelling |
| [197] | Flax/Epoxy | DNS | Diffusion, swelling |
| [198] | Woven composites | AH | Diffusion |
| [112] | GFRP | AH/NH | Swelling |
| [199] | GFRP | AH | Degradation |
| [200] | High-Vf polymers | AH/NH | Diffusion |
| [201] | GFRP | AH | Diffusion, swelling |
| [202] | GFRP | NH | Diffusion |
| [203] | GFRP | NH | Diffusion, degradation, fracture |
| [204] | Woven composites | NH | Diffusion |
| [205,206] | GFRP | NH | Diffusion, degradation |
| [207] | Concrete | CH | Diffusion, swelling, degradation, fracture |
| [208] | Polyamide composites | CH | Diffusion, swelling, degradation, damage |
| [202,209,210] | GFRP | CH | Diffusion, swelling, degradation, fracture |
| [211] | Titanium composites | Other | Diffusion, degradation |
| [212] | Braided composites | Other | Degradation, fracture |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krauklis, A.E.; Karl, C.W.; Rocha, I.B.C.M.; Burlakovs, J.; Ozola-Davidane, R.; Gagani, A.I.; Starkova, O. Modelling of Environmental Ageing of Polymers and Polymer Composites—Modular and Multiscale Methods. Polymers 2022, 14, 216. https://doi.org/10.3390/polym14010216
Krauklis AE, Karl CW, Rocha IBCM, Burlakovs J, Ozola-Davidane R, Gagani AI, Starkova O. Modelling of Environmental Ageing of Polymers and Polymer Composites—Modular and Multiscale Methods. Polymers. 2022; 14(1):216. https://doi.org/10.3390/polym14010216
Chicago/Turabian StyleKrauklis, Andrey E., Christian W. Karl, Iuri B. C. M. Rocha, Juris Burlakovs, Ruta Ozola-Davidane, Abedin I. Gagani, and Olesja Starkova. 2022. "Modelling of Environmental Ageing of Polymers and Polymer Composites—Modular and Multiscale Methods" Polymers 14, no. 1: 216. https://doi.org/10.3390/polym14010216
APA StyleKrauklis, A. E., Karl, C. W., Rocha, I. B. C. M., Burlakovs, J., Ozola-Davidane, R., Gagani, A. I., & Starkova, O. (2022). Modelling of Environmental Ageing of Polymers and Polymer Composites—Modular and Multiscale Methods. Polymers, 14(1), 216. https://doi.org/10.3390/polym14010216