Wide-Ranging Multitool Study of Structure and Porosity of PLGA Scaffolds for Tissue Engineering
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussions
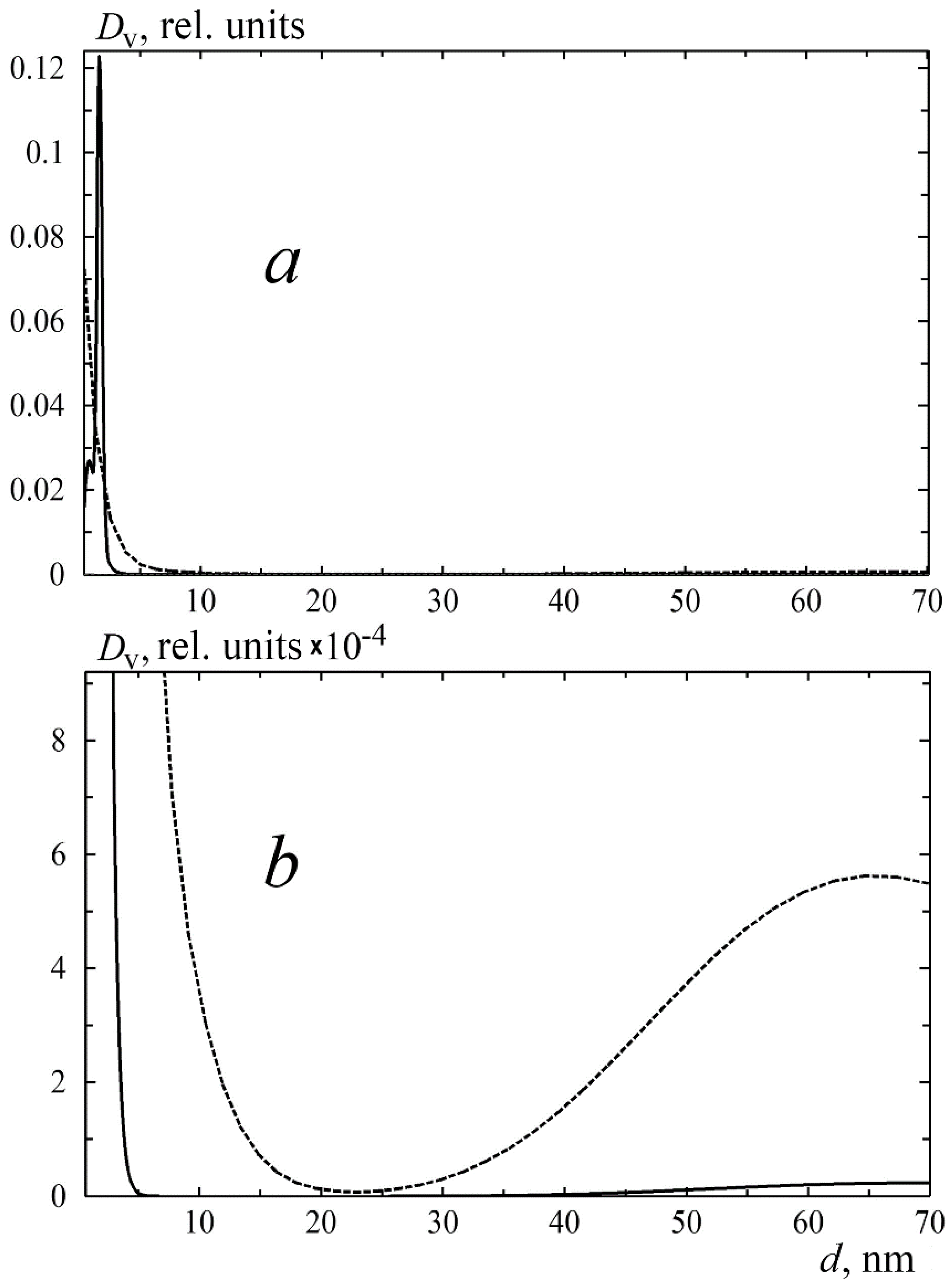
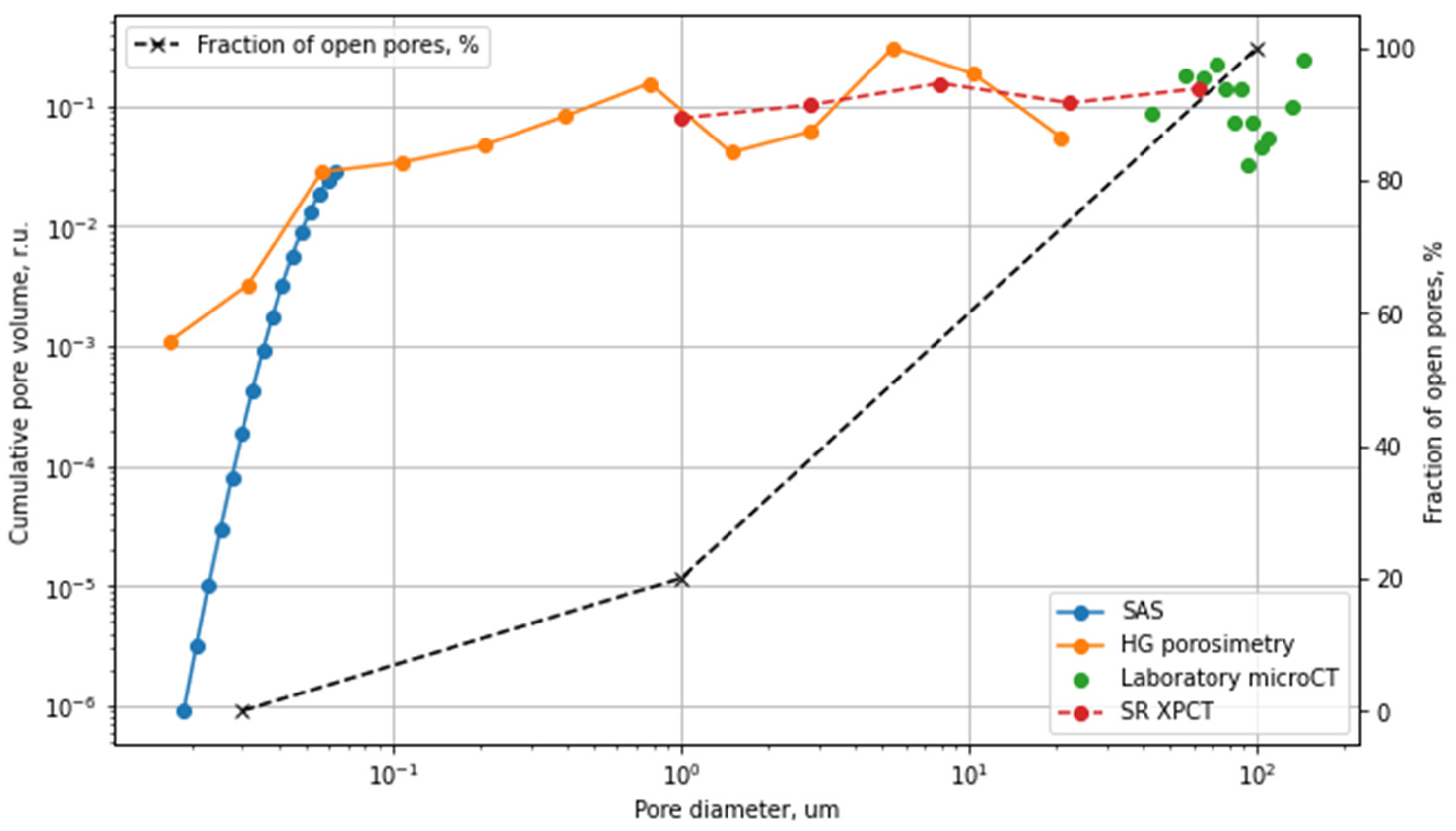
3.1. Small-Angle X-ray Scattering (SAXS)
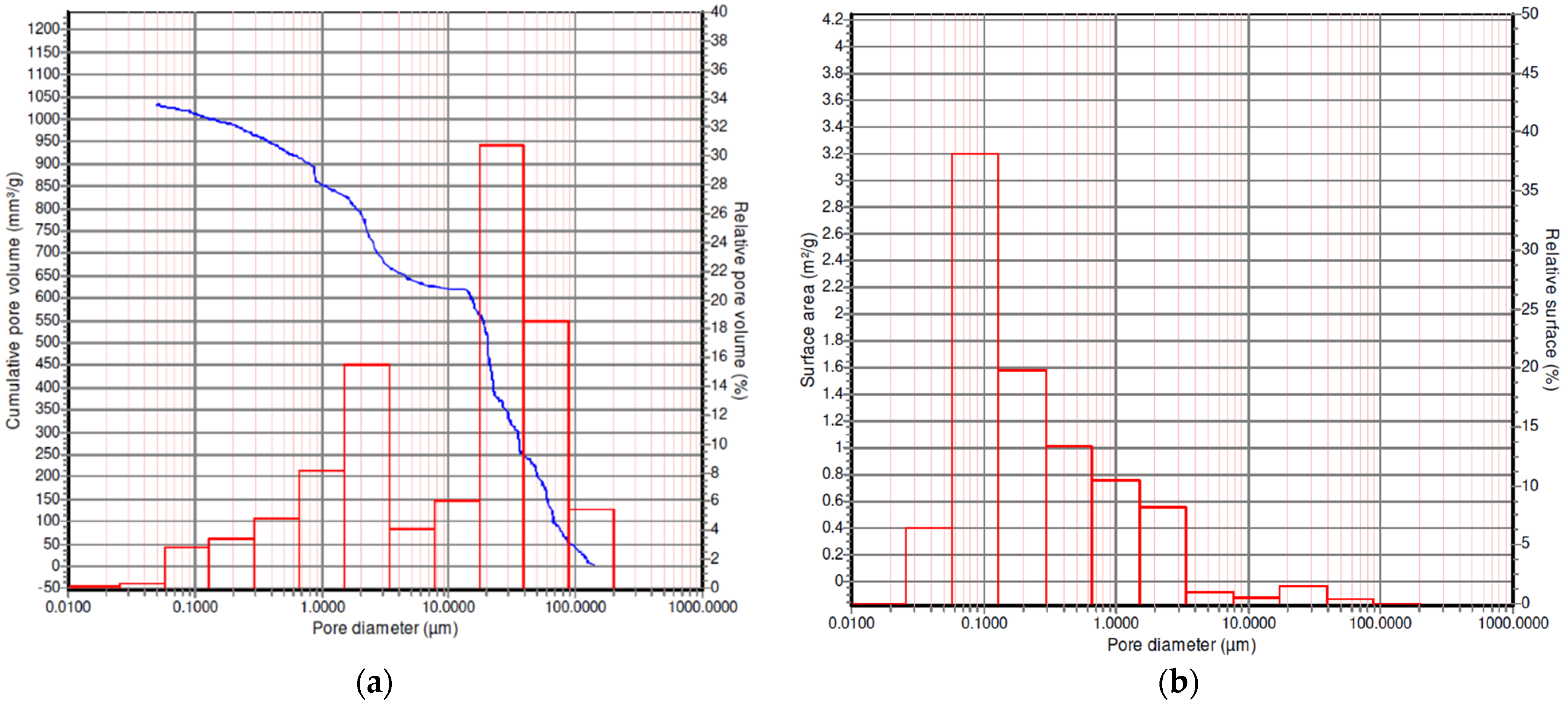
3.2. Helium Pycnometry and Mercury Intrusion Porosimetry
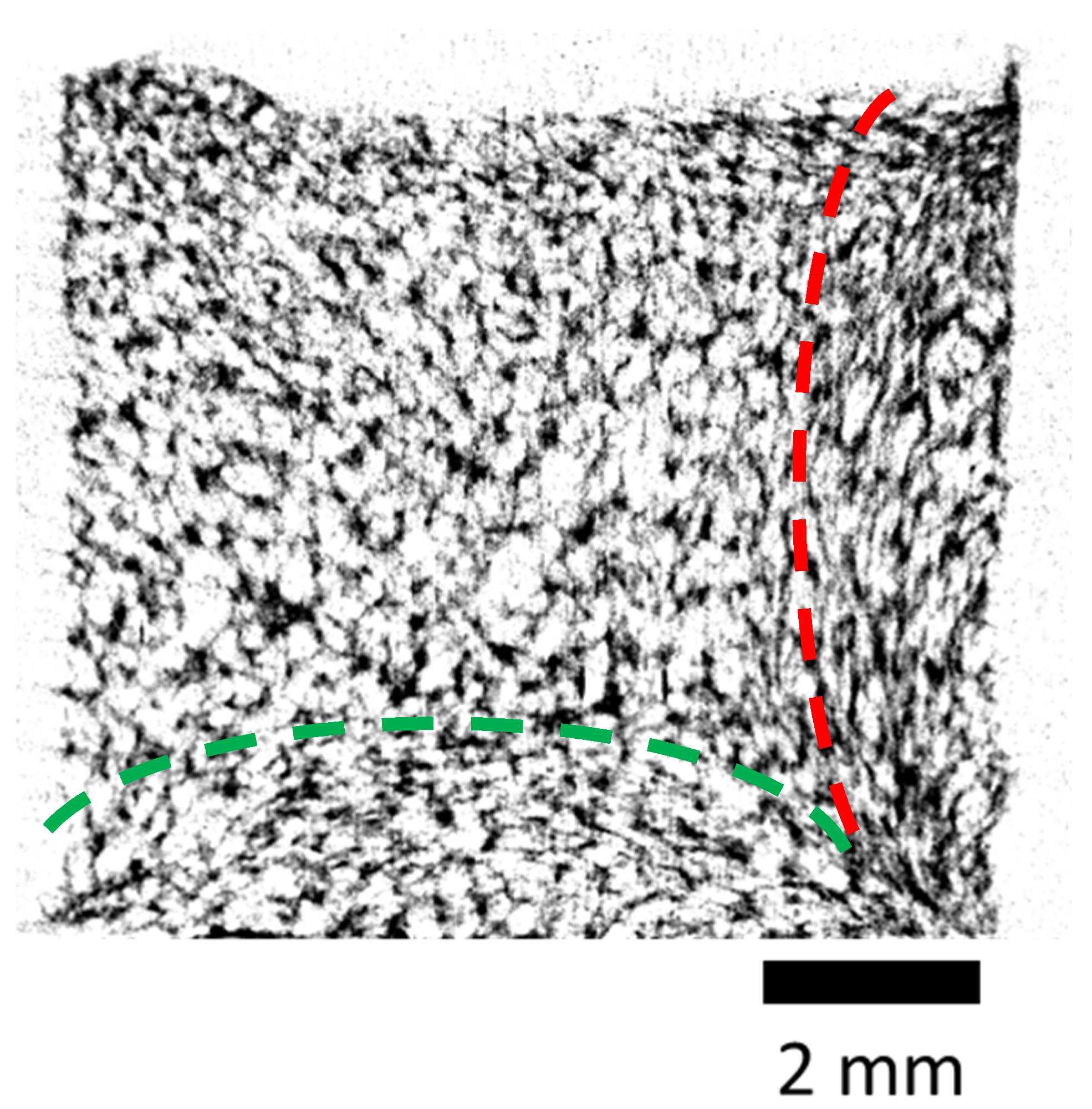
3.3. X-ray MicroCT
- (1)
- for each point belonging to the pores, the Euclidean distance Ed(x,y,z) to the nearest matrix edge was calculated;
- (2)
- to determine the radii of the pores (approximating that the pores are spherical), the positions of local maxima of function Ed(x,y,z) were found (distance to the closest border) and these values used as the radii of the pores. The coordinates of the maxima were used as the centers inscribed in the spheres of the pores. This step is similar to the approach implemented in [49], in which the method was used to analyze the thickness of the wall, instead of the pore size, as is the case here;
- (3)
- the “watershed search” segmentation method [50], with the starting points in the positions of the local maxima identified earlier, was used for three-dimensional segmentation;
- (4)
- using a pseudo-random color scale, the three-dimensional segmented areas were colored (Figure 6);
- (5)
- for each segmented element, the volume and effective radius of the sphere was calculated.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ratner, B.D.; Hoffman, A.S.; Schoen, F.J.; Lemons, J.E. Biomaterials Science. An Introduction to Materials in Medicine, 3rd ed.; Academic Press: Boston, MA, USA, 2012. [Google Scholar]
- Niaounakis, M. Biopolymers: Applications and Trends; Elsevier BV: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Pan, J. Modelling Degradation of Bioresorbable Polymeric Medical Devices; Woodhead Publishing: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Manavitehrani, I.; Fathi, A.; Badr, H.; Daly, S.; Negahi Shirazi, A.; Dehghani, F. Biomedical applications of biodegradable polyes-ters. Polymers 2016, 8, 20. [Google Scholar] [CrossRef]
- Pan, Z.; Ding, J.D. Poly(lactide-co-glycolide) porous scaffolds for tissue engineering and regenerative medicine. Interface Focus 2012, 2, 366–377. [Google Scholar] [CrossRef]
- Tsung, J.; Burgess, D.J. Biodegradable polymers in drug delivery systems. In Fundamentals and Applications of Controlled Release Drug Delivery; Siepmann, J., Siegel, R.A., Rathbone, M.J., Eds.; Springer: Boston, MA, USA, 2012; pp. 107–123. [Google Scholar]
- Makadia, H.K.; Siegel, S.J. Poly lactic-co-glycolic acid (PLGA) as biodegradable controlled drug delivery carrier. Polymers 2011, 3, 1377–1397. [Google Scholar] [CrossRef]
- Nair, L.S.; Laurencin, C.T. Biodegradable polymers as biomaterials. Prog. Polym. Sci. 2007, 32, 762–798. [Google Scholar] [CrossRef]
- Gentile, P.; Chiono, V.; Carmagnola, I.; Hatton, P.V. An overview of poly(lactic-co-glycolic) acid (PLGA)-based biomaterials for bone tissue engineering. Int. J. Mol. Sci. 2014, 15, 3640–3659. [Google Scholar] [CrossRef]
- Lanao, R.P.F.; Jonker, A.M.; Wolke, J.G.C.; Jansen, J.A.; van Hest, J.C.M.; Leeuwenburgh, S.C.G. Physicochemical properties and ap-plications of poly(lactic-co-glycolic acid) for use in bone regeneration. Tissue Eng. Part B Rev. 2013, 19, 380–390. [Google Scholar] [CrossRef]
- Rodriguez, F.; Cohen, C.; Ober, C.K.; Archer, L. Principles of Polymer Systems, 5th ed.; Taylor & Francis: New York, NY, USA, 2003. [Google Scholar]
- Boland, E.L.; Shine, R.; Kelly, N.; Sweeney, C.A.; McHugh, P.E. A review of material degradation modelling for the analysis and design of bioabsorbable stents. Ann. Biomed. Eng. 2016, 44, 341–356. [Google Scholar] [CrossRef] [PubMed]
- Li, S.M. Hydrolytic degradation characteristics of aliphatic polyesters derived from lactic and glycolic acids. J. Biomed. Mater. Res. 1999, 48, 342–353. [Google Scholar] [CrossRef]
- Engineer, C.; Parikh, J.; Raval, A. Review on hydrolytic degradation behavior of biodegradable polymers from controlled drug delivery system. Trends Biomater. Artif. Organs 2011, 25, 79–85. [Google Scholar]
- Von Burkersroda, F.; Schedl, L.; Göpferich, A. Why degradable polymers undergo surface erosion or bulk erosion. Biomaterials 2002, 23, 4221–4231. [Google Scholar] [CrossRef]
- Borovikov, P.I.; Antonov, E.N.; Dunaev, A.G.; Krotova, L.I.; Sviridov, A.P.; Fatkhudinov, T.H.; Popov, V.K. Model of aliphatic polyesters hydrolysis comprising water and oligomers diffusion. Polym. Degrad. Stab. 2019, 159, 70–78. [Google Scholar] [CrossRef]
- Hollister, S.J. Porous scaffold design for tissue engineering. Nat. Mater. 2005, 4, 518–524. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, F.J. Biomaterials & scaffolds for tissue engineering. Mater. Today 2011, 14, 88–95. [Google Scholar]
- Sampath, U.G.T.; Ching, Y.C.; Chuah, C.H.; Sabariah, J.J.; Lin, P.-C. Fabrication of porous materials from natural/synthetic biopolymers and their composites. Materials 2016, 9, 991. [Google Scholar] [CrossRef] [PubMed]
- Lowell, S.; Shields, J.E.; Thomas, M.A.; Thommes, M. Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density; Springer: New York, NY, USA, 2004. [Google Scholar]
- Feigin, L.A.; Svergun, D.I. Structure Analysis by Small-Angle X-ray and Neutron Scattering; Plenum Press: New York, NY, USA, 1987; p. 321. [Google Scholar]
- Stange, U.; Scherf-Clavel, M.; Gieseler, H.J. Application of gas pycnometry for the density measurement of freeze-dried products. Pharm. Sci. 2013, 102, 4087–4099. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.G.T.; Horn, J.C.; Bleakney, M.; Siderius, D.W.; Espinal, L. Understanding material characteristics through signature traits from helium pycnometry. Langmuir 2019, 35, 2115–2122. [Google Scholar] [CrossRef]
- Pirard, R.; Heinrichs, B.; Cantfort, O.; Pirard, J.-P. Mercury porosimetry applied to low density xerogels; relation between structure and mechanical properties. J. Sol Gel Sci. Tech. 1998, 13, 335–339. [Google Scholar] [CrossRef]
- Hao, N.; Wang, Y.L.; Mao, L.T.; Liu, Q. The fractal characteristic analysis of coal pore structure based on mercury intrusion porosimetry. Adv. Civil Ind. Eng. 2013, 4, 353–356. [Google Scholar] [CrossRef]
- Al-Raoush, R.; Willson, C. Extraction of physically realistic pore network properties from three-dimensional synchrotron X-ray microtomography images of unconsolidated porous media systems. J. Hydrol. 2005, 300, 44–64. [Google Scholar] [CrossRef]
- Cooper, A. Porous Materials and Supercritical Fluids. Adv. Mater. 2003, 15, 1049–1059. [Google Scholar] [CrossRef]
- Gualandi, C. Porous Polymeric Bioresorbable Scaffolds for Tissue Engineering; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bogorodskii, S.E.; Krotova, L.I.; Mironov, A.V.; Popov, V.K. Fabrication of highly porous bioresorbable polymer matrices us-ing supercritical carbon dioxide. Russ. J. Phys. Chem. B 2013, 7, 916–923. [Google Scholar] [CrossRef]
- Barry, J.J.A.; Silva, M.M.C.G.; Popov, V.K.; Shakeheff, K.M.; Howdle, S.M. Supercritical carbon dioxide: Putting the fizz into bio-materials. Phil. Trans. R. Soc. A 2006, 364, 249–261. [Google Scholar] [CrossRef]
- Baldino, L.; Cardea, S.; Reverchon, E. Natural composite aerogels production by supercritical gel drying. Chem. Eng. Trans. 2015, 43, 739–744. [Google Scholar]
- Ho, S.T.; Hutmacher, D.W. A comparison of micro CT with other techniques used in the characterization of scaffolds. Biomaterials 2006, 27, 1362–1376. [Google Scholar] [CrossRef]
- Grémare, A.; Guduric, V.; Bareille, R.; Heroguez, V.; Latour, S.; L’Heureux, N.; Fricain, J.-C.; Catros, S.; le Nihouannen, D. Characterization of printed PLA scaffolds for bone tissue engineering. J. Biomed. Mater. Res. Part A 2018, 106, 887–894. [Google Scholar] [CrossRef]
- Tai, H.; Mather, M.L.; Howard, D.; Wang, W.; White, L.J.; Crowe, J.A.; Morgan, S.P.; Chandra, A.; Williams, D.J.; Howdle, S.M.; et al. Control of pore size and structure of tissue engineering scaffolds produced by supercritical fluid processing. Eur. Cells Mater. 2007, 14, 64–77. [Google Scholar] [CrossRef]
- Lemon, G.; Reinwald, Y.; White, L.J.; Howdle, S.M.; Shakesheff, K.M.; King, J.R. Interconnectivity analysis of supercritical CO2-foamed scaffolds. Comput. Methods Programs Biomed. 2012, 106, 139–149. [Google Scholar] [CrossRef][Green Version]
- Bogorodskii, S.E.; Zarkhina, T.S.; Kuznetsov, E.V.; Minaeva, S.A.; Popov, V.K.; Solov’Eva, A.B.; Timashev, P.S. Morphological changes of the polylactic acid microstructure under the action of supercritical carbon dioxide. Russ. J. Phys. Chem. B 2014, 8, 924–931. [Google Scholar] [CrossRef]
- Mogilevsky, L.Y.; Dembo, A.T.; Svergun, D.I.; Feigin, L.A. Automatic small-angle X-ray diffractometer with position-sensitive detector. Crystallography 1984, 29, 587–591. (In Russian) [Google Scholar]
- State Standard R8.698-2010. Dimensional Parameters of Nanoparticles and Thin Films. Measurement Technique with a Small-Angle X-ray Diffractometer; Standardinform: Moscow, Russia, 2010; p. 41. (In Russian)
- Svergun, D.I.; Konarev, P.V.; Volkov, V.V.; Koch, M.H.J.; Sager, W.F.C.; Smeets, J.; Blokhuis, E.M. A small angle X-ray scattering study of the droplet–cylinder transition in oil–rich sodium bis(2–ethylhexyl) sulfosuccinate microemulsions. J. Chem. Phys. 2000, 113, 1651–1665. [Google Scholar] [CrossRef]
- Franke, D.; Petoukhov, M.V.; Konarev, P.V.; Panjkovich, A.; Tuukkanen, A.; Mertens, H.D.T.; Kikhney, A.G.; Hajizadeh, N.R.; Franklin, J.M.; Jeffries, C.M.; et al. ATSAS 2.8: A comprehensive data analysis suite for small-angle scattering from macromolecular solutions. J. Appl. Crystallogr. 2017, 50, 1212–1225. [Google Scholar] [CrossRef] [PubMed]
- Schulz, G.V. Über die Beziehung zwischen Reaktionsgeschwindigkeit und Zusammensetzung des Reaktionsproduktes bei Makropolymerisationsvorgängen. Z. Phys. Chem. Abt. 1935, 30, 379–398. [Google Scholar]
- Buzmakov, A.V.; Asadchikov, V.E.; Zolotov, D.A.; Roshchin, B.S.; Dymshits, Y.M.; Shishkov, V.A.; Chukalina, M.V.; Ingacheva, A.S.; Ichalova, D.E.; Krivonosov, Y.S.; et al. Laboratory Microtomographs: Design and Data Processing Algorithms. Crystallogr. Rep. 2018, 63, 1057–1061. [Google Scholar] [CrossRef]
- Rau, C. Imaging with Coherent Synchrotron Radiation: X-ray Imaging and Coherence Beamline (I13) at Diamond Light Source. Synchrotron Radiat. News 2017, 30, 19–25. [Google Scholar] [CrossRef]
- Bodey, A.J.; Rau, C. Launch of the I13-2 data beamline at the Diamond Light Source synchrotron. J. Phys. Conf. Ser. 2017, 849, 12038. [Google Scholar] [CrossRef]
- Atwood, R.C.; Bodey, A.J.; Price, S.W.T.; Basham, M.; Drakopoulos, M. A high-throughput system for high-quality tomographic reconstruction of large datasets at Diamond Light Source. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140398. [Google Scholar] [CrossRef]
- Wadeson, N.; Basham, M. Savu: A Python-based, MPI framework for simultaneous processing of multiple, N-dimensional, large tomography datasets. arXiv 2016, arXiv:1610.08015. [Google Scholar]
- Vo, N.T.; Atwood, R.C.; Drakopoulos, M. Radial lens distortion correction with sub-pixel accuracy for X-ray micro-tomography. Opt. Express 2015, 23, 32859–32868. [Google Scholar] [CrossRef] [PubMed]
- Grady, L. Random Walks for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1768–1783. [Google Scholar] [CrossRef]
- Komlev, V.; Mastrogiacomo, M.; Pereira, R.C.; Peyrin, F.; Rustichelli, F.; Cancedda, R. Biodegradation of porous calcium phosphate scaffolds in an ectopic bone formation model studied by X-ray computed microtomograph. Eur. Cells Mater. 2010, 19, 136–146. [Google Scholar] [CrossRef]
- Najman, L.; Schmitt, M. Watershed of a continuous function. Signal Process. 1994, 38, 99–112. [Google Scholar] [CrossRef]
- Asadchikov, V.E.; Senin, R.A.; Blagov, A.E.; Buzmakov, A.V.; Gulimova, V.I.; Zolotov, D.A.; Orekhov, A.S.; Osadchaya, A.S.; Podurets, K.M.; Savel’Ev, S.V.; et al. Comparison of the data of X-ray microtomography and fluorescence analysis in the study of bone-tissue structure. Crystallogr. Rep. 2012, 57, 700–707. [Google Scholar] [CrossRef]




| Sample Mass, g | Skeletal Density, g/cm3 | Bulk Density, g/cm3 | Apparent Density, g/cm3 |
|---|---|---|---|
| 0.0476 | 0.7891 | 0.5012 | 1.0353 |
| Specific Pore Volume, mm³/g | Specific Pore Surface Area, m²/g | Average Pore Diameter, μm | Median Pore Diameter, μm |
|---|---|---|---|
| 1033.58 | 3.538 | 1.1686 | 20.2424 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buzmakov, A.V.; Dunaev, A.G.; Krivonosov, Y.S.; Zolotov, D.A.; Dyachkova, I.G.; Krotova, L.I.; Volkov, V.V.; Bodey, A.J.; Asadchikov, V.E.; Popov, V.K. Wide-Ranging Multitool Study of Structure and Porosity of PLGA Scaffolds for Tissue Engineering. Polymers 2021, 13, 1021. https://doi.org/10.3390/polym13071021
Buzmakov AV, Dunaev AG, Krivonosov YS, Zolotov DA, Dyachkova IG, Krotova LI, Volkov VV, Bodey AJ, Asadchikov VE, Popov VK. Wide-Ranging Multitool Study of Structure and Porosity of PLGA Scaffolds for Tissue Engineering. Polymers. 2021; 13(7):1021. https://doi.org/10.3390/polym13071021
Chicago/Turabian StyleBuzmakov, Alexey V., Andrey G. Dunaev, Yuriy S. Krivonosov, Denis A. Zolotov, Irina G. Dyachkova, Larisa I. Krotova, Vladimir V. Volkov, Andrew J. Bodey, Victor E. Asadchikov, and Vladimir K. Popov. 2021. "Wide-Ranging Multitool Study of Structure and Porosity of PLGA Scaffolds for Tissue Engineering" Polymers 13, no. 7: 1021. https://doi.org/10.3390/polym13071021
APA StyleBuzmakov, A. V., Dunaev, A. G., Krivonosov, Y. S., Zolotov, D. A., Dyachkova, I. G., Krotova, L. I., Volkov, V. V., Bodey, A. J., Asadchikov, V. E., & Popov, V. K. (2021). Wide-Ranging Multitool Study of Structure and Porosity of PLGA Scaffolds for Tissue Engineering. Polymers, 13(7), 1021. https://doi.org/10.3390/polym13071021








