Determination by Relaxation Tests of the Mechanical Properties of Soft Polyacrylamide Gels Made for Mechanobiology Studies
Abstract
1. Introduction
2. Materials and Methods
2.1. Polyacrylamide (PAM) Hydrogels Preparation
2.2. Poly-Dimethylsiloxane (PDMS) Preparation
2.3. Mechanobiology Test with Fibroblast Culture
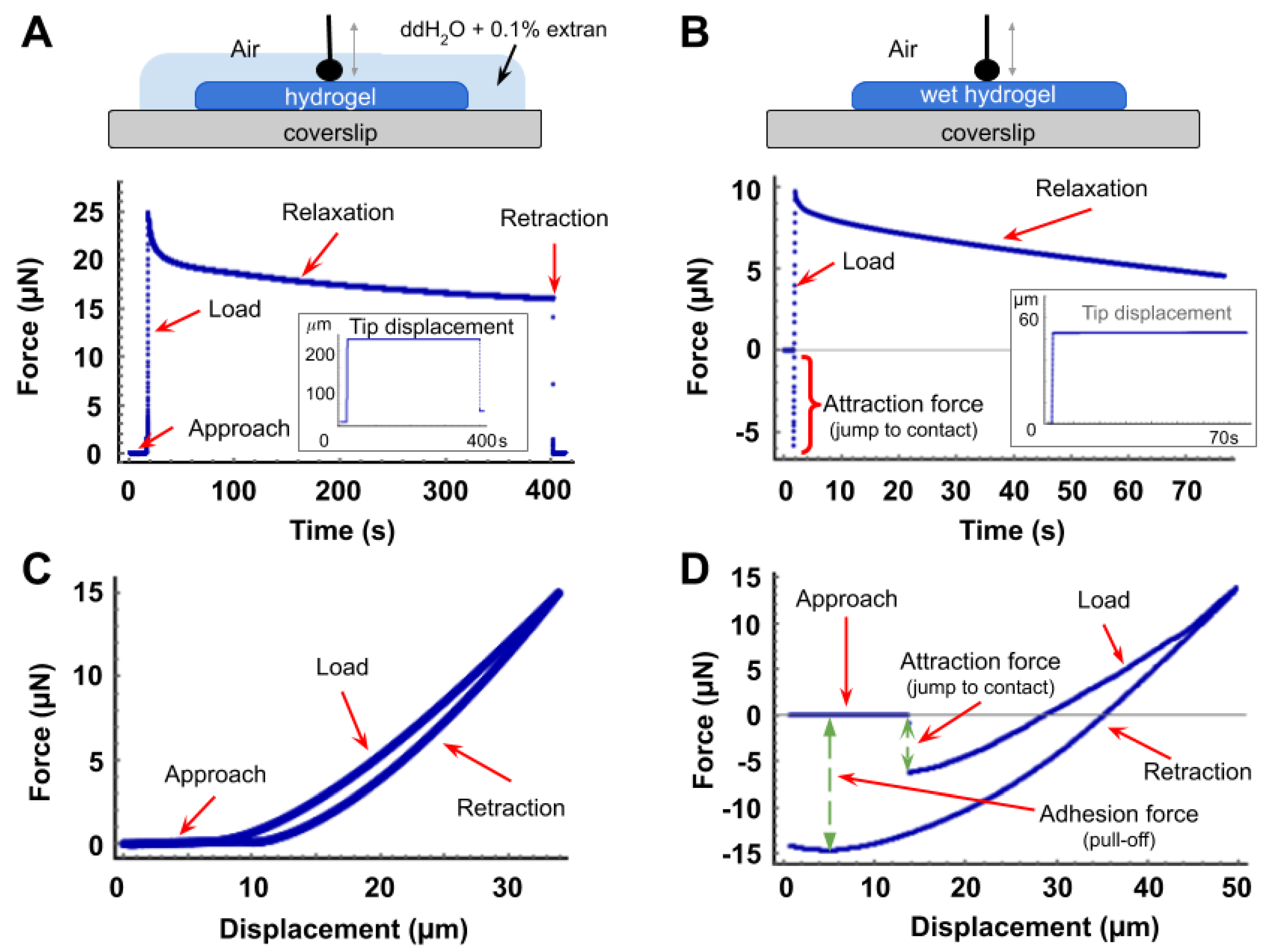
2.4. Microindentation and Relaxation Tests
2.5. Force Curves Processing
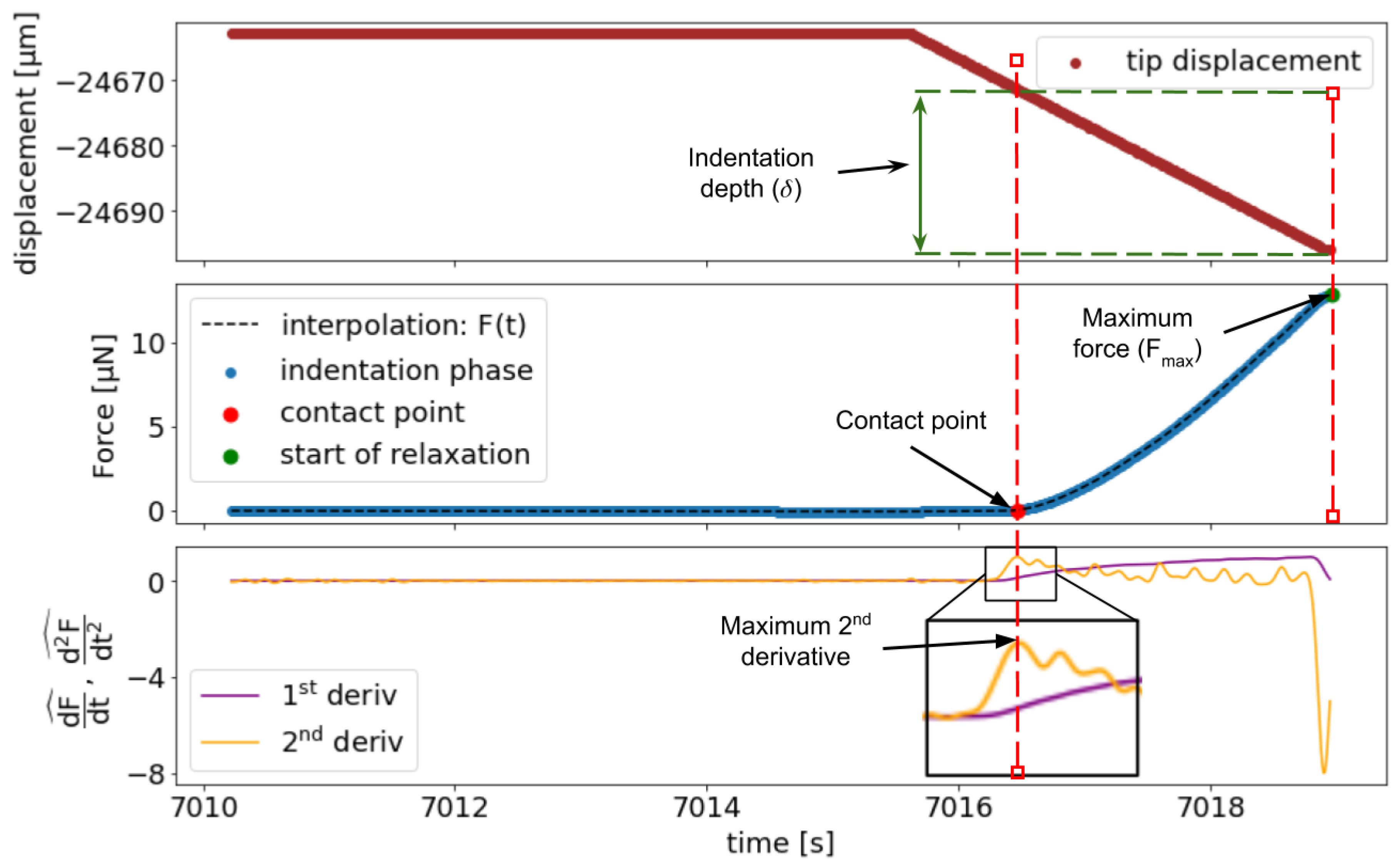
2.5.1. Determination of the Contact Point
2.5.2. Indentation Data Analysis
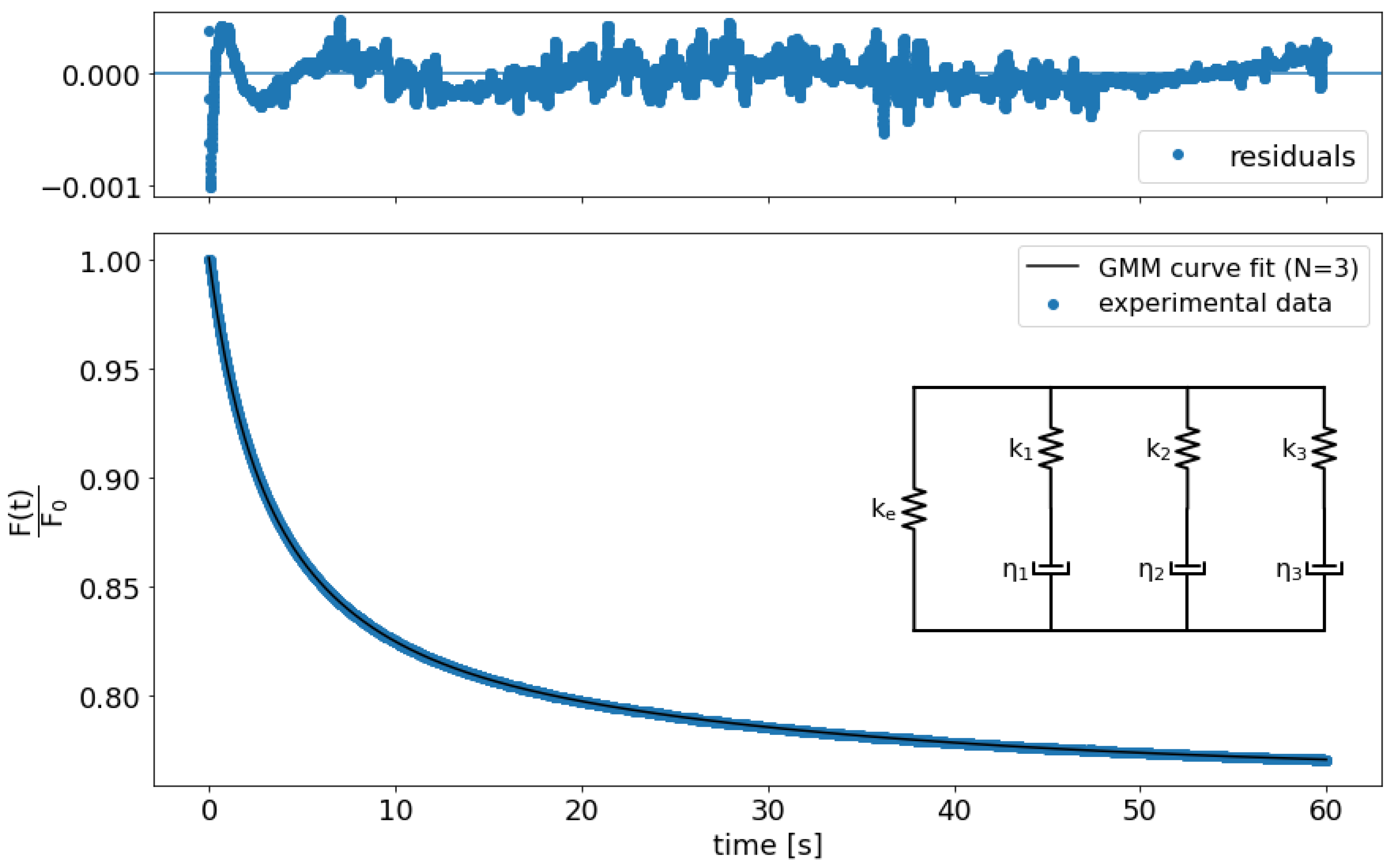
2.5.3. Relaxation Data Analysis
2.6. Statistical Analysis
3. Results
3.1. Force Curves and Correction for Tip Displacement
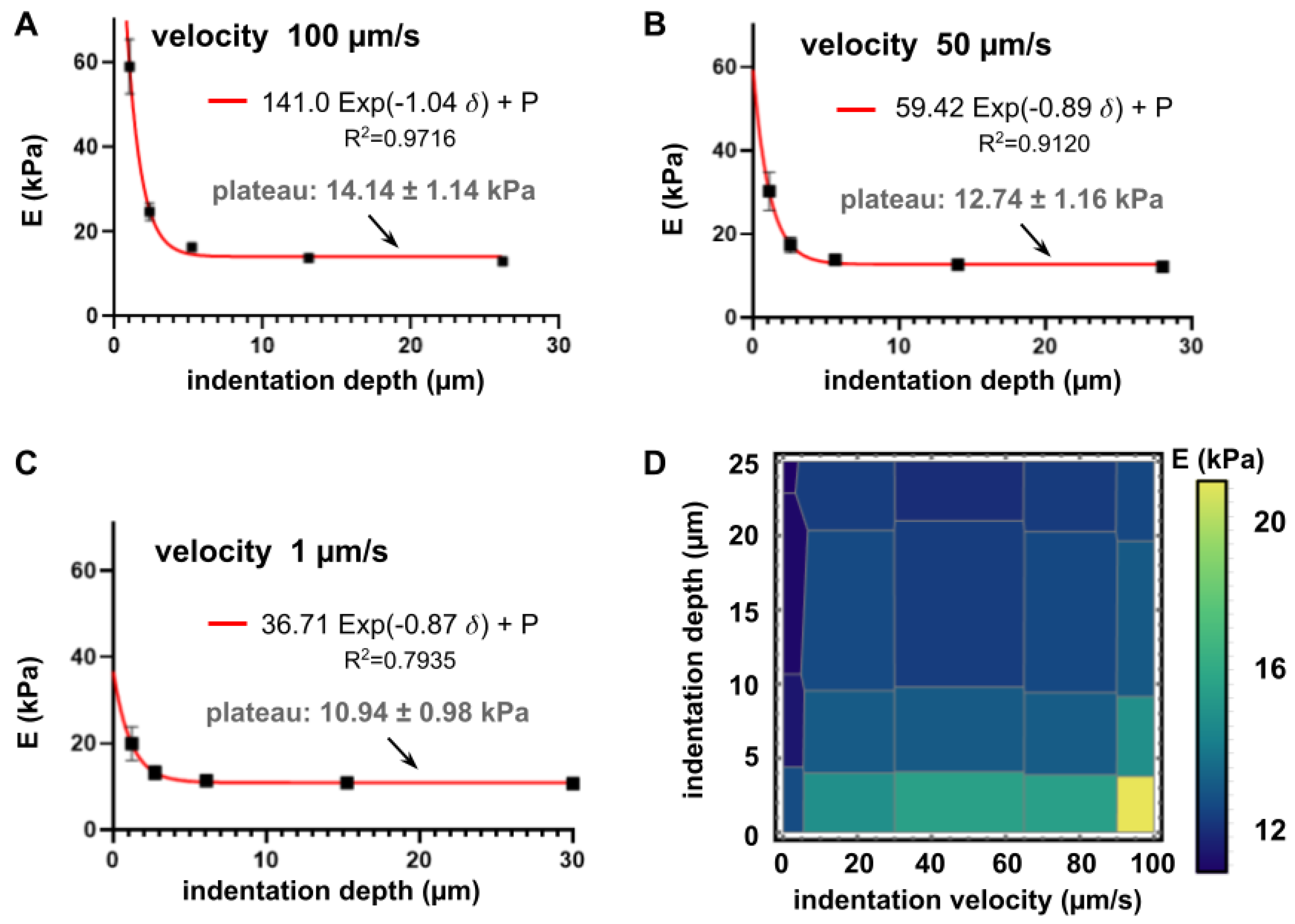
3.2. Influence of Velocity and Depth of Indentation
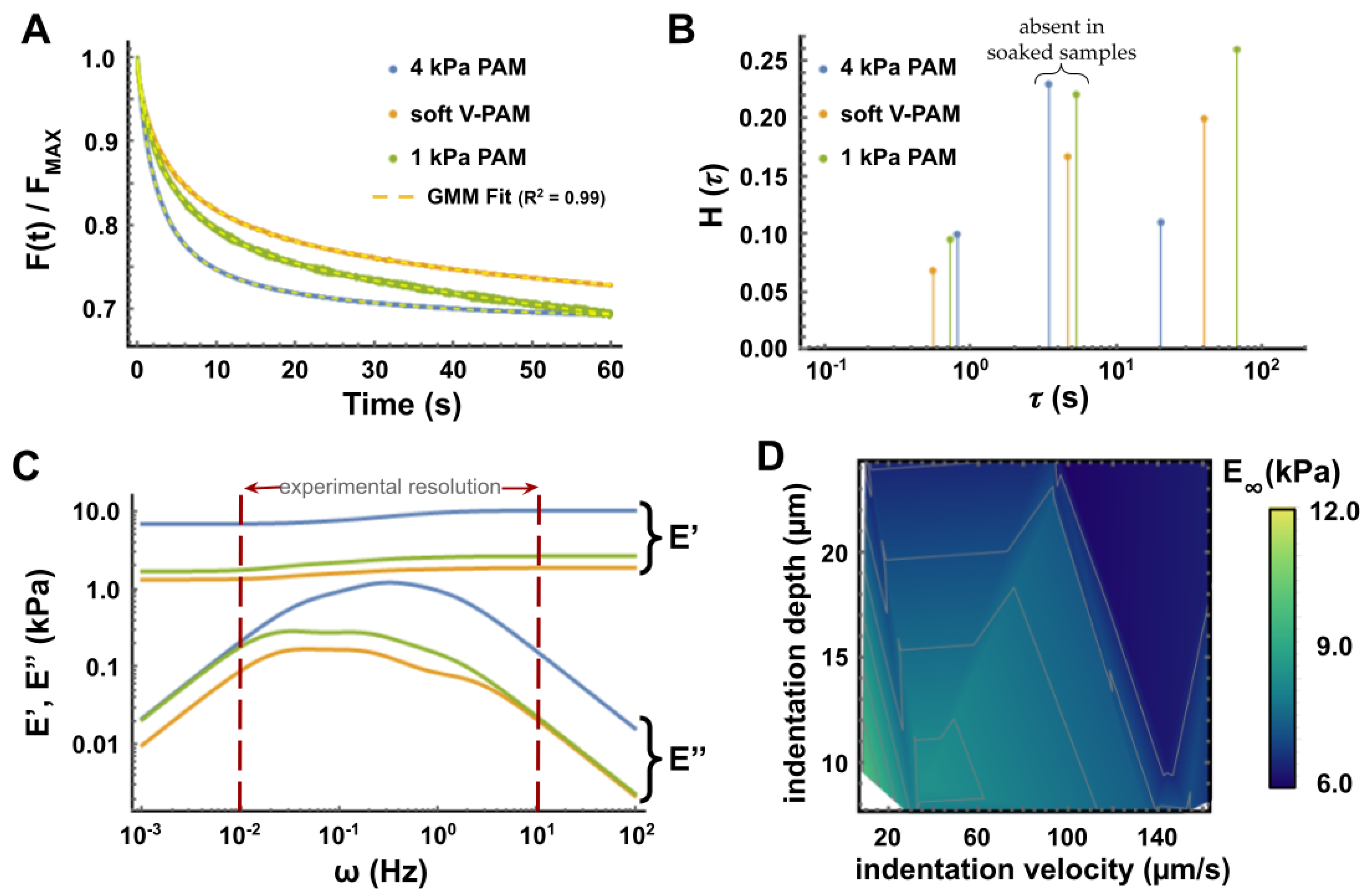
3.3. Relaxation Tests to Characterize PAM Mechanical Properties
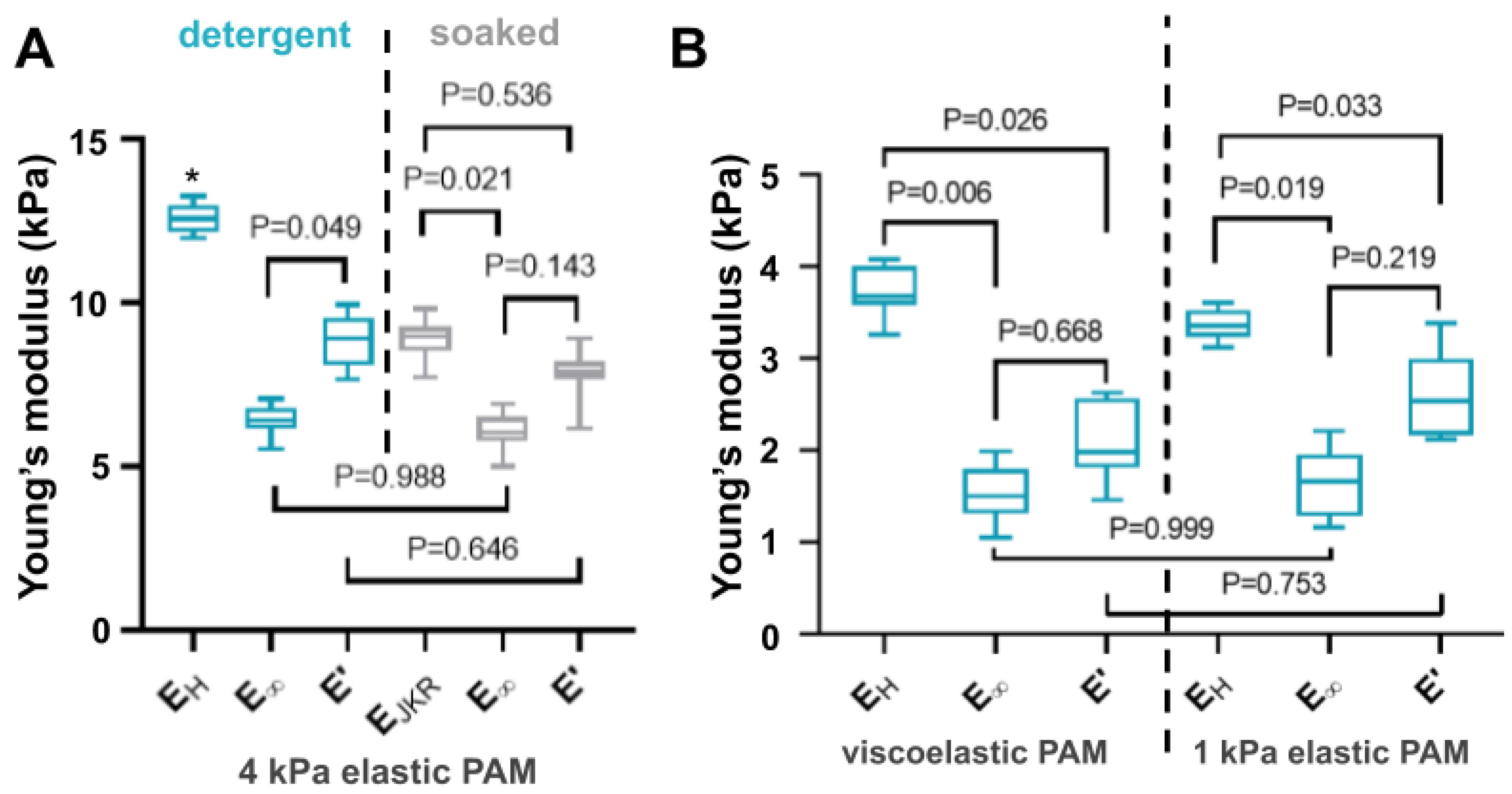
3.4. Comparison between Microindentation and Relaxation Mechanical Tests
| 4kPa PAM (kPa) | 4kPa PAM (kPa) | Soft V-PAM (kPa) | 1kPa PAM (kPa) | Stiff PAM (kPa) | PDMS 10:1 (MPa) | PDMS 15:1 (MPa) | ||
|---|---|---|---|---|---|---|---|---|
| measurement conditions | soaked | detergent | detergent | detergent | soaked | dry | dry | |
| reported values [reference] | Eref | 4.47 ± 1.19 [5] | - | 1.723 1 [22] | 1.10 ± 0.34 [5] | 34.88 [5] | 1.35–2.01 [67] | 0.9–1.2 [37] |
| micro indentation | E | 8.92 ± 0.55 | 12.60 ± 0.42 | 3.73 ± 0.27 | 3.37 ± 0.17 | 38.72 ± 8.71 | 0.91 ± 0.09 | 0.63 ± 0.01 |
| relaxation tests | E∞ | 6.00 ± 0.57 | 6.41 ± 0.44 | 1.55 ± 0.31 | 1.63 ± 0.39 | 36.01 ± 2.67 | 1.61 ± 0.48 | 0.61 ± 0.17 |
| E′ | 8.25 ± 1.47 | 8.78 ± 0.80 | 2.09 ± 0.40 | 2.57 ± 0.50 | 39.93 ± 2.54 | 1.68 ± 0.47 | 0.65 ± 0.16 | |
3.5. Relevance for Cellular Mechanobiology: Cell Response to PAM Hydrogels of Different Mechanical Properties
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
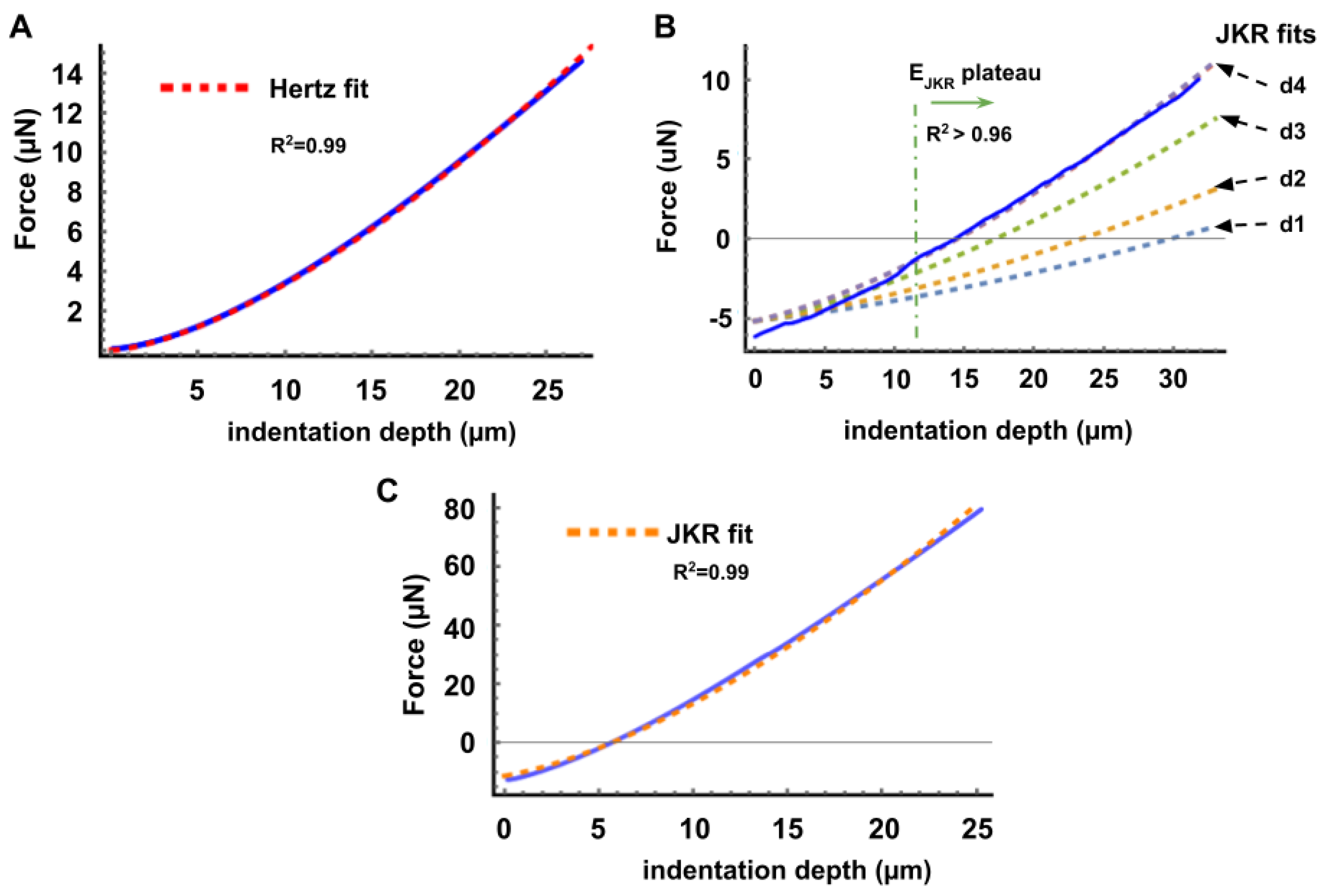
Appendix A. Notes on FD Curve Processing and Analysis


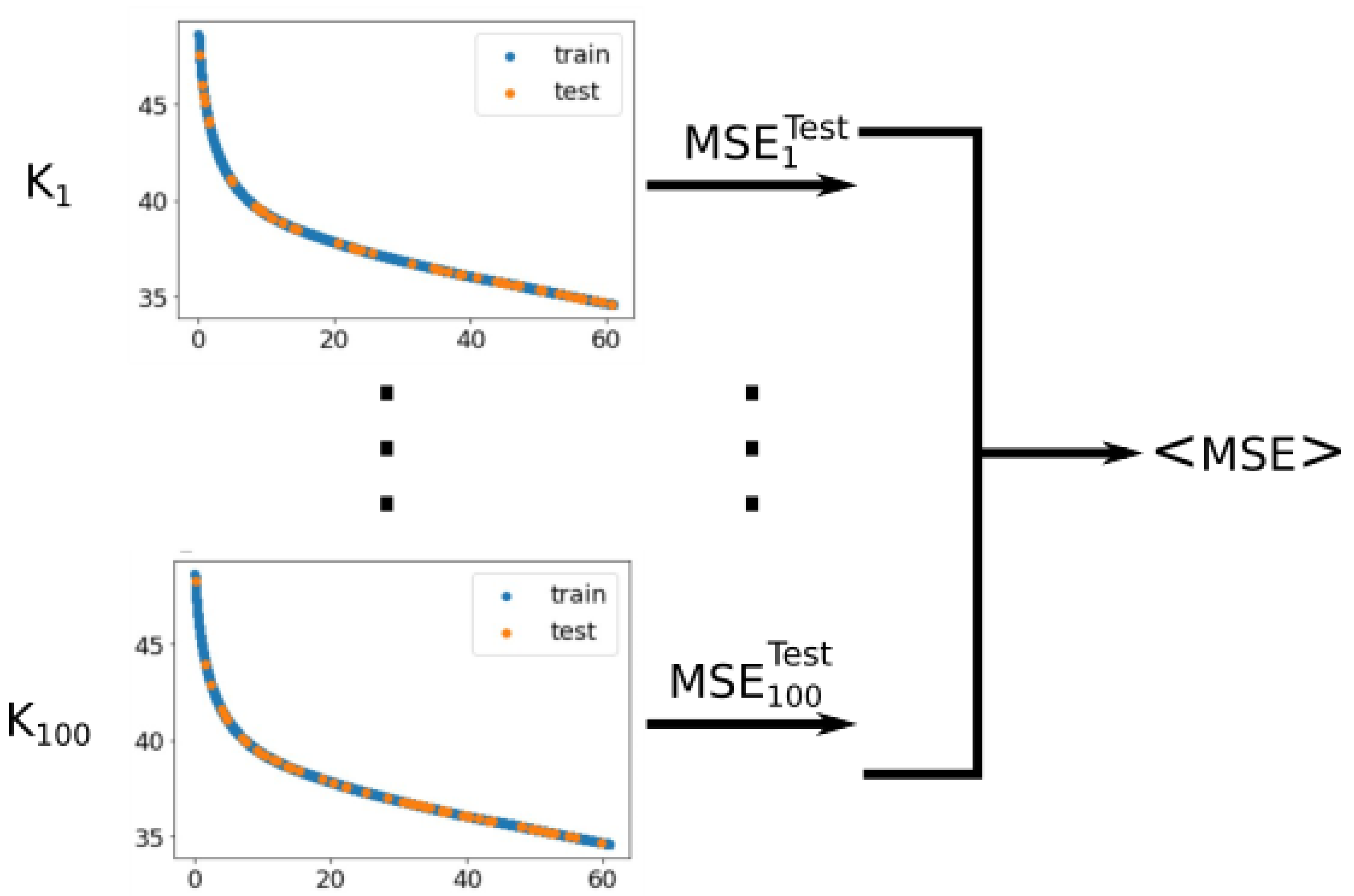
Appendix B. Notes on the Criterion of Cross Validation to Determine a Proper Fitting
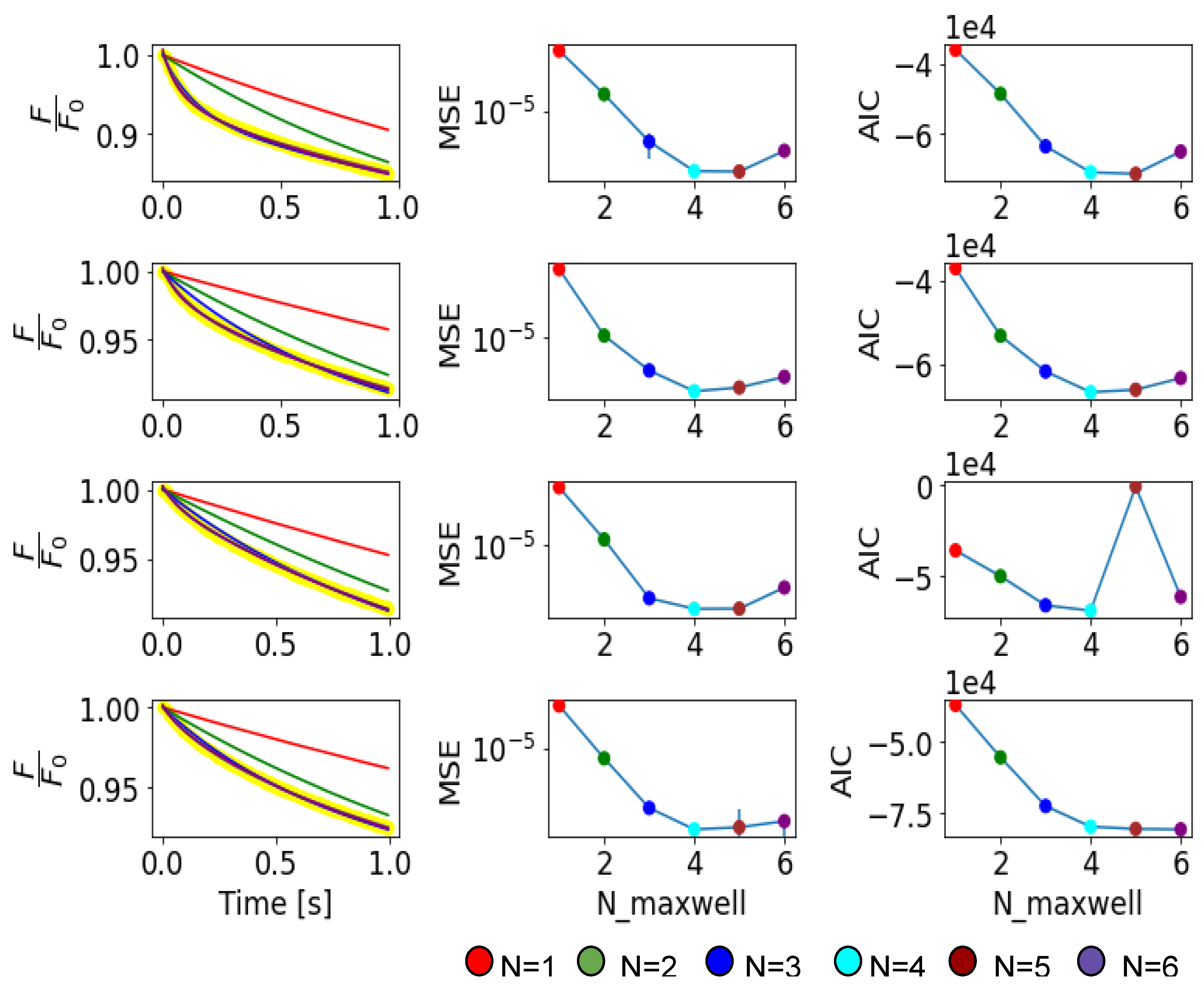
Appendix C. Validation and Comparison with Other Methods

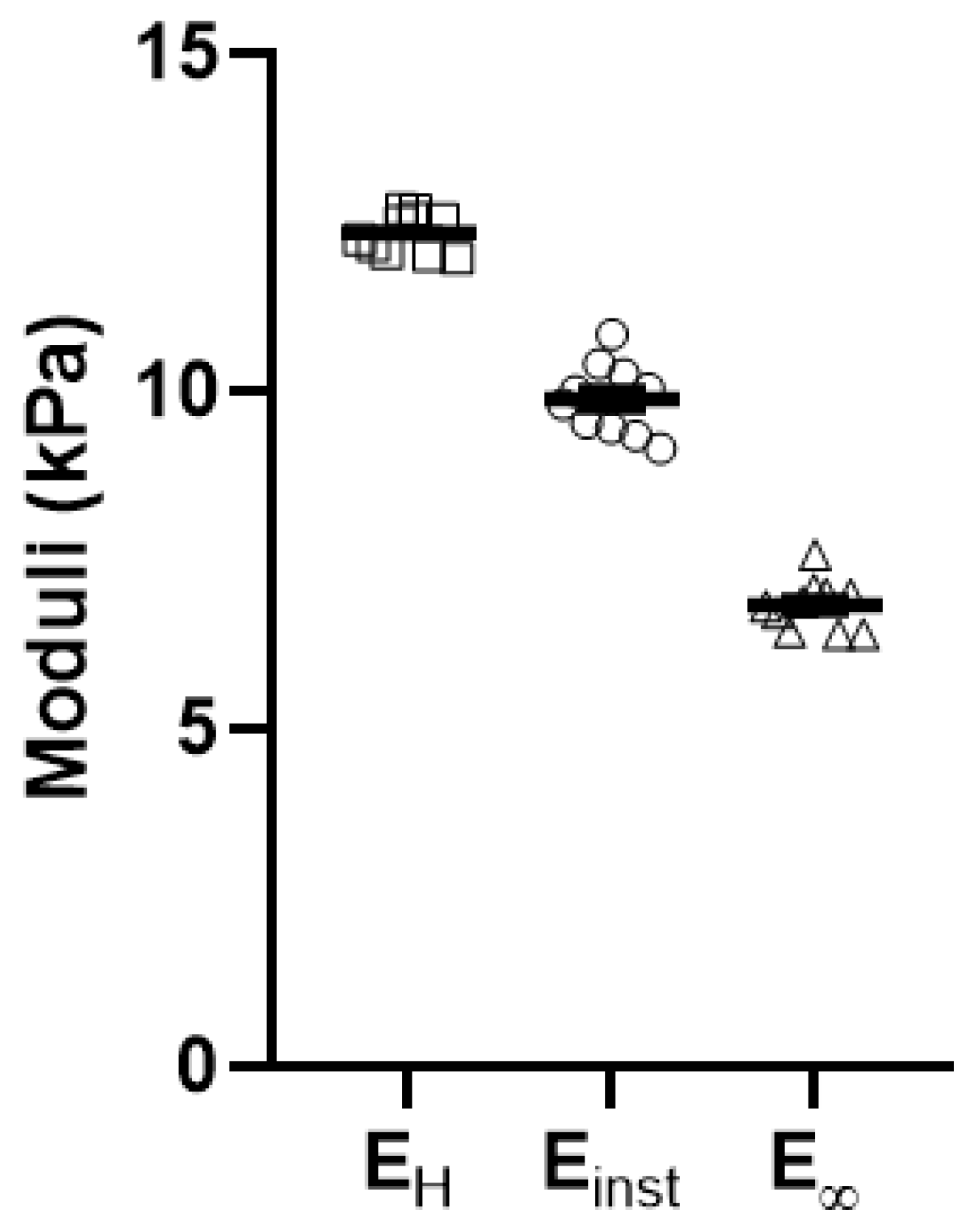
| EH | Einst | E∞ | |
|---|---|---|---|
| r (EH, Ei) | 1.000 | 0.556 | 0.924 |
References
- Roca-Cusachs, P.; Conte, V.; Trepat, X. Quantifying forces in cell biology. Nat. Cell Biol. 2017, 19, 742–751. [Google Scholar] [CrossRef]
- DuFort, C.C.; Paszek, M.J.; Weaver, V.M. Balancing forces: Architectural control of mechanotransduction. Nat. Rev. Mol. Cell Biol. 2011, 12, 308–319. [Google Scholar] [CrossRef] [PubMed]
- Iskratsch, T.; Wolfenson, H.; Sheetz, M.P. Appreciating force and shape—The rise of mechanotransduction in cell biology. Nat. Rev. Mol. Cell Biol. 2014, 15, 825–833. [Google Scholar] [CrossRef] [PubMed]
- Charrier, E.E.; Pogoda, K.; Wells, R.G.; Janmey, P.A. Control of cell morphology and differentiation by substrates with independently tunable elasticity and viscous dissipation. Nat. Commun. 2018, 9, 1–13. [Google Scholar] [CrossRef]
- Tse, J.R.; Engler, A.J. Preparation of Hydrogel Substrates with Tunable Mechanical Properties. Curr. Protoc. Cell Biol. 2010, 47, 10.16.1–10.16.16. [Google Scholar] [CrossRef]
- Ondeck, M.G.; Kumar, A.; Placone, J.K.; Plunkett, C.M.; Matte, B.F.; Wong, K.C.; Fattet, L.; Yang, J.; Engler, A.J. Dynamically stiffened matrix promotes malignant transformation of mammary epithelial cells via collective mechanical signaling. Proc. Natl. Acad. Sci. USA 2019, 116, 3502–3507. [Google Scholar] [CrossRef] [PubMed]
- Caliari, S.R.; Perepelyuk, M.; Soulas, E.M.; Lee, G.Y.; Wells, R.G.; Burdick, J.A. Gradually softening hydrogels for modeling hepatic stellate cell behavior during fibrosis regression. Integr. Biol. 2016, 8, 720–728. [Google Scholar] [CrossRef] [PubMed]
- Rosales, A.M.; Vega, S.L.; DelRio, F.W.; Burdick, J.A.; Anseth, K.S. Hydrogels with Reversible Mechanics to Probe Dynamic Cell Microenvironments. Angew. Chem. Int. Ed. 2017, 56, 12132–12136. [Google Scholar] [CrossRef]
- Al Mayah, A. Biomechanics of Soft Tissues: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781351135818. [Google Scholar]
- Desai, S.S.; Tung, J.C.; Zhou, V.X.; Grenert, J.P.; Malato, Y.; Rezvani, M.; Español-Suñer, R.; Willenbring, H.; Weaver, V.M.; Chang, T.T. Physiological ranges of matrix rigidity modulate primary mouse hepatocyte function in part through hepatocyte nuclear factor 4 alpha. Hepatology 2016, 64, 261–275. [Google Scholar] [CrossRef]
- Chaudhuri, O.; Gu, L.; Klumpers, D.; Darnell, M.; Bencherif, S.A.; Weaver, J.C.; Huebsch, N.; Lee, H.-P.; Lippens, E.; Duda, G.N.; et al. Hydrogels with tunable stress relaxation regulate stem cell fate and activity. Nat. Mater. 2016, 15, 326–334. [Google Scholar] [CrossRef]
- Wu, P.-H.; Aroush, D.R.-B.; Asnacios, A.; Chen, W.-C.; Dokukin, M.E.; Doss, B.L.; Durand-Smet, P.; Ekpenyong, A.; Guck, J.; Guz, N.V.; et al. A comparison of methods to assess cell mechanical properties. Nat. Methods 2018, 15, 491–498. [Google Scholar] [CrossRef]
- Griffin, M.; Premakumar, Y.; Seifalian, A.; Butler, P.E.; Szarko, M. Biomechanical Characterization of Human Soft Tissues Using Indentation and Tensile Testing. J. Vis. Exp. 2016. [Google Scholar] [CrossRef]
- Lin, D.C.; Dimitriadis, E.K.; Horkay, F. Robust Strategies for Automated AFM Force Curve Analysis—II: Adhesion-Influenced Indentation of Soft, Elastic Materials. J. Biomech. Eng. 2007, 129, 904–912. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.-R.; Raghunathan, V.K.; Garland, S.P.; Morgan, J.T.; Russell, P.; Murphy, C.J. Automated AFM force curve analysis for determining elastic modulus of biomaterials and biological samples. J. Mech. Behav. Biomed. Mater. 2014, 37, 209–218. [Google Scholar] [CrossRef]
- Sawicka, A.; Babataheri, A.; Dogniaux, S.; Barakat, A.I.; Gonzalez-Rodriguez, D.; Hivroz, C.; Husson, J. Micropipette force probe to quantify single-cell force generation: Application to T-cell activation. Mol. Biol. Cell 2017, 28, 3229–3239. [Google Scholar] [CrossRef] [PubMed]
- Neuman, K.C.; Nagy, A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2008, 5, 491–505. [Google Scholar] [CrossRef] [PubMed]
- Mihai, L.A.; Goriely, A. How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170607. [Google Scholar] [CrossRef]
- Amar, M.B. Nonlinear visco-elasticity of soft tissues under cyclic deformations. Int. J. Non Linear Mech. 2018, 106, 238–244. [Google Scholar] [CrossRef]
- Gong, Z.; Szczesny, S.E.; Caliari, S.R.; Charrier, E.E.; Chaudhuri, O.; Cao, X.; Lin, Y.; Mauck, R.L.; Janmey, P.A.; Burdick, J.A.; et al. Matching material and cellular timescales maximizes cell spreading on viscoelastic substrates. Proc. Natl. Acad. Sci. USA 2018, 115, E2686–E2695. [Google Scholar] [CrossRef]
- Chaudhuri, O.; Cooper-White, J.; Janmey, P.A.; Mooney, D.J.; Shenoy, V.B. Effects of extracellular matrix viscoelasticity on cellular behaviour. Nature 2020, 584, 535–546. [Google Scholar] [CrossRef]
- Charrier, E.E.; Pogoda, K.; Li, R.; Park, C.Y.; Fredberg, J.J.; Janmey, P.A. A novel method to make viscoelastic polyacrylamide gels for cell culture and traction force microscopy. APL Bioeng. 2020, 4, 036104. [Google Scholar] [CrossRef]
- Mandal, K.; Gong, Z.; Rylander, A.; Shenoy, V.B.; Janmey, P.A. Opposite responses of normal hepatocytes and hepatocellular carcinoma cells to substrate viscoelasticity. Biomater. Sci. 2020, 8, 1316–1328. [Google Scholar] [CrossRef] [PubMed]
- Swoger, M.; Gupta, S.; Charrier, E.E.; Bates, M.; Hehnly, H.; Patteson, A.E. Vimentin intermediate filaments mediate cell shape on visco-elastic substrates. bioRxiv 2020. [Google Scholar] [CrossRef]
- Discher, D.E.; Smith, L.; Cho, S.; Colasurdo, M.; García, A.J.; Safran, S. Matrix Mechanosensing: From Scaling Concepts in ’Omics Data to Mechanisms in the Nucleus, Regeneration, and Cancer. Annu. Rev. Biophys. 2017, 46, 295–315. [Google Scholar] [CrossRef]
- Kim, S.; Uroz, M.; Bays, J.L.; Chen, C.S. Harnessing Mechanobiology for Tissue Engineering. Dev. Cell 2021. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Nieto, M.; Mendoza-Flores, P.; García-Ortiz, D.; Montes-de-Oca, L.M.; Mendoza-Villa, M.; Barrón-González, P.; Espinosa, G.; Menchaca, J.L. Viscoelastic properties of doxorubicin-treated HT-29 cancer cells by atomic force microscopy: The fractional Zener model as an optimal viscoelastic model for cells. Biomech. Modeling Mechanobiol. 2020, 19, 801–813. [Google Scholar] [CrossRef] [PubMed]
- Lekka, M.; Laidler, P. Applicability of AFM in cancer detection. Nat. Nanotechnol. 2009, 4, 72. [Google Scholar] [CrossRef]
- Galluzzi, M.; Biswas, C.S.; Wu, Y.; Wang, Q.; Du, B.; Stadler, F.J. Space-resolved quantitative mechanical measurements of soft and supersoft materials by atomic force microscopy. NPG Asia Mater. 2016, 8, e327. [Google Scholar] [CrossRef]
- Rheinlaender, J.; Dimitracopoulos, A.; Wallmeyer, B.; Kronenberg, N.M.; Chalut, K.J.; Gather, M.C.; Betz, T.; Charras, G.; Franze, K. Cortical cell stiffness is independent of substrate mechanics. Nat. Mater. 2020, 19, 1019–1025. [Google Scholar] [CrossRef]
- Gavara, N. Combined strategies for optimal detection of the contact point in AFM force-indentation curves obtained on thin samples and adherent cells. Sci. Rep. 2016, 6, 21267. [Google Scholar] [CrossRef]
- Guimarães, C.F.; Gasperini, L.; Marques, A.P.; Reis, R.L. The stiffness of living tissues and its implications for tissue engineering. Nat. Rev. Mater. 2020, 5, 351–370. [Google Scholar] [CrossRef]
- Kalcioglu, Z.I.; Mahmoodian, R.; Hu, Y.; Suo, Z.; Van Vliet, K.J. From macro- to microscale poroelastic characterization of polymeric hydrogels via indentation. Soft Matter 2012, 8, 3393–3398. [Google Scholar] [CrossRef]
- Cretu, A.; Castagnino, P.; Assoian, R. Studying the Effects of Matrix Stiffness on Cellular Function using Acrylamide-based Hydrogels. J. Vis. Exp. JoVE 2010, 42, e2089. [Google Scholar] [CrossRef] [PubMed]
- Flores-Merino, M.V.; Chirasatitsin, S.; Lopresti, C.; Reilly, G.C.; Battaglia, G.; Engler, A.J. Nanoscopic mechanical anisotropy in hydrogel surfaces. Soft Matter 2010, 6, 4466–4470. [Google Scholar] [CrossRef]
- Takigawa, T.; Morino, Y.; Urayama, K.; Masuda, T. Poisson’s ratio of polyacrylamide (PAAm) gels. Polym. Gels Netw. 1996, 4, 1–5. [Google Scholar] [CrossRef]
- Jin, C.; Ma, C.; Yang, Z.; Lin, H. A Force Measurement Method Based on Flexible PDMS Grating. Appl. Sci. 2020, 10, 2296. [Google Scholar] [CrossRef]
- Serna-Márquez, N.; Rodríguez-Hernández, A.; Ayala-Reyes, M.; Martínez-Hernández, L.O.; Peña-Rico, M.Á.; Carretero-Ortega, J.; Hautefeuille, M.; Vázquez-Victorio, G. Fibrillar Collagen Type I Participates in the Survival and Aggregation of Primary Hepatocytes Cultured on Soft Hydrogels. Biomimetics 2020, 5, 30. [Google Scholar] [CrossRef]
- Vázquez-Victorio, G.; Rodríguez-Hernández, A.; Cano-Jorge, M.; Monroy-Romero, A.X.; Macías-Silva, M.; Hautefeuille, M. Fabrication of Adhesive Substrate for Incorporating Hydrogels to Investigate the Influence of Stiffness on Cancer Cell Behavior. Methods Mol. Biol. 2021, 2174, 277–297. [Google Scholar]
- Meyer, K.; Morales-Navarrete, H.; Seifert, S.; Wilsch-Braeuninger, M.; Dahmen, U.; Tanaka, E.M.; Brusch, L.; Kalaidzidis, Y.; Zerial, M. Bile canaliculi remodeling activates YAP via the actin cytoskeleton during liver regeneration. Mol. Syst. Biol. 2020, 16, e8985. [Google Scholar] [CrossRef]
- Dimitriadis, E.K.; Horkay, F.; Maresca, J.; Kachar, B.; Chadwick, R.S. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophys. J. 2002, 82, 2798–2810. [Google Scholar] [CrossRef]
- Kohn, J.C.; Ebenstein, D.M. Eliminating adhesion errors in nanoindentation of compliant polymers and hydrogels. J. Mech. Behav. Biomed. Mater. 2013, 20, 316–326. [Google Scholar] [CrossRef]
- Style, R.W.; Hyland, C.; Boltyanskiy, R.; Wettlaufer, J.S.; Dufresne, E.R. Surface tension and contact with soft elastic solids. Nat. Commun. 2013, 4, 2728. [Google Scholar] [CrossRef]
- Tabor, D. Surface Forces and Surface Interactions. In Plenary and Invited Lectures; Academic Press: Cambridge, MA, USA, 1977; pp. 3–14. [Google Scholar]
- Efremov, Y.M.; Bagrov, D.V.; Kirpichnikov, M.P.; Shaitan, K.V. Application of the Johnson–Kendall–Roberts model in AFM-based mechanical measurements on cells and gel. Colloids Surf. B Biointerfaces 2015, 134, 131–139. [Google Scholar] [CrossRef]
- Ciavarella, M.; Xu, Y.; Jackson, R.L. The generalized Tabor parameter for adhesive rough contacts near complete contact. J. Mech. Phys. Solids 2019, 122, 126–140. [Google Scholar] [CrossRef]
- Ebenstein, D.M.; Wahl, K.J. A comparison of JKR-based methods to analyze quasi-static and dynamic indentation force curves. J. Colloid Interface Sci. 2006, 298, 652–662. [Google Scholar] [CrossRef] [PubMed]
- Ebenstein, D.M. Nano-JKR force curve method overcomes challenges of surface detection and adhesion for nanoindentation of a compliant polymer in air and water. J. Mater. Res. 2011, 26, 1026–1035. [Google Scholar] [CrossRef]
- Kraus, M.A.; Schuster, M.; Kuntsche, J.; Siebert, G.; Schneider, J. Parameter identification methods for visco- and hyperelastic material models. Glass Struct. Eng. 2017, 2, 147–167. [Google Scholar] [CrossRef]
- Walcott, S.; Sun, S.X. A mechanical model of actin stress fiber formation and substrate elasticity sensing in adherent cells. Proc. Natl. Acad. Sci. USA 2010, 107, 7757–7762. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.M.; Mohan, A.C.; Oyen, M.L.; Zhao, X.H. Separating viscoelasticity and poroelasticity of gels with different length and time scales. Acta Mech. Sin. 2014, 30, 20–27. [Google Scholar] [CrossRef]
- Lee, K.-Y.; Case, E.D. Effects of adhesion on the effective Young’s modulus in glass slide/glue laminates. J. Mater. Sci. 1996, 31, 2253–2264. [Google Scholar] [CrossRef]
- Rico, F.; Roca-Cusachs, P.; Gavara, N.; Farré, R.; Rotger, M.; Navajas, D. Probing mechanical properties of living cells by atomic force microscopy with blunted pyramidal cantilever tips. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005, 72, 021914. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, J.; Xu, G.-K.; Wang, G.-F. Are elastic moduli of biological cells depth dependent or not? Another explanation using a contact mechanics model with surface tension. Soft Matter 2018, 14, 7534–7541. [Google Scholar] [CrossRef] [PubMed]
- Esteki, M.H.; Alemrajabi, A.A.; Hall, C.M.; Sheridan, G.K.; Azadi, M.; Moeendarbary, E. A new framework for characterization of poroelastic materials using indentation. Acta Biomater. 2020, 102, 138–148. [Google Scholar] [CrossRef]
- Wen, J.H.; Vincent, L.G.; Fuhrmann, A.; Choi, Y.S.; Hribar, K.C.; Taylor-Weiner, H.; Chen, S.; Engler, A.J. Interplay of matrix stiffness and protein tethering in stem cell differentiation. Nat. Mater. 2014, 13, 979–987. [Google Scholar] [CrossRef] [PubMed]
- Subramani, R.; Izquierdo-Alvarez, A.; Bhattacharya, P.; Meerts, M.; Moldenaers, P.; Ramon, H.; Van Oosterwyck, H. The Influence of Swelling on Elastic Properties of Polyacrylamide Hydrogels. Front. Mater. 2020, 7. [Google Scholar] [CrossRef]
- Hui, C.Y.; Lin, Y.Y.; Chuang, F.C.; Shull, K.R.; Lin, W.C. A contact mechanics method for characterizing the elastic properties and permeability of gels. J. Polym. Sci. B Polym. Phys. 2006, 44, 359–370. [Google Scholar] [CrossRef]
- Cacopardo, L.; Guazzelli, N.; Nossa, R.; Mattei, G.; Ahluwalia, A. Engineering hydrogel viscoelasticity. J. Mech. Behav. Biomed. Mater. 2019, 89, 162–167. [Google Scholar] [CrossRef]
- Mattei, G.; Cacopardo, L.; Ahluwalia, A.A. Engineering Gels with Time-Evolving Viscoelasticity. Materials 2020, 13, 438. [Google Scholar] [CrossRef]
- Chim, Y.H.; Mason, L.M.; Rath, N.; Olson, M.F.; Tassieri, M.; Yin, H. A one-step procedure to probe the viscoelastic properties of cells by Atomic Force Microscopy. Sci. Rep. 2018, 8, 1–12. [Google Scholar] [CrossRef]
- Vázquez-Victorio, G.; Peto-Gutiérrez, C.; Díaz-Bello, B.; Cano-Jorge, M.; Pérez-Calixto, D.; Jiménez-Escobar, A.; Espinosa-Matías, S.; Lara Martínez, R.; Courson, R.; Malaquin, L.; et al. Building a microfluidic cell culture platform with stiffness control using Loctite 3525 glue. Lab Chip 2019, 19, 3512–3525. [Google Scholar] [CrossRef]
- Wahl, A.; Dinet, C.; Dillard, P.; Nassereddine, A.; Puech, P.-H.; Limozin, L.; Sengupta, K. Biphasic mechanosensitivity of T cell receptor-mediated spreading of lymphocytes. Proc. Natl. Acad. Sci. USA 2019, 116, 5908–5913. [Google Scholar] [CrossRef] [PubMed]
- Saez, A.; Anon, E.; Ghibaudo, M.; Du Roure, O.; Di Meglio, J.-M.; Hersen, P.; Silberzan, P.; Buguin, A.; Ladoux, B. Traction forces exerted by epithelial cell sheets. J. Phys. Condens. Matter 2010, 22, 194119. [Google Scholar] [CrossRef] [PubMed]
- Mouser, V.H.M.; Melchels, F.P.W.; Visser, J.; Dhert, W.J.A.; Gawlitta, D.; Malda, J. Yield stress determines bioprintability of hydrogels based on gelatin-methacryloyl and gellan gum for cartilage bioprinting. Biofabrication 2016, 8, 035003. [Google Scholar] [CrossRef] [PubMed]
- Valero, D.E. Compression Testing and Measurement of Material Properties of a Double Network Hydrogel. Ph.D. Thesis, Massachussetts Institute of Technology, Cambridge, MA, USA, 2015. [Google Scholar]
- Kim, M.; Moon, B.-U.; Hidrovo, C.H. Enhancement of the thermo-mechanical properties of PDMS molds for the hot embossing of PMMA microfluidic devices. J. Micromech. Microeng. 2013, 23, 095024. [Google Scholar] [CrossRef]
- Grinnell, F.; Ho, C.-H. The effect of growth factor environment on fibroblast morphological response to substrate stiffness. Biomaterials 2013, 34, 965–974. [Google Scholar] [CrossRef] [PubMed]
- Pocaterra, A.; Romani, P.; Dupont, S. YAP/TAZ functions and their regulation at a glance. J. Cell Sci. 2020, 133. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Calixto, D.; Amat-Shapiro, S.; Zamarrón-Hernández, D.; Vázquez-Victorio, G.; Puech, P.-H.; Hautefeuille, M. Determination by Relaxation Tests of the Mechanical Properties of Soft Polyacrylamide Gels Made for Mechanobiology Studies. Polymers 2021, 13, 629. https://doi.org/10.3390/polym13040629
Pérez-Calixto D, Amat-Shapiro S, Zamarrón-Hernández D, Vázquez-Victorio G, Puech P-H, Hautefeuille M. Determination by Relaxation Tests of the Mechanical Properties of Soft Polyacrylamide Gels Made for Mechanobiology Studies. Polymers. 2021; 13(4):629. https://doi.org/10.3390/polym13040629
Chicago/Turabian StylePérez-Calixto, Daniel, Samuel Amat-Shapiro, Diego Zamarrón-Hernández, Genaro Vázquez-Victorio, Pierre-Henri Puech, and Mathieu Hautefeuille. 2021. "Determination by Relaxation Tests of the Mechanical Properties of Soft Polyacrylamide Gels Made for Mechanobiology Studies" Polymers 13, no. 4: 629. https://doi.org/10.3390/polym13040629
APA StylePérez-Calixto, D., Amat-Shapiro, S., Zamarrón-Hernández, D., Vázquez-Victorio, G., Puech, P.-H., & Hautefeuille, M. (2021). Determination by Relaxation Tests of the Mechanical Properties of Soft Polyacrylamide Gels Made for Mechanobiology Studies. Polymers, 13(4), 629. https://doi.org/10.3390/polym13040629





