Electromagnetic Interference Shielding of Metal Coated Ultrathin Nonwoven Fabrics and Their Factorial Design
Abstract
1. Introduction
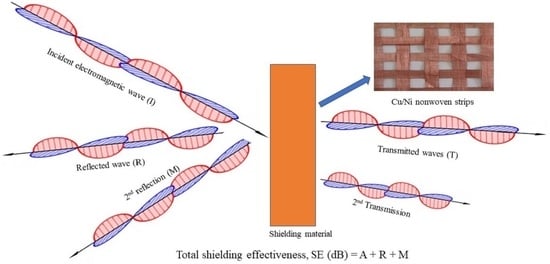
Electromagnetic Shielding Mechanism
2. Materials
3. Methods
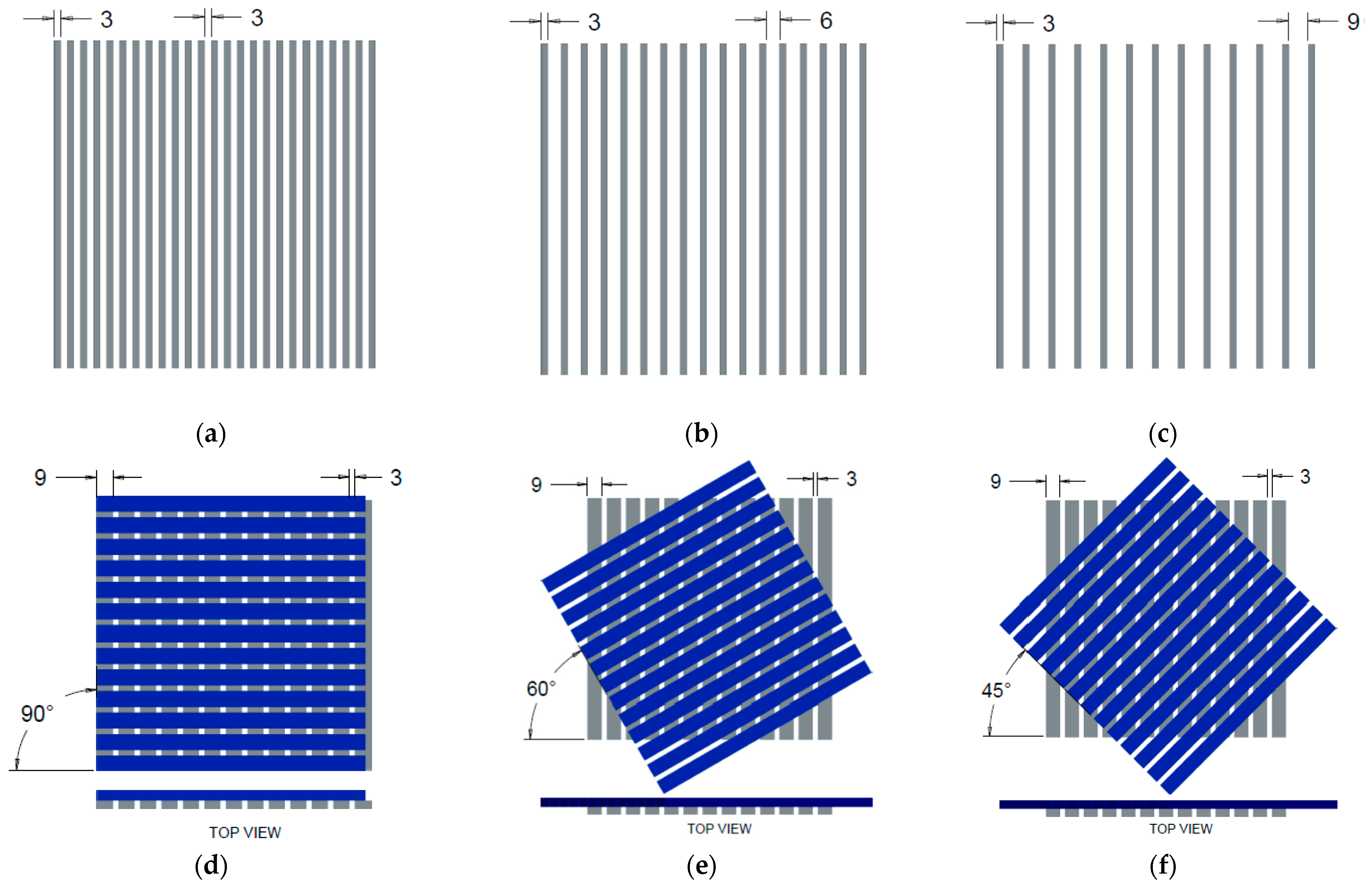
3.1. Experimental Design
3.2. Electromagnetic Shielding Effectiveness
4. Results and Discussion
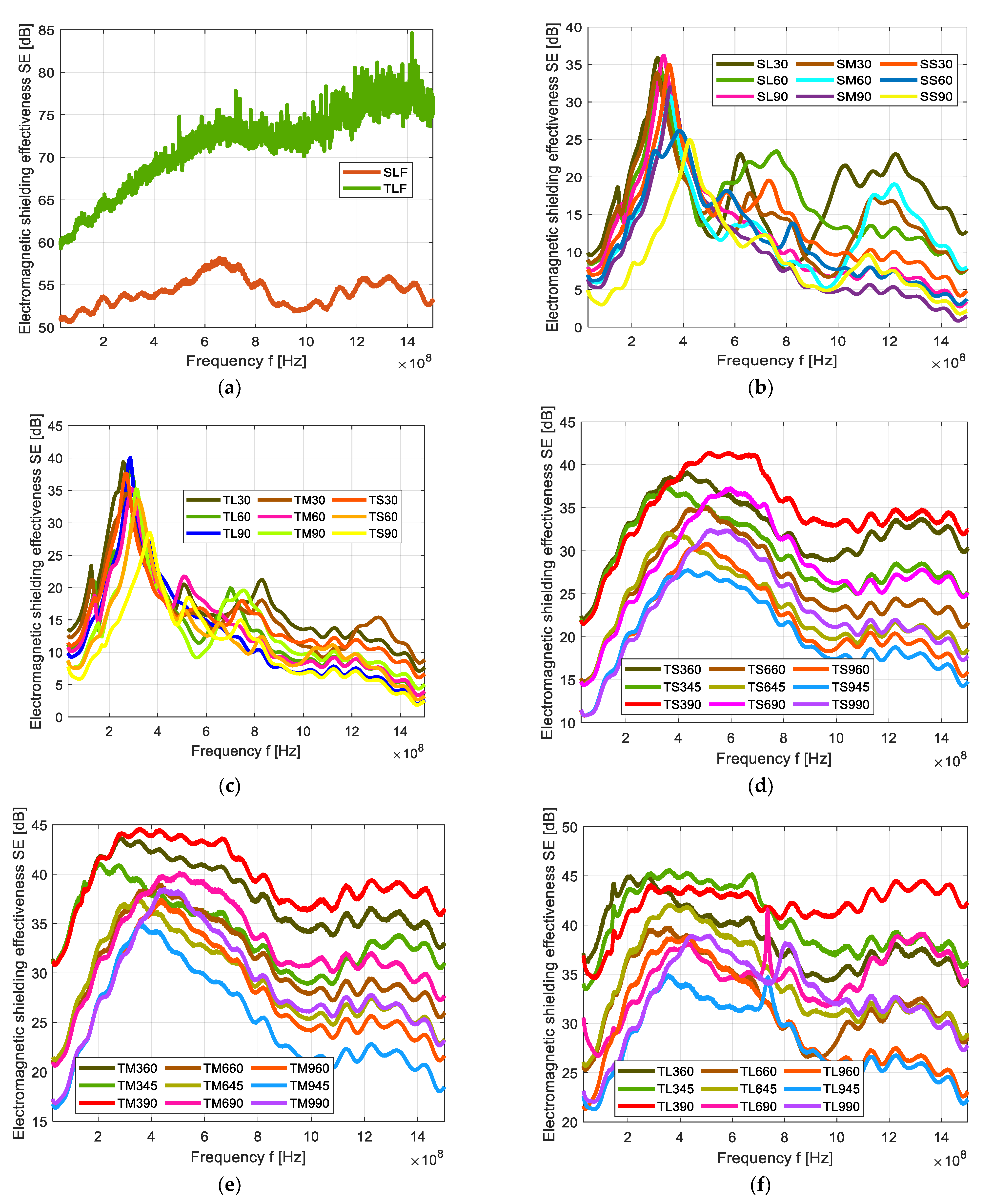
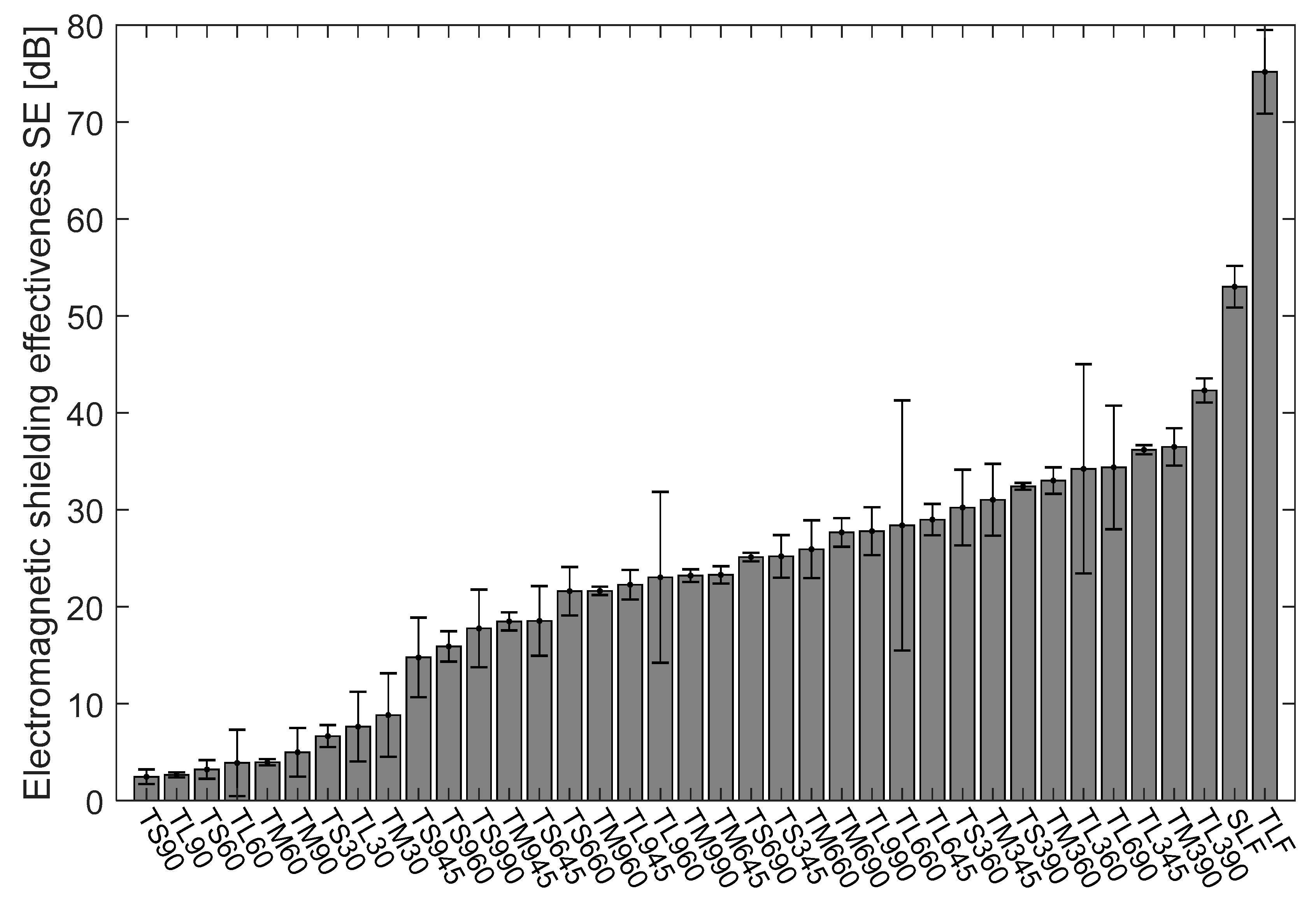
4.1. Electromagnetic Shielding Effectiveness of Cu/Ni NW Samples
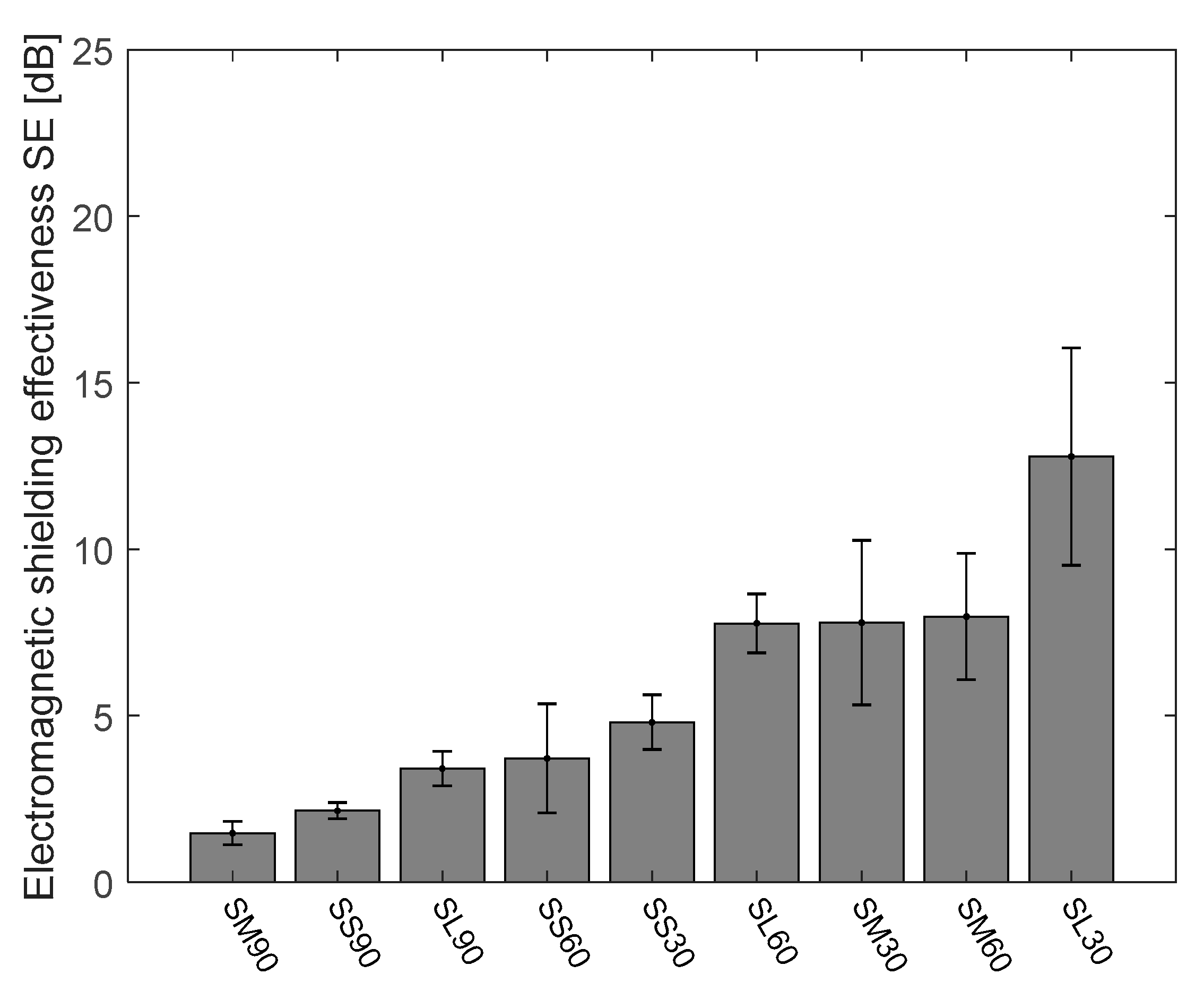
4.2. Electromagnetic Shielding Effectiveness of Cu/Ni NW Strip Samples at 1.5 GHz Frequency
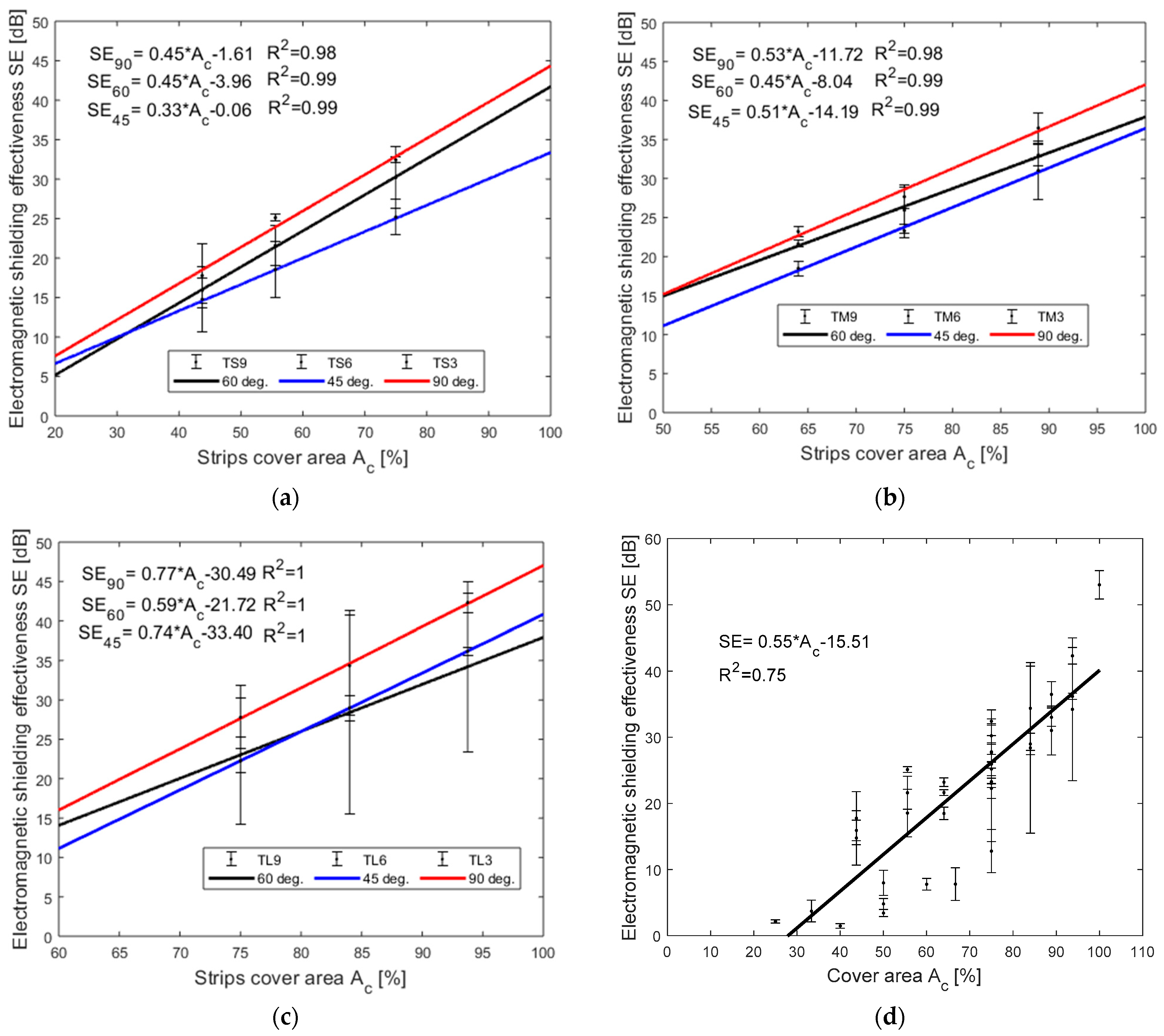
4.3. Effect of Electromagnetic Shielding Effectiveness on the Cover Area of Strips
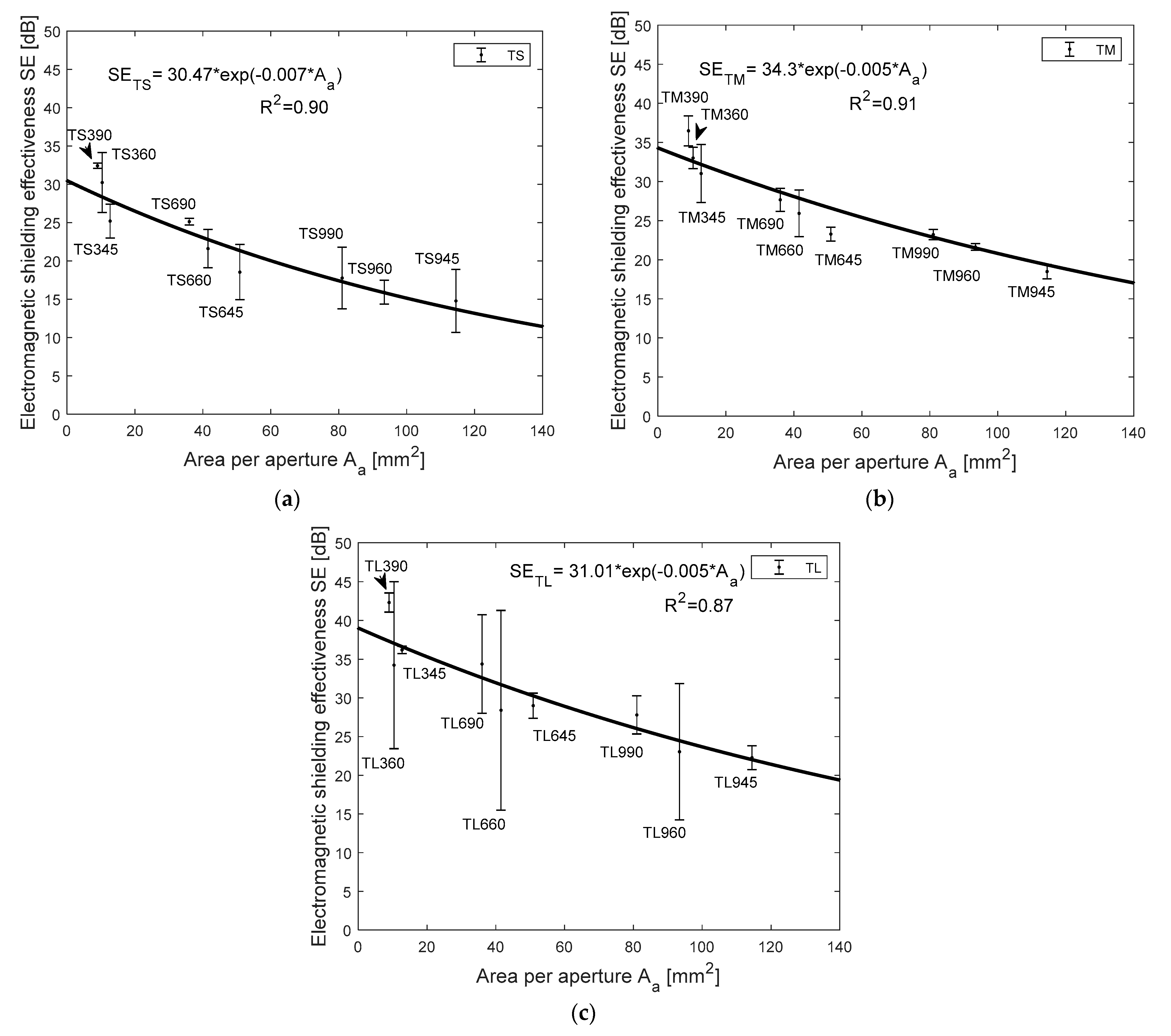
4.4. Influence of Area per Aperture at Different Laying Angle and its Effect on SE Results
4.5. Design of Experiment
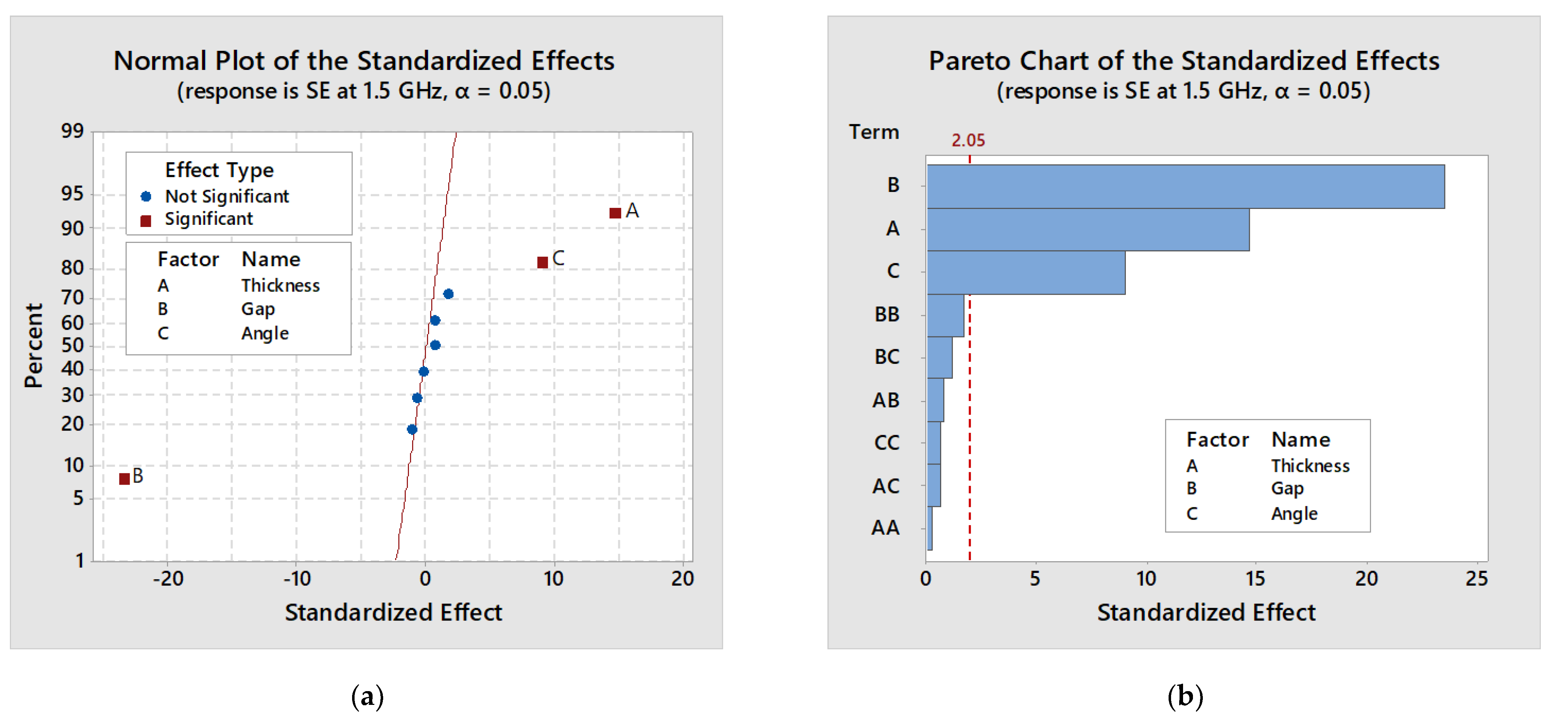
4.5.1. Analysis of Variance
4.5.2. Regression Equation in Uncoded Units
4.5.3. Standardized Effect Charts
4.5.4. Main Effect Plot
4.5.5. Interaction Plot
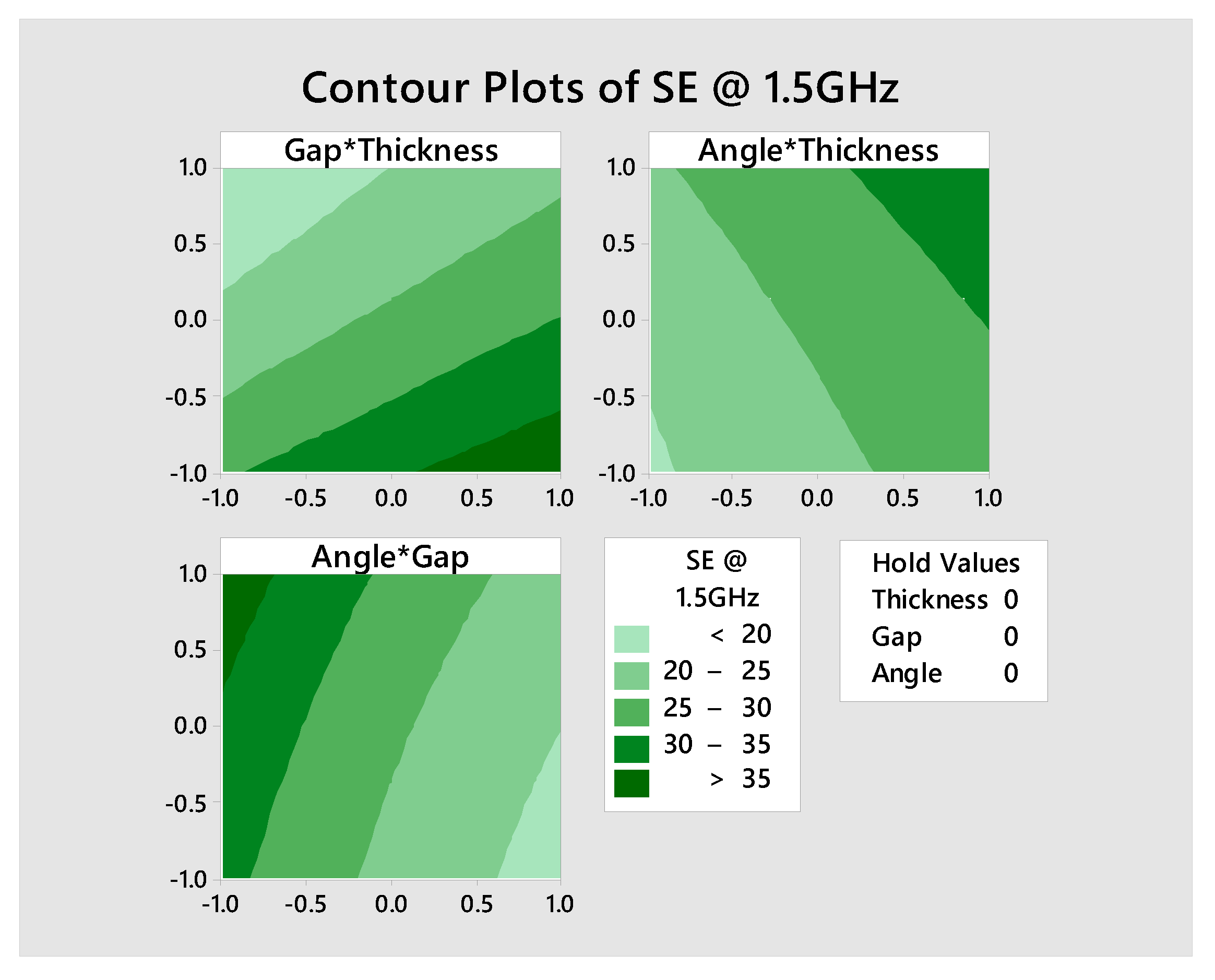
4.5.6. Contour Plot
5. Conclusions
Author Contributions
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barnes, F.S.; Greenebaum, B. (Eds.) Bioengineering and Biophysical Aspects of Electromagnetic Fields, 3rd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2006; ISBN 0849395399. [Google Scholar]
- Martin, R. (Ed.) Epidemiology of Electromagnetic Fields, 2nd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2008; ISBN 9781466568167. [Google Scholar]
- Lin, J.C. (Ed.) Electromagnetic Fields in Biological Systems; Taylor & Francis Group: Boca Raton, FL, USA, 2012; ISBN 9781439860625. [Google Scholar]
- Ott, H.W. Electromagnetic Compatibility Engineering; John Wiley& Sons, Inc.: Somerset, NJ, USA, 2009; ISBN 9780470189306. [Google Scholar]
- Geetha, S.; Kumar, K.K.S.; Rao, C.R.K.; Vijayan, M.; Trivedi, D.C. EMI shielding: Methods and materials—A review. J. Appl. Polym. Sci. 2009, 112, 2073–2086. [Google Scholar] [CrossRef]
- Kaynak, A.; Håkansson, E. Characterization of conducting polymer coated fabrics at microwave frequencies. Int. J. Cloth. Sci. Technol. 2009, 21, 117–126. [Google Scholar] [CrossRef]
- Yanılmaz, M.; Saraç, A.S. A review: Effect of conductive polymers on the conductivities of electrospun mats. Text. Res. J. 2014, 84, 1325–1342. [Google Scholar] [CrossRef]
- Uzun, S.; Han, M.; Strobel, C.J.; Hantanasirisakul, K.; Goad, A.; Dion, G.; Gogotsi, Y. Highly conductive and scalable Ti3C2T -coated fabrics for efficient electromagnetic interference shielding. Carbon 2021, 174, 382–389. [Google Scholar] [CrossRef]
- Wu, X.; Chen, Y.; Liang, K.; Yu, X.; Zhuang, Q.; Yang, Q.; Liu, S.; Liao, S.; Li, N.; Zhang, H. Fe2O3 Nanowire Arrays on Ni-Coated Yarns as excellent electrodes for High Performance Wearable Yarn-Supercapacitor. J. Alloys Compd. 2020, 158156. [Google Scholar] [CrossRef]
- Šafářová, V.; Militký, J. Electromagnetic shielding properties of woven fabrics made from high-performance fibers. Text. Res. J. 2014, 84, 1255–1267. [Google Scholar] [CrossRef]
- Liang, R.; Cheng, W.; Xiao, H.; Shi, M.; Tang, Z.; Wang, N. A calculating method for the electromagnetic shielding effectiveness of metal fiber blended fabric. Text. Res. J. 2018, 88, 973–986. [Google Scholar] [CrossRef]
- Ortlek, H.G.; Saracoglu, O.G.; Saritas, O.; Bilgin, S. Electromagnetic shielding characteristics of woven fabrics made of hybrid yarns containing metal wire. Fibers Polym. 2012, 13, 63–67. [Google Scholar] [CrossRef]
- Perumalraj, R.; Nalankilli, G.; Balasaravanan, T.R.; Roshanraja, K.; Shyamsundar, G.; Dasaradan, B.S. Electromagnetic shielding tester for conductive textile materials. Indian J. Fibre Text. Res. 2010, 35, 361–365. [Google Scholar]
- Li, T.-T.; Wang, R.; Lou, C.-W.; Lin, M.-C.; Lin, J.-H. Manufacture and effectiveness evaluations of high-modulus electromagnetic interference shielding/puncture resisting composites. Text. Res. J. 2013, 83, 1796–1807. [Google Scholar] [CrossRef]
- Lai, K.; Sun, R.-J.; Chen, M.-Y.; Wu, H.; Zha, A.-X. Electromagnetic Shielding Effectiveness of Fabrics with Metallized Polyester Filaments. Text. Res. J. 2007, 77, 242–246. [Google Scholar] [CrossRef]
- Roh, J.-S.; Chi, Y.-S.; Kang, T.J.; Nam, S.-W. Electromagnetic Shielding Effectiveness of Multifunctional Metal Composite Fabrics. Text. Res. J. 2008, 78, 825–835. [Google Scholar] [CrossRef]
- Yang, K.; Periyasamy, A.P.; Venkataraman, M.; Militký, J.; Kremenakova, D.; Vecernik, J.; Pulíček, R. Resistance against Penetration of Electromagnetic Radiation for Ultra-light Cu/Ni-Coated Polyester Fibrous Materials. Polymers 2020, 12, 2029. [Google Scholar] [CrossRef]
- Yu, Z.-C.; He, H.; Lu, Y.; Zhang, J.-F.; Lou, C.-W.; Chen, A.-P.; Lin, J.-H. Functional Properties and Electromagnetic Shielding Behaviour of Elastic Warp-knitted Fabrics. Fibres Text. East. Eur. 2015, 23, 78–83. [Google Scholar] [CrossRef]
- Tunakova, V.; Tunak, M.; Bajzik, V.; Ocheretna, L.; Arabuli, S.; Кизимчук, О.П.; Vlasenko, V. Hybrid knitted fabric for electromagnetic radiation shielding. J. Eng. Fibers Fabr. 2020, 15, 15. [Google Scholar] [CrossRef]
- D4935-10 ASTM Standard Test Method for Measuring the Electromagnetic Shielding Effectiveness of Planar Materials; ASTM International: West Conshohocken, PA, USA, 2010.
- Vojtech, L.; Neruda, M. Design of radiofrequency protective clothing containing silver nanoparticles. Fibres Text. East. Eur. 2013, 101, 141–147. [Google Scholar]
- Palanisamy, S.; Tunakova, V.; Militky, J. Fiber-based structures for electromagnetic shielding – comparison of different materials and textile structures. Text. Res. J. 2017, 88, 1992–2012. [Google Scholar] [CrossRef]
- Kardarian, K.; Busani, T.; Osório, I.; Domingos, H.; Igreja, R.; Franco, R.; Cortez, J. Sintering of nanoscale silver coated textiles, a new approach to attain conductive fabrics for electromagnetic shielding. Mater. Chem. Phys. 2014, 147, 815–822. [Google Scholar] [CrossRef]
- Engin, F.Z.; Usta, I. Electromagnetic shielding effectiveness of polyester fabrics with polyaniline deposition. Text. Res. J. 2013, 84, 903–912. [Google Scholar] [CrossRef]
- Tian, M.; Du, M.; Qu, L.; Chen, S.; Zhu, S.; Han, G. Electromagnetic interference shielding cotton fabrics with high electrical conductivity and electrical heating behavior via layer-by-layer self-assembly route. RSC Adv. 2017, 7, 42641–42652. [Google Scholar] [CrossRef]
- Safarova, V.; Militký, J. Electromagnetic Field Shielding Fabrics with Increased Comfort Properties. Adv. Mater. Res. 2013, 677, 161–168. [Google Scholar] [CrossRef]
- Šafářová, V.; Militký, J. Multifunctional metal composite textile shields against electromagnetic radiation-effect of various parameters on electromagnetic shielding effectiveness. Polym. Compos. 2015, 38, 309–323. [Google Scholar] [CrossRef]
- Romero, S.F.; Rodríguez, P.L.; Bocanegra, D.E.; Martinez, D.P.; Cancela, M.A. Comparing Open Area Test Site and Resonant Chamber for Unmanned Aerial Vehicle’s High-Intensity Radiated Field Testing. IEEE Trans. Electromagn. Compat. 2018, 60, 1704–1711. [Google Scholar] [CrossRef]
- Valente, R.V.; De Ruijter, C.; Vlasveld, D.; Van Der Zwaag, S.; Groen, W. Setup for EMI Shielding Effectiveness Tests of Electrically Conductive Polymer Composites at Frequencies up to 3.0 GHz. IEEE Access 2017, 5, 16665–16675. [Google Scholar] [CrossRef]
- Ozen, M.S.; Sancak, E.; Beyit, A.; Usta, I.; Akalin, M. Investigation of electromagnetic shielding properties of needle-punched nonwoven fabrics with stainless steel and polyester fiber. Text. Res. J. 2012, 83, 849–858. [Google Scholar] [CrossRef]
- Krzysztofik, W.J.; Borowiec, R.; Bieda, B. Some consideration on shielding effectiveness testing by means of the nested reverberation chambers. Radioengineering 2011, 20, 766–774. [Google Scholar]
- Duran, D.; Kadoğlu, H. Electromagnetic shielding characterization of conductive woven fabrics produced with silver-containing yarns. Text. Res. J. 2014, 85, 1009–1021. [Google Scholar] [CrossRef]
- MEFTEX 20. Available online: https://www.meftex.cz/en/meftex-20/p-3/ (accessed on 1 October 2020).
- Kenett, R.S.; Zacks, S.; Amberti, D. Modern Industrial Statistics, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2014; ISBN 9781118456064. [Google Scholar]
- FTTS-FA-003 Specified Requirements of Electromagnetic Shielding Textiles; The Committee for Conformity Assessment of Accreditation and Certification on Functional and Technical Textiles: New Taipei City, Taiwan, 2005; Volume 2.0, Available online: https://www.ftts.org.tw/estandard (accessed on 6 October 2020).



| Parameters * | Values |
|---|---|
| Areal density (g/m2) | 24.56 ± 2.69 |
| Thickness (mm) | 0.087 ± 0.006 |
| Tensile strength in MD (N/50 mm) | 25 [33] |
| Tensile strength in CD (N/50 mm) | 16 [33] |
| Surface resistivity (Ω) | 2.1 ± 0.28 |
| No. of Layers | Angle of Layers (°) | Strip Thickness (mm) | Gap between the Strips (mm) | ||
|---|---|---|---|---|---|
| 3 | 6 | 9 | |||
| One | 0 | SS30 | SM30 | SL30 | 3 |
| SS60 | SM60 | SL60 | 6 | ||
| SS90 | SM90 | SL90 | 9 | ||
| Two | 0 | TS30 | TM30 | TL30 | 3 |
| TS60 | TM60 | TL60 | 6 | ||
| TS90 | TM90 | TL90 | 9 | ||
| 45 | TS345 | TM345 | TL345 | 3 | |
| 60 | TS360 | TM360 | TL360 | ||
| 90 | TS390 | TM390 | TL390 | ||
| 45 | TS645 | TM645 | TL645 | 6 | |
| 60 | TS660 | TM660 | TL660 | ||
| 90 | TS690 | TM690 | TL690 | ||
| 45 | TS945 | TM945 | TL945 | 9 | |
| 60 | TS960 | TM960 | TL960 | ||
| 90 | TS990 | TM990 | TL990 | ||
| Single-layer of fabric | SLF | ||||
| Two-layers of fabric | TLF | ||||
| Factors | Levels | Response | ||
|---|---|---|---|---|
| Strip thickness (A) | −1 | 0 | +1 | EMI SE (dB) |
| Gap between the strips (B) | −1 | 0 | +1 | |
| Angles of layers (C) | −1 | 0 | +1 | |
| Grade | Excellent | Very Good | Good | Moderate | Fair |
|---|---|---|---|---|---|
| Range (dB) | SE > 60 | 60 ≥ SE > 50 | 50 ≥ SE > 40 | 40 ≥ SE > 30 | 30 ≥ SE > 20 |
| Grade | Excellent | Very Good | Good | Moderate | Fair |
|---|---|---|---|---|---|
| Range (dB) | SE > 30 | 30 ≥ SE > 20 | 20 ≥ SE > 10 | 10 ≥ SE > 7 | 7 ≥ SE > 5 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9 | 2355.05 | 261.67 | 94.92 | 0.000 |
| Linear | 3 | 2334.18 | 778.06 | 282.24 | 0.000 |
| Thickness | 1 | 592.96 | 592.96 | 215.09 | 0.000 |
| Gap | 1 | 1517.86 | 1517.86 | 550.59 | 0.000 |
| Angle | 1 | 223.36 | 223.36 | 81.02 | 0.000 |
| Square | 3 | 9.33 | 3.11 | 1.13 | 0.354 |
| Thickness*Thickness | 1 | 0.22 | 0.22 | 0.08 | 0.779 |
| Gap*Gap | 1 | 7.81 | 7.81 | 2.83 | 0.103 |
| Angle*Angle | 1 | 1.09 | 1.09 | 0.40 | 0.534 |
| 2-Way Interactions | 3 | 8.96 | 2.99 | 1.08 | 0.371 |
| Thickness*Gap | 1 | 1.59 | 1.59 | 0.58 | 0.453 |
| Thickness*Angle | 1 | 1.02 | 1.02 | 0.37 | 0.549 |
| Gap*Angle | 1 | 3.82 | 3.82 | 1.39 | 0.249 |
| Error | 29 | 79.95 | 2.76 | - | - |
| Lack-of-Fit | 3 | 12.99 | 4.33 | 1.68 | 0.196 |
| Pure Error | 26 | 66.96 | 2.58 | - | - |
| Total | 38 | 2435.00 | - | - | |
| S | R-sq | R-sq(adj) | R-sq(pred) | - | - |
| 1.66035 | 96.72% | 95.70% | 94.25% | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palanisamy, S.; Tunakova, V.; Hu, S.; Yang, T.; Kremenakova, D.; Venkataraman, M.; Petru, M.; Militky, J. Electromagnetic Interference Shielding of Metal Coated Ultrathin Nonwoven Fabrics and Their Factorial Design. Polymers 2021, 13, 484. https://doi.org/10.3390/polym13040484
Palanisamy S, Tunakova V, Hu S, Yang T, Kremenakova D, Venkataraman M, Petru M, Militky J. Electromagnetic Interference Shielding of Metal Coated Ultrathin Nonwoven Fabrics and Their Factorial Design. Polymers. 2021; 13(4):484. https://doi.org/10.3390/polym13040484
Chicago/Turabian StylePalanisamy, Sundaramoorthy, Veronika Tunakova, Shi Hu, Tao Yang, Dana Kremenakova, Mohanapriya Venkataraman, Michal Petru, and Jiri Militky. 2021. "Electromagnetic Interference Shielding of Metal Coated Ultrathin Nonwoven Fabrics and Their Factorial Design" Polymers 13, no. 4: 484. https://doi.org/10.3390/polym13040484
APA StylePalanisamy, S., Tunakova, V., Hu, S., Yang, T., Kremenakova, D., Venkataraman, M., Petru, M., & Militky, J. (2021). Electromagnetic Interference Shielding of Metal Coated Ultrathin Nonwoven Fabrics and Their Factorial Design. Polymers, 13(4), 484. https://doi.org/10.3390/polym13040484