An Artificial Lens Capsule with a Lens Radial Stretching System Mimicking Dynamic Eye Focusing
Abstract
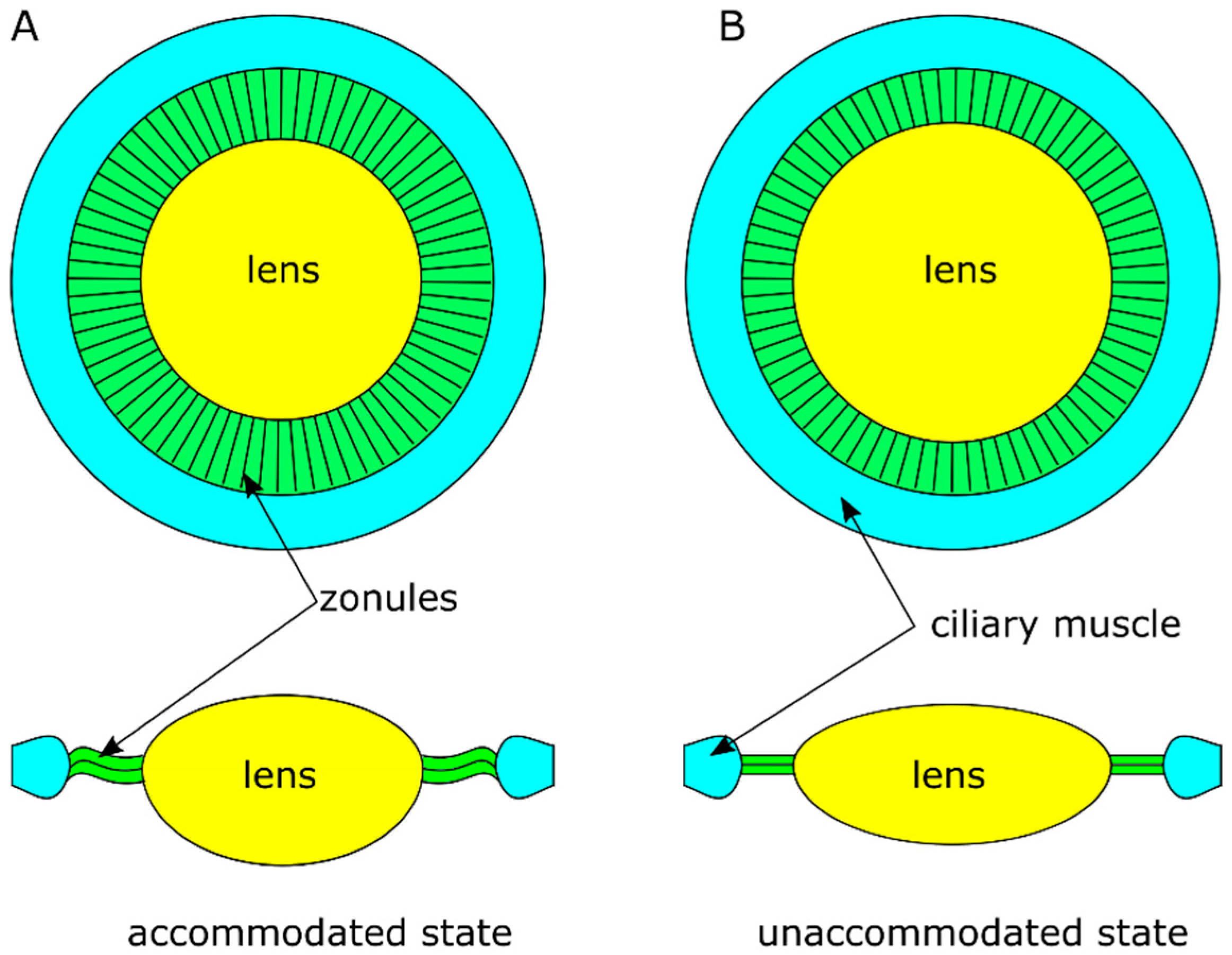
1. Introduction
2. Materials and Methods
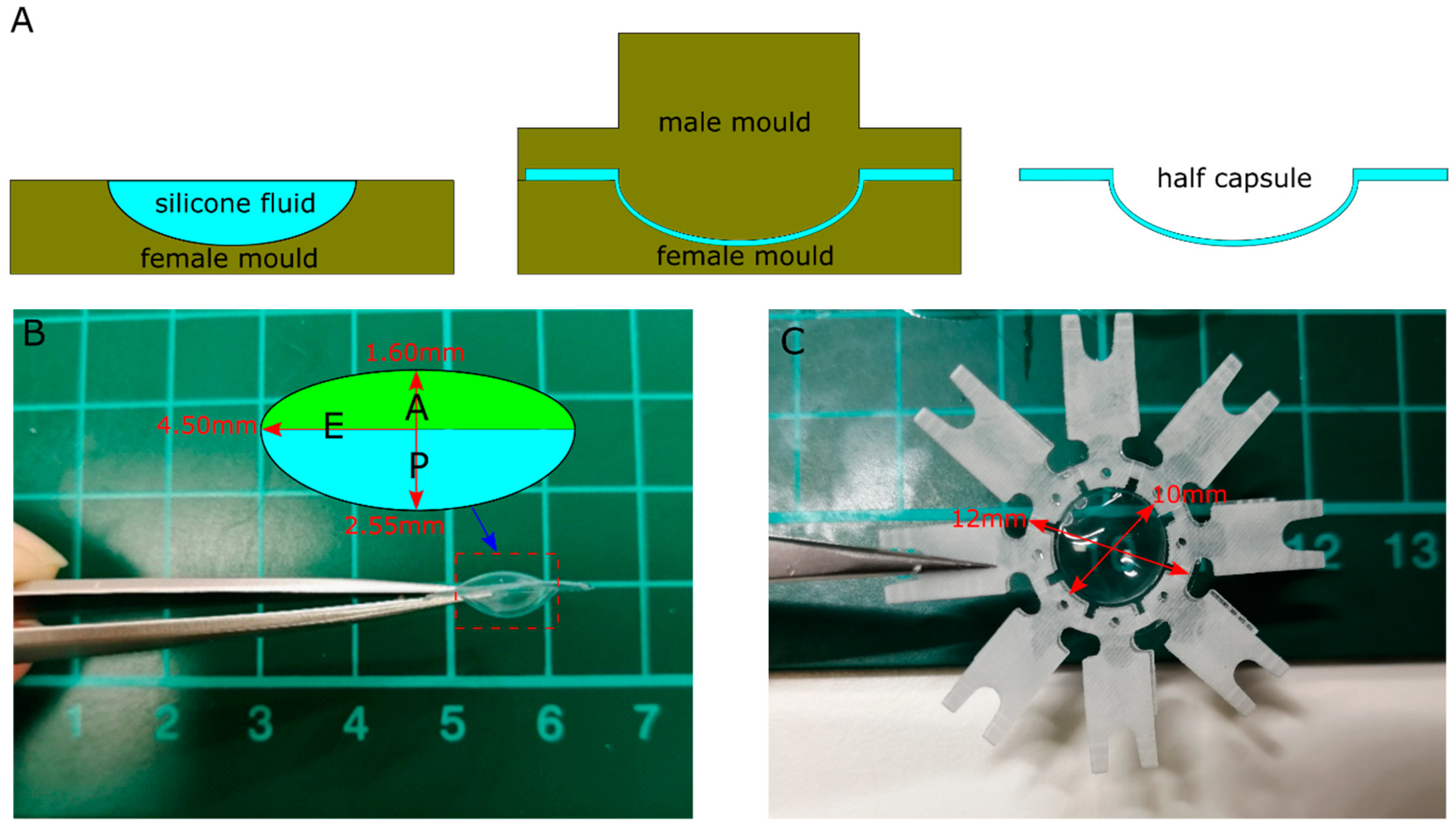
2.1. Preparation of Artificial Lens Capsule (ALC)
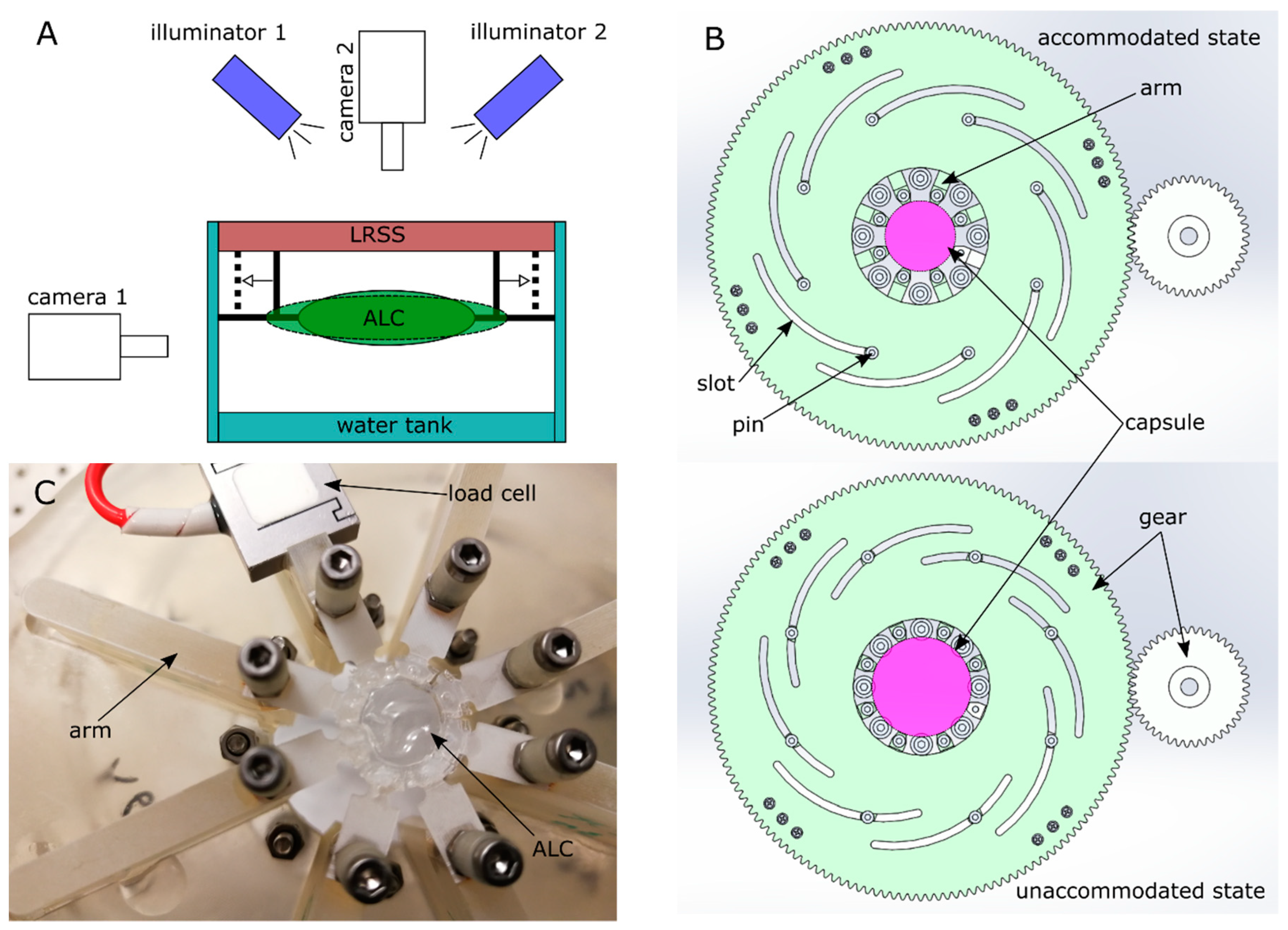
2.2. Stretching Test Mimicking Accommodation
3. Results
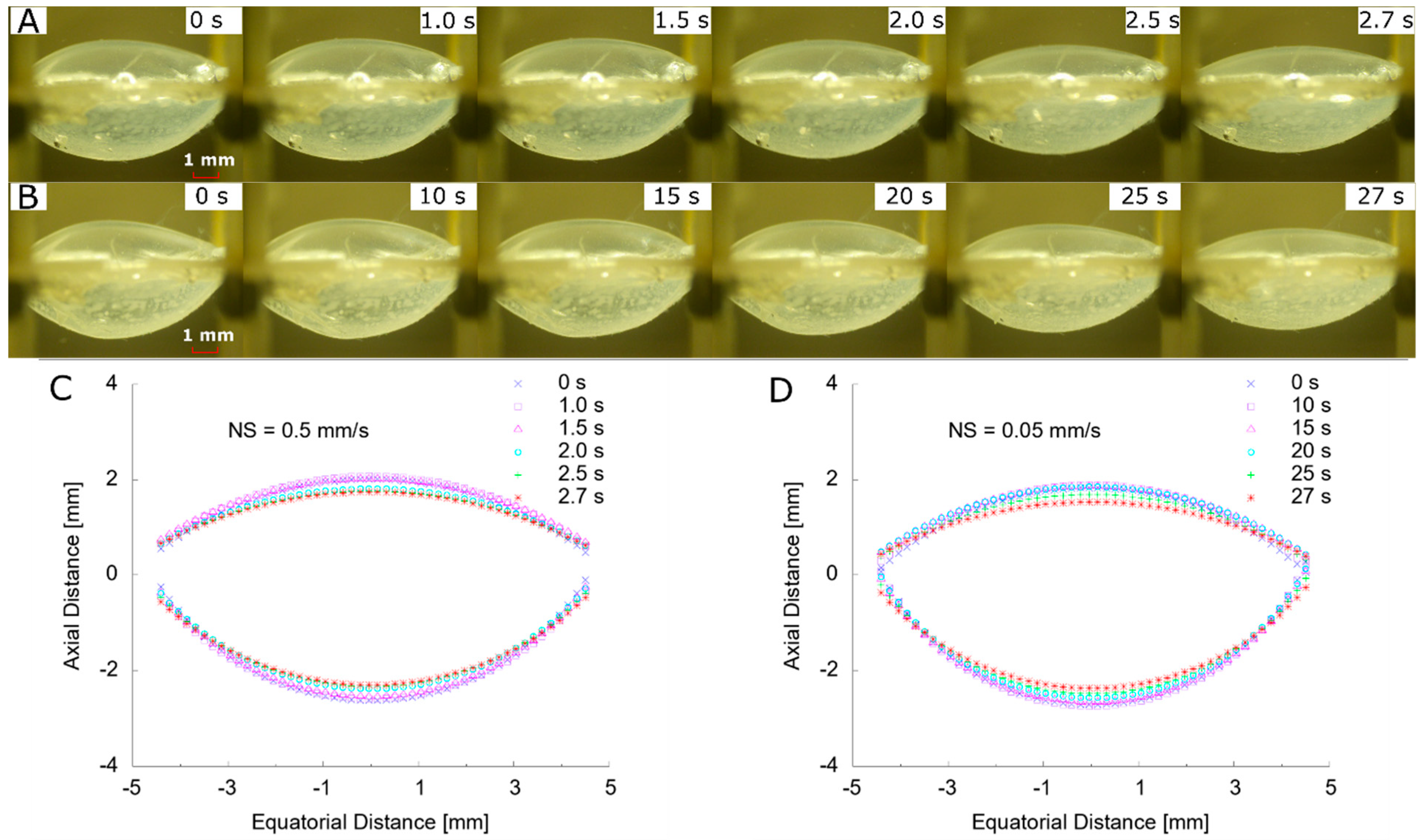
3.1. Change of Diameter
3.2. Change of Profile
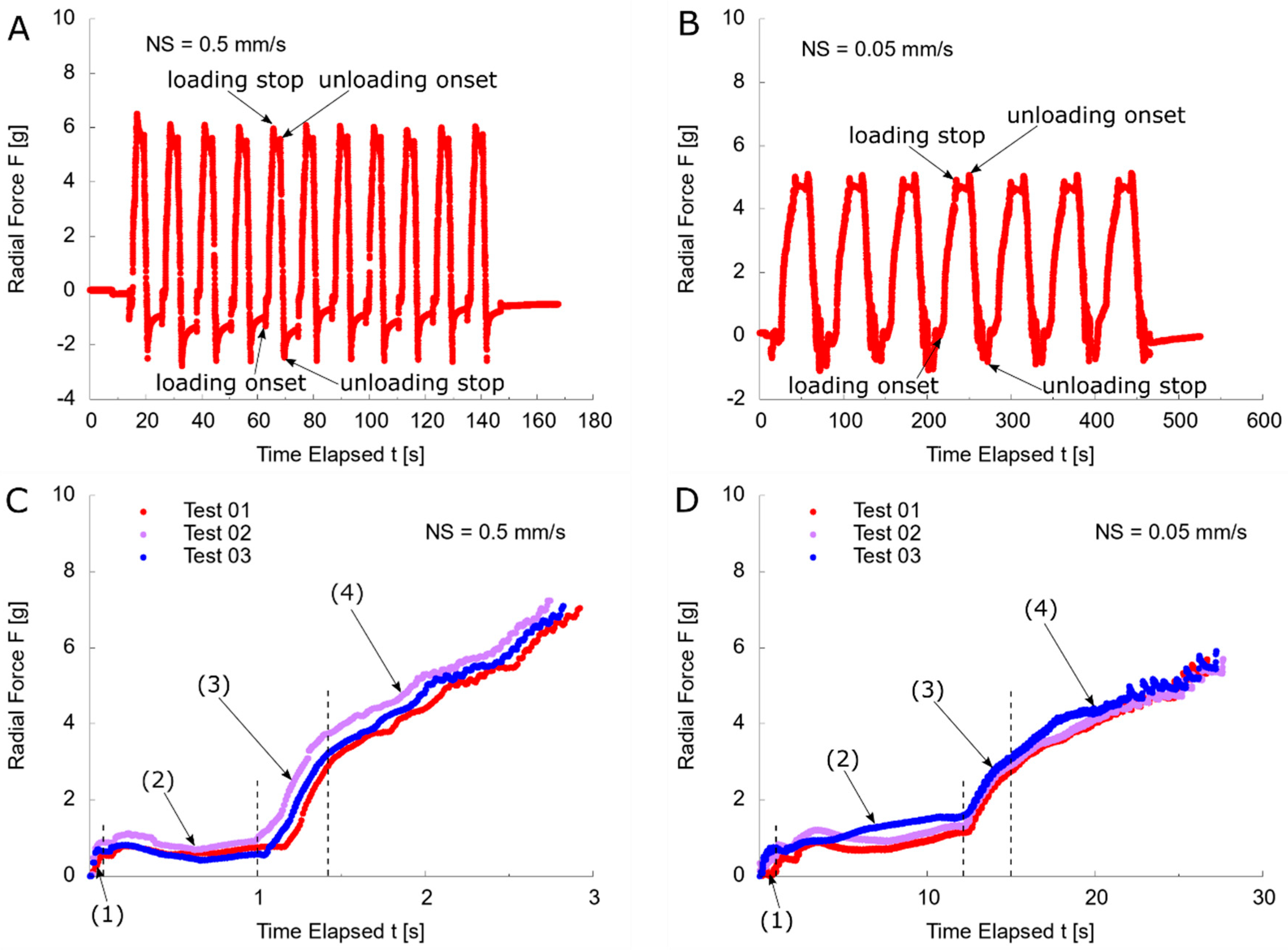
3.3. Reaction Force
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Wang, K.; Pierscionek, B.K. Biomechanics of the human lens and accommodative system: Functional relevance to physiological states. Prog. Retin. Eye Res. 2019, 71, 114–131. [Google Scholar] [CrossRef]
- Fisher, R.F. The force of contraction of the human ciliary muscle during accommodation. J. Physiol. 1977, 270, 51–74. [Google Scholar] [CrossRef] [PubMed]
- Wolffsohn, J.S.; Davies, L.N. Presbyopia: Effectiveness of correction strategies. Prog. Retin. Eye Res. 2019, 68, 124–143. [Google Scholar] [CrossRef] [PubMed]
- Heys, K.R.; Cram, S.L.; Truscott, R.J.W. Massive increase in the stiffness of the human lens nucleus with age: The basis for presbyopia? Mol. Vis. 2004, 10, 956–963. [Google Scholar] [PubMed]
- Sheppard, A.L.; Davies, L.N. The effect of ageing on in vivo human ciliary muscle morphology and contractility. Investig. Ophthalmol. Vis. Sci. 2011, 52, 1809–1816. [Google Scholar] [CrossRef]
- Ovenseri-Ogbomo, G.O.; Oduntan, O.A. Mechanism of accommodation: A review of theoretical propositions. Afr. Vis. Eye Heal. 2015, 74, 1–6. [Google Scholar] [CrossRef]
- Helmholtz, H. Ueber die Accommodation des Auges. Arch. Opthalmol. 1855, 1, 1–74. [Google Scholar] [CrossRef]
- Fisher, R.F. The Elastic Constants of the Human Lens. J. Physiol. 1971, 212, 147–180. [Google Scholar] [CrossRef] [PubMed]
- Wilkes, R.P.; Reilly, M.A. A pre-tensioned finite element model of ocular accommodation and presbyopia. Int. J. Adv. Eng. Sci. Appl. Math. 2016, 8, 25–38. [Google Scholar] [CrossRef]
- Fisher, R.F. Elastic constants of the human lens capsule. J. Physiol. 1969, 201, 1–19. [Google Scholar] [CrossRef]
- Fisher, R.F. The Significance of the Shape of the Lens and Capsular Energy Changes in Accommodation. J. Physiol. 1969, 201, 21–47. [Google Scholar] [CrossRef]
- Ziebarth, N.M.; Borja, D.; Arrieta, E.; Aly, M.; Manns, F.; Dortonne, I.; Nankivil, D.; Jain, R.; Parel, J.M. Role of the lens capsule on the mechanical accommodative response in a lens stretcher. Investig. Ophthalmol. Vis. Sci. 2008, 49, 4490–4496. [Google Scholar] [CrossRef]
- Krag, S.; Olsen, T.; Andreassewf, T.T. Biomechanical Characteristics of the Human Anterior Lens Capsule in Relation to Age. Investig. Ophthalmol. Vis. Sci. 1997, 38, 357–363. [Google Scholar]
- Alió, J.L.; Ben-Nun, J. Study of the Force Dynamics at the Capsular Interface Related to Ciliary Body Stimulation in a Primate Model. J. Refract. Surg. 2015, 31, 124–128. [Google Scholar] [CrossRef] [PubMed]
- Glasser, A. Adrian Glasser Restoration of accommodation: Surgical options for correction of presbyopia. Clin. Exp. Optom. 2008, 91, 279–295. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, A.L.; Bashir, A.; Wolffsohn, J.S.; Davies, L.N. Accommodating intraocular lenses: A review of design concepts, usage and assessment methods. Clin. Exp. Optom. 2010, 93, 441–452. [Google Scholar] [CrossRef]
- Tomás-Juan, J.; Murueta-Goyena Larrañaga, A. Axial movement of the dual-optic accommodating intraocular lens for the correction of the presbyopia: Optical performance and clinical outcomes. J. Optom. 2015, 8, 67–76. [Google Scholar] [CrossRef] [PubMed]
- Pepose, J.S.; Burke, J.S.; Qazi, M.A. Accommodating intraocular lenses. Asia-Pac. J. Ophthalmol. 2017, 6, 350–357. [Google Scholar] [CrossRef]
- Krag, S.; Andreassen, T.T. Mechanical properties of the human lens capsule. Prog. Retin. Eye Res. 2003, 22, 749–767. [Google Scholar] [CrossRef]
- Jardine, G.J.; Wong, G.C.; Elsnab, J.R.; Gale, B.K.; Ambati, B.K. Endocapsular carousel technique phacoemulsification. J. Refract. Surg. 2011, 37, 433–437. [Google Scholar] [CrossRef]
- Danielsen, C.C. Tensile mechanical and creep properties of Descemet’s membrane and lens capsule. Exp. Eye Res. 2004, 79, 343–350. [Google Scholar] [CrossRef]
- Pedrigi, R.M.; David, G.; Dziezyc, J.; Humphrey, J.D. Regional mechanical properties and stress analysis of the human anterior lens capsule. Vis. Res. 2007, 47, 1781–1789. [Google Scholar] [CrossRef]
- Pierscionek, B.K. In Vitro Alteration of Human Lens Curvatures by Radial Stretching. Exp. Eye Res. 1993, 57, 629–635. [Google Scholar] [CrossRef]
- Webb, J.N.; Dong, C.; Bernal, A.; Scarcelli, G. Simulating the Mechanics of Lens Accommodation via a Manual Lens Stretcher. J. Vis. Exp. 2018, 8–13. [Google Scholar] [CrossRef]
- Ehrmann, K.; Ho, A.; Parel, J.M. Biomechanical analysis of the accommodative apparatus in primates. Clin. Exp. Optom. 2008, 91, 302–312. [Google Scholar] [CrossRef]
- Pierscionek, B.K. Age-Related Response of Human Lenses to Stretching Forces. Exp. Eye Res. 1995, 60, 325–332. [Google Scholar] [CrossRef]
- Glasser, A. Restoration of accommodation. Curr. Opin. Ophthalmol. 2006, 17, 12–18. [Google Scholar] [CrossRef]
- Pellegrino, A.; Burd, H.J.; Pinilla Cortés, L.; D’Antin, J.C.; Petrinic, N.; Barraquer, R.I.; Michael, R. Anterior lens capsule strains during simulated accommodation in porcine eyes. Exp. Eye Res. 2018, 168, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.F.; Ennifer Wakelyf, J. The elastic constants and ultrastructural organization of a basement membrane (lens capsule). Proc. R. Soc. Lond. Ser. B. Biol. Sci. 1976, 193, 335–358. [Google Scholar]
- Meththananda, I.M.; Parker, S.; Patel, M.P.; Braden, M. The relationship between Shore hardness of elastomeric dental materials and Young’s modulus. Dent. Mater. 2009, 25, 956–959. [Google Scholar] [CrossRef] [PubMed]
- Gent, A.N. On the relation between indentation hardness and Young’s modulus. Rubber Chem. Technol. 1958, 31, 896–906. [Google Scholar] [CrossRef]
- Cortés, L.P.; Burd, H.J.; Montenegro, G.A.; D’Antin, J.C.; Mikielewicz, M.; Barraquer, R.I.; Michael, R. Experimental protocols for Ex vivo lens stretching tests to investigate the biomechanics of the human accommodation apparatus. Investig. Ophthalmol. Vis. Sci. 2015, 56, 2926–2932. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Michael, R.; Mikielewicz, M.; Gordillo, C.; Montenegro, G.A.; Pinilla Cortés, L.; Barraquer, R.I. Elastic properties of human lens zonules as a function of age in presbyopes. Investig. Ophthalmol. Vis. Sci. 2012, 53, 6109–6114. [Google Scholar] [CrossRef]
- Ehrmann, K.; Ho, A.; Parel, J.-M. Ex vivo accommodation simulator II: Concept and preliminary results. In Ophthalmic Technologies XIV; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; Volume 5314, pp. 48–58. [Google Scholar]
- Harwood, J.A.C.; Mullins, L.; Payne, A.R. Stress softening in natural rubber vulcanizates. Part II. Stress softening effects in pure gum and filler loaded rubbers. J. Appl. Polym. Sci. 1965, 9, 3011–3021. [Google Scholar] [CrossRef]
- Diani, J.; Fayolle, B.; Gilormini, P.; Diani, J.; Fayolle, B.; Gilormini, P. A review on the Mullins effect. Eur. Polym. J. 2009, 45, 601–612. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Tinard, V.; Fond, C. The modelling of nonlinear rheological behaviour and Mullins effect in High Damping Rubber. Int. J. Solids Struct. 2015, 75–76, 235–246. [Google Scholar] [CrossRef]
- Bernardi, L.; Hopf, R.; Ferrari, A.; Ehret, A.E.; Mazza, E. On the large strain deformation behavior of silicone-based elastomers for biomedical applications. Polym. Test. 2017, 58, 189–198. [Google Scholar] [CrossRef]
- Manns, F.; Parel, J.M.; Denham, D.; Billotte, C.; Ziebarth, N.; Borja, D.; Fernandez, V.; Aly, M.; Arrieta, E.; Ho, A.; et al. Optomechanical response of human and monkey lenses in a lens stretcher. Investig. Ophthalmol. Vis. Sci. 2007, 48, 3260–3268. [Google Scholar] [CrossRef]
- Sheppard, A.L.; John Evans, C.; Singh, K.D.; Wolffsohn, J.S.; Dunne, M.C.M.; Davies, L.N. Three-dimensional magnetic resonance imaging of the phakic crystalline lens during accommodation. Investig. Ophthalmol. Vis. Sci. 2011, 52, 3689–3697. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.F.; Pettet, B.E. The postnatal growth of the capsule of the human crystalline lens. J. Anat. 1972, 112, 207–214. [Google Scholar] [PubMed]
- Barraquer, R.I.; Michael, R.; Abreu, R.; Lamarca, J.; Tresserra, F. Human lens capsule thickness as a function of age and location along the sagittal lens perimeter. Investig. Ophthalmol. Vis. Sci. 2006, 47, 2053–2060. [Google Scholar] [CrossRef]
- Fisher, R.F. The Mechanics of Accommodation in Relation to Presbyopia. Eye 1988, 2, 646–649. [Google Scholar] [CrossRef] [PubMed]
- Krag, S.; Andreassen, T.T. Mechanical properties of the human posterior lens capsule. Investig. Ophthalmol. Vis. Sci. 2003, 44, 691–696. [Google Scholar] [CrossRef] [PubMed]
- Kasthurirangan, S.; Markwell, E.L.; Atchison, D.A.; Pope, J.M. MRI study of the changes in crystalline lens shape with accommodation and aging in humans. J. Vis. 2011, 11, 19. [Google Scholar] [CrossRef] [PubMed]
- Hermans, E.A.; Dubbelman, M.; van der Heijde, G.L.; Heethaar, R.M. Estimating the external force acting on the human eye lens during accommodation by finite element modelling. Vis. Res. 2006, 46, 3642–3650. [Google Scholar] [CrossRef] [PubMed]
- Nankivil, D.; Heilman, B.M.; Durkee, H.; Manns, F.; Ehrmann, K.; Kelly, S.; Arrieta-Quintero, E.; Parel, J.M. The zonules selectively alter the shape of the lens during accommodation based on the location of their anchorage points. Investig. Ophthalmol. Vis. Sci. 2015, 56, 1751–1760. [Google Scholar] [CrossRef] [PubMed]
- Strenk, S.A.; Semmlow, J.L.; Strenk, L.M.; Munoz, P.; Gronlund-Jacob, J.; DeMarco, J.K. Age-related changes in human ciliary muscle and lens: A magnetic resonance imaging study. Investig. Ophthalmol. Vis. Sci. 1999, 40, 1162–1169. [Google Scholar]
- Reilly, M.A.; Hamilton, P.D.; Perry, G.; Ravi, N. Comparison of the behavior of natural and refilled porcine lenses in a robotic lens stretcher. Exp. Eye Res. 2009, 88, 483–494. [Google Scholar] [CrossRef]
- Dubbelman, M.; Van Der Heijde, G.L. The shape of the aging human lens: Curvature, equivalent refractive index and the lens paradox. Vis. Res. 2001, 41, 1867–1877. [Google Scholar] [CrossRef]
- Reilly, M.A.; Hamilton, P.D.; Ravi, N. Dynamic multi-arm radial lens stretcher: A robotic analog of the ciliary body. Exp. Eye Res. 2008, 86, 157–164. [Google Scholar] [CrossRef]
- Dubbelman, M.; Van Der Heijde, G.L.; Weeber, H.A. Change in shape of the aging human crystalline lens with accommodation. Vis. Res. 2005, 45, 117–132. [Google Scholar] [CrossRef] [PubMed]
- Reilly, M.A. A quantitative geometric mechanics lens model: Insights into the mechanisms of accommodation and presbyopia. Vis. Res. 2014, 103, 20–31. [Google Scholar] [CrossRef] [PubMed]

| Lens Diameter D [mm] | Curvature Radius | Sagittal Distance H [mm] | ||
|---|---|---|---|---|
| NS = 0.5 mm/s | ||||
| Accommodated | 9.078 ± 0.003 | 7.338 ± 0.079 | −5.360 ± 0.092 | 4.674 ± 0.031 |
| Unaccommodated | 9.921 ± 0.056 | 9.416 ± 0.079 | −6.376 ± 0.053 | 4.063 ± 0.016 |
| Increment | 0.843 ± 0.055 | 2.079 ± 0.072 | −1.015 ± 0.104 | −0.610 ± 0.016 |
| NS = 0.05 mm/s | ||||
| Accommodated | 10.313 ± 0.054 | 7.010 ± 0.225 | −4.853 ± 0.117 | 4.617 ± 0.014 |
| Unaccommodated | 11.073 ± 0.056 | 9.288 ± 0.186 | −5.782 ± 0.126 | 3.937 ± 0.077 |
| Increment | 0.878 ± 0.045 | 2.278 ± 0.226 | −0.929 ± 0.098 | −0.680 ± 0.070 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Wolffsohn, J.S.; Gomes de Oliveira, O.; Davies, L.N. An Artificial Lens Capsule with a Lens Radial Stretching System Mimicking Dynamic Eye Focusing. Polymers 2021, 13, 3552. https://doi.org/10.3390/polym13203552
Wei H, Wolffsohn JS, Gomes de Oliveira O, Davies LN. An Artificial Lens Capsule with a Lens Radial Stretching System Mimicking Dynamic Eye Focusing. Polymers. 2021; 13(20):3552. https://doi.org/10.3390/polym13203552
Chicago/Turabian StyleWei, Huidong, James S. Wolffsohn, Otavio Gomes de Oliveira, and Leon N. Davies. 2021. "An Artificial Lens Capsule with a Lens Radial Stretching System Mimicking Dynamic Eye Focusing" Polymers 13, no. 20: 3552. https://doi.org/10.3390/polym13203552
APA StyleWei, H., Wolffsohn, J. S., Gomes de Oliveira, O., & Davies, L. N. (2021). An Artificial Lens Capsule with a Lens Radial Stretching System Mimicking Dynamic Eye Focusing. Polymers, 13(20), 3552. https://doi.org/10.3390/polym13203552








