Solvent-Free Ultrasonic Dispersion of Nanofillers in Epoxy Matrix
Abstract
1. Introduction
2. Materials and Methods
2.1. Matrix and Nanofillers
2.2. Oxidation
2.3. Dispersion
2.4. Three-Roll Mill
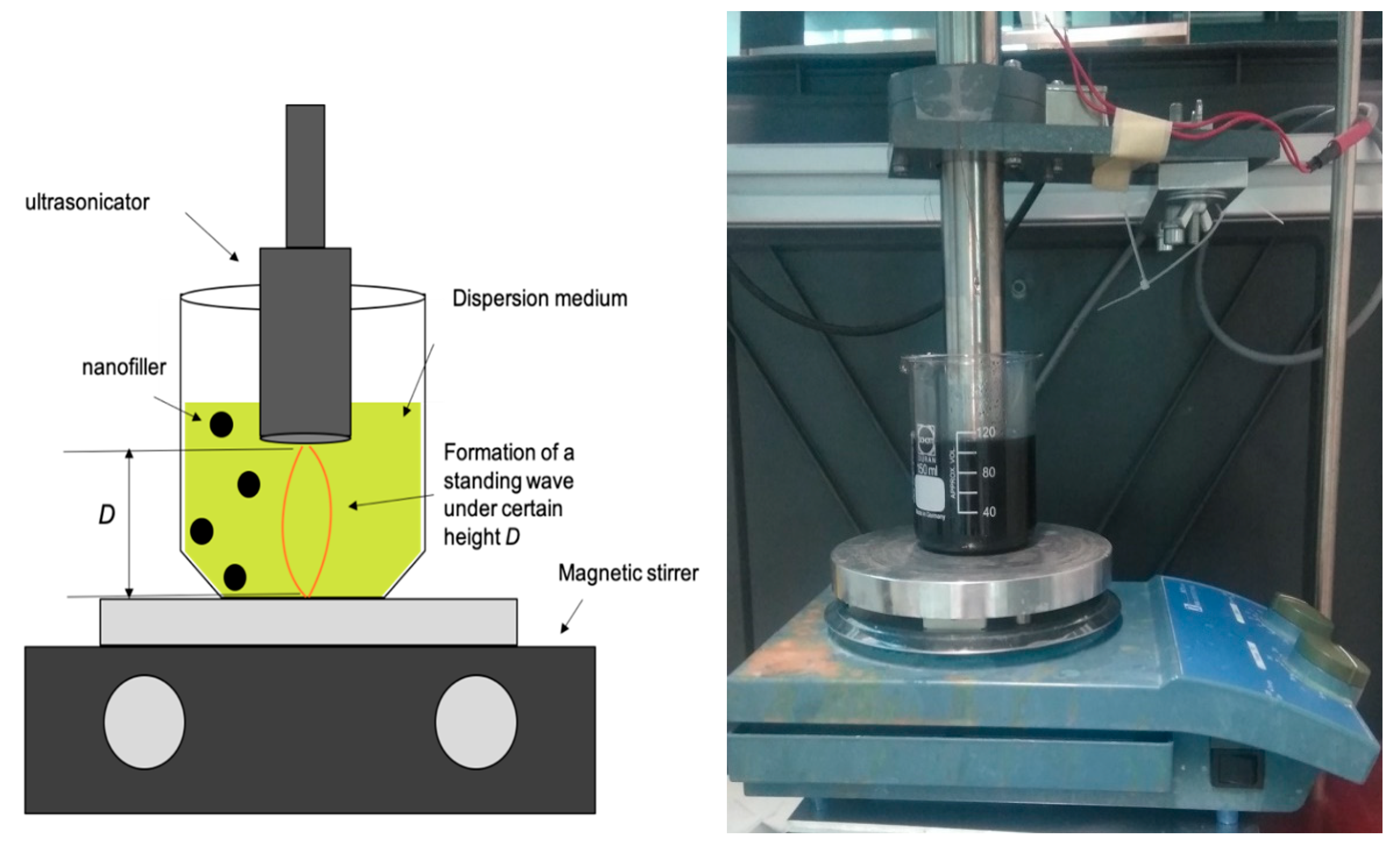
2.5. Ultrasonication
2.6. Microscopy
2.7. Rheology
3. Results
3.1. Oxidation State of the CNT by XPS
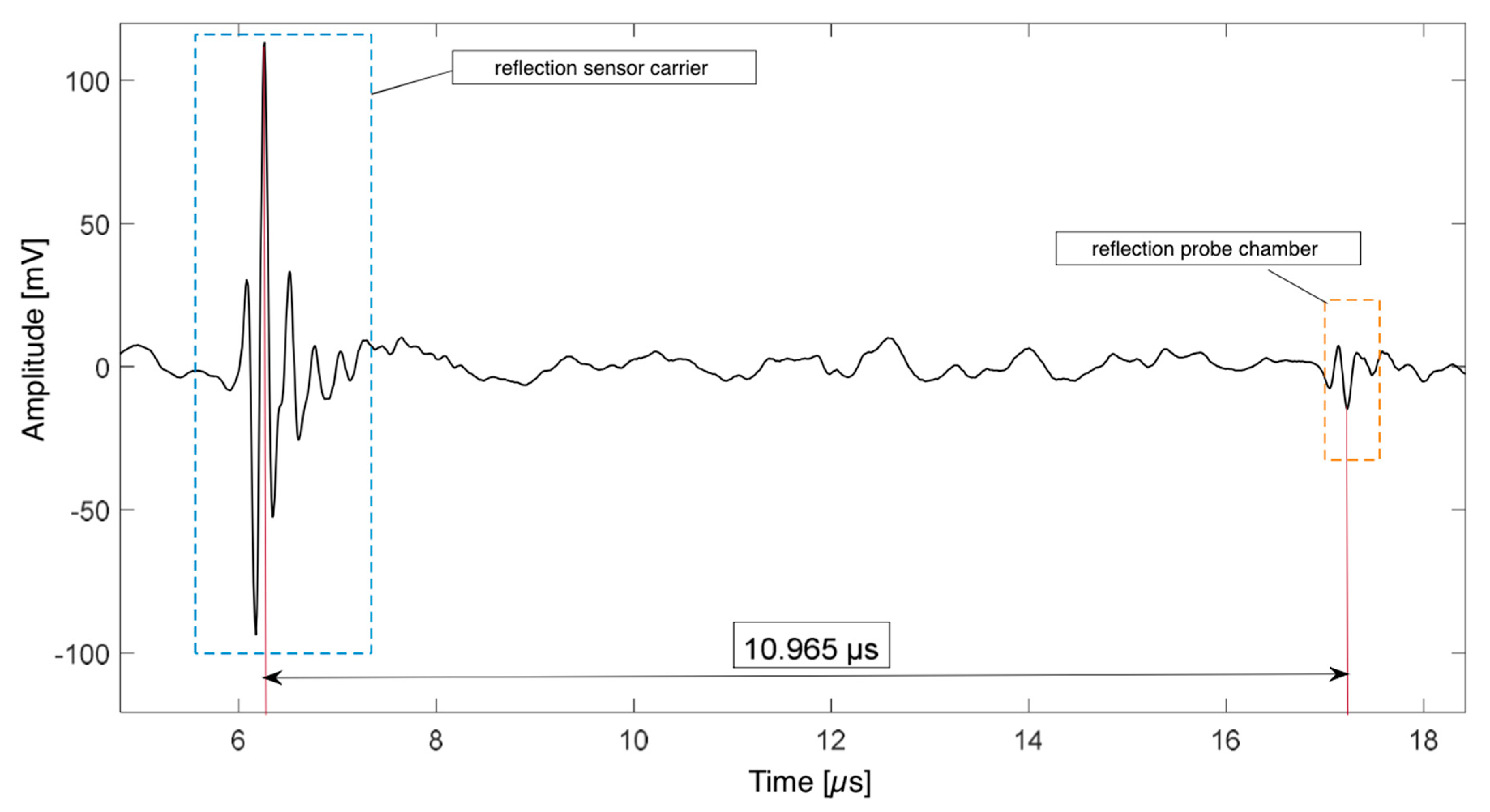
3.2. Determination of Hardeners’ Speed of Sound and Optimal Sonicator Height
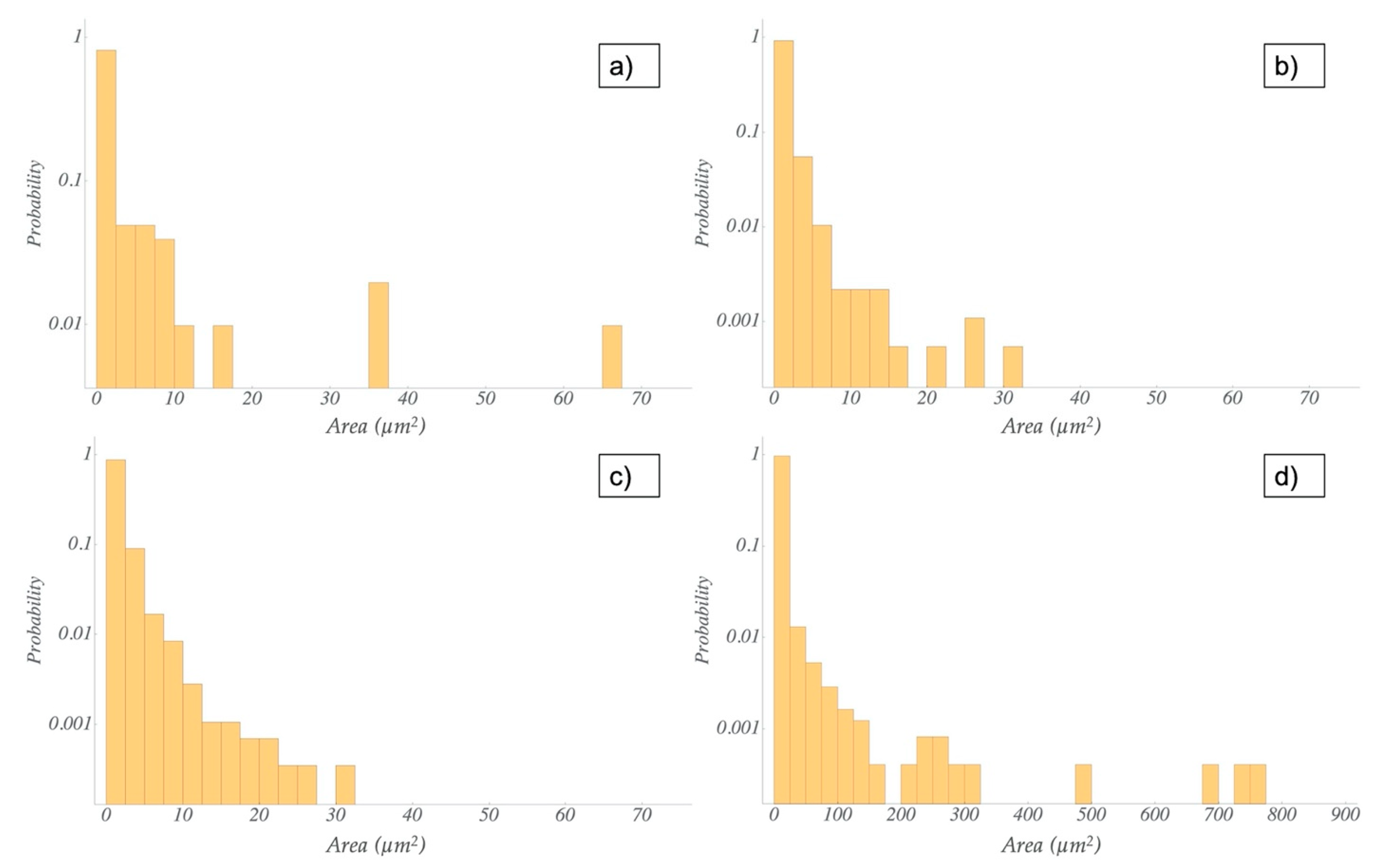
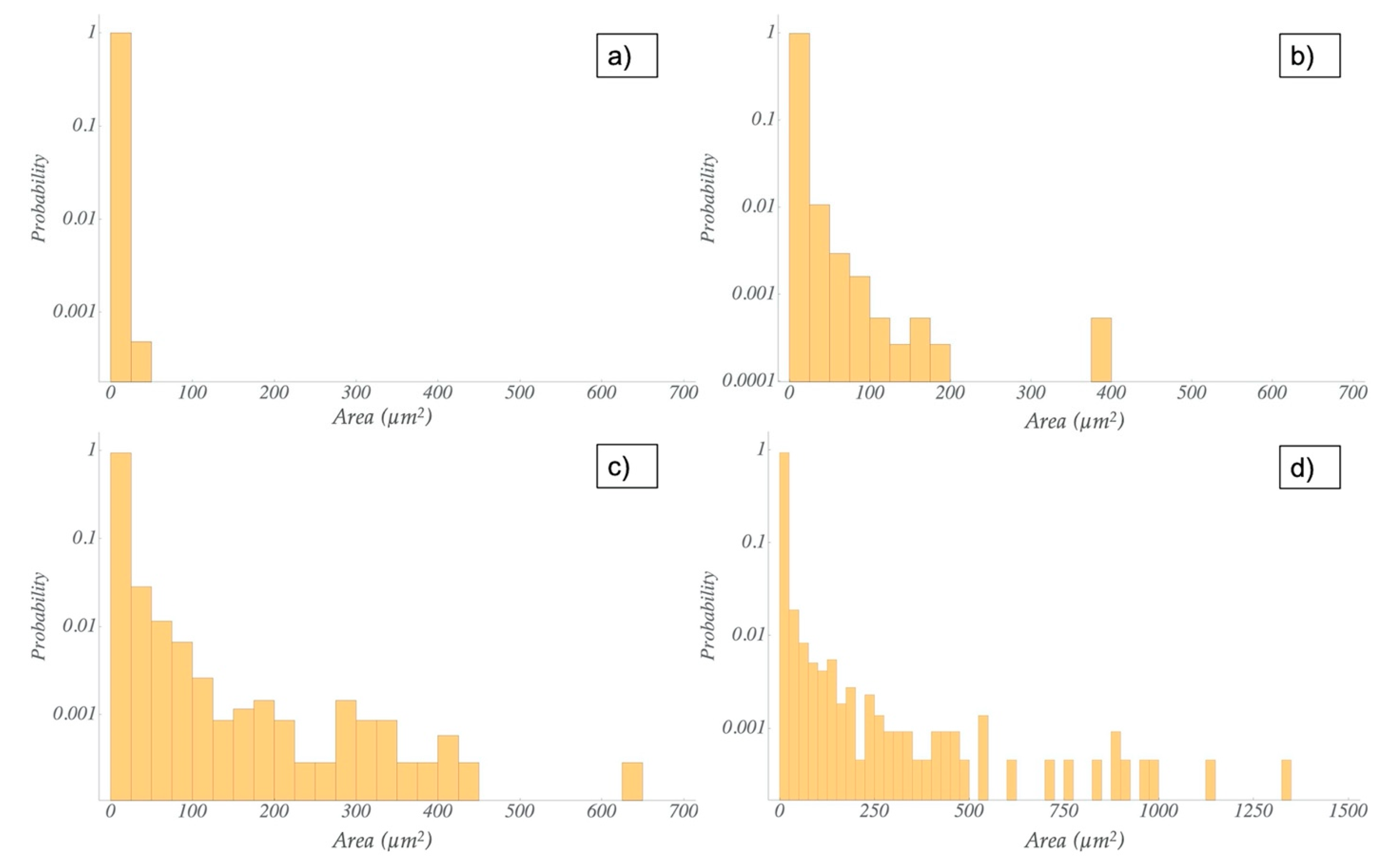
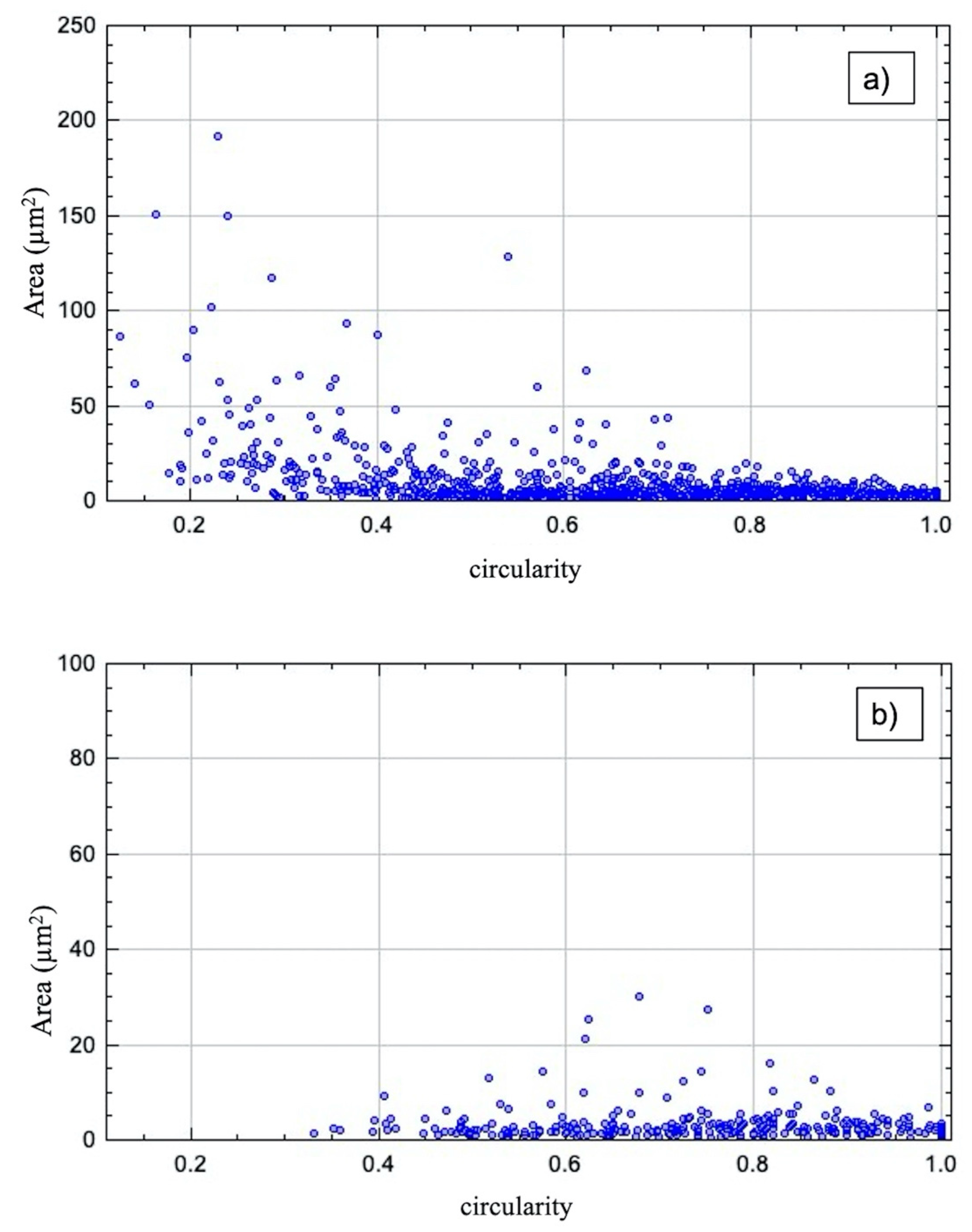
3.3. Microscopic Characterization of TRM and US Dispersions
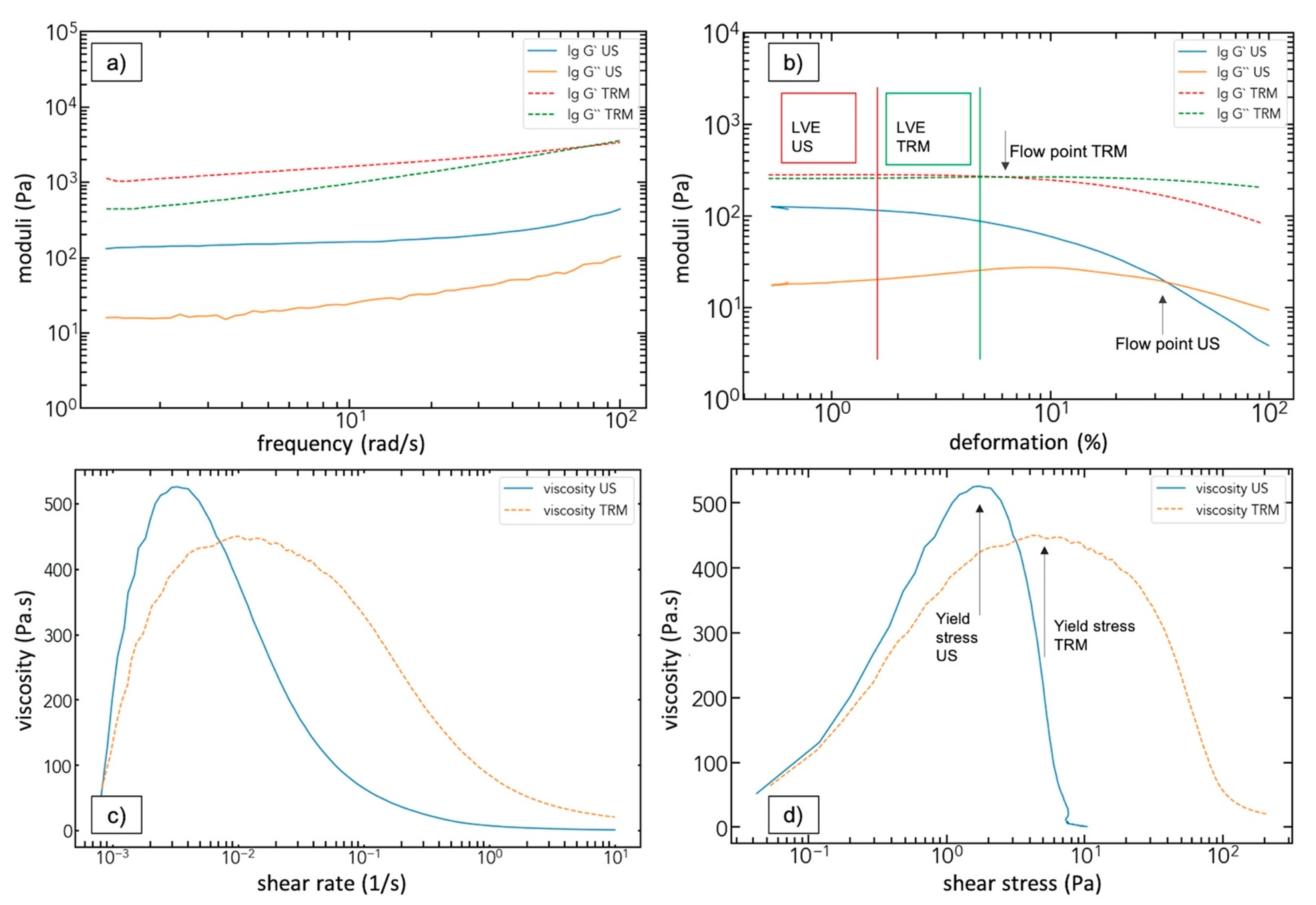
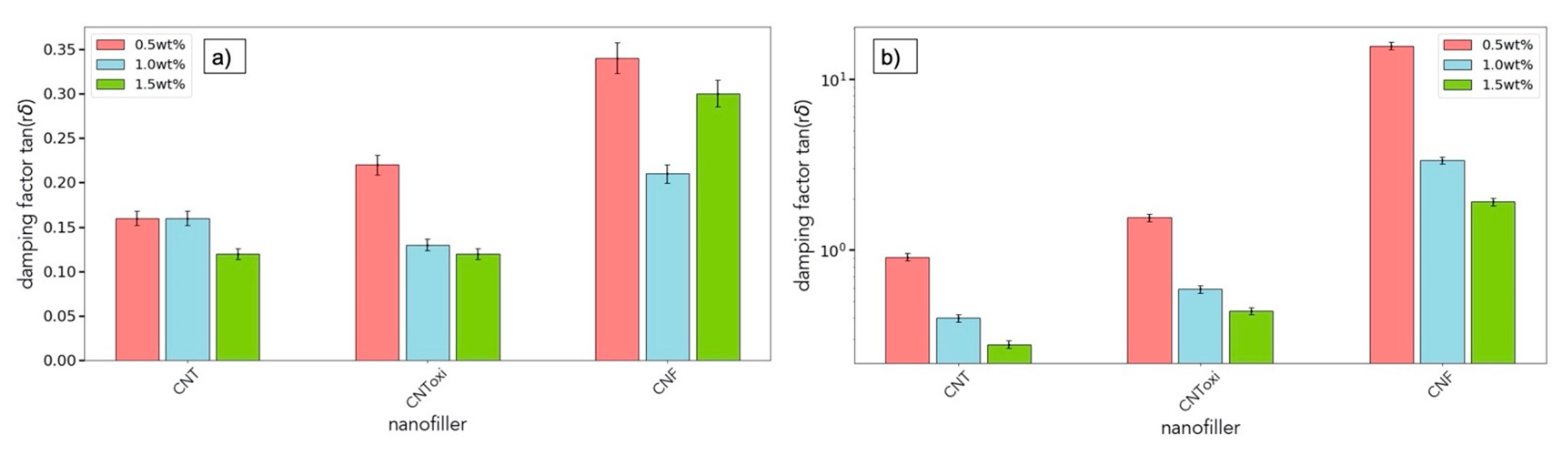
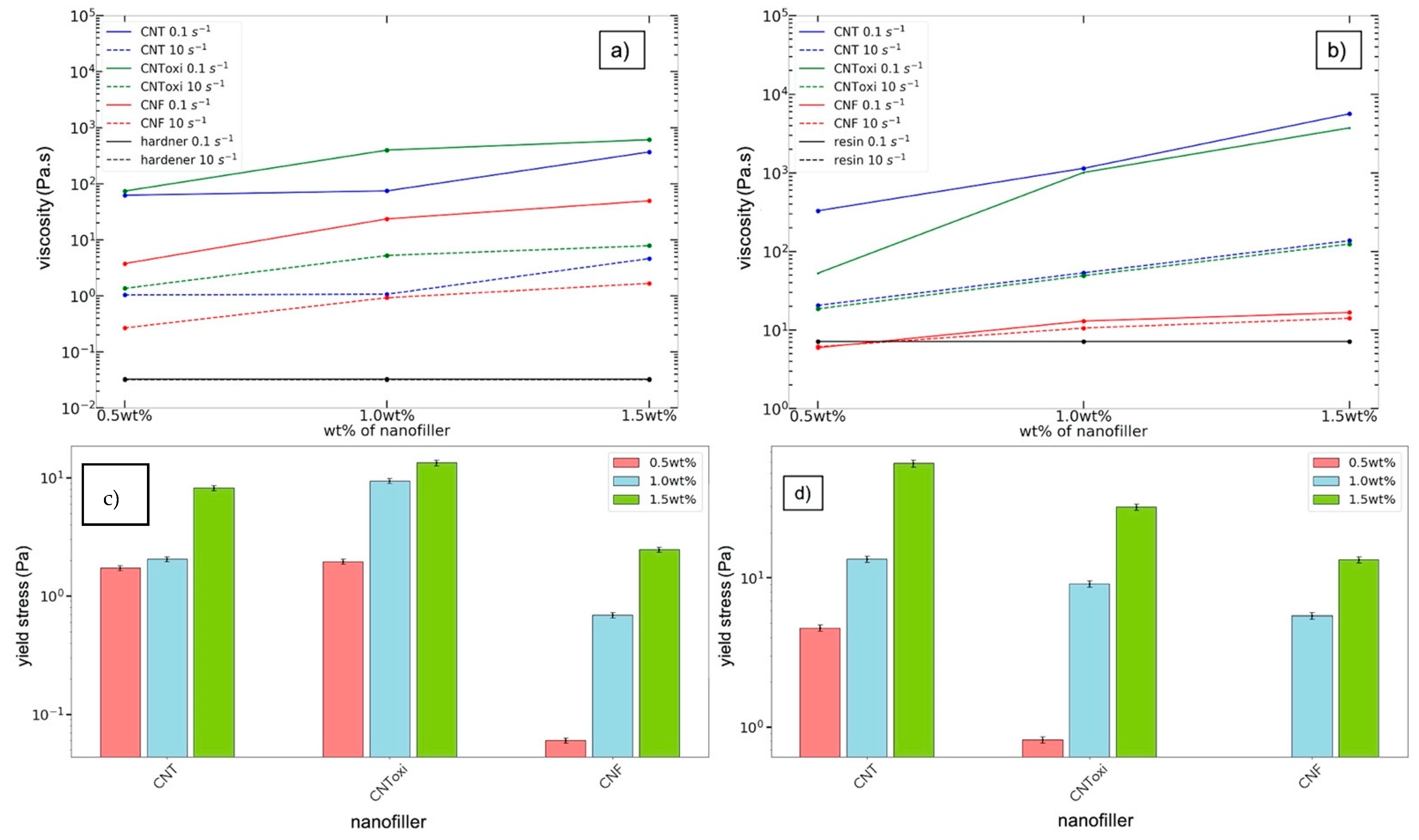
3.4. Rheological Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, M.-F.; Lourie, O.; Dyer, M.J.; Moloni, K.; Kelly, T.F.; Ruoff, R.S. Strength and Breaking Mechanism of Multiwalled Carbon Nanotubes Under Tensile Load. Science 2000, 287, 637–640. [Google Scholar] [CrossRef] [PubMed]
- Berber, S.; Kwon, Y.-K.; Tománek, D. Unusually High Thermal Conductivity of Carbon Nanotubes. Phys. Rev. Lett. 2000, 84, 4613–4616. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, J.; Wei, F. A treatment method to give separated multi-walled carbon nanotubes with high purity, high crystallization and a large aspect ratio. Carbon 2003, 41, 2939–2948. [Google Scholar] [CrossRef]
- Feng, L.; Xie, N.; Zhong, J. Carbon Nanofibers and Their Composites: A Review of Synthesizing, Properties and Applications. Materials 2014, 7, 3919–3945. [Google Scholar] [CrossRef] [PubMed]
- Karger-Kocsis, J.; Mahmood, H.; Pegoretti, A. All-carbon multi-scale and hierarchical fibers and related structural composites: A review. Compos. Sci. Technol. 2020, 186, 107932. [Google Scholar] [CrossRef]
- Netravali, A.N.; Mittal, K.L.; Nicolais, L. Fiber Surface Treatment: Relevance to Interfacial Characteristics. Wiley Encycl. Compos. 2012, 1–19. [Google Scholar] [CrossRef]
- Romhány, G.; Czigány, T.; Karger-Kocsis, J. Failure Assessment and Evaluation of Damage Development and Crack Growth in Polymer Composites Via Localization of Acoustic Emission Events: A Review. Polym. Rev. 2017, 57, 397–439. [Google Scholar] [CrossRef]
- Khare, R.; Bose, S. Carbon Nanotube Based Composites—A Review. J. Miner. Mater. Charact. Eng. 2005, 4, 31–46. [Google Scholar] [CrossRef]
- Arrigo, R.; Teresi, R.; Gambarotti, C.; Parisi, F.; Lazzara, G.; Dintcheva, N.T. Sonication-Induced Modification of Carbon Nanotubes: Effect on the Rheological and Thermo-Oxidative Behaviour of Polymer-Based Nanocomposites. Materials 2018, 11, 383. [Google Scholar] [CrossRef]
- Datsyuk, V.; Kalyva, M.; Papagelis, K.; Parthenios, J.; Tasis, D.; Siokou, A.; Kallitsis, I.; Galiotis, C. Chemical oxidation of multiwalled carbon nanotubes. Carbon 2008, 46, 833–840. [Google Scholar] [CrossRef]
- Stobinski, L.; Lesiak, B.; Kövér, L.; Tóth, J.; Biniak, S.; Trykowski, G.; Judek, J. Multiwall carbon nanotubes purification and oxidation by nitric acid studied by the FTIR and electron spectroscopy methods. J. Alloy. Compd. 2010, 501, 77–84. [Google Scholar] [CrossRef]
- Singer, G.; Siedlaczek, P.; Sinn, G.; Rennhofer, H.; Mičušík, M.; Omastova, M.; Unterlass, M.M.; Wendrinsky, J.; Milotti, V.; Fedi, F.; et al. Acid Free Oxidation and Simple Dispersion Method of MWCNT for High-Performance CFRP. Nanomaterials 2018, 8, 912. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Liang, R.; Wang, B.; Zhang, C. Load-transfer in functionalized carbon nanotubes/polymer composites. Chem. Phys. Lett. 2008, 457, 371–375. [Google Scholar] [CrossRef]
- Ma, P.-C.; Siddiqui, N.A.; Marom, G.; Kim, J.-K. Dispersion and functionalization of carbon nanotubes for polymer-based nanocomposites: A review. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1345–1367. [Google Scholar] [CrossRef]
- Olowojoba, G.; Sathyanarayana, S.; Caglar, B.; Kiss-Pataki, B.; Mikonsaari, I.; Hübner, C.; Elsner, P. Influence of process parameters on the morphology, rheological and dielectric properties of three-roll-milled multiwalled carbon nanotube/epoxy suspensions. Polymer 2013, 54, 188–198. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.-W. Processing-structure-multi-functional property relationship in carbon nanotube/epoxy composites. Carbon 2006, 44, 3022–3029. [Google Scholar] [CrossRef]
- Ha, J.-H.; Lee, S.-E.; Sung-Chul, L.; Park, H.L. Effect of Dispersion by Three-Roll Milling on Electrical Properties and Filler Length of Carbon Nanotube Composites. Materials 2019, 12, 3823. [Google Scholar] [CrossRef]
- Sesis, A.; Hodnett, M.; Memoli, G.; Wain, A.J.; Jurewicz, I.; Dalton, A.B.; Carey, J.D.; Hinds, G. Influence of Acoustic Cavitation on the Controlled Ultrasonic Dispersion of Carbon Nanotubes. J. Phys. Chem. B 2013, 117, 15141–15150. [Google Scholar] [CrossRef]
- Wu, Z.; Mitra, S. Length reduction of multi-walled carbon nanotubes via high energy ultrasonication and its effect on their dispersibility. J. Nanoparticle Res. 2014, 16, 1–7. [Google Scholar] [CrossRef]
- Fuge, R.; Liebscher, M.; Schröfl, C.; Oswald, S.; Leonhardt, A.; Büchner, B.; Mechtcherine, V. Fragmentation characteristics of undoped and nitrogen-doped multiwalled carbon nanotubes in aqueous dispersion in dependence on the ultrasonication parameters. Diam. Relat. Mater. 2016, 66, 126–134. [Google Scholar] [CrossRef]
- Dehghan, M.; Al-Mahaidi, R.; Sbarski, I. Investigation of CNT modification of epoxy resin in CFRP strengthening systems. Polym. Compos. 2014, 37, 1021–1033. [Google Scholar] [CrossRef]
- LaRosa, C.; Patra, N.; Salerno, M.; Mikac, L.; Meri, R.M.; Ivanda, M. Preparation and characterization of polycarbonate/multiwalled carbon nanotube nanocomposites. Beilstein J. Nanotechnol. 2017, 8, 2026–2031. [Google Scholar] [CrossRef] [PubMed]
- Rezazadeh, V.; Pourhossaini, M.R.; Salimi, A. Effect of amine-functionalized dispersant on cure and electrical properties of carbon nanotube/epoxy nanocomposites. Prog. Org. Coat. 2017, 111, 389–394. [Google Scholar] [CrossRef]
- Frømyr, T.R.; Hansen, F.K.; Olsen, T. The Optimum Dispersion of Carbon Nanotubes for Epoxy Nanocomposites: Evolution of the Particle Size Distribution by Ultrasonic Treatment. J. Nanotechnol. 2012, 2012, 1–14. [Google Scholar] [CrossRef]
- Guadagno, L.; De Vivo, B.; Di Bartolomeo, A.; Lamberti, P.; Sorrentino, A.; Tucci, V.; Vertuccio, L.; Vittoria, V. Effect of functionalization on the thermo-mechanical and electrical behavior of multi-wall carbon nanotube/epoxy composites. Carbon 2011, 49, 1919–1930. [Google Scholar] [CrossRef]
- Kim, M.; Park, Y.-B.; Okoli, O.I.; Zhang, C. Processing, characterization, and modeling of carbon nanotube-reinforced multiscale composites. Compos. Sci. Technol. 2009, 69, 335–342. [Google Scholar] [CrossRef]
- Lee, K.P.; Leese, H.S.; Mattia, D. Water flow enhancement in hydrophilic nanochannels. Nanoscale 2012, 4, 2621. [Google Scholar] [CrossRef]
- Lugod, C.B.; Auresenia, J. Effect of magnetic field on the synthesis of carbon nanotubes using MPECVD. In MATEC Web of Conferences; EDP Sciences: Paris, France, 2019; Volume 268, p. 05004. [Google Scholar]
- Shanthi, C.; Porpatham, R.K.; Pappa, N. Image analysis for particle size distribution. Int. J. Eng. Technol. 2014, 6, 1340–1345. [Google Scholar]
- Meeuw, H.; Wisniewski, V.K.; Fiedler, B. Frequency or Amplitude?—Rheo-Electrical Characterization of Carbon Nanoparticle Filled Epoxy Systems. Polymer 2018, 10, 999. [Google Scholar] [CrossRef]
- Ibanescu, C.; Danu, M.; Nanu, A.; Lungu, M.; Simionescu, B.C. Stability of Disperse Systems Estimated Using Rheological Oscillatory Shear Tests. Rev. Roum. Chim. 2010, 55, 933–940. [Google Scholar]
- Lu, K. Rheological behavior of carbon nanotube-alumina nanoparticle dispersion systems. Powder Technol. 2007, 177, 154–161. [Google Scholar] [CrossRef]
- Wu, D.; Wu, L.; Zhang, M.; Zhao, Y. Viscoelasticity and thermal stability of polylactide composites with various functionalized carbon nanotubes. Polym. Degrad. Stab. 2008, 93, 1577–1584. [Google Scholar] [CrossRef]
- Wang, G.; Guo, B.; Xu, J.; Li, R. Rheology, crystallization behaviors, and thermal stabilities of poly(butylene succinate)/pristine multiwalled carbon nanotube composites obtained by melt compounding. J. Appl. Polym. Sci. 2011, 121, 59–67. [Google Scholar] [CrossRef]
- Song, Y.S. Rheological characterization of carbon nanotubes/poly(ethylene oxide) composites. Rheol. Acta 2006, 46, 231–238. [Google Scholar] [CrossRef]
- Kim, J.A.; Seong, D.G.; Kang, T.J.; Youn, J.R. Effects of surface modification on rheological and mechanical properties of CNT/epoxy composites. Carbon 2006, 44, 1898–1905. [Google Scholar] [CrossRef]
- Singer, G.; Siedlaczek, P.; Sinn, G.; Kirner, P.H.; Schuller, R.; Wan-Wendner, R.; Lichtenegger, H.C. Vacuum Casting and Mechanical Characterization of Nanocomposites from Epoxy and Oxidized Multi-Walled Carbon Nanotubes. Molecule 2019, 24, 510. [Google Scholar] [CrossRef]
- Domun, N.; Hadavinia, H.; Zhang, T.; Sainsbury, T.; Liaghat, G.H.; Vahid, S. Improving the fracture toughness and the strength of epoxy using nanomaterials—A review of the current status. Nanoscale 2015, 7, 10294–10329. [Google Scholar] [CrossRef]
- Verdejo, R.; Barroso-Bujans, F.; Rodriguez-Perez, M.A.; De Saja, J.A.; Arroyo, M.; Lopez-Manchado, M.A. Carbon nanotubes provide self-extinguishing grade to silicone-based foams. J. Mater. Chem. 2008, 18, 3933–3939. [Google Scholar] [CrossRef]
- Mezger, T.G. Das Rheologie Handbuch: 5; Farbe Und Lack: Hannover, Germany, 2016. [Google Scholar]
- Berg, J. An Introduction to Interfaces and Colloids: The Bridge to Nanoscience; World Science: Singapore, 2009; pp. 1–785. [Google Scholar]
- Markgraf, W.; Watts, C.W.; Whalley, W.R.; Hrkac, T.; Horn, R. Influence of organic matter on rheological properties of soil. Appl. Clay Sci. 2012, 64, 25–33. [Google Scholar] [CrossRef]
- Fan, Z.; Advani, S. Rheology of multiwall carbon nanotube suspensions. J. Rheol. 2007, 51, 585–604. [Google Scholar] [CrossRef]
- Wu, J.; Guo, J.; Zhang, Q.; Gao, L.; Li, H.; Deng, H.; Jiang, W.; Sui, G.; Yang, X. Effect of different amino functionalized carbon nanotubes on curing behavior and mechanical properties of carbon fiber/epoxy composites. Polym. Compos. 2016, 39, E733–E744. [Google Scholar] [CrossRef]
- Pötschke, P.; Fornes, T.; Paul, D.R. Rheological behavior of multiwalled carbon nanotube/polycarbonate composites. Polymer 2002, 43, 3247–3255. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J.; Moldenaers, P.; Vermant, J. Assessment of the Dispersion Quality in Polymer Nanocomposites by Rheological Methods. Macromol. Mater. Eng. 2011, 296, 331–340. [Google Scholar] [CrossRef]
- Chan, C.-M.; Wu, J.; Li, J.-X.; Cheung, Y.-K. Polypropylene/calcium carbonate nanocomposites. Polymer 2002, 43, 2981–2992. [Google Scholar] [CrossRef]
- Böhm, G.G.A.; Nguyen, M.N. Flocculation of carbon black in filled rubber compounds. I. Flocculation occurring in unvulcanized compounds during annealing at elevated temperatures. J. Appl. Polym. Sci. 1995, 55, 1041–1050. [Google Scholar] [CrossRef]


| TRM Gap | Step 1 | Step 2 | Step 3 | Step 4 | Step 4 Shear Force (N/mm) |
|---|---|---|---|---|---|
| Gap 1 size (µm) ± 1 µm | 120 | 30 | 15 | 5 | variable |
| Gap 2 size (µm) ± 1 µm | 40 | 10 | 5 | 0 | 5 |
| n | D (mm) |
|---|---|
| 1 | 40.0 ± 0.3 |
| 2 | 80.0 ± 0.5 |
| 3 | 120.0 ± 0.7 |
| Filler Amount | CNT US | CNToxi US | CNF US | CNT TRM | CNToxi TRM | CNF TRM |
|---|---|---|---|---|---|---|
| Feret diameter Cut off (µm) ± 2 μm | ||||||
| 0.5 wt% | 44 | 21 | 9 | 9 | 8 | 6 |
| 1.0 wt% | 50 | 32 | 14 | 20 | 11 | 11 |
| 1.5 wt% | 49 | 36 | 19 | 22 | 10 | 20 |
| 0.5 wt% semi d. | 80 | / | / | 69 | / | / |
| Feret diameter Maximum (µm) ± 2 μm | ||||||
| 0.5 wt% | 48 | 47 | 9 | 13 | 9 | 11 |
| 1.0 wt% | 71 | 59 | 14 | 24 | 18 | 13 |
| 1.5wt% | 72 | 74 | 46 | 22 | 10 | 20 |
| 0.5 wt% semi d. | 180 | / | / | 92 | / | / |
| Filler Amount | CNT | CNToxi | CNF | CNT Semi | CNT | CNToxi | CNF | CNT Semi |
|---|---|---|---|---|---|---|---|---|
| Yield point (%) | Ultrasonication | Three-roll mill | ||||||
| 0.5 wt% | 1.27 ± 0.06 | 1.40 ± 0.07 | 0.37 ± 0.02 | 1.08 ± 0.05 | 5.7 ± 0.3 | 3.8 ± 0.2 | / | 0.61 ± 0.03 |
| 1.0 wt% | 0.29 ± 0.01 | 1.07 ± 0.05 | 1.43 ± 0.07 | / | 2.5 ± 0.2 | 2.1 ± 0.2 | 1.18 ± 0.06 | / |
| 1.5 wt% | 0.93 ± 0.04 | 1.03 ± 0.05 | 0.20 ± 0.01 | / | 1.69 ± 0.08 | 1.60 ± 0.08 | 0.65 ± 0.03 | / |
| Flow point (%) | Ultrasonication | Three-roll mill | ||||||
| 0.5 wt% | 34 ± 4 | 23 ± 3 | 2.1 ± 0.3 | 24 ± 3 | 5.8 ± 0.6 | / | / | 8.9 ± 0.9 |
| 1.0 wt% | 42 ± 5 | 27 ± 3 | 35 ± 4 | / | 27 ± 3 | 8.3 ± 0.9 | / | / |
| 1.5 wt% | 37 ± 4 | 37 ± 4 | 1.6 ± 0.2 | / | 31 ± 4 | 11 ± 2 | / | / |
| Filler Amount | CNT | CNToxi | CNF | CNT | CNToxi | CNF | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G’:G” | Ultrasonication at 2 rad/s | Three-roll mill at 2 rad/s | ||||||||||
| 0.5 wt% | 8.9 ± 0.5 | 6.9 ± 0.4 | 1.6 ± 0.1 | 2.1 ± 0.1 | 0.9 ± 0.1 | 0.01 ± 0.01 | ||||||
| 1.0 wt% | 7.1 ± 0.4 | 8.5 ± 0.5 | 5.9 ± 0.3 | 3.6 ± 0.2 | 1.9 ± 0.1 | 0.34 ± 0.02 | ||||||
| 1.5 wt% | 8.5 ± 0.5 | 8.8 ± 0.5 | 2.4 ± 0.2 | 4.7 ± 0.3 | 2.3 ± 0.2 | 0.67 ± 0.03 | ||||||
| Moduli slopes Ultrasonication M | Moduli slopes Three-roll mill M | |||||||||||
| slope | ∆G’/∆f | ∆G’’/∆f | ∆G’/∆f | ∆G’’/∆f | ∆G’/∆f | ∆G’’/∆f | ∆G’/∆f | ∆G’’/∆f | ∆G’/∆f | ∆G’’/∆f | ∆G’/∆f | ∆G’’/∆f |
| 0.5 wt% | 2.67 ± 0.05 | 0.85 ± 0.01 | 2.63 ± 0.03 | 0.87 ± 0.01 | 1.18 ± 0.03 | 0.58 ± 0.02 | 34 ± 1 | 24 ± 1 | 5.9 ± 0.2 | 15.4 ± 0.2 | 8.08 ± 0.04 | 0.8 ± 0.2 |
| 1.0 wt% | 4.1 ± 0.3 | 1.05 ± 0.07 | 4.6 ± 0.2 | 1.54 ± 0.02 | 0.06 ± 0.01 | 0.61 ± 0.01 | 25 ± 2 | 24.6 ± 0.5 | 33 ± 1 | 33 ± 1 | 15.2 ± 0.2 | 5.42 ± 0.07 |
| 1.5 wt% | 6.4 ± 0.4 | 2.24 ± 0.05 | 8.5 ± 0.1 | 2.21 ± 0.02 | 5.1 ± 0.1 | 1.32 ± 0.04 | 61 ± 3 | 41 ± 1 | 82 ± 3 | 57 ± 2 | 20.1 ± 0.3 | 8.3 ± 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanghellini, B.; Knaack, P.; Schörpf, S.; Semlitsch, K.-H.; Lichtenegger, H.C.; Praher, B.; Omastova, M.; Rennhofer, H. Solvent-Free Ultrasonic Dispersion of Nanofillers in Epoxy Matrix. Polymers 2021, 13, 308. https://doi.org/10.3390/polym13020308
Zanghellini B, Knaack P, Schörpf S, Semlitsch K-H, Lichtenegger HC, Praher B, Omastova M, Rennhofer H. Solvent-Free Ultrasonic Dispersion of Nanofillers in Epoxy Matrix. Polymers. 2021; 13(2):308. https://doi.org/10.3390/polym13020308
Chicago/Turabian StyleZanghellini, Benjamin, Patrick Knaack, Sebastian Schörpf, Karl-Heinz Semlitsch, Helga C. Lichtenegger, Bernhard Praher, Maria Omastova, and Harald Rennhofer. 2021. "Solvent-Free Ultrasonic Dispersion of Nanofillers in Epoxy Matrix" Polymers 13, no. 2: 308. https://doi.org/10.3390/polym13020308
APA StyleZanghellini, B., Knaack, P., Schörpf, S., Semlitsch, K.-H., Lichtenegger, H. C., Praher, B., Omastova, M., & Rennhofer, H. (2021). Solvent-Free Ultrasonic Dispersion of Nanofillers in Epoxy Matrix. Polymers, 13(2), 308. https://doi.org/10.3390/polym13020308









