Constitutive Modelling of Polylactic Acid at Large Deformation Using Multiaxial Strains
Abstract
:1. Introduction
- Biaxial testing, in the form of planar extension, provides a strain field that is more general than uniaxial testing and explores the effectiveness of the material model in more general conditions. The results provide a measure of anisotropy.
- Stress relaxation allows for direct observation of the elastic component of the stress in the form of steady-state behaviour. This aids the derivation of material parameters and puts a limit on the extent of the entropic contribution to strain-hardening.
2. Materials and Methods
2.1. Material and Preparation
2.2. Differential Scanning Calorimetry (DSC)
2.3. Uniaxial Experiments
2.4. Biaxial Experiments
3. Results
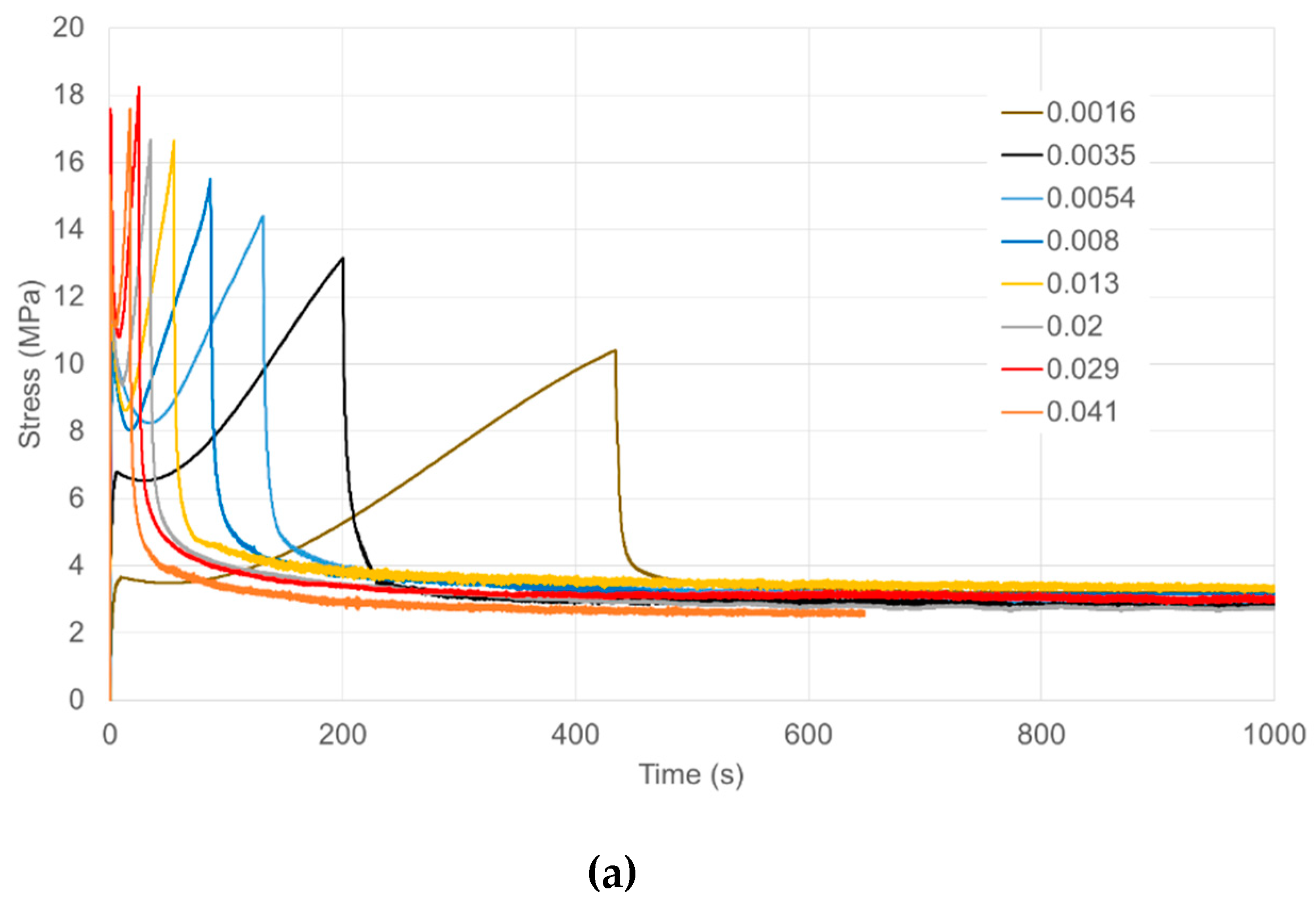
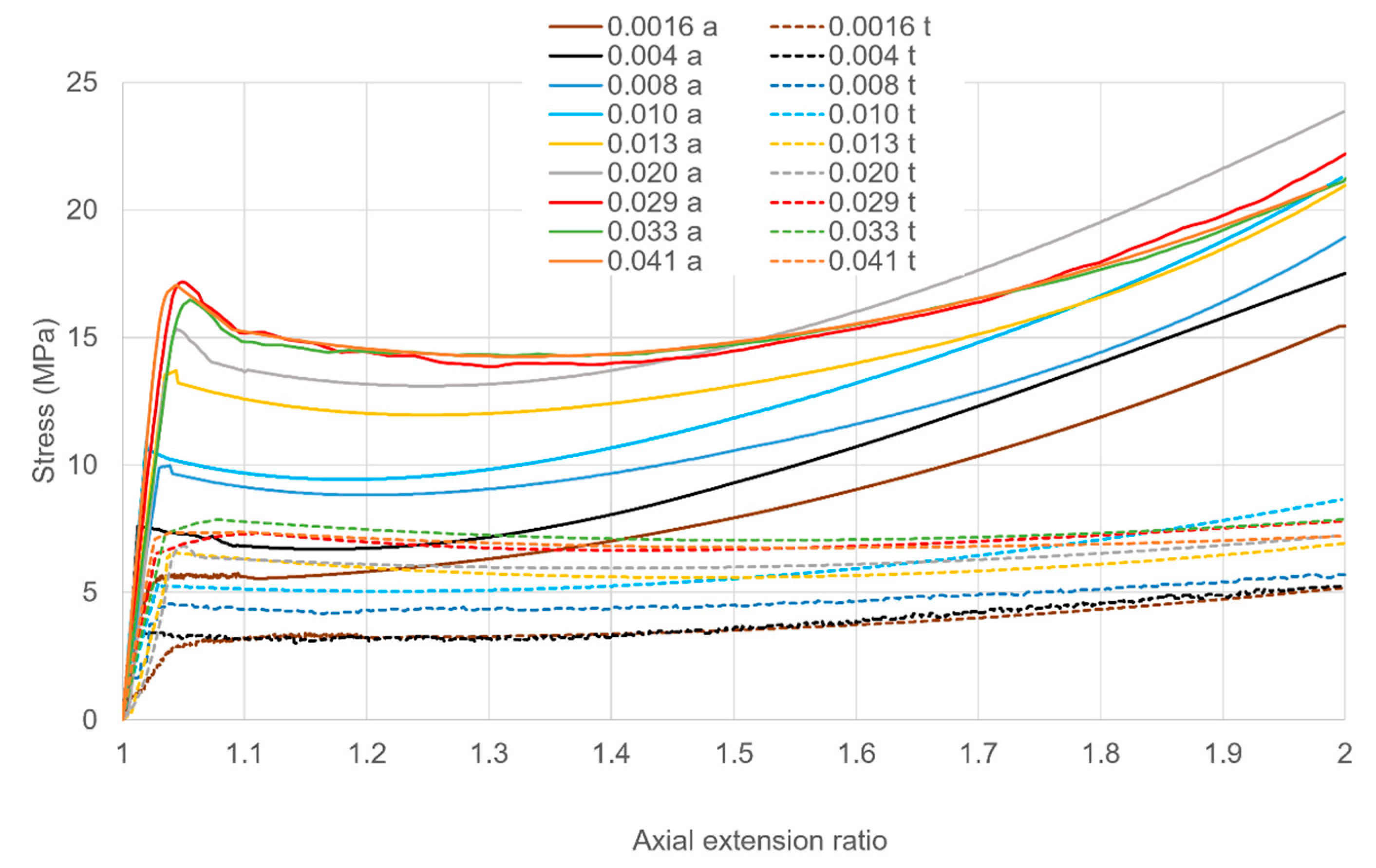
3.1. Uniaxial Yield and Stress Relaxation
3.2. Yield and Stress Relaxation in Planar Extension
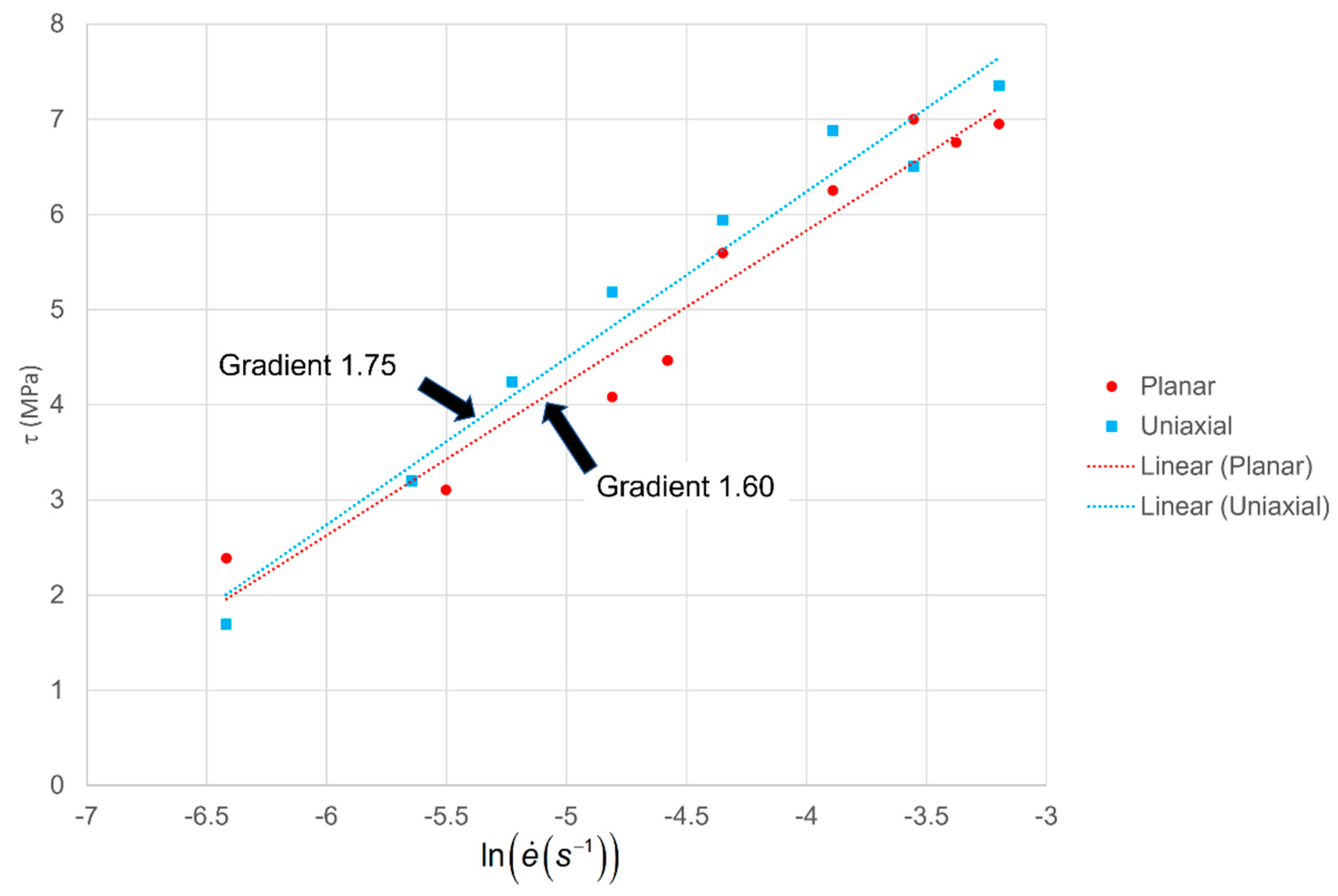
4. Analysis of Yield
5. Modelling
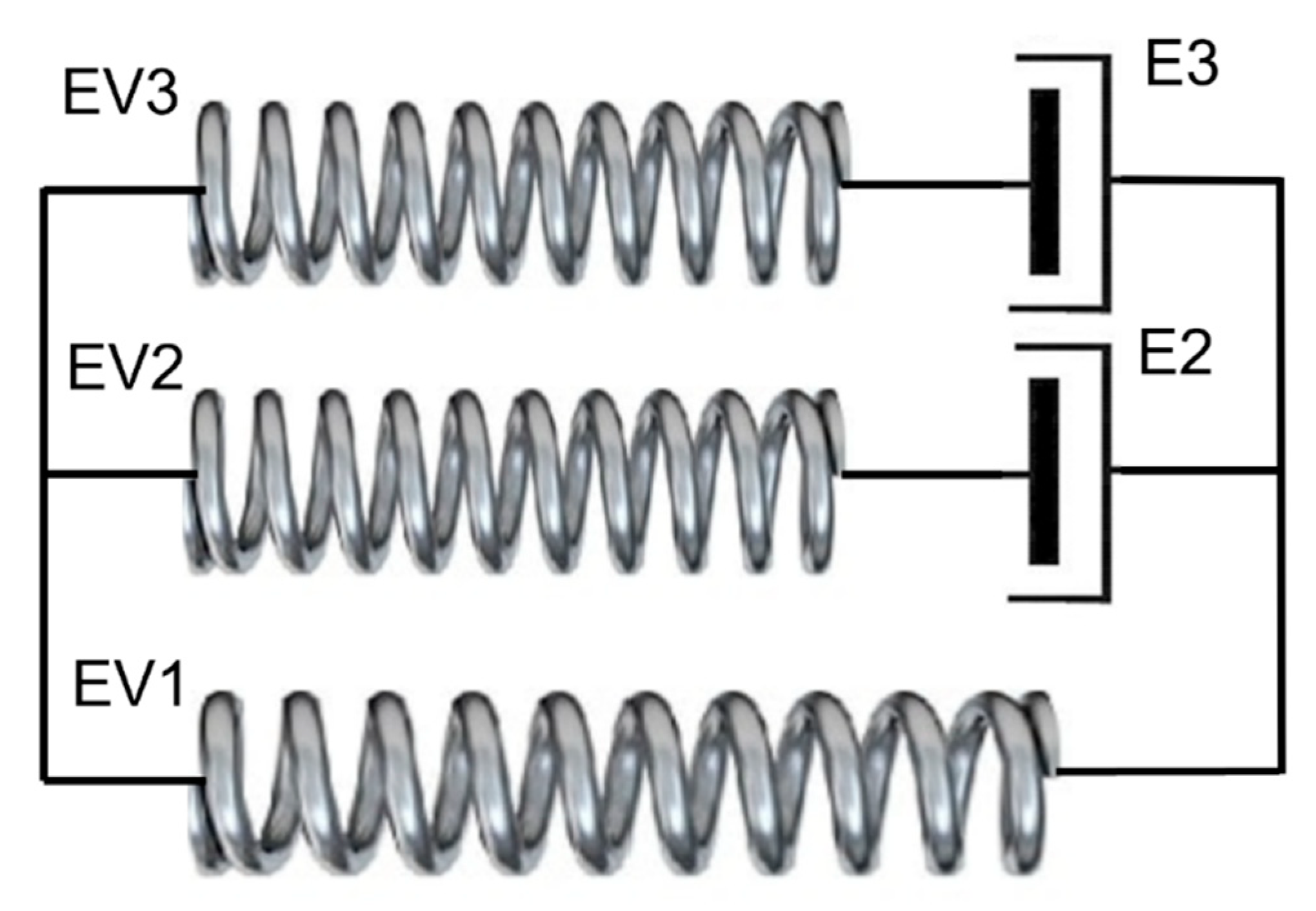
5.1. Elementary Formulation
5.2. Results for Elementary Model
5.3. Modelling with Stress Drops
5.3.1. Uniaxial Strains
5.3.2. Planar Strains
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cosate de Andrade, M.F.; Souza, P.M.S.; Cavalett, O.; Morales, A.R. Life cycle assessment of poly(lactic acid) (PLA): Comparison between chemical recycling. Mechanical recycling and composting. J. Polym. Environ. 2016, 24, 372–384. [Google Scholar] [CrossRef]
- Maga, D.; Hiebel, M.; Thonemann, N. Life cycle assessment of recycling options for polylactic acid. Resour. Conserv. Recycl. 2019, 149, 86–96. [Google Scholar] [CrossRef]
- Shojaeiarani, J.; Bajwa, D.S.; Rehovsky, C.; Bajwa, S.G.; Vahidi, G. Deterioration in the Physico-Mechanical and Thermal Properties of Biopolymers Due to Reprocessing. Polymers 2019, 11, 58. [Google Scholar] [CrossRef] [Green Version]
- Hebda, M.; McIlroy, C.; Whiteside, B.R.; Caton-Rose, F.; Coates, P.D. A method for predicting geometric characteristics of polymer deposition during fused-filament-fabrication. Addit. Manuf. 2019, 27, 99–108. [Google Scholar] [CrossRef] [Green Version]
- Athanasiou, K.A.; Niederauer, G.G.; Agrawal, C.M. Sterilization, toxicity, biocompatibility and clinical applications of polylactic acid/polyglycolic acid copolymers. Biomaterials 1996, 17, 93–102. [Google Scholar] [CrossRef]
- Brkaric, M.; Baker, K.C.; Israel, R.; Harding, T.; Montgomery, D.M.; Herkowit, H.N. Early failure of bioabsorbable anterial cervical fusion plates. J. Spinal Disord. Tech. 2007, 20, 248–254. [Google Scholar] [CrossRef]
- Smit, T.H.; Engels, T.A.P.; Wuisman, P.I.J.M.; Govaert, L.E. Time-dependent mechanical strength of 70/30 poly(l,dl-lactide): Shedding light on the premature failure of degradable spinal cages. Spine 2008, 33, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rebelo, R.; Fernandes, M.; Fangueiro, R. Biopolymers in medical implants: A brief review. Proc. Eng. 2017, 200, 236–243. [Google Scholar] [CrossRef]
- Sweeney, J.; Collins, T.L.D.; Coates, P.D.; Ward, I.M. Application of an elastic model to the large deformation, high temperature stretching of polypropylene. Polymer 1997, 38, 5991–5999. [Google Scholar] [CrossRef]
- Haward, R.N.; Thackray, G. The use of a mathematical model to describe isothermal stress-strain curves in glassy thermoplastics. Proc. Roy. Soc. A 1968, 302, 453–472. [Google Scholar]
- Arruda, E.M.; Boyce, M.C. Evolution of plastic anisotropy in amorphous polymers during finite straining. Int. J. Plast. 1993, 9, 697–720. [Google Scholar] [CrossRef]
- Hoy, R.S.; Robbins, M.O. Strain hardening of polymer glasses: Entanglements, energetics and plasticity. Phys. Rev. E 2008, 77, 031801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoy, R.S.; O’Hern, C.S. Viscoplasticity and large-scale chain relaxation in glassy-polymeric strain hardening. Phys. Rev. 2010, 82, 041803. [Google Scholar] [CrossRef] [Green Version]
- Mahajan, D.K. Basu sumit investigations into the applicability of rubber elastic analogy to hardening in glassy polymers. Model. Simul. Mater. Sci. Eng. 2010, 18, 025001. [Google Scholar] [CrossRef]
- Wendlandt, M.; Tervoort, T.A.; Sutter, U.W. Strain-hardening of cross-linked glassy poly(methyl methacrylate). J. Polym. Sci. Part B Polym. Phys. 2010, 48, 1464–1472. [Google Scholar] [CrossRef]
- Billon, N. New constitutive modeling for time-dependent mechanical behavior of polymers close to glass transition: Fundamentals and experimental validation. J. Appl. Polym. Sci. 2012, 125, 4390–4401. [Google Scholar] [CrossRef] [Green Version]
- Edwards, S.F.; Vilgis, T. The effect of entanglements in rubber elasticity. Polymer 1986, 27, 483. [Google Scholar] [CrossRef]
- Sweeney, J.; O’Connor, C.P.J.; Spencer, P.E.; Pua, H.; Caton-Rose, P.; Martin, P.J. A material model for multiaxial stretching and stress relaxation of polypropylene under process conditions. Mech. Mater. 2012, 54, 55–69. [Google Scholar] [CrossRef]
- Fotheringham, D.G.; Cherry, B.W. The role of recovery forces in the deformation of linear polyethylene. J. Mater. Sci. 1978, 13, 951–964. [Google Scholar] [CrossRef]
- Sweeney, J.; Bonner, M.; Ward, I.M. Modelling of loading, stress relaxation and stress recovery in a shape memory polymer. J. Mech. Behav. Biomed. Mater. 2014, 37, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Wei, H.; Menary, G.; Buchanan, F.; Yan, S.; Nixon, J. Experimental characterisation of the behaviour of PLLA for stretch blow moulding of bioresorbable vascular scaffolds. Int. J. Mater. Form. 2021, 14, 375–389. [Google Scholar] [CrossRef] [Green Version]
- Al-Itry, R.; Lamnawar, K.; Maazouz, A.; Billon, N.; Combeaud, C. Effect of the simultaneous biaxial stretching on the structural and mechanical properties of PLA, PBAT and their blends at rubbery state. Eur. Polym. J. 2015, 68, 288–301. [Google Scholar] [CrossRef]
- Kmett, A. Litauszki development of poly (lactide acid) foams with thermally expandable microspheres. Polymers 2020, 12, 463. [Google Scholar] [CrossRef] [Green Version]
- Jia, S.; Yu, D.; Zhu, Y.; Wang, Z.; Chen, L.; Fu, L. Morphology, crystallization and thermal behaviors of PLA-based composites: Wonderful effects of hybrid GO/PEG via dynamic impregnating. Polymers 2017, 9, 528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buckley, C.P.; Dooling, P.J.; Harding, J.; Ruiz, C. Deformation of thermosetting resins at impact rates of strain. Part 2: Constitutive model with rejeuvenation. J. Mech. Phys. Solids 2004, 52, 2355–2377. [Google Scholar] [CrossRef]
- Turner, J.A.; Menary, G.H.; Martin, P.J.; Yan, S. Modelling the temperature dependent biaxial response of poly(ether-ether-ketone) above and below the glass transition for thermoforming applications. Polymers 2019, 11, 1042. [Google Scholar] [CrossRef] [Green Version]
- Bonet, J.; Wood, R.W. Nonlinear Continuum Mechanics for Finite Element Analysis; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers, 3rd ed.; Wiley: Chichester, UK, 2013. [Google Scholar]
- Ayyub, B.M.; McCuen, R.H. Probability, Statistics and Reliability for Engineers and Scientists; Taylor and Francis Group: Milton Park, UK, 2011; ISBN 9781439895337. [Google Scholar]
- Nazarenko, S.; Bensason, S.; Hiltner, A.; Baer, E. The effect of temperature and pressure on necking of polycarbonate. Polymer 1994, 35, 3883–3892. [Google Scholar] [CrossRef]
- Truss, R.W.; Duckett, R.A.; Ward, I.M. Effect of hydrostatic pressure on the yield and fracture of polyethylene in torsion. J. Mater. Sci. 1981, 16, 1689–1699. [Google Scholar] [CrossRef]
- Bauwens-Crowet, C.; Bauwens, J.-C.; Homes, G. The temperature dependence of yield of polycarbonate in uniaxial compression and tensile tests. J. Mater. Sci. 1972, 7, 176. [Google Scholar] [CrossRef]
- Buckley, C.P.; Jones, D.C.; Jones, D.P. Hot drawing of poly(ethylene terephthalate) under biaxial stress: Application of a three-dimensional glass-rubber model. Polymer 1996, 37, 2403–2414. [Google Scholar] [CrossRef]
- Ho, J.; Govaert, L.; Utz, M. Plastic deformation of glassy polymers: Correlation between shear activation volume and entanglement density. Macromolecules 2013, 36, 7398–7404. [Google Scholar] [CrossRef]
- Van Breemen, L.C.A.; Engels, T.A.P.; Klompen, E.T.J.; Senden, D.J.A.; Govaert, L.E. Rate- and temperature-dependent strain softening in solid polymers. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1757–1771. [Google Scholar] [CrossRef]
- Di Aola, M.; Pirrotta, A.; Valenza, A. Visco-elastic behavior through fractional calculus: An easier method for best fitting experimental results. Mech. Mater. 2011, 43, 799–806. [Google Scholar] [CrossRef] [Green Version]
- Falla, G.; Zingaeles, M. Advanced materials modelling via fractional calculus: Challenges and perspectives. Phil. Trans. Roy. Soc. A 2020, 3678, 20200050. [Google Scholar] [CrossRef]
- Fabrizio, M.; Lazzari, B.; Nibbi, R. Existence ans stability for a visco-plastic material via a fractional constitutive equation. Math. Methods Appl. Sci. 2017, 40, 6305–6315. [Google Scholar] [CrossRef]
- Halsey, G.; White, H.J.; Eyring, H. Mechanical properties of textiles, I. Text. Res. J. 1945, 15, 295–311. [Google Scholar] [CrossRef]
- Guiu, F.; Pratt, P.L. Stress relaxation and the plastic deformation of solids. Phys. Status Solidi. 1964, 6, 111–120. [Google Scholar] [CrossRef]
- Kaliske, M.; Rothert, H. On the finite element implementation of rubber-like materials at finite strains. Eng. Comput. 1997, 14, 216–232. [Google Scholar] [CrossRef]
- Hutchinson, J.M. Physical ageing in polymers. Prog. Polym. Sci. 1995, 20, 703–760. [Google Scholar] [CrossRef]




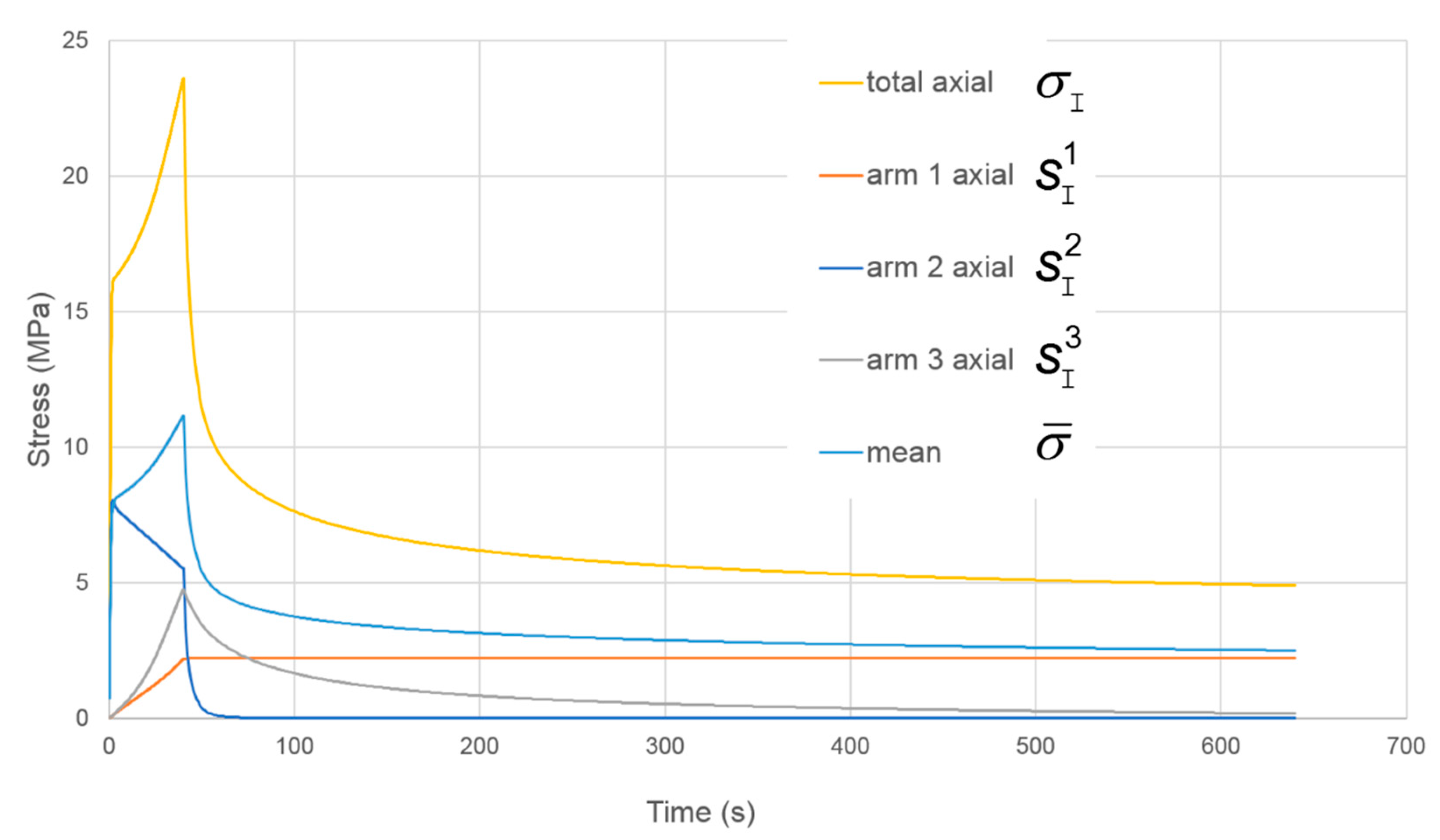
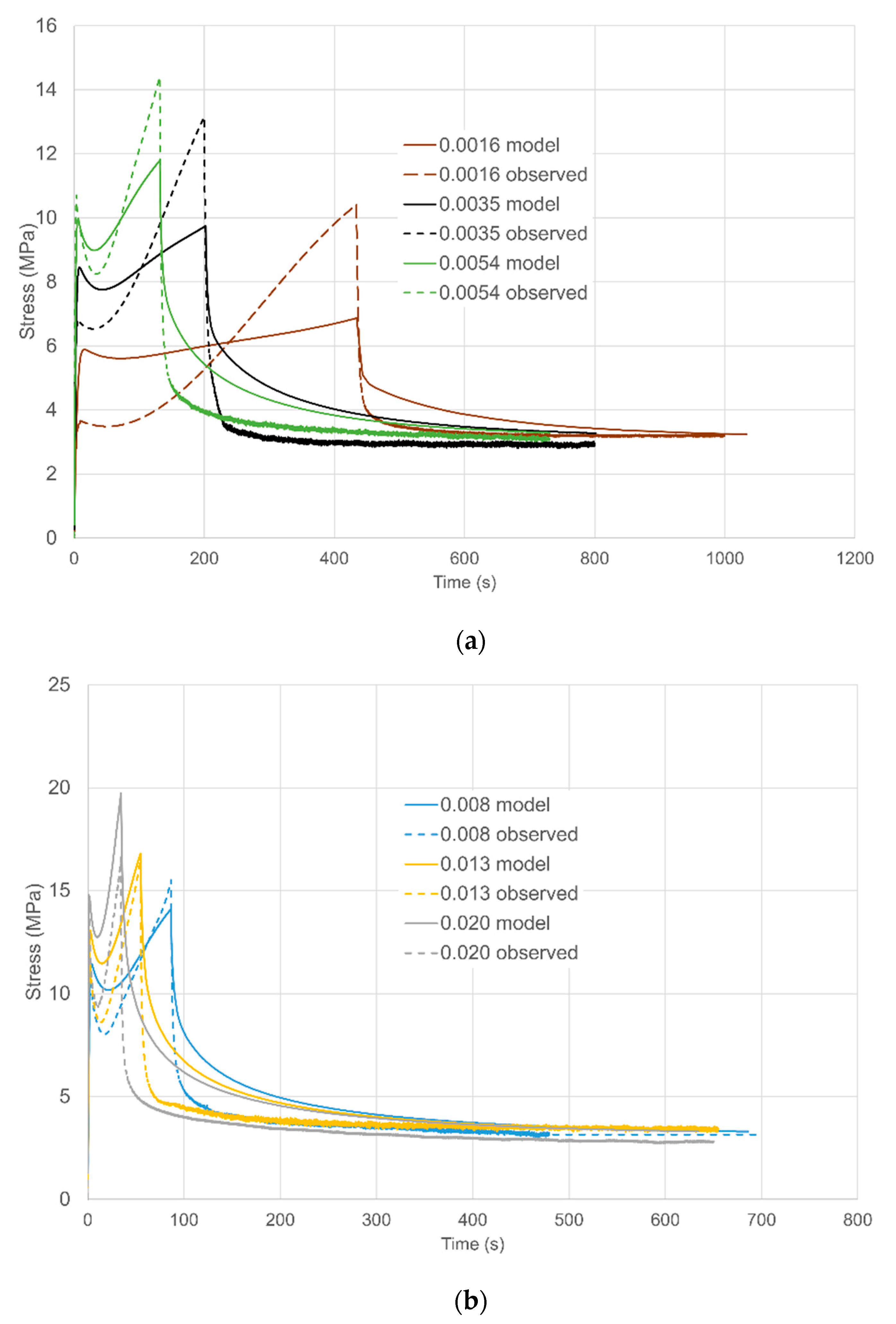
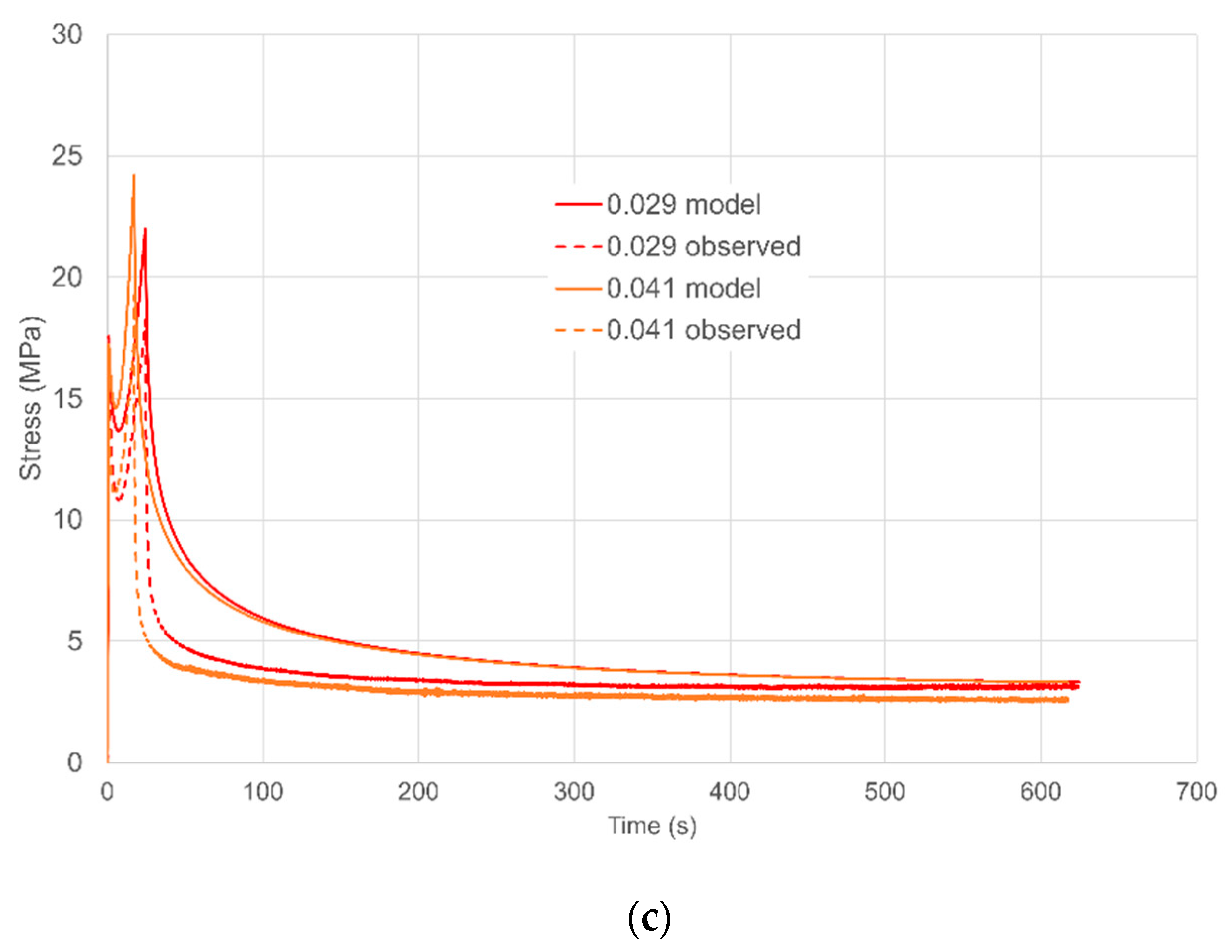




| Nc MPa | Ns MPa | B MPa | α | η | Vs MPa−1 | Vp MPa−1 | ||
|---|---|---|---|---|---|---|---|---|
| Arm 1 | 0 | 4.48 | 950 | 0.216 | 1.60 | - | - | - |
| Arm 2 | 190 | 0 | 0 | 0 | 0.50 | 0.10 | 7 × 10−4 | |
| Arm 3 | 1.0 | 0.0 | 0.36 | 0.0 | 0.25 | 0.05 | 4 × 10−3 |
| r | |||
|---|---|---|---|
| 0.50 | 0.58 | 0.65 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sweeney, J.; Spencer, P.; Thompson, G.; Barker, D.; Coates, P. Constitutive Modelling of Polylactic Acid at Large Deformation Using Multiaxial Strains. Polymers 2021, 13, 2967. https://doi.org/10.3390/polym13172967
Sweeney J, Spencer P, Thompson G, Barker D, Coates P. Constitutive Modelling of Polylactic Acid at Large Deformation Using Multiaxial Strains. Polymers. 2021; 13(17):2967. https://doi.org/10.3390/polym13172967
Chicago/Turabian StyleSweeney, John, Paul Spencer, Glen Thompson, David Barker, and Phil Coates. 2021. "Constitutive Modelling of Polylactic Acid at Large Deformation Using Multiaxial Strains" Polymers 13, no. 17: 2967. https://doi.org/10.3390/polym13172967
APA StyleSweeney, J., Spencer, P., Thompson, G., Barker, D., & Coates, P. (2021). Constitutive Modelling of Polylactic Acid at Large Deformation Using Multiaxial Strains. Polymers, 13(17), 2967. https://doi.org/10.3390/polym13172967







