Glass Transition in Rice Pasta as Observed by Combined Neutron Scattering and Time-Domain NMR
Abstract
:1. Introduction
2. Materials and Methods
2.1. Pasta Preparation and Composition
2.2. Differential Scanning Calorimetry
2.3. NMR Measurements and Data Analysis
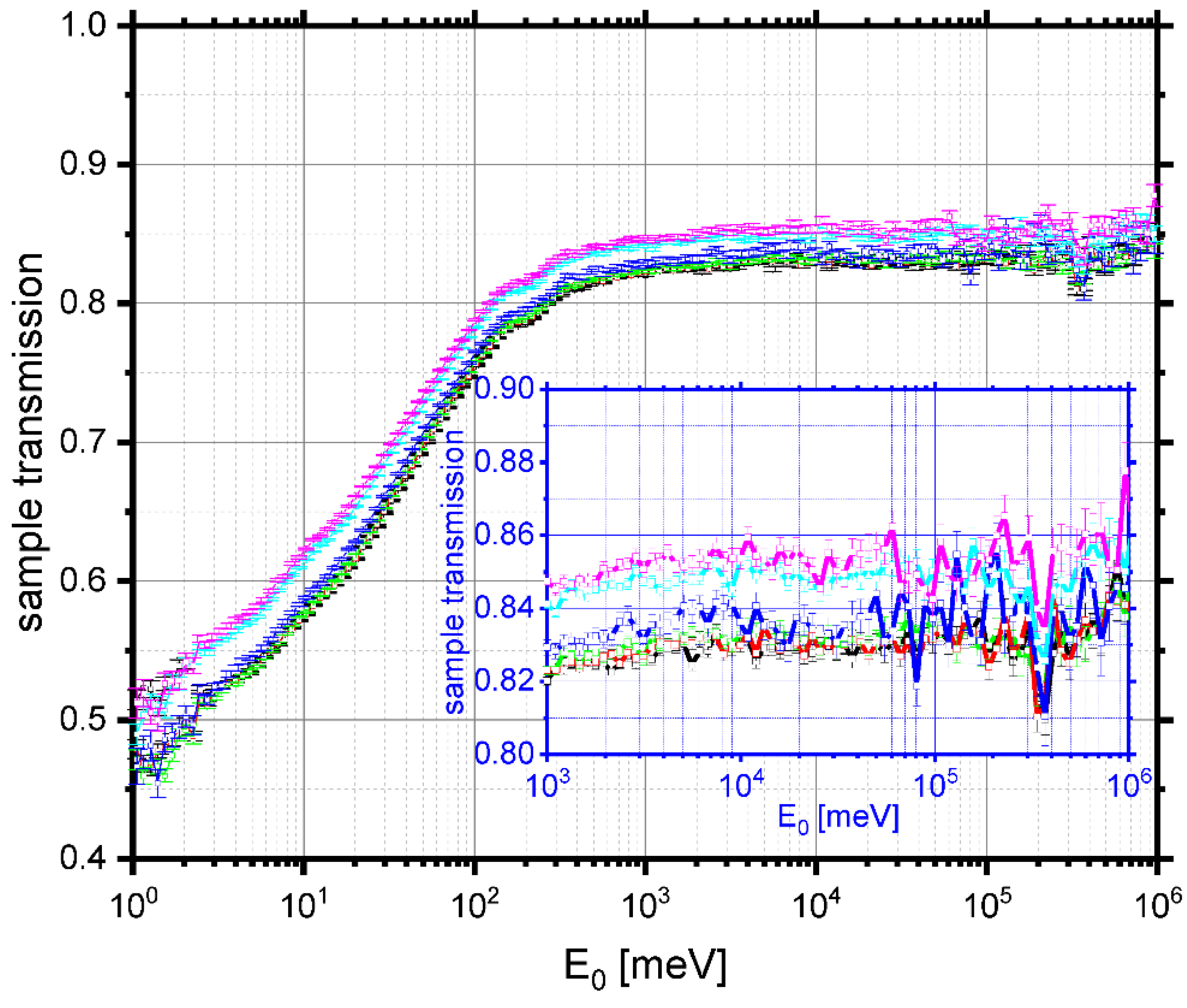
2.4. Neutron Scattering Experiments
3. Results and Discussion
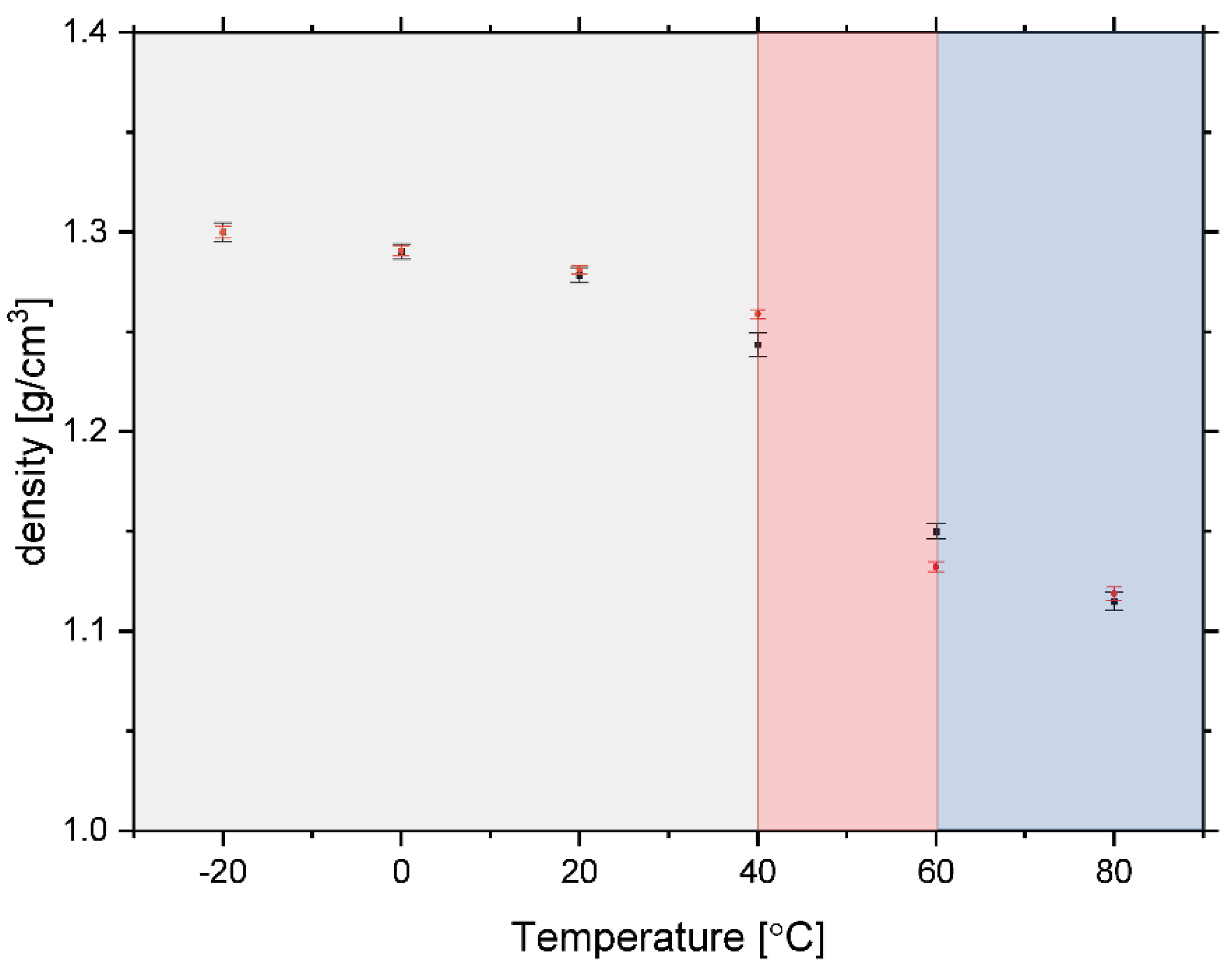
3.1. Glass Transition by DSC
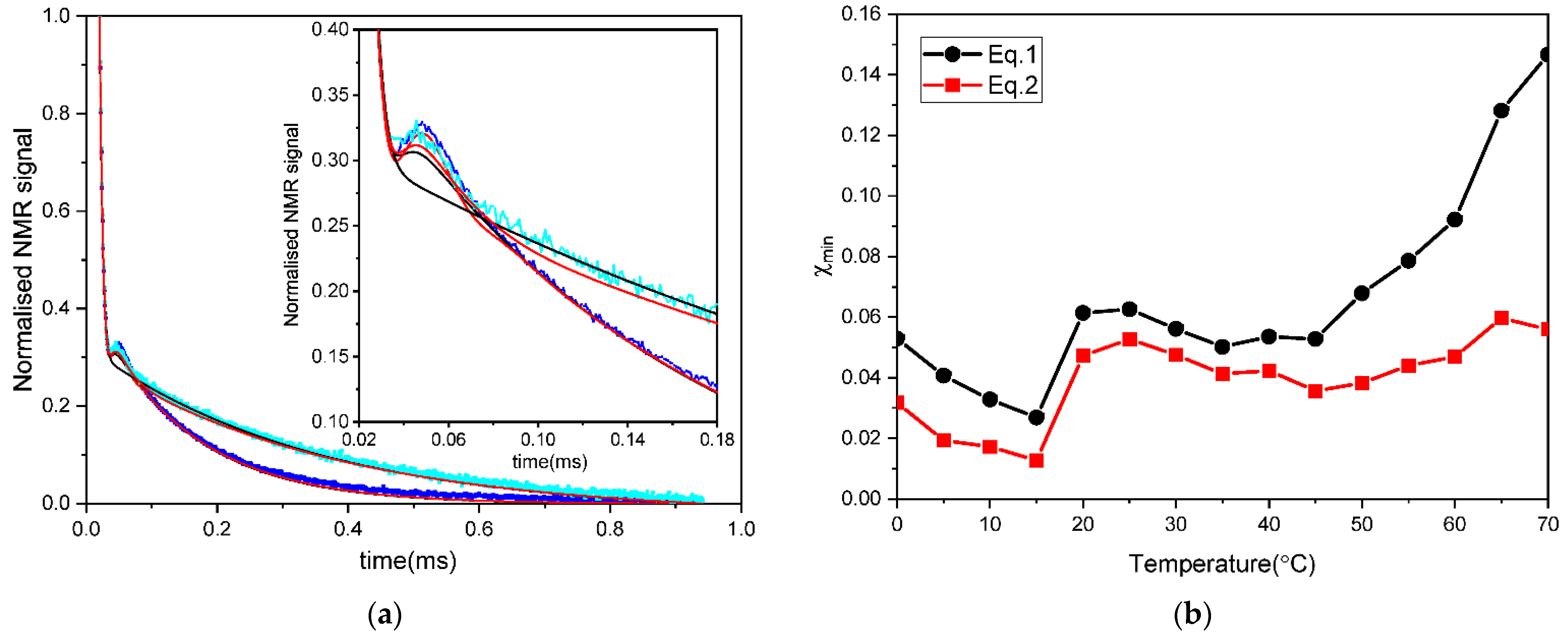
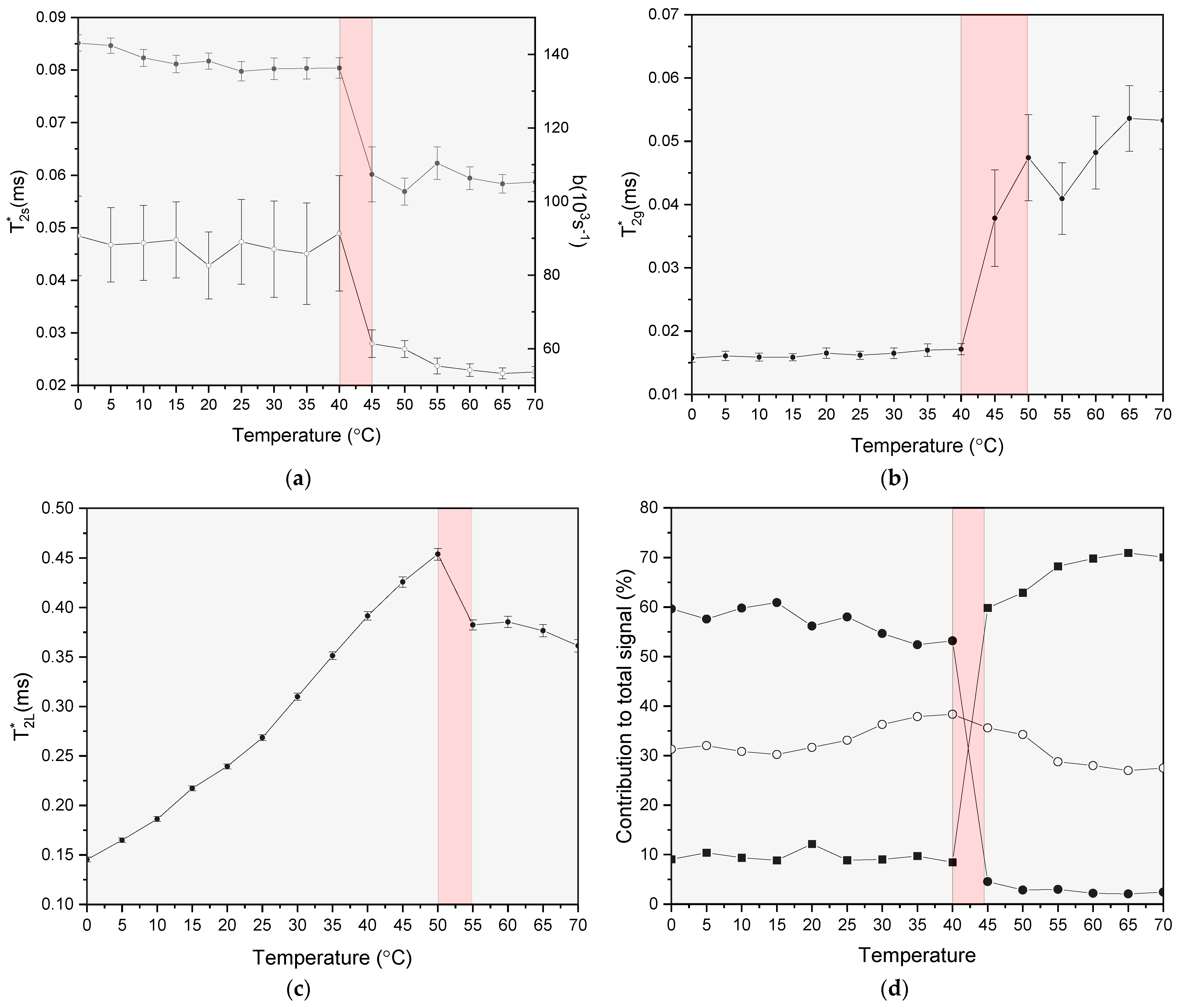
3.2. Glass Transition in Rice Pasta by NMR Analysis
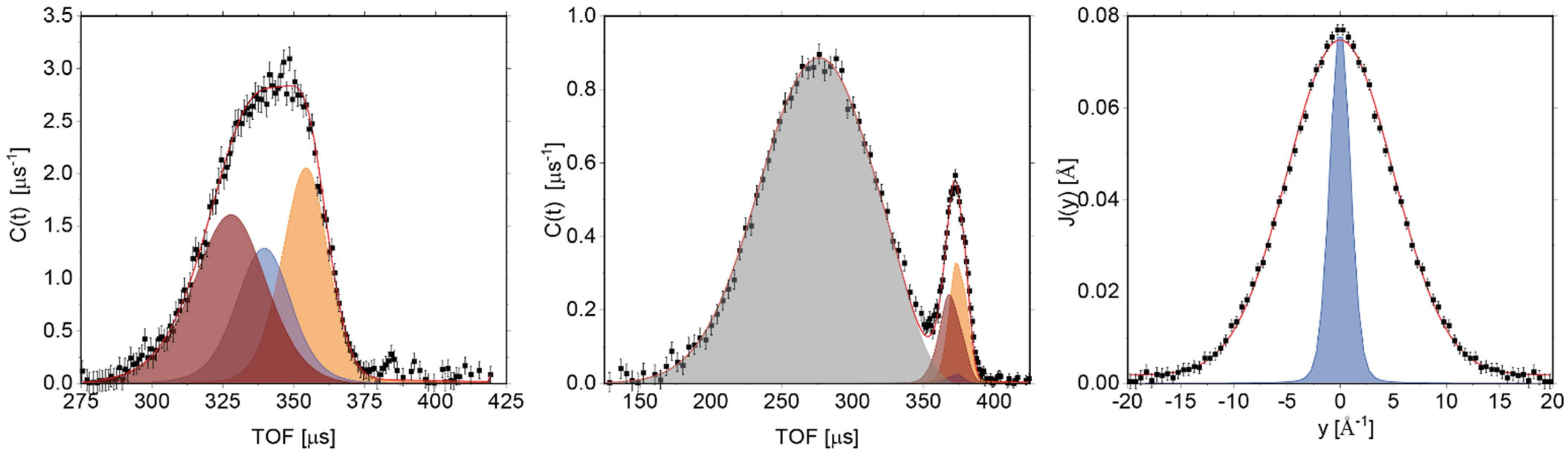
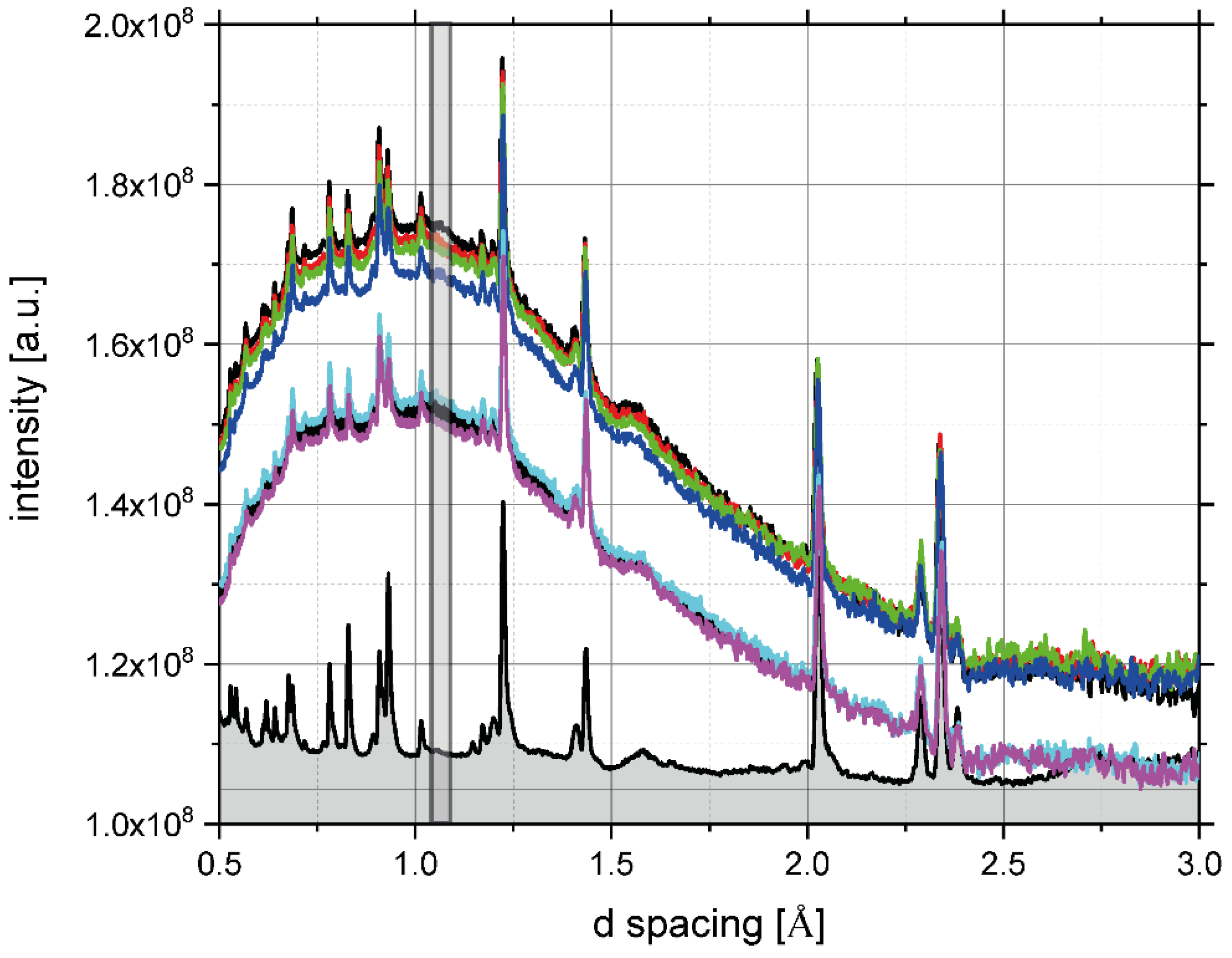
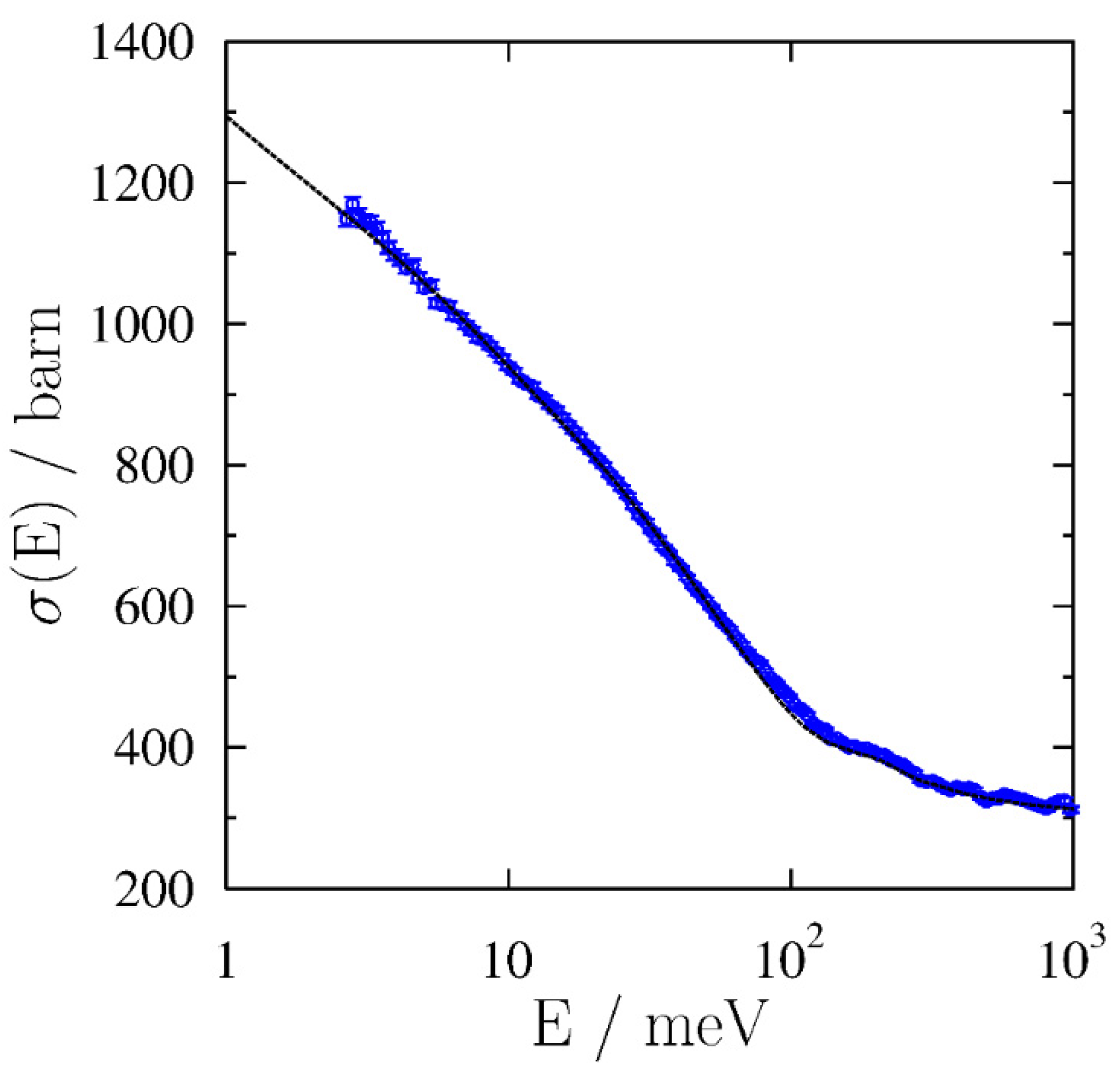
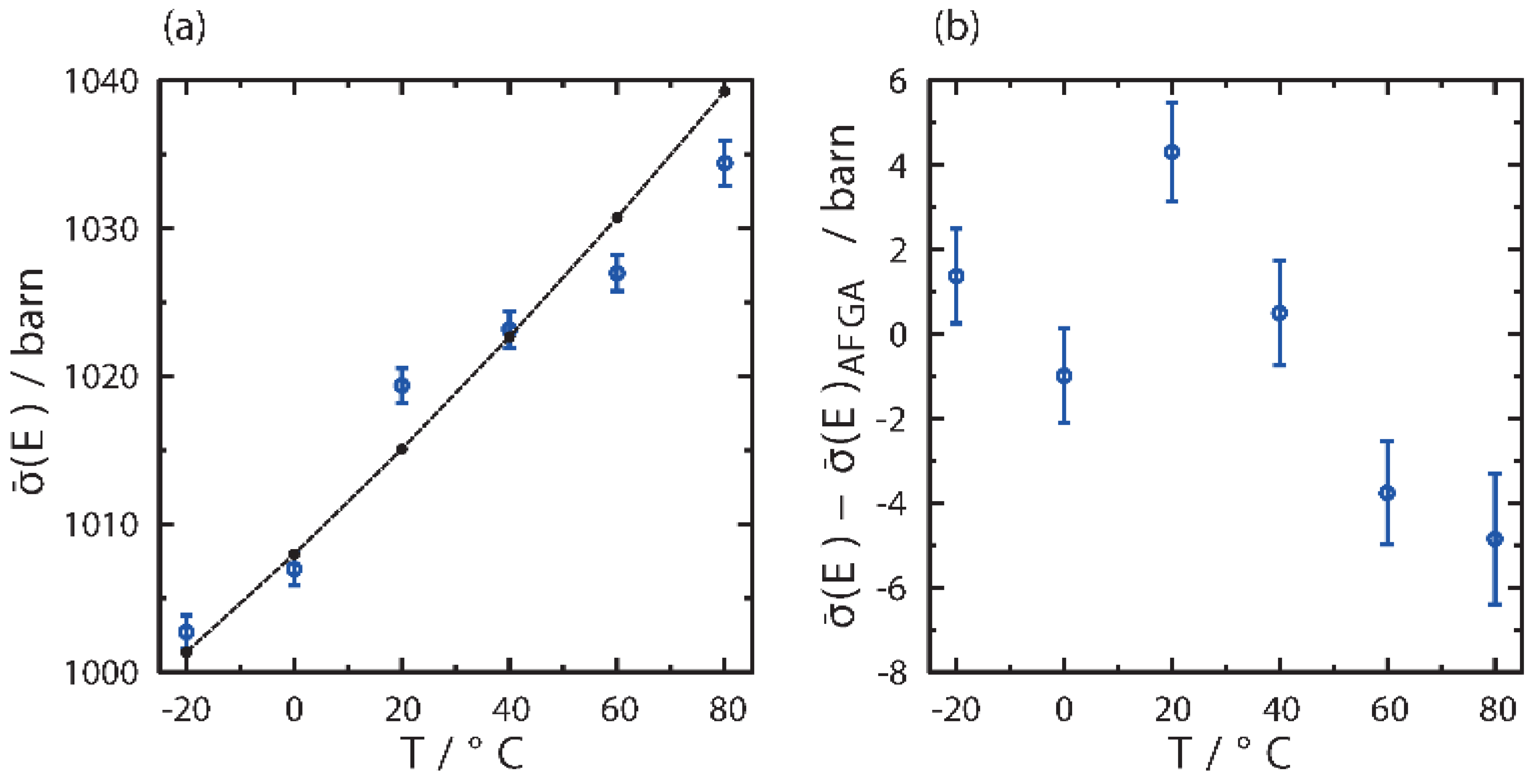
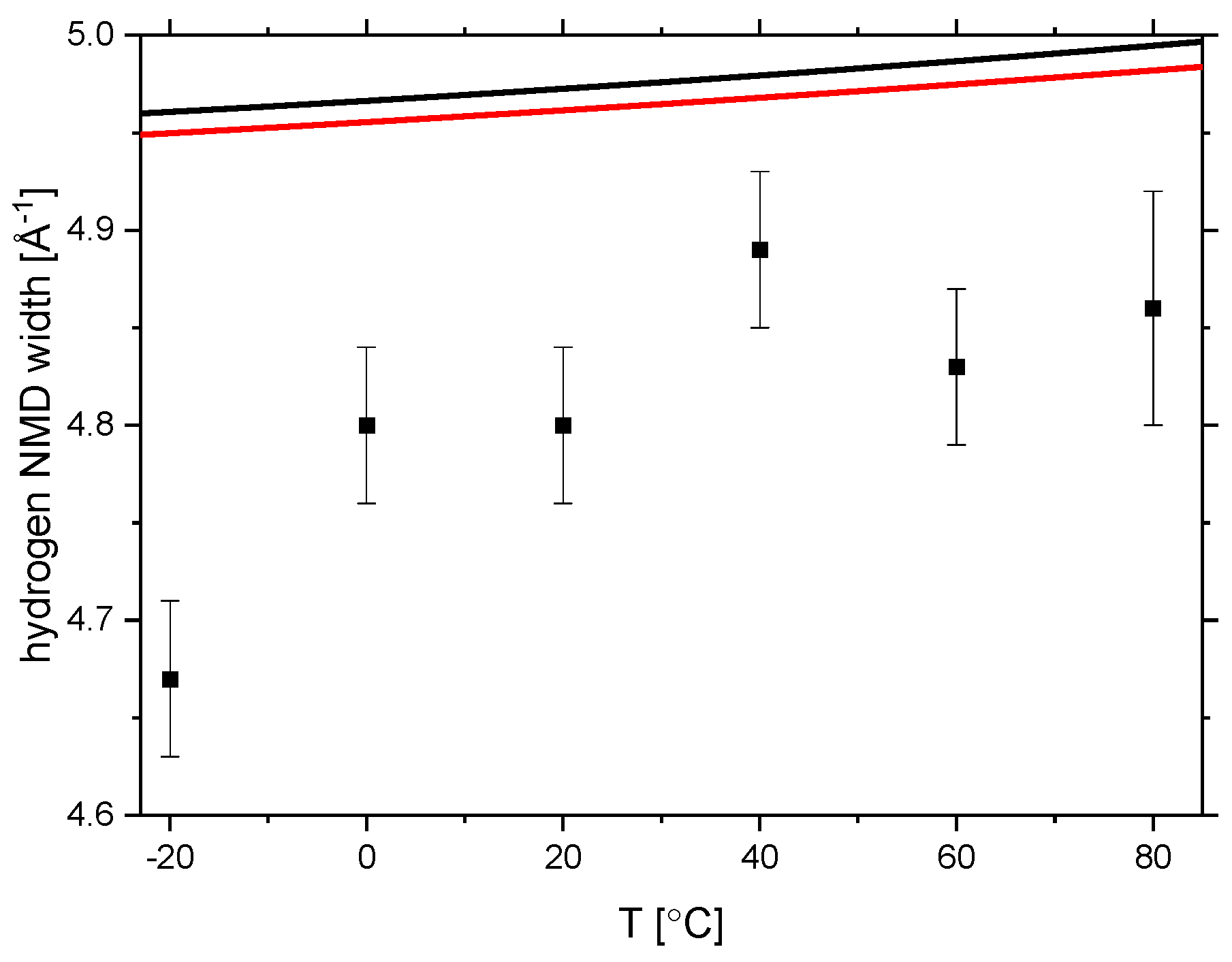
3.3. Glass Transition by Neutron Experiments
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carlstedt, J.; Wojtasz, J.; Fyhr, P.; Kocherbitov, V. Hydration and the phase diagram of acid hydrolyzed potato starch. Carbohydr. Polym. 2014, 112, 569–577. [Google Scholar] [CrossRef]
- Herawat, H.; Kusnandar, F.; Adawiyah, D.R.; Budijanto, S.; Rahman, M.S. Thermal characteristics and state diagram of extruded instant artificial rice. Thermochim. Acta 2014, 593, 50–57. [Google Scholar] [CrossRef]
- Homer, S.; Kelly, M.; Day, L. Determination of the thermo-mechanical properties in starch and starch/gluten systems at low moisture content—A comparison of DSC and TMA. Carbohydr. Polym. 2014, 108, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Monnier, X.; Maigret, J.-E.; Lourdin, D.; Saiter, A. Glass transition of anhydrous starch by fast scanning calorimetry. Carbohydr. Polym. 2017, 173, 77–83. [Google Scholar] [CrossRef]
- Rahman, M.S.; Senadeera, W.; Al-Alawi, A.; Truong, T.; Bhandari, B.; Al-Saidi, G. Thermal Transition Properties of Spaghetti Measured by Differential Scanning Calorimetry (DSC) and Thermal Mechanical Compression Test (TMCT). Food Bioprocess Technol. 2011, 4, 1422–1431. [Google Scholar] [CrossRef]
- Roudaut, G.; Wallecan, J. New insights on the thermal analysis of low moisture composite foods. Carbohydr. Polym. 2015, 115, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Cangialosi, D. Dynamics and thermodynamics of polymer glasses. J. Phys. Condens. Mat. 2014, 26, 153101. [Google Scholar] [CrossRef] [PubMed]
- Ojovan, M.I.; Louzguine-Luzgin, D.V. Revealing Structural Changes at Glass Transition via Radial Distribution Functions. J. Phys. Chem. B 2020, 124, 3186–3194. [Google Scholar] [CrossRef]
- Stanzione, J.F.; Strawhecker, K.E.; Wool, R.P. Observing the twinkling fractal nature of the glass transition. J. Non-Cryst. Solids 2011, 357, 311–319. [Google Scholar] [CrossRef]
- Albert, S.; Bauer, T.; Michl, M.; Biroli, G.; Bouchaud, J.P.; Loidl, A.; Lunkenheimer, P.; Tourbot, R.; Wiertel-Gasquet, C.; Ladieu, F. Fifth-order susceptibility unveils growth of thermodynamic amorphous order in glass-formers. Science 2016, 352, 1308–1311. [Google Scholar] [CrossRef] [Green Version]
- Kalichevsky, M.; Jaroszkiewicz, E.; Ablett, S.; Blanshard, J.; Lillford, P. The Glass-Transition of Amylopectin Measured by DSC, DMTA and NMR. Carbohydr. Polym. 1992, 18, 77–88. [Google Scholar] [CrossRef]
- Ruan, R.; Long, Z.; Chen, P.; Huang, V.; Almaer, S.; Taub, I. Pulse NMR study of glass transition in maltodextrin. J. Food Sci. 1999, 64, 6–9. [Google Scholar] [CrossRef]
- Ruan, R.R.; Long, Z.Z.; Song, A.J.; Chen, P.L. Determination of the glass transition temperature of food polymers using low field NMR. Food Sci. Technol.-Lebensm.-Wiss. Technol. 1998, 31, 516–521. [Google Scholar] [CrossRef]
- Lin, X.; Ruan, R.; Chen, P.; Chung, M.; Ye, X.; Yang, T.; Doona, C.; Wagner, T. NMR state diagram concept. J. Food Sci. 2006, 71, R136–R145. [Google Scholar] [CrossRef]
- Kumagai, H.; MacNaughtan, W.; Farhat, I.A.; Mitchell, J.R. The influence of carrageenan on molecular mobility in low moisture amorphous sugars. Carbohydr. Polym. 2002, 48, 341–349. [Google Scholar] [CrossRef]
- Partanen, R.; Marie, V.; MacNaughtan, W.; Forssell, P.; Farhat, I. H-1 NMR study of amylose films plasticised by glycerol and water. Carbohydr. Polym. 2004, 56, 147–155. [Google Scholar] [CrossRef]
- Roudaut, G.; Farhat, I.; Poirier-Brulez, F.; Champion, D. Influence of water, temperature and sucrose on dynamics in glassy starch-based products studied by low field H-1 NMR. Carbohydr. Polym. 2009, 77, 489–495. [Google Scholar] [CrossRef]
- Ying, R.; Saulnier, L.; Rondeau-Mouro, C. Films of arabinoxylans and beta-glucans extracted from cereal grains: Molecular motions by TD-NMR. Carbohydr. Polym. 2011, 86, 812–822. [Google Scholar] [CrossRef]
- Mayers, J.; Reiter, G. The VESUVIO electron volt neutron spectrometer. Meas. Sci. Technol. 2012, 23, 045902. [Google Scholar] [CrossRef]
- Senesi, R.; Andreani, C.; Bowden, Z.; Colognesi, D.; Degiorgi, E.; Fielding, A.L.; Mayers, J.; Nardone, M.; Norris, J.; Praitano, M.; et al. VESUVIO: A novel instrument for performing spectroscopic studies in condensed matter with eV neutrons at the ISIS facility. Phys. B 2000, 276, 200–201. [Google Scholar] [CrossRef]
- Andreani, C.; Krzystyniak, M.; Romanelli, G.; Senesi, R.; Fernandez-Alonso, F. Electron-volt neutron spectroscopy: Beyond fundamental systems. Adv. Phys. 2017, 66, 1–73. [Google Scholar] [CrossRef]
- Andreani, C.; Senesi, R.; Krzystyniak, M.; Romanelli, G.; Fernandez-Alonso, F. Chapter 7—Atomic Quantum Dynamics in Materials Research. In Experimental Methods in the Physical Sciences; Fernandez-Alonso, F., Price, D.L., Eds.; Academic Press: Cambridge, MA, USA, 2017; Volume 49, pp. 403–457. [Google Scholar]
- Andreani, C.; Senesi, R.; Krzystyniak, M.; Romanelli, G.; Fernandez-Alonso, F.F. Experimental studies of nuclear quantum effects in condensed matter: The case of water. Riv. Nuovo Cimento 2018, 41, 291–340. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Romanelli, G.; Fabian, M.; Gutmann, M.; Festa, G.; Arcidiacono, L.; Gigg, M.; Druzbicki, K.; Andreani, C.; Senesi, R.; et al. VESUVIO plus: The Current Testbed for a Next-generation Epithermal Neutron Spectrometer. J. Phys. Conf. Ser. 2018, 1021, 012026. [Google Scholar] [CrossRef]
- Seel, A.G.; Krzystyniak, M.; Fernandez-Alonso, F. The VESUVIO Spectrometer Now and When? J. Phys. Conf. Ser. 2014, 571, 012006. [Google Scholar] [CrossRef] [Green Version]
- Dawidowski, J.; Palomino, L.A.R.; Romanelli, G.; Krzystyniak, M. Procedure for the determination of effective temperatures employing VESUVIO spectrometer. J. Phys. Conf. Ser. 2018, 1055, 012013. [Google Scholar] [CrossRef]
- Di Giulio, A.; Zanetti, M.; Romanelli, G.; Krzystyniak, M.; Senesi, R.; Fernandez-Alonso, F. A McStas simulation of the incident neutron beam on the VESUVIO spectrometer. J. Phys. Conf. Ser. 2018, 1055, 012014. [Google Scholar] [CrossRef]
- Jackson, S.; Krzystyniak, M.; Seel, A.G.; Giggi, M.; Richards, S.E.; Fernandez-Alonso, F. VESUVIO Data Analysis Goes MANTID. J. Phys. Conf. Ser. 2014, 571, 012009. [Google Scholar] [CrossRef]
- Robledo, J.I.; Dawidowski, J.; Damian, J.I.M.; Skoro, G.; Bovo, C.; Romanelli, G. Measurement of neutron total cross sections at the VESUVIO spectrometer. Nucl. Instrum. Methods A 2020, 971, 164096. [Google Scholar] [CrossRef]
- Romanelli, G.; Krzystyniak, M.; Senesi, R.; Raspino, D.; Boxall, J.; Pooley, D.; Moorby, S.; Schooneveld, E.; Rhodes, N.; Andreani, C. Characterisation of the incident beam and current diffraction capabilities on the VESUVIO spectrometer. Meas Sci. Technol. 2017, 28, 095501. [Google Scholar] [CrossRef]
- Martellucci, M.; Romanelli, G.; Valeri, S.; Cottone, D.; Andreani, C.; Senesi, R. The neutron cross section of barite-enriched concrete for radioprotection shielding in the range 1 meV-1 keV. Eur. Phys. J. Plus 2021, 136, 259. [Google Scholar] [CrossRef]
- Capelli, S.C.; Romanelli, G. An effective hydrogen scattering cross section for time-of-flight neutron experiments with simple organic molecules. J. Appl. Crystallogr. 2019, 52, 1233–1237. [Google Scholar] [CrossRef]
- Colognesi, D.; Demmel, F.; Filabozzi, A.; Pietropaolo, A.; Pozio, A.; Romanelli, G.; Santucci, A.; Tosti, S. Proton Dynamics in Palladium-Silver: An Inelastic Neutron Scattering Investigation. Molecules 2020, 25, 5587. [Google Scholar] [CrossRef]
- Damian, J.I.M.; Dawidowski, J.; Granada, R.J.; Cantargi, F.; Romanelli, G.; Helman, C.; Krzystyniak, M.; Skoro, G.; Roubtsov, D. Experimental validation of the temperature behavior of the ENDF/B-VIII.0 thermal scattering kernel for light water. EPJ Web. Conf. 2020, 239, 14001. [Google Scholar] [CrossRef]
- Palomino, L.A.R.; Dawidowski, J.; Damian, J.I.M.; Cuello, G.J.; Romanelli, G.; Krzystyniak, M. Neutron total cross-section of hydrogenous and deuterated 1-and 2-propanol and n-butanol measured using the VESUVIO spectrometer. Nucl. Instrum. Methods A 2017, 870, 84–89. [Google Scholar] [CrossRef] [Green Version]
- Palomino, L.A.R.; Dawidowski, J.; Helman, C.; Damian, J.I.M.; Romanelli, G.; Krzystyniak, M.; Rudic, S.; Cuello, G.J. Determination of the scattering cross section of calcium using the VESUVIO spectrometer. Nucl. Instrum. Methods A 2019, 927, 443–450. [Google Scholar] [CrossRef]
- Romanelli, G.; Onorati, D.; Ulpiani, P.; Cancelli, S.; Perelli-Cippo, E.; Damian, J.I.M.; Capelli, S.C.; Croci, G.; Muraro, A.; Tardocchi, M.; et al. Thermal neutron cross sections of amino acids from average contributions of functional groups. J. Phys. Condens Mat. 2021, 33, 285901. [Google Scholar] [CrossRef]
- Romanelli, G.; Rudic, S.; Krzystyniak, M.; Fernandez-Alonso, F.; Fornalski, D.; Kibble, M.; Goodway, C.; Bones, J.; Probert, M.; Skoro, G. Robust measurement of para-ortho H-2 ratios to characterise the ISIS hydrogen moderators. J. Phys. Conf. Ser. 2018, 1021, 259. [Google Scholar] [CrossRef]
- Romanelli, G.; Rudic, S.; Zanetti, M.; Andreani, C.; Fernandez-Alonso, F.; Gorini, G.; Krzystyniak, M.; Skoro, G. Measurement of the para-hydrogen concentration in the ISIS moderators using neutron transmission and thermal conductivity. Nucl. Instrum. Methods A 2018, 888, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Krzystyniak, M.; Druzbicki, K.; Romanelli, G.; Gutmann, M.J.; Rudic, S.; Imberti, S.; Fernandez-Alonso, F. Nuclear dynamics and phase polymorphism in solid formic acid. Phys. Chem. Chem. Phys. 2017, 19, 9064–9074. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Syrykh, G.; Stolyarov, A.; Sadykov, R.A.; Armstrong, J.; da Silva, I.; Romanelli, G.; Fernandez-Alonso, F. Mass-selective neutron spectroscopy of glassy versus polycrystalline structures in binary mixtures of beryllium and zirconium. J. Phys. Conf. Ser. 2018, 1055, 012004. [Google Scholar] [CrossRef] [Green Version]
- Onorati, D.; Andreani, C.; Arcidiacono, L.; Fernandez-Alonso, F.; Festa, G.; Krzystyniak, M.; Romanelli, G.; Ulpiani, P.; Senesi, R. Gamma background characterization on VESUVIO: Before and after the moderator upgrade. J. Phys. Conf. Ser. 2018, 1055, 012009. [Google Scholar] [CrossRef]
- Onorati, D.; Romanelli, G.; Ulpiani, P.; Cazzaniga, C.; Preziosi, E.; Arcidiacono, L.; Festa, G.; Andreani, C.; Senesi, R.; Morone, M.C. FLUKA simulations and benchmark measurements of the YAP(Ce) scintillators installed on the VESUVIO spectrometer. Nucl. Instrum. Methods A 2020, 969, 164012. [Google Scholar] [CrossRef]
- Ulpiani, P.; Romanelli, G.; Arcidiacono, L.; Onorati, D.; Festa, G.; Krzystyniak, M.; Schooneveld, E.; Fernandez-Alonso, F.; Andreani, C.; Senesi, R. Enhancement of counting statistics and noise reduction in the forward-scattering detectors on the VESUVIO spectrometer. J. Phys. Conf. Ser. 2018, 1055, 012008. [Google Scholar] [CrossRef] [Green Version]
- Ulpiani, P.; Romanelli, G.; Onorati, D.; Parmentier, A.; Festa, G.; Schooneveld, E.; Cazzaniga, C.; Arcidiacono, L.; Andreani, C.; Senesi, R. Optimization of detection strategies for epithermal neutron spectroscopy using photon-sensitive detectors. Rev. Sci. Instrum. 2019, 90, 073901. [Google Scholar] [CrossRef]
- Dawidowski, J.; Bermejo, F.J.; Barquin, L.F.; Gorria, P.; Barandiaran, J.M.; Evans, A.C.; Mayers, J. Short-time dynamics on a metallic glass as probed by deep inelastic neutron scattering. Phys. Lett. A 1996, 214, 59–64. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Druzbicki, K.; Rudic, S.; Fabian, M. Positional, isotopic mass and force constant disorder in molybdate glasses and their parent metal oxides as observed by neutron diffraction and Compton scattering. J. Phys. Commun. 2020, 4, 095027. [Google Scholar] [CrossRef]
- Blostein, J.J.; Dawidowski, J.; Granada, J.R. Analysis of mean kinetic energies in H2O/D2O mixtures by neutron total cross-section measurements. Phys. B 2006, 385, 69–71. [Google Scholar] [CrossRef]
- Dawidowski, J.; Palomino, L.A.R.; Daman, J.I.M.; Blostein, J.J.; Cuello, G.J. Effective temperatures and scattering cross sections in water mixtures determined by Deep Inelastic Neutron Scattering. Ann. Nucl. Energy 2016, 90, 247–255. [Google Scholar] [CrossRef]
- Granada, J.R.; Dawidowski, J.; Mayer, R.E.; Gillette, V.H. Thermal-Neutron Cross-Section and Transport-Properties of Polyethylene. Nucl. Instrum. Methods A 1987, 261, 573–578. [Google Scholar] [CrossRef]
- Palomino, L.A.R.; Dawidowski, J.; Blosteinl, J.J.; Cuello, G.J. New prospects of VESUVIO applied to measurements in water mixtures. J. Phys. Conf. Ser. 2014, 571, 012008. [Google Scholar] [CrossRef] [Green Version]
- Vinales, A.D.; Dawidowski, J.; Damian, J.I.M. Neutron total cross-section model for liquids and its application to light water. Ann. Nucl. Energy 2011, 38, 1687–1692. [Google Scholar] [CrossRef]
- AOAC. AOAC method 2001.11.Crude Protein in animal feed, forage (plant tissue), grain and oil seeds. In Official Methods of Analysis of AOAC International, 18th ed.; AOAC International: Gaithersburg, MD, USA; Arlington, VA, USA, 2005. [Google Scholar]
- AOAC. AOAC Official Method 925.32, Fat in Eggs. Acid hydrolysis method. In Official Methods of Anaysis of AOAC International, 19th ed.; AOAC International: Gaithersburg, MD, USA; Arlington, VA, USA, 2012. [Google Scholar]
- Liu, Y.T.; Bhandari, B.; Zhou, W.B. Glass transition and enthalpy relaxation of amorphous food saccharides: A review. J. Agric. Food Chem. 2006, 54, 5701–5717. [Google Scholar] [CrossRef]
- Monserrat, D.; Vispa, A.; Pardo, L.C.; Tolchenov, R.; Mukhopadhyay, S.; Fernandez-Alonso, F. FABADA Goes MANTID to Answer an Old Question: How Many Lines Are There? J. Phys. Conf. Ser. 2015, 663, 012009. [Google Scholar] [CrossRef]
- Pardo, L.C.; Rovira-Esteva, M.; Busch, S.; Ruiz-Martin, M.D.; Tamarit, J.L. FABADA: A Fitting Algorithm for Bayesian Analysis of DAta. J. Phys. Conf. Ser. 2011, 325, 012006. [Google Scholar] [CrossRef] [Green Version]
- Vispa, A.; Rovira-Esteva, M.; Ruiz-Martin, M.D.; Busch, S.; Unruh, T.; Pardo, L.C.; Tamarit, J.L. Microscopic dynamics of glycerol: A QENS study. J. Phys. Conf. Ser. 2014, 549, 012013. [Google Scholar] [CrossRef]
- Romanelli, G.; Hewer, B.; Krzystyniak, M.; Gigg, M.; Tolchenov, R.; Mukhopadhyay, S.; Fernandez-Alonso, F. Data analysis of neutron Compton scattering experiments using MANTID. J. Phys. Conf. Ser. 2018, 1055, 012016. [Google Scholar] [CrossRef]
- Andreani, C.; Colognesi, D.; Mayers, J.; Reiter, G.; Senesi, R. Measurement of momentum distribution of lightatoms and molecules in condensed matter systems using inelastic neutron scattering. Adv. Phys. 2005, 54, 377–469. [Google Scholar] [CrossRef]
- Fernandez-Alonso, F.; Price, D.L. Neutron Scattering: Applications in Biology, Chemistry, and Materials Science; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Rahman, M.S.; Kasapis, S.; Guizani, N.; Al-Amri, O.S. State diagram of tuna meat: Freezing curve and glass transition. J. Food Eng. 2003, 57, 321–326. [Google Scholar] [CrossRef]
- AleidaJ, S.; Martin, N.; AlejandroJ, M.; Guy, D.V.; Denis, L. Glass transition temperatures of a ready to eat breakfast cereal formulation and its main components determined by DSC and DMTA. Carbohydr. Polym. 2009, 76, 528–534. [Google Scholar] [CrossRef]
- Chung, H.J.; Lee, E.J.; Lim, S.T. Comparison in glass transition and enthalpy relaxation between native and gelatinized rice starches. Carbohydr. Polym. 2002, 48, 287–298. [Google Scholar] [CrossRef]
- Chen, C.-M.; Yeh, A.-I. Effect of Amylose Content on Expansion of Extruded Rice Pellet. Cereal Chem. 2001, 78, 261–266. [Google Scholar] [CrossRef]
- Perdon, A.; Siebenmorgen, T.J.; Mauromoustakos, A. Glassy State Transition and Rice Drying: Development of a Brown Rice State Diagram. Cereal Chem. 2000, 77, 708–713. [Google Scholar] [CrossRef] [Green Version]
- Cao, W.; Nishiyama, Y.; Koide, S. Physicochemical, mechanical and thermal properties of brown rice grain with various moisture contents. Int. J. Food Sci. Technol. 2004, 39, 899–906. [Google Scholar] [CrossRef]
- van den Dries, I.J.; van Dusschoten, D.; Hemminga, M.A. Mobility in maltose-water glasses studied with H-1 NMR. J. Phys. Chem. B 1998, 102, 10483–10489. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: Oxford, UK; New York, NY, USA, 1983; p. 618. [Google Scholar]
- Hills, B.; Pardoe, K. Proton and Deuterium Nmr-Studies of the Glass-Transition in a 10-Percent Water-Maltose Solution. J. Mol. Liq. 1995, 63, 229–237. [Google Scholar] [CrossRef]
- Derbyshire, W.; van den Bosch, M.; van Dusschoten, D.; MacNaughtan, W.; Farhat, I.A.; Hemminga, M.A.; Mitchell, J.R. Fitting of the beat pattern observed in NMR free-induction decay signals of concentrated carbohydrate-water solutions. J. Magn. Reson. 2004, 168, 278–283. [Google Scholar] [CrossRef] [PubMed]
- Peleg, M. A dissenting view on glass transition summary. Food Technol. 1997, 51, 30–31. [Google Scholar]
- Abdul-Redah, T.; Krzystyniak, M.; Chatzidimitriou-Dreismann, C.A. Neutron Compton scattering from water studied with the double-difference technique. Phys. Rev. B 2005, 72, 052202. [Google Scholar] [CrossRef]
- Andreani, C.; Ceriotti, M.; Fernandez-Alonso, F.; Gorini, G.; Krzystyniak, M.; Parmentier, A.; Parker, S.; Seel, A.; Senesi, R.; Walewski, L. Discussion: Measurement and Instrumentation. J. Phys. Conf. Ser. 2014, 571, 012010. [Google Scholar] [CrossRef] [Green Version]
- Frost, K.; Kaminski, D.; Kirwan, G.; Lascaris, E.; Shanks, R. Crystallinity and structure of starch using wide angle X-ray scattering. Carbohydr. Polym. 2009, 78, 543–548. [Google Scholar] [CrossRef]
- Nara, S.; Mori, A.; Komiya, T. Study on Relative Crystallinity of Moist Potato Starch. Starch Stärke 1978, 30, 111–114. [Google Scholar] [CrossRef]
- Liu, H.; Chaudhary, D.; Tade, M.O. Atomistic dynamic modelling of amylose fragments with different hydration and glycerol concentration: Equilibrium behaviour and Tg estimation. In Proceedings of the Chemeca 2011: Engineering a Better World, Sydney Hilton Hotel, Sydney, Australia, 18–21 September 2011. [Google Scholar]
- Abiad, M.G.; Carvajal, M.T.; Campanella, O.H. A Review on Methods and Theories to Describe the Glass Transition Phenomenon: Applications in Food and Pharmaceutical Products. Food Eng. Rev. 2009, 1, 105–132. [Google Scholar] [CrossRef]
- Bernazzani, P.; Peyyavula, V.K.; Agarwal, S.; Tatikonda, R.K. Evaluation of the phase composition of amylose by FTIR and isothermal immersion heats. Polymer 2008, 49, 4150–4158. [Google Scholar] [CrossRef]
- Capron, I.; Robert, P.; Colonna, P.; Brogly, M.; Planchot, V. Starch in rubbery and glassy states by FTIR spectroscopy. Carbohydr. Polym. 2007, 68, 249–259. [Google Scholar] [CrossRef]
- Jha, P.; Dharmalingam, K.; Nishizu, T.; Katsuno, N.; Anandalakshmi, R. Effect of Amylose-Amylopectin Ratios on Physical, Mechanical, and Thermal Properties of Starch-Based Bionanocomposite Films Incorporated with CMC and Nanoclay. Starch-Starke 2020, 72, 1900121. [Google Scholar] [CrossRef]
- Mejia, C.D.; Mauer, L.J.; Hamaker, B.R. Similarities and differences in secondary structure of viscoelastic polymers of maize alpha-zein and wheat gluten proteins. J. Cereal Sci. 2007, 45, 353–359. [Google Scholar] [CrossRef]
- Mousia, Z.; Farhat, I.A.; Pearson, M.; Chesters, M.A.; Mitchell, J.R. FTIR microspectroscopy study of composition fluctuations in extruded amylopectin-gelatin blends. Biopolymers 2001, 62, 208–218. [Google Scholar] [CrossRef] [PubMed]
- Rindlav, A.; Hulleman, S.H.D.; Gatenholm, P. Formation of starch films with varying crystallinity. Carbohydr. Polym. 1997, 34, 25–30. [Google Scholar] [CrossRef]
- Terao, W.; Mori, T.; Fujii, Y.; Koreeda, A.; Kabeya, M.; Kojima, S. Boson peak dynamics of natural polymer starch investigated by terahertz time-domain spectroscopy and low-frequency Raman scattering. Spectrochim. Acta A 2018, 192, 446–450. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witek, M.; Krzystyniak, M.; Romanelli, G.; Witczak, T. Glass Transition in Rice Pasta as Observed by Combined Neutron Scattering and Time-Domain NMR. Polymers 2021, 13, 2426. https://doi.org/10.3390/polym13152426
Witek M, Krzystyniak M, Romanelli G, Witczak T. Glass Transition in Rice Pasta as Observed by Combined Neutron Scattering and Time-Domain NMR. Polymers. 2021; 13(15):2426. https://doi.org/10.3390/polym13152426
Chicago/Turabian StyleWitek, Magdalena, Maciej Krzystyniak, Giovanni Romanelli, and Teresa Witczak. 2021. "Glass Transition in Rice Pasta as Observed by Combined Neutron Scattering and Time-Domain NMR" Polymers 13, no. 15: 2426. https://doi.org/10.3390/polym13152426
APA StyleWitek, M., Krzystyniak, M., Romanelli, G., & Witczak, T. (2021). Glass Transition in Rice Pasta as Observed by Combined Neutron Scattering and Time-Domain NMR. Polymers, 13(15), 2426. https://doi.org/10.3390/polym13152426






