3D Modelling of Mass Transfer into Bio-Composite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Parameters for Water Vapor Transfer
- Effective moisture diffusivity value of each phase matrix and particle.
- The boundary concentrations of water vapor in the PHBV matrix in contact with dry air and with humid air (relative humidity of 95%). These concentrations were determined using the experimental water vapor sorption isotherm of PHBV film at 20 °C.
- Water vapor partition coefficient , calculated as the slope of the linear relation between the water concentration in PHBV matrix and WSF particles, obtained from experimental water vapor sorption isotherm at 20 °C for matrix and particles.
| Sample | Diffusivity a | Permeability
| Upper Boundary Concentration a | Lower Boundary Concentration a | Partition Coefficient a |
|---|---|---|---|---|---|
| PHBV matrix | b | ||||
| WSF particle | c | - | - |
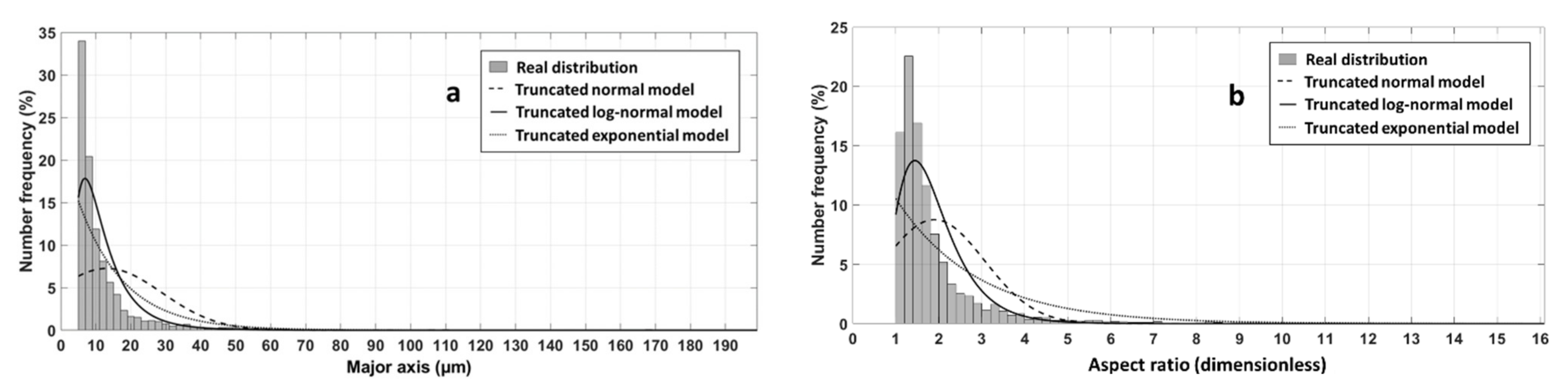
2.2. 2D Image Analysis
2.3. 3D Structure Generation
2.4. Mathematical Modelling and Geometry
2.4.1. 3D Structure Generation
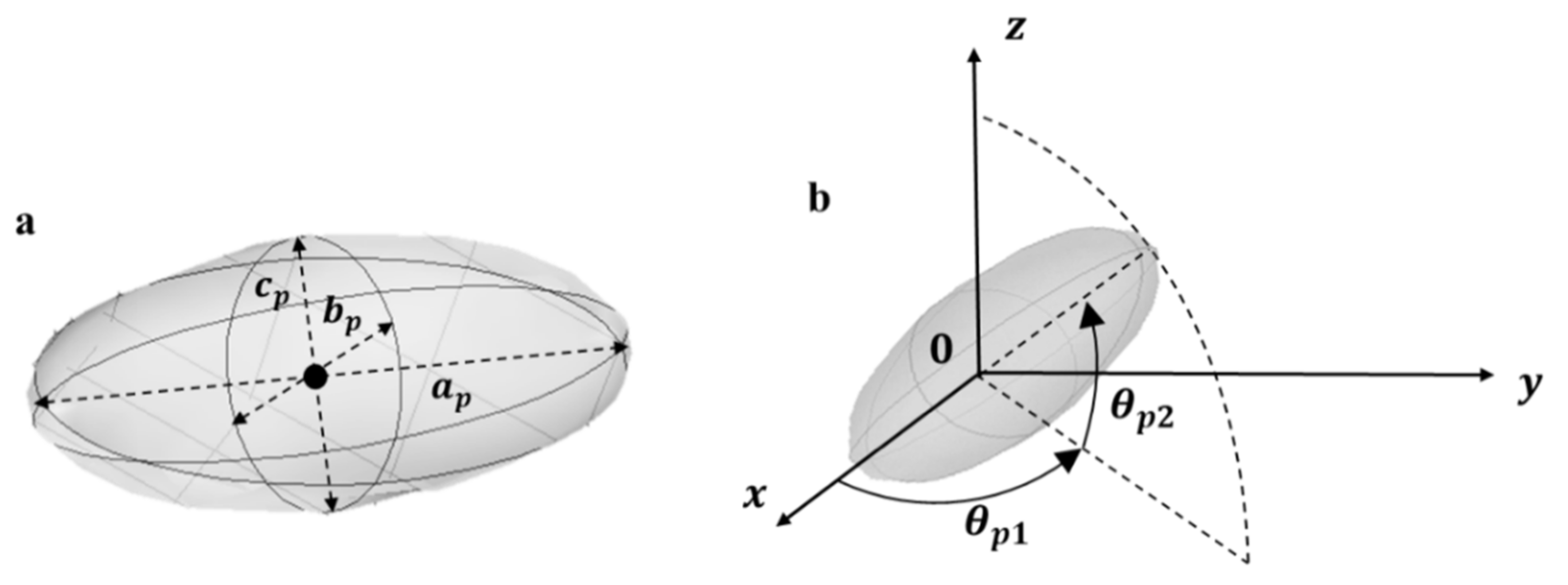
- Step 1. The position (center coordinates ) and orientation (azimuth and elevation angle) are randomly drawn using uniform distributions.
- Step 2. The non-overlapping of the particle with the horizontal faces of the RVE ( and ) and with the existing particles is tested.
2.4.2. Governing Equations
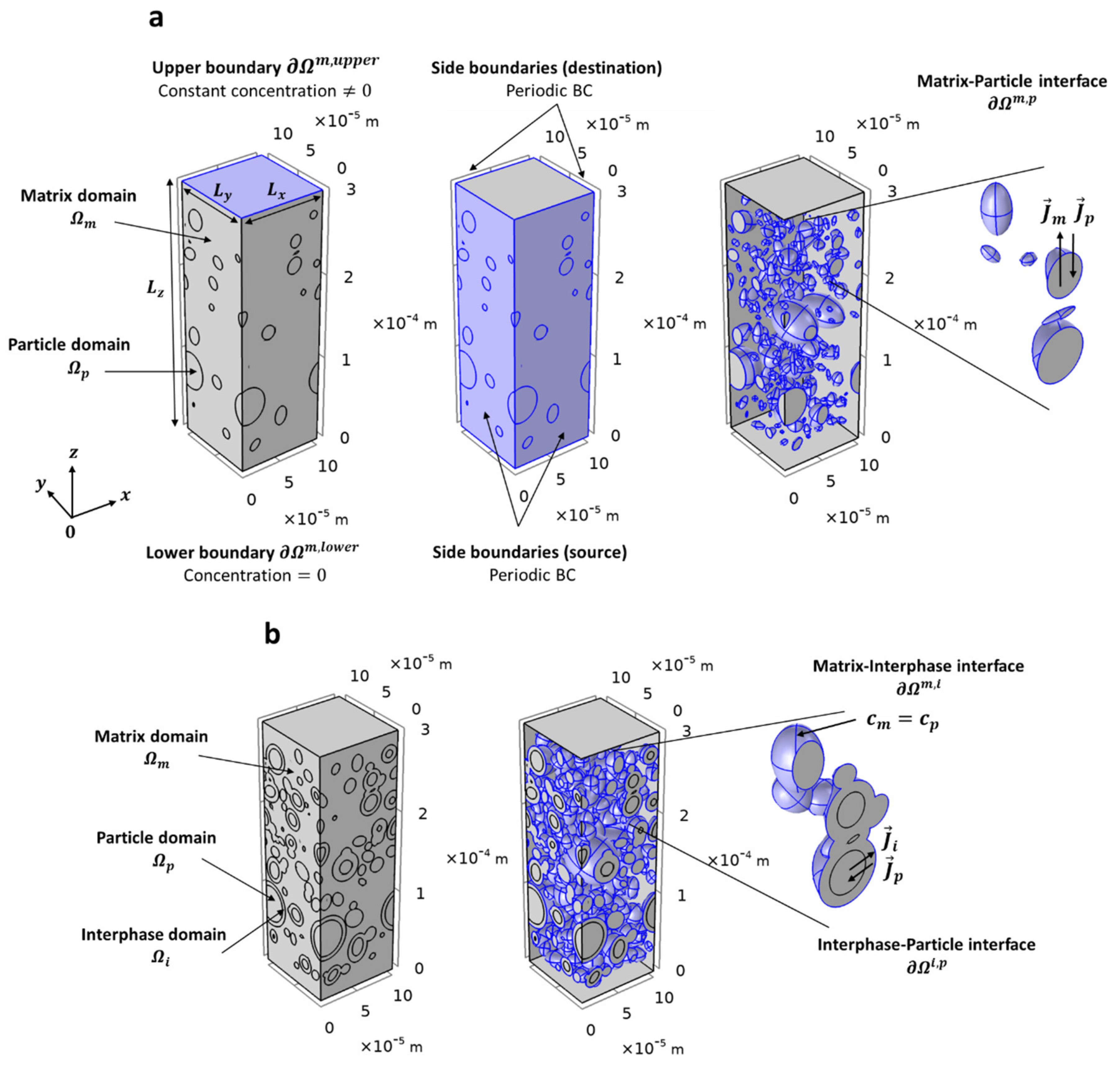
2.4.3. Boundary Conditions
2.4.4. Effective Permeability Evaluation
2.5. Numerical Simulations
3. Results and Discussion
3.1. From Particle Morphology to 3D Structure Generation
3.2. Simulations of Two-Phase Model
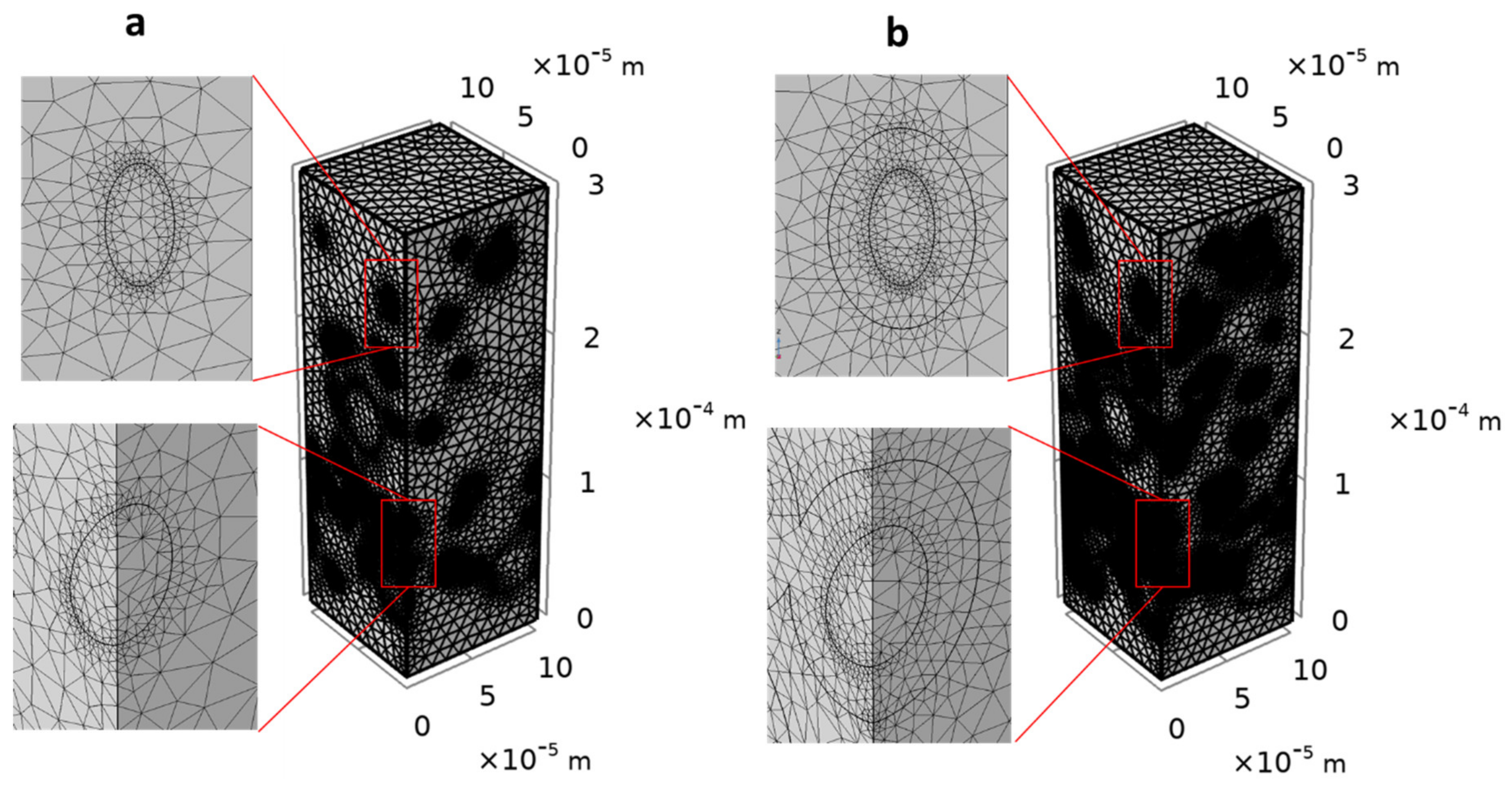
3.2.1. Selection of Mesh and RVE Sizes
3.2.2. Selection of the Number of Structures to Analyze
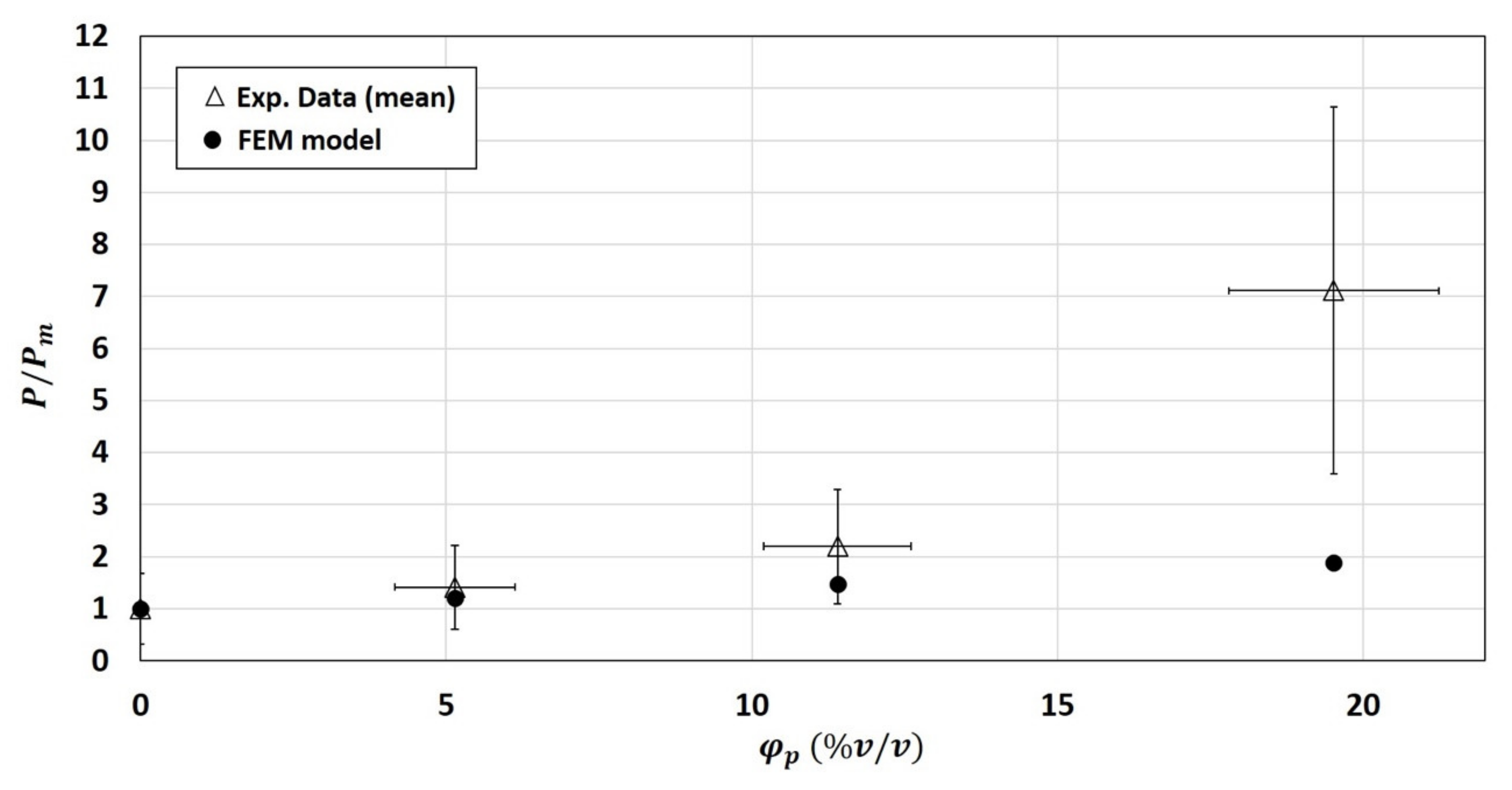
3.2.3. Numerical Results of the 2-Phase Model
- the physical properties of the fiber particle and especially its diffusivity value would be modified once embedded into the polymer matrix compare to the one measure on the native component,
- the diffusivity of the polymer matrix, measured before fiber particles addition, would be modified after fiber particles addition and therefore not well representative of what occurs in the composite material,
- the presence of an interphase, third compartment with its own physical properties, at the interface matrix/particle would influence the overall permeability into the composite.
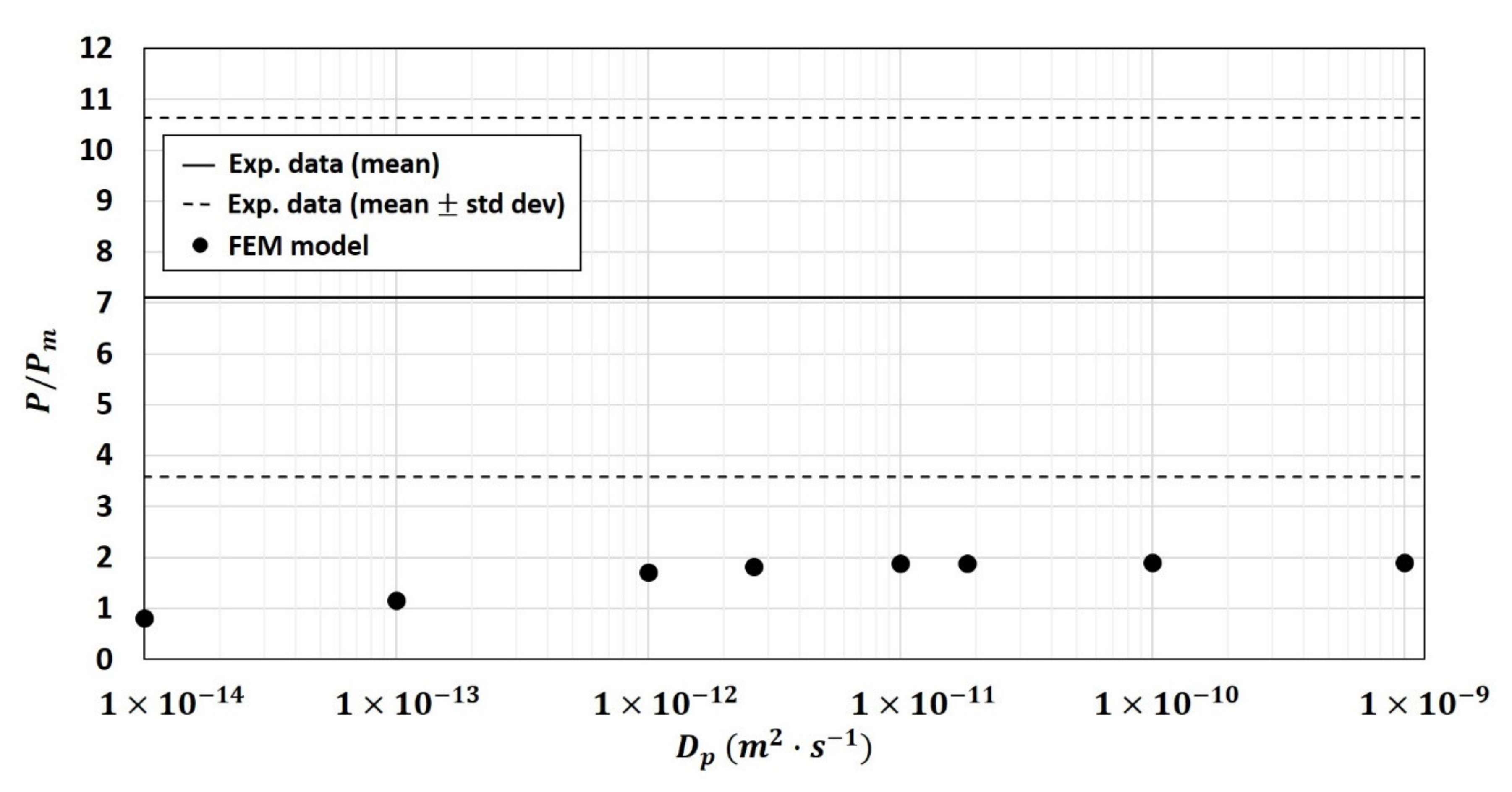
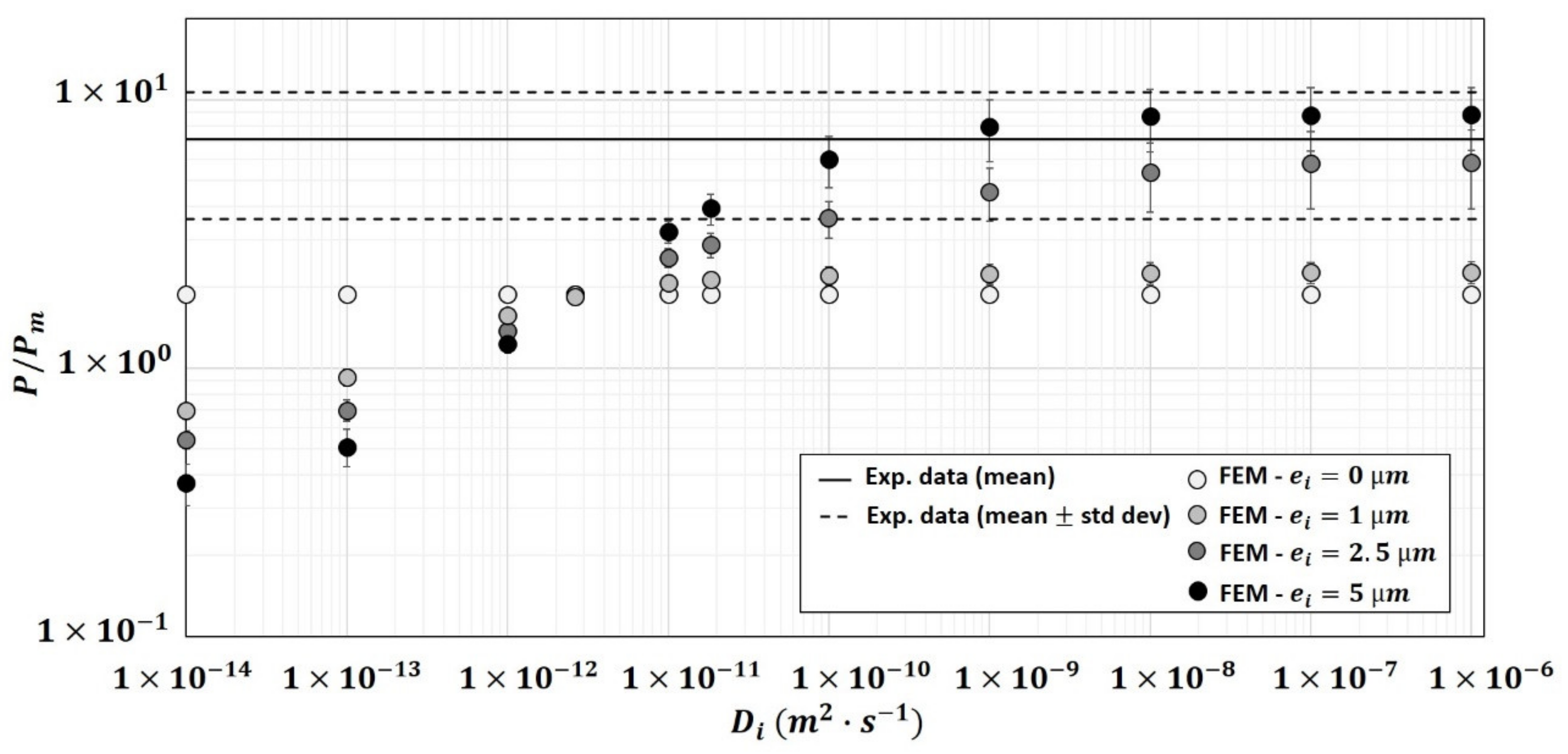
3.2.4. Modification of Particles Diffusivity Values in the Two-Phase Model
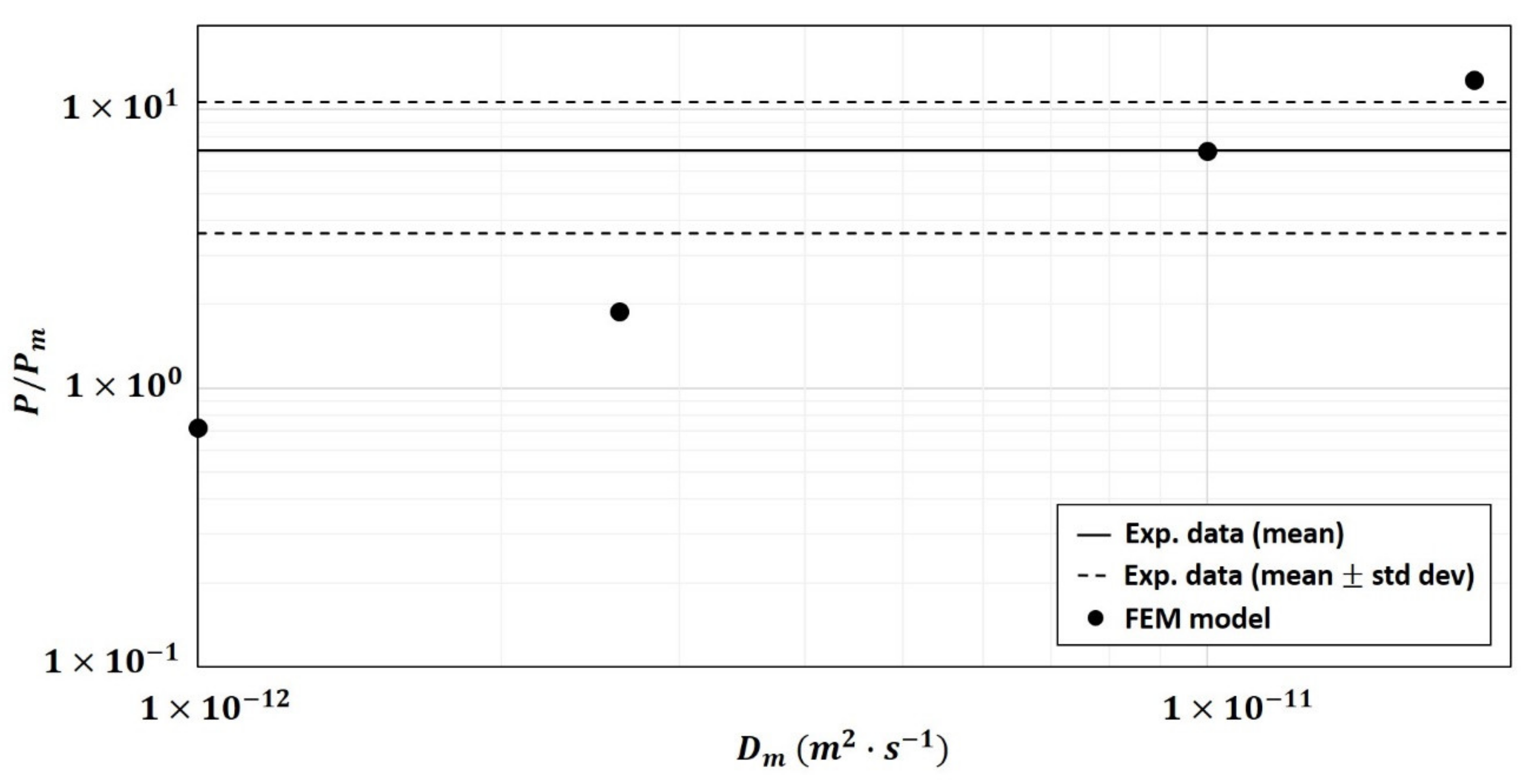
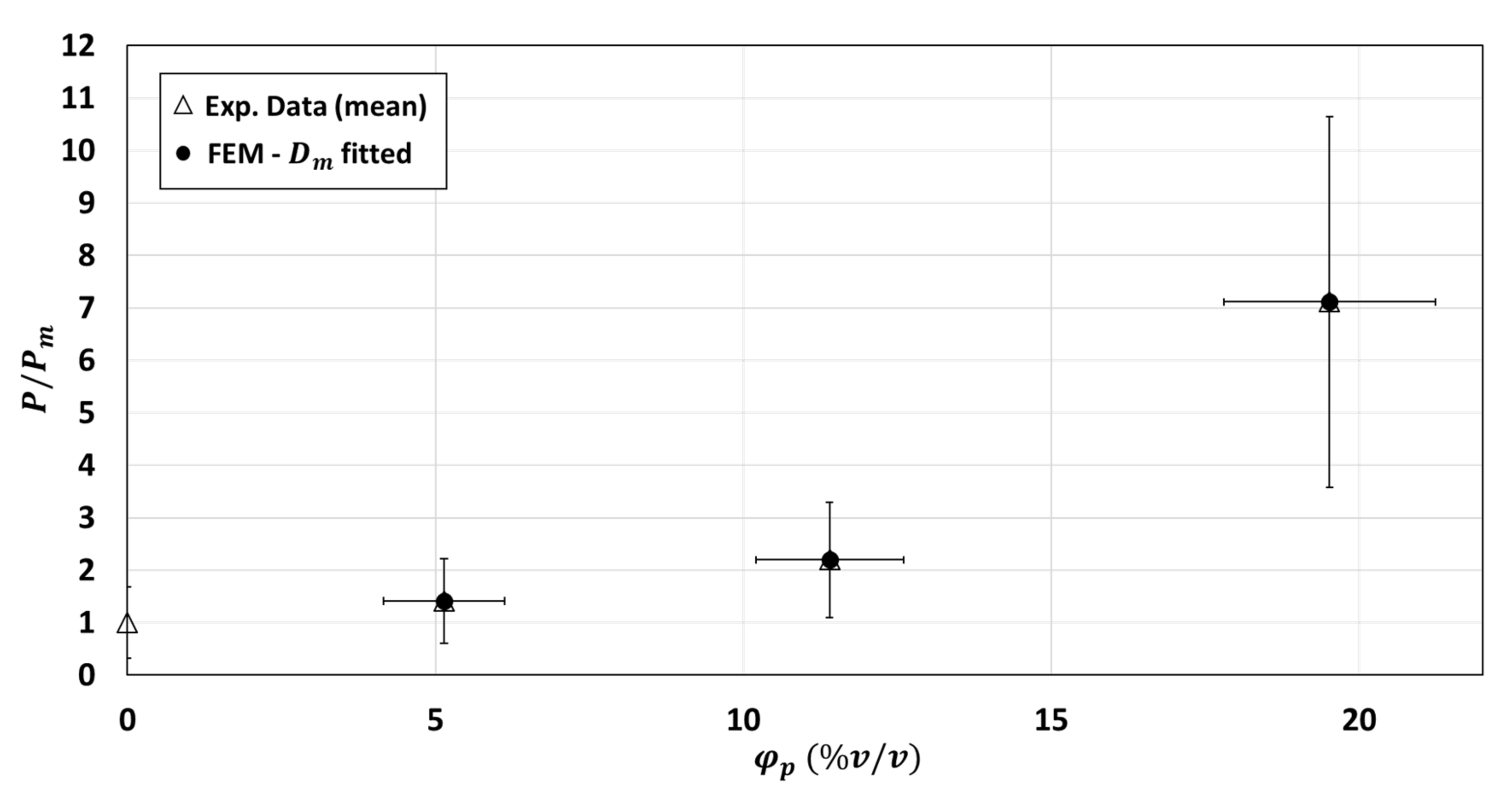
3.2.5. Modification of Matrix Diffusivity Values in the Two-Phase Model
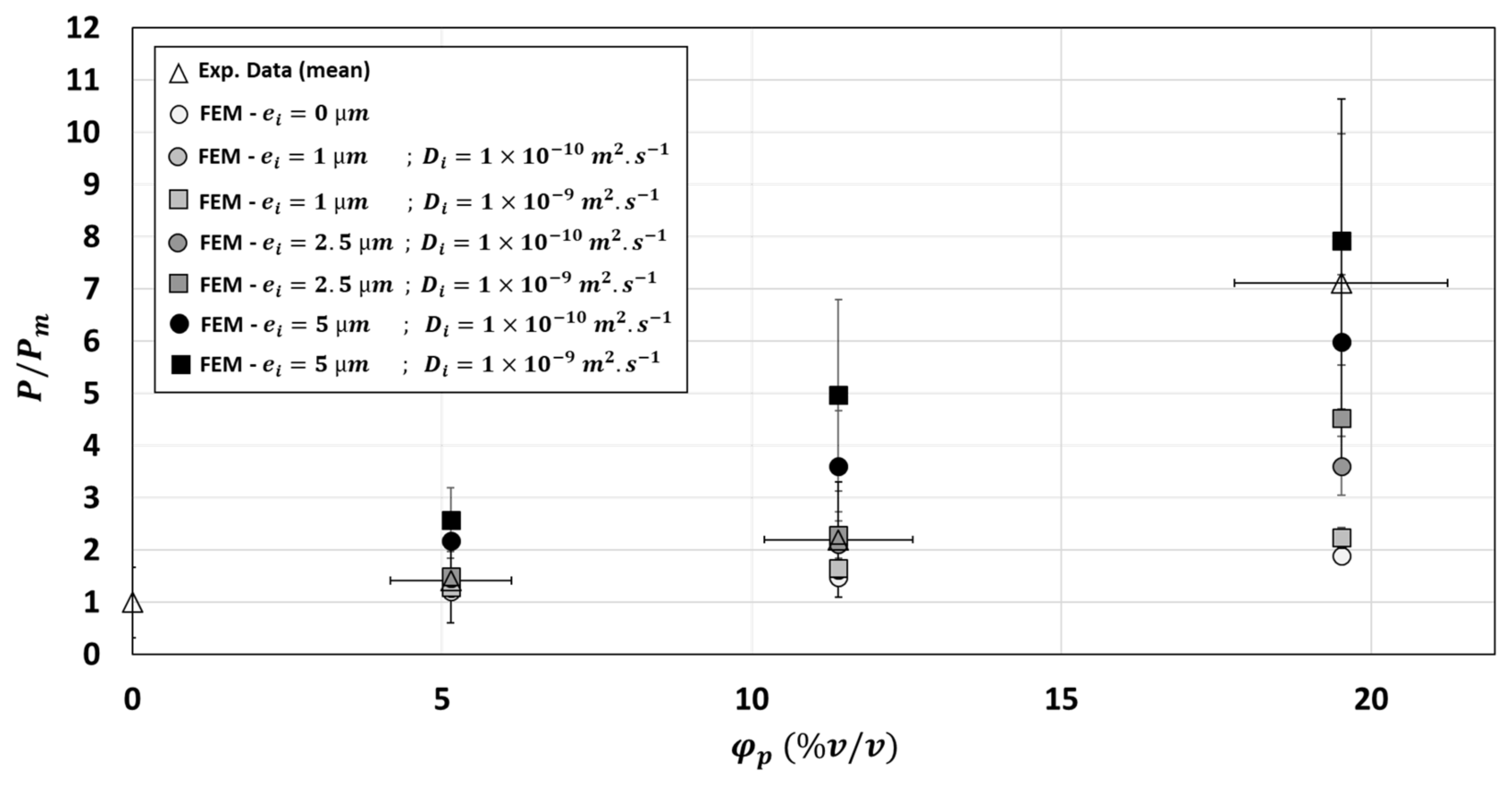
3.3. Simulations of Three-Phase Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| RVE | Representative Volume Element |
| FEM | Finite Element Method |
| PHBV | Poly(3-HydroxyButyrate-co-3-HydroxyValerate) |
| WSF | Wheat Straw Fibers |
| 2D, 3D | Two and Three Dimension |
| E | Mean |
| SD | Standard Deviation |
| Probability Density Function | |
| CDF | Cumulative Distribution Function |
| cte | Constant value |
| Latin symbols | |
| RVE length along x-axis, y-axis and z-axis | |
| Major, minor and third axis of the particle | |
| Center coordinates of the particle | |
| Diffusivity of water vapor in the phase k | |
| Permeability of water vapor in the phase k | |
| Permeability of water vapor in the composite | |
| Concentration of water vapor in the phase k | |
| Molar surface flux vector of water vapor in the phase k | |
| Water vapor pressure differential across the film | |
| K | Partition coefficient: concentration ratio between particles and matrix at equilibrium (-) |
| M | Velocity (non-physical property) |
| Interphase thickness | |
| Number of particles (-) | |
| Greek symbols | |
| Aspect ratio: ratio between major and minor axis of the particle ( (-) | |
| Volume fraction of the phase k: ratio between the volume of the phase k and the composite volume | |
| Molar flux (along z-axis) of water vapor across a composite face | |
| Azimuth angle: angle between the x-axis and the orthogonal projection of the semi-major axis onto the xy-plane (degree°) | |
| Elevation angle: angle between the semi-major axis and its orthogonal projection onto the xy-plane (degree°) | |
| Subscripts | |
| m | Matrix |
| p | Particle |
| i | Interphase |
Appendix A
References
- Angellier-Coussy, H.; Guillard, V.; Guillaume, C.; Gontard, N. Role of packaging in the smorgasbord of action for sustainable food consumption. Agro Food Ind. Hi Tech 2013, 24, 15–19. [Google Scholar]
- Guillard, V.; Gaucel, S.; Fornaciari, C.; Angellier-coussy, H.; Buche, P.; Gontard, N. The Next Generation of Sustainable Food Packaging to Preserve Our Environment in a Circular Economy Context. Front. Nutr. 2018, 5, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berthet, M.-A.; Angellier-Coussy, H.; Chea, V.; Guillard, V.; Gastaldi, E.; Gontard, N. Sustainable food packaging: Valorising wheat straw fibres for tuning PHBV-based composites properties. Compos. Part A Appl. Sci. Manuf. 2015, 72, 139–147. [Google Scholar] [CrossRef]
- Berthet, M.A.; Angellier-Coussy, H.; Guillard, V.; Gontard, N. Vegetal fiber-based biocomposites: Which stakes for food packaging applications? J. Appl. Polym. Sci. 2016, 133. [Google Scholar] [CrossRef]
- Cui, Y.; Kumar, S.; Rao Kona, B.; van Houcke, D. Gas barrier properties of polymer/clay nanocomposites. RSC Adv. 2015, 5, 63669–63690. [Google Scholar] [CrossRef]
- Zid, S.; Zinet, M.; Espuche, E. Modeling Diffusion Mass Transport in Multiphase Polymer Systems for Gas Barrier Applications: A Review. J. Polym. Sci. 2018, 56, 621–638. [Google Scholar] [CrossRef] [Green Version]
- Monsalve-Bravo, G.M. Modeling permeation through mixed-matrix membranes: A review. Processes 2018, 6, 172. [Google Scholar] [CrossRef] [Green Version]
- Fricke, H. The maxwell-wagner dispersion in a suspension of ellipsoids. J. Phys. Chem. 1951, 57, 934–937. [Google Scholar] [CrossRef]
- Barrer, R.M.; Petropoulos, J.H. Diffusion in heterogeneous media: Lattice and parallelepipeds in a continuous phase. J. Appl. Phys. 1961, 12, 691–697. [Google Scholar] [CrossRef]
- Petropoulos, J.H. A comparative study of approaches applied to the permeability of binary composite polymeric materials. J. Polym. Sci. Polym. Phys. Ed. 1985, 23, 1309–1324. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism 1873. Available online: https://www.nature.com/articles/007478a0 (accessed on 7 July 2021).
- Gonzo, E.E.; Parentis, M.L.; Gottifredi, J.C. Estimating models for predicting effective permeability of mixed matrix membranes. J. Memb. Sci. 2006, 277, 46–54. [Google Scholar] [CrossRef]
- Rafiq, S.; Maulud, A.; Man, Z.; Ibrahim, M.; Mutalib, A.; Ahmad, F.; Khan, A.U.; Khan, A.L.; Ghauri, M.; Muhammad, N. Modelling in Mixed Matrix Membranes for Gas Separation. Can. J. Chem. Eng. 2015, 93, 88–95. [Google Scholar] [CrossRef]
- Thoury-Monbrun, V.; Angellier-Coussy, H.; Guillard, V.; Legland, D.; Gaucel, S. Impact of Two-Dimensional Particle Size Distribution on Estimation of Water Vapor Diffusivity in Micrometric Size Cellulose Particles. Materials 2018, 11, 1712. [Google Scholar] [CrossRef] [Green Version]
- Rafiq, S.; Man, Z.; Maulud, A.; Muhammad, N.; Maitra, S. Separation of CO 2 from CH 4 using polysulfone/polyimide silica nanocomposite membranes. Sep. Purif. Technol. 2012, 90, 162–172. [Google Scholar] [CrossRef]
- Papadokostaki, K.G.; Minelli, M.; Doghieri, F.; Petropoulos, J.H. A fundamental study of the extent of meaningful application of Maxwell’s and Wiener’s equations to the permeability of binary composite materials. Part II: A useful explicit analytical approach. Chem. Eng. Sci. 2015, 131, 353–359. [Google Scholar] [CrossRef]
- Monsalve-bravo, G.M.; Smart, S.; Bhatia, S.K. Simulation of multicomponent gas transport through mixed-matrix membranes. J. Memb. Sci. 2019, 577, 219–234. [Google Scholar] [CrossRef] [Green Version]
- Sharifzadeh, M.; Zamani Pedram, M.; Ebadi Amooghin, A. A new permeation model in porous filler–based mixed matrix membranes for CO2 separation. Greenh. Gases Sci. Technol. 2019, 9, 719–742. [Google Scholar] [CrossRef]
- Jiang, N.; Li, Y.; Li, D.; Yu, T.; Li, Y.; Xu, J.; Li, N.; Marrow, T.J. 3D finite element modeling of water diffusion behavior of jute/PLA composite based on X-ray computed tomography. Compos. Sci. Technol. 2020, 199, 108313. [Google Scholar] [CrossRef]
- Qiao, R.; Catherine Brinson, L. Simulation of interphase percolation and gradients in polymer nanocomposites. Compos. Sci. Technol. 2009, 69, 491–499. [Google Scholar] [CrossRef]
- Petsi, A.J.; Burganos, V.N. Interphase layer effects on transport in mixed matrix membranes. J. Memb. Sci. 2012, 421–422, 247–257. [Google Scholar] [CrossRef]
- Zid, S.; Zinet, M.; Espuche, E. 3D numerical analysis of mass diffusion in (nano) composites: The effect of the filler-matrix interphase on barrier properties. Model. Simul. Mater. Sci. Eng. 2020, 28, 75003. [Google Scholar] [CrossRef]
- Petropoulos, J.H.; Papadokostaki, K.G.; Doghieri, F.; Minelli, M. A fundamental study of the extent of meaningful application of Maxwell’s and Wiener’s equations to the permeability of binary composite materials. Part III: Extension of the binary cubes model to 3-phase media. Chem. Eng. Sci. 2015, 131, 360–366. [Google Scholar] [CrossRef]
- Wolf, C.; Guillard, V.; Angellier-Coussy, H.; Silva, G.D.G.; Gontard, N. Water vapor sorption and diffusion in wheat straw particles and their impact on the mass transfer properties of biocomposites. J. Appl. Polym. Sci. 2016, 133, 1–12. [Google Scholar] [CrossRef]
- David, G.; Gontard, N.; Angellier-Coussy, H. Mitigating the Impact of Cellulose Particles on the Performance of Biopolyester-Based Composites by Gas-Phase Esterification. Polymers 2019, 11, 200. [Google Scholar] [CrossRef] [Green Version]
- Berthet, M.-A.; Angellier-Coussy, H.; Machado, D.; Hilliou, L.; Staebler, A.; Vicente, A.; Gontard, N. Exploring the potentialities of using lignocellulosic fibres derived from three food by-products as constituents of biocomposites for food packaging. Ind. Crops Prod. 2015, 69, 110–122. [Google Scholar] [CrossRef]
- Wolf, C. Multi-Scale Modelling of Structure and Mass Transfer Relationships in Nano- and Micro- Composites for Food Packaging. Ph.D. Thesis, University of Montpellier, Montpellier, France, 2014. Available online: https://tel.archives-ouvertes.fr/tel-02178975 (accessed on 7 July 2021).
- Berthet, M.-A. Biocomposites Durables pour l’Emballage Alimentaire, À Partir de Sous-Produits de l’Industrie Alimentaire: Relations Procédé-Structure-Propriétés. Ph.D. Thesis, University of Montpellier, Montpellier, France, 2014. [Google Scholar]
- Tschopp, M.A. 3-D Synthetic Microstructure Generation with Ellipsoid Particles; Technical Report; Defense Technical Information Center: Fort Belvoir, VA, USA, 2017. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Separation Through Dialysis. 2008. Available online: https://www.comsol.ch/forum/thread/attachment/16637/dialysis_comsol-2156.PDF (accessed on 7 July 2021).
- Zid, S.; Zinet, M.; Espuche, E. 3D Mass Diffusion in Ordered Nanocomposite Systems: Finite Element Simulation and Phenomenological Modeling. J. Polym. Sci. Part B Polym. Phys. 2019, 57, 51–61. [Google Scholar] [CrossRef] [Green Version]
- Liang, M.; Feng, K.; He, C.; Li, Y.; An, L.; Guo, W. A meso-scale model toward concrete water permeability regarding aggregate permeability. Constr. Build. Mater. 2020, 261, 120547. [Google Scholar] [CrossRef]
- Hedenqvist, M.; Gedde, U.W. Diffusion of small-molecule penetrants in semicrystalline polymers. Prog. Polym. Sci. 1996, 21, 299–333. [Google Scholar] [CrossRef]
- Trifol, J.; Plackett, D.; Szabo, P.; Daugaard, A.E.; Baschetti, M.G. Effect of Crystallinity on Water Vapor Sorption, Diffusion, and Permeation of PLA-Based Nanocomposites. ACS Omega 2020, 5, 15362–15369. [Google Scholar] [CrossRef]
- Kim, J.-K.; Hodzic, A. Nanoscale characterisation of thickness and properties of interphase in polymer matrix composites. J. Adhes. 2003, 79, 383–414. [Google Scholar] [CrossRef]
- Joliff, Y.; Rekik, W.; Belec, L.; Chailan, J.F. Study of the moisture/stress effects on glass fibre/epoxy composite and the impact of the interphase area. Compos. Struct. 2014, 108, 876–885. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabbej, M.; Guillard, V.; Angellier-Coussy, H.; Wolf, C.; Gontard, N.; Gaucel, S. 3D Modelling of Mass Transfer into Bio-Composite. Polymers 2021, 13, 2257. https://doi.org/10.3390/polym13142257
Kabbej M, Guillard V, Angellier-Coussy H, Wolf C, Gontard N, Gaucel S. 3D Modelling of Mass Transfer into Bio-Composite. Polymers. 2021; 13(14):2257. https://doi.org/10.3390/polym13142257
Chicago/Turabian StyleKabbej, Marouane, Valérie Guillard, Hélène Angellier-Coussy, Caroline Wolf, Nathalie Gontard, and Sébastien Gaucel. 2021. "3D Modelling of Mass Transfer into Bio-Composite" Polymers 13, no. 14: 2257. https://doi.org/10.3390/polym13142257
APA StyleKabbej, M., Guillard, V., Angellier-Coussy, H., Wolf, C., Gontard, N., & Gaucel, S. (2021). 3D Modelling of Mass Transfer into Bio-Composite. Polymers, 13(14), 2257. https://doi.org/10.3390/polym13142257







