Viscoelastic Effects on Drop Deformation Using a Machine Learning-Enhanced, Finite Element method
Abstract
1. Introduction
2. Materials and Methods
2.1. Finite Element Discretization
2.1.1. Governing Equations
2.1.2. Interface Capturing Technique
2.2. Computational Implementation
2.2.1. Machine Learning Enhancement
2.2.2. PETSc-Based Solver


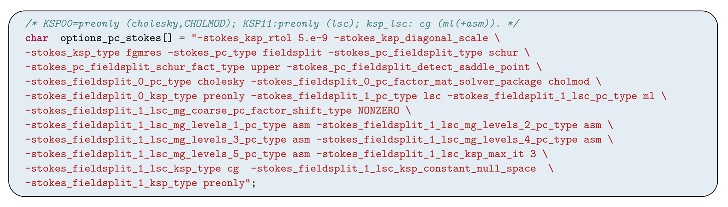
2.2.3. Boundary Conditions
3. Results and Discussion
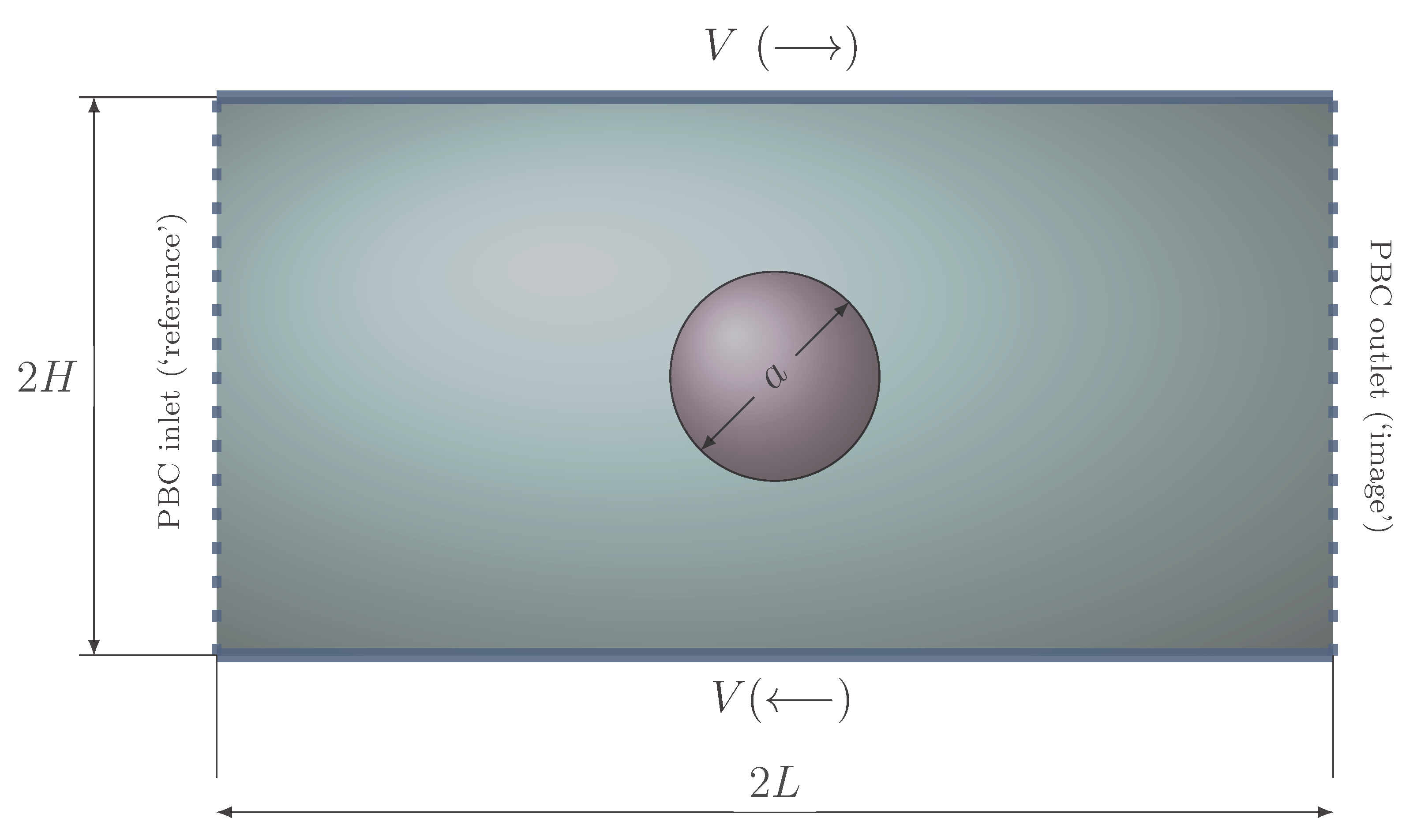
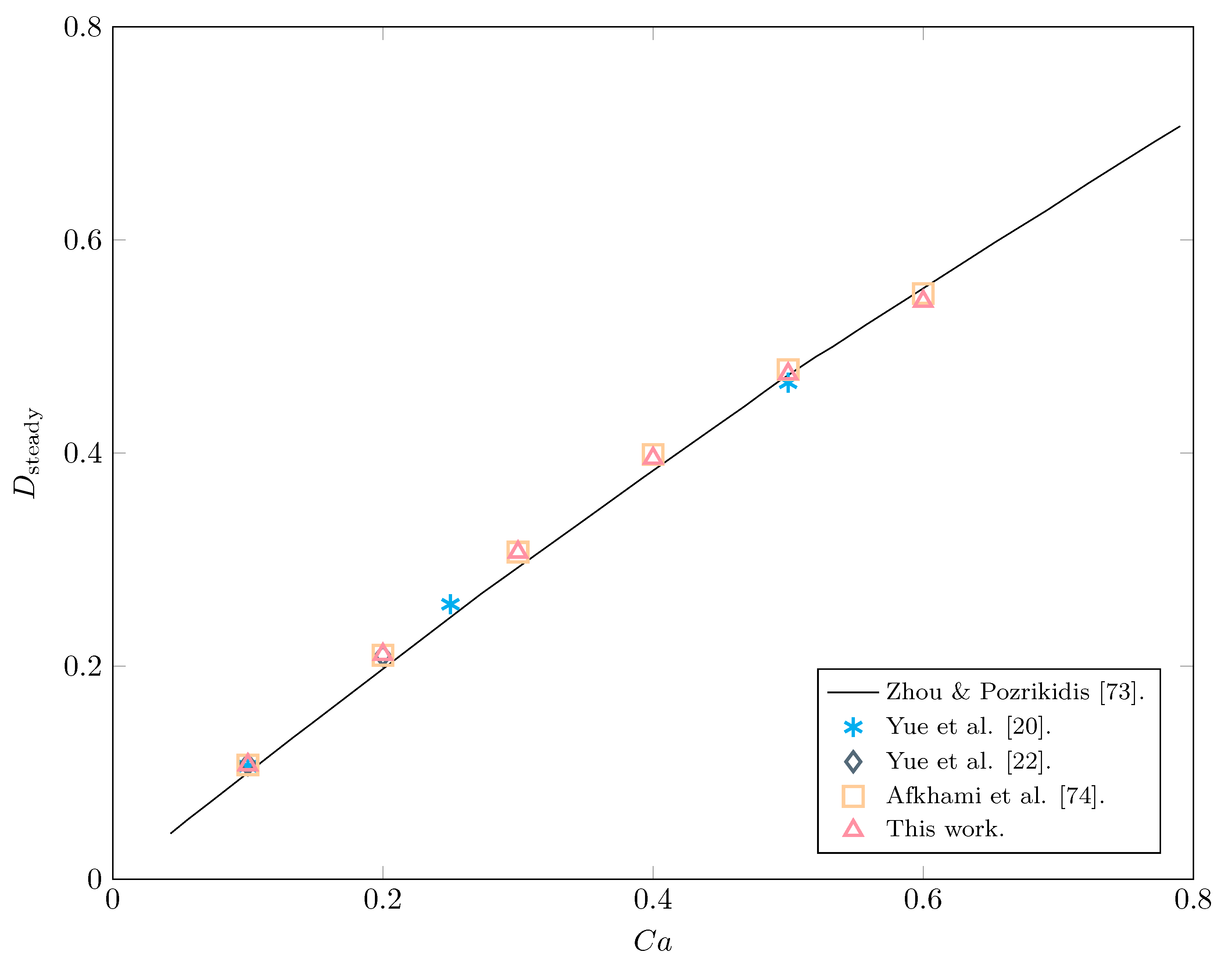
3.1. Drop Deformation in Steady, Shear Flow
3.1.1. Newtonian Drop in a Newtonian Matrix
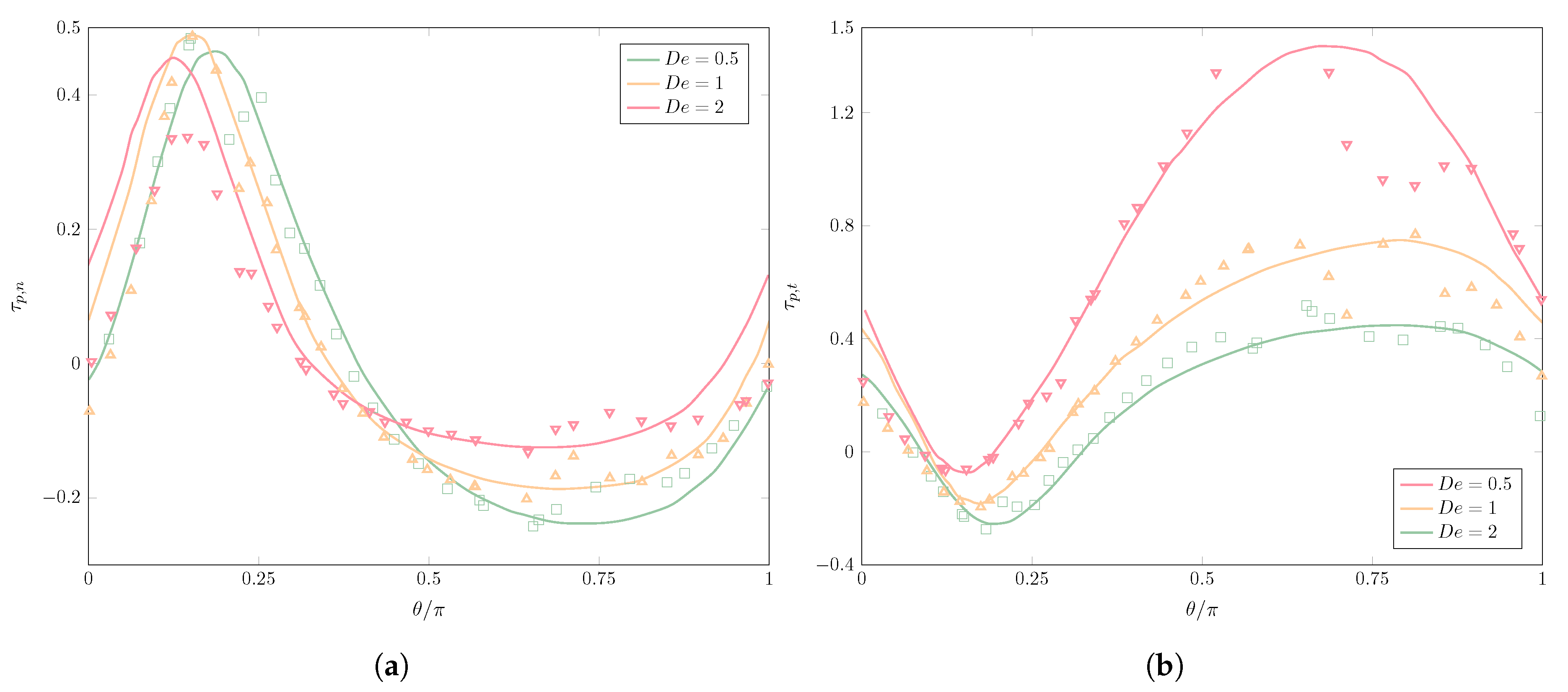
3.1.2. Viscoelastic Drop in a Newtonian Matrix
3.2. Drop Deformation in Buoyancy-Driven Flow
3.2.1. Convergence Results
3.2.2. Impact of CSRBF smoothness on the polymer stress tensor
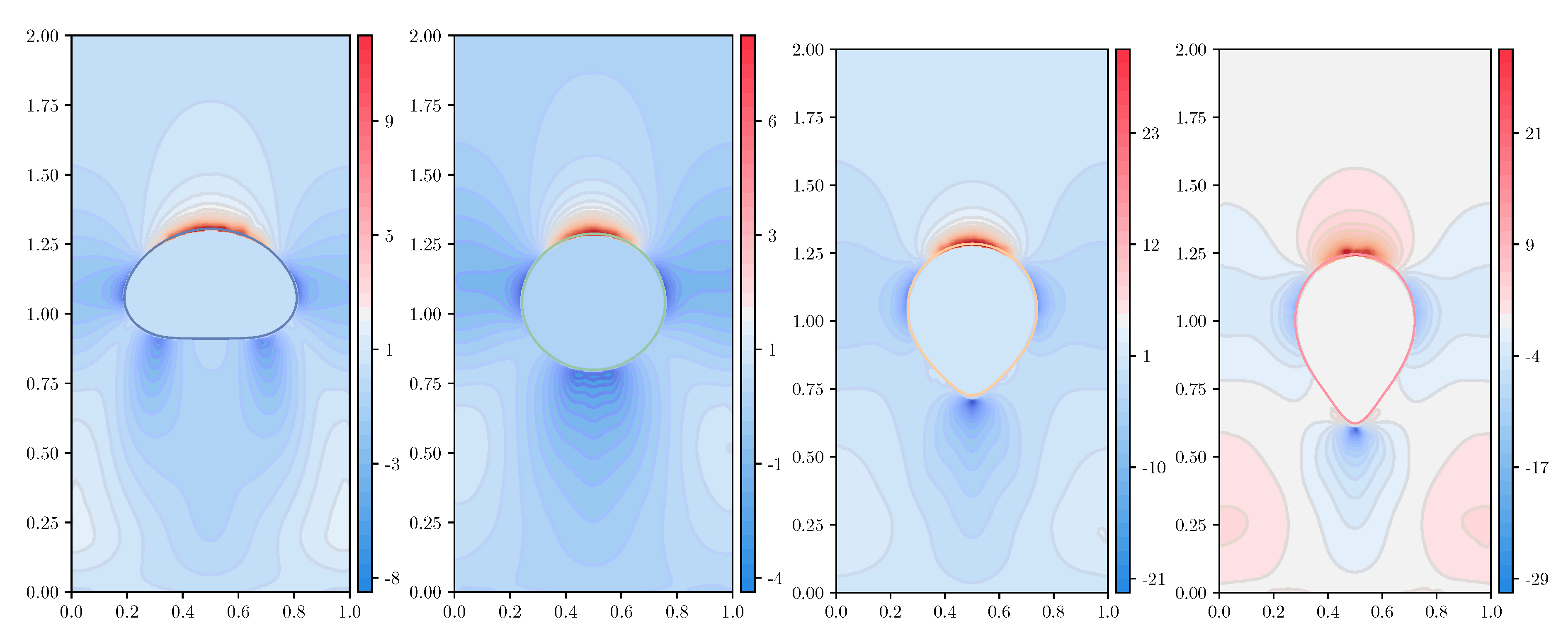
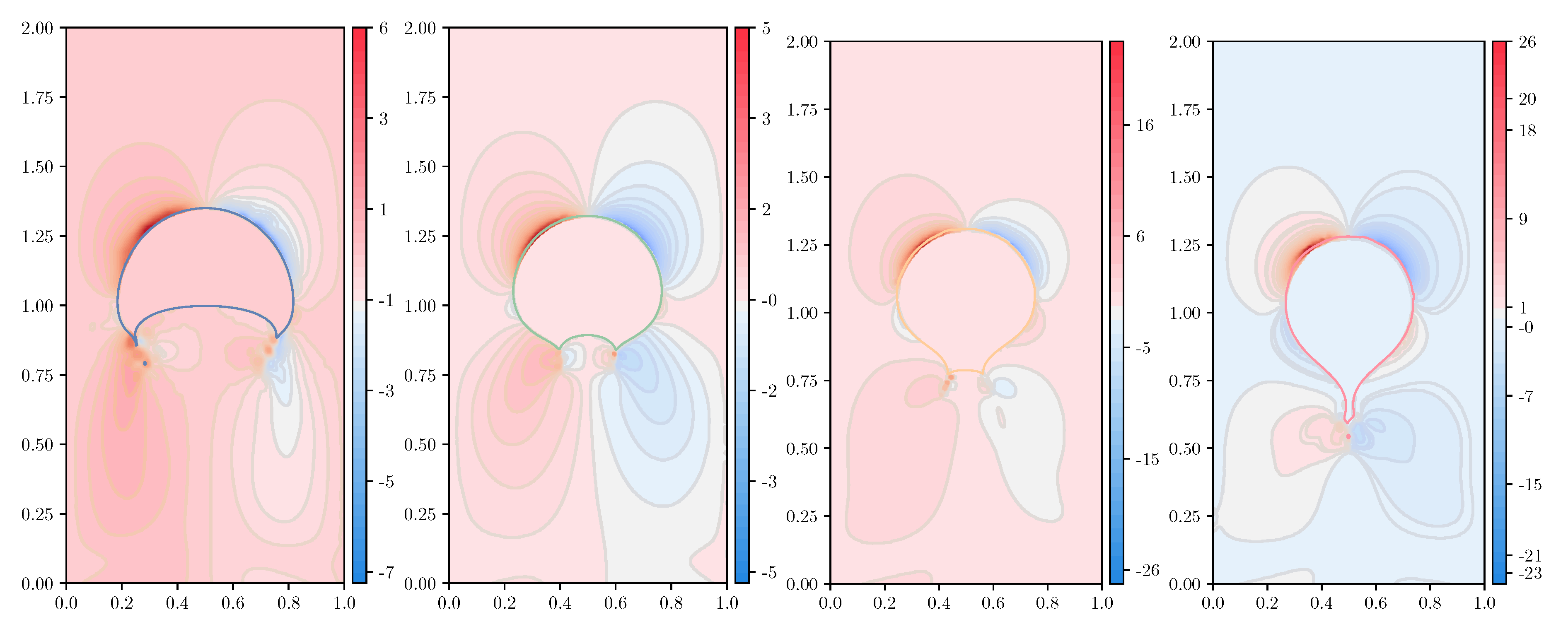
3.2.3. Flow Pattern under Increasing Viscoelastic Effects
4. Conclusions
Funding
Conflicts of Interest
Abbreviations
| Viscosity of the continuous phase | |
| Droplet viscosity | |
| Density of the continuous phase | |
| Droplet density | |
| Polymer (“extra-”)stress tensor | |
| Shear component of the polymer stress tensor | |
| Normal stress difference of the polymer stress tensor | |
| Level set function | |
| Compactly-supported Wendland function | |
| Support size of the CSRBF | |
| Trial basis function | |
| b | FENE extensibility parameter |
| c | Concentration parameter |
| Droplet circularity | |
| Time step size | |
| h | Grid size of the uniform, unstructured mesh |
| p | Pressure field |
| Velocity field | |
| s | Approximation interpolant of the CSRBF |
| D | Deformation parameter |
| Number of uncorrelated dumbbells per ensemble | |
| Number of ensembles of polymer particles | |
| Number of marker particles | |
| Capillary number | |
| Froude number | |
| Reynolds number | |
| Weber number | |
| ALE | Arbitrary Lagrangian-Eulerian method |
| BD | Brownian Dynamics simulations |
| CSRBF | Compactly-Supported Radial Basis Function |
| FEM | Finite Element Method |
| FENE | Finitely Extensible Non-linear Elastic model |
| LS | Level Set method |
| LSC | Least Squares Commutator preconditioner |
| ML | Machine Learning |
| NN | Nearest Neighbor |
| PBC | Periodic Boundary Conditions |
| PLS | Particle Level Set |
| RBF | Radial Basis Function |
| VOF | Volume-Of-Fluid method |
| [l c] | Vector of interpolation coefficients for the CSRBF |
| K | Discrete matrix system |
| PETSc | Portable, Extensible Toolkit for Scientific Computation |
References
- Zenit, R.; Feng, J. Hydrodynamic Interactions among Bubbles, Drops, and Particles in Non-Newtonian Liquids. Annu. Rev. Fluid Mech. 2018, 50, 505–534. [Google Scholar] [CrossRef]
- Aytouna, M.; Paredes, J.; Shahidzadeh-Bonn, N.; Moulinet, S.; Wagner, C.; Amarouchene, Y.; Eggers, J.; Bonn, D. Drop Formation in Non-Newtonian Fluids. Phys. Rev. Lett. 2013, 110, 034501. [Google Scholar] [CrossRef] [PubMed]
- Prieto-López, L.O.; Xu, J.; Cui, J. Magnetic-Responsive Bendable Nozzles for Open Surface Droplet Manipulation. Polymers 2019, 11, 1792. [Google Scholar] [CrossRef] [PubMed]
- Feigl, K.; Baniabedalruhman, A.; Tanner, F.X.; Windhab, E.J. Numerical simulations of the breakup of emulsion droplets inside a spraying nozzle. Phys. Fluids 2016, 28, 123103. [Google Scholar] [CrossRef]
- Fortelný, I.; Jůza, J. Description of the Droplet Size Evolution in Flowing Immiscible Polymer Blends. Polymers 2019, 11, 761. [Google Scholar] [CrossRef] [PubMed]
- Mohammad Karim, A. Experimental dynamics of Newtonian and non-Newtonian droplets impacting liquid surface with different rheology. Phys. Fluids 2020, 32, 043102. [Google Scholar] [CrossRef]
- Prieto, J.L. Stochastic particle level set simulations of buoyancy-driven droplets in non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 2015, 226, 16–31. [Google Scholar] [CrossRef]
- Faulde, M.; Siemes, E.; Wöll, D.; Jupke, A. Fluid Dynamics of Microgel-Covered Drops Reveal Impact on Interfacial Conditions. Polymers 2018, 10, 809. [Google Scholar] [CrossRef]
- Elgeti, S.; Sauerland, H. Deforming fluid domains within the finite element method: Five mesh-based tracking methods in comparison. Arch. Comput. Method. E. 2016, 23, 323–361. [Google Scholar] [CrossRef]
- Donea, J.; Huerta, A.; Ponthot, J.P.; Rodriguez-Ferran, A. Encyclopedia of Computational Mechanics Vol. 1: Fundamentals., Chapter 14: Arbitrary Lagrangian-Eulerian Methods; Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Bo, W.; Shashkov, M. Adaptive reconnection-based arbitrary Lagrangian Eulerian method. J. Comput. Phys. 2015, 299, 902–939. [Google Scholar] [CrossRef]
- Kenamond, M.; Shashkov, M. The distribution-based remapping of the nodal mass and momentum between arbitrary meshes for staggered arbitrary Lagrangian-Eulerian hydrodynamics. Comput. Fluids 2020, 201, 104469. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- López, J.; Hernández, J.; Gómez, P.; Faura, F. A volume of fluid method based on multidimensional advection and spline interface reconstruction. J. Comput. Phys. 2004, 195, 718–742. [Google Scholar] [CrossRef]
- López, J.; Hernández, J.; Gómez, P.; Faura, F. Non-convex analytical and geometrical tools for volume truncation, initialization and conservation enforcement in VOF methods. J. Comput. Phys. 2019, 392, 666–693. [Google Scholar] [CrossRef]
- Sethian, J.A.; Smereka, P. Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef]
- Gibou, F.; Fedkiw, R.; Osher, S. A review of level-set methods and some recent applications. J. Comput. Phys. 2018, 353, 82–109. [Google Scholar] [CrossRef]
- Enright, D.; Fedkiw, R.; Ferziger, J.; Mitchell, I. A Hybrid Particle Level Set Method for Improved Interface Capturing. J. Comput. Phys. 2002, 183, 83–116. [Google Scholar] [CrossRef]
- Thome, J.R. Encyclopedia of Two-Phase Heat Transfer and Flow III; World Scientific Publishing: Singapore, 2018. [Google Scholar] [CrossRef]
- Yue, P.; Feng, J.J.; Liu, C.; Shen, J. A diffuse-interface method for two-phase complex fluids. J. Fluid Mech. 2004, 515, 293–317. [Google Scholar] [CrossRef]
- Yue, P.; Feng, J.J.; Liu, C.; Shen, J. Transient drop deformation upon startup of shear in viscoelastic fluids. Phys. Fluids 2005, 17, 123101. [Google Scholar] [CrossRef]
- Yue, P.; Feng, J.J.; Liu, C.; Shen, J. Viscoelastic effects on drop deformation in steady shear. J. Fluid Mech. 2005, 540, 427–437. [Google Scholar] [CrossRef]
- Pillapakkam, S.B.; Singh, P.; Blackmore, D.; Aubry, N. Transient and steady state of a rising bubble in a viscoelastic fluid. J. Fluid Mech. 2007, 589, 215–252. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Laso, M. Numerical simulation of bubble dynamics in a Phan-Thien-Tanner liquid: Non-linear shape and size oscillatory response under periodic pressure. Ultrasonics 2010, 50, 758–776. [Google Scholar] [CrossRef] [PubMed]
- Castillo, E.; Baiges, J.; Codina, R. Approximation of the two-fluid flow problem for viscoelastic fluids using the level set method and pressure enriched finite element shape functions. J. Non-Newtonian Fluid Mech. 2015, 225, 37–53. [Google Scholar] [CrossRef]
- Fraggedakis, D.; Pavlidis, M.; Dimakopoulos, Y.; Tsamopoulos, J. On the velocity discontinuity at a critical volume of a bubble rising in a viscoelastic fluid. J. Fluid Mech. 2016, 789, 310–346. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Cheng, Z. Direct Numerical Simulation of Gas-Liquid Drag-Reducing Cavity Flow by the VOSET Method. Polymers 2019, 11, 596. [Google Scholar] [CrossRef] [PubMed]
- Xie, C.; Xu, K.; Mohanty, K.; Wang, M.; Balhoff, M.T. Nonwetting droplet oscillation and displacement by viscoelastic fluids. Phys. Rev. Fluids 2020, 5, 063301. [Google Scholar] [CrossRef]
- Keunings, R. Micro-macro methods for the multiscale simulation of viscoelastic flow using molecular models of kinetic theory. In Rheology Reviews; Binding, D.M., Walters, K., Eds.; British Society of Rheology: Aberystwyth, UK, 2004; pp. 67–98. [Google Scholar]
- Degond, P.; Lozinski, A.; Owens, R.G. Kinetic models for dilute solutions of dumbbells in non-homogeneous flows revisited. J. Non-Newtonian Fluid Mech. 2010, 165, 509–518. [Google Scholar] [CrossRef][Green Version]
- Müller, M.; de Pablo, J.J. Computational Approaches for the Dynamics of Structure Formation in Self-Assembling Polymeric Materials. Annu. Rev. Mater. Res. 2013, 43, 1–34. [Google Scholar] [CrossRef]
- Stephanou, P.; Kröger, M. Tumbling-Snake Model for Polymeric Liquids Subjected to Biaxial Elongational Flows with a Focus on Planar Elongation. Polymers 2018, 10, 329. [Google Scholar] [CrossRef]
- Megariotis, G.; Vogiatzis, G.; Sgouros, A.; Theodorou, D. Slip Spring-Based Mesoscopic Simulations of Polymer Networks: Methodology and the Corresponding Computational Code. Polymers 2018, 10, 1156. [Google Scholar] [CrossRef] [PubMed]
- Laso, M.; Öttinger, H.C. Calculation of viscoelastic flow using molecular models: The CONNFFESSIT approach. J. Non-Newtonian Fluid Mech. 1993, 47, 1–20. [Google Scholar] [CrossRef]
- Cormenzana, J.; Ledda, A.; Laso, M.; Debbaut, B. Calculation of free surface flows using CONNFFESSIT. J. Rheol. 2001, 45, 237–258. [Google Scholar] [CrossRef]
- Grande, E.; Laso, M.; Picasso, M. Calculation of variable-topology free surface flows using CONNFFESSIT. J. Non-Newtonian Fluid Mech. 2003, 113, 127–145. [Google Scholar] [CrossRef]
- Prieto, J.L. SLEIPNNIR: A multiscale, particle level set method for Newtonian and non-Newtonian interface flows. Comput. Methods Appl. Mech. Eng. 2016, 307, 164–192. [Google Scholar] [CrossRef]
- Prieto, J.L.; Bermejo, R.; Laso, M. A semi-Lagrangian micro-macro method for viscoelastic flow calculations. J. Non-Newtonian Fluid Mech. 2010, 165, 120–135. [Google Scholar] [CrossRef][Green Version]
- Bajaj, M.; Bhat, P.P.; Prakash, J.R.; Pasquali, M. Multiscale simulation of viscoelastic free surface flows. J. Non-Newtonian Fluid Mech. 2006, 140, 87–107. [Google Scholar] [CrossRef]
- Xu, X.; Ouyang, J.; Li, W.; Liu, Q. SPH simulations of 2D transient viscoelastic flows using Brownian Configuration Fields. J. Non-Newtonian Fluid Mech. 2014, 208–209, 59–71. [Google Scholar] [CrossRef]
- Hulsen, M.A.; van Heel, A.P.G.; van den Brule, B.H.A.A. Simulation of viscoelastic flows using Brownian Configuration Fields. J. Non-Newtonian Fluid Mech. 1997, 70, 79–101. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: New york, NY, USA, 2014. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Doblies, A.; Boll, B.; Fiedler, B. Prediction of Thermal Exposure and Mechanical Behavior of Epoxy Resin Using Artificial Neural Networks and Fourier Transform Infrared Spectroscopy. Polymers 2019, 11, 363. [Google Scholar] [CrossRef]
- Jackson, N.E.; Bowen, A.S.; de Pablo, J.J. Efficient Multiscale Optoelectronic Prediction for Conjugated Polymers. Macromolecules 2020, 53, 482–490. [Google Scholar] [CrossRef]
- Kopal, I.; Harničárová, M.; Valíček, J.; Krmela, J.; Lukáč, O. Radial Basis Function Neural Network-Based Modeling of the Dynamic Thermo-Mechanical Response and Damping Behavior of Thermoplastic Elastomer Systems. Polymers 2019, 11, 1074. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekaran, A.; Kim, C.; Venkatram, S.; Ramprasad, R. A Deep Learning Solvent-Selection Paradigm Powered by a Massive Solvent/Nonsolvent Database for Polymers. Macromolecules 2020, 53, 4764–4769. [Google Scholar] [CrossRef]
- Ma, M.; Lu, J.; Tryggvason, G. Using statistical learning to close two-fluid multiphase flow equations for a simple bubbly system. Phys. Fluids 2015, 27, 092101. [Google Scholar] [CrossRef]
- Ladický, L.; Jeong, S.; Solenthaler, B.; Pollefeys, M.; Gross, M. Data-Driven Fluid Simulations Using Regression Forests. ACM Trans. Graph. 2015, 34, 1–9. [Google Scholar] [CrossRef]
- Gibou, F.; Hyde, D.; Fedkiw, R. Sharp interface approaches and deep learning techniques for multiphase flows. J. Comput. Phys. 2019, 380, 442–463. [Google Scholar] [CrossRef]
- Öttinger, H.C. Stochastic Processes in Polymeric Fluids: Tools and Examples for Developing Simulation Algorithms; Springer: Berlin, Germany, 1996. [Google Scholar]
- Prieto, J.L. An RBF-reconstructed, polymer stress tensor for stochastic, particle-based simulations of non-Newtonian, multiphase flows. J. Non-Newtonian Fluid Mech. 2016, 227, 90–99. [Google Scholar] [CrossRef]
- Bermejo, R.; Prieto, J.L. A Semi-Lagrangian Particle Level Set Finite Element Method for Interface Problems. SIAM J. Sci. Comput. 2013, 35, A1815–A1846. [Google Scholar] [CrossRef][Green Version]
- Cheng, L.T.; Tsai, Y.H. Redistancing by flow of time dependent eikonal equation. J. Comput. Phys. 2008, 227, 4002–4017. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Tantau, T. The TikZ and PGF Packages. Comprehensive TEX Archive Network, CTAN. 2020. Available online: http://mirrors.ctan.org/graphics/pgf/base/doc/pgfmanual.pdf (accessed on 24 July 2020).
- Ramachandran, P.; Varoquaux, G. Mayavi: 3D Visualization of Scientific Data. Comput. Sci. Eng. 2011, 13, 40–51. [Google Scholar] [CrossRef]
- Pandas Development Team. Pandas-Dev/Pandas: Pandas. 2020. Available online: https://doi.org/10.5281/zenodo.3509134 (accessed on 24 July 2020).
- Schaback, R.; Wendland, H. Kernel techniques: From machine learning to meshless methods. Acta Numerica 2006, 15, 543–639. [Google Scholar] [CrossRef]
- Carr, J.C.; Beatson, R.K.; Cherrie, J.B.; Mitchell, T.J.; Fright, W.R.; McCallum, B.C.; Evans, T.R. Reconstruction and Representation of 3D Objects with Radial Basis Functions. In SIGGRAPH’2001: Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques; Association for Computing Machinery: New York, NY, USA, 2001; pp. 67–76. [Google Scholar]
- Ohtake, Y.; Belyaev, A.; Seidel, H.P. 3D scattered data interpolation and approximation with multilevel compactly supported RBFs. Graph. Models 2005, 67, 150–165. [Google Scholar] [CrossRef]
- Wendland, H. Scattered Data Approximation; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Brown, J.; Brune, P.; Buschelman, K.; Dalcin, L.; Dener, A.; Eijkhout, V.; Gropp, W.D.; et al. PETSc Web Page. Available online: https://www.mcs.anl.gov/petsc (accessed on 24 July 2020).
- Dean, E.J.; Glowinski, R. On some finite element methods for the numerical simulation of incompressible viscous flow. In Incompressible Computational Fluid Dynamics; Gunzburger, M.D., Nicolaides, R.A., Eds.; Cambridge University Press: New York, NY, USA, 1993; pp. 109–150. [Google Scholar]
- Sousa, F.S.; Oishi, C.M.; Buscaglia, G.C. Spurious transients of projection methods in microflow simulations. Comput. Methods Appl. Mech. Eng. 2015, 285, 659–693. [Google Scholar] [CrossRef]
- Elman, H.; Howle, V.; Shadid, J.; Shuttleworth, R.; Tuminaro, R. A taxonomy and comparison of parallel block multi-level preconditioners for the incompressible Navier-Stokes equations. J. Comput. Phys. 2008, 227, 1790–1808. [Google Scholar] [CrossRef]
- Elman, H.C.; Silvester, D.J.; Wathen, A.J. Finite Elements and Fast Iterative Solvers: With Applications in Incompressible Fluid Dynamics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Davis, T.A.; Hager, W.W. Dynamic Supernodes in Sparse Cholesky Update/Downdate and Triangular Solves. ACM Trans. Math. Softw. 2009, 35, 27:1–27:23. [Google Scholar] [CrossRef]
- Golub, G.H.; Loan, C.F.V. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2012. [Google Scholar]
- Gee, M.; Siefert, C.; Hu, J.; Tuminaro, R.; Sala, M. ML 5.0 Smoothed Aggregation User’s Guide; Technical Report SAND2006-2649; Sandia National Laboratories: Livermore, CA, USA, 2006. [Google Scholar]
- Pask, J.; Klein, B.; Sterne, P.; Fong, C. Finite-element methods in electronic-structure theory. Comput. Phys. Commun. 2001, 135, 1–34. [Google Scholar] [CrossRef]
- Sukumar, N.; Pask, J.E. Classical and enriched finite element formulations for Bloch-periodic boundary conditions. Int. J. Numer. Methods Eng. 2009, 77, 1121–1138. [Google Scholar] [CrossRef]
- Zhou, H.; Pozrikidis, C. The flow of suspensions in channels: Single files of drops. Phys. Fluids 1993, 5, 311–324. [Google Scholar] [CrossRef]
- Afkhami, S.; Yue, P.; Renardy, Y. A comparison of viscoelastic stress wakes for two-dimensional and three-dimensional Newtonian drop deformations in a viscoelastic matrix under shear. Phys. Fluids 2009, 21, 072106. [Google Scholar] [CrossRef]
- Balla, M.; Kavuri, S.; Tripathi, M.K.; Sahu, K.C.; Govindarajan, R. Effect of viscosity and density ratios on two drops rising side by side. Phys. Rev. Fluids 2020, 5, 013601. [Google Scholar] [CrossRef]
- Hassager, O. Negative wake behind bubbles in non-Newtonian liquids. Nature 1979, 279, 402–403. [Google Scholar] [CrossRef] [PubMed]
- Prieto, J.L.; Carpio, J. A-SLEIPNNIR: A multiscale, anisotropic adaptive, particle level set framework for moving interfaces. Transport equation applications. J. Comput. Phys. 2019, 377, 89–116. [Google Scholar] [CrossRef]

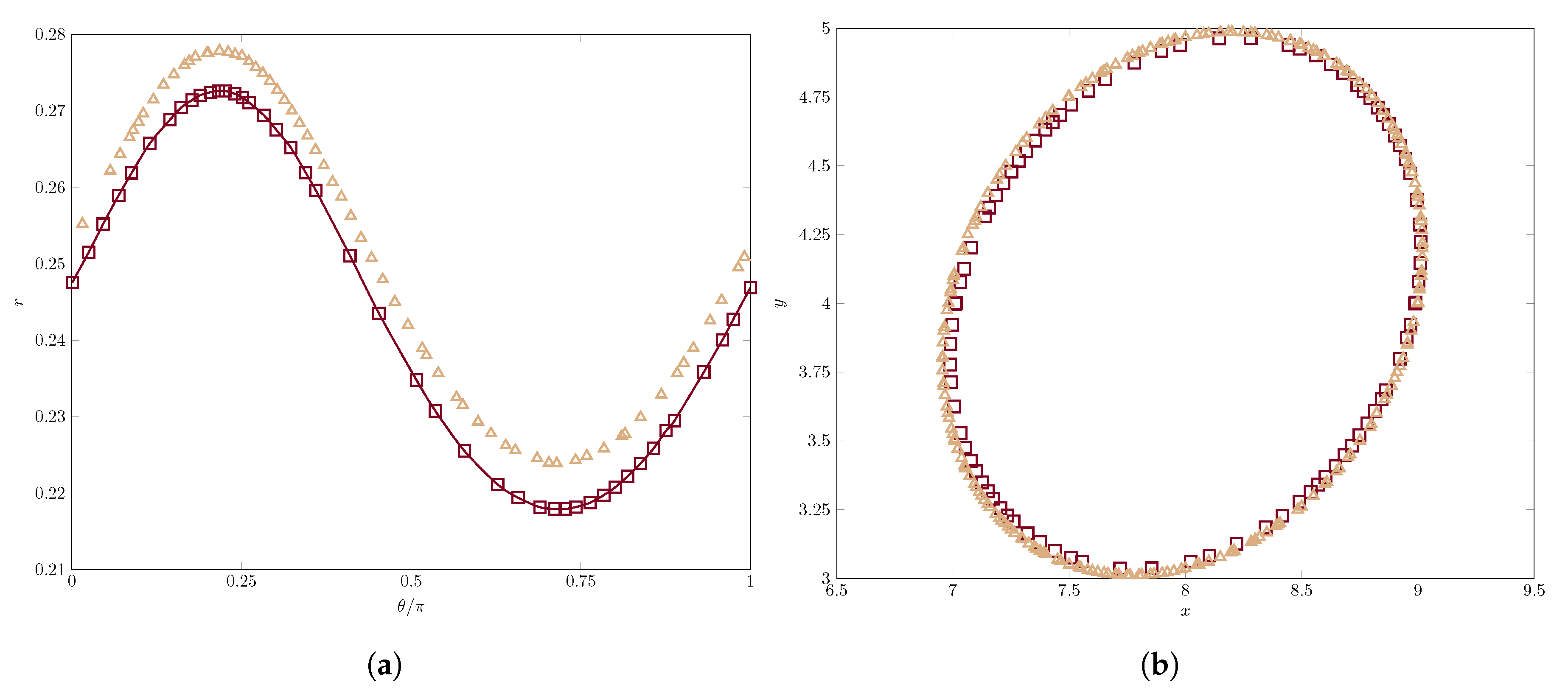


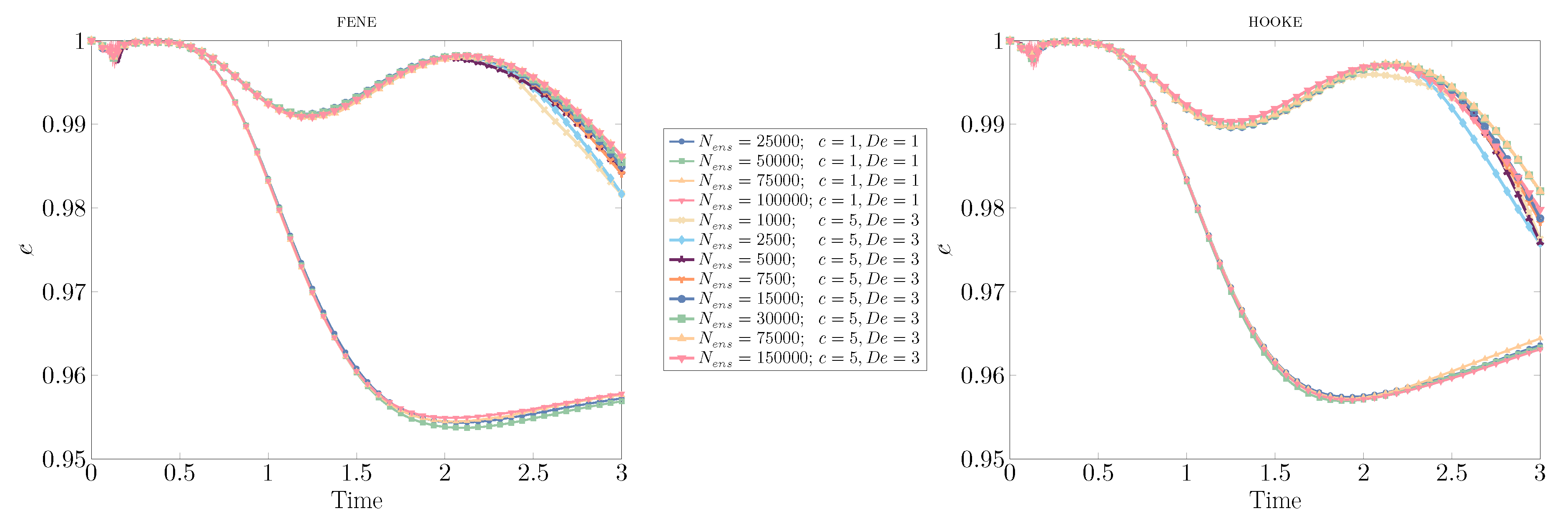




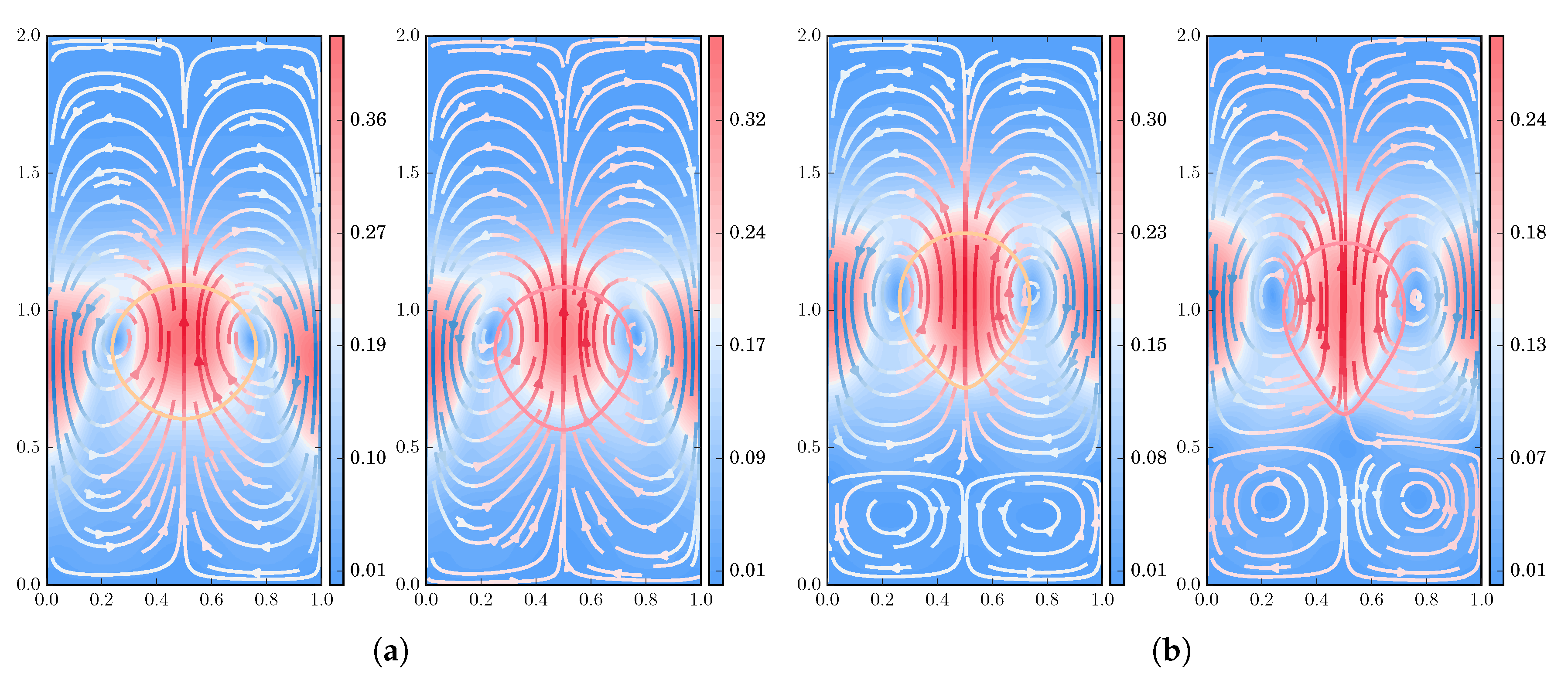
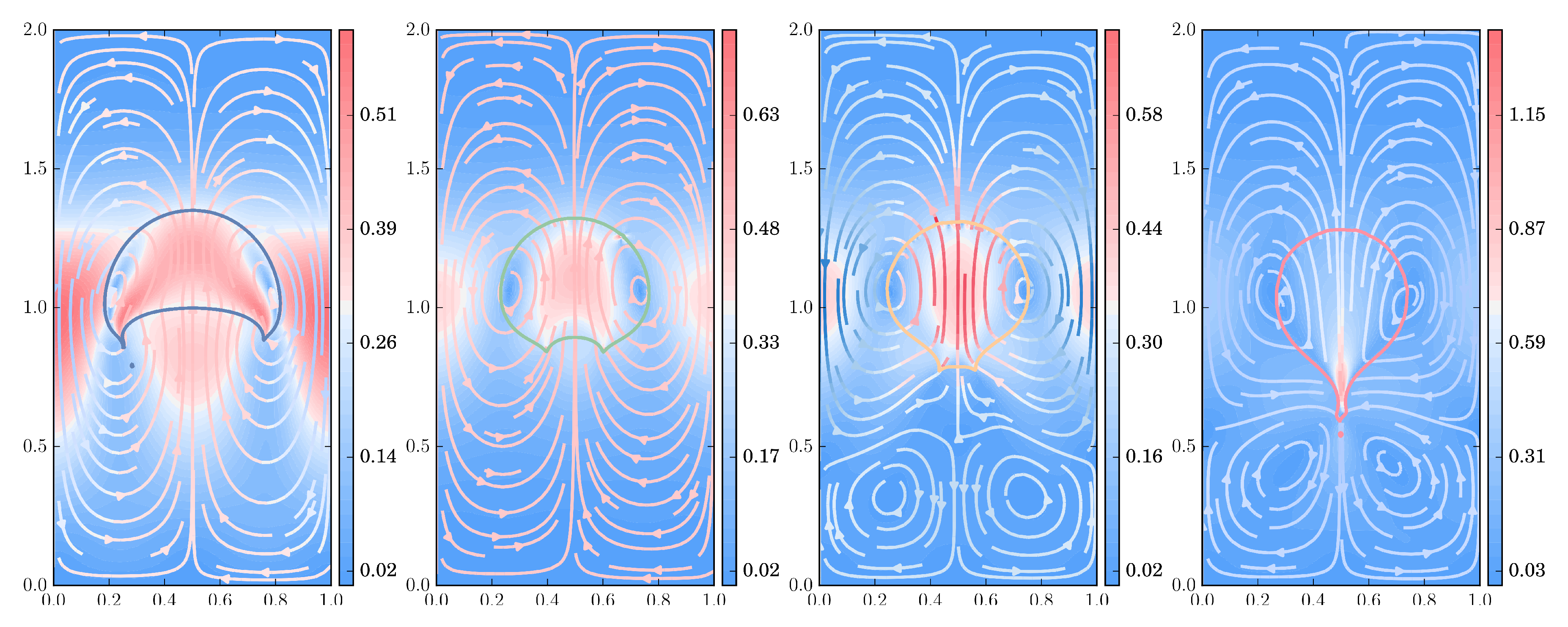
| Density Ratio | ||||
|---|---|---|---|---|
| 10 | 150,000/5000 | 75,000/10,000 | 50,000/15,000 | 37,500/20,000 |
| 1000 | 150,000/5000 | 50,000/15,000 | 15,000/50,000 | 15,000/5000 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prieto, J.L. Viscoelastic Effects on Drop Deformation Using a Machine Learning-Enhanced, Finite Element method. Polymers 2020, 12, 1652. https://doi.org/10.3390/polym12081652
Prieto JL. Viscoelastic Effects on Drop Deformation Using a Machine Learning-Enhanced, Finite Element method. Polymers. 2020; 12(8):1652. https://doi.org/10.3390/polym12081652
Chicago/Turabian StylePrieto, Juan Luis. 2020. "Viscoelastic Effects on Drop Deformation Using a Machine Learning-Enhanced, Finite Element method" Polymers 12, no. 8: 1652. https://doi.org/10.3390/polym12081652
APA StylePrieto, J. L. (2020). Viscoelastic Effects on Drop Deformation Using a Machine Learning-Enhanced, Finite Element method. Polymers, 12(8), 1652. https://doi.org/10.3390/polym12081652





