Characterization of Rough PTFE Surfaces by the Modified Wilhelmy Balance Technique
Abstract
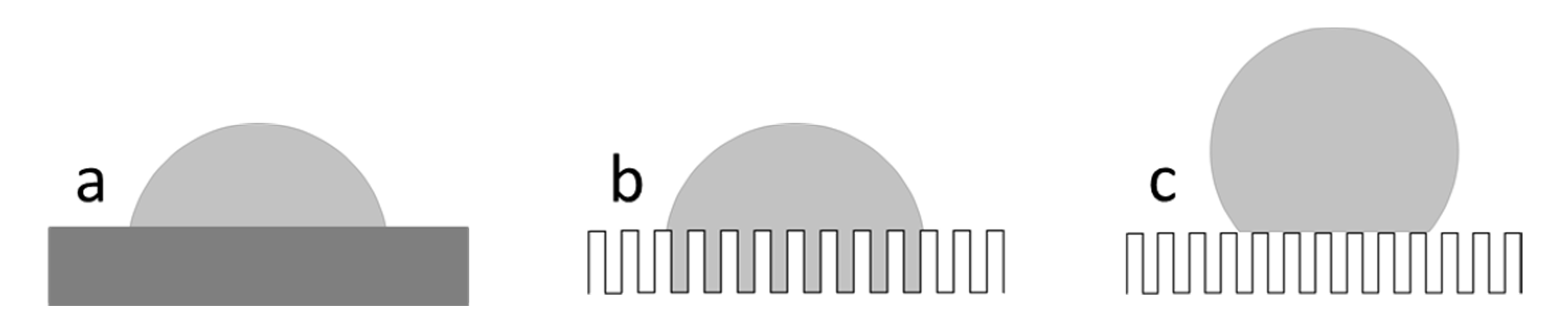
1. Introduction
2. Materials and Methods
3. Results
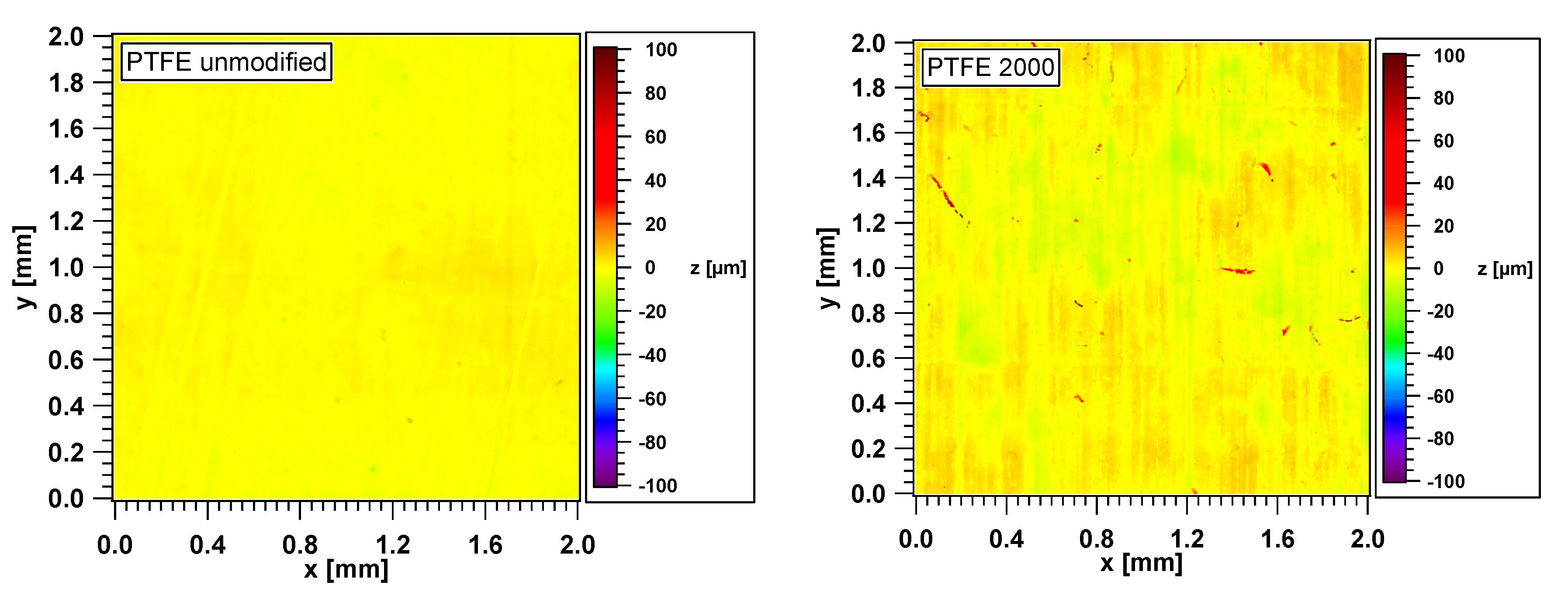
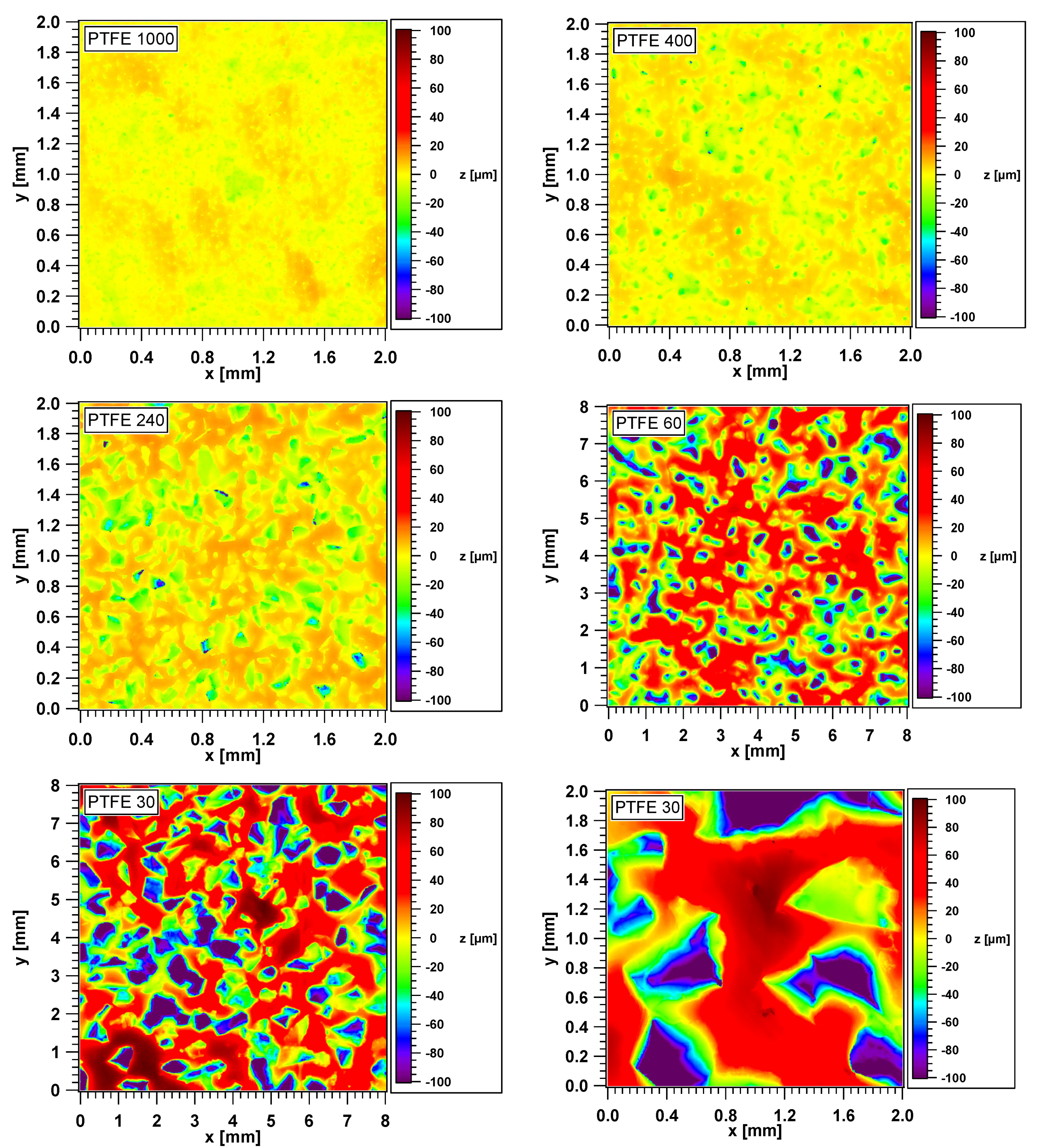
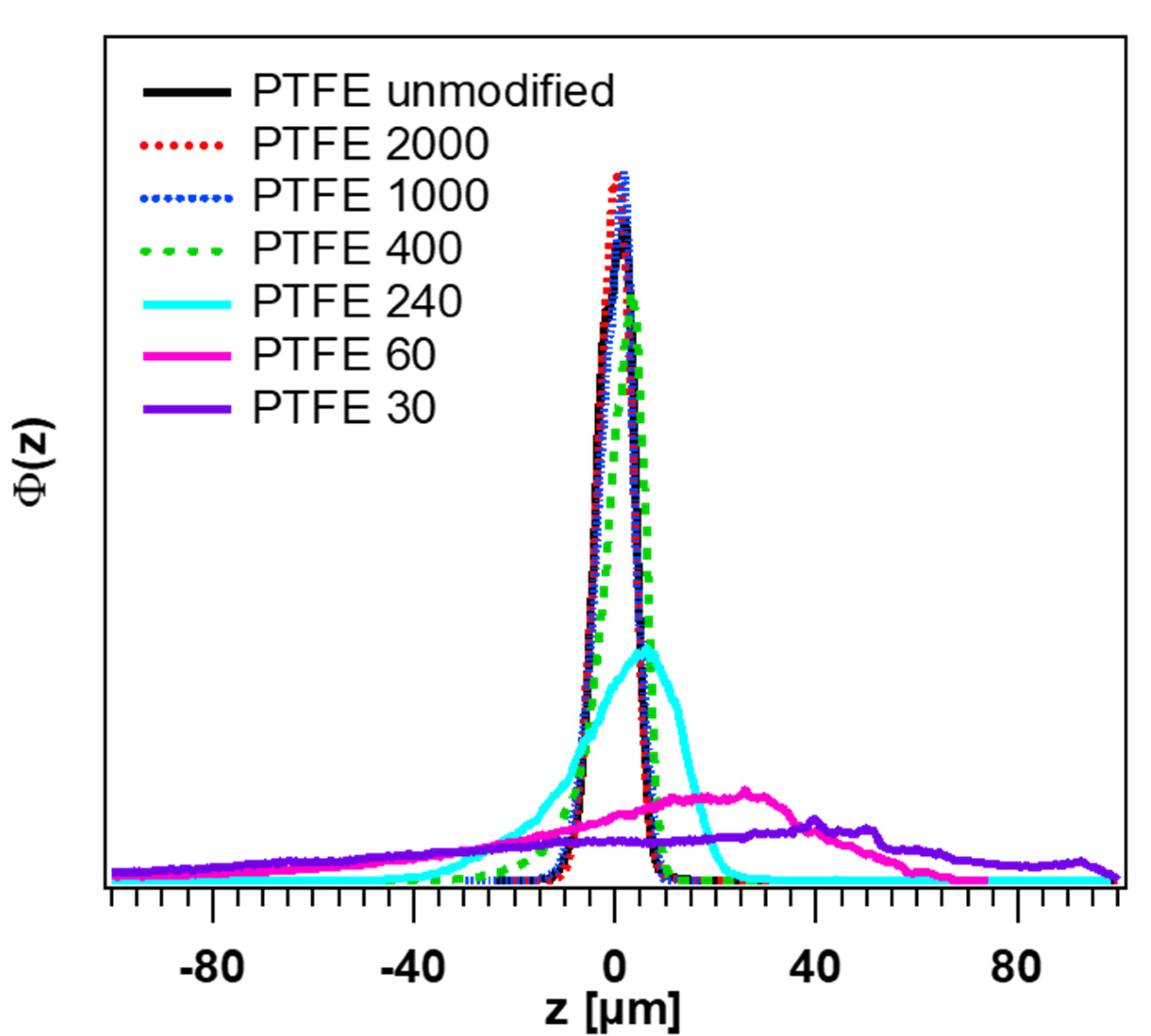
3.1. Topography and Height Distributions of the PTFE Surfaces
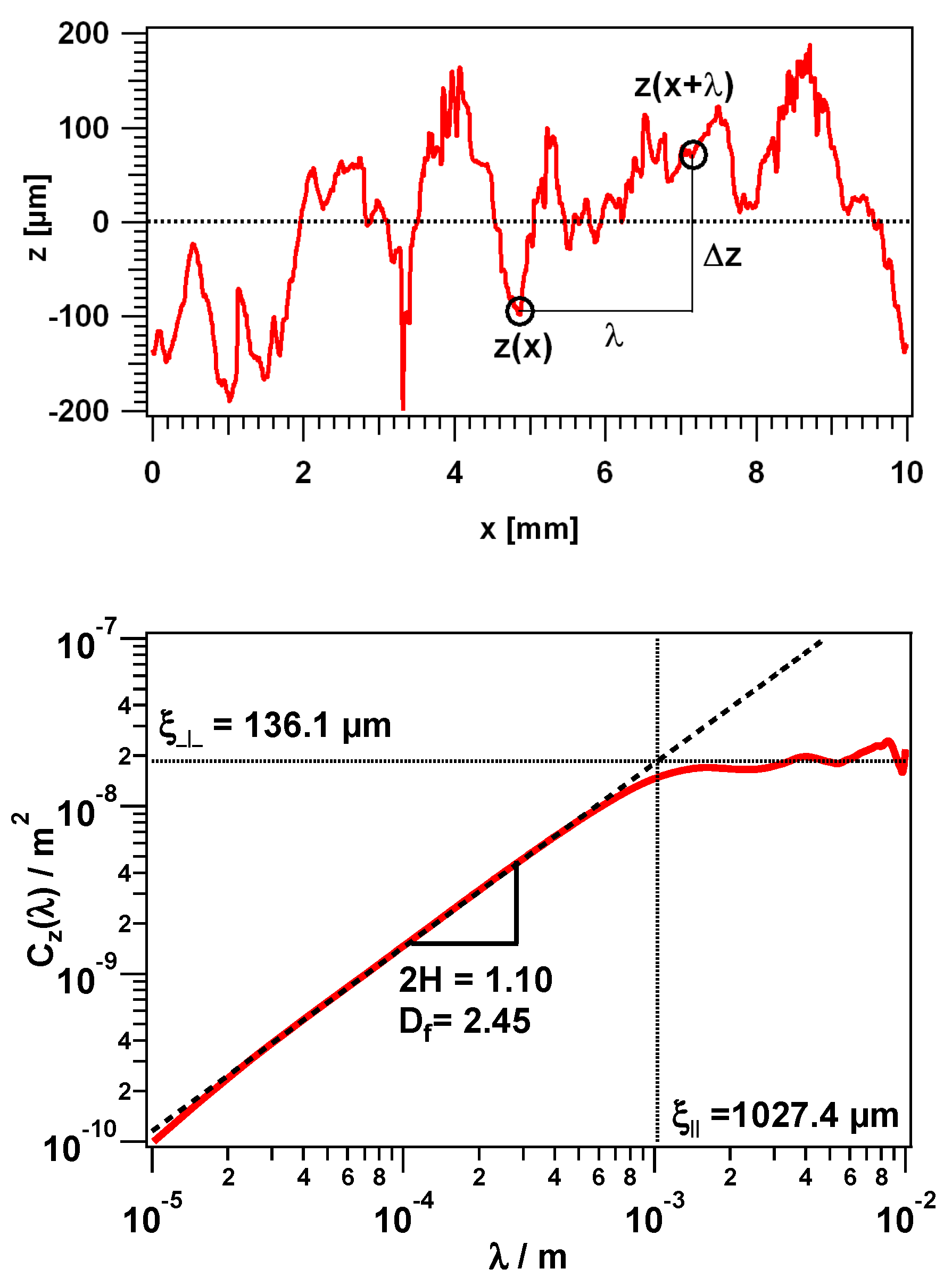
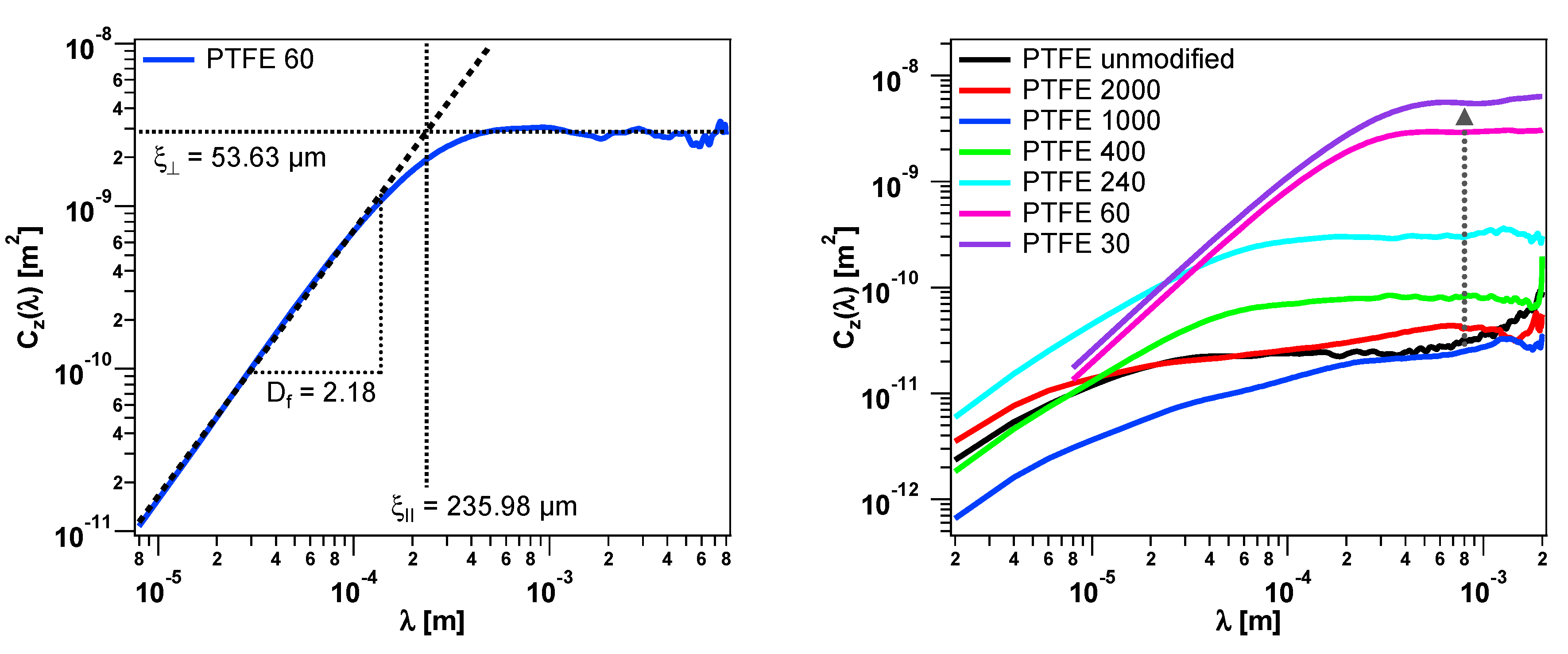
3.2. Height Difference Correlation Function and Fractal Descriptors of the PTFE Surfaces
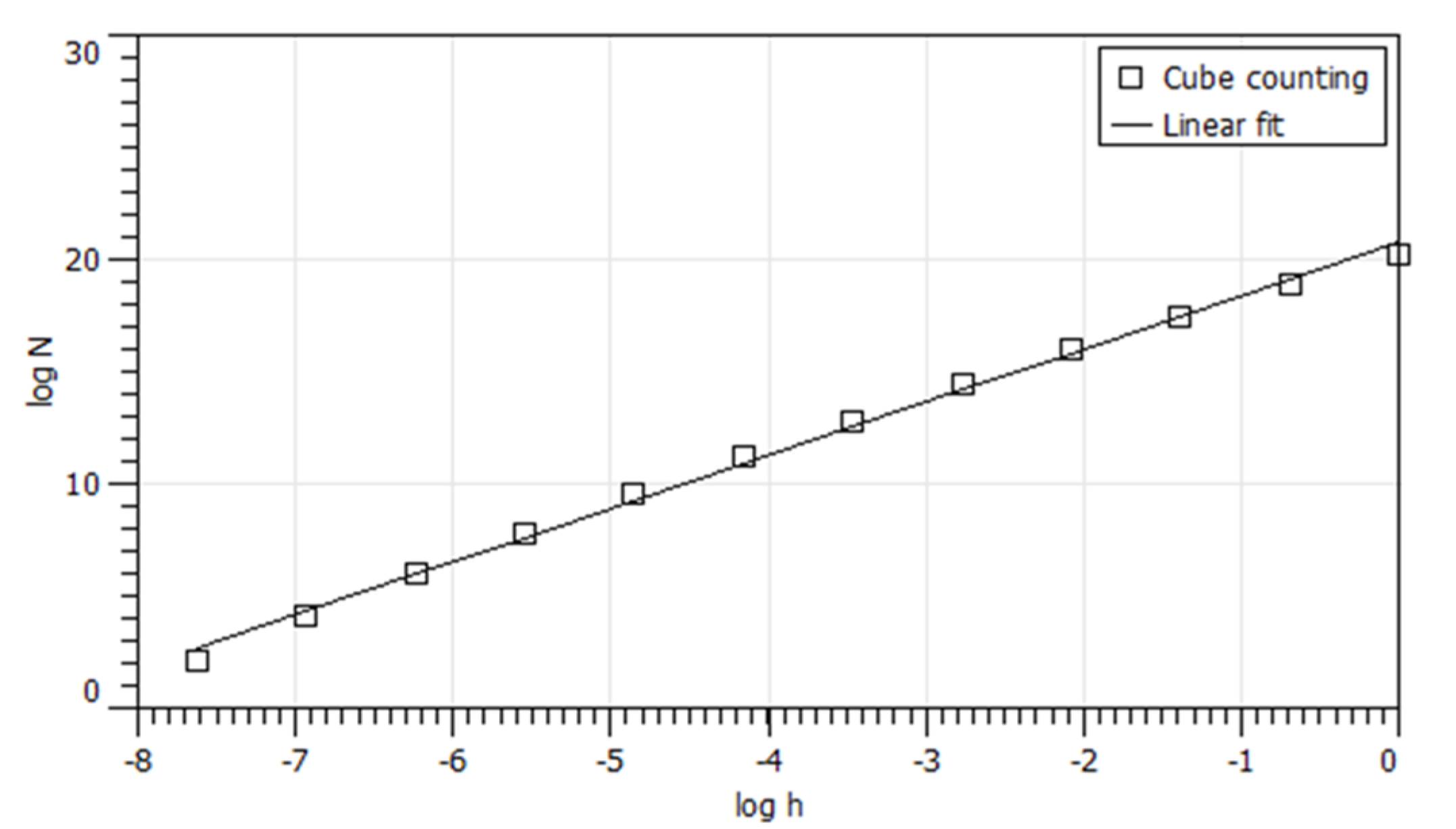
3.3. Cube Counting Method and Calculation of Fractal Descriptors of the PTFE Surfaces
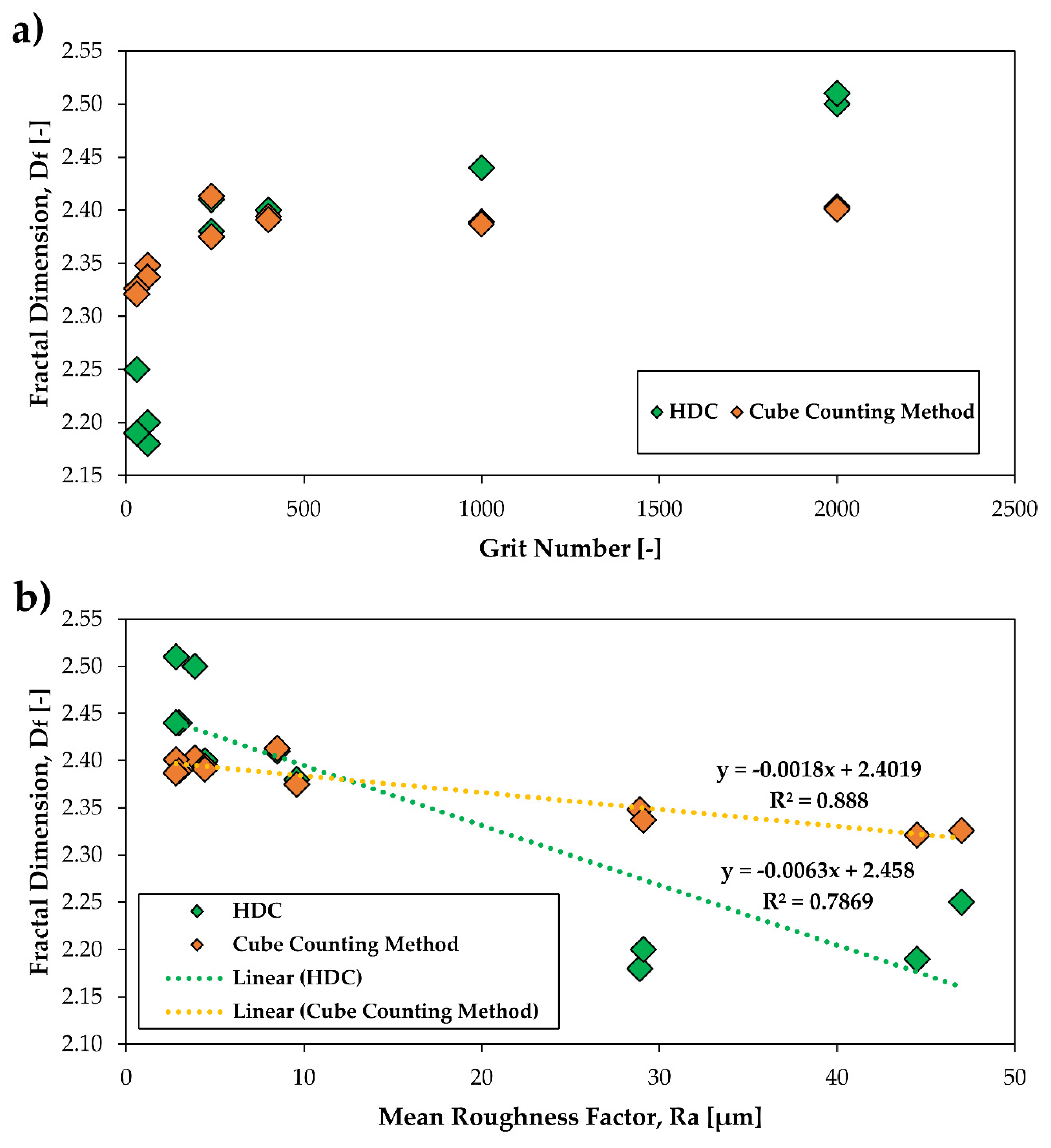
3.4. The Relationship between the Fractal Dimension Df and the Grit Number as Well as the Mean Roughness Ra
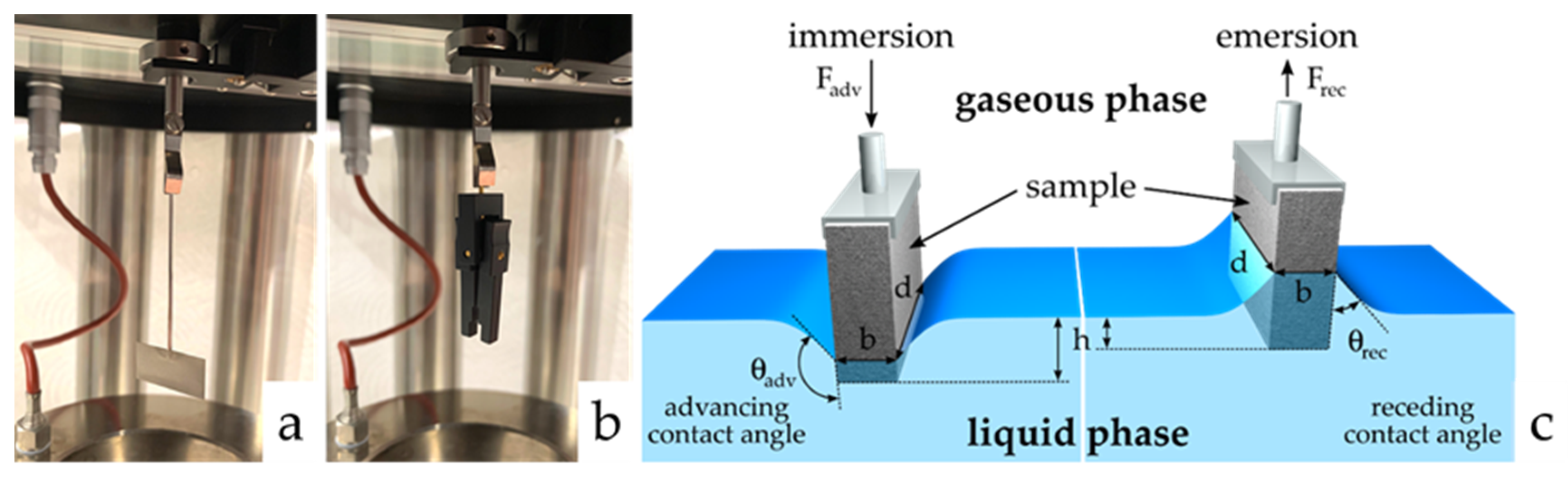
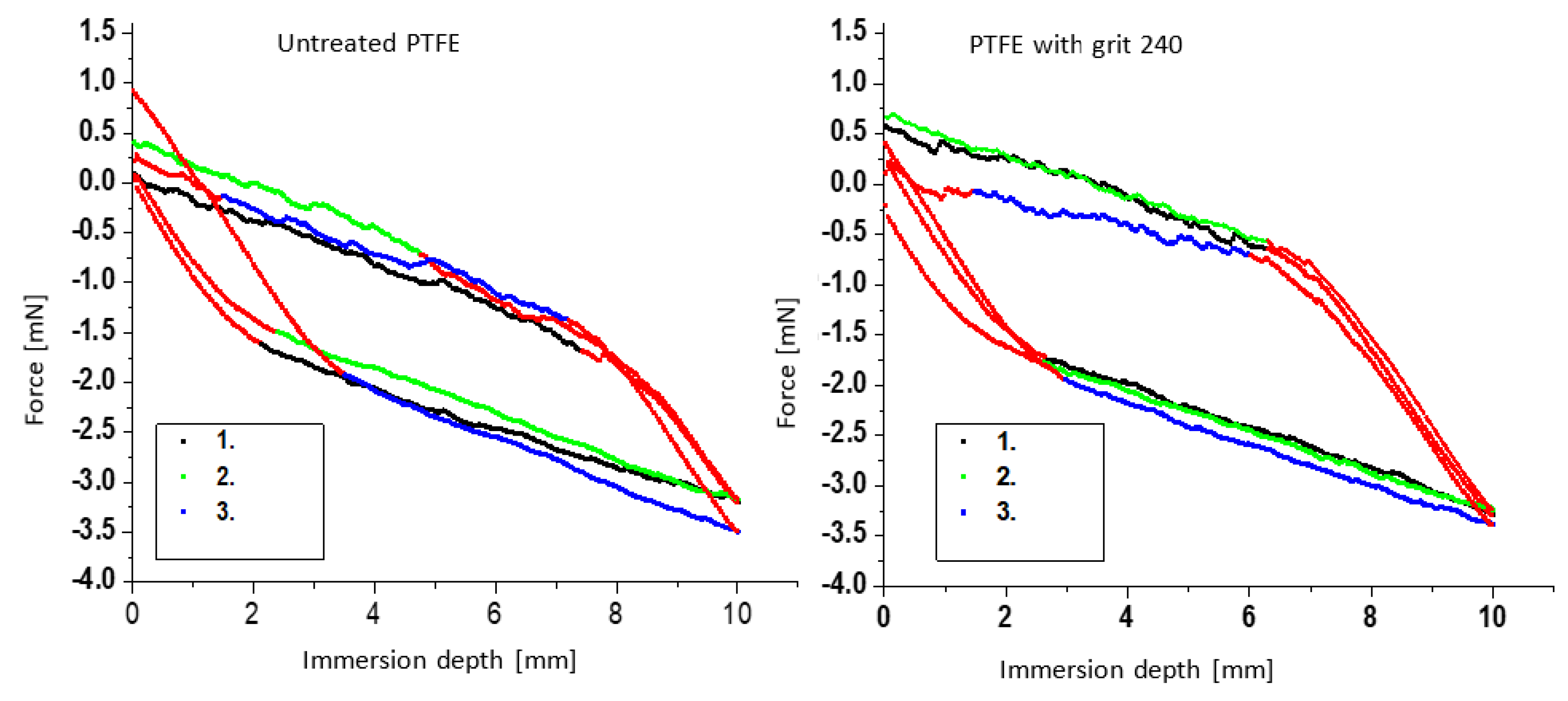
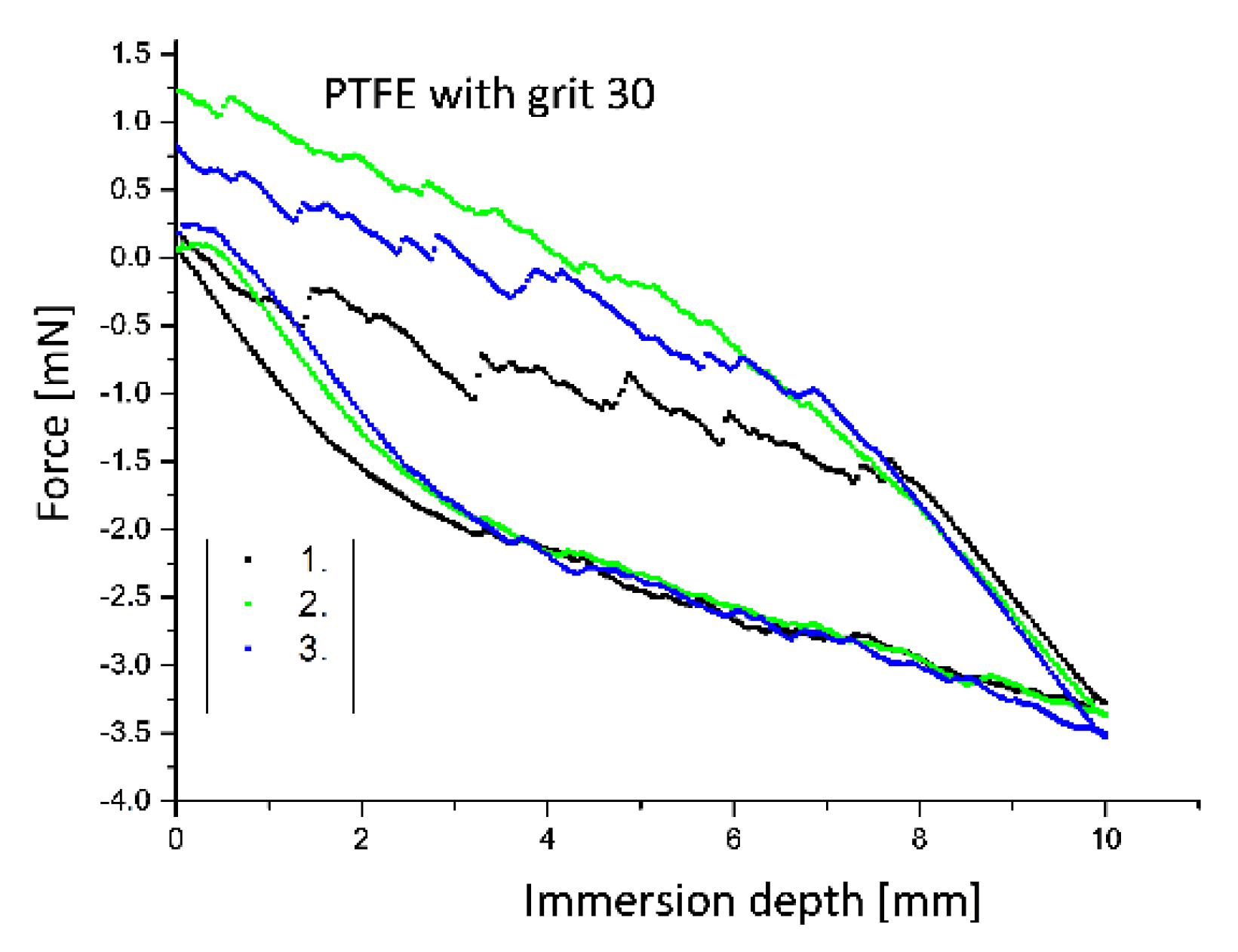
3.5. Determination of Contact Angles by the Modified Wilhelmy Balance Technique
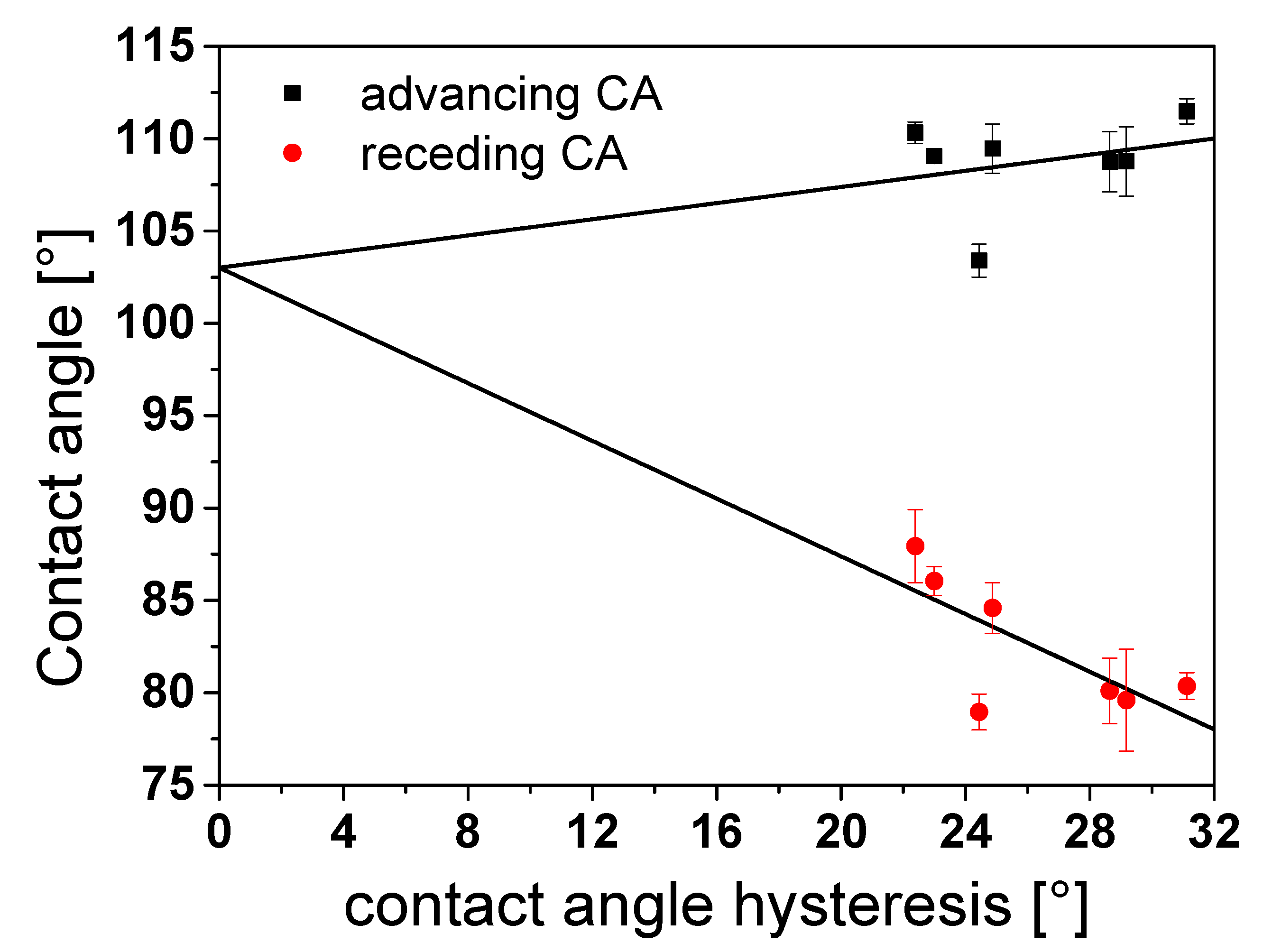
3.6. Determination of the Equilibrium Contact Angle of Rough PTFE Surfaces
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yamamoto, M.; Nishikawa, N.; Mayama, H.; Nonomura, Y.; Yokojima, S.; Nakamura, S.; Uchida, K. Theoretical Explanation of the Lotus Effect: Superhydrophobic Property Changes by Removal of Nanostructures from the Surface of a Lotus Leaf. Langmuir 2015, 26, 7355–7363. [Google Scholar] [CrossRef] [PubMed]
- Barthlott, W.; Neinhuis, C. Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 1997, 202, 1–8. [Google Scholar] [CrossRef]
- Koch, K.; Bhushan, B.; Barthlott, W. Diversity of structure, morphology and wetting of plant surfaces. Soft Matter 2008, 4, 1943–1963. [Google Scholar] [CrossRef]
- Golovin, K.; Kobaku, S.P.R.; Hyun Lee, D.; DiLoreto, E.T.; Mabry, J.M.; Tuteja, A. Designing durable icephobic surfaces. Sci. Adv. 2016, 2, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Xue, J.; Wang, Y.; Chen, Q.; Ding, J.; Wan, Q. Ice-phobic Coatings Based on Silicon-Oil-Infused Polydimethylsiloxane. ACS Appl. Mater. Interfaces 2013, 5, 4053–4062. [Google Scholar] [CrossRef] [PubMed]
- Dorrer, C.; Rühe, J. Some thoughts on superhydrophobic wetting. Soft Matter 2009, 5, 51–61. [Google Scholar] [CrossRef]
- Bain, C.D.; Whitesides, G.M. Depth sensitivity of wetting: Monolayers of omega-mercapto ethers on gold. J. Am. Chem. Soc. 1988, 110, 5897–5898. [Google Scholar] [CrossRef]
- Meiron, T.S.; Marmur, A.; Saguy, I.S. Contact angle measurement on rough surfaces. J. Colloid Interface Sci. 2004, 274, 637–644. [Google Scholar] [CrossRef]
- Wolansky, G.; Marmur, A. Apparent contact angles on rough surfaces: The Wenzel equation revisited. Colloids Surf. A: Physicochem. Eng. Asp. 1999, 156, 381–388. [Google Scholar] [CrossRef]
- Young, T. Miscellaneous Works; Peacock, G., Ed.; Murray: London, UK, 1855; p. 418. [Google Scholar]
- Koch, K.; Barthlott, W. Superhydrophobic and Superhydrophilic Plant Surfaces: An Inspiration for Biomimetic Materials. Philos. Trans. R. Soc. A 2009, 367, 1487–1509. [Google Scholar] [CrossRef]
- Kim, S.H. Fabrication of Superhydrophobic Surfaces. J. Adhes. Sci. Technol. 2008, 22, 235–250. [Google Scholar] [CrossRef]
- Jeevahan, J.; Chandrasekaran, M.; Joseph, G.B.; Durairaj, R.B.; Mageshwaran, G.J. Superhydrophobic surfaces: A review on fundamentals, applications, and challenges. J. Coat. Technol. Res. 2018, 15, 231–250. [Google Scholar] [CrossRef]
- Lafuma, A.; Queéreé, D. Superhydrophobic States. Nat. Mater. 2003, 2, 457–460. [Google Scholar] [CrossRef]
- Erbil, H.Y.; Demirel, A.L.; Avcı, Y.; Mert, O. Transformation of a Simple Plastic into a Superhydrophobic Surface. Science 2003, 299, 1377–1380. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.F.; Mondal, B.; Lyons, A.M. Fabricating Superhydrophobic Polymer Surfaces with Excellent Abrasion Resistance by a Simple Lamination Templating Method. ACS Appl. Mater. Interfaces 2011, 3, 3508–3514. [Google Scholar] [CrossRef] [PubMed]
- de Givenchy, E.T.; Amigoni, S.; Martin, C.; Andrada, G.; Caillier, L.; Géribaldi, S.; Guittard, F. Fabrication of Superhydrophobic PDMS Surfaces by Combining Acidic Treatment and Perfluorinated Monolayers. Langmuir 2009, 25, 6448–6453. [Google Scholar] [CrossRef]
- Marmur, A. Solid-Surface Characterization by Wetting. Annu. Rev. Mater. Res 2009, 39, 473–489. [Google Scholar] [CrossRef]
- Karl, C.W.; Rahimi, W.; Lang, A.; Giese, U.; Klüppel, M.; Geisler, H. Characterization of modified elastomer surfaces by wetting-A review. KGK Rubberpoint 2018, 71, 19–31. [Google Scholar]
- Marmur, A.; Della Volpe, C.; Alidad, S.S.; Jaroslaw, A.; Drelich, W. Contact angles and wettability: Towards common and accurate terminology. Surf. Innov. 2017, 5, 3–8. [Google Scholar] [CrossRef]
- Karl, C.W.; Busse, L.; Klüppel, M. Varnish Coating of Elastomers: Morphology, Friction and Surface Energies. In Proceedings of the 9th Rubber Fall Colloquium, Hanover, Germany, 3–5 November 2010. [Google Scholar]
- Johnson, R.E., Jr.; Dettre, R.H. Contact Angle Hysteresis. In Contact Angle, Wettability and Adhesion; ACS Advances in Chemistry Series, 43; Fowkes, F.M., Ed.; American Chemical Society: Washington, DC, USA, 1964; pp. 112–135. [Google Scholar] [CrossRef]
- Eick, J.D.; Good, R.G.; Neumann, A.W. Thermodynamics of contact angles. II. Rough solid surfaces. J. Colloid Interface Sci. 1975, 53, 235–248. [Google Scholar] [CrossRef]
- Johnson, R.E., Jr.; Dettre, R.H. Contact Angle Hysteresis. J. Phys. Chem. 1964, 68, 1744–1750. [Google Scholar] [CrossRef]
- Neumann, A.W.; Good, R.J.J. Thermodynamics of contact angles. I. Heterogeneous solid surfaces. Colloid Interface Sci. 1972, 38, 341–358. [Google Scholar] [CrossRef]
- Penn, L.S.; Miller, B.J. A study of the primary cause of contact angle hysteresis on some polymeric solids. Colloid Interface Sci. 1980, 78, 238–241. [Google Scholar] [CrossRef]
- Good, R.J. Surface and Colloid Science; Good, R.J., Stromberg, R.R., Eds.; Plenum Press: New York, NY, USA, 1979; Volume 11. [Google Scholar]
- Andrade, J.D.; Smith, L.M.; Gregonis, D.E. Surface and Interfacial Aspects of Biomedical Polymers; Andrade, J.D., Ed.; Plenum Press: New York, NY, USA, 1985; Volume 1, Chapter 7. [Google Scholar]
- Extrand, C.W.; Kumagai, Y. Liquid Drops on an Inclined Plane: The Relation between Contact Angles, Drop Shape, and Retentive Force. J. Colloid Interface Sci. 1995, 170, 515–521. [Google Scholar] [CrossRef]
- Extrand, C.W.; Kumagai, Y. An Experimental Study of Contact Angle Hysteresis. J. Colloid Interface Sci. 1997, 191, 378–383. [Google Scholar] [CrossRef] [PubMed]
- Schulze, R.-D.; Possart, W.; Kamusewitz, H.; Bischof, C. Young’s equilibrium contact angle on rough solid surfaces. Part I. An empirical determination. J. Adhes. Sci. Technol. 1989, 3, 39–48. [Google Scholar] [CrossRef]
- Extrand, C.W.; In Moon, S. Contact Angles on Spherical Surfaces. Langmuir 2008, 24, 9470–9473. [Google Scholar] [CrossRef]
- Montes Ruiz-Cabello, F.J.; Rodríguez-Valverde, M.A.; Cabrerizo-Vilchez, M.A. Contact Angle Hysteresis on Polymer Surfaces: An Experimental Study. J. Adhes. Sci. Technol. 2011, 25, 2039–2049. [Google Scholar] [CrossRef]
- Pericet-Camara, R.; Moraila-Martinez, L.C.; Rodriguez-Valverde, M.A.; Cabrerizo-Vilchez, M.A. Hysteretic behaviour of static and dynamic contact angles on various polymer surfaces: A comparative study. In Proceedings of the Third Iberic Meeting on Colloids and Interfaces, Granada, Spain, 6–9 December 2009. [Google Scholar]
- Strobel, M.; Lyons, C.S. An Essay on Contact Angle Measurements. Plasma Process. Polym. 2011, 8, 8–13. [Google Scholar] [CrossRef]
- Mack, J.L. The Determination of Contact Angles from Measurements of the Dimensions of Small Bubbles and Drops. I. The Spheroidal Segment Method for Acute Angles. J. Phys. Chem. 1936, 40, 159–167. [Google Scholar] [CrossRef]
- Atefi, E.; Mann, J.A.; Tavana, H. A Robust Polynomial Fitting Approach for Contact Angle Measurements. Langmuir 2013, 29, 5677–5688. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.-W.; Lin, S.-Y. A method for correcting the contact angle from the θ/2 method. Colloids Surf. A: Physicochem. Eng. Asp. 2003, 220, 199–210. [Google Scholar] [CrossRef]
- Chen, P.; Kwok, D.Y.; Prokop, R.M.; del Rio, O.I.; Susnar, S.S.; Neumann, A.W. Axisymmetric Drop Shape Analysis (ADSA) and its Applications. Stud. Interface Sci. 1998, 6, 61–138. [Google Scholar]
- Stalder, A.F.; Melchior, T.; Mueller, M.; Sage, D.; Blu, T.; Unser, M. Low-bond axisymmetric drop shape analysis for surface tension and contact angle measurements of sessile drops. Colloids Surf. A 2010, 364, 72–81. [Google Scholar] [CrossRef]
- Konduru, V. Static and Dynamic Contact Angle Measurement on Rough Surfaces Using Sessile Drop Profile Analysis with Application to Water Management in Low Temperature Fuel Cells. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2010. [Google Scholar]
- Vuckovac, M.; Latikka, M.; Liu, K.; Huhtamäkia, T.; Ras, R.H.A. Uncertainties in contact angle goniometry. Soft Matter 2019, 15, 7089–7096. [Google Scholar] [CrossRef]
- Butt, H.-J.; Roisman, I.V.; Brinkmann, M.; Papadopoulos, P.; Vollmer, D.; Semprebon, C. Characterization of super liquid-repellent surfaces. Curr. Opin. Colloid Interface Sci. 2014, 19, 343–354. [Google Scholar] [CrossRef]
- Xu, Z.N. A noise-resistant ADSA-PH algorithm for superhydrophobic surface’s static contact angle evaluation. AIP Adv. 2017, 7, 035210. [Google Scholar] [CrossRef]
- Heib, F.; Schmitt, M. Statistical Contact Angle Analyses with the High-Precision Drop Shape Analysis (HPDSA) Approach: Basic Principles and Applications. Coatings 2016, 6, 57. [Google Scholar] [CrossRef]
- Volpe, C.D.; Siboni, S. The Wilhelmy method: A critical and practical review. Surf. Innov. 2018, 6, 120–132. [Google Scholar] [CrossRef]
- Park, J.; Pasaogullari, U.; Bonville, L. Wettability measurements of irregular shapes with Wilhelmy plate method. Appl. Surf. Sci. 2018, 27, 273–280. [Google Scholar] [CrossRef]
- Karl, C.W.; Klüppel, M. Characterization of Elastomers by Wetting: Roughness and Chemical Heterogeneity. Chem. Listy 2011, 105, 233–234. [Google Scholar]
- Miller, J.D.; Veeramasuneni, S.; Drelich, J.; Yalamanchili, M.R.; Yamauchi, G. Effect of roughness as determined by atomic force microscopy on the wetting properties of PTFE thin films. Polym. Eng. Sci. 1996, 36, 1849–1855. [Google Scholar] [CrossRef]
- Yadav, R.P.; Kumar, T.; Baranwal, V.; Kumar, M.; Priya, P.K.; Pandey, S.N.; Mittal, A.K. Fractal characterization and wettability of ion treated silicon surfaces. J. Appl. Phys. 2017, 121, 055301. [Google Scholar] [CrossRef]
- Jain, R.; Pitchumani, R. Fractal Model for Wettability of Rough Surfaces. Langmuir 2017, 33, 7181–7190. [Google Scholar] [CrossRef] [PubMed]
- ISO 6344-1:1998. Coated Abrasives—Grain Size Analysis—Part 1: Grain Size Distribution Test; ISO: Geneva, Switzerland, 1998. [Google Scholar]
- ISO 6344-2:1998. Coated Abrasives—Grain Size Analysis—Part 2: Determination of Grain Size Distribution of Macrogrits P12 to P220; ISO: Geneva, Switzerland, 1998. [Google Scholar]
- ISO 4287:1997. Geometrical Product Specifications (GPS)–Surface Texture: Profile Method–Terms, Definitions and Surface Texture Parameters; ISO: Geneva, Switzerland, 1997. [Google Scholar]
- Erbil, H.Y. Surface Chemistry of Solid and Liquid Interfaces; Blackwell Publishing: Oxford, UK, 2006. [Google Scholar]
- Volpe, C.D.; Cassinelli, C.; Morra, M. Wilhelmy Plate Measurements on Poly (N-isopropylacrylamide)-Grafted Surfaces. Langmuir 1998, 14, 4650–4656. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Die Fraktale Geometrie der Natur; Birkhäuser-Verlag: Basel, Switzerland, 1991. [Google Scholar]
- Rado, Z. A Study of Road Surface Texture and Its Relationship to Friction. Ph.D. Thesis, Pennsylvania State University, State College, PA, USA, 1994. [Google Scholar]
- Thomas, T.R. Rough Surfaces, 2nd ed.; Imperial College Press: London, UK, 1999. [Google Scholar]
- Klüppel, M.; Heinrich, G. Rubber friction on self-affine road tracks. Rubber Chem. Technol. 2000, 73, 578–606. [Google Scholar] [CrossRef]
- Douketis, C.; Wang, Z.; Haslett, T.L.; Moskovits, M. Fractal character of cold-deposited silver films determined by low-temperature scanning tunneling microscopy. Phys. Rev. B 1995, 51, 11022. [Google Scholar] [CrossRef]
- Zahn, W.; Zösch, A. The dependence of fractal dimension on measuring conditions of scanning probe microscopy. Fresenius’ J. Anal. Chem. 1999, 365, 168–172. [Google Scholar] [CrossRef]
- Zhang, X.; Jackson, R.L. An Analysis of the Multiscale Structure of Surfaces with Various Finishes. Tribol. Trans. 2017, 60, 121–134. [Google Scholar] [CrossRef]
- Nonomura, Y.; Seino, E.; Abe, S.; Mayama, H. Preparation and Characterization of Fractal Elastomer Surfaces. J. Oleo Sci. 2013, 62, 587–590. [Google Scholar] [CrossRef]
- Nezadal, M.; Zmeskal, O.; Buchnicek, M. The Box-Counting: Critical Study; Technical University of Brno, Faculty of Chemistry, Institute of Physical and Applied Chemistry: Brno, Czech Republic, 2001. [Google Scholar]
- Militký, J.; Bajzík, V. Surface Roughness and Fractal Dimension. J. Text. Inst. 2001, 92, 91–113. [Google Scholar] [CrossRef]
- Karl, C.W. Untersuchungen zur Tribologie und zum Benetzungsverhalten von Elastomerkompositen. Ph.D. Thesis, University of Hanover, Hannover, Germany, 2014. [Google Scholar]
- Johnson, R.E.; Dettre, R.H. Wettability and contact angle. In Surface and Colloid Science; Matijevic, E., Ed.; Wiley-Interscience: New York, NY, USA, 1969; Volume 2, pp. 85–153. [Google Scholar]
- Tavana, H.; Yang, G.; Yip, C.M.; Appelhans, D.; Zschoche, S.; Grundke, K.; Hair, M.L.; Neumann, W.A. Stick−Slip of the Three-Phase Line in Measurements of Dynamic Contact Angles. Langmuir 2006, 22, 628–636. [Google Scholar] [CrossRef] [PubMed]
- Kopczynska, A. Oberflächenspannungsphänomene bei Kunststoffen–Bestimmung und Anwendung. Ph.D. Thesis, University of Erlangen, Erlangen, Germany, 2008. [Google Scholar]
- Orejon, D.; Sefiane, K.; Shanahan, M.E.R. Stick–Slip of Evaporating Droplets: Substrate Hydrophobicity and Nanoparticle Concentration. Langmuir 2011, 27, 12834–12843. [Google Scholar] [CrossRef] [PubMed]
| Sample (side) | [µm] | [µm] | [-] |
|---|---|---|---|
| PTFE unmodified (A) | 5.57 | 31.21 | 2.56 |
| PTFE unmodified (B) | 1.78 | 171.95 | 2.71 |
| PTFE 2000 (A) | 6.32 | 21.61 | 2.50 |
| PTFE 2000 (B) | 7.15 | 91.74 | 2.51 |
| PTFE 1000 (A) | 5.31 | 54.73 | 2.44 |
| PTFE 1000 (B) | 5.08 | 49.61 | 2.44 |
| PTFE 400 (A) | 8.86 | 44.74 | 2.40 |
| PTFE 400 (B) | 8.83 | 45.29 | 2.40 |
| PTFE 240 (A) | 17.88 | 48.39 | 2.38 |
| PTFE 240 (B) | 16.51 | 48.11 | 2.41 |
| PTFE 60 (A) | 53.63 | 235.98 | 2.18 |
| PTFE 60 (B) | 54.99 | 222.79 | 2.20 |
| PTFE 30 (A) | 77.95 | 425.35 | 2.25 |
| PTFE 30 (B) | 78.15 | 288.12 | 2.19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karl, C.W.; Krauklis, A.E.; Lang, A.; Giese, U. Characterization of Rough PTFE Surfaces by the Modified Wilhelmy Balance Technique. Polymers 2020, 12, 1528. https://doi.org/10.3390/polym12071528
Karl CW, Krauklis AE, Lang A, Giese U. Characterization of Rough PTFE Surfaces by the Modified Wilhelmy Balance Technique. Polymers. 2020; 12(7):1528. https://doi.org/10.3390/polym12071528
Chicago/Turabian StyleKarl, Christian W., Andrey E. Krauklis, Andrej Lang, and Ulrich Giese. 2020. "Characterization of Rough PTFE Surfaces by the Modified Wilhelmy Balance Technique" Polymers 12, no. 7: 1528. https://doi.org/10.3390/polym12071528
APA StyleKarl, C. W., Krauklis, A. E., Lang, A., & Giese, U. (2020). Characterization of Rough PTFE Surfaces by the Modified Wilhelmy Balance Technique. Polymers, 12(7), 1528. https://doi.org/10.3390/polym12071528








