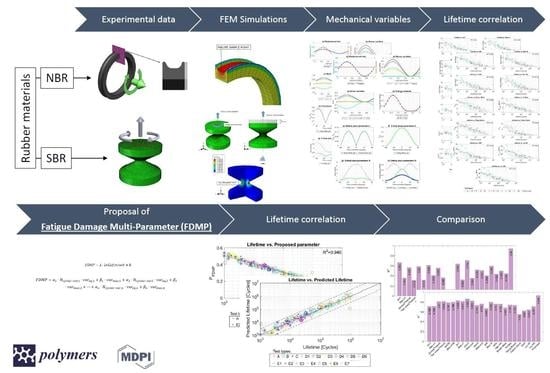
A New Multiparameter Model for Multiaxial Fatigue Life Prediction of Rubber Materials
Abstract
1. Introduction
2. State-of-the-Art Review of Fatigue Damage Parameters for Rubber Materials
2.1. Fatigue Damage Parameters Based on Stresses, Strains, and Energy
2.2. Fatigue Damage Parameters Based on the Critical Plane
2.2.1. Cracking Energy Density (CED)
2.2.2. Fatemi-Socie Parameter
2.2.3. Smith–Watson–Topper Parameter
2.2.4. Liu I and Liu II Parameters
2.2.5. Findley Parameter
2.2.6. Brown –Miller Parameter
2.2.7. Wang –Brown Parameter
2.2.8. McDiarmid Parameter
3. Proposed Fatigue Damage Multi-Parameter (FDMP) for Multiaxial Fatigue Analysis
3.1. Proposed Fatigue Multi-Parameter
- αi: Weights for each variable (amplitude and mean value) taken into account
- βi: Weights for each variable (maximum value) taken into account
- Ncycles-var,i: Number of cycles experienced by variable i during one load cycle.
- The value of vareq,i is defined in Equations (13) and (14):
- γi: Coefficient in order to take into account the mean value of each variable
3.2. Methodology for Validation of the Proposed Model (FDMP)
- Numerical simulation of each of the tests for each of the specimens and each of the materials.
- Obtaining and calculation of the evolution of 20 mechanical variables throughout a load cycle.
- Calculation of the number of cycles, amplitude, maximum value, and average value of each variable for each load cycle.
- Correlation of the calculated values with the fatigue life of each material and obtaining the parameter R2.
- Calculation of weights and coefficients for the model proposed in this work for each of the test batteries.
- Application of the proposed model, correlation with the fatigue life of each material and obtaining the parameter R2.
- Comparison of the R2 parameters of all the fatigue variables considered.
- The obtained results are analysed in detail in Section 7: Discussion.
3.3. Experimental Data for Model Validation
3.3.1. Mars and Fatemi Experimental Data Description (NBR Tests)
3.3.2. Ayoub Experimental Data Description (SBR Tests)
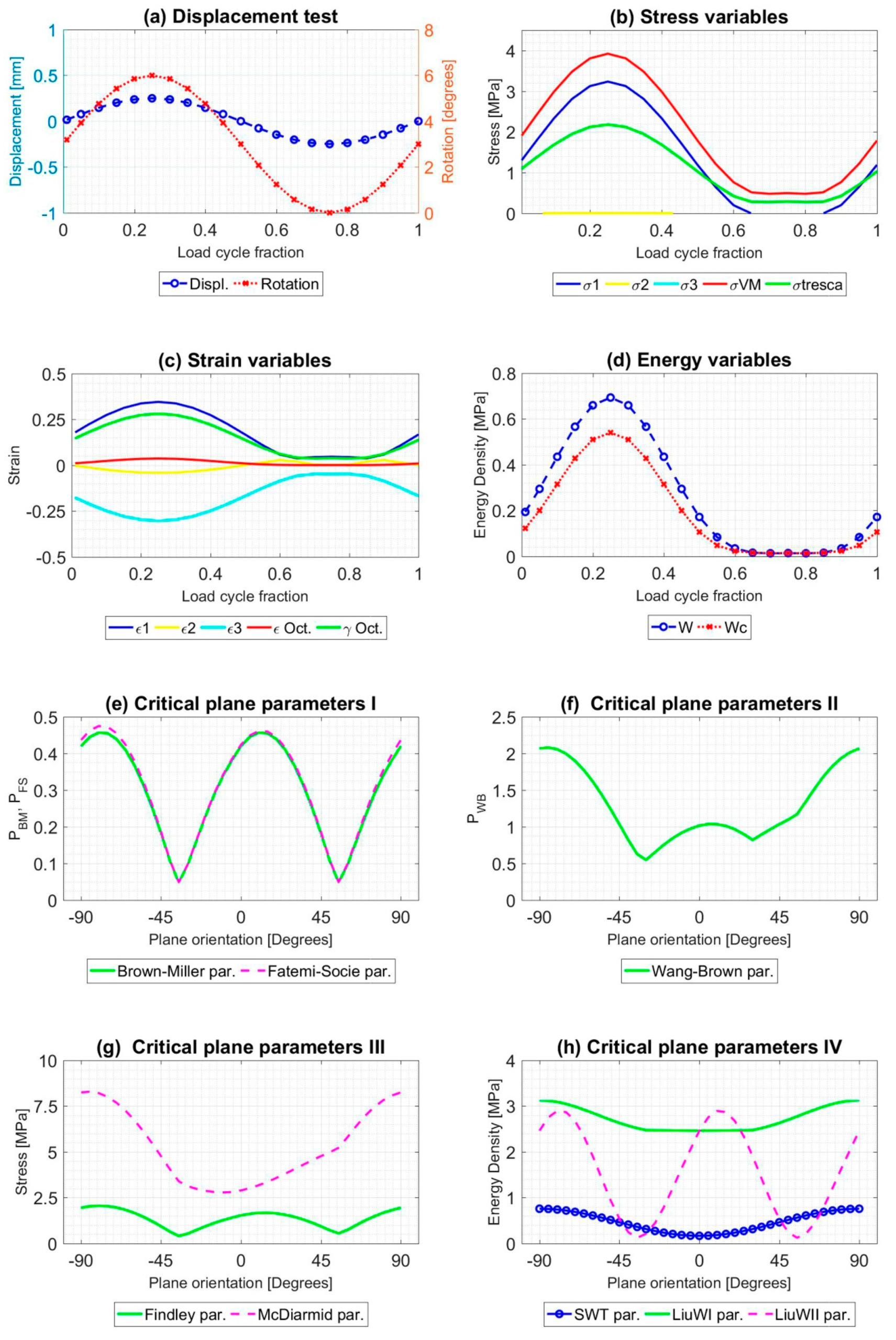
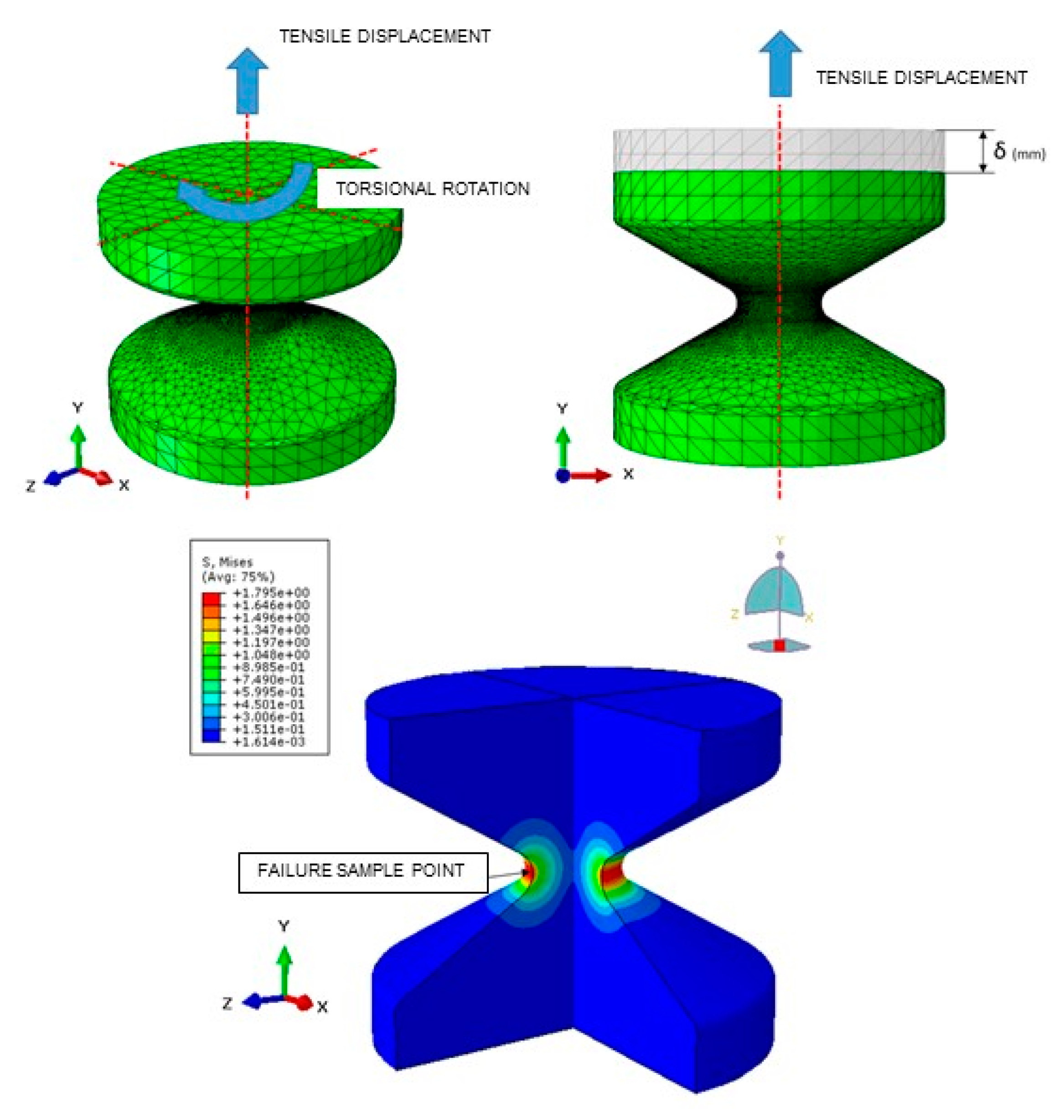
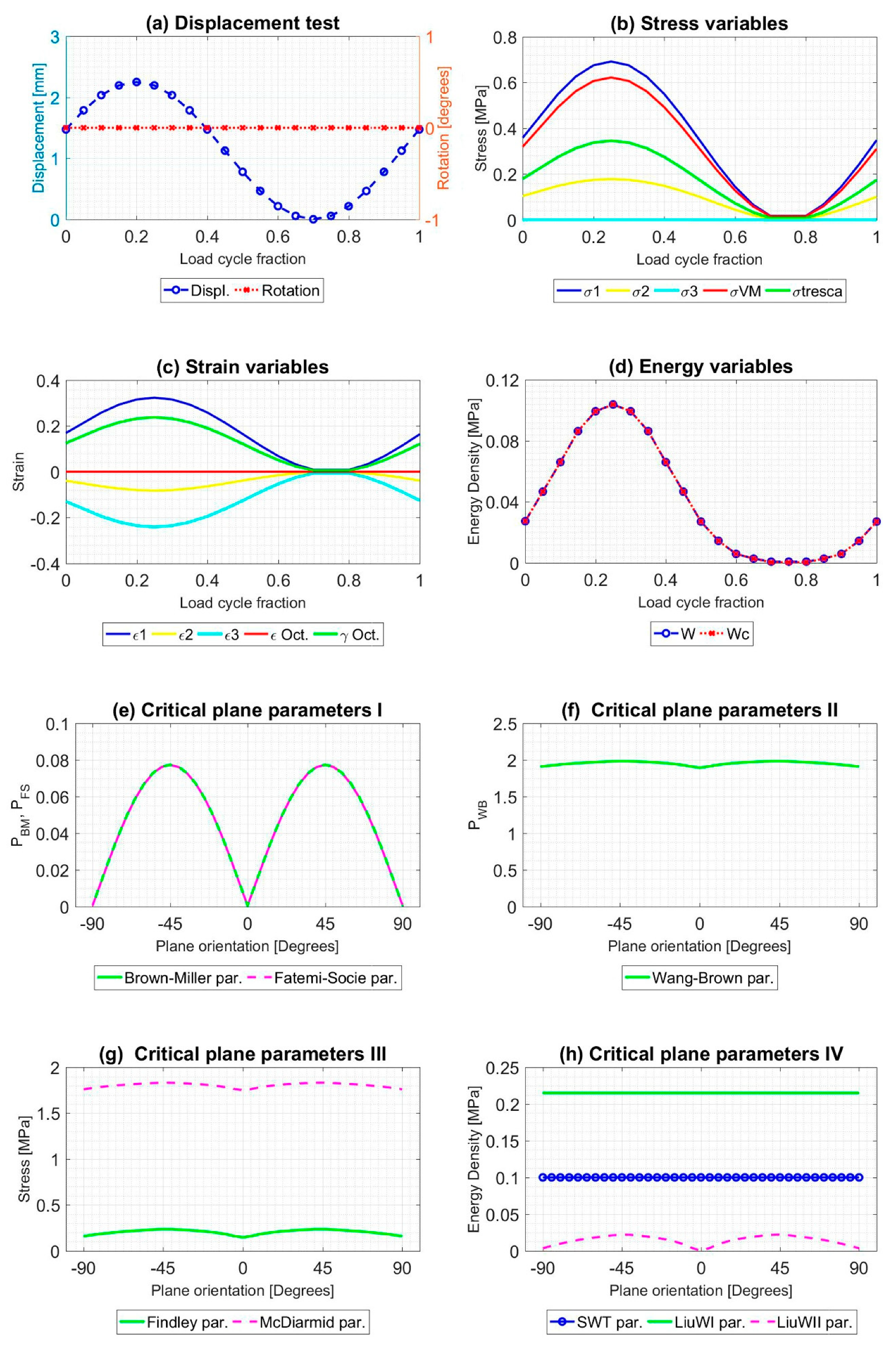
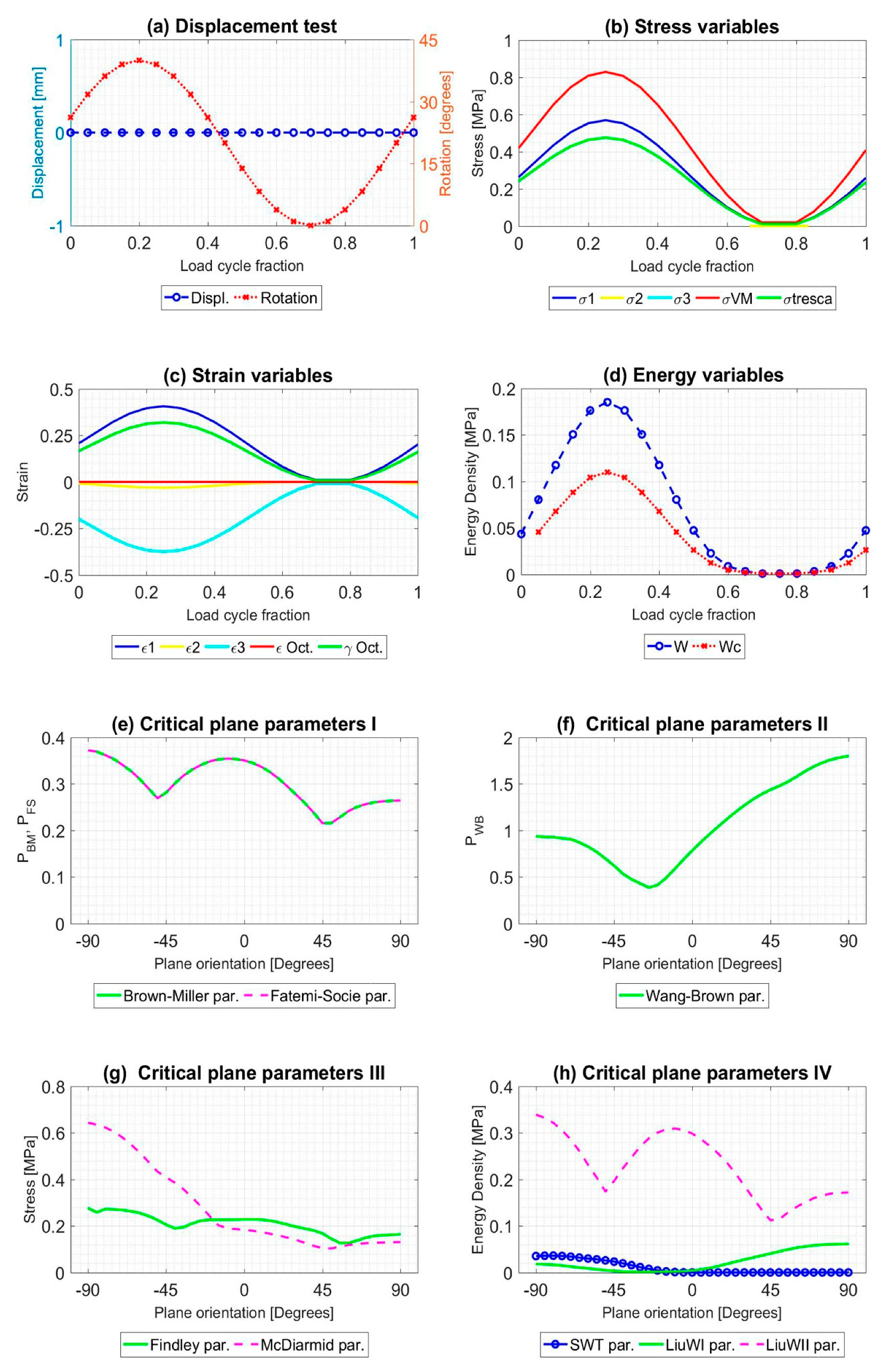
4. Numerical Simulations and Results
4.1. NBR Numerical Simulations and Results
4.2. SBR Numerical Simulations and Results
5. Fatigue Lifetime Correlation
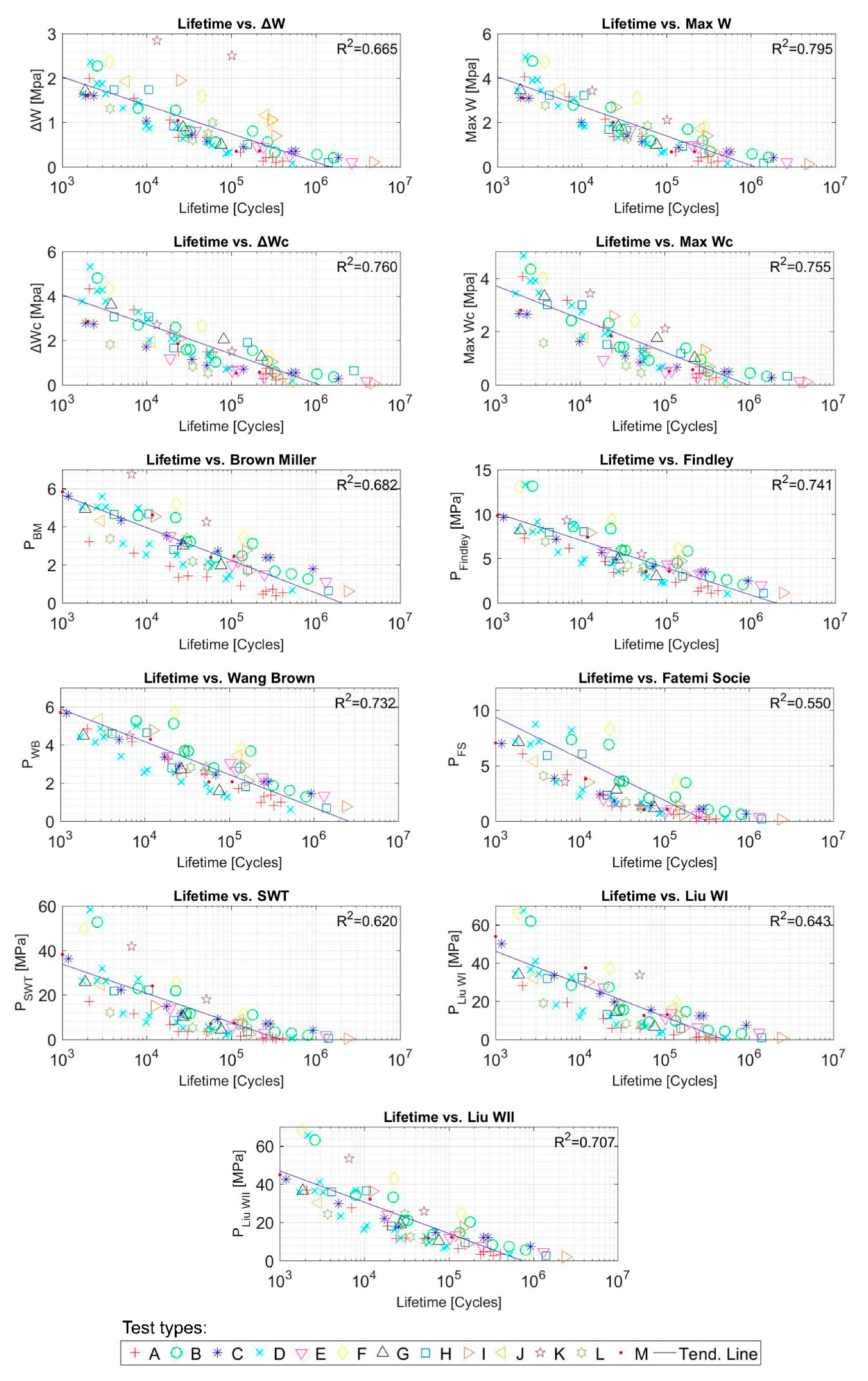
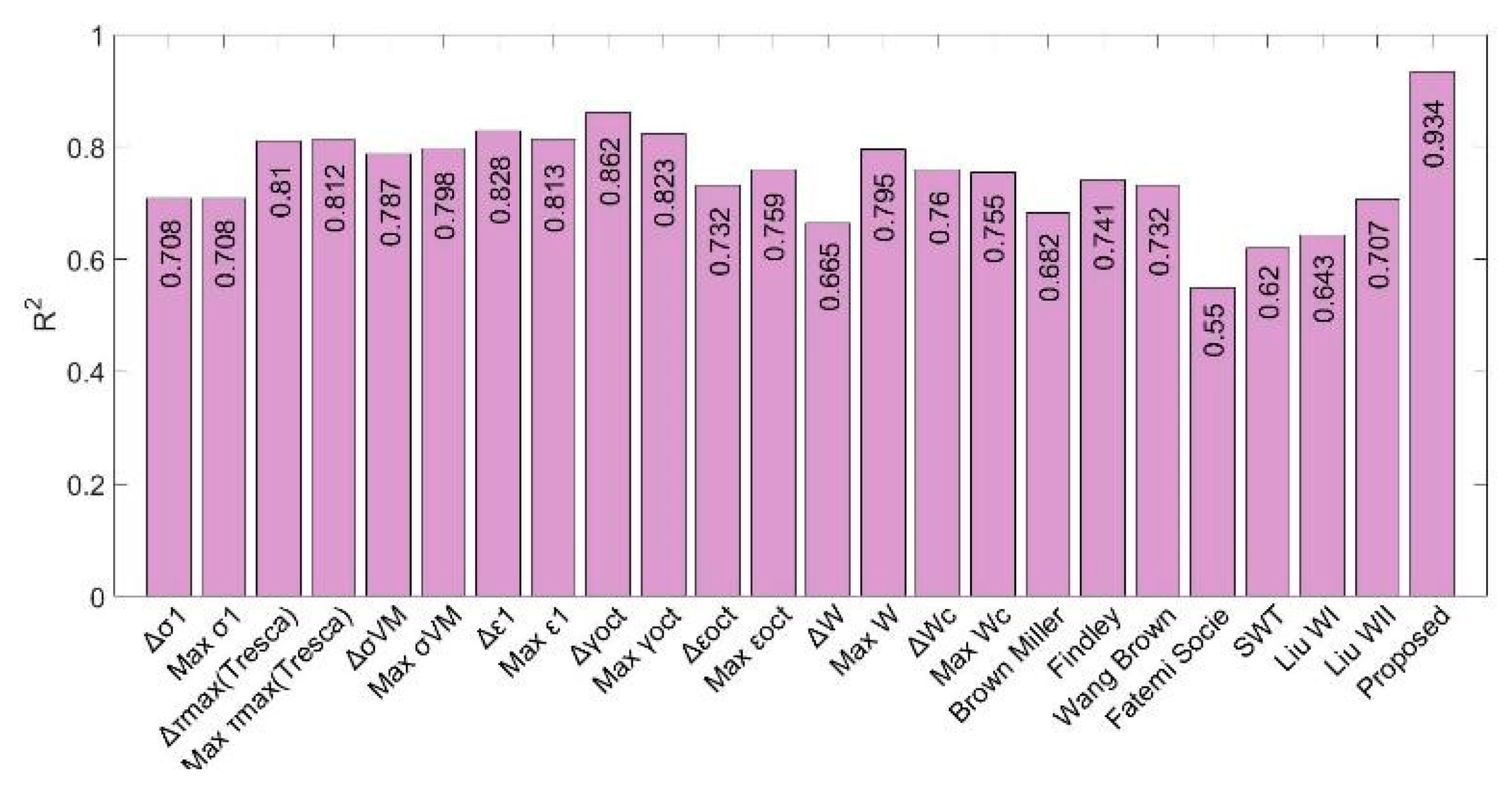
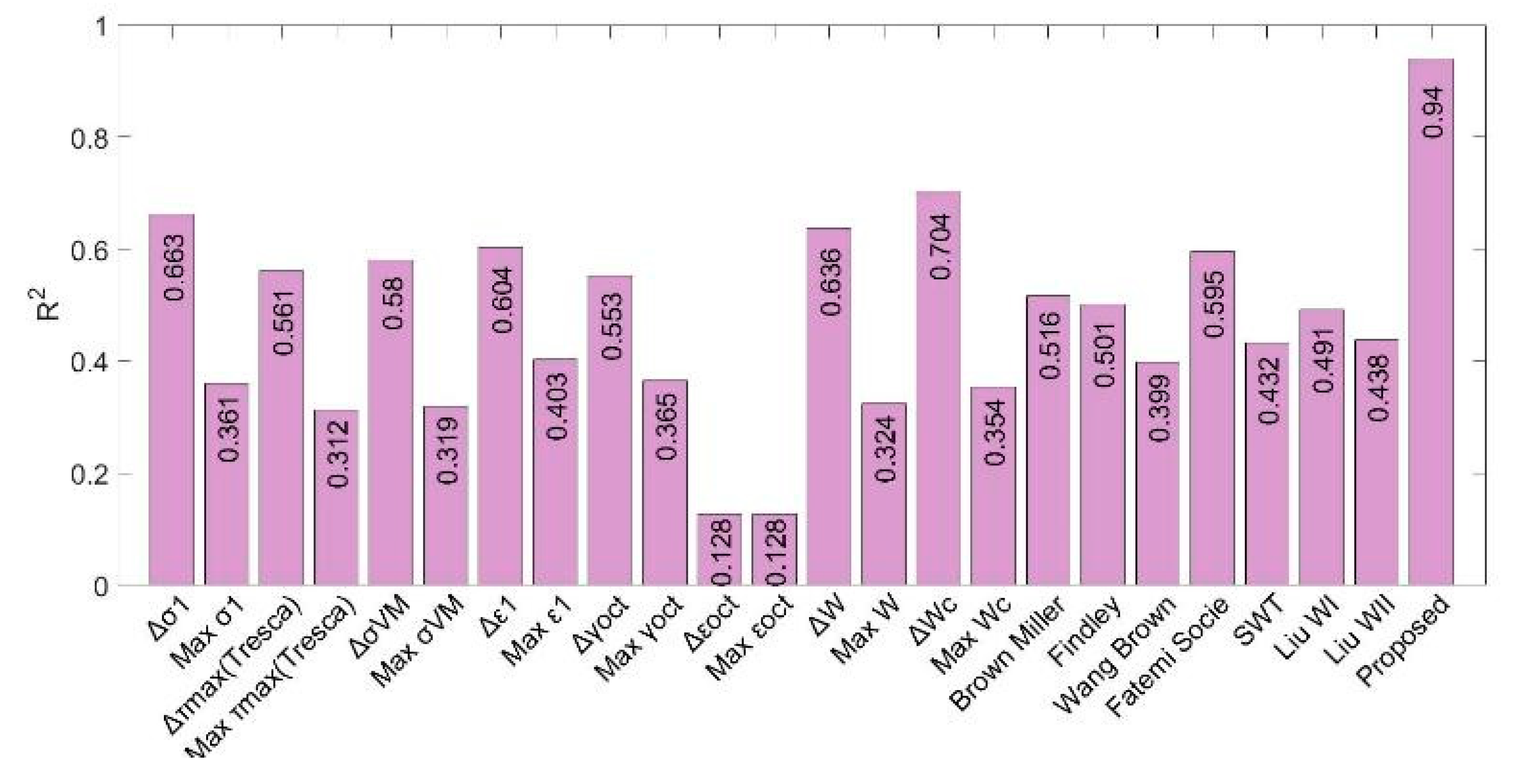
5.1. NBR–Fatigue Parameters Correlation
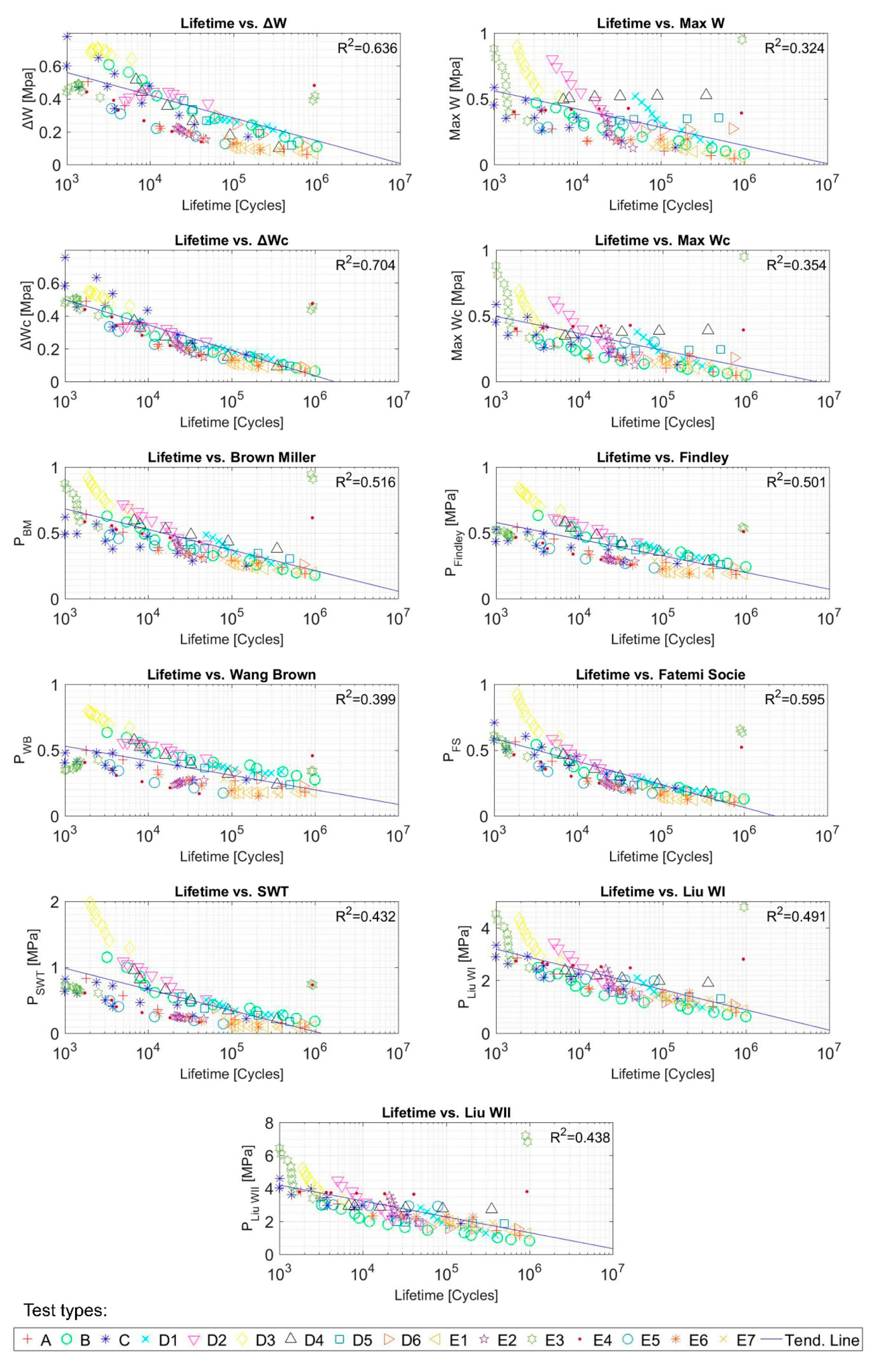
5.2. SBR–Fatigue Parameters Correlation
6. Application of the Proposed Fatigue Damage Multi-Parameter (FDMP)
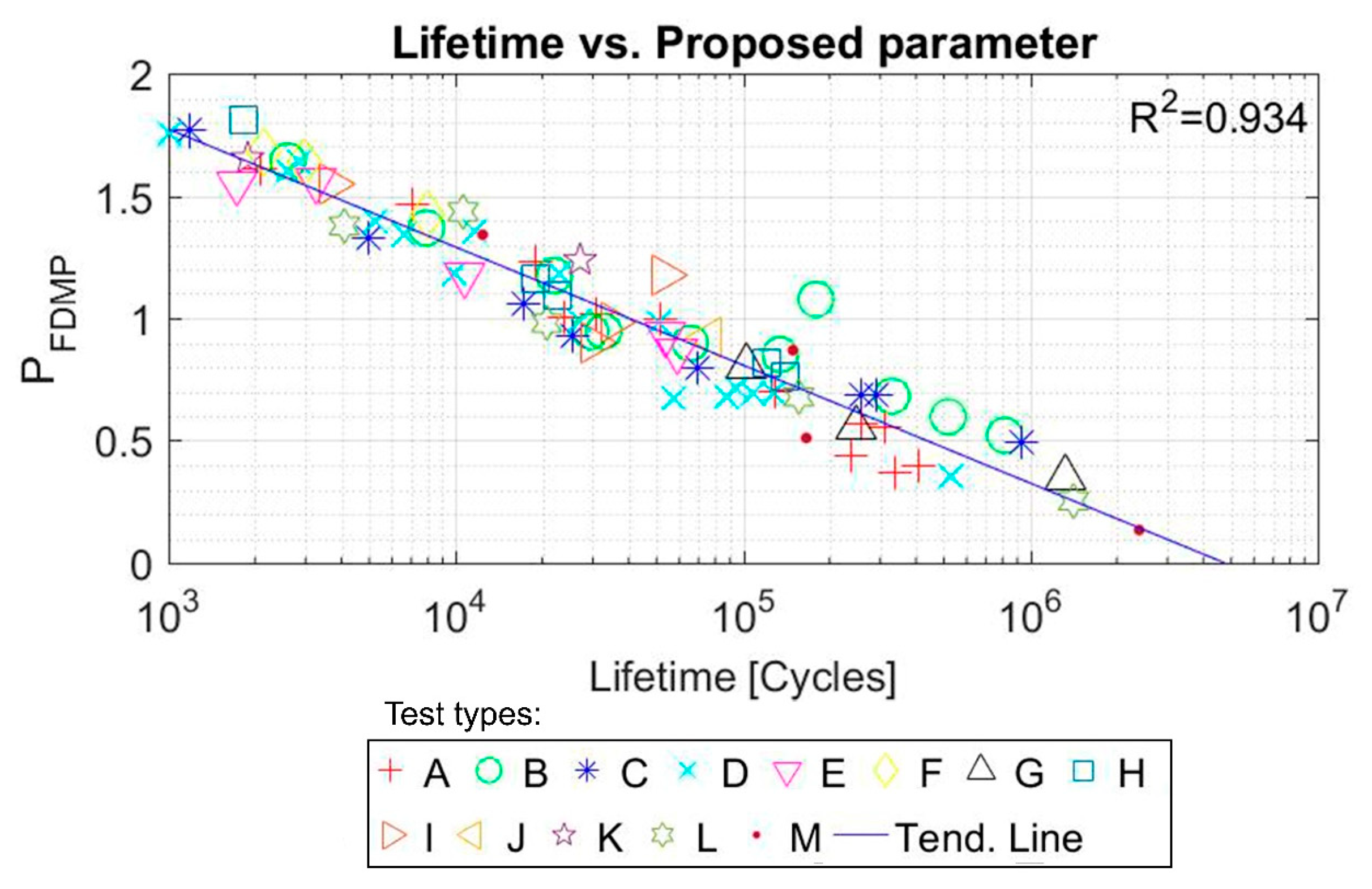
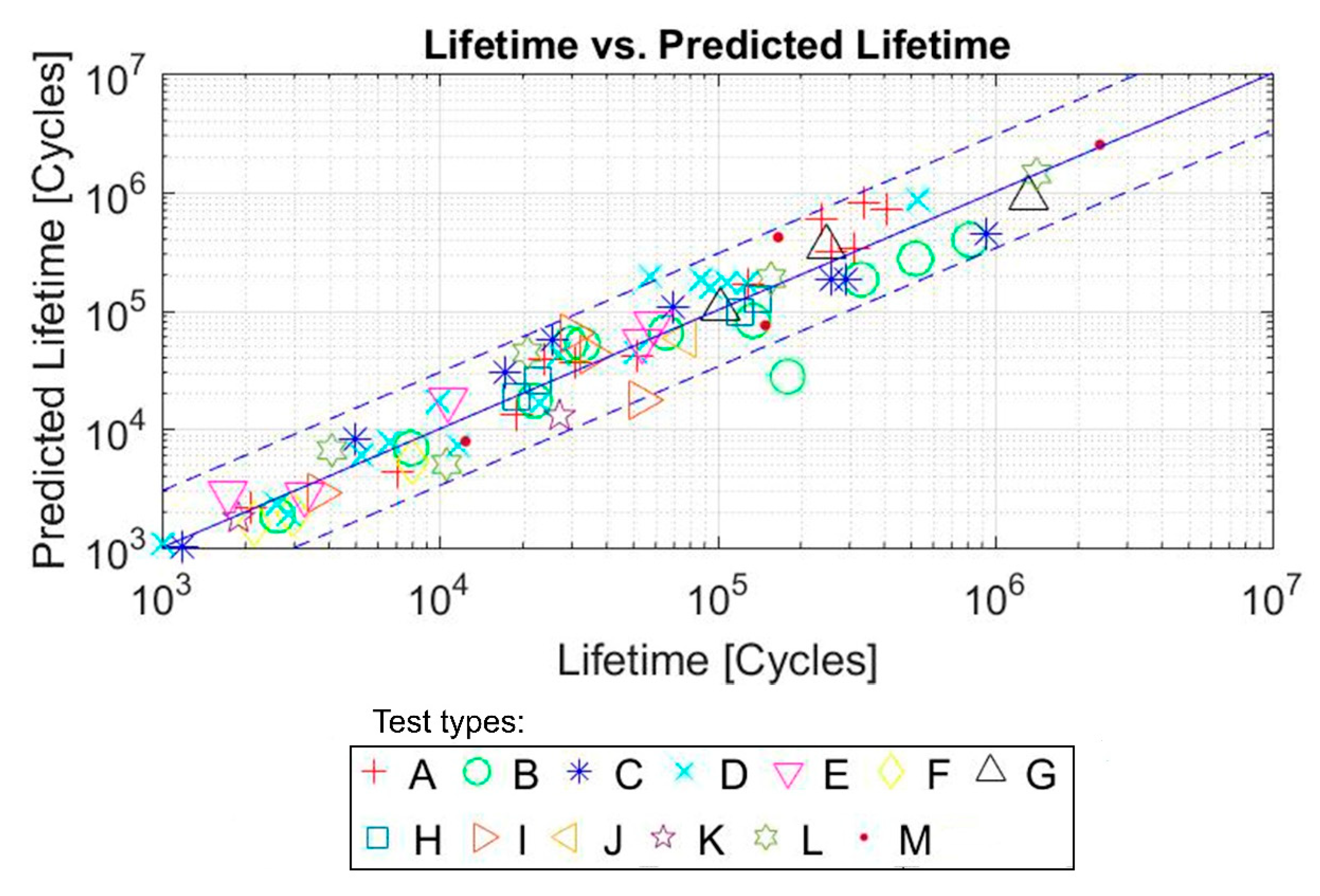
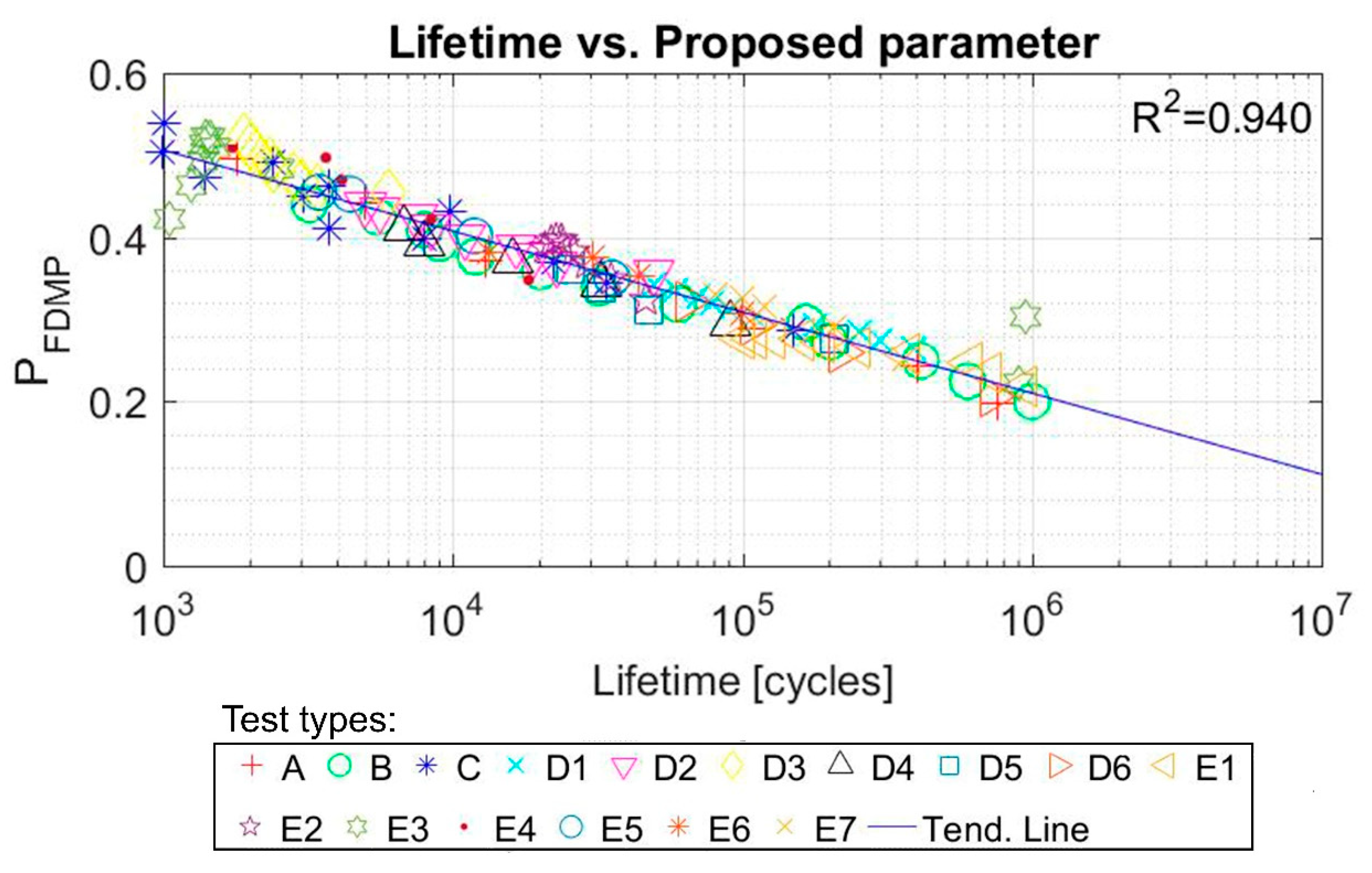
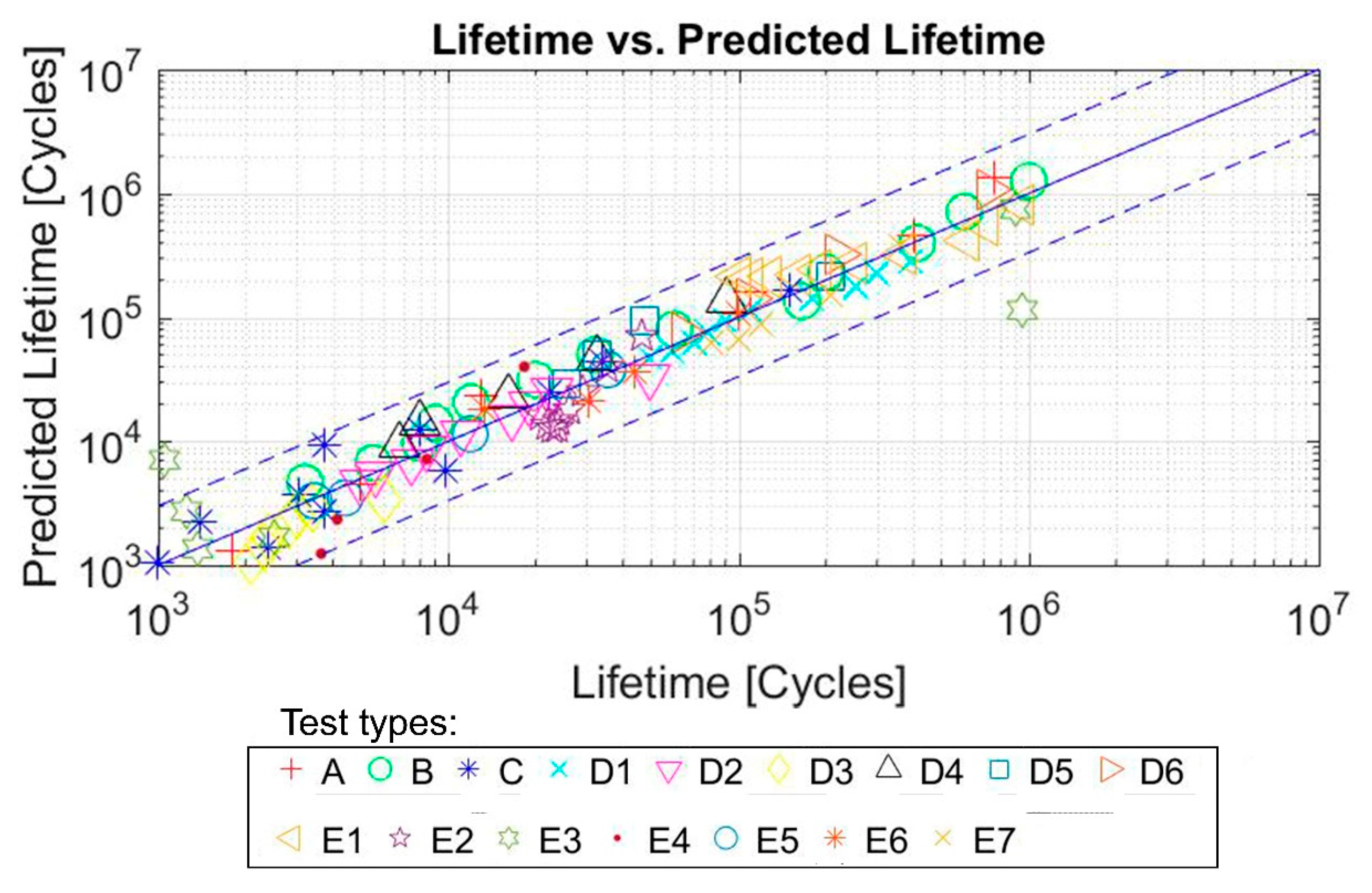
6.1. NBR – FDMP Results
6.2. SBR–FDMP Results
7. Discussion
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CED | Cracking Energy Density |
| FDMP | Fatigue Damage Multi-Parameter |
| FEM | Finite Element Method |
| HCF | High Cycle Fatigue |
| NBR | Acrylonitrile Butadiene Rubber |
| NR | Natural Rubber |
| PBM | Brown-Miller parameter |
| PFS | Fatemi-Socie parameter |
| PWB | Wang-Brown parameter |
| R2 | Coefficient of determination |
| SBR | Styrene-Butadiene Rubber |
| SED | Strain Energy Density |
| SWT | Smith-Watson-Topper |
References
- Dufton, P.W. Thermoplastic Elastomers; Smithers Rapra Publishing: Shrewsbury, UK, 2001. [Google Scholar]
- Delogu, M.; Del Pero, F.; Pierini, M. Lightweight design solutions in the automotive field: Environmental modelling based on fuel reduction value applied to diesel turbocharged vehicles. Sustainability 2016, 8, 1167. [Google Scholar] [CrossRef]
- Koltzenburg, S.; Maskos, M.; Nuyken, O. Elastomers. In Polymer Chemistry; Springer: Berlin/Heidelberg, Germany, 2017; pp. 477–491. ISBN 978-3-662-49279-6. [Google Scholar]
- Ciampa, F.; Mahmoodi, P.; Pinto, F.; Meo, M. Recent advances in active infrared thermography for non-destructive testing of aerospace components. Sensors 2018, 18, 609. [Google Scholar] [CrossRef] [PubMed]
- Markl, E.; Lackner, M. Devulcanization technologies for recycling of tire-derived rubber: A review. Materials 2020, 13, 1246. [Google Scholar] [CrossRef] [PubMed]
- Araujo-Morera, J.; Santana, M.H.; Verdejo, R.; López-Manchado, M.A. Giving a second opportunity to tire waste: An alternative path for the development of sustainable self-healing styrene-butadiene rubber compounds overcoming the magic triangle of tires. Polymers 2019, 11, 2122. [Google Scholar] [CrossRef] [PubMed]
- Buss, A.H.; Kovaleski, J.L.; Pagani, R.N.; da Silva, V.L.; de Silva, J.M. Proposal to reuse rubber waste from end-of-life tires using thermosetting resin. Sustainability 2019, 11, 6997. [Google Scholar] [CrossRef]
- Rodgers, B. Rubber Compounding: Chemistry and Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Szczypinski-Sala, W.; Lubas, J. Tribological characteristic of a ring seal with graphite filler. Materials 2020, 13, 311. [Google Scholar] [CrossRef]
- Liang, B.; Yang, X.; Wang, Z.; Su, X.; Liao, B.; Ren, Y.; Sun, B. Influence of randomness in rubber materials parameters on the reliability of rubber O-ring seal. Materials 2019, 12, 1566. [Google Scholar] [CrossRef]
- Yoon, S.H.; Winters, M.; Siviour, C.R. High strain-rate tensile characterization of EPDM rubber using non-equilibrium loading and the virtual fields method. Exp. Mech. 2016, 56, 25–35. [Google Scholar] [CrossRef]
- Arghavan, A.; Kashyzadeh, K.R.; Asfarjani, A.A. Investigating effect of industrial coatings on fatigue damage. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Kapellweg, Switzerland, 2011. [Google Scholar]
- Gobbato, M.; Kosmatka, J.B.; Conte, J.P. A recursive bayesian approach for fatigue damage prognosis: An experimental validation at the reliability component level. Mech. Syst. Signal Process. 2014. [Google Scholar] [CrossRef]
- Pfingstl, S.; Steiner, M.; Tusch, O.; Zimmermann, M. Crack detection zones: Computation and validation. Sensors 2020, 20, 2568. [Google Scholar] [CrossRef]
- Seichter, S.; Archodoulaki, V.M.; Koch, T.; Holzner, A.; Wondracek, A. Investigation of different influences on the fatigue behaviour of industrial rubbers. Polym. Test. 2017. [Google Scholar] [CrossRef]
- Abdelaziz, N.M.; Ayoub, G.; Colin, X.; Benhassine, M.; Mouwakeh, M. New developments in fracture of rubbers: Predictive tools and influence of thermal aging. Int. J. Solids Struct. 2019. [Google Scholar] [CrossRef]
- Neuhaus, C.; Lion, A.; Johlitz, M.; Heuler, P.; Barkhoff, M.; Duisen, F. Fatigue behaviour of an elastomer under consideration of ageing effects. Int. J. Fatigue 2017. [Google Scholar] [CrossRef]
- Duan, X.; Shangguan, W.B.; Li, M.; Rakheja, S. Measurement and modelling of the fatigue life of rubber mounts for an automotive powertrain at high temperatures. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016. [Google Scholar] [CrossRef]
- Loo, M.S.; Le Cam, J.B.; Andriyana, A.; Robin, E.; Coulon, J.F. Effect of swelling on fatigue life of elastomers. Polym. Degrad. Stab. 2016. [Google Scholar] [CrossRef]
- Ruellan, B.; Le Cam, J.B.; Jeanneau, I.; Canévet, F.; Mortier, F.; Robin, E. Fatigue of natural rubber under different temperatures. Int. J. Fatigue 2019. [Google Scholar] [CrossRef]
- Zhou, Y.; Jerrams, S.; Betts, A.; Farrell, G.; Chen, L. The influence of particle content on the equi-biaxial fatigue behaviour of magnetorheological elastomers. Mater. Des. 2015. [Google Scholar] [CrossRef]
- Spagnoli, A.; Terzano, M.; Brighenti, R.; Artoni, F.; Carpinteri, A. How soft polymers cope with cracks and notches. Appl. Sci. 2019, 9, 1086. [Google Scholar] [CrossRef]
- Guo, H.; Li, F.; Wen, S.; Yang, H.; Zhang, L. Characterization and quantitative analysis of crack precursor size for rubber composites. Materials 2019, 12, 3442. [Google Scholar] [CrossRef]
- Li, F.; Liu, J.; Mars, W.V.; Chan, T.W.; Lu, Y.; Yang, H.; Zhang, L. Crack precursor size for natural rubber inferred from relaxing and non-relaxing fatigue experiments. Int. J. Fatigue 2015. [Google Scholar] [CrossRef]
- Wada, S.; Zhang, R.; Mannava, S.R.; Vasudevan, V.K.; Qian, D. Simulation-based prediction of cyclic failure in rubbery materials using nonlinear space-time finite element method coupled with continuum damage mechanics. Finite Elem. Anal. Des. 2018. [Google Scholar] [CrossRef]
- Nyaaba, W.; Frimpong, S.; Anani, A. Fatigue damage investigation of ultra-large tire components. Int. J. Fatigue 2019. [Google Scholar] [CrossRef]
- Feng, X.; Li, Z.; Wei, Y.; Chen, Y.; Kaliske, M.; Zopf, C.; Behnke, R. A novel method for constitutive characterization of the mechanical properties of uncured rubber. J. Elastomers Plast. 2016, 48, 523–534. [Google Scholar] [CrossRef]
- Carleo, F.; Barbieri, E.; Whear, R.; Busfield, J.J.C. Limitations of viscoelastic constitutive models for carbon-black reinforced rubber in medium dynamic strains and medium strain rates. Polymers 2018, 10, 988. [Google Scholar] [CrossRef] [PubMed]
- Mars, W.V.; Ellul, M.D. Fatigue characterization of a thermoplastic elastomer. Rubber Chem. Technol. 2017. [Google Scholar] [CrossRef]
- Cruanes, C.; Lacroix, F.; Berton, G.; Méo, S.; Ranganathan, N. Study of the fatigue behavior of a synthetic rubber undergoing cumulative damage tests. Int. J. Fatigue 2016. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, X.; Gu, B. Modeling and experimental validation of interfacial fatigue damage in fiber-reinforced rubber composites. Polym. Eng. Sci. 2018. [Google Scholar] [CrossRef]
- Luo, P.; Yao, W.; Wang, Y.; Li, P. A survey on fatigue life analysis approaches for metallic notched components under multi-axial loading. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 3870–3890. [Google Scholar] [CrossRef]
- Narynbek, U.K.; Huneau, B.; Verron, E.; Béranger, A.S.; Heuillet, P. True stress controlled fatigue life experiments for elastomers. Int. J. Fatigue 2017. [Google Scholar] [CrossRef]
- Sun, C.; Du, Z.; Nagarajan, S.; Zhao, H.; Wen, S.; Zhao, S.; Zhang, P.; Zhang, L. Impact of uniaxial tensile fatigue on the evolution of microscopic and mesoscopic structure of carbon black filled natural rubber. R. Soc. Open Sci. 2019. [Google Scholar] [CrossRef]
- Gehrmann, O.; El Yaagoubi, M.; El Maanaoui, H.; Meier, J. Lifetime prediction of simple shear loaded filled elastomers based on the probability distribution of particles. Polym. Test. 2019. [Google Scholar] [CrossRef]
- Mars, W.V.; Fatemi, A. A literature survey on fatigue analysis approaches for rubber. Int. J. Fatigue 2002, 24, 949–961. [Google Scholar] [CrossRef]
- Moon, B.; Lee, J.; Park, S.; Seok, C.S. Study on the aging behavior of natural rubber/butadiene rubber (NR/BR) blends using a parallel spring model. Polymers 2018, 10, 658. [Google Scholar] [CrossRef]
- Zhang, J.; Xue, F.; Wang, Y.; Zhang, X.; Han, S. Strain energy-based rubber fatigue life prediction under the influence of temperature. R. Soc. Open Sci. 2018. [Google Scholar] [CrossRef] [PubMed]
- Poulain, X.; Lefèvre, V.; Lopez-Pamies, O.; Ravi-Chandar, K. Damage in elastomers: Nucleation and growth of cavities, micro-cracks, and macro-cracks. Int. J. Fract. 2017. [Google Scholar] [CrossRef]
- Huneau, B.; Masquelier, I.; Marco, Y.; Le Saux, V.; Noizet, S.; Schiel, C.; Charrier, P. Fatigue crack initiation in a carbon black-filled natural rubber. Rubber Chem. Technol. 2016. [Google Scholar] [CrossRef]
- Rubio-Mateos, A.; Rivero, A.; Ukar, E.; Lamikiz, A. Influence of elastomer layers in the quality of aluminum parts on finishing operations. Metals 2020, 10, 289. [Google Scholar] [CrossRef]
- Lei, T.; Zhang, Y.-W.; Kuang, D.-L.; Yang, Y.-R. Preparation and properties of rubber blends for high-damping-isolation bearings. Polymers 2019, 11, 1374. [Google Scholar] [CrossRef]
- Zanchet, A. Elastomeric composites containing SBR industrial scraps devulcanized by microwaves: Raw material, not a trash. Recycling 2020, 5, 3. [Google Scholar] [CrossRef]
- Shen, M.-Y.; Chiou, Y.-C.; Tan, C.-M.; Wu, C.-C.; Chen, W.-J. Effect of wall thickness on stress-strain response and buckling behavior of hollow-cylinder rubber fenders. Materials 2020, 13, 1170. [Google Scholar] [CrossRef]
- Fatemi, A.; Mars, W.V. Multiaxial fatigue of rubber: Part II: Experimental observations and life predictions. Fatigue Fract. Eng. Mater. Struct. 2005, 28, 523–538. [Google Scholar]
- Ayoub, G.; Naït-Abdelaziz, M.; Zaïri, F.; Gloaguen, J.M.; Charrier, P. Fatigue life prediction of rubber-like materials under multiaxial loading using a continuum damage mechanics approach: Effects of two-blocks loading and R ratio. Mech. Mater. 2012. [Google Scholar] [CrossRef]
- Lu, C. Etude du Comportement Mécanique et des Mécanismes D’endommagement des Élastomères en Fatigue et en Fissuration Par Fatigue. Ph.D. Thesis, CNAM, Paris, France, 1991. [Google Scholar]
- Abraham, F.; Alshuth, T.; Jerrams, S. The effect of minimum stress and stress amplitude on the fatigue life of non strain crystallising elastomers. Mater. Des. 2005, 26, 239–245. [Google Scholar] [CrossRef]
- André, N.; Cailletaud, G.; Piques, R. Others haigh diagram for fatigue crack initiation prediction of natural rubber components. Kautsch. Gummi Kunstst. 1999, 52, 120–123. [Google Scholar]
- Andre, N. Critère local d’amorçage de fissure en fatigue dans un élastomère de type NR. Ph.D. Thesis, Ecole Nationale Supérieure des Mines de Paris, Paris, France, 1999. [Google Scholar]
- Shaker, R.; Rodrigue, D. Rotomolding of thermoplastic elastomers based on low-density polyethylene and recycled natural rubber. Appl. Sci. 2019, 9, 5430. [Google Scholar] [CrossRef]
- Wang, W.T.; Xiao, S.H.; Huang, J.L.; Xie, X.X. Investigation on rubber isolator’s fatigue life prediction under uniaxial tensile load. Zhendong Yu Chongji J. Vib. Shock 2014. [Google Scholar] [CrossRef]
- Woo, C.S.; Kim, W.D.; Kwon, J. Do a study on the material properties and fatigue life prediction of natural rubber component. Mater. Sci. Eng. A 2008. [Google Scholar] [CrossRef]
- Suryatal, B.; Phakatkar, H.; Rajkumar, K.; Thavamani, P. Fatigue life estimation of an elastomeric pad by ε-N curve and FEA. J. Surf. Eng. Mater. Adv. Technol. 2015. [Google Scholar] [CrossRef]
- Li, Q.; Wen, Z.-W.; He, G.; Yuan, M.-H.; Zhu, W.-D. Fatigue life prediction of a rubber mount based on the continuum damage mechanics. J. Macromol. Sci. Part B 2019, 58, 947–958. [Google Scholar] [CrossRef]
- Roberts, B.J.; Benzies, J.B. The relationship between uniaxial and equibiaxial fatigue in gum and carbon black filled vulcanizates. Proc. Rubbercon 1977, 77, 1–2. [Google Scholar]
- Greensmith, H.W.; Mullins, L.; Thomas, A.G. The Chemistry and Physics of Rubber Like Substances; Wiley: New York, NY, USA, 1963. [Google Scholar]
- Mars, W.V.; Fatemi, A. Multiaxial fatigue of rubber: Part I: Equivalence criteria and theoretical aspects. Fatigue Fract. Eng. Mater. Struct. 2005, 28, 515–522. [Google Scholar] [CrossRef]
- Mars, W.V.; Fatemi, A. Criteria for fatigue crack nucleation in rubber under multiaxial loading. Const. Model. Rubber 2001, 2, 213–222. [Google Scholar]
- Peng, Y.; Liu, G.; Quan, Y.; Zeng, Q. Cracking energy density calculation of hyperelastic constitutive model and its application in rubber fatigue life estimations. J. Appl. Polym. Sci. 2016. [Google Scholar] [CrossRef]
- Verron, E. Prediction of fatigue crack initiation in rubber with the help of configurational mechanics. In Constitutive Models for Rubber-Proceedings; CRC Press: Boca Raton, FL, USA, 2005; Volume 4, p. 3. [Google Scholar]
- Verron, E.; Le Cam, J.-B.; Gornet, L. A multiaxial criterion for crack nucleation in rubber. Mech. Res. Commun. 2006, 33, 493–498. [Google Scholar] [CrossRef]
- Barbash, K.P.; Mars, W.V. Critical plane analysis of rubber bushing durability under road loads. In Proceedings of the SAE World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2016. [Google Scholar]
- Mars, W.V.; Wei, Y.; Hao, W.; Bauman, M.A. Computing tire component durability via critical plane analysis. Tire Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Fatemi, A.; Socie, D.F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 149–165. [Google Scholar] [CrossRef]
- Smith, K.; Topper, T.H.; Watson, P. A stress-strain function for the fatigue of metals (Stress-strain function for metal fatigue including mean stress effect). J. Mater. 1970, 5, 767–778. [Google Scholar]
- Liu, K.C. A method based on virtual strain-energy parameters for multiaxial fatigue life prediction. In Advances in Multiaxial Fatigue; ASTM International: West Conshohocken, PA, USA, 1993. [Google Scholar]
- Findley, W.N. Fatigue of Metals Under Combinations of Stresses; Division of Engineering, Brown University: Providence, RI, USA, 1956. [Google Scholar]
- Brown, M.W.; Miller, K.J. A theory for fatigue failure under multiaxial stress-strain conditions. Proc. Inst. Mech. Eng. 1973, 187, 745–755. [Google Scholar] [CrossRef]
- Wang, C.H.; Brown, M.W. Life prediction techniques for variable amplitude multiaxial fatigue—Part 1: Theories. J. Eng. Mater. Technol. 1996, 118, 367–370. [Google Scholar] [CrossRef]
- Kandil, F.A.; Brown, M.W.; Miller, K.J. Biaxial low-cycle fatigue failure of 316 stainless steel at elevated temperatures. In Mechanical Behaviour and Nuclear Applications of Stainless Steel at Elevated Temperatures; Maney Pub.: London, UK, 1982. [Google Scholar]
- McDiarmid, D.L. A general criterion for high cycle multiaxial fatigue failure. Fatigue Fract. Eng. Mater. Struct. 1991, 14, 429–453. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear optimization using the generalized reduced gradient method. Rev. Fr. Autom Inf Rech Oper 1974. [Google Scholar] [CrossRef]
- Brown, A.M. A step-by-step guide to non-linear regression analysis of experimental data using a Microsoft Excel spreadsheet. Comput. Methods Programs Biomed. 2001. [Google Scholar] [CrossRef]
- Baschnagel, F.; Härdi, R.; Triantafyllidis, Z.; Meier, U.; Terrasi, G. Pietro Fatigue and durability of laminated carbon fibre reinforced polymer straps for bridge suspenders. Polymers 2018, 10, 169. [Google Scholar] [CrossRef] [PubMed]
- Tobajas, R.; Elduque, D.; Ibarz, E.; Javierre, C.; Canteli, A.F.; Gracia, L. Visco-hyperelastic model with damage for simulating cyclic thermoplastic elastomers behavior applied to an industrial component. Polymers 2018, 10, 668. [Google Scholar] [CrossRef]




| No | Test (Type-Number) | δmax (mm) | δmin (mm) | θmax (°) | θmin (°) | Pa (N) | Pm (N) | Ta (Nm) | Tm (Nm) | Offset (°) | Lifetime (Cycles) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A1 | 1.27 | 0 | 0 | 0 | 1136 | 581 | 0 | 1 | 0 | 339,167 |
| 83 | I4 | 3.55 | 0 | 14 | 0 | 1645 | 638 | 60 | 47 | 180 | 12,408 |
| Test | Test Type | F (Hz) | dmax (mm) | dmin (mm) | θmax (°) | θmin (°) | Lifetime (Cycles) |
|---|---|---|---|---|---|---|---|
| 1 | A | 5 | 2.25 | 0 | 0 | 0 | 760,000 |
| 128 | E7 | 5 | 3.8 | 1.75 | 0 | 0 | 363,500 |
| n | Variable | γn | αn | βn |
|---|---|---|---|---|
| 1 | σ1 | 0.550 | 0.017 | −0.188 |
| 2 | σ2 | 0.932 | −0.139 | 0.253 |
| 3 | σ3 | 1.000 | −0.068 | −0.134 |
| 4 | ε1 | 12.152 | −0.153 | 2.580 |
| 5 | ε2 | 1.000 | 1.500 | −0.912 |
| 6 | ε3 | 1.000 | 0.283 | 4.470 |
| 7 | SED | −1.715 | 0.151 | 0.071 |
| n | Variable | γn | αn | βn |
|---|---|---|---|---|
| 1 | σ1 | 0.006 | 319.264 | −160.034 |
| 2 | σ2 | 1.000 | −1.371 | 0.962 |
| 3 | σ3 | 1.000 | −0.563 | 1.188 |
| 4 | ε1 | 0.006 | −25.018 | 13.890 |
| 5 | ε2 | 1.000 | −0.412 | −0.297 |
| 6 | ε3 | 1.000 | −0.144 | −1.452 |
| 7 | SED | −0.093 | 16.546 | −8115 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tobajas, R.; Elduque, D.; Ibarz, E.; Javierre, C.; Gracia, L. A New Multiparameter Model for Multiaxial Fatigue Life Prediction of Rubber Materials. Polymers 2020, 12, 1194. https://doi.org/10.3390/polym12051194
Tobajas R, Elduque D, Ibarz E, Javierre C, Gracia L. A New Multiparameter Model for Multiaxial Fatigue Life Prediction of Rubber Materials. Polymers. 2020; 12(5):1194. https://doi.org/10.3390/polym12051194
Chicago/Turabian StyleTobajas, Rafael, Daniel Elduque, Elena Ibarz, Carlos Javierre, and Luis Gracia. 2020. "A New Multiparameter Model for Multiaxial Fatigue Life Prediction of Rubber Materials" Polymers 12, no. 5: 1194. https://doi.org/10.3390/polym12051194
APA StyleTobajas, R., Elduque, D., Ibarz, E., Javierre, C., & Gracia, L. (2020). A New Multiparameter Model for Multiaxial Fatigue Life Prediction of Rubber Materials. Polymers, 12(5), 1194. https://doi.org/10.3390/polym12051194