Non-Uniform Curvature Model and Numerical Simulation for Anti-Symmetric Cylindrical Bistable Polymer Composite Shells
Abstract
1. Introduction
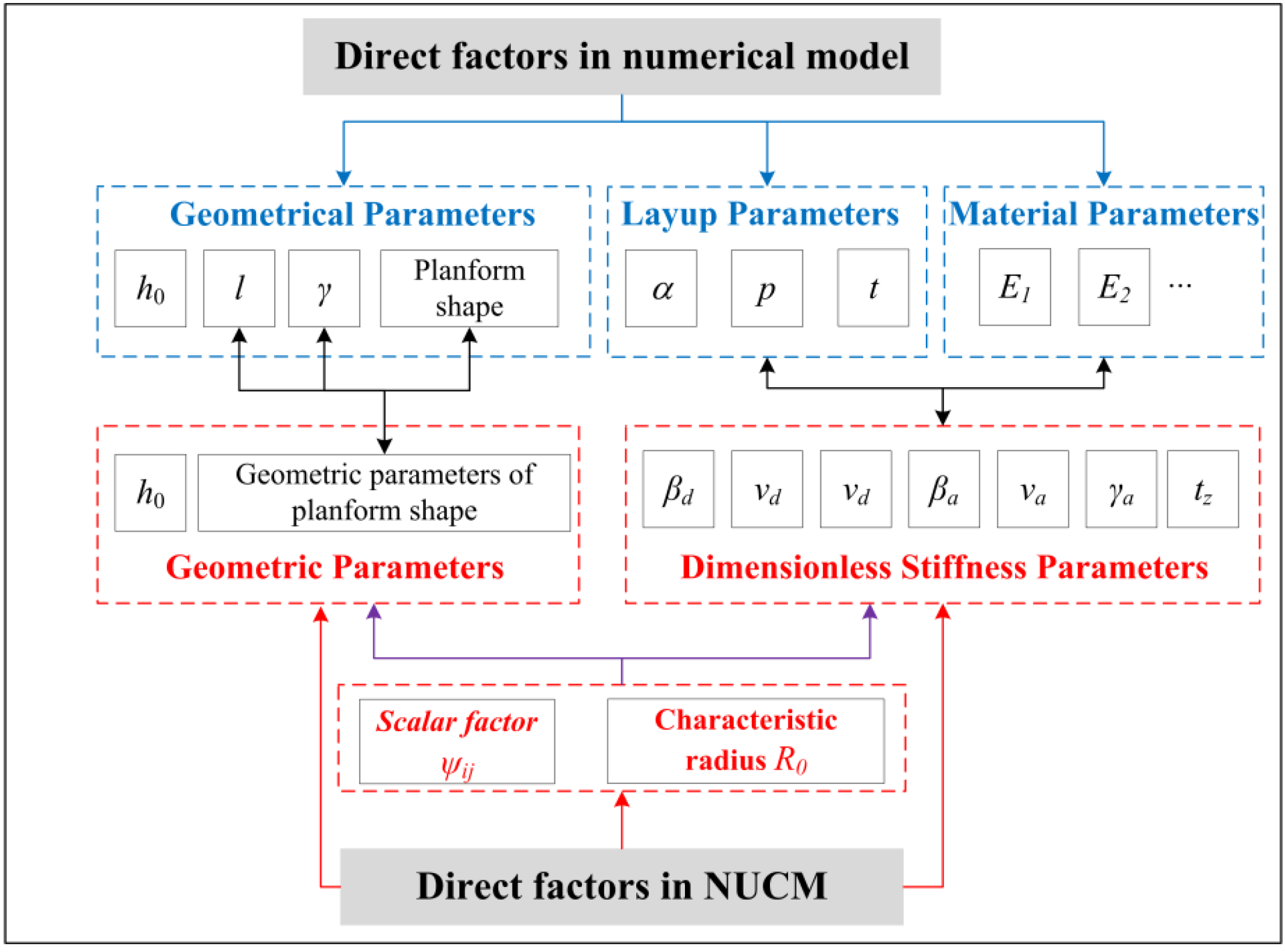
2. Analytical Model
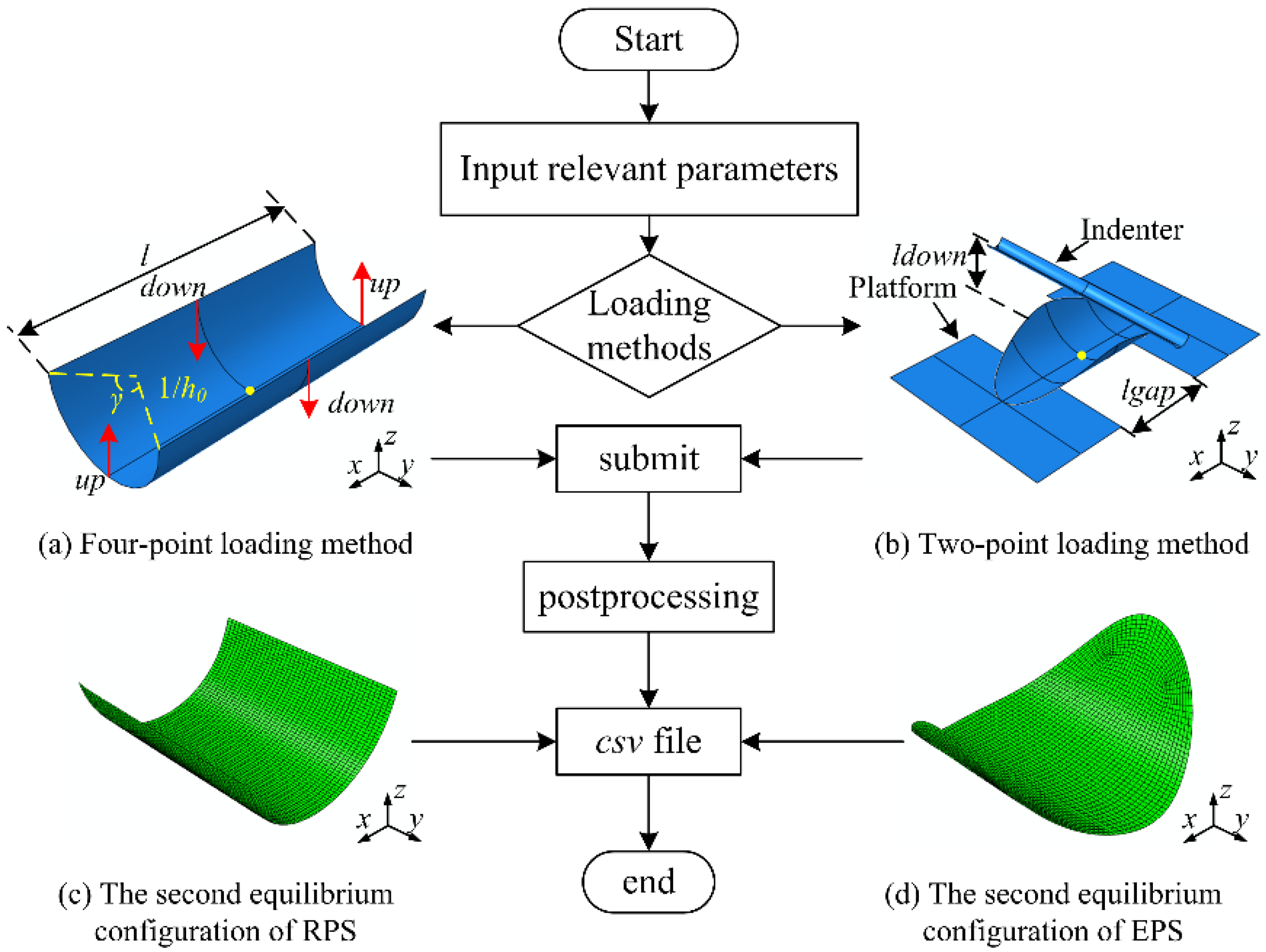
3. Finite Element Analysis
4. Result and Discussion
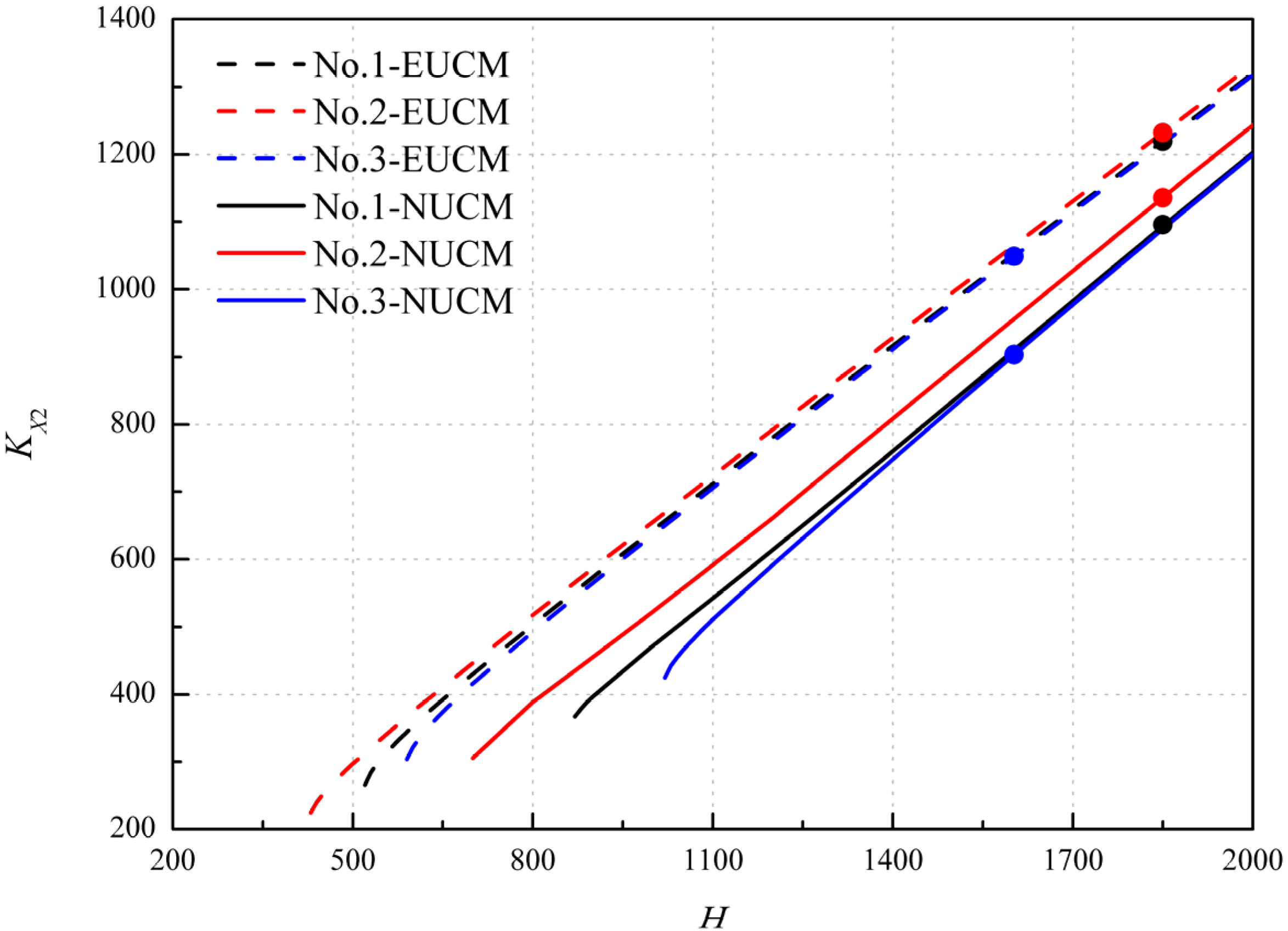
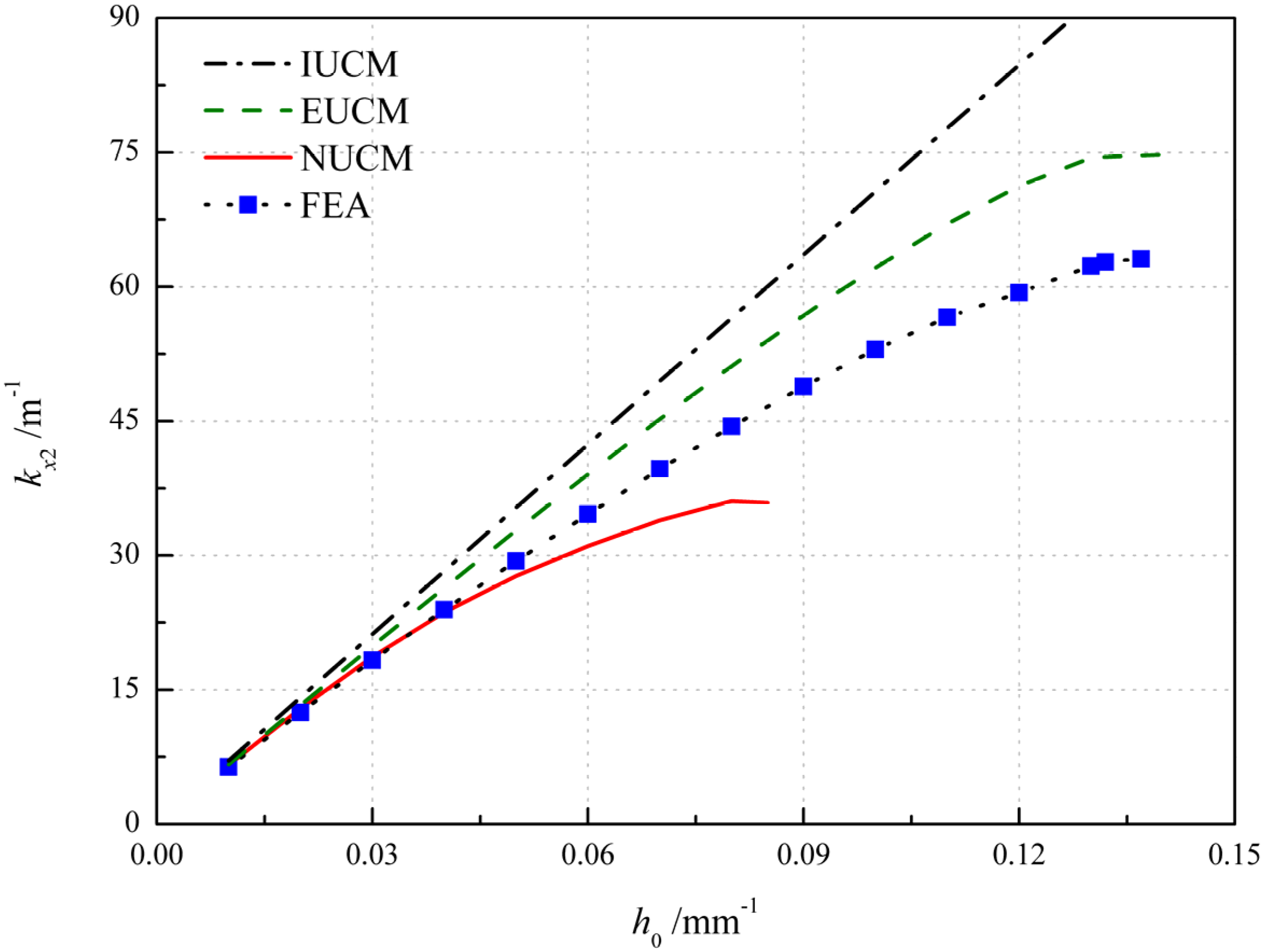
4.1. Validation of Accuracy
4.2. Factors Affecting the Bistability
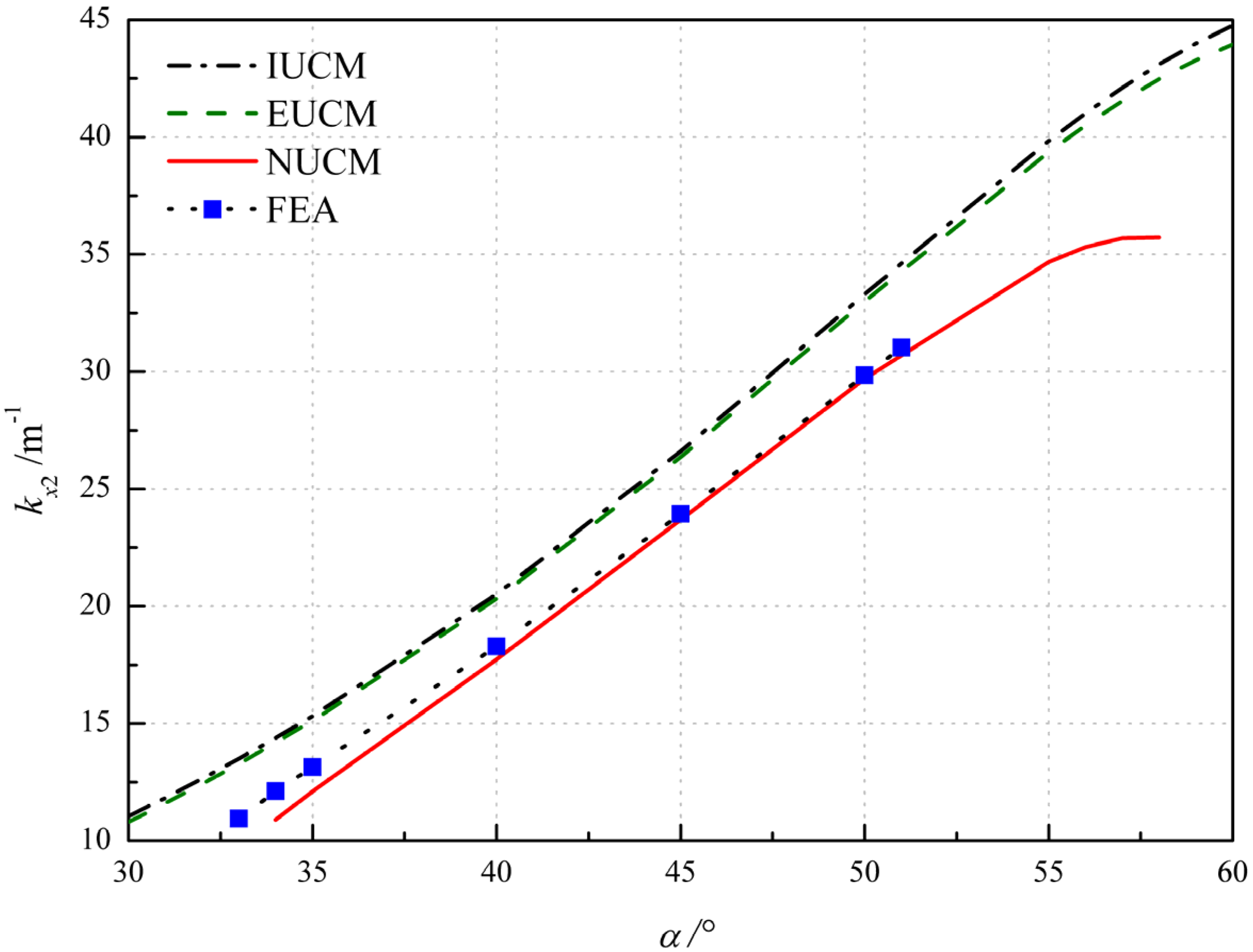
4.2.1. Influence of Scalar Factor and Characteristic Radius
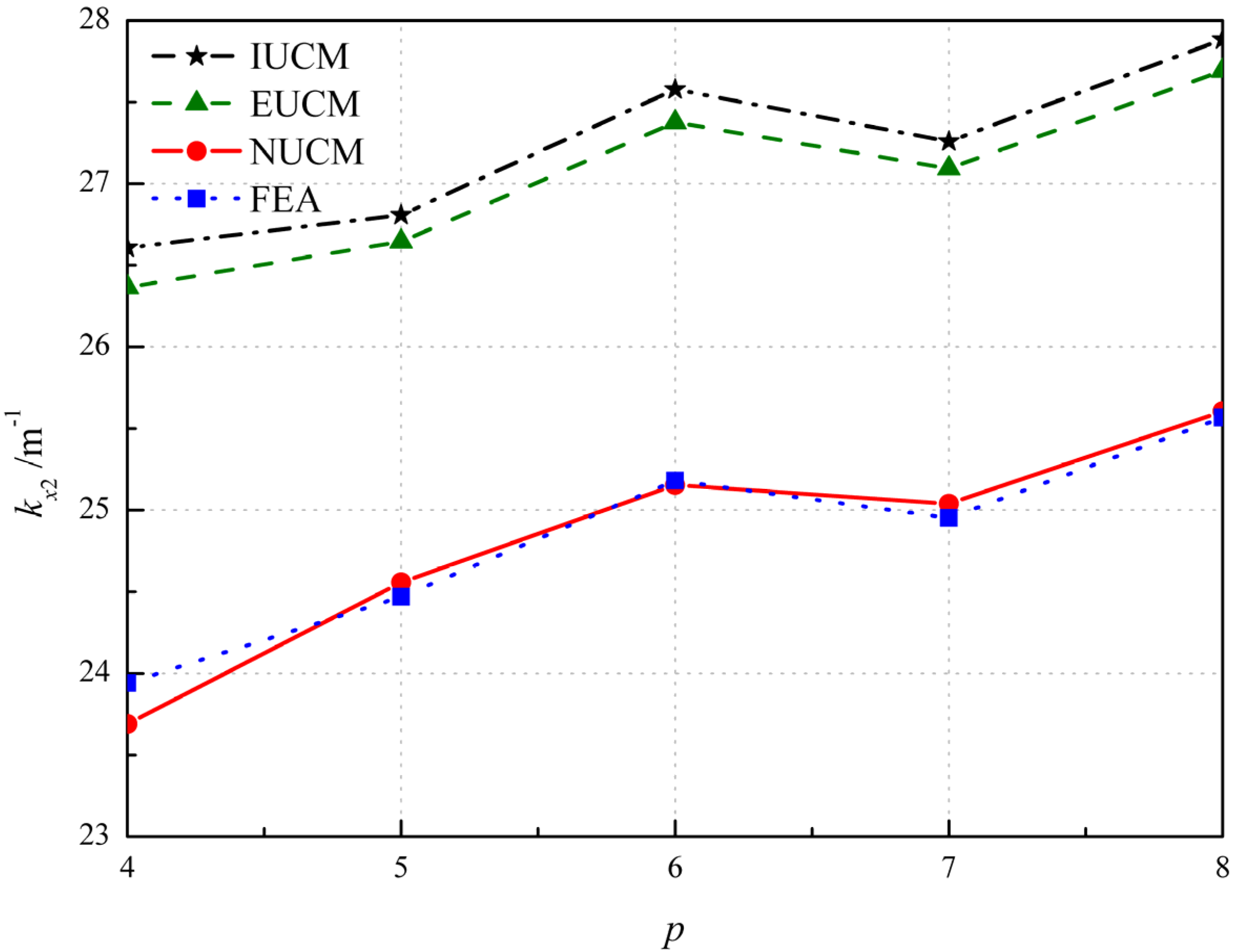
4.2.2. Influence of Layup Parameters
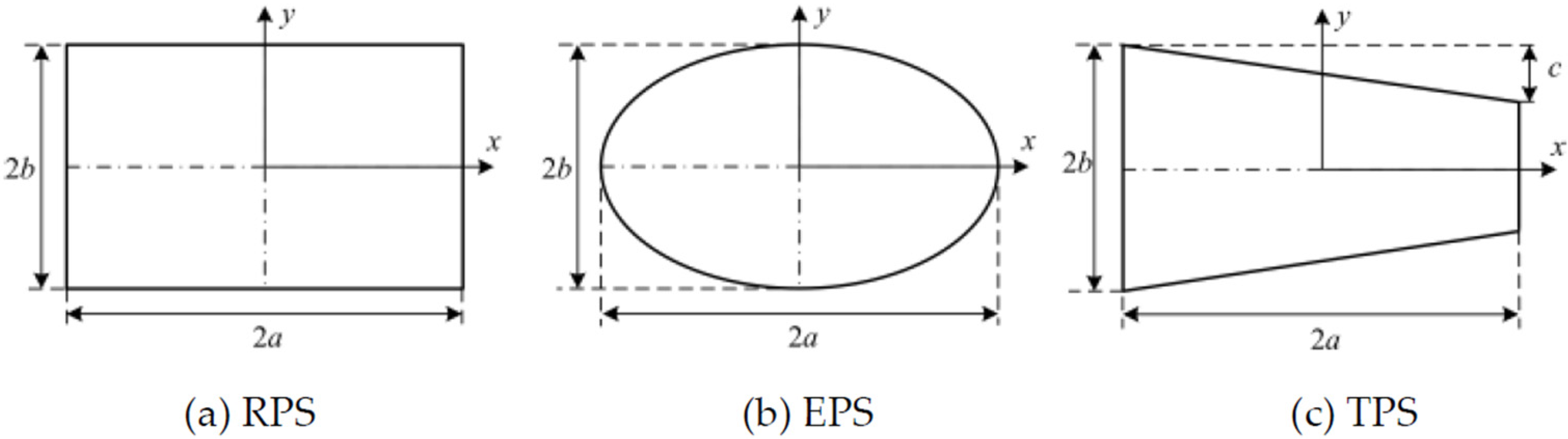
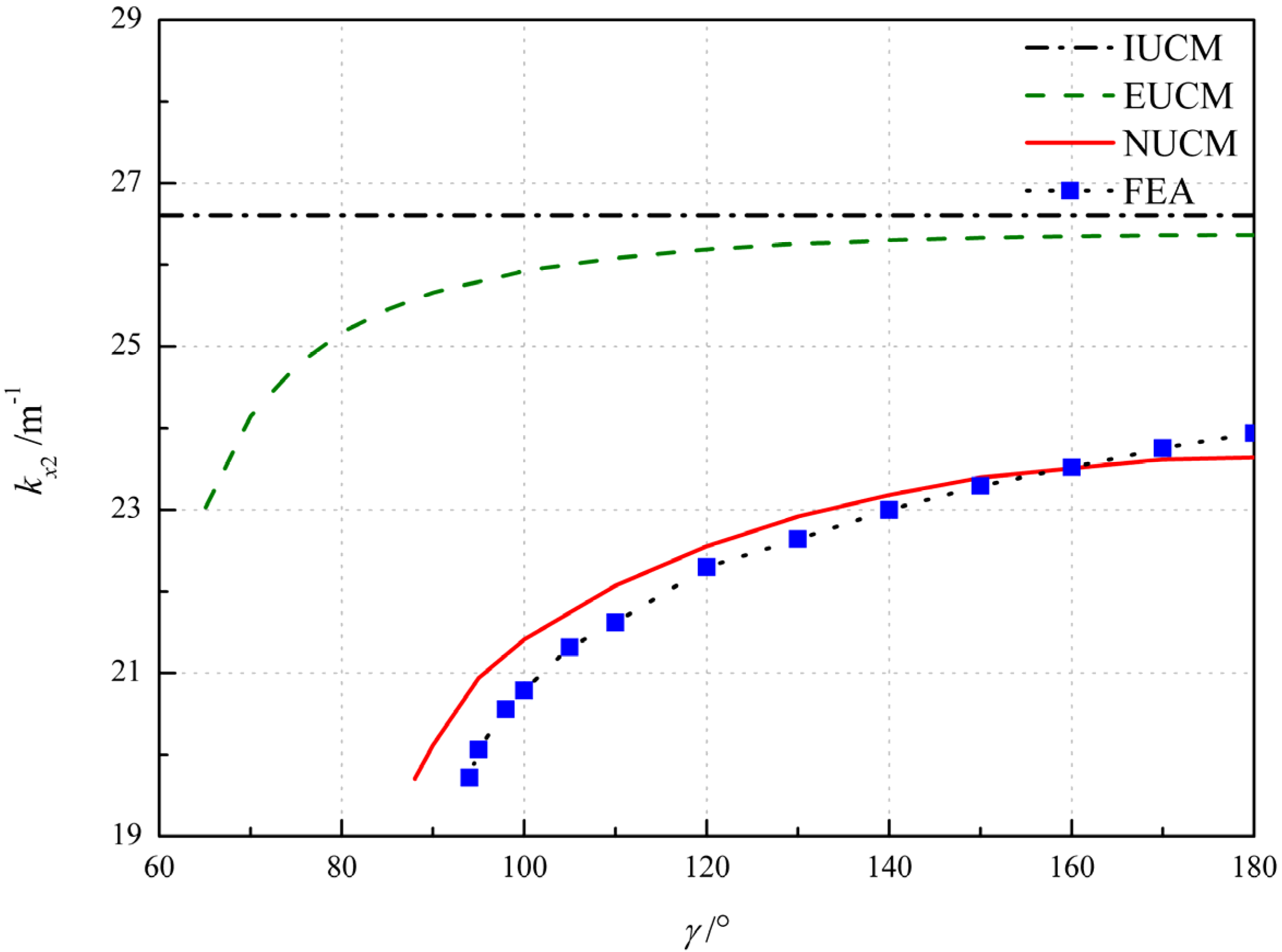
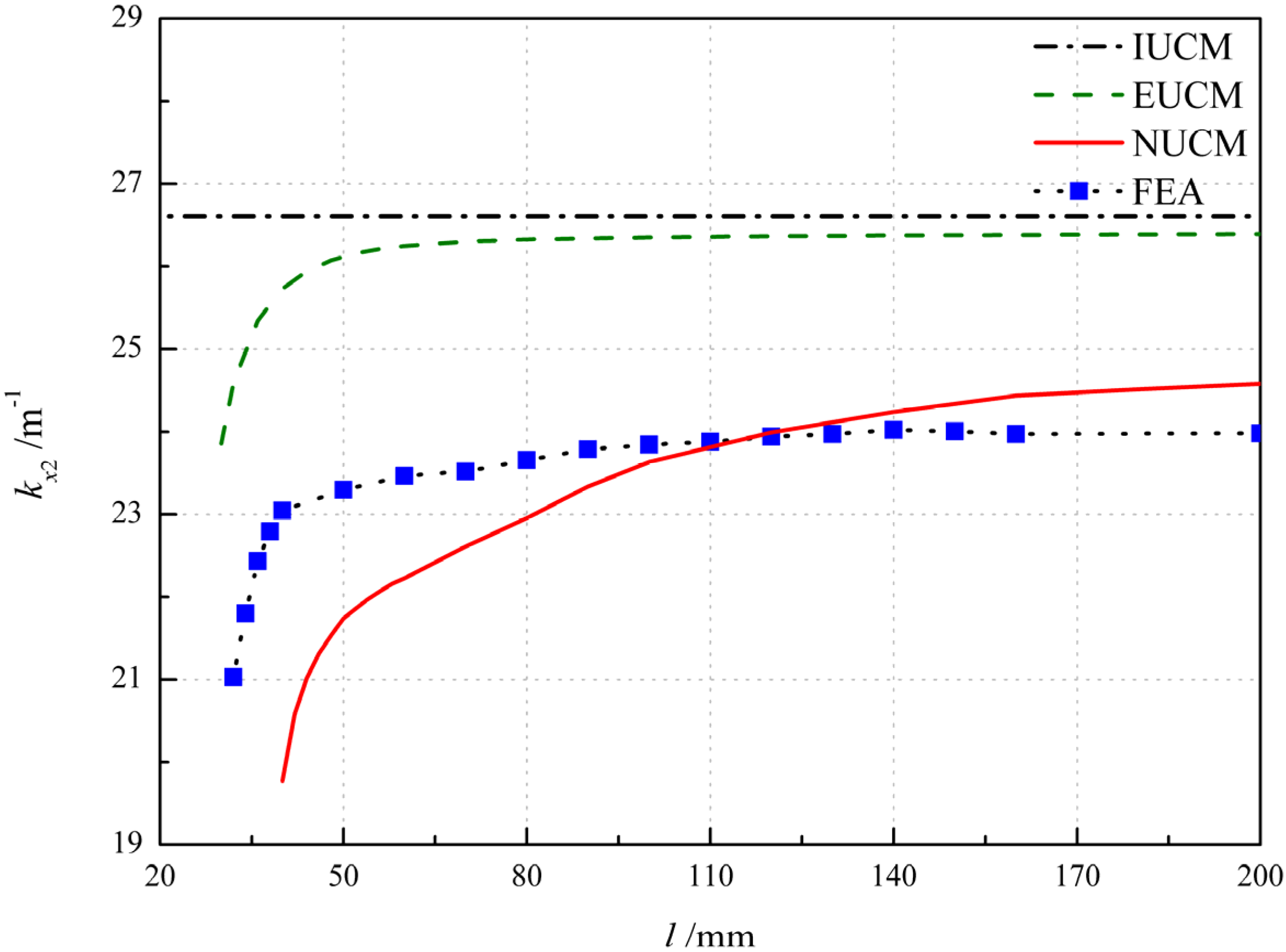
4.2.3. Influence of Geometrical Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Zhang, Z.; Li, Y.; Yu, X.; Li, X.; Wu, H.; Wu, H.; Jiang, S.; Chai, G. Bistable morphing composite structures: A review. Thin-Walled Struct. 2019, 142, 74–97. [Google Scholar] [CrossRef]
- Daynes, S.; Weaver, M. Review of shape-morphing automobile structures: Concepts and outlook. Proc. Inst. Mech. Eng. Part D 2013, 227, 1603–1622. [Google Scholar] [CrossRef]
- Kuder, I.; Fasel, U.; Ermanni, P.; Arrieta, A.F. Concurrent design of a morphing aerofoil with variable stiffness bi-stable laminates. Smart Mater. Struct. 2016, 25, 115001. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, W.; Wu, H.; Wu, H.; Jiang, S.; Chai, G. A rigid thick Miura-Ori structure driven by bistable carbon fibre-reinforced polymer cylindrical shell. Compos. Sci. Technol. 2018, 167, 411–420. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, Z.; Zhang, H.; Li, Y.; Wu, H.; Jiang, S.; Chai, G. An origami-inspired cube pipe structure with bistable anti-symmetric CFRP shells driven by magnetic field. Smart Mater. Struct. 2019, 28, 025028. [Google Scholar] [CrossRef]
- Kim, S.; Koh, J.; Lee, J.; Ryu, J.; Cho, M.; Cho, K. Flytrap-inspired robot using structurally integrated actuation based on bistability and a developable surface. Bioinspiration Biomim. 2014, 9, 036004. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Yu, X. Magnetic actuation bionic robotic gripper with bistable morphing structure. Compos. Struct. 2019, 229, 111422. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, D.; Wu, H.; Bao, Y.; Chai, G. Non-contact magnetic driving bioinspired Venus flytrap robot based on bistable anti-symmetric CFRP structure. Compos. Struct. 2016, 135, 17–22. [Google Scholar] [CrossRef]
- Chiacchiari, S.; Romeo, F.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Vibration energy harvesting from impulsive excitations via a bistable nonlinear attachment—Experimental study. Mech. Syst. signal Process. 2019, 125, 185–201. [Google Scholar] [CrossRef]
- Pan, D.; Ma, B.; Dai, F. Experimental investigation of broadband energy harvesting of a bi-stable composite piezoelectric plate. Smart Mater. Struct. 2017, 26, 035045. [Google Scholar] [CrossRef]
- Hamouche, W.; Maurini, C.; Vidoli, S.; Vincenti, A. Multi-parameter actuation of a neutrally stable shell: A flexible gear-less motor. Proc. R. Soc. A 2017, 473, 20170364. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chen, B.; Lu, C.; Wu, H.; Wu, H.; Jiang, S.; Chai, G. A novel thermo-mechanical anti-icing/de-icing system using bi-stable laminate composite structures with superhydrophobic surface. Compos. Struct. 2017, 180, 933–943. [Google Scholar] [CrossRef]
- Daynes, S.; Diaconu, C.; Potter, K.; Weaver, P.M. Bistable prestressed symmetric laminates. J. Compos. Mater. 2009, 44, 1119–1137. [Google Scholar] [CrossRef]
- Jiang, X.; Pezzulla, M.; Shao, H.; Ghosh, T.K.; Holmes, D.P. Snapping of bistable, prestressed cylindrical shells. Europhys. Lett. 2018, 122, 64003. [Google Scholar] [CrossRef]
- Kebadze, E.; Guest, S.D.; Pellegrino, S. Bistable prestressed shell structures. Int. J. Solids Struct. 2004, 41, 2801–2820. [Google Scholar] [CrossRef]
- Seffen, K.A.; Guest, S.D. Prestressed morphing bistable and neutrally stable shells. J. Appl. Mech. 2011, 78, 011002. [Google Scholar] [CrossRef]
- Hyer, M. Some observations on the cured shape of thin unsymmetric laminates. J. Compos. Mater. 1981, 15, 175–194. [Google Scholar] [CrossRef]
- Iqbal, K.; Pellegrino, S. Bi-stable composite shells. In Proceedings of the 41st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, GA, USA, 3–6 April 2000; Volume 3. [Google Scholar]
- Zhang, Z.; Wu, H.; He, X.; Wu, H.; Bao, Y.; Chai, G. The bistable behaviors of carbon-fiber/epoxy anti-symmetric composite shells. Compos. Part B 2013, 47, 190–199. [Google Scholar] [CrossRef]
- Guest, S.; Pellegrino, S. Analytical models for bistable cylindrical shells. Proc. R. Soc. A 2006, 2067, 839–854. [Google Scholar] [CrossRef]
- Seffen, K. ‘Morphing’ bistable orthotropic elliptical shallow shells. Proc. R. Soc. A 2007, 463, 67–83. [Google Scholar] [CrossRef]
- Vidoli, S.; Maurini, C. Tristability of thin orthotropic shells with uniform initial curvature. Proc. R. Soc. A 2008, 464, 2949–2966. [Google Scholar] [CrossRef]
- Iqbal, K.; Pellegrino, S.; Daton-Lovett, A. Bi-stable composite slit tubes. In IUTAM-IASS Symposium on Deployable Structures: Theory and Applications; Springer: Dordrecht, The Netherlands, 2000; pp. 153–162. [Google Scholar]
- Galletly, D.A.; Guest, S.D. Bistable composite slit tubes. I. A beam model. Int. J. Solids Struct. 2004, 41, 4517–4533. [Google Scholar] [CrossRef]
- Galletly, D.A.; Guest, S.D. Bistable composite slit tubes. II. A shell model. Int. J. Solids Struct. 2004, 41, 4503–4516. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Wu, H.; Chen, D.; Yang, J.; Wu, H.; Jiang, S.; Chai, G. Viscoelastic bistable behaviour of antisymmetric laminated composite shells with time-temperature dependent properties. Thin-Walled Struct. 2018, 122, 403–415. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, H.; Ye, G.; Yang, J.; Kitipornchai, S.; Chai, G. Experimental study on bistable behaviour of anti-symmetric laminated cylindrical shells in thermal environments. Compos. Struct. 2016, 144, 24–32. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, H.; Ye, G.; Wu, H.; He, X.; Chai, G. Systematic experimental and numerical study of bistable snap processes for anti-symmetric cylindrical shells. Compos. Struct. 2014, 112, 368–377. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, G.; Wu, H.; Yang, J.; Kitipornchai, S.; Chai, G. Bistable behaviour and microstructure characterization of carbon fiber/epoxy resin anti-symmetric laminated cylindrical shell after thermal exposure. Compos. Sci. Technol. 2017, 138, 91–97. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, G.; Wu, H.; Chen, D.; Chai, G. Thermal effect and active control on bistable behaviour of anti-symmetric composite shells with temperature-dependent properties. Compos. Struct. 2015, 124, 263–271. [Google Scholar] [CrossRef]
- Chai, H.; Li, Y.; Zhang, Z.; Sun, M.; Wu, H.; Jiang, S. Systematic analysis of bistable anti-symmetric composite cylindrical shells and variable stiffness composite structures in hygrothermal environment. Int. J. Adv. Manuf. Technol. 2020, 1–17. [Google Scholar] [CrossRef]
- Calladine, C. Theory of Shell Structures; Cambridge university press: Cambridge, UK, 1989. [Google Scholar]
- Fernandes, A.; Maurini, C.; Vidoli, S. Multiparameter actuation for shape control of bistable composite plates. Int. J. Solids Struct. 2010, 47, 1449–1458. [Google Scholar] [CrossRef]
- Hamouche, W.; Maurini, C. Vincenti, A.; Vidoli, S. Basic criteria to design and produce multistable shells. Meccanica 2016, 51, 2305–2320. [Google Scholar] [CrossRef]
- Vidoli, S. Discrete approximations of the Föppl–Von Kármán shell model: From coarse to more refined models. Int. J. Solids Struct. 2013, 50, 1241–1252. [Google Scholar] [CrossRef]
- Brunetti, M.; Vincenti, A.; Vidoli, S. A class of morphing shell structures satisfying clamped boundary conditions. Int. J. Solids Struct. 2016, 82, 47–55. [Google Scholar] [CrossRef]
- Brunetti, M.; Vidoli, S.; Vincenti, A. Bistability of orthotropic shells with clamped boundary conditions: An analysis by the polar method. Compos. Struct. 2018, 194, 388–397. [Google Scholar] [CrossRef]
- Pirrera, A.; Avitabile, D.; Weaver, P.M. Bistable plates for morphing structures: A refined analytical approach with high-order polynomials. Int. J. Solids Struct. 2010, 47, 3412–3425. [Google Scholar] [CrossRef]
- Pirrera, A.; Avitabile, D.; Weaver, P. On the thermally induced bistability of composite cylindrical shells for morphing structures. Int. J. Solids Struct. 2012, 49, 685–700. [Google Scholar] [CrossRef]
- Ciarlet, P. A justification of the von Kármán equations. Arch. Ration. Mech. Anal. 1980, 73, 349–389. [Google Scholar] [CrossRef]
- Logg, A.; Mardal, K.-A.; Wells, G. Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hyer, M. The room-temperature shapes of four-layer unsymmetric cross-ply laminates. J. Compos. Mater. 1982, 16, 318–340. [Google Scholar] [CrossRef]
- Emam, S.; Inman, D. A review on bistable composite laminates for morphing and energy harvesting. Appl. Mech. Rev. 2015, 67, 060803. [Google Scholar] [CrossRef]
- Coburn, B.; Pirrera, A.; Weaver, P.M. Vidoli, S. Tristability of an orthotropic doubly curved shell. Compos. Struct. 2013, 96, 446–454. [Google Scholar] [CrossRef]
- Giomi, L.; Mahadevan, L. Multi-stability of free spontaneously curved anisotropic strips. Proc. R. Soc. A 2011, 468, 511–530. [Google Scholar] [CrossRef]
| E1/GPa | E2/GPa | G12(13)/GPa | v12 | α1/(10−6/°C) | α2/(10−6/°C) |
|---|---|---|---|---|---|
| 108 | 7.07 | 5.17 | 0.31 | −2.1 | 64.33 |
| Average Curvature | IUCM [20] | EUCM [21] | QVCM [35] | NUCM | FEA |
|---|---|---|---|---|---|
| kx2/m−1 | 26.61 | 26.36 | 11.98 | 23.69 | 23.94 |
| ky2/m−1 | 0 | 0.16 | 8.01 | 2.07 | 2.81 |
| Number of Plies p | kx2/m−1(NUCM) | kx2/m−1(FEA) | Error |
|---|---|---|---|
| 4 | 23.69 | 23.94 | 1.05% |
| 5 | 24.56 | 24.47 | −0.36% |
| 6 | 25.15 | 25.18 | 0.10% |
| 7 | 25.04 | 24.95 | −0.35% |
| 8 | 25.61 | 25.57 | −0.15% |
| Angle of Embrace γ/° | kx2/m−1(NUCM) | kx2/m−1(FEA) | Error |
|---|---|---|---|
| 180 | 23.64 | 23.94 | 1.24% |
| 160 | 23.51 | 23.52 | 0.05% |
| 140 | 23.18 | 23.00 | −0.79% |
| 120 | 22.55 | 22.30 | −1.14% |
| 100 | 21.41 | 20.78 | −3.01% |
| 95 | 20.94 | 20.06 | −4.38% |
| h0/mm−1 | kx2/m−1(EUCM) | kx2/m−1(NUCM) | kx2/m−1(FEA) | Error-1 | Error-2 |
|---|---|---|---|---|---|
| 0.01 | 6.65 | 6.60 | 6.37 | 4.36% | 3.68% |
| 0.02 | 13.27 | 12.93 | 12.45 | 6.62% | 3.83% |
| 0.03 | 19.85 | 18.69 | 18.30 | 8.50% | 2.12% |
| 0.04 | 26.36 | 23.69 | 23.94 | 10.11% | 1.04% |
| 0.05 | 32.78 | 27.70 | 29.36 | 11.66% | −5.67% |
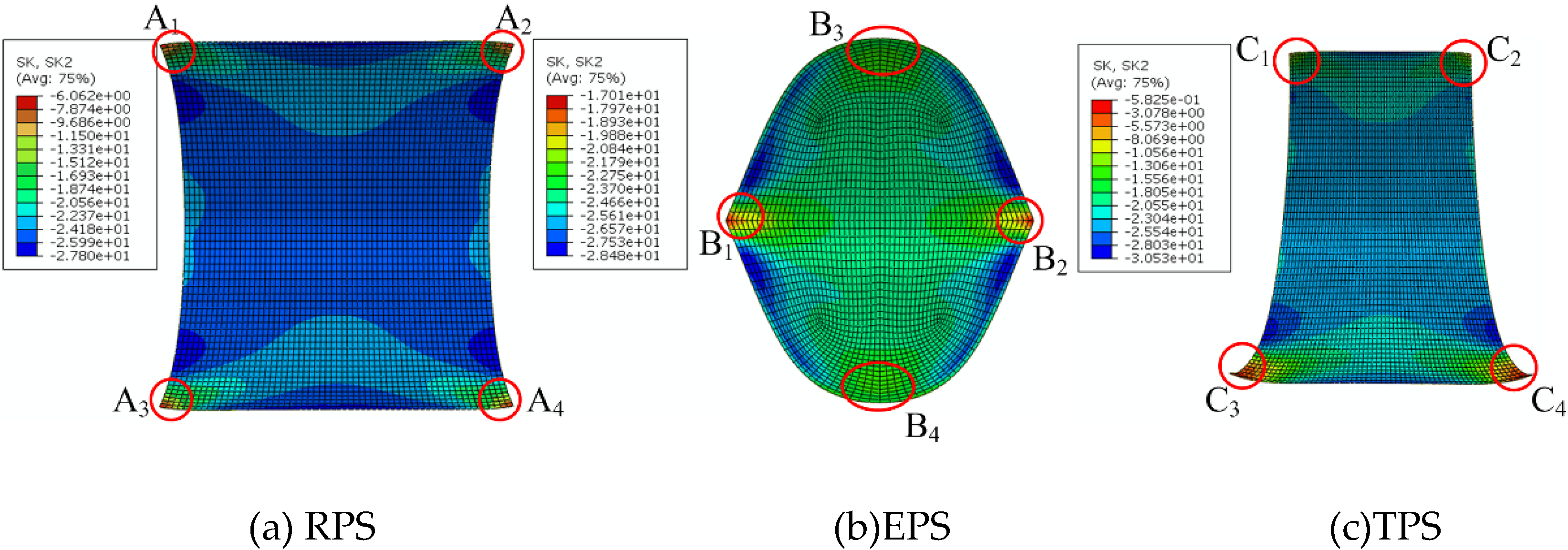
| Planform Shape | kx2/m−1(EUCM) | kx2/m−1(NUCM) | kx2/m−1(FEA) | Error-1 | Error-2 |
|---|---|---|---|---|---|
| RPS | 26.36 | 23.69 | 23.94 | 10.11% | −1.04% |
| EPS | 26.30 | 23.98 | 24.46 | 7.52% | −1.96% |
| TPS | 26.54 | 24.48 | 22.16 | 19.76% | 10.47% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Yu, X.; Wu, H.; Sun, M.; Li, X.; Wu, H.; Jiang, S. Non-Uniform Curvature Model and Numerical Simulation for Anti-Symmetric Cylindrical Bistable Polymer Composite Shells. Polymers 2020, 12, 1001. https://doi.org/10.3390/polym12051001
Zhang Z, Yu X, Wu H, Sun M, Li X, Wu H, Jiang S. Non-Uniform Curvature Model and Numerical Simulation for Anti-Symmetric Cylindrical Bistable Polymer Composite Shells. Polymers. 2020; 12(5):1001. https://doi.org/10.3390/polym12051001
Chicago/Turabian StyleZhang, Zheng, Xiaochen Yu, Helong Wu, Min Sun, Xianghao Li, Huaping Wu, and Shaofei Jiang. 2020. "Non-Uniform Curvature Model and Numerical Simulation for Anti-Symmetric Cylindrical Bistable Polymer Composite Shells" Polymers 12, no. 5: 1001. https://doi.org/10.3390/polym12051001
APA StyleZhang, Z., Yu, X., Wu, H., Sun, M., Li, X., Wu, H., & Jiang, S. (2020). Non-Uniform Curvature Model and Numerical Simulation for Anti-Symmetric Cylindrical Bistable Polymer Composite Shells. Polymers, 12(5), 1001. https://doi.org/10.3390/polym12051001






