Rheological Model and Transition Velocity Equation of a Polymer Solution in a Partial Pressure Tool
Abstract
:1. Introduction
2. Methodology
2.1. Physical Experiments
- The YP-B2003 electronic balance was used to measure dry powder of the HPAM and experimental water in proportion to prepare a polymer solution with a concentration of 1000 mg/L;
- The polymer mother liquor was dissolved and agitated using the EURO-ST D S25 electronic agitator at 250 r/min for 2.5 h and then left to stand for 2 h to ensure full dispersion of the solution molecules and a uniform system;
- The thermostatic circulation system was started in the RS-150 rheometer, heated to 45 °C, and put in homeostasis for 15 min. The prepared solution was put into a preheated measuring outer cylinder, and the temperature was kept constant for 20 min so that the temperature of each point of the sample could reach the testing temperature;
- The shear rate was set from 1 to 1000 s−1, the rheometer was started, and the rheometer’s viscosity option was selected for testing. When the indication viscosity value was basically stable, recording was started, and then recording was performed every 5 min. Four viscosity values were recorded continuously, and if the deviations between the first value and the three other values did not exceed 5%, the system was considered to have reached dynamic equilibrium.
2.2. Laminar Flow Model of the Polymer Solution in the Partial Pressure Tool
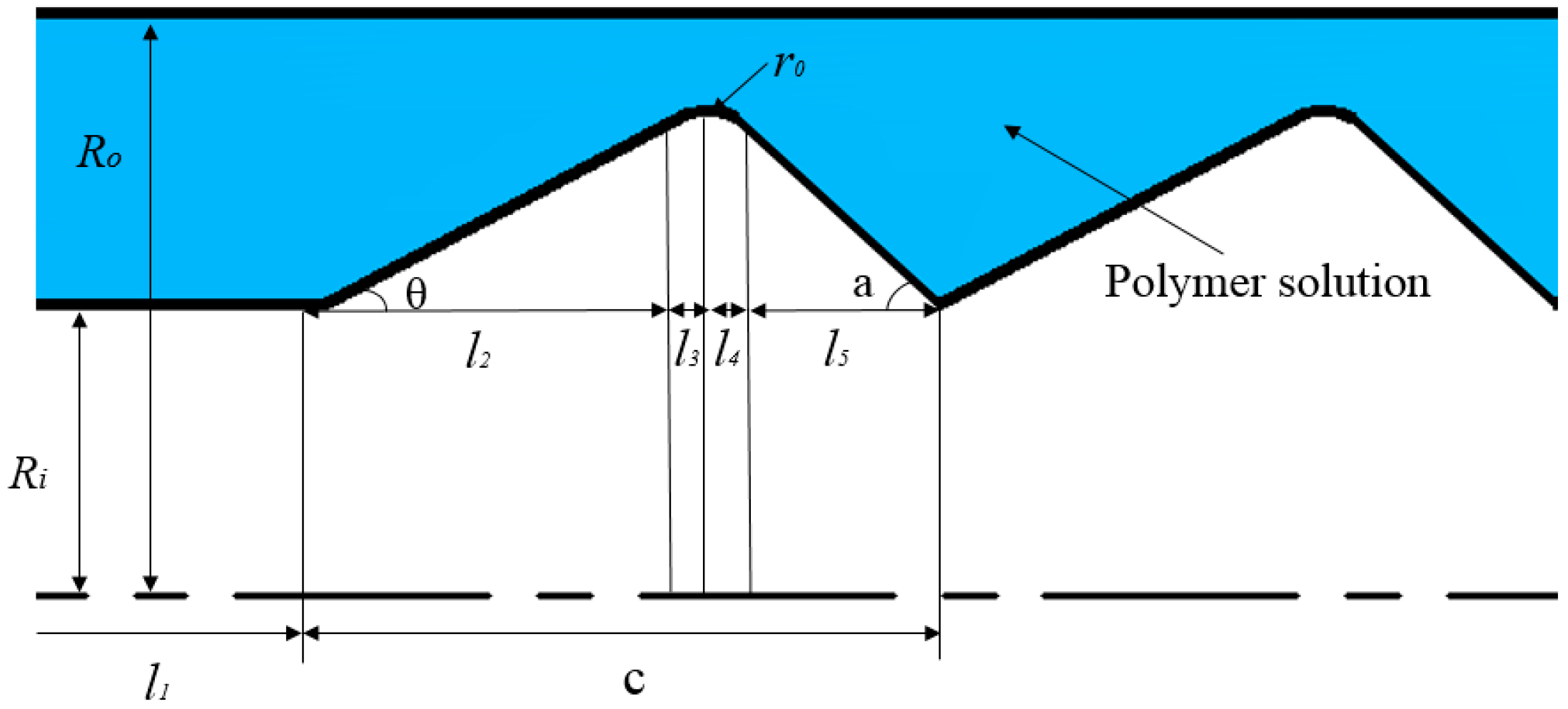
2.2.1. Physical Model of the Partial Pressure Tool
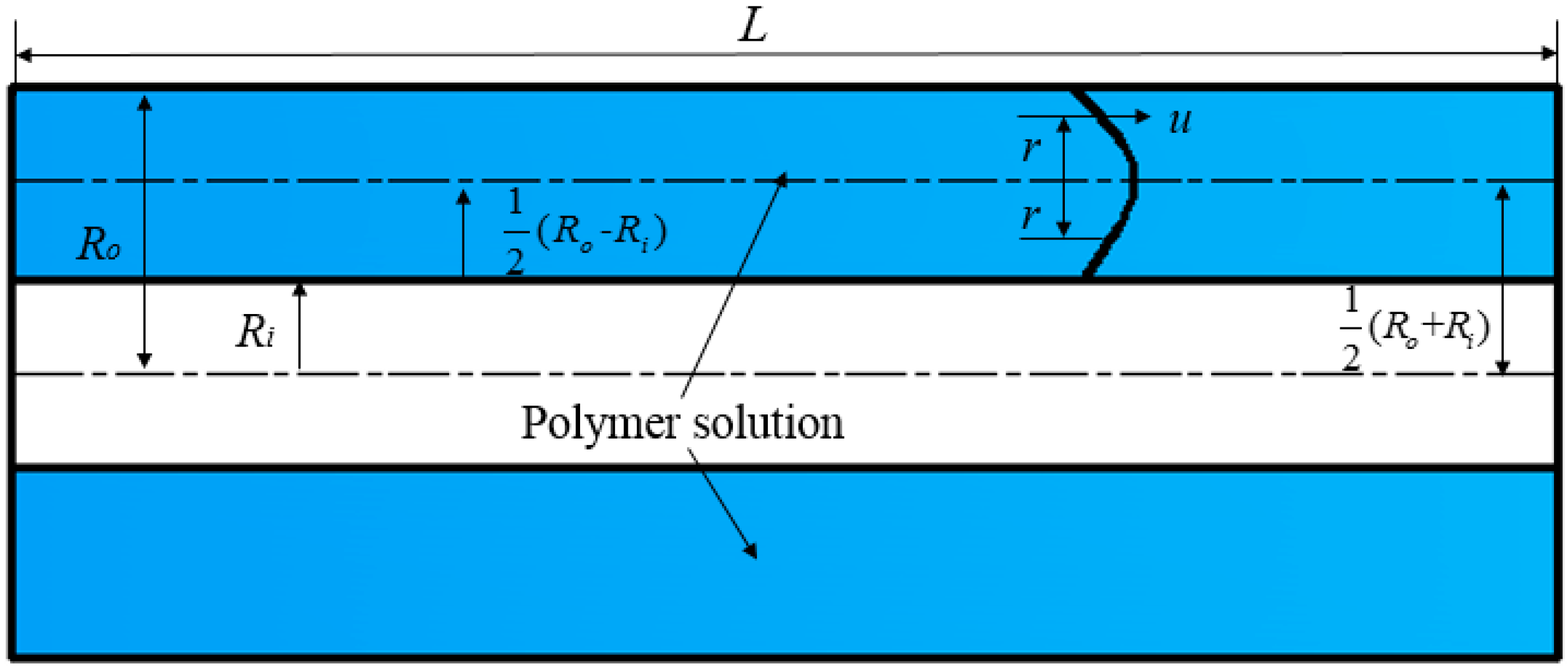
2.2.2. Flow Model of the Polymer Solution in the Annular Flow Channel of the Partial Pressure Tool
2.2.3. Flow Model of the Polymer Solution in the Throttling Section of the Partial Pressure Tool
- When , the polymer solution flows in the annulus flow channel:
- When , the polymer solution flows into the throttling section and flows through the contraction part of the throttling section:
- When , the polymer solution flows into the throttling section and flows through the middle arc contraction part of the throttling section:
- When , the polymer solution flows into the throttling section and flows through the middle arc expansion part of the throttling section
- When , the polymer solution flows into the throttling section and flows through the contraction part of the throttling section
2.2.4. Transition Velocity of the Polymer Solution in the Partial Pressure Tool
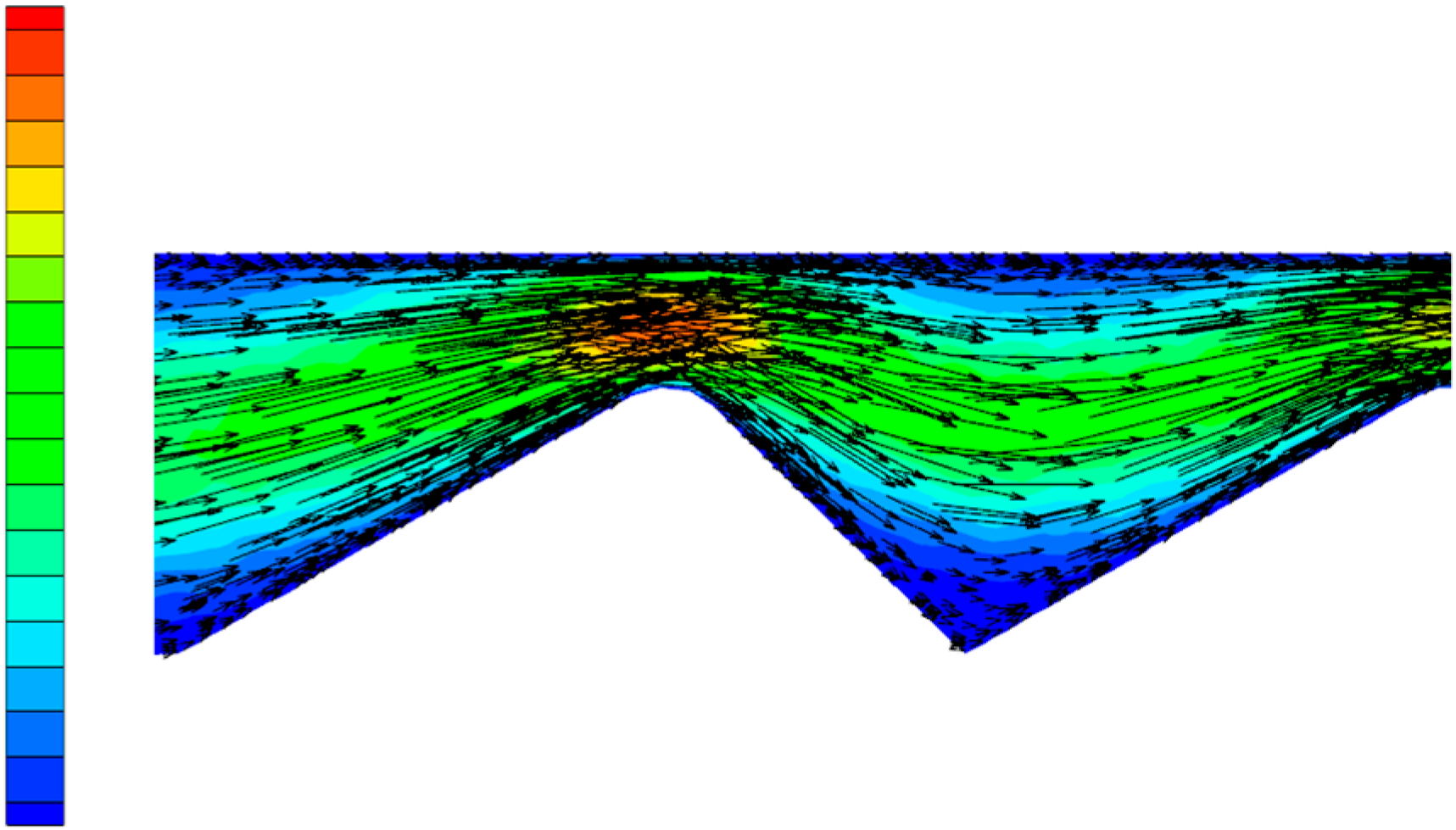
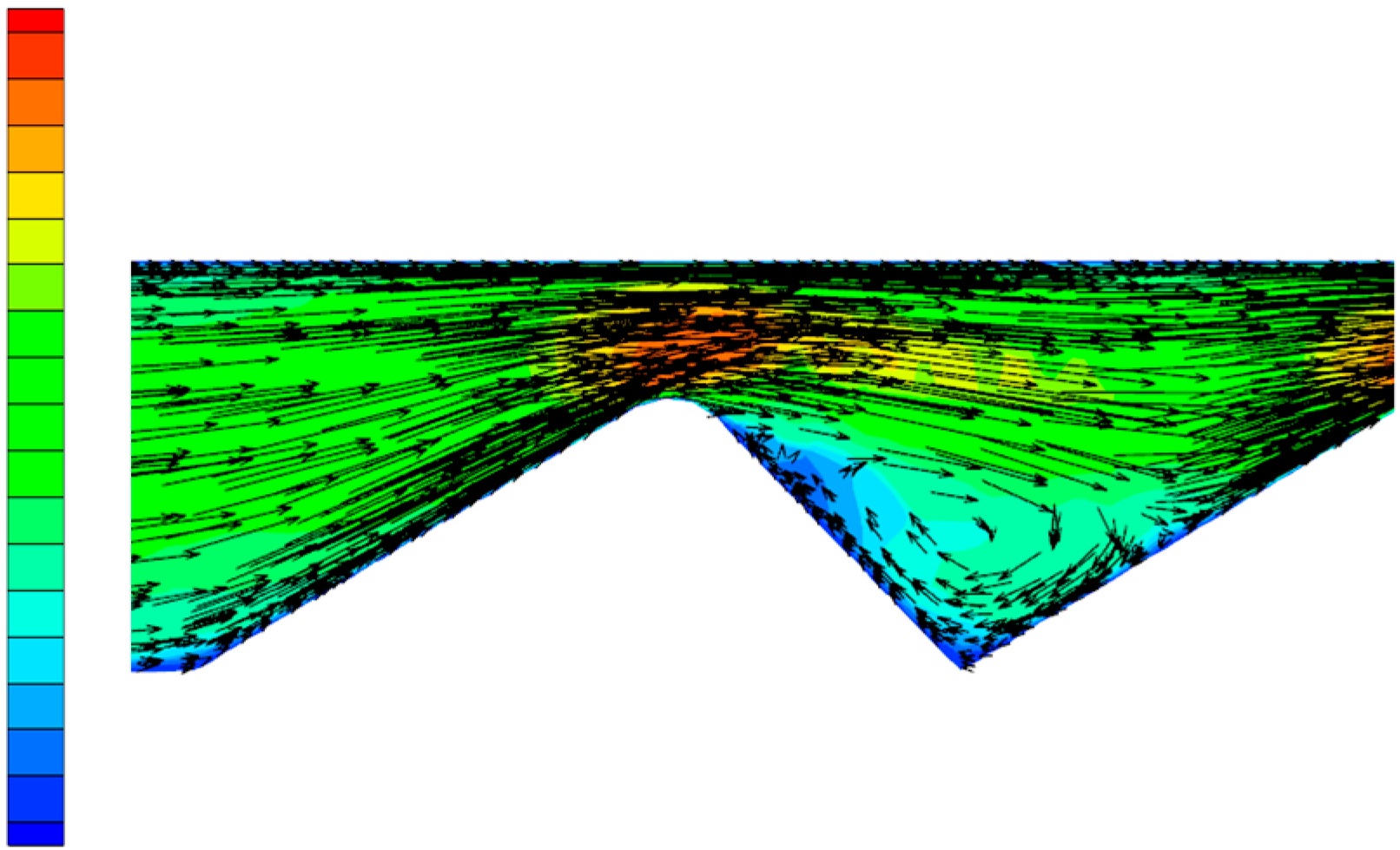
3. Numerical Solution of Polymer Solution Flow in the Partial Pressure Tool
4. Conclusions
- (1)
- According to the deduced rheological equation, the pressure and apparent viscosity of the polymer solution flowing through the partial pressure tools are related to the characteristics of the polymer solution and the structural parameters of the partial pressure tools;
- (2)
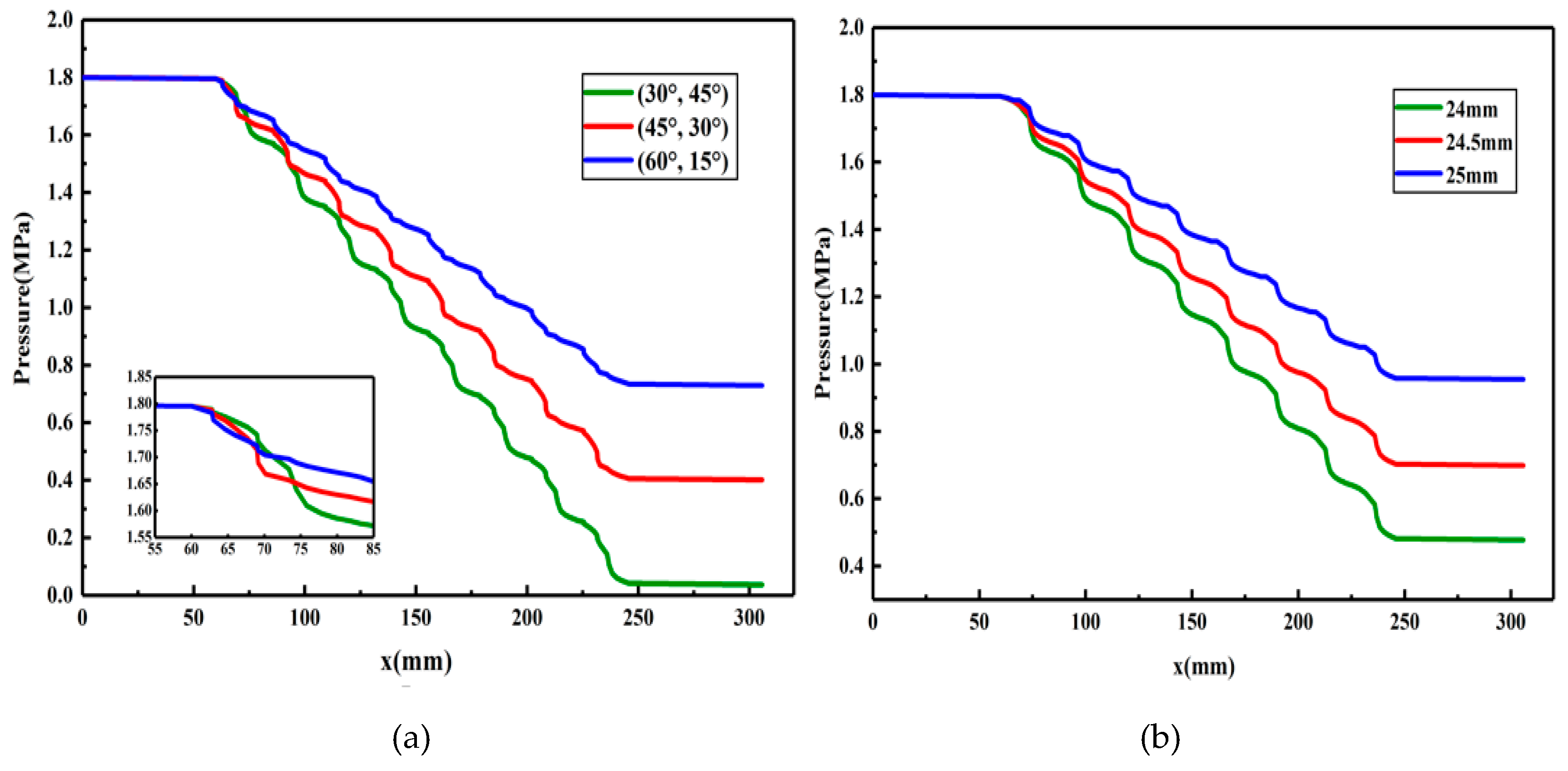
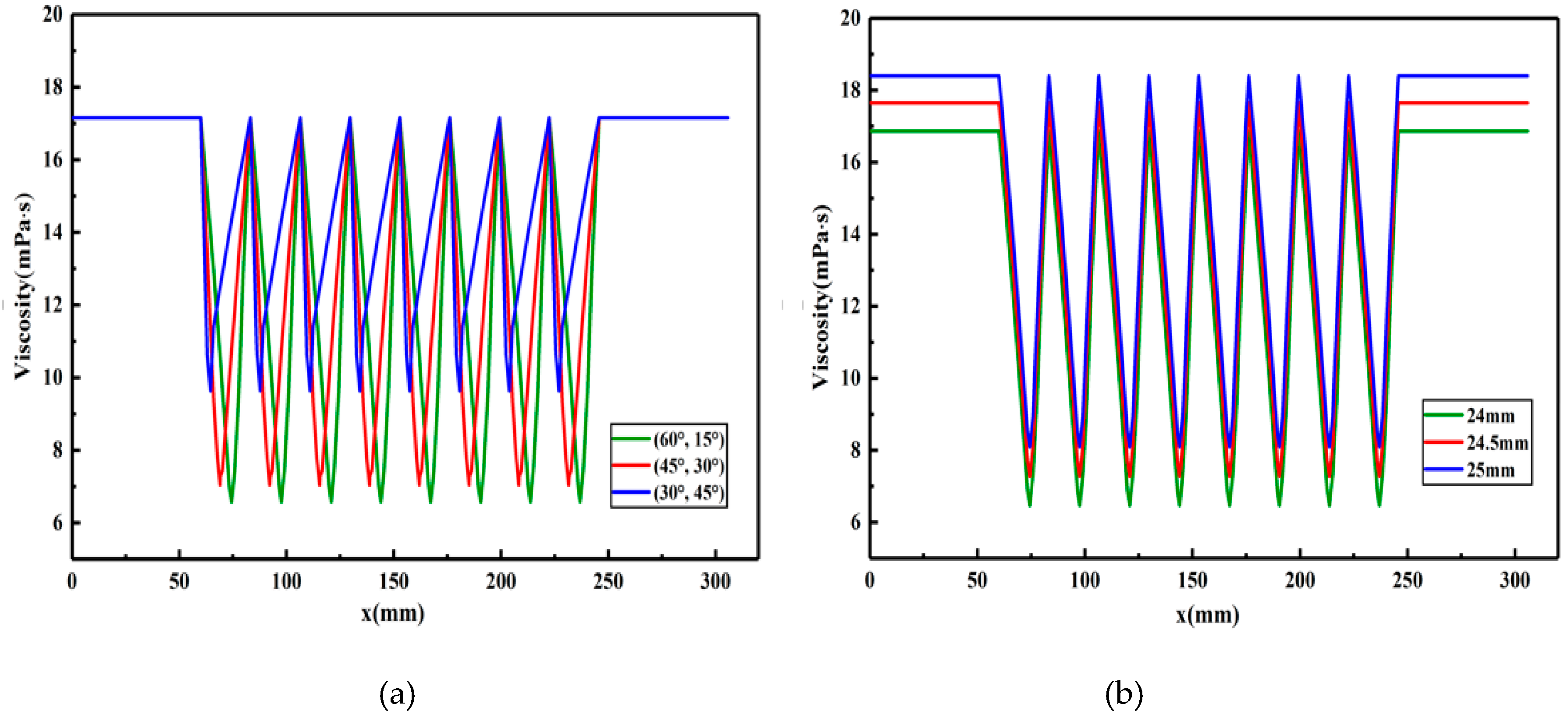
- When the polymer solution passes through the throttling section of the partial pressure tool, with decreasing front groove angle (and consequently increasing rear groove angle) and decreasing outer cylinder radius, the total pressure drop of the polymer solution increases. When the front groove angle and rear groove angle are 30° and 45°, respectively, the pressure drop reaches a maximum value of 1.77 MPa, and when the outer cylinder radius is 24 mm, the pressure drop reaches a maximum value of 1.32 MPa;
- (3)
- The apparent viscosity of the polymer solution is the same before and after flowing through the partial pressure tool. With increasing front groove angle (and consequently decreasing rear groove angle), the rate of the apparent viscosity decrease increases; however, the magnitude of the decrease is reduced. With increasing outer cylinder radius, the initial value of the apparent viscosity of the polymer solution increases.
- (4)
- Based on the concept of stability factor, the transition velocity equation is established, and the transition velocity of the polymer solution is calculated to be 50.29 m/s. When the velocity exceeds 50.29 m/s, the flow of the polymer solution changes from a laminar state to a turbulent state.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shao, Z.B.; Zhou, J.S.; Sun, G. Studies on Mechanical degradation of partially hydrolized polyacrylamidein course of polymer flooding: Changes in relative molecular mass, viscosity and related parameters. Oilfield Chem. 2005, 22, 73–76. [Google Scholar]
- Belden, W.M. Design and operations micellar-polymer pilot project facilities bell creek field. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, WY, USA, 14–16 May 1980. [Google Scholar]
- Wu, D.; Ai, G.; Chen, Y.; Han, L.; Lin, S.; Meng, X.; Liang, H. Rheology and stability of IOR produced liquid in daqing oilfield. In Proceedings of the SPE Asia Pacific Improved Oil Recovery Conference, Kuala Lumpur, Malaysia, 25–26 October 1999. [Google Scholar]
- Meyers, J.J. Alkaline-Surfactant-Polymer flood of the west kiehl, minnelusa unit. In Proceedings of the SPE/DOE Eighth Symposium on Enhanced Oil Recovery, Tulsa, Oklahoma, 22–24 April 1992. [Google Scholar]
- Clark, S.R. Design and Application of an Alkaline-Surfactant-Polymer Recovery System for the West Kiehl Field. SPE Adv. Technol. Ser. 1993, 1, 172–179. [Google Scholar] [CrossRef]
- Denny, D. Effect of elasticity on displacement efficiency: High concentration polymer flooding. J. Pet. Technol. 2009, 61, 50–51. [Google Scholar] [CrossRef]
- Wassmuth, F.R.; Gree, N.K. Polymer flood application to improve heavy oil recovery at east bodo. J. Can. Pet. Technol. 2009, 48, 55–61. [Google Scholar] [CrossRef]
- White, P.D.; Moss, J.T. Thermal Recovery Methods; PennWell Publishing Company: Tulsa, OK, USA, 1983. [Google Scholar]
- Swulius, T.M. Porosity calibration of neutron logs, SACROC unit. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 16–19 September 1984. [Google Scholar]
- Lerma, M.K.; Giuliani, M.A. Cost-effective methods of profile control in mature waterflood injectors. In Proceedings of the SPE Western Regional Meeting, Long Beach, CA, USA, 23–25 March 1994. [Google Scholar]
- Yin, H.J.; Wang, D.M.; Zhong, H.Y. Study on flow behavoirs of viscoelastic polymer solution in micropore with dead end. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Lee, S.J.; Kim, D.H.; Huh, C.; Pope, G.A. Development of a comprehensive rheological property database for EOR polymers. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Silva, I.P.G.; Aguiar, A.A.; Amaury, A.; Rezende, V.P.; Viviane, P. A polymer flooding mechanism for mature oil fields: Laboratory measurements and field results interpretation. J. Pet. Sci. Eng. 2018, 161, 468–475. [Google Scholar] [CrossRef]
- Li, H.C. Overview of separate injection technique for polymer flooding in Daqing oilfield. Oil Gas Geol. 2012, 33, 296–301. [Google Scholar]
- Geng, C.H.; Liu, Q.W. Study on Polymer Single Pipe Layered Injection Process. Pet. Geol. Oilfield Dev. Daqing 2006, 25, 38–41. [Google Scholar]
- Wu, G.H.; Chen, C.K.; Ju, S.H. On the flow of a polymer melt passing over a transverse slot. J. Polym. Eng. 1999, 19, 175–196. [Google Scholar] [CrossRef]
- Huang, B.; Li, X.; Fu, C.; Wang, Y.; Cheng, H. Study rheological behavior of polymer solution in different-medium-injection-tool. Polymers 2019, 11, 319. [Google Scholar] [CrossRef]
- Malkus, D.S.; Bernstein, B. Flow of a curtiss-bird fluid over a transverse slot using the finite element drift-function method. J. Non-Newton. Fluid Mech. 1984, 16, 77–116. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, H.Q.; Yang, Y.J. Pressure distribution on the wall of the inner cylinder reciprocating axially to the unsteady flow of viscoelastic fluid in eccentric annulus. J. Hydrodyn. 2006, 18, 606–612. [Google Scholar] [CrossRef]
- Hidema, R.; Murao, I.; Komoda, Y.; Suzuki, H. Effects of the extensional rheological properties of polymer solutions on vortex shedding and turbulence characteristics in a two-dimensional turbulent flow. J. Non-Newton. Fluid Mech. 2018, 254, 1–11. [Google Scholar] [CrossRef]
- Wouter, J.T.; Robert, R. Dissipation in unsteady turbulence. Phys. Rev. Fluids 2017, 2, 022601. [Google Scholar]
- Xin, X.K.; Yu, G.M.; Chen, Z.G.; Wu, K.L.; Dong, X.H.; Zhu, Z.Y. Effect of polymer degradation on polymer flooding in heterogeneous reservoirs. Polymers 2018, 10, 857. [Google Scholar] [CrossRef]
- Al-Shakry, B.; Skauge, T.; Shiran, B.S.; Skauge, A. Impact of mechanical degradation on polymer injectivity in porous media. Polymers 2018, 10, 742. [Google Scholar] [CrossRef]
- Takamure, K.; Sakai, Y.; Ito, Y.; Iwano, K.; Hayase, T. Dissipation scaling in the transition region of turbulent mixing layer. Int. J. Heat Fluid Flow 2019, 75, 77–85. [Google Scholar] [CrossRef]
- Dodge, D.W.; Metzner, A.B. Turbulent flow of non-newtonian systems. AICHE J. 2010, 5, 189–204. [Google Scholar] [CrossRef]
- Chen, J.G.; Zhou, Y.; Antonia, R.A.; Zhou, T.M. Characteristics of the turbulent energy dissipation rate in a cylinder wake. J. Fluid Mech. 2018, 835, 271–300. [Google Scholar] [CrossRef]
- Shukhman, I.G.; Tewner, S.W.; Cohen, J. Vortical disturbances in a linearly stratifed linear shear flow. I. linear theory. Phys. Fluids 2015, 27, 024104. [Google Scholar] [CrossRef]
- Vassilicos, J.C. Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 2015, 47, 95–114. [Google Scholar] [CrossRef]
- Liu, N.Z.; Wang, Y.R.; Liu, X.L.; Liu, C.J. Stability of non-newtonian fluid and its flow pattern discrimination. Nat. Gas Ind. 2003, 23, 53–57. [Google Scholar]
- Liu, C.J.; Liu, H.X. Discussion on the z value of the quasi number for judging liquid flow state. J. Southwest Pet. Inst. 1981, 2, 12–23. [Google Scholar]
- Manneville, P. Laminar-turbulent patterning in transitional flows. Entropy 2017, 19, 316. [Google Scholar] [CrossRef]
- Gavrilov1, A.A.; Rudyak, V.Y. Direct numerical simulation of the turbulent flows of power-law fluids in a circular pipe. Thermophys. Aeromech. 2016, 23, 473–486. [Google Scholar] [CrossRef]
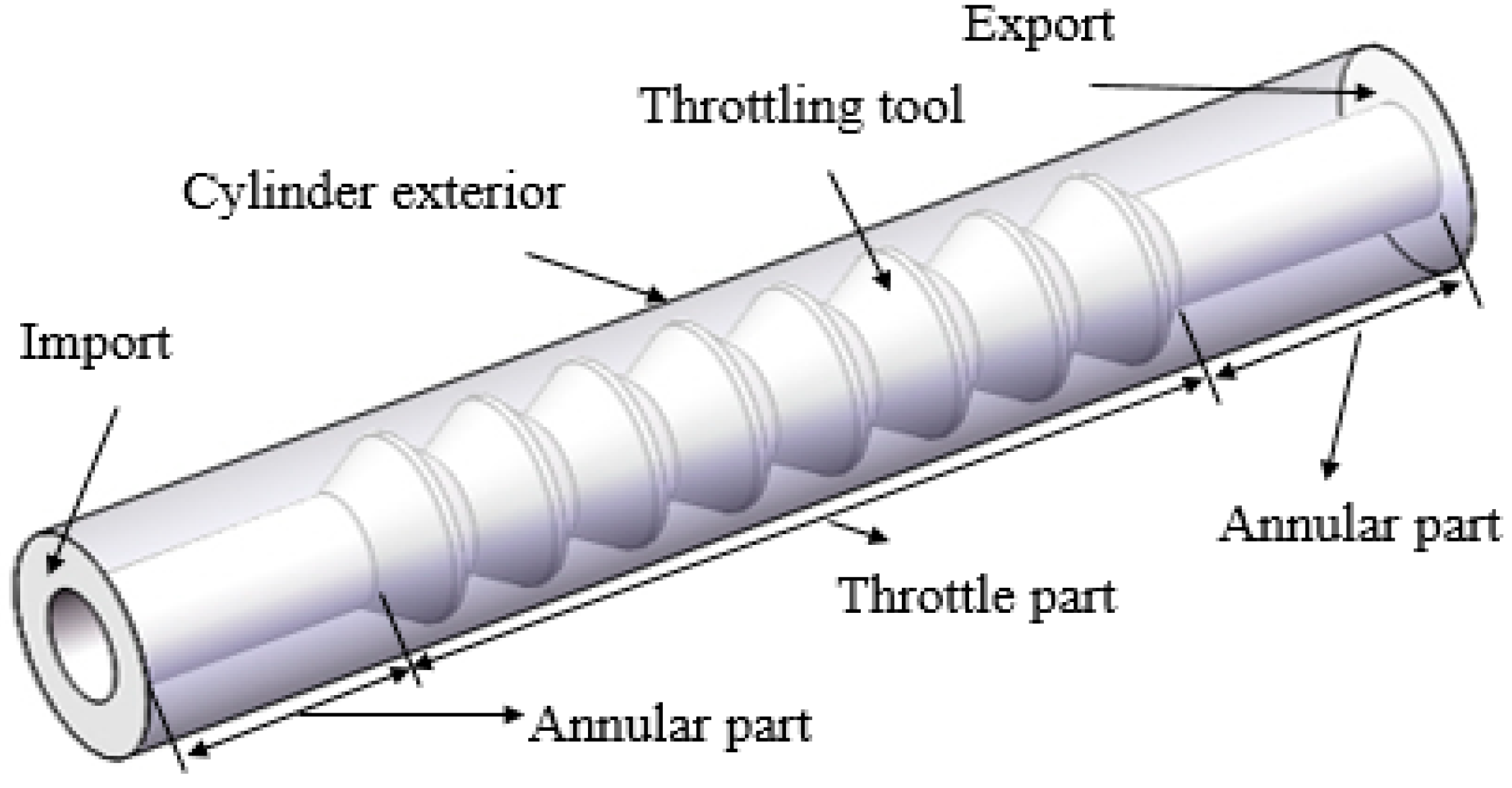
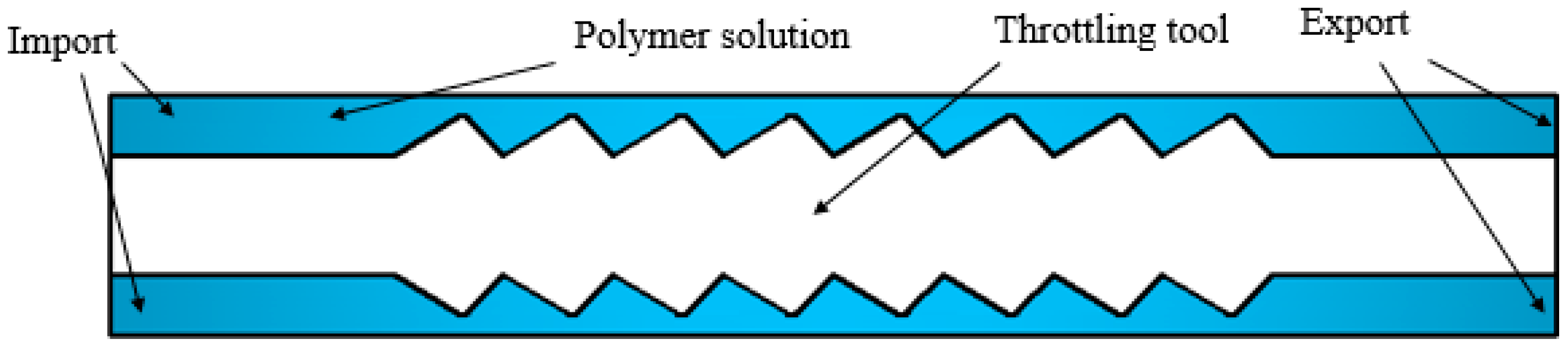
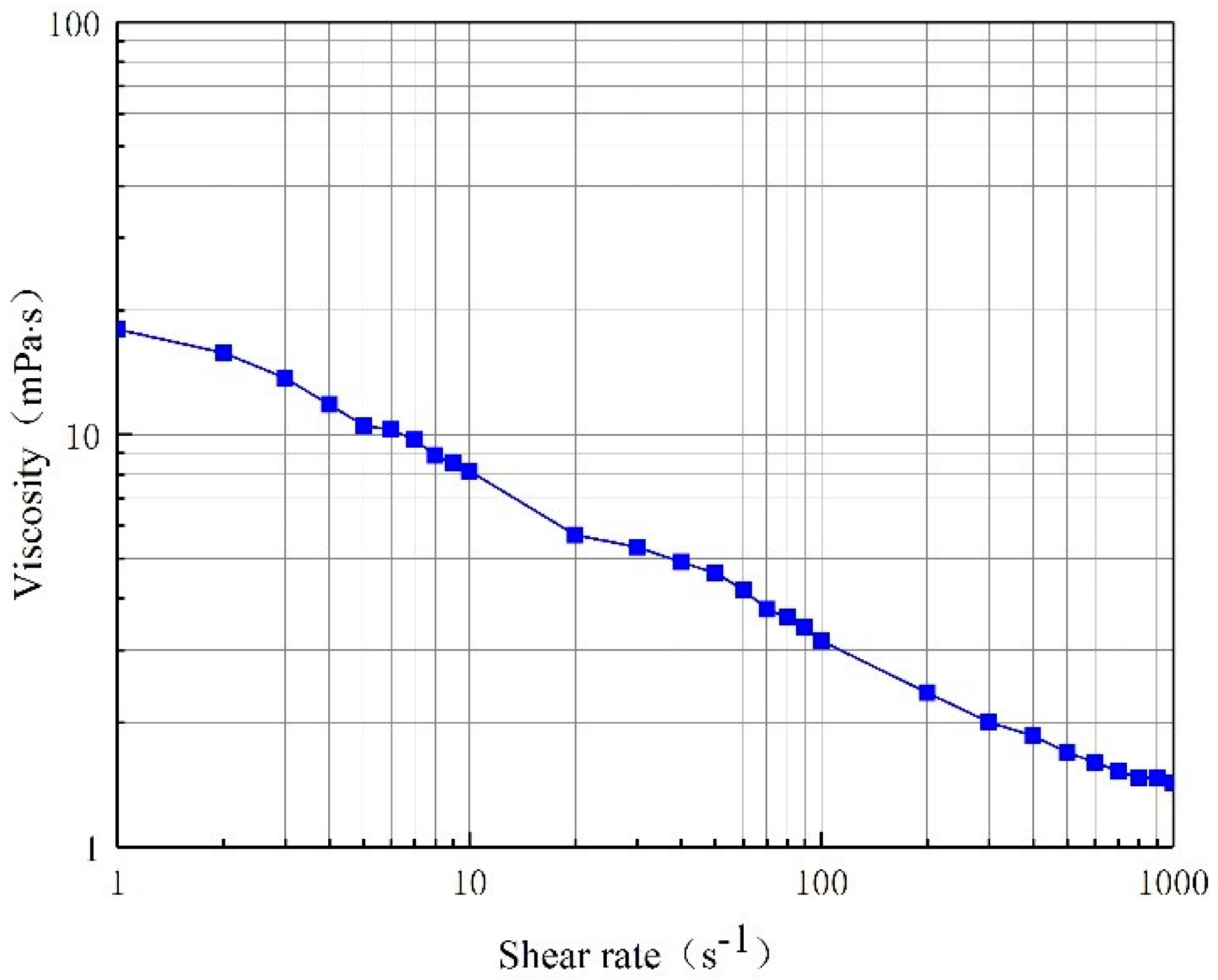


| Chemical Composition | Na+, K+ | HCO3− | CO32− | SO42− | Cl− | Mg2+ | Ca2+ |
|---|---|---|---|---|---|---|---|
| Concentration(mg/L) | 132.53 | 52.65 | 22.38 | 25.17 | 28.72 | 7.69 | 14.28 |
| Radius of the Outer Cylinder (mm) | Radius of the Inner Cylinder (mm) | Length of the Annular Flow Channel L (mm) |
|---|---|---|
| 24 | 12 | 60 |
| Angle (°) | Angle (°) | Length (mm) | Length (mm) | Length (mm) | Length (mm) | Length (mm) | Radius (mm) | Radius (mm) | Radius (mm) |
|---|---|---|---|---|---|---|---|---|---|
| 30 | 45 | 60 | 13.392 | 1 | 1.414 | 7.414 | 2 | 24 | 12 |
| Concentration (mg/L) | Consistency Coefficient k | Rheological Index n | Constitutive Equation |
|---|---|---|---|
| 1000 | 20.26 | 0.61 |
| Angle (°) | Angle (°) | Length (mm) | Length (mm) | Length (mm) | Length (mm) | Length (mm) | Radius (mm) | Radius (mm) | Radius (mm) |
|---|---|---|---|---|---|---|---|---|---|
| 30 | 45 | 60 | 13.392 | 1 | 1.414 | 7.414 | 2 | 24 | 12 |
| 45 | 30 | 60 | 7.732 | 1.414 | 1 | 12.841 | 2 | 24 | 12 |
| 60 | 15 | 60 | 2.830 | 1.732 | 0.518 | 17.542 | 2 | 24 | 12 |
| 30 | 45 | 60 | 13.392 | 1 | 1.414 | 7.414 | 2 | 24 | 12 |
| 30 | 45 | 60 | 13.392 | 1 | 1.414 | 7.414 | 2 | 24.5 | 12 |
| 30 | 45 | 60 | 13.392 | 1 | 1.414 | 7.414 | 2 | 25 | 12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, B.; Hu, X.; Fu, C.; Liu, C.; Wang, Y.; An, X. Rheological Model and Transition Velocity Equation of a Polymer Solution in a Partial Pressure Tool. Polymers 2019, 11, 855. https://doi.org/10.3390/polym11050855
Huang B, Hu X, Fu C, Liu C, Wang Y, An X. Rheological Model and Transition Velocity Equation of a Polymer Solution in a Partial Pressure Tool. Polymers. 2019; 11(5):855. https://doi.org/10.3390/polym11050855
Chicago/Turabian StyleHuang, Bin, Xinyu Hu, Cheng Fu, Chongjiang Liu, Ying Wang, and Xu An. 2019. "Rheological Model and Transition Velocity Equation of a Polymer Solution in a Partial Pressure Tool" Polymers 11, no. 5: 855. https://doi.org/10.3390/polym11050855
APA StyleHuang, B., Hu, X., Fu, C., Liu, C., Wang, Y., & An, X. (2019). Rheological Model and Transition Velocity Equation of a Polymer Solution in a Partial Pressure Tool. Polymers, 11(5), 855. https://doi.org/10.3390/polym11050855




