One-Dimensional Theoretical Solution and Two-Dimensional Numerical Simulation for Functionally-Graded Piezoelectric Cantilever Beams with Different Properties in Tension and Compression
Abstract
1. Introduction
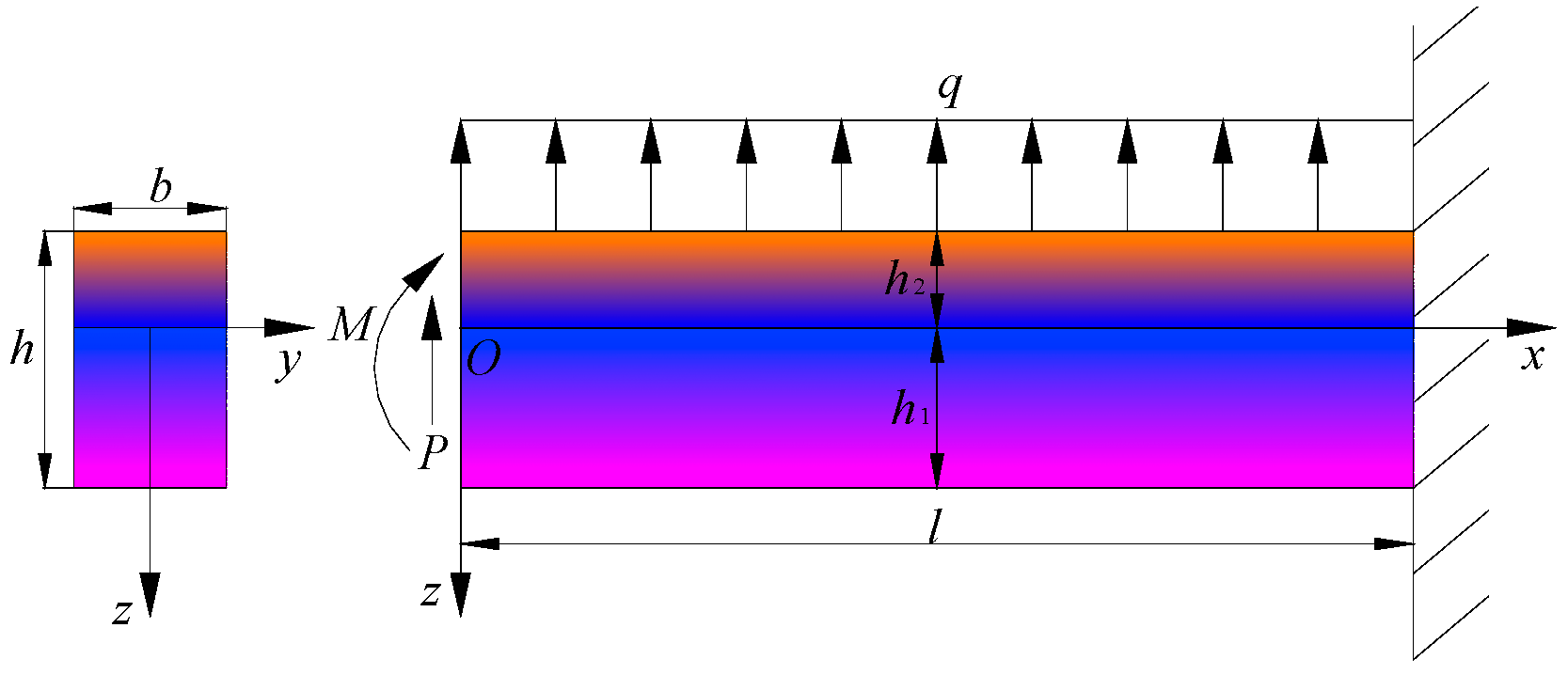
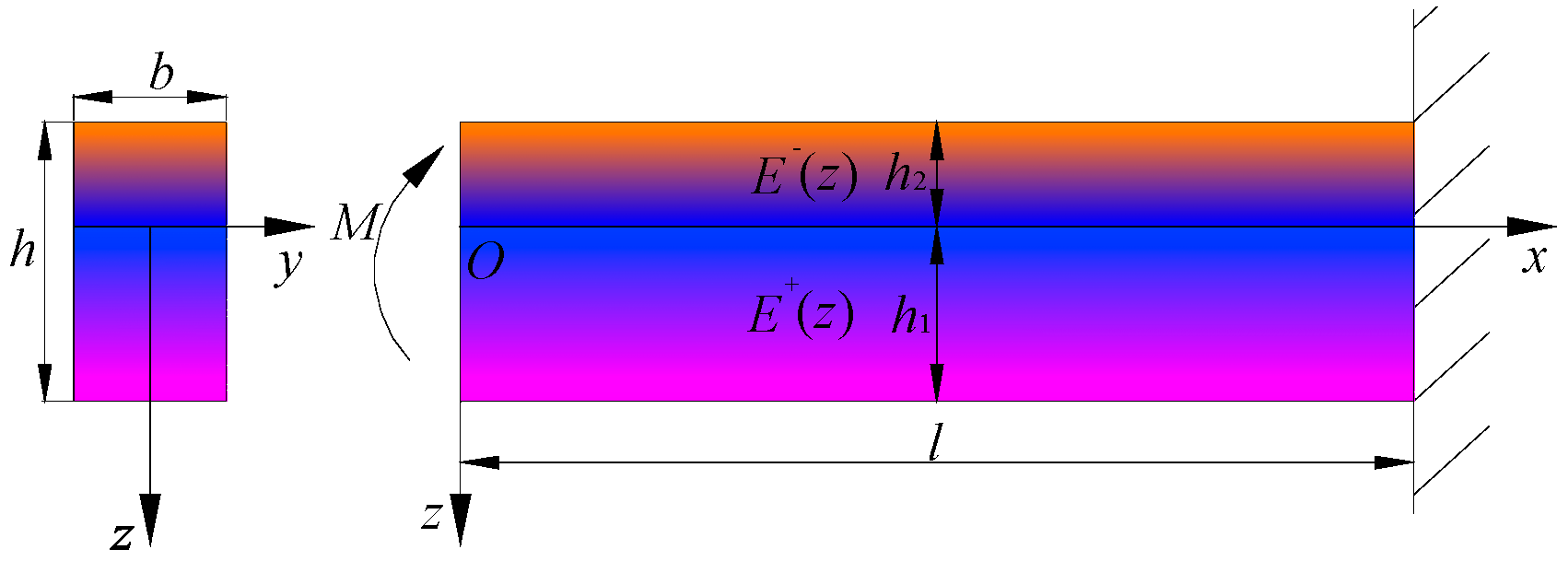
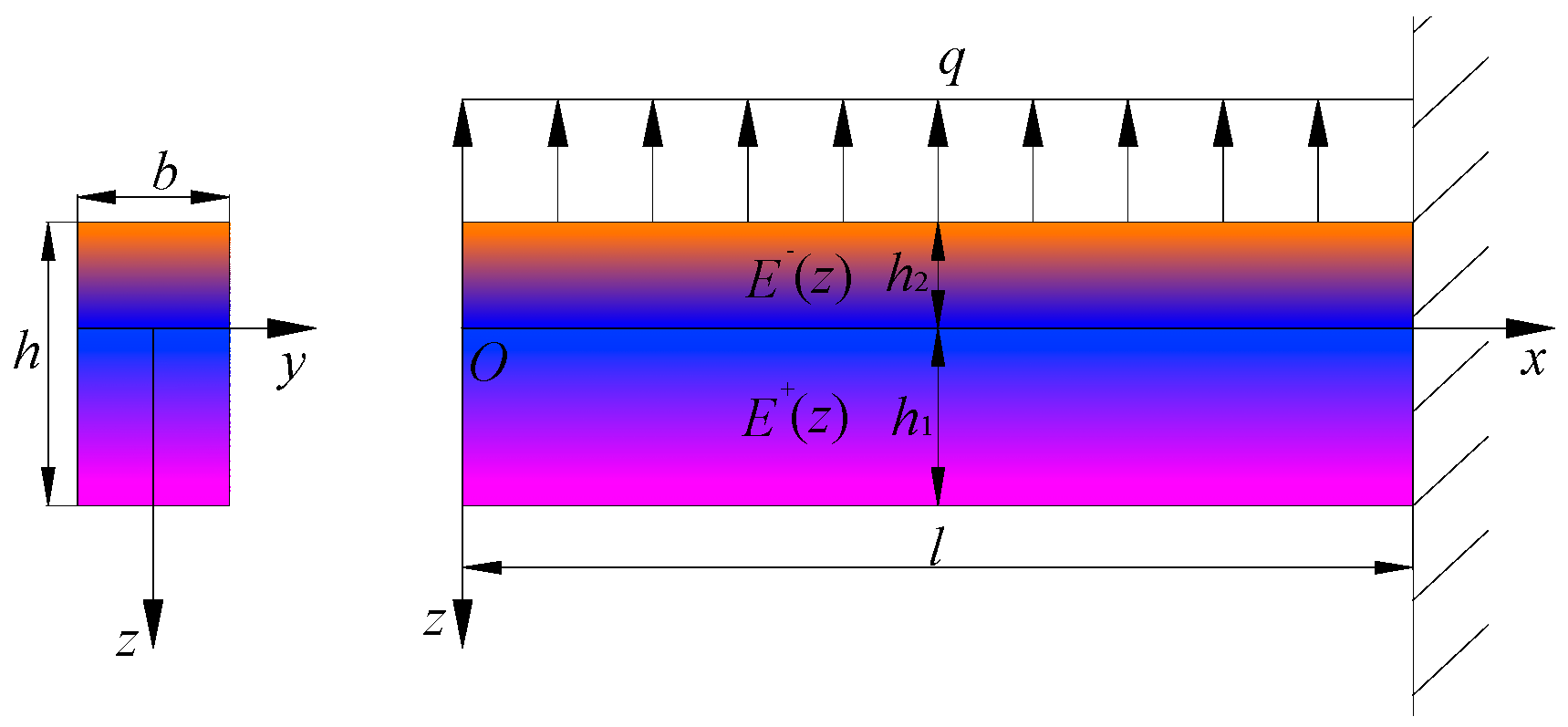
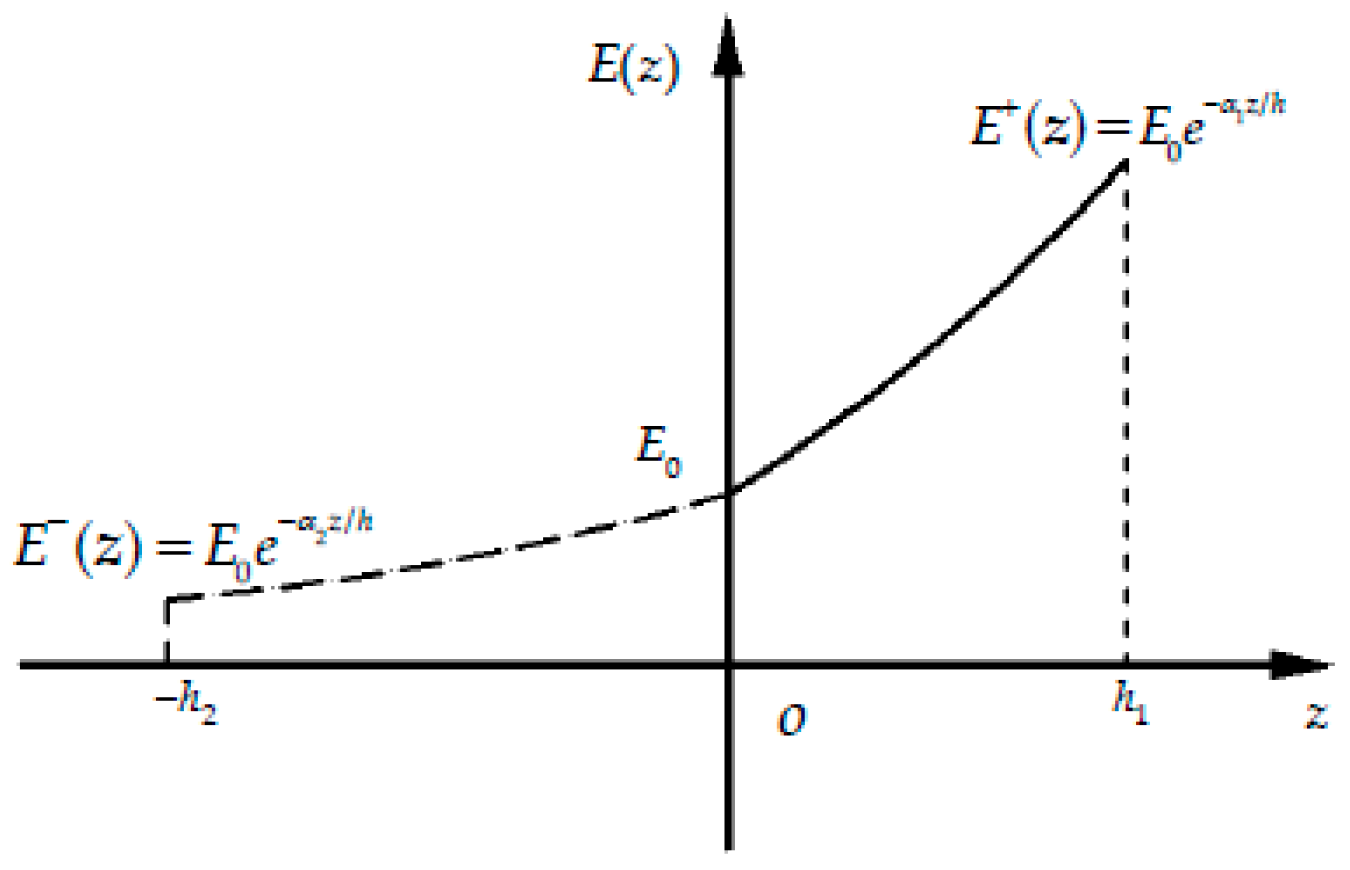
2. The Problem Description
3. One-Dimensional Theoretical Solution
3.1. Mechanical Stress and Deflection
3.2. Electrical Displacement
4. Two-Dimensional Numerical Simulation
4.1. Constitutive Equation of Piezoelectrical Materials
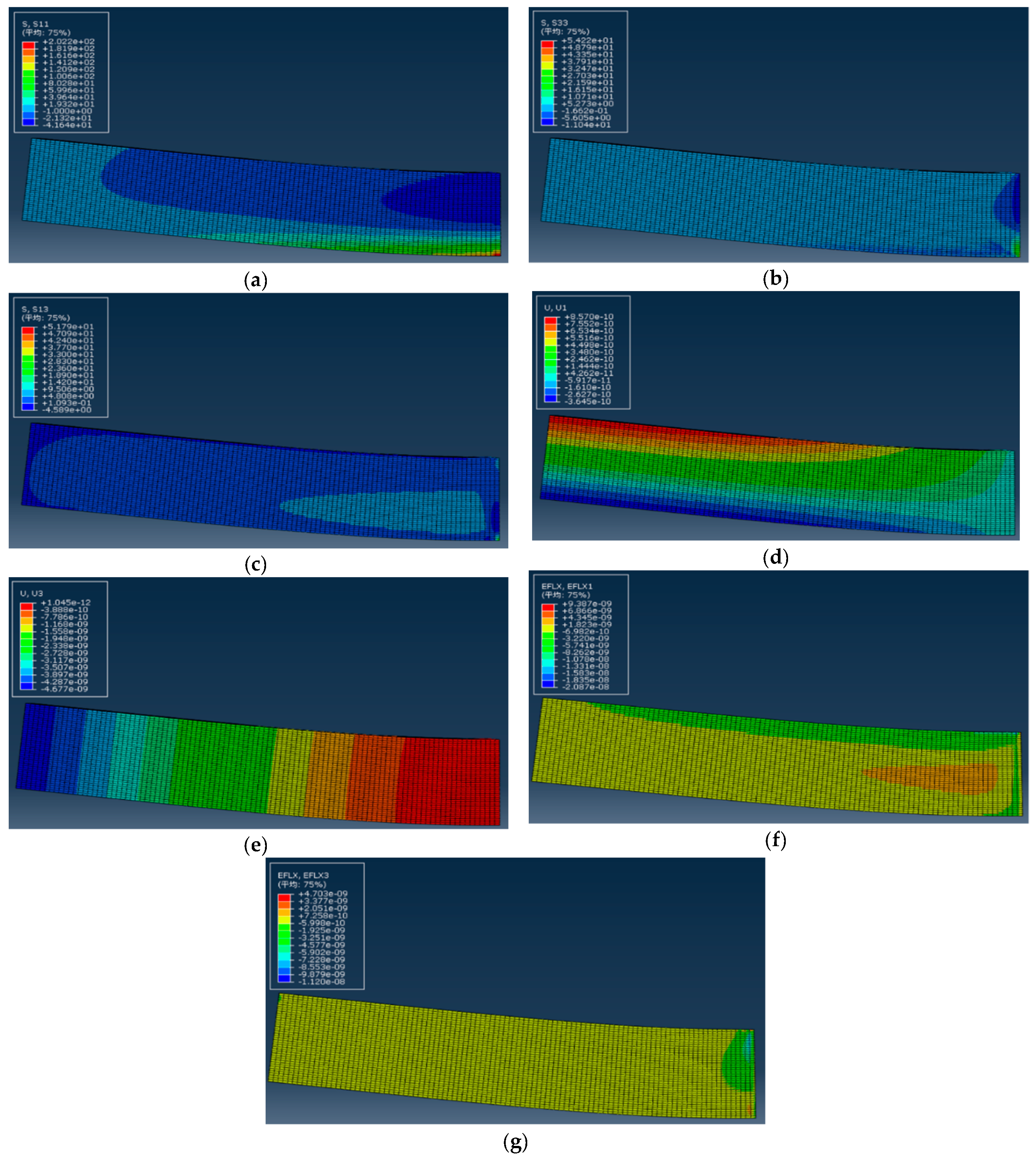
4.2. Modeling and Simulation
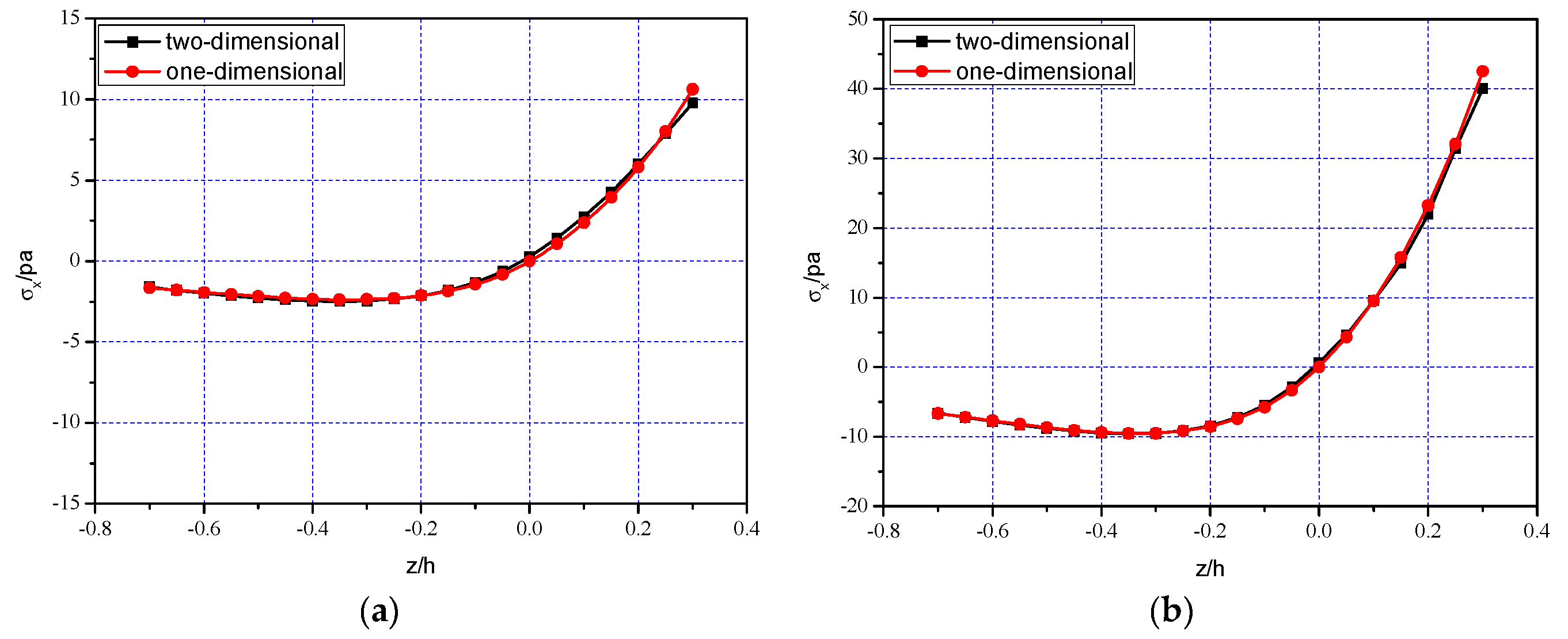
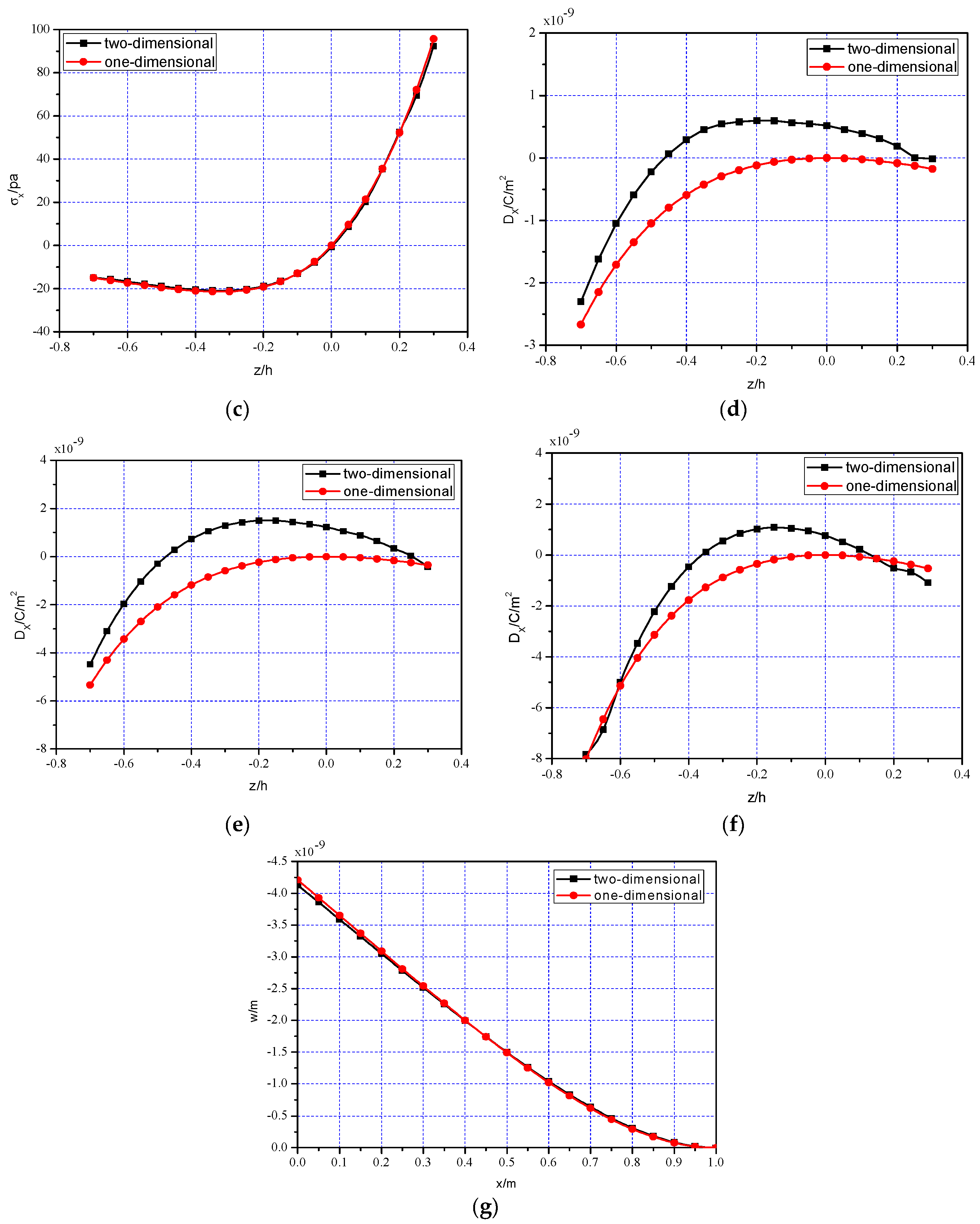
5. Comparisons and Discussions
5.1. Comparison of One-Dimensional Solution and Two-Dimensional Simulation
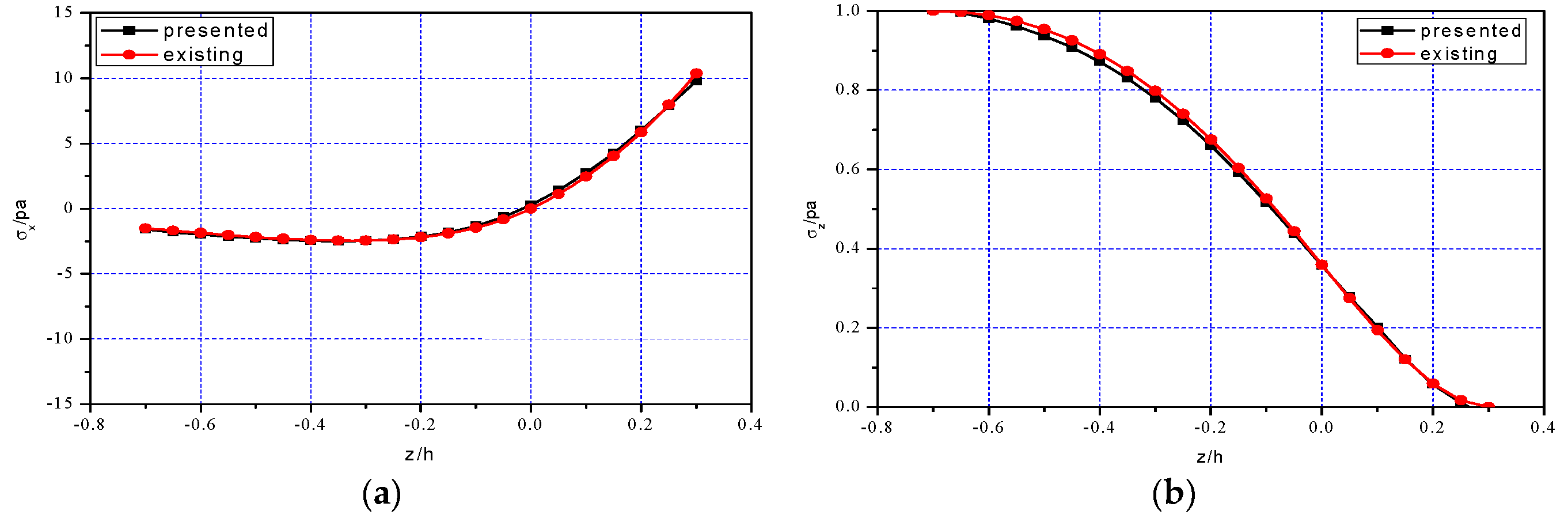
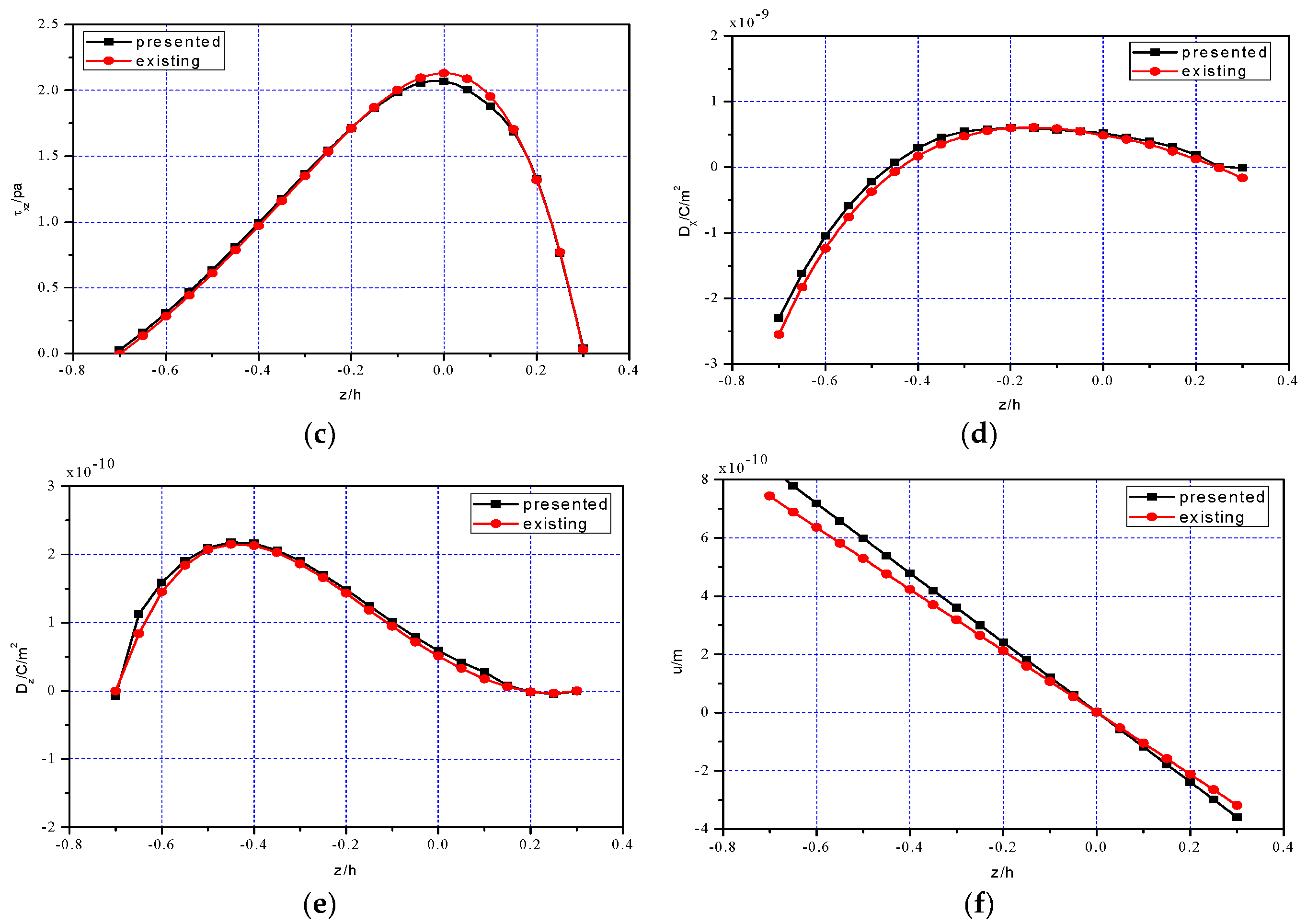
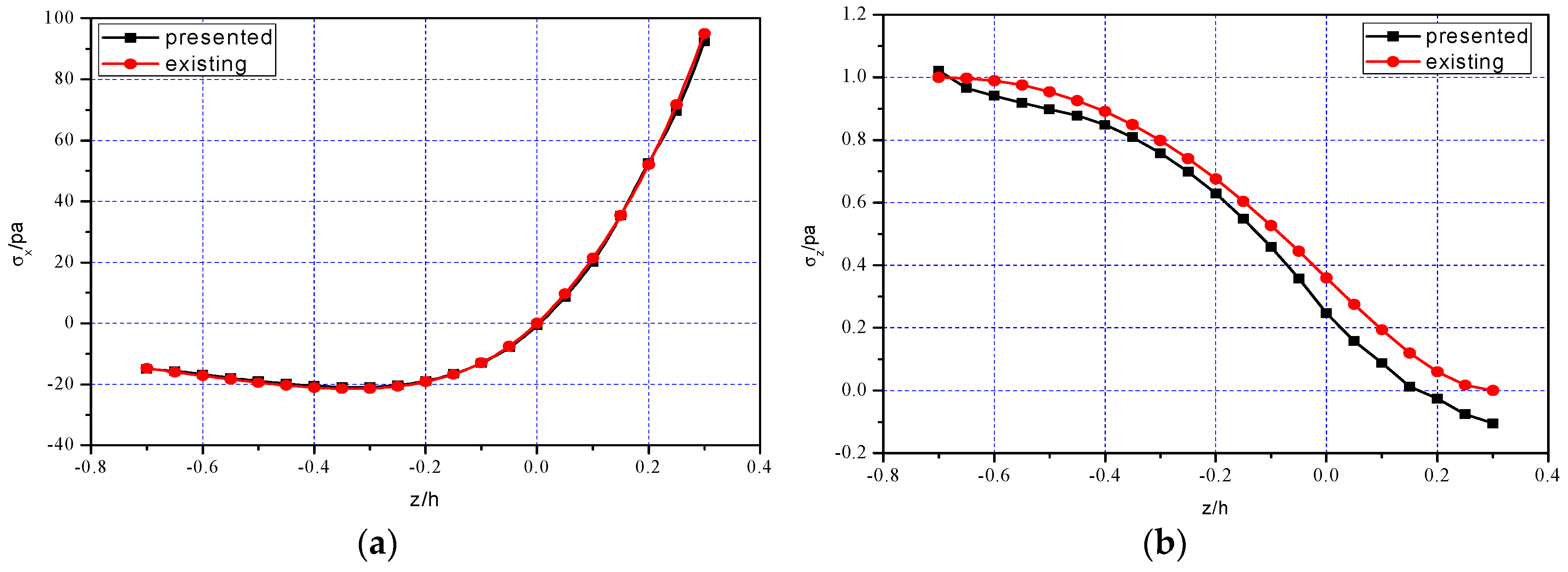
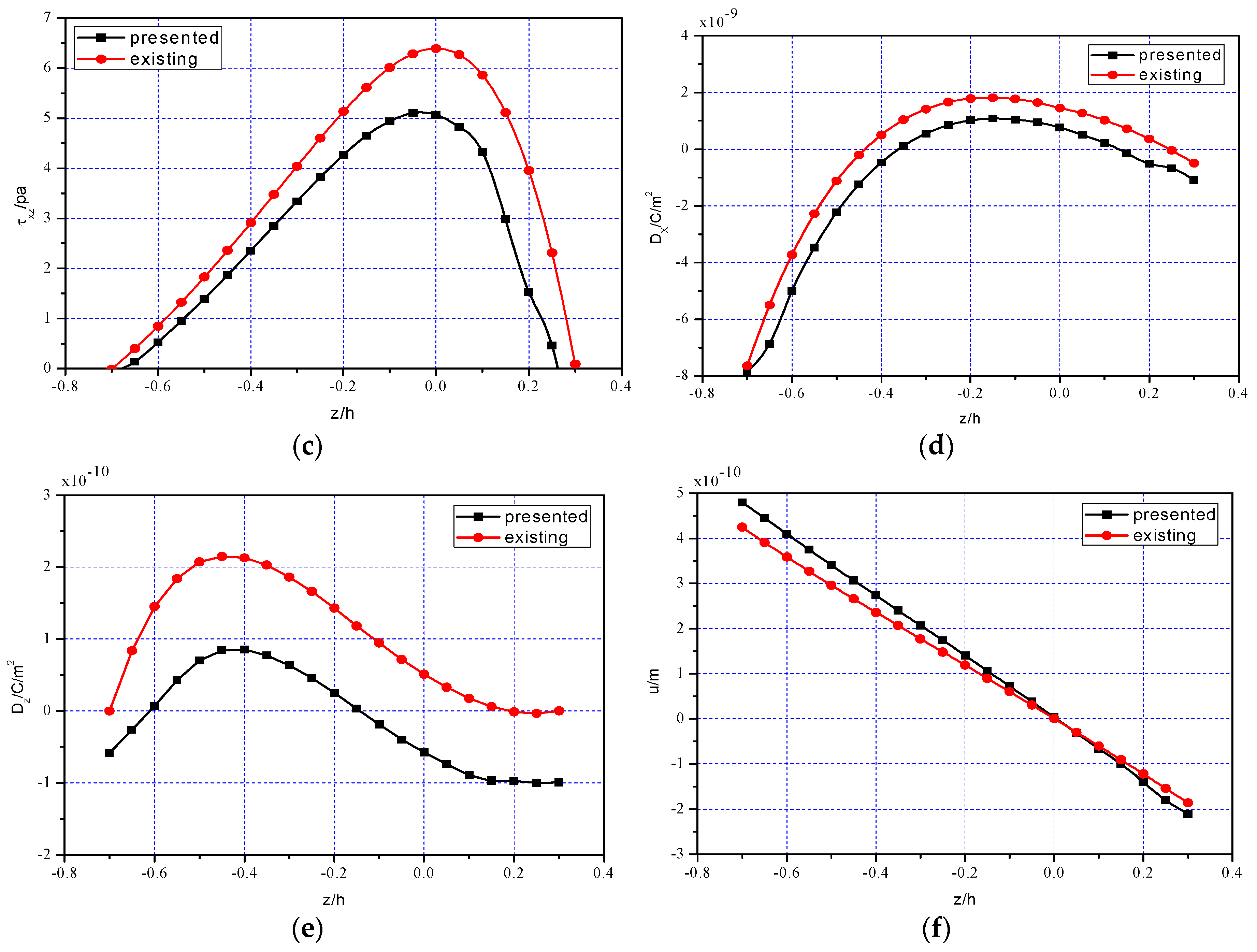
5.2. Comparison of Two-Dimensional Numerical Simulation and Existing Solution
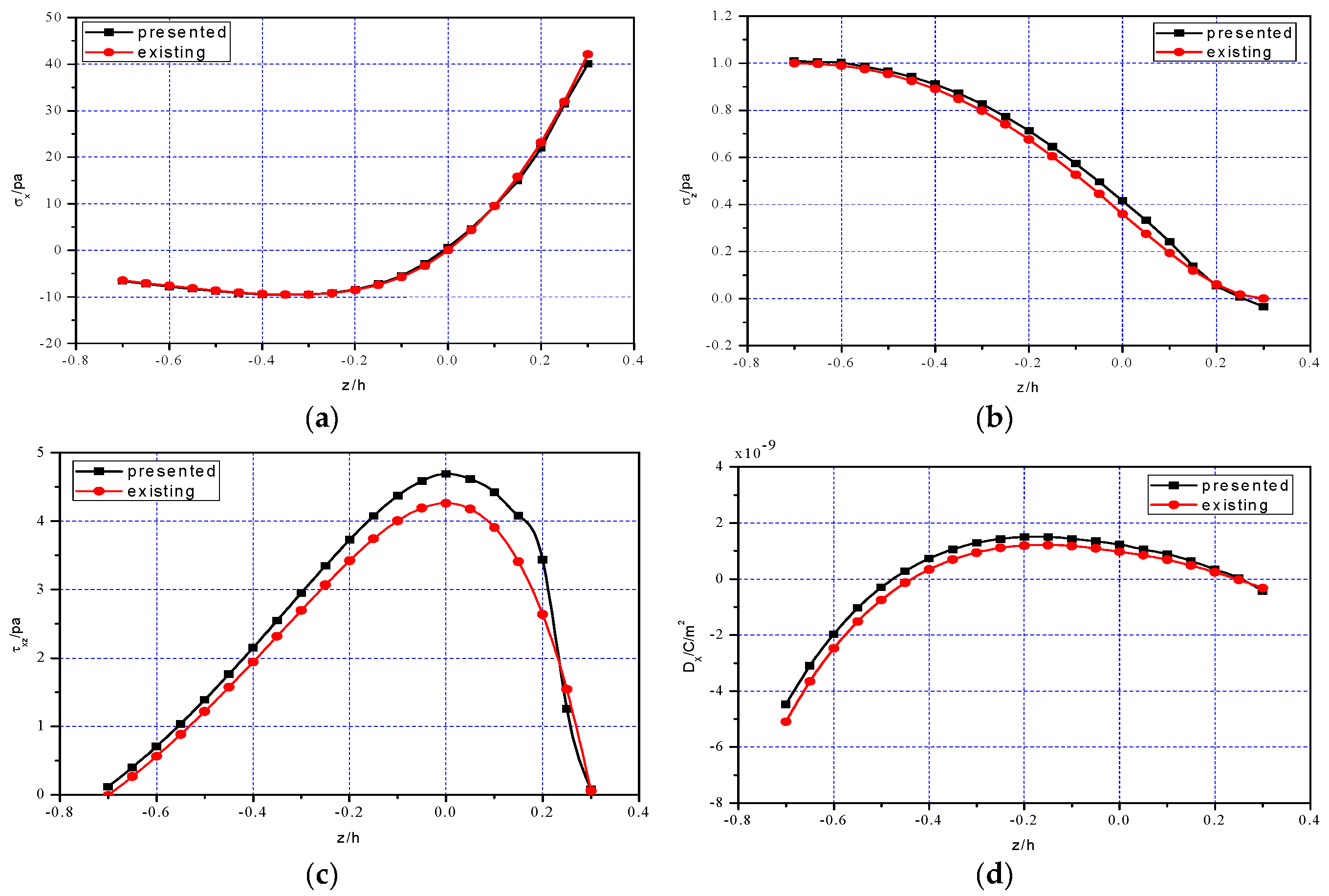
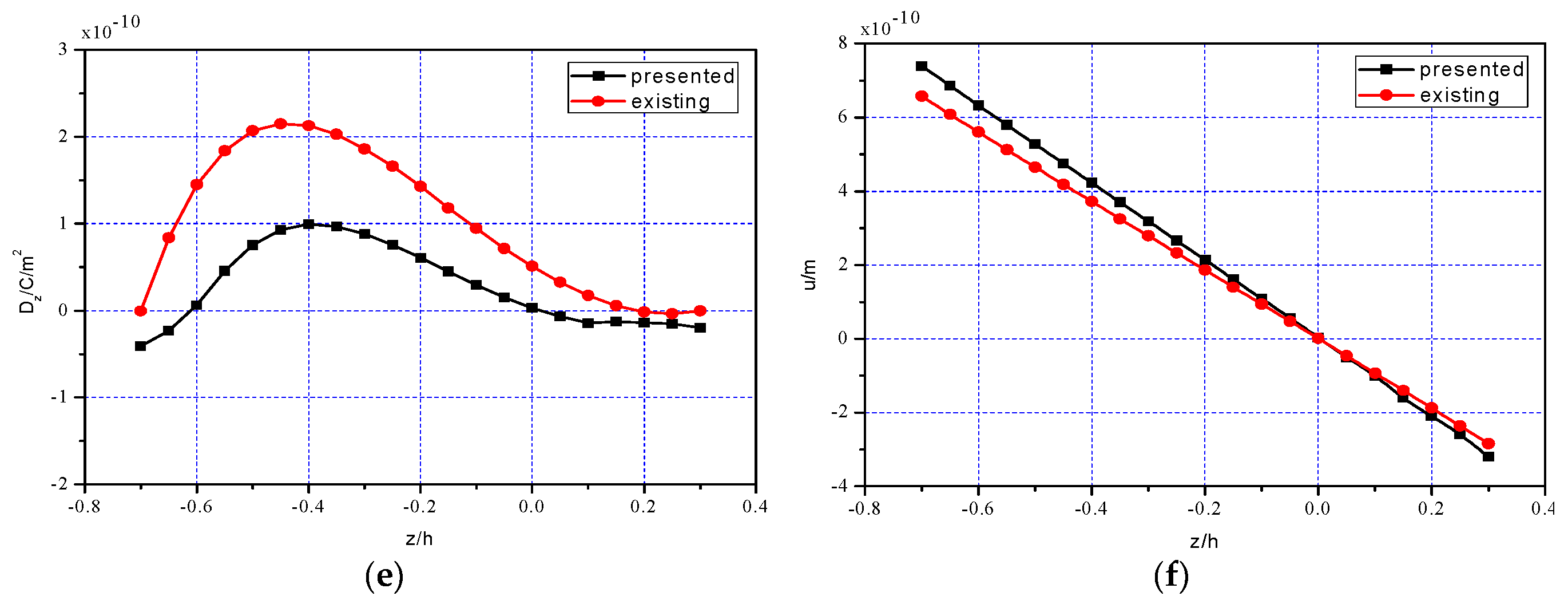
5.3. Comparison of One-Dimensional Theoretical Solution and Existing Solutions
5.4. Evolution for One-Dimensional Theoretical Solution
5.5. Discussion on Flexible FGPM Cantilever Beam
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, Y.; Gong, L.; Hu, X.; Zhao, Y.; Chen, H.; Feng, L.; Zhang, D. Aligned P(VDF-TrFE) nanofibers for enhanced piezoelectric directional strain sensing. Polymers 2018, 10, 364. [Google Scholar] [CrossRef] [PubMed]
- Kaczmarek, H.; Królikowski, B.; Chylińska, M.; Klimiec, E.; Bajer, D. Piezoelectric films based on polyethylene modified by aluminosilicate filler. Polymers 2019, 11, 1345. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, V.F.; Correia, D.M.; Ribeiro, C.; Fernandes, M.M.; Lanceros-Méndez, S. Fluorinated polymers as smart materials for advanced biomedical applications. Polymers 2018, 10, 161. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Wu, Y.S.; Kan, E.C.; Fan, J. Breathable and flexible piezoelectric ZnO@PVDF fibrous nanogenerator for wearable applications. Polymers 2018, 10, 745. [Google Scholar] [CrossRef] [PubMed]
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Zhu, X.; Meng, Z. Operational principle, fabrication and displacement characteristics of a functionally gradient piezoelectric ceramic actuator. Sens. Actuators A Phys. 1995, 48, 169–176. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, Q.; Meng, Z. A functionally gradient piezoelectric actuator prepared by powder metallurgical process in PNN-PZ-PT system. J. Mater. Sci. Lett. 1995, 14, 516–518. [Google Scholar] [CrossRef]
- Kruusing, A. Analysis and optimization of loaded cantilever beam microactuators. Smart Mater. Struct. 2000, 9, 186–196. [Google Scholar] [CrossRef]
- Wang, C.M.; Ang, K.K.; Ajit, A. Shape control of laminated cantilevered beams with piezoelectric actuators. J. Intell. Mater. Syst. Struct. 1999, 10, 164–175. [Google Scholar] [CrossRef]
- Yang, S.; Ngoi, B. Shape control of beams by piezoelectric actuators. AIAA J. 2015, 38, 2292–2298. [Google Scholar] [CrossRef]
- Smits, J.G.; Dalke, S.I.; Cooney, T.K. The constituent equations of piezoelectric bimorphs. Sens. Actuators A Phys. 1991, 28, 41–61. [Google Scholar] [CrossRef]
- Elshafei, M.A.; Farid, A.; Omer, A.A. Modeling of torsion actuation of beams using inclined piezoelectric actuators. Arch. Appl. Mech. 2015, 85, 171–189. [Google Scholar] [CrossRef]
- Yu, T.; Zhong, Z. Bending analysis of a functionally graded piezoelectric cantilever beam. Sci. China G Phys. Mech. Astron. 2007, 50, 97–108. [Google Scholar] [CrossRef]
- Zhong, Z.; Yu, T. Electroelastic analysis of functionally graded piezoelectric material beam. J. Intell. Mater. Syst. Struct. 2008, 19, 707–713. [Google Scholar] [CrossRef]
- Huang, D.J.; Ding, H.J.; Chen, W.Q. Piezoelasticity solutions for functionally graded piezoelectric beams. Smart Mater. Struct. 2007, 16, 687–695. [Google Scholar] [CrossRef]
- Huang, D.J.; Ding, H.J.; Chen, W.Q. Analysis of functionally graded and laminated piezoelectric cantilever actuators subjected to constant voltage. Smart Mater. Struct. 2008, 17, 1–11. [Google Scholar] [CrossRef]
- Shi, Z.F.; Chen, Y. Functionally graded piezoelectric cantilever beam under load. Arch. Appl. Mech. 2004, 74, 237–247. [Google Scholar] [CrossRef]
- Xiang, H.J.; Shi, Z.F. Electrostatic analysis of functionally graded piezoelectric cantilevers. J. Intell. Mater. Syst. Struct. 2007, 18, 719–726. [Google Scholar] [CrossRef]
- Yao, R.X.; Shi, Z.F. Steady-State forced vibration of functionally graded piezoelectric beams. J. Intell. Mater. Syst. Struct. 2011, 22, 769–779. [Google Scholar] [CrossRef]
- Shi, Z.F.; Li, J.L.; Yao, R.X. Solution modification of a piezoelectric bimorph cantilever under loads. J. Intell. Mater. Syst. Struct. 2015, 26, 2028–2041. [Google Scholar] [CrossRef]
- Barak, M.M.; Currey, J.D.; Weiner, S.; Shahar, R. Are tensile and compressive Young’s moduli of compact bone different. J. Mech. Behav. Biomed. Mater. 2009, 2, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Destrade, M.; Gilchrist, M.D.; Motherway, J.A.; Murphy, J.G. Bimodular rubber buckles early in bending. Mech. Mater. 2010, 42, 469–476. [Google Scholar] [CrossRef]
- Ambartsumyan, S.A. Elasticity Theory of Different Moduli; Wu, R.F.; Zhang, Y.Z., Translators; China Railway Publishing House: Beijing, China, 1986. [Google Scholar]
- Zhang, Y.Z.; Wang, Z.F. Finite element method of elasticity problem with different tension and compression moduli. Comput. Struct. Mech. Appl. 1989, 6, 236–245. [Google Scholar]
- Ye, Z.M.; Chen, T.; Yao, W.J. Progresses in elasticity theory with different moduli in tension and compression and related FEM. Mech. Eng. 2004, 26, 9–14. [Google Scholar]
- Sun, J.Y.; Zhu, H.Q.; Qin, S.H.; Yang, D.L.; He, X.T. A review on the research of mechanical problems with different moduli in tension and compression. J. Mech. Sci. Technol. 2010, 24, 1845–1854. [Google Scholar] [CrossRef]
- He, X.T.; Wang, Y.Z.; Shi, S.J.; Sun, J.Y. An electroelastic solution for functionally graded piezoelectric material beams with different moduli in tension and compression. J. Intell. Mater. Syst. Struct. 2018, 29, 1649–1669. [Google Scholar] [CrossRef]
- Yao, W.J.; Ye, Z.M. Analytical solution for bending beam subject to lateral force with different modulus. Appl. Math. Mech. 2004, 25, 1107–1117. [Google Scholar]
- He, X.T.; Li, W.M.; Sun, J.Y.; Wang, Z.X. An elasticity solution of functionally graded beams with different moduli in tension and compression. Mech. Adv. Mater. Struct. 2018, 25, 143–154. [Google Scholar] [CrossRef]
- Li, X.; Dong, J.; Sun, J.Y.; He, X.T. One-dimensional and two-dimensional analytical solutions for functionally graded beams with different moduli in tension and compression. Materials 2018, 11, 830. [Google Scholar] [CrossRef]
- Yang, D.Q.; Liu, Z.X. Analytical solution for bending of a piezoelectric cantilever beam under an end load. Chin. Q. Mech. 2003, 24, 327–333. [Google Scholar]
- Ruan, X.P.; Danforth, S.C.; Safari, A.; Chou, T.W. Saint-Venant end effects in piezoceramic materials. Int. J. Solids Struct. 2000, 37, 2625–2637. [Google Scholar] [CrossRef]
- He, X.T.; Chen, S.L.; Sun, J.Y. Applying the equivalent section method to solve beam subjected to lateral force and bending-compression column with different moduli. Int. J. Mech. Sci. 2007, 49, 919–924. [Google Scholar] [CrossRef]
- Merupo, V.I.; Guiffard, B.; Seveno, R.; Tabellout, M.; Kassiba, A. Flexoelectric response in soft polyurethane films and their use for large curvature sensing. J. Appl. Phys. 2017, 122, 144101. [Google Scholar] [CrossRef]
- Seveno, R.; Guiffard, B. Ultra large deflection of thin PZT/aluminum cantilever beam. Funct. Mater. Lett. 2018, 8, 1550051. [Google Scholar] [CrossRef]
- He, X.T.; Chen, S.L. Biparametric perturbation solution of large deflection problem of cantilever beams. Appl. Math. Mech. 2006, 27, 453–460. [Google Scholar] [CrossRef]
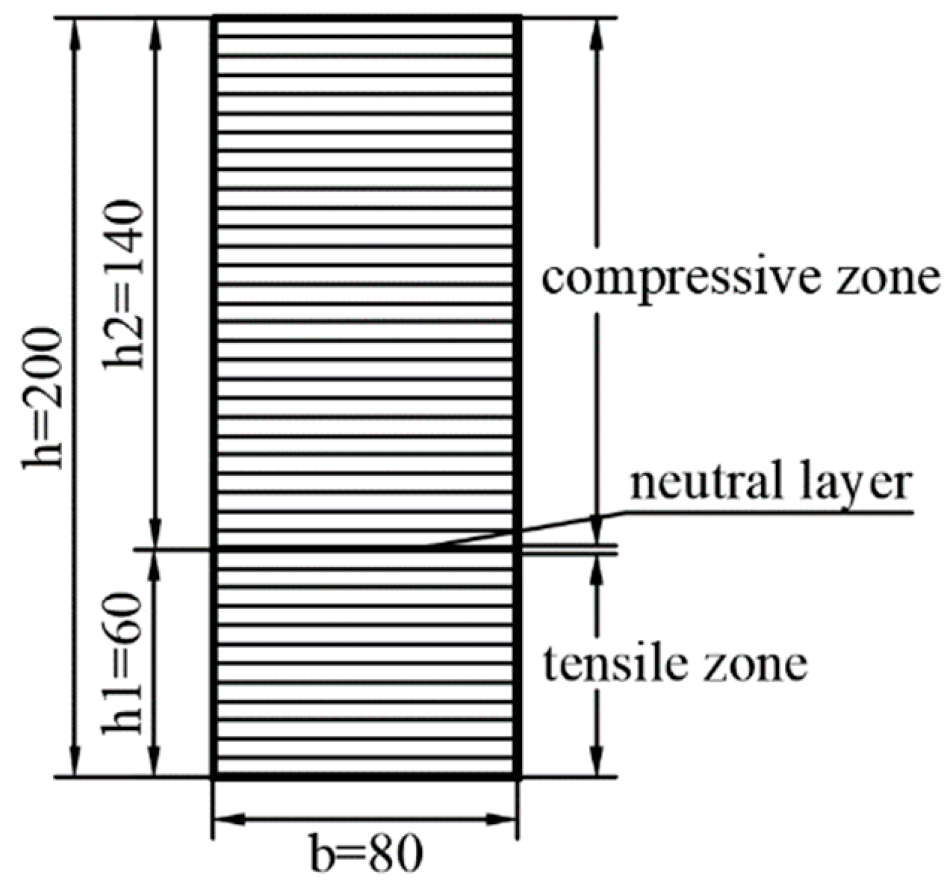
| Elastic Constant (10−12 m2·N−1) | Piezoelectric Constant (10−12 C·N−1) | Dielectric Constant (10−8 F·m−1) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 12.4 | −3.98 | −5.52 | 16.1 | 39.1 | −135 | 300 | 525 | 1.301 | 1.151 |
| ABAQUS Simulation (Pa) | Theoretical Solution (Pa) | Relative Errors % | |
|---|---|---|---|
| −0.7 | −1.5745 | −1.6675 | 5.58 |
| −0.6 | −1.9871 | −1.9294 | 2.99 |
| −0.5 | −2.2859 | −2.1703 | 5.33 |
| −0.4 | −2.4750 | −2.3437 | 5.60 |
| −0.3 | −2.4741 | −2.3727 | 4.27 |
| −0.2 | −2.1492 | −2.1352 | 0.66 |
| −0.1 | −1.3278 | −1.4411 | 7.86 |
| 0.0 | 0.2813 | 0 | - |
| 0.1 | 2.7493 | 2.3760 | 15.71 |
| 0.2 | 5.9989 | 5.8042 | 3.35 |
| 0.3 | 9.7701 | 10.6338 | 8.12 |
| ABAQUS Simulation (10−9 m) | Theoretical Solution (10−9 m) | Relative Errors % | |
|---|---|---|---|
| 0.0 | −4.1261 | −4.2083 | 1.95 |
| 0.1 | −3.5882 | −3.6474 | 1.62 |
| 0.2 | −3.0502 | −3.0884 | 1.24 |
| 0.3 | −2.5167 | −2.5364 | 0.78 |
| 0.4 | −1.9961 | −1.9998 | 0.19 |
| 0.5 | −1.4993 | −1.4905 | 0.59 |
| 0.6 | −1.0408 | −1.0235 | 1.69 |
| 0.7 | −0.6385 | −0.6174 | 3.42 |
| 0.8 | −0.3132 | −0.2940 | 6.54 |
| 0.9 | −0.0896 | −0.0787 | 13.91 |
| 1.0 | 0.0000 | 0 | - |
| ABAQUS (Pa) | Analytical (Pa) | Errors % | ABAQUS (Pa) | Analytical (Pa) | Errors % | |
|---|---|---|---|---|---|---|
| −0.7 | −1.5745 | −1.5004 | 4.94 | 0.0257 | 0.0000 | - |
| −0.6 | −1.9871 | −1.8570 | 7.01 | 0.3090 | 0.2817 | 9.69 |
| −0.5 | −2.2859 | −2.1748 | 5.11 | 0.6349 | 0.6086 | 4.32 |
| −0.4 | −2.4760 | −2.3987 | 3.22 | 0.9928 | 0.9693 | 2.42 |
| −0.3 | −2.4741 | −2.4451 | 1.19 | 1.3638 | 1.3474 | 1.22 |
| −0.2 | −2.1492 | −2.1921 | 1.96 | 1.7137 | 1.7110 | 0.16 |
| −0.1 | −1.3278 | −1.4598 | 9.04 | 1.9818 | 2.0034 | 1.08 |
| 0.0 | 0.2813 | 0 | - | 2.0697 | 2.1306 | 2.86 |
| 0.1 | 2.7493 | 2.4601 | 11.76 | 1.8770 | 1.9534 | 3.91 |
| 0.2 | 5.9989 | 5.8575 | 2.41 | 1.3238 | 1.3181 | 0.43 |
| 0.3 | 9.7701 | 10.3926 | 5.99 | 0.0377 | 0.0306 | 23.20 |
| ABAQUS (10−10 m) | Analytical (10−10 m) | Errors % | |
|---|---|---|---|
| −0.7 | 8.3955 | 7.4356 | 12.91 |
| −0.6 | 7.1834 | 6.3564 | 13.01 |
| −0.5 | 5.9828 | 5.2900 | 13.10 |
| −0.4 | 4.7887 | 4.2308 | 13.19 |
| −0.3 | 3.5975 | 3.1756 | 13.29 |
| −0.2 | 2.4065 | 2.1214 | 13.44 |
| −0.1 | 1.2138 | 1.0660 | 13.86 |
| 0.0 | 0.0178 | 0.0088 | - |
| 0.1 | −1.1818 | −1.0522 | 12.32 |
| 0.2 | −2.3855 | −2.1174 | 12.66 |
| 0.3 | −3.5941 | −3.1873 | 12.76 |
| ABAQUS (10−9 C/m2) | Analytical (10−9 C/m2) | Errors % | ABAQUS (10−9 C/m2) | Analytical (10−9 C/m2) | Errors % | |
|---|---|---|---|---|---|---|
| −0.7 | −2.3014 | −2.5480 | 9.68 | −0.0769 | 0.0000 | - |
| −0.6 | −1.0508 | −1.2423 | 15.42 | 1.5915 | 1.4459 | 10.07 |
| −0.5 | −0.2199 | −0.3746 | 41.30 | 2.1005 | 2.0677 | 1.59 |
| −0.4 | 0.2929 | 0.1685 | 73.83 | 2.1626 | 2.1316 | 1.45 |
| −0.3 | 0.5455 | 0.4712 | 15.77 | 1.9038 | 1.8621 | 2.24 |
| −0.2 | 0.5982 | 0.5957 | 0.42 | 1.4800 | 1.4252 | 3.85 |
| −0.1 | 0.5651 | 0.5883 | 3.94 | 1.0100 | 0.9440 | 6.99 |
| 0.0 | 0.5199 | 0.4832 | 7.60 | 0.5887 | 0.5098 | 15.48 |
| 0.1 | 0.3928 | 0.3416 | 14.99 | 0.2730 | 0.1741 | 56.81 |
| 0.2 | 0.1905 | 0.1211 | 57.31 | −0.0166 | −0.0157 | 5.73 |
| 0.3 | −0.0088 | −0.1640 | 94.63 | −0.0074 | 0.0000 | - |
| Material Types of Beams | Modulus of Elasticity | Bending Stiffness |
|---|---|---|
| Classical beams | ||
| Bimodular beams [33] | , where | |
| Bimodular FGM beams [29] | , where and is neutral layer modulus | , where |
| Bimodular FGPM beams (this study) | , where and are neutral layer modulus | , where and |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.-T.; Yang, Z.-X.; Jing, H.-X.; Sun, J.-Y. One-Dimensional Theoretical Solution and Two-Dimensional Numerical Simulation for Functionally-Graded Piezoelectric Cantilever Beams with Different Properties in Tension and Compression. Polymers 2019, 11, 1728. https://doi.org/10.3390/polym11111728
He X-T, Yang Z-X, Jing H-X, Sun J-Y. One-Dimensional Theoretical Solution and Two-Dimensional Numerical Simulation for Functionally-Graded Piezoelectric Cantilever Beams with Different Properties in Tension and Compression. Polymers. 2019; 11(11):1728. https://doi.org/10.3390/polym11111728
Chicago/Turabian StyleHe, Xiao-Ting, Zhi-Xin Yang, Hong-Xia Jing, and Jun-Yi Sun. 2019. "One-Dimensional Theoretical Solution and Two-Dimensional Numerical Simulation for Functionally-Graded Piezoelectric Cantilever Beams with Different Properties in Tension and Compression" Polymers 11, no. 11: 1728. https://doi.org/10.3390/polym11111728
APA StyleHe, X.-T., Yang, Z.-X., Jing, H.-X., & Sun, J.-Y. (2019). One-Dimensional Theoretical Solution and Two-Dimensional Numerical Simulation for Functionally-Graded Piezoelectric Cantilever Beams with Different Properties in Tension and Compression. Polymers, 11(11), 1728. https://doi.org/10.3390/polym11111728






