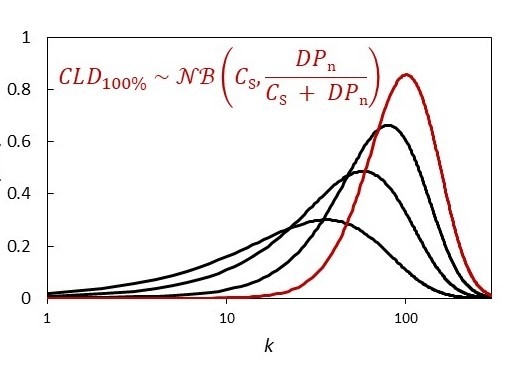
The Chain Length Distribution of an Ideal Reversible Deactivation Radical Polymerization
Abstract
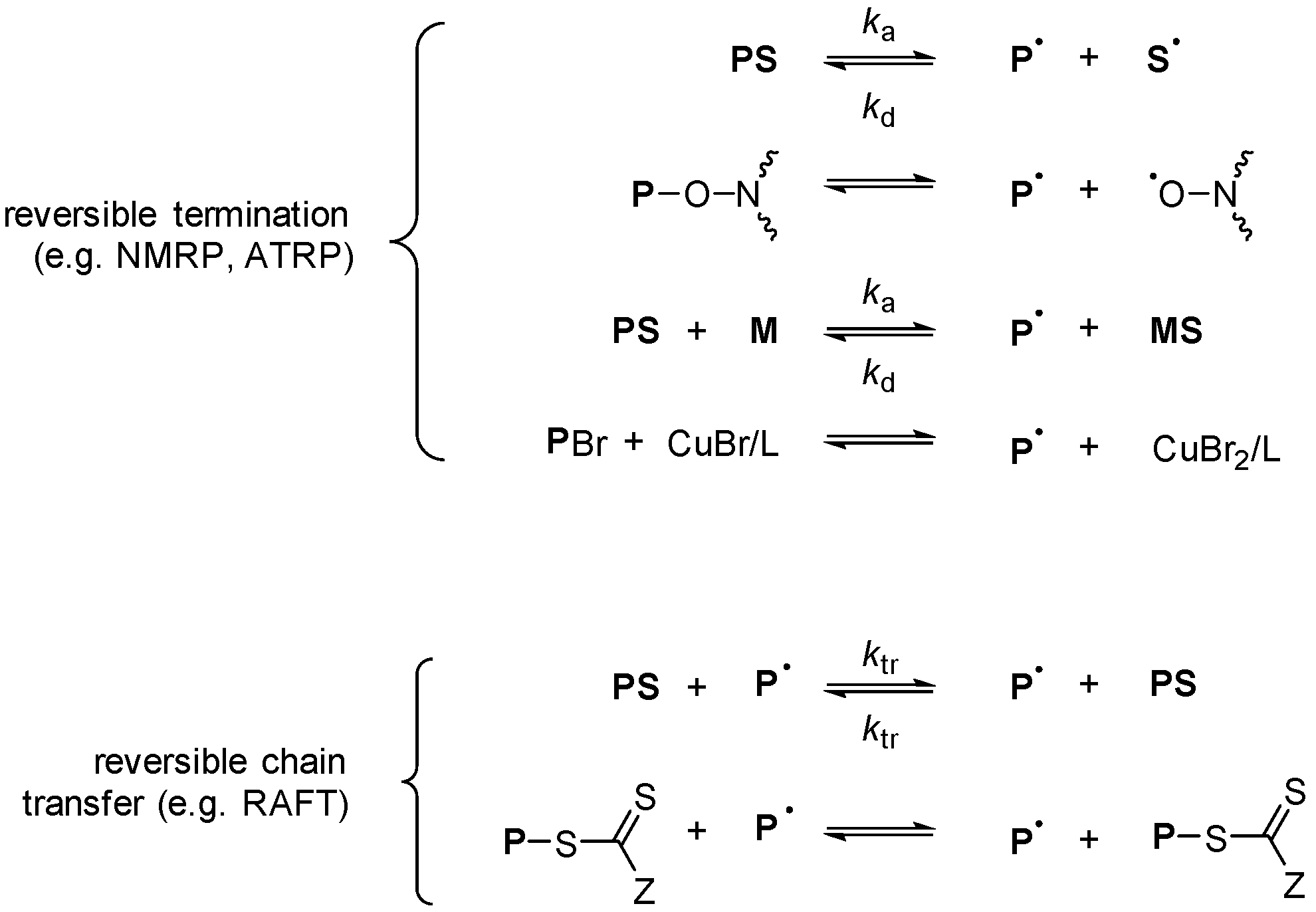
1. Introduction
2. Materials and Methods
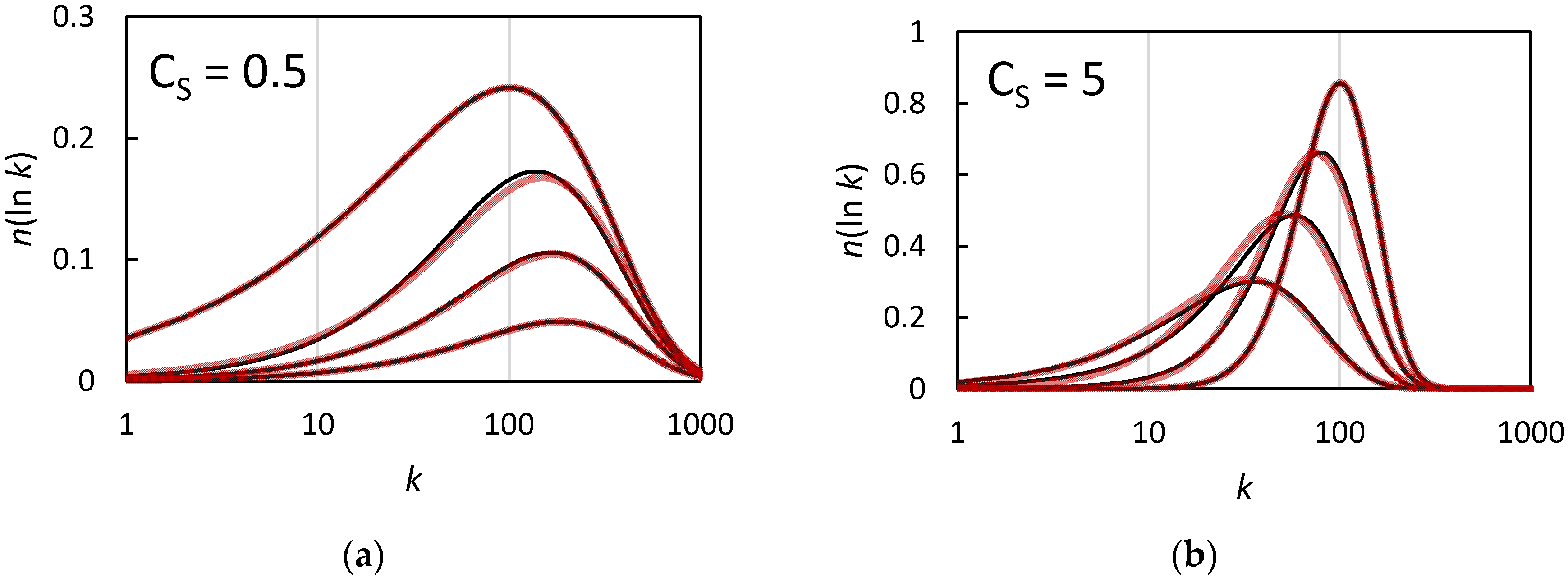
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Jenkins, A.D.; Jones, R.G.; Moad, G. Terminology for reversible-deactivation radical polymerization previously called “controlled” radical or “living” radical polymerization (IUPAC Recommendations 2010). Pure Appl. Chem. 2010, 82, 483–491. [Google Scholar] [CrossRef]
- Zamfir, M.; Lutz, J.-F. Ultra-precise insertion of functional monomers in chain-growth polymerizations. Nat. Commun. 2012, 3, 1138. [Google Scholar] [CrossRef]
- Lutz, J.-F.; Schmidt, B.V.K.J.; Pfeifer, S. Tailored Polymer Microstructures Prepared by Atom Transfer Radical Copolymerization of Styrene and N-substituted Maleimides. Macromol. Rapid Commun. 2011, 32, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Anastasaki, A.; Waldron, C.; Wilson, P.; Boyer, C.; Zetterlund, P.B.; Whittaker, M.R.; Haddleton, D. High Molecular Weight Block Copolymers by Sequential Monomer Addition via Cu(0)-Mediated Living Radical Polymerization (SET-LRP): An Optimized Approach. ACS Macro Lett. 2013, 2, 896–900. [Google Scholar] [CrossRef]
- Gody, G.; Maschmeyer, T.; Zetterlund, P.B.; Perrier, S. Rapid and quantitative one-pot synthesis of sequence-controlled polymers by radical polymerization. Nat. Commun. 2013, 4, 2505. [Google Scholar] [CrossRef] [PubMed]
- Gody, G.; Maschmeyer, T.; Zetterlund, P.B.; Perrier, S. Pushing the Limit of the RAFT Process: Multiblock Copolymers by One-Pot Rapid Multiple Chain Extensions at Full Monomer Conversion. Macromolecules 2014, 47, 3451–3460. [Google Scholar] [CrossRef]
- Gody, G.; Maschmeyer, T.; Zetterlund, P.B.; Perrier, S. Exploitation of the Degenerative Transfer Mechanism in RAFT Polymerization for Synthesis of Polymer of High Livingness at Full Monomer Conversion. Macromolecules 2014, 47, 639–649. [Google Scholar] [CrossRef]
- Engelis, N.G.; Anastasaki, A.; Nurumbetov, G.; Truong, N.P.; Nikolaou, V.; Shegiwal, A.; Whittaker, M.R.; Davis, T.P.; Haddleton, D.M. Sequence-controlled methacrylic multiblock copolymers via sulfur-free RAFT emulsion polymerization. Nat. Chem. 2017, 9, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Wenn, B.; Martens, A.C.; Chuang, Y.M.; Gruber, J.; Junkers, T. Efficient multiblock star polymer synthesis from photo-induced copper-mediated polymerization with up to 21 arms. Polym. Chem. 2016, 7, 2720–2727. [Google Scholar] [CrossRef]
- Gody, G.; Zetterlund, P.B.; Perrier, S.; Harrisson, S. The limits of precision monomer placement in chain growth polymerization. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Molecular Size Distribution in Ethylene Oxide Polymers. J. Am. Chem. Soc. 1940, 62, 1561–1565. [Google Scholar] [CrossRef]
- Goto, A.; Fukuda, T. Kinetics of living radical polymerization. Prog. Polym. Sci. 2004, 29, 329–385. [Google Scholar] [CrossRef]
- Mueller, A.H.E.; Zhuang, R.; Yan, D.; Litvinenko, G. Kinetic Analysis of “Living” Polymerization Processes Exhibiting Slow Equilibria. 1. Degenerative Transfer (Direct Activity Exchange between Active and “Dormant” Species). Application to Group Transfer Polymerization. Macromolecules 1995, 28, 4326–4333. [Google Scholar] [CrossRef]
- Müller, A.H.E.; Litvinenko, G.; Yan, D. Kinetic Analysis of “Living” Polymerization Systems Exhibiting Slow Equilibria. 4. “Dissociative” Mechanism of Group Transfer Polymerization and Generation of Free Ions in Cationic Polymerization. Macromolecules 1996, 29, 2346–2353. [Google Scholar] [CrossRef]
- Nicolas, J.; Guillaneuf, Y.; Lefay, C.; Bertin, D.; Gigmes, D.; Charleux, B. Nitroxide-mediated polymerization. Prog. Polym. Sci. 2013, 38, 63–235. [Google Scholar] [CrossRef]
- Matyjaszewski, K.; Xia, J. Atom Transfer Radical Polymerization. Chem. Rev. 2001, 101, 2921–2990. [Google Scholar] [CrossRef] [PubMed]
- Moad, G.; Rizzardo, E.; Thang, S.H. Living Radical Polymerization by the RAFT Process. Aust. J. Chem. 2005, 58, 379–410. [Google Scholar] [CrossRef]
- Mastan, E.; Zhu, S. A Molecular Weight Distribution Polydispersity Equation for the ATRP System: Quantifying the Effect of Radical Termination. Macromolecules 2015, 48, 6440–6449. [Google Scholar] [CrossRef]
- Mastan, E.; Li, X.; Zhu, S. Modeling and theoretical development in controlled radical polymerization. Prog. Polym. Sci. 2015, 45, 71–101. [Google Scholar] [CrossRef]
- Gold, L. Statistics of Polymer Molecular Size Distribution for an Invariant Number of Propagating Chains. J. Chem. Phys. 1958, 28, 91–99. [Google Scholar] [CrossRef]
- Mueller, A.H.E.; Yan, D.; Litvinenko, G.; Zhuang, R.; Dong, H. Kinetic Analysis of “Living” Polymerization Processes Exhibiting Slow Equilibria. 2. Molecular Weight Distribution for Degenerative Transfer (Direct Activity Exchange between Active and “Dormant” Species) at Constant Monomer Concentration. Macromolecules 1995, 28, 7335–7338. [Google Scholar] [CrossRef]
- Tobita, H. Molecular Weight Distribution of Living Radical Polymers. Macromol. Theory Simul. 2006, 15, 12–22. [Google Scholar] [CrossRef]
- Tobita, H. Fundamental Molecular Weight Distribution of RAFT Polymers. Macromol. React. Eng. 2008, 2, 371–381. [Google Scholar] [CrossRef]
- Konkolewicz, D.; Hawkett, B.S.; Gray-Weale, A.; Perrier, S. RAFT Polymerization Kinetics: Combination of Apparently Conflicting Models. Macromolecules 2008, 41, 6400–6412. [Google Scholar] [CrossRef]
- Konkolewicz, D.; Hawkett, B.S.; Gray-Weale, A.; Perrier, S. RAFT polymerization kinetics: How long are the cross-terminating oligomers? J. Polym. Sci. A Polym. Chem. 2009, 47, 3455–3466. [Google Scholar] [CrossRef]
- Konkolewicz, D.; Siauw, M.; Gray-Weale, A.; Hawkett, B.S.; Perrier, S. Obtaining Kinetic Information from the Chain-Length Distribution of Polymers Produced by RAFT. J. Phys. Chem. B 2009, 113, 7086–7094. [Google Scholar] [CrossRef] [PubMed]
- Bartko, J.J. A Note on the Negative Binomial Distribution. Technometrics 1962, 4, 609–610. [Google Scholar] [CrossRef]
- Hilbe, J.M. Negative Binomial Regression, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Grimmett, G.R.; Stirzaker, D.R. Probability and Random Processes, 3rd ed.; Oxford University Press: Oxford, UK, 2001; pp. 148–155. [Google Scholar]
- Mastan, E.; Zhu, S. Method of moments: A versatile tool for deterministic modeling of polymerization kinetics. Eur. Polym. J. 2015, 68, 139–160. [Google Scholar] [CrossRef]
- Qi, S.; Klushin, L.I.; Skvortsov, A.M.; Schmid, F. Polydisperse Polymer Brushes: Internal Structure, Critical Behavior, and Interaction with Flow. Macromolecules 2016, 49, 9665–9683. [Google Scholar] [CrossRef]
- Patil, R.R.; Turgman-Cohen, S.; Šrogl, J.; Kiserow, D.; Genzer, J. On-Demand Degrafting and the Study of Molecular Weight and Grafting Density of Poly(methyl methacrylate) Brushes on Flat Silica Substrates. Langmuir 2015, 31, 2372–2381. [Google Scholar] [CrossRef] [PubMed]
- Schaeffel, D.; Yordanov, S.; Staff, R.H.; Kreyes, A.; Zhao, Y.; Schmidt, M.; Landfester, K.; Hofkens, J.; Butt, H.-J.; Crespy, D.; Koynov, K. Fluorescence Correlation Spectroscopy in Dilute Polymer Solutions: Effects of Molar Mass Dispersity and the Type of Fluorescent Labeling. ACS Macro Lett. 2015, 4, 171–176. [Google Scholar] [CrossRef]
- Lynd, N.A.; Meuler, A.J.; Hillmyer, M.A. Polydispersity and block copolymer self-assembly. Prog. Polym. Sci. 2008, 33, 875–893. [Google Scholar] [CrossRef]
- Schulz, G.V. Über die Kinetik der Kettenpolymerisationen. V. Z. Phys. Chem. 1939, B43, 25–46. [Google Scholar] [CrossRef]
- Zimm, B.H. Apparatus and Methods for Measurement and Interpretation of the Angular Variation of Light Scattering; Preliminary Results on Polystyrene Solutions. J. Chem. Phys. 1948, 16, 1099–1117. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harrisson, S. The Chain Length Distribution of an Ideal Reversible Deactivation Radical Polymerization. Polymers 2018, 10, 887. https://doi.org/10.3390/polym10080887
Harrisson S. The Chain Length Distribution of an Ideal Reversible Deactivation Radical Polymerization. Polymers. 2018; 10(8):887. https://doi.org/10.3390/polym10080887
Chicago/Turabian StyleHarrisson, Simon. 2018. "The Chain Length Distribution of an Ideal Reversible Deactivation Radical Polymerization" Polymers 10, no. 8: 887. https://doi.org/10.3390/polym10080887
APA StyleHarrisson, S. (2018). The Chain Length Distribution of an Ideal Reversible Deactivation Radical Polymerization. Polymers, 10(8), 887. https://doi.org/10.3390/polym10080887