Dynamic and Static Mechanical Properties of Crosslinked Polymer Matrices: Multiscale Simulations and Experiments
Abstract
:1. Introduction
2. Methodology
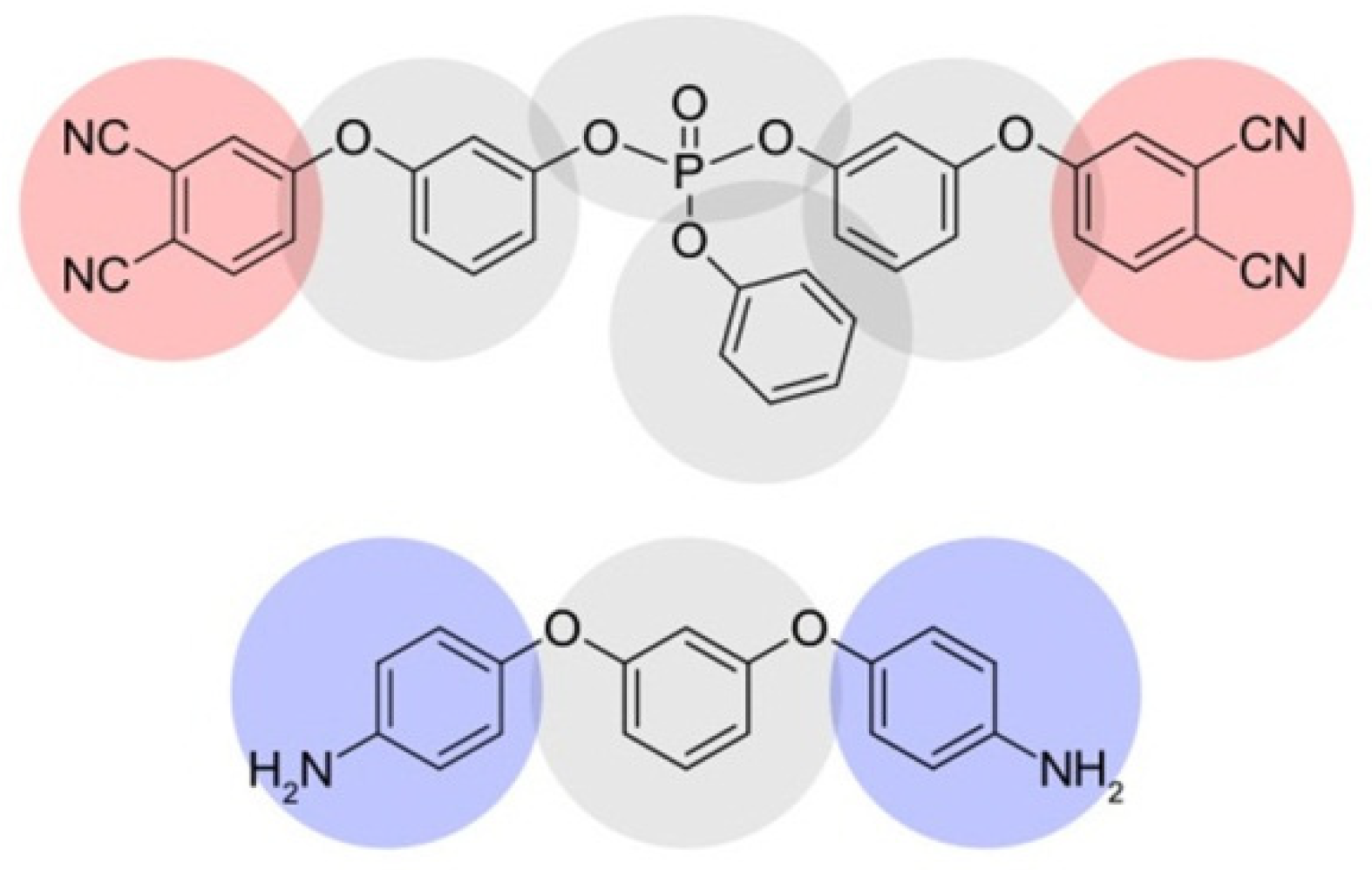
2.1. Coarse-Grained Model
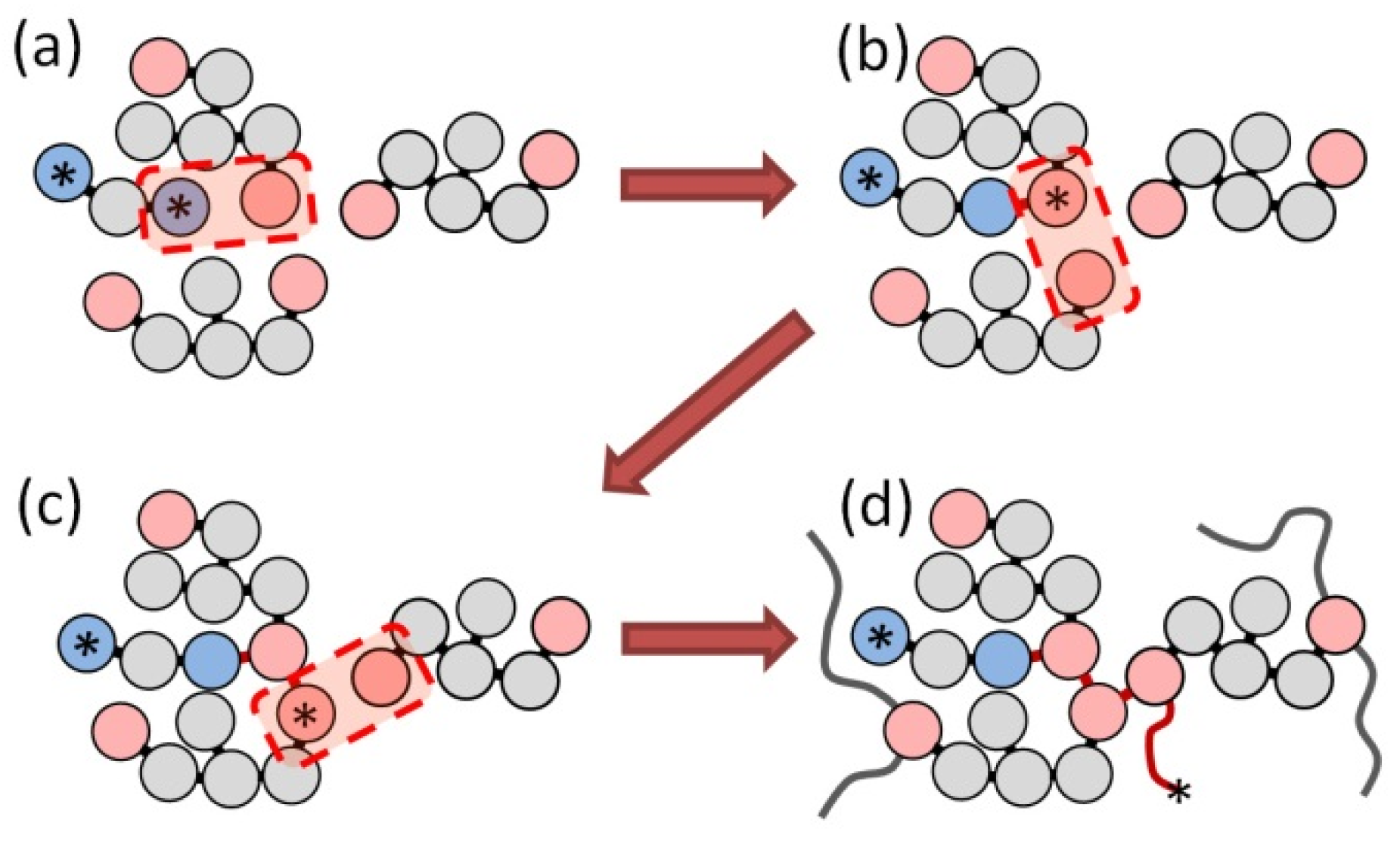
2.2. Simulation of Curing Process at CG Level
- Initiation reaction, when terminal beads of the initiator and monomer molecule form a bond and the corresponding monomer particle takes an active state from the initiator terminal bead (asterisk in Figure 2a,b); and
2.3. Mechanical Properties of CG Networks
2.4. Reverse Mapping of CG Networks
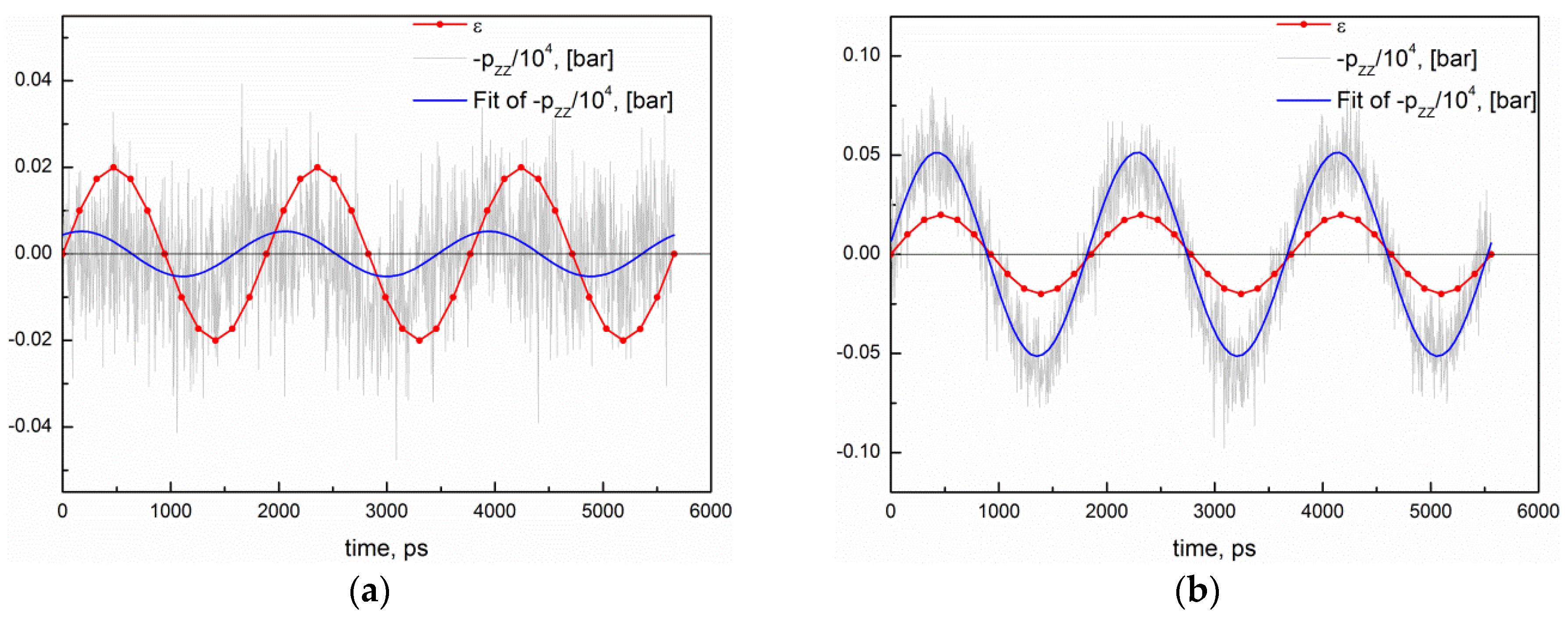
2.5. MD Simulations of Physical Properties of Atomistic Networks
3. Experimental
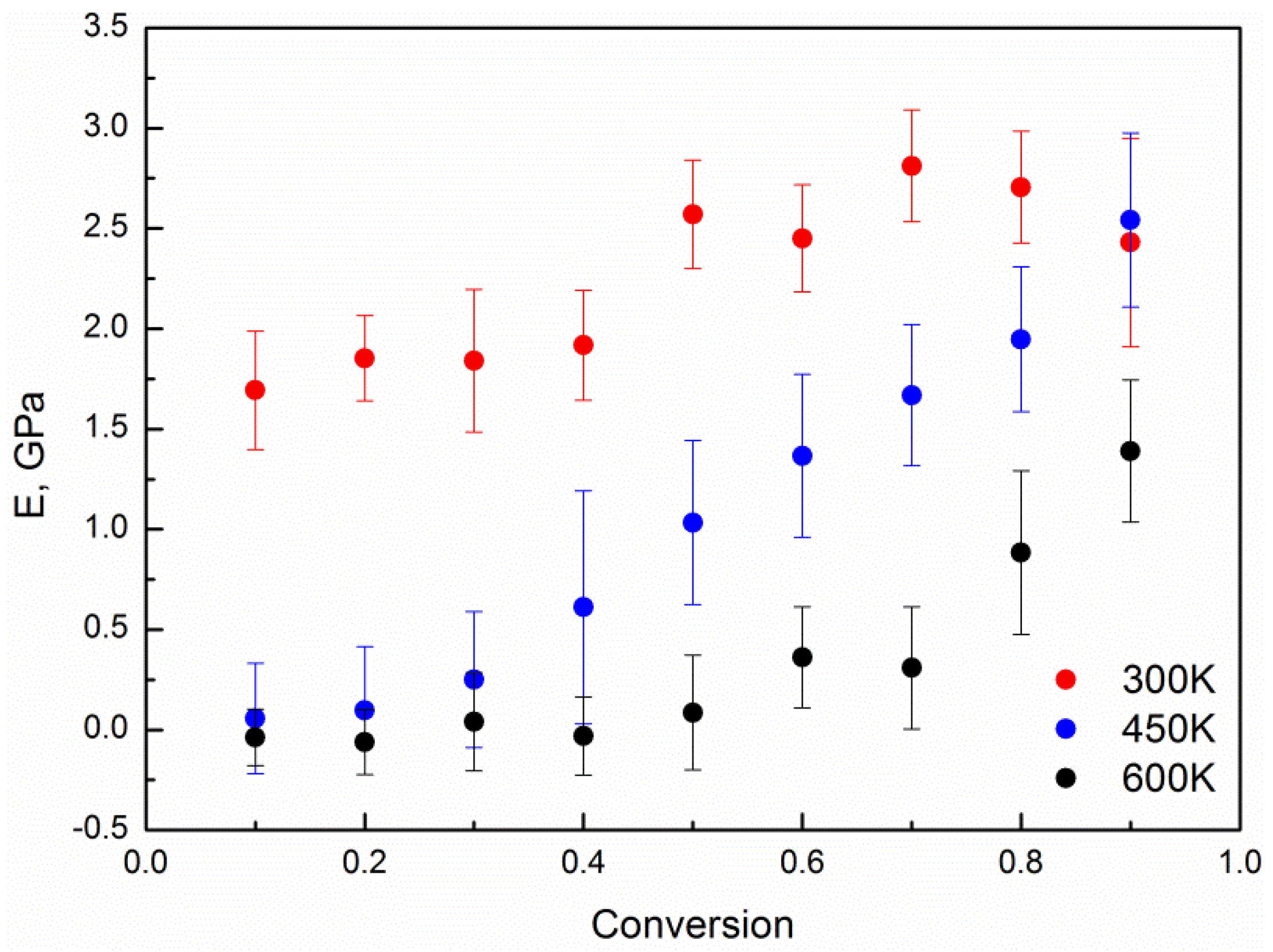
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Keller, T.M.; Griffith, J.R. Polyphenylether-Bridged Polyphthalocyanine. U.S. Patent 4,259,471, 31 March 1981. [Google Scholar]
- Dominguez, D.D.; Jones, H.N.; Keller, T.M. The effect of curing additive on the mechanical properties of phthalonitrile-carbon fiber composites. Polym. Compos. 2004, 25, 554–561. [Google Scholar] [CrossRef]
- Sastri, S.B.; Armistead, J.P.; Keller, T.M. Phthalonitrile-carbon fiber composites. Polym. Compos. 1996, 17, 816–822. [Google Scholar] [CrossRef]
- Dominguez, D.D.; Keller, T.M. Low-melting phthalonitrile oligomers: Preparation, polymerization and polymer properties. High Perform. Polym. 2006, 18, 283–304. [Google Scholar] [CrossRef]
- Keller, T.M.; Dominguez, D.D.; Laskoski, M. Oligomeric bisphenol A-based PEEK-like phthalonitrile-cure and polymer properties. J. Polym. Sci. Part A Polym. Chem. 2016, 54, 3769–3777. [Google Scholar] [CrossRef]
- Laskoski, M.; Neal, A.; Schear, M.B.; Keller, T.M.; Ricks-Laskoski, H.L.; Saab, A.P. Oligomeric aliphatic-aromatic ether containing phthalonitrile resins. J. Polym. Sci. Part A Polym. Chem. 2015, 53, 2186–2191. [Google Scholar] [CrossRef]
- Laskoski, M.; Dominguez, D.D.; Keller, T.M. Synthesis and properties of aromatic ether phosphine oxide containing oligomeric phthalonitrile resins with improved oxidative stability. Polymer 2007, 48, 6234–6240. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, R.; Yu, X.; Naito, K.; Qu, X.; Zhang, Q. A high temperature polymer of phthalonitrile-substituted phosphazene with low melting point and good thermal stability. J. Appl. Polym. Sci. 2015, 132, 42606. [Google Scholar] [CrossRef]
- Xu, S.; Han, Y.; Guo, Y.; Luo, Z.; Ye, L.; Li, Z.; Zhou, H.; Zhao, Y.; Zhao, T. Allyl phenolic-phthalonitrile resins with tunable properties: Curing, processability and thermal stability. Eur. Polym. J. 2017, 95, 394–405. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Zhou, H.; Lin, X.; Zhao, T.; Zhang, M.; Xu, C. Self-catalyzed silicon-containing phthalonitrile resins with low melting point, excellent solubility and thermal stability. J. Appl. Polym. Sci. 2014, 131, 40919. [Google Scholar] [CrossRef]
- Bulgakov, B.A.; Sulimov, A.V.; Babkin, A.V.; Kepman, A.V.; Malakho, A.P.; Avdeev, V.V. Dual-curing thermosetting monomer containing both propargyl ether and phthalonitrile groups. J. Appl. Polym. Sci. 2017, 134, 44786. [Google Scholar] [CrossRef]
- Dzhevakov, P.B.; Korotkov, R.F.; Bulgakov, B.A.; Babkin, A.V.; Kepman, A.V.; Avdeev, V.V. Synthesis and polymerization of disiloxane Si–O–Si-linked phthalonitrile monomer. Mendeleev Commun. 2016, 26, 527–529. [Google Scholar] [CrossRef]
- Babkin, A.V.; Zodbinov, E.B.; Bulgakov, B.A.; Kepman, A.V.; Avdeev, V.V. Low-melting siloxane-bridged phthalonitriles for heat-resistant matrices. Eur. Polym. J. 2015, 66, 452–457. [Google Scholar] [CrossRef]
- Zhou, H.; Badashah, A.; Luo, Z.; Liu, F.; Zhao, T. Preparation and property comparison of ortho, meta, and para autocatalytic phthalonitrile compounds with amino group. Polym. Adv. Technol. 2011, 22, 1459–1465. [Google Scholar] [CrossRef]
- Sastri, S.B.; Armistead, J.P.; Keller, T.M.; Sorathia, U. Phthalonitrile-glass fabric composites. Polym. Compos. 1997, 18, 48–54. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, H.; Tang, H.; Yang, X.; Xu, M.; Liu, X. Preparation and properties of bisphenol A-based bis-phthalonitrile composite laminates. J. Appl. Polym. Sci. 2013, 129, 2621–2628. [Google Scholar] [CrossRef]
- Zong, L.; Liu, C.; Guo, Y.; Wang, J.; Jian, X. Thermally stable phthalonitrile resins based on multiple oligo (aryl ether)s with phenyl-s-triazine moieties in backbones. RSC Adv. 2015, 5, 77027–77036. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, M.; Pan, H.; Jia, K.; Liu, X. Effect of ortho-diallyl bisphenol A on the processability of phthalonitrile-based resin and their fiber-reinforced laminates. Polym. Eng. Sci. 2016, 56, 150–157. [Google Scholar] [CrossRef]
- Bulgakov, B.A.; Sulimov, A.V.; Babkin, A.V.; Afanasiev, D.V.; Solopchenko, A.V.; Afanaseva, E.S.; Kepman, A.V.; Avdeeva, V.V. Flame-retardant carbon fiber reinforced phthalonitrile composite for high-temperature applications obtained by resin transfer molding. Mendeleev Commun. 2017, 27, 257–259. [Google Scholar] [CrossRef]
- Bulgakov, B.A.; Sulimov, A.V.; Babkin, A.V.; Timoshkin, I.A.; Solopchenko, A.V.; Kepman, A.V.; Avdeev, V.V. Phthalonitrile-carbon fiber composites produced by vacuum infusion process. J. Compos. Mater. 2017, 51, 4157–4164. [Google Scholar] [CrossRef]
- Babkin, A.V.; Sulimov, A.V.; Bulgakov, B.A.; Kepman, A.V. Phosphorus-containing phthalonitrile resin for VIMP and RTM processing. In SAMPE Conf. Proc.; Society for the Advancement of Material and Process Engineering: Seattle, WA, USA, 2017; pp. 713–724. [Google Scholar]
- Bulgakov, B.A.; Babkin, A.V.; Dzhevakov, P.B.; Bogolyubov, A.A.; Sulimov, A.V.; Kepman, A.V.; Kolyagin, Y.G.; Guseva, D.V.; Rudyak, V.Y.; Chertovich, A.V. Low-melting phthalonitrile thermosetting monomers with siloxane- and phosphate bridges. Eur. Polym. J. 2016, 84, 205–217. [Google Scholar] [CrossRef]
- Thornton, A.W.; Simon, C.M.; Kim, J.; Kwon, O.; Deeg, K.S.; Konstas, K.; Pas, S.J.; Hill, M.R.; Winkler, D.A.; Haranczyk, M.; et al. Materials genome in action: Identifying the performance limits of physical hydrogen storage. Chem. Mater. 2017, 29, 2844–2854. [Google Scholar] [CrossRef] [PubMed]
- Keten, S.; Xu, Z.; Ihle, B.; Buehler, M.J. Nanoconfinement controls stiffness, strength and mechanical toughness of β-sheet crystals in silk. Nat. Mater. 2010, 9, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Gavrilov, A.A.; Komarov, P.V.; Khalatur, P.G. Thermal properties and topology of epoxy networks: A multiscale simulation methodology. Macromolecules 2015, 48, 206–212. [Google Scholar] [CrossRef]
- Pavlov, A.S.; Khalatur, P.G. Fully atomistic molecular dynamics simulation of nanosilica-filled crosslinked polybutadiene. Chem. Phys. Lett. 2016, 653, 90–95. [Google Scholar] [CrossRef]
- Shudo, Y.; Izumi, A.; Hagita, K.; Nakao, T.; Shibayama, M. Structure-mechanical property relationships in crosslinked phenolic resin investigated by molecular dynamics simulation. Polymer 2017, 116, 506–514. [Google Scholar] [CrossRef]
- Guseva, D.V.; Chertovich, A.V.; Rudyak, V.Y. Systematic study of glass transition in low-molecular phthalonitriles: Insight from computer simulations. J. Chem. Phys. 2016, 145, 144503. [Google Scholar] [CrossRef] [PubMed]
- Rudyak, V.Y.; Gavrilov, A.A.; Guseva, D.V.; Chertovich, A.V. Complex curing pathways and their influence on the phthalonitrile resin hardening and elasticity. Macromol. Theory Simul. 2017, 26, 1700015. [Google Scholar] [CrossRef]
- Guseva, D.V.; Rudyak, V.Y.; Komarov, P.V.; Sulimov, A.V.; Bulgakov, B.A.; Chertovich, A.V. Crosslinking mechanisms, structure and glass transition in phthalonitrile resins: Insight from computer multiscale simulations and experiments. J. Polym. Sci. Part B Polym. Phys. 2018, 56, 362–374. [Google Scholar] [CrossRef]
- Bulgakov, B.A.; Babkin, A.V.; Bogolyubov, A.A.; Afanas’eva, E.S.; Kepman, A.V. Mechanical and physicochemical properties of matrices for fiber reinforced plastics based on low-melting phthalonitrile monomers. Russ. Chem. Bull. 2016, 65, 287–290. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Koelman, J.M.V.A.; Hoogerbrugge, P.J. Dynamic simulations of hard-sphere suspensions under steady shear. Europhys. Lett. 1993, 21, 363–368. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Berezkin, A.V.; Kudryavtsev, Y.V. Simulation of end-coupling reactions at a polymer−polymer interface: The mechanism of interfacial roughness development. Macromolecules 2011, 44, 112–121. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Chertovich, A.V.; Khalatur, P.G.; Khokhlov, A.R. Study of the mechanisms of filler reinforcement in elastomer nanocomposites. Macromolecules 2014, 47, 5400–5408. [Google Scholar] [CrossRef]
- Li, C.; Strachan, A. Molecular scale simulations on thermoset polymers: A review. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 103–122. [Google Scholar] [CrossRef]
- Augustine, D.; Mathew, D.; Nair, C.P.R. One component propargyl phthalonitrile novolac: Synthesis and characterization. Eur. Polym. J. 2015, 71, 389–400. [Google Scholar] [CrossRef]
- Sheng, L.; Yin, C.; Xiao, J. A novel phthalonitrile monomer with low post cure temperature and short cure time. RSC Adv. 2016, 6, 22204–22212. [Google Scholar] [CrossRef]
- Sun, H.; Mumby, S.J.; Maple, J.R.; Hagler, A.T. An ab initio CFF93 all-atom force field for polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. [Google Scholar] [CrossRef]
- Spoel, D.V.D.; Lindahl, E.; Hess, B.; Buuren, A.R.V.; Apol, E.; Meulenhoff, P.J.; Tieleman, D.P.; Sijbers, A.L.T.M.; Feenstra, K.A.; Drunen, R.V.; et al. Gromacs User Manual Version 4.5.6. 2010. Available online: http://www.gromacs.org (accessed on 18 July 2018).
- Spoel, D.V.D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comp. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- LAMMPS Users Manual 16 Jul 2018 version. Sandia National Laboratories, Sandia Corporation, 2017. Available online: http://lammps.sandia.gov (accessed on 18 July 2018).
- Menard, K.P. DMA: Introduction to the Technique, Its Applications and Theory; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Research Computing Center of Lomonosov Moscow State University. Available online: http://hpc.msu.ru (accessed on 18 July 2018).
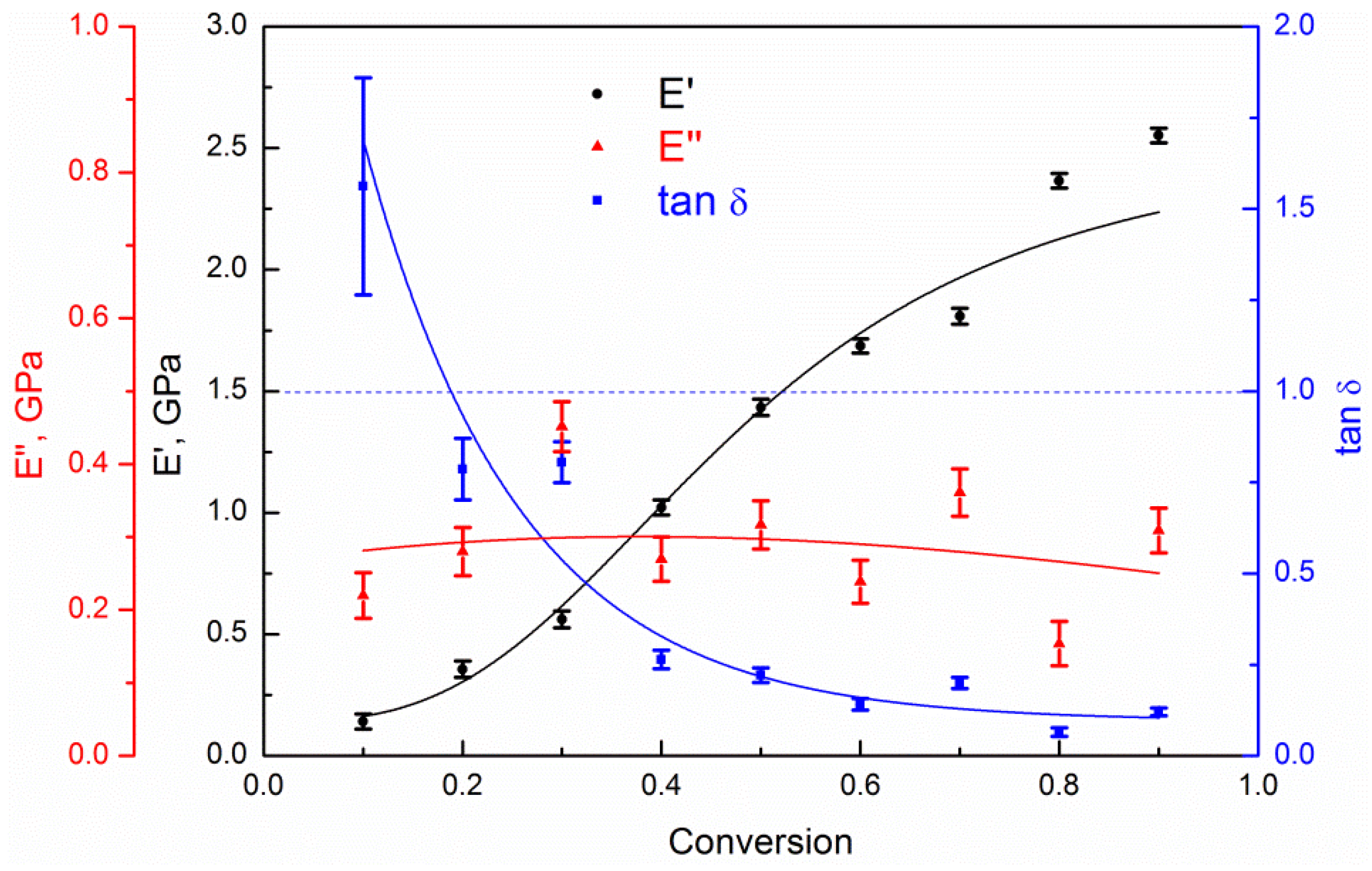
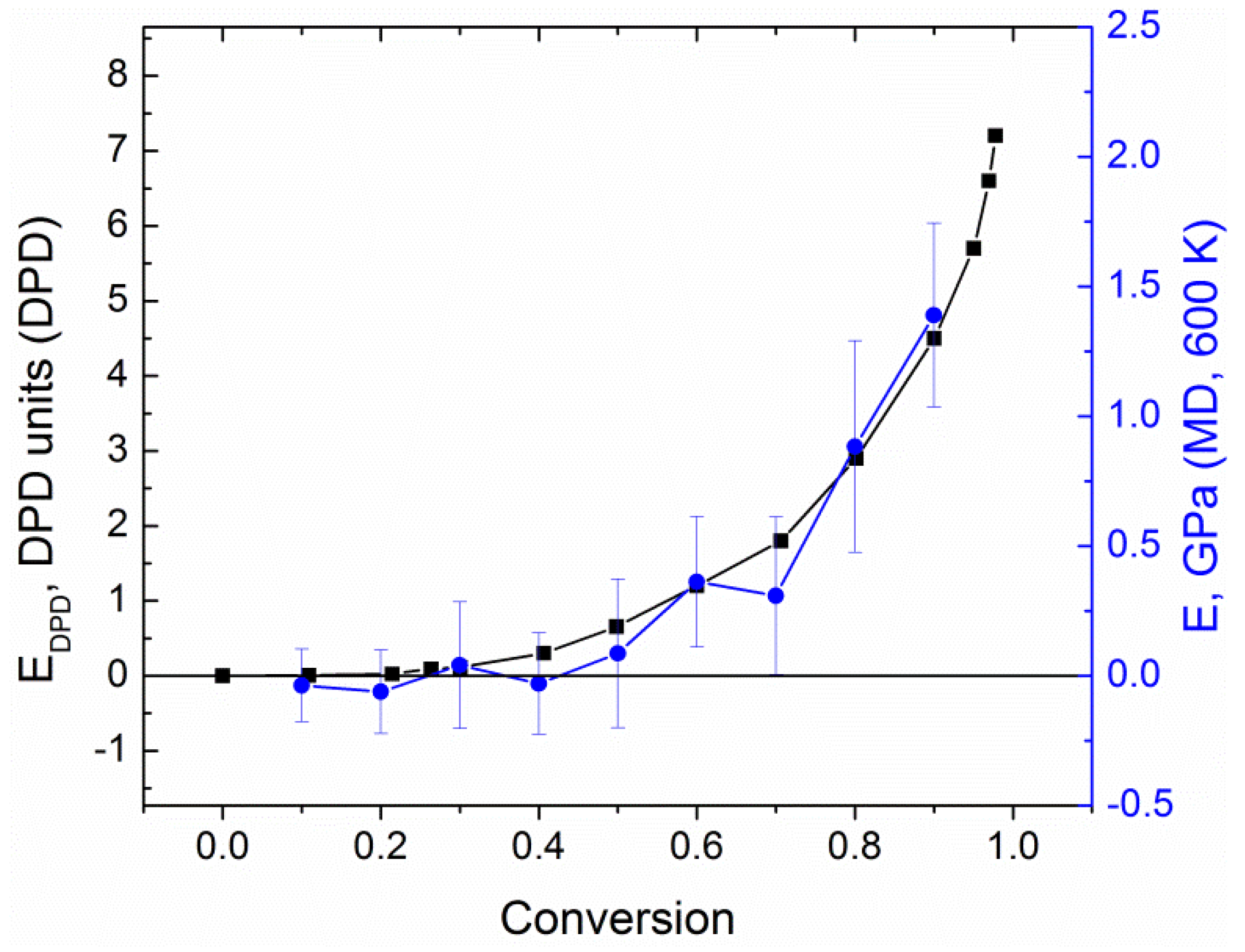
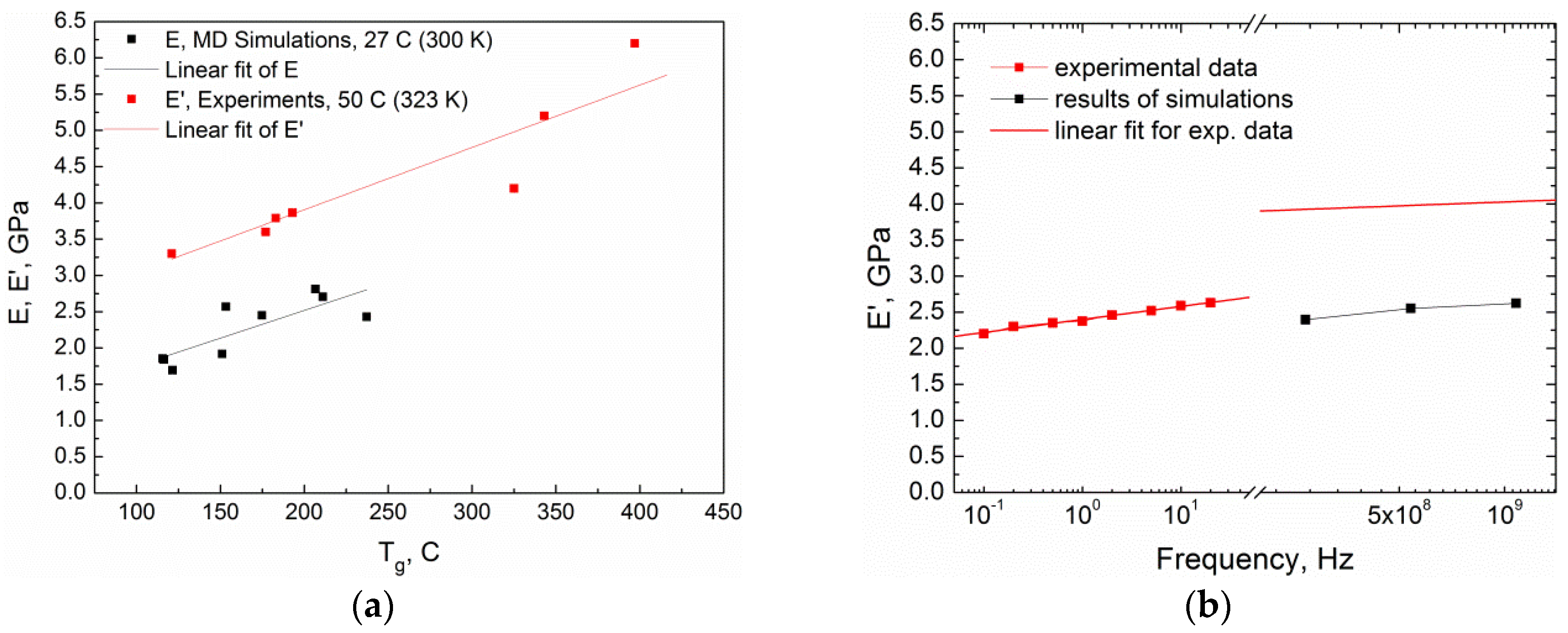
| Curing Temperature, °C (K) | Curing Time, hours | E′ @ 1 Hz, MPa | E″ @ 1 Hz, MPa | Tg, °C | ||||
|---|---|---|---|---|---|---|---|---|
| 323 K | 450 K | 600 K | 323 K | 450 K | 600 K | |||
| Curing | ||||||||
| 200 (473) | 6 | 3300 | 12.5 | – | 149 | 16 | – | 121 |
| Post-curing | ||||||||
| 250 (523) | 3 | 3600 | 984 | – | 141 | 262 | – | 177 |
| 250 (523) | 6 | 3790 | 2170 | – | 144 | 206 | – | 183 |
| 300 (573) | 3 | 3865 | 2150 | 48.5 | 190 | 163 | 48 | 193 |
| 300 (573) | 6 | 4200 | 2557 | 665.6 | 137 | 167 | 141 | 325 |
| 350 (623) | 3 | 5200 | 4190 | 2154 | 205 | 261 | 344 | 343 |
| 350 (623) | 6 | 6200 | 5500 | 3780 | 204 | 261 | 298 | 397 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guseva, D.V.; Rudyak, V.Y.; Komarov, P.V.; Bulgakov, B.A.; Babkin, A.V.; Chertovich, A.V. Dynamic and Static Mechanical Properties of Crosslinked Polymer Matrices: Multiscale Simulations and Experiments. Polymers 2018, 10, 792. https://doi.org/10.3390/polym10070792
Guseva DV, Rudyak VY, Komarov PV, Bulgakov BA, Babkin AV, Chertovich AV. Dynamic and Static Mechanical Properties of Crosslinked Polymer Matrices: Multiscale Simulations and Experiments. Polymers. 2018; 10(7):792. https://doi.org/10.3390/polym10070792
Chicago/Turabian StyleGuseva, Daria V., Vladimir Yu. Rudyak, Pavel V. Komarov, Boris A. Bulgakov, Alexander V. Babkin, and Alexander V. Chertovich. 2018. "Dynamic and Static Mechanical Properties of Crosslinked Polymer Matrices: Multiscale Simulations and Experiments" Polymers 10, no. 7: 792. https://doi.org/10.3390/polym10070792
APA StyleGuseva, D. V., Rudyak, V. Y., Komarov, P. V., Bulgakov, B. A., Babkin, A. V., & Chertovich, A. V. (2018). Dynamic and Static Mechanical Properties of Crosslinked Polymer Matrices: Multiscale Simulations and Experiments. Polymers, 10(7), 792. https://doi.org/10.3390/polym10070792





