Ferroelectric Self-Poling in GeTe Films and Crystals
Abstract
:1. Introduction
2. Materials and Methods
2.1. Crystal and Thin Film Growth
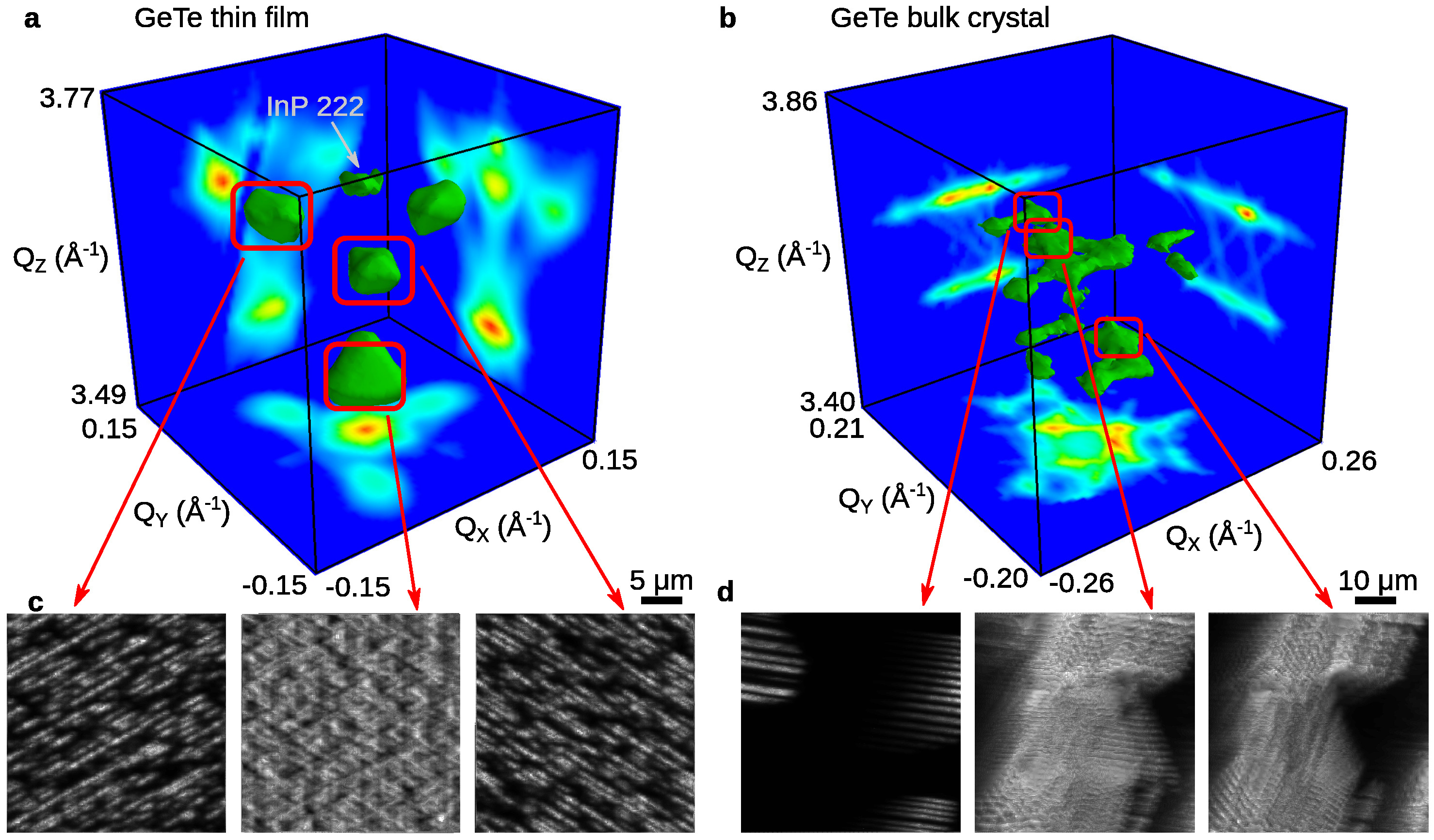
2.2. Scanning X-Ray Diffraction
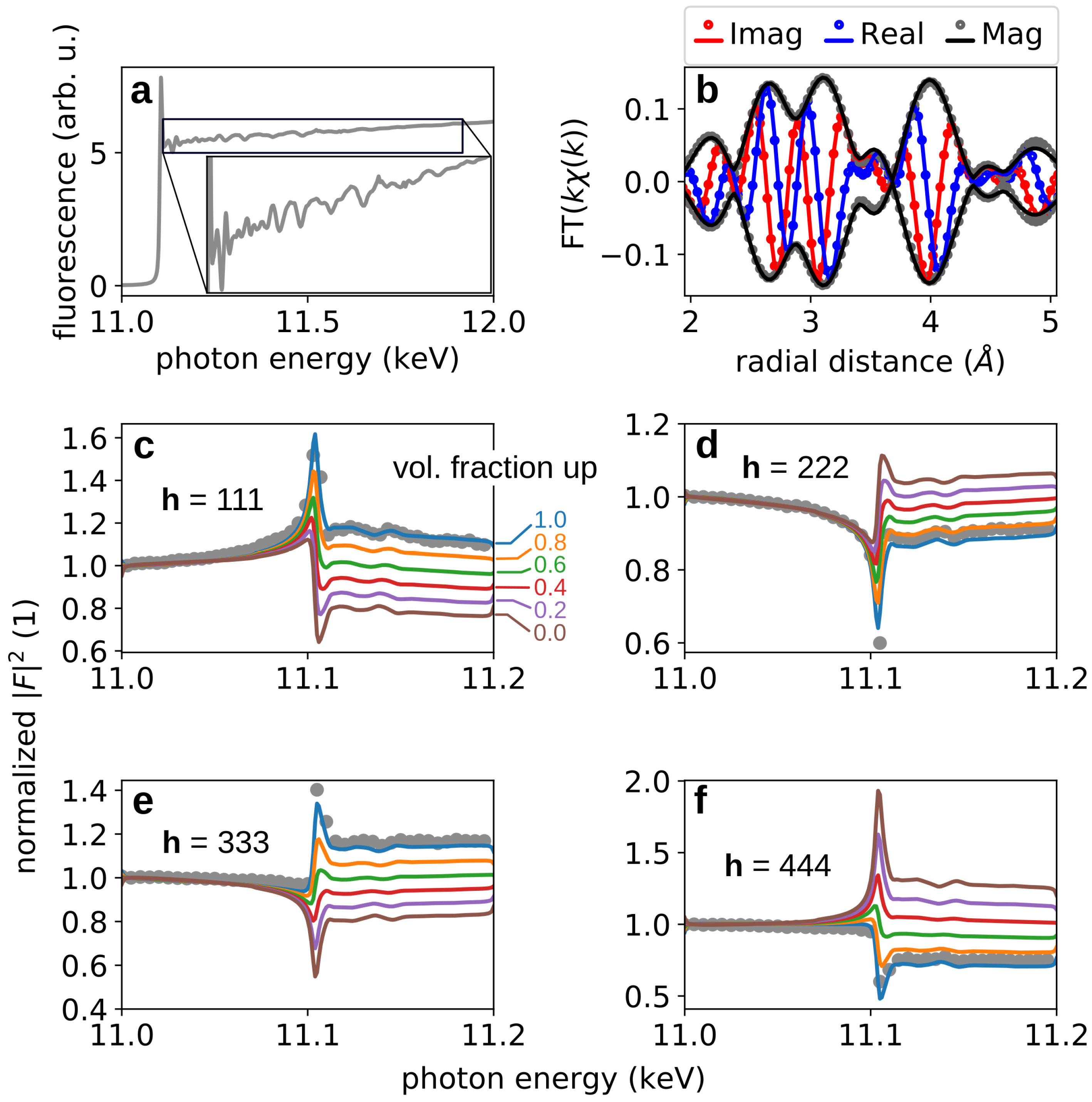
2.3. X-Ray Absorption Fine Structure Spectroscopy and Anomalous Diffraction
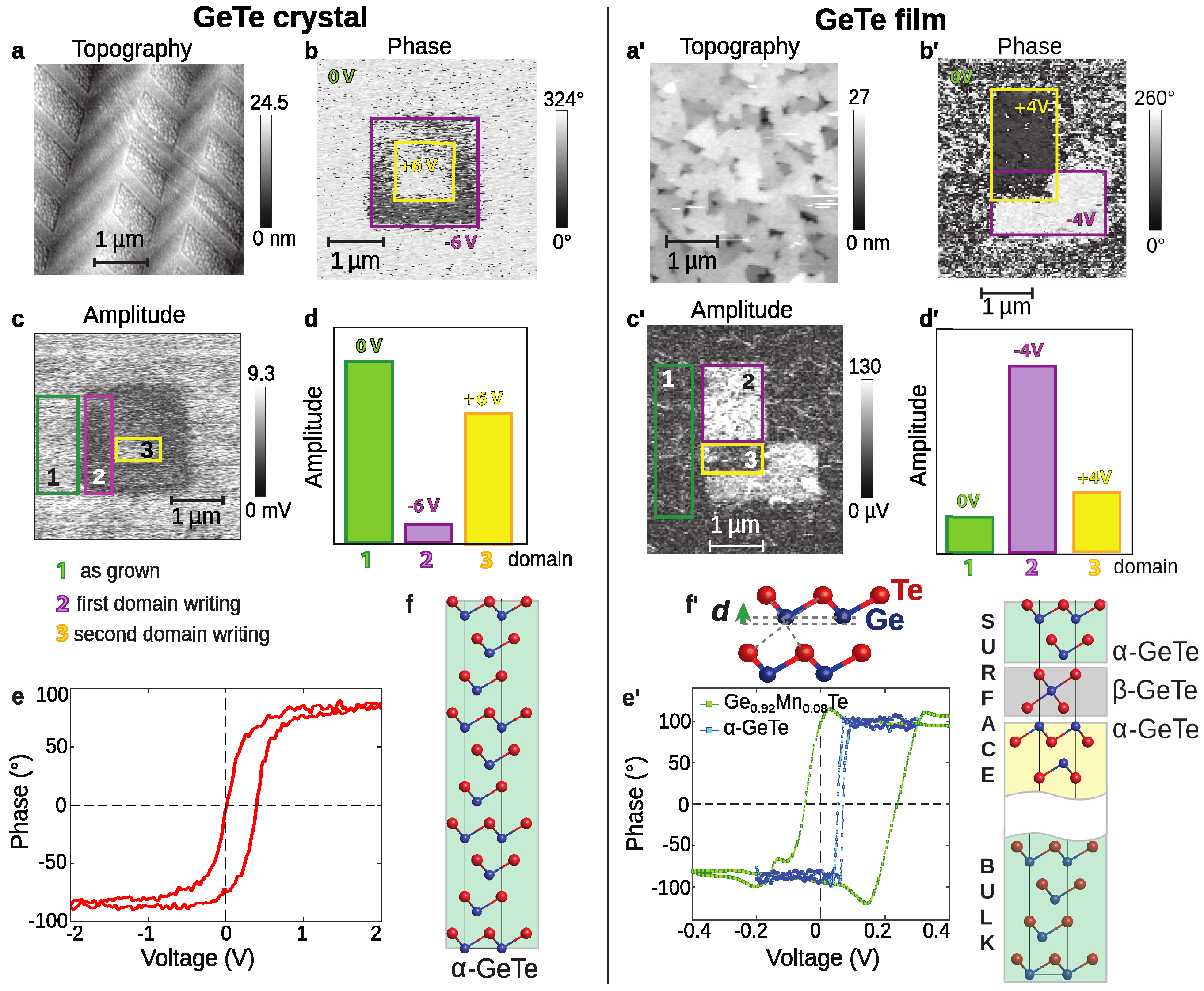
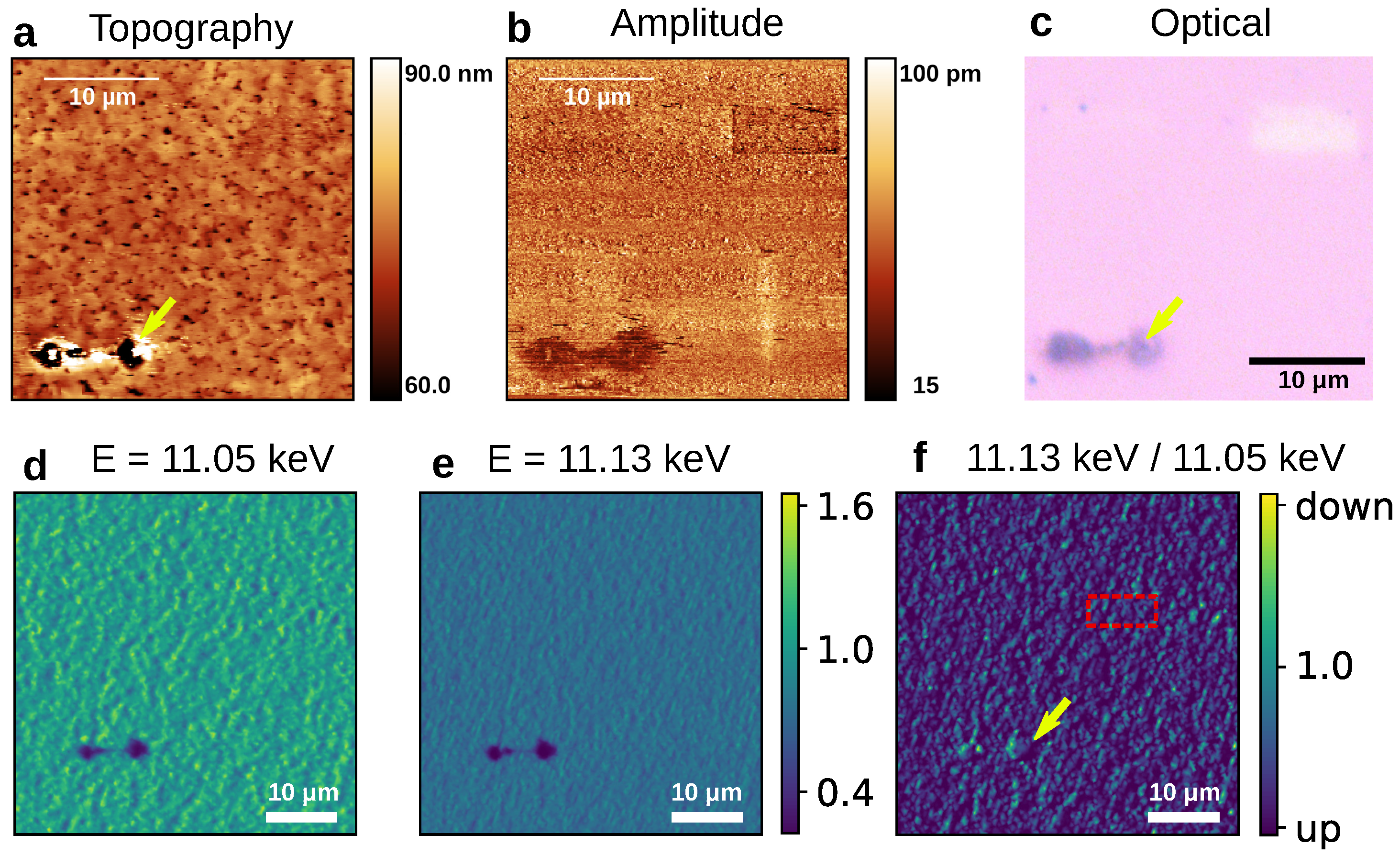
2.4. FE Domains Probed by Piezo-Force Scanning Microscopy
3. Results and Discussion
3.1. Self-Polarized State
3.2. Self-Poling of GeTe Surface Versus Bulk
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194–198. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.Z.; Kane, C.L. Colloquium:Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Dil, J.H. Spin- and angle-resolved photoemission on topological materials. Electron. Struct. 2019, 1, 023001. [Google Scholar] [CrossRef] [Green Version]
- Rashba, E.I. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 1960, 2, 1109–1122. [Google Scholar]
- Di Sante, D.; Barone, P.; Bertacco, R.; Picozzi, S. Electric Control of the Giant Rashba Effect in Bulk GeTe. Adv. Mater. 2013, 25, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Krempaský, J.; Volfová, H.; Muff, S.; Pilet, N.; Landolt, G.; Radović, M.; Shi, M.; Kriegner, D.; Holý, V.; Braun, J.; et al. Disentangling bulk and surface Rashba effects in ferroelectric α-GeTe. Phys. Rev. B 2016, 94, 205111. [Google Scholar] [CrossRef]
- Liebmann, M.; Rinaldi, C.; Di Sante, D.; Kellner, J.; Pauly, C.; Wang, R.N.; Boschker, J.E.; Giussani, A.; Bertoli, S.; Cantoni, M.; et al. Giant Rashba-Type Spin Splitting in Ferroelectric GeTe(111). Adv. Mater. 2016, 28, 560–565. [Google Scholar] [CrossRef]
- Elmers, H.J.; Wallauer, R.; Liebmann, M.; Kellner, J.; Morgenstern, M.; Wang, R.N.; Boschker, J.E.; Calarco, R.; Sánchez-Barriga, J.; Rader, O.; et al. Spin mapping of surface and bulk Rashba states in ferroelectric α-GeTe(111) films. Phys. Rev. B 2016, 94, 201403. [Google Scholar] [CrossRef]
- Krempaský, J.; Fanciulli, M.; Pilet, N.; Minár, J.; Khan, W.; Muntwiler, M.; Bertran, F.; Muff, S.; Weber, A.P.; Strocov, V.N.; et al. Spin-resolved electronic structure of ferroelectric α-GeTe and multiferroic Ge1−xMnxTe. J. Phys. Chem. Solids 2019, 128, 237–244. [Google Scholar] [CrossRef]
- Pawley, G.S.; Cochran, W.; Cowley, R.A.; Dolling, G. Diatomic Ferroelectrics. Phys. Rev. Lett. 1966, 17, 753–755. [Google Scholar] [CrossRef]
- Muir, J.A.; Beato, V. Phase transformations in the system GeSe-GeTe. J. Less Common Met. 1973, 33, 333–340. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Boucherle, J.X.; von Schnering, H.G. Neutron diffraction study on the structural phase transition in GeTe. J. Phys. C Solid State Phys. 1987, 20, 1431–1440. [Google Scholar] [CrossRef]
- Kriegner, D.; Furthmüller, J.; Kirchschlager, R.; Endres, J.; Horak, L.; Cejpek, P.; Reichlova, H.; Marti, X.; Primetzhofer, D.; Ney, A.; et al. Ferroelectric phase transitions in multiferroic Ge1−xMnxTe driven by local lattice distortions. Phys. Rev. B 2016, 94, 054112. [Google Scholar] [CrossRef] [PubMed]
- Kolobov, A.V.; Kim, D.J.; Giussani, A.; Fons, P.; Tominaga, J.; Calarco, R.; Gruverman, A. Ferroelectric switching in epitaxial GeTe films. APL Mater. 2014, 2, 066101. [Google Scholar] [CrossRef]
- Spaldin, N.A. Analogies and Differences between Ferroelectrics and Ferromagnets. In Physics of Ferroelectrics: A Modern Perspective, Topics Appl. Physics; Rabe, K., Ahn, C.H., Triscone, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 105, pp. 175–218. [Google Scholar]
- Matsunaga, T.; Fons, P.; Kolobov, A.V.; Tominaga, J.; Yamada, N. The order-disorder transition in GeTe: Views from different length-scales. Appl. Phys. Lett. 2011, 99, 231907. [Google Scholar] [CrossRef]
- Lencer, D.; Salinga, M.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Wuttig, M. A map for phase-change materials. Nat. Mater. 2008, 7, 972–977. [Google Scholar] [CrossRef]
- Shportko, K.; Kremers, S.; Woda, M.; Lencer, D.; Robertson, J.; Wuttig, M. Resonant bonding in crystalline phase-change materials. Nat. Mater. 2008, 7, 653–658. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Wang, X.; Bu, Z.; Zheng, L.; Zhou, B.; Xiong, F.; Chen, Y.; Pei, Y. High-Performance GeTe Thermoelectrics in Both Rhombohedral and Cubic Phases. J. Am. Chem. Soc. 2018, 140, 16190–16197. [Google Scholar] [CrossRef]
- Srinivasan, B.; Gellé, A.; Gucci, F.; Boussard-Pledel, C.; Fontaine, B.; Gautier, R.; Halet, J.F.; Reece, M.J.; Bureau, B. Realizing a stable high thermoelectric zT ∼ 2 over a broad temperature range in Ge1−x−yGaxSbyTe via band engineering and hybrid flash-SPS processing. Inorg. Chem. Front. 2019, 6, 63–73. [Google Scholar] [CrossRef]
- Przybylinska, H.; Springholz, G.; Lechner, R.T.; Hassan, M.; Wegscheider, M.; Jantsch, W.; Bauer, G. Magnetic-Field-Induced Ferroelectric Polarization Reversal in the Multiferroic Ge1−xMnxTe Semiconductor. Phys. Rev. Lett. 2014, 112, 047202. [Google Scholar] [CrossRef]
- Krempaský, J.; Muff, S.; Bisti, F.; Fanciulli, M.; Volfová, H.; Weber, A.P.; Pilet, N.; Warnicke, P.; Bertran, F.; Ebert, H.; et al. Entanglement and manipulation of the magnetic and spin-orbit order in multiferroic Ge1−xMnxTe. Nat. Commun. 2016, 7, 13071. [Google Scholar] [CrossRef] [PubMed]
- Krempaský, J.; Muff, S.; Minár, J.; Pilet, N.; Fanciulli, M.; Weber, A.P.; Guedes, E.B.; Caputo, M.; Müller, E.; Volobuev, V.V.; et al. Operando Imaging of All-Electric Spin Texture Manipulation in Ferroelectric and Multiferroic Rashba Semiconductors. Phys. Rev. X 2018, 8, 021067. [Google Scholar] [CrossRef] [Green Version]
- Krempaský, J.; Springholz, G.; Minár, J.; Dil, J.H. α-GeTe and (GeMn)Te semiconductors: A new paradigm for spintronics. AIP Conf. Proc. 2018, 1996, 020026. [Google Scholar]
- Deringer, V.L.; Lumeij, M.; Dronskowski, R. Ab Initio Modeling of α-GeTe(111) Surfaces. J. Phys. Chem. C 2012, 116, 15801–15811. [Google Scholar] [CrossRef]
- Lechner, R.T.; Springholz, G.; Hassan, M.; Groiss, H.; Kirchschlager, R.; Stangl, J.; Hrauda, N.; Bauer, G. Phase separation and exchange biasing in the ferromagnetic IV-VI semiconductor Ge1−xMnxTe. Appl. Phys. Lett. 2010, 97, 023101. [Google Scholar] [CrossRef]
- Chahine, G.A.; Richard, M.I.; Homs-Regojo, R.A.; Tran-Caliste, T.N.; Carbone, D.; Jaques, V.L.R.; Grifone, R.; Boesecke, P.; Katzer, J.; Costina, I.; et al. Imaging of strain and lattice orientation by quick scanning X-ray microscopy combined with three-dimensional reciprocal space mapping. J. Appl. Crystallogr. 2014, 47, 762–769. [Google Scholar] [CrossRef]
- Stangl, J.; Mocuta, C.; Diaz, A.; Metzger, T.H.; Bauer, G. X-ray diffraction as a local probe tool. ChemPhysChem 2009, 10, 2923–2930. [Google Scholar] [CrossRef] [PubMed]
- Hrauda, N.; Zhang, J.; Wintersberger, E.; Etzelstorfer, T.; Mandl, B.; Stangl, J.; Carbone, D.; Holý, V.; Jovanović, V.; Biasotto, C.; et al. X-ray nanodiffraction on a single SiGe quantum dot inside a functioning field-effect transistor. Nano Lett. 2011, 11, 2875–2880. [Google Scholar] [CrossRef]
- Chahine, G.A.; Zoellner, M.H.; Richard, M.I.; Guha, S.; Reich, C.; Zaumseil, P.; Capellini, G.; Schroeder, T.; Schülli, T.U. Strain and lattice orientation distribution in SiN/Ge complementary metal-oxide-semiconductor compatible light emitting microstructures by quick X-ray nano-diffraction microscopy. Appl. Phys. Lett. 2015, 106, 071902. [Google Scholar] [CrossRef]
- Schäfer, N.; Chahine, G.A.; Wilkinson, A.J.; Schmid, T.; Rissom, T.; Schülli, T.U.; Abou-Ras, D. Microstrain distributions in polycrystalline thin films measured by X-ray microdiffraction. J. Appl. Crystallogr. 2016, 49, 632. [Google Scholar] [CrossRef]
- Kriegner, D.; Harcuba, P.; Vesely, J.; Lesnik, A.; Bauer, G.; Springholz, G.; Holy, V. Twin domain imaging in topological insulator Bi2Te3 and Bi2Se3 epitaxial thin films by scanning X-ray nanobeam microscopy and electron backscatter diffraction. J. Appl. Crystallogr. 2017, 50, 369–377. [Google Scholar] [CrossRef] [PubMed]
- Ravel, B.; Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radat. 2005, 12, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Kelly, S.D.; Stern, E.A.; Ingalls, R. Determining crystalline atomic positions using XAFS, a new addition to the UWXAFS analysis package. J. Synchrotron Radat. 2001, 8, 311–313. [Google Scholar] [CrossRef] [PubMed]
- Azimonte, C.; Granado, E.; Terashita, H.; Park, S.; Cheong, S.W. Polar atomic displacements in multiferroics observed via anomalous X-ray diffraction. Phys. Rev. B 2010, 81, 012103. [Google Scholar] [CrossRef]
- Richter, C.; Zschornak, M.; Novikov, D.; Mehner, E.; Nentwich, M.; Hanzig, J.; Gorfman, S.; Meyer, D.C. Picometer polar atomic displacements in strontium titanate determined by resonant X-ray diffraction. Nat. Commun. 2018, 9, 178. [Google Scholar] [CrossRef] [PubMed]
- Pietsch, U.; Holý, V.; Baumbach, T. High-Resolution X-ray Scattering; Springer: New York, NY, USA, 2004. [Google Scholar]
- Brown, P.J.; Fox, A.G.; Maslen, E.N.; O’Keefe, M.A.; Willis, B.T.M. Intensity of diffracted intensities. In International Tables for Crystallography; Prince, E., Ed.; Wiley Online Library: Hoboken, NJ, USA, 2006; Volume C, Chapter 6.1; p. 554. [Google Scholar]
- Sasaki, S. Numerical Tables of Anomalous Scattering Factors Calculated by the Cromer and Liberman’s Method; Technical Report; KEK–88-14; National Lab. for High Energy Physics: Tsukuba, Japan, 1989. [Google Scholar]
- Atomic Scattering Factor Files. Available online: http://henke.lbl.gov/optical_constants/asf.html (accessed on 1 November 2018).
- Cross, J.O.; Elam, W.T.; Woicik, J.C.; Sorensen, L.B. Reliability of structural parameters determined from DAFS data using the iterative dispersion integral algorithm. J. Synchrotron Radiat. 1999, 6, 335–337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalinin, S.V.; Bonnell, D.A. Electric Scanning Probe Imaging and Modification of Ferroelectric Surfaces. In Nanoscale Characterisation of Ferroelectric Materials; Gruverman, M.A.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Pilet, N.; Raabe, J.; Stevenson, S.E.; Romer, S.; Bernard, L.; McNeill, C.R.; Fink, R.H.; Hug, H.J.; Quitmann, C. Nanostructure characterization by a combined X-ray absorption/scanning force microscopy system. Nanotechnology 2012, 23, 475708. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.S.; Kim, B.S.; Cho, C.W.; Oh, M.W.; Min, B.K.; Park, S.D.; Lee, H.W. Herringbone structure in GeTe-based thermoelectric materials. Acta Mater. 2015, 91, 83–90. [Google Scholar] [CrossRef]
- Vermeulen, P.A.; Kumar, A.; ten Brink, G.H.; Blake, G.R.; Kooi, B.J. Unravelling the Domain Structures in GeTe and LaAlO3. Cryst. Growth Des. 2016, 16, 5915. [Google Scholar] [CrossRef]
- Wang, R.; Boschker, J.E.; Bruyer, E.; Sante, D.D.; Picozzi, S.; Perumal, K.; Giussani, A.; Riechert, H.; Calarco, R. Toward Truly Single Crystalline GeTe Films: The Relevance of the Substrate Surface. J. Phys. Chem. C 2014, 118, 29724–29730. [Google Scholar] [CrossRef]
- Polatoglou, H.M.; Theodorou, G.; Economou, N.A. Bonding in cubic and rhombohedral GeTe. J. Phys. C Solid State Phys. 1983, 16, 817. [Google Scholar] [CrossRef]
- Li, B.; Li, G.; Yin, Q.; Zhu, Z.; Ding, A.; Cao, W. Pinning and depinning mechanism of defect dipoles in PMnN–PZT ceramics. J. Phys. D Appl. Phys. 2005, 38, 1107–1111. [Google Scholar] [CrossRef]
- Kanno, I.; Fujii, S.; Kamada, T.; Takayama, R. Piezoelectric properties of c-axis oriented Pb(Zr,Ti)O3 thin films. Appl. Phys. Lett. 1997, 70, 1378–1380. [Google Scholar] [CrossRef]
- Pike, G.E.; Warren, W.L.; Dimos, D.; Tuttle, B.A.; Ramesh, R.; Lee, J.; Keramidas, V.G.; Evans, J.T., Jr. Voltage offsets in (Pb,La)(Zr,Ti)O3 thin films. Appl. Phys. Lett. 1995, 66, 484–486. [Google Scholar] [CrossRef]
- Chen, X.; Zou, Y.; Yuan, G.; Zeng, M.; Liu, J.M.; Yin, J.; Liu, Z. Temperature Gradient Introduced Ferroelectric Self-Poling in BiFeO3 Ceramics. J. Am. Ceram. Soc. 2013, 96, 3788–3792. [Google Scholar] [CrossRef]
- Nukala, P.; Ren, M.; Agarwal, R.; Berger, J.; Liu, G.; Johnson, A.T.C.; Agarwal, R. Inverting polar domains via electrical pulsing in metallic germanium telluride. Nat. Commun. 2017, 8, 15033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.Y.; Liu, G.; Sando, D.; Nagarajan, V.; Seidel, J. Morphology-dependent photo-induced polarization recovery in ferroelectric thin films. Appl. Phys. Lett. 2017, 111, 092902. [Google Scholar] [CrossRef]
- Rubio-Marcos, F.; Ochoa, D.A.; Del Campo, A.; García, M.A.; Castro, G.R.; Fernández, J.F.; García, J.E. Reversible optical control of macroscopic polarization in ferroelectrics. Nat. Photonics 2018, 12, 29–32. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kriegner, D.; Springholz, G.; Richter, C.; Pilet, N.; Müller, E.; Capron, M.; Berger, H.; Holý, V.; Dil, J.H.; Krempaský, J. Ferroelectric Self-Poling in GeTe Films and Crystals. Crystals 2019, 9, 335. https://doi.org/10.3390/cryst9070335
Kriegner D, Springholz G, Richter C, Pilet N, Müller E, Capron M, Berger H, Holý V, Dil JH, Krempaský J. Ferroelectric Self-Poling in GeTe Films and Crystals. Crystals. 2019; 9(7):335. https://doi.org/10.3390/cryst9070335
Chicago/Turabian StyleKriegner, Dominik, Gunther Springholz, Carsten Richter, Nicolas Pilet, Elisabeth Müller, Marie Capron, Helmut Berger, Václav Holý, J. Hugo Dil, and Juraj Krempaský. 2019. "Ferroelectric Self-Poling in GeTe Films and Crystals" Crystals 9, no. 7: 335. https://doi.org/10.3390/cryst9070335
APA StyleKriegner, D., Springholz, G., Richter, C., Pilet, N., Müller, E., Capron, M., Berger, H., Holý, V., Dil, J. H., & Krempaský, J. (2019). Ferroelectric Self-Poling in GeTe Films and Crystals. Crystals, 9(7), 335. https://doi.org/10.3390/cryst9070335





