High-Density Well-Aligned Dislocations Introduced by Plastic Deformation in Bi1−xSbx Topological Insulator Single Crystals
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
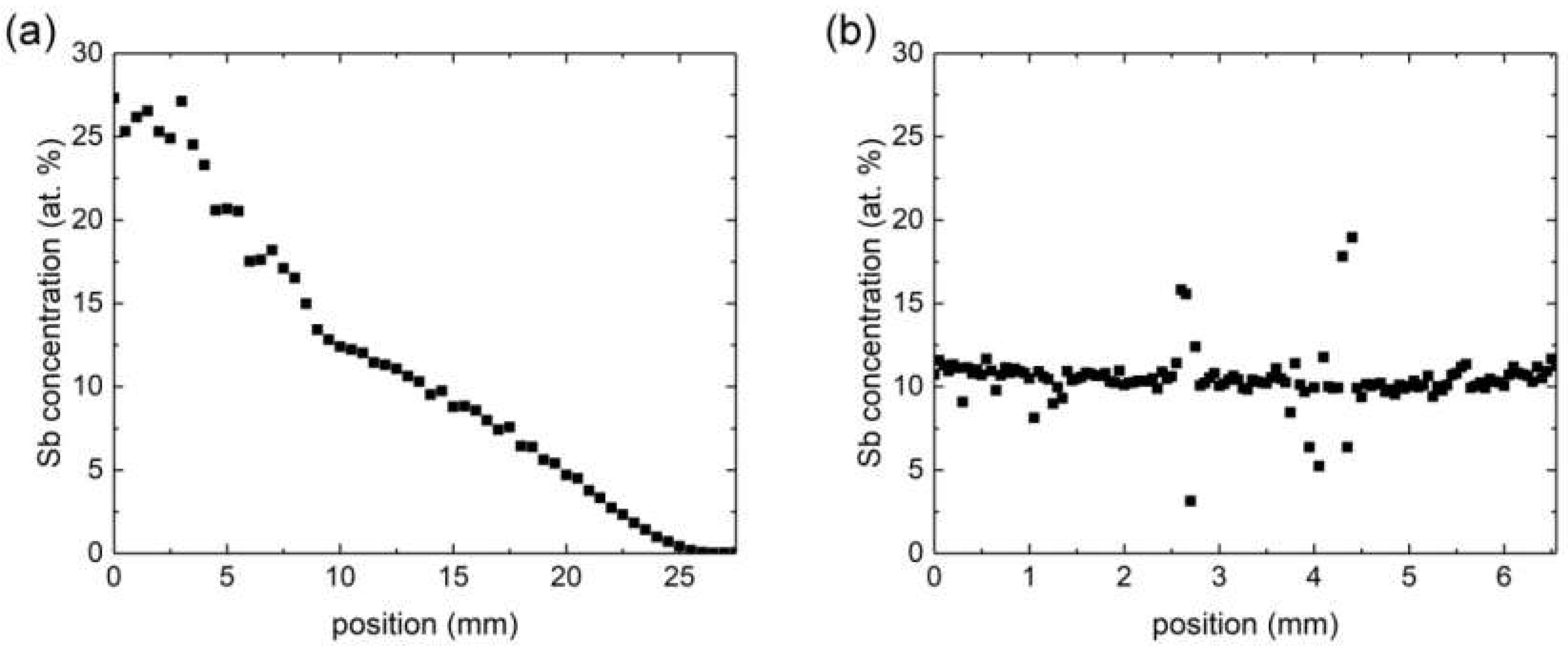
3.1. Crystal Growth
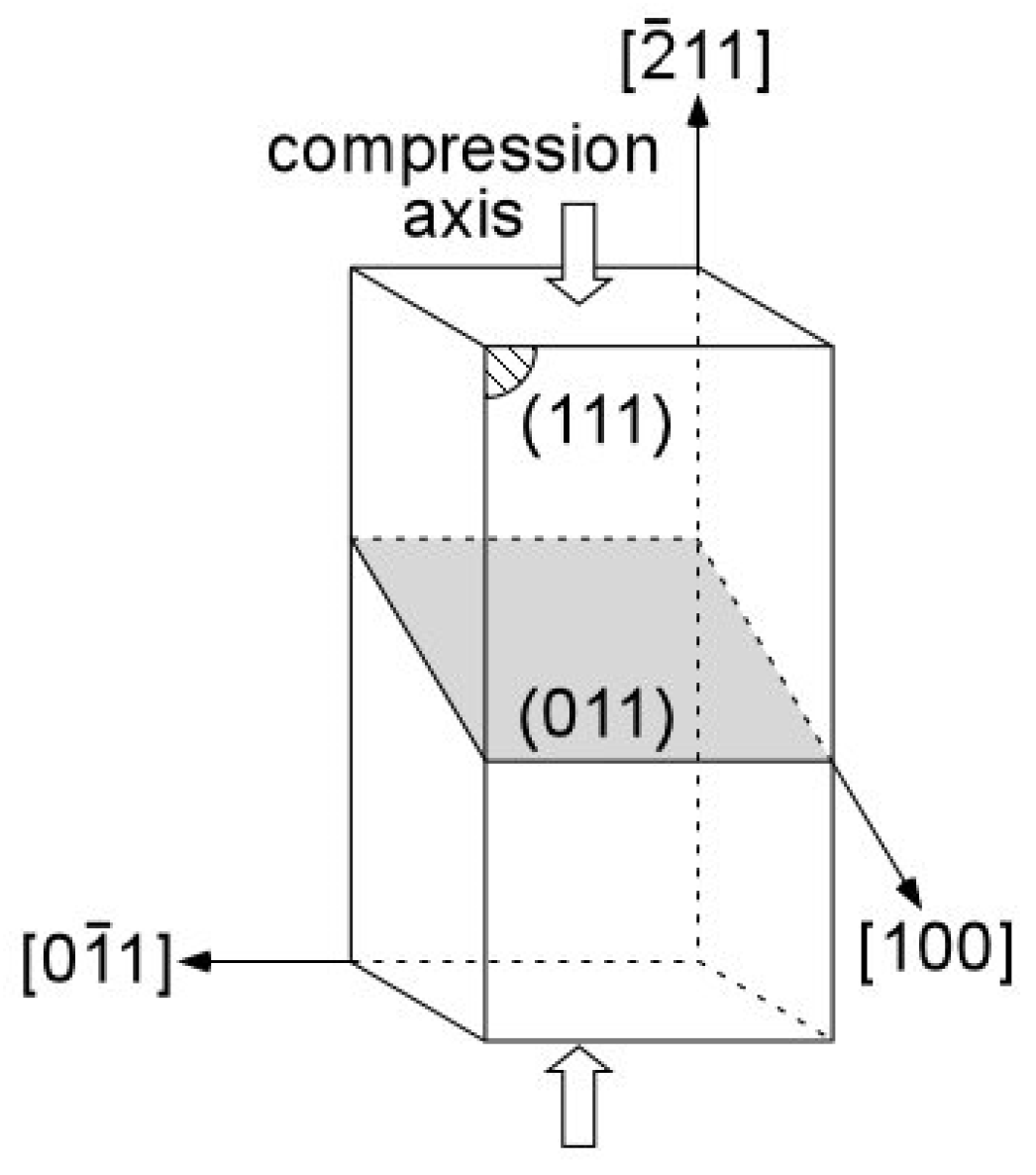
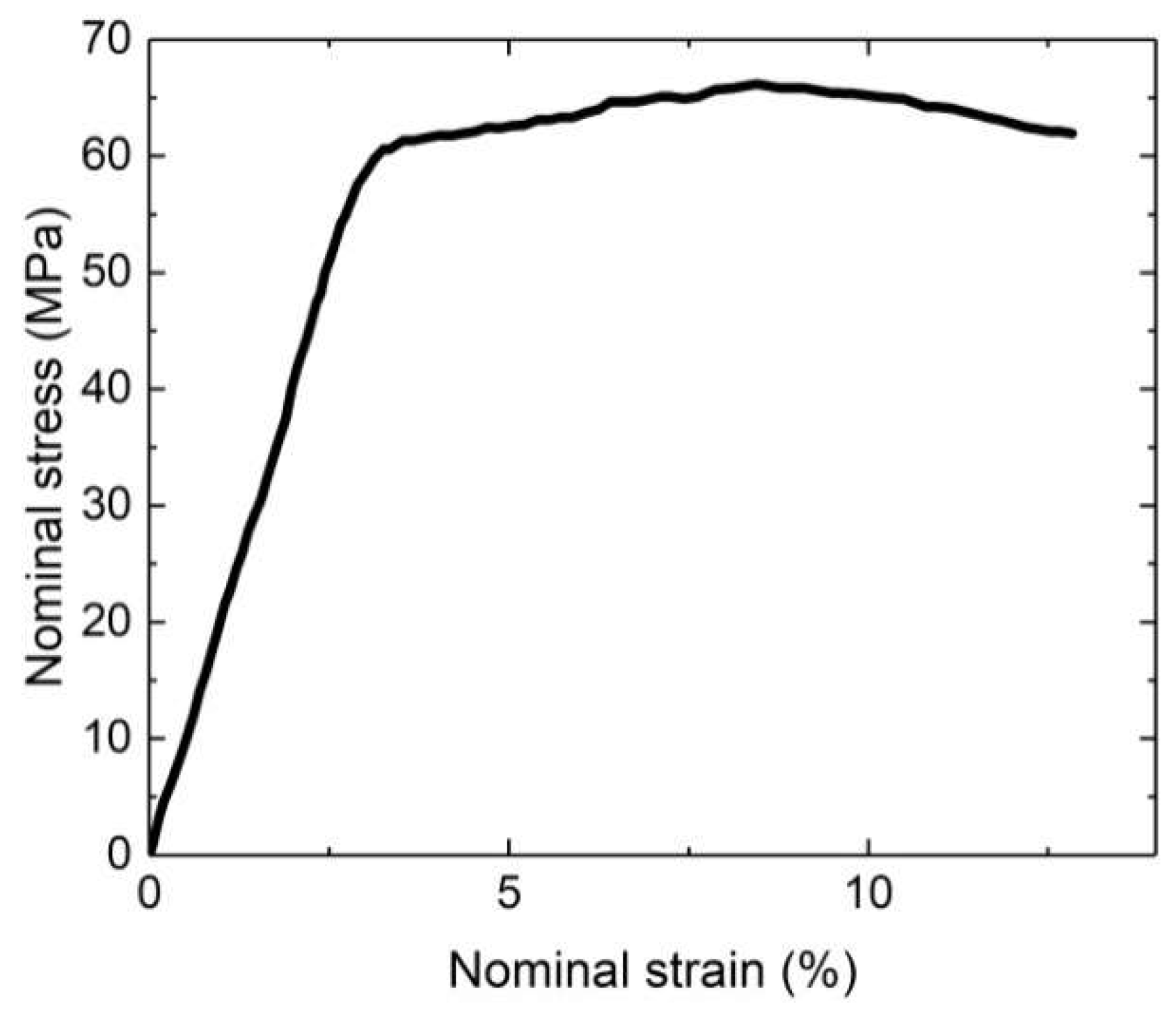
3.2. Plastic Deformation
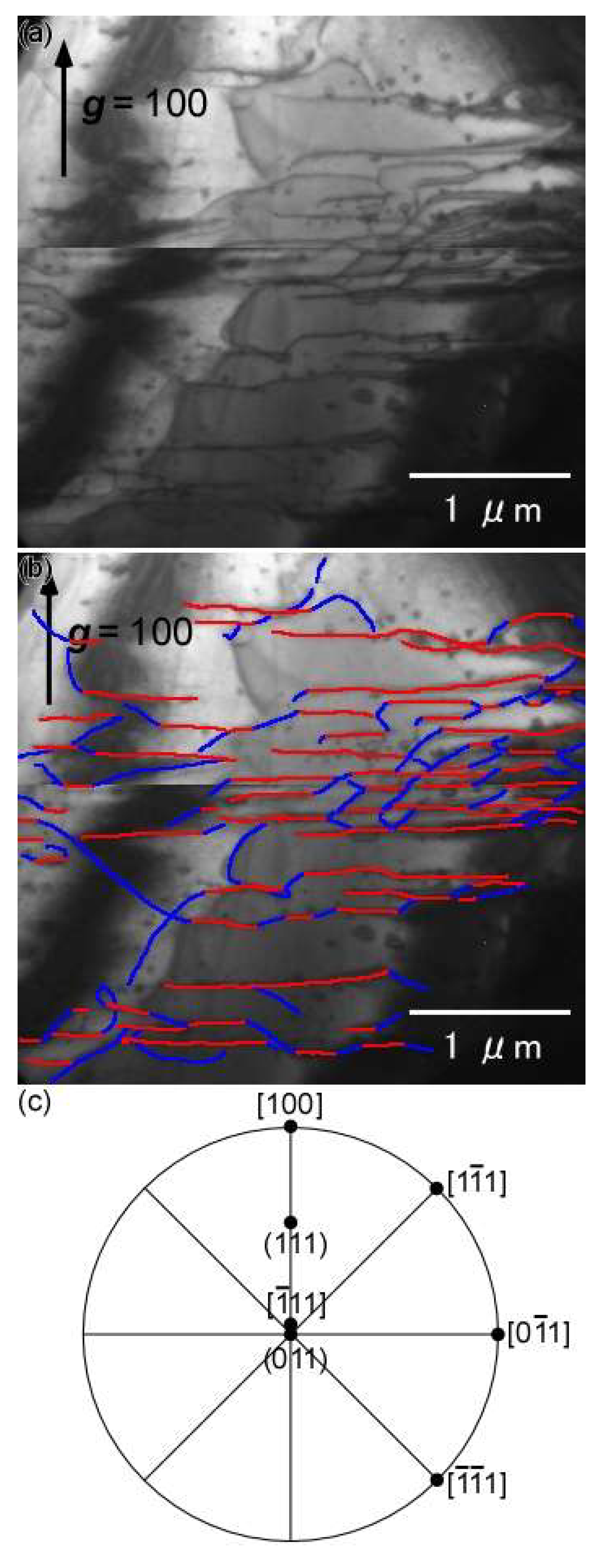
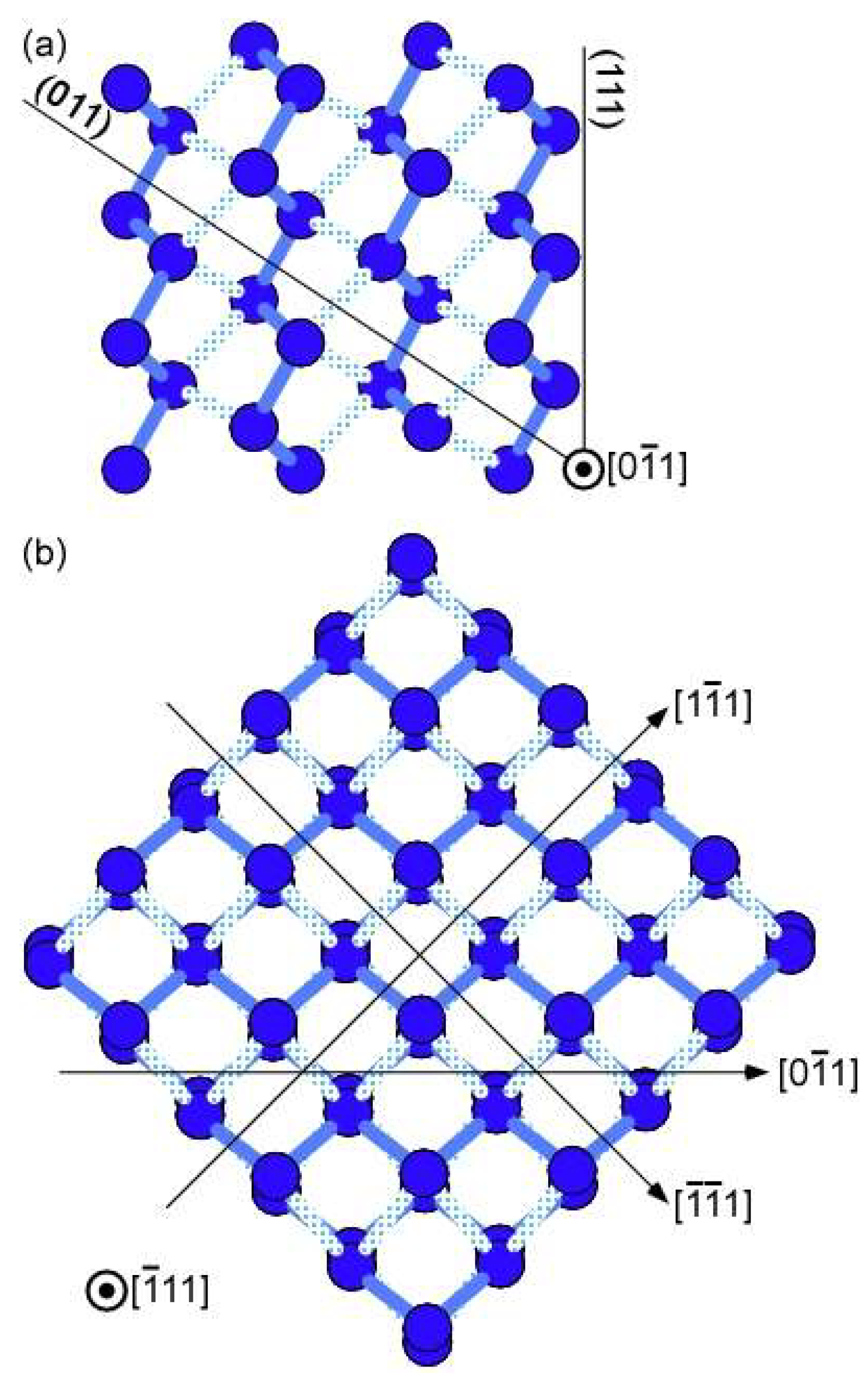
3.3. TEM Observations of Dislocations Introduced by Plastic Deformation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hasan, M.Z.; Kane, C.L. Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn. 2013, 82, 102001. [Google Scholar] [CrossRef]
- Ran, Y.; Zhang, Y.; Vishwanath, A. One-dimensional topologically protected modes in topological insulators with lattice dislocations. Nat. Phys. 2009, 5, 298–303. [Google Scholar] [CrossRef]
- Moore, J.E.; Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 2007, 75, 121306. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological insulators in three dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [PubMed]
- Tretiakov, O.A.; Abanov, A.; Murakami, S.; Sinova, J. Large thermoelectric figure of merit for three-dimensional topological Anderson insulators via line dislocation engineering. Appl. Phys. Lett. 2010, 97, 073108. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Topological insulators with inversion symmetry. Phys. Rev. B 2007, 76, 045302. [Google Scholar] [CrossRef]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970–974. [Google Scholar] [CrossRef]
- Ellett, M.R.; Horst, R.B.; Williams, L.R.; Cuff, K.F. Shubnikov-de Haas investigations of the Bi1−xSbx (0 < x < 0.3) system. J. Phys. Soc. Jpn. 1996, 21, 666–672. [Google Scholar]
- Imura, K.; Takane, Y.; Tanaka, A. Weak topological insulator with protected gapless helical states. Phys. Rev. B 2011, 84, 035443. [Google Scholar] [CrossRef]
- Yoshimura, Y.; Matsumoto, A.; Takane, Y.; Imura, K. Perfectly conducting channel on the dark surface of weak topological insulators. Phys. Rev. B 2013, 88, 045408. [Google Scholar] [CrossRef]
- Slager, R.-J.; Mesaros, A.; Juricic, V.; Zaanen, J. Interplay between electronic topology and crystal symmetry: Dislocation-line modes in topological band insulators. Phys. Rev. B 2014, 90, 241403. [Google Scholar] [CrossRef]
- Hamasaki, H.; Tokumoto, Y.; Edagawa, K. Dislocation conduction in Bi-Sb topological insulators. Appl. Phys. Lett. 2017, 110, 092105. [Google Scholar] [CrossRef]
- Otake, S.; Motohashi, Y. Plastic deformation and dislocation etch-pit distribution for the primary glide system on bismuth single crystals. J. Jpn. Inst. Met. Mater. 1973, 37, 44–51. [Google Scholar] [CrossRef][Green Version]
- Motohashi, Y.; Otake, S. Plastic deformation and dislocation etch-pit distribution due to the glide system for bismuth single crystals. J. Jpn. Inst. Met. Mater. 1973, 37, 978–985. [Google Scholar] [CrossRef][Green Version]
- Yanaka, Y.; Kariya, Y.; Watanabe, H.; Hokazono, H. Plastic deformation behavior and mechanism of bismuth single crystals in principal axes. Mater. Trans. 2016, 57, 819–823. [Google Scholar] [CrossRef]
- Yanaka, Y.; Kariya, Y.; Watanabe, H.; Hokazono, H. Influence of temperature on plastic deformation behavior and mechanism of bismuth single crystals. J. Electron. Mater. 2018, 47, 594–603. [Google Scholar] [CrossRef]
- Otake, S.; Namazuea, H.; Matsuno, N. Critical resolved shear stresses of two slip systems in bismuth single crystals. Jpn. J. Appl. Phys. 1980, 19, 433–437. [Google Scholar] [CrossRef]
- Steegmuller, C.; Daniel, J.S. Slip in bismuth. J. Less Common Met. 1972, 27, 81–85. [Google Scholar] [CrossRef]
- Matsuo, T.; Suzuki, H. Effect of plastic deformation on the thermal conductivity of bismuth crystals. J. Phys. Soc. Jpn. 1976, 41, 1692–1698. [Google Scholar] [CrossRef]
- Mooser, E.; Peason, W.B. The crystal structures and properties of the group VB to VIIB elements and of compounds formed between them. J. Phys. Chem. Solids 1958, 7, 65–77. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tokumoto, Y.; Fujiwara, R.; Edagawa, K. High-Density Well-Aligned Dislocations Introduced by Plastic Deformation in Bi1−xSbx Topological Insulator Single Crystals. Crystals 2019, 9, 317. https://doi.org/10.3390/cryst9060317
Tokumoto Y, Fujiwara R, Edagawa K. High-Density Well-Aligned Dislocations Introduced by Plastic Deformation in Bi1−xSbx Topological Insulator Single Crystals. Crystals. 2019; 9(6):317. https://doi.org/10.3390/cryst9060317
Chicago/Turabian StyleTokumoto, Yuki, Riku Fujiwara, and Keiichi Edagawa. 2019. "High-Density Well-Aligned Dislocations Introduced by Plastic Deformation in Bi1−xSbx Topological Insulator Single Crystals" Crystals 9, no. 6: 317. https://doi.org/10.3390/cryst9060317
APA StyleTokumoto, Y., Fujiwara, R., & Edagawa, K. (2019). High-Density Well-Aligned Dislocations Introduced by Plastic Deformation in Bi1−xSbx Topological Insulator Single Crystals. Crystals, 9(6), 317. https://doi.org/10.3390/cryst9060317




