Electro-Optical Switching of Dual-Frequency Nematic Liquid Crystals: Regimes of Thin and Thick Cells
Abstract
1. Introduction
2. Materials and Methods
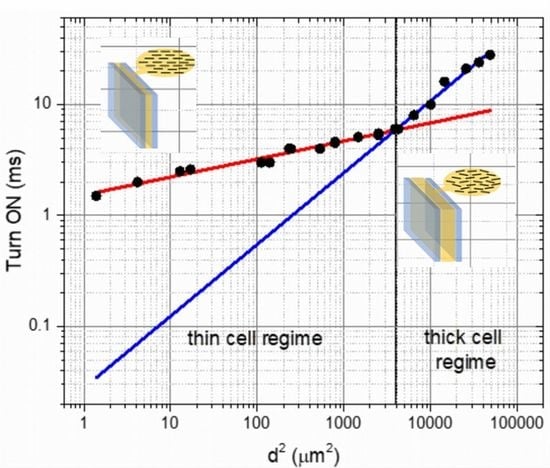
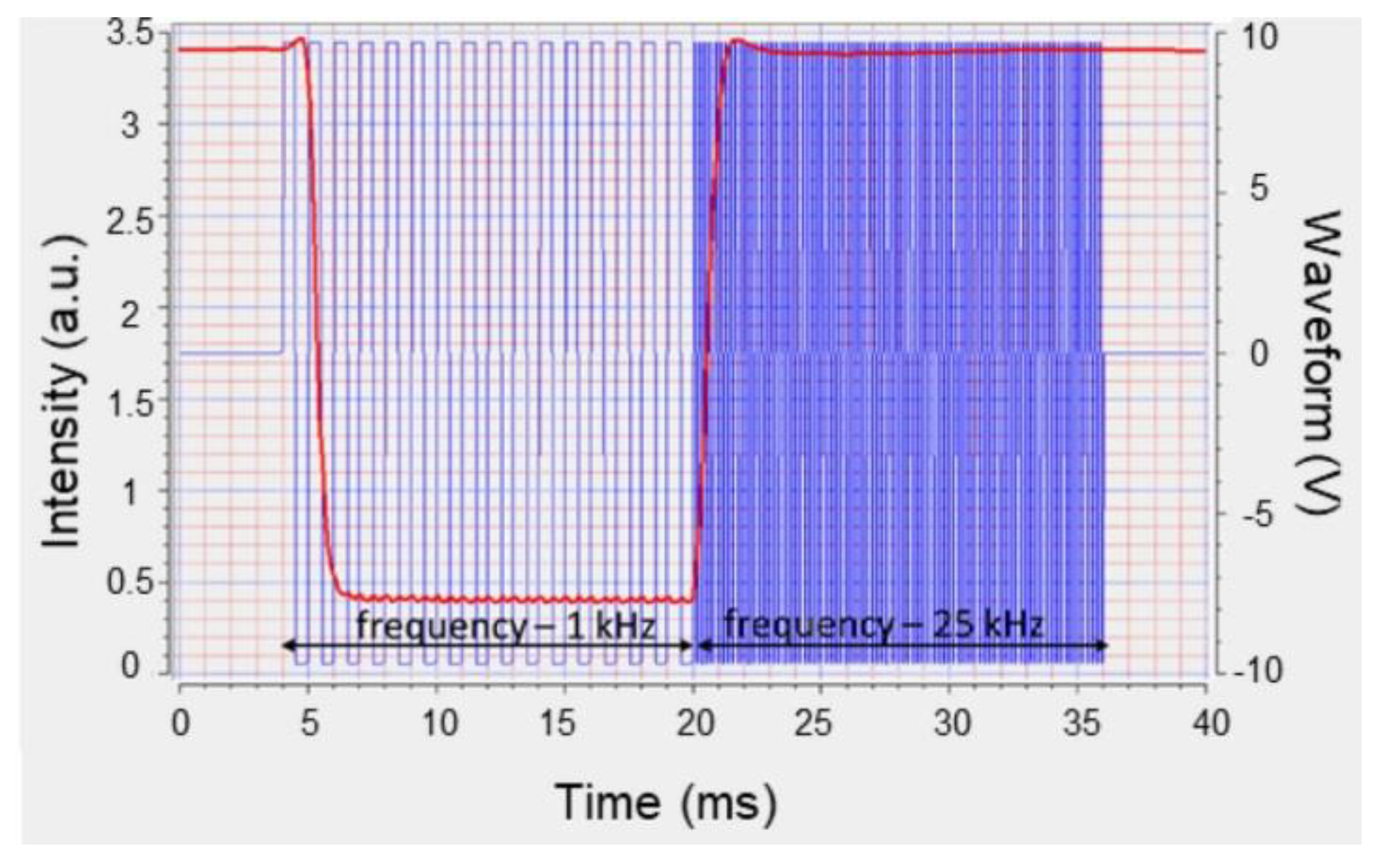
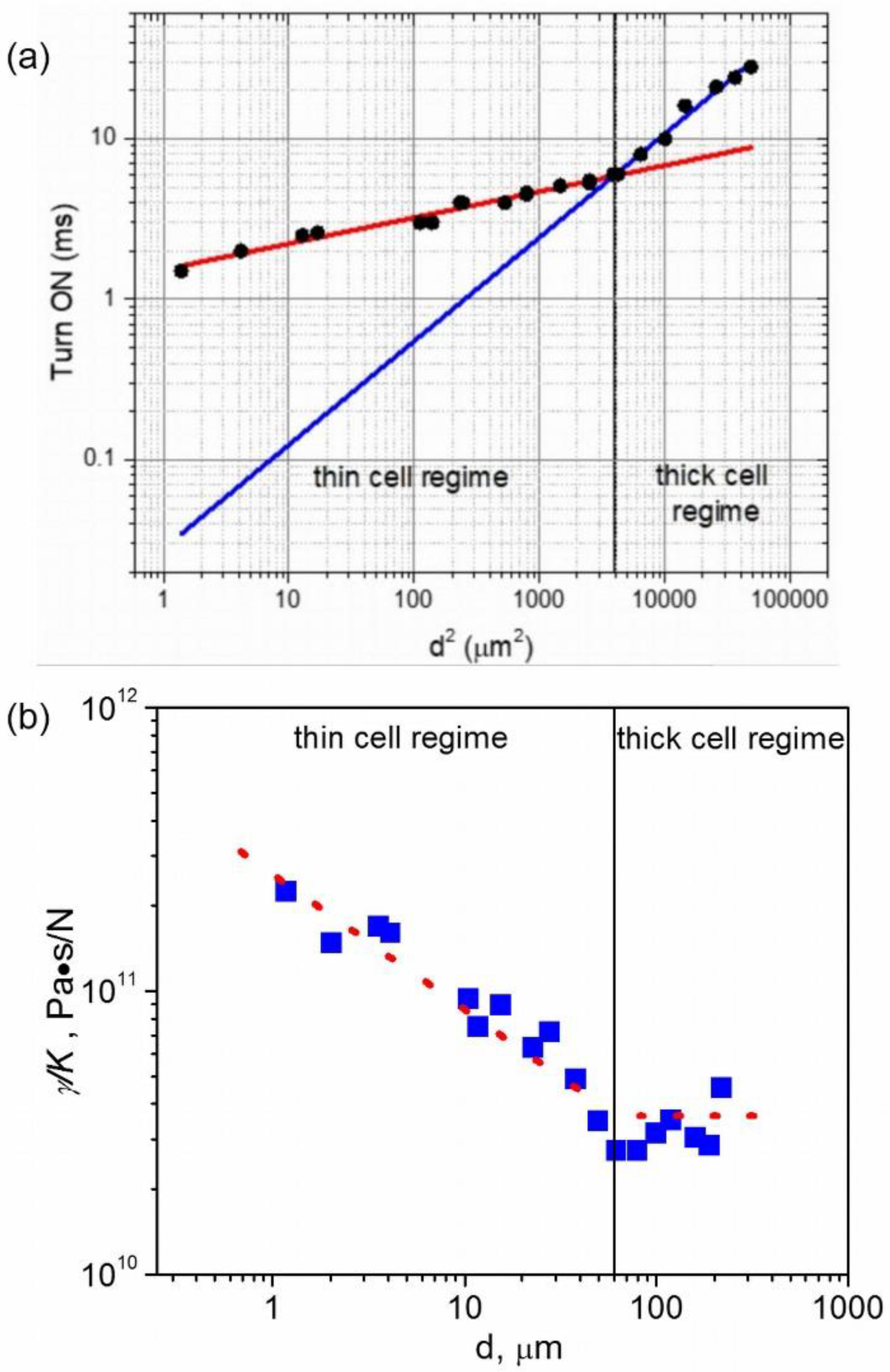
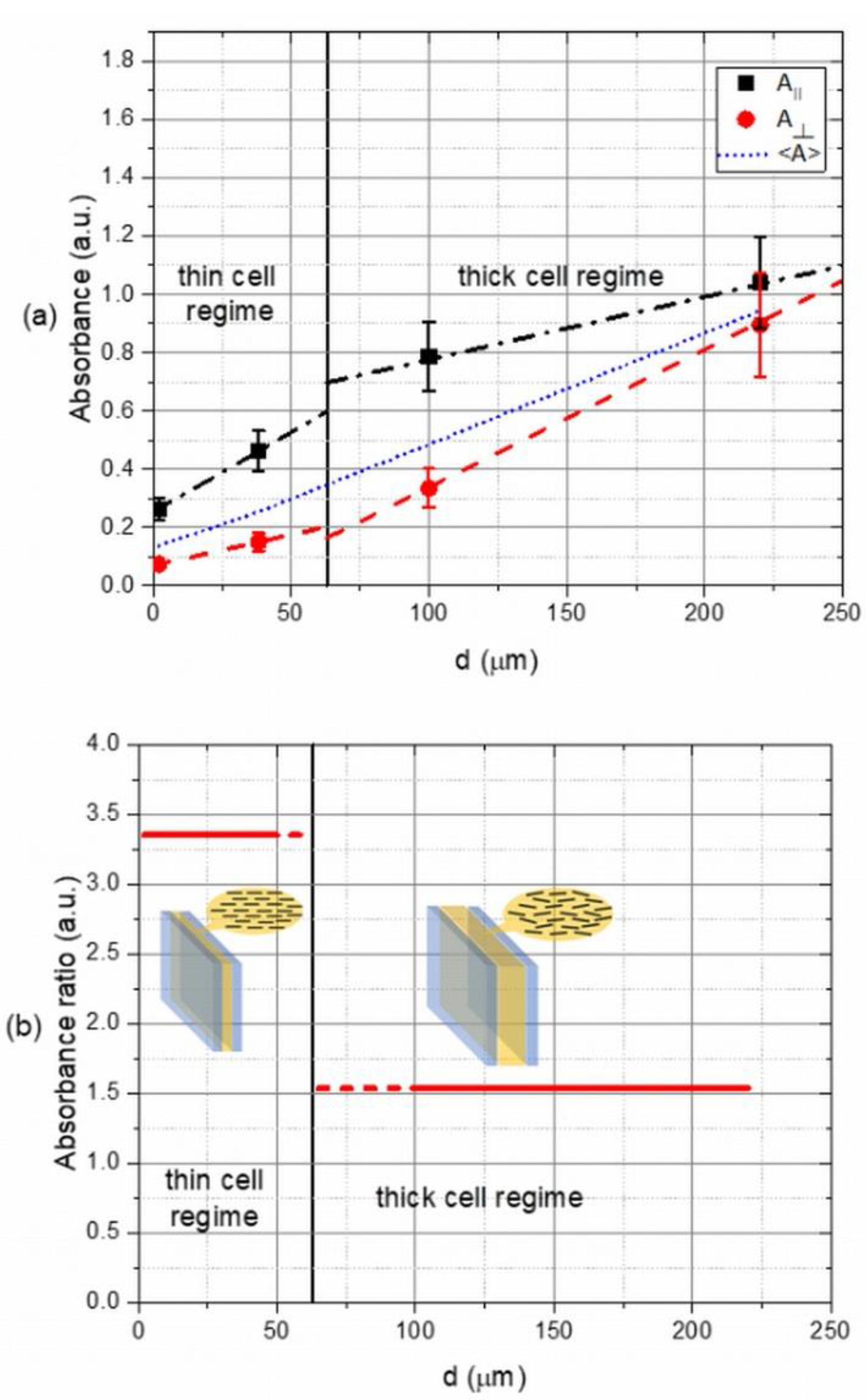
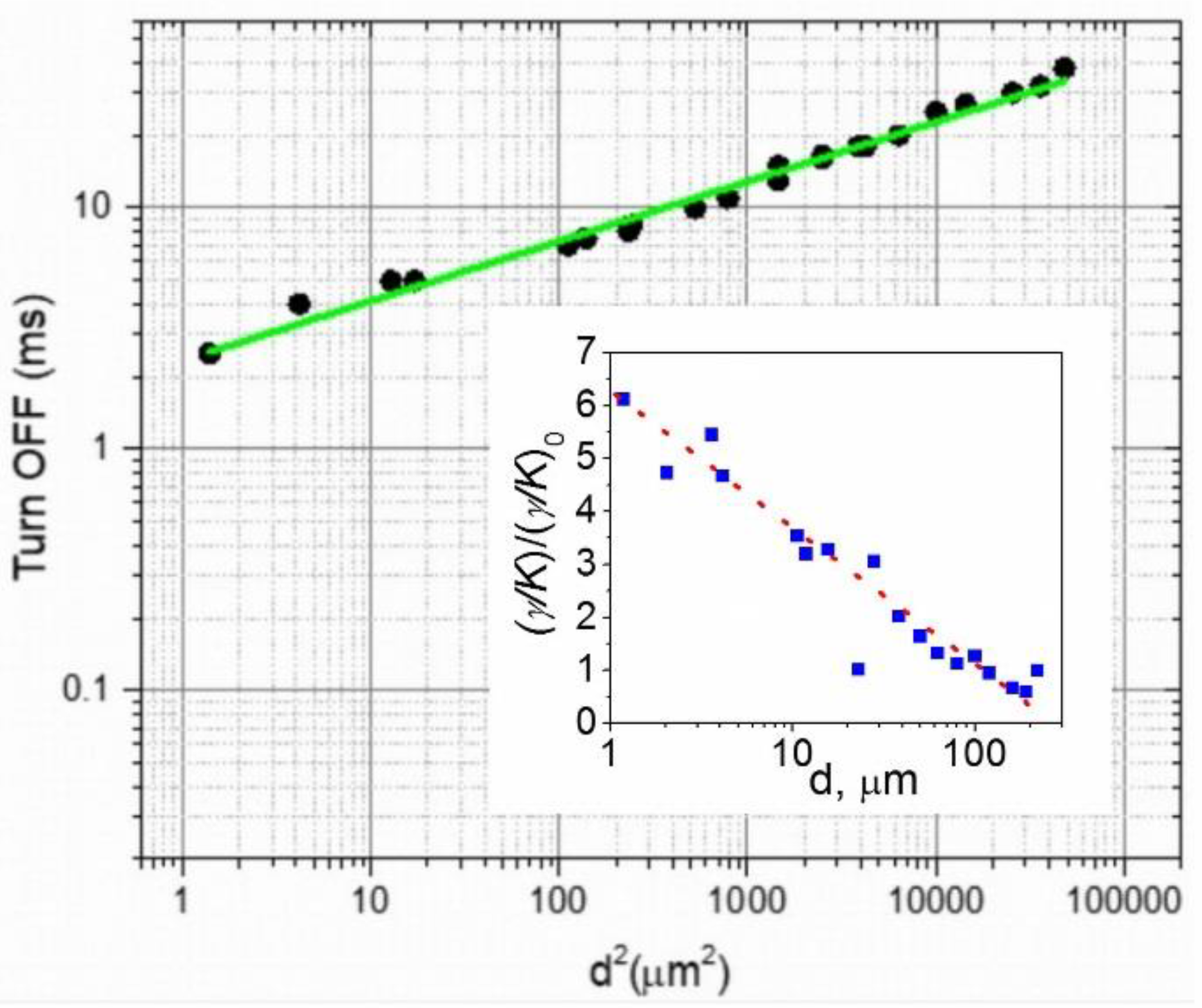
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Castellano, J.A. Liquid crystal display applications past, present & future. Liq. Cryst. Today 1991, 1, 4–6. [Google Scholar]
- Arines, J. Impact of liquid crystals in active and adaptive optics. Materials 2009, 2, 549–561. [Google Scholar] [CrossRef]
- Camley, R.; Celinski, Z.; Garbovskiy, Y.; Glushchenko, A. Liquid crystals for signal processing applications in themicrowave andmillimeter wave frequency ranges. Liq. Cryst. Rev. 2018, 6, 17–52. [Google Scholar] [CrossRef]
- Khoo, I.-C. Liquid Crystals; Wiley & Sons Inc.: Hoboken, NJ, USA, 2007; p. 368. [Google Scholar]
- Nie, X.; Lu, R.; Xianyu, H.; Wu, T.X.; Wu, S.T. Anchoring energy and cell gap effects on liquid crystal response time. J. Appl. Phys. 2007, 101, 103110. [Google Scholar] [CrossRef]
- He, Z.; Gou, F.; Chen, R.; Yin, K.; Zhan, T.; Wu, S.-T. Liquid Crystal Beam Steering Devices: Principles, Recent Advances, and Future Developments. Crystals 2019, 9, 292. [Google Scholar] [CrossRef]
- Di Pietro, V.M.; Residori, S.; Bortolozzo, U.; Jullien, A.; Forget, N. Dynamical optical response of nematic liquid crystal cells through electrically driven Fréedericksz transition: Influence of the nematic layer thickness. Opt. Express 2018, 26, 10716–10728. [Google Scholar] [CrossRef]
- Mucha, M.; Nastal, E. Complex study of reorientational dynamics of the liquid crystal in PDLC films. Liq. Cryst. 1997, 23, 749–758. [Google Scholar] [CrossRef]
- Melnyk, O.; Garbovskiy, Y.; Glushchenko, A. Science and technology of stressed liquid crystals: Display and non-display applications. Phase Transit. 2017, 90, 773–779. [Google Scholar] [CrossRef]
- Wen, C.-H. High Birefringence and Low Viscosity Liquid Crystals. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2006; p. 148. [Google Scholar]
- Dąbrowski, R.; Kula, P.; Herman, J. High Birefringence Liquid Crystals. Crystals 2013, 3, 443–482. [Google Scholar] [CrossRef]
- Xianyu, H.; Wu, S.T.; Lin, C.L. Dual frequency liquid crystals: A review. Liq. Cryst. 2009, 36, 717–726. [Google Scholar] [CrossRef]
- Mrukiewicz, M.; Perkowski, P.; Piecek, W.; Mazur, R.; Chojnowska, O.; Garbat, K. Two-step switching in dual-frequency nematic liquid crystal mixtures. J. Appl. Phys. 2015, 118, 173104. [Google Scholar] [CrossRef]
- Pianelli, A.; Parka, J.; Perkowski, P.; Caputo, R.; Otón, E.; Mrukiewicz, M.; Mazur, R.; Sielezin, K.; Garbat, K. Investigations of dual-frequency nematic liquid crystals doped with dichroic dye. Liq. Cryst. 2018, 1–12. [Google Scholar] [CrossRef]
- Oh-e, M.; Kondo, K. Response mechanism of nematic liquid crystals using the in-plane switching mode. Appl. Phys. Lett. 1996, 69, 623–625. [Google Scholar] [CrossRef]
- Wu, S.T. Design of a liquid crystal based tunable electrooptic filter. Appl. Opt. 1989, 28, 48–52. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.T.; Wu, C.S. High-speed liquid-crystal modulators using transient nematic effect. J. Appl. Phys. 1989, 65, 527–532. [Google Scholar] [CrossRef]
- Yu, J.-P.; Chen, S.; Fan, F.; Cheng, J.-R.; Xu, S.-T.; Wang, X.-H.; Chang, S.-J. Tunable terahertz wave-plate based on dual-frequency liquid crystal controlled by alternating electric field. Opt. Express 2018, 26, 663–673. [Google Scholar] [CrossRef] [PubMed]
- Duan, W.; Chen, P.; Ge, S.-J.; Liang, X.; Hu, W. A Fast-Response and Helicity-Dependent Lens Enabled by Micro-Patterned Dual-Frequency Liquid Crystals. Crystals 2019, 9, 111. [Google Scholar] [CrossRef]
- Li, B.-X.; Xiao, R.-L.; Paladugu, S.; Shiyanovskii, S.V.; Lavrentovich, O.D. Dye-doped dual-frequency nematic cells as fast-switching polarization-independent shutters. Opt. Express 2019, 27, 3861–3866. [Google Scholar] [CrossRef]
- Mrukiewicz, M.; Perkowski, P.; Garbat, K.; Dabrowski, R.; Parka, J. Dielectric properties of compounds creating dual frequency nematic liquid crystals. Acta Phys. Pol. A 2013, 124, 940–945. [Google Scholar] [CrossRef]
- Bennis, N.; Herman, J.; Kalbarczyk, A.; Kula, P.; Jaroszewicz, L.R. Multifrequency driven nematics. Crystals 2019, 9, 275. [Google Scholar] [CrossRef]
- Li, Y.W.; Kwok, H.S. Bistable twisted-bend and twisted-nematic liquid crystal display. Appl. Phys. Lett. 2009, 95, 2009–2011. [Google Scholar] [CrossRef]
- Yin, Y. Dielectric Relaxation and Electro-Optical Effects in Nematic Liquid Crystals. Ph.D. Thesis, Kent State University, Kent, OH, USA, 2007; p. 113. [Google Scholar]
- Golovin, A.B.; Shiyanovskii, S.V.; Lavrentovich, O.D. Fast switching dual-frequency liquid crystal optical retarder, driven by an amplitude and frequency modulated voltage. Appl. Phys. Lett. 2003, 83, 3864–3866. [Google Scholar] [CrossRef]
- Kumar, S. Liquid Crystals: Experimental Study of Physical Properties and Phase Transitions; Cambridge University Press: Cambridge, UK, 2008; p. 487. [Google Scholar]
- Nishikawa, M.; West, J.L. Order Parameter of Liquid Crystal on Polyimide with Polarized Ultraviolet-Light Exposure. Jpn. J. Appl. Phys. 2002, 38, L331–L333. [Google Scholar] [CrossRef]
- Uchida, T.; Shishido, C.; Seki, H.; Wada, M. Guest-Host Interactions in Liquid Crystals. Mol. Cryst. Liq. Cryst. 1977, 39, 39–52. [Google Scholar] [CrossRef]
| Optical Properties (at λ = 550 nm) | Dielectric Properties | ||
|---|---|---|---|
| ne | 1.7192 | ∆ε at 1 kHZ | 3.00 |
| no | 1.4978 | ∆ε at 50 kHz | −2.8 |
| ∆n | 0.2214 | fcross | 18 kHz |
| Cell Thickness (µm) | Applied Voltage (V) | Cell Thickness (µm) | Applied Voltage (V) | Cell Thickness (µm) | Applied Voltage (V) |
|---|---|---|---|---|---|
| 1.18 | 10 | 15.62 | 50 | 50.00 | 85 |
| 2.04 | 12 | 23.00 | 60 | 62.31 | 90 |
| 3.58 | 20 | 23.007 | 60 | 65.11 | 90 |
| 4.13 | 22 | 28.01 | 75 | 100 | 120 |
| 10.55 | 40 | 28.10 | 75 | 150 | 130 |
| 11.81 | 40 | 38.17 | 80 | 200 | 140 |
| 15.31 | 50 | 38.22 | 80 | 220 | 190 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melnyk, O.; Garbovskiy, Y.; Bueno-Baques, D.; Glushchenko, A. Electro-Optical Switching of Dual-Frequency Nematic Liquid Crystals: Regimes of Thin and Thick Cells. Crystals 2019, 9, 314. https://doi.org/10.3390/cryst9060314
Melnyk O, Garbovskiy Y, Bueno-Baques D, Glushchenko A. Electro-Optical Switching of Dual-Frequency Nematic Liquid Crystals: Regimes of Thin and Thick Cells. Crystals. 2019; 9(6):314. https://doi.org/10.3390/cryst9060314
Chicago/Turabian StyleMelnyk, Olha, Yuriy Garbovskiy, Dario Bueno-Baques, and Anatoliy Glushchenko. 2019. "Electro-Optical Switching of Dual-Frequency Nematic Liquid Crystals: Regimes of Thin and Thick Cells" Crystals 9, no. 6: 314. https://doi.org/10.3390/cryst9060314
APA StyleMelnyk, O., Garbovskiy, Y., Bueno-Baques, D., & Glushchenko, A. (2019). Electro-Optical Switching of Dual-Frequency Nematic Liquid Crystals: Regimes of Thin and Thick Cells. Crystals, 9(6), 314. https://doi.org/10.3390/cryst9060314