1. Introduction
Brine is an important liquid mineral resource which is usually rich in lithium, potassium, boron and many other rare elements [
1]. Obtaining elements that are enriched in liquid or are an ore is the premise of many methods. How these resources are exploited environmentally and effectively is significant for sustainable development. At present, there are many ways to extract boron from salt-lake brine, such as extraction, precipitation and electrodialysis, and the solar pond method is now widely adopted [
2,
3]. The effectiveness of the prefractionation of salt mined from brine is closely related to the property of the product and operational conditions of crystallization. However, it is difficult for boron to be enriched, which causes problems not only for the extraction and purification of boron but also for the whole production process, such as separation and purification. Researchers found that there are many forms of boron precipitation, but borax decahydrate was the main type that resulted from carbonate-type brine [
4]. For this reason, borax decahydrate was chosen to study the changes of solubility and metastable zone width (MSZW) to deliver fundamental information for the exploitation and utilization of carbonate-type brine.
Some researchers [
5,
6,
7] have studied the crystalline properties of borax decahydrate and found that the effects of the impurities were complex. Gürbüz and Özdemir [
8] studied the effects of CaCl
2 and MgCl
2 and found that the MSZW broadened. Jiaoyu investigated the influence of KCl [
9], LiCl [
10] and Li
2SO
4 [
11] in detail with the use of the laser technique. The solubility became higher and the MSZW became wider in all the experiments. Most researchers attributed these changes to cations, with much less emphasis being placed on the study of anion effects. The majority of these researchers only reported data of a single salt, which is not suitable for brine systems, which are complex systems composed of different kinds of salts. In this paper, we have investigated the mixing effects of CO
32−, Cl
−, and SO
42− on the solubility and MSZW of borax decahydrate in simulated carbonate-type brine. Then, the experimental MSZW data of different cooling/heating rates,
R, were analyzed and discussed in the context of three-dimensional nucleation theory.
2. Nucleation Theory Model, 3D Nucleation Theory
Nucleation is the first and most important step of crystallization, which is closely related to the metastable zone width (MSZW). MSZW is defined as the temperature/concentration difference between nucleation and dissolution, and there are two different forms: supercooling and supersaturation. Many researchers have investigated the determination, control and prediction of the MSZW of products in a variety of systems as it is an important parameter in industrial production. However, the MSZW is closely related to the kind and concentration of impurities, temperature, stirring, seeds and many other factors, which makes it difficult to perform a further study. Over recent decades, many researchers have put forward models to describe the MSZW data, such as Nývlt’s approaches, self-consistent Nývlt’s-like approaches, Kubota’s approaches and the classical 3D nucleation theory model [
12]. Compared with other models, the 3D nucleation theory model has one remarkable advantage: The 3D nucleation theory model is based on the classical theory of 3D nucleation instead of empirical relations. This allows every parameter to have a well-defined physical background. Therefore, using the classical 3D nucleation theory model, the effects of impurity on the MSZW can be explained from the perspective of thermodynamics and kinetics by the corresponding parameters.
According to the 3D nucleation theory, the nucleation rate (
J) can be written as follows:
where
J is the number of nuclei formed in a unit volume (1 cm
3) for an infinitesimally short nucleation time;
A is the pre-exponential factor related to the kinetics of formation of nuclei in growth medium;
γ is the solid–liquid interfacial energy;
V is the molecular volume;
kB is the Boltzmann constant;
Tlim is the nucleation temperature; and
S is the supersaturation ratio when primary nucleation occurs. According to the solution theory, the correlation between the supersaturation ratio and the maximum temperature difference can be written as follows:
where
c0 and
clim are the actual and the saturation concentrations of the solute at a given temperature, respectively;
T0 is the dissolution temperature; Δ
Tmax is the difference between
T0 and
Tlim; and
RG and Δ
disH refer to the universal gas constant and the dissolution enthalpy, respectively.
Concerning the effects of the cooling/heating rate
R (
R = Δ
T/Δ
t) on the rate of nucleation, and in combination with Equation (2), the formula below is attained:
where
f is defined as the number of particles per unit volume and is dominated by aggregation and diffusion processes in the solution. Combining Equations (1) and (2), we obtain the following equation:
From Equations (3) and (4), one may write:
which, upon taking a logarithm on both sides and rearranging the equation, gives us
where
It is evident from Equation (6) that a linear relationship exists between the value of (ΔT0/ΔTmax)2 and lnR. The value of the interfacial energy γ, the kinetic factor A and other parameters can be calculated by the slope F1 and intercept F according to the formulas above.
3. Experimental Section
3.1. Materials and Apparatus
The Na2B4O7·10H2O supplied from the Tianjin Damao Chemical Reagent Factory was recrystallized from the aqueous solution to a mass fraction purity of more than 99.9%. Na2CO3, Na2SO4 and NaCl (reference reagent) were provided by the Tianjin Yongda Chemical Reagent Development Centre (purity ≥ 99.95%). Water (resistivity, 18.25 MΩ·cm) was deionized from a water purification system (UPT-II-20T, Chengdu Ultrapure Technology Co., Ltd., Chengdu, China) before being used in the experiments.
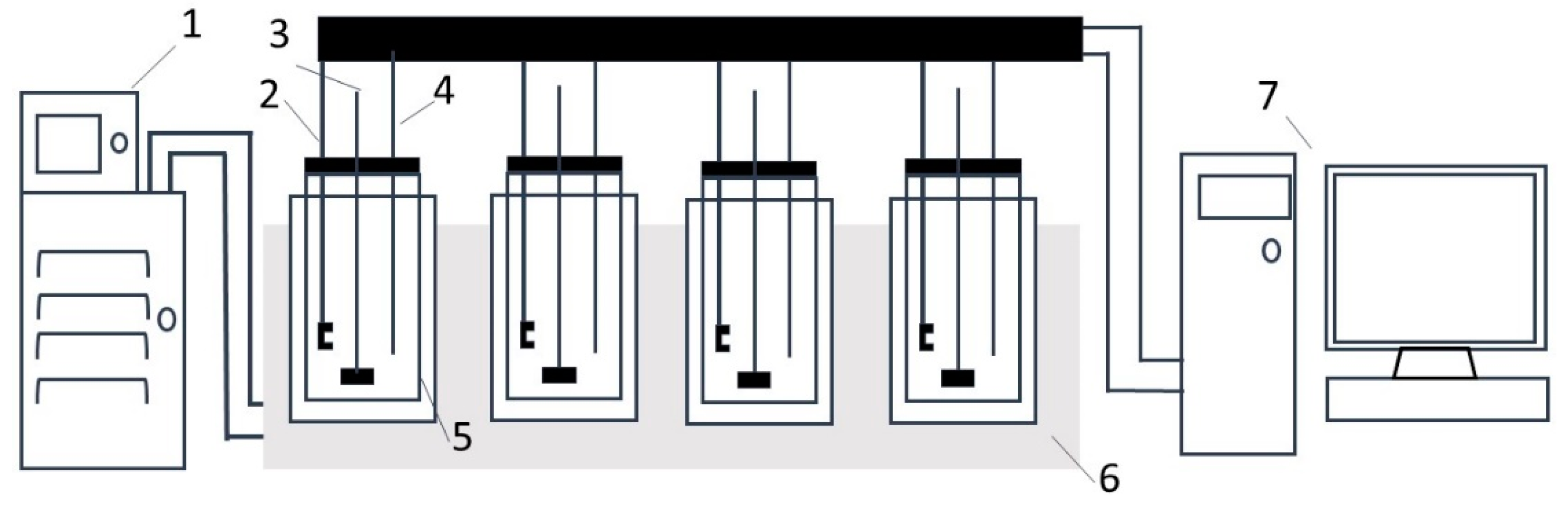
All experiments were performed using Crystal Scan (E1061, HEL, London, UK). As shown in
Figure 1, the instrument consists of seven parts. The cooling rate control was accomplished by a programmable thermostatic bath (FP50-ME, Julabo, Seelbach, Germany) assisted by a computer. The crystallizer was a 100 mL glass vessel with an internal overhead stirrer, temperature sensor and turbidity sensor. The turbidity meter was employed to detect nucleation/dissolution. The digital thermometer with a precision of ±0.01 °C was used to measure the temperature of the prepared solution. Additionally, the crystallizer was made airtight so that the loss of solvent due to evaporation could be minimized. There were four crystallizers, meaning that four independent experiments could be performed simultaneously. The X-ray diffraction (XRD) analysis (XPert Powder, Panalytical, Almelo, Holland) was used to confirm the identity of the solid phase that crystallized from the solutions.
3.2. Experimental Procedure
The MSZW of Na2B4O7·10H2O in the mixture of Na2CO3, NaCl and Na2SO4 was measured by the conventional polythermal method. About 60 g of Na2SO4-NaCl-Na2CO3-Na2B4O7-H2O mixture was prepared in 100 mL of the crystallizer. The mixture was heated/cooled at five different rates (55 K/h, 45 K/h, 35 K/h, 25 K/h and 15 K/h) with a constant stirring rate of 300 rpm. The mixture was heated more than 5 K above the saturation temperature and maintained for 10 min to ensure complete dissolution; then, the supersaturated solution was generated. Subsequently, the mixture was cooled down at the same constant rate. The variation of turbidity was used to determine whether nucleation formation or dissolution occurred. Turbidity decreased with increasing temperature and remained unchanged under complete dissolution. The nucleation that occurred resulted in a sudden increase in turbidity at lower temperatures. Correspondingly, the temperature during the formation and dissolution of the nuclei was taken as T1 and T2, respectively. The saturation temperature T0 was obtained from the extrapolation to 0 K/min of T2-R lines at each of the solution concentrations. The MSZW of borax was represented by the maximum degree of supercooling ΔTmax (ΔTmax = T0 − T1).
Chemical analysis was employed to determine the contents of the mixture. The boron content was determined by mannitol conversion acid−base titration. The Cl− ions were determined by Hg(NO3)2 titration with diphenyl carbazone and bromophenol blue as an indicator at pH 3. The CO32− ion concentration was obtained by HCl titration. The gravimetric method for the determination of SO42− was used. The accuracy of these analyses was about 0.1% to 0.3%.
4. Results and Discussion
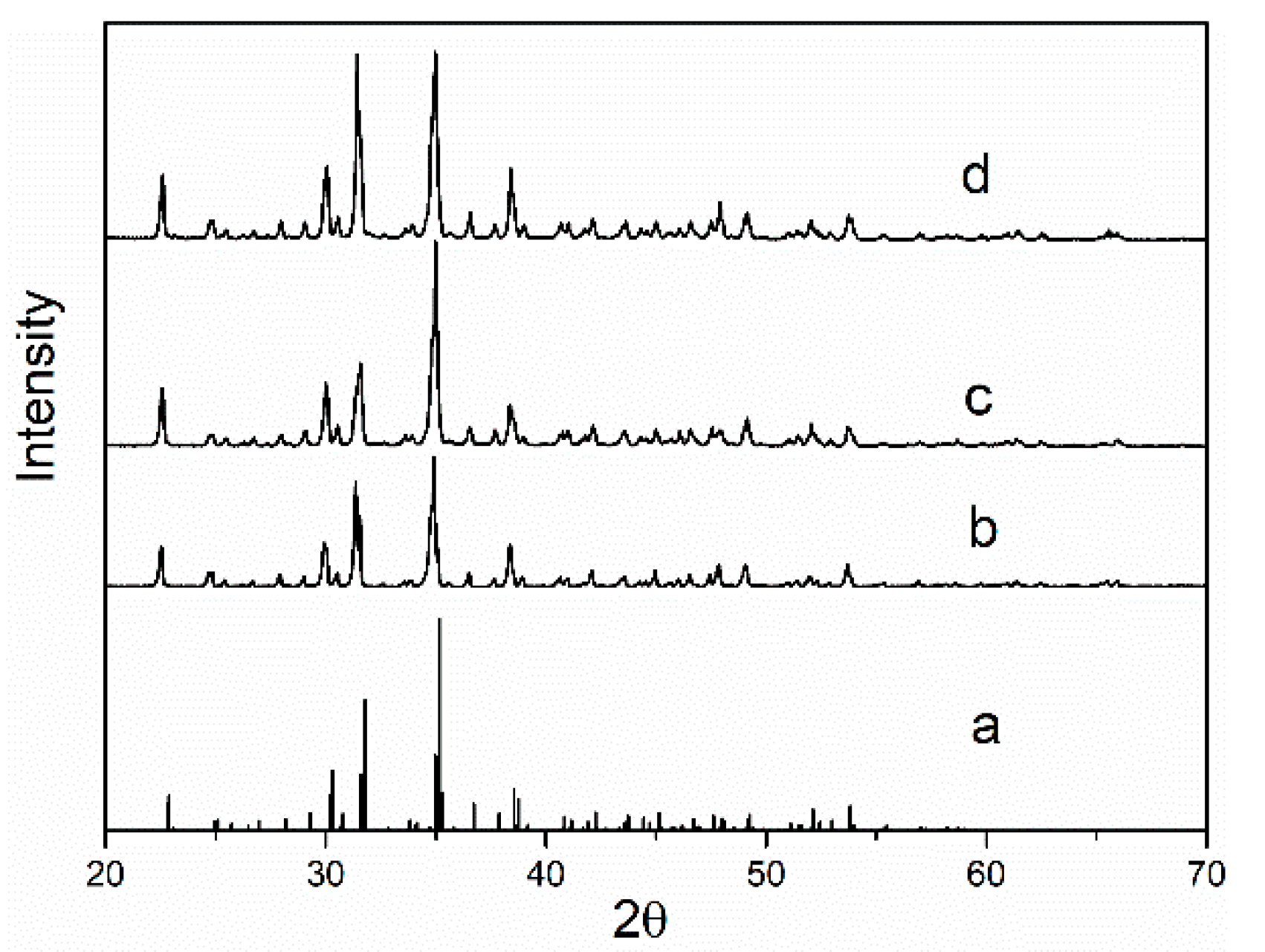
4.1. XRD Analysis
The XRD patterns of borax obtained from pure water, NaCl-Na
2CO
3-Na
2B
4O
7-H
2O systems and NaCl-Na
2SO
4-Na
2CO
3-Na
2B
4O
7-H
2O carbonate were investigated, respectively, as shown in
Figure 2. It can be seen that the X-ray diffraction patterns are identical according to the reference data from joint committee on power diffraction standards (JCPDS), the reference code is 01-75-1078 [
13].
4.2. Solubility
Since super-saturation determines the crystal nucleation rate, it is vital to measure the solubility precisely in the presence of impurities. The solubility of borax decahydrate in pure water was determined first; the results were in good agreement with the literature values indicating that the method was reliable [
14].
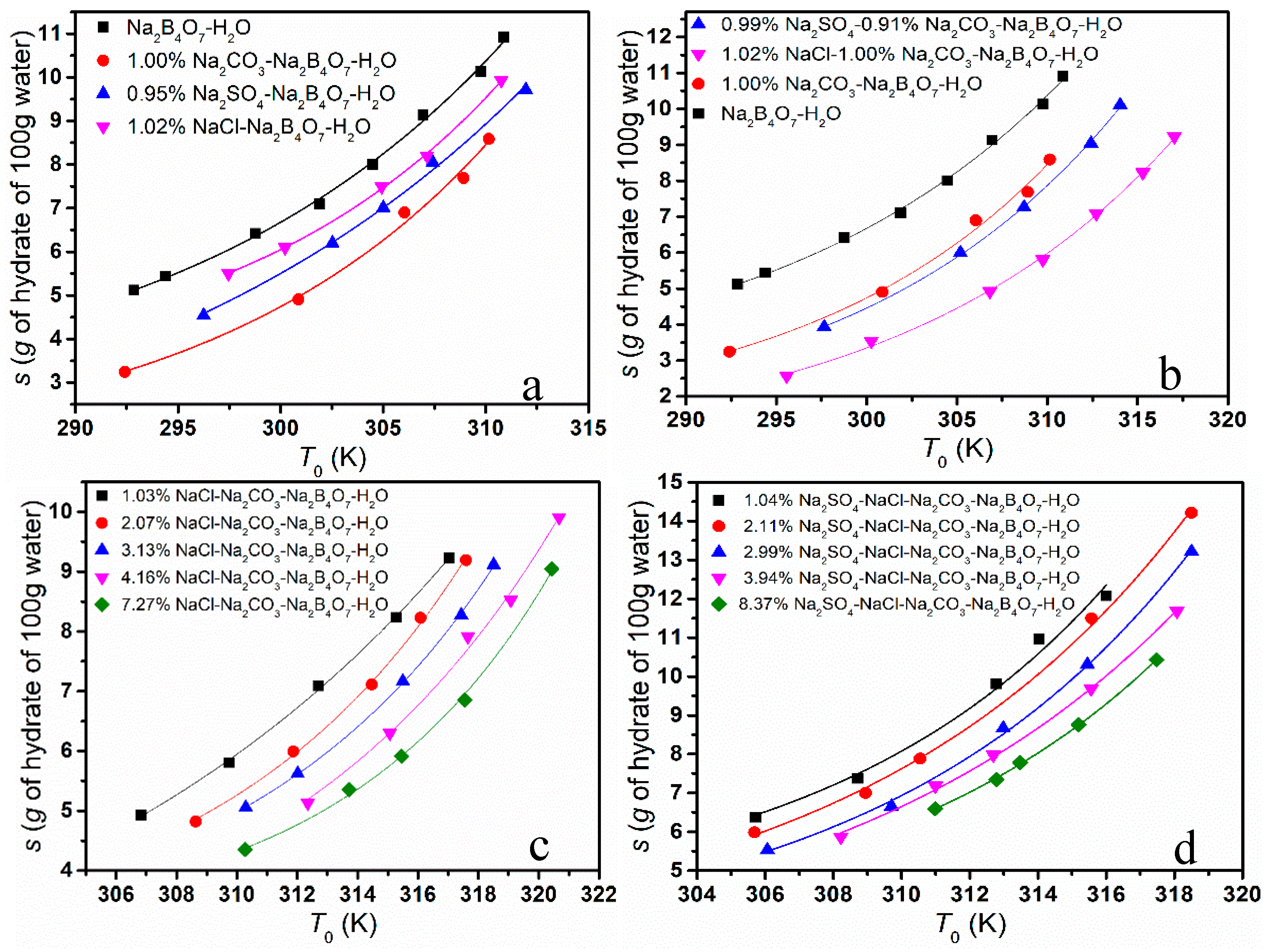
The solubility of borax decahydrate in different systems was determined as demonstrated in
Figure 3. As shown in
Figure 3a–d, the existence of NaCl, Na
2SO
4 and Na
2CO
3 suppressed the solubility of Na
2B
4O
7·10H
2O in simulated brine. As can be seen from
Figure 3a, the effect on the solubility of borax is Na
2CO
3 > Na
2SO
4 > NaCl; from
Figure 3b, the addition of Na
2SO
4 had less of an effect on the solubility of borax than that of NaCl in the Na
2CO
3-Na
2B
4O
7-H
2O system; from
Figure 3c,d, we can find that the solubility of Na
2B
4O
7·10H
2O gradually decreased with the addition of NaCl and Na
2SO
4.
The phenomenon above could be explained from the following aspects. Firstly, the common ion effect is one of the main influencing factors. NaCl, Na2SO4 and Na2CO3 are strong electrolytes and hydrolyze completely, which leads to the concentration of Na+ in the solution being greater within the impurities than in the pure solution. As the dissolution–precipitate equilibrium moved towards the precipitate, the solubility of Na2B4O7·10H2O was reduced. Due to the difference in molecular weight, when the mass fraction is the same, the concentration of Na+ is different, and the effect on the solubility is also different. Secondly, the effect could be ascribed to the salt effect. The addition of NaCl, Na2SO4 and Na2CO3 increases the total concentration of ions in the solution, which increases the interaction between ions, reduces the chance of combining to form borax molecules and increases the solubility. The salt effect is closely related to the activity coefficient of the solution. According to the calculation of the ion strength of solutions at the same mass fraction, we found that the ion strength of Na2SO4 solution and Na2CO3 solution was much greater than that of NaCl solution. Therefore, the salt effect of Na2SO4 and Na2CO3 is stronger than that of NaCl. Furthermore, intermolecular interactions such as hydrogen bonds would affect the solubility. The hydrogen bond strength of CO32− is stronger than that of SO42−, as there are differences in the structure and distribution of the charge.
In conclusion, the solubility of borax in brine is affected by various factors. The common effect is the most important factor, but the salt effect also has a significant effect when the impurity types and concentration in the system increase.
4.3. Thermodynamic Functions
Dissolution enthalpy and dissolution entropy are important factors when investigating the dissolution behaviour of a solute in different solvents. When the solubility of borax in different solutions is available, they can be obtained from the Van’t Hoff equation as per Equation (10).
where Δ
disH and Δ
disS are the dissolution enthalpy and entropy, respectively,
RG is the gas constant (8.314 J·mol
−1·K
−1) and
χ is the mole fraction. The standard dissolution enthalpy and standard dissolution entropy can be calculated from the experimental molar fraction solubility data by the ideal Van’t Hoff model.
The calculated dissolution enthalpy and entropy of borax are shown in
Table 1. The calculated dissolution enthalpy and entropy of borax are 67.99 kJ·mol
−1 and 34.75 J·mol
−1·K
−1, respectively, which is in good agreement with the values of Lange’s handbook of chemistry (34.20 kJ·mol
−1 and 66.80 J·mol
−1·K
−1) [
15].
The dissolution entropy is a measure of uncertainty, and the dissolution enthalpy is the thermal effect of solute dissolution in the solution at a given temperature and pressure. The value of dissolution enthalpy positive indicates endothermic reaction, while negative means exothermic reaction. As shown in
Table 1, the dissolution enthalpy and entropy were positive, which indicates that the dissolution was endothermic and entropy-driven. Furthermore, the dissolution enthalpy and entropy increase with the increased concentration of Na
2SO
4 and NaCl. The higher value of Δ
disH means that the more energy the dissolution needs, the lower the resulting solubilities. The results showed that the trend of dissolution enthalpy and solubility was consistent.
4.4. Metastable Zone Width
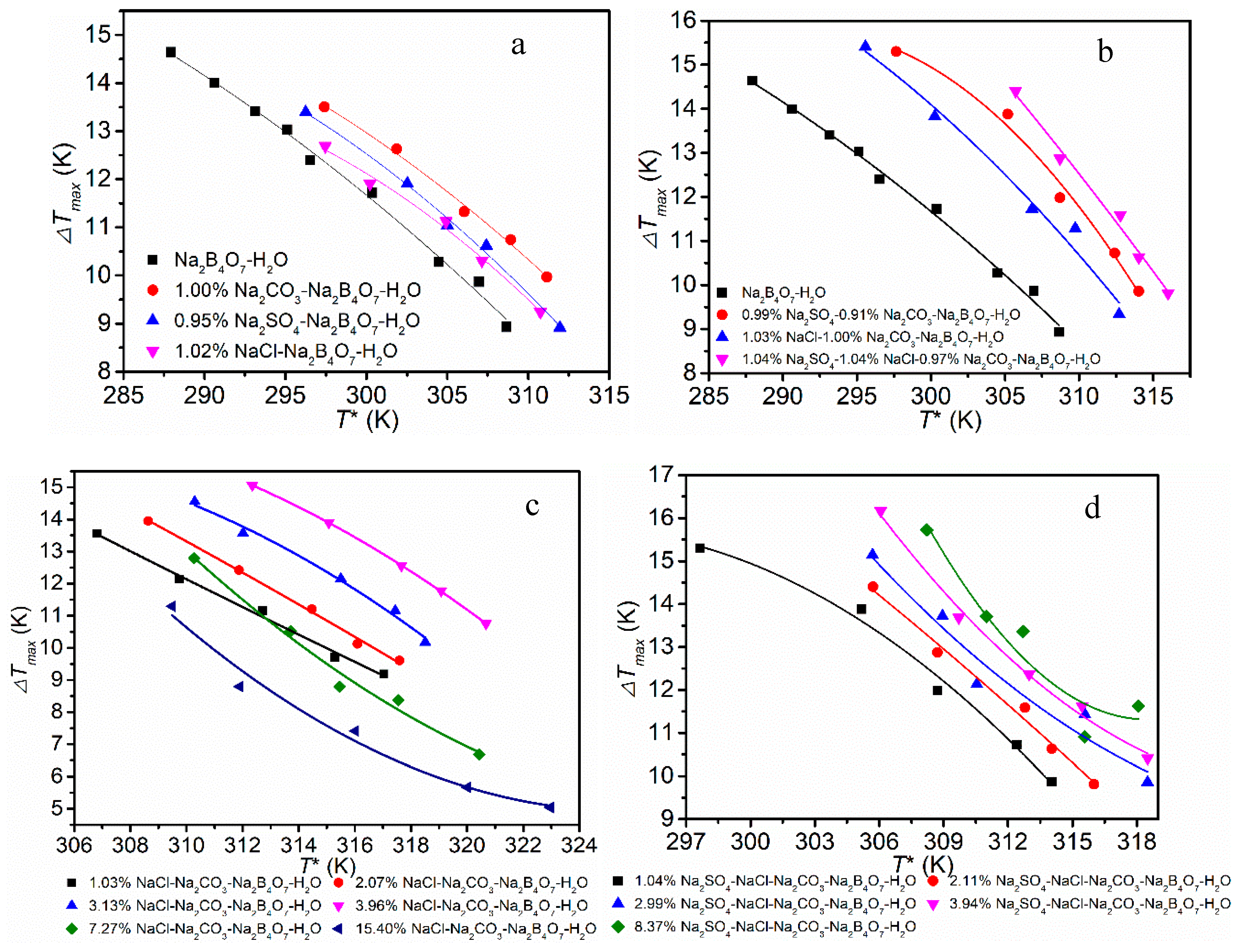
The quality of crystals to a large extent is determined by nucleation. To apply control on nucleation, a full understanding of nucleation is critical. Measuring the metastable zone width (MSZW) is an effective method to understand the nucleation. The MSZW data of Na
2B
4O
7·H
2O in different systems are plotted in
Figure 4. As can be seen from
Figure 4a, the addition of NaCl, Na
2CO
3 and Na
2SO
4 widens the MSZW of borax. The order of the influence is Na
2CO
3 > Na
2SO
4 > NaCl. From
Figure 4b, we find that the effect of Na
2CO
3 and Na
2SO
4 is greater than Na
2CO
3 and NaCl, and the result is consistent with
Figure 4a. As seen in
Figure 4c, the effects of NaCl depend on the concentration. At first, there was a noticeable increase in the MSZW of borax decahydrate with the addition of NaCl impurity, but the MSZW suddenly became narrowed when the concentration of NaCl increased to some extent. As seen in
Figure 4d, the addition of Na
2SO
4 widens the MSZW, but the effect of Na
2SO
4 was different from that of NaCl, which exhibited no relationship with the concentration in the range studied.
We found that this phenomenon is common in studies of chlorides on the MSZW of borate [
9,
16,
17,
18], but it only considers the effects of the cation and ignores the effect of Cl
−. As so many chlorides have similar effects on the MSZW of borate, it was concluded that Cl
− played a crucial role in nucleation. This could be explained by different mechanisms of the nuclear process. The impurities can occupy the active growth sites to suppress nucleation. Meanwhile, the combination increases the interfacial tension of the nucleus and energy barriers for crystal nucleation [
19]. Furthermore, the amount of free water was reduced with the addition of impurities, which increased the chance of nucleation. As the number of active growth sites was limited, when the opposite effects on MSZW were considered together, a critical value could be observed. The MSZW widened when below the value and narrowed when above it. The effect of Na
2SO
4 was greater than that of NaCl. This was mainly due to the fact that the volume of SO
42− was much bigger than that of Cl
−, it had stronger suppression effects on the ion diffusion process and delayed the crystal nucleation process. As the Cl
− has a smaller volume, higher electronegativity and can occupy the active growth sites more quickly, transition is more likely.
By comparing
Figure 3 and
Figure 4, it can be found that there is a certain correlation between solubility and MSZW. Since the addition of impurities will reduce the solubility, a higher temperature is required to dissolve the same amount of borax, and this will inevitably lead to an increase of the saturation temperature (
T0). From the definition of the MSZW (Δ
Tmax =
T0 −
T1), the increase of saturate temperature will lead to the widening of the MSZW. The MSZW can also be expressed by the maximum degree of supersaturation (Δ
Smax =
S0 −
S1, where
S0 and
S1 are the actual concentration and saturation concentration, respectively). The addition of impurities reduces the solubility, which means the saturation concentration of the solution decreases at a given temperature. Obviously, this widens the MSZW.
4.5. Nucleation Parameters, Explanation of MSZW Changes
According to the classical 3D nucleation theory model, plots of (
T0/Δ
Tmax)
2 against ln
R for borax in different mass fractions of NaCl and Na
2SO
4 display a linear relationship. The value of the solid–liquid interfacial energy
γ and the kinetic factor
A for borax decahydrate can be calculated by the slope and intercept by Equations (7)–(9) and are listed in
Table 2,
Table 3 and
Table 4, respectively.
As can be seen from the table above, the values of
A are much bigger in the pure solution than the impure solution, and they increase with the increase of temperature. Comparing
Table 3 and
Table 4, the values of
A in the Na
2SO
4-NaCl-Na
2CO
3-Na
2B
4O
7-H
2O system are bigger than the NaCl-Na
2CO
3-Na
2B
4O
7-H
2O system. According to Sangwal [
20,
21,
22], constant
A was associated with the kinetics of the formation of nuclei in the growth medium. An impurity absorbing on the nucleus surface would lead to a decrease in the value of
A caused by physically occupying or blocking the active sites for the attachment of growth units on the growing nuclei. The value of
A also depends on the temperature. The higher the temperature, the faster the molecules move, which speeds up the nucleation process and increases the value of
A. From Equation (4), we can see that the nucleation rate
J is proportional to
A. The increase in
A will result in a higher nucleation rate, which leads to a narrower MSZW.
The solid–liquid interfacial energy
γ is also an important thermodynamic parameter that indicates the ability of the solute to crystallize from the solution. As shown in
Table 2,
Table 3 and
Table 4, the type of impurity has little effect on the estimated solid–liquid interfacial energy
γ, but
γ increases with the concentration of the impurity. The values of
γ are mainly affected by the temperature when the concentration and kind of impurity are the same. As the temperature goes up, the values of
γ go down. It can be seen from Equation (1) that the solid–liquid interfacial energy
γ has a large effect on the crystal nucleation rate [
23]. The smaller
γ is, the less resistance it has for borax molecules to enter the crystal embryo to form nucleation, that is, the lower the nuclear barrier is, the easier nucleation is, and therefore the MSZW would narrow. Otherwise, the increase in
γ increases the nucleation barrier and suppresses nucleation, and the MSZW widens. The change of
γ could explain the influence of NaCl on MSZW effectively. The addition of NaCl can adsorb on the surface of the crystal nucleus, resulting in the decrease of
γ. However, the number of active sites on the crystal nucleus surface is limited. The addition of continuous NaCl would not result in an increase in the interfacial energy but decrease it when all active growth sites were occupied. The
γ value could also be used to indicate the ability of the solute to be crystallized spontaneously; the lower the value, the easier it is for borax to be crystallized. This represents another way of evaluating the changes of solubilities in different systems.
5. Conclusions
The development and utilization of brine resources cannot be separated from crystallization. How and when the valuable elements are enriched in brine is of great significance to exploit brine. In order to further understand the boron enrichment process in carbonate-type brine, we have studied the changes in solubility and MSZW of borax in the simulated brine system. The solubility and MSZW were measured by the conventional polythermal method with turbidity technology.
The experimental data showed that Na2SO4, NaCl and Na2CO3 had a salt-out effect on borax. Comparing the solubility of borax in NaCl-Na2CO3-Na2B4O7-H2O and Na2SO4-NaCl-Na2CO3-Na2B4O7-H2O, we found that the salt effect also plays a large role. In general, the results of the common ion effect are the largest. However, when the system becomes more complex, due to the increase of ionic strength and the decrease of activity coefficients, the interaction between ions in the solution becomes stronger, making it difficult to combine and form borax molecules. From the experimental molar fraction solubility data by the ideal Van’t Hoff model, the standard dissolution enthalpy and standard dissolution entropy could be calculated. According to the value of ΔdisH and ΔdisS, all cases are endothermic and entropy-driven. We also found that with the increase of NaCl and Na2SO4, values of ΔdisH and ΔdisS also increase, and this means that more energy is needed to dissolve borax. This leads to a decrease in solubility. This explains the decrease of solubility from the thermodynamic point of view.
The presence of impurities will affect the nucleation of borax: NaCl, Na2SO4, and Na2CO3 result in the broadening of the MSZW. Nevertheless, the effect of NaCl depends on concentration. The MSZW becomes wider at first, then narrows with the addition of NaCl. It was concluded that Cl− could suppress the nucleation rate by occupying the active growth sites and thereby broadening the MSZW. Some parameters are calculated by using the classical 3D nucleation theory to explain these phenomena. The nucleation factor A is related to the nucleation kinetics in the growth medium. Raising the temperature makes the particles move faster, which is reflected in an increase in the value of A. According to the classical 3D nucleation theory, the nucleation rate will increase with the increase of A, so the MSZW narrows. The solid–liquid interface energy γ is related to the nuclear barrier. The larger γ is, the higher the barrier is, the more difficult it is to nucleate, and the wider MSZW is. Due to the effect of adsorption, the addition of impurities increases the γ. However, the number of active sites is limited. Correspondingly, there is a critical concentration, and the MSZW widened below the value and narrowed above it.
The findings of this investigation complement those of earlier studies. The systems we studied are closer to the actual brine composition. These parameters are very useful in the whole process, such as improving yield and quality of production, especially in carbonate-type brine. Moreover, further works are needed to fully understand the crystallization of borates in brine.
Author Contributions
J.C. participated in all procedures including the design of the study, carrying out the laboratory work, data analysis and drafting the manuscript. J.P. participated in the design of the study and drafted the manuscript. X.W. carried out the analyses. Y.D. and W.L. conceived the study. All authors gave final approval for publication.
Acknowledgments
This work was supported by the National Key R&D Program of China (No. 2017YFC0602805); the National Natural Science Foundation of Qaidam Salt Lake Chemical Science Research Joint Fund (No. U1607103); the National Natural Science Foundation for the Youth (No. 21501187); the Enterprise Project (No. 2015-6300-101).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Helvaci, C.; Palmer, M.R. Origin and Distribution of Evaporite Borates: The Primary Economic Sources of Boron. Elements 2017, 13, 249–254. [Google Scholar] [CrossRef]
- Zhu, C.; Dong, Y.; Yun, Z.; Hao, Y.; Wang, C.; Dong, N.; Li, W. Study of lithium exploitation from carbonate subtype and sulfate type salt-lakes of Tibet. Hydrometallurgy 2014, 149, 143–147. [Google Scholar] [CrossRef]
- Jiangjiang, Y.; Mianping, Z.; Lijun, T.; Qian, W.; Zhen, N.; Lingzhong, B. Comparative study of lithium extraction from the carbonate brine between solar pond and laboratory simulation experiment. Chem. Ind. Eng. Prog. 2013, 32, 1248–1256. [Google Scholar] [CrossRef]
- Yufeng, W. Hydrochemical Characteristics of Zabuye Salt Lake in Tibet. Master’s Thesis, Jinan University, Guangzhou, China, June 2015. [Google Scholar]
- Sahin, O.; Aslan, F.; Ozdemir, M.; Durgun, M. Determination of kinetic parameters of crystal growth rate of borax in aqueous solution by usingthe rotatingdisc technique. J. Cryst. Growth 2004, 270, 604–614. [Google Scholar] [CrossRef]
- Ćosić, M.; Kaćunić, A.; Kuzmanić, N. The Investigation of the Influence of Impeller Blade Inclination on Borax Nucleation and Crystal Growth Kinetics. Chem. Eng. Commun. 2016, 203, 1497–1506. [Google Scholar] [CrossRef]
- Akrap, M.; Kuzmanić, N.; Kardum, J.P. Impeller geometry effect on crystallization kinetics of borax decahydrate in a batch cooling crystallizer. Chem. Eng. Res. Des. 2012, 90, 793–802. [Google Scholar] [CrossRef]
- Gurbuz, H.; Ozdemir, B. Experimental determination of the metastable zone width of borax decahydrate by ultrasonic velocity measurement. J. Cryst. Growth 2003, 252, 343–349. [Google Scholar] [CrossRef]
- Peng, J.; Dong, Y.; Nie, Z.; Kong, F.; Meng, Q.; Li, W. Solubility and Metastable Zone Width Measurement of Borax Decahydrate in Potassium Chloride Solution. J. Chem. Eng. Data 2012, 57, 890–895. [Google Scholar] [CrossRef]
- Peng, J.; Nie, Z.; Li, L.; Wang, L.; Dong, Y.; Li, W. Solubility and Metastable Zone Width of Sodium Tetraborate Decahydrate in a Solution Containing Lithium Chloride. J. Chem. Eng. Data 2013, 58, 1288–1293. [Google Scholar] [CrossRef]
- Peng, J.; Dong, Y.; Wang, L.; Li, L.; Li, W.; Feng, H. Effect of Impurities on the Solubility, Metastable Zone Width, and Nucleation Kinetics of Borax Decahydrate. Ind. Eng. Chem. Res. 2014, 53, 12170–12178. [Google Scholar] [CrossRef]
- Sangwal, K. Novel Approach to Analyze Metastable Zone Width Determined by the Polythermal Method: Physical Interpretation of Various Parameters. Cryst. Growth Des. 2009, 9, 942–950. [Google Scholar] [CrossRef]
- Levy, H.A.; Lisensky, G.C. Crystal Structures of Sodium Sulfate Decahydrate (Glauber’s Salt) and Sodium Tetraborate Decahydrate (Borax). Acta Cryst. 1978, 34, 3502–3510. [Google Scholar] [CrossRef]
- Ceyhana, A.A.; Sahinb, O.; Bulutcua, A.N. Crystallization kinetics of the borax decahydrate. J. Cryst. Growth 2007, 300, 440–447. [Google Scholar] [CrossRef]
- Lange, N.A.; Speight, J.G. Lange’s Handbook of Chemistry, 16th ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Lin, C.; YaPing, D.; QinFen, M.; HaiTao, F.; Wu, L. Study of the metastable zone of H3BO3 in the SrCl2-H3BO3-H2O system. J. Beijing Univ. Chem Technol. 2008, 35, 29–33. [Google Scholar] [CrossRef]
- Qingfen, M.; Yaping, D.; Fanzhia, K.; Haitaoa, F.; Wu, L. Study on the Metastable Zone Property of Boric Acid in Different Concentrations of MgCl2 and NaCl Solutions. Acta Chim. Sin. 2010, 68, 1699–1706. [Google Scholar]
- Sayan, P.; Ulrich, J. Effect of Various Impurities on the Metastable Zone Width of Boric Acid. Cryst. Res. Technol. 2001, 36, 411–417. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Reed Educational and Professional Publishing: London, UK, 2014. [Google Scholar]
- Nishinaga, T. Handbook of Crystal Growth, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Sangwal, K. Effect of impurities on the metastable zone width of solute–solvent systems. J. Cryst. Growth 2009, 311, 4050–4061. [Google Scholar] [CrossRef]
- Sangwal, K. Some features of metastable zone width of various systems determined by polythermal method. Cryst. Eng. Commun. 2011, 13, 489–501. [Google Scholar] [CrossRef]
- Sangwal, K. Recent developments in understanding of the metastable zone width of different solute−solvent systems. J. Cryst. Growth 2011, 318, 103–109. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).