The Orientation of Strain-Induced Crystallites in Uniaxially-Strained, Thin and Wide Bands Made from Natural Rubber

Abstract

Vulcanized natural rubber (unfilled and filled with 20 phr carbon black) is strained. We suppress the macroscopic formation of fiber symmetry by choosing strip-shaped samples ("pure-shear geometry") and investigate the orientation of the resulting crystallites by two-dimensional wide-angle X-ray diffraction (WAXD), additionally rotating the sample tape about the straining direction. Indications of a directed reinforcing effect of the strain-induced crystallization (SIC) in the thin strip are found. In the filled material fewer crystallites are oriented and the orientation distribution of the oriented crystallites is less perfect. The results confirm, that it is important for the evaluation of crystallinity under deformation to check, whether fiber symmetry can be assumed. This has consequences in particular on the quantitative interpretation of space-resolved scanning experiments in the vicinity of crack tips. Furthermore it raises the question, whether there is an asymmetric reinforcing effect of the SIC in the vicinity of crack tips inside natural rubber.

1. Introduction

Strain-induced crystallization (SIC) is one of the most important factors for the outstanding mechanical properties of natural rubber. It was extensively investigated with a focus on homogeneous uniaxial strain [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Nevertheless, we can assume that even under macroscopic uniaxial stress local deviations from the fiber symmetry occur. Especially in the case of pre-cracked respectively damaged samples, the strain field is often highly inhomogeneous. This influences the strain-induced crystallization and it must be expected that the residual crystallinity and crystallite orientation, e.g., around a crack tip, will be inhomogeneous, as well. To study deviations from the simplest assumption of fiber symmetry, one can stretch thin, broad strips. Such tensile tests with samples of "pure-shear geometry" [11,14] are in the focus of different studies.

In our present study we pre-stretch thin, wide strips of natural rubber and study the material by wide-angle X-ray diffraction (WAXD) at a synchrotron beamline. Crystalline reflections in the patterns are related to crystallites which have been formed by straininduced crystallization (SIC). If we could assume the validity of fiber symmetry, then a single WAXD pattern would suffice at least for an approximate structural analysis [17]. This assumption is not valid for “pure-shear” experiments. Thus in order to explore a sufficient part of the reciprocal space we rotate the sample tape about the straining direction with respect to the X-ray beam. In this way we collect structural information on the deviation from fiber symmetry.

Such tests are rarely performed, although they are always necessary when the deformation of the material suggests deviations from the fiber symmetry. Such deviations can be expected not only in pure-shear experiments, but also in spatially resolved investigations of morphology in the vicinity of crack tips, and this is a target of ongoing work.

The aim of our paper is the exemplary investigation of the morphology by WAXD in the case of violation of fiber symmetry in a "pure-shear" [17] loading experiment of natural rubber and the estimation of information, which can then be obtained by rotation of the sample in the X-ray beam.

2. Materials and Methods

2.1. Sample Preparation and Deformation

Samples of vulcanized natural rubber, unfilled and filled with 20 phr carbon black (NR0 and NR20), were investigated. The samples have the commonly used so-called “pure-shear geometry” with the dimensions of 80 mm (width) × 10 mm (height) × 1 mm (thickness) [11,14,18]. A bulge on both sides with a diameter of 5 mm enables a defined clamping of the samples. According to the high width compared to the thickness, transversal deformation during stretching is mainly thinning of the sample, while the width remains nearly constant. On the free sample length two lines were applied for optical strain estimation.

The samples were externally quasi-statically stretched to stretch ratios of 5:1 and 6:1, respectively, named NR0_5, NR0_6 for the unfilled grade and a stretch ratio of 5:1 for the filled grade named NR20_5. In the stretched state they were fixed within a frame and put with this frame into the beam.

2.2. Synchrotron WAXD Measurements

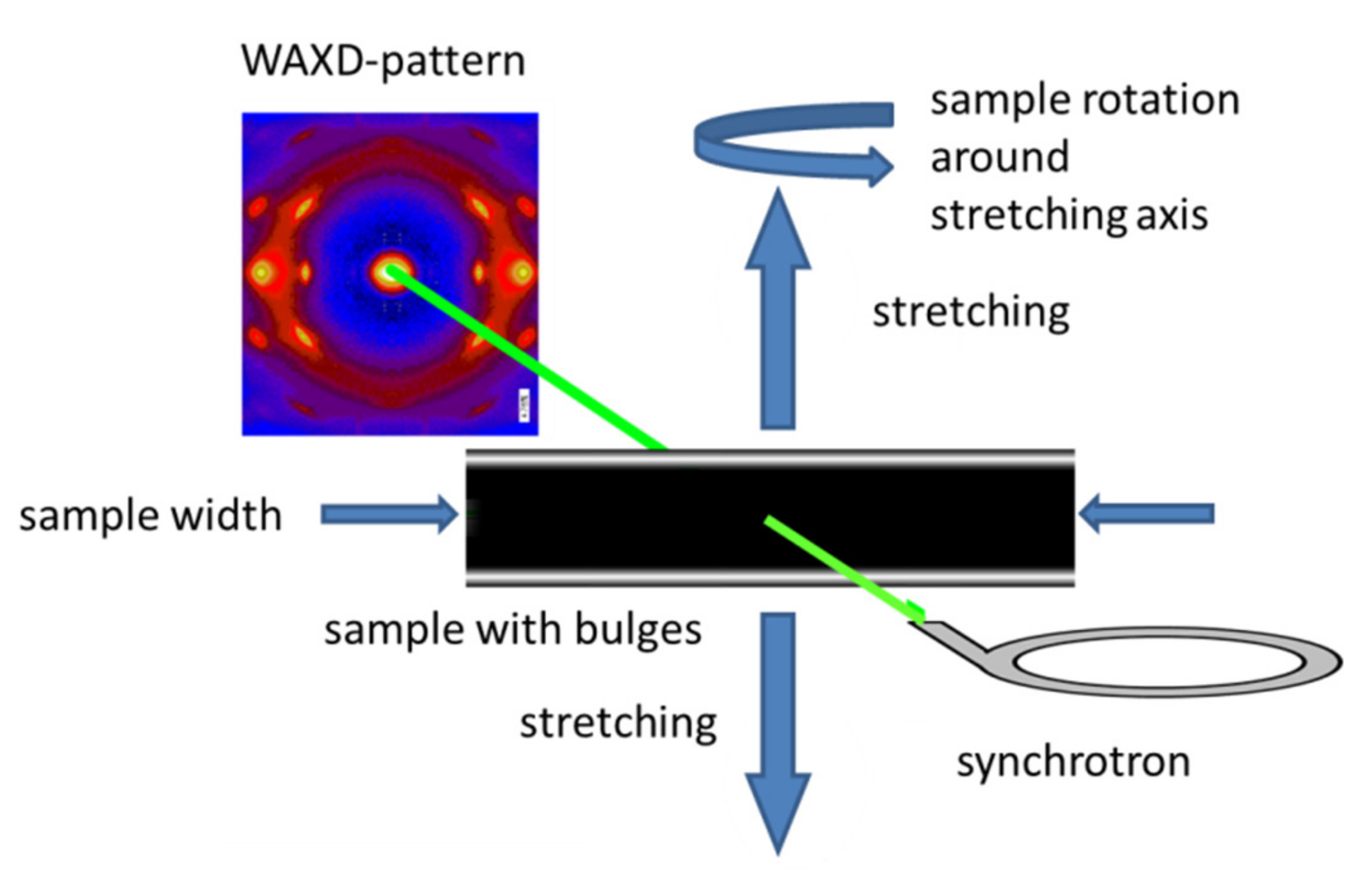
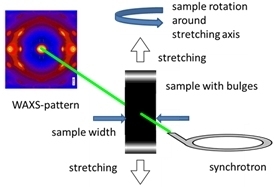
Synchrotron WAXD measurements were performed at DESY, Hamburg, beamline P03 with a micro beam. A wavelength of 0.094 nm (energy of 13.2 keV) and a beam size of about 20 µm × 20 µm were used [19]. The general arrangement of the measurements is shown in Figure 1.

For the measurement a PILATUS 300k detector (Dectris Ltd.) was used with a pixel size of 0.172 mm and a sample-to-detector distance of 206 mm. The intensity of the incoming beam was measured with an ionization chamber, the intensity of the transmitted beam by a beamstop diode.

While for samples with small width the assumption of fiber symmetry is normally valid, here samples with high width with respect to the thickness were investigated. Due to the geometry the width of the samples remained mainly constant during stretching. So, the stretch ratio was inverse to the thickness reduction.

The samples were investigated at seven different rotation angles of the sample with respect to the beam from −45° to 45° in steps of 15 degrees. At each arrangement 10 patterns were captured scanning along the sample in stretching direction with a step width of 1 mm and with an exposure time of 1 s.

2.3. Primary Data Processing

For the samples, absorption coefficients (µ) of 0.418 mm⁻¹ (NR0) and 0.44 mm⁻¹ (NR20) were estimated. The raw patterns were corrected with respect to the beam intensity, the background scattering and the sample thickness, which depends on the stretch ratio as well as on the tilting angle.

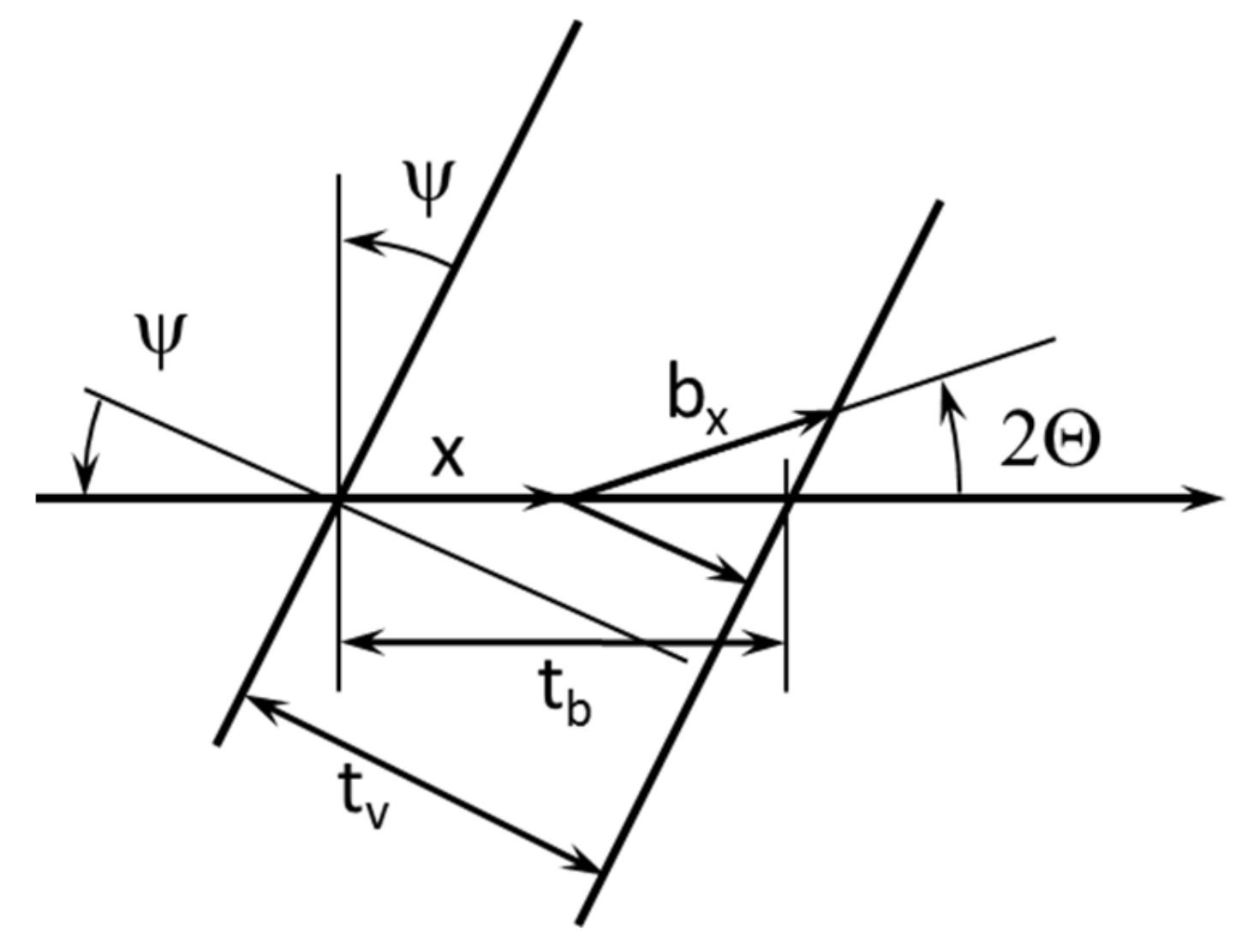
Due to the tilting of the sample, the X-ray path within the sample, x + b_x, was dependent on the tilting angle ψ (Figure 2). Additionally, the paths of the two scattered signals at ±2Θ were different from each other.

The intensity of the scattered beam changed according to the rotation of the sample via the angle ψ, respectively the different paths of the scattered beam through the sample. In analogy to the derivation of Stribeck for normal-transmission geometry [17], the scattering intensity S(2Θ) may be expressed as:

$$S\left(2\Theta \right)=\frac{I_{t_b}\left(2\Theta \right)}{I_{0}F{t}_b} \exp \left(\frac{\mu t_b\cos (\psi )}{\cos \left(\psi +2\Theta \right)}\right)$$

(1)

with the F being the cross section of the beam. I₀ is the intensity of the incoming beam, I_tb the intensity under the angle 2Θ.

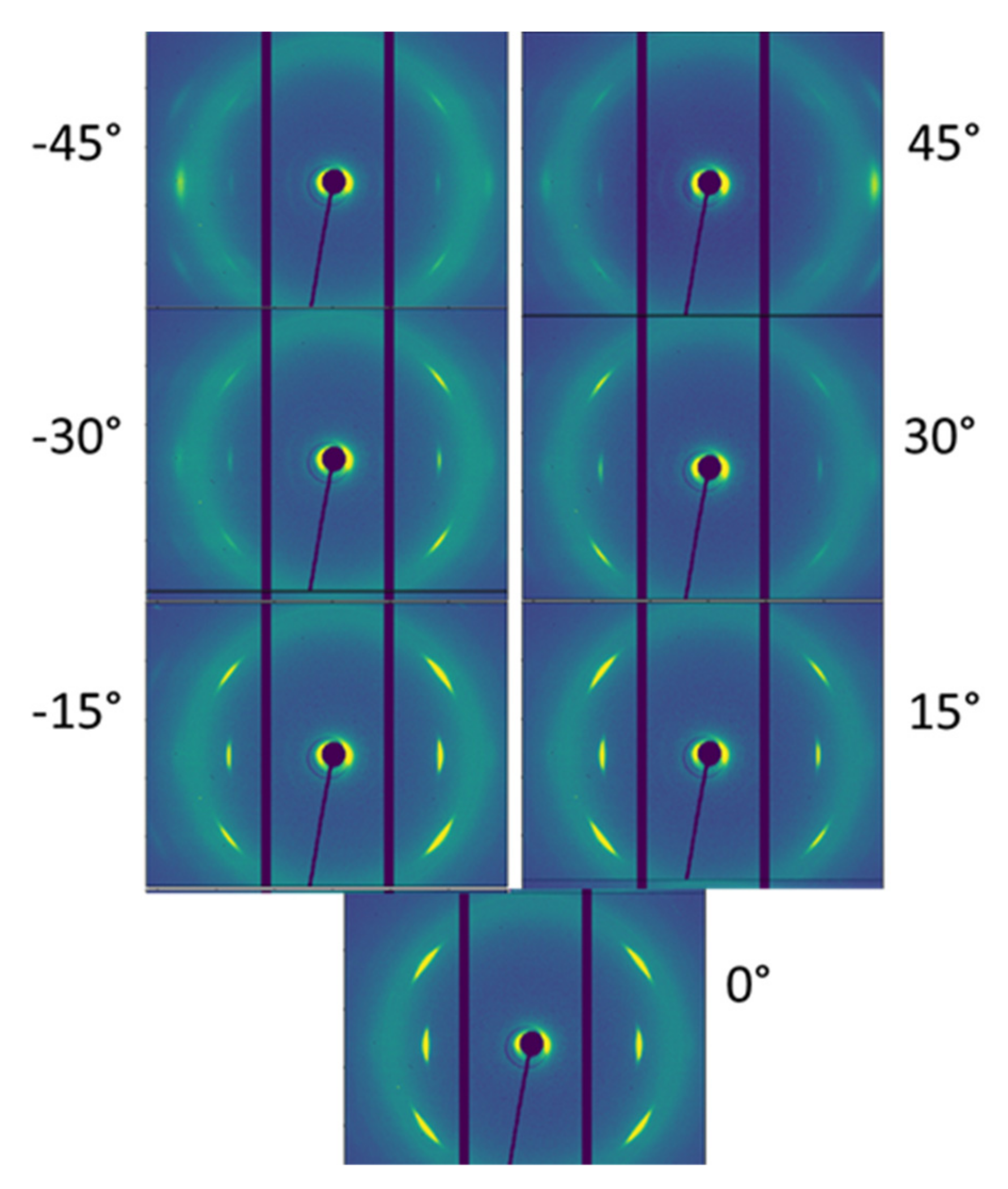
The patterns for NR0_5, corrected by this way, are shown in Figure 3.

It is obvious, that there was a very strong dependence of the intensities of the individual peaks on the rotation angle of the sample. This confirms that there is no fiber symmetry within the samples.

Generally it is obvious, that the c-axis of the crystallites was strongly oriented with respect to tensile axis. The further discussion is focused on the equatorial peaks (2 0 0) and (1 2 0), the information of the peak (2 0 1) is nearly identical to the information of the peak (2 0 0).

The characterization of the crystalline peaks was done via integrating the peak area after subtraction of the underlying amorphous halo.

3. Estimation of the Crystallite Orientation Function

3.1. Crystallographic Characterization of Strain-Induced Crystallites in Natural Rubber

The crystal structure of natural rubber was intensively investigated in the past. Takahashi and Kumano [5] gave a comprehensive overview about these investigations. The unit cell is monoclinic with parameters a = 12.41 Å, b = 8.81 Å, fiber axis c = 8.23 Å, and β = 93.1°. The structure factors of the reflections (2 0 0) and (1 2 0) are $\left|F_{200}\right|$ = 128.91 and $\left|F_{120}\right|$ = 290.91, respectively [4]. The geometry is very similar to the orthorhombic cell, reported by Nyburg [1] which was used for reasons of simplicity for the further evaluation.

3.2. Peak Intensities and Crystallite Orientation

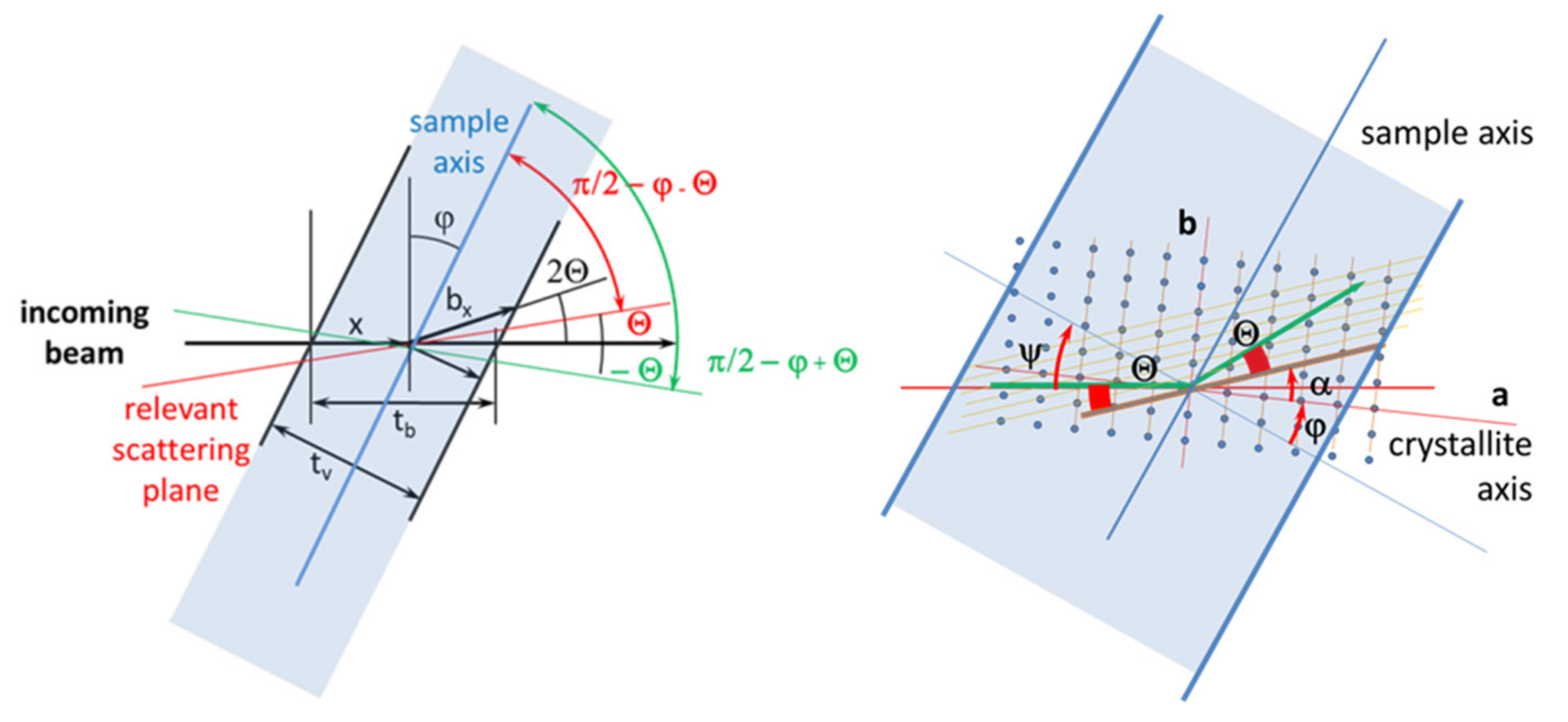
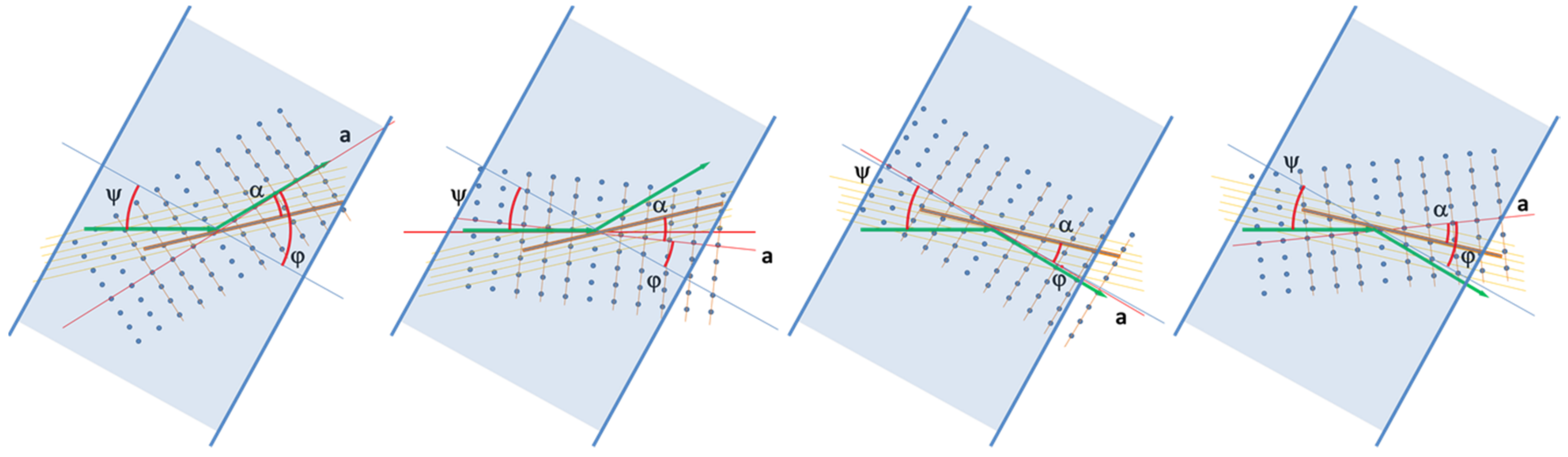
The general alignment of the sample with respect to the beam and a scattering crystallite within the sample are shown in Figure 4.

The characteristic peaks of a pattern appear if the Bragg condition is fulfilled. So we get for the left and right equatorial peak (2 0 0) with 2 Θ₂₀₀ = ±8.682° and α₂₀₀ = 0° always one possible orientation of crystallites ψ + φ_1/2. For each of the (1 2 0) peaks with 2 Θ₁₂₀ = ±12.808° and α₁₂₀ = ±70.48° we get always two possible orientations of the scattering crystallites according to Equation (2):

$$\begin{gathered} 2{\Theta }_{hkl}=2\left(\psi +{\phi }_1-{\alpha }_{hkl}\right), \\ 2{\Theta }_{hkl}=2\left(\psi +{\phi }_2+{\alpha }_{hkl}\right), \\ 2{\Theta }_{hkl}=-2\left(\psi +{\phi }_3+{\alpha }_{hkl}\right), \\ 2{\Theta }_{hkl}=-2\left(\psi +{\phi }_4-{\alpha }_{hkl}\right), \end{gathered}$$

(2)

or:

$${\phi }_{1/2}={\Theta }_{hkl}-\psi \pm {\alpha }_{hkl} \mathrm{and} {\phi }_{3/4}={\Theta }_{hkl}+\psi \pm {\alpha }_{hkl},$$

(3)

where α is the angle between the a-axis of the crystallite and the scattering crystalline plane, ψ the angle between the incoming beam and the sample normal and φ the angle between the sample normal and the a-axis of the crystallite. In Figure 5 the different orientations of the crystalline lattice with respect to beam and sample are shown for illustration.

We assume a random (uniform) orientation of crystallites, superimposed with a Gaussian distribution of oriented crystallites as approach according to

$$X\left(\phi \right)=C_0+C_1\exp \left(-\frac{{\left(\phi \right)}^2}{2{\sigma }^2}\right),$$

(4)

with the intensity-constants C₀ for the randomly oriented crystallites and C₁ for the oriented crystallites with a variance σ² respectively a standard deviation σ over the orientation angle φ in degree, the scattering intensity of the crystallite peaks can be estimated by:

$$I_{hkl+}\left(\psi \right)={\left|F_{hkl}\right|}^2*\left(X\left({\phi }_1\right)+X\left({\phi }_2\right)\right) \mathrm{resp}. I_{hkl-}\left(\psi \right)={\left|F_{hkl}\right|}^2*\left(X\left({\phi }_3\right)+X\left({\phi }_4\right)\right).$$

(5)

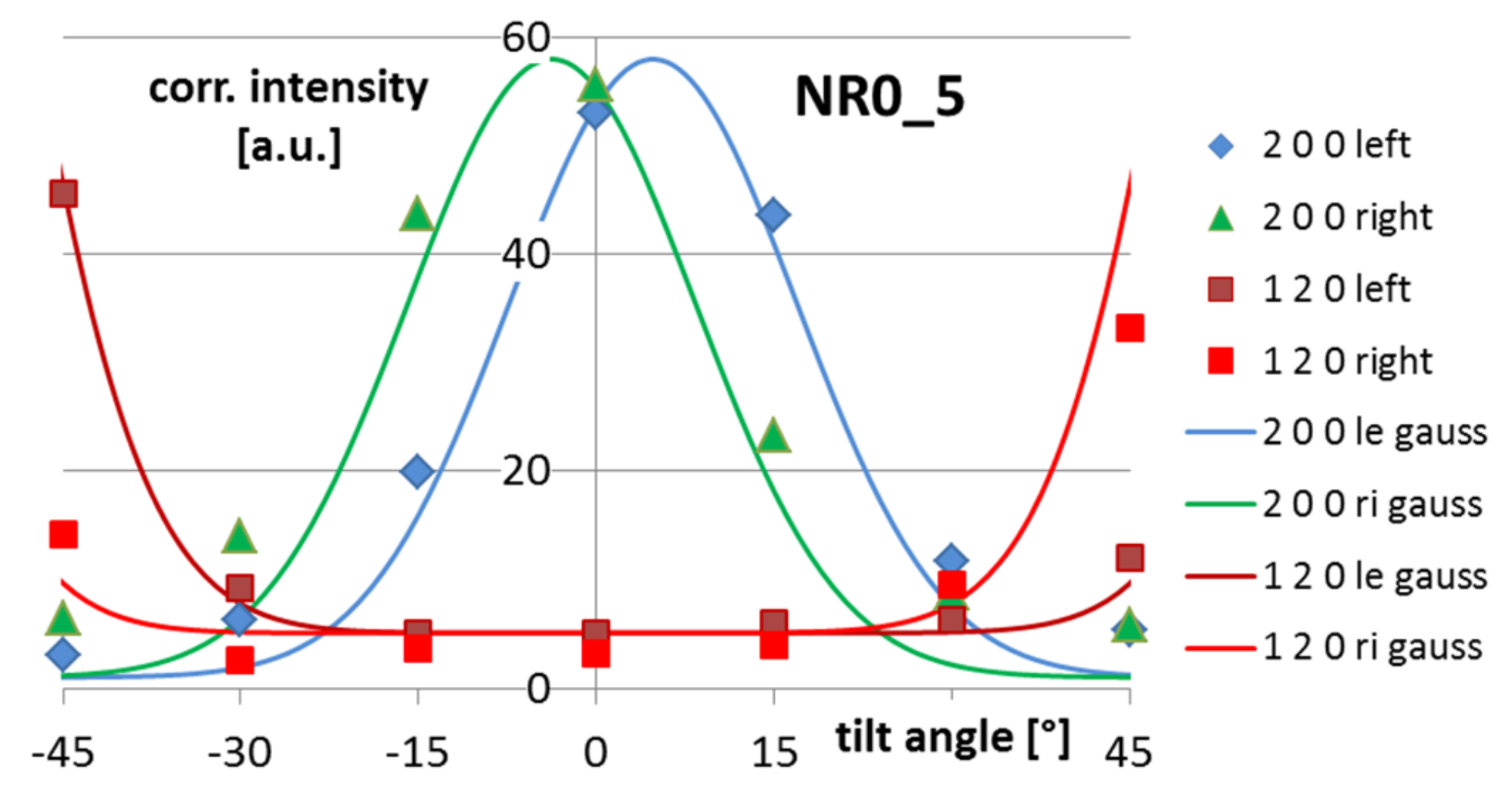
This enables a quite good description of the peak intensities in a very pragmatic way (Figure 6). The parameters for the description, estimated via a least square fit, are summarized in

Table 1. Parameters of the orientation distribution of the a-axis of crystallites in the different NR-samples. C₀ and C₁ and so c_oriented and c_random are estimated for the measurements and not normalized.

Sample	C0 [a.u.]	C1 [a.u.]	σ [rad]	coriented [a.u.]	crandom [a.u.]	coriented/ctotal
NR0_5	0.5	28.5	0.21	864	90	91%
NR0_6	0.2	61	0.19	1697	36	98%
NR20_5	2	18.1	0.35	907	360	72%

. A unique set of parameters (C₀, C₁, σ) fits all the intensities of the different reflections, while each of the parameters has a certain physical meaning. For the interpretation of the parameters their individual error was estimated to be less than 10%.

It is clear, that here an obviously small amount of randomly distributed crystallites are found. A large number of the crystallites are strongly oriented in that way, that the a-axis of the crystallites has a preferred orientation vertical to the sample surface. The standard deviation of 0.21 resp. 12.1° in the present case means, that 68.3% of the oriented crystallites are oriented within ±12.1 or 90% of the crystallites are oriented within ±1.645 σ respectively within ±19.9 around a vertical direction to the sample surface.

The amounts of random and oriented crystallites can be estimated by integration of Equation (4) yielding:

$$\begin{gathered} c_{random}={{\displaystyle \int }}_{-\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{C}_0 d\phi =\pi * C_0 \\ {c}_{oriented}={{\displaystyle \int }}_{-\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{C}_1\exp \left(-\frac{{\left(\phi \right)}^2}{2{\sigma }^2}\right) d\phi =\sqrt{2\pi {\sigma }^2}{C}_1 \end{gathered}$$

(6)

From the estimated amounts of oriented and random crystallites the relative amount of oriented crystallites can be estimated as 91% (Table 1).

3.3. Influence of Strain on the Crystallite Orientation Function

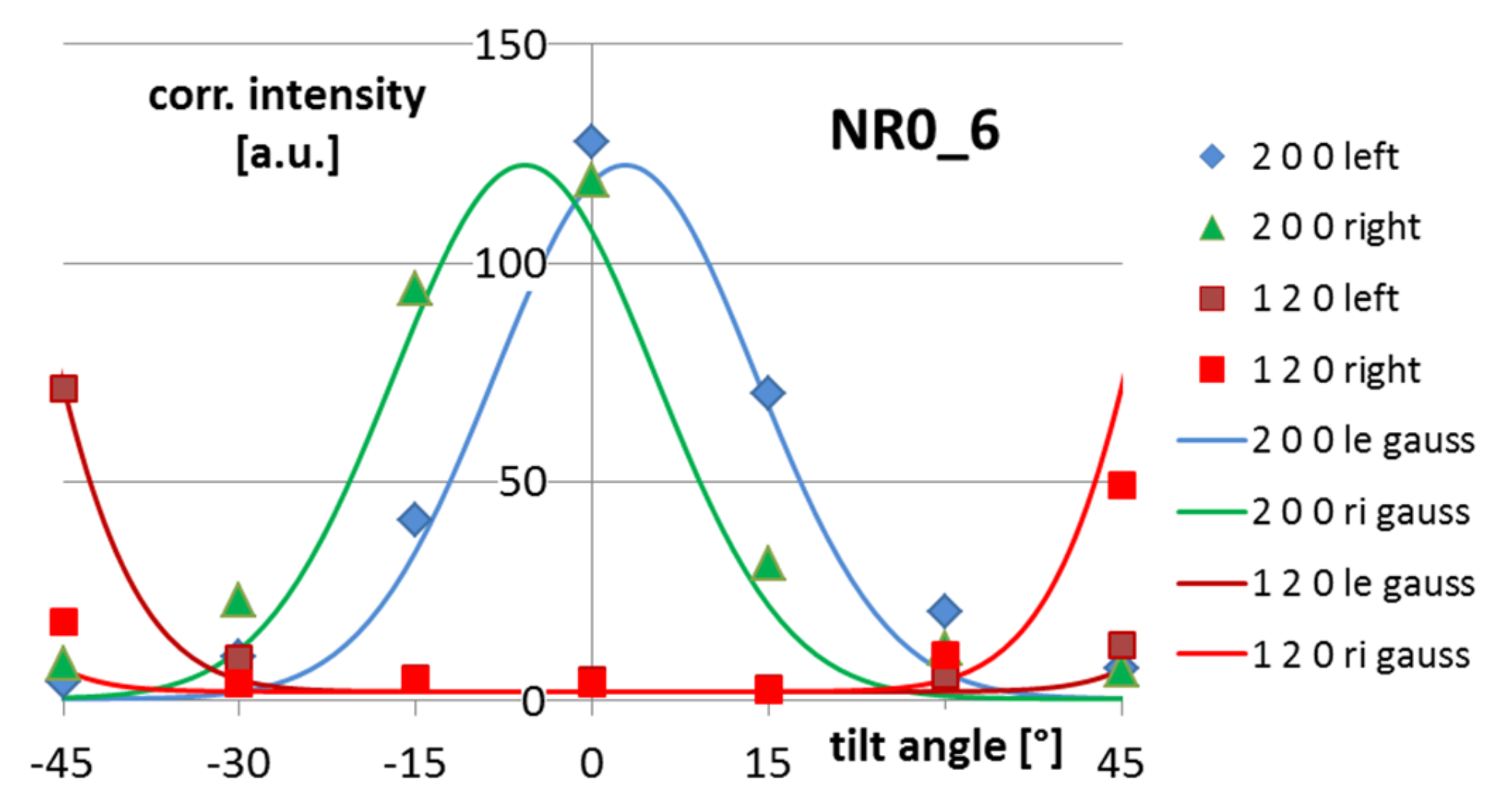
With an increase of the stretch ratio, here from 5:1 to 6:1 for NR0, the scattering intensities over the rotation angle change slightly (Figure 7).

During the ongoing stretching, mainly the orientation distribution becomes narrower to a value of σ = 0.19 = 11.1°, that means, that 68.3% of the crystallites are oriented within ±11.1° or 90% of the crystallites within ±18.3° around a vertical direction to the sample surface, the content of randomly oriented crystallites vanishes almost completely. Simultaneously the amount of randomly distributed crystallites is strongly reduced. Finally 98% of the crystallites are oriented, see also Table 1.

3.4. Influence of Filler Content on the Crystallite Orientation

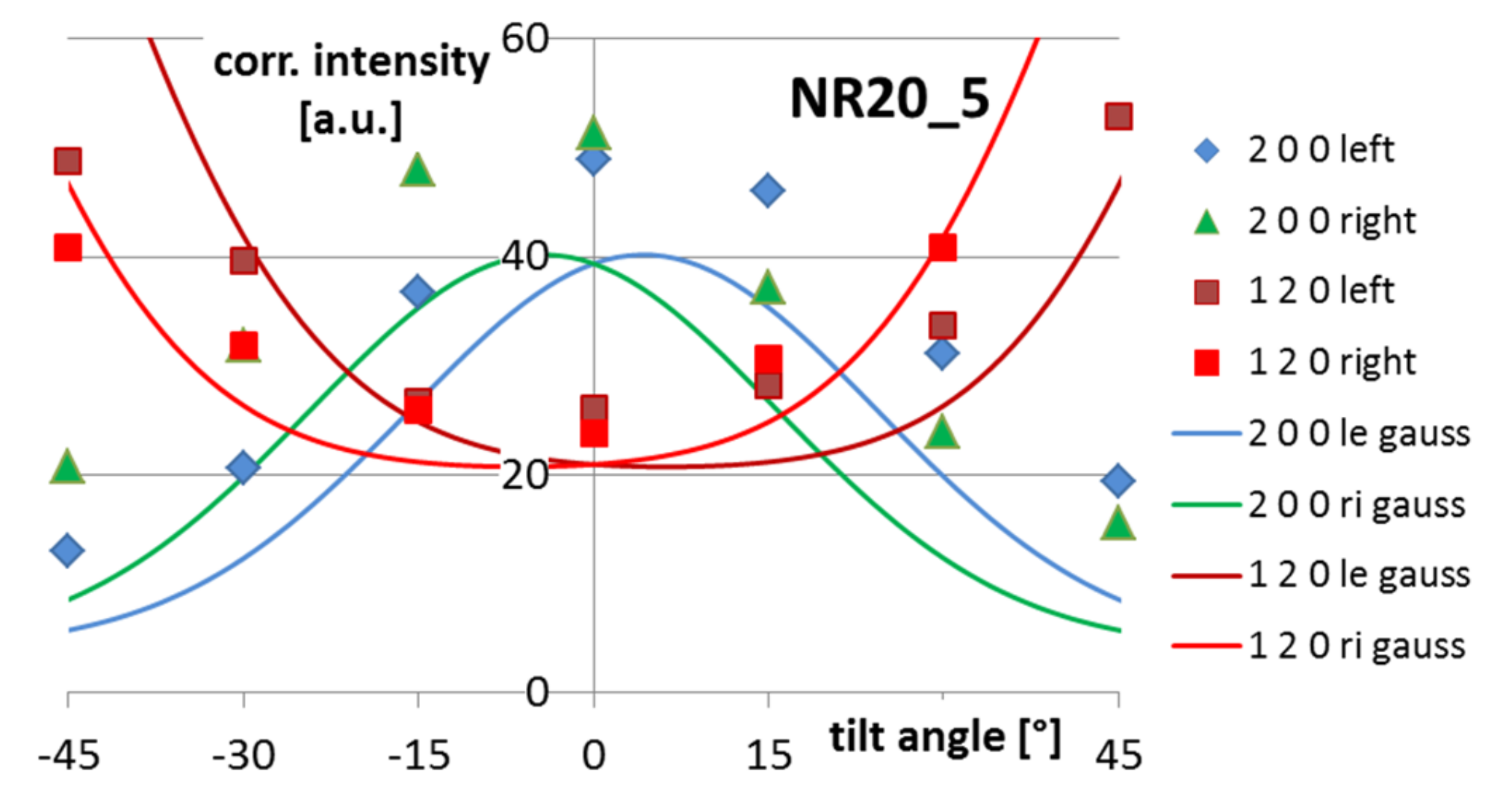
In the case of filled natural rubber (NR), the superstructure is remarkably different. The general orientation of the crystallites is similar with a preferred orientation of the a-axis perpendicular to the sample surface, but the orientation distribution is much wider with a standard deviation of 0.35 respectively 20° or 90% of crystallites oriented within ±32.9° around a vertical direction to the sample surface. Additionally, an enormous amount of randomly distributed crystallites appears, (Figure 8). Using Equation (6) the amount of oriented crystallites can be estimated to be 72%. Generally it must be realized, that fitting the crystallite distribution by the approach according to Equation (4) is much worse than in the case of unfilled NR.

The parameters, describing all the orientation distributions of the crystallites, are summarized in Table 1.

3.5. Crystallite Orientation in Tensile Direction

The width of orientation distribution of the crystallites in stretching direction can be estimated by the width of the equatorial reflections in azimuthal direction. In

Table 2. Width of the orientation distribution (deviation from stretching direction), approximated by a Gaussian distribution, in degrees.

Reflection	2 0 0	1 2 0
NR0_5	10	12
NR0_6	11	11.6
NR20_5	16	16

the values are summarized.

3.6. Crystallite Size, Estimated by the Scherrer Formula

The Scherrer formula enables a rough estimation of crystallite sizes in certain directions. It is:

$$L_{hkl}=\frac{K\lambda }{\Delta \left(2\Theta \right)\cos \left({\Theta }_0\right)}$$

(7)

where L_hkl is the size of the crystallite perpendicular to the lattice plane (h k l), λ the wavelength of the used radiation, Δ(2Θ) the total half width of the reflection, Θ₀ the Bragg angle in radians and K the dimensionless Scherrer-shape factor in the order of 1.

The mean sizes of the crystallites in different directions estimated by the Scherrer formula are summarized in

Table 3. Size of crystallites of strain-induced crystallization (SIC) in natural rubber (NR) samples at different stretch ratio in nm, estimated by the Scherrer formula.

Reflection	2 0 0	1 2 0
NR0_5	25	8.8
NR0_6	26.1	8.9
NR20_5	19.6	7.6

.

4. Discussion

Comparing the 10 patterns captured at each strain/rotation angle shows no significant difference. This confirms that the crystalline structure within the sample is quite homogeneous at a scale of microns.

In contrast to that, investigating a stretched pure shear sample under different angles shows a strong dependence of the individual crystalline reflections at the same strain. This is a clear indication, that there is no fiber symmetry in the samples, caused by the geometrical constraint due to the pure shear geometry of the samples.

The evaluation of the different peaks enables the estimation of the orientation of the strain-induced crystallites of the samples. It can be well described by a Gaussian distribution superimposed to a certain amount of randomly distributed crystallites; all of them are aligned in tensile direction. It is found, that the a-axis of the oriented crystallites is mainly directed perpendicular to the sample surface.

The amount of randomly distributed crystallites found in unfilled natural rubber decreases strongly with increasing strain. At a stretch ratio of 6:1 nearly all crystallites are oriented. Simultaneously, with increasing strain the orientation of the crystallites becomes slightly narrower, while the size of the individual crystallites remains mainly constant. It is not totally clear, whether the total amount of crystallinity increases strongly during this increase of strain.

In the case of CB-filled natural rubber the establishment of strain-induced crystallization is remarkably influenced by the presence of filler. The sizes of crystallites are, compared with the unfilled rubber, generally smaller, and the orientation of crystallites becomes wider. Furthermore, the amount of crystallites oriented with respect to their a-axis is remarkable smaller than in the case of the unfilled samples. Obviously, this is mainly caused by the constraint of crystallization due to the limited space between adjacent filler particles, and not only by the inhomogeneous strain due to the constraining sample geometry.

5. Conclusions

The investigations show that a constraining geometry as well as fillers have a clear impact on the orientation of strain-induced crystallites in natural rubber. Due to the reinforcing effect of the crystallites this will have an impact not only on the mechanical behavior of anisotropic loaded rubber materials, but also on their crack growth resistance. The anisotropic load ahead of the crack tip will influence the orientation of crystallites in the vicinity of the crack tip and, in this way, the details of the failure process.

These details of this influence will be the topic of further investigations.