Flow Instabilities of Coupled Rotation and Thermal-Solutal Capillary Convection of Binary Mixture in Czochralski Configuration

Abstract

In order to understand the flow instabilities of coupled rotation and thermal-solutal capillary convection of binary mixture in a Czochralski configuration subjected to simultaneous radial thermal and solutal gradients, a series of three-dimensional direct numerical simulation have been conducted. The capillary ratio of the silicon-germanium mixture is −0.2. The rotation Reynolds numbers of crystal and crucible, Re_s and Re_c range from 0 to 3506 and 0 to 1403, respectively. Results show that the basic flow is axisymmetric and steady. It has rich flow structures in the meridian plane, depending on the competitions among the driving forces. With the increase of thermocapillary and rotation Reynolds numbers, the basic flow will transit to three dimensional oscillatory flow. For different combination of rotation rate and thermocapillary Reynolds number, the oscillatory flow can be displayed as spoke patterns which is steady in time but oscillate in space, spoke patterns propagate in azimuthal direction, rotational waves or coexistence of spokes and rotational waves. The crucible rotation has an inhibitory effect on the flow instability, inducing the monotonically increase of critical value for flow transitions, however, for crystal rotation, the critical thermocapillary Reynolds number increases at first and then decreases. When the rotation rate is large, two flow transitions are captured.

1. Introduction

Thermal-solutal capillary convection is ubiquitous in nature and commonly encountered in industrial processes [1,2]. In the material processing industry, the crystal growth process is an important example that the qualities of the crystal materials are closely affected by the flow instabilities resulting from the buoyancy and thermal-solutal convections, since the oscillatory flow induces impurity striations in the crystals [3,4]. Especially, under microgravity conditions, the effect of gravity is minimized [5] and the effect of thermal-solutal capillary flow generated by surface tension gradient is highlighted [6,7,8]. Czochralski (Cz) crystal growth technology is an important method for producing crystals, where a rod-mounted seed crystal dipped into melt and carefully pulled out by controlling the thermal and concentration gradients, crystal rotation and pulling rates [9,10]. Thus, the thermal-solutal capillary forces generated by the surface tension gradient, the centrifugal and Coriolis forces induced by rotation are coupled and make the flow become very complex. Therefore, further understanding of such coupled flow and ensuing instabilities is expected to improve the quality of crystal growth.

Thermal-solutal capillary convection has been extensively investigated in previous studies. Most of the works have been focused on the flow instabilities in a horizontal mixture layer with vertical temperature and concentration gradients [7]. McTaggart [11] has carried out linear stability analysis on the flow instabilities in a thin and infinitely extended fluid layer heated from below or above [12]. Results showed that neglecting the buoyancy effect, thermal and solutal capillary convection induced by surface tension gradient is more likely to be the onset of instabilities, which are closely related to the directions of the thermal and solutal capillary forces. When the thermal and soultal capillary forces are in the same direction, the onset of instability is in the form of stationary convection; otherwise, it is presented as oscillatory convection. Then, Ho and Chang [13] verified McTaggart’s [11] results and extended the investigation to double diffusive Marangoni instability. The nonlinear analysis pointed out that the finite amplitude steady rolls can suppress the oscillatory instability. Afterwards, many investigations have been devoted to study the coupled thermal-solutal capillary and buoyancy flows [14,15,16,17]. Results have showed that the thermal-solutal capillary flow and buoyancy flow are coupled in different scales, generating different flow patterns and making diversity of instabilities types [18,19].

For the tangential temperature and solute concentration gradients, Bergman [20] has numerically investigated the thermal-soultal convection in a rectangular cavity. It has been indicated that without buoyancy effect, even though the overall Marangoni number is zero, the convection may occur. Also, the interactions of thermal and soultal capillary effects induce variations in temperatures and concentration distributions, which generate several flow patterns. Zhan et al. [21,22] have performed numerical simulations on the thermal-solutal capillary convection in a cubic cavity with a constant temperature and concentration gradients. The effect of aspect ratio, Lewis number and Prandtl number on the flow instability were investigated. They reported three different oscillatory modes and found that the onset of instability correlates with a supercritical Hopf bifurcation. Later, Yu et al. [23] and Chen et al. [24,25] have performed simulations on the flow pattern transitions of binary mixture with a -1 capillary ratio in an annular pool, which is a simplified model for Cz configuration. Various types of flow patterns were observed with the increase of the thermocapillary Reynolds number, such as concentric rolls, petal-like, spokes, rosebud-like patterns and vibrating spoke patterns.

On the other hand, during the Cz crystal growth process for pure liquid, it was found that not only the thermal flows but also the rotation plays an import role in the flow instabilities. Back to 1989, Jones [26] experimentally investigated the flow transitions in the Czochralski configuration. During the experiments, four types of flow patterns were observed. Jones [26] concluded that the flow patterns are closely dependent on the rotation rate. Afterward, investigations on the effect of rotation on the thermal convection for pure liquid sprung up in the past decades [27,28,29]. Results showed that when the thermocapillary Reynolds number exceeds threshold values, the basic flow transits to the three-dimensional(3D) oscillatory flow, which is shown as standing waves or spoke patterns. With the influence of rotation, the oscillatory flow behaves as travelling waves, the oscillation amplitude and wave numbers vary with the rotation rate [30]. In our previous work [31,32,33], a series of numerical simulations on the convections of silicon melt in a Cz configuration have been conducted. The critical conditions for flow transitions have been determined and the stability diagrams have been mapped and several mechanisms for flow instabilities have been identified, such as Rayleigh-Marangoni-Benard instability, baroclinic instability, hydrothermal wave, as well as the elliptic and shear instabilities. Also, it has been approved that in the shallow Cz configuration, the buoyancy effect is negligible.

For the binary mixture in a rotating system with imposed temperature and concentration gradients, the thermal-solutal capillary and buoyancy forces, as well as the centrifugal and Coriolis forces are coupled together [34]. The characteristics of such coupled flows remain unclear and how the rotation influences the thermal-solutal capillary flow and the ensuing instabilities are unknown. The main objective of our work is to investigate the coupling effect of rotation and thermal-solutal capillary convection. Therefore, in this paper, a series of 3D numerical simulations have been conducted to investigate the coupling effect of rotation and thermal-solutal capillary convection of binary mixture in Czochralski configuration, subjected to simultaneous radial thermal and solutal gradients. In order to extract and analyze the coupled rotation and surface tension effect, buoyancy effect has been neglected.

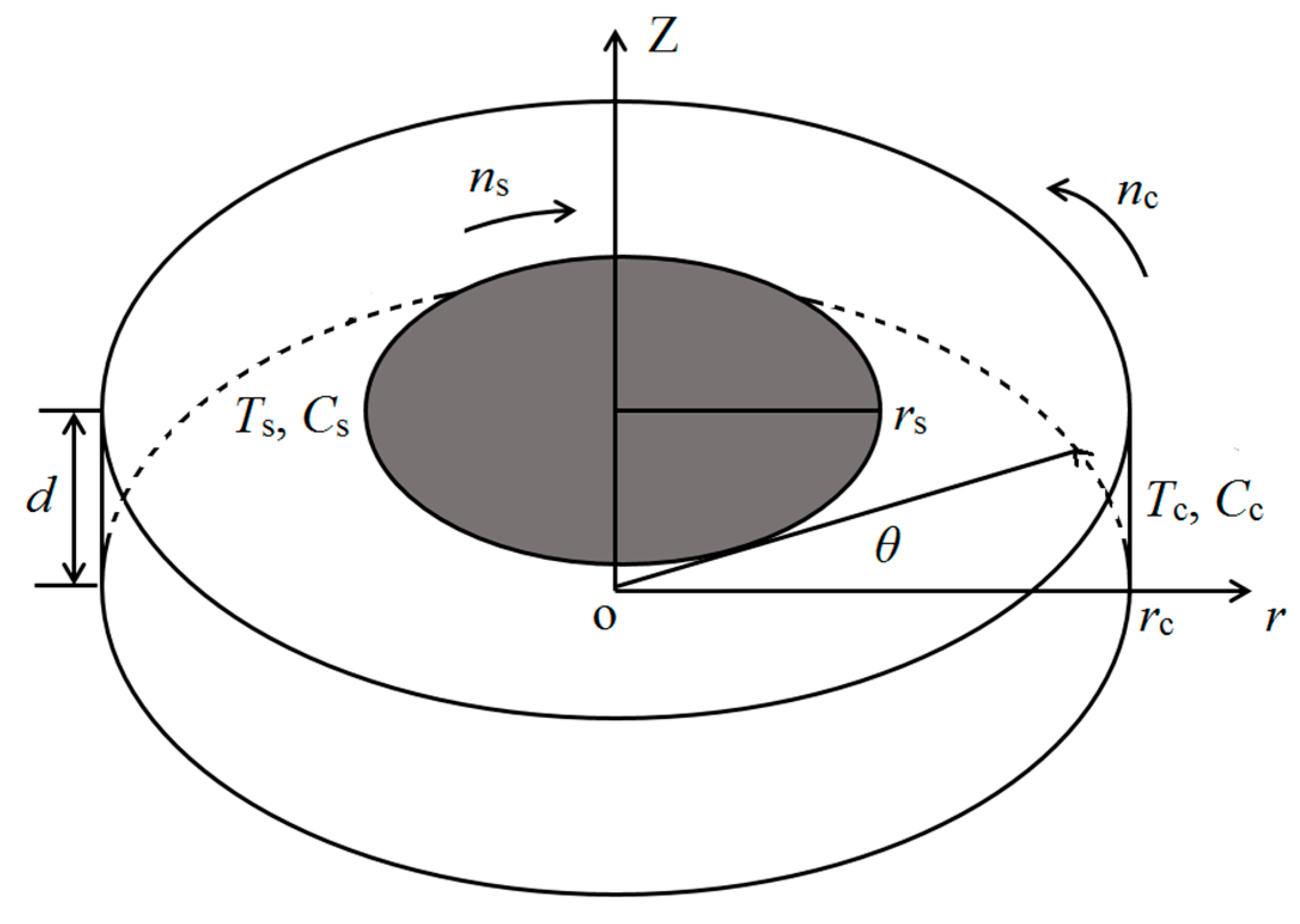
2. Physical and Mathematical Model

2.1. Basic Assumptions and Governing Equations

The physical model is schematically shown in Figure 1. The shallow cylindrical crucible of depth d and radius r_c is filled with Ge_1−xSi_x melt and a disk with radius r_s locating on the free surface. The disk and crucible rotate at constant rate n_s (r/min) and n_c (r/min), respectively. The crystal/disk interface and the sidewall of crucible are maintained at temperature and solute concentration T_s = T_m, C_s and T_c, C_c, (T_c > T_s, C_c > C_s), respectively. T_m is the melting point temperature of GeSi melt. The subscript s and c represent the crystal and crucible, respectively. The flow is laminar. The melt is an incompressible fluid with constant physical parameters. The melt top surface and melt/disk interface are flat and non-deformable. It is unrealistic to employ flat interface in Cz configuration [35,36] but the flat interface assumption adopted in this work is helpful to elucidate the effect of rotation on the thermal-solutal capillary convections. On the free surface, the thermocapillary and solutocapillary forces are taken into account. The solid-liquid interface satisfies no-slip condition. The surface tension σ changes linearly with temperature and concentration, which is defined as

$$\sigma (T,C)={\sigma }_0-{\gamma }_T(T-T_s)-{\gamma }_C(C-C_s)$$

(1)

where σ₀ = σ (T_s, C_s), γ_T = (∂σ/∂T)_C, γ_C = (∂σ/∂C)_T.

By applying r_c, r_c²/ν, ν/r_c and ρν2/r_c2 as the reference scales for length, time, velocity and pressure, respectively, the dimensionless governing equations can be expressed as follows, where ν is the kinematic viscosity, ρ is the density.

$$\nabla \cdot \mathit{V}=0$$

(2)

$$\frac{\partial \mathit{V}}{\partial \tau }+\mathit{V}\cdot \nabla \mathit{V}=-\nabla P+{\nabla }^2\mathit{V}$$

(3)

$$\frac{\partial \Theta }{\partial \tau }+\mathit{V}\cdot \nabla \Theta =\frac{1}{Pr}{\nabla }^2\Theta$$

(4)

$$\frac{\partial \Phi }{\partial \tau }+\mathit{V}\cdot \nabla \Phi =\frac{1}{Sc}{\nabla }^2\Phi$$

(5)

where Θ = (T − T_s)/(T_c − T_s) is the non-dimensional temperature, Φ = (C − C_s)/(C_c − C_s) represents the non-dimensional concentration, τ is the non-dimensional time, P is the non-dimensional pressure and V = V (V_R, V_θ, V_Z) is the non-dimensional velocity vector, respectively.

2.2. Boundary and Initial Conditions

The boundary conditions are expressed as follow:

At fluid/crystal interface, constant temperature T_s and solute concentration C_s are imposed (Z = D = d/r_c, R ≤ R_s = r_s/r_c, 0 ≤ θ < 2π):

$$V_R=V_Z=0,V_{\theta }=R{e}_s\frac{R}{R_s},\Phi =\Theta =0$$

(6)

At the free surface, thermal and solutal capillary forces are taken into account (Z = D, R_s < R < 1, 0 ≤ θ < 2π):

$$\frac{\partial V_R}{\partial Z}=-R{e}_T\frac{\partial \Theta }{\partial R}-R{e}_{Con}\frac{\partial \Phi }{\partial R},\frac{\partial V_{\theta }}{\partial Z}=-R{e}_T\frac{\partial \Theta }{R\cdot \partial \theta }-R{e}_{Con}\frac{\partial \Phi }{R\cdot \partial \theta }$$

(7)

$$V_Z=0,\frac{\partial \Phi }{\partial Z}=\frac{\partial \Theta }{\partial Z}=0$$

(8)

At the crucible’s sidewall, the temperature and solute concentration are kept as T_c and C_c (0 ≤ Z ≤ D, R = 1, 0 ≤ θ < 2π):

V_R = V_Z = 0, V_θ = Re_c, Φ = Θ = 1

(9)

At the bottom (Z = 0, R < 1, 0 ≤ θ < 2π):

$$V_R=V_Z=0,V_{\theta }=R{e}_c\cdot R,\frac{\partial \Phi }{\partial Z}=\frac{\partial \Theta }{\partial Z}=0$$

(10)

Primary conductive state is used as the initial condition (τ = 0):

$$V_R=V_Z=V_{\theta }=0,\Phi =\Theta =\frac{\ln (R/R_s)}{\ln (R_c/R_s)},R_s<R<1;\Theta =0,R\le R_s$$

(11)

The thermocapillary Reynolds number and solutocapillary Reynolds number are respectively defined as:

$$R{e}_T=\frac{{\gamma }_T(T_c-T_s)r_c}{\mu \nu },R{e}_{Con}=\frac{{\gamma }_C(T_c-T_s)r_c}{\mu \nu }$$

(12)

The rotation Reynolds numbers of crystal and crucible are respectively defined as:

$$R{e}_s=\frac{2\pi r_s{n}_s{r}_c}{60\nu },R{e}_c=\frac{2\pi n_c{r}_c^2}{60\nu }$$

(13)

The capillary ratio R_σ is used to describe the interaction between the solutal and thermal capillary effect:

$$R_{\sigma }=\frac{{\gamma }_C(C_c-C_s)}{{\gamma }_T(T_c-T_s)}$$

(14)

2.3. Calculation Conditions and Numerical Method

The tested fluid is Ge_0.98Si_0.02 melt and the thermophyscial properties at T_m = 1271.3 K are listed in

Table 1. Physical parameters of Ge_0.98Si_0.02 melt.

Property	Symbol	Unit	Value
Density	ρ	kg/m3	5246.00
Thermal diffusivity	α	m2/s	2.20 × 10−5
Viscosity	μ	kg/(m·s)	7.34 × 10−4
Mass diffusivity of species	D	m2/s	1.00 × 10−8
Temperature coefficient of surface tension	γT	N/(m·k)	8.10 × 10−5
Concentration coefficient of surface tension	γC	N/m	−0.54
Prandtl number	Pr	-	6.37 × 10−3
Schmidt	Sc		2.90
Lewis number	Le	-	2197.80

. The capillary ratio is considered to be R_σ = −0.2, which is one of the typical capillary ratios generated by the segregation during Czochralski crystal growth [37]. The radius ratio R (R = r_s/r_c) is 0.5 and the aspect ratio Г(Г = d/r_c) is 0.1. The disk and crucible of rotation Reynolds numbers, Re_s and Re_c range from 0 to 1870 and 0 to 1403, respectively.

The governing equation and the boundary conditions are discretized by the finite volume method. The convective term adopted the QUICK (Quadratic Upwind Interpolation of Convection Kinematics) scheme and diffusion term is solved by central-difference approximation. SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm is used to handle the coupling of pressure and velocity. The iterative equation will converge when the maximum error is less than 10⁻⁵. During the simulations, the dimensionless time steps from 2.2 × 10⁻⁶ to 2.5 × 10⁻⁵ are chosen. Convergence at each time step is assumed the maximum relative error of all these fundamental equations among the computational domain gets below 10⁻⁵.

Non-uniform staggered grid is applied in the system. Near the free surface, crystal interface and crucible’s sidewall, the grids are encrypted. The mesh convergence is carefully checked. As listed in the

Table 2. Variation of non-dimensional wave number m and velocity fluctuation V_ave with grid when Re_T = 2000.

Grids	m	Vave
40R × 20Z × 90θ	8	50.40
60R × 20Z × 90θ	8	50.10
80R × 30Z × 120θ	8	50.05
120R × 40Z × 160θ	8	50.47

, different grids produce similar surface oscillation patterns. The wave number does not change with the grid. The difference of the average velocity on the free surface is small with an error then than 1% between two fine meshes. Therefore, the mesh of 80^R × 30^Z × 120^θ adopted in the paper is sufficient for accurate simulation.

In order to validate the current numerical scheme, we performed three-dimensional simulation study on the double-diffusive convection in a cubic cavity that investigated by Zhan et al. [7]. The simulation has been carefully done under the same condition by Zhan et al. [7], that Re_T = 200, Le = 10. As shown in Figure 2, it is found that the presented temperature, concentration, as well as velocity distributions are almost the same with the results of Zhan et al. These validations provide confidence to the accuracy of the numerical scheme.

3. Results and Discussion

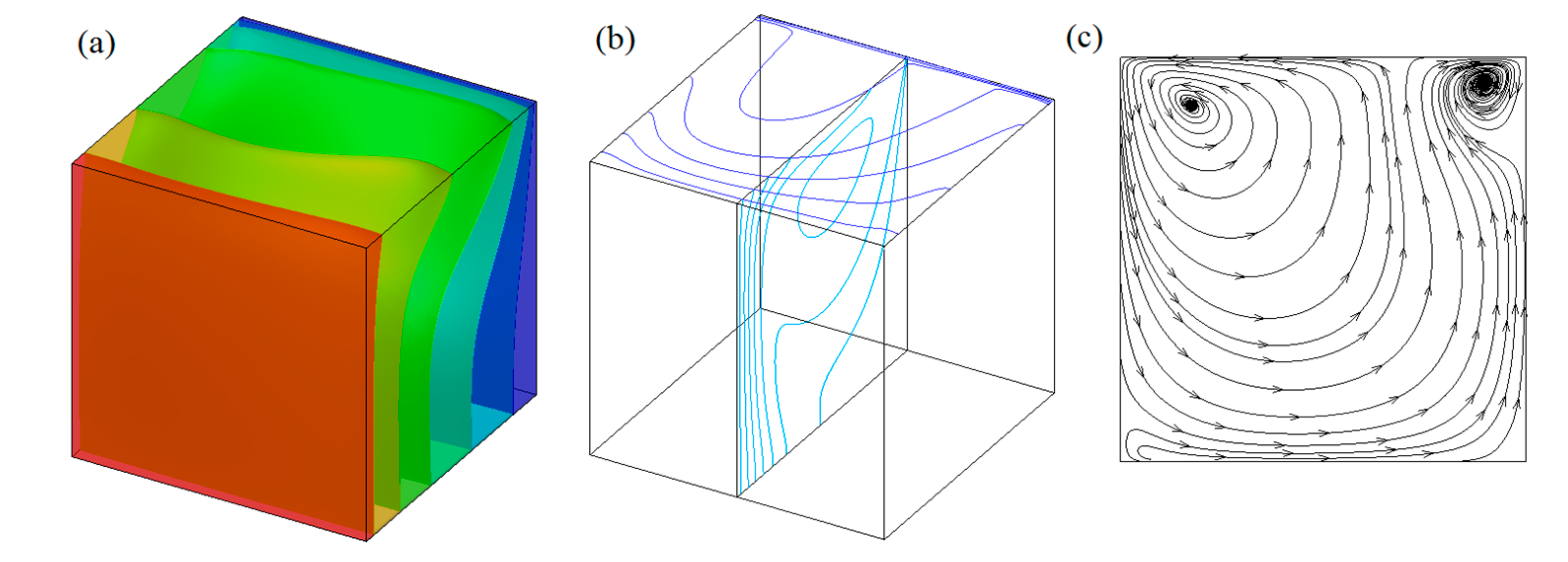
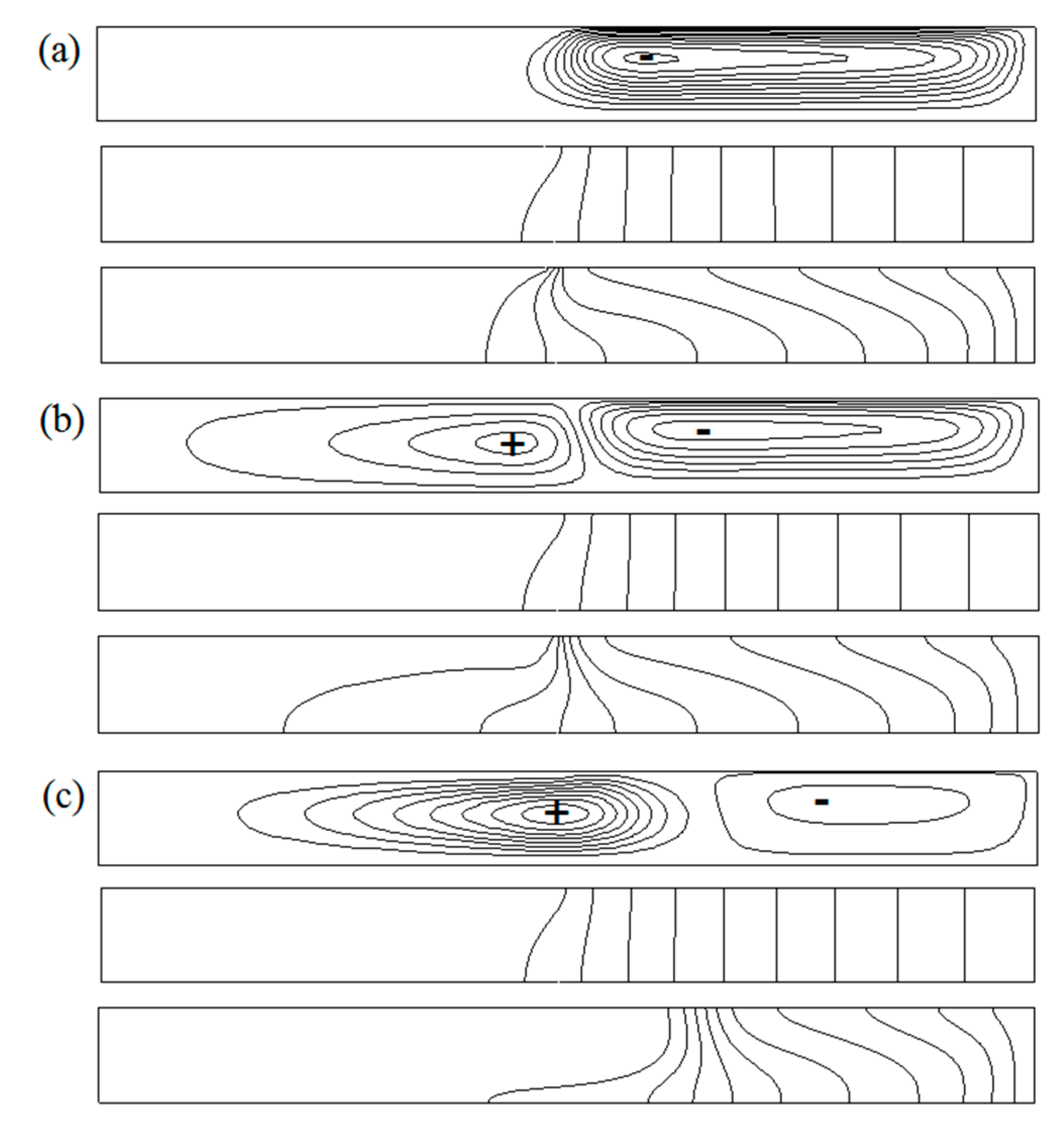
3.1. Basic Flow

When the thermal-capillary and the rotation Reynolds numbers are relatively small, the combined rotation and thermal-solutal capillary flow is steady and axisymmetric. This type of flow is called basic flow. Due to the circulation in the meridional plane generated by the thermal-solutal capillary forces, the centrifugal and Coriolis forces created by the rotation of the crystal or crucible, several types of basic flow structure are observed. The velocity field is displayed in terms of the non-dimensional stream function ψ, which is defined as

$$U=-\frac{1}{R}\frac{\partial \psi }{\partial Z},W=\frac{1}{R}\frac{\partial \psi }{\partial R}$$

(15)

This definition results in the positive values of ψ for clockwise circulation flows and negative values of counterclockwise circulation flows.

For the mixture investigated in this paper, the capillary ratio is −0.2, the negative sign describes the fact that the thermocapillary force is always opposite to the solutal-capillary force and the value of 0.2 indicate that the thermal-capillary effect is much larger than the solutal-capillary effect. Without rotation, the basic flow is dominated by the thermocapillary force. Figure 3 shows the streamlines, isotherms and iso-concentration lines of the basic flow at the meridian plane. When the Re_T is less than a threshold value, the thermocapillary force drives the surface fluid flows from the hot crucible’s sidewall to the crystal/fluid interface, then a return flow appears in the liquid bulk, generating a counterclockwise convection roll cell. This flow structure is similar with that of the pure liquid in a Cz model [31,32]. For the temperature profile, the isotherms are almost parallel to the sidewall, except the isotherm near the crystal. Compared with the isotherms, the iso-concentration lines are more distorted and more sensitive to the flow, as shown in Figure 3a. This is because the Lewis number of the mixture is much larger than unit, hence the thermal diffusion is much faster than mass diffusion, creating greater deformation of iso-concentration lines. With the increase of Re_T, the flow is enhanced, the maximum value of the stream function is increased to 0.37, the isotherms change very little, while the iso-concentration lines near the crystal and the sidewall become denser, indicating larger concentration gradients, as shown in Figure 3b.

When the crystal or crucible rotation is considered, the combined rotation-thermal-solutal capillary flow is dominated by the competition among the driving forces. For a small rotation rate of crystal, the flow is still mainly driven by the thermal-solutal forces, as shown in Figure 4a. As the increase of crystal rotation rate, the centrifugal force induced by the crystal rotation pumps the surface fluid out towards the crucible’s sidewall, thus, a clockwise circulation appears underneath the crystal, as shown in Figure 4b. Meanwhile, for this case, the rotation driven flow is not strong enough to completely inhibit the thermal-solutal capillary flow. Therefore, two counter rotating cells coexist in the flow field and flow intensity of the clockwise cell is weaker than that of the counterclockwise cell. When the value of Re_s further increases to 702, as shown in Figure 4c the rotation driven flow is much stronger than the thermal-solutal capillary flow, the flow field is mainly occupied by the clockwise circulation, a smaller counterclockwise rotating cell appears near the sidewall. Since the strong effect of the crystal rotation, the concentration profile near the crystal is more uniform.

On the other hand, when the crystal is kept in steady condition but the crucible rotates with Re_c = 468, the centrifugal and thermal capillary forces are imposed in the same direction. Since the crucible has large contact area with the mixture, the counterclockwise circulation occupies the whole flow field, as shown in Figure 5a. Compared with the case shown in Figure 3a, with the increase of Re_c, the combined rotational-thermal-solutal capillary flow is enhanced. As Re_c is increased from 468 to 1403, the maximum value of the stream function is increased from 0.22 to 0.81, as shown in Figure 5b. For this case, the rolling cell shifts to the crystal side and the iso-concentration line near the crystal curves to the sidewall. When the rotation of the crystal and crucible are both considered, the flow structure is related with the competitions among the driving forces, including the centrifugal and Coriolis forces driven by crystal and crucible rotations, thermal and solutal capillary forces. For example, when the Re_T is kept at 400 but Re_s is increased to 468, the counter rotating cells are observed, for the clockwise circulation driven by the combined crucible rotation and thermocapillary force, the maximum value of the stream function is 0.15, which is even smaller than the case of Re_c = 468, as shown in Figure 5c. This is because that the centrifugal forces generated by crystal and crucible rotations are in the opposite direction, hence, when the co-rotation of crystal and crucible is considered, the flow generated by the crucible rotation is weakened.

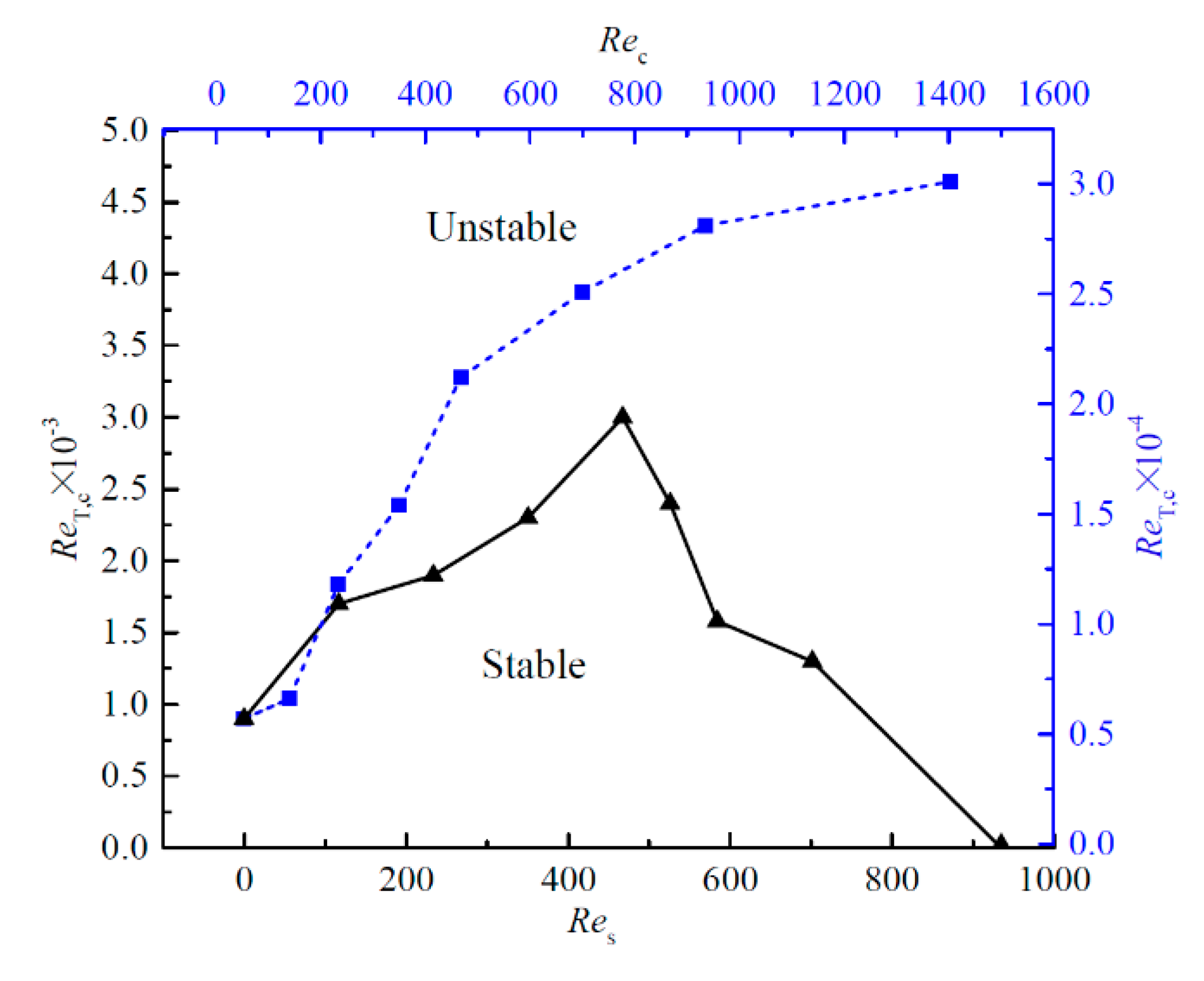
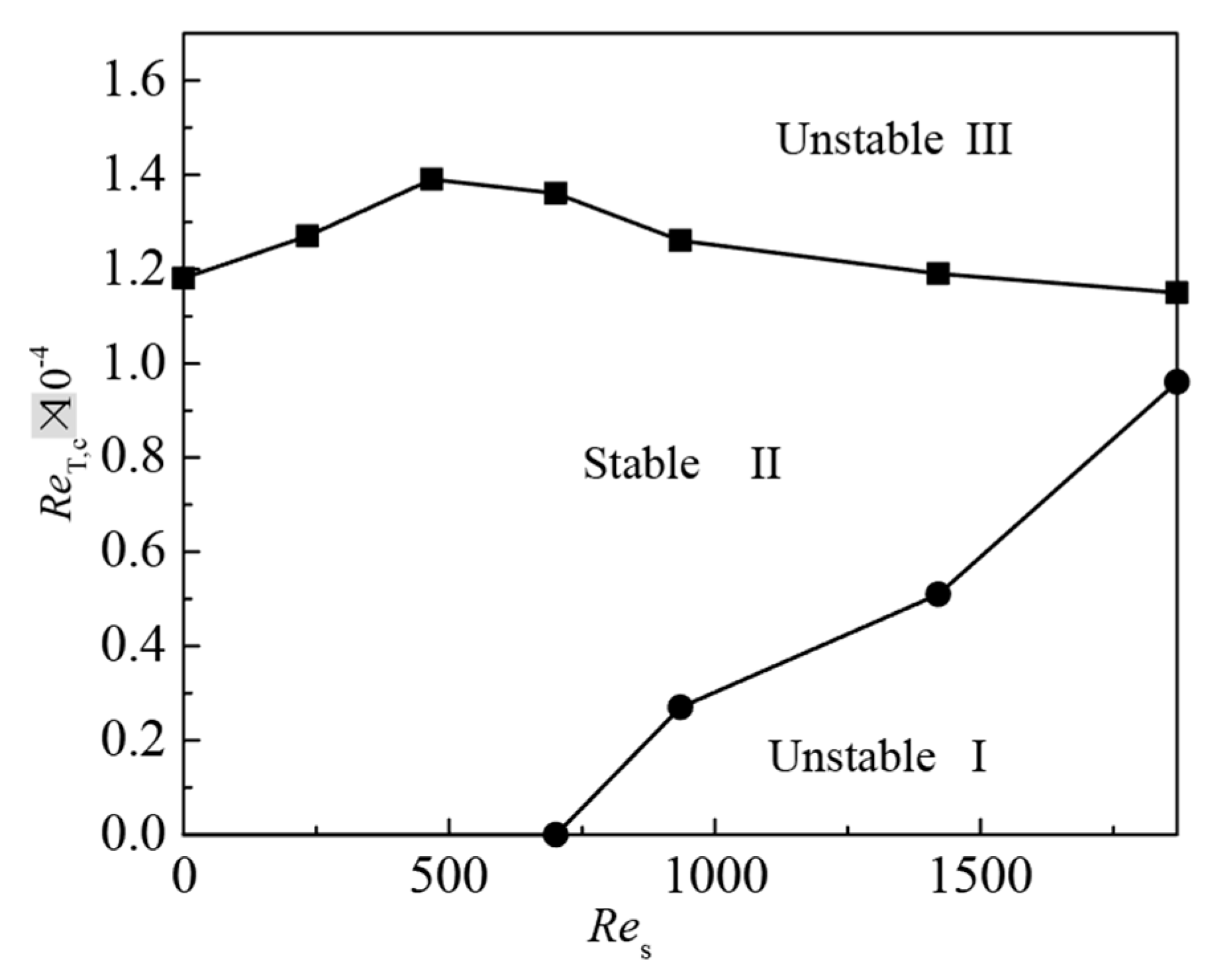
3.2. Critical Conditions for the Flow Destabilization

With or without rotation, once the thermocapillary Reynolds number exceeds a threshold number, the 3D disturbances will be incubated and the amplitudes increase with time, finally, the three-dimensional oscillatory flow is formed, then the two dimensional basic flow will transit to the three-dimensional oscillatory flow. During the initial growth process, the intensity of any disturbance (X) increases exponentially, which can be expressed by [38]

$$X\left(R,\theta ,Z,\tau \right)=X_0\left(R,\theta ,Z\right)\exp \left[\left(\beta +i{\beta }_I\right)\tau \right]$$

(16)

where β is the growth rate constant of the disturbance and β_I represent the time-dependent oscillatory characteristics of the disturbance. The value of β can be determined from the slope of the semi-logarithmic plot of concentration versus τ. Then, the critical thermocapillary Reynolds number Re_T,c for the formation of three dimensional flow can be determined by plotting β versus Re_T, which is defined as the neutral stability limit (β = 0).

Figure 6 shows the critical conditions for the flow transition when the crystal or crucible rotates. It is found that without rotation, the critical conditions for the flow transition from basic thermo-soultal capillary flow to the 3D oscillatory flow is about 900, which is smaller than that of the pure fluid [31,32]. When the crucible starts rotating, the value of Re_T,c increases monotonically, indicating that the rotation of crucible has an inhibitory effect on the thermo-soultal capillary flow instability. Meanwhile, as the increase of crystal rotation rate, the centrifugal force generated by rotation is opposite to that of the thermocapillary force, which suppresses the radial inward flow and depresses the flow instability, thus, the Re_T,c increases with the increasing Re_s. However, with the further increase of crystal rotation, the cells generated by rotation is shearing with the circulation produced by thermo-soultal capillary flow, the disturbance is enhanced, thus, the critical value of Re_T,c is decreased. It should be noted that when Re_s is increased to 950, the rotation driven flow is dominated, no stable state is observed.

When the crystal co-rotates with crucible, the flow undergoes two transitions. For a typical example of Re_c = 234, with the increase of Re_T, the flow transits from basic flow to three dimensional oscillatory flow. The critical value of Re_T,c is increased first and then decreased with the increase of Re_s. This variation trend is similar with that shown in Figure 6. When the Re_s further increases to 700, the rotation driven flow behaves as an unstable 3D oscillatory flow, even though the Re_T is zero, as shown in Figure 7, this rotation dominated state is denoted as unstable state I. When the small temperature and concentration gradient is imposed, the rotation driven unstable flow is exhibited and the flow will transit to the stable state II. With a larger Re_s, a larger value of Re_T is expected to exhibit the rotation driven flow, this the curve for the transition from state I to state II is ascending. For a further increase of Re_T, the thermo-solutal capillary force is enlarged and drives the flow lose stability again and then undergoes a second transition to the unstable state III.

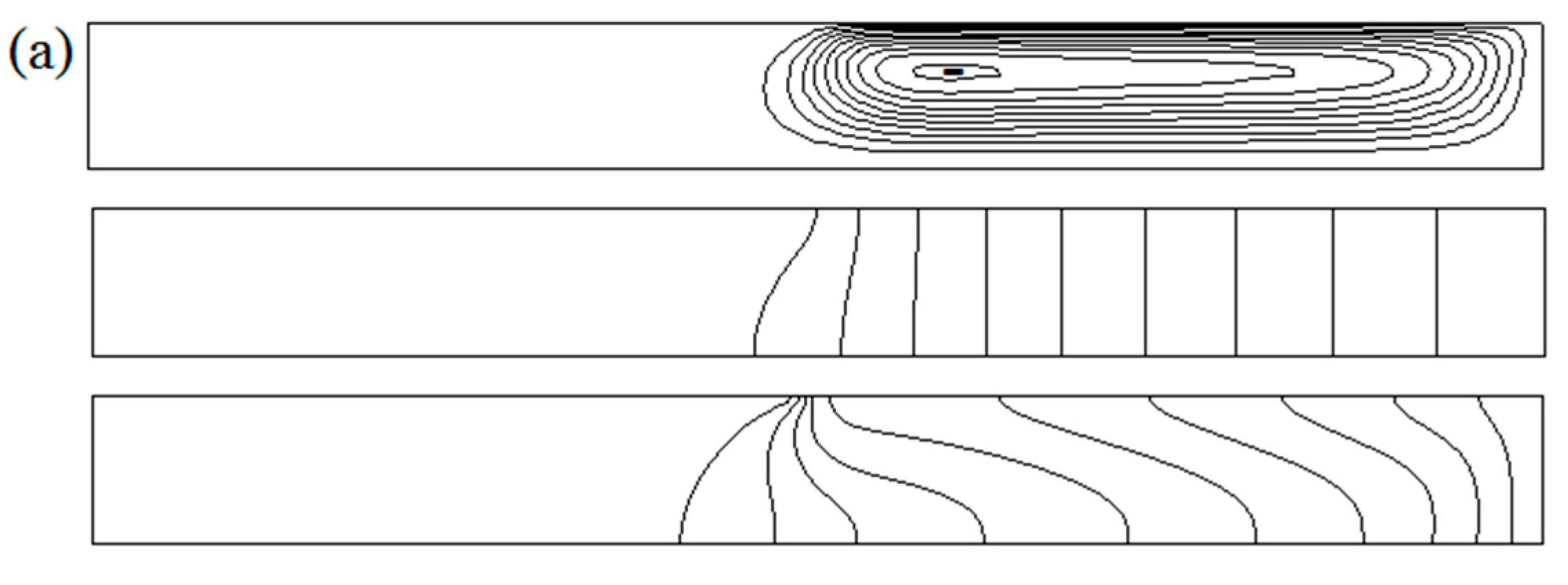
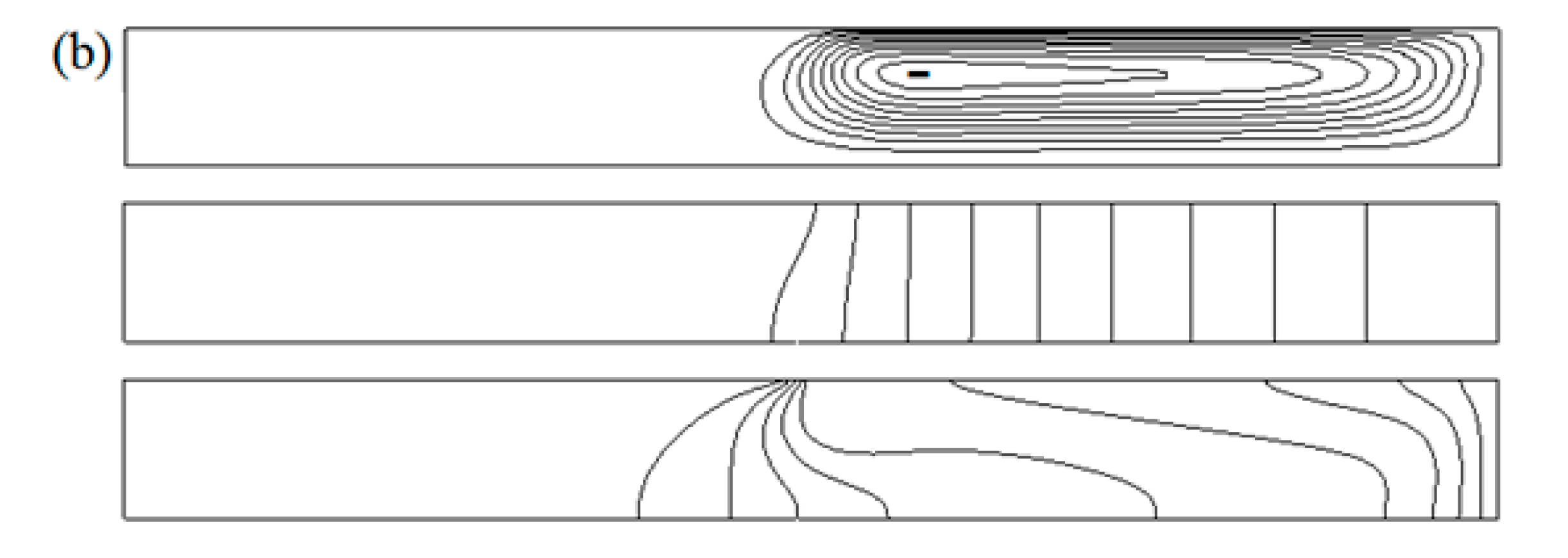
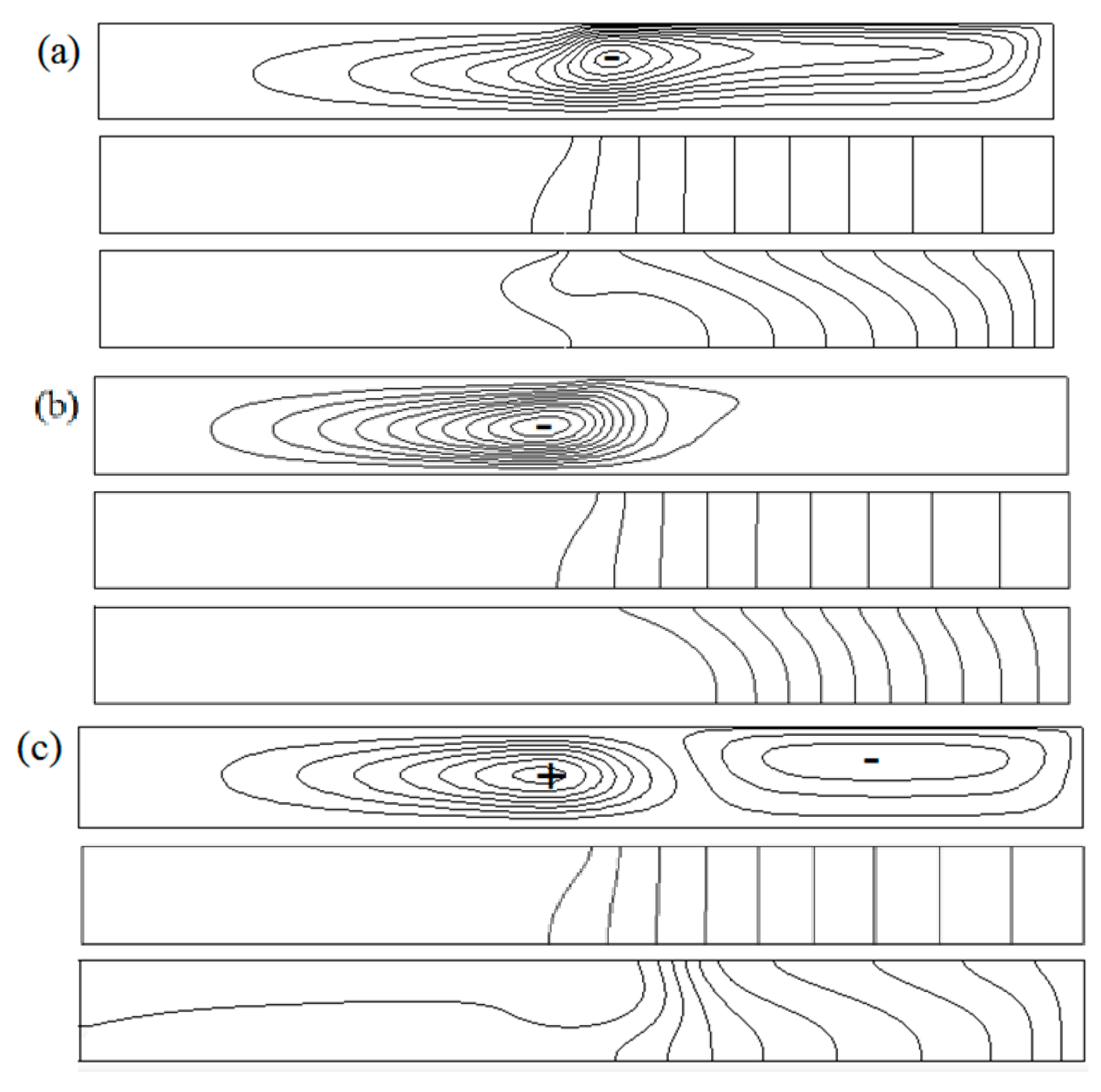
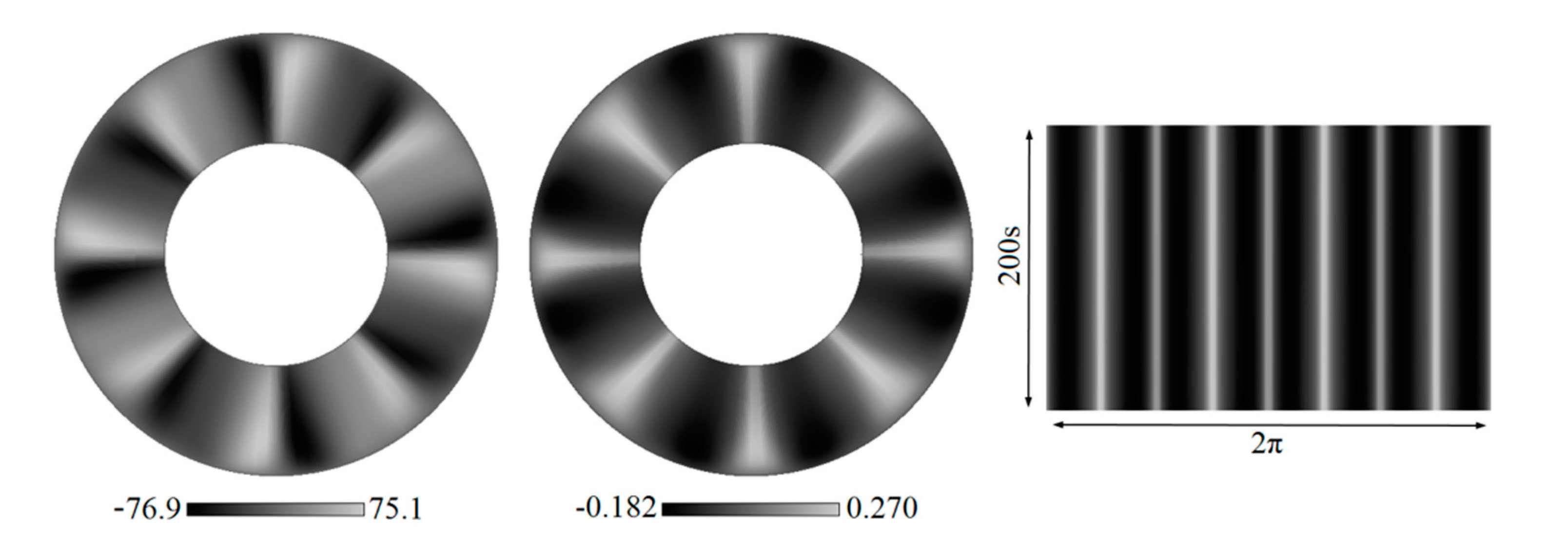
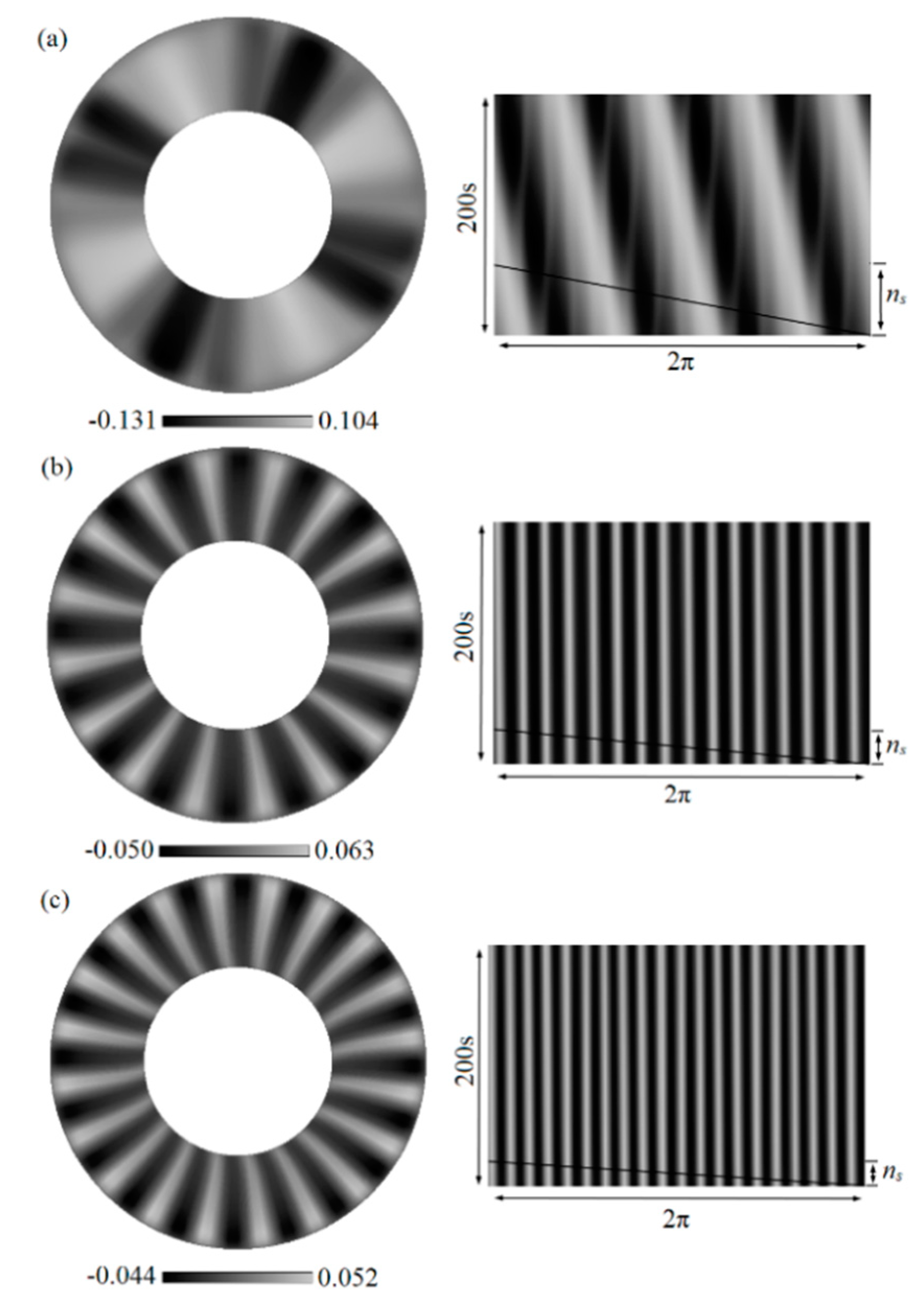
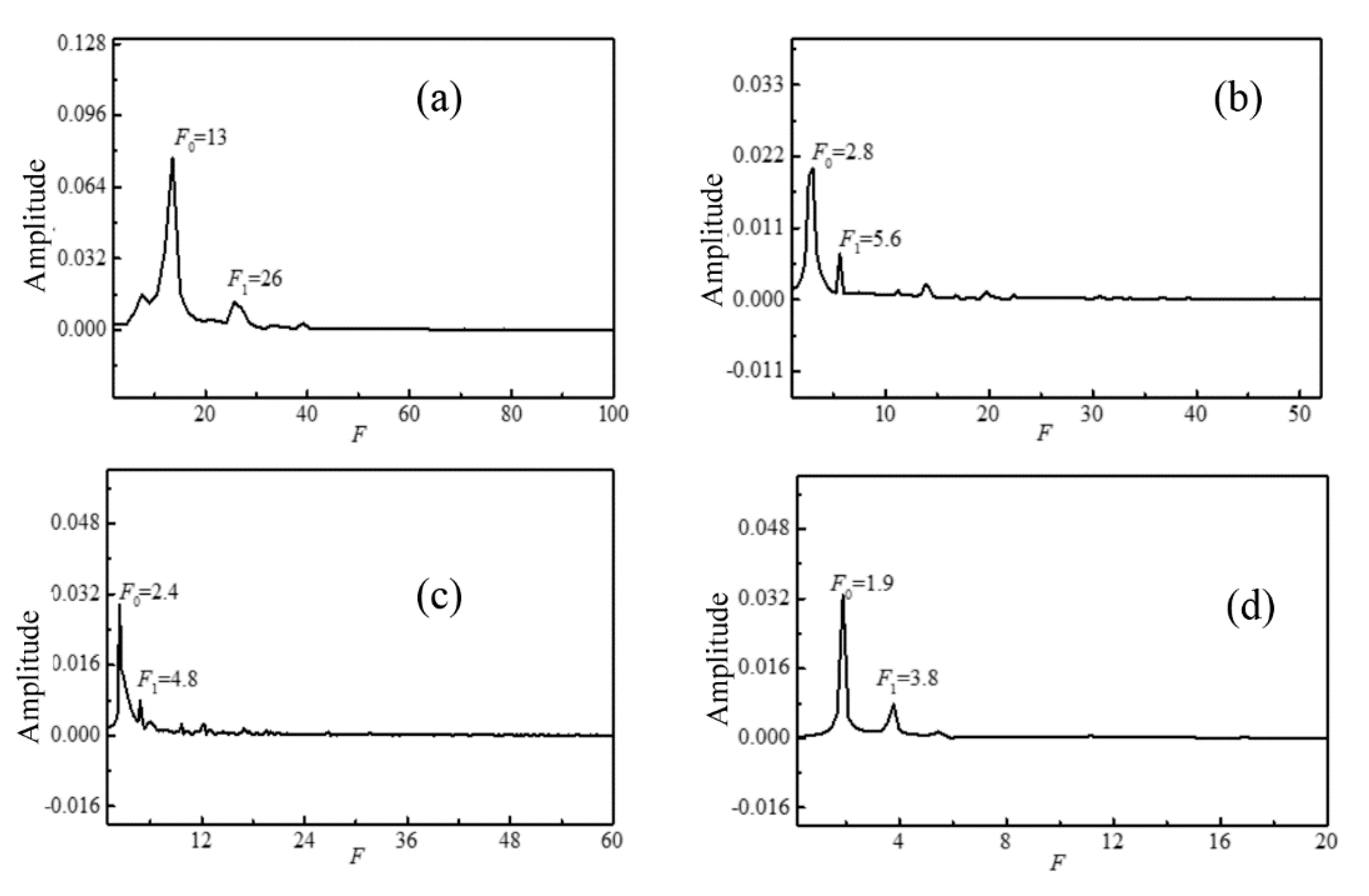
3.3. Three-Dimensional Oscillatory Flow

In order to obtain the three-dimensional disturbances, fluctuation (δζ) of a physical quantity ζ is introduced as follows,

$$\delta \zeta (R,\theta ,Z,\tau )=\zeta (R,\theta ,Z,\tau )-\frac{1}{2\pi }{\displaystyle {\int }_0^{2\pi }\zeta (R,\theta ,Z,\tau )}d\theta$$

(17)

where ζ can be non-dimensional temperature Θ, concentration Φ or velocity V.

Without rotation, the surface patterns are shown as spokes. Since the Schmidt number, which is defined as the ratio of momentum diffusivity and mass diffusivity, is much larger than the Prandtl number, compared with the concentration oscillatory, the temperature fluctuation is very small and always consists with the concentration fluctuation, thus, in the following discussions about the surface patterns, only the oscillation patterns of concentration and azimuthal velocity are shown. As seen in Figure 8, the 3D oscillatory concentration and velocity are shown as spoke patterns with wave number of 7. From the spatiotemporal diagram (STD), 7 vertical lines are displayed, which indicates that the flow is steady in time but fluctuates in space. This pattern corresponds to a series of circulating cells lined up side by side in the azimuthal direction.

When the crystal starts to rotate, the surface oscillation patterns transfers with the rotation rate. As shown in Figure 9a, when Re_s is set to be 234, the surface concentration fluctuations are still displayed as spokes. However, compared with Figure 8, the oscillation amplitude and wave number are decreased, since the small rotation rate can depress the flow instability. On the other hand, under the influence of crystal rotation, the surface fluctuations slightly rotate in the same direction as that of crystal, the STD is presented as series of inclined line. Also, the propagation velocity of such concentration fluctuations is much smaller than that of crystal rotation. With the increase of rotation rate, the effect of rotation driven flow is enhanced, the thermal-solutal capillary flow is weakened, then the fluctuation amplitude is decreased. The surface patterns are back to the steady state but the wave number increases from 16 to 20, as Re_s increases from 468 to 701, as shown in Figure 9b,c. Meanwhile, the corresponding Fourier spectra of the surface concentration fluctuations at a monitor point P (R = 0.55) are shown in Figure 10. Obviously, there are two peaks marked as F₀ and F₁, respectively and F₀ = 1/2F₁. Shen et al. [39] also experimentally reported that two or three frequencies exist when the thermal flow of a pure liquid transfers to the 3D oscillatory in a rotating Czochralski system. Moreover, as the increase of crystal rotation rate, the main frequencies decreases, simultaneously, the wave number increases, thus the period of the oscillation is increased but the propagation velocity is decreased.

When the rotation rate is large, the rotation driven flow is dominant. As discussed in Figure 6, the rotational flow is unstable even without temperature and concentration gradient. For these cases, with the increase of Re_T, the flow undergoes two transitions. The free surface patterns depend on the competitions among the driving forces. As shown in Figure 11a, for a small temperature and concentration gradient, the surface pattern is shown as a typical rotation wave with wave number of 4. The azimuthal rotation velocity is slightly less than that of Re_s. When Re_T is increased to 2.2 × 10³, the oscillation amplitude is decreased, since the rotation driven flow is inhibited by the contrary thermal-solutal convection, as shown in Figure 11b. With further increase of Re_T, the flow instability is totally inhibited and the 3D oscillatory flow transits to the stable 2D basic flow. When the Re_T increases to 3.0 × 10³, the rotation driven flow and the thermal-solutal capillary flow are comparable. As shown in Figure 11c, the surface oscillation pattern is superimposed by two group of waves, one the rotation wave, another one is the spoke wave. The corresponding STD is also composed two group of lines, one is inclined to the left, one is series of vertical lines. As Re_T continues increasing to 6.0 × 10³, the thermal-solutal capillary flow enhanced, the surface oscillation is shown as spoke pattern, which corresponds to the unstable state III. In this state, the flow is dominated by the thermal-solutal convection, as shown in Figure 11d.

When strength of the crystal rotation driven flow and thermal-solutal convection are comparable, the surface pattern is affected by both two factors. As displayed in Figure 12, when Re_s is 1403, the surface concentration fluctuations are similar as spoke pattern generated by thermal-solutal capillary force but different with the zero rotation case, from the STD, it can be seen that the STD consist of a series of vertical wavy lines. As the increase of Re_s, the vertical wave lines become inclined lines and the surface waves near the crystal propagate in azimuthal direction. When the Re_s is increased to 3506, as shown in Figure 12c, the crystal rotation driven flow generated a typical rotational wave with a wave number of 3. The maximum oscillation is located near the crucible sidewall. For this case, the rotation driven unstable flow is almost the same as that in the pure liquid without temperature and concentration gradients, as reported in previous work [31].

In order to show the characteristics of the unstable flow inside the crucible, the circumferential views of concentration fluctuations are plotted in Figure 13. It is shown that as the crystal rotates, the oscillation waves always propagate in the same direction with that of crystal. However, the penetration depth of the surface oscillation is depending on the competition of the thermal-solutal capillary flow and the rotation driven flow. For the given value of Re_T, when the rotation rate is relatively small, the oscillations almost occupy the whole crucible, from the surface to the bottom, the oscillation pattern is almost the same, as shown in Figure 13a,b. When the value of Res is increased to 935, in the upper side of the crucible, the flow is co-dominated by the rotation and thermal-solutal capillary convections, the corresponding surface pattern is similar as that shown in Figure 11c. In the lower part of the crucible, the vertical lines disappear and the flow is almost dominated by the rotation driven flow. For the further increase of Res, the rotation domination area moves to the lower part, in the crucible, two groups of waves are clearly observed, as shown in Figure 11d,e. When the value of Re_s is increased to 3506, the rotation wave number is decreased to 3 and the dominant the whole flow field, as shown in Figure 11f.

As previously discussed, in present calculation range of Re_c, the critical Re_T for the flow transition always increase with the increase of Re_c. For the 3D oscillatory flow, the surface patterns do not change too much with the crucible rotation rate. However, since the contact area of crucible is larger, the propagation velocity of the surface wave is almost dominated by the crucible rotation rate. As shown in Figure 14, when Re_c = 234, the surface spokes with wave number of 16 almost rotate in the same rate as the crucible. When Re_c is increased to 701, the flow instability is depressed, the fluctuation is weakened. Then, the wave number is decreased, since the energy need to be dissipated is less. The corresponding circumferential view of the fluctuations are shown in Figure 15. It is noted that the concentration oscillations are mainly located near the free surface and the lower part of the crucible. When Re_c is kept at 234 and the Re_s is increased to 3506, the spokes near the crystal are twisted, the correspond STD is consisted of a series of wavy lines inkling to the left, as shown in Figure 14c. Compared with the crystal rotation case (shown in Figure 12c), the oscillation magnitude is decreased, since the centrifugal forces driven by the crystal and crucible are opposite, inducing the depressing effect on the rotation driven flow. In addition, from the Figure 15c, it is clearly observed that the near the free surface, the unstable thermal-solutal capillary flow is dominated and is presented as a series of circulating cells lined up side by side in the azimuthal direction. However, in the lower part of the crucible, the crystal rotation driven waves with wave number of 3 is dominant, which is consisted with the case that shown in Figure 13f.

4. Conclusions

The coupled rotation and thermal-solutal capillary convections in a typical Czochralski configuration with radial temperature and concentration gradients has been investigated by three-dimensional numerical simulations. The main conclusions are drawn as follows:

(1)

For the small Reynolds numbers, the basic flow represents as two-dimensional steady flow. Depending on the competitions among the driving forces, the flow structure is presented as meridional circulations in counter-clockwise or clockwise direction. When the strength of the driving forces are comparable, two opposite cells can coexist in the flow field.

(2)

When the Re_T exceeds a critical value, the basic flow will transit to the three-dimensional oscillatory state. For crucible rotation, the critical value of Re_T increases monotonically with the increase of crucible rotation rate. For crystal rotation, the variation trend for the critical Re_T increase first and then decreases with the increase of Re_s. For the co-rotation of crucible and crystal, two critical values of Re_T are obtained. When the rotation driven flow is dominated, the flow is named as unstable state I; with the increase of Re_T, the flow will transit to stable state II, then the thermal-solutal capillary will dominate the flow and drives the flow lose its stability again and transits to unstable state III.

(3)

The oscillatory flow patterns are closely related with the competitions among the rotation and thermal-solutal capillary forces. Without rotation, the surface spoke pattern is steady in time but oscillate in space. With crystal rotation, the surface will transit to spokes propagating in azimuthal direction, rotation waves, also, the spokes and rotation waves may coexist, these waves overlap and interweave in the flow field. The crucible rotation mainly dominants the propagation velocity of the surface fluctuation waves.