Interplay of Spin and Spatial Anisotropy in Low-Dimensional Quantum Magnets with Spin 1/2
Abstract
1. Introduction
2. Spatial Anisotropy of the Exchange Coupling: From the Chain to the Square Lattice
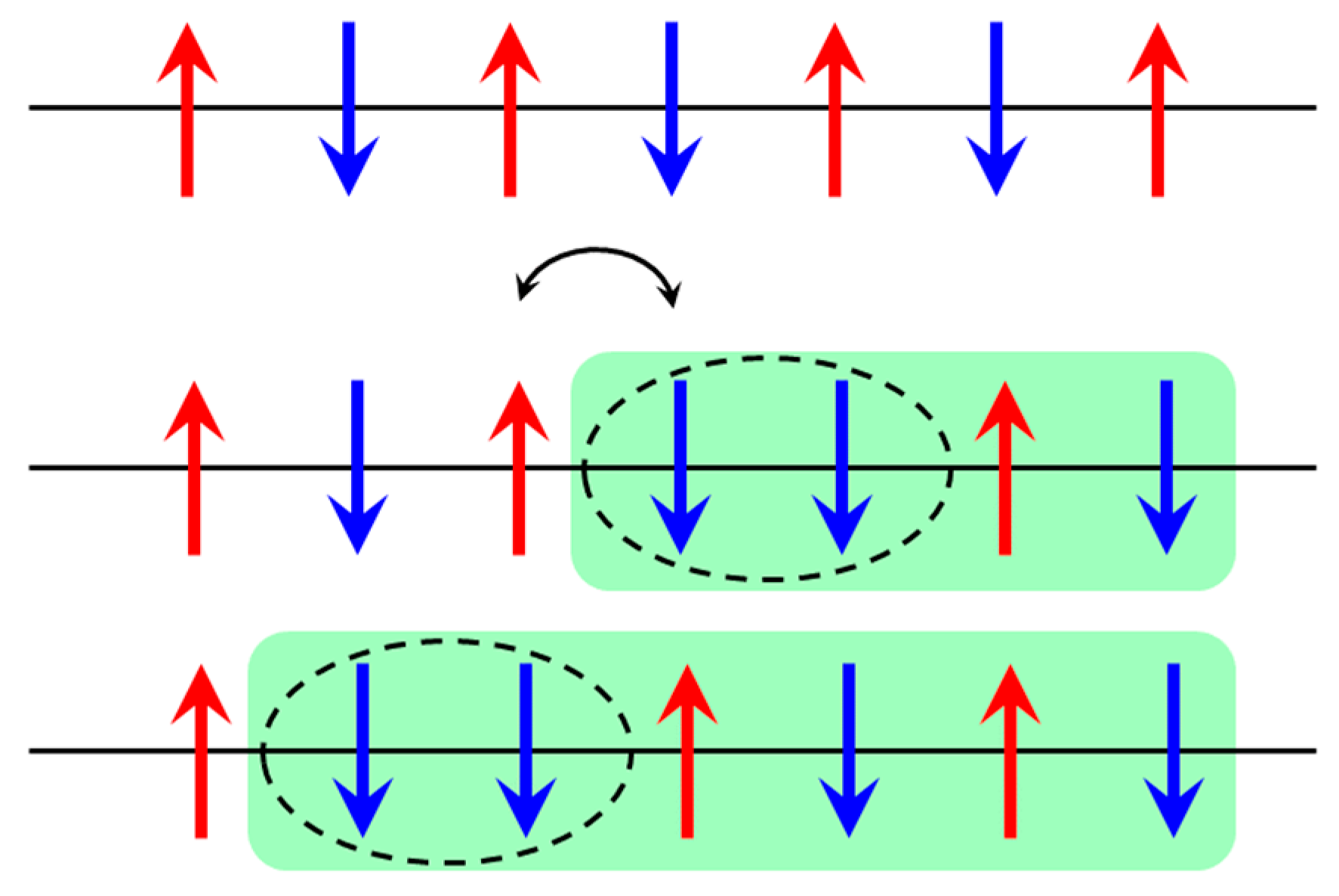
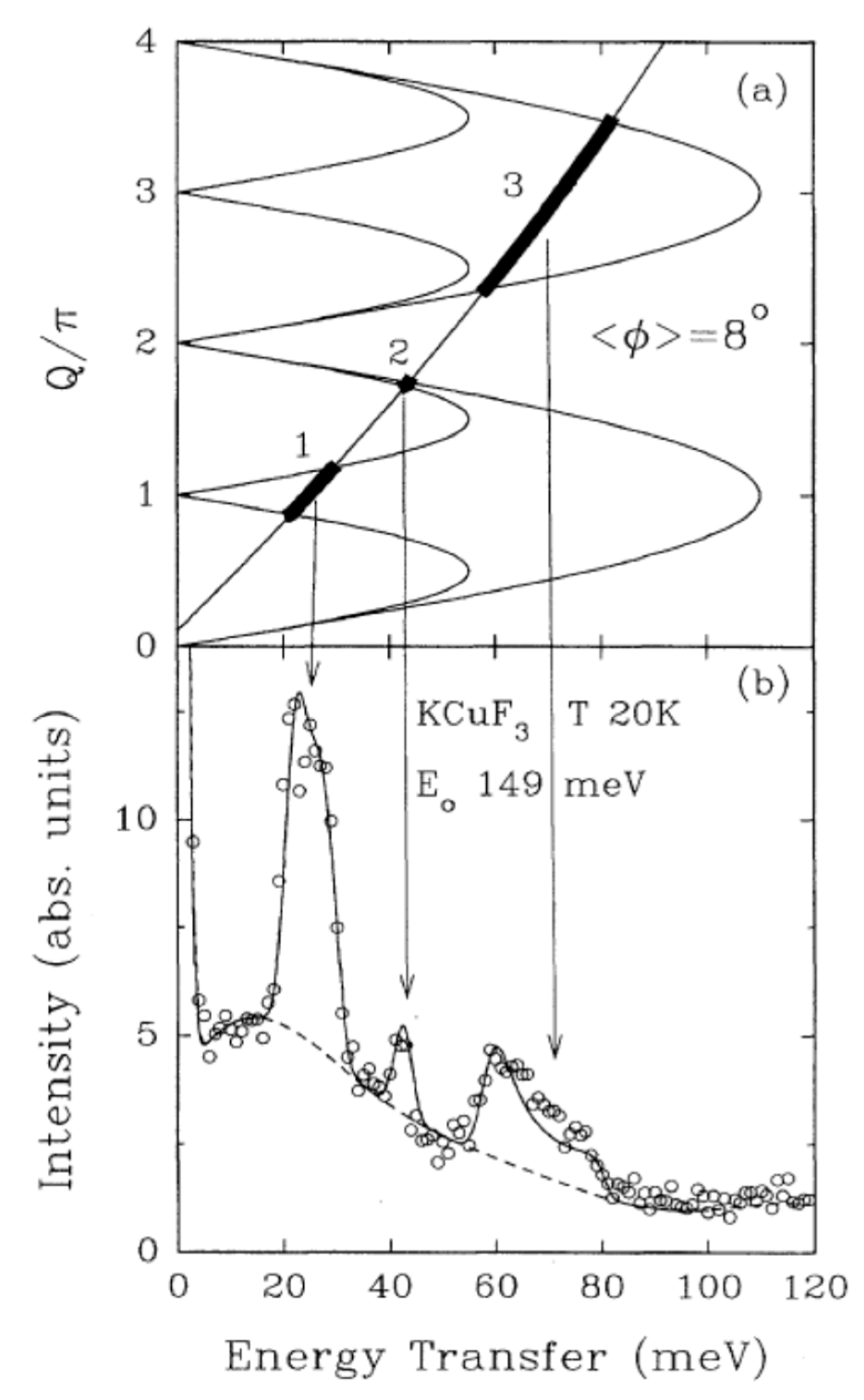
2.1. The S = 1/2 Heisenberg Antiferromagnetic Chain
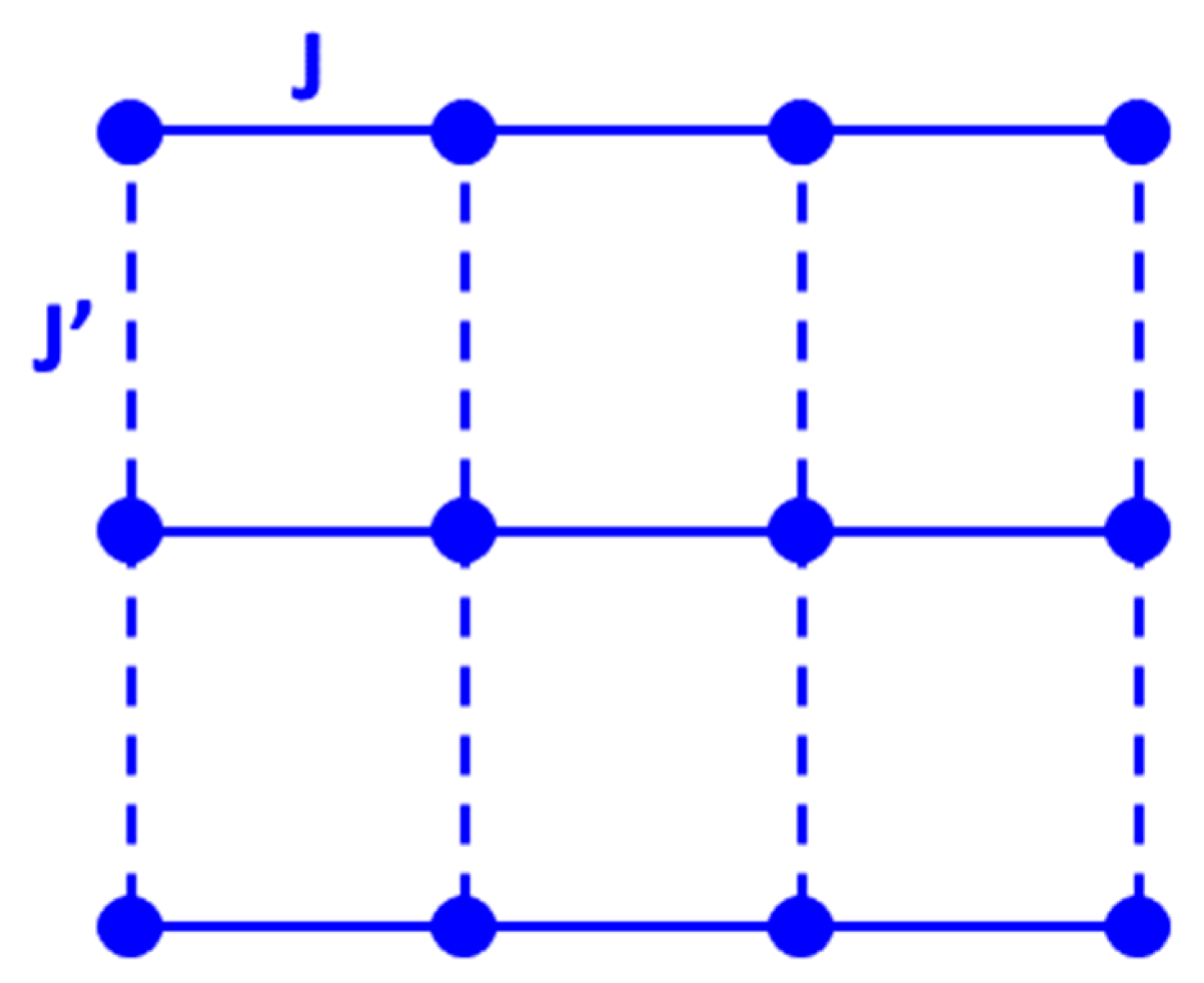
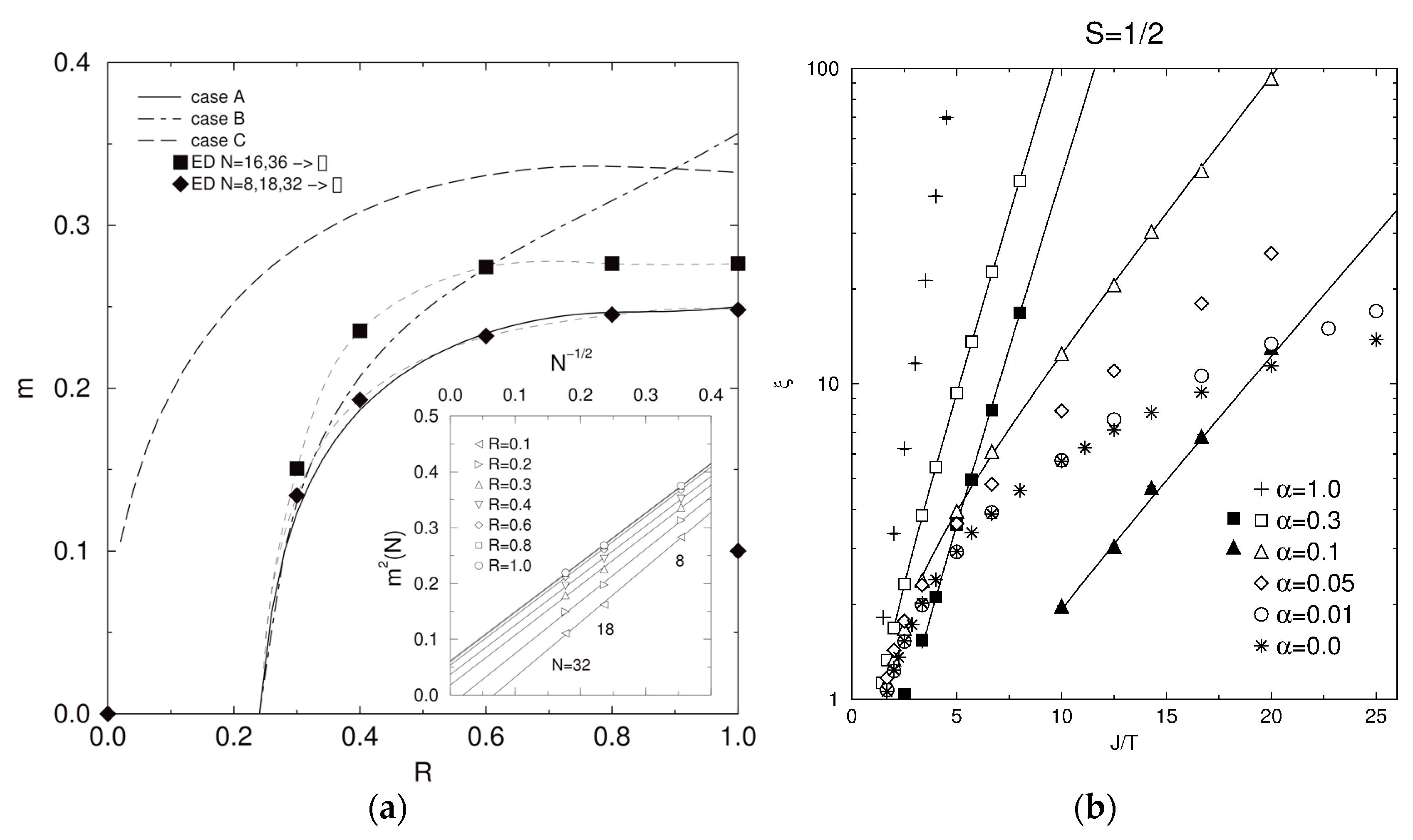
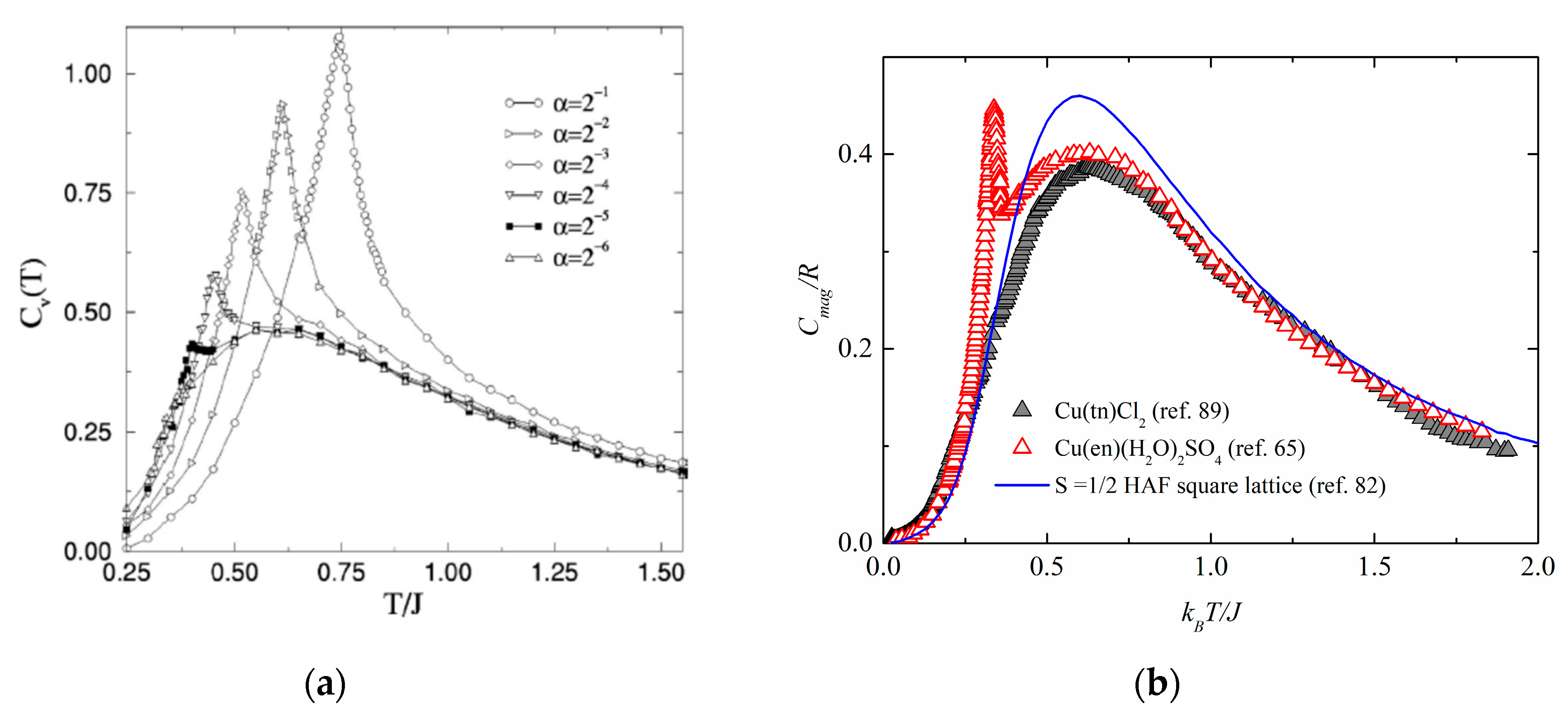
2.2. The S = 1/2 Heisenberg Antiferromagnet on the Spatially Anisotropic Square Lattice
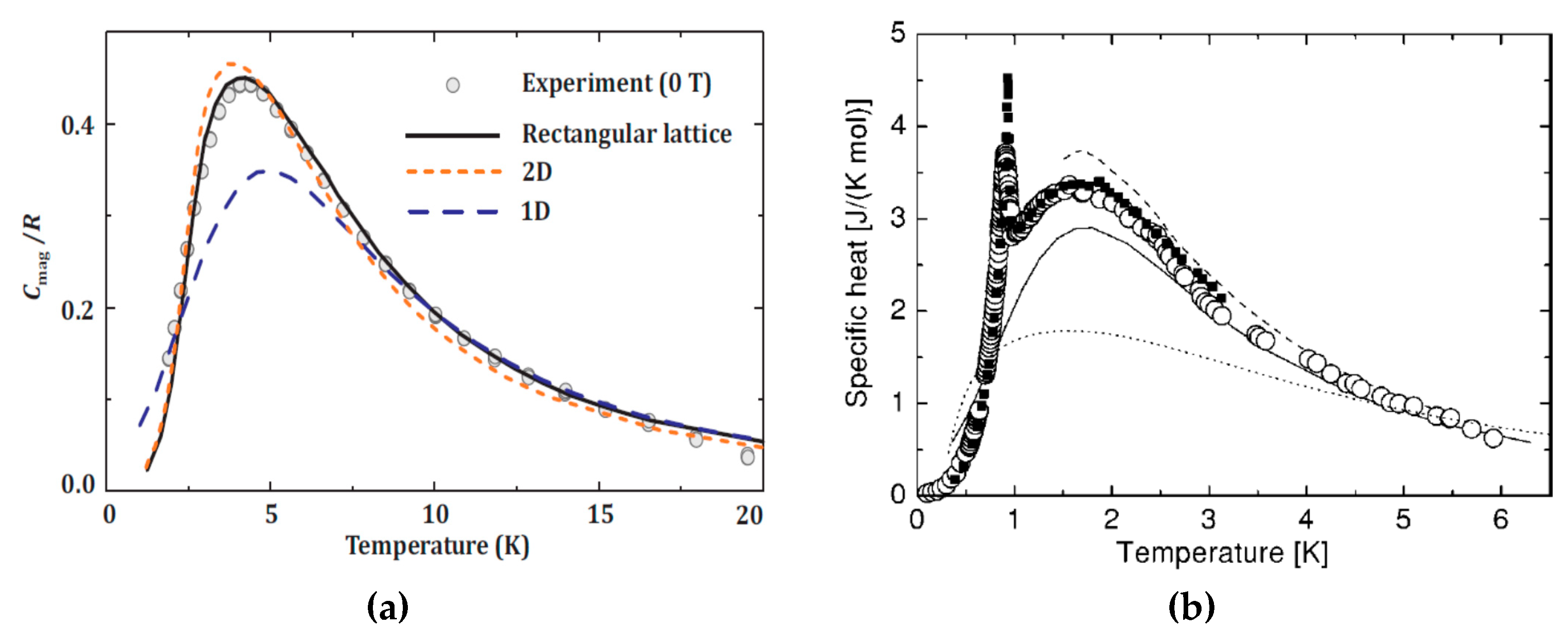
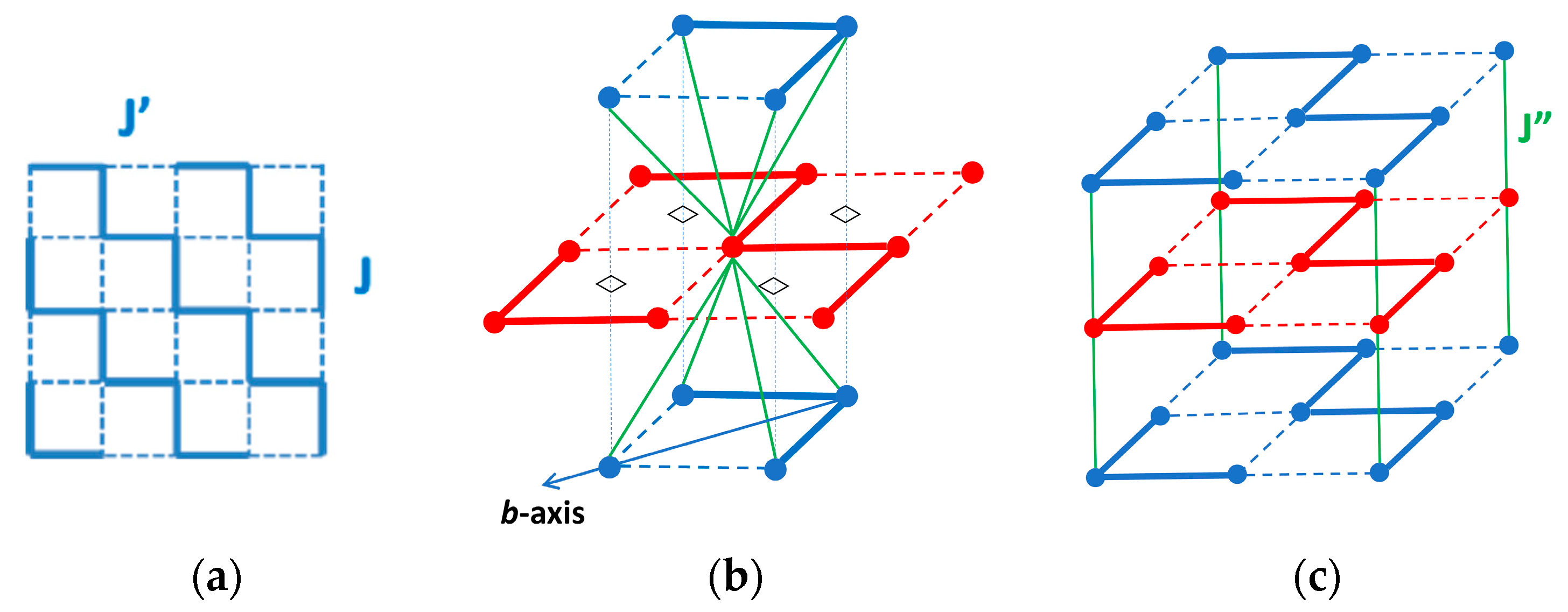
2.3. The Crossover from 2D to 3D
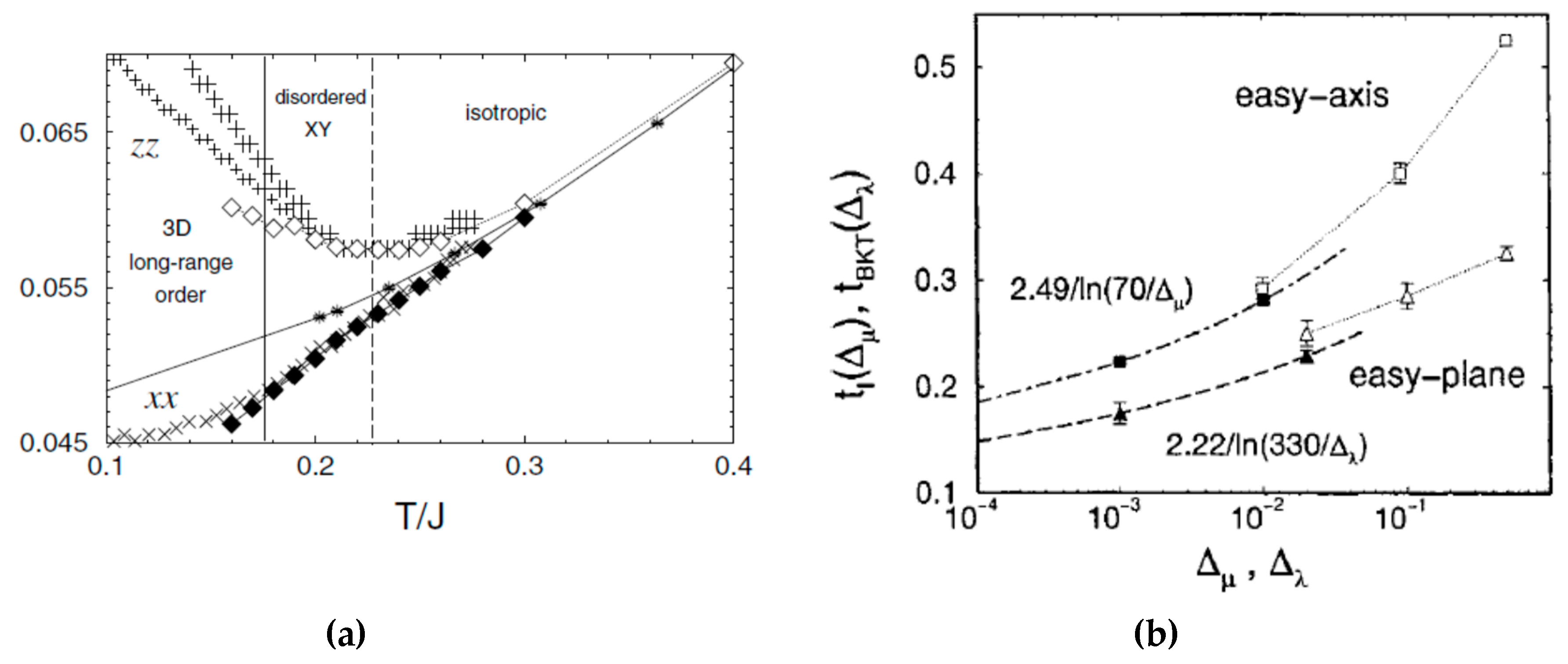
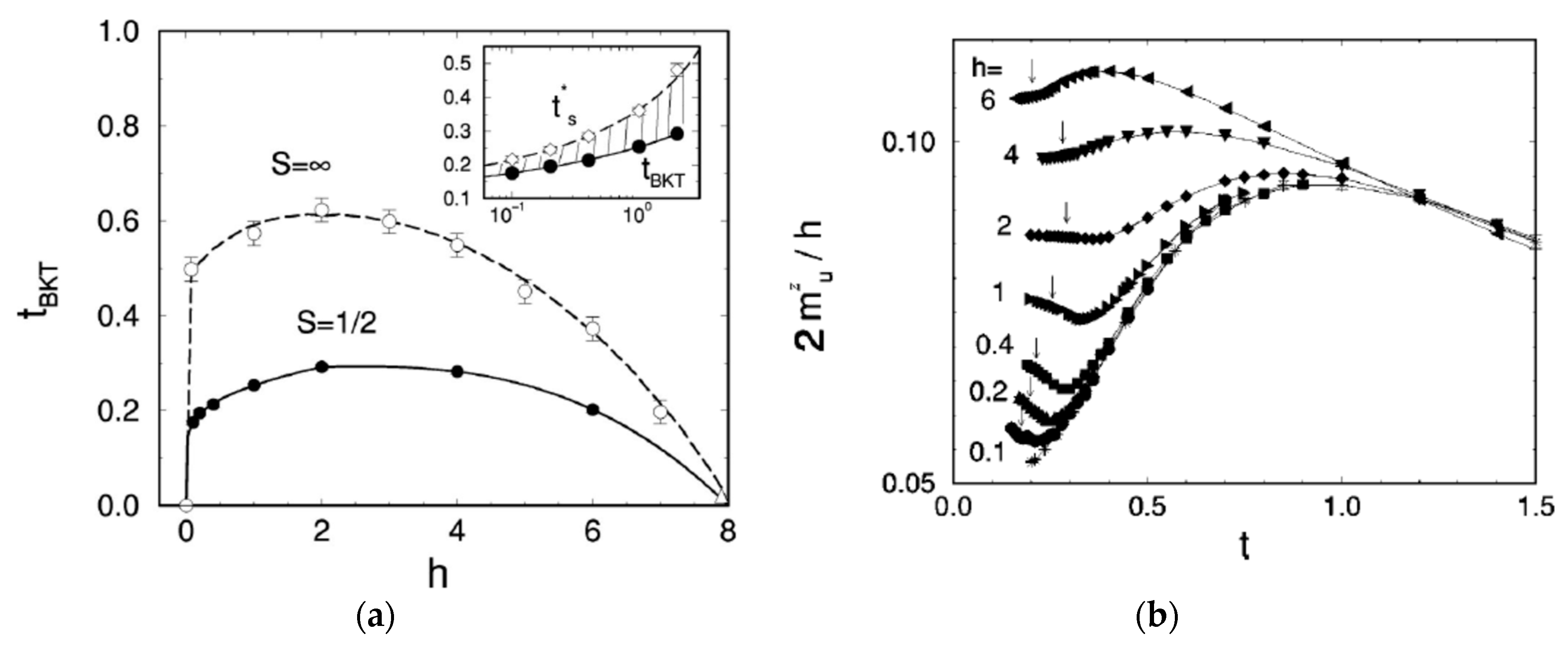
3. The Effect of the Spin Anisotropy and Magnetic Field in the S = 1/2 HAF on the Square Lattice
3.1. B = 0
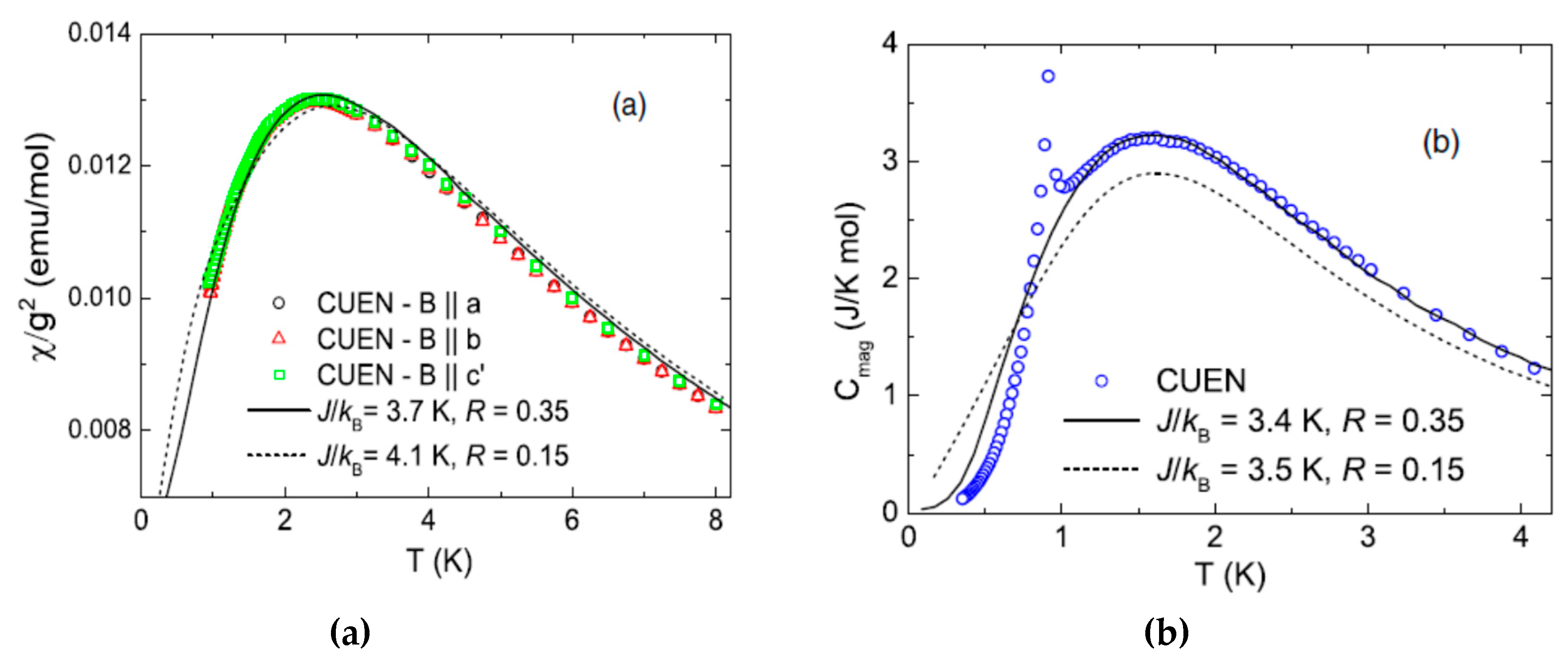
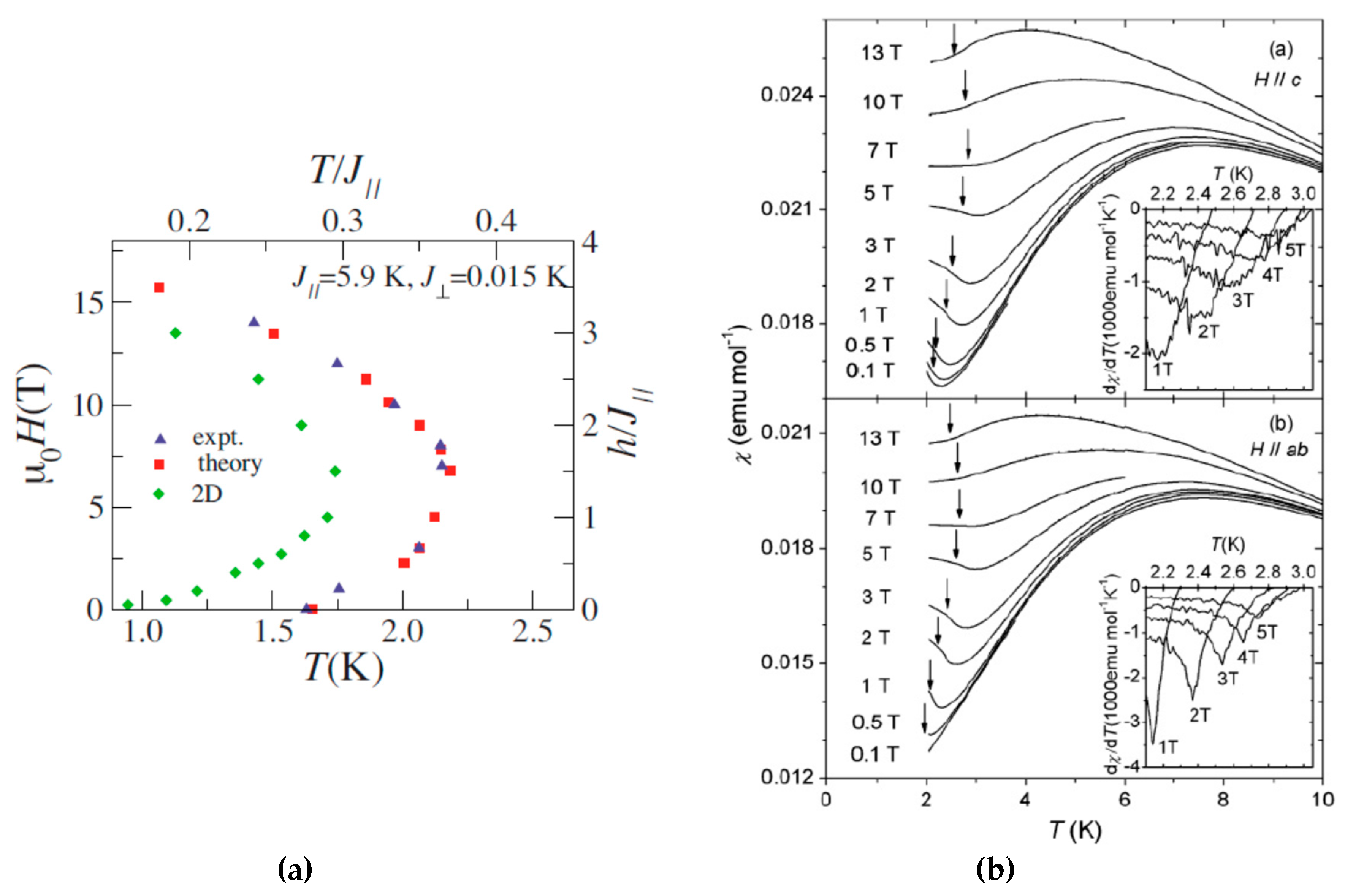
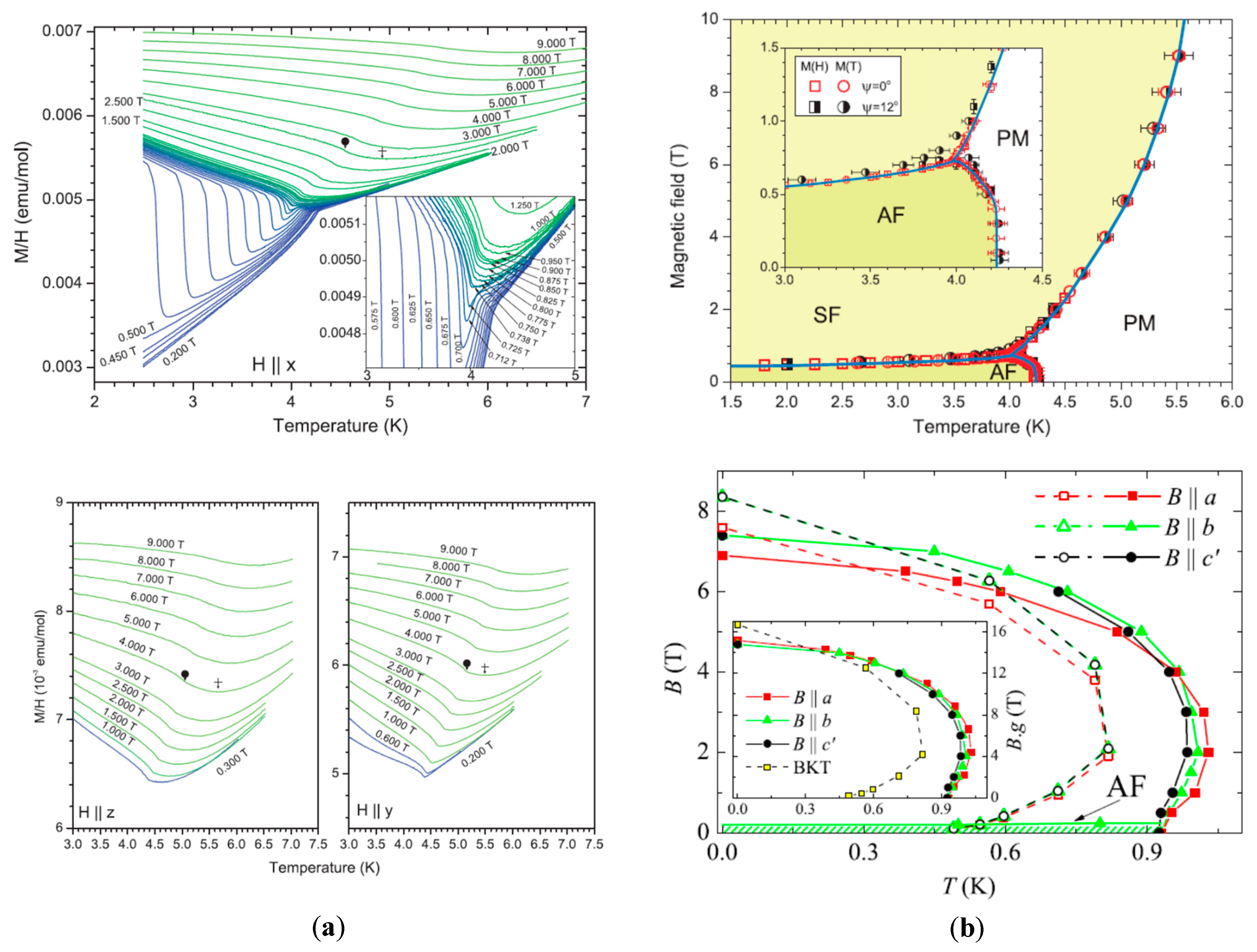
3.2. B ≠ 0
4. Summary and Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Domb, C. On the Theory of Cooperative Phenomena in Crystals. Adv. Phys. 1960, 9, 149–361. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133–1136. [Google Scholar] [CrossRef]
- Stanley, H.E.; Kaplan, T.A. Possibility of a Phase Transition for the Two-Dimensional Heisenberg Model. Phys. Rev. Lett. 1966, 17, 913–915. [Google Scholar] [CrossRef]
- Wegner, F. Spin-Ordering in a Planar Classical Heisenberg Model. Z. Phys. 1967, 206, 465–470. [Google Scholar] [CrossRef]
- Stanley, H.E. Dependence of Critical Properties on Dimensionality of Spins. Phys. Rev. Lett. 1968, 20, 589–592. [Google Scholar] [CrossRef]
- Moore, M.A. Additional Evidence for a Phase Transition in the Plane-Rotator and Classical Heisenberg Models for Two-Dimensional Lattices. Phys. Rev. Lett. 1968, 23, 861–863. [Google Scholar] [CrossRef]
- Berezinskii, V.L. Destruction of Long-range Order in One-dimensional and Two-dimensional Systems having a Continuous Symmetry Group I. Classical Systems. Sov. Phys. JETP 1971, 32, 493–500. [Google Scholar]
- Berezinskii, V.L. Destruction of Long-range Order in One-dimensional and Two-dimensional Systems Possessing a Continuous Symmetry Group. II. Quantum Systems. Sov. Phys. JETP 1971, 34, 610–616. [Google Scholar]
- Kosterlitz, M.J.; Thouless, D.J. Ordering, Metastability and Phase Transitions in Two-Dimensional Systems. J. Phys. C 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Minnhagen, P. The Two-Dimensional Coulomb Gas, Vortex Unbinding, and Superfluid-Superconducting Films. Rev. Modern Phys. 1987, 59, 1001–1066. [Google Scholar] [CrossRef]
- de Jongh, L.J.; Miedema, A.R. Experiments on Simple Magnetic Model Systems. Adv. Phys. 1974, 23, 1–260. [Google Scholar] [CrossRef]
- Müller, G.; Thomas, H.; Beck, H.; Bonner, J.C. Quantum Spin Dynamics of the Antiferromagnetic Linear Chain in Zero and Nonzero Magnetic Field. Phys. Rev. B 1981, 24, 1429–1467. [Google Scholar] [CrossRef]
- Mikeska, H.J. Solitons in a One-Dimensional Magnet with an Easy Plane. J. Phys. C 1978, 11, L29–L32. [Google Scholar] [CrossRef]
- Mikeska, H.J.; Steiner, M. Solitary Excitations in One-Dimensional Magnets. Adv. Phys. 1991, 40, 191–356. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Continuum Dynamics of the 1-D Heisenberg Antiferromagnet: Identification with the O(3) Nonlinear Sigma Model. Phys. Lett. A 1983, 93, 464–468. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Nonlinear Field Theory of Large-Spin Heisenberg Antiferromagnets: Semiclassically Quantized Solitons of the One-Dimensional Easy-Axis Néel State. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Renard, J.P.; Verdaguer, M.; Regnault, L.P.; Erkelens, W.A.C.; Rossat-Mignod, J.; Stirling, W.G. Presumption for a Quantum Energy Gap in the Quasi-One-Dimensional S = 1 Heisenberg Antiferromagnet Ni(C2H8N2)2NO2(ClO4). Europhys. Lett. 1987, 3, 945–951. [Google Scholar] [CrossRef]
- Ma, S.; Broholm, C.; Reich, D.H.; Sternlieb, B.J.; Erwin, R.W. Dominance of Long-Lived Excitations in the Antiferromagnetic Spin-1 Chain NENP. Phys. Rev. Lett. 1992, 69, 3571–3574. [Google Scholar] [CrossRef]
- Dagotto, E. Correlated Electrons in High-Temperature Superconductors. Rev. Mod. Phys. 1994, 66, 763–840. [Google Scholar] [CrossRef]
- Huse, D.A.; Elser, V. Simple Variational Wave Functions for Two-Dimensional Heisenberg Spin-½ Antiferromagnets. Phys. Rev. Lett. 1988, 60, 2531–2534. [Google Scholar] [CrossRef] [PubMed]
- Shastry, B.S.; Sutherland, B. Exact Ground-State of a Quantum-Mechanical Antiferromagnet. Physica B & C 1981, 108, 1069–1070. [Google Scholar] [CrossRef]
- Bernhard, B.H.; Canals, B.; Lacroix, C. Green’s Function Approach to the Magnetic Properties of the Kagomé Antiferromagnet. Phys. Rev. B 2002, 66, 104424. [Google Scholar] [CrossRef]
- Savary, L.; Balents, L. Quantum Spin Liquids: A Review. Rep. Prog. Phys. 2017, 80, 016502. [Google Scholar] [CrossRef] [PubMed]
- Scholwöck, U.; Richter, J.; Farnel, D.J.J.; Bishop, R.F. Quantum Magnetism, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-540-40066-0. [Google Scholar]
- Blundel, S.J.; Pratt, F.L. Organic and Molecular Magnets. J. Phys. Condens. Matter 2004, 16, R771–R828. [Google Scholar] [CrossRef]
- Meier, F.; Levy, J.; Loss, D. Quantum Computing with Spin Cluster Qubits. Phys. Rev. Lett. 2003, 90, 047901. [Google Scholar] [CrossRef]
- Jenkins, M.D.; Duan, Y.; Diosdado, B.; García-Ripoll, J.J.; Gaita-Ariño, A.; Giménez-Saiz, C.; Alonso, P.J.; Coronado, E.; Luis, F. Coherent Manipulation of Three-Qubit States in a Molecular Single-Ion Magnet. Phys. Rev. B 2017, 95, 064423. [Google Scholar] [CrossRef]
- Gaudenzi, R.; Burzurí, E.; Maegawa, S.; van der Zant, H.S.J.; Luis, F. Quantum Landauer Erasure with a Molecular Nanomagnet. Nat. Phys. 2018, 14, 565–568. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wei, H.L.; Zhang, Z.Q.; Zhang, L. Anisotropic Magnetocaloric Effect in Nanostructured Magnetic Clusters. Phys. Rev. Lett. 2001, 87, 157203. [Google Scholar] [CrossRef]
- Zhitomirski, M.E. Enhanced Magnetocaloric effect in Frustrated Magnets. Phys. Rev. B 2003, 67, 104421. [Google Scholar] [CrossRef]
- Trippe, C.; Honecker, A.; Klümper, A.; Ohanyan, V. Exact Calculation of the Magnetocaloric Effect in the spin-1/2 XXZ Chain. Phys. Rev. B 2010, 81, 054402. [Google Scholar] [CrossRef]
- Thomas, L.; Lionti, F.; Ballou, R.; Gatteschi, D.; Sessoli, R.; Barbara, B. Macroscopic Quantum Tunnelling of Magnetization in a Single Crystal of Nanomagnets. Nature 1996, 383, 145–147. [Google Scholar] [CrossRef]
- Radu, T.; Wilhelm, H.; Yushankhai, V.; Kovrizhin, D.; Coldea, R.; Tylczynski, Z.; Lühmann, T.; Steglich, F. Bose-Einstein Condensation of Magnons in Cs2CuCl4. Phys. Rev. Lett. 2005, 95, 127202. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H.; Dorner, U.; Zoller, P. Dynamics of a Quantum Phase Transition. Phys. Rev. Lett. 2005, 95, 105701. [Google Scholar] [CrossRef] [PubMed]
- Blanc, N.; Trinh, J.; Dong, L.; Bai, X.; Aczel, A.A.; Mourigal, M.; Balents, L.; Siegrist, T.; Ramirez, A.P. Quantum Criticality among Entangled Spin Chains. Nat. Phys. 2018, 14, 273–276. [Google Scholar] [CrossRef]
- Kasahara, Y.; Sugii, K.; Ohnishi, T.; Shimozawa, M.; Yamashita, M.; Kurita, N.; Tanaka, H.; Nasu, J.; Motome, Y.; Shibauchi, T.; et al. Unusual Thermal Hall Effect in a Kitaev Spin Liquid Candidate α-RuCl3. Phys. Rev. Lett. 2018, 120, 217205. [Google Scholar] [CrossRef]
- Affleck, I.; Lieb, E. A Proof of Part of Haldane’s Conjecture on Spin Chains. Lett. Math. Phys. 1986, 12, 57–69. [Google Scholar] [CrossRef]
- Affleck, I.; Kennedy, T.; Lieb, E.H.; Tasaki, H. Rigorous Results on Valence-Bond Ground States in Antiferromagnets. Phys. Rev. Lett. 1987, 59, 799–802. [Google Scholar] [CrossRef]
- Giamarchi, T. Quantum Physics in One Dimension, 1st ed.; Clarendon Press: Oxford, UK, 2003; ISBN 9780198525004. [Google Scholar]
- Tennant, D.H.; Cowley, R.A.; Nagler, S.E.; Tsvelik, A.M. Measurement of the Spin-Excitation Continuum in One-Dimensional KCuF3 using Neutron Scattering. Phys. Rev. B 1995, 52, 13368–13380. [Google Scholar] [CrossRef]
- Coldea, R.; Tennant, D.A.; Cowley, R.A.; McMorrow, D.F.; Dorner, B.; Tylczynski, Z. Quasi-1D S = 1/2 Antiferromagnet Cs2CuCl4 in a Magnetic Field. Phys. Rev. Lett. 1997, 79, 151–154. [Google Scholar] [CrossRef]
- Stone, M.B.; Reich, D.H.; Broholm, C.; Lefmann, K.; Rischel, C.; Landee, C.P.; Turnbull, M.M. Extended Quantum Critical Phase in a Magnetized Spin-1/2 Antiferromagnetic Chain. Phys. Rev. Lett. 2003, 91, 037205. [Google Scholar] [CrossRef] [PubMed]
- Bonner, J.C.; Fisher, M.E. Linear Magnetic Chains with Anisotropic Coupling. Phys. Rev. 1964, 135, A640–A658. [Google Scholar] [CrossRef]
- Blöte, H.W.J. The Specific Heat of Magnetic Linear Chains. Physica B & C 1975, 79, 427–466. [Google Scholar] [CrossRef]
- Klümper, A.; Johnston, D.C. Thermodynamics of the Spin-1/2 Antiferromagnetic Uniform Heisenberg Chain. Phys. Rev. Lett. 2000, 84, 4701–4704. [Google Scholar] [CrossRef] [PubMed]
- Johnston, D.C.; Kremer, R.K.; Troyer, M.; Wang, X.; Klümper, A.; Bud’ko, S.L.; Panchula, A.F.; Canfield, P.C. Thermodynamics of Spin S = 1/2 Antiferromagnetic Uniform and Alternating-Exchange Heisenberg Chains. Phys. Rev. B 2000, 61, 9558–9606. [Google Scholar] [CrossRef]
- Tarasenko, R.; Čižmár, E.; Orendáčová, A.; Kuchár, J.; Černák, J.; Prokleška, J.; Sechovský, V.; Orendáč, M. S = 1/2 Heisenberg Antiferromagnetic Spin Chain [Cu(dmbpy)(H2O)2SO4] (dmbpy = 4,4′-dimethyl-2,2′-bipyridine): Synthesis, Crystal Structure and Enhanced Magnetocaloric Effect. Solid State Sci. 2014, 28, 14–19. [Google Scholar] [CrossRef]
- Piazza, B.D.; Mourigal, M.; Christensen, N.B.; Nilsen, G.J.; Tregenna-Piggott, P.; Perring, T.G.; Enderle, M.; McMorrow, D.F.; Ivanov, D.A.; Ronnow, H.M. Fractional Excitations in the Square-Lattice Quantum Antiferromagnet. Nat. Phys. 2015, 11, 62–68. [Google Scholar] [CrossRef]
- Chakravarty, S.; Halperin, B.I.; Nelson, D.R. Low-Temperature Behavior of Two-Dimensional Quantum Antiferromagnets. Phys. Rev. Lett. 1988, 60, 1057–1060. [Google Scholar] [CrossRef]
- Chakravarty, S.; Halperin, B.I.; Nelson, D.R. Two-Dimensional Quantum Heisenberg Antiferromagnet at Low Temperatures. Phys. Rev. B 1989, 39, 2344–2371. [Google Scholar] [CrossRef]
- Makivić, M.S.; Ding, H.-Q. Two-Dimensional Spin-1/2 Heisenberg Antiferromagnet: A Quantum Monte Carlo Study. Phys. Rev. B 1991, 43, 3562–3574. [Google Scholar] [CrossRef]
- Cuccoli, A.; Tognetti, V.; Vaia, R.; Verrucchi, P. Two-Dimensional Quantum Heisenberg Antiferromagnet: Effective-Hamiltonian Approach to the Thermodynamics. Phys. Rev. B 1997, 56, 14456–14468. [Google Scholar] [CrossRef]
- Kim, J.-K.; Troyer, M. Low Temperature Behavior and Crossovers of the Square Lattice Quantum Heisenberg Antiferromagnet. Phys. Rev. Lett. 1998, 80, 2705–2708. [Google Scholar] [CrossRef]
- Orendáč, M.; Orendáčová, A.; Černák, J.; Feher, A. Magnetic Specific Heat Analysis of Cu(C2H8N2)2Ni(CN)4: A Quasi-Two-Dimensional Heisenberg Antiferromagnet. Solid State Commun. 1995, 94, 833–835. [Google Scholar] [CrossRef]
- Hanko, J.; Orendáč, M.; Kuchár, J.; Žák, Z.; Černák, J.; Orendáčová, A.; Feher, A. Hydrogen Bonds Mediated Magnetism in Cu(bmen)2Pd(CN)4. Solid State Commun. 2007, 142, 128–131. [Google Scholar] [CrossRef]
- Turnbull, M.M.; Albrecht, A.S.; Jameson, G.B.; Landee, C.P. High-Field Magnetization Studies of Two-Dimensional Copper Antiferromagnets. Mol. Cryst. Liq. Cryst. 1999, 335, 245–252. [Google Scholar] [CrossRef]
- Xiao, F.; Woodward, F.M.; Landee, C.P.; Turnbull, M.M.; Mielke, C.; Harrison, N.; Lancaster, T.; Blundell, S.J.; Baker, P.J.; Babkevich, P.; et al. Two-Dimensional XY Behavior Observed in Quasi-Two-Dimensional Quantum Heisenberg Antiferromagnets. Phys. Rev. B 2009, 79, 134412. [Google Scholar] [CrossRef]
- Clarke, S.J.; Harrison, A.; Mason, T.E.; Visser, D. Characterisation of Spin-Waves in Copper(II) Deuteroformate Tetradeuterate: A Square S = 1/2 Heisenberg Antiferromagnet. Solid State Commun. 1999, 112, 561–564. [Google Scholar] [CrossRef]
- Zhou, P.; Drumheller, J.E.; Rubenacker, G.V.; Halvorson, K.; Willett, R.D. Novel Low-Dimensional Spin 1/2 Antiferromagnets: Two-Halide Exchange Pathways in A2CuBr4 Salts. J. Appl. Phys. 1991, 69, 5804. [Google Scholar] [CrossRef]
- Woodward, F.M.; Landee, C.P.; Giantsidis, J.; Turnbull, M.M.; Richardson, C. Structure and Magnetic Properties of (5BAP)2CuBr4: Magneto-Structural Correlations of Layered S = 1/2 Heisenberg Antiferromagnets. Inorg. Chim. Acta 2001, 324, 324–330. [Google Scholar] [CrossRef]
- Woodward, F.M.; Albrecht, A.S.; Wynn, C.M.; Landee, C.P.; Turnbull, M.M. Two-Dimensional S = 1/2 Heisenberg Antiferromagnets: Synthesis, Structure, and Magnetic Properties. Phys. Rev. B 2002, 65, 144412. [Google Scholar] [CrossRef]
- Coomer, F.C.; Bondah-Jagalu, V.; Grant, K.J.; Harrison, A.; McIntyre, G.J.; Rønnow, H.M.; Feyerherm, R.; Wand, T.; Meißner, M.; Visser, D.; et al. Neutron Diffraction Studies of Nuclear and Magnetic Structures in the S = 1/2 Square Heisenberg Antiferromagnets (d6-5 CAP)2CuX4 (X = Br and Cl). Phys. Rev. B 2007, 75, 094424. [Google Scholar] [CrossRef]
- Kajňaková, M.; Orendáč, M.; Orendáčová, A.; Vlček, A.; Černák, J.; Kravchyna, O.V.; Anders, A.G.; Bałanda, M.; Park, J.-H.; Feher, A.; et al. Cu(H2O)2(C2H8N2)SO4: A Quasi-Two-Dimensional S = 1/2 Heisenberg Antiferromagnet. Phys. Rev. B 2005, 71, 014435. [Google Scholar] [CrossRef]
- Potočňák, I.; Vavra, M.; Čižmár, E.; Tibenská, K.; Orendáčová, A.; Steinbornc, D.; Wagner, C.; Dušek, M.; Fejfarová, K.; Schmidt, H.; et al. Low-Dimensional Compounds Containing Cyano Groups. XIV. Crystal Structure, Spectroscopic, Thermal and Magnetic Properties of [CuL2][Pt(CN)4] Complexes (L=ethylenediamine or N,N-dimethylethylenediamine). J. Solid State Chem. 2006, 179, 1965–1976. [Google Scholar] [CrossRef]
- Zeleňák, V.; Orendáčová, A.; Císařová, I.; Černák, J.; Kravchyna, O.V.; Park, J.-H.; Orendáč, M.; Anders, A.G.; Feher, A.; Meisel, M.W. Magneto-Structural Correlations in Cu(tn)Cl2 (tn = 1,3-Diaminopropane): Two-Dimensional Spatially Anisotropic Triangular Magnet Formed by Hydrogen Bonds. Inorg. Chem. 2006, 45, 1774–1782. [Google Scholar] [CrossRef] [PubMed]
- Vlček, A.; Orendáč, M.; Orendáčová, A.; Kajňaková, M.; Papageorgiou, T.; Chomič, J.; Černák, J.; Massa, W.; Feher, A. Magneto-Structural Correlation in Cu(NH3)2Ag2(CN)4. Crystal Structure, Magnetic and Thermodynamic Properties of an S = 1/2 Low-Dimensional Heisenberg Antiferromagnet. Solid State Sci. 2007, 9, 116–125. [Google Scholar] [CrossRef]
- Sedláková, L.; Tarasenko, R.; Potočňák, I.; Orendáčová, A.; Kajňaková, M.; Orendáč, M.; Starodub, V.A.; Anders, A.G.; Kravchyna, O.; Feher, A. Magnetic Properties of S = 1/2 Two-Dimensional Quantum Antiferromagnet Cu(D2O)2(C2H6D2N2)SO4. Solid State Commun. 2008, 147, 239–241. [Google Scholar] [CrossRef]
- Orendáč, M.; Čižmár, E.; Orendáčová, A.; Tkáčová, J.; Kuchár, J.; Černák, J. Enhanced Magnetocaloric Effect in Quasi-One-Dimensional S = 1/2 Heisenberg Antiferromagnet [Cu(dmen)2(H2O)]SiF6. J. Alloys Compd. 2014, 586, 34–38. [Google Scholar] [CrossRef]
- Parola, A.; Sorella, S.; Zhong, Q.F. Realization of a Spin Liquid in a Two Dimensional Quantum Antiferromagnet. Phys. Rev. Lett. 1993, 71, 4393–4396. [Google Scholar] [CrossRef]
- Ihle, D.; Schindelin, C.; Weiße, A.; Fehske, H. Magnetic Order-Disorder Transition in the Two-Dimensional Spatially Anisotropic Heisenberg Model at Zero Temperature. Phys. Rev. B 1999, 60, 9240–9243. [Google Scholar] [CrossRef]
- Affleck, I.; Halperin, B. On a Renormalization Group Approach to Dimensional Crossover. J. Phys. A Math. Gen. 1996, 29, 2627–2631. [Google Scholar] [CrossRef]
- Sandvik, A.W. Multichain Mean-Field Theory of Quasi-One-Dimensional Quantum Spin Systems. Phys. Rev. Lett. 1999, 83, 3069–3072. [Google Scholar] [CrossRef]
- Kim, Y.J.; Birgeneau, R.J. Monte Carlo Study of the S = 1/2 and S = 1 Heisenberg Antiferromagnet on a Spatially Anisotropic Square Lattice. Phys. Rev. B 2000, 62, 6378–6384. [Google Scholar] [CrossRef]
- Jiang, F.-J.; Kämpfer, F.; Nyfeler, M. Monte Carlo Determination of the Low-Energy Constants of a Spin-1/2 Heisenberg Model with Spatial Anisotropy. Phys. Rev. B 2009, 80, 033104. [Google Scholar] [CrossRef]
- Keith, B.C.; Landee, C.P.; Valleau, T.; Turnbull, M.M.; Harrison, N. Two-Dimensional Spin-1/2 Rectangular Heisenberg antiferromagnets: Simulation and Experiment. Phys. Rev. B 2011, 84, 104442, Erratum Phys. Rev. B 2011, 84, 229901, doi:10.1103/PhysRevB.84.229901. [Google Scholar] [CrossRef]
- Cliffe, M.J.; Lee, J.; Paddison, J.A.M.; Schott, S.; Mukherjee, P.; Gaultois, M.W.; Manuel, P.; Sirringhaus, H.; Dutton, S.E.; Grey, C.P. Low-Dimensional Quantum Magnetism in Cu(NCS)2: A Molecular Framework Material. Phys. Rev. B 2018, 97, 144421. [Google Scholar] [CrossRef]
- Nath, R.; Padmanabhan, M.; Baby, S.; Thirumurugan, A.; Ehlers, D.; Hemmida, M.; Krug von Nidda, H.-A.; Tsirlin, A.A. Quasi-Two-Dimensional S = 1/2 Magnetism of Cu[C6H2(COO)4][C2H5NH3]2. Phys. Rev. B 2015, 91, 054409. [Google Scholar] [CrossRef]
- Tarasenko, R.; Orendáčová, A.; Čižmár, E.; Maťaš, S.; Orendáč, M.; Potočňák, I.; Siemensmeyer, K.; Zvyagin, S.; Wosnitza, J.; Feher, A. Spin Anisotropy in Cu(en)(H2O)2SO4: A Quasi-Two-Dimensional S = 1/2 Spatially Anisotropic Triangular-Lattice Antiferromagnet. Phys. Rev. B 2013, 87, 174401. [Google Scholar] [CrossRef]
- Sýkora, R.; Legut, D. Magnetic Interactions in a Quasi-One-Dimensional Antiferromagnet Cu(H2O)2(en)SO4. J. Appl. Phys. 2014, 115, 17B305. [Google Scholar] [CrossRef]
- Lederová, L.; Orendáčová, A.; Chovan, J.; Strečka, J.; Verkholyak, T.; Tarasenko, R.; Legut, D.; Sýkora, R.; Čižmár, E.; Tkáč, V.; et al. Realization of a Spin-1/2 Spatially Anisotropic Square Lattice in a Quasi-Two-Dimensional Quantum Antiferromagnet Cu(en)(H2O)2SO4. Phys. Rev. B 2017, 95, 054436. [Google Scholar] [CrossRef]
- Barbero, N.; Shiroka, T.; Landee, C.P.; Pikulski, M.; Ott, H.-R.; Mesot, J. Pressure and Magnetic Field Effects on a Quasi-Two-Dimensional Spin-1/2 Heisenberg Antiferromagnet. Phys. Rev. B 2016, 93, 054425. [Google Scholar] [CrossRef]
- Goddard, P.A.; Singleton, J.; Franke, I.; Möller, J.S.; Lancaster, T.; Steele, A.J.; Topping, C.V.; Blundell, S.J.; Pratt, F.L.; Baines, C.; et al. Control of the Third Dimension in Copper-Based Square-Lattice Antiferromagnets. Phys. Rev. B 2016, 93, 094430. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Tamekuni, Y.; Iwasaki, Y.; Otsuka, R.; Hosokoshi, Y.; Kida, T.; Hagiwara, M. Magnetic Properties of a Quasi-Two-Dimensional S = 1/2 Heisenberg Antiferromagnet with Distorted Square Lattice. Phys. Rev. B 2017, 95, 235135. [Google Scholar] [CrossRef]
- Siurakshina, L.; Ihle, D.; Hayn, R. Theory of Magnetic Order in the Three-Dimensional Spatially Anisotropic Heisenberg Model. Phys. Rev. B 2000, 61, 14601–14606. [Google Scholar] [CrossRef]
- Sengupta, P.; Sandvik, A.W.; Singh, R.R.P. Specific Heat of Quasi-Two-Dimensional Antiferromagnetic Heisenberg Models with Varying Interplanar Couplings. Phys. Rev. B 2003, 68, 094423. [Google Scholar] [CrossRef]
- Yasuda, C.; Todo, S.; Hukushima, K.; Alet, F.; Keller, M.; Troyer, M.; Takayama, H. Néel Temperature of Quasi-Low-Dimensional Heisenberg Antiferromagnets. Phys. Rev. Lett. 2005, 94, 217201. [Google Scholar] [CrossRef] [PubMed]
- Orendáčová, A.; Čižmár, E.; Sedláková, L.; Hanko, J.; Kajňaková, M.; Orendáč, M.; Feher, A.; Xia, J.S.; Yin, L.; Pajerowski, D.M.; et al. Interplay of Frustration and Magnetic Field in the Two-Dimensional Quantum Antiferromagnet Cu(tn)Cl2. Phys. Rev. B 2009, 80, 144418. [Google Scholar] [CrossRef]
- Kohama, Y.; Jaime, M.; Ayala-Valenzuela, O.E.; McDonald, R.D.; Mun, E.D.; Corbey, J.F.; Manson, J.L. Field-Induced XY and Ising Ground States in a Quasi-Two-Dimensional S = 1/2 Heisenberg Antiferromagnet. Phys. Rev. B 2011, 84, 184402. [Google Scholar] [CrossRef]
- Irkhin, V.Y.; Katanin, A.A. Thermodynamics of Isotropic and Anisotropic Layered Magnets: Renormalization-Group Approach and 1/N Expansion. Phys. Rev. B 1998, 57, 379–391. [Google Scholar] [CrossRef]
- Hathaway, B.J.; Billing, D.E. The Electronic Properties and Stereochemistry of Mono-Nuclear Complexes of the Copper(II) Ion. Coord. Chem. Rev. 1970, 5, 143–207. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Povarov, K.Y.; Smirnov, A.I.; Landee, C.P. Switching of Anisotropy and Phase Diagram of the Heisenberg Square-Lattice S = 1/2 Antiferromagnet Cu(pz)2(ClO4)2. Phys. Rev. B 2013, 87, 214402. [Google Scholar] [CrossRef]
- Ihle, D.; Schindelin, C.; Fehske, H. Magnetic Order in the Quasi-Two-Dimensional Easy-Plane XXZ Model. Phys. Rev. B 2001, 64, 054419. [Google Scholar] [CrossRef]
- Cuccoli, A.; Roscilde, T.; Vaia, R.; Verrucchi, P. Detection of XY Behavior in Weakly Anisotropic Quantum Antiferromagnets on the Square Lattice. Phys. Rev. Lett. 2003, 90, 167205. [Google Scholar] [CrossRef] [PubMed]
- Cuccoli, A.; Roscilde, T.; Tognetti, V.; Vaia, R.; Verrucchi, P. Quantum Monte Carlo Study of S = 1/2 Weakly Anisotropic Antiferromagnets on the Square Lattice. Phys. Rev. B 2003, 67, 104414. [Google Scholar] [CrossRef]
- Pereira, A.R.; Pires, A.S.T. Dynamics of Vortices in a Two-Dimensional Easy-Plane Antiferromagnet. Phys. Rev. B 1995, 51, 996–1002. [Google Scholar] [CrossRef]
- Cuccoli, A.; Gori, G.; Vaia, R.; Verrucchi, P. Phase Diagram of the Two-Dimensional Quantum Antiferromagnet in a Magnetic Field. J. Appl. Phys. 2006, 99, 08H503. [Google Scholar] [CrossRef]
- de Groot, H.J.M.; de Jongh, L.J. Phase Diagrams of Weakly Anisotropic Heisenberg Antiferromagnets, Nonlinear Excitations (Solitons) and Random-Field Effects. Physica B & C 1986, 141, 1–36. [Google Scholar] [CrossRef]
- Landau, D.P.; Binder, K. Phase Diagrams and Critical Behavior of a Two-Dimensional Anisotropic Heisenberg Antiferromagnet. Phys. Rev. B 1981, 24, 1391–1403. [Google Scholar] [CrossRef]
- Holtschneider, M.; Selke, W.; Leidl, R. Two-Dimensional Anisotropic Heisenberg Antiferromagnet in a Magnetic Field. Phys. Rev. B 2005, 72, 064443. [Google Scholar] [CrossRef]
- Zhou, C.; Landau, D.P.; Schulthess, T.C. Hidden Zero-Temperature Bicritical Point in the Two-Dimensional Anisotropic Heisenberg Model: Monte Carlo Simulations and Proper Finite-Size Scaling. Phys. Rev. B 2006, 74, 064407. [Google Scholar] [CrossRef]
- Pelissetto, A.; Vicari, E. Multicritical Behavior of Two-Dimensional Anisotropic Antiferromagnets in a Magnetic Field. Phys. Rev. B 2007, 76, 024436. [Google Scholar] [CrossRef]
- Pires, A.S.T. Kosterlitz-Thouless Transition in a Two-Dimensional Isotropic Antiferromagnet in a Uniform Field. Phys. Rev. B 1994, 50, 9592–9594. [Google Scholar] [CrossRef]
- Cuccoli, A.; Roscilde, T.; Vaia, R.; Verrucchi, P. Field-Induced XY Behavior in the S = 1/2 Antiferromagnet on the Square Lattice. Phys. Rev. B 2003, 68, 060402. [Google Scholar] [CrossRef]
- Cuccoli, A.; Roscilde, T.; Vaia, R.; Verrucchi, P. XY Behaviour of the 2D Antiferromagnet in a Field. J. Magn. Magn. Mater. 2004, 884, 272–276. [Google Scholar] [CrossRef]
- Sengupta, P.; Batista, C.D.; McDonald, R.D.; Cox, S.; Singleton, J.; Huang, L.; Papageorgiou, T.P.; Ignatchik, O.; Herrmannsdörfer, T.; Manson, J.L.; et al. Nonmonotonic Field Dependence of the Néel Temperature in the Quasi-Two-Dimensional Magnet [Cu(HF2)(pyz)2]BF4. Phys. Rev. B 2009, 79, 060409. [Google Scholar] [CrossRef]
- Tsyrulin, N.; Xiao, F.; Schneidewind, A.; Link, P.; Rønnow, H.M.; Gavilano, J.; Landee, C.P.; Turnbull, M.M.; Kenzelmann, M. Two-Dimensional Square-Lattice S = 1/2 Antiferromagnet Cu(pz)2(ClO4)2. Phys. Rev. B 2010, 81, 134409. [Google Scholar] [CrossRef]
- Fortune, N.A.; Hannahs, S.T.; Landee, C.P.; Turnbull, M.M.; Xiao, F. Magnetic-Field-Induced Heisenberg to XY Crossover in a Quasi-2D Quantum Antiferromagnet. J. Phys. Conf. Ser. 2014, 568, 042004. [Google Scholar] [CrossRef]
- Glazkov, V.N.; Krasnikova, Y.; Rodygina, I.; Tarasenko, R.; Orendáčová, A. Low-Temperature Antiferromagnetic Resonance of Quasi-2D Magnet Cu(en)(H2O)2SO4. In Proceedings of the International Symposium Spin Waves 2018, St. Petersburg, Russia, 3–8 June 2018. [Google Scholar]
- Kubo, Y.; Kurihara, S. Tunable Rotons in Square-Lattice Antiferromagnets under Strong Magnetic Fields. Phys. Rev. B 2014, 90, 014421. [Google Scholar] [CrossRef]
- Powalski, M.; Uhrig, G.S.; Schmidt, K.P. Roton Minimum as a Fingerprint of Magnon-Higgs Scattering in Ordered Quantum Antiferromagnets. Phys. Rev. Lett. 2015, 115, 207202. [Google Scholar] [CrossRef]
- Orendáčová, A.; Kajňaková, M.; Černák, J.; Park, J.-H.; Čižmár, E.; Orendáč, M.; Vlček, A.; Kravchyna, O.V.; Anders, A.G.; Feher, A.; et al. Hydrogen Bond Mediated Magnetism in [CuII(en)2(H2O)][CuII(en)2Ni2CuI2(CN)10]∙2H2O. Chem. Phys. 2005, 309, 115–125. [Google Scholar] [CrossRef]
- Brown, S.; Cao, J.; Musfeldt, J.L.; Conner, M.M.; McConnel, A.C.; Southerland, H.I.; Manson, J.L.; Schlueter, J.A.; Phillips, M.D.; Turnbull, M.M.; et al. Hydrogen Bonding and Multiphonon Structure in Copper Pyrazine Coordination Polymers. Inorg. Chem. 2007, 46, 8577–8583. [Google Scholar] [CrossRef] [PubMed]
- Legut, D.; Sýkora, R.; Wdowik, U.D.; Orendáčová, A. Mechanical Properties of the Quasi-One-Dimensional Antiferromagnet Cu(en)(H2O)2SO4. J. Nanosci. Nanotechnol. 2018, 18, 3016–3018. [Google Scholar] [CrossRef] [PubMed]
- Perren, G.; Möller, J.S.; Hüvonen, D.; Podlesnyak, A.A.; Zheludev, A. Spin Dynamics in Pressure-Induced Magnetically Ordered Phases in (C4H12N2)Cu2Cl6. Phys. Rev. B 2015, 92, 054413. [Google Scholar] [CrossRef]
- O’Neal, K.R.; Zhou, J.; Cherian, J.G.; Turnbull, M.M.; Landee, C.P.; Jena, P.; Liu, Z.; Musfeldt, J.L. Pressure-Induced Structural Transition in Copper Pyrazine Dinitrate and Implications for Quantum Magnetism. Phys. Rev. B 2016, 93, 104409. [Google Scholar] [CrossRef]
- Cini, A.; Mannini, M.; Totti, F.; Fittipaldi, M.; Spina, G.; Chumakov, A.; Rüffer, R.; Cornia, A.; Sessoli, R. Mössbauer Spectroscopy of a Monolayer of Single Molecule Magnets. Nat. Commun. 2018, 9, 480. [Google Scholar] [CrossRef]
- Campbell, V.E.; Tonelli, M.; Cimatti, I.; Moussy, J.-B.; Tortech, L.; Dappe, Y.J.; Rivie, E.; Guillot, R.; Delprat, S.; Mattana, R.; et al. Engineering the Magnetic Coupling and Anisotropy at the Molecule–Magnetic Surface Interface in Molecular Spintronic Devices. Nat. Commun. 2016, 7, 13646. [Google Scholar] [CrossRef]
- Laskowska, M.; Kityk, I.; Dulski, M.; Jędryka, J.; Wojciechowski, A.; Jelonkiewicz, J.; Wojtyniak, M.; Laskowski, Ł. Functionalized Mesoporous Silica Thin Films as a Tunable Nonlinear Optical Material. Nanoscale 2017, 9, 12110–12123. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orendáčová, A.; Tarasenko, R.; Tkáč, V.; Čižmár, E.; Orendáč, M.; Feher, A. Interplay of Spin and Spatial Anisotropy in Low-Dimensional Quantum Magnets with Spin 1/2. Crystals 2019, 9, 6. https://doi.org/10.3390/cryst9010006
Orendáčová A, Tarasenko R, Tkáč V, Čižmár E, Orendáč M, Feher A. Interplay of Spin and Spatial Anisotropy in Low-Dimensional Quantum Magnets with Spin 1/2. Crystals. 2019; 9(1):6. https://doi.org/10.3390/cryst9010006
Chicago/Turabian StyleOrendáčová, Alžbeta, Róbert Tarasenko, Vladimír Tkáč, Erik Čižmár, Martin Orendáč, and Alexander Feher. 2019. "Interplay of Spin and Spatial Anisotropy in Low-Dimensional Quantum Magnets with Spin 1/2" Crystals 9, no. 1: 6. https://doi.org/10.3390/cryst9010006
APA StyleOrendáčová, A., Tarasenko, R., Tkáč, V., Čižmár, E., Orendáč, M., & Feher, A. (2019). Interplay of Spin and Spatial Anisotropy in Low-Dimensional Quantum Magnets with Spin 1/2. Crystals, 9(1), 6. https://doi.org/10.3390/cryst9010006




