The Crystal Structure of Defect KBB’O₆ Pyrochlores (B,B’: Nb,W,Sb,Te) Revisited from Neutron Diffraction Data

Abstract

Three defect pyrochlores KNbWO₆·xH₂O, KNbTeO₆ and KSbWO₆ were synthesized by solid state reaction at 750 °C, from stoichiometric mixtures of K₂C₂O₄, Sb₂O₃, Nb₂O₅, WO₃ and 20% excess TeO₂. A neutron powder diffraction (NPD) data analysis allowed unveiling some structural features. They are all defined in the cubic $Fd\overline{3}m$ space group symmetry, with α = 10.5068(1) Å, 10.2466(1) Å and 10.2377(1) Å, respectively. Difference Fourier synthesis for KNbWO₆·xH₂O clearly showed the presence of crystallization water, with extra O’ oxygen and H⁺ atoms that were located from NPD data. These O’ oxygen atoms are placed at 32e Wyckoff sites, conforming a K₂O’ sublattice interpenetrated with the covalent framework constituted by (Nb,W)O₆ octahedra. The H⁺ ions coordinate the O’ atoms at partially occupied 96g Wyckoff sites while K⁺ ions shift also along 32e sites, but closer to the 16c special site (0,0,0). By contrast, extra H₂O molecules are absent in the other two pyrochlores: in KNbTeO₆ and KSbWO₆ K⁺ ions are shifted along 32e (x,x,x) sites further away from the origin than for the previous material, and the higher covalency of the octahedral network determines more compact structures, with shorter B–O distances and narrower B–O–B angles in the proposed AB₂O₆ defect pyrochlore structure.

1. Introduction

Pyrochlore oxides, both natural and synthetic ceramics, have been extensively studied over the years because of their properties of technological interest, associated with their appealing electrical, dielectric, magnetic, optical, or catalytic properties [1], what makes them interesting candidates for catalysts and photocatalysts [2,3], promising solid fuel cell electrodes [4,5], superconductors [6], and nuclear waste treatment materials [7], among others. These materials are mostly cubic, defined in the $Fd\overline{3}m$ (No 227) space group, Z = 8. They have a general crystallographic formula A₂B₂O₆O′; B atoms are normally transition or p-block metals, whereas A are more voluminous alkali, alkali-earth or rare-earth elements. The crystal structure consists of a covalent B₂O₆ network of BO₆ corner-sharing octahedra with an approximate B–O–B angle of 130°, and the A₂O′ sublattice forms an interpenetrating network that does not interact much with the former. It is also well known that A₂B₂O₆ or even AB₂O₆ stoichiometries are also stable. They are called defect pyrochlores due to the partial absence of A cations and O’ oxygen atoms [1].

In an early work, we prepared and characterized an oxide with pyrochlore structure and composition KSbTeO₆ [8]. Among its properties, the one that caught our attention is its ability to enact K-ion diffusion, due to its open framework that contains three-dimensional interconnected channels. An appealing derivative of this material is the (H₃O)SbTeO₆ defect pyrochlore, prepared by ion exchange from the former oxide in sulfuric acid at 453 K for 12 h [9]. This hydronium-containing material is appealing since a proton conductivity comparable to that of Nafion^© was described above 160 °C [10]. These results prompted us for the search of alternative defect pyrochlores that could offer similar A-atom ion diffusion, involving subsequent acidic and/or catalytic properties. Instead of Sb^V and Te^VI we successfully introduced pentavalent niobium or hexavalent tungsten, in materials with nominal stoichiometry KSbWO₆, KNbTeO₆, or KNbWO₆ following a similar synthesis procedure.

Pioneering reports on the mentioned pyrochlores have been published: Antimony tungstates were obtained by solid state reaction and hydrothermal reactions in acidic media [11,12], while niobium tungstates and tellurates were also obtained by solid state reaction [13,14,15,16]. Within the preliminary structural studies carried out on these materials, XRD patterns were analyzed and Rietveld refinements were performed in order to determine the elements positions, cell volume, isotropic thermal parameters and, in some cases, main angles and distances [7,11]. In this work we performed a more exhaustive structural analysis from neutron powder diffraction data, accessing to more precise positions and anisotropic displacement factors for oxygen and potassium ions. Moreover, Fourier syntheses unveiled a more complex formula for the defect pyrochlore KNbWO₆·1.17(6) H₂O, similar to that previously reported for KNbWO₆·0.69D₂O [17].

2. Experimental Section

Samples with nominal stoichiometry KNbWO₆ (hereafter named KNbW), KNbTeO₆ (KNbTe) and KSbWO₆ (KSbW) were prepared by solid-state reaction between monohydrated potassium oxalate (K₂C₂O₄·H₂O, Carlo Erba, Milano, Italy) and Sb₂O₃ (Alfa Aesar, Karlsruhe, Germany) Nb₂O₅ (Strem, Newburgport, USA), WO₃ (Merck, Darmstadt, Germany) and TeO₂ (Alfa Aesar, Karlsruhe, Germany) oxides as pertinent. The molar ratios were set to 1:1:2 for the tungsten materials, while a 1:1:2.4 ratio was employed for KNbTe, providing an excess of TeO₂ to compensate for volatilization losses. Starting mixtures were thoroughly ground and calcined at 823 and 1023 K for 12 h at each temperature, with intermediate grindings that ensured total reaction, achieving homogeneous and fine white, light-yellow and light-brown powders, respectively.

The initial products characterization was carried out by XRD with a Bruker-AXS D8 Advance diffractometer (40 kV, 30 mA) (Bruker-AXS, Karlsruhe, Germany) controlled by the DIFFRACT^PLUS software, in Bragg–Brentano reflection geometry, with Cu K_α radiation (λ = 1.5418 Å). To remove Cu K_β radiation a nickel filter was used. NPD experiments were carried out in the D2B high-resolution powder diffractometer (λ = 1.59468(1) Å) at the Institut Laue-Langevin, in Grenoble, France. About 2 to 3 g of each sample were contained in a vanadium can. The full diffraction patterns were collected in 2 h of measurement time.

The crystal structures were refined by the Rietveld method [18] with the software FULLPROF (Grenoble, France, version Nov. 2016) [19]. The coherent scattering lengths of K, Sb, Nb, Te, W, O and H were 3.67, 5.57, 7.054, 5.80, 4.86, 5.803 and −3.739 fm, respectively. For generating the line shape of the diffraction peaks a pseudo-Voigt function was chosen. In the final Rietveld fit the following parameters were refined: scale factor, background coefficients, zero-point error, pseudo-Voigt profile function parameters corrected for asymmetry, atomic coordinates, anisotropic atomic displacement parameters for all atoms, and the occupancy factors of certain atoms.

Thermogravimetric analysis (TGA) curve was obtained using a Stanton STA 781 instrument, (London, UK). The temperature was measured with an accuracy of ±1 K. Analysis was carried out in an air flow at a heating rate of 10 K·min⁻¹. About 64.5 mg of powder sample was used.

3. Results and Discussion

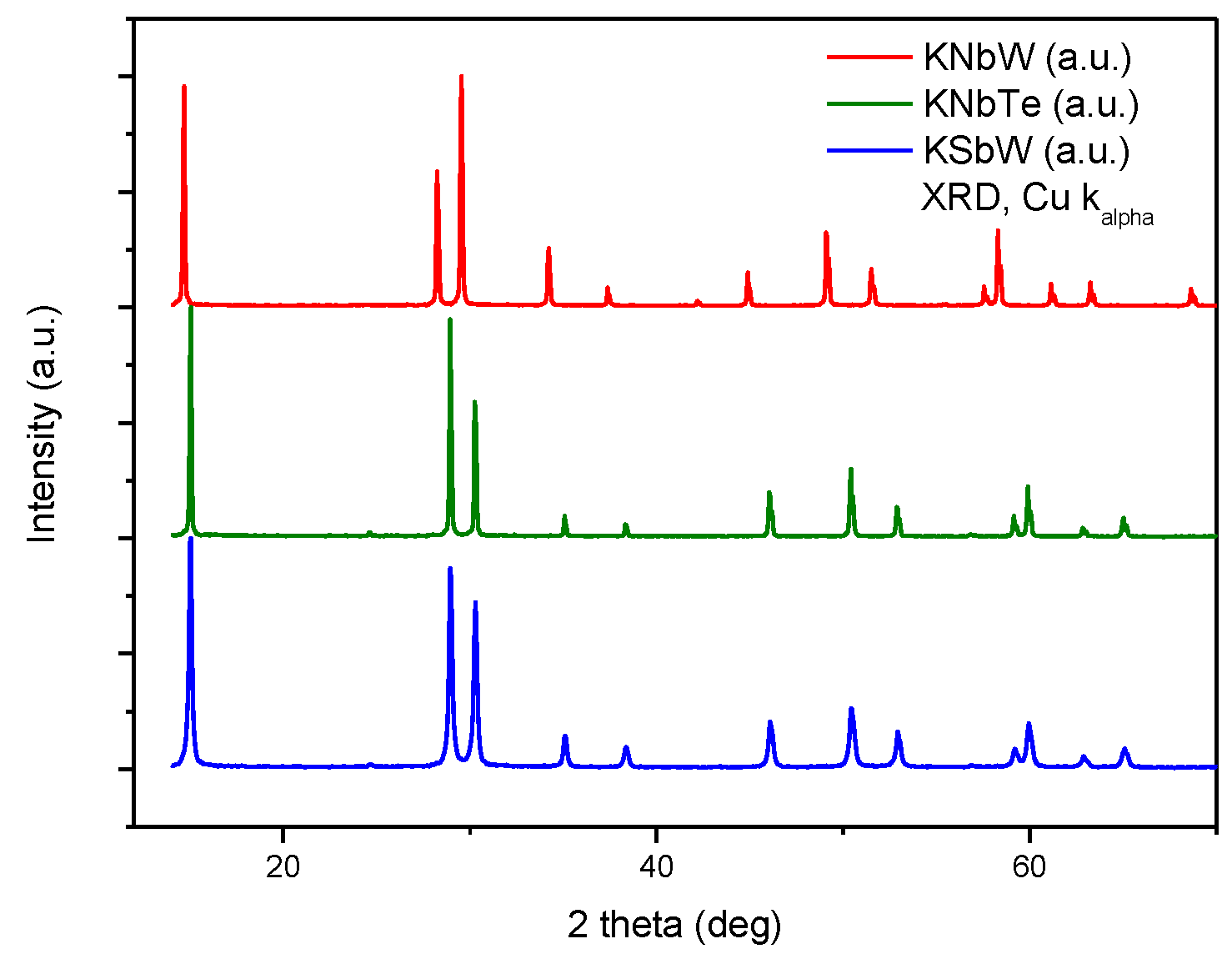
The oxides were obtained as well-crystallized powders, as suggested by the sharp peaks obtained in the XRD diagrams, shown all together in Figure 1. These patterns were used for the Pattern Matching analysis carried out prior to NPD Rietveld refinements. For this purpose, the unit-cell parameters, $Fd\overline{3}m$ space group symmetry and initial background points were given as input data. Characteristic pyrochlore structures were then confirmed, with a = 10.5068(1) Å, 10.2466(1) Å and 10.2377(1) Å for KNbW, KNbTe and KSbW, respectively. Given their monochromaticity, well-defined peak shape and unique features of neutrons, including the absence of form factor and the contrasting scattering factors even for light elements like O, NPD data were used for the crystal structure refinement, spanning a total 2θ range from 10 to 150°.

A first Rietveld refinement was performed based on the proposed structural model for KSbTeO₆ pyrochlore [8], with the origin choice No. 2 of the space group $Fd\overline{3}m$ (No 227), in which B^V (Nb or Sb) and B^VI (W or Te) atoms were statistically distributed over the 16d (½,½,½) sites, and the O oxygen atoms were placed at 48f (x,⅛,⅛) positions. K atoms were considered to be located at 32e (x,x,x) sites, being free to shift along the main diagonal of the unit cell. Although KNbTe and KSbW were properly fitted with this model, significant discrepancies between observed and calculated intensities were obtained for the KNbW sample, implying that some information on the remaining scattering density has not been correctly considered in the starting model. 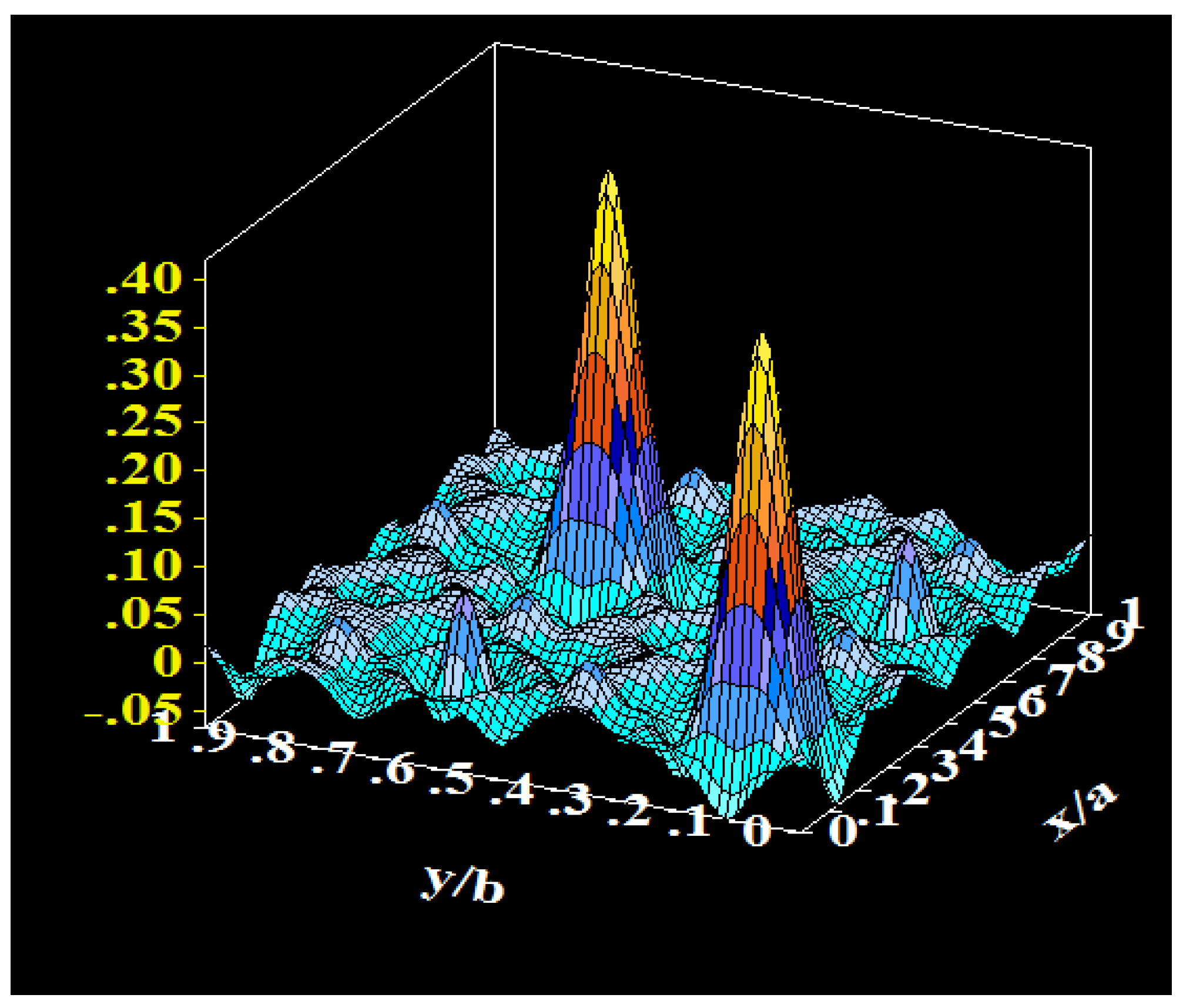R_Bragg factor for this initial model was above 10 %. A difference Fourier synthesis (performed over the difference between observed and calculated structure factors) was then carried out, in order to get information on the missing atoms in the model. The attained difference Fourier map allowed us to locate missing O’ atoms at 32e (x,x,x) sites and H atoms at 96g (x,x,z) positions. Figure 2 illustrates the Fourier peaks corresponding to the oxygen nuclear density (O’) of the missing water molecules. The introduction of O’ and H atoms in the structural refinement, based on the work by Murphy et al. [17], allowed an entire reduction of the Fourier Difference Map features and a decrease of the R_Bragg factor down to 1.96%. Large atomic displacement parameters (B) of 2.8 Ų and about 15(2) Ų were obtained for O’ and H atoms respectively, indicating a labile character for inserted water molecules. A good agreement between the observed and simulated patterns was achieved in all cases. The Rietveld plots from NPD data, including the observed, calculated and difference profiles for each sample, as well as the allowed Bragg positions, are shown in Figure 3.

Table 1. Unit–cell, fractional atomic coordinates, atomic displacement parameters, refined occupancy factors and Rietveld agreement factors of KNbW, KNbTe and KSbW, with cubic space group $Fd\overline{3}m$ (No. 227) and Z = 8, from NPD data at 298 K (λ = 1.59468(1) Å).

Pyrochlore	KNbW	KNbTe	KSbW
a (Å)	10.5068(1)	10.2466(1)	10.2377(1)
V(Å)3	1159.87(2)	1075.83(1)	1073.04(2)
K, 32e (x,x,x)
x	0.0083(7)	0.1043(6)	0.1008(5)
β11 = β22 = β33 *	-	63(8)	74(7)
β12 = β13 = β23 *	-	−12(4)	−2(4)
Beq (Å2)	0.8(1)	2.6(3)	3.1(3)
focc	0.2500	0.2500	0.2500
(BV,BVI), 16d (½,½,½)	NbV,WVI	NbV,TeVI	SbV,WVI
β11 = β22 = β33 *	38(1)	18.0(7)	32.6(9)
β12 = β13 = β23 *	−6(1)	−1.6(6)	−2.0(9)
Beq (Å2)	1.66(4)	0.76(3)	1.37(4)
focc *(BV,BVI)	0.5000/0.5000	0.5000/0.5000	0.5000/0.5000
O, 48f (x,⅛,⅛)
x	0.4406(1)	0.4329(1)	0.43355(9)
β11 *	23(1)	25(1)	38(1)
β22 = β33 *	25.6(9)	29.3(8)	33.9(9)
β23 *,**	−3(1)	−14.8(8)	−16.7(9)
Beq (Å2)	1.10(1)	1.16(4)	1.48(5)
focc	1.0000	1.0000	1.0000
O’, 32e (x,x,x)
x	0.0830(6)	-	-
Beq (Å2)	2.8	-	-
focc	0.29(1)	-	-
H, 96g (x,x,z)
x	0.3386(9)	-	-
z	0.028(5)	-	-
β11 = β22 *	7(1) × 10	-	-
β33 *	9(1) × 102	-	-
β12 *	−19(9)	-	-
β13 = β23 *	3(2) × 10	-	-
Beq (Å2)	15(2)	-	-
focc	0.195(4)	-	-
Reliability Factors
Rp (%)	2.07	4.47	2.93
Rwp (%)	2.95	6.24	3.95
Rexp (%)	1.48	2.07	2.16
χ2	3.98	9.08	3.35
RBragg (%)	1.96	2.48	2.09

* Anisotropic Betas (×10⁴). ** β₁₂ = β₁₃ = 0.

gathers all the crystallographic information from the NPD refinements, including the agreement factors. Also, main distances and angles between B^V/B^VI and O for the main covalent lattice, and K and O’ as sub-lattice are summarized in

Table 2. Main interatomic distances (Å) and angles (°) at 298 K.

Pyrochlore	KNbW	KNbTe	KSbW
K–O(×3)	2.716(7)	2.959(6)	2.932(5)
(×3)	2.756(7)	3.379(6)	3.377(5)
K–O’(×3)	2.484(10)	-	-
(×3)	2.778(10)	-	-
(BV,BVI)–O(×6)	1.9593(4)	1.9375(4)	1.9334(4)
H–O’(×3)	1.17(6)	-	-
(BV,BVI)–O–(BV,BVI)	142.865(15)	138.418(15)	138.798(15)
O–(BV,BVI)–O	88.71(5)	88.15(6)	88.41(6)
	91.29(3)	91.85(3)	91.59(3)

.

The presence of water molecules in KNbW is concomitant with its abnormally large unit-cell parameter (α = 10.5068(1) Å): from the ionic radii [20] of both hexacoordinated Nb⁺⁵ and W⁺⁶, the KNbW pyrochlore should have an intermediate unit-cell parameter between those of KNbTe (10.2466(1) Å) and KSbW (10.2377(1) Å). The exceptional expansion of the pyrochlore network is especially driven by the presence of O’ oxygen, which partially occupies a site normally occupied by A atoms in defect pyrochlores, displacing K to a near (0,0,0) position and conforming the A₂O’ sub-lattice interleaved with the B₂O₆ framework.

The presence of extra O’ oxygens, in addition to the high background values at low angles for the NPD pattern of KNbW indeed suggested the existence of water in the structure. A thermogravimetric analysis was performed for this sample, shown in Figure 4: a weight loss of 4.9(4) % was observed, corresponding to 1.18(9) water molecules per formula unit of the pyrochlore. The structural refinement including O’ and H atoms led to a crystallographic formula KNbWO₆·1.17(6) H₂O. It is noticeable that when the sample is cooled down to room temperature after the thermogravimetric analysis, the weight indicated a slow mass recovery similar to the loss weight, suggesting that the KNbW sample is extremely hygroscopic and after some time it retakes water from the air atmosphere. The present results are similar to those reported in Ref [17] about the water insertion reactions of the pyrochlore KNbWO₆; where the authors describe a formula KNbWO₆·0.69D₂O. The present material, with a superior water contents, also exhibits a correspondingly large unit-cell parameter (10.5068(1) vs. 10.5019(2) Å [17]).

Similar Fourier syntheses carried out for the two other pyrochlores, KNbTe and KSbW, did not show any significant features, excluding a spontaneous water insertion phenomenon.

As shown in Table 1, the position for K ions within the pyrochlore unit cell is rather different in KNbW with respect to the two other pyrochlores. Although we found K located at 32e site (x = 0.0083(7)), it is significantly closer to (0,0,0), yet clearly not occupying the 16c special site. It is worth mentioning that both K and O’ positions are close to those reported in Ref. [17] (0.0083(7) vs. 0.0143(7) and 0.0830(6) vs. 0.0857(4), respectively). For KNbTe and KSbW, x = 0.1043(6) and 0.1008(5), respectively. 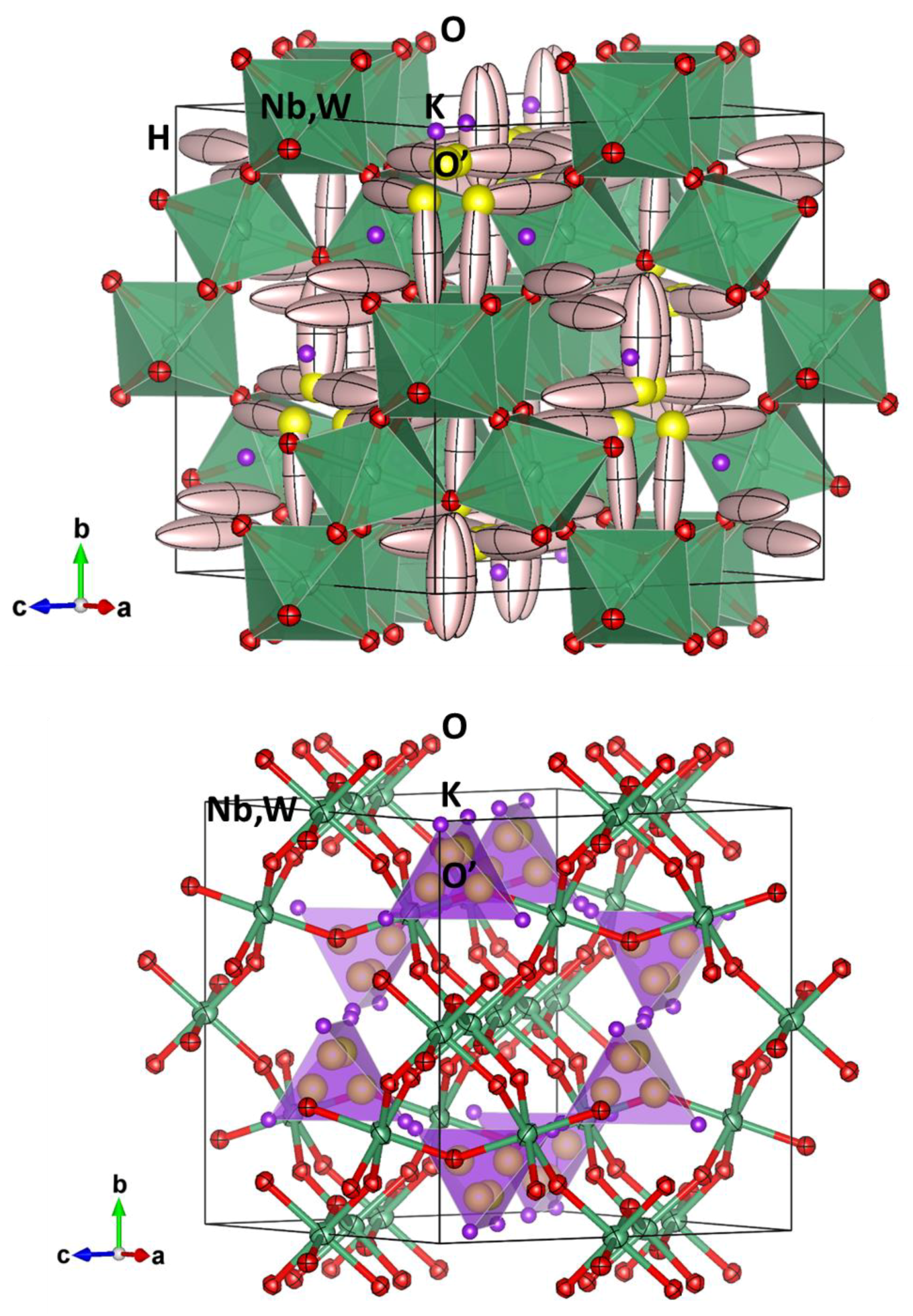Figure 5 shows two views of crystal structure of the KNbW pyrochlore, where Nb/W, O and H atoms are displayed with their displacement ellipsoids and K and O’ as isotropic atoms, all with a 75% probability. For KNbW, the O and Nb/W ellipsoids are quite regular, close to spheres. The K₂O’ sub-lattice has been highlighted as purple tetrahedra (Figure 5b), where distances between K and O’ are between 2.48−2.78 Å (Table 2). Here H atoms were removed for a clearer view. K atoms are expected to be little mobile or labile, in comparison to the other AB₂O₆ defect pyrochlores, where no O’ is present and a weaker steric impediment should be found for K⁺ diffusion. The high equivalent atomic displacement parameter of H atoms (15(2) Ų; Table 1) may correspond to highly mobile water molecules where the H atoms are dynamically oscillating between adjacent 96g positions. Overall Atomic Displacement parameter of O’ atoms (2.8 Ų) could not be refined due to a strong divergence; it was therefore slowly modified by hand until the Reliability Factors were minimized. The H–O distance (1.17(6) Å) is slightly longer than usually observed in free H₂O molecules (~1 Å) since there are strong interactions with the pyrochlore cage that weaken the O–H bond.

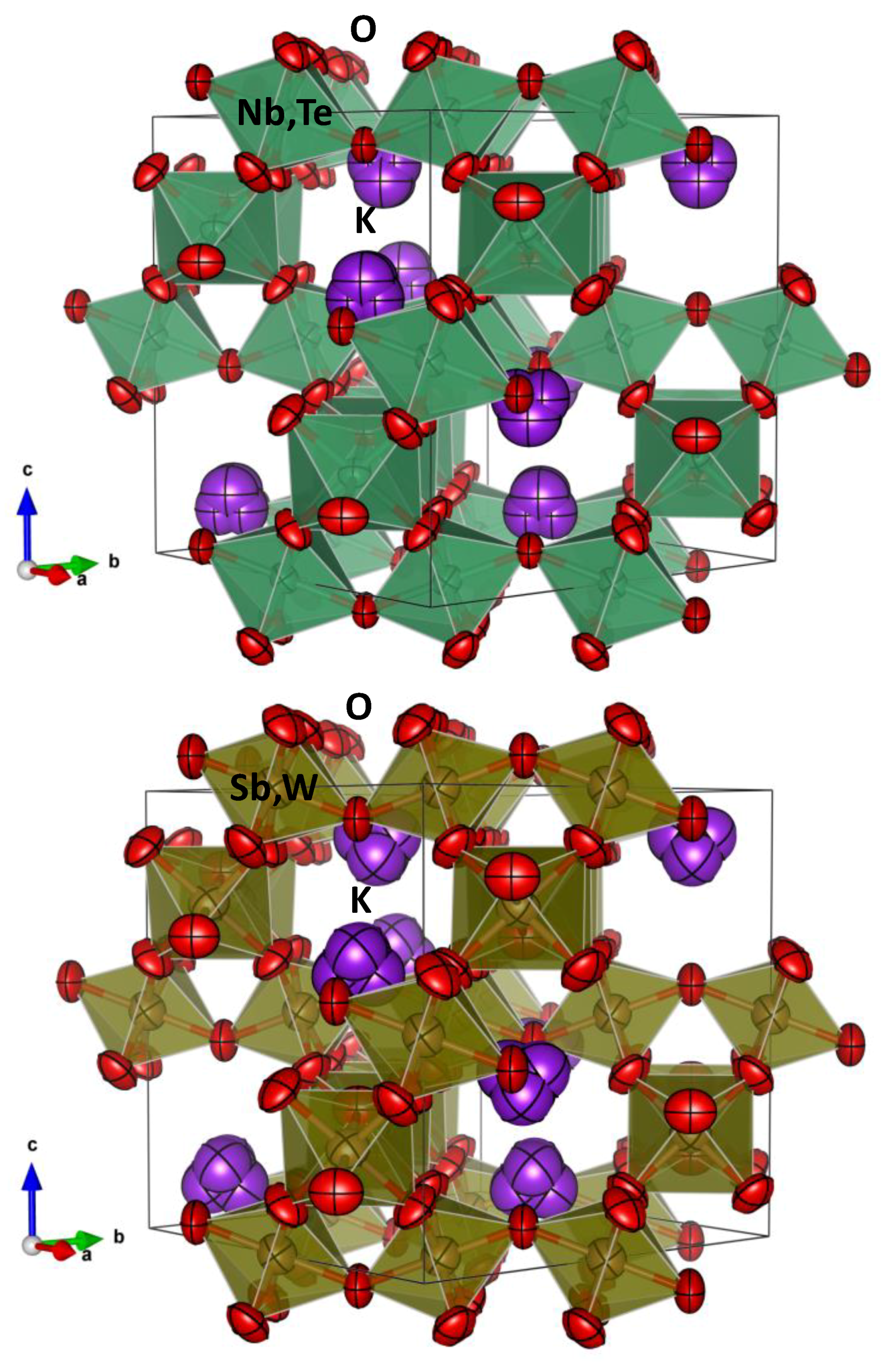
Figure 6 displays a representation of (a) KNbTe and (b) KSbW pyrochlores. Both panels show the anisotropic displacement parameters with 99% probability for all the atoms. The channels are clearly visible along the [1$\overline{1}$. 0] direction; within these channels the K⁺ atoms are expected to diffuse, and permit ionic exchange, as observed in KSbTeO₆. In all three KNbW, KNbTe and KSbW samples, pictures show K tetrahedra where the K⁺ ions are statistically distributed at 32e Wyckoff positions with a ¼ occupancy factor; that is to say that, statistically, only one tetrahedron corner is actually a K atom, while the three other are empty. In KNbW, the occupancy of 32e sites by K⁺ ions or water molecules in adjacent cages is statistical.

In KNbTe the tetrahedral boxes allocating K atoms are slightly larger compared to KSbW, as corresponds to the greater x (K) coordinates. For KNbW, shorter K–O distances are observed (Table 2), since H₂O molecules are accommodated within the same tetrahedral cages. Regarding the (B^V,B^VI)–O distances, they are notably longer in KNbW (1.9593(4) Å) with respect to KNbTe (1.9375(4) Å) and KSbW (1.9334(4) Å); this is certainly connected with the presence in the two last compounds of a p-block element, giving more covalent, stronger and shorter bonds to oxygen atoms. In any case, these values are slightly shorter (0.05 Å on average) to the expected ones of 2.00 Å, 1.98 Å and 1.98 Å from the Shannon’s mean ionic radius sum, respectively [20]. It is noteworthy that for all three compounds the (B^V,B^VI)O₆ octahedra are actually slightly axially distorted, although they exhibit six equal (B^V,B^VI)–O distances. Another notorious difference is the wider (B^V,B^VI)–O–(B^V,B^VI) angle between adjacent octahedra in KNbW pyrochlore (142.865(15)° versus 138.418(15)° and 138.798(15)° for KNbW vs. KNbTe and KSbW, respectively), which is translated into a more open and thus greater main network, constituted by (B^V,B^VI)O₆ corner-shared octahedra. As mentioned in the introduction, this lattice forms a three-dimensional tunnel framework in which the K cations are located and are expected to move freely. This feature grants the high ion conductivity in pyrochlore-type materials, and is exploited by ion-exchange of K for hydronium groups, giving rise to acid catalysts [21].

In a previous report on the closely related KSbTeO₆ material, K⁺ ions occupy 32e Wyckoff sites with x = 0.126(3); this was virtually an 8a site (⅛,⅛,⅛) within experimental error [8]. By contrast, in this present work we found that K coordinates for all three pyrochlores [x (K) = 0.0083(7), 0.1043(6) and 0.1008(5) Å for KNbW, KNbTe and KSbW, respectively] are considerably away from the 8a (⅛,⅛,⅛) Wyckoff site, unambiguously verifying that K atoms locate in 32e sites. Taking the example of KNbTe, K atoms are coordinated to six oxygen atoms only, forming a deformed octahedron. Figure 7 shows the KO₆ pseudo-octahedra for the KNbTe sample, where K–O distances form short (2.959(6) Å) and long (3.379(6) Å) bonds, labelled with “S” and “L”, respectively. Only one out of four K of the tetrahedra are represented. Also, Nb, Te and unbonded O atoms are hidden for the sake of clarity.

As final consideration, the fact that KNbW is hydrated whereas KNbTe or KSbW are not is certainly related to the presence in the two last compounds of p-block elements (Sb and Te), with a superior electronegativity, which are able to form strongly covalent bonds to oxygen. The octahedral B₂O₆ framework is, therefore, much more covalent in character for the Sb or Te-containing pyrochlores. The O oxygen atoms of this framework are, thus, less prone to form additional bonds, even the subtle H bonds that are expected to exist between the inserted water molecules in the pyrochlore cages and the octahedral framework. In consequence, this covalent framework is not able to host additional water molecules for KNbTe or KSbW.

4. Conclusions

Three defect pyrochlores were obtained by a solid-state procedure, and their crystal structures refined from NPD data at RT in the cubic $Fd\overline{3}m$ symmetry. KNbW, KNbTe and KSbW contain a covalent network formed by vertex-sharing (B^V,B^VI)O₆ octahedra, but exhibit conspicuous structural differences. KNbW possess an interleaved K₂O’ network, given the presence of water molecules (within the crystalline structure) and therefore extra O’ oxygen atoms at special 32e positions; consequently K ions are pushed close to 16c (0,0,0) sites, forming K₄ tetrahedra. On the other hand, the more covalent nature of the (B,B’)–O interaction for Sb and Te determine shorter (B,B’)–O bonds and narrower B–O–B angles, in significantly smaller unit cells. The present structural data forecast ionic exchange easiness for KNbTe and KSbW.