Influence of Abrasive Shape on the Abrasion and Phase Transformation of Monocrystalline Silicon
Abstract
:1. Introduction
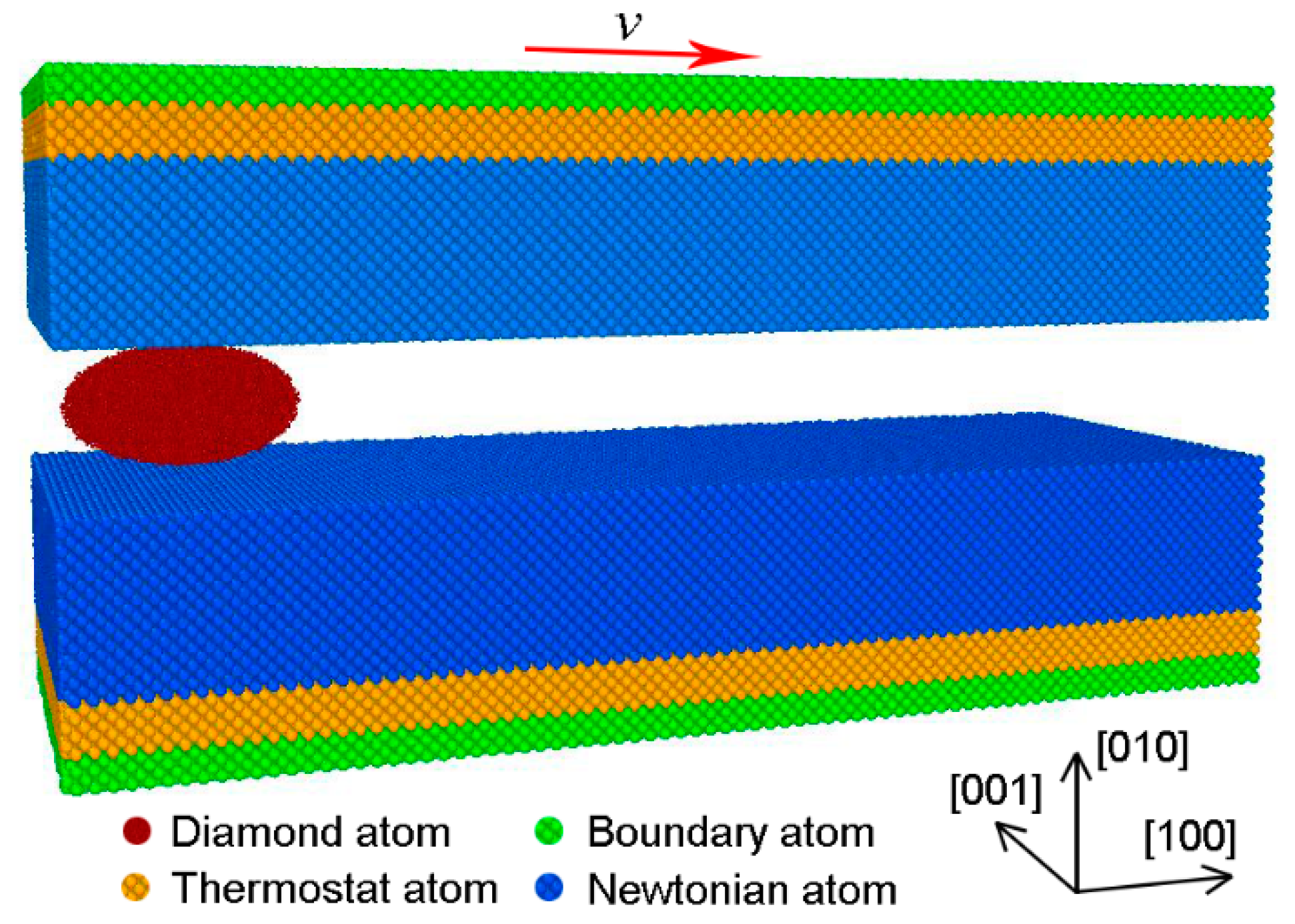
2. Simulation Model and Methodology
3. Results and Discussion
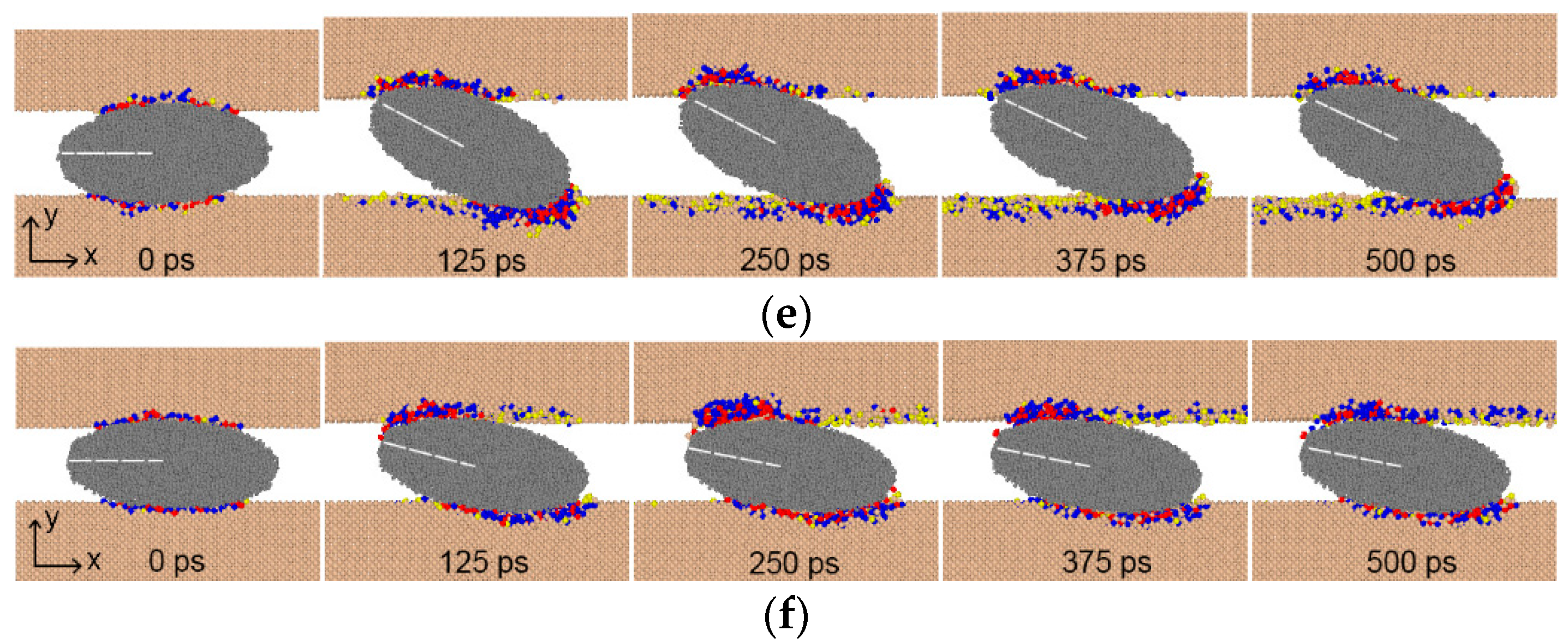
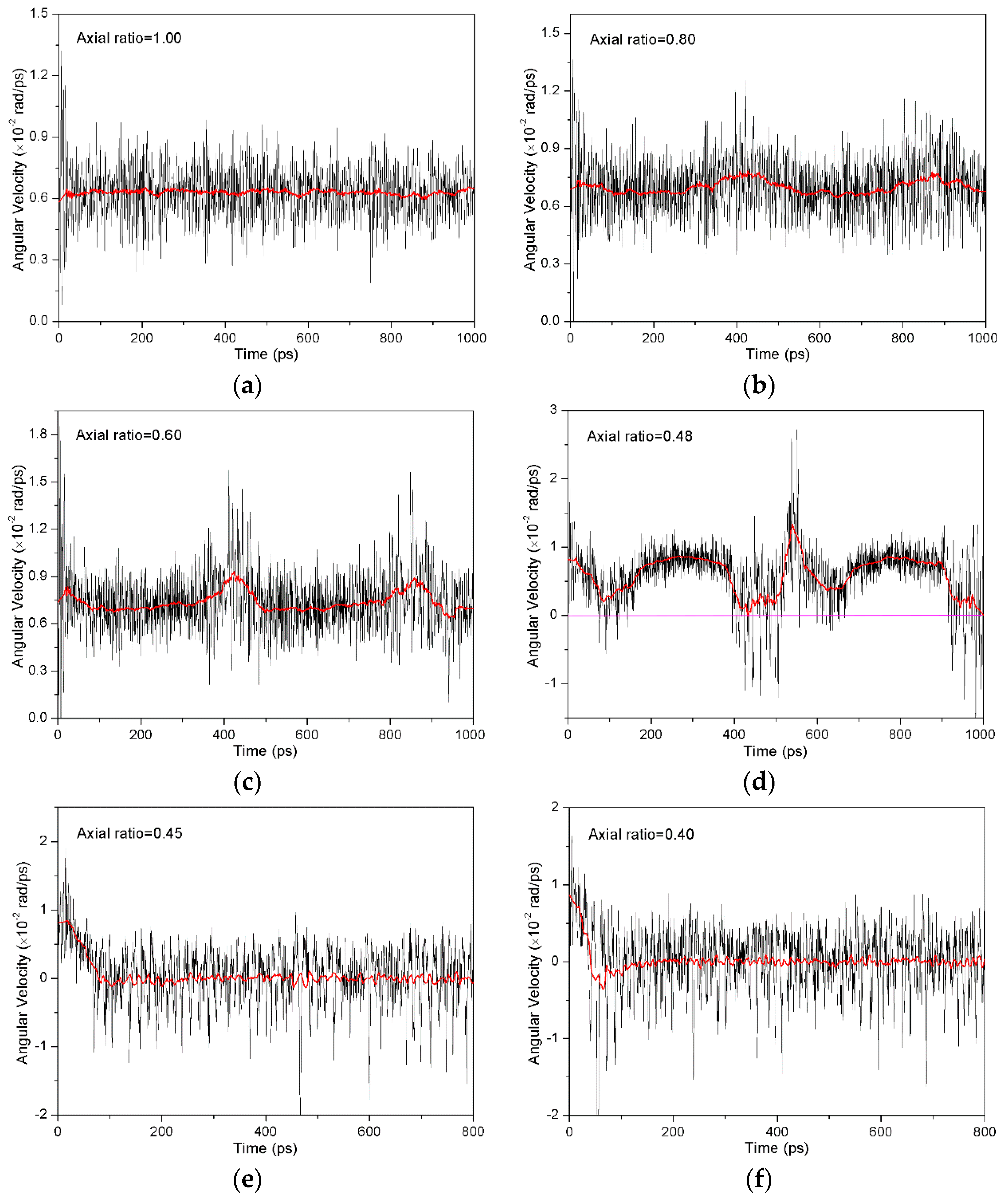
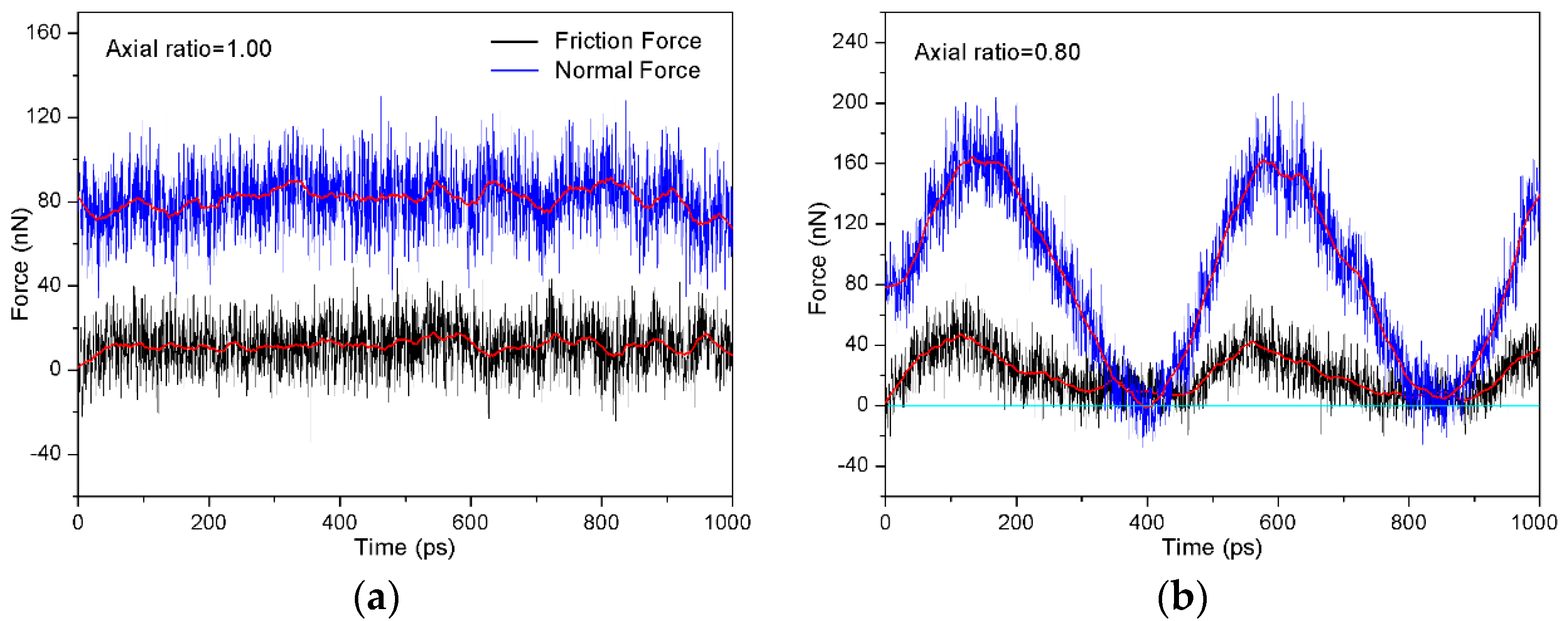
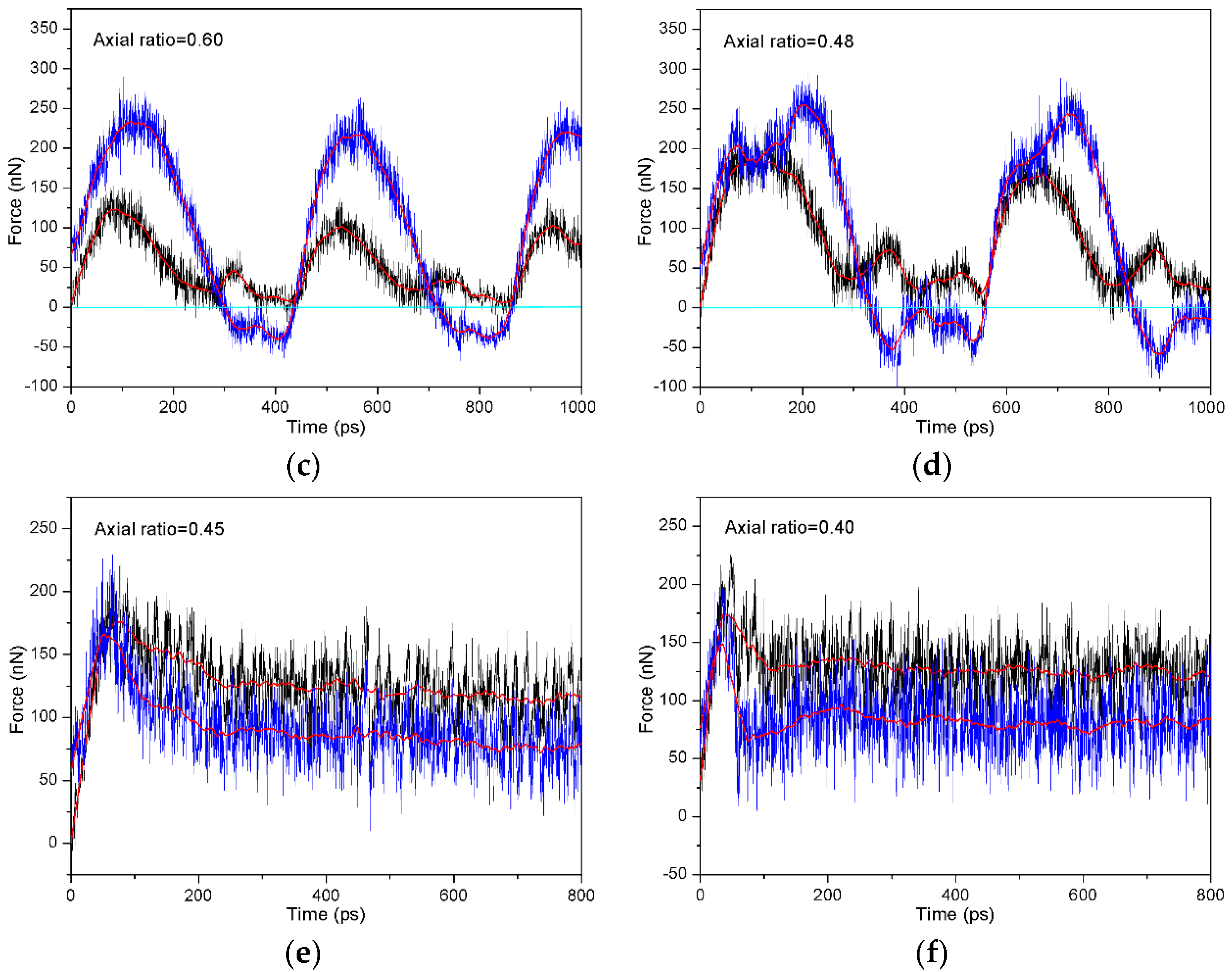
3.1. Movement Pattern of Abrasive Particle
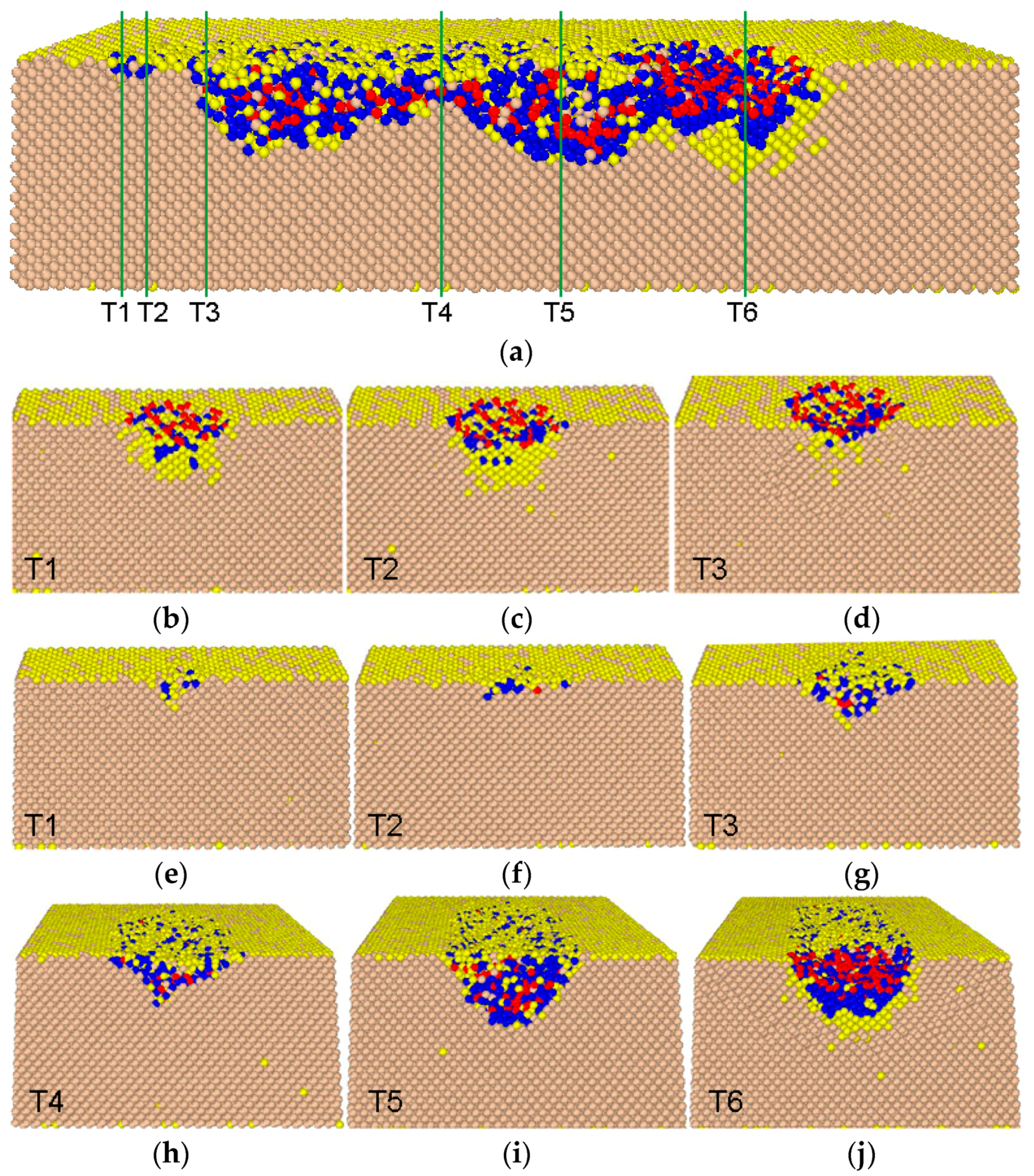
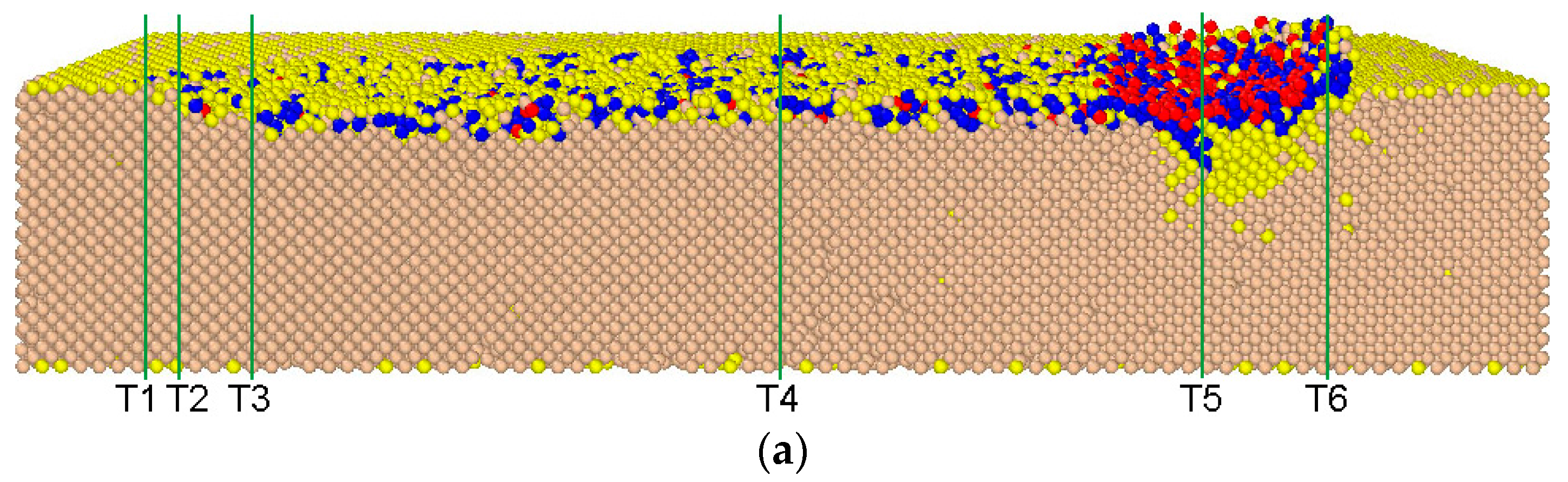
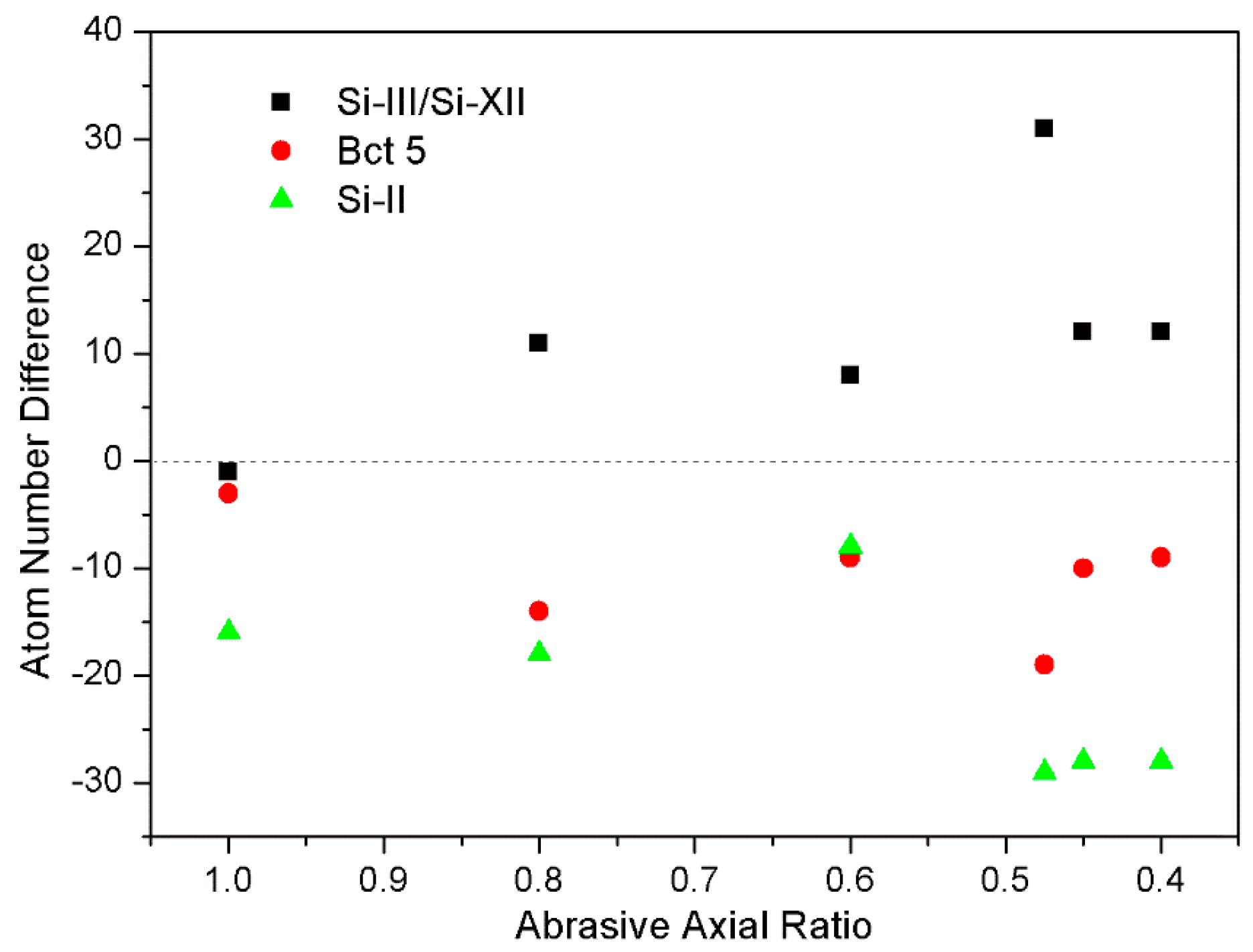
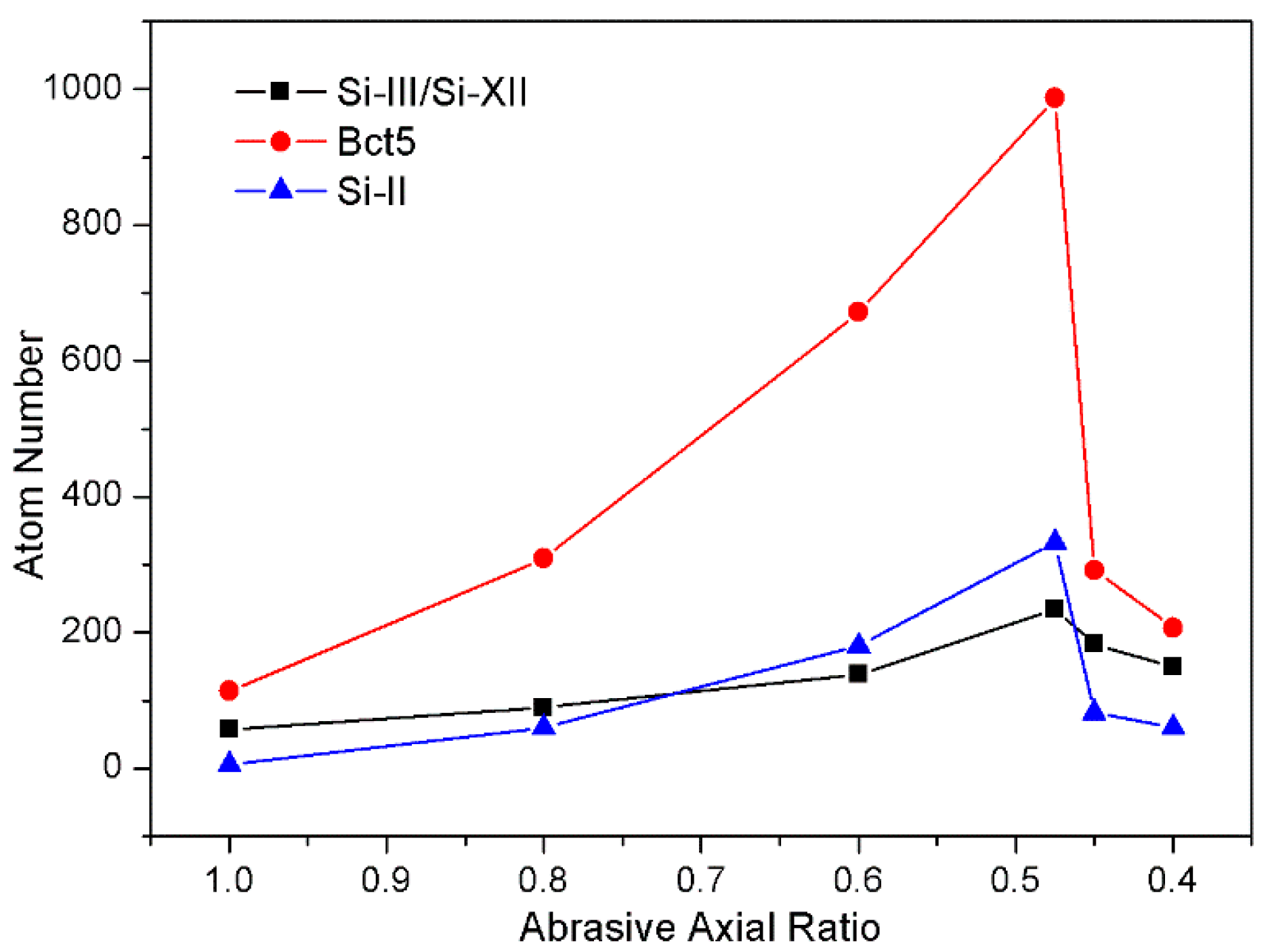
3.2. Phase Transformation of Monocrystalline Silicon
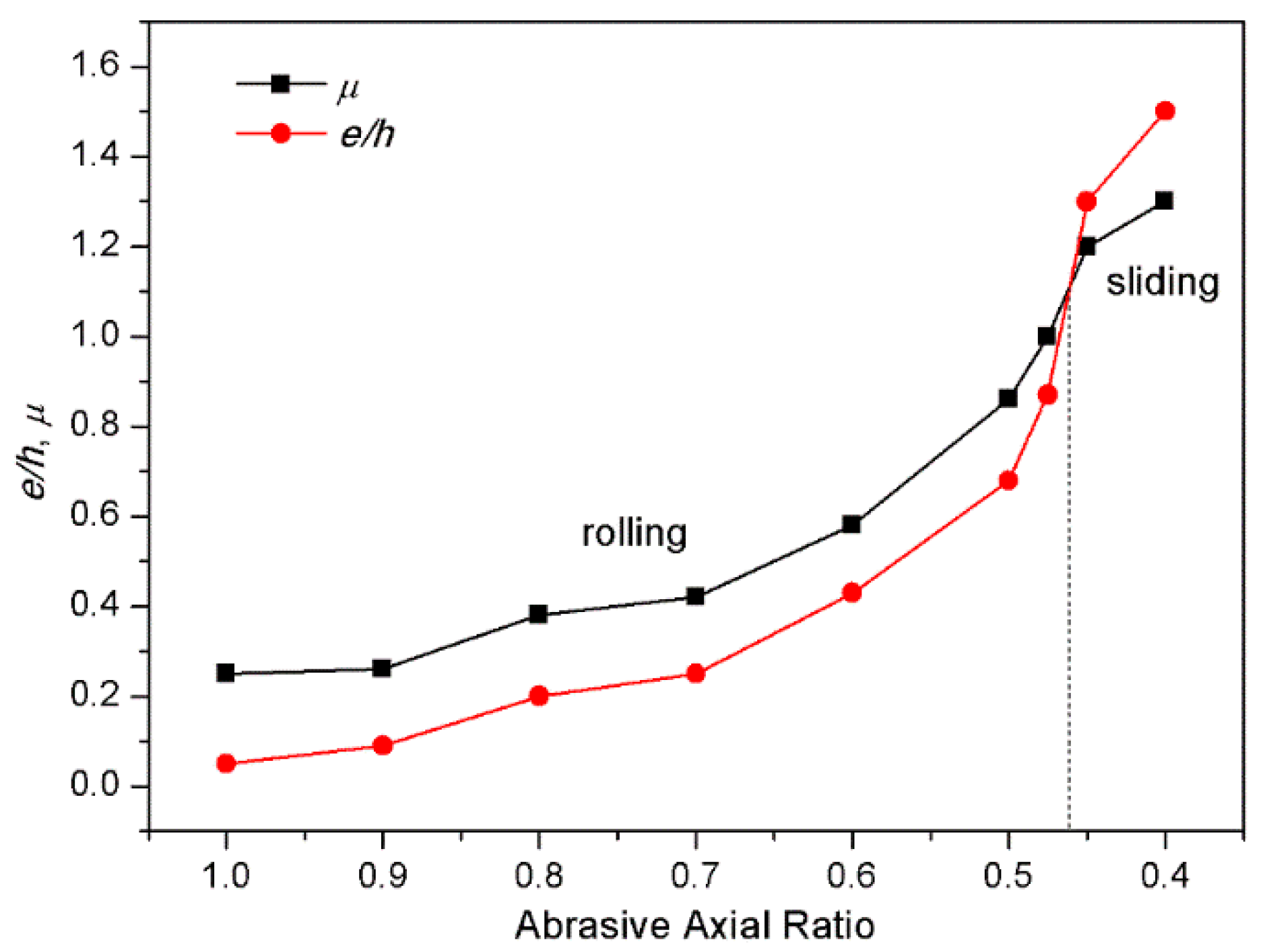
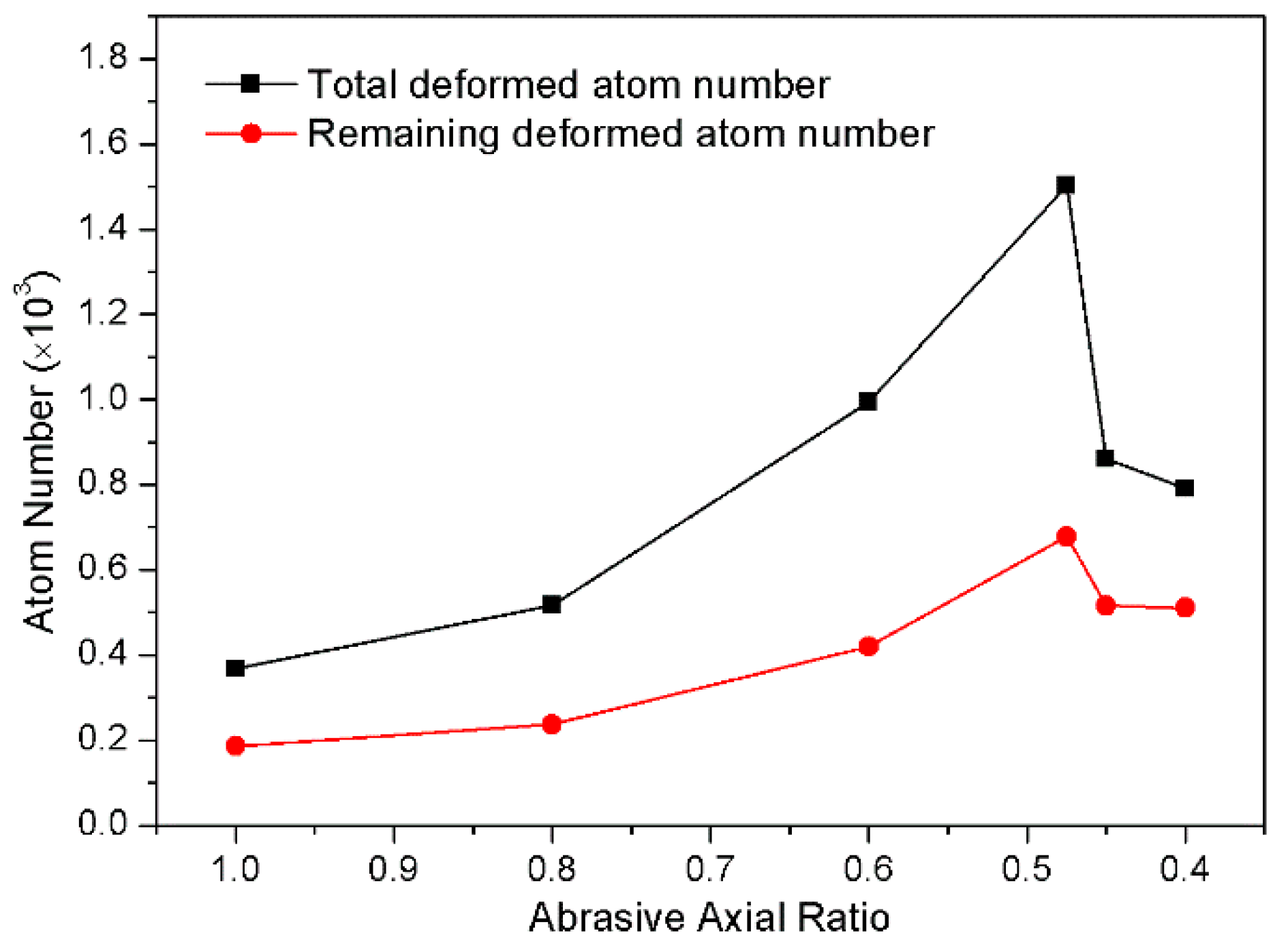
4. Damage Evaluation of Monocrystalline Silicon
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huang, H.; Yan, J.W. New insights into phase transformations in single crystal silicon by controlled cyclic nanoindentation. Scr. Mater. 2015, 102, 35–38. [Google Scholar] [CrossRef]
- Zhang, L.C.; Tang, C.Y. Friction and wear of diamond–silicon nano-systems: Effect of moisture and surface roughness. Wear 2013, 302, 929–936. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, H.W.; Yang, Y.H.; Huang, H.; Ma, Z.C.; Shao, M.K. Evaluation of repeated single-point diamond turning on the deformation behavior of monocrystalline silicon via molecular dynamic simulations. Appl. Phys. A 2014, 116, 141–150. [Google Scholar] [CrossRef]
- Kim, D.E.; Oh, S.I. Atomistic simulation of structural phase transformations in monocrystalline silicon induced by nanoindentation. Nanotechnology 2006, 17, 2259–2265. [Google Scholar] [CrossRef]
- Subhash, G.; Corwin, A.D.; de Boer, M.P. Evolution of Wear Characteristics and Frictional Behavior in MEMS devices. Tribol. Lett. 2014, 1, 177–189. [Google Scholar] [CrossRef]
- Alsem, D.H.; Dugger, M.T.; Stach, E.A.; Ritchie, R.O. Microscale friction and sliding wear of polycrystalline silicon thin structural films in ambient air. J. Microelectromech. S 2008, 17, 1144–1145. [Google Scholar] [CrossRef]
- Shen, S.; Meng, Y.; Zhang, W. Characteristics of the wear process of side-wall surfaces in bulk-fabricated Si-MEMS devices in nitrogen gas environment. Tribol. Lett. 2012, 47, 455–466. [Google Scholar] [CrossRef]
- Kasai, T.; Bhushan, B. Physics and tribology of chemical mechnical planarization. J. Phys. Condens. Matter 2008, 20, 225011. [Google Scholar] [CrossRef]
- Luo, J.F.; Dornfeld, D.A. Material removal mechanism in chemical mechanical polishing: Theory and modeling. IEEE Trans. Semicond. Manuf. 2001, 14, 112–133. [Google Scholar]
- Luo, J.F.; Dornfeld, D.A. Material removal regions in chemical mechanical planarization for submicron integrated circuit fabrication: Coupling effects of slurry chemicals, abrasive size distribution, and wafer-pad contact area. IEEE Trans. Semicond. Manuf. 2003, 16, 45–56. [Google Scholar]
- Anantheshwara, K.; Lockwood, A.J.; Mishra, R.K.; Inkson, B.J.; Bobji, M.S. Dynamical evolution of wear particles in nanocontacts. Tribol. Lett. 2012, 45, 229–235. [Google Scholar] [CrossRef]
- Gupta, M.C.; Ruoff, A.L. Static compression of silicon in the [100] and in the [111] directions. J. Appl. Phys. 1980, 51, 1072–1075. [Google Scholar] [CrossRef]
- Clarke, D.R.; Kroll, M.C.; Kirchner, P.D.; Cook, R.F. Amorphization and conductivity of silicon and germanium induced by indentation. Phys. Rev. Lett. 1988, 60, 2156–2159. [Google Scholar] [CrossRef] [PubMed]
- Mann, A.B.; Van, H.D.; Pethica, J.B.; Bowes, P.; Weihs, T.P. Contact resistance and phase transformations during nanoindentation of silicon. Philos. Mag. A 2002, 82, 1921–1929. [Google Scholar] [CrossRef]
- Bradby, J.E.; Williams, J.S.; Swain, M.V. In situ electrical characterization of phase transformations in Si during indentation. Phys. Rev. B 2003, 67, 085205. [Google Scholar] [CrossRef]
- Oliver, M.R. Chemical Mechanical Planarization of Semiconductor Materials; Springer: Heidelberg, Germany, 2004. [Google Scholar]
- Su, Y.T. Investigation of removal rate properties of a floating polishing process. J. Electrochem. Soc. 2000, 147, 2290–2296. [Google Scholar] [CrossRef]
- Fang, L.; Zhao, J.; Li, B.; Sun, K. Movement patterns of ellipsoidal particle in abrasive flow machining. J. Mater. Process. Technol. 2009, 209, 6048–6056. [Google Scholar] [CrossRef]
- Zhang, L.; Tanaka, H. Atomic scale deformation in silicon monocrystals induced by two-body and three-body contact sliding. Tribol. Int. 1998, 31, 425–433. [Google Scholar] [CrossRef]
- Mylvaganam, K.; Zhang, L.C. Nanotwinning in monocrystalline silicon upon nanoscratching. Scr. Mater. 2011, 65, 214–216. [Google Scholar] [CrossRef]
- Du, X.C.; Zhao, H.W.; Zhang, L.; Yang, Y.H.; Xu, H.L.; Fu, H.S.; Li, L.J. Molecular dynamics investigations of mechanical behaviours in monocrystalline silicon due to nanoindentation at cryogenic temperatures and room temperature. Sci. Rep. 2015, 5, 16275. [Google Scholar] [CrossRef] [PubMed]
- Eyben, P.; Clemente, F.; Vanstreels, K.; Pourtois, G.; Clarysse, T.; Duriau, E.; Hantschel, T. Analysis and modeling of the high vacuum scanning spreading resistance microscopy nanocontact on silicon. J. Vac. Sci. Technol. B 2010, 28, 401–406. [Google Scholar] [CrossRef]
- Kim, D.E.; Oh, S.I. Deformation pathway to high-pressure phases of silicon during nanoindentation. J. Appl. Phys. 2008, 104, 013502. [Google Scholar] [CrossRef]
- Sun, J.P.; Fang, L.; Han, J.; Han, Y.; Chen, H.W.; Sun, K. Abrasive wear of nanoscale single crystal silicon. Wear 2013, 307, 119–126. [Google Scholar] [CrossRef]
- Sun, J.P.; Fang, L.; Han, J.; Han, Y.; Chen, H.W.; Sun, K. Phase transformations of mono-crystal silicon induced by two-body and three-body abrasion in nanoscale. Comput. Mater. Sci. 2014, 82, 140–150. [Google Scholar] [CrossRef]
- Hu, C.Z.; Bai, M.L.; Lv, J.Z.; Kou, Z.H.; Li, X.J. Molecular dynamics simulation on the tribology properties of two hard nanoparticles (diamond and silicon dioxide) confined by two iron blocks. Tribol. Int. 2015, 90, 297–305. [Google Scholar] [CrossRef]
- Eder, S.J.; Feldbauer, G.; Bianchi, D.; Cihak-Bayr, U.; Betz, G.; Vernes, A. Applicability of macroscopic wear and friction laws on the atomic length scale. Phys. Rev. Lett. 2015, 115, 025502. [Google Scholar] [CrossRef] [PubMed]
- Ewen, J.P.; Gattinoni, C.; Thakkar, F.M.; Morgan, N.; Spikes, H.A.; Dini, D. Nonequilibrium molecular dynamics investigation of the reduction in friction and wear by carbon nanoparticles between iron surfaces. Tribol. Lett. 2016, 63, 38. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.N.; Miao, N.M. Polymethylmethacrylate (PMMA)/CeO2 hybrid particles for enhanced chemical mechanical polishing performance. Tribol. Int. 2015, 82, 211–217. [Google Scholar] [CrossRef]
- Tersoff, J. Modelling solid-state chemistry: Interatomic potentials for multicomponent system. Phys. Rev. B 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical model for the structural properties of silicon. Phys. Rev. Lett. 1986, 56, 632–635. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Shi, C.; Zhang, P.; Zhang, L.; Huang, H.; Yan, J. Research on the effects of machining-induced subsurface damages on mono-crystalline silicon via molecular dynamics simulation. Appl. Surf. Sci. 2012, 259, 66–71. [Google Scholar] [CrossRef]
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Constant-pressure equations of motion. Phys. Rev. A 1986, 34, 2499–2500. [Google Scholar] [CrossRef]
- Fang, L.; Zhou, Q.D. A statistical model describing wear traces in three-body abrasion. Lubr. Sci. 1995, 2, 47–53. [Google Scholar] [CrossRef]
- Fang, L.; Kong, X.L.; Zhou, Q.D. A wear tester capable of monitoring and evaluating the movement pattern of abrasive particles in three-body abrasion. Wear 1992, 159, 115–120. [Google Scholar]
- Fang, L.; Kong, X.L.; Su, J.Y.; Zhou, Q.D. Movement patterns of abrasive particles in three-body abrasion. Wear 1993, 162, 782–789. [Google Scholar] [CrossRef]
- Fang, L.; Zhou, Q.D.; Rao, Q.C. An experimental simulation of cutting wear in three-body abrasion. Wear 1998, 218, 188–194. [Google Scholar] [CrossRef]
- Shi, J.Q.; Chen, J.; Wei, X.Q.; Fang, L.; Sun, K.; Sun, J.P.; Han, J. Influence of normal load on the three-body abrasion behaviour of monocrystalline silicon with ellipsoidal particle. RSC Adv. 2017, 7, 30929–30940. [Google Scholar] [CrossRef]
- Fang, L.; Sun, K.; Shi, J.Q.; Zhu, X.Z.; Zhang, Y.N.; Chen, J.; Sun, J.P.; Han, J. Movement patterns of ellipsoidal particles with different axial ratios in three-body abrasion of monocrystalline copper: A large scale molecular dynamics study. RSC Adv. 2017, 7, 26790–26800. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. The Friction and Lubrification of Solids; Clarendon Press: Oxford, UK, 1950–1954; Volume 1. [Google Scholar]
- Moore, D.F. Principles and Applications of Tribology; Pergamon Press Ltd.: Oxford, UK, 1975. [Google Scholar]
- Zhu, P.Z.; Hu, Y.Z.; Ma, T.B.; Wang, H. Molecular Dynamics Study on Friction Due to Ploughing and Adhesion in Nanometric Scratching Process. Tribol. Lett. 2011, 41, 41–46. [Google Scholar] [CrossRef]
- Coffey, T.; Krim, J. C60 Molecular Bearings and the Phenomenon of Nanomapping. PRL 2006, 96, 186104. [Google Scholar] [CrossRef] [PubMed]
- Braun, O.M.; Tosatti, E. Rack-and-pinion effects in molecular rolling friction. Philos. Mag. Lett. 2008, 88, 509–517. [Google Scholar] [CrossRef]
- Ren, J.Q.; Zhao, J.S.; Dong, Z.G.; Liu, P.K. Molecular dynamics study on the mechanism of AFM-based nanoscratching process with water-layer lubrication. Appl. Surf. Sci. 2015, 346, 84–98. [Google Scholar] [CrossRef]

| γ = b/a | 1.00 | 0.80 | 0.60 | 0.48 | 0.45 | 0.40 |
|---|---|---|---|---|---|---|
| a (x-axis)/Å | 40 | 40 | 40 | 40 | 40 | 40 |
| b (y-axis)/Å | 40 | 32 | 24 | 19 | 18 | 16 |
| c (z-axis)/Å | 40 | 40 | 40 | 40 | 40 | 40 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Wei, X.; Chen, J.; Sun, K.; Fang, L. Influence of Abrasive Shape on the Abrasion and Phase Transformation of Monocrystalline Silicon. Crystals 2018, 8, 32. https://doi.org/10.3390/cryst8010032
Shi J, Wei X, Chen J, Sun K, Fang L. Influence of Abrasive Shape on the Abrasion and Phase Transformation of Monocrystalline Silicon. Crystals. 2018; 8(1):32. https://doi.org/10.3390/cryst8010032
Chicago/Turabian StyleShi, Junqin, Xinqi Wei, Juan Chen, Kun Sun, and Liang Fang. 2018. "Influence of Abrasive Shape on the Abrasion and Phase Transformation of Monocrystalline Silicon" Crystals 8, no. 1: 32. https://doi.org/10.3390/cryst8010032
APA StyleShi, J., Wei, X., Chen, J., Sun, K., & Fang, L. (2018). Influence of Abrasive Shape on the Abrasion and Phase Transformation of Monocrystalline Silicon. Crystals, 8(1), 32. https://doi.org/10.3390/cryst8010032





