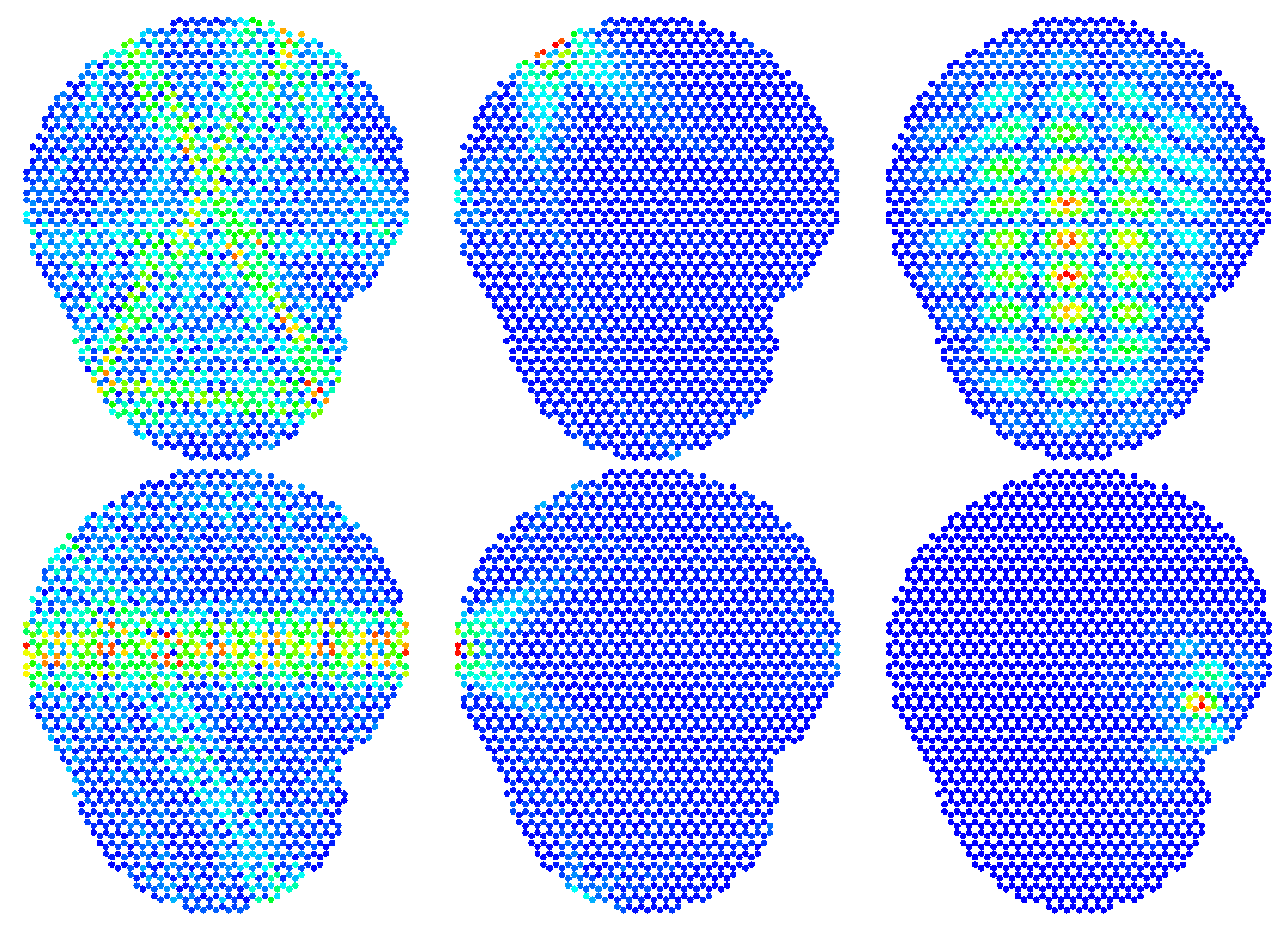1. Introduction
The isolation of graphene [
1], a monoatomic layer of carbon atoms arranged in a honeycomb (hexagonal) lattice, has stimulated recently considerable interest in two-dimensional (2D) structures. Most of the interest has come from the extraordinary electronic band structure [
2,
3] of graphene. It stems solely from the symmetry properties of the honeycomb lattice, which is formed by two interpenetrating triangular lattices [
4]. Another important feature of graphene is its soft structure. Graphene shares many properties of soft membranes [
5] due to the fact that it has out-of-plane vibrational modes [
6,
7,
8] that are not found in 3D crystals. These modes, also called flexural modes [
2], play a crucial role in many applications. In addition, if one of the dimensions is shrunk to zero, one can have graphene ribbons, or carbon nanotubes [
9] obtained by rolling graphene along a given direction and reconnecting the carbon bonds. These structures are one-dimensional (1D). Finally, the carbon atoms can be arranged spherically to form fullerene molecules [
10]. These are zero-dimensional (0D) structures with discrete energy states. They can be obtained from graphene by wrapping the sheet into a sphere [
11].
Recently [
12], we have introduced an algebraic approach to lattice systems particularly well suited to study 2D lattices, which is a generalization of that to molecules (0D) [
13] applied in [
14] and to linear lattices [
15]. It was used in [
12] to calculate energy dispersion relations (EDR) and the density of states (DOS) of flexural one-dimensional (1d) out-of-plane vibrations, both analytically and numerically. The numerical simulations were done on linear lattices with
n sites and on square and hexagonal lattices with
sites. In this article, we study unusual localization properties of the wave functions of the hexagonal lattice (graphene), which are not present in other types of 2D lattices. The wave functions are obtained by means of the algebraic model.
One peculiarity of graphene sheets is the existence of zero-energy electronic states that are nonvanishing only at the sheet boundary and accordingly are called edge states. Such states were predicted to be localized at clean zigzag edges [
16,
17,
18,
19], or more generally, at parts of the boundary where the particle-hole sublattice symmetry is not broken [
20]. Previous studies focused on these edge states [
21]. They occur in the energy region where the dispersion relation of graphene is linear [
2,
3]. The band structure, however, becomes more complex with increasing energy and eventually the dispersion relation becomes quadratic [
22]. The transition takes place at the van Hove singularities in the DOS, which generally occur in two-dimensional crystals with a periodic structure [
23]. There, the wave functions exhibit a further peculiar feature both in square and in hexagonal lattices, namely striped flexural modes, which, when frozen, produce the so-called ripples. Various edge geometries and edge states have been studied experimentally in graphene [
24,
25,
26,
27]. Furthermore, van Hove singularities have been observed in measurements [
28,
29,
30,
31,
32]. In the vicinity of a van Hove singularity, the DOS diverges logarithmically. Accordingly, arbitrarily weak distortions in the graphene structure might produce large effects in the electronic properties. Similarly, edge states might be affected by distortions of the edge structure, which, actually, were detected in the experiments. We present results on the robustness of the localization exhibited by the wave functions at zero energy [
21] and at the van Hove singularities with respect to perturbations in the lattice structure and to the choice of the boundary shape. In addition, the connection with soft membranes will become apparent when analyzing the wave functions.
The algebraic method can be used both for bosons and fermions (electrons). The structure of the equations is identical and depends only on the symmetry of the unit cell of the lattice, for the honeycomb lattice. The problem of out-of-plane vibrations of the lattice is therefore formally identical to that of the electronic band structure of the lattice, except for the replacement of boson operators with fermion operators. The only difference is that, while for bosons, we can put any number at each site, for fermions, we can put only one at each site (or two if spin is taken into account). This analogy will be also briefly mentioned.
First, we briefly outline the main features of the algebraic model in
Section 2. The associated algebraic Hamiltonian, actually, has a structure similar to that of the corresponding tight-binding Hamiltonian [
2]. In
Section 3 and
Section 4, we review the salient features of the wave functions of finite-size square and hexagonal lattices, respectively. Finally, we investigate in
Section 5 the unusual localization properties of the wave functions in terms of participation ratios. Here, we consider hexagonal lattices of rectangular and of Africa shape. Classical billiards of corresponding shapes exhibit integrable and chaotic dynamics, respectively. In References [
33,
34], the spectral properties of artificial graphene billiards of these shapes were studied experimentally and shown to depend on the properties of the classical dynamics. Similarly, we will demonstrate that the choice of a hexagonal lattice with the shape of the billiard with chaotic dynamics leads to stronger localization of the edge states and the states in the vicinity of the van Hove singularities than that with integrable dynamics.
2. Algebraic Model
The algebraic model of crystal vibrations, denoted in short here AMC, has been introduced in detail in Reference [
12]. Therefore, we will review only briefly its main ideas. The AMC consists in inserting an algebra
g at each site
i and coupling the algebra at site
i with that at site
j. The model is a generalization of the algebraic approach to molecules (0D) [
13]. For one-dimensional (1d) vibrations, the algebra is
, for two-dimensional (2d) vibrations, it is
, and for three-dimensional (3d) vibrations, it is
. One-dimensional vibrations have been studied both in molecules (0D) [
14], and in polymers (1D) [
15,
35,
36]. Applications to 2D lattices were introduced in [
12], where both harmonic and anharmonic vibrations were studied.
The
algebra at each site can be realized with two boson operators
[
37]. The elements of
are
For harmonic vibrations, we need to consider only the Heisenberg–Weyl algebra
obtained from Equation (
1) by the process of contraction [
38].
The algebraic Hamiltonian of the lattice takes then the general form
where the sum goes over the
n lattice sites. The last term is also called “hopping” or “exchange” Majorana operator
because it was introduced by Majorana in 1937 [
39] in the context of nuclear physics. Within the algebraic theory of molecules [
13], it was introduced in 1991 [
14]. This Hamiltonian is identical to that of the Bose–Hubbard model [
40], except that, for applications in crystal vibrations,
is large and positive, and
U,
V are small,
. In this article, we take
and consider the simplified form
where we have expanded the Majorana interaction into one between nearest neighbors with interaction coefficient
, and one between next-to-nearest neighbors with coefficient
, etc. The coefficients
are symmetry adapted to reflect the symmetry of the unit cell. Our sign convention for these coefficients is that of Reference [
12], and they are assumed to be positive.
In a previous publication [
12], we have studied the energy eigenvalues of the Hamiltonian Equation (
4) and, from those, we have obtained the EDR and the DOS for linear (1D), square and hexagonal (2D) lattices, with symmetry
,
, and
, respectively. In this article, we study the corresponding eigenfunctions. In particular, we consider here the fundamental vibrations of the lattice, obtained by diagonalizing the Hamiltonian Equation (
4) in the
n-dimensional basis
where
denotes the state with one quantum of vibration (phonon) at location
i. The wave functions in this basis, called the local basis, are written as
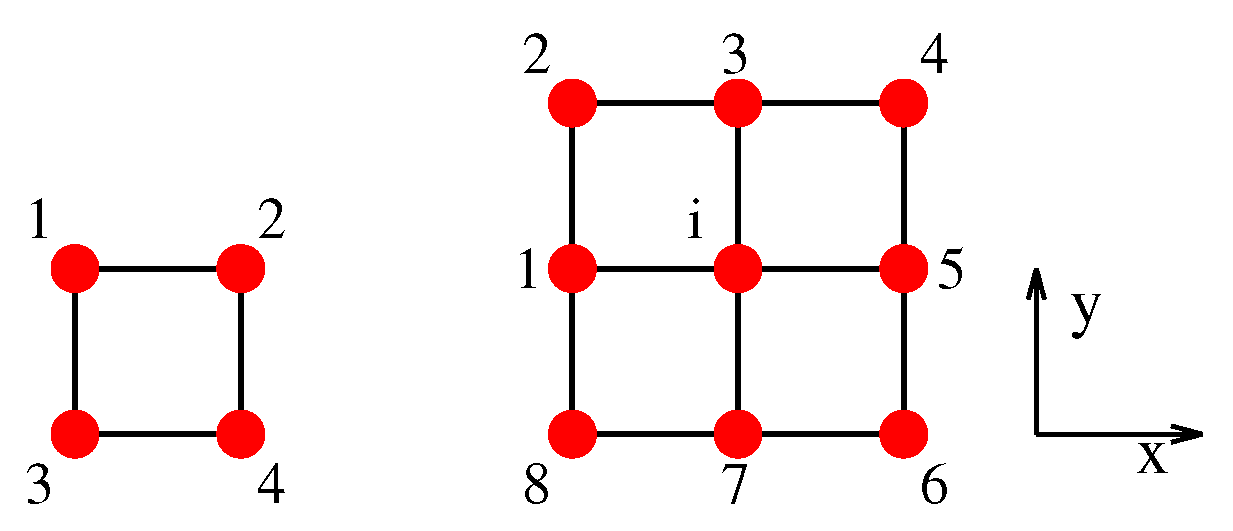
3. Square Lattice
The symmetry adaptation of this lattice,
Figure 1, was discussed in [
12]. The basis vectors
and
generating the lattice and the reciprocal lattice, respectively, are given as
Within a unit cell, with symmetry
, we have two types of interactions, nearest-neighbor,
, and next-to-nearest neighbor,
. The coordinates of the four nearest neighbors of the atom at lattice site
i in
Figure 1 are given as
those of the next-to-nearest neighbors by
The EDR including both interactions is given by [
9]
Here,
and
are the components of
in the reciprocal lattice basis,
, and the sign convention for
is that of [
12,
41]. Accordingly, in terms of the components
and
, the EDR is given by [
12,
41,
42]
In
Figure 2, we show the corresponding energy surface (left) and the plot of isofrequency contours (right) in the quasimomentum plane
.
The DOS is obtained from Equation (
11) by integration,
where
is Dirac’s
-function. For
it is given by [
12]
where
and
is a complete elliptic integral of the first kind. For
, i.e., only nearest-neighbor interactions, the DOS takes the simple form
Both in Equations (
13) and (
14), the DOS has a logarithmic singularity, called a van Hove singularity [
23] (vHs). The upper panels in
Figure 3 show the DOS for six different values of
with
fixed for a finite-size square shaped square lattice with
sites and Dirichlet boundary conditions. Equation (
11) provides the EDR of an infinitely extended square lattice. For a finite-size sheet, the values of
and
are discretized, depending on the shape of the sheet. Numerically, the determination of the eigenvalues and wave functions of a lattice with
N atoms involves the diagonalization of an
N-dimensional matrix. The eigenvector component
, with
and
denoting the discretized coordinates
and quasimomenta
, respectively, yields the amplitude of the wave function associated with the eigenvalue at the corresponding lattice site [
43].
We also determined the quasimomenta corresponding to the eigenstates. For this, we computed the momentum distributions, which were obtained from the Fourier transform of the wave functions
,
It is peaked at the quasimomenta associated with the state .
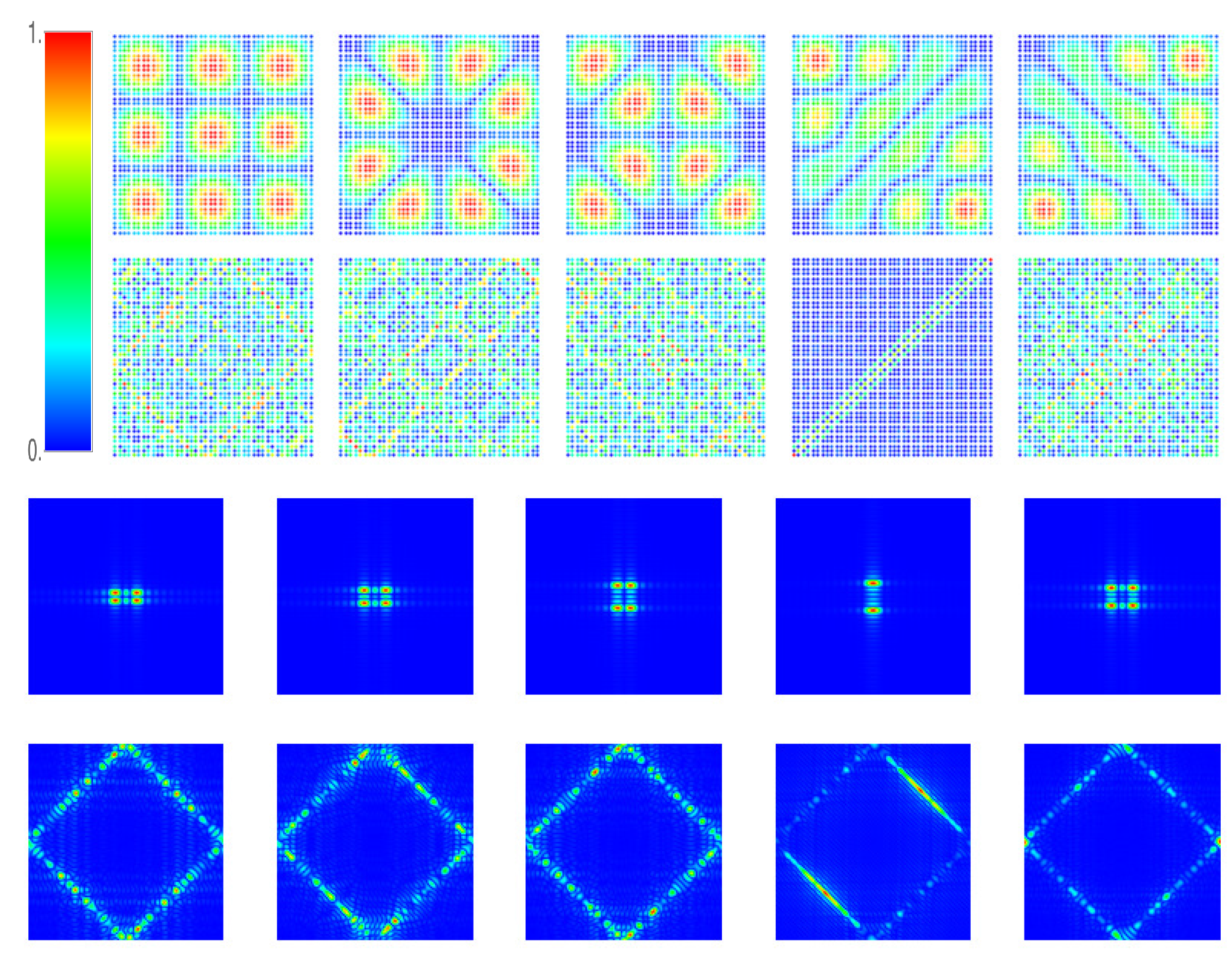
We display examples for these wave functions and the associated momentum distributions in
Figure 4. We consider to this end the case of a square shaped lattice with
sites, which was cut out parallel to the basis vectors
from an infinitely extended square lattice. The total number of states is here
. In
Figure 4, we show the squared wave functions, i.e., the intensities
, obtained numerically by diagonalizing the Hamiltonian Equation (
4). At the lower band edge, shown in the first row of
Figure 4, the wave functions represent vibrations of the lattice as a membrane. Around the vHs at
, shown in the second row of
Figure 4, we have the occurrence of some unusual features consisting of stripes, particularly evident for the wave function
. This spatial localization will be discussed further in
Section 5. At the upper the band edge the wave functions represent again membrane-like vibrations of the lattice. These wave functions, with the index counted from the upper band edge down, differ from those counted from the lower band edge up only in the signs of their components. The figures also include momentum distributions. They are peaked around the minimum and the maximum of the EDR for eigenvalues close to the band edges, and along the equipotential contour connecting the saddle points of the EDR around the van Hove singularities.
The results in
Figure 4 are for a square lattice with square-shape and Dirichlet boundary conditions. Similar studies have been done for square lattices with a rectangular shape of the boundary. Furthermore, we considered square and rectangular shaped sheets, which were cut out of a square lattice not along the rows of the square lattice but along diagonal lines, i.e., along next-to-nearest neighbor atoms. For a square-shaped boundary, the wave function patterns are similar to those shown in
Figure 4 at the band edges. This is in accordance with the findings of Reference [
33], that, at the band edges, the spectral properties of a lattice only depend on the shape of the sheet. At the van Hove singularities, we again observe the occurrence of stripes in the wave function patterns; however, here they are parallel to the sides of the sheet, not to the diagonal as in
Figure 4. In conclusion, the striped structure of the wave functions observed at the van Hove singularities persists independently of the shape of the sheet.
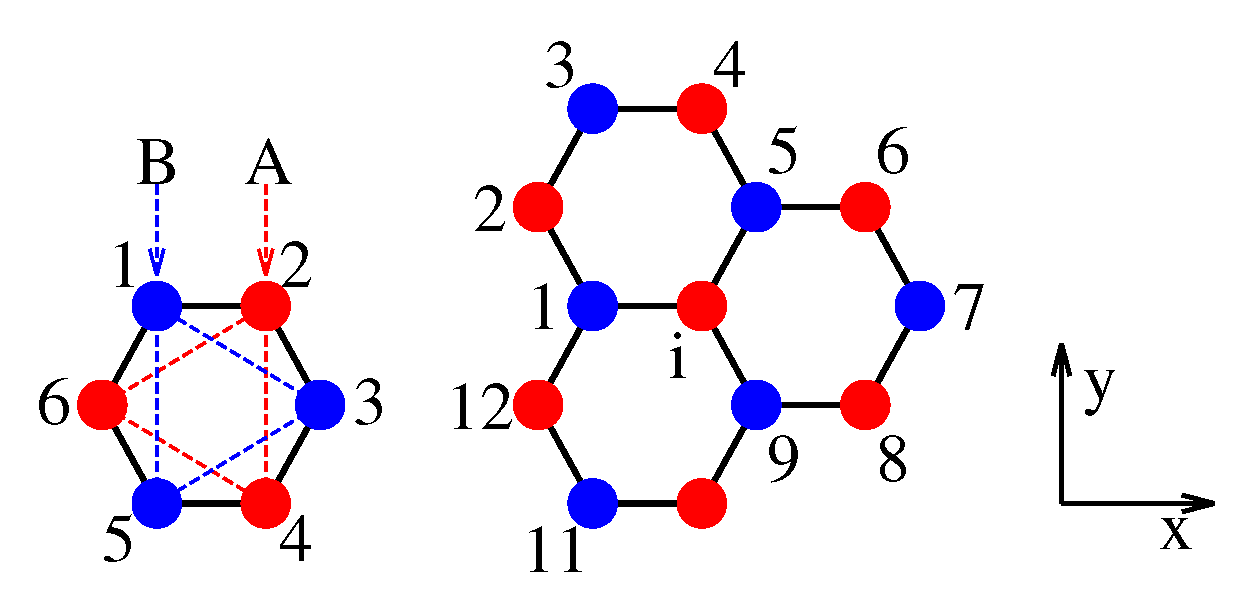
4. Hexagonal Lattice
The spectral properties of the hexagonal lattice are of particular interest in applications to graphene [
2] and artificial graphene [
22,
33,
44]. The symmetry adaptation of this lattice,
Figure 5, was discussed in [
12]. The unit cell can also be viewed as composed of two triangular subcells A and B. The basis vectors
and
generating each triangular lattice and the reciprocal lattice, respectively, are given as
with
a denoting the distance between neighboring atoms. Within the unit cell, with symmetry
, we have three types of interactions, nearest neighbor,
, next-to-nearest neighbor,
, and third neighbor,
. The interaction
couples atoms within the same subcell, while
and
couple atoms in subcell A with those in subcell B. The coordinates of the three nearest neighbors of the atom at lattice site
i in
Figure 5 are given as
Since the hexagonal lattice is composed of two interpenetrating triangular lattices, one has to diagonalize a
matrix
in order to obtain the EDR for an infinite-size hexagonal lattice [
4]. Taking into account only nearest-neighbor interactions, the off-diagonal elements are given as
Choosing
, the diagonalization of Equation (18) yields for the EDR in terms of the components
and
of
in the reciprocal lattice basis
and with
,
in the
plane
The EDR including the next-to-nearest neighbor interactions is given by [
2,
12]
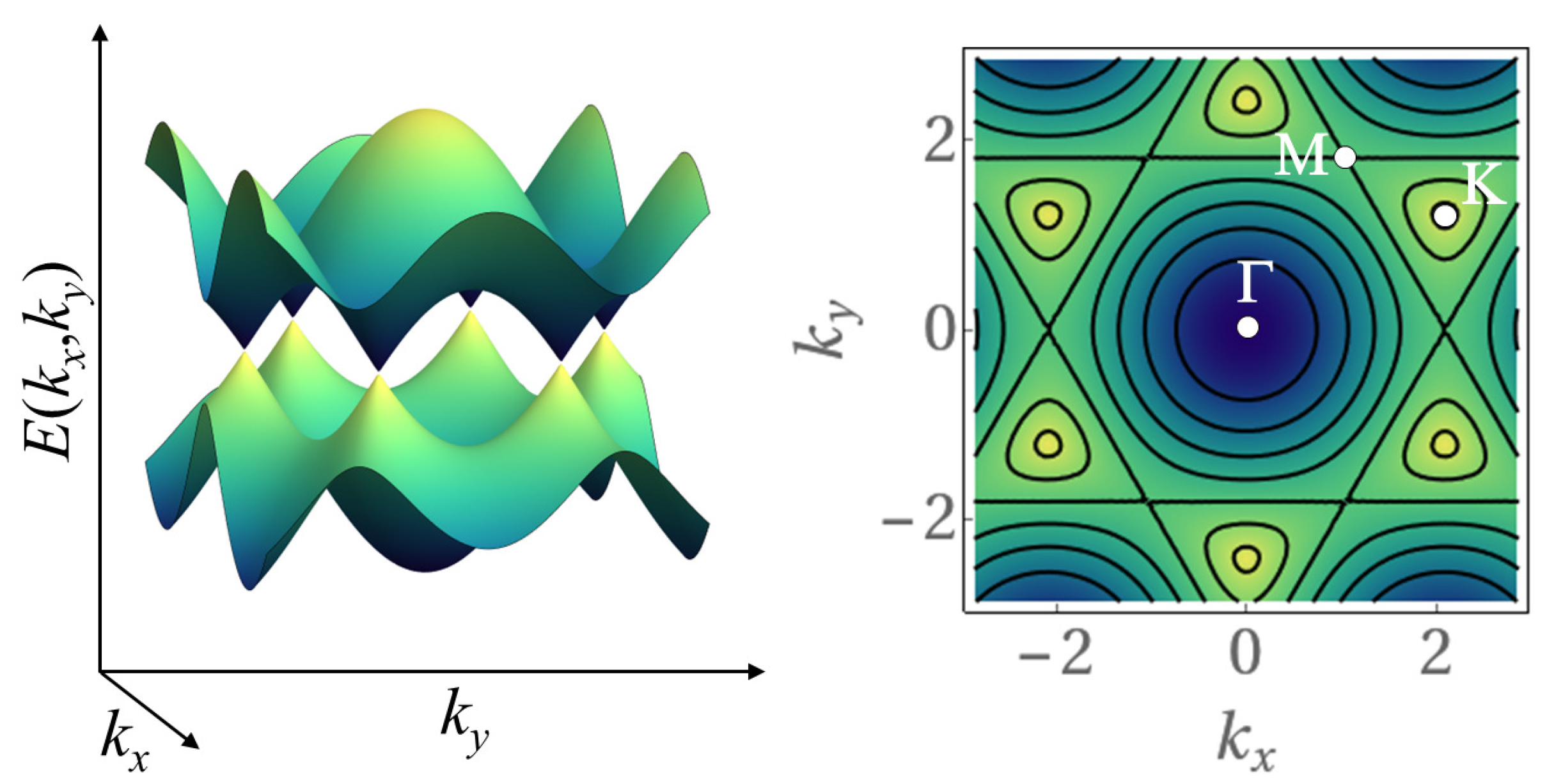
Figure 6, left panel, shows the two sheets of the energy surface, Equation (21), of an infinite size hexagonal lattice, in the quasimomentum plane
, where
and
are varied within the first Brillouin zone. The energy surfaces touch each other conically at the corners of the first Brillouin zone. The right panel shows the corresponding plot of isofrequency contours in the quasimomentum plane
.
The DOS associated with Equations (20) and (21) can be written in explicit analytic form [
45] in terms of an elliptic integral
where
,
,
. This function has two van Hove singularities (vHs
) at
and a Dirac point (DP) at
. Equations (
21) and (
22) provide the EDR of an infinite-size hexagonal lattice. We are interested in wave function properties of finite sheets. The corresponding quasimomentum components
take discrete values
, which depend on the shape of the sheet. Furthermore, for finite-size lattices, the DOS has an additional peak at
. The upper panels in
Figure 7 show the DOS of a hexagonal lattice with Africa shape [
22,
34] and Dirichlet boundary conditions for six different values of
with
fixed and
. The peak at
is attributed to the edge states that are localized along the zigzag edges in the lattice structure. Note that the positions of the van Hove singularities vHs
and also of the DP are slightly shifted with increasing
as expected from tight-binding model calculations [
46].
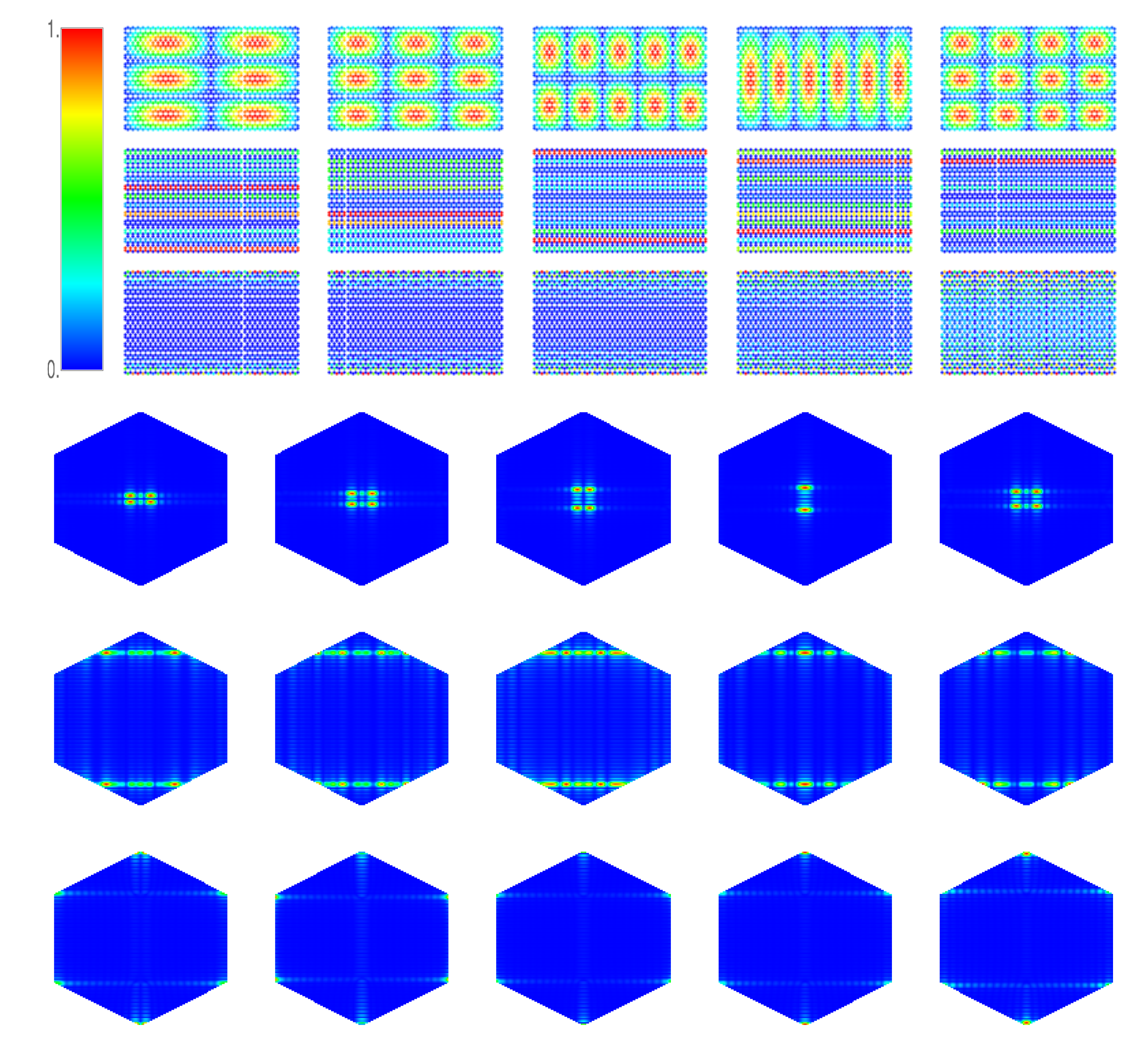
For the general case of a sheet with
N sites, the energies and wave functions can be obtained by diagonalizing an
N-dimensional matrix. We show in
Figure 8 the wave functions of a hexagonal lattice with rectangular shape with
sites and Dirichlet boundary conditions, including both space and momentum distributions. The zigzag edges are parallel to the longer sides of the rectangle and the lattice consists of in total 24 rows of 34 and 35 lattice sites, respectively. At the lower band edge, see the first row of
Figure 8, the wave functions represent vibrations of the lattice as a membrane, similarly as in the square lattice. Around the vHs
, shown in the second row of
Figure 8, the wave functions exhibit a striking structure consisting of stripes along interior zigzag lines. This behavior, already seen in the square lattice, is even more pronounced here. Around the DP, see the third row of
Figure 8, we observe the above mentioned edge states. Their wave functions are concentrated at the zigzag edges of the lattice, and are vanishingly small everywhere else. The situation repeats at the vHs
, with clear stripes, and at the upper band edge, with membrane-like vibrations. The only difference between the wave functions at the lower and upper band edges is the sign of wave-function components at the sites of the lattice,
. The fourth to sixth rows in
Figure 8 show the corresponding momentum distributions. Near the lower band edge (fourth row), they are peaked around the
point of the EDR, on equienergy lines of the M points close to the vHs (see fifth row) and around the K points in the vicinity of the DP (sixth row).
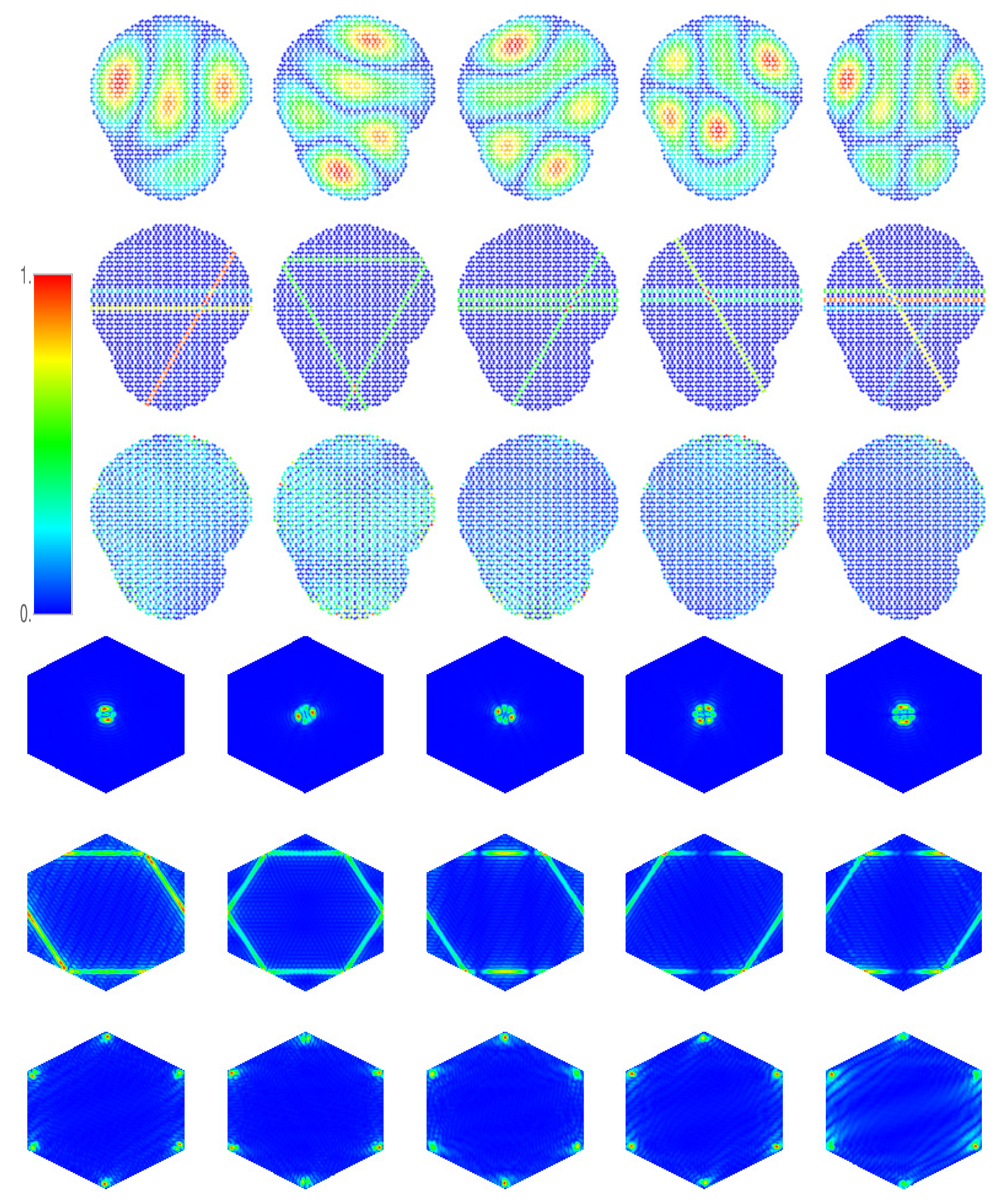
The results in
Figure 8 are for a rectangular shape of the lattice. In view of the remarkable properties of the wave functions at the van Hove singularities, we have also investigated the wave functions for more complicated shapes, in particular the Africa shape [
22,
34,
47,
48,
49]. We show in
Figure 9 again the wave functions at the lower band edge (first row), the vHs
(second row), and the DP (third row) for Dirichlet boundary conditions. For such shapes, we also observe the extraordinary features described in the paragraphs above. In addition, at both van Hove singularities, the stripes appear along
all three equivalent zigzag directions. Two of these, inclined at angles
to the horizontal axis, were not seen in the rectangular shape due to boundary effects. In addition, the momentum distributions are extended to the whole hexagonal equienergy contour corresponding to the vHs, in contrast to the rectangular shape, fifth row in
Figure 8.
5. Localization Properties
We illustrated in the previous sections that the wave functions of the square and hexagonal lattice are localized into stripes at the van Hove singularities and for the latter in addition at the zigzag edges around the DP. In this section, we quantify the localization in terms of participation ratios [
50,
51] in the local basis, defined for 2D lattices through the wave function components
at sites
with
denoting the discretized quasimomenta
as
Similar results are obtained for the Shannon entropy [
52]. Note that, in order to reproduce the DOS of real graphene, nonzero second- and third-neighbor interactions had to be introduced [
9,
53]. Accordingly, we are particularly interested here in how localization is influenced by (i) the addition of second- and third-neighbor interactions, and (ii) noise affecting the hopping coefficients
,
and
. For this, we keep
fixed and vary
and
. Since, in general, in a square lattice
, we can neglect it in the study of their localization properties. In hexagonal lattices, on the other hand,
[
33], so, in the corresponding studies, we simply chose
and
and
with opposite sign [
54].
Figure 3 shows the DOS (upper panels) and the corresponding participation ratio of the fundamental vibration of a square lattice with Dirichlet boundary conditions and square shape for six different values of
. Here, the values of the hopping coefficients
are the same for each lattice site. We see from this figure that around the vHs-energy
, states of increased localization persist even for large values of the relative strength
of the second-neighbor interactions, identified by small values of
around the singularity. However, a close inspection reveals that the minimum
jumps abruptly from
at
to a value saturated at
, for an infinitesimally small value
, as checked numerically down to
. The corresponding striped eigenstate for
is nonvanishing only along one of the diagomals and the two neighboring ones. For
, it spreads into states resembling the eigenstates of a lattice with pure second-neighbor interaction, i.e.,
(not shown here), in which the vibration involves only one half of the lattice sites. This is reflected in the fact that the saturation value of
at the vHs for
equals one half of the value corresponding to the ground state, which is
, indicating that the wave function components are nonzero on one half of the sites. Accordingly, stripes are not present in the square lattice for
independently of the shape of the boundary.
Figure 7 shows the participation ratios of the fundamental vibrations of the hexagonal lattice with an Africa shape. The corresponding results for a rectangular shape are not shown because they are qualitatively similar to those for the Africa shape. As stated above, we included third-nearest neighbor interactions in this case where we chose
. Similarly to the situation in the square lattice discussed above, this figure indicates remarkable localization properties. In particular, the minimum value of
at the DP (
) is practically independent of
, underlining the robustness of the edge states. However, the minimum values of
near the lower and the upper van Hove singularities (
) show a jump at small values of
, from
to
for the Africa shape and from
to
for the rectangular one. These values for
already indicate that the localization as compared to the ground state, where
equals half the number of sites, is stronger in the former case than in the latter. In contrast to the square lattice, the peculiar striped states persist for the van Hove singularities even though they are broader above
as indicated by the respective participation ratio. Above
, a third peak appears in the DOS near the upper band edge. There, at the vHs
, the stripes disappear with increasing
and the wave functions become more and more localized at the armchair edges, that is, e.g., in the hexagonal lattice with rectangular shaped at the shorter sides. This is illustrated in the upper rows of
Figure 10 and
Figure 11.
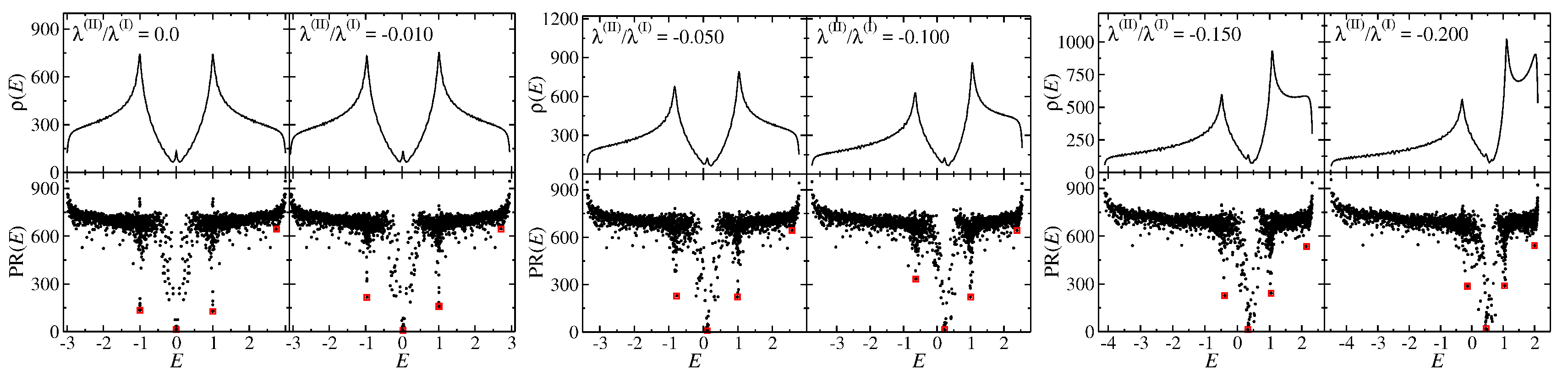
Examples are shown for wave functions at minimal values of the participation ratio close to the vHs, the vHs and the peak in the DOS appearing above for . In both cases, the wave functions are localized in broadened stripes along interior zigzag edges at the vHs, strongly localized at armchair edges at the vHs and within the lattice at the third peak in the DOS. Note that this feature at the vHs is opposite to that near the DP, where the wave functions are localized at the zigzag edges. This persistence of the striped structure at vHs and its disappearance at the vHs and the simultaneous increase of the localization at the armchair edges is reflected in the corresponding participation ratios.
Substantially different behaviors between the square and the hexagonal lattices are observed under the influence of noise. We introduce the noise by generating individual hopping coefficients
,
at each site
in the general Hamiltonian of Equation (
3) randomly with a uniform distribution, yielding
, where we again set
. Here,
denotes the average value across the whole lattice and
denotes the noise strength with respect to
at site
.
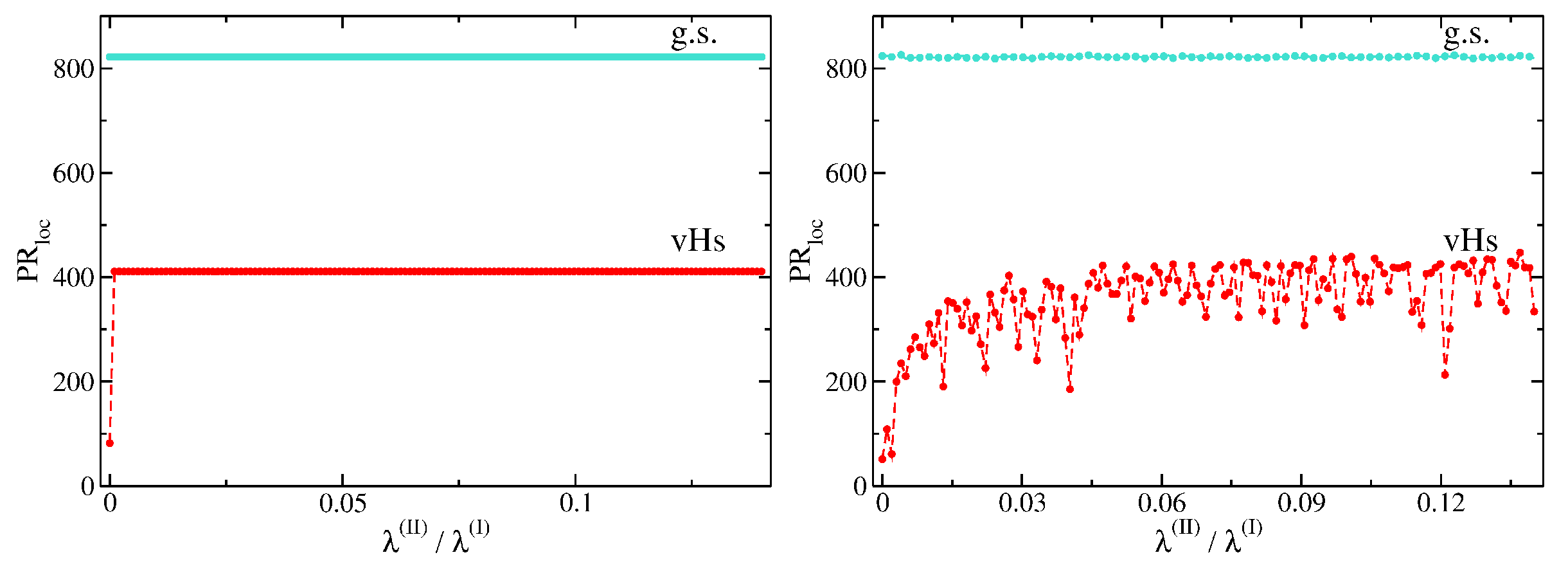
In
Figure 12, we show the evolution of the participation ratios of the vHs-states compared to that of the ground states (g.s.) of the square lattice as a function of
without noise (left) and with noise of relative strength
(right). Note that the state with
in the noiseless case at
is due to the formation of stripes in the wave function structure (see
Section 5). Evidently, noise leads to an enhancement of localization at the vHs for
. For
, the wave function is nonvanishingly only along one of the diagonals, as reflected in the corresponding participation ratio,
. With increasing
, the eigenstate at the vHs delocalizes not abruptly, but smoothly until it saturates at
for
.
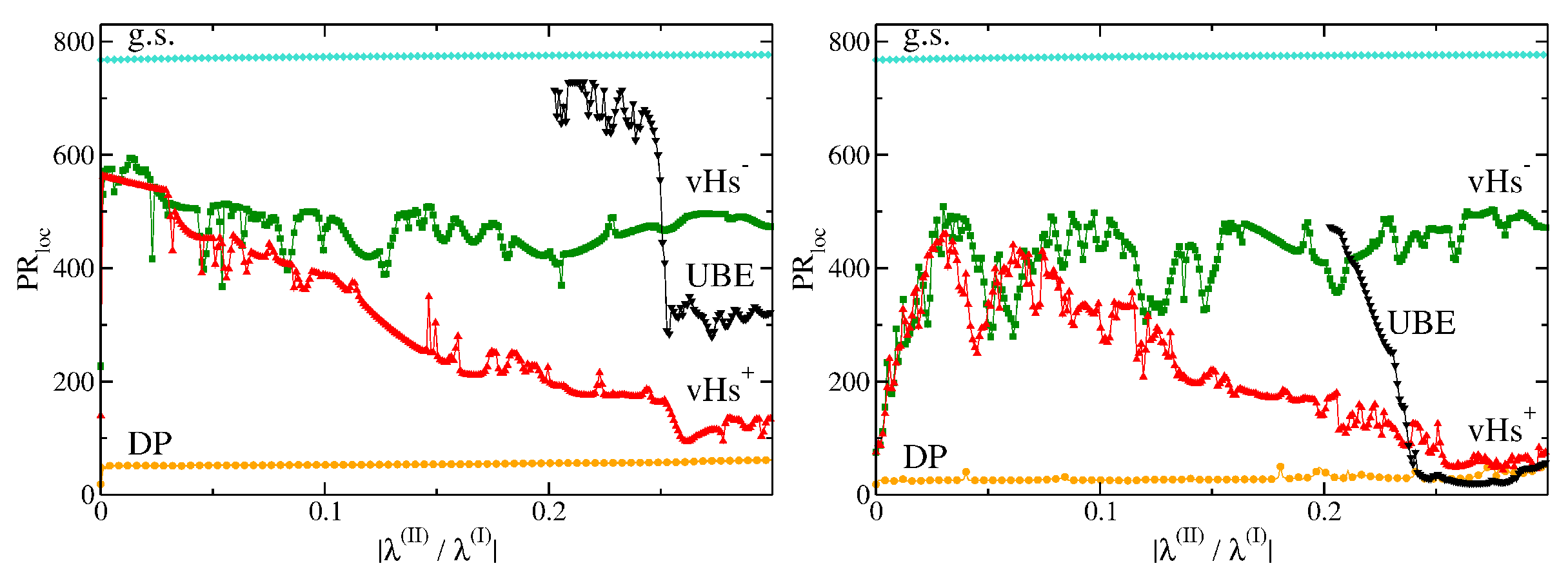
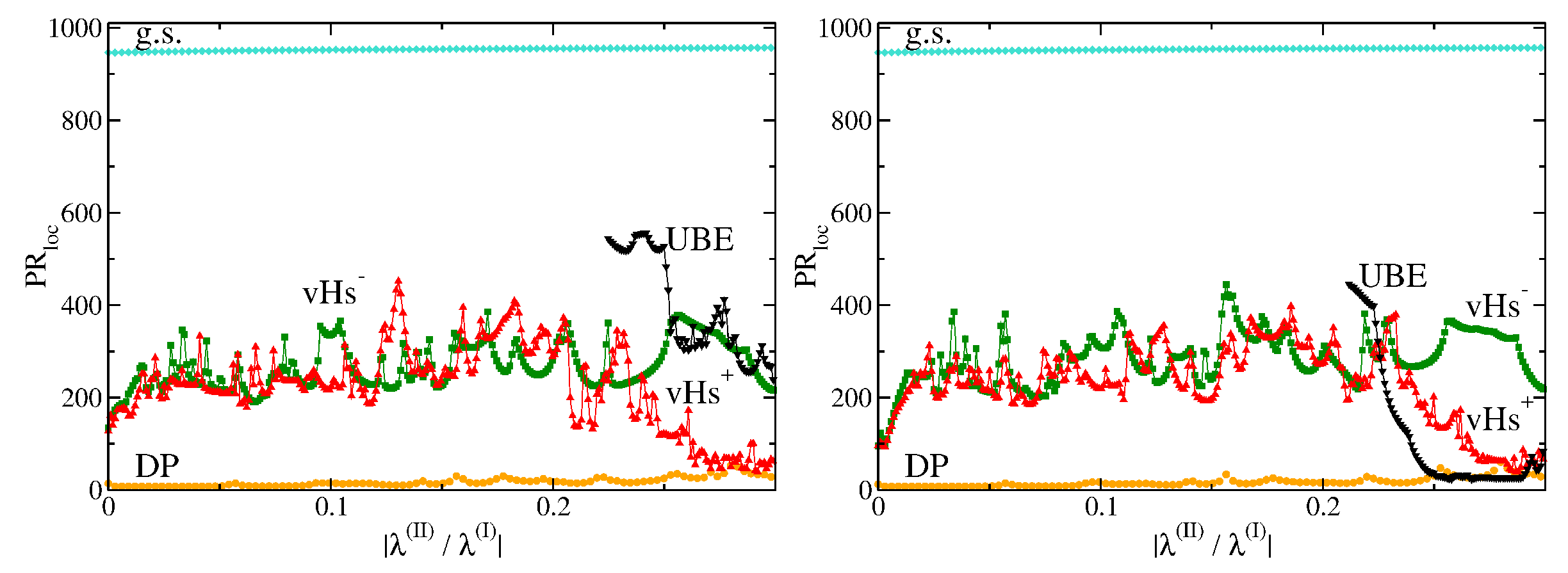
Similarly to the square, the noise in the hexagonal lattice acts against, and surpasses, the effect of delocalization caused by the second- and third-neighbor interaction, as can be seen in
Figure 13 and
Figure 14. Compared to the noiseless situation with an abrupt jump for
(left panels), in the noisy case, increasing
induces instead a gradual rise in
(right panels). In contrast to the square lattice, the localization of the striped states at the vHs
is enhanced in the noiseless case even for
, where saturation of the participation ratio takes place. The minimal participation ratio at the vHs
gradually decreases with increasing
for the rectangular shape both with and without noise until it saturates at around
similar to that at the third peak appearing in the DOS above
. The localization of the latter is considerably enhanced when turning on the noise. Similar results are obtained for the Africa shape; however, there the minimal participation ratio at the vHs
starts to decrease only at
, simultaneously with the occurrence of the third peak in the DOS at the upper band edge.
In all, the localization is stronger in the hexagonal lattice with the shape of a classically chaotic Africa billiard than in that with the shape of a rectangle with classically integrable dynamics. From these observations, we may conclude that both the introduction of noise and the choice of the shape of a billiard with classically chaotic dynamics enhance the localization at the peaks in the DOS. The comparison of the wave functions in the upper and lower rows of
Figure 10 and
Figure 11 clearly corroborates this behavior.
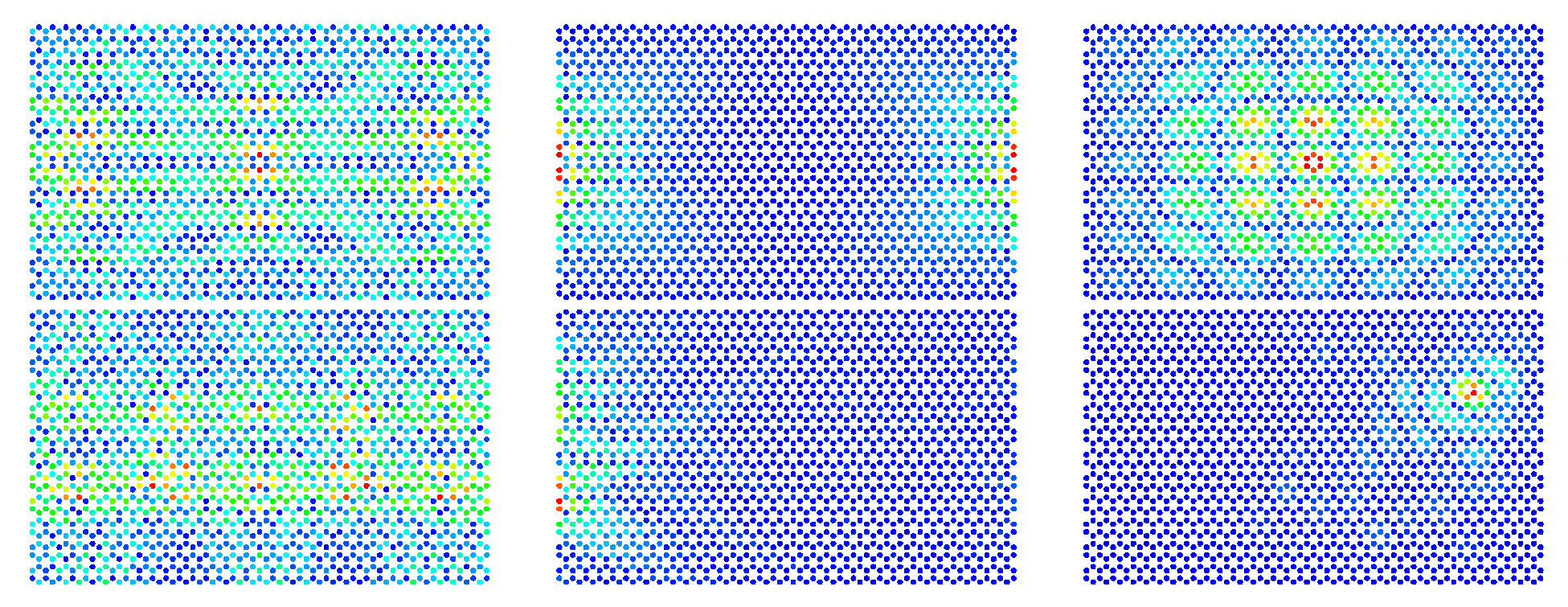
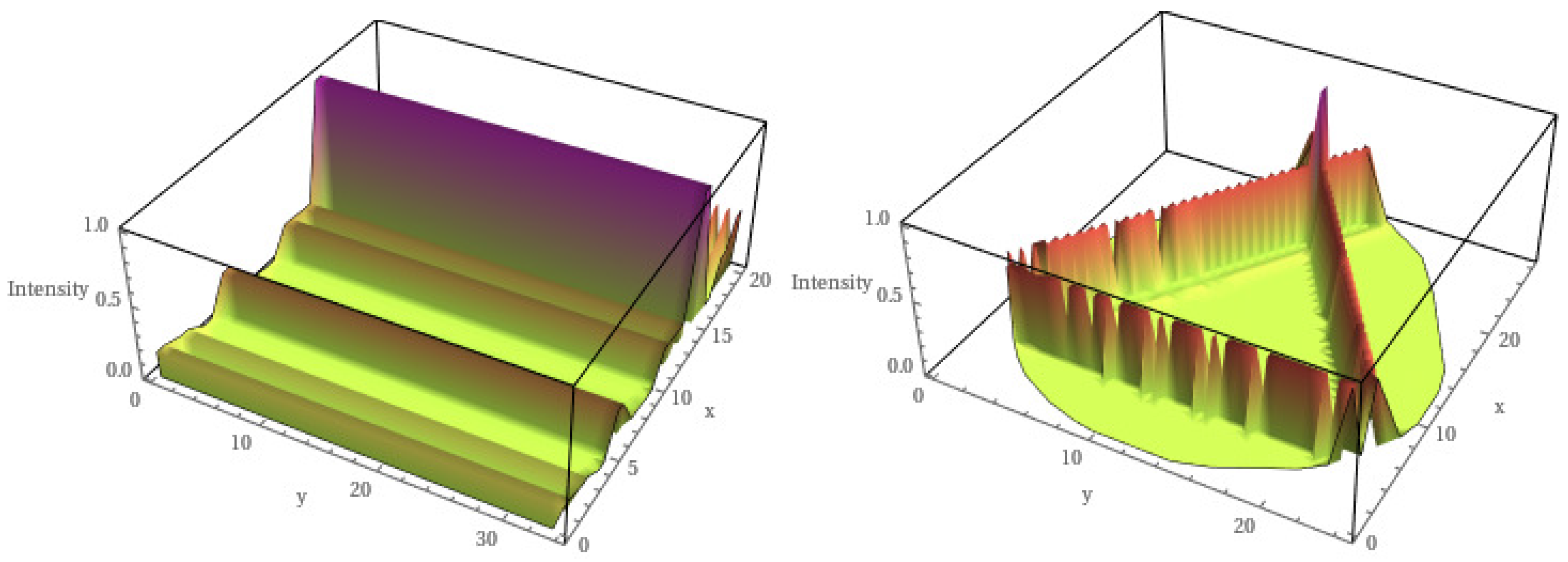
Finally, in order to illustrate the main object of study of this article, i.e., the striped structure in the wave functions, we show in
Figure 15, the smoothed probability density
corresponding to such vibrations at the van Hove singularities of hexagonal lattices with rectangular (left) and Africa-shaped (right) boundaries. This figure shows clearly the ripples of flexural modes in graphene-like materials.
We also note that physically relevant values of
are
for a Lennard–Jones potential,
for artificial graphene [
12] and
for graphene [
53], thus we expect that the effects discussed above can be realized experimentally. Although we do not report it, these localization properties persist also for other shapes of the boundary, like sectors from a circle [
55].
In our previous papers [
12,
22], a connection was made between van Hove singularities and excited state quantum phase transitions (ESQPT) whose definition is given in [
56,
57]. In relation to this connection, we note that the localization properties of the
model described here appear to be the same as those of
models, described in [
58]. The explicit relation between van Hove singularities (and their associated striped wave functions) and ESQPT will be discussed in a forthcoming publication.