Analysis of Diffracted Intensities from Finite Protein Crystals with Incomplete Unit Cells
Abstract
:1. Introduction
2. Materials and Methods
2.1. Construction of a Model for the Average Diffracted Intensity Distribution
2.1.1. The Whole-Pattern Fitting Model
2.1.2. Crystal Dimensions
2.2. Simulations
2.2.1. Crystal Surfaces
3. Results and Discussion
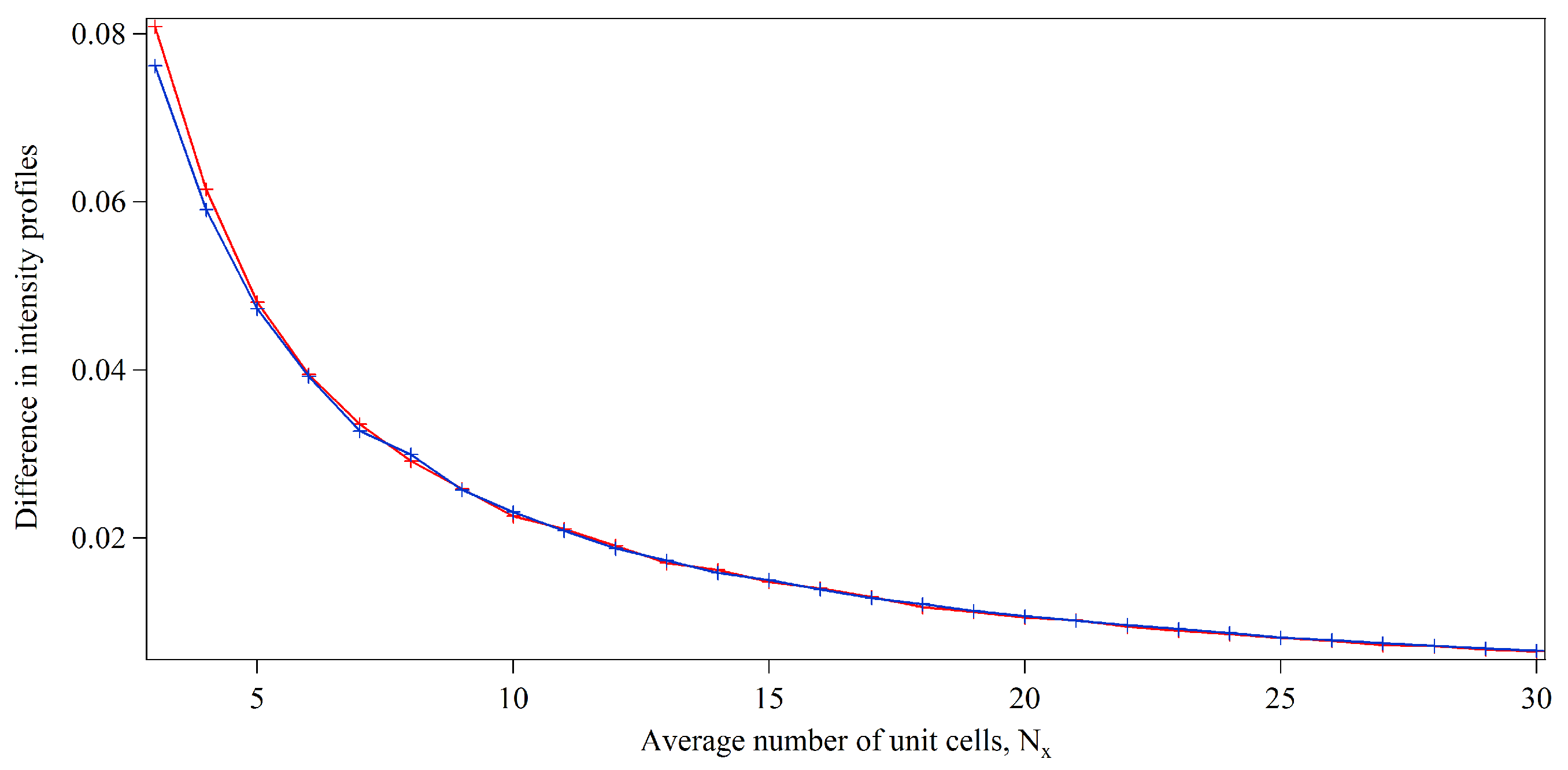
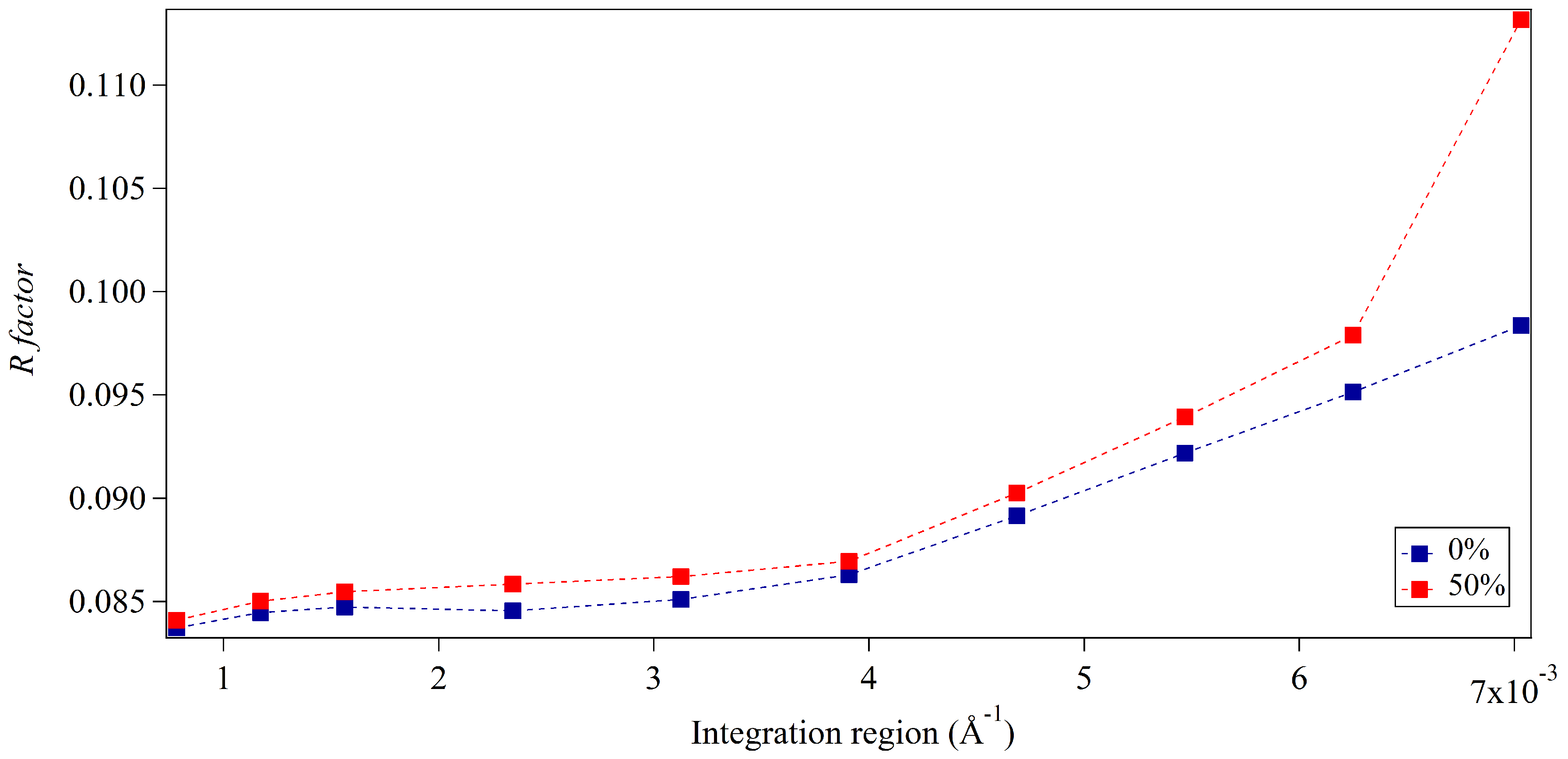
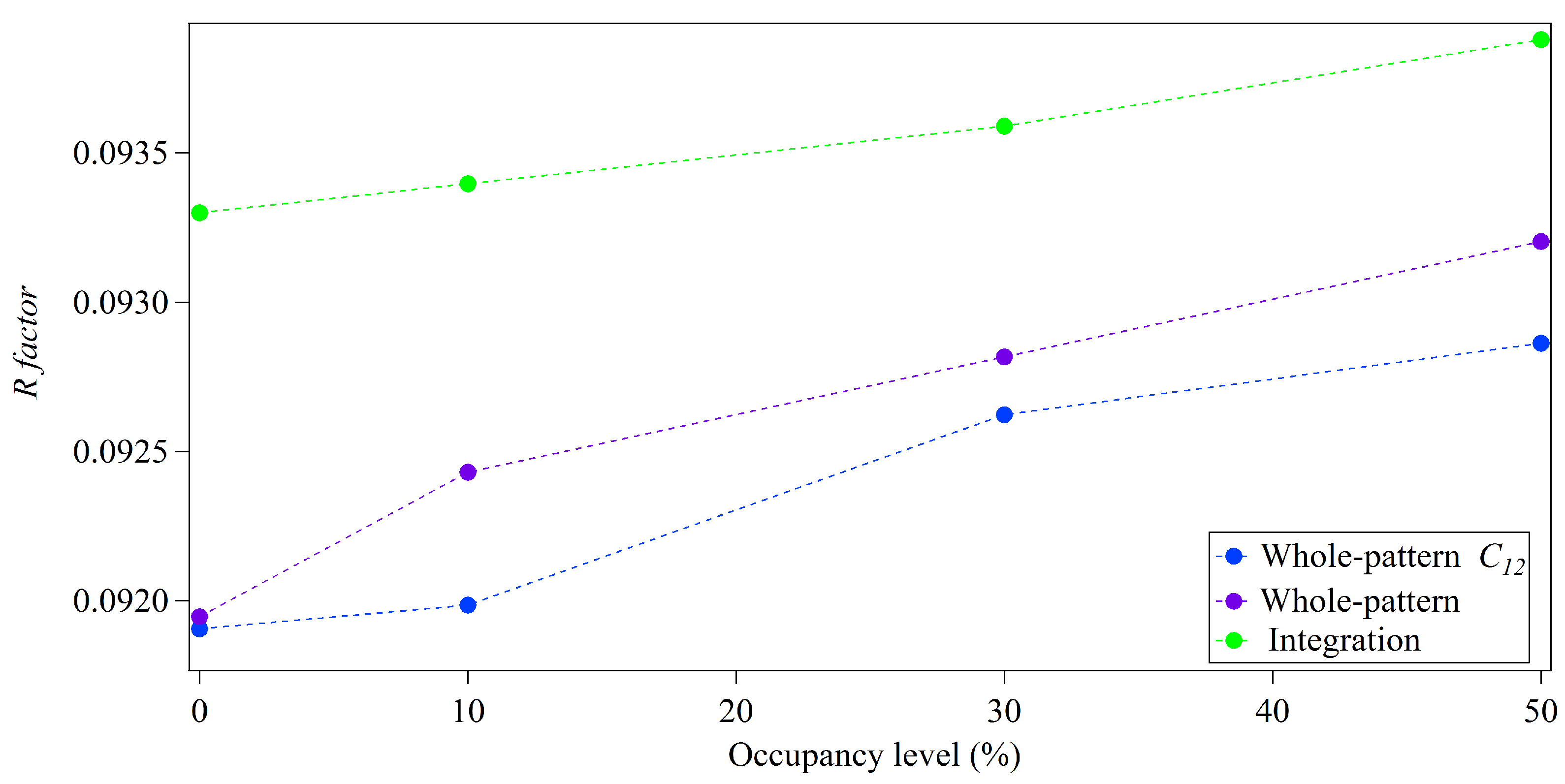
3.1. Integration Analysis for Incomplete Unit Cells
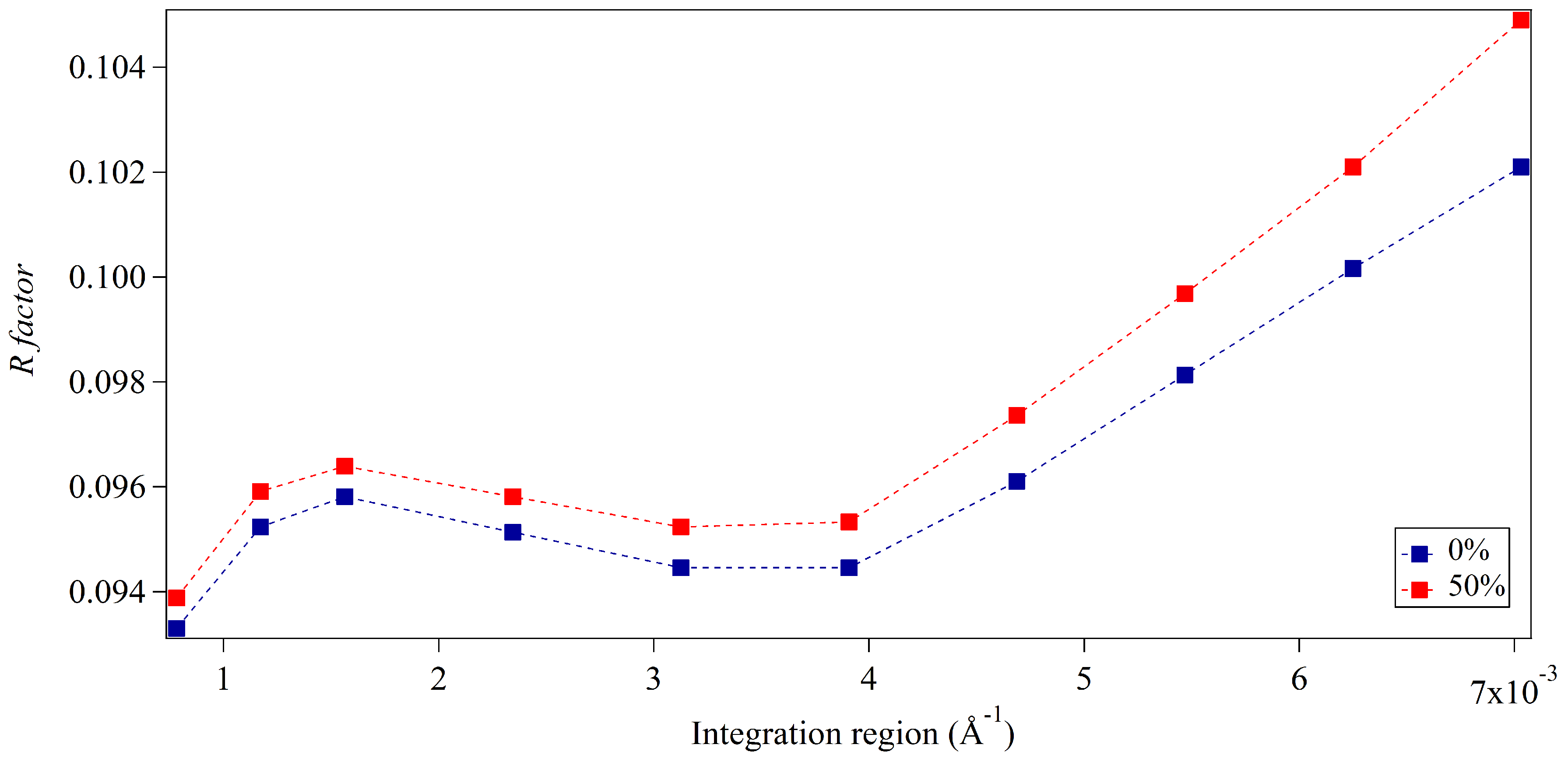
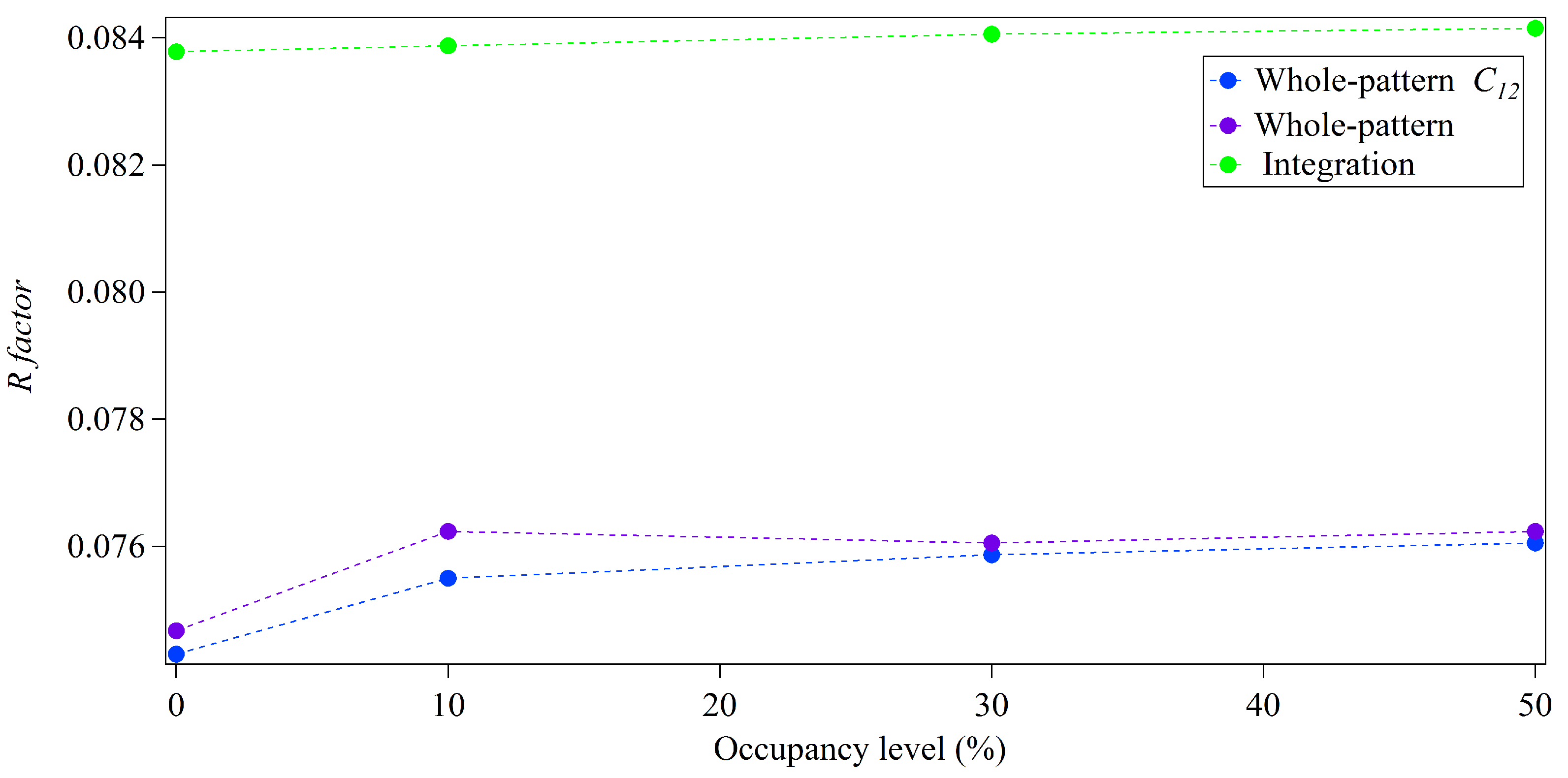
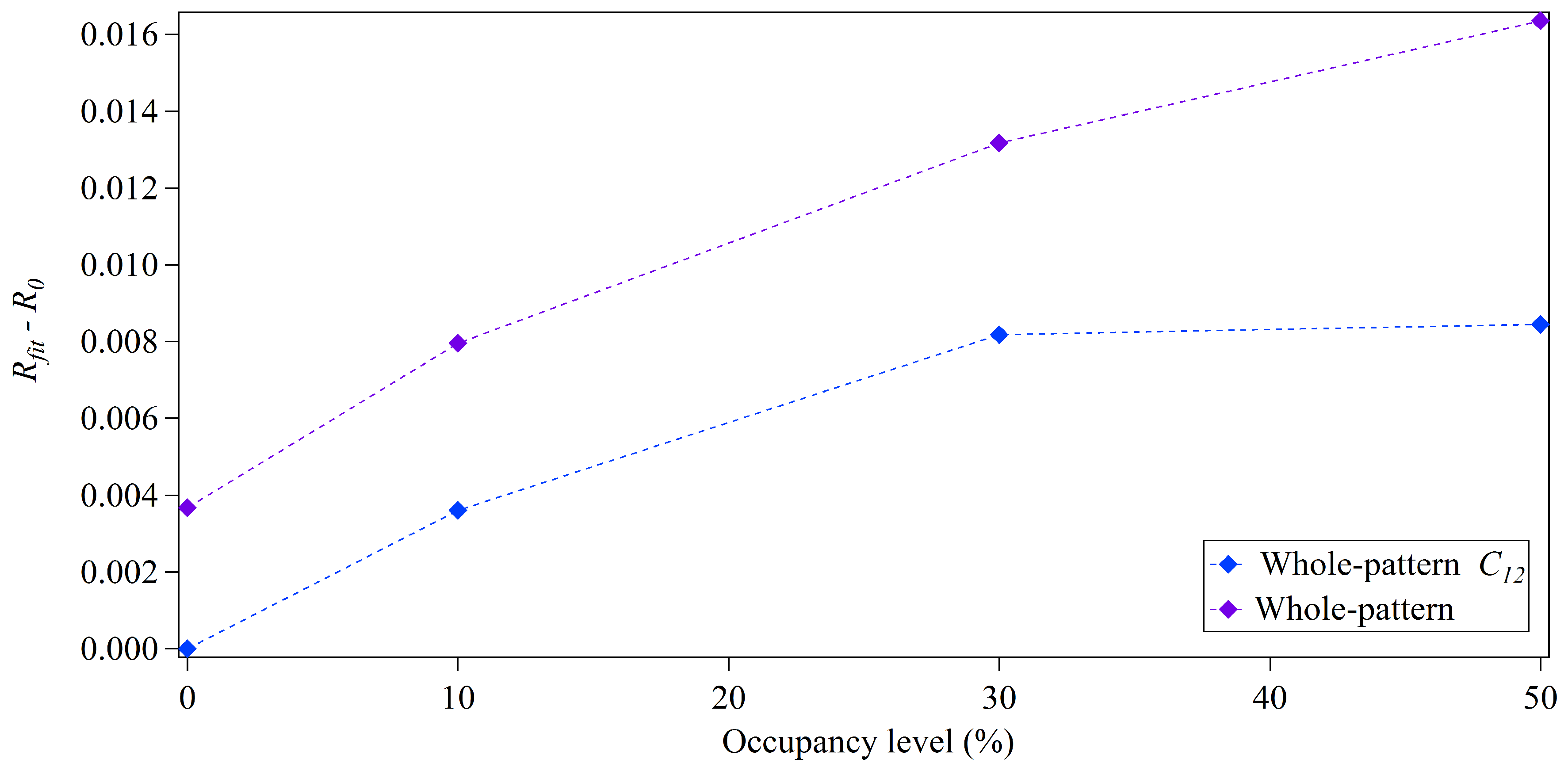
3.2. Whole-Pattern Fitting and Integration Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SXC | serial X-ray crystallography |
| XFELs | X-ray free-electron lasers |
| microED | micro electron diffraction |
Appendix A
- (1)
- Equal numbers of each sub-unit. The unit cell is defined by 1,2 packing order with .
- (2)
- Equal numbers of each sub-unit. The unit cell is defined by 2,1 packing order with .
- (3)
- . The unit cell is not defined. For this case,.
- (4)
- . The unit cell is not defined. For this case,.
References
- Chapman, H.N.; Fromme, P.; Barty, A.; White, T.A.; Kirian, R.A.; Aquila, A.; Hunter, M.S.; Schulz, J.; DePonte, D.P.; Weierstall, U.; et al. Femtosecond X-ray protein nanocrystallography. Nature 2011, 470, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Stellato, F.; Oberthür, D.; Liang, M.; Bean, R.; Gati, C.; Yefanov, O.; Barty, A.; Burkhardt, A.; Fischer, P.; Galli, L.; et al. Room-temperature macromolecular serial crystallography using synchrotron radiation. IUCrJ 2014, 1, 204–212. [Google Scholar] [CrossRef] [PubMed]
- Gati, C.; Bourenkov, G.; Klinge, M.; Rehders, D.; Stellato, F.; Oberthür, D.; Yefanov, O.; Sommer, B.P.; Mogk, S.; Duszenko, M.; et al. Serial crystallography on in vivo grown microcrystals using synchrotron radiation. IUCrJ 2014, 1, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.; Nannenga, B.L.; Iadanza, M.G.; Gonen, T. Three-dimensional electron crystallography of protein microcrystals. ELife 2013, 2, e01345. [Google Scholar] [CrossRef] [PubMed]
- Nannenga, B.L.; Shi, D.; Leslie, A.G.W.; Gonen, T. High-resolution structure determination by continuous-rotation data collection in MicroED. Nat. Methods 2014, 11, 927–930. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.; Nannenga, B.L.; de la Cruz, M.J.; Liu, J.; Sawtelle, S.; Calero, G.; Reyes, F.E.; Hattne, J.; Gonen, T. The collection of MicroED data for macromolecular crystallography. Nat. Protoc. 2016, 11, 895–904. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, G.; Basu, S.; Liu, H.; Zuo, J.M.; Spence, J.C.H. Solving protein nanocrystals by cryo-EM diffraction: Multiple scattering artifacts. Ultramicroscopy 2015, 148, 87–93. [Google Scholar] [CrossRef] [PubMed]
- Patterson, A.L. The Scherrer Formula for X-ray Particle Size Determination. Phys. Rev. 1939, 56, 978–982. [Google Scholar] [CrossRef]
- Langford, J.I.; Wilson, A.J.C. Scherrer after sixty years: A survey and some new results in the determination of crystallite size. J. Appl. Crystallogr. 1978, 11, 102–113. [Google Scholar] [CrossRef]
- Holzwarth, U.; Gibson, N. The Scherrer equation versus the ’Debye-Scherrer equation’. Nat. Nanotechnol. 2011, 6, 534. [Google Scholar] [CrossRef] [PubMed]
- Yefanov, O.; Gati, C.; Bourenkov, G.; Kirian, R.A.; White, T.A.; Spence, J.C.H.; Chapman, H.N.; Barty, A. Mapping the continuous reciprocal space intensity distribution of X-ray serial crystallography. Philos. Trans. R. Soc. B 2014, 369, 20130333. [Google Scholar] [CrossRef] [PubMed]
- Hunter, M.S.; DePonte, D.P.; Shapiro, D.A.; Kirian, R.A.; Wang, X.; Starodub, D.; Marchesini, S.; Weierstall, U.; Doak, R.B.; Spence, J.C.H.; et al. X-ray Diffraction from Membrane Protein Nanocrystals. Biophys. J. 2011, 100, 198–206. [Google Scholar] [CrossRef] [PubMed]
- Kirian, R.A.; Bean, R.J.; Beyerlein, K.R.; Yefanov, O.M.; White, T.A.; Barty, A.; Chapman, H.N. Phasing coherently illuminated nanocrystals bounded by partial unit cells. Philos. Trans. R. Soc. B 2014, 369, 20130331. [Google Scholar] [CrossRef] [PubMed]
- Spence, J.C.H.; Kirian, R.A.; Wang, X.; Weierstall, U.; Schmidt, K.E.; White, T.; Barty, A.; Chapman, H.N.; Marchesini, S.; Holton, J. Phasing of coherent femtosecond X-ray diffraction from size-varying nanocrystals. Opt. Express 2011, 19, 2866–2873. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J. Phase Retrieval Algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [PubMed]
- Miao, J.; Sayre, D.; Chapman, H.N. Phase retrieval from the magnitude of the Fourier transforms of nonperiodic objects. J. Opt. Soc. Am. A 1998, 15, 1662–1669. [Google Scholar] [CrossRef]
- Kirian, R.A.; Bean, R.J.; Beyerlein, K.R.; Barthelmess, M.; Yoon, C.H.; Wang, F.; Capotondi, F.; Pedersoli, E.; Barty, A.; Chapman, H.N. Direct phasing of finite crystals illuminated with a free-electron laser. Phys. Rev. X 2015, 5, 011015. [Google Scholar] [CrossRef]
- Liu, H.; Zatsepin, N.A.; Spence, J.C.H. Ab-initio phasing using nanocrystal shape transforms with incomplete unit cells. IUCrJ 2013, 1, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.P.J.; Millane, R.P. Diffraction by nanocrystals. J. Opt. Soc. Am. A 2013, 30, 2627–2634. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.P.J.; Millane, R.P. Diffraction by nanocrystals II. J. Opt. Soc. Am. A 2014, 31, 1730–1737. [Google Scholar] [CrossRef] [PubMed]
- Dilanian, R.A.; Williams, S.R.; Martin, A.V.; Streltsov, V.A.; Quiney, H.M. Whole-pattern fitting technique in serial femtosecond nanocrystallography. IUCrJ 2016, 3, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Le Bail, A.; Duroy, H.; Fourquet, J.L. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mater. Res. Bull. 1988, 23, 447–452. [Google Scholar] [CrossRef]
- Rodriguez, J.A.; Ivanova, M.I.; Sawaya, M.R.; Cascio, D.; Reyes, F.E.; Shi, D.; Sangwan, S.; Guenther, E.L.; Johnson, L.M.; Zhang, M.; et al. Structure of the toxic core of α-synuclein from invisible crystals. Nature 2015, 525, 486–490. [Google Scholar] [CrossRef] [PubMed]
- Sawaya, M.R.; Rodriguez, J.; Cascio, D.; Collazo, M.J.; Shi, D.; Reyes, F.E.; Hattne, J.; Gonen, T.; Eisenberg, D.S. Ab initio structure determination from prion nanocrystals at atomic resolution by MicroED. Proc. Natl. Acad. Sci. USA 2016, 113, 11232–11236. [Google Scholar] [CrossRef] [PubMed]
- Guinier, A. X-ray Diffraction in Crystals, Imperfect Crystals, and Amorphous Bodies; W. H. Freeman and Company: San Francisco, CA, USA, 1963. [Google Scholar]
- Ino, T.; Minami, N. X-ray diffraction by small crystals. Acta Crystallogr. Sect. A 1979, 35, 163–170. [Google Scholar]
- Bogan, M.J. X-ray free electron lasers motivate bioanalytical characterization of protein nanocrystals: Serial femtosecond crystallography. Anal. Chem. 2013, 85, 3464–3471. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Carney, P.J.; Chang, J.C.; Guo, Z.; Villanueva, J.M.; Stevens, J. Structure and receptor binding preferences of recombinant human A(H3N2) virus hemagglutinins. Virology 2015, 477, 18–31. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Vaguine, A.A.; Richelle, J.; Wodak, S.J. SFCHECK: A unified set of procedures for evaluating the quality of macromolecular structure-factor data and their agreement with the atomic model. Acta Crystallogr. D Biol. Crystallogr. 1999, 55, 191–205. [Google Scholar] [CrossRef] [PubMed]
- Winn, M.D.; Ballard, C.C.; Cowtan, K.D.; Dodson, E.J.; Emsley, P.; Evans, P.R.; Keegan, R.M.; Krissinel, E.B.; Leslie, A.G.W.; McCoy, A.; et al. Overview of the CCP4 suite and current developments. Acta Crystallogr. D Biol. Crystallogr. 2011, 67, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.J.C. The probability distribution of X-ray intensities. Acta Crystallogr. 1949, 2, 318–321. [Google Scholar] [CrossRef]
- Patterson, A.L. A Fourier Series Method for the Determination of the Components of Interatomic Distances in Crystals. Phys. Rev. 1934, 46, 372–376. [Google Scholar] [CrossRef]
- Kirian, R.A.; Wang, X.; Weierstall, U.; Schmidt, K.E.; Spence, J.C.H.; Hunter, M.; Fromme, P.; White, T.; Chapman, H.N.; Holton, J. Femtosecond protein nanocrystallography-data analysis methods. Opt. Express 2010, 18, 5713–5723. [Google Scholar] [CrossRef] [PubMed]
- Kirian, R.A.; White, T.A.; Holton, J.M.; Chapman, H.N.; Fromme, P.; Barty, A.; Lomb, L.; Aquila, A.; Maia, F.R.N.C.; Martin, A.V.; et al. Structure-factor analysis of femtosecond micro-diffraction patterns from protein nanocrystals. Acta Crystallogr. Sect. A 2011, 67, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Ayyer, K.; Yefanov, O.M.; Oberthür, D.; Roy-Chowdhury, S.; Galli, L.; Mariani, V.; Basu, S.; Coe, J.; Conrad, C.E.; Fromme, R.; et al. Macromolecular diffractive imaging using imperfect crystals. Nature 2016, 530, 202–206. [Google Scholar] [CrossRef] [PubMed]
- Dilanian, R.A.; Streltsov, V.A.; Quiney, H.M.; Nugent, K.A. Continuous X-ray diffractive field in protein nanocrystallography. Acta Crystallogr. Sect. A 2013, 69, 108–118. [Google Scholar] [CrossRef] [PubMed]
- Wolf, E. New theory of partial coherence in the space-frequency domain. Part I: Spectra and cross spectra of steady-state sources. J. Opt. Soc. Am. 1982, 72, 343–351. [Google Scholar] [CrossRef]
- Nave, C.; Sutton, G.; Evans, G.; Owen, R.; Rau, C.; Robinson, I.; Stuart, D.I. Imperfection and radiation damage in protein crystals studied with coherent radiation. J. Synchrotron Radiat. 2016, 23, 228–237. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williams, S.R.; Dilanian, R.A.; Quiney, H.M.; Martin, A.V. Analysis of Diffracted Intensities from Finite Protein Crystals with Incomplete Unit Cells. Crystals 2017, 7, 220. https://doi.org/10.3390/cryst7070220
Williams SR, Dilanian RA, Quiney HM, Martin AV. Analysis of Diffracted Intensities from Finite Protein Crystals with Incomplete Unit Cells. Crystals. 2017; 7(7):220. https://doi.org/10.3390/cryst7070220
Chicago/Turabian StyleWilliams, Sophie R., Ruben A. Dilanian, Harry M. Quiney, and Andrew V. Martin. 2017. "Analysis of Diffracted Intensities from Finite Protein Crystals with Incomplete Unit Cells" Crystals 7, no. 7: 220. https://doi.org/10.3390/cryst7070220
APA StyleWilliams, S. R., Dilanian, R. A., Quiney, H. M., & Martin, A. V. (2017). Analysis of Diffracted Intensities from Finite Protein Crystals with Incomplete Unit Cells. Crystals, 7(7), 220. https://doi.org/10.3390/cryst7070220




