Elastic, Mechanical and Phonon Behavior of Wurtzite Cadmium Sulfide under Pressure
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Ullah, N.; Ullah, H.; Murtaza, G.; Khenata, R.; Ali, S. Structural phase transition and optoelectronic properties of ZnS under pressure. J. Opt. Adv. Mater. 2015, 17, 1272. [Google Scholar]
- Bouhemadou, A.; Haddadi, K.; Khenata, R.; Rached, D.; Bin-Omran, S. Structural, elastic and thermodynamic properties under pressure and temperature effects of MgIn2S4 and CdIn2S4. Phys. B Condens. Matter 2012, 407, 2295. [Google Scholar] [CrossRef]
- Seddik, T.; Semari, F.; Khenata, R.; Bouhemadou, A.; Amrani, B. High pressure phase transition and elastic properties of Lutetium chalcogenides. Phys. B Condens. Matter 2010, 405, 394. [Google Scholar] [CrossRef]
- Duan, D.; Liu, Y.; Ma, Y.; Liu, Z.; Cui, T.; Liu, B.; Zou, G. Ab initio studies of solid bromine under high pressure. Phys. Rev. B 2007, 76, 104113. [Google Scholar] [CrossRef]
- Duan, D.; Huang, X.; Tian, F.; Li, D.; Yu, H.; Liu, Y.; Ma, Y.; Liu, B.; Cui, T. Pressure-induced decomposition of solid hydrogen sulfide. Phys. Rev. B 2015, 91, 180502(R). [Google Scholar] [CrossRef]
- Ouendadji, S.; Ghemid, S.; Meradji, H.; El Haj Hassan, F. Theoretical study of structural, electronic, and thermal properties of CdS, CdSe and CdTe compounds. Comput. Mater. Sci. 2011, 50, 1460. [Google Scholar] [CrossRef]
- Benkabou, F.; Aourag, H.; Certier, M. Atomistic study of zinc-blende CdS, CdSe, ZnS, and ZnSe from molecular dynamics. Mater. Chem. Phys. 2000, 66, 10–16. [Google Scholar] [CrossRef]
- Deligoz, E.; Colakoglu, K.; Ciftci, Y. Elastic, electronic, and lattice dynamical properties of CdS, CdSe, and CdTe. Phys. B Condens. Matter 2006, 373, 124–130. [Google Scholar] [CrossRef]
- Grünwald, M.; Zayak, A.; Neaton, J.B.; Geissler, P.L.; Rabani, E. Transferable pair potentials for CdS and ZnS crystals. J. Chem. Phys. 2012, 136, 234111. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.J.; Li, Y.; Ji, G.F. High-Pressure Phase Transitions and Thermodynamic Behaviors of Cadmium Sulfide. Acta Phys. Pol. A 2011, 120, 501–506. [Google Scholar] [CrossRef]
- Wright, K.; Gale, J.D. Interatomic potentials for the simulation of the zinc-blende and wurtzite forms of ZnS and CdS: Bulk structure, properties, and phase stability. Phys. Rev. B 2004, 70, 035211. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Li, H.; Li, X.; Lin, C.; Xiao, W.; Liu, J. High pressure-induced phase transitions in CdS up to 1 Mbar. J. Appl. Phys. 2013, 113, 083509. [Google Scholar] [CrossRef]
- Fan, Z.; Koster, R.S.; Wang, S.; Fang, C.; Yalcin, A.O.; Tichelaar, F.D.; Zandbergen, H.W.; van Huis, M.A.; Vlugt, T.J.H. A transferable force field for CdS-CdSe-PbS-PbSe solid systems. J. Chem. Phys. 2014, 141, 244503. [Google Scholar] [CrossRef] [PubMed]
- Gale, J.D. Empirical potential derivation for ionic materials. Philos. Mag. B 1996, 73, 3–19. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday 1997, 93, 629. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simulat. 2003, 29, 291. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: Capabilities and prospects. Z. Kristallogr. 2005, 220, 552. [Google Scholar] [CrossRef]
- Walsh, A.; Sokol, A.A.; Catlow, C.R.A. Computational Approaches to Energy Materials, 1st ed.; John Wiley & Sons, Ltd.: West Sussex, UK, 2013; p. 101. [Google Scholar]
- Valerio, M.E.G.; Jackson, R.A.; de Lima, J.F. Derivation of potentials for the rare-earth fluorides, and the calculation of lattice and intrinsic defect properties. J. Phys. Condens. Matter 2000, 12, 7727. [Google Scholar] [CrossRef]
- Güler, E.; Güler, M. High pressure elastic properties of wurtzite aluminum nitrate. Chin. J. Phys. 2014, 52, 1625–1635. [Google Scholar]
- Dick, B.G.; Overhauser, A.W. Theory of the Dielectric Constants of Alkali Halide Crystals. Phys. Rev. 1958, 112, 90. [Google Scholar] [CrossRef]
- Ewald, P.P. Die Berechnung optischer und elektrostatischer Gitterpotentiale. Ann. Phys. 1921, 64, 253. [Google Scholar] [CrossRef]
- Archer, T.D.; Birse, S.E.A.; Dove, M.T.; Redfern, S.; Gale, J.D.; Cygan, R.T. An interatomic potential model for carbonates allowing for polarization effects. Phys. Chem. Miner. 2003, 30, 416. [Google Scholar] [CrossRef]
- Ayala, A.P. Atomistic simulations of the pressure-induced phase transitions in BaF2 crystals. J. Phys. Condens. Matter 2001, 13, 11741. [Google Scholar] [CrossRef]
- Chisholm, J.A.; Lewis, D.W.; Bristowe, P.D. Classical simulations of the properties of group-III nitrides. J. Phys. Condens. Matter 1999, 11, L235–L239. [Google Scholar] [CrossRef]
- Kilo, M.; Jackson, R.A.; Borchardt, G. Computer modelling of ion migration in zirconia. Phil. Mag. 2003, 83, 3309. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Broyden, G.C. The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations. J. Inst. Math. Appl. 1970, 6, 76. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317. [Google Scholar] [CrossRef]
- Goldfarb, D. A family of variable-metric methods derived by variational means. Math. Comput. 1970, 24, 23. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Adachi, S. Handbook on Physical Properties of Semiconductors; Kluwer: Boston, MA, USA, 2004; Volume 1. [Google Scholar]
- Hirsekorn, S. Elastic properties of polycrystals. Textures Microstruct. 1990, 12, 1–14. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; B.G. Teubner: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Angew. Z. Math. Mech. 1929, 9, 55. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Clarendon: Oxford, UK, 1956. [Google Scholar]
- Bolef, D.I.; Melamed, N.T.; Menes, M. Elastic constants of hexagonal cadmium sulfide. J. Phys. Chem. Solids 1960, 17, 143. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823. [Google Scholar] [CrossRef]
- Guo, X.J.; Xu, B.; Liu, Z.Y.; Yu, D.L.; He, J.L.; Guo, L.C. Theoretical Hardness of Wurtzite-Structured Semiconductors. Chin. Phys. Lett. 2008, 25, 2158. [Google Scholar]
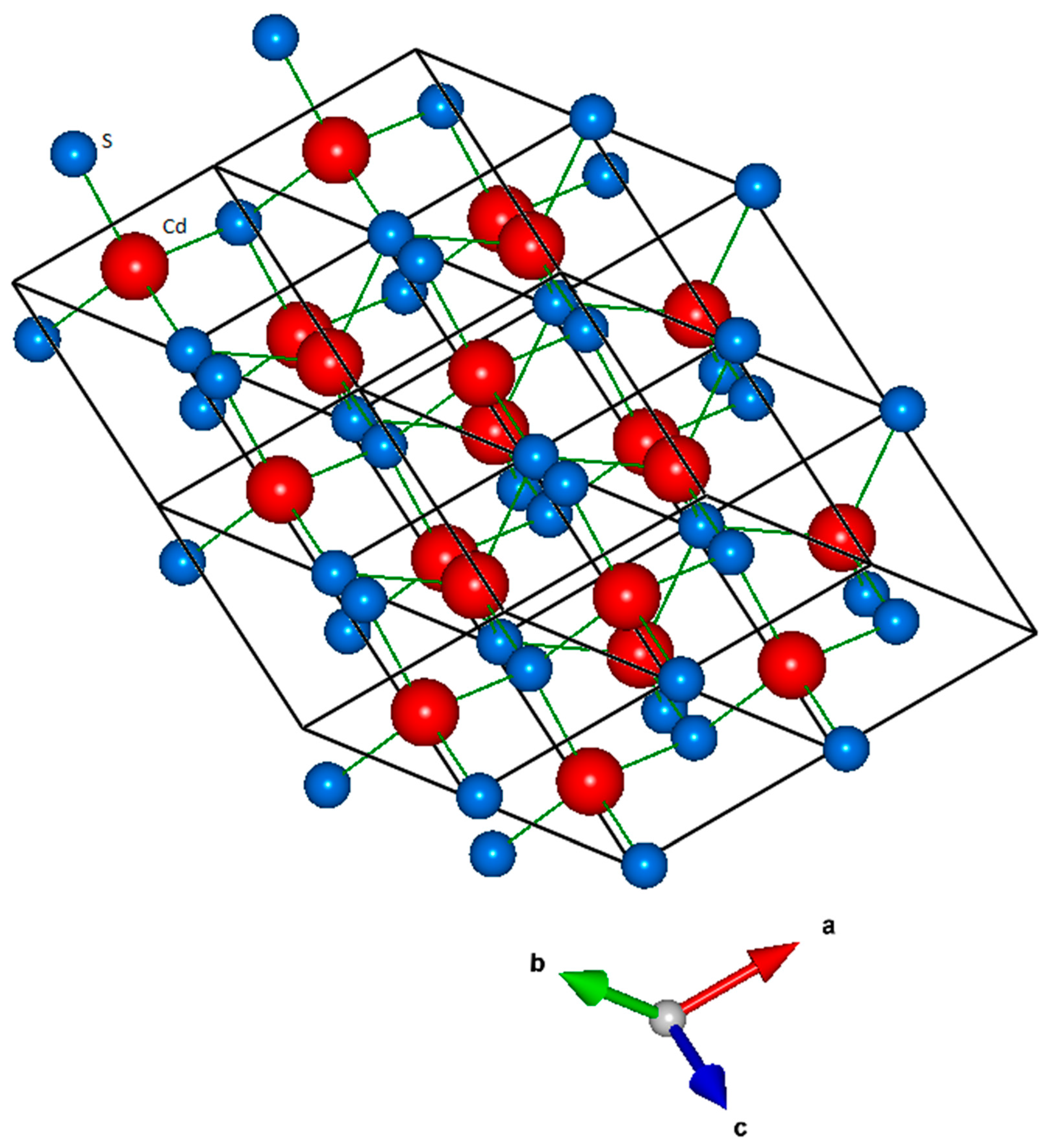


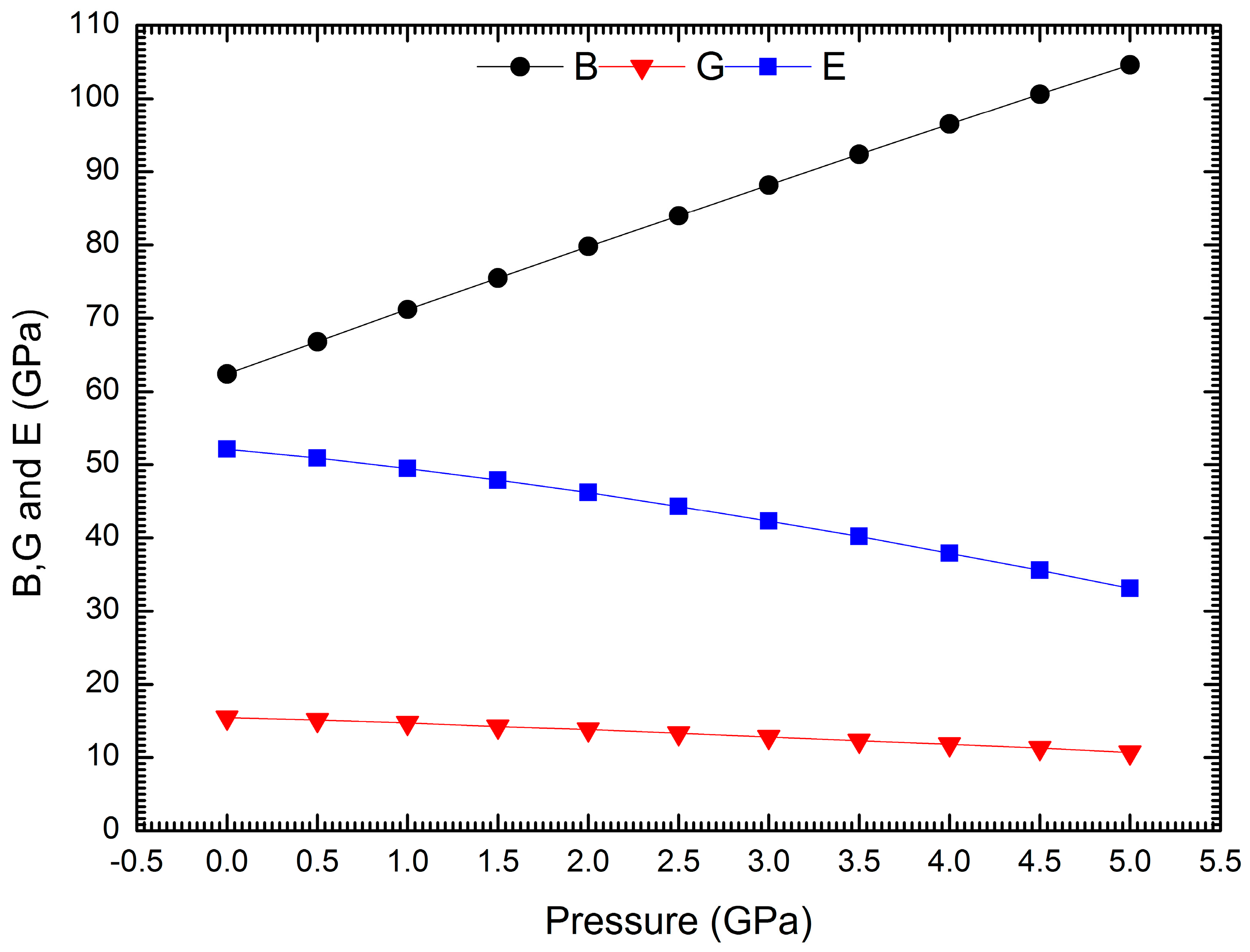
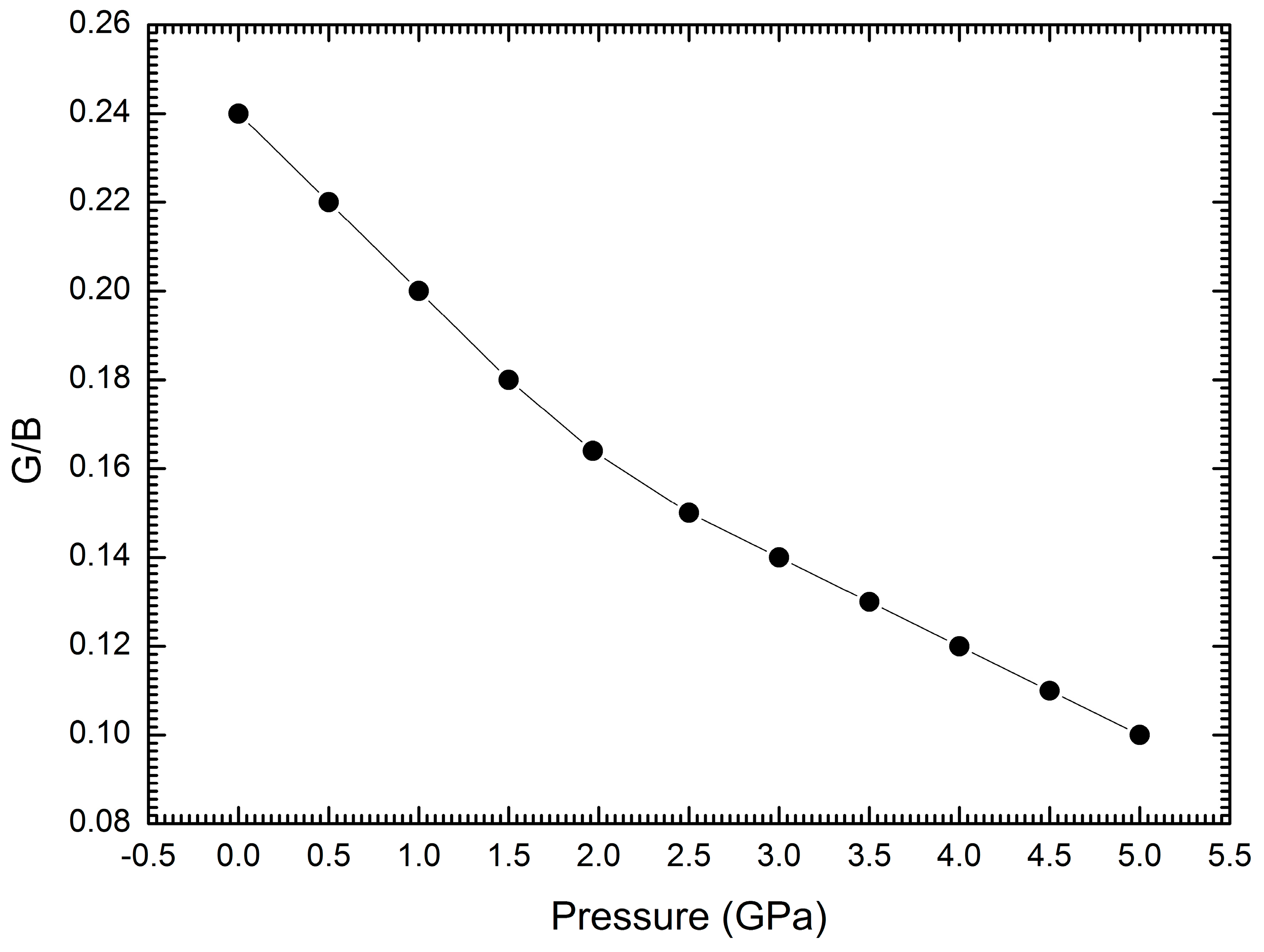


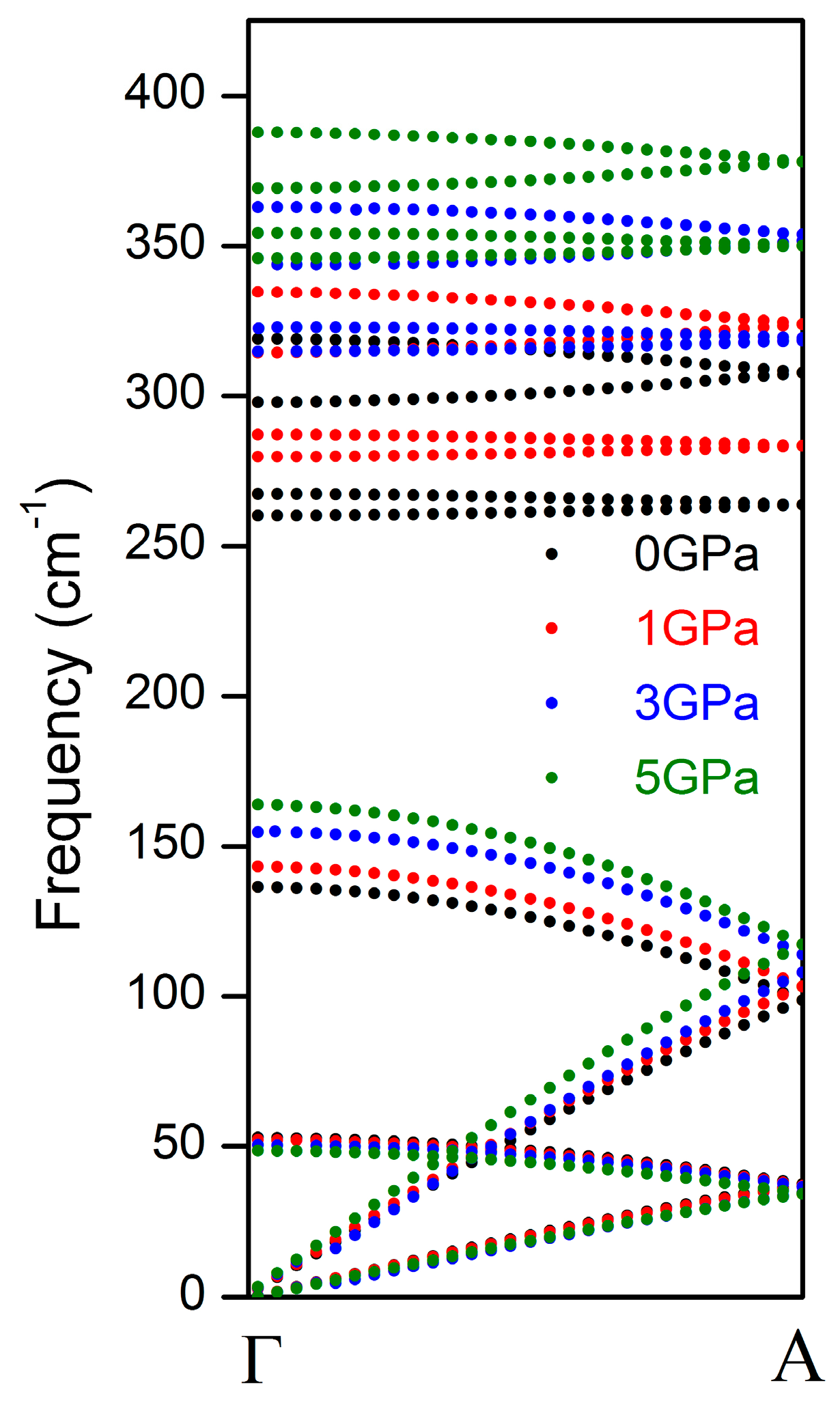

| Interaction | A (eV) | ρ (Å) | C (eV·Å6) |
|---|---|---|---|
| CdC-SC | 1.26 × 109 | 0.107 | 53.5 |
| SC-SC | 4.68 × 103 | 0.374 | 120 |
| Parameter | Exp [33] | Present | Ref [9] | Ref [10] | Ref [11] | Ref [41] |
|---|---|---|---|---|---|---|
| C11 (GPa) | 84.3 | 85.2 | 107.3 | 93.9 | 102.8 | 80.5 |
| C12 (GPa) | 52.1 | 56.2 | 35.8 | 57.6 | 45.4 | 45.0 |
| C13(GPa) | 46.3 | 48.4 | 15.9 | 50.1 | 47.5 | 37.1 |
| C33 (GPa) | 93.9 | 85.3 | 144.3 | 105.2 | 113.3 | 87.0 |
| C44 (GPa) | 14.8 | 14.5 | 20.5 | 15.8 | 32.4 | 15.2 |
| B (GPa) | 62.7 | 62.4 | 54.0 | 68.9 | 66.4 | 54.0 |
| E (GPa) | 48.1 | 52.0 | 51.0 | |||
| G (GPa) | - | 15.4 | 18.5 | |||
| VS (km/s) | 1.84 | 1.77 | ||||
| VL (km/s) | 4.24 | 4.11 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Güler, M.; Güler, E. Elastic, Mechanical and Phonon Behavior of Wurtzite Cadmium Sulfide under Pressure. Crystals 2017, 7, 164. https://doi.org/10.3390/cryst7060164
Güler M, Güler E. Elastic, Mechanical and Phonon Behavior of Wurtzite Cadmium Sulfide under Pressure. Crystals. 2017; 7(6):164. https://doi.org/10.3390/cryst7060164
Chicago/Turabian StyleGüler, Melek, and Emre Güler. 2017. "Elastic, Mechanical and Phonon Behavior of Wurtzite Cadmium Sulfide under Pressure" Crystals 7, no. 6: 164. https://doi.org/10.3390/cryst7060164
APA StyleGüler, M., & Güler, E. (2017). Elastic, Mechanical and Phonon Behavior of Wurtzite Cadmium Sulfide under Pressure. Crystals, 7(6), 164. https://doi.org/10.3390/cryst7060164





