1. Introduction
Cast glass-coated amorphous micro- and nanowires (CGCAMNW) are very interesting materials from a theoretical standpoint as well as for the practical applications.
A simple production technology of cast glass-coated amorphous micro- and nanowires (CGCFMWs) was first introduced in 1924 by Taylor [
1]. Later, in the period 1950–1964, this method was significantly modified by Ulitovsky. Modified Taylor–Ulitovsky method allows producing large amounts of such microwires. Interest in the cast glass-coated microwires has greatly increased over the last few years, mainly due to their technological applications, in particular, as sensor elements in various devices [
2,
3]. Consequently, preparation of CGCFMWs by the Taylor–Ulitovsky method and the study of their magnetic properties were reported in many publications by various research groups [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29]. It is essential that the microwires are manufactured using a rapid solidification technique. However, the main peculiarity of the aforementioned microwires is the simultaneous rapid solidification of metallic alloy covered by glass [
2,
3,
4,
5,
6,
7,
8,
9].
Therefore, the other families of amorphous magnetic wires produced by co-called “in-rotating-water quenching” or melt-extraction methods present the distinctive magnetic properties since their magnetoelastic anisotropy and magnetic domain structures are different.
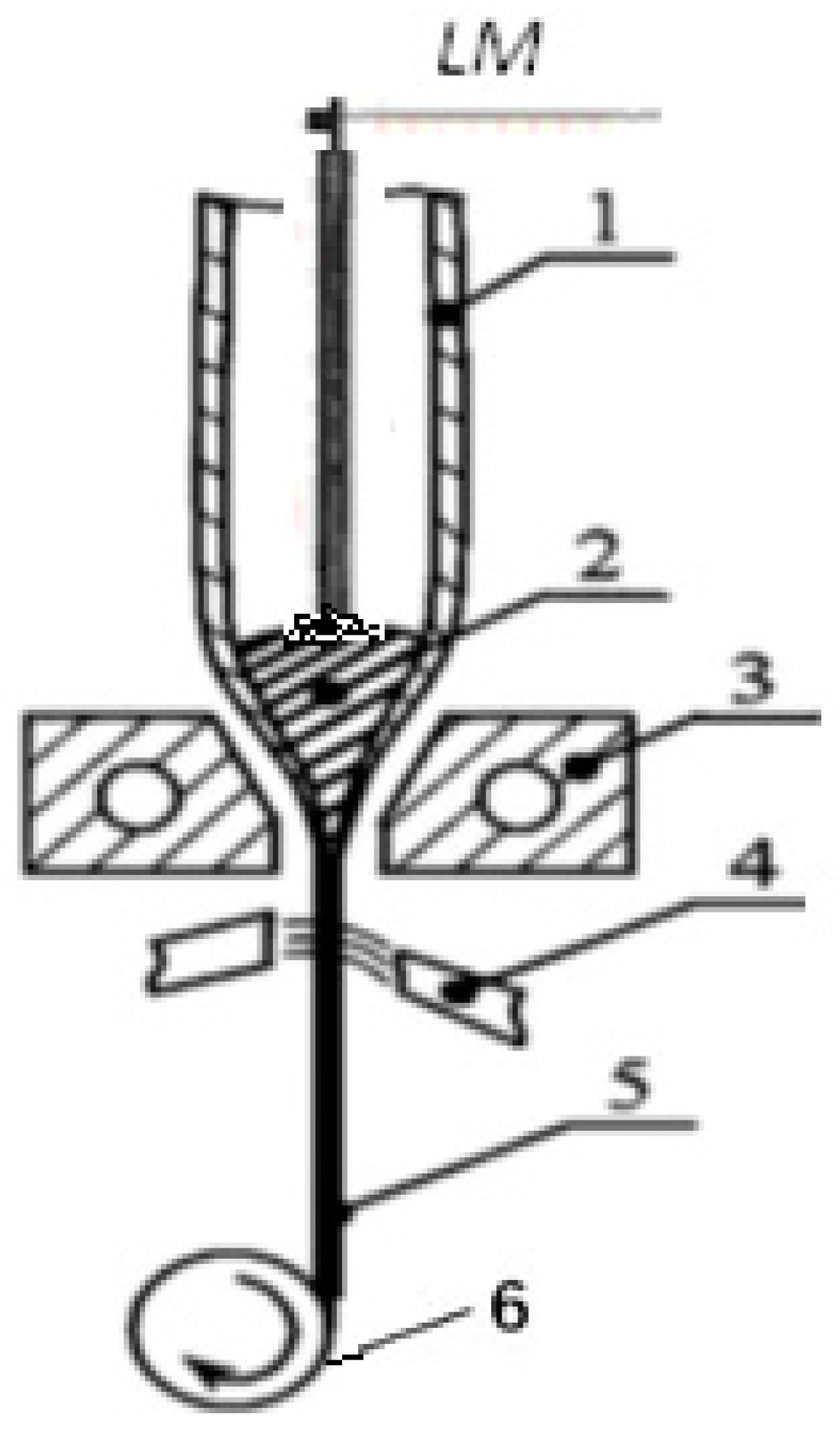
Technological aspects of the Taylor–Ulitovsky method for the production of the cast glass-coated microwires, which can have the different microstructure and composition of the metallic core, are presented below. If a continuous production process of casting glass-coated amorphous magnetic microwires is carried out, a metal alloy rod (named LM) is inserted into the glass tube 1.
In this process, a few grams of the metallic alloy are placed inside a glass tube located directly within a high frequency induction heater (see
Figure 1). The metallic alloy is heated up to the melting point to form a droplet. Under suitable conditions the molten metal fills the glass capillary and so a microwire is formed when its metallic core is completely coated with a glass cladding. In order to regulate the diameter of the microwire’s metallic core, a vacuum controller is used to regulate the pressure inside the glass tube. Thus, the geometrical characteristics of the obtained microwires are determined not only by the physical properties of the glass and the metal, but also by the diameter of the initial glass tube, and the parameters of the heating inductor. The microstructure and, hence, properties of the manufactured microwire mostly depend on the cooling rate, which can be controlled by a cooling mechanism, by which the metal-filled capillary enters into a stream of a cooling liquid (water or oil) on its way to the receiving coil. The magnetic properties of the microwire are largely attributed to the composition and microstructure of the metallic core. The casting method offers the possibility of fast cooling and solidification of a liquid metal in a nonequilibrium process, which leads to the formation of various metastable metal phases. Depending on the critical cooling rates, different metastable metal phases can be formed: the supersaturated solid solution, nanocrystalline, microcrystalline and crystalline phases. The values of the critical quenching (cooling) rates that gives rise to a metastable (or supersaturated) state of the microwire metallic core are 10
4–10
7 K/s [
2,
6,
7].
The main advantages of this method for the production of the cast glass-coated microwires are as follows [
2,
3,
5,
6,
7]:
The production of the continuous long pieces of a microwire up to 10
4 m (in the case of a drip process). For a continuous process (see
Figure 1), the length of a microwire is not limited.
A wide range of variations in the geometric parameters (typically the metallic core diameter D
m is in a range of 0.5–70 µm, and a glass-coating thickness is in a range of 1–50 µm (
Figure 2)).
The control and adjustment of the geometric parameters (the inner metallic core diameter Dm and glass thickness) during production.
The reproducibility of the physical properties and geometric parameters of the microwires in mass production.
Figure 3 shows the machine for the preparation of CGCFMWs by the Taylor–Ulitovsky method, which were manufactured in Moldova. This machine can produce cast glass-coated microwires of different types with a broad range of the core diameters, as was indicated above.
We also provided an analysis of residual stresses arising in glass-coated microwires and reviewed the prospective applications of glass-coated microwires (see below).
2. Experimental Installation for Measuring Magnetic Properties
An installation has been developed for measuring of magnetic properties of microwires. The magnetic loops of sample
1 were measured by the standard induction method (
Figure 4). Pickup (
2) the magnetic loops of sample
1 were measured by the standard induction method (
Figure 4).
Pickup (2) and compensating (3) coils were placed symmetrically in magnetizing coil 4 (connected to a linear-sweep power supply 5) in which a magnetic field from 0 to 10 Oe with a frequency of 10–60 Hz was created.
The analog differential signal from the pickup coil (after compensation in switching unit 6) was digitized and integrated in unit 7 to the shape of the integral hysteresis curve. The correctness of the integration process was verified with known reference specimens and compensating (3) coils were placed symmetrically in magnetizing coil 4 (connected to a linear-sweep power supply 5) in which a magnetic field from 0 to 10 Oe with a frequency of 10–60 Hz was created.
The analog differential signal from the pickup coil (after compensation in switching unit 6) was digitized and integrated in unit 7 to the shape of the integral hysteresis curve. The correctness of the integration process was verified with known reference specimens.
3. The Effect of Heat Treatment on the Coercive Force
Annealing (with the annealing time sufficient for the relaxation of the amorphous structure) up to the temperature when the process of formation of micro-nano crystals starts (~400 °C) is of practical interest. Residual stresses relaxation by annealing can produce irreversible changes of magnetic properties (i.e., coercive field, H
c) allowing optimization of magnetic properties of microwires. At temperatures above 400 °C, the formations of a nano- or microcrystalline phases in CGCFMWs were observed (this temperature is designated as T
cr) [
11,
12,
13,
14,
15,
16,
17].
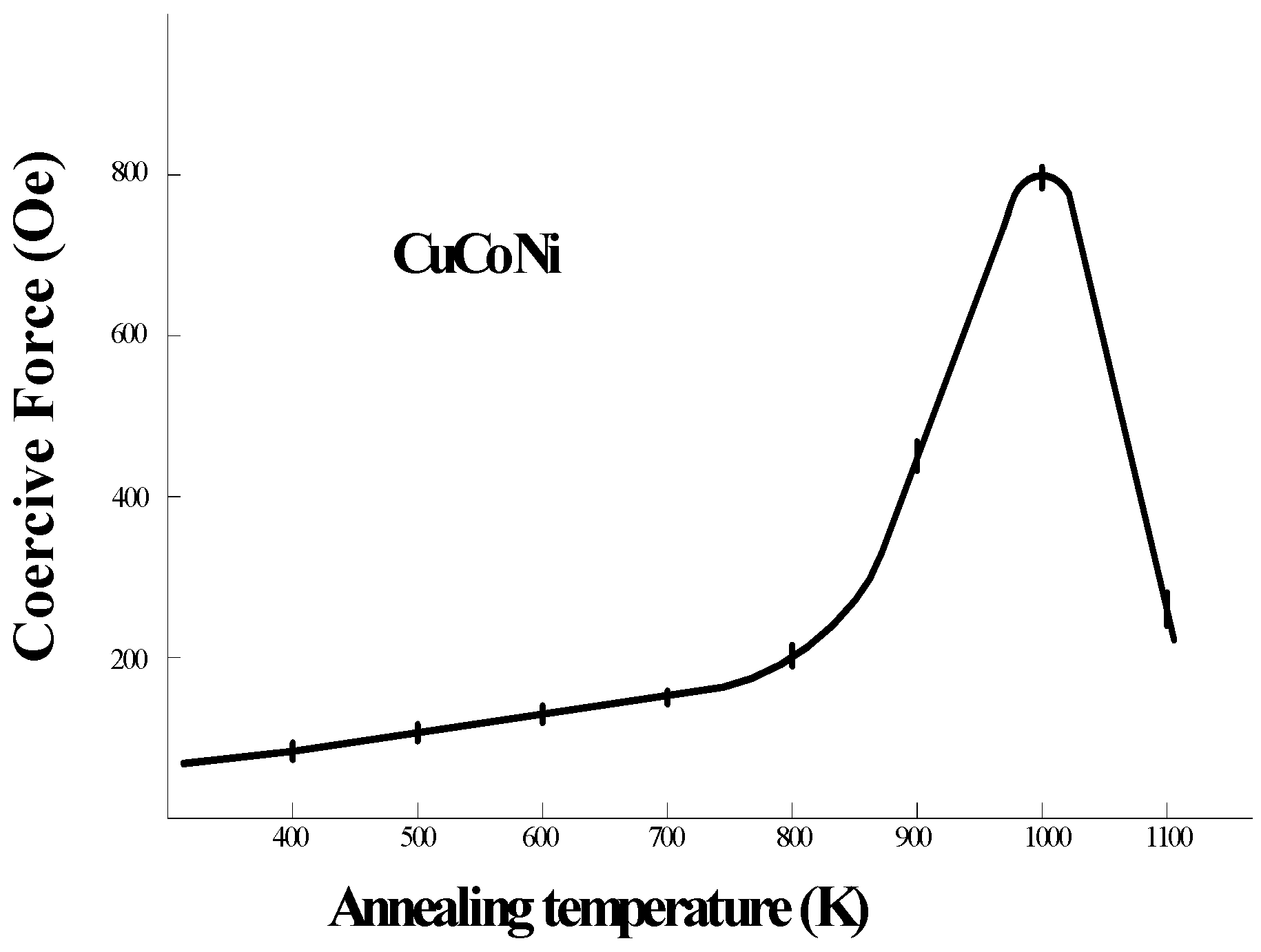
Figure 5 shows a typical dependence of the coercive field on annealing temperature reflecting the relaxation of the residual stresses and first stages of the crystallization processes. It is worth noting that in some compositions of magnetic microwires the heat treatment at temperatures below T
cr can improve the CGCFMWs magnetic properties, i.e., decrease the values of σ
H and H
c [
14,
15,
16].
The compositions that we have used are characterized by a high thermal stability; i.e., by a sufficiently high T
cr-value. In the present study, we used the specimens with the glass coating thickness of about (7–10) μm. The coercive force, H
cm is varied in the range of (0.5–1.5) Oe at room temperature. In spite of a quite broad range of initial H
cm-values, the correlation of H
c/H
cm remains unchanged within the error bars (-up to 20%) and fits within the dependence shown in
Figure 5 [
5,
6,
7,
8].
The structure of the nanocrystalline alloy consists of nanometric grains, with average size about 10 nm, embedded in the residual amorphous matrix. Properties of alloys at the nanoscale depend on the composition, size of constituting nanocrystals, as well as on their distribution within the amorphous phase [
11,
12,
13,
14,
15,
16,
17]. Microwires with hard magnetic properties can be obtained by suitable thermal treatments (see
Figure 6).
On the basis of Becker–Volmer theory, the following approximate expression holds:
where: exp{E
1,2/kT}, describes the low-temperature processes with the energy of activation E
1,2.
The expression:
describes high-temperature processes, for which G is the change in the Gibbs energy, of irreversible phase transitions associated with the crystallization.
In the classical nucleation theory (of Becker–Volmer), an inverse value is generally used, which determines the rate of the nucleation.
For the theoretical description of the above phenomena Formula (1) can be generalized for the case of structural changes.
At low temperatures, the value of exp{−G/kT} is small (as-compared to a unity); therefore, formula:
can be used.
At high temperatures, Formula (1) can be written as follows:
The main dependence is now determined by the product exp (G/kT), determining the irreversible relaxation. Note that the proposed model allowing suggesting that
where S
1 is the entropy change decreasing with the relaxation of the initial amorphous state into more stable one but also amorphous state, and S
2 is the entropy change increasing during the transition from the metastable state to the stable polycrystalline state.
Consequently, with the entropy increasing, the system passes into a more stable state. Therefore, the variation of the switching field also decreases. Thus, the generalization of the presented equation can be justified on the thermodynamic basis.
The result provided here as a proof of a stronger dependence of Hc for the irreversible processes that are described by the exp (G/kT) product during the high-temperature treatment.
Regardless of the application, in designing inductive components, the use of nanocrystalline cores typically provides the following advantages [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]:
Reduced weight
Reduced losses on the coil due to reduction in number of turns
Extended temperature range
Increased durability and stability of properties.
High accuracy for measuring devices
4. Evaluation of Residual Stresses
The main technological parameters for the production of the glass-coated microwires are presented below.
According to the previous analysis [
6], the most significant effect on the geometry of such microwire comes from the glass properties. The microwire radius
Rg (the outer radius of the glass shell) is estimated as follows:
where
k is the parameter, which is dependent on a casting rate (0 <
k < 1); ρ is the average microwire density;
Vd is the casting rate; σ
s is the surface tension; and η is the dynamical viscosity of the glass:
where ε ~ 2·10 kJ/mol, Δ
H ~ 10
2 kJ/mol,
R is the universal gas constant, η
0 and
c are the material constants (
c ~ 0.4–0.9).
Special attention is paid to the parameters determining the casting and cooling rates that are responsible for the microstructure of the cast glass-coated microwires. So, the dynamical viscosity η is very important parameter whose value has characteristic temperature dependence. A typical temperature dependence of the dynamical viscosity is shown below in
Figure 7. The temperature region where the casting process can be implemented is indicated by the dashed lines.
Formula (6) suggests the following:
If the value of the casting rate is extremely low, then the value of
Rc is high and we obtain the formula similar to that given in [
5,
6,
7]:
where
k = 1/3.
If the casting rate is sufficiently high, we obtain for
Rc:
where
k = 2/3.
At the theoretical limit of extremely high casting rate, i.e., when
k→1, we obtain:
Finally, we present the results on theoretical simulation for the residual stresses in the microwire metallic core. The origin of the residual stresses is a difference in the thermal expansion coefficients of a metal and of glass. A simple theory for the distribution of the residual stresses in the metallic core of the microwire was proposed in the works [
4,
5,
6,
7,
8,
9,
10,
11].
In cylindrical coordinates, the residual stresses are characterized by the axial, radial and tangential components which, at a first approximation, do not depend on the radial coordinate [
5,
6,
7,
8,
9]:
where
Rm is the metallic core radius of microwire;
where
Ym is the Young’s modulus of metal and
Yg is the Young’s modulus of glass:
where α
m and α
g are the thermal expansion coefficients of the metal and glass, respectively;
T* is the effective solidification temperature of the composite microwire (when both the metallic core and the glass-coating (cladding) are solidified) and
T is the experimental temperature.
We will provide below the more accurate model used for the residual stresses at the microwires.
The metallic strand from its axis up to the certain internal radius b preserves the liquid state (parameter b has a certain value depending on the defined metallic alloy composition and cooling rate).
In contrast, the metallic core from b up to Rm, which has only the elastic residual stresses, freezes earlier.
1. So, at
b <
r < Rm, this model gives (see [
5,
8]):
where ν is the Poisson’s coefficient.
2. In addition, at
r < b, this model gives (see [
5,
8]):
where
K is the thermoelastic constant of metal.
(Note that a rigorous solution should be obtained by the lacing of Formulas (11)–(16) (see [
5])).
Formulas (11)–(16) adequately explain the experiments concerning ferromagnetic resonance (FR) and natural ferromagnetic resonance (NFR) (see [
4,
9,
19]).
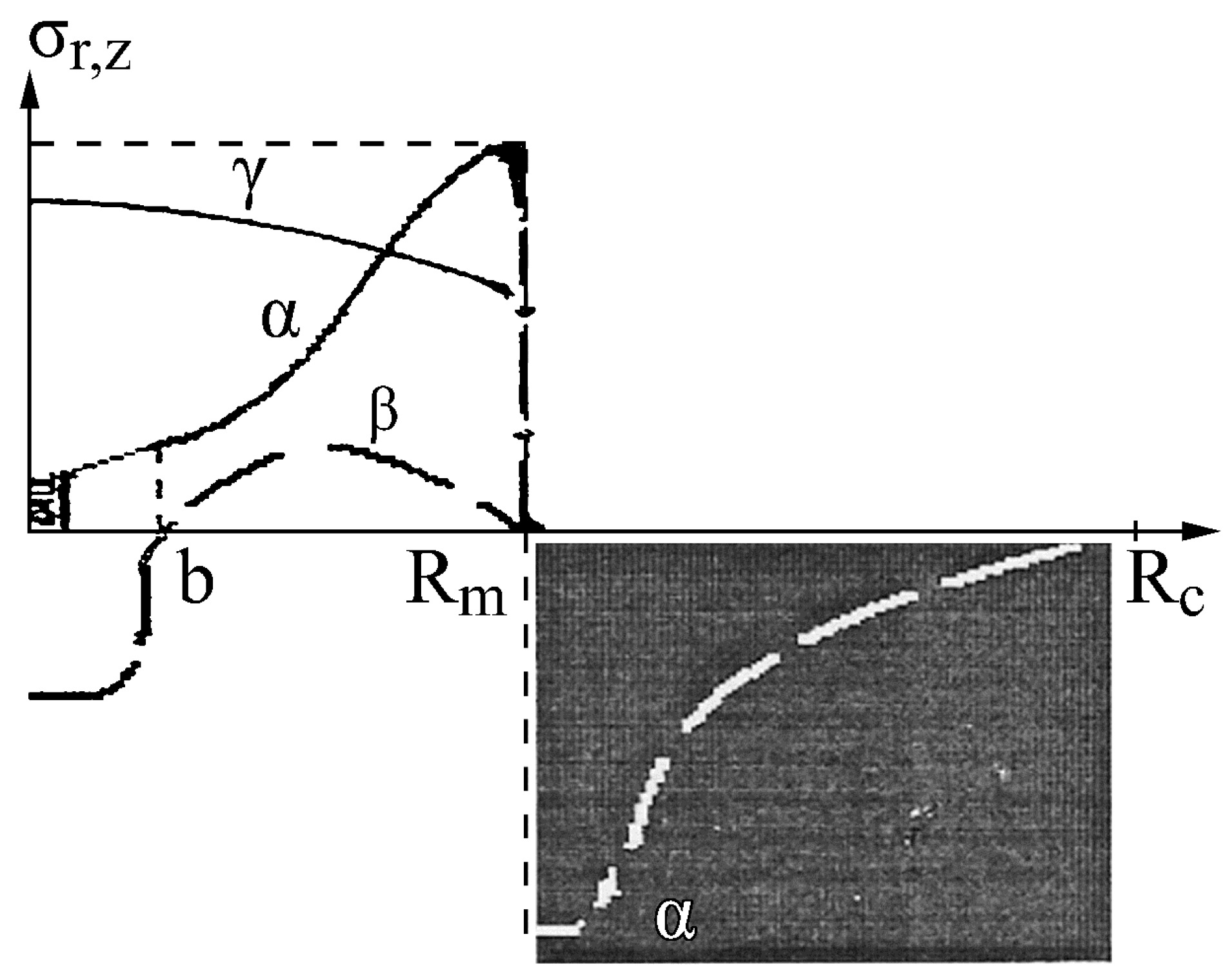
We suggested a model in which the residual stresses σ
r and σ
z in the CGCAMNW monotonically decrease towards the strand center (see
Figure 8). This model differs from the models in [
10].
5. Application of Microwires
The microwire are of great importance in a wide spectrum of applications, most of which are related to wireless telecommunications systems, such as telephone, broadcast satellite television, or satellite global positioning. Radar systems are also very useful for detecting mobile targets in air, sea for air-traffic control or missile tracking radars, and for a wide variety of remote sensing systems. In addition, resonance phenomena appearing at microwave frequencies offer an opportunity for novel applications in systems medical diagnosis and treatment or just new effects in basic science. In all these cases, the involved phenomena are characterized by high frequency electromagnetic waves.
The glass-coating for the magnetic microwires, in addition to protecting the metallic nucleus from corrosion and providing electrical insulation, induces large mechanical stresses in the metallic nucleus [
2,
3,
4,
5,
6,
7,
8,
9].
They can exhibit an exciting microwave behavior exploited in numerous technological applications requiring elements for absorption of electromagnetic radiation.
The composite prepared from magnetically soft glass-coated microwires embedded in an elastomeric matrix are promising for applications in electromagnetic shields (see
Figure 9 and
Figure 10) [
18,
19,
20,
21,
22,
23,
24,
25]. Thus, 1-mm-thick shields are capable for attenuating of electromagnetic radiation in a frequency range of 3–16 GHz by 20–30 dB, which can be used in aircraft equipment operating in the super high frequency range, e.g., radar altimeters (4.3 GHz), microwave landing systems (5.0–5.1 GHz), Doppler navigation systems (8.8 GHz), and weather radars (9.375 GHz). Other advantages of such shields are their excellent mechanical flexibility due to the elastomeric matrix as well as good adherence to various surfaces.
The absorbing characteristic of a screen made from microwires with natural resonance in the range of frequencies 10–12 GHz [
5,
9] are as follows: the measurement error was less than 10% for the frequency, while the spread of the attenuation factor was 5–7 dB.
As we mentioned above, the glass-coated microwires have physical properties that are tuneable by the composition and microstructure of the metallic core. These are the functional materials that can be used as both individual materials and fillers for the composites. For example, the glass-coated microwires can possess excellent magnetic properties (Giant magnetoimpedance effect of fast magnetizxation switching) that make them very suitable as the sensing elements of devices for diverse technological applications [
17,
26,
27,
28,
29].
It has been established that the bistability of glass-coated micro- and nanowires fully correlates with natural ferromagnetic resonance (NFR). The lower the NFR frequency is, the smaller the coercive force is [
5,
9]. In fact, low–NFR-frequency glass-coated micro- and nanowires can be used as magnetic field sensors that use the so-called asymmetric giant magneto-impedance (GMI) effect (see [
17,
18,
19,
25,
26,
27]). We accept that the asymmetric GMI is equivalent to the NFR with a sufficiently small natural ferromagnetic resonance frequency.
The glass-coated ferromagnetic microwires embedded in a cellulose matrix can be used as validating elements in security devices for autentification of a counterfeit products. For instance, use of specially designed detectors for sensing of the ferromagnetic microwires in paper can be suitable for the autentification of documents. The geometry of the microwires prepared from soft magnetic alloys is compatible with the size of the cellulosic fibers.
Glass-coated microwires embedded in different matrices have already found numerous applications in: miniaturized high-voltage transformers, elements for magnetic encoding, the sensitive elements of magnetic sensors, electromagnetic shields, anti-shoplifting labeling, security elements for authentication of products and documents, access control points, and floor heating systems, etc.
6. Conclusions
We described the main technological parameters for the production of the cast glass-coated microwires. The continuous casting method for glass-coated microwires (Taylor–Ulitovsky method) has some limitations determined by the physical properties of a metal and of glass. A range of the working temperatures for casting is specific for the given composition of a metallic alloy and a certain type of glass, i.e., for each pair of a metallic alloy and glass, the working temperature depends on the viscosity of the glass and the metal and on other physical properties.
Particular attention has been paid to the parameters determining a microstructure of the cast glass-coated microwires (crystalline, microcrystalline, or nanocrystalline).
We have written simple analytic expressions for the residual stresses in the microwire metallic core, which clearly show their dependence on the ratio of the microwire radius to the metallic nucleus radius and on the ratio of the Young’s modules of the glass and metal (see Formulas (11)–(14)). The theoretical simulation in accordance with the thermoelastic relaxation theory show that the residual stresses increase from the axis of microwire up to the surface of its metallic core, which corresponds to the previously obtained experimental data. Thus, at the preparation of the cast glass-coated microwires by the Taylor–Ulitovsky method, the residual stresses attain the maximum values on the metallic core surface. This theory also explains the activation mechanism of the domain wall motion in the cast glass-coated microwires, giving the Arrhenius temperature dependence for the magnetic coercivity.
The specific feature of the cast glass-coated microwires is a presence of the residual stresses arising from a difference of the thermal expansion coefficients of the metallic alloy and the glass-coating. This feature is the main factor determining the physical properties of such microwires, particularly their magnetic properties.
As a result, the cast glass-coated ferromagnetic microwires exhibit a residual magnetization due to a specific distribution of the residual stresses. This property of the studied microwires can be used for a design of the long-term magnetic storage elements and other electronic devices based, for example, on the domain wall propagation.
We have overviewed the applications of glass-coated microwires in composites for absorption characteristics of shielding. We assume that the main property micro- and nanowires is magnetization reversal bistability in cast glass-coated micro- and nanowires. Glass-coated micro- and nanowires bistability can be explained using theories designed for calculating residual stresses.