Analysis of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals
Abstract
:1. Introduction
2. Analysis of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals with the MTMM
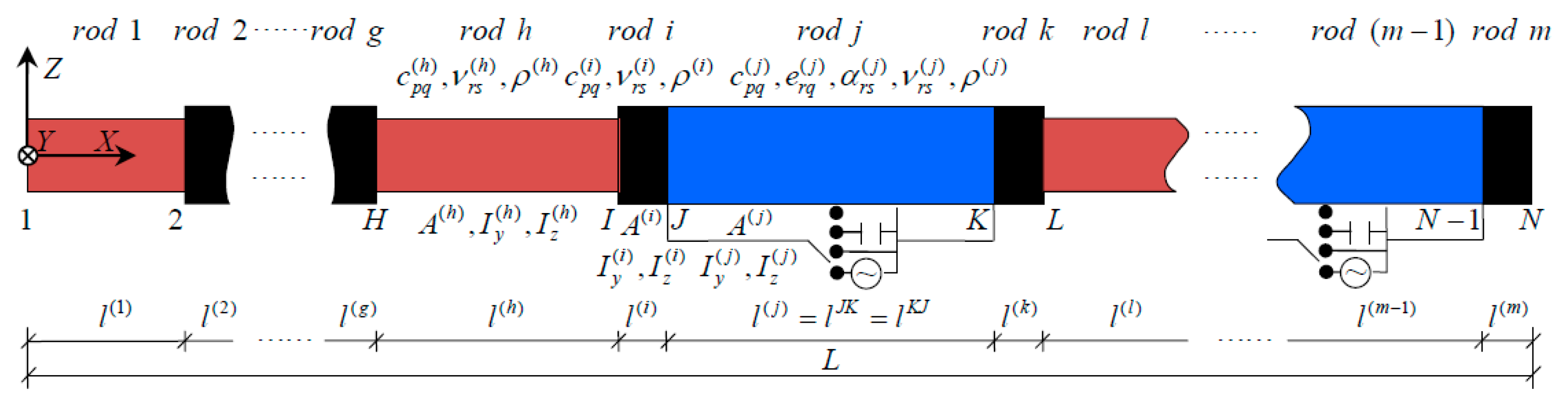
2.1. Basic Model
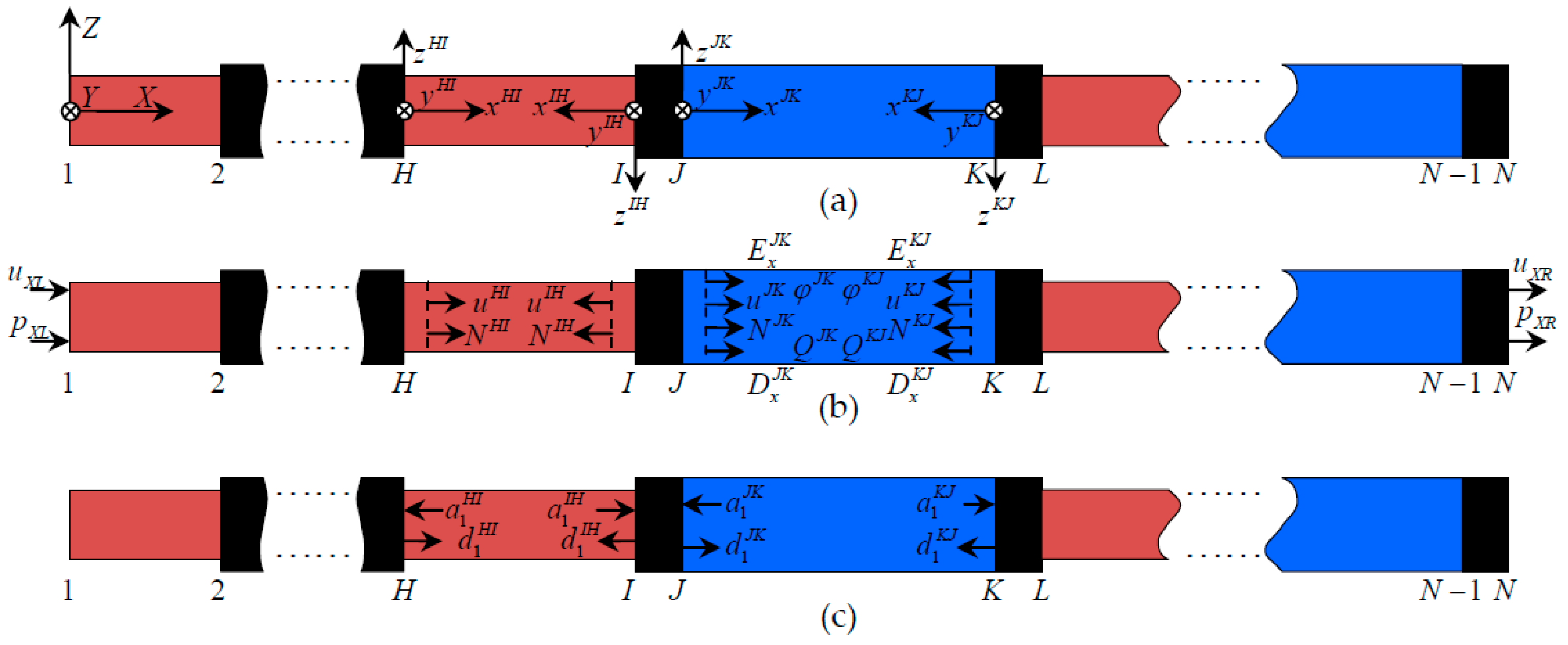
2.2. Coordinate Systems and Physical Variables
2.3. Governing Equations and Wave Solutions of a Constituent Rod
2.4. Transfer Matrix of a Member
2.5. Transfer Matrix of a Joint
2.6. Global Transfer Matrix of the Unit Cell
2.7. Dispersion Relation of Infinite Periodic Structures
2.8. Global Transfer Relation of Finite Periodic Structures
3. Numerical Examples
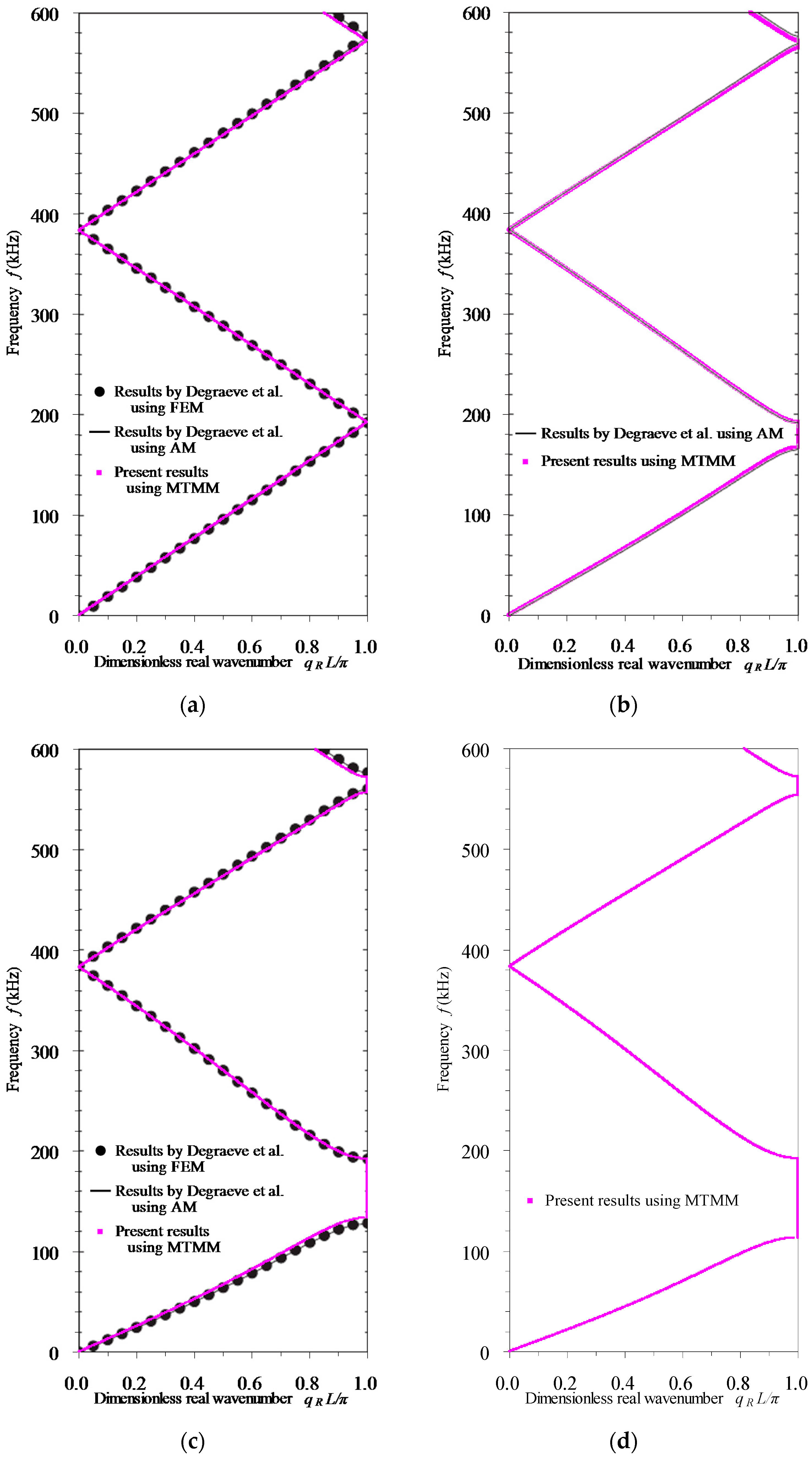
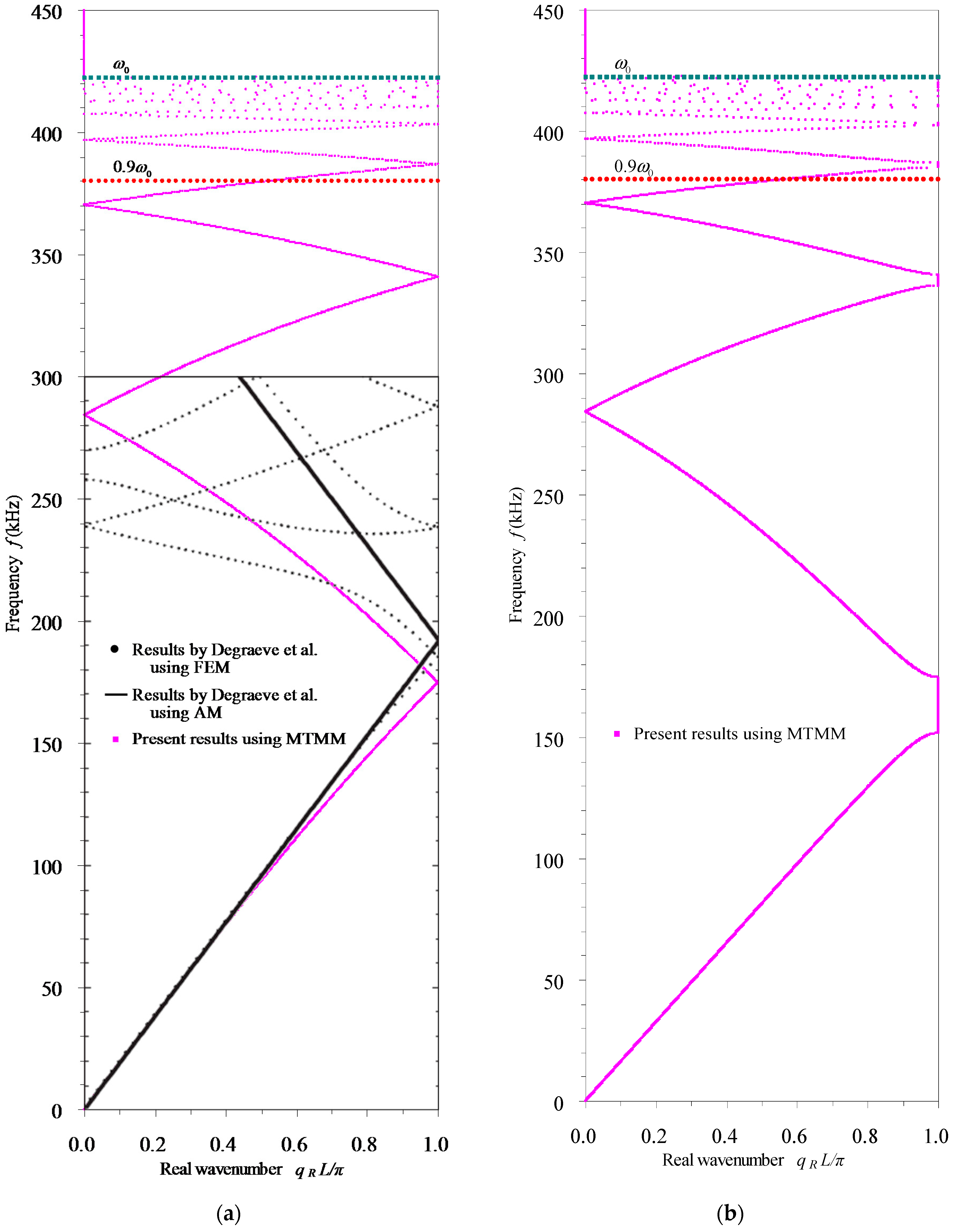
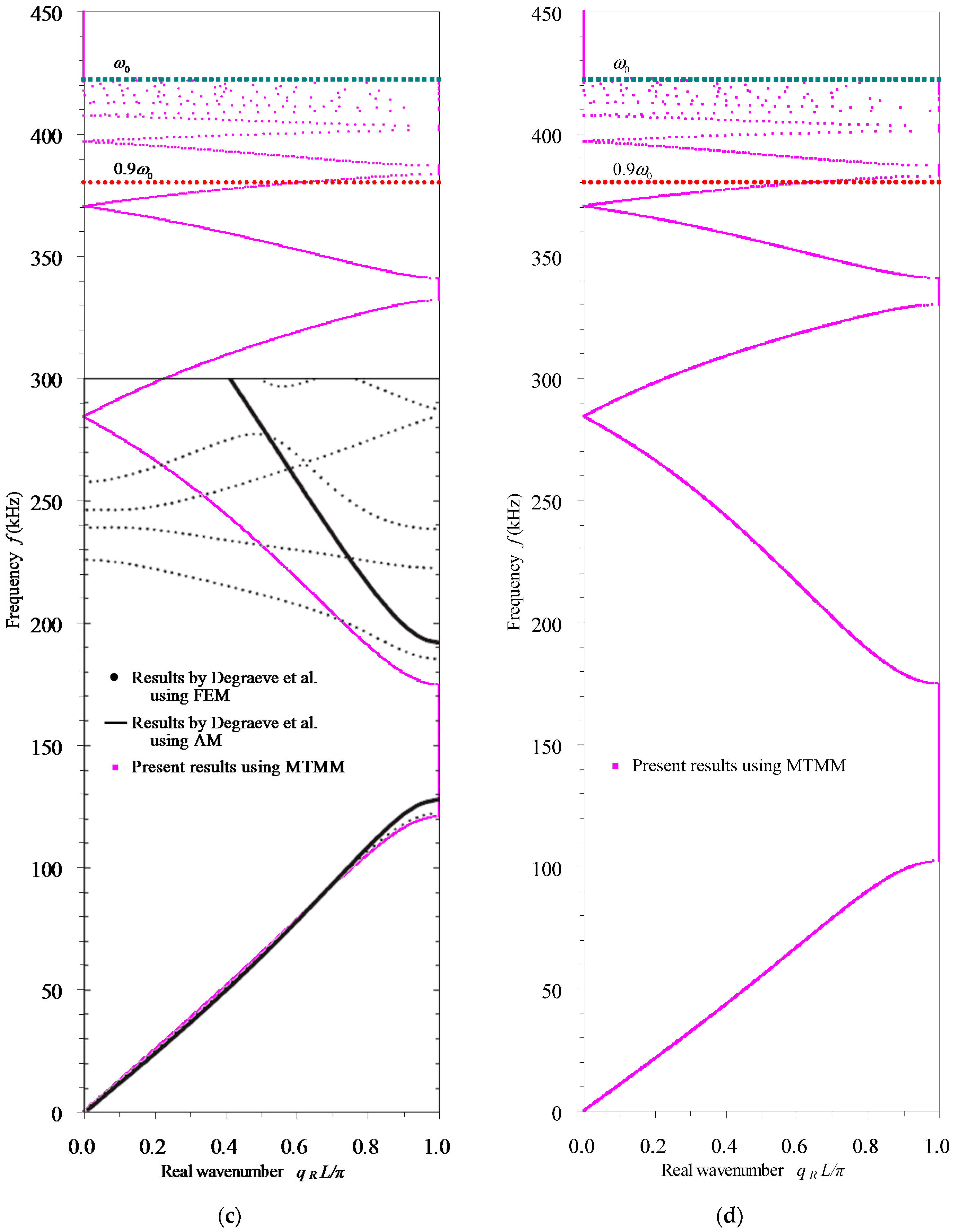
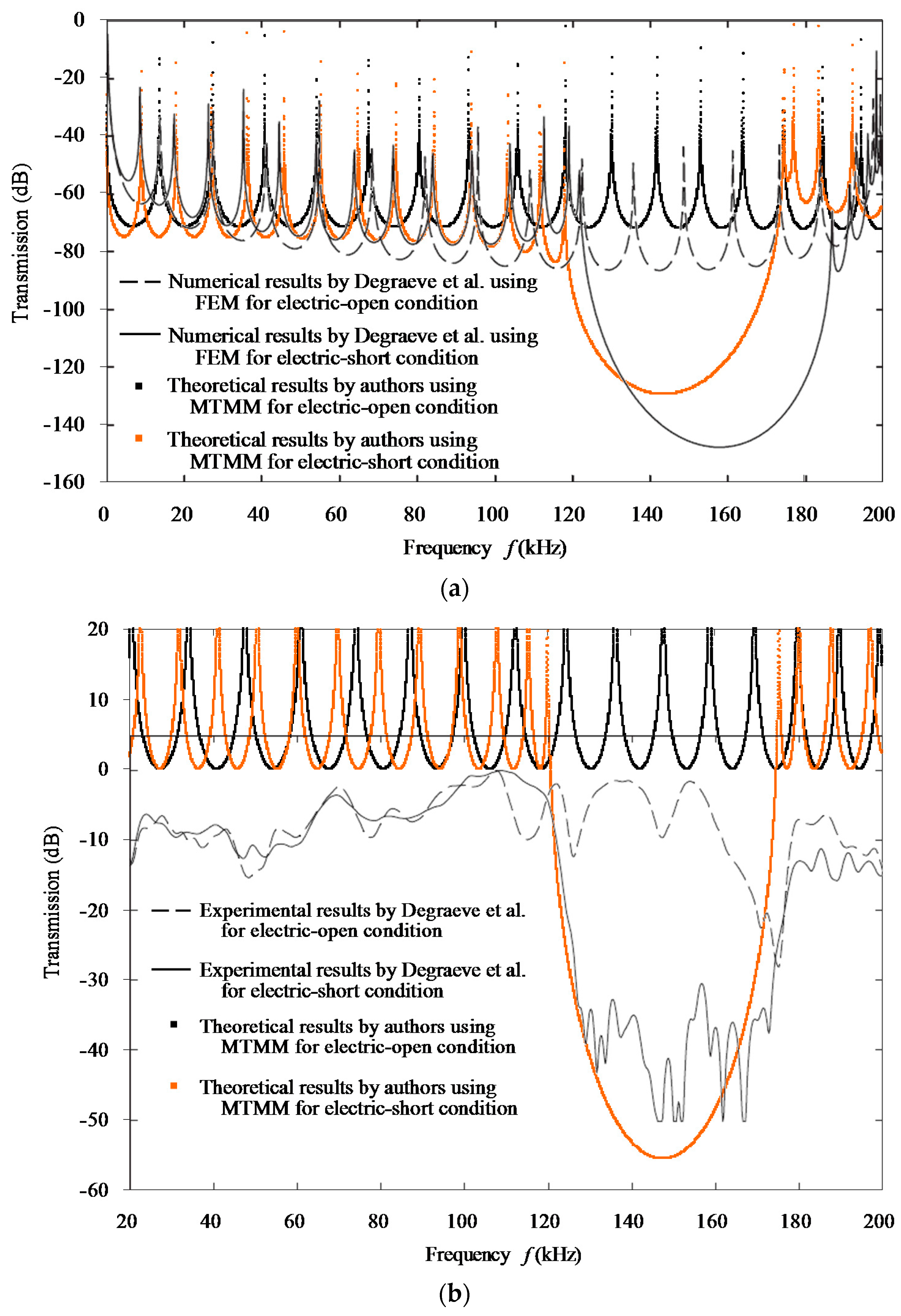
3.1. Validation of the Proposed MTMM
3.2. Passive Control of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals
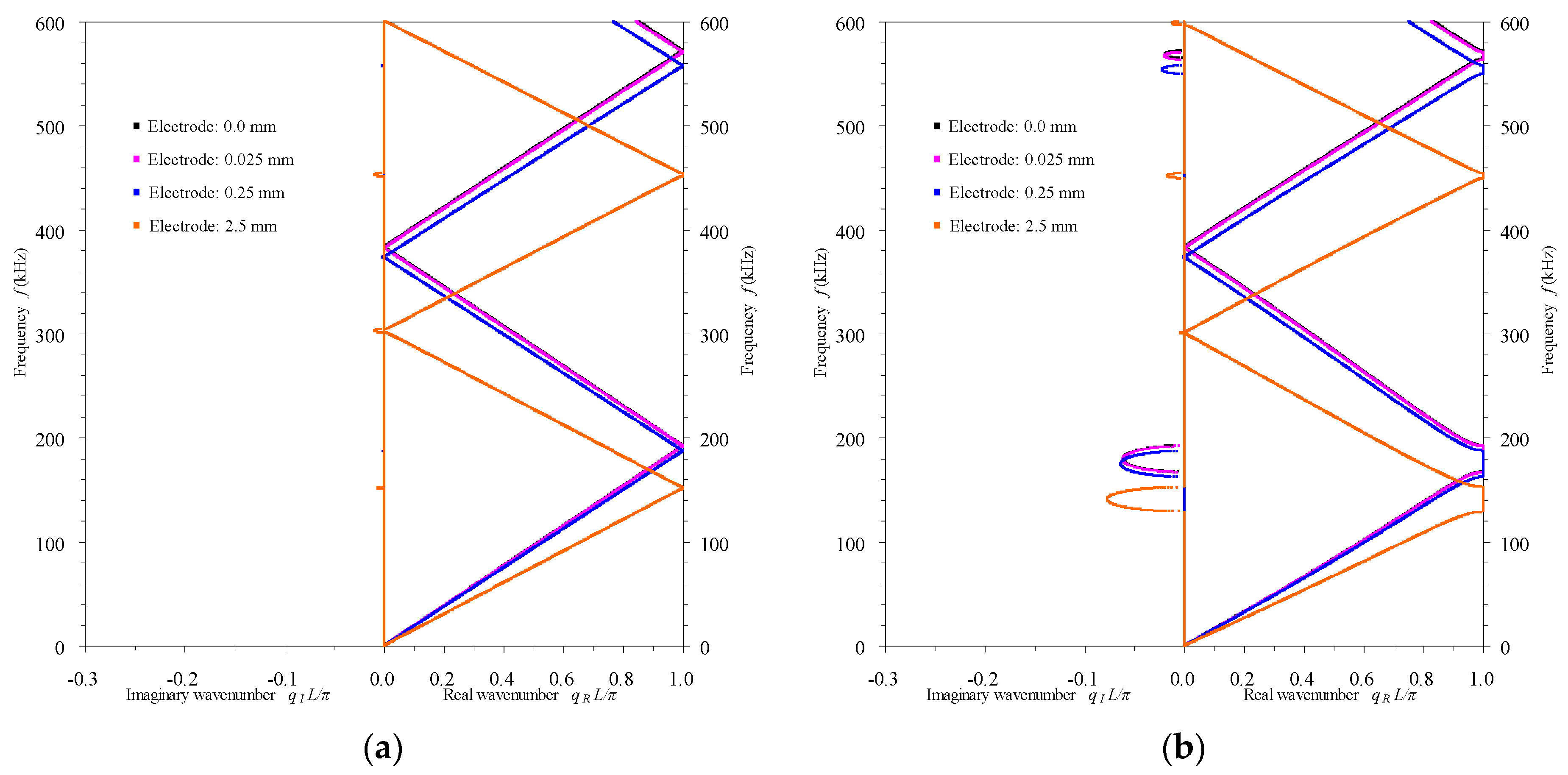
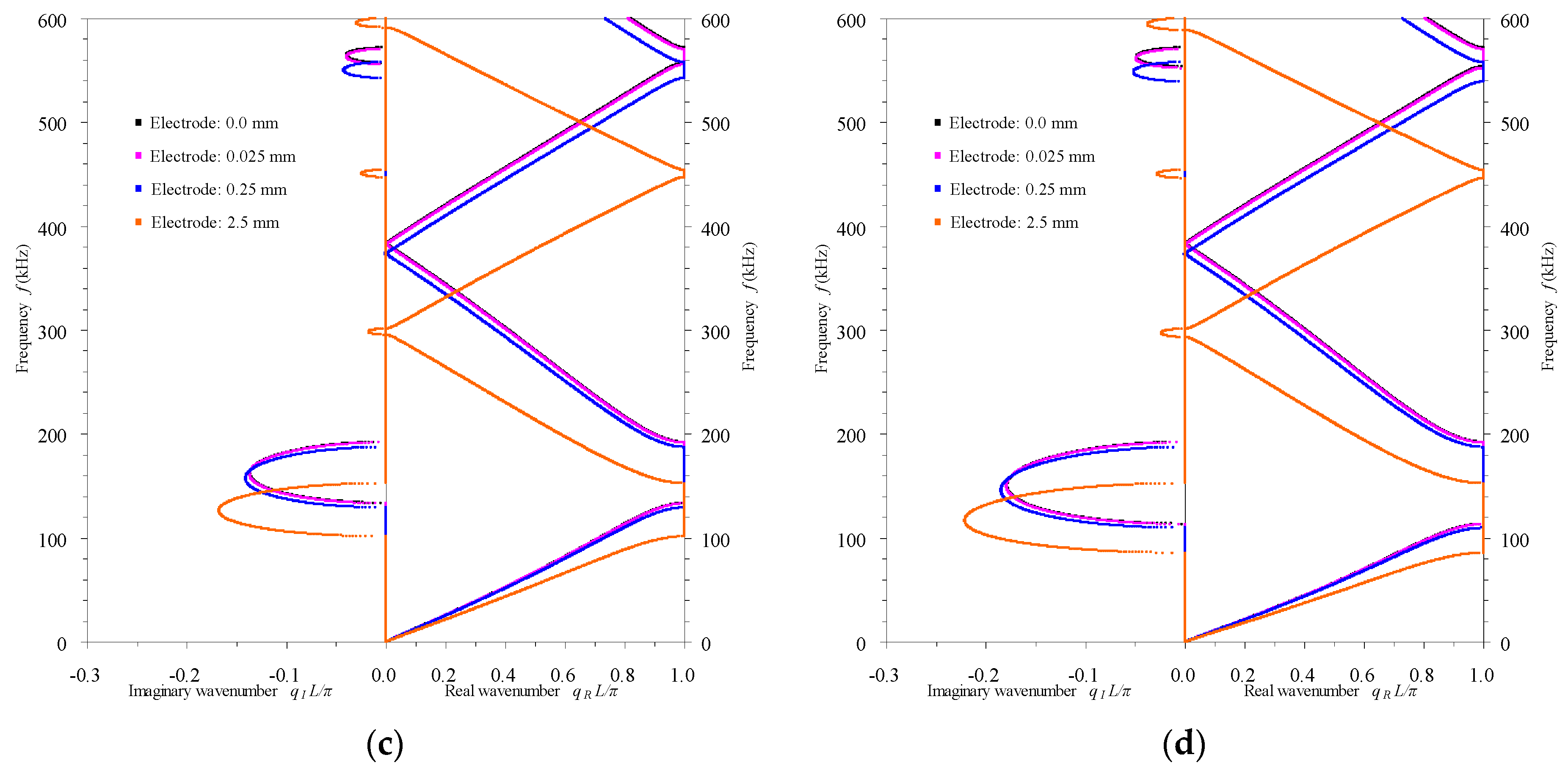
3.2.1. Influence of the Electrode’s Thickness
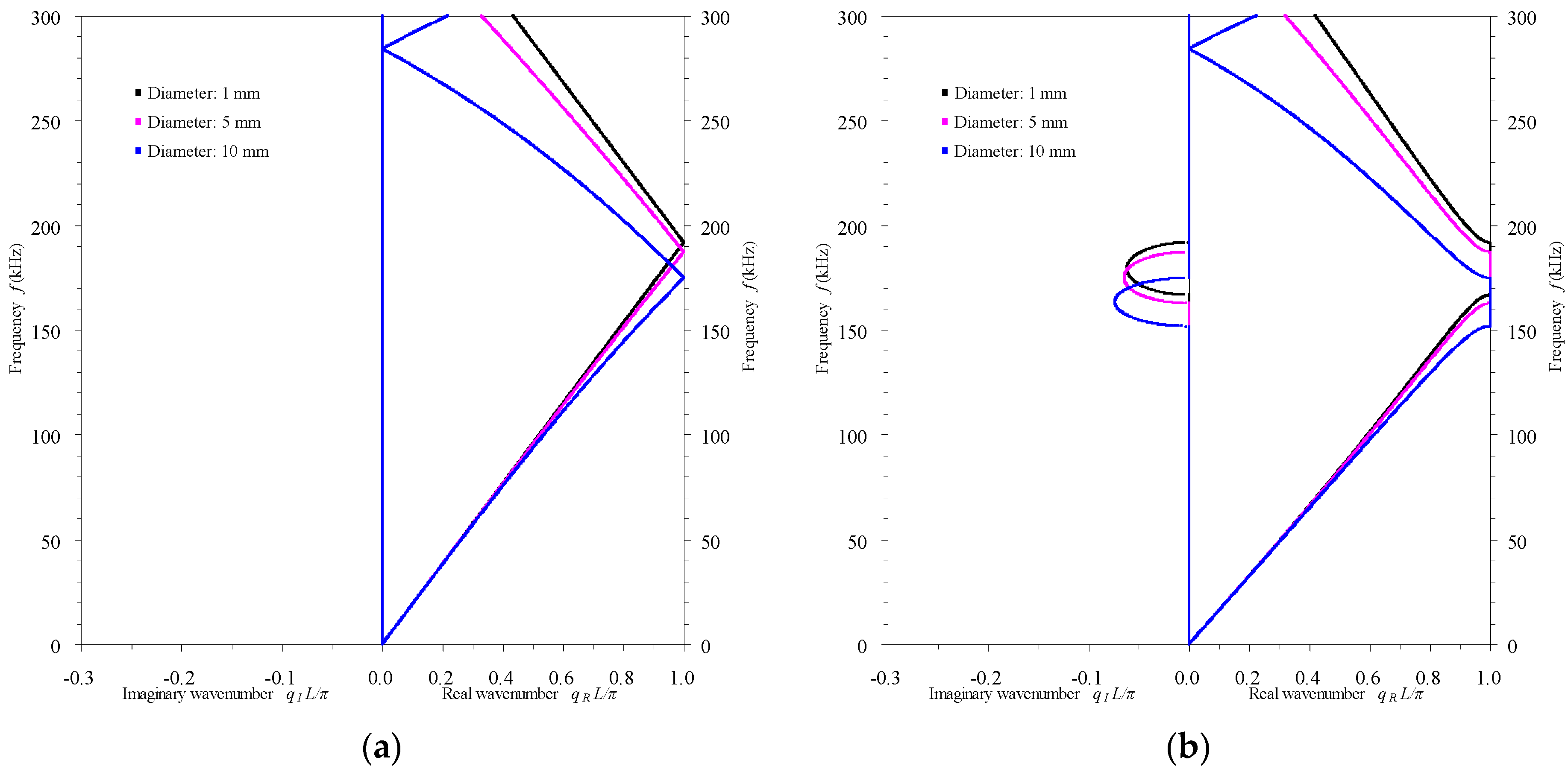
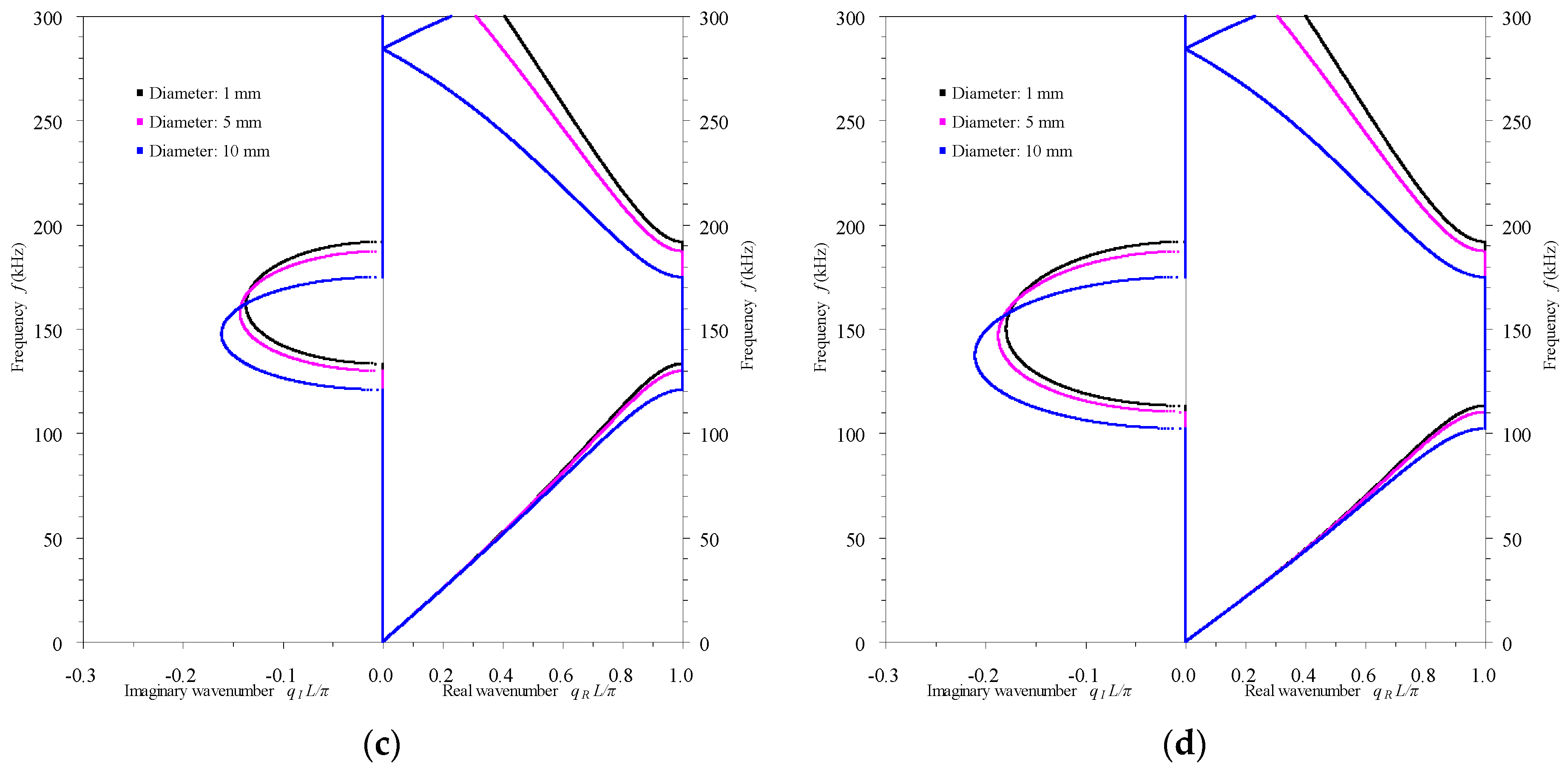
3.2.2. Influence of the Rod’s Cross-Sectional Dimension
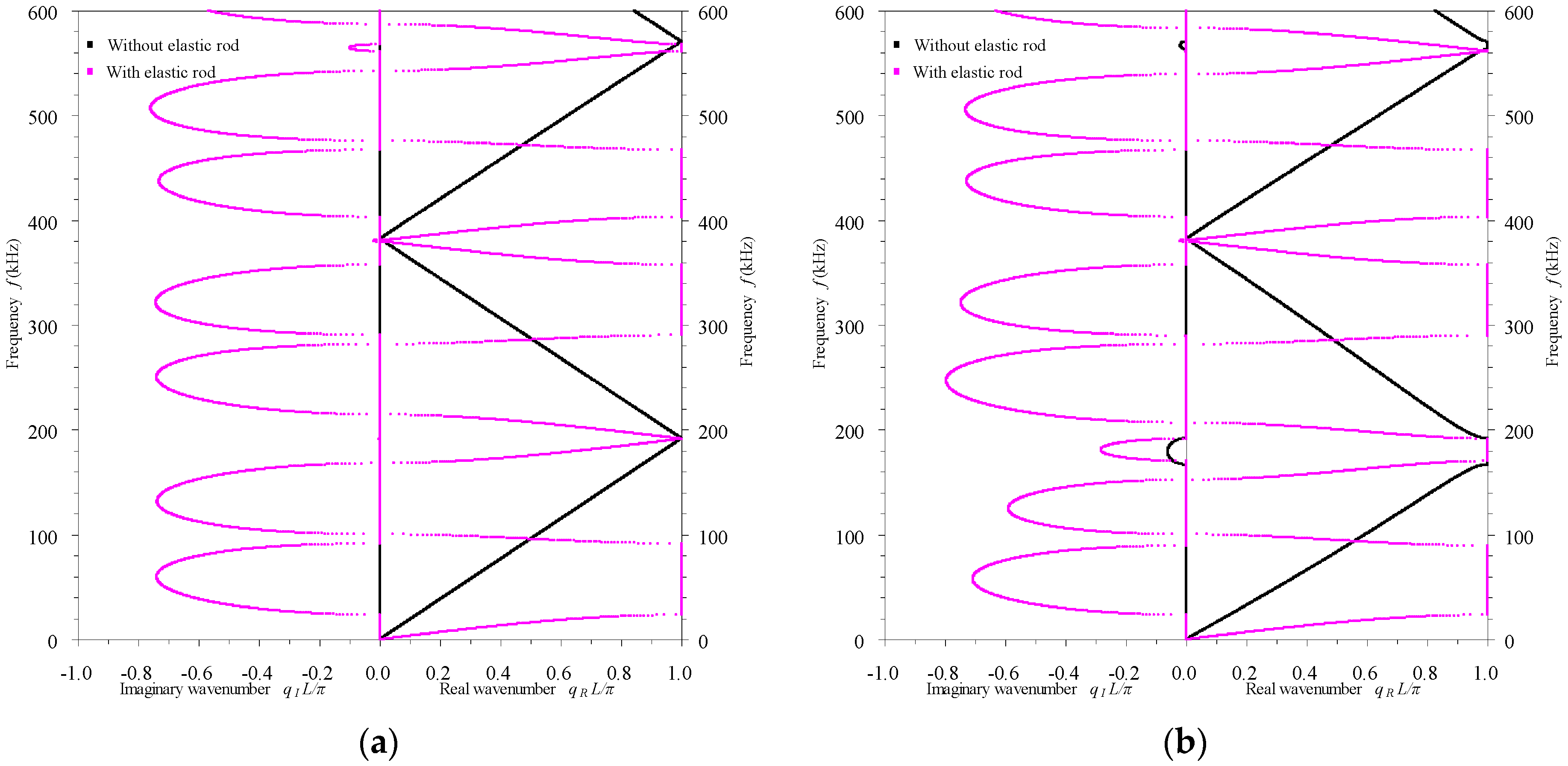
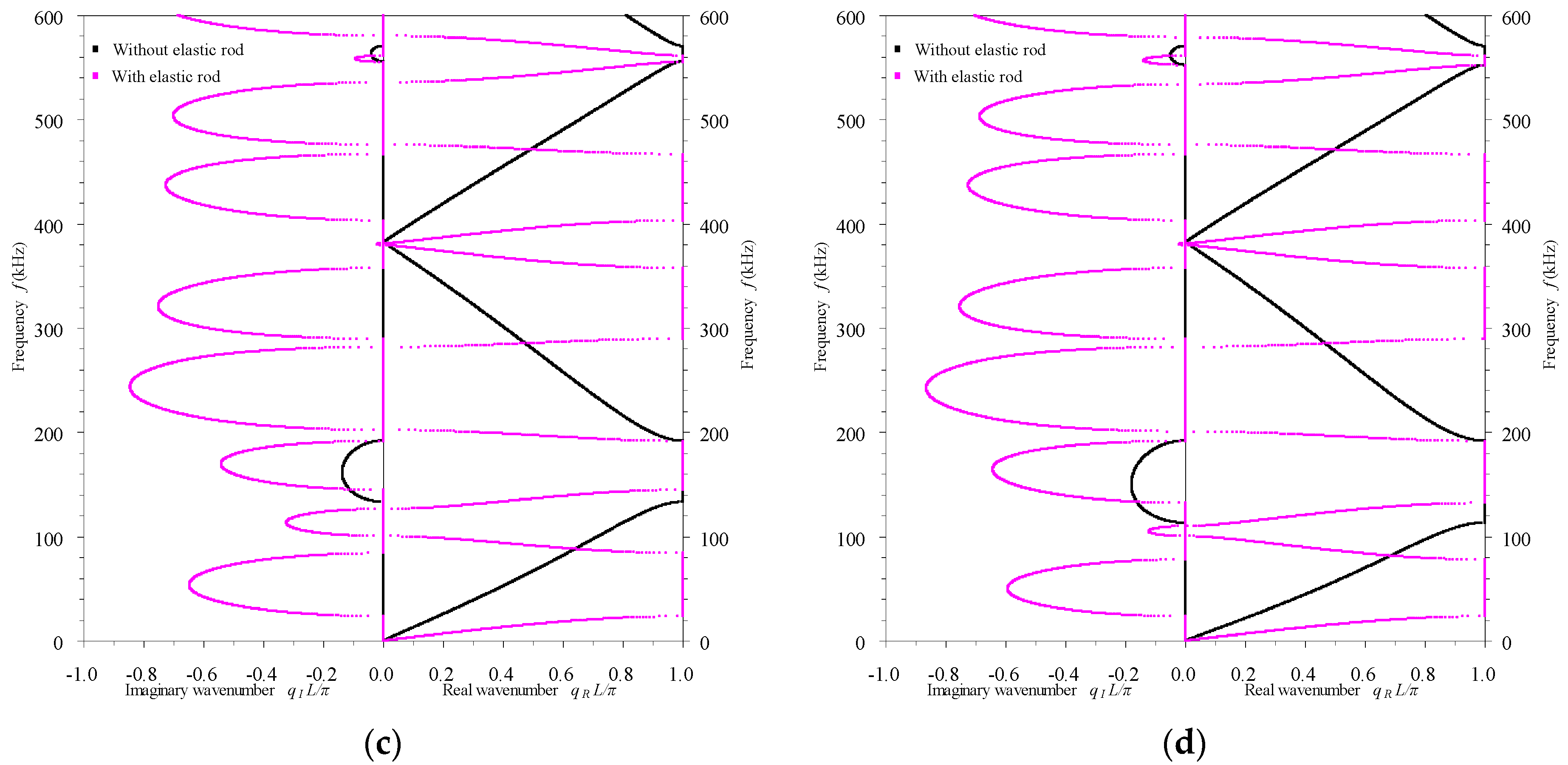
3.2.3. Influence of the Elastic Rod Insert
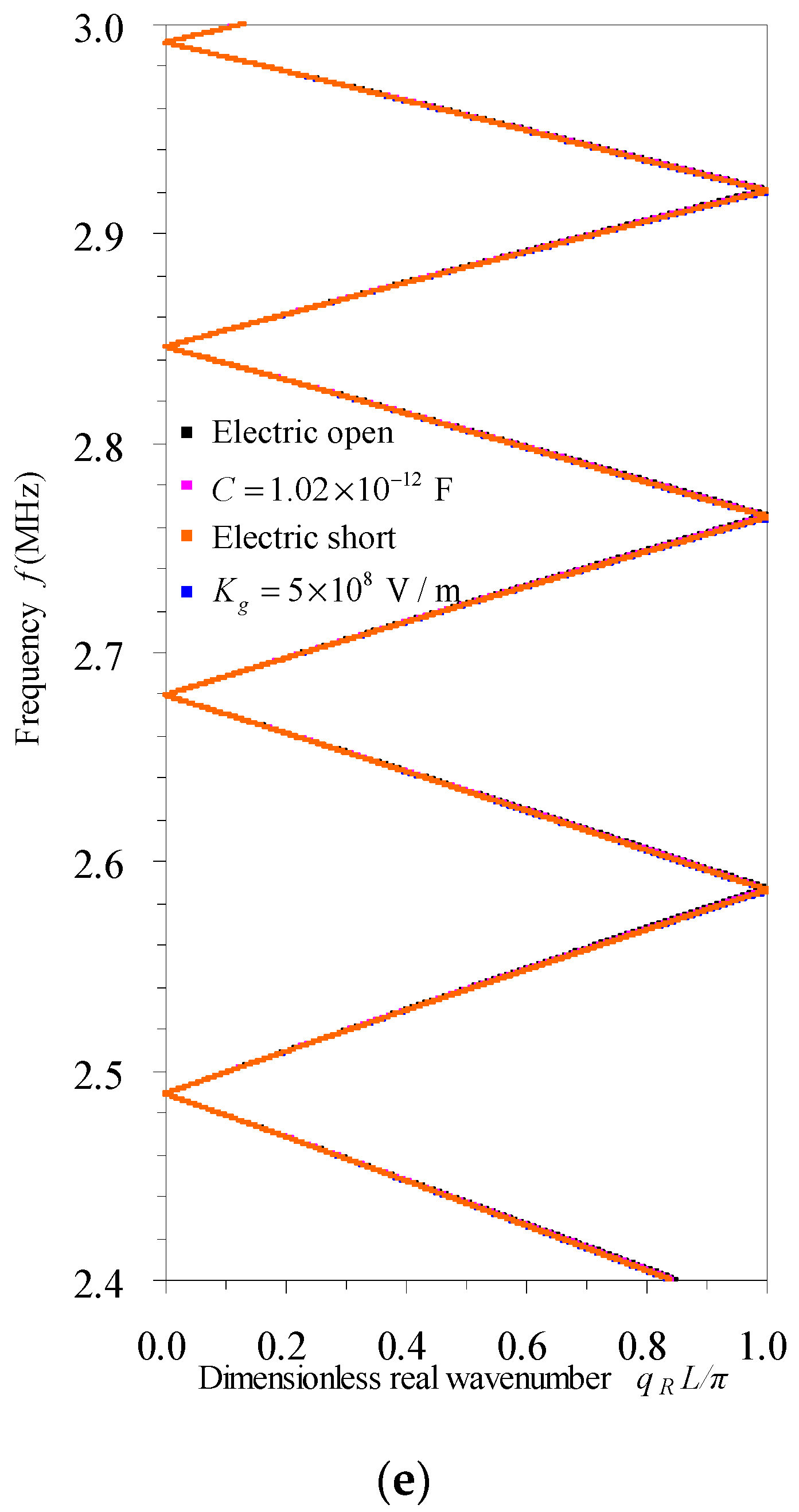
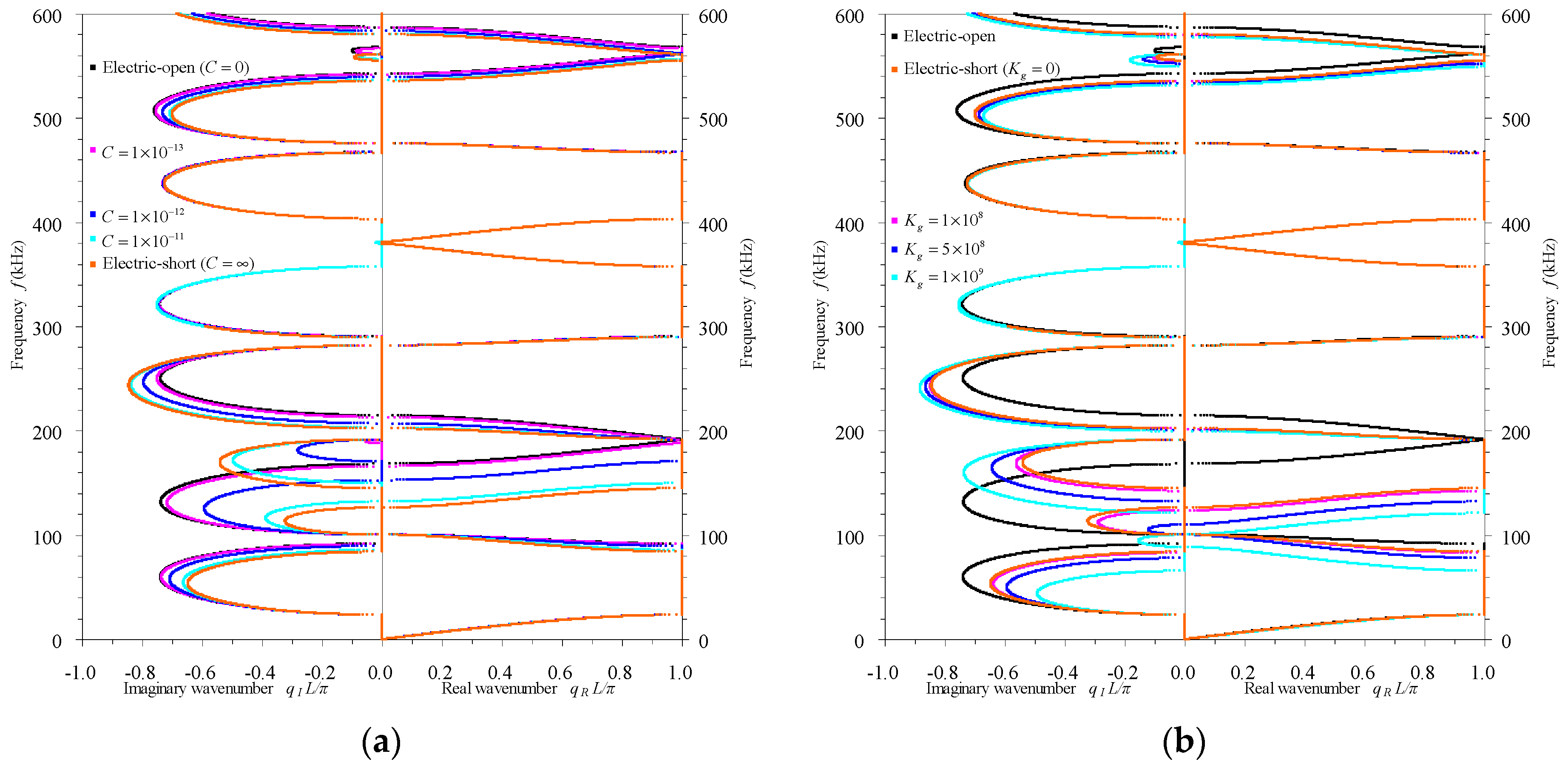
3.3. Active Control of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals
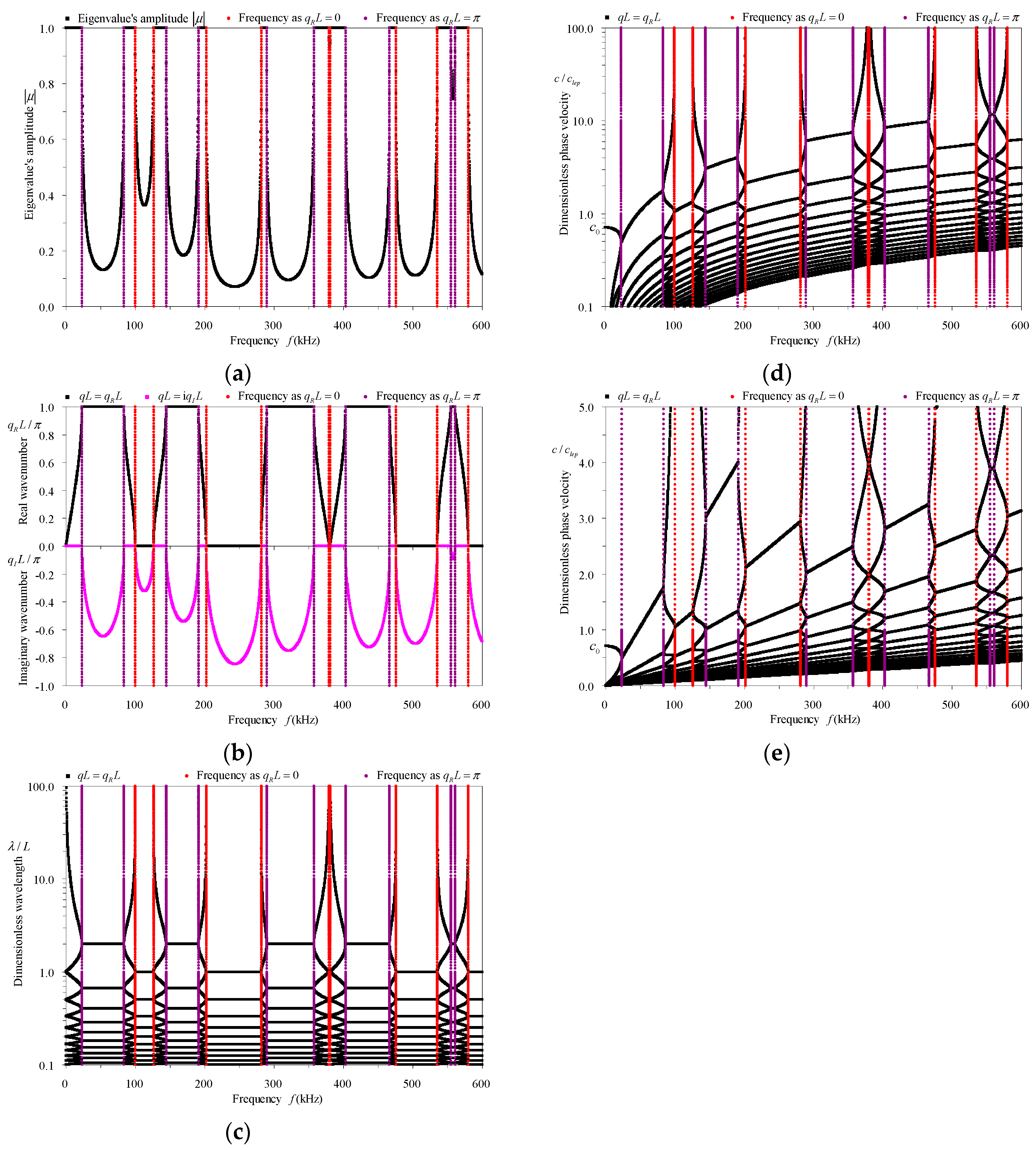
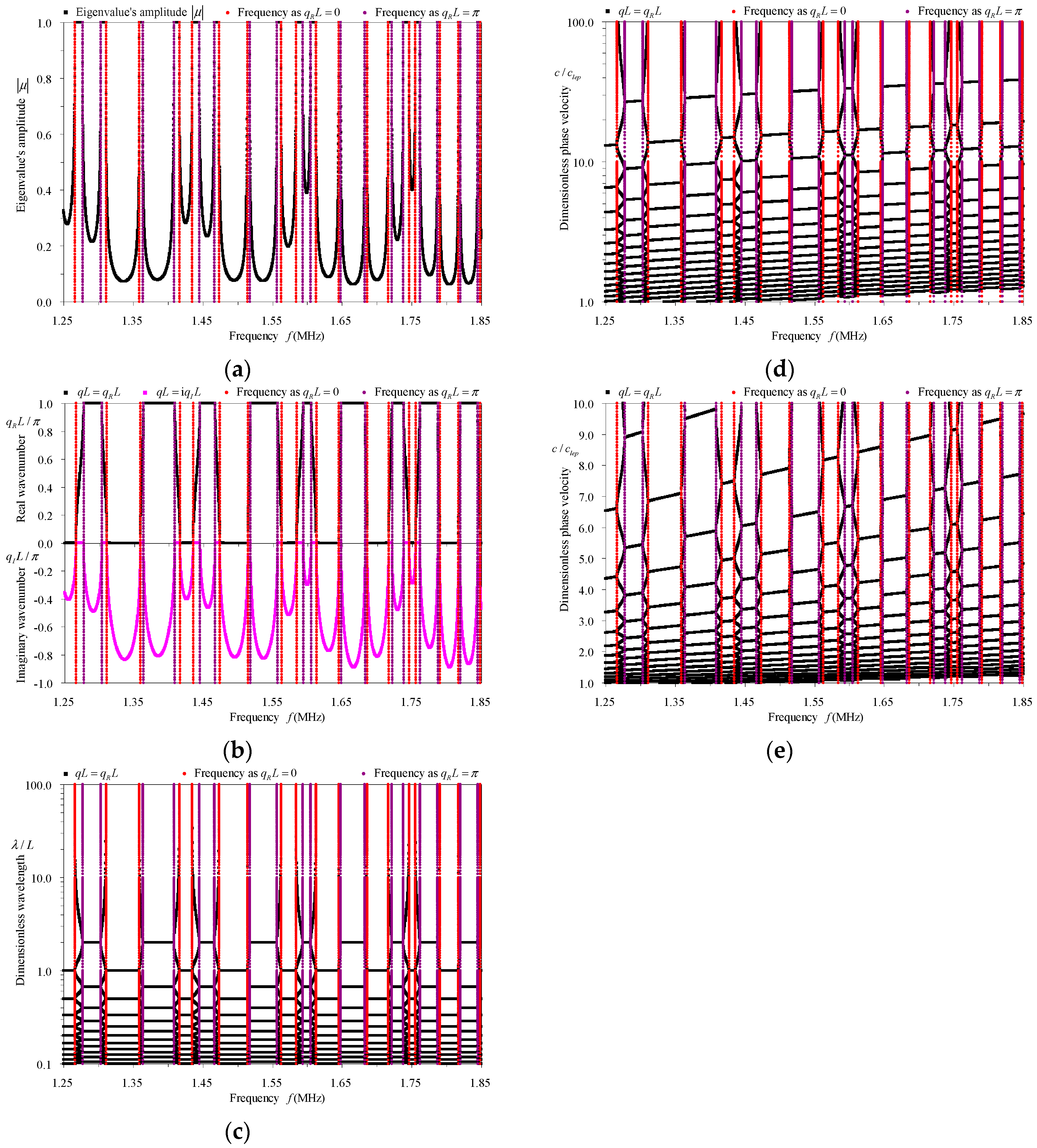
3.4. Dispersion Properties of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals
- (1)
- The eigenvalue’s amplitude spectra, which cannot be obtained by MRRM [5], demonstrate clearly the width, the central frequencies and the bounding frequencies of the pass-bands () and the stop-bands (). They also reflect the attenuation amplitudes of waves in the stop-bands, which are verified by the attenuation constant () spectra. The eigenvalue’s amplitude spectra cannot indicate the properties of waves in the pass-bands, but the phase constant spectra do.
- (2)
- In these frequency-related dispersion curves, the bounding frequencies of the odd and even order stop-bands correspond to and ( is a natural number), respectively. Within the stop-bands, the real part () of the complex wavenumber , which cannot be computed by the MRRM [5] but obtained here by the MTMM, have the same phases as their boundaries. In the wavelength spectra, the representations corresponding to these two kinds of phases are horizontal lines and . In the phase velocity spectra, they correspond to inclined lines that pass through the origin and have slopes , respectively. The lines determined by the above formulas and the lines of bounding frequencies form the grids to draw the spectra in the corresponding frequency-related dispersion curves.
4. Conclusions
- (1)
- The proposed analytical MTMM provides an alternative analysis method for the complex band structures and transmission spectra till to ( is the minimum critical frequency) within which the Love rod theory is valid. Its effectiveness is validated by some numerical examples.
- (2)
- In passive mode, the electrode’s thickness and the rod’s cross-sectional dimension can be used to slightly adjust the band structures of the rod-type piezoelectric phononic crystals, while the elastic rod insert is able to enormously alter the band structures.
- (3)
- In active mode, the switchable electrical boundaries among electric-short, applied electric capacity, electric-open and applied feedback control conditions is effective for modulating some of the band structures that are related to the electromechanical coupling of the rod-type piezoelectric phononic crystals. The tunable capacity and control gain in the applied electric capacity and applied feedback control cases, respectively, can also be used for tuning the propagation of longitudinal waves. The band structures of the electric-short condition play a referential role for designing the active control scheme.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MTMM | Modified Transfer Matrix Method |
| MRRM | Method of Reverberation-Ray Matrix |
| TMM | Transfer Matrix Method |
| FEM | Finite Element Method |
| AM | Analytical Method |
Appendix A
Appendix B
References
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Deymier, P.A. (Ed.) Acoustic Metamaterials and Phononic Crystals; Springer: Berlin, Germany, 2013.
- Asiri, S.; Baz, A.; Pines, D. Periodic struts for gearbox support system. J. Vib. Control 2005, 11, 709–721. [Google Scholar] [CrossRef]
- Asiri, S. Vibration isolation of automotive vehicle engine using periodic mounting systems. Proc. SPIE 2005, 5760, 526–537. [Google Scholar]
- Guo, Y.Q.; Fang, D.N. Analysis and interpretation of longitudinal waves in periodic multiphase rods using the method of reverberation-ray matrix combined with the Floquet-Bloch theorem. ASME J. Vib. Acoust. 2014, 136, 011006. [Google Scholar] [CrossRef]
- Ruzzene, M.; Baz, A. Attenuation and localization of wave propagation in periodic rods using shape memory inserts. Smart Mater. Struct. 2000, 9, 805–816. [Google Scholar] [CrossRef]
- Ruzzene, M.; Baz, A. Control of wave propagation in periodic composite rods using shape memory inserts. ASME J. Vib. Acoust. 2000, 122, 151–159. [Google Scholar] [CrossRef]
- Ding, R.; Su, X.L.; Zhang, J.J.; Gao, Y.W. Tunability of longitudinal wave band gaps in one dimensional phononic crystal with magnetostrictive material. J. Appl. Phys. 2014, 115, 074104. [Google Scholar] [CrossRef]
- Baz, A. Active control of periodic structures. ASME J. Vib. Acoust. 2001, 123, 472–479. [Google Scholar] [CrossRef]
- Thorp, O.; Ruzzene, M.; Baz, A. Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches. Smart Mater. Struct. 2001, 10, 979–989. [Google Scholar] [CrossRef]
- Chen, S.B.; Wen, J.H.; Wang, G.; Yu, D.L.; Wen, X.S. Improved modeling of rods with periodic arrays of shunted piezoelectric patches. J. Intell. Mater. Syst. Struct. 2012, 23, 1613–1621. [Google Scholar]
- Lossouarn, B.; Aucejo, M.; Deu, J.-F. Multimodal coupling of periodic lattices and application to rod vibration damping with a piezoelectric network. Smart Mater. Struct. 2015, 24, 045018. [Google Scholar] [CrossRef]
- Lossouarn, B.; Aucejo, M.; Deu, J.-F. Multimodal vibration damping through a periodic array of piezoelectric patches connected to a passive network. Proc. SPIE 2015, 9431, 94311A. [Google Scholar]
- Singh, A.; Pines, D.J.; Baz, A. Active/passive reduction of vibration of periodic one-dimensional structures using piezoelectric actuators. Smart Mater. Struct. 2004, 13, 698–711. [Google Scholar] [CrossRef]
- Asiri, S.; Baz, A.; Pines, D. Active periodic struts for a gearbox support system. Smart Mater. Struct. 2006, 15, 1707–1714. [Google Scholar] [CrossRef]
- Asiri, S. Tunable mechanical filter for longitudinal vibrations. Shock Vib. 2007, 14, 377–391. [Google Scholar] [CrossRef]
- Asiri, S. Broadband vibration attenuation using hybrid periodic rods. J. Eng. Res. 2008, 5, 7–19. [Google Scholar]
- Li, F.M.; Wang, Y.S.; Chen, A.L. Wave localization in randomly disordered periodic piezoelectric rods. Acta Mech. Solida Sin. 2006, 19, 50–57. [Google Scholar]
- Wang, Y.Z.; Li, F.M.; Kishimoto, K.; Wang, Y.S.; Huang, W.H. Wave localization in randomly disordered periodic piezoelectric rods with initial stress. Acta Mech. Solida Sin. 2008, 21, 529–535. [Google Scholar] [CrossRef]
- Degraeve, S.; Granger, C.; Dubus, B.; Vasseur, J.O.; Thi, M.P.; Hladky-Hennion, A.-C. Bragg band gaps tunability in an homogeneous piezoelectric rod with periodic electrical boundary conditions. J. Appl. Phys. 2014, 115, 194508. [Google Scholar] [CrossRef]
- Kutsenko, A.A.; Shuvalov, A.L.; Poncelet, O.; Darinskii, A.N. Quasistatic stopband and other unusual features of the spectrum of a one-dimensional piezoelectric phononic crystal controlled by negative capacitance. C. R. Mec. 2015, 343, 680–688. [Google Scholar] [CrossRef]
- Ponge, M.-F.; Dubus, B.; Granger, C.; Vasseur, J.O.; Thi, M.P.; Hladky-Hennion, A.-C. Theoretical and experimental analyses of tunable Fabry-Perot resonators using piezoelectric phononic crystals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1114–1121. [Google Scholar] [CrossRef] [PubMed]
- Degraeve, S.; Granger, C.; Dubus, B.; Vasseur, J.O.; Thi, M.P.; Hladky, A.C. Tunability of Bragg band gaps in one-dimensional piezoelectric phononic crystals using external capacitances. Smart Mater. Struct. 2015, 24, 085013. [Google Scholar] [CrossRef]
- Degraeve, S.; Granger, C.; Dubus, B.; Vasseur, J.O.; Thi, M.P.; Hladky-Hennion, A.-C. Tunability of a one-dimensional elastic/piezoelectric phononic crystal using external capacitances. Acta Acust. United Acust. 2015, 101, 494–501. [Google Scholar] [CrossRef]
- Kutsenko, A.A.; Shuvalov, A.L.; Poncelet, O.; Darinskii, A.N. Tunable effective constants of the one-dimensional piezoelectric phononic crystal with internal connected electrodes. J. Acoust. Soc. Am. 2015, 137, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Vasilenko, A.V.; Rogacheva, N.N. The effective characteristics and electroelastic state of active composite elements. PMM-J. Appl. Math. Mech. 2011, 75, 463–471. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity, 4th ed.; Cambridge University Press: Cambridge, UK, 1927; p. 428. [Google Scholar]
- Graff, K.F. Wave Motion in Elastic Solids; Ohio State University Press: Columbus, OH, USA, 1975; pp. 108–125. [Google Scholar]
- Doyle, J.F. Wave Propagation in Structures, 2nd ed.; Springer: New York, NY, USA, 1997. [Google Scholar]
- Ravindra, B. Love-theoretical analysis of periodic system of rods. J. Acoust. Soc. Am. 1999, 106, 1183–1186. [Google Scholar] [CrossRef] [PubMed]
- Brillouin, L. Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices, 2nd ed.; Dover Publications: New York, NY, USA, 1953. [Google Scholar]
- Mead, D.J. Wave propagation in continuous periodic structures: Research contributions from Southampton, 1964–1995. J. Sound Vib. 1996, 190, 495–524. [Google Scholar] [CrossRef]
- ANSI/IEEE Std 176-1987. IEEE Standard on Piezoelectricity; IEEE: New York, NY, USA, 1988; pp. 6–8. [Google Scholar]
- Tiersten, H.F. Linear Piezoelectric Plate Vibrations; Plenum Press: New York, NY, USA, 1969; pp. 41–50. [Google Scholar]
- Auld, B.A. Acoustic Fields and Waves in Solids; John Wiley & Sons: New York, NY, USA, 1973; Volume I. [Google Scholar]
- Bronshtein, I.N.; Semendyayev, K.A.; Musiol, G.; Muehlig, H. Handbook of Mathematics, 5th ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Mead, D.J. Wave propagation and natural modes in periodic systems: I. Mono-coupled systems. J. Sound Vib. 1975, 40, 1–18. [Google Scholar] [CrossRef]
| Electrical Boundary Conditions | Associated Mathematical Formulas | Expressions of | Expressions of |
|---|---|---|---|
| Electric-open | |||
| Applied electric capacity | |||
| Electric-short | |||
| Applied feedback control | |||
| Electrical Boundary Conditions | Expressions of | Expressions of | |
| Electric-open | |||
| Applied electric capacity | |||
| Electric-short | |||
| Applied feedback control | |||
| Materials | Stiffness Constants () | |||||||||
| PZT-5H | 117.0 | 126.0 | 126.0 | 84.1 | 84.1 | 79.5 | ||||
| Brass | 162.46 | 162.46 | 162.46 | 82.58 | 82.58 | 82.58 | ||||
| Epoxy | 6.98 | 6.98 | 6.98 | 3.76 | 3.76 | 3.76 | ||||
| Materials | Poisson’s Ratios | Piezoelectric Constants () | Dielectric Constants () | |||||||
| PZT-5H | 0.41 | 0.41 | 23.3 | −6.5 | −6.5 | 13.02 | ||||
| Brass | 0.337 | 0.337 | — | — | — | — | ||||
| Epoxy | 0.35 | 0.35 | — | — | — | — | ||||
| Materials | Mass Density () | Length () | Cross-Sectional Area () | Cross-Sectional Moments of Inertia () | ||||||
| PZT-5H | 7500 | 10 | 1/4 | 1/64 | 1/64 | |||||
| Brass | 8320 | 0.025 | 1/4 | 1/64 | 1/64 | |||||
| Epoxy | 1180 | 10 | 1/4 | 1/64 | 1/64 | |||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Guo, Y. Analysis of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals. Crystals 2016, 6, 45. https://doi.org/10.3390/cryst6040045
Li L, Guo Y. Analysis of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals. Crystals. 2016; 6(4):45. https://doi.org/10.3390/cryst6040045
Chicago/Turabian StyleLi, Longfei, and Yongqiang Guo. 2016. "Analysis of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals" Crystals 6, no. 4: 45. https://doi.org/10.3390/cryst6040045
APA StyleLi, L., & Guo, Y. (2016). Analysis of Longitudinal Waves in Rod-Type Piezoelectric Phononic Crystals. Crystals, 6(4), 45. https://doi.org/10.3390/cryst6040045






