Influence of Boron on Initial Austenite Grain Size and Hot Deformation Behavior of Boron Microalloyed Steels
Abstract
:1. Introduction
2. Results and Discussion
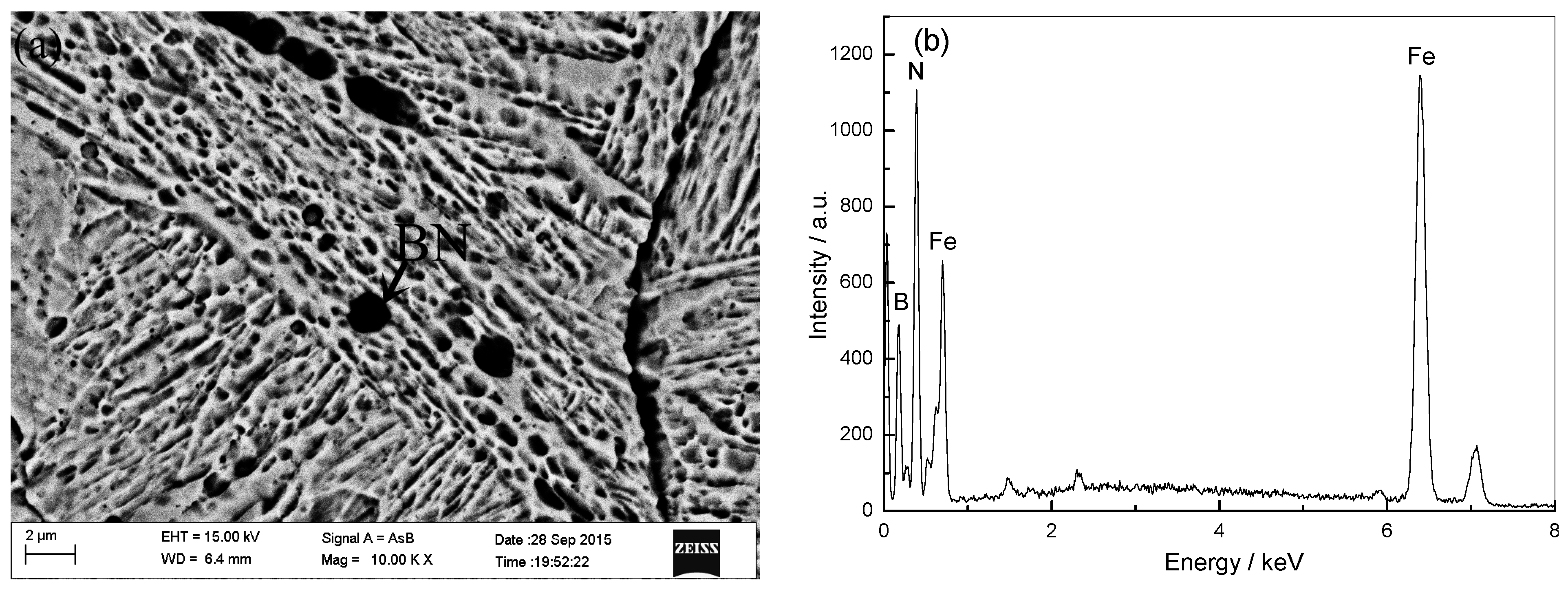
2.1. Influence of Boron Content on Initial Austenite Grain

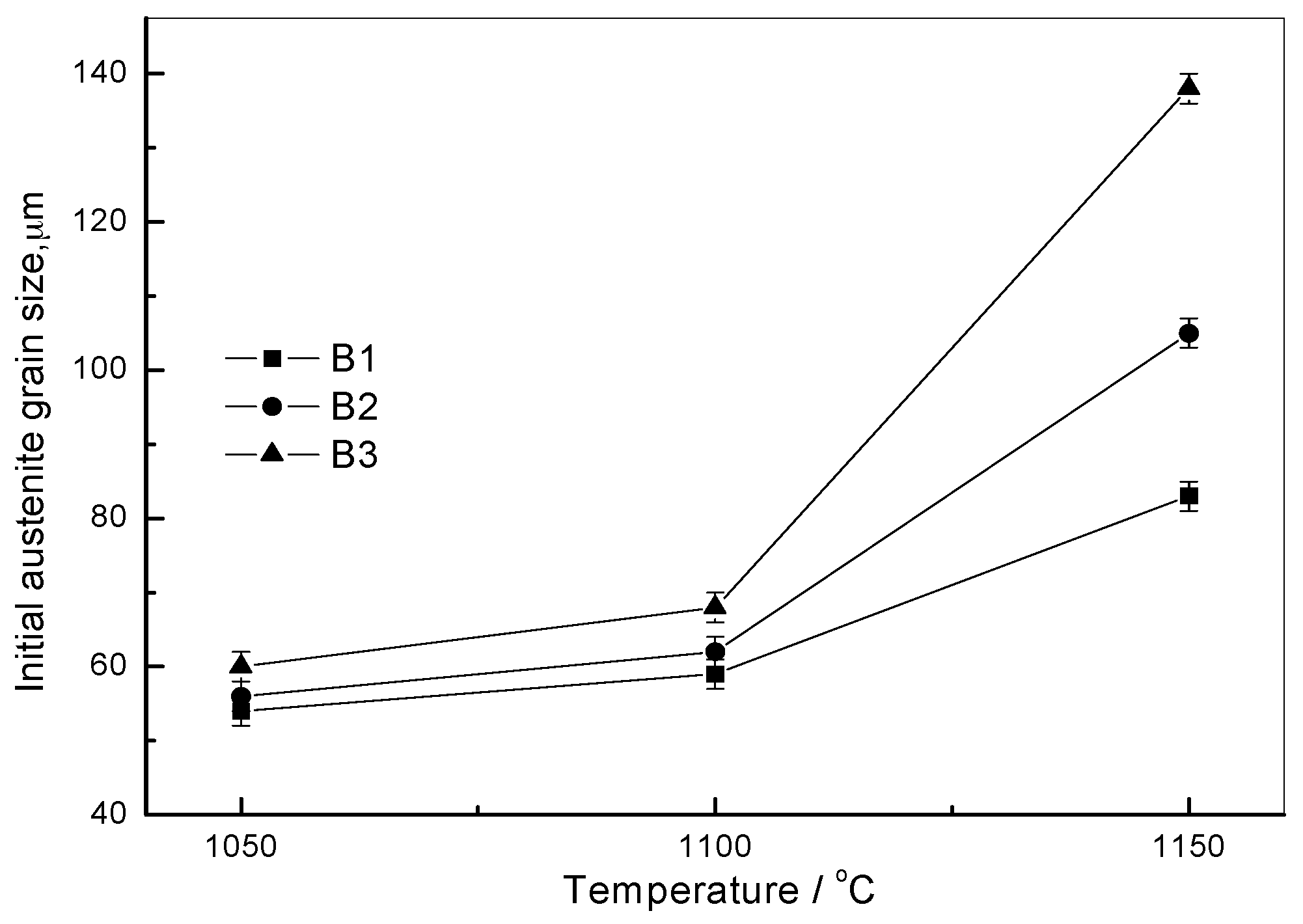
| Steels | 1050 °C | 1100 °C | 1150 °C |
|---|---|---|---|
| B1 | 54 | 59 | 83 |
| B2 | 56 | 62 | 105 |
| B3 | 60 | 68 | 138 |

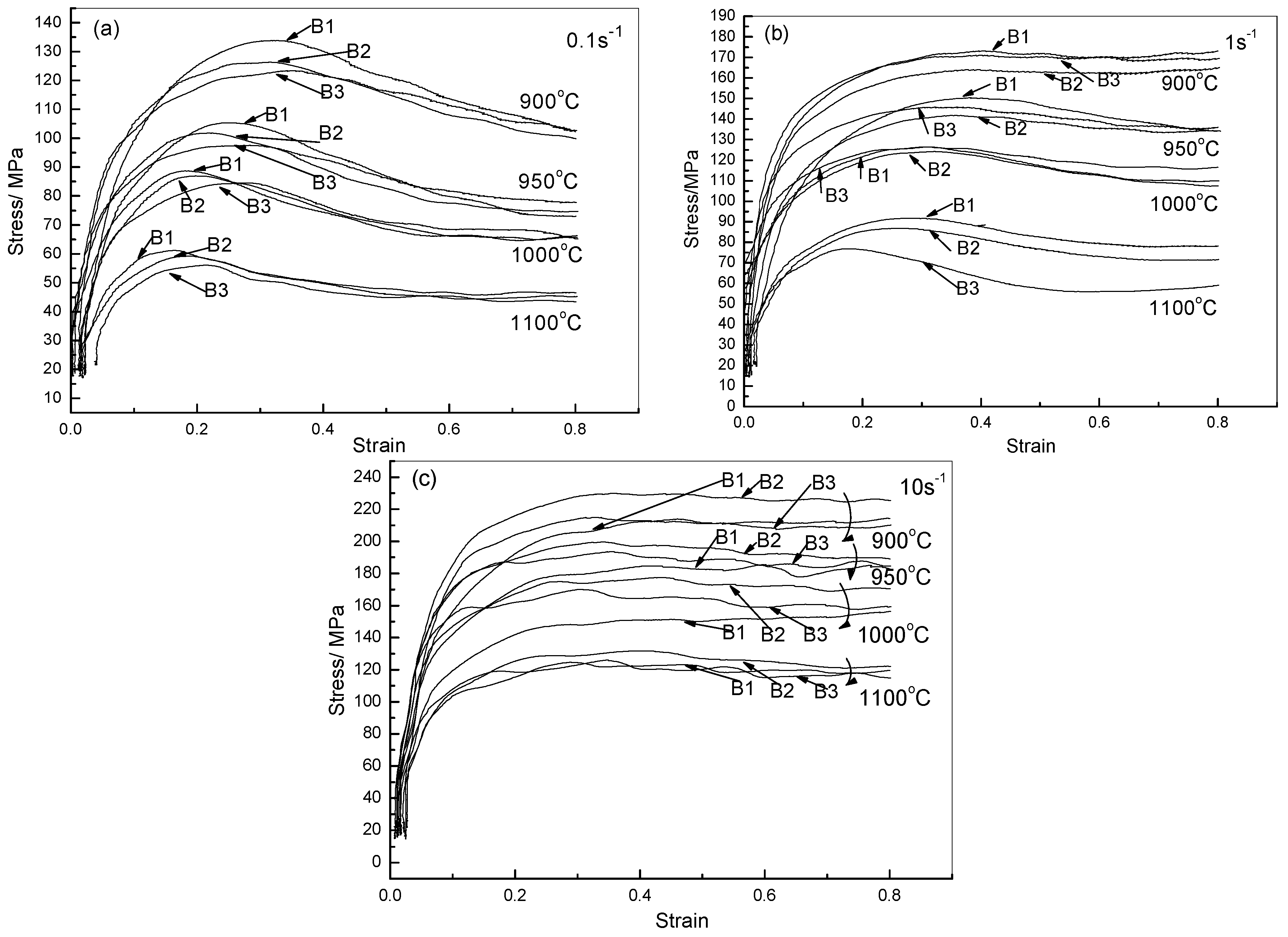
2.2. Influence of Boron Content on Hot Deformation Behavior
2.2.1. Flow Stress Curves
2.2.2. Constitutive Analysis
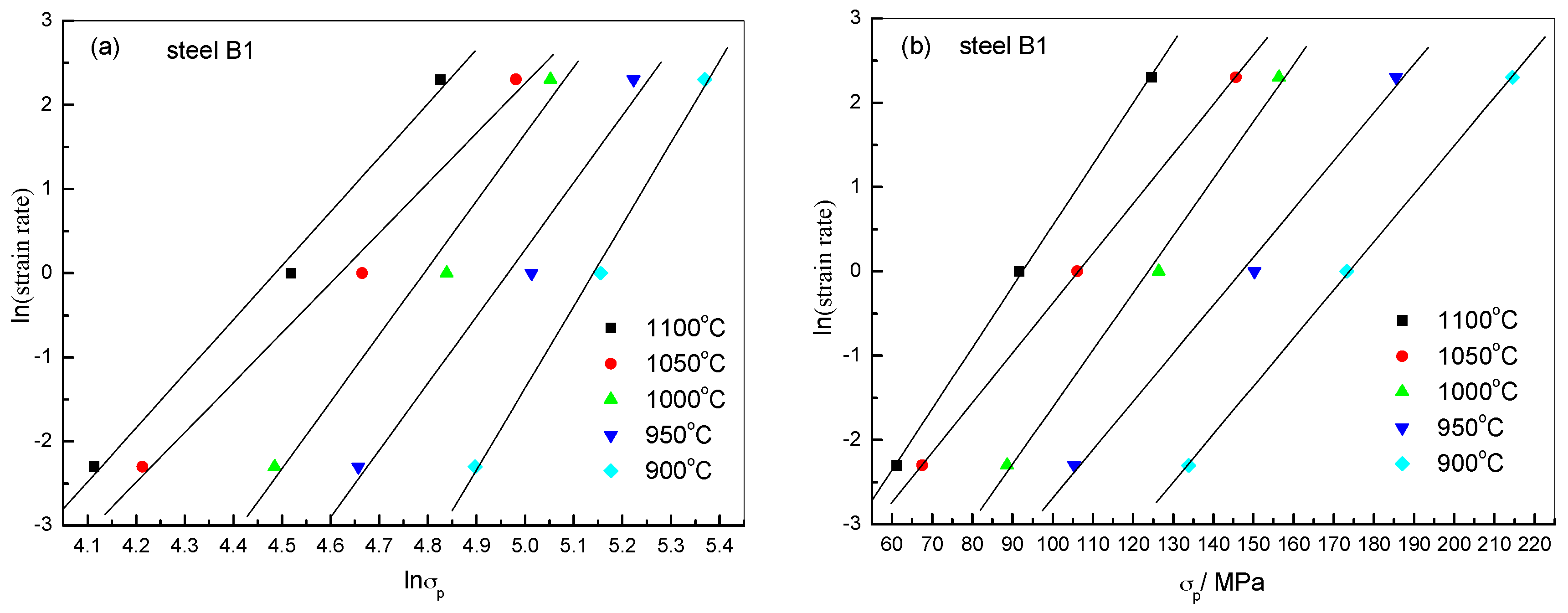
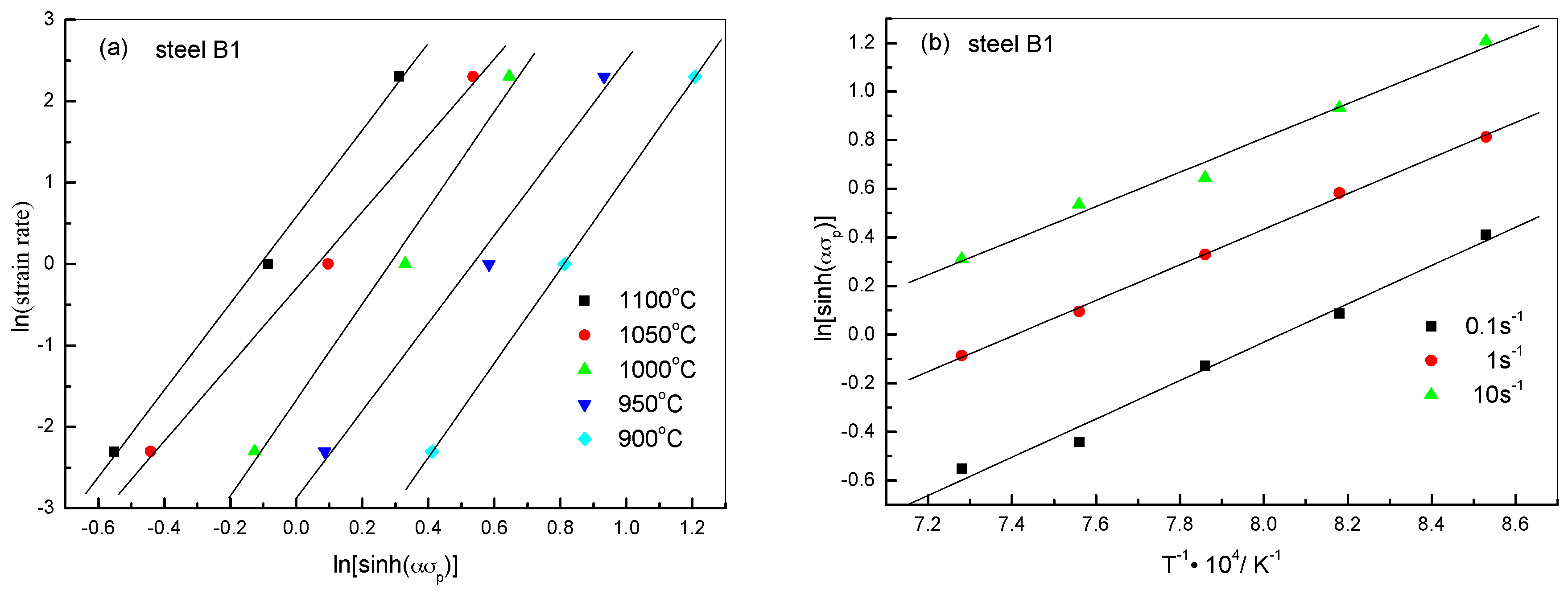
| Steels | β | n1 | α | n | Q (kJ/mol) | A |
|---|---|---|---|---|---|---|
| B1 | 0.0607 | 6.7717 | 0.0090 | 5.4195 | 316.86 | 1.501 × 1012 |
| B2 | 0.0465 | 6.0033 | 0.0078 | 4.8760 | 286.45 | 4.495 × 1011 |
| B3 | 0.0506 | 5.6940 | 0.0089 | 4.6014 | 277.91 | 6.009 × 1010 |
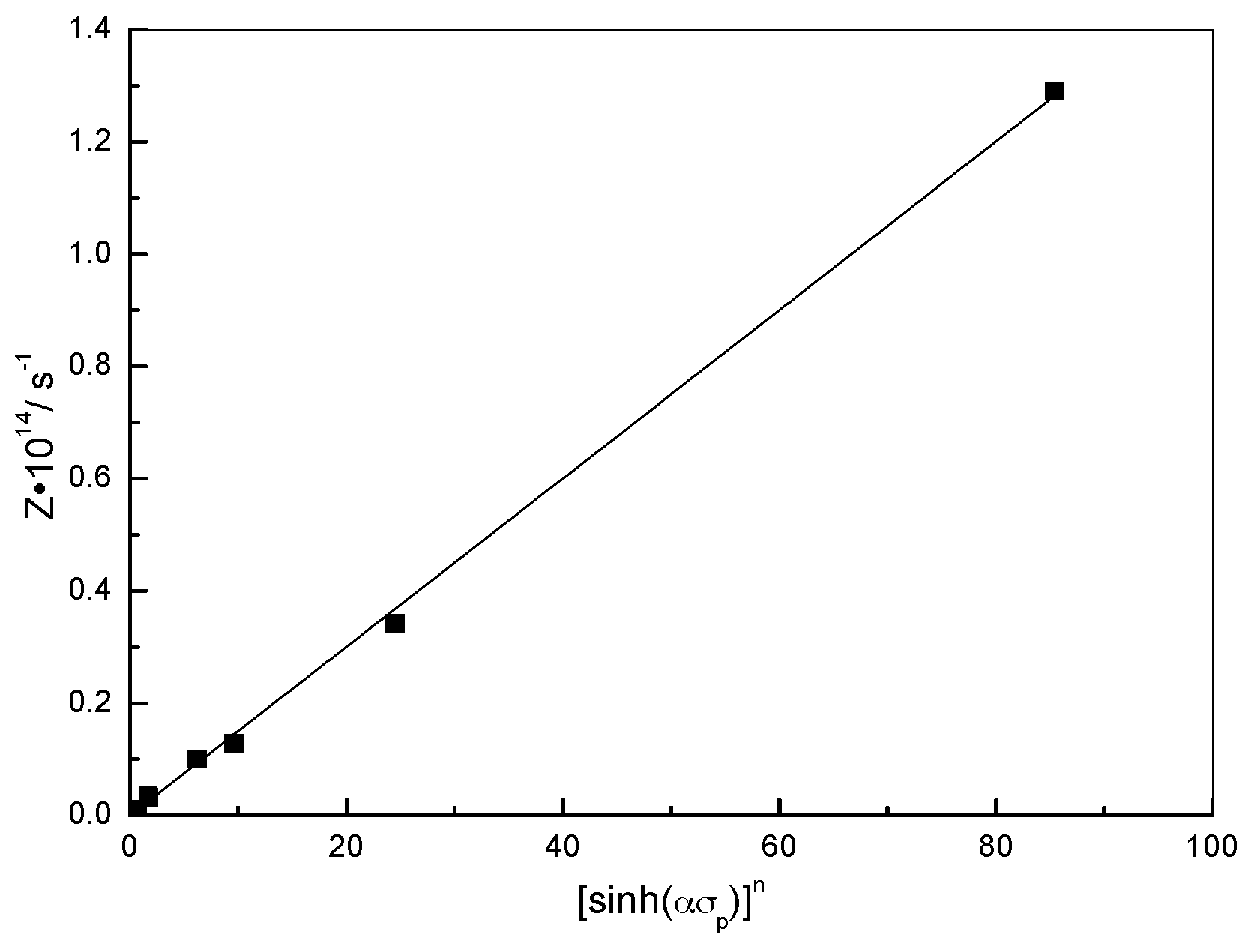
2.2.3. Critical DRX Parameters
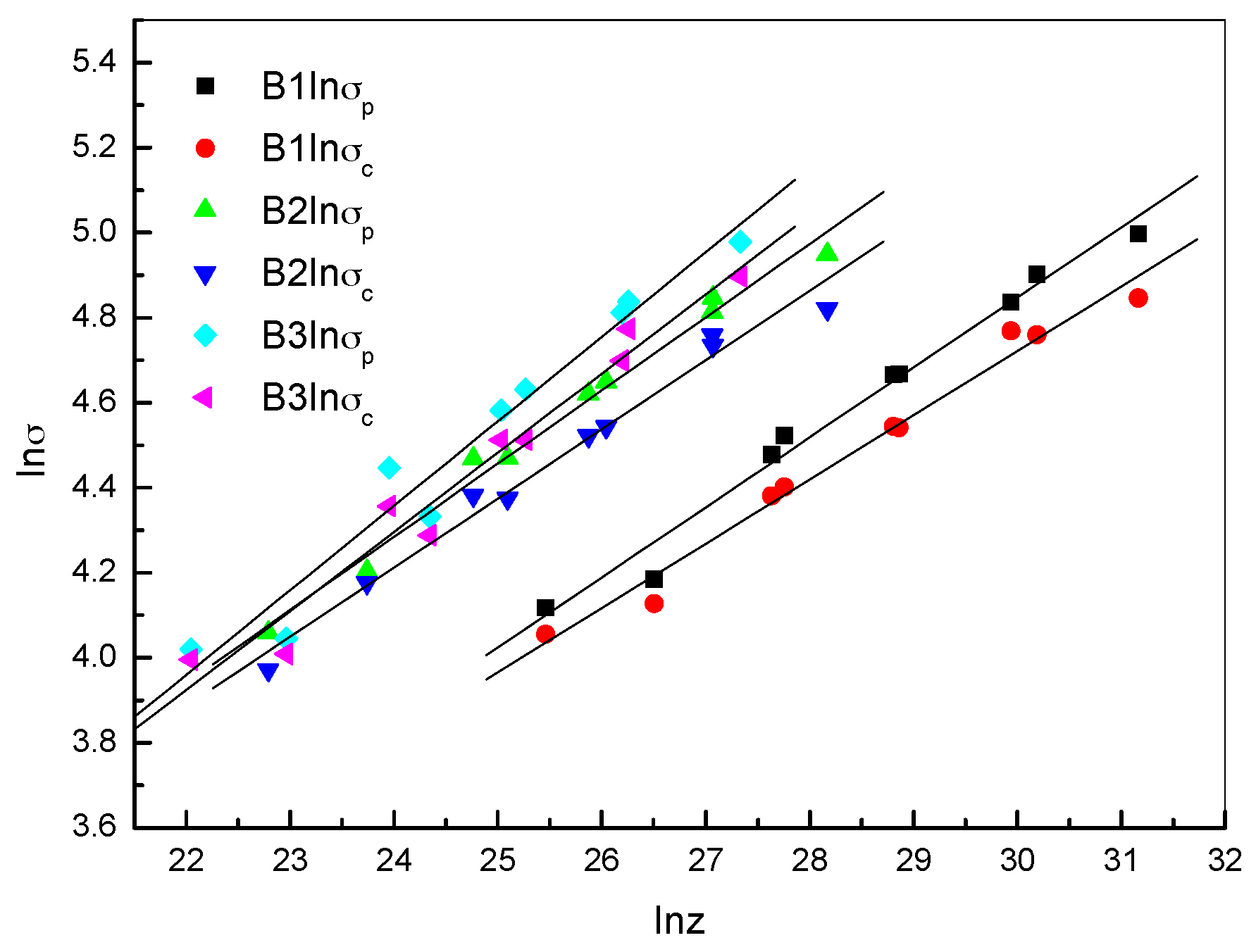
| Steel B1 | Steel B2 | Steel B3 | |
|---|---|---|---|
| lnσp-lnZ | lnσp = 0.16465 lnZ − 0.09199 | lnσp = 0.17208 lnZ + 0.15473 | lnσp = 0.19057 lnZ − 0.40797 |
| lnσc-lnZ | lnσc = 0.15116 lnZ + 0.18716 | lnσc = 0.16276 lnZ + 0.30586 | lnσc = 0.18593 lnZ − 0.16590 |
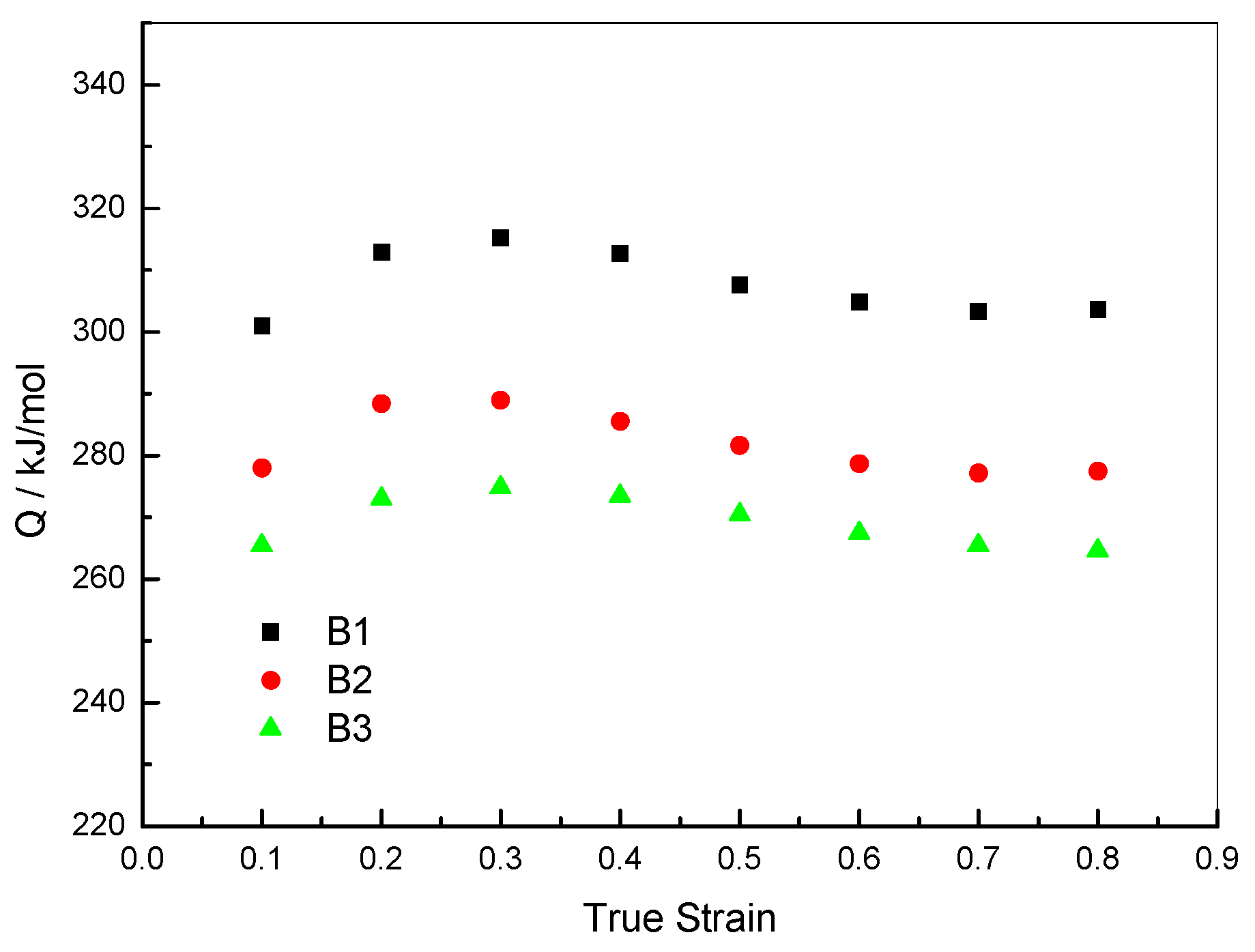
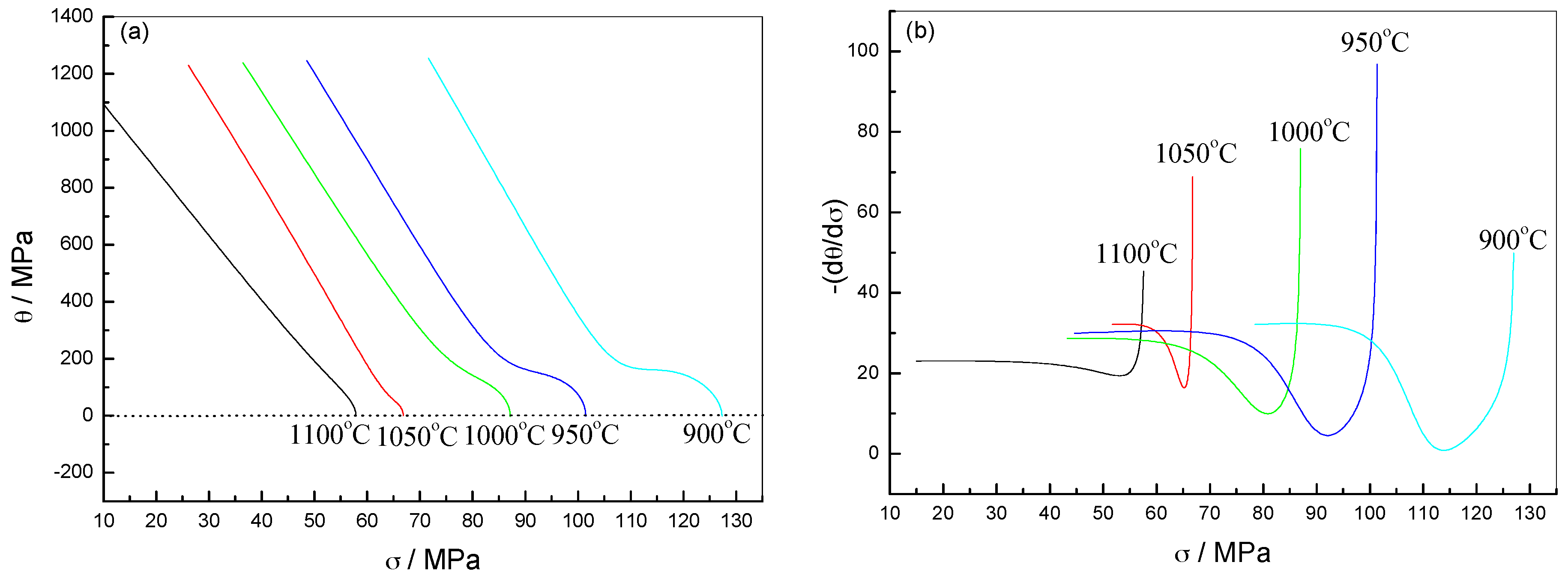
2.2.4. Analysis of DRX Behaviors

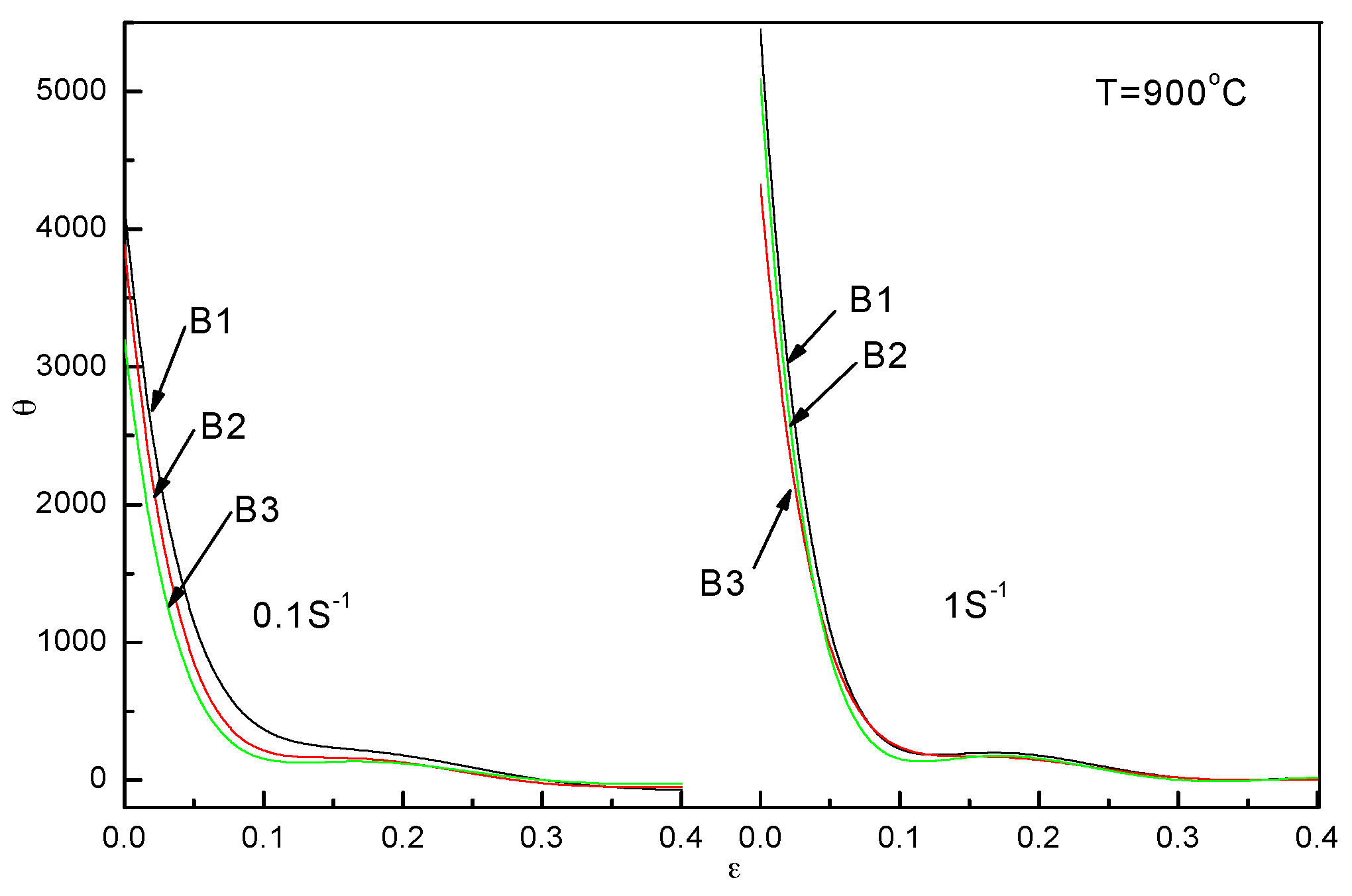
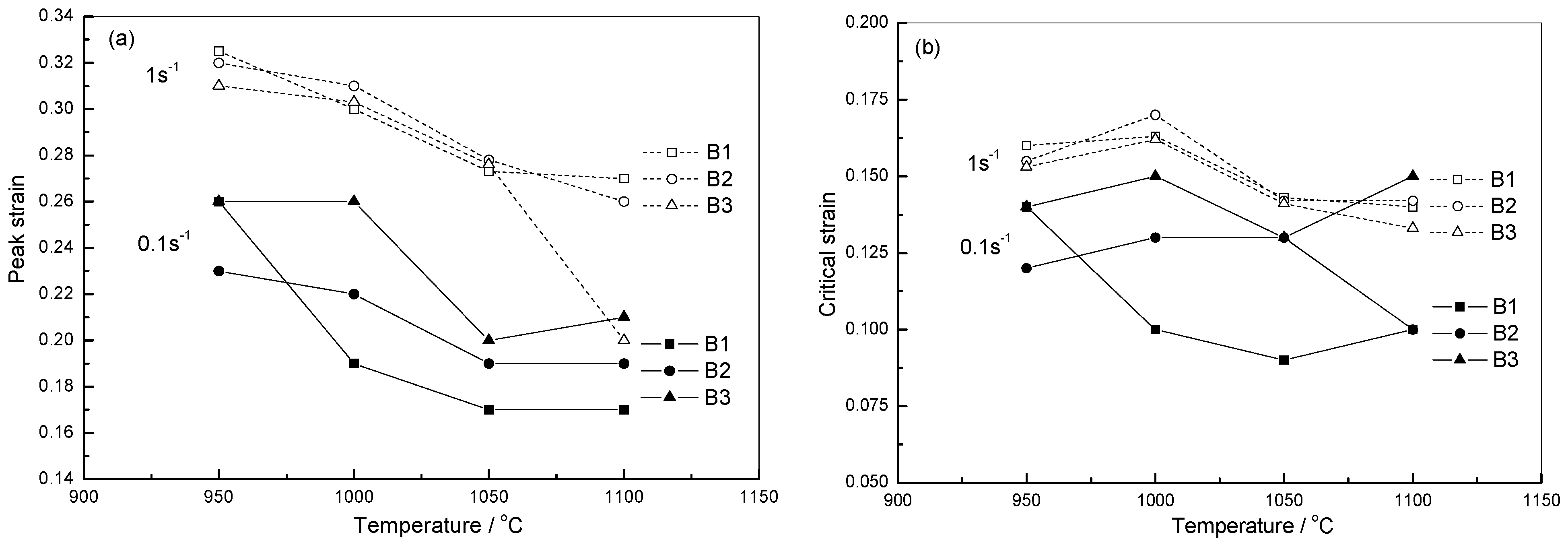
3. Experimental Section
| Steels | C | Si | Mn | S | P | Al | B | N |
|---|---|---|---|---|---|---|---|---|
| B1 | 0.18 | 0.184 | 0.619 | 0.025 | 0.016 | 0.051% | 0.002 | 0.004 |
| B2 | 0.18 | 0.191 | 0.626 | 0.025 | 0.016 | 0.049% | 0.004 | 0.004 |
| B3 | 0.18 | 0.196 | 0.626 | 0.025 | 0.016 | 0.049% | 0.006 | 0.004 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Abid, N.H.; Al-Rub, R.K.A.; Palazotto, A.N. Computational modeling of the effect of equiaxed heterogeneous microstructures on strength and ductility of dual phase steels. Comput. Mater. Sci. 2015, 103, 20–37. [Google Scholar] [CrossRef]
- Al-Rub, R.K.A.; Ettehad, M.; Palazotto, A.N. Microstructural modeling of dual phase steel using a higher-order gradient plasticity-damage model. Int. J. Solids Struct. 2015, 58, 178–189. [Google Scholar] [CrossRef]
- Eghbali, B.; Abdollah-zadeh, A. Influence of deformation temperature on the ferrite grain refinement in a low carbon Nb-Ti microalloyed steel. J. Mater. Process. Technol. 2006, 180, 44–48. [Google Scholar] [CrossRef]
- Jun, H.J.; Kang, J.S.; Seo, D.H.; Kang, K.B.; Park, C.G. Effects of deformation and boron on microstructure and continuous cooling transformation in low carbon HSLA steels. Mater. Sci. Eng. A 2006, 422, 157–162. [Google Scholar] [CrossRef]
- Han, F.; Wang, B.C.; Suh, D.W.; Wang, Z.C.; Lee, D.L.; Kim, S.J. Effect of Molybdenum and Chromium on Hardenability of Low-Carbon Boron-Added Steels. Met. Mater. Int. 2008, 14, 667–672. [Google Scholar] [CrossRef]
- Wu, B.P.; Li, L.H.; Wu, J.T.; Wang, Z.; Wang, Y.B.; Chen, X.F.; Dong, J.X.; Li, J.T. Effect of boron addition on the microstructure and stress-rupture properties of directionally solidified superalloys. Int. J. Miner. Metall. Mater. 2014, 21, 1120–1126. [Google Scholar] [CrossRef]
- Chapman, M.A.V.; Faulkner, R.G. Computer modelling of grain boundary segregation. Acta Metall. 1982, 31, 677–689. [Google Scholar] [CrossRef]
- Nishibata, T.; Kojima, N. Effect of quenching rate on hardness and microstructure of hot-stamped steel. J. Alloys Compd. 2013, 577, S549–S557. [Google Scholar] [CrossRef]
- Devaa, A.; Jha, B.K.; Mishra, N.S. Influence of boron on strain hardening behavior and ductility of low carbon hot rolled steel. Mater. Sci. Eng. A 2011, 528, 7375–7380. [Google Scholar] [CrossRef]
- Terzic, A.; Calcagnotto, M.; Guk, S.; Schulz, T.; Kawalla, R. Influence of Boron on transformation behavior during continuous cooling of low alloyed steels. Mater. Sci. Eng. A 2013, 584, 32–40. [Google Scholar] [CrossRef]
- Mun, D.J.; Shin, E.J.; Choi, Y.W.; Lee, J.S.; Koo, Y.M. Effects of cooling rate, austenitizing temperature and austenite deformation on the transformation behavior of high-strength boron steel. Mater. Sci. Eng. A 2012, 545, 214–224. [Google Scholar] [CrossRef]
- Shigesato, G.; Fujishiro, T.; Hara, T. Grain Boundary Segregation Behavior of Boron in Low-Alloy Steel. Metall. Mater. Trans. A 2014, 45, 1876–1882. [Google Scholar] [CrossRef]
- Mejía, I.; Jacuinde, A.B.; Maldonado, C.; Cabrera, J.M. Determination of the critical conditions for the initiation of dynamic recrystallization in boron microalloyed steels. Mater. Sci. Eng. A 2011, 528, 4133–4140. [Google Scholar] [CrossRef]
- Mejía, I.; López-Chipres, E.; Maldonado, C.; Bedolla-Jacuinde, A.; Cabrera, J.M. Modeling of the hot deformation behavior of boron microalloyed steels under uniaxial hot-compression conditions. Int. J. Mater. Res. 2008, 99, 1336–1345. [Google Scholar] [CrossRef]
- López-Chipres, E.; Mejía, I.; Maldonado, C.; Bedolla-Jacuinde, A.; El-Wahabi, M.; Cabrera, J.M. Hot flow behavior of boron microalloyed steels. Mater. Sci. Eng. A 2008, 480, 49–55. [Google Scholar] [CrossRef]
- Kim, S.I.; Choi, S.H.; Lee, Y. Influence of phosphorous and boron on dynamic recrystallization and microstructures of hot-rolled interstitial free steel. Mater. Sci. Eng. A 2005, 406, 125–133. [Google Scholar] [CrossRef]
- Banks, K.; Stumpf, W.; Tuling, A. Inconsistent flow stress in low carbon boron steels during finishing. Mater. Sci. Eng. A 2006, 421, 307–316. [Google Scholar] [CrossRef]
- Stumpf, W.; Banks, K. The hot working characteristics of a boron bearing and a conventional low carbon steel. Mater. Sci. Eng. A 2006, 418, 86–94. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.M.; Guo, Z.Y.; Wang, Y.Q.; Li, C.G.; Lan, L.Y. AlN Precipitates and Microstructure in Non-oriented Electrical Steels Produced by Twin-roll Casting Process. Acta Metall. Sin. 2013, 26, 483–488. [Google Scholar] [CrossRef]
- Liang, Y.J.; Che, Y.C. Thermodynamics Date of Inorganic Matter; Northeastern University Press: Shenyang, China, 1993; p. 449. [Google Scholar]
- Li, P.S.; Xiao, L.J.; Xie, Z. Thermodynamic Analysis of AlN and BN Competitive Precipitation in Low Carbon Steel. J. Iron Steel Res. 2009, 21, 16–18. [Google Scholar]
- Bao, H.S.; Fu, W.T.; Cheng, S.C.; Liu, Z.D.; Yang, G. An investigation on Boronnitride (BN) Compound in T122 Heat Resistant Steel. Iron Steel 2005, 40, 68–71. [Google Scholar]
- Chown, L.H.; Cornish, L.A. Investigation of hot ductility in Al-killed boron steels. Mater. Sci. Eng. A 2008, 494, 263–275. [Google Scholar] [CrossRef]
- Meysami, M.; Mousavi, S.A.A.A. Study on the behavior of medium carbon vanadium microalloyed steel by hot compression test. Mater. Sci. Eng. A 2011, 528, 3049–3055. [Google Scholar] [CrossRef]
- Wei, H.L.; Liu, G.Q.; Zhao, H.T.; Kang, R.M. Hot deformation behavior of two C-Mn-Si based and C-Mn-Al based microalloyed high-strength steels: A comparative study. Mater. Des. 2013, 50, 484–490. [Google Scholar] [CrossRef]
- Jahazi, M.; Jonas, J.J. The non-equilibrium segregation of boron on original and moving austenite grain boundaries. Mater. Sci. Eng. A 2002, 335, 49–61. [Google Scholar] [CrossRef]
- Stewart, G.R.; Jonas, J.J.; Montheillet, F. Kinetics and Critical Conditions for the Initiation of Dynamic Recrystallization in 304 Stainless Steel. ISIJ Int. 2004, 44, 1581–1589. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta Mater. 1996, 44, 127–136. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Initiation of Dynamic Recrystallization in Constant Strain Rate Hot Deformation. ISIJ Int. 2003, 43, 684–691. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Critical Strain for Dynamic Recrystallization in Variable Strain Rate Hot Deformation. ISIJ Int. 2003, 43, 692–700. [Google Scholar] [CrossRef]
- Sherby, O.D. Factors affecting the high temperature strength of polcyrystalline solids. Factors affecting the high temperature strength of polcyrystalline solids. Acta Metall. 1962, 10, 135–147. [Google Scholar] [CrossRef]
- Wray, P.J. Effect of carbon content on the plastic flow of plain carbon steels at elevated temperatures. Metall. Mater. Trans. A 1982, 13, 125–134. [Google Scholar] [CrossRef]
- Wei, H.L.; Liu, G.Q.; Zhao, H.T.; Zhang, M.H. Effect of carbon content on hot deformation behaviors of vanadium microalloyed steels. Mater. Sci. Eng. A 2014, 596, 112–120. [Google Scholar] [CrossRef]
- Wang, X.M.; He, X.L. Effect of Boron Addition on Structure and Properties of Low Carbon Bainitic Steels. ISIJ Int. 2003, 42, S38–S46. [Google Scholar] [CrossRef]
- Barnett, M.R.; Kelly, G.L.; Hodgson, P.D. Inferring dynamic recrystallization in ferrite using the kinetics of static recrystallization. Metall. Mater. Trans. A 2002, 33, 1893–1900. [Google Scholar] [CrossRef]
- Fernández, A.I.; Uranga, P.; López, B.; Rodriguez-Ibabe, J.M. Dynamic recrystallization behavior covering a wide austenite grain size range in Nb and Nb–Ti microalloyed steels. Mater. Sci. Eng. A. 2003, 361, 367–376. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.-l.; Xue, X.-x.; Yang, H. Influence of Boron on Initial Austenite Grain Size and Hot Deformation Behavior of Boron Microalloyed Steels. Crystals 2015, 5, 592-607. https://doi.org/10.3390/cryst5040592
Gao Y-l, Xue X-x, Yang H. Influence of Boron on Initial Austenite Grain Size and Hot Deformation Behavior of Boron Microalloyed Steels. Crystals. 2015; 5(4):592-607. https://doi.org/10.3390/cryst5040592
Chicago/Turabian StyleGao, Yong-liang, Xiang-xin Xue, and He Yang. 2015. "Influence of Boron on Initial Austenite Grain Size and Hot Deformation Behavior of Boron Microalloyed Steels" Crystals 5, no. 4: 592-607. https://doi.org/10.3390/cryst5040592
APA StyleGao, Y.-l., Xue, X.-x., & Yang, H. (2015). Influence of Boron on Initial Austenite Grain Size and Hot Deformation Behavior of Boron Microalloyed Steels. Crystals, 5(4), 592-607. https://doi.org/10.3390/cryst5040592





