One-, Two-, and Three-Dimensional Hopping Dynamics
Abstract
: Hopping dynamics in glass has been known for quite a long time. In contrast, hopping dynamics in smectic-A (SmA) and hexatic smectic-B (HexB) liquid crystals (LC) has been observed only recently. The hopping in SmA phase occurs among the smectic layers (one-dimensionally), while hopping in HexB phase occurs inside the layers (two-dimensionally). The hopping dynamics in SmA and HexB liquid crystal phases is investigated by parallel soft-core spherocylinders, while three-dimensional hopping dynamics in inherent glassy states is investigated by systems of Weeks–Chandler–Andersen (WCA) spheres. The temperature dependence of diffusion coefficients of hopping in SmA phase can be described by the Arrhenius equation characteristic of activation process. In HexB LC phase, the diffusion coefficients saturate at higher temperatures. In a system of WCA spheres, the values and temperature dependence of diffusion coefficients depend on the observed states.1. Introduction
First, we would like to clarify what we mean by “hopping dynamics” in this review. The term “hopping” is used scientifically in several classical concepts mentioned below. Disorder and aperiodicity are common concepts underlying hopping dynamics.
Hopping motion of individual particles or molecules from its original position to nearby positions. The time trapped in positions (which is called “sites”) is much longer compared with the time that takes the individuals to hop among them. The sites are defined as geometrical positions surrounded by potential barriers.
Hopping conduction on a background matrix. Conduction of heat [1] and electric current [2–4] is mainly discussed in this context.
Thermally activated transfer of the “total system” between the metastable states (free-energy minima).
In this article, we treat type (a) hopping dynamics. Type (c) refers to a theoretical treatment of the system by the total energy (or order parameter), not considering the dynamics of the constituent elements of the system. This type of analysis is used, for instance, to discuss the aging effect in glass at lower temperature (typically below the mode-coupling temperature) [5]. Six-fold bond orientational order parameter C6 of the total system in hexatic smectic B (HexB) liquid crystal shows transfer among different metastable states (Figures 8 and 9 of [6]) and can be classified as type (c) hopping. Although both types (a) and (c) of hopping occur in HexB LC phase and glass, type (c) does not concern us here since we are interested in the hopping dynamics of individual particles/molecules.
In the systems we discuss here, molecular/particle movement is always three dimensional. However, the hopping dynamics occur only in a restricted dimension. For instance, hopping dynamics in SmA phase occurs among the stacked smectic layers, though there is also liquid-like diffusion inside the layers. Thus the direction of the hopping is quasi one-dimensional, but the movement of the particles occurs in all directions. In the HexB LC phase, the particles only diffuse inside the layers in a hopping manner, however undulation of the layers (local movements perpendicular to the layers) is very important for the stability of the HexB phase. Thus the hopping is only quasi two-dimensional.
In this article, we also stress the thermodynamic aspect of the states where hopping dynamics exist. In liquid crystalline phases, hopping dynamics occurs in thermodynamic equilibrium phases as well as thermodynamic metastable states. When we refer to thermodynamic metastable states, the system is in one of the local minima of the free energy function where the thermal fluctuation at that temperature cannot drive the system to transfer to another state in the observed time duration. Here, the thermodynamic situation underlying the hopping dynamics is clear, i.e., the thermodynamic variables are well defined. Dynamical relaxation processes where the thermodynamic quantities change along the relaxation are omitted. We also omit polydispersed systems, because there is no clear-cut thermodynamic reference state, since the crystalline structure is not known in most cases. When a thermodynamic reference state is absent, it is not clear whether the observed dynamics is a relaxation process or a dynamics characteristic of a certain state. The calculations reported here were possible due to the stable and high precision symplectic integrators designed for simulating soft matter [7]. It is important to keep not only the energy but also the symplectic structure for high-quality molecular dynamics (MD) simulations of well-defined thermodynamic states. For strongly anisotropic systems, such as in smectic liquid crystals, the time scales of the fluctuation parallel and perpendicular to the layers are quite different. Hence, to properly simulate the dynamics and thermodynamics, the simulation method has to accommodate anisotropic fluctuations [8]. Reduced simulation units [9] are used to present the results here, unless otherwise stated. In systems of parallel soft-core spherocylinders used as a model of liquid crystals, additional scaling laws exist [10], which define a set of corresponding states.
2. One-Dimensional Hopping in Liquid Crystal Phase
Molecular dynamics studies in 1992 showed that in the Sm LC phase, there is molecular diffusion not only in the direction parallel to the Sm layers but also slightly in the direction perpendicular to the layers [11]. In addition, the pair-distribution function gz in the direction perpendicular to the Sm layers showed that the probability to find a molecule in between the layers is negligibly small compared with that inside the layers, suggesting that the time that the molecules exist between two layers is much shorter compared with that inside the layers. Naturally these two facts suggested that hopping dynamics is occurring among the layers. Later on, it was shown that the molecular rotation around the short axis will enhance the diffusion perpendicular to Sm layers [12,13].
Recently, experimental observations of dynamical phenomena in the scale of individual rod-like particle have been reported. The hopping-like diffusion among the smectic layers are clearly discerned in system of viruses [14,15], where the length of the rods far exceeds the diameter (aspect ratio larger than 100) and the diffusion parallel to the rods is dominant, Dz/Dxy ≫ 1. The stiffness of the viruses affects the anisotropy of the diffusion where in systems of stiff viral rods Dxy becomes more pronounced [16]. Preliminary observation of the dynamics of colloidal silica rods [17] in the smectic phase suggests larger values of Dxy than Dz. Interlayer diffusion is also studied by MD simulations in a model of rod–sphere mixture [18], hard-core spherocylinders [19], and in atomic detailed sexithiophene [20]. The ratio is much smaller for these simulated shorter particles (molecules), but still Dz/Dxy > 1 [18,20] or Dz/Dxy ≃ 1 [19] in the SmA phase. Experimental studies of thermotropic smectic phases show Dxy/Dz ≥ 1 [21]. The effect of flexibility of the molecules in hopping-like diffusion in the smectic phase also has been discussed [22].
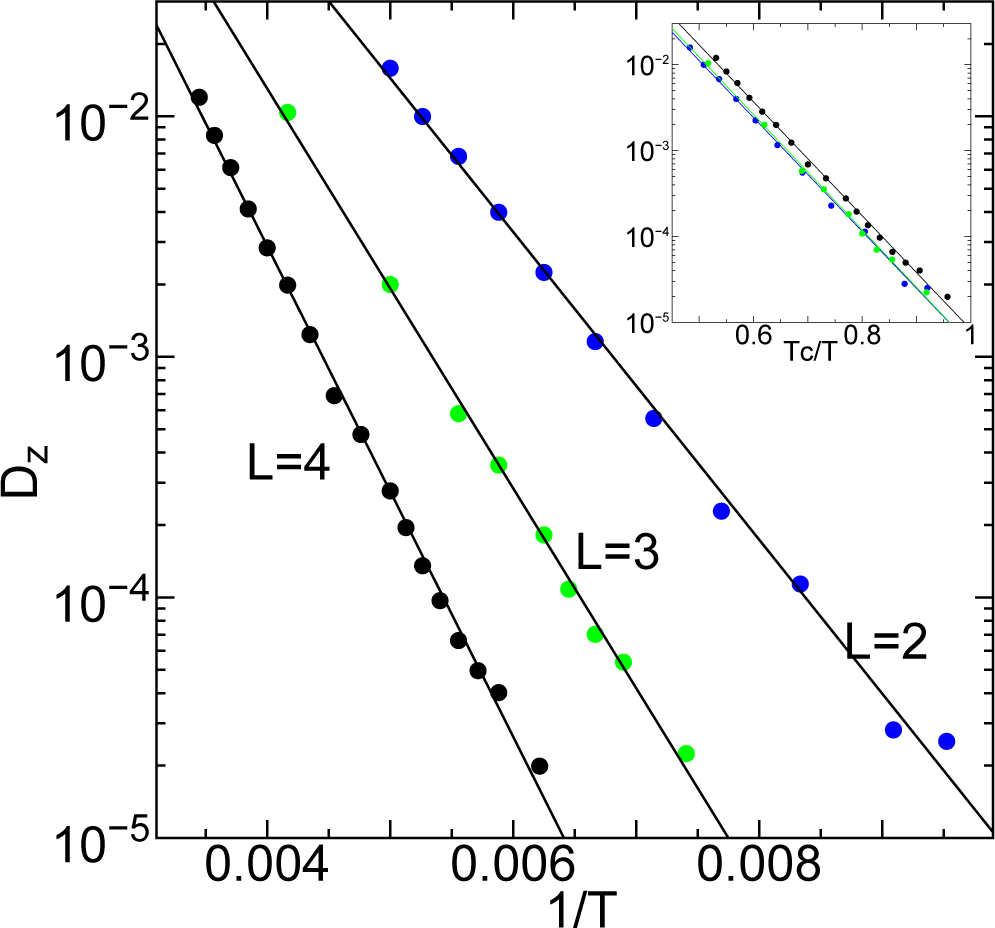
Here we report diffusion in the SmA phase of purely repulsive soft parallel spherocylinders that interact through minimum distance [6,23]. Figure 1 shows the diffusion coefficient parallel to the particle long axis versus inverse of the temperature T. In the inset, the temperature is scaled by the HexB–SmA phase transition temperature Tc. The temperature dependence of the diffusion coefficient Dz is described by the Arrhenius equation,
At the transition from HexB to SmA phase, in the layers, the area per particle jump to a higher value showing a behavior of first order transition. Thus, in the SmA phase, the layers are completely melted and liquid-like. As a result, the diffusion coefficients inside the layers Dxy are much higher compared with Dz shown in Figure 1. We show the ratio Dxy/Dz in the SmA phase in Figure 2. In parallel spherocylinders, the values of the diffusion coefficients Dxy and Dz are higher for shorter particles at the same temperature. However, the ratio Dxy/Dz is higher when the particles are longer as shown in Figure 2.
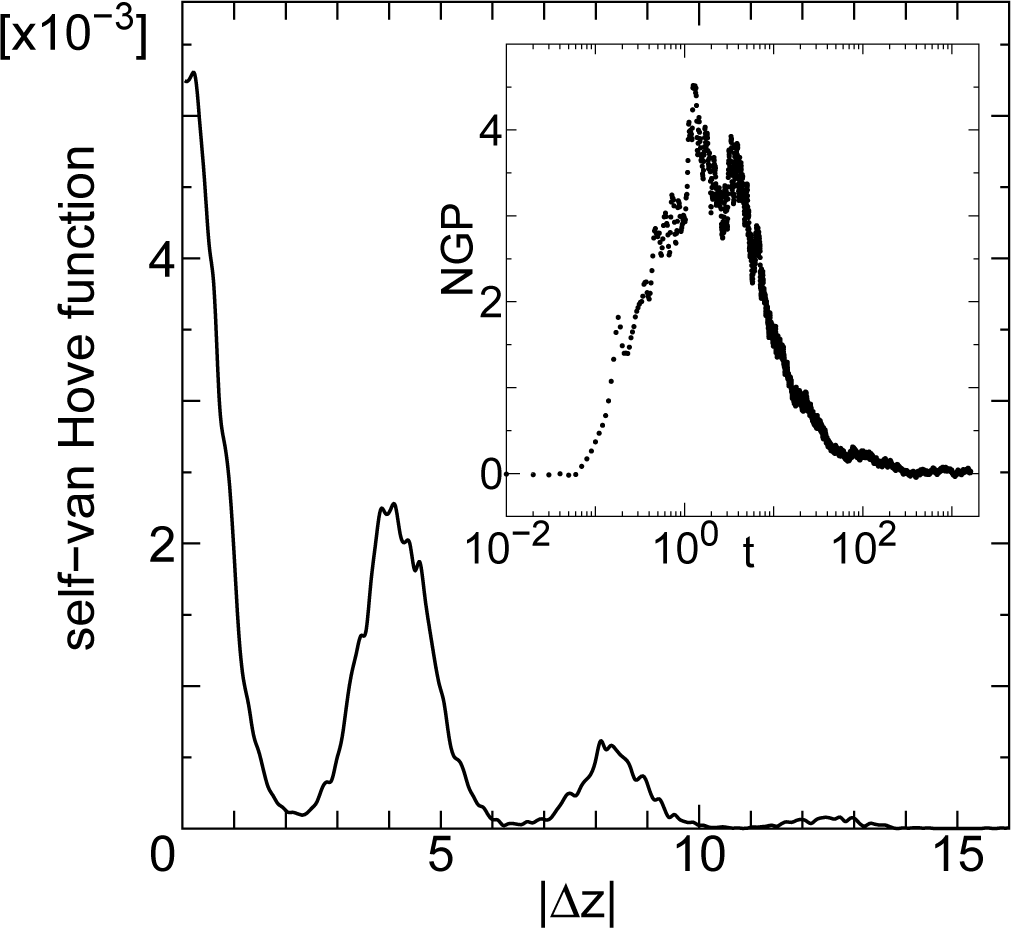
In Figure 3, we show van Hove self-correlation function
3. Two-Dimensional Hopping in Liquid Crystal Phase
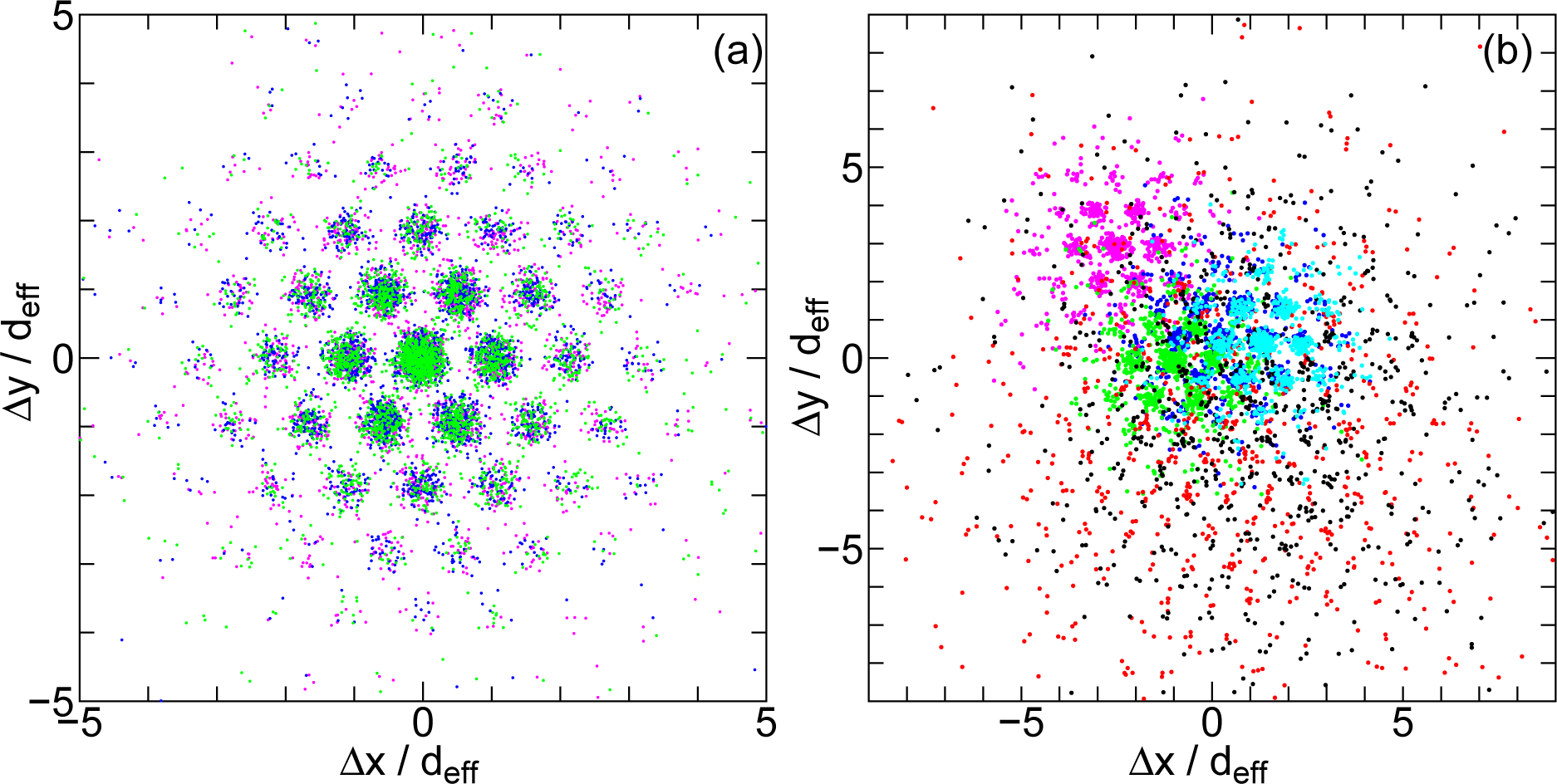
Despite the abundance in literature about experimental studies of HexB LC phase, there are only a number of simulation studies of the HexB LC phase [6,23–27]. Monte Carlo simulation is a method using statistical sampling, and by nature the dynamics that it discusses have limited significance. However, hopping-like dynamics has been reported in Monte Carlo simulation and used as a criterion to define the boundary between solid and HexB phases [27]. By MD simulations, thermodynamic equilibrium HexB phase [23] and many thermodynamic metastable HexB states [6] has been investigated. In both HexB states, thermodynamic equilibrium and metastable, the hopping nature of the dynamics is clearly observed in the displacement plots. In the displacements plot of HexB LC, the positional displacement in the xy-plane is plotted for all the particles in the system where the particles on different layers are projected on a single plane. In Figure 4, we show two examples of the displacement plots where the hopping nature of the displacements can be observed. In Figure 4b where there are 6 layers, in addition to the hopping dynamics in each layer, a relative diffusive motion of the layers can be discerned. In our simulation, the number of layers in the system slightly affects the value of six-fold bond orientational order parameter in the HexB (see inset in Figure 6 of [23]). When there are a large number of layers in the system, the correlation among the layers seems to be reduced and the relative diffusion of the layers enhanced even in the thermal equilibrium HexB phase. In metastable HexB states, the strength of the correlation among the layers depends on each state (see Figure 10 of [6]).
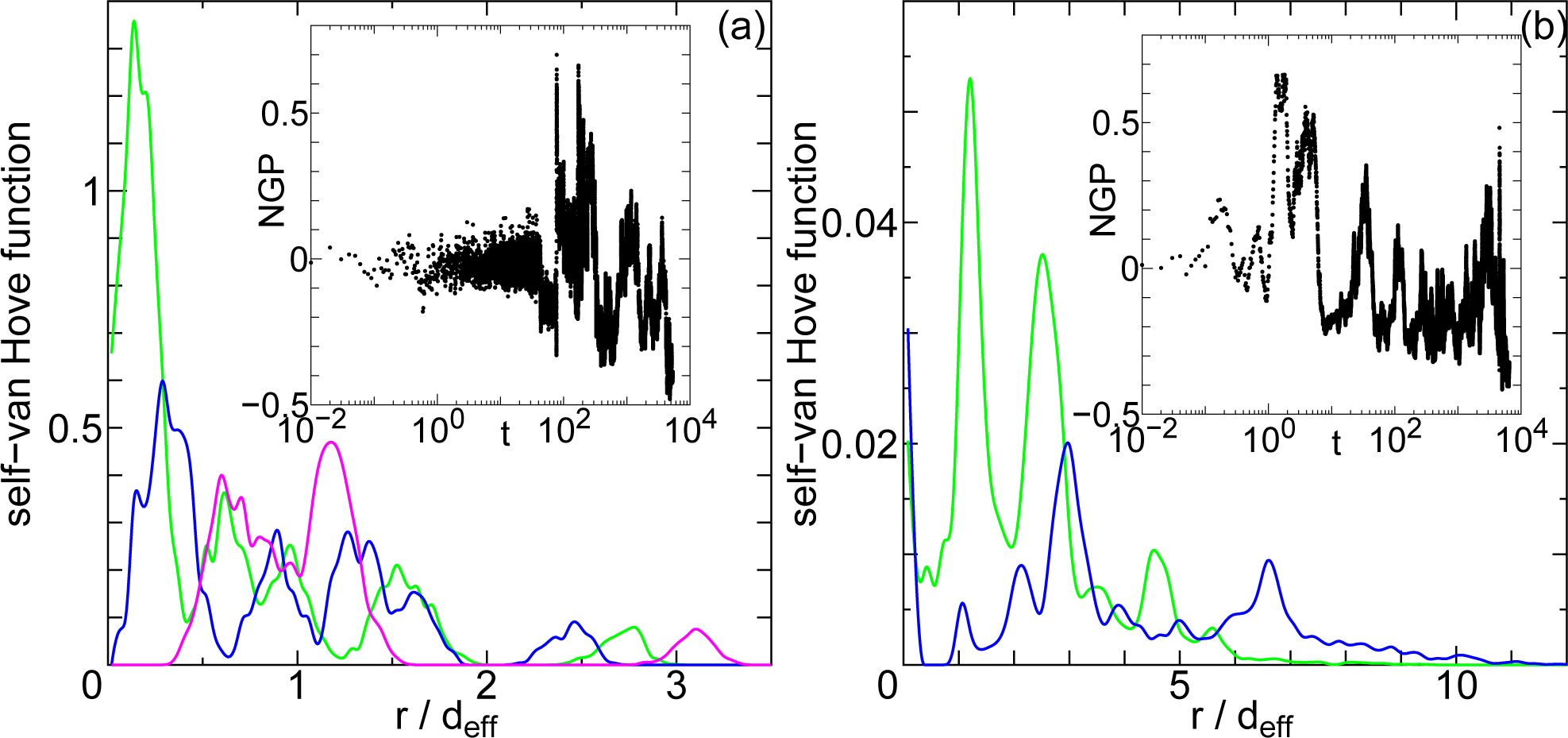
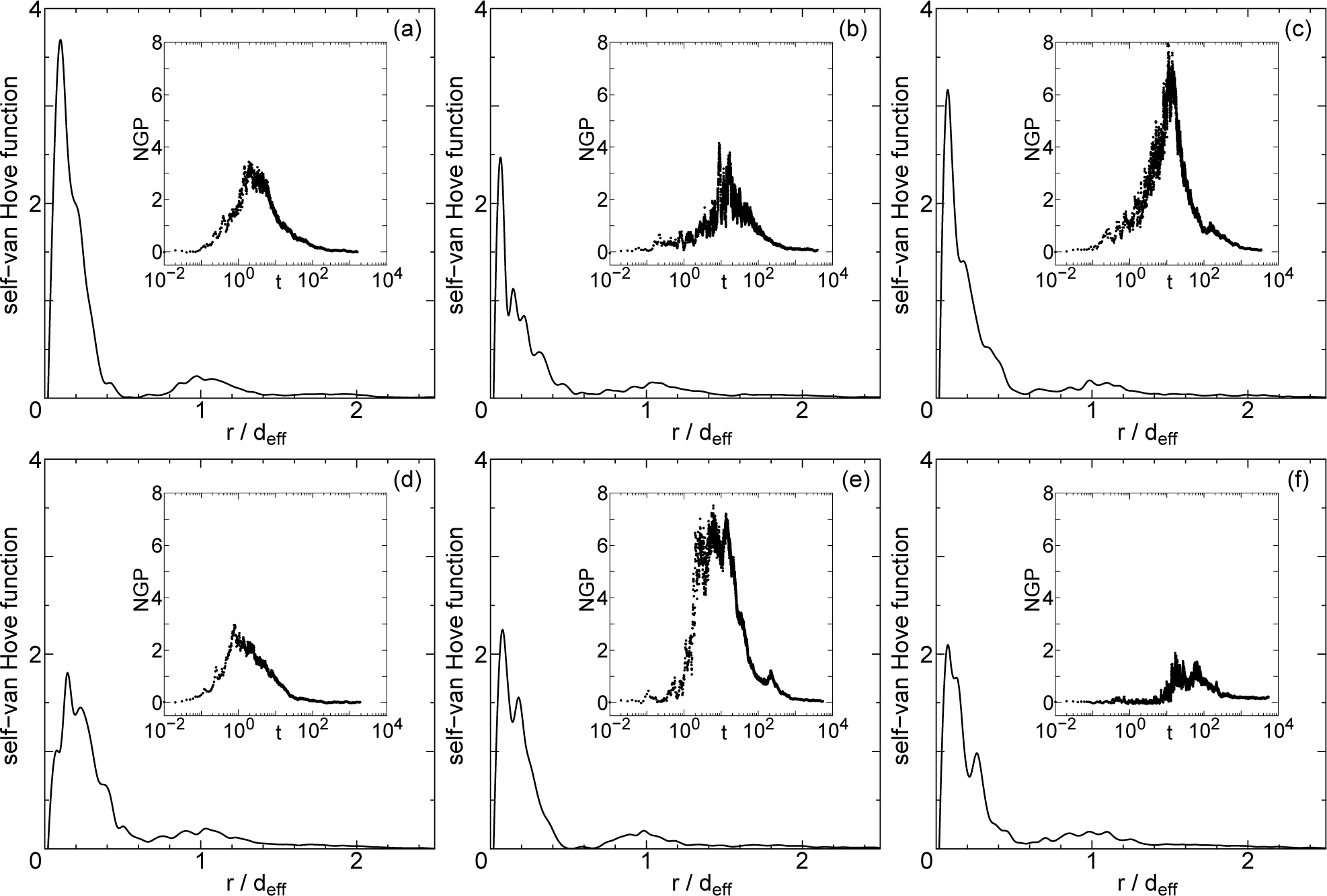
In Figure 5, we show the self van Hove correlation function F (rxy, t) in HexB phase. At temperature T = 66 where hopping is a rare event, the self correlation function shows existence of interstitials. In Figure 5a, for a longer time duration (blue line compared with the green), the position of the 5th peak at 2.5deff, where deff is the effective diameter, shows that a certain amount of particles have not diffused away but returned closer to the original position. This type of forward–backward hopping process is widely observed in the HexB phase and clearly appears in the MSD curve, making the determination of the diffusion coefficients difficult. At higher temperatures, the distance between the peaks in the self-correlation function are approximately deff, and the peaks diffuse away as shown in Figure 5b. In this figure, both lines are for the same time duration Δt = 50, however the way the peaks diffuse are quite different, showing the strong intermittent nature of HexB hopping diffusion. The heterogeneous nature can be seen especially in the blue line, where some peaks distant from the origin, for instance at r = 3deff, show high probability of existence, indicating that the particles do not evenly diffuse away. At temperatures T = 66 and T = 120, the effective diameters are respectively deff = 0.6981 and deff = 0.6661. The non-Gaussian parameters in the HexB phase show the strong nature of intermittency that persists through the observation time.
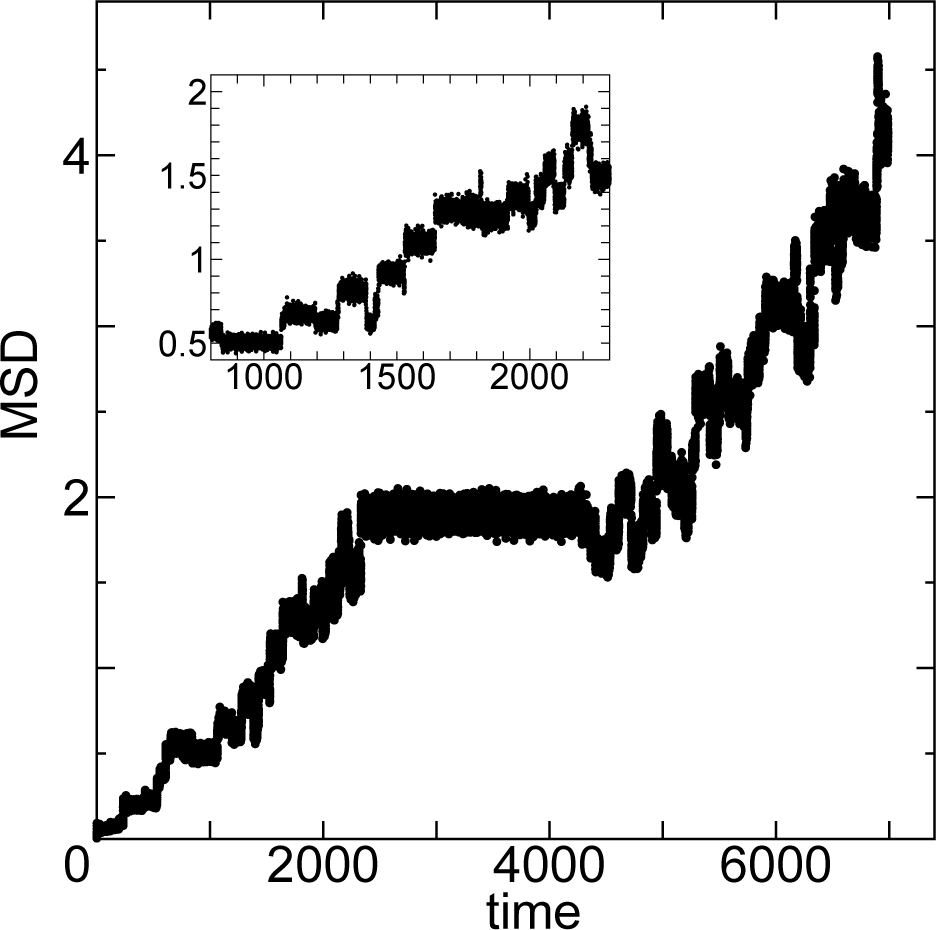
We show in Figure 6 the mean square displacements (MSD) in the HexB phase of parallel spherocylinders of length L = 3 at T = 62. The inset shows MSD for time t = 800 through 2300. We clearly see the intermittent and fractal-like character of the hopping diffusion in different time scales. There exists a plateau for time duration Δt = 2037 showing that the heterogeneity extends through the whole system (N = 1344) of this simulation.
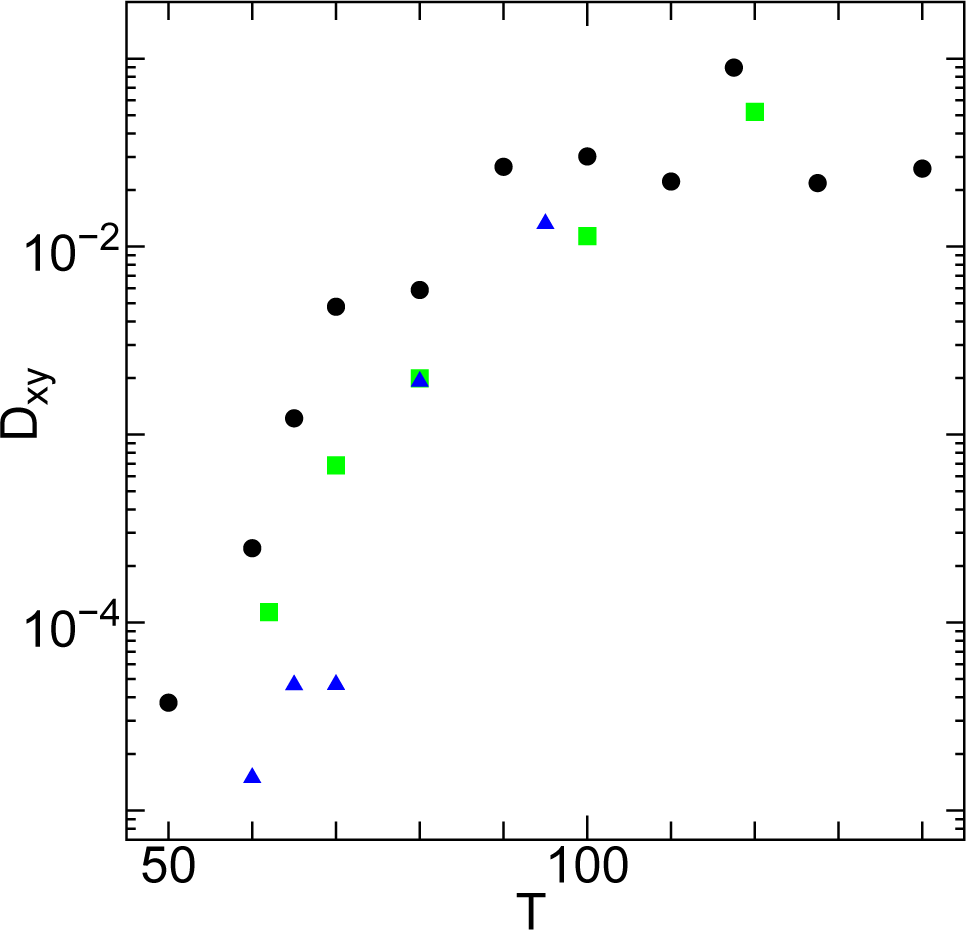
As seen from Figure 6, the system in the HexB phase is strongly intermittent and heterogeneous, where the waiting time is dispersed in many orders. Because of the reasons mentioned above, the evaluation of the diffusion coefficients is difficult in the HexB phase. Nevertheless, we try to estimate the temperature dependence of the diffusion coefficients Dxy. In the HexB phase, the layers show strong undulation but the particles do not diffuse among different layers, thus Dz = 0 in HexB. We remind the readers that the HexB–SmA phase transition is clearly first order in our model just as many experimental systems [28,29]. In Figure 7, the diffusion coefficient Dxy is shown against temperature T. There is a sharp increase in the values of Dxy at low temperatures T < 90. However, the values of Dxy seem to saturate for higher temperatures in the HexB phase.
4. Three-Dimensional Hopping in Monodispersed Glass
An early report of single component fluids of purely repulsive soft-spheres in dense metastable states [30] shows that the particle dynamics changes its basic characteristics from continuous fluid-like displacements to hopping of individual particles, in density region higher than the normal liquid range.
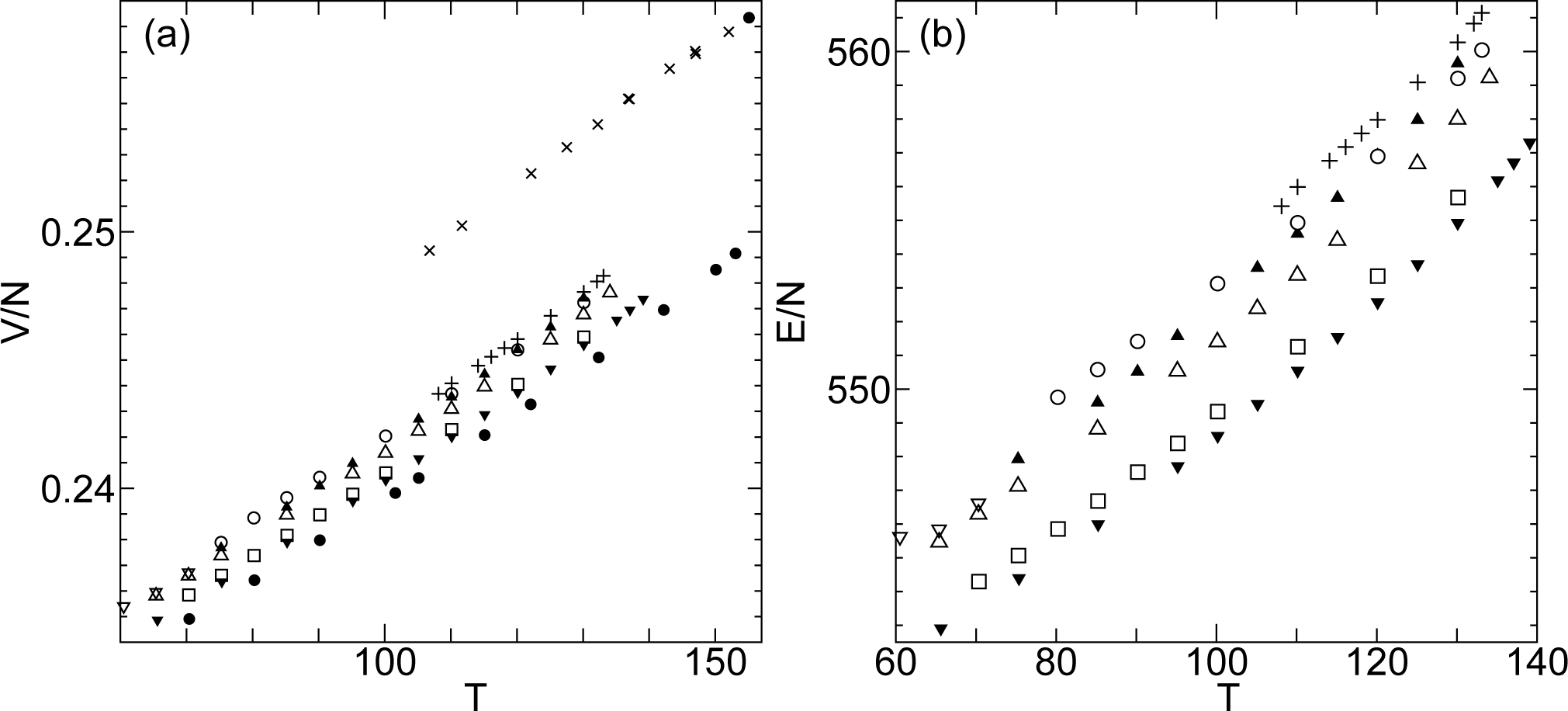
The simulated system we discuss here consists of monodispersed (single component) soft-spheres of WCA potential, i.e., repulsive part of Lennard-Jones spheres. The metastable states, where the hopping dynamics is reported here, were first reported in [7] as amorphous solids. A more detailed analysis using a different barostat was done in [31], where three different hopping states were reported. Here, additional symplectic calculations are reported using the metastable states, reported in [7] (depicted by Symbol ▽; K = 20 with T = 97 (state A), 98 (state C), 101 (state B), and 104 (state F) in Figure 11 of [7]), as initial configurations. The number of particles is N = 1344, barostat piston mass M = 10−3 and mass of thermostat K = 1000. Notice that the barostat used in these calculations yield very small system size effects compared with conventional barostats. The volume and potential energy per particle of WCA spheres at pressure P = 104 are shown in Figure 8. In addition to the thermal equilibrium phases, there exist eight thermodynamic metastable states, i.e., supercooled liquid, hopping states A, B, C, D, E, F, and amorphous solid. Since our thermodynamic metastable states correspond to local minima of free energy surrounded by free energy barriers that cannot be overcome by thermal fluctuation at that temperature, the structures obtained by our method correspond to the so-called inherent structures in the glass community. The high densities of states A–F hint that there might be some relation to the low entropy state predicted by a cooperative excitation theory that treats thermodynamic properties of fragile glass forming liquids [32,33]. Although the density differences of the hopping states are small, the dynamics are quite different. In the high density state E, the system is strongly heterogeneous and divided into active and inactive regions. The hopping dynamics is strongly anisotropic and show a cooperative string-like motion. We show in Figure 9 displacement plots of state E where the relative displacements show an elongated helical structure. Such cooperative string-like motions are reported in many glassy systems by experiments and by simulations [34–40], where the thermodynamic situation is not necessarily clear; the systems might be only in a thermodynamic relaxation mode, in contrast to our system. In state A, the mobile particles are distributed in the inactive surroundings. In this state A, the particles are hopping to relatively well-defined sites and the structure seems to be maintained by a domino effect; the inherent structures of these states seem to be maintained by the dynamic hopping stream of the mobile particles.
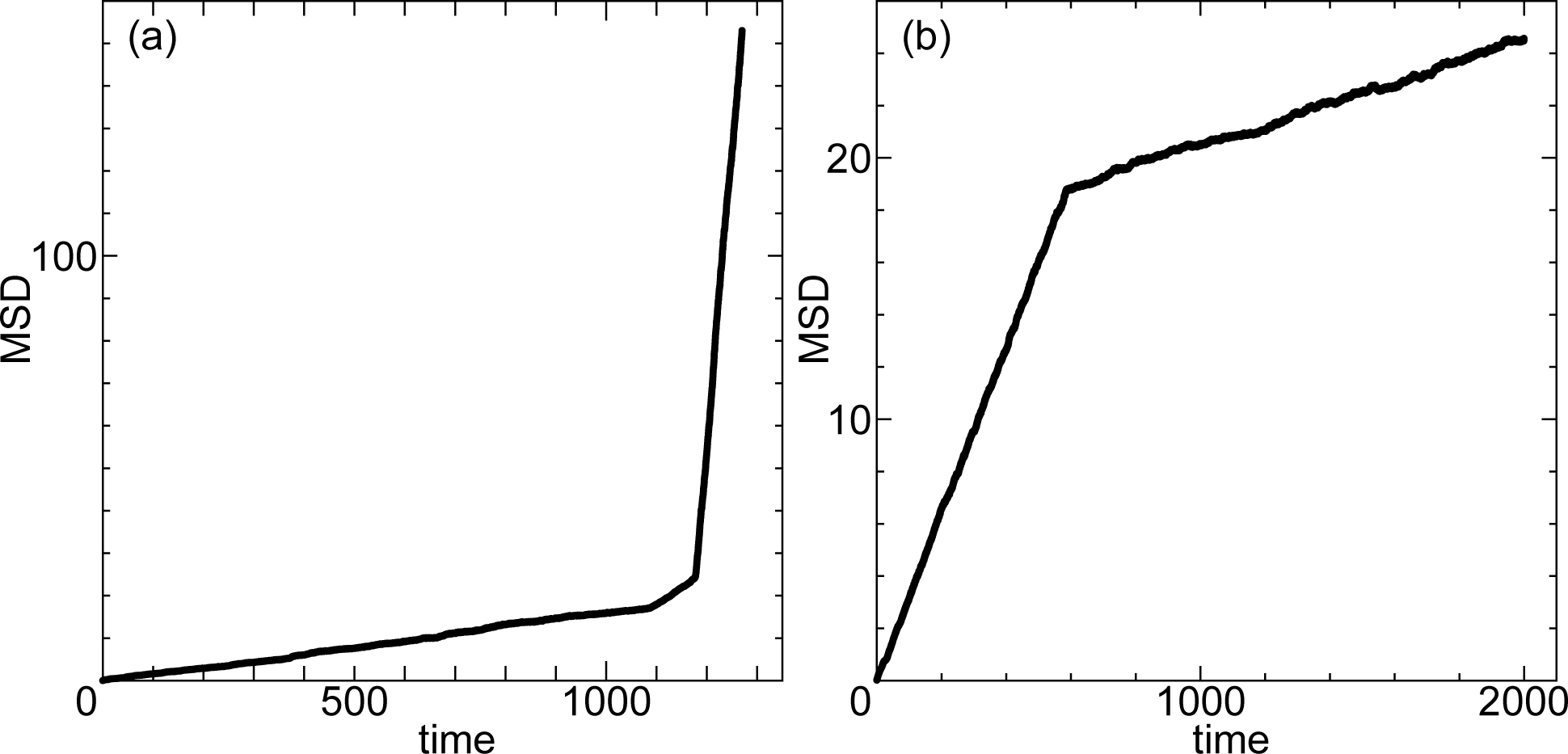
The radial distribution function (RDF) of the hopping states A, B, C, D, E and F are shown in Figure 10. As seen in Figure 10c, crystalline-like feature strongly appears in state C. Crystalline-like structures are also observed in experimental systems of glass. In an experimental system of supercooled monodispersed colloidal fluid, large fraction of particles are found to show face-centered cubic or hexagonal closed packing characteristics [41]. High density glass is obtained by vapor deposition of ethylbenzene on cold substrates, in addition to thermodynamically unstable low density glass [42]. When the temperature is raised in this system, a structural relaxation occurs to the unstable low density glass, while high density glass transforms directly to supercooled liquid [43]. States of WCA spheres also melted when kept at temperature T = 140 for state E, at T = 135 for states A and B, at T = 134 for state C and D, and at T = 131 for state F. State B kept at T = 135 remained to be so for a certain time, i.e., for t = 1087 (i.e., 1.087 × 107 calculation time-steps), and melted to state D and later on at time t = 1177 to supercooled liquid. The mean square displacement (MSD) clearly shows the two stage melting process (Figure 11a). The value of diffusion coefficient changes from 2.71 × 10−3, to 1.32 × 10−2, and finally to 2.33 × 10−1. Note that the RDF of the intermediate melted state D shown in Figure 11a is similar to state B (Figure 10). State C remained until time t = 332 and melted directly to supercooled liquid at temperature T = 134. As shown in Figure 11b, state D, which exists only for a small temperature range, is observed to transform to state E at T = 105 where the value of diffusion coefficient changes from 5.33 × 10−3 to 6.68 × 10−4 at time t = 587.
In Figure 12, we show the self van Hove correlation function F(rxyz, t) in the hopping states A, B, C, D, and E of WCA spheres. In all states, hopping to the nearest neighbors can be discerned. In the insets, the 3D NGP are shown against duration of time t. Each state shows different characteristic of NGP. Note that in state F, the value of NGP converges at around 0.18, suggesting that the scale of heterogeneity in space is larger compared with other states of WCA spheres and has reached the order of the system size.
In the hopping states, in a short time duration, the feature of hopping dynamics with intermittency appears in the MSDs. However, for a long time duration (but much shorter time duration needed for the HexB phase) the MSDs smooth out and increase linearly against time, which allows us to measure the diffusion coefficient with a linear fit. In Figure 13 the diffusion coefficients Dxyz of the hopping dynamics in states A–F and supercooled liquid are shown. Each state shows different temperature dependence of the diffusion coefficients. Note that the diffusion coefficients show close values for states B and C at temperature T = 110, where the inherent structures were strikingly different (Figure 10). State D with the largest volume difference compared with the crystal phase (Figure 8) has the largest diffusion coefficient. However as shown in Figure 11b, at T = 105, state D becomes unstable and transforms to state E. The temperature range of stability of state D is 106 ≤ T ≤ 133. State A shows the second largest Dxyz, and is stable at 80 ≤ T ≤ 133. A drastic decrease in the mobility of particles occurs for state A at T = 70, 65, and 60. We identify these states as amorphous solid. It takes a certain time for state A to solidify, for instance at T = 65 the MSD ceases to increase after t = 1145 (1.145 × 107 time steps). The volume and the potential energy of the amorphous solid is denoted by ▽ in Figure 8. At temperature T = 65, the volume of amorphous solid and state B cannot be distinguished, but the RDF is clearly different. At temperatures where amorphous solids (obtained from state A) are observed, the MSDs of states B and C still show linear increase against time. The RDFs of states A and F are similar as shown in Figure 10, the values and temperature dependence of the diffusion coefficients are quite different. The RDFs of states B and D are similar as shown in Figure 10, but the values of Dxyz are an order different and the existing temperature range (as shown in Figure 8) is smaller for state D. Note that these simulations are independent calculations conducted under constant pressure and temperature. This is in contrast to conventional methods that usually use rapid temperature control (much faster than the relaxation rates), usually called supercooling, to obtain glass. The supercooled liquid state(×) in our calculation depicted in Figure 8 is also a thermodynamic metastable state, surrounded by free energy barriers that cannot be overcome by the thermal fluctuations in those temperatures. The supercooled liquid of WCA spheres cannot exist at temperatures T ≤ 100 under pressure P = 104.
5. Discussion
We have seen quasi one-, two-, and three-dimensional hopping in thermodynamically well-defined situations, i.e., in thermodynamic equilibrium and metastable states confined in energy barriers that cannot be overcome by thermal fluctuations at the observed temperature. One- and two-dimensional hopping occur in thermal equilibrium phases while two- and three-dimensional hopping occur in thermodynamic metastable states. The HexB LC is the only state observed so far that shows hopping dynamics in both thermal equilibrium and metastable states. Hopping dynamics has been extensively discussed in the context of supercooled liquids and glassy systems but the thermodynamic situation in these systems is not necessarily clear. We are aware that there exists a community for which the term glass is only related to relaxation processes where the thermodynamics is irrelevant. It is stressed again that we are concerned with the thermodynamic situation and discuss the hopping dynamics on the same footing.
The evidence is that in a well-defined thermodynamic situation of simple models, when the scale of time and space is large enough, the diffusion is normal, i.e., MSD shows a linear increase against time. The hopping event becomes quite rare in low temperatures, which makes a reasonable ensemble average difficult, although observations of large systems or long time duration deny anomalous diffusion in these systems. The time duration to get a reasonable MSD curve for linear fitting is at least one order longer for the HexB LC phase compared with that of the hopping states in systems of WCA spheres. Although these two systems show hopping dynamics in nearly the same temperature range, the length scale of the heterogeneity is larger for the HexB LC phase. Intermittency appears strongly in the non-Gaussian parameter of HexB phase.
In the smectic A phase, the temperature range involved in hopping dynamics is higher, although similar or longer time durations, compared with systems of WCA spheres, is necessary to get a MSD curve suited for linear fitting. Only in the SmA phase will the temperature dependence of diffusion coefficients show a well-known behavior of Equation (1).
By making the model more complex, the scale of time and space where anomaly appears can be elongated. A binary system widely used for investigating glassy systems is one example. As shown in this manuscript, even for a simple model in a well-defined thermodynamic situation, there are several metastable states where anomaly appears at different scales of time and space. However, when the scale of time and space is large enough, the anomaly disappears.
Acknowledgments
This work was partly supported by KAKENHI No. 23540458.
Appendix: Simulation Models and Method
This appendix gives a short summary of the simulation models and method; the reader is referred to [7,23] for further information.
A monodisperse (single component) system of WCA spheres (repulsive part of Lennard-Jones potential) [44] with full translational degree of freedom is used to obtain hopping dynamics of glassy states in Section 4. Analysis of systems of WCA spheres using the Andersen’s barostat [45] was done in [31]. Compared with the barostat in [7] used in this study, the Andersen’s barostat yield much larger system size effect, and the range of applicable piston mass M is narrower.
Model for SmA and HexB Liquid Crystal Phases
The model used in Sections 2 and 3 is parallel soft spherocylinders described by the minimum distance between lines representing the long axis of the two spherocylinders;
The phase sequence that appears in this model system is crystal → HexB LC → SmA LC, where the transition from crystal to HexB LC phase is continuous and the transition from HexB to SmA LC phase is first order.
Symplectic Integrator Designed for Simulating Soft Matter
A symplectic integrator is an integrator that preserves the structure of the canonical Hamiltonian equations of motion.
The barostat [8] used in the simulations has been designed to overcome the difficulties of simulating liquid crystal phases where there exist large differences in the viscoelastic properties depending on direction. With an anisotropic factor in the cell dynamics, the barostat reduces the system size effect drastically. System size effects can be discerned only at higher temperatures close to the phase transition (see for instance the inset in Figure 6 of [23]). The Hamiltonian of the new barostat is splittable and yields an explicit symplectic integration formula.
An explicit symplectic integration formula [46] of the Nosé–Poincaré thermostat [47–49] (Hamitonian version of Nosé–Hoover thermostat) is used in our simulation. The actual calculation is done in the extended phase space [50]. The time scaling function between the extended phase space and the original phase space allows relative entropy estimation between different states obtained from the same initial configuration [7,23].
The advantage of the new method is that not only thermodynamic equilibrium phases but also metastable states can be obtained by constant pressure and temperature processes. Thus inherent structures are obtained in a thermodynamically well-defined situation where the temperature and pressure are fixed.
References
- Michalski, J. Thermal conductivity of amorphous solids above the plateau: Molecular-dynamics study. Phys. Rev. B 1992, 45, 7054–7065. [Google Scholar]
- Kogan, Sh. Electron glass: Intervalley transition and hopping conduction noise. Phys. Rev. B 1998, 57, 9736–9744. [Google Scholar]
- Karayanni, M.; Papavassiliou, G.; Fardis, M.; Milia, F.; Dolinšek, J. Protonic inter-H-bond motion and ionic conductivity in hydrogen-bonded proton glasses. Phys. Rev. B 1999, 59, 3534–3539. [Google Scholar]
- Murugavel, S.; Roling, B. AC Conductivity Spectra of Alkali Tellurite Glasses: Composition-Dependent Deviations from the Sommerfield Scaling. Phys. Rev. Lett. 2002, 89, 195902:1–195902:4. [Google Scholar]
- Rinn, B.; Maass, P.; Bouchaud, J.-P. Hopping in glass configuration space: Subaging and generalized scaling laws. Phys. Rev. B 2001, 64, 104417:1–104417:15. [Google Scholar]
- Aoki, K.M.; Yoneya, M. Order parameter discretization in metastable states of hexatic smectic B liquid crystal. J. Phys. Soc. Jpn. 2011, 80, 124603:1–124603:7. [Google Scholar]
- Aoki, K.M. Symplectic integrators designed for simulating soft matter. J. Phys. Soc. Jpn. 2008, 77, 044003:1–044003:11. [Google Scholar]
- Aoki, K.M.; Yoneya, M.; Yokoyama, H. Molecular dynamic simulation methods for anisotropic liquids. J. Chem. Phys. 2004, 120, 5576–5584. [Google Scholar]
- Allen, M.P.; Tildsley, D.J. Appendix B REDUCED NITS. In Computer Simulation of Liquids; Claredon Press: Oxford, UK, 1987. [Google Scholar]
- Aoki, K.M.; Yonezawa, F. Scaling properties of systems of soft-core parallel spherocylinders near the crystal-smectic transition. Phys. Rev. E 1993, 48, 2025–2027. [Google Scholar]
- Aoki, K.M.; Yonezawa, F. Constant-pressure molecular-dynamics simulations of crystal-smectic transition in systems of soft parallel spherocylinders. Phys. Rev. A 1992, 46, 6541–6549. [Google Scholar]
- Aoki, K.M.; Akiyama, T. Investigation of liquid crystalline phases by means of constant-pressure molecular-dynamics simulation. Mol. Cryst. Liq. Cryst. 1995, 262, 543–553. [Google Scholar]
- Aoki, K.M.; Akiyama, T. Molecular dynamics simulations of liquid cryatl phase transitions. Mol. Cryst. Liq. Cryst. 1997, 299, 45–50. [Google Scholar]
- Lettinga, M.P.; Grelet, E. Self-diffusion of rodlike viruses through smectic layers. Phys. Rev. Lett. 2007, 99, 197802:1–197802:4. [Google Scholar]
- Grelet, E.; Lettinga, M.P.; Bier, M.; van Roij, R.; van der Schoot, P. Dynamical and structural insights into the smectic phase of rod-like particles. J. Phys. Condens. Matter 2008, 20, 494213:1–494213:6. [Google Scholar]
- Pouget, E.; Grelet, E.; Lettinga, M.P. Dynamics in the smectic phase of stiff viral rods. Phys. Rev. E 2011, 84, 041704:1–041704:6. [Google Scholar]
- Kuijk, A.; Byelov, D.V.; Petukhov, A.V.; van Blaaderen, A.; Imhof, A. Phase behavior of colloidal silica rods. Faraday Discuss 2012, 159, 181–199. [Google Scholar]
- Cinacchi, G.; de Gaetani, L. Diffusion in the lamellar phase of rod-sphere mixture. J. Chem. Phys. 2009, 131, 104908:1–104908:8. [Google Scholar]
- Patti, A.; El Masri, D.; van Roij, R.; Dijkstra, M. Stringlike clusters and cooperative interlayer permeation in smectic liquid cryatals formed by colloidal rods. Phy. Rev. Lett. 2009, 103, 248304:1–248304:4. [Google Scholar]
- Pizzirusso, A.; Savini, M.; Muccioli, L.; Zannoni, C. An atomistic simulation of the liquid-crystalline phases of sexithiophene. J. Mater. Chem. 2011, 21, 125–133. [Google Scholar]
- Krüger, G.J. Diffusion in thermotropic liquid crystals. Phys. Rep. 1982, 82, 229–269. [Google Scholar]
- Mukherjee, B.; Peter, C.; Kremer, K. Multiscale Simulation of Liquid Crystalline Phase Transitions, Proceedings of ILCC2012, Mainz, Germany, 19—24 August, 2012.
- Aoki, K.M.; Yoneya, M.; Yokoyama, H. Entropy and heat capacity calculations of simulated crystal-hexatic smectic-B-smectic-A liquid-crystal phase transition. Phys. Rev. E 2010, 81, 021701:1–021701:5. [Google Scholar]
- Martiínez-Haya, B.; Cuetos, A. Stability of nematic and smectic phases in rod-like mesogens with orientation-dependent attractive interactions. J. Phys. Chem. B 2007, 111, 8150–8157. [Google Scholar]
- De Gaetani, L.; Tani, A. Sixfold bond orientational properties of a model liquid crystal in the dimensional crossover of B phases: A computer simulation study. J. Chem. Phys. 2007, 126, 064909:1–064909:5. [Google Scholar]
- Brannigan, G.; Brown, F.L.H. Solvent-free simulation of fluid membrane bilayer. J. Chem. Phys. 2004, 120, 1059–1071. [Google Scholar]
- Brannigan, G.; Tamboli, A.C.; Brown, F.L.H. The role of molecular shape in bilayer elasticity and phase behavior. J. Chem. Phys. 2004, 121, 3259–3271. [Google Scholar]
- Kutnjak, Z.; Garland, C.W. Generalized smecitc-hexatic phase diagram. Phys. Rev. E 1998, 57, 3105–3020. [Google Scholar]
- Mercuri, F.; Marinelli, M.; Zammit, U.; Huang, C.C.; Finotello, D. Critial behavior of thermal parameters at the smectic-A–hexatic-B and smectic-A–smectic-C phase transitions in liquid crystals. Phys. Rev. E 2003, 68, 051705:1–051705:10. [Google Scholar]
- Ullo, J.; Yip, S. Dynamical correlation in dense metastable fluids. Phys. Rev. A 1989, 39, 5877–5886. [Google Scholar]
- Yamamoto, T.; Fujiwara, S.; Aoki, K.M.; Sogo, K.; Ohnishi, S. Glassy dynamics in metastable steady states of single-component systems; 1-19-8 Shin-Yokohama, Kohoku-Ku, Yokohama 222-0033, Japan, Unpublished work; 2011. [Google Scholar]
- Matyushov, D.V.; Angell, C.A. Two-Gaussian excitation model for the glass transition. J. Chem. Phys. 2005, 123, 034506:1–034506:12. [Google Scholar]
- Matyushov, D.V.; Angell, C.A. Gaussian excitations model for glass-former dynamics and thermodynamics. J. Chem. Phys. 2007, 126, 094501:1–094501:19. [Google Scholar]
- Donati, C.; Douglas, J.F.; Kob, W.; Plimpton, S.J.; Poole, P.H.; Glotzer, S.C. Stringlike cooperative motion in a supercooled liquid. Phys. Rev. Lett. 1998, 80, 2338–2341. [Google Scholar]
- Donati, C.; Glotzer, S.C.; Poole, P.H.; Kob, W.; Plimpton, S.J. Spatial correlations of mobility and immobility in a glass-forming Lennard-Jones liquid. Phys. Rev. E 1999, 60, 3107–3119. [Google Scholar]
- Perera, D.N.; Harrowell, P. Relaxation dynamics and their spatial distribution in a two dimensional glass-forming mixture. J. Chem. Phys. 1999, 111, 5441–5454. [Google Scholar]
- Caprion, D.; Matsui, J.; Schober, H.R. Dynamics heterogeneity of relaxations in glassesand liquids. Phys. Rev. Lett. 2000, 85, 4293–4296. [Google Scholar]
- Widmer-Cooper, A.; Harrowell, P.; Fynewever, H. How reproducible are dynamic heterogeneities in a supercooled liquid? Phys. Rev. Lett. 2004, 93, 135701:1–135701:4. [Google Scholar]
- Gebremichael, Y.; Vogel, M.; Glotzer, S.C. Particle dynamics and the development of string-like motion in a simulated monoatomic supercooled liquid. J. Chem. Phys. 2004, 120, 4415–4427. [Google Scholar]
- Li, M.; Wang, C.-Z.; Mendelev, M.I.; Ho, K.-M. Molecular dynamics investigation of dynamical heterogeneity and local structure in the supercooled liquid and glass states of Al. Phys. Rev. B 2008, 77, 184202:1–184202:11. [Google Scholar]
- Gasser, U.; Schofield, A.; Weitz, D.A. Local order in a supercooled colloidal fluid observed by confocal microscopy. J. Phys. Condens. Matter 2003, 15, S375–S385. [Google Scholar]
- Ishii, K.; Nakayama, H.; Hirabayashi, S.; Moriyama, R. Anomalously high-density glass of ethylbenzene prepared by vapor deposition at temperatures close to the glass-transition temperature. Chem. Phys. Lett. 2008, 459, 109–112. [Google Scholar]
- Ishii, K.; Yokoyama, Y.; Moriyama, R.; Nakayama, H. Liquid-liquid relaxation in the supercooled liquid state of ethylbenzene: Thermal studies using a prototype DTA sensor for the study of vapor-deposited samples. Chem. Lett. 2010, 39, 958–960. [Google Scholar]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar]
- Andersen, H.C. Molecular dynamics simulation at constant pressure and/or temperature. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar]
- Nosé, S. An improved symplectic integrator for Nosé-Poincaré thermostat. J. Phys. Soc. Jpn. 2001, 70, 75–77. [Google Scholar]
- Dettmann, C.P.; Morriss, G.P. Hamiltonian reformulation and pairing of Lyapunov exponents for Nosé-Hoover dynamics. Phys. Rev. E 1997, 55, 3693–3696. [Google Scholar]
- Bond, S.D.; Leimkuhler, B.J.; Laird, B.B. The Nosé-Poincaré method for constant temperature molecular dynamics. J. Comput. Phys. 1999, 151, 114–134. [Google Scholar]
- Sturgeon, J.B.; Laird, B.B. Symplectic algorithm for constant-pressure molecular dynamics using a Nosé-Poincaré thermostat. J. Chem. Phys. 2000, 112, 3474–3482. [Google Scholar]
- Struckmeier, J. Hamiltonian dynamics on the symplectic extended phase space for autonomous and non-autonomous systems. J. Phys. A 2005, 38, 1257–1278. [Google Scholar]




© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Aoki, K.M.; Fujiwara, S.; Sogo, K.; Ohnishi, S.; Yamamoto, T. One-, Two-, and Three-Dimensional Hopping Dynamics. Crystals 2013, 3, 315-332. https://doi.org/10.3390/cryst3020315
Aoki KM, Fujiwara S, Sogo K, Ohnishi S, Yamamoto T. One-, Two-, and Three-Dimensional Hopping Dynamics. Crystals. 2013; 3(2):315-332. https://doi.org/10.3390/cryst3020315
Chicago/Turabian StyleAoki, Keiko M., Susumu Fujiwara, Kiyoshi Sogo, Shuhei Ohnishi, and Takenori Yamamoto. 2013. "One-, Two-, and Three-Dimensional Hopping Dynamics" Crystals 3, no. 2: 315-332. https://doi.org/10.3390/cryst3020315
APA StyleAoki, K. M., Fujiwara, S., Sogo, K., Ohnishi, S., & Yamamoto, T. (2013). One-, Two-, and Three-Dimensional Hopping Dynamics. Crystals, 3(2), 315-332. https://doi.org/10.3390/cryst3020315



