Applications of Random Nonlinear Photonic Crystals Based on Strontium Tetraborate
Abstract
:1. Introduction
2. Orthorhombic Strontium Tetraborate (α-SBO)

3. Applications of NPC SBO
3.1. Generation of Deep UV Radiation in NPC SBO
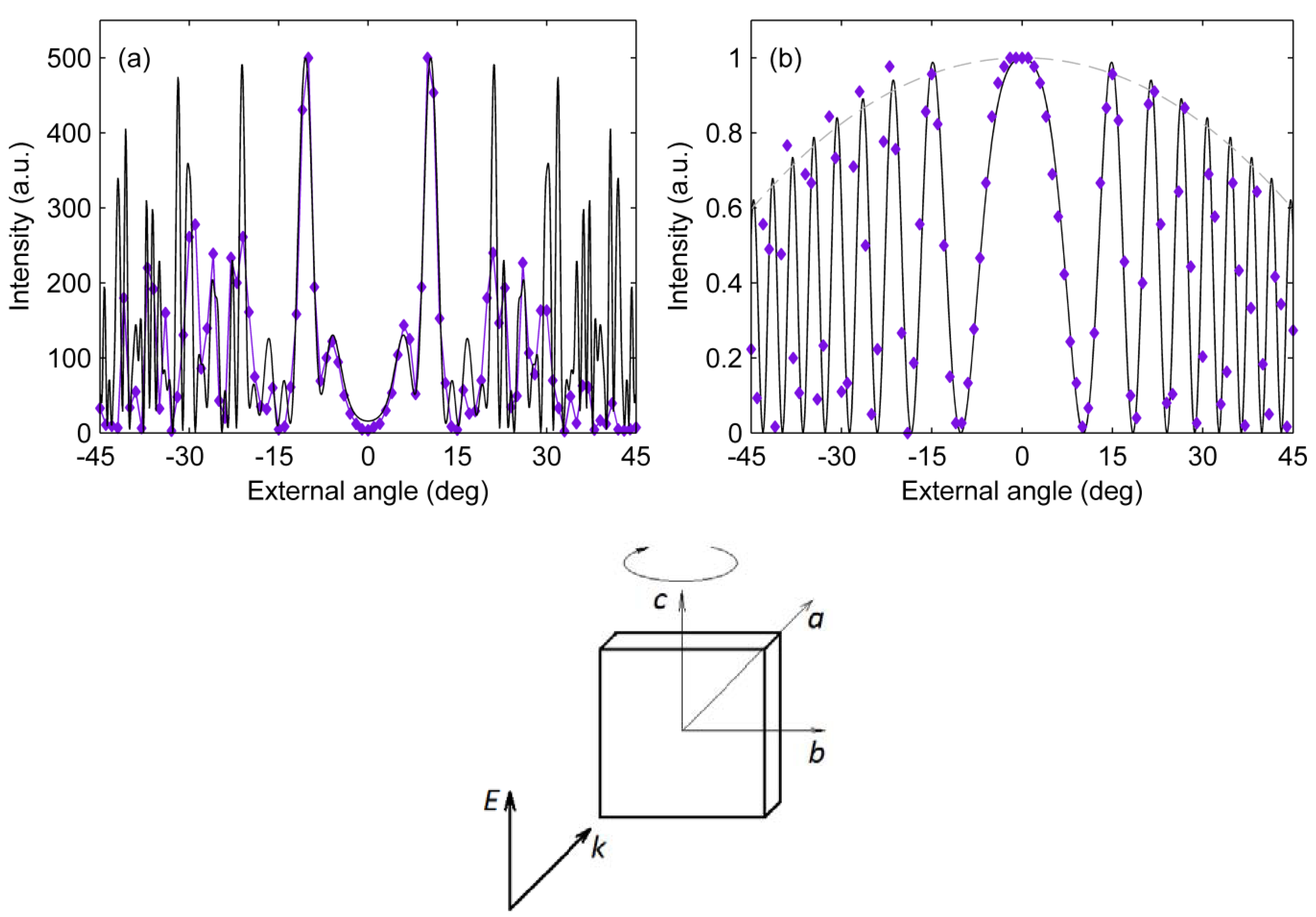
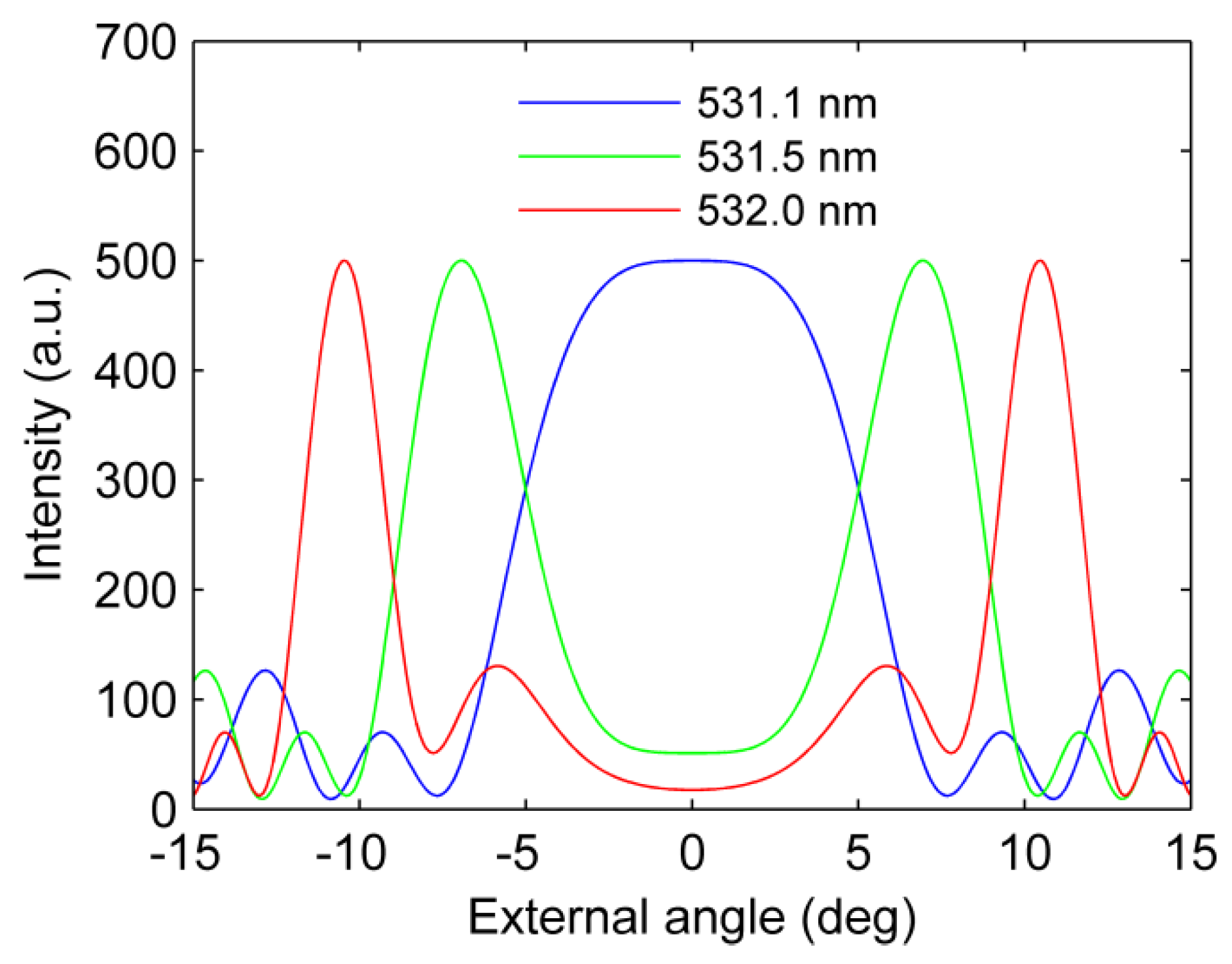
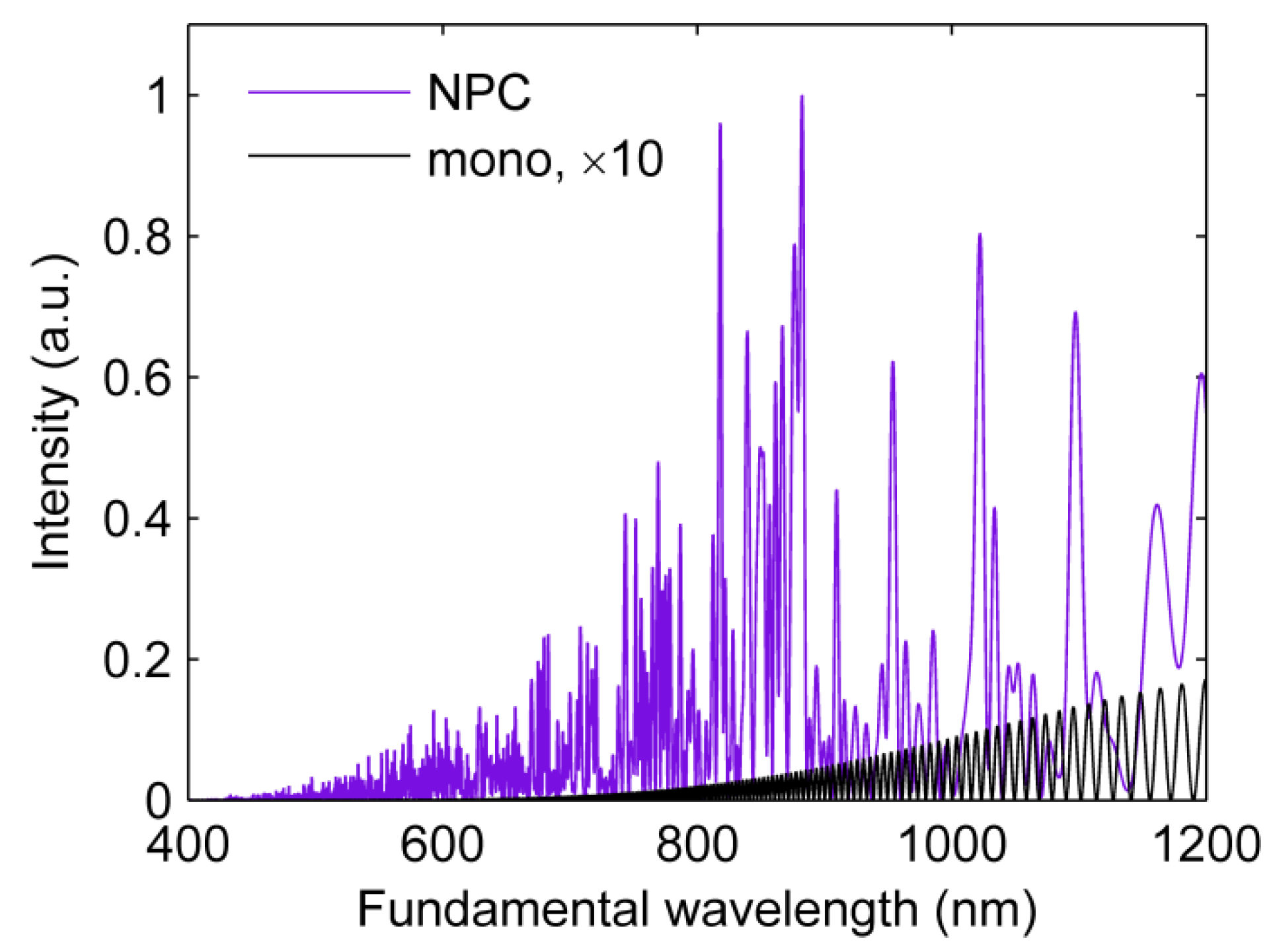
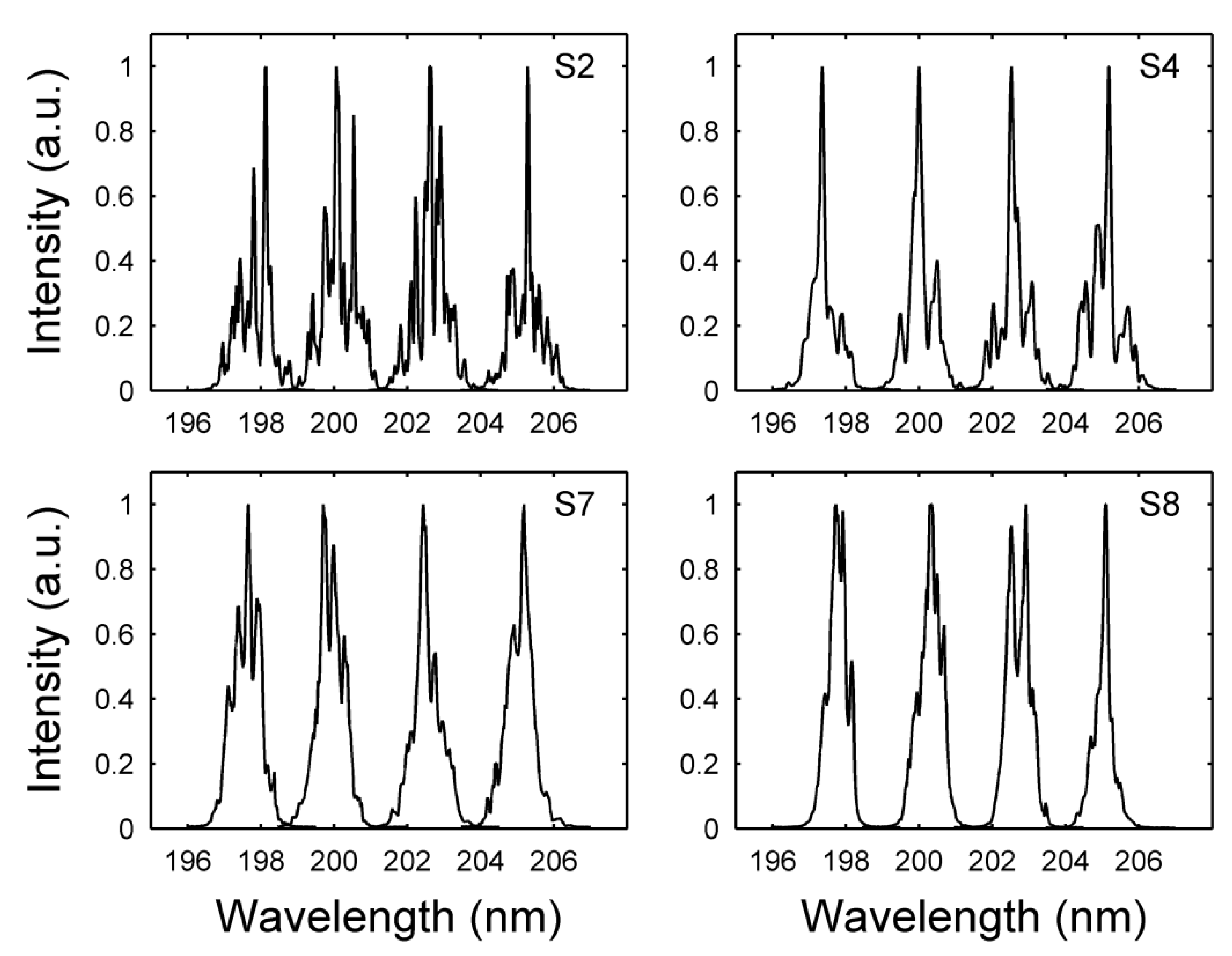
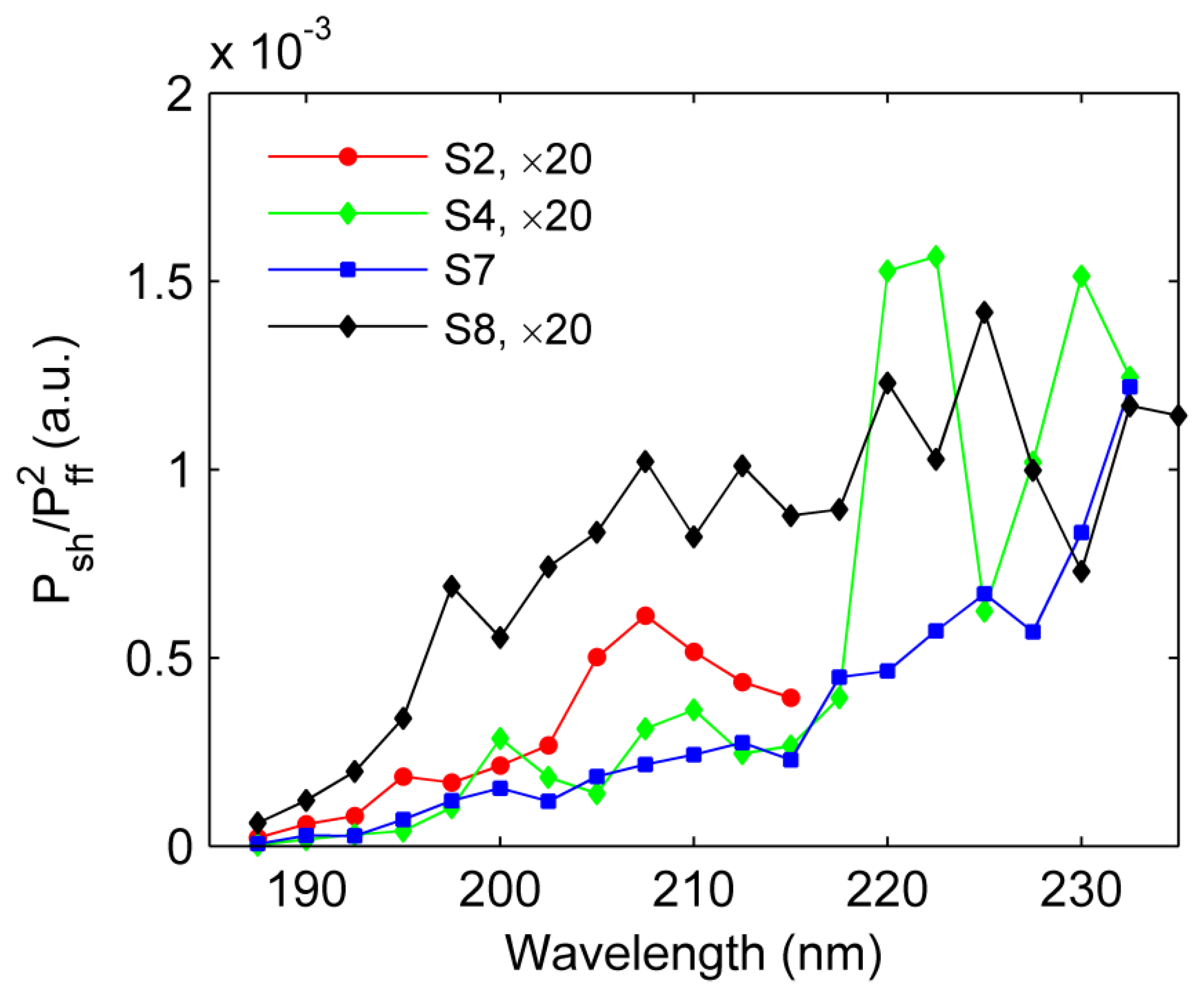
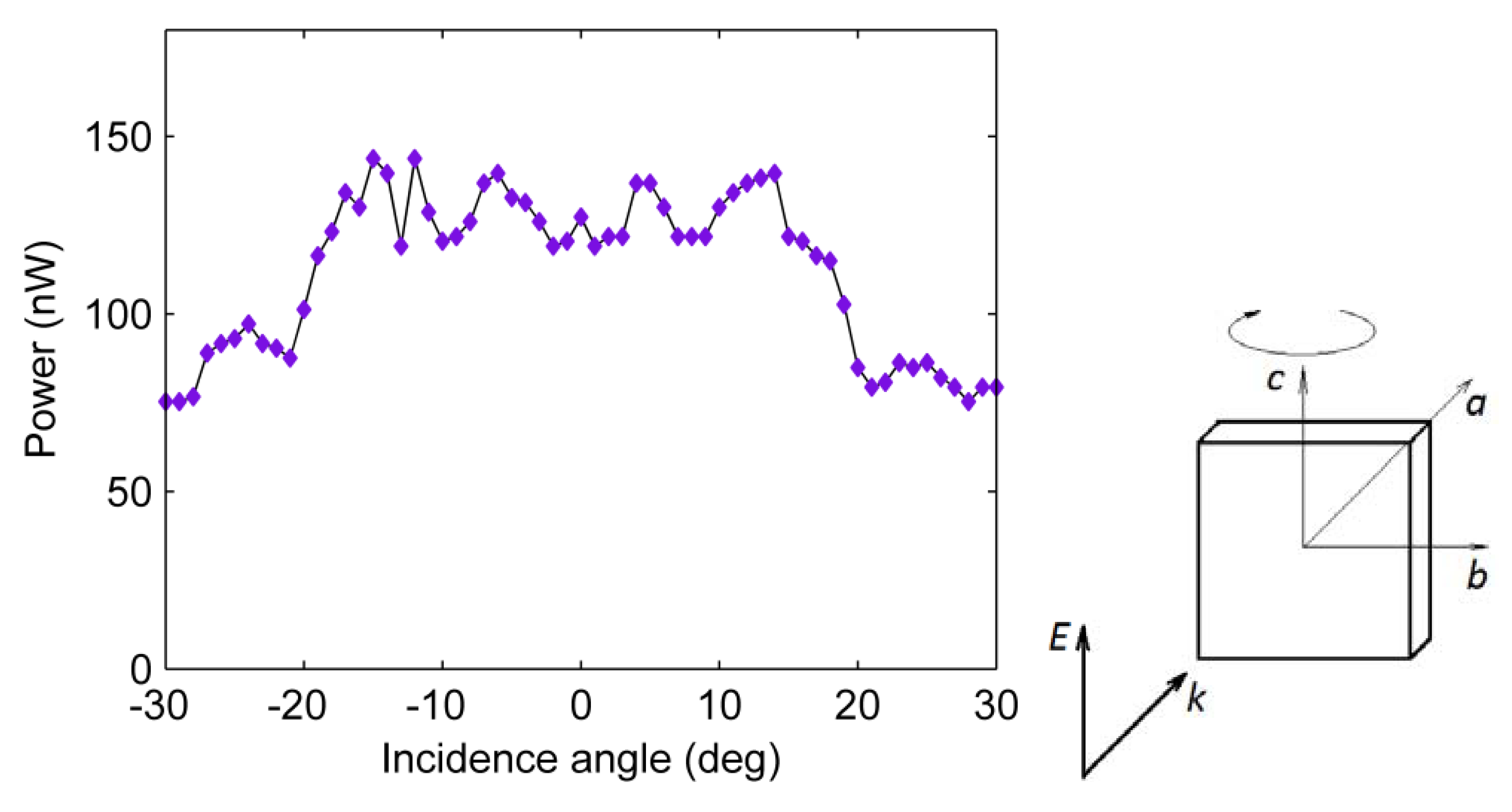
3.2. Fs Pulses Diagnostics Using NPC SBO
3.2.1. RQPM Scheme
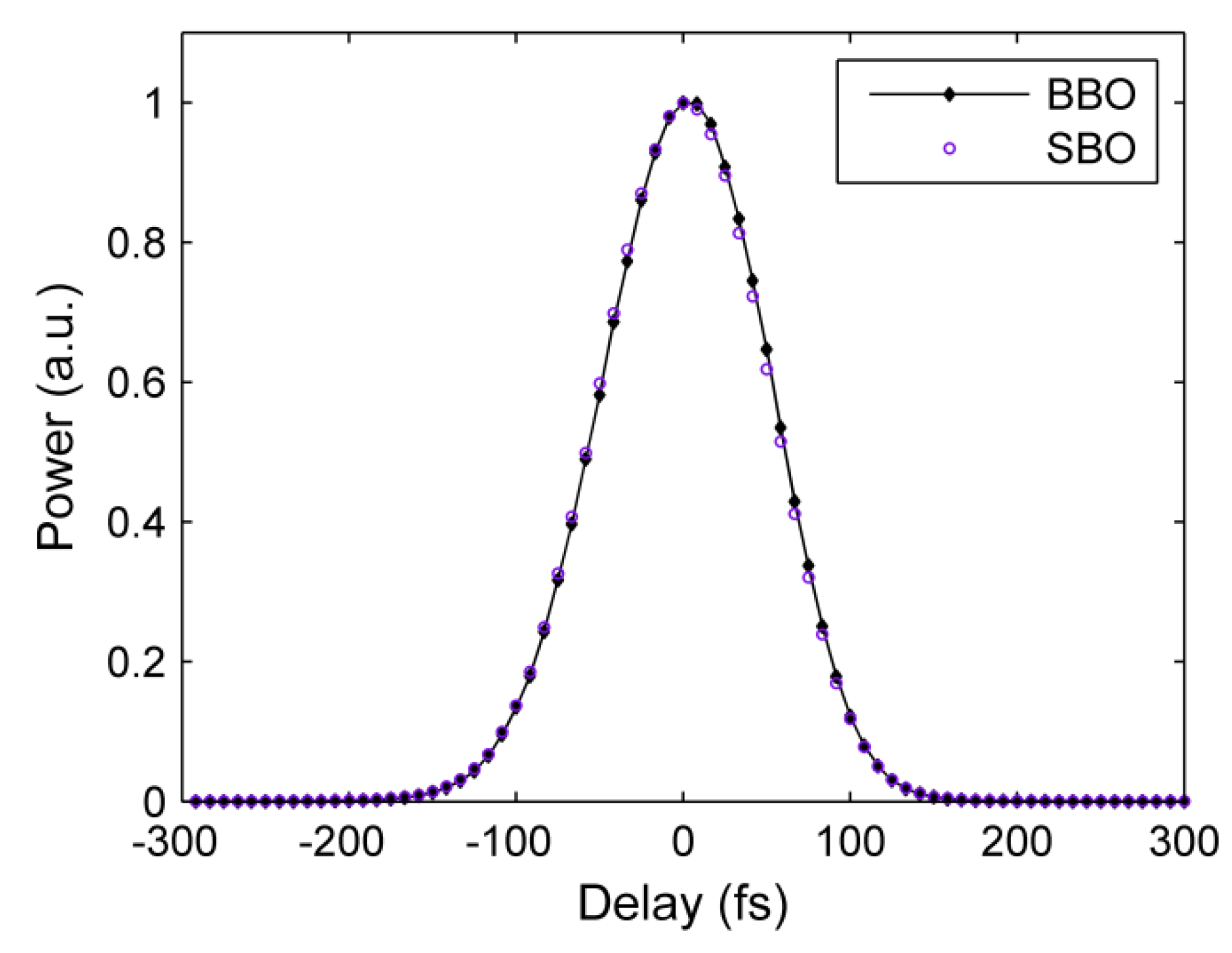
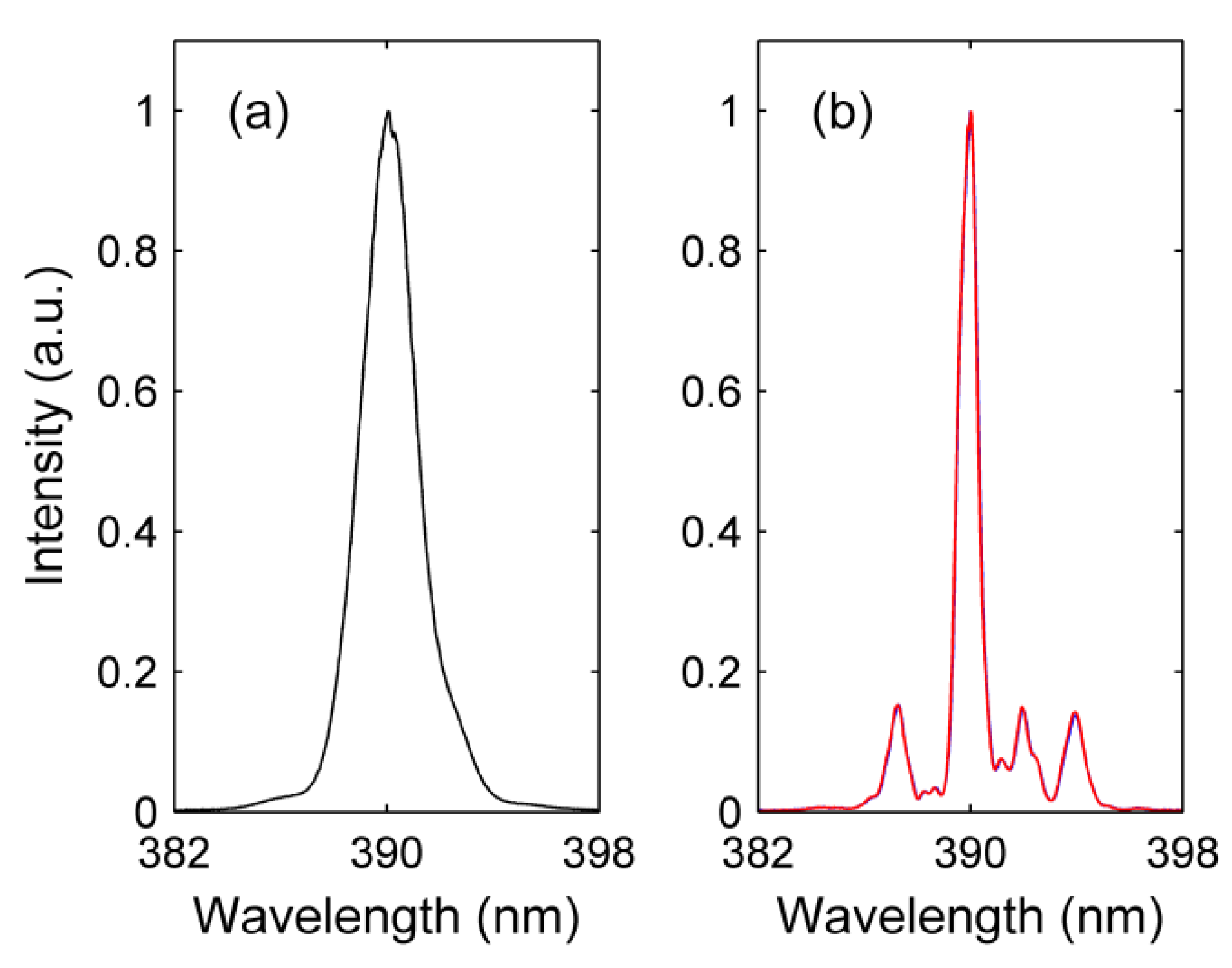
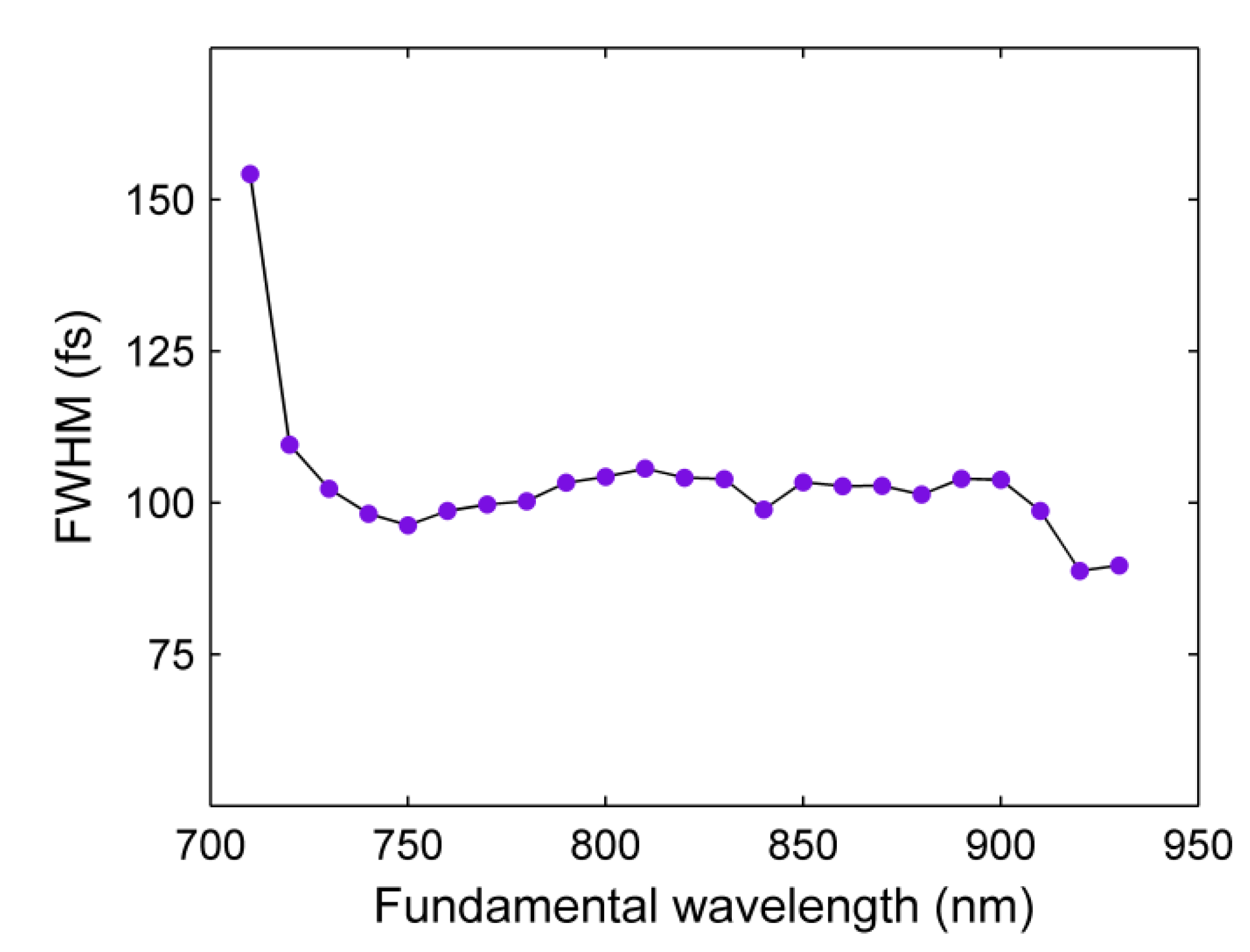
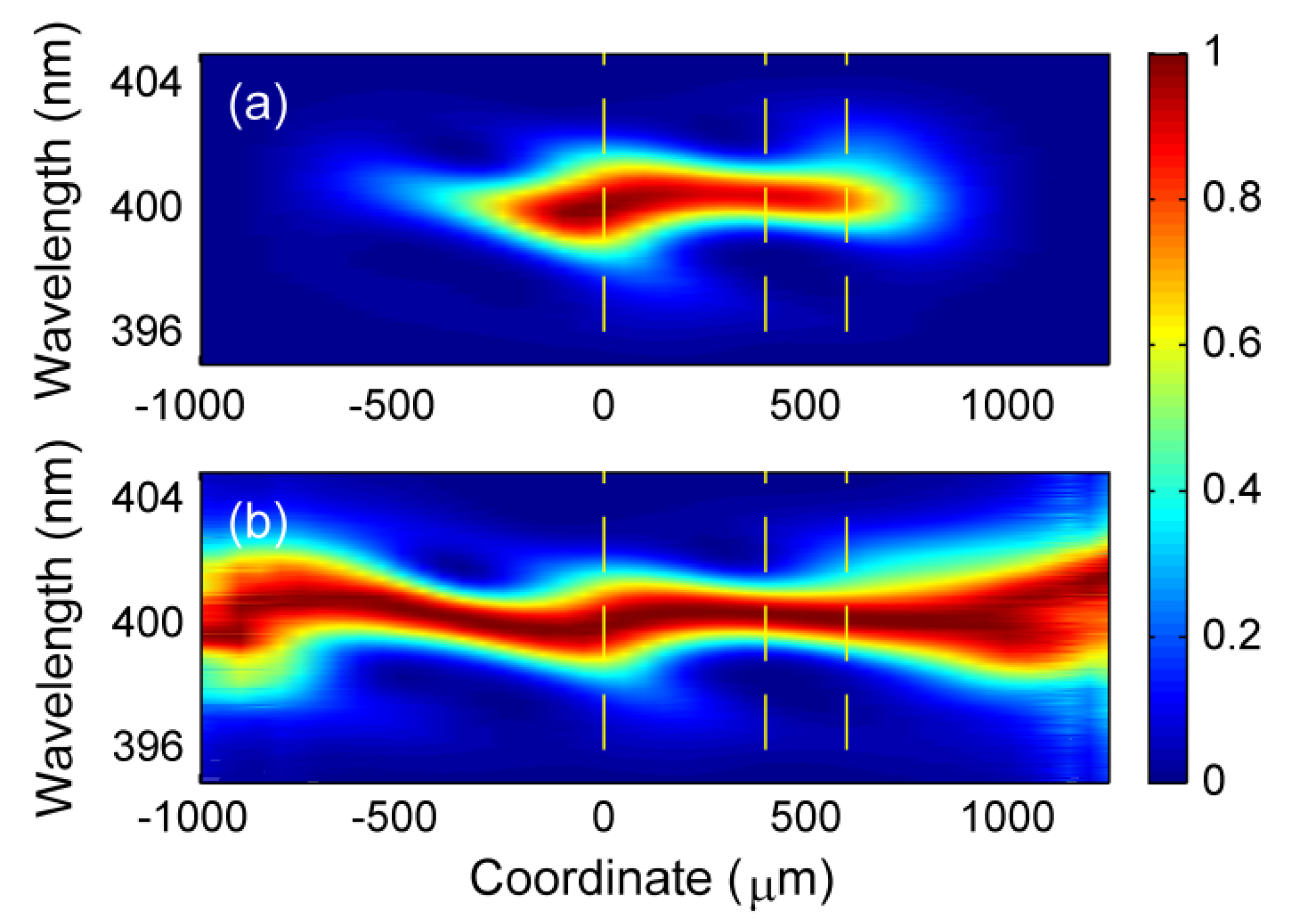
3.2.2. Autocorrelation Measurements Using Nonlinear Diffraction from Virtual Beam
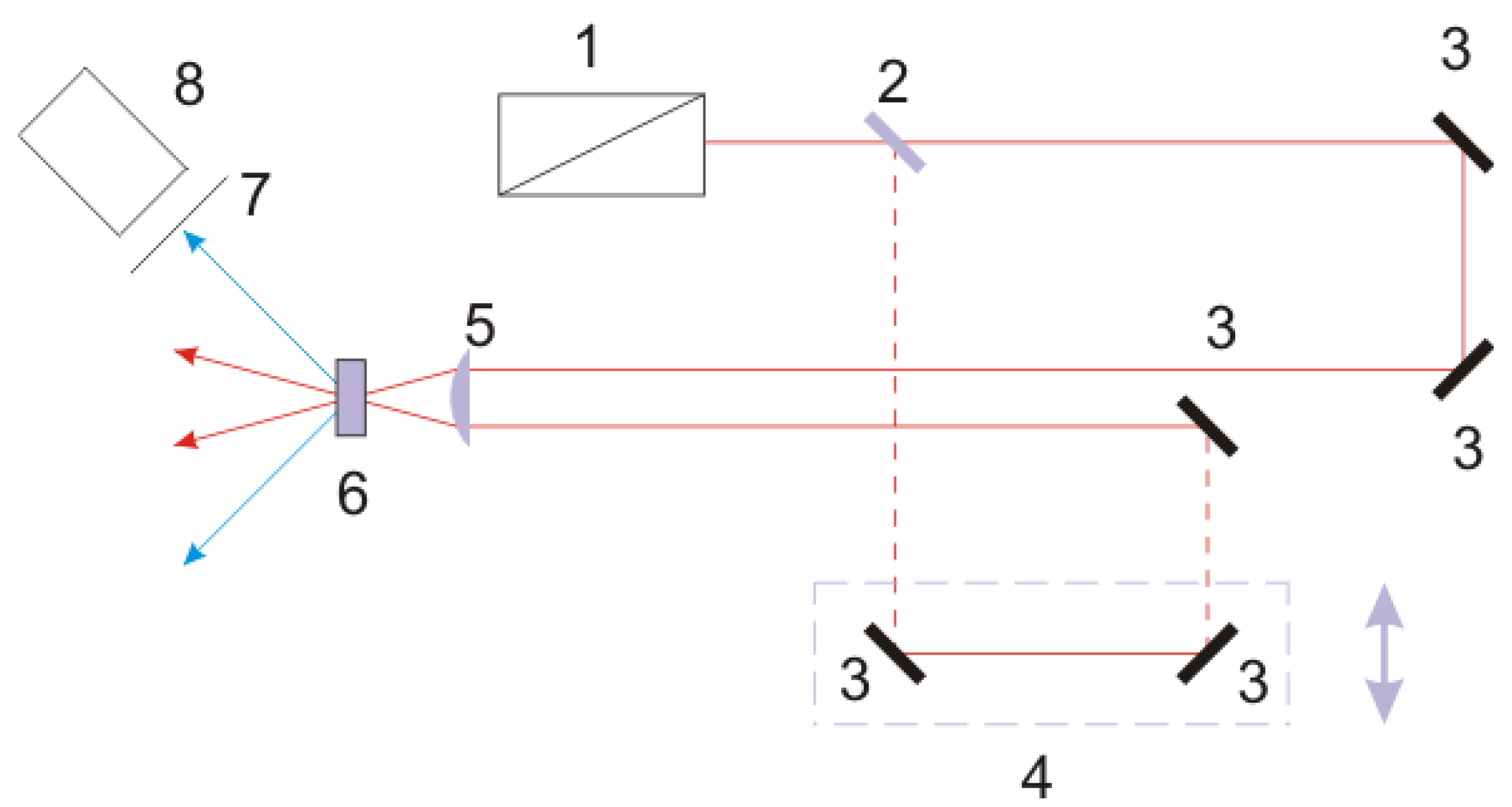
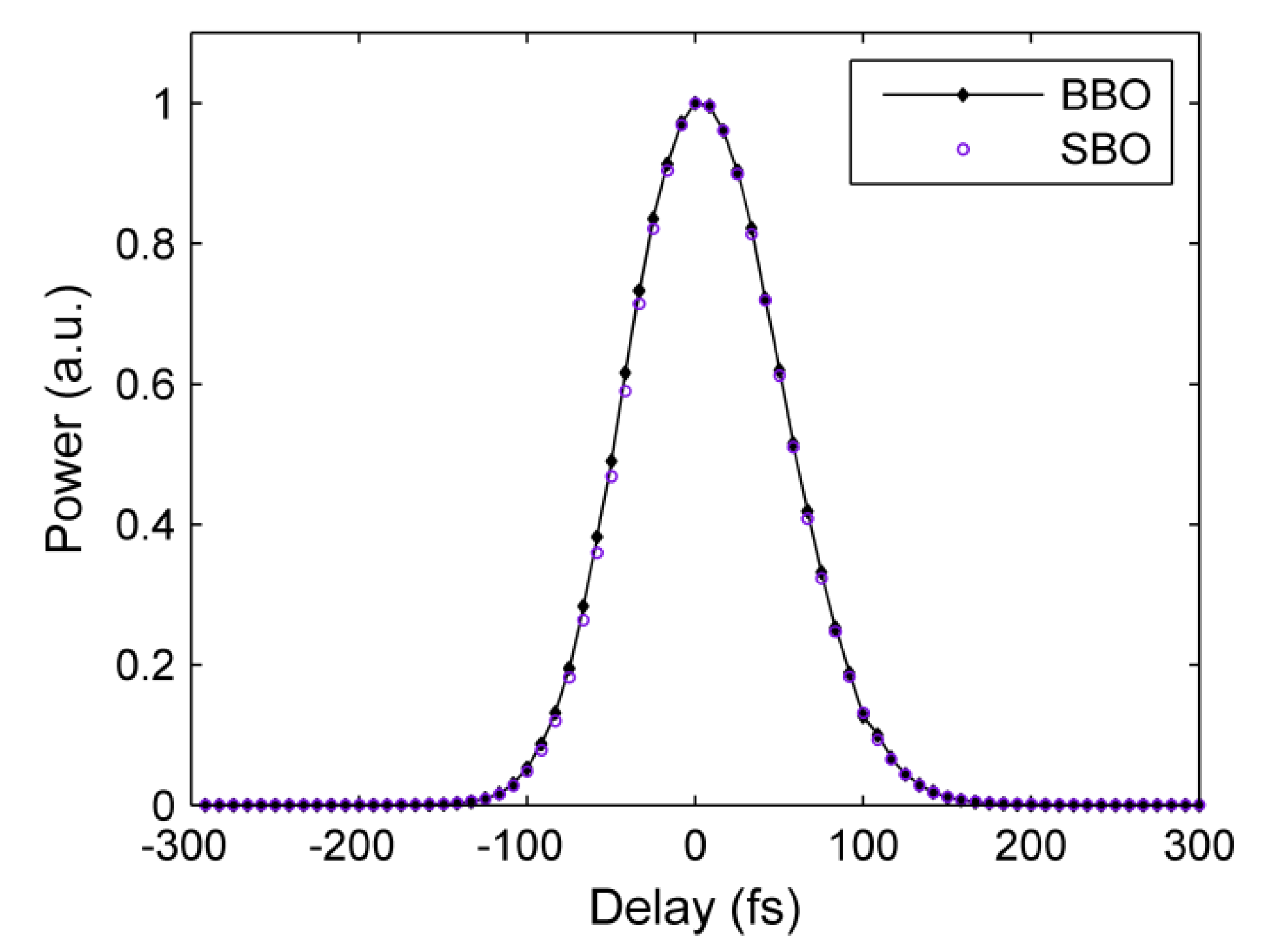
4. Conclusions
Acknowledgments
Conflict of Interest
References and Notes
- Joannopoulos, J.D.; Meade, R.D.; Winn, J.N. Photonic Crystals; Princeton University Press: Princeton, NJ, USA, 2008; p. 286. [Google Scholar]
- Berger, V. Nonlinear photonic crystals. Phys. Rev. Lett. 1998, 81, 4136–4139. [Google Scholar] [CrossRef]
- Armstrong, A.; Bloembergen, N.; Ducuing, J.; Pershan, P.S. Interactions between light waves in a nonlinear dielectric. Phys. Rev. 1962, 127, 1918–1939. [Google Scholar] [CrossRef]
- Fejer, M.M.; Magel, G.A.; Jundt, D.H.; Byer, R.L. Quasi-Phase-Matched second harmonic generation: Tuning and tolerances. IEEE J. Quant. Electron. 1992, 28, 2631–2654. [Google Scholar] [CrossRef]
- Arie, A.; Voloch, N.C. Periodic, quasi-periodic and random quadratic nonlinear photonic crystals. Laser Photon. Rev. 2010, 4, 355–373. [Google Scholar] [CrossRef]
- Baudrier-Raybaut, M.; Haidar, R.; Kupecek, P.; Lemasson, P.; Rosencher, E. Random quasi-phase-matching in bulk polycrystalline isotropic nonlinear materials. Nature 2004, 432, 374–376. [Google Scholar] [CrossRef]
- Morozov, E.Y.; Chirkin, A.S. Stochastic quasi-phase matching in nonlinear-optical crystals with an irregular domain structure. Quantum Electron. 2004, 34, 227–232. [Google Scholar] [CrossRef]
- Fischer, R.; Saltiel, S.M.; Neshev, D.N.; Krolikovski, W.; Kivshar, Y.S. Broadband femtosecond frequency doubling in random media. Appl. Phys. Lett. 2006, 89, 1–3. [Google Scholar]
- Aleksandrovsky, A.S.; Vyunishev, A.M.; Zaitsev, A.I.; Zamkov, A.V.; Arkhipkin, V.G. Detection of randomized nonlinear photonic crystal structure in a non-ferroelectric crystal. J. Opt. A, Pure Appl. Opt. 2007, 9, S334–S338. [Google Scholar] [CrossRef]
- Aleksandrovsky, A.S.; Vyunishev, A.M.; Shakhura, I.E.; Zaitsev, A.I.; Zamkov, A.V. Random quasi-phase-matching in nonlinear photonic crystal structure of strontium tetraborate. Phys. Rev. A 2008, 78, 31802–31806. [Google Scholar] [CrossRef]
- Shutov, I.V.; Chirkin, A.S. Consecutive high-order harmonic generation and formation of subfemtosecond light pulses in aperiodical nonlinear photonic crystals. Phys. Rev. A 2008, 78. [Google Scholar]
- Sheng, Y.; Ma, D.L.; Ren, M.L.; Chai, W.Q.; Li, Z.Y.; Koynov, K.; Krolikowski, W. Broadband second harmonic generation in one-dimensional randomized nonlinear photonic crystal. Appl. Phys. Lett. 2011, 99. [Google Scholar]
- Simagina, L.V.; Mishina, E.D.; Semin, S.V.; Ilyin, N.A.; Volk, T.R.; Gainutdinov, R.V.; Ivleva, L.I. Second harmonic generation in microdomain gratings fabricated in strontium-barium niobate crystals with an atomic force microscope. J. Appl. Phys. 2011, 110. [Google Scholar]
- Petrov, V.; Rotermund, F.; Noack, F.; Ringling, J.; Kittelmann, O.; Komatsu, R. Frequency conversion of Ti:Sapphire-Based femtosecond laser systems to the 200-nm spectral region using nonlinear optical crystals. IEEE J. Sel. Top. Quantum Electron. 1999, 5, 1532–1542. [Google Scholar] [CrossRef]
- Kurimura, S.K; Harada, M.; Muramatsu, K.; Ueda, M.; Adachi, M.; Yamada, T.; Ueno, T. Quartz revisits nonlinear optics: Twinned crystal for quasi-phase matching. Opt. Mater. Express 2011, 1, 1367–1375. [Google Scholar] [CrossRef]
- Petrov, V.; Noack, F.; Shen, D.Z.; Feng, P.; Shen, G.Q.; Wang, X.Q.; Komatsu, R.; Alex, V. Application of the nonlinear crystal SrB4O7 for ultrafast diagnostics converting to wavelengths as short as 125 nm. Opt. Lett. 2004, 29, 373–375. [Google Scholar] [CrossRef]
- Zinenko, V.I.; Pavlovskii, M.S.; Zaitsev, A.I.; Krylov, A.S.; Shinkorenko, A.S. Vibrational spectra and elastic piezoelectric and polarization properties of the α-SrB4O7 crystal. J. Exp. Theor. Phys. 2012, 115, 455–461. [Google Scholar]
- Zaitsev, A.I.; Aleksandrovsky, A.S.; Vasiliev, A.D.; Zamkov, A.V. Domain structure in strontium tetraborate single crystal. J. Cryst. Growth 2008, 310, 1–4. [Google Scholar] [CrossRef]
- Aleksandrovsky, A.S.; Vyunishev, A.M.; Zaitsev, A.I.; Slabko, V.V. Random-Quasi-Phase matched conversion of broadband radiation in a nonlinear photonic crystal. Phys. Rev. A 2010, 82. [Google Scholar]
- Aleksandrovsky, A.S.; Vyunishev, A.M.; Zaitsev, A.I.; Ikonnikov, A.A.; Pospelov, G.I.; Rovskii, V.E.; Slabko, V.V. Deep-UV generation in an SBO crystal with an irregular domain structure. Quantum Electron. 2011, 41, 748–753. [Google Scholar] [CrossRef]
- Aleksandrovsky, A.S.; Vyunishev, A.M.; Shakhura, I.E.; Zaitsev, A.I.; Zamkov, A.V. Nonlinear optical processes in domain structures of strontium tetraborate. Opt. Spectrosc. 2009, 107, 359–362. [Google Scholar] [CrossRef]
- Aleksandrovsky, A.S.; Vyunishev, A.M.; Zaitsev, A.I.; Ikonnikov, A.A.; Pospelov, G.I. Ultrashort pulses characterization by nonlinear diffraction from virtual beam. Appl. Phys. Lett. 2011, 98. [Google Scholar]
- Aleksandrovsky, A.S.; Vyunishev, A.M.; Zaitsev, A.I.; Pospelov, G.I.; Slabko, V.V. Diagnostics of fs pulses by noncollinear random quasi-phase-matched frequency. Appl. Phys. Lett. 2011, 99. [Google Scholar]
- Saltiel, S.M.; Neshev, D.N.; Krolikowski, W.; Voloch-Bloch, N.; Arie, A.; Bang, O.; Kivshar, Y.S. Nonlinear diffraction from a virtual beam. Phys. Rev. Lett. 2010, 104. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Aleksandrovsky, A.S.; Vyunishev, A.M.; Zaitsev, A.I. Applications of Random Nonlinear Photonic Crystals Based on Strontium Tetraborate. Crystals 2012, 2, 1393-1409. https://doi.org/10.3390/cryst2041393
Aleksandrovsky AS, Vyunishev AM, Zaitsev AI. Applications of Random Nonlinear Photonic Crystals Based on Strontium Tetraborate. Crystals. 2012; 2(4):1393-1409. https://doi.org/10.3390/cryst2041393
Chicago/Turabian StyleAleksandrovsky, Aleksandr S., Andrey M. Vyunishev, and Alexandre I. Zaitsev. 2012. "Applications of Random Nonlinear Photonic Crystals Based on Strontium Tetraborate" Crystals 2, no. 4: 1393-1409. https://doi.org/10.3390/cryst2041393
APA StyleAleksandrovsky, A. S., Vyunishev, A. M., & Zaitsev, A. I. (2012). Applications of Random Nonlinear Photonic Crystals Based on Strontium Tetraborate. Crystals, 2(4), 1393-1409. https://doi.org/10.3390/cryst2041393



