Infrared and Raman Studies of Charge Ordering in Organic Conductors, BEDT-TTF Salts with Quarter-Filled Bands
Abstract
:1. Introduction
2. Detection and Analysis of Charge Order
2.1. Site Charge and Fluctuation
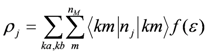
 is the Bloch function of the mth band, nM is the number of molecules in a unit cell, nj is the number operator at the jth site, and f(ε) is the Fermi distribution function for a hole. The site charge is the integrated valence electron at each site below a Fermi level. Therefore, the site-charge distribution is sometimes non-uniform even in a metal, if the site in a unit cell is crystallographically non-equivalent. If the amplitude of charge order Δρ is small, a small portion of the valence electrons near the Fermi level contribute to the charge disproportionation, while in the case of large Δρ, most valence electrons participate in the charge disproportionation as the band structure entirely changes
is the Bloch function of the mth band, nM is the number of molecules in a unit cell, nj is the number operator at the jth site, and f(ε) is the Fermi distribution function for a hole. The site charge is the integrated valence electron at each site below a Fermi level. Therefore, the site-charge distribution is sometimes non-uniform even in a metal, if the site in a unit cell is crystallographically non-equivalent. If the amplitude of charge order Δρ is small, a small portion of the valence electrons near the Fermi level contribute to the charge disproportionation, while in the case of large Δρ, most valence electrons participate in the charge disproportionation as the band structure entirely changes 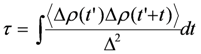
2.2. Charge-Sensitive Mode of BEDT-TTF

2.3. Electron-Molecular Vibration (EMV) Coupling in BEDT-TTF
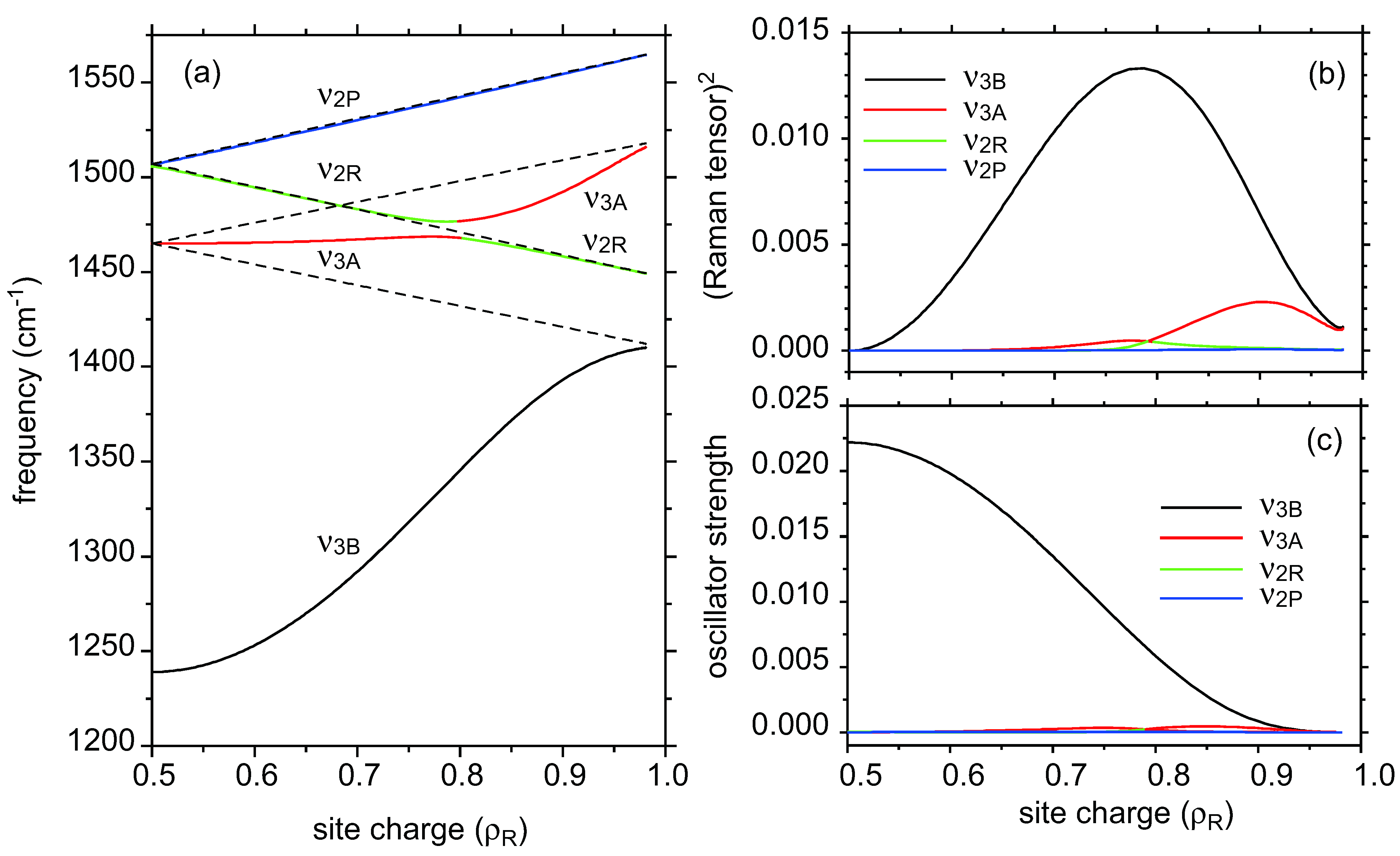
2.4. The Line Shape of Charge-Sensitive Mode

 ) and correlation time
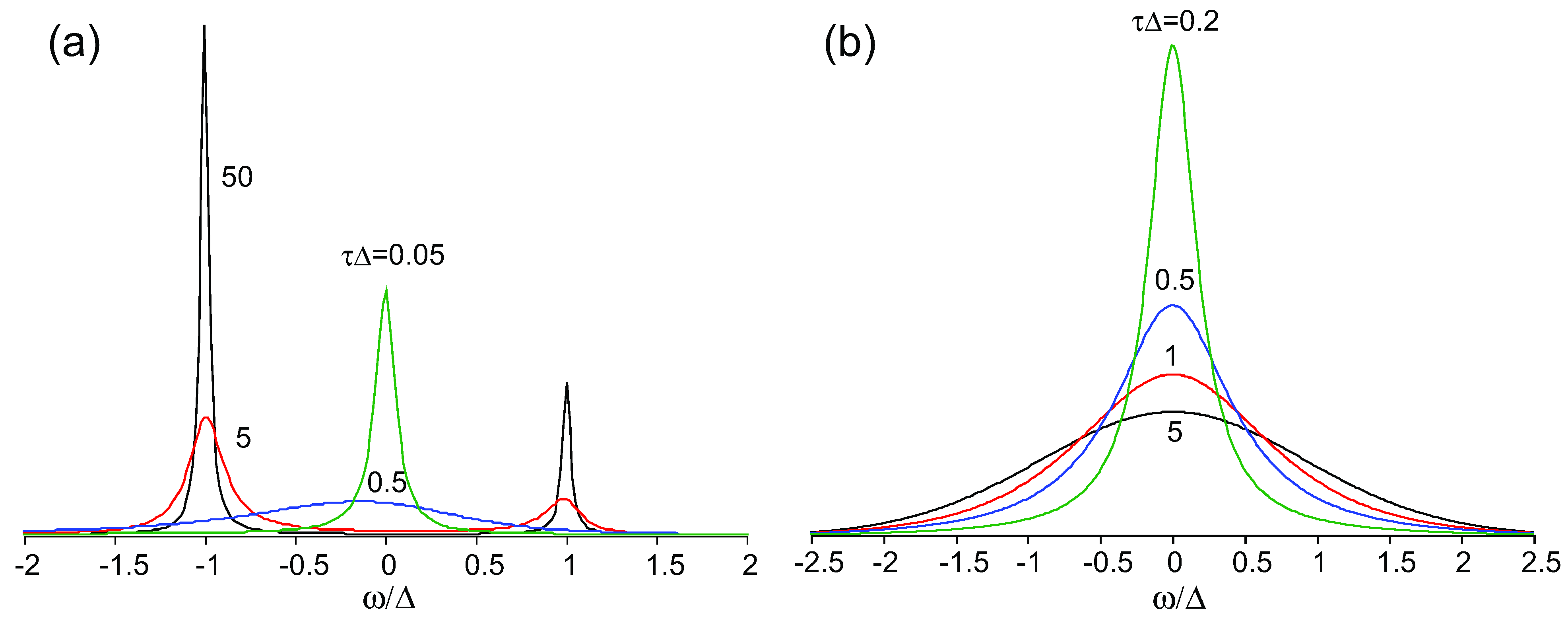
) and correlation time  , where Δρ = ρ(t) − 1/2 is the time-dependent site-charge variation from the average site charge 1/2. This charge fluctuation modulates the frequencies of ν27 and ν2 with an amplitude Δf and correlation time τ. When the site charge fluctuates stochastically between two values such as ρR and ρP and thus the frequency fluctuates between ωR and ωP with a transition rate γ, then the line shape of the charge-sensitive mode is described by the following equation [58].
, where Δρ = ρ(t) − 1/2 is the time-dependent site-charge variation from the average site charge 1/2. This charge fluctuation modulates the frequencies of ν27 and ν2 with an amplitude Δf and correlation time τ. When the site charge fluctuates stochastically between two values such as ρR and ρP and thus the frequency fluctuates between ωR and ωP with a transition rate γ, then the line shape of the charge-sensitive mode is described by the following equation [58].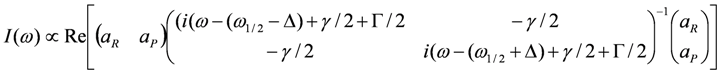
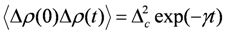 , where Δc is the amplitude of the fluctuation and γ is the decay rate. In this case, the modulation of the site charge is transformed to a modulation of the frequency of the charge-sensitive mode, and the line shape of the charge-sensitive mode is given by the following equation [59,60],
, where Δc is the amplitude of the fluctuation and γ is the decay rate. In this case, the modulation of the site charge is transformed to a modulation of the frequency of the charge-sensitive mode, and the line shape of the charge-sensitive mode is given by the following equation [59,60], 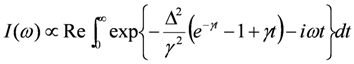
3. β″-(BEDT-TTF)(TCNQ)
3.1. Crystal Structure and Superlattice
 , the proposed model of this superstructure is shown in Figure 5. TCNQ is connected by a center of symmetry (4kF modulation) and BEDT-TTF is located on the center of symmetry. Therefore, the two TCNQs in the unit cell are crystallographically equivalent, whereas the two BEDT-TTFs are non-equivalent. These superlattice spots disappear at around 170 K. However, the vibronic bands of TCNQ still remain after the superlattice spots vanish. This result implies that the short-range ordered 4kF modulation remains in the TCNQ stack or another superlattice forms. According to the X-ray diffraction study by Nogami, a new superlattice spot for 2a × 2c was found below 170 K. [63]. In any case, the valence electron in the TCNQ stack is localized within the dimer, and the valence electron in the pseudo-one-dimensional BEDT-TTF band is responsible for the charge carriers.
, the proposed model of this superstructure is shown in Figure 5. TCNQ is connected by a center of symmetry (4kF modulation) and BEDT-TTF is located on the center of symmetry. Therefore, the two TCNQs in the unit cell are crystallographically equivalent, whereas the two BEDT-TTFs are non-equivalent. These superlattice spots disappear at around 170 K. However, the vibronic bands of TCNQ still remain after the superlattice spots vanish. This result implies that the short-range ordered 4kF modulation remains in the TCNQ stack or another superlattice forms. According to the X-ray diffraction study by Nogami, a new superlattice spot for 2a × 2c was found below 170 K. [63]. In any case, the valence electron in the TCNQ stack is localized within the dimer, and the valence electron in the pseudo-one-dimensional BEDT-TTF band is responsible for the charge carriers.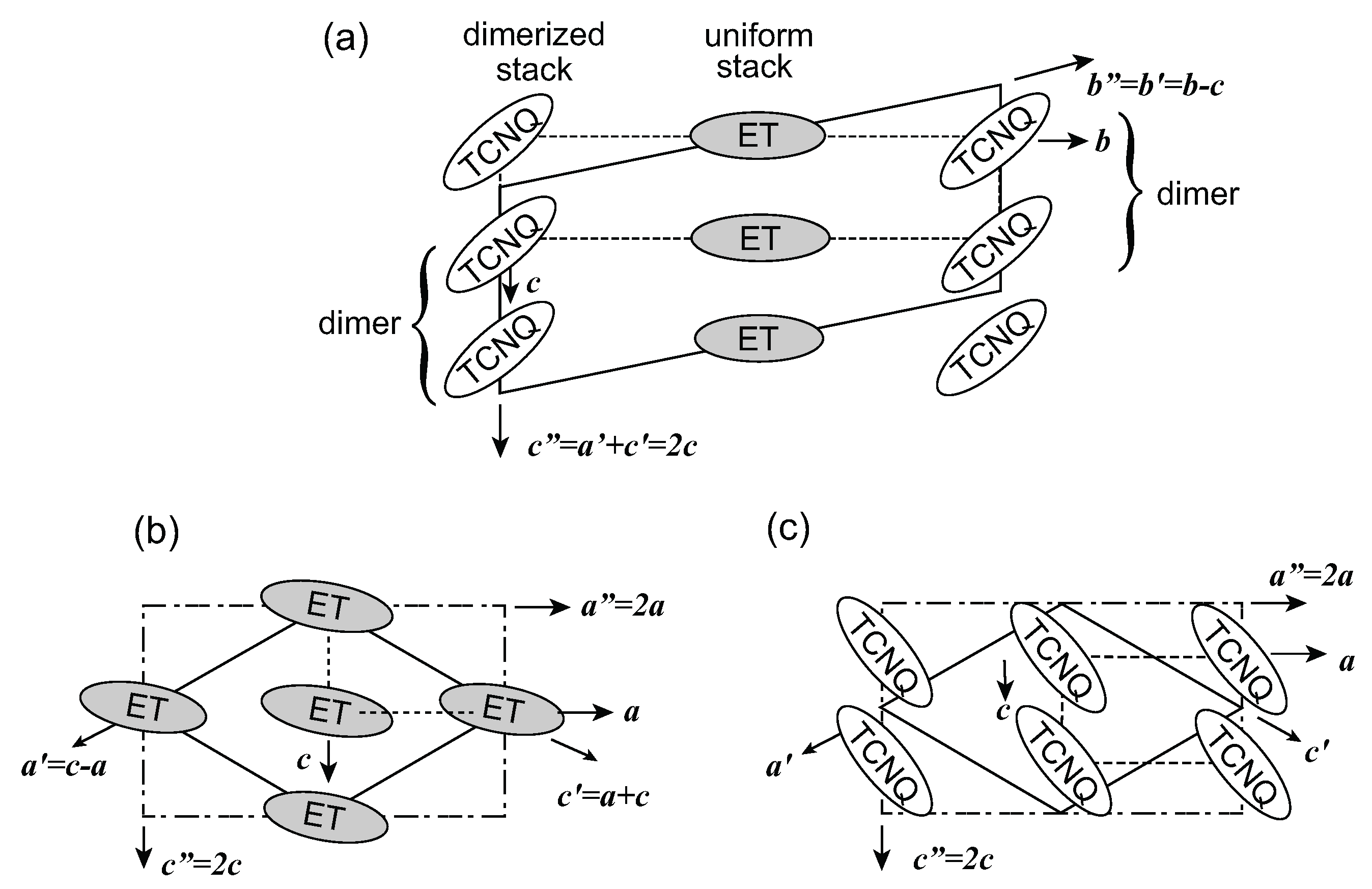
3.2. Crossover from Uniform Metal to Charge-Ordered Metal
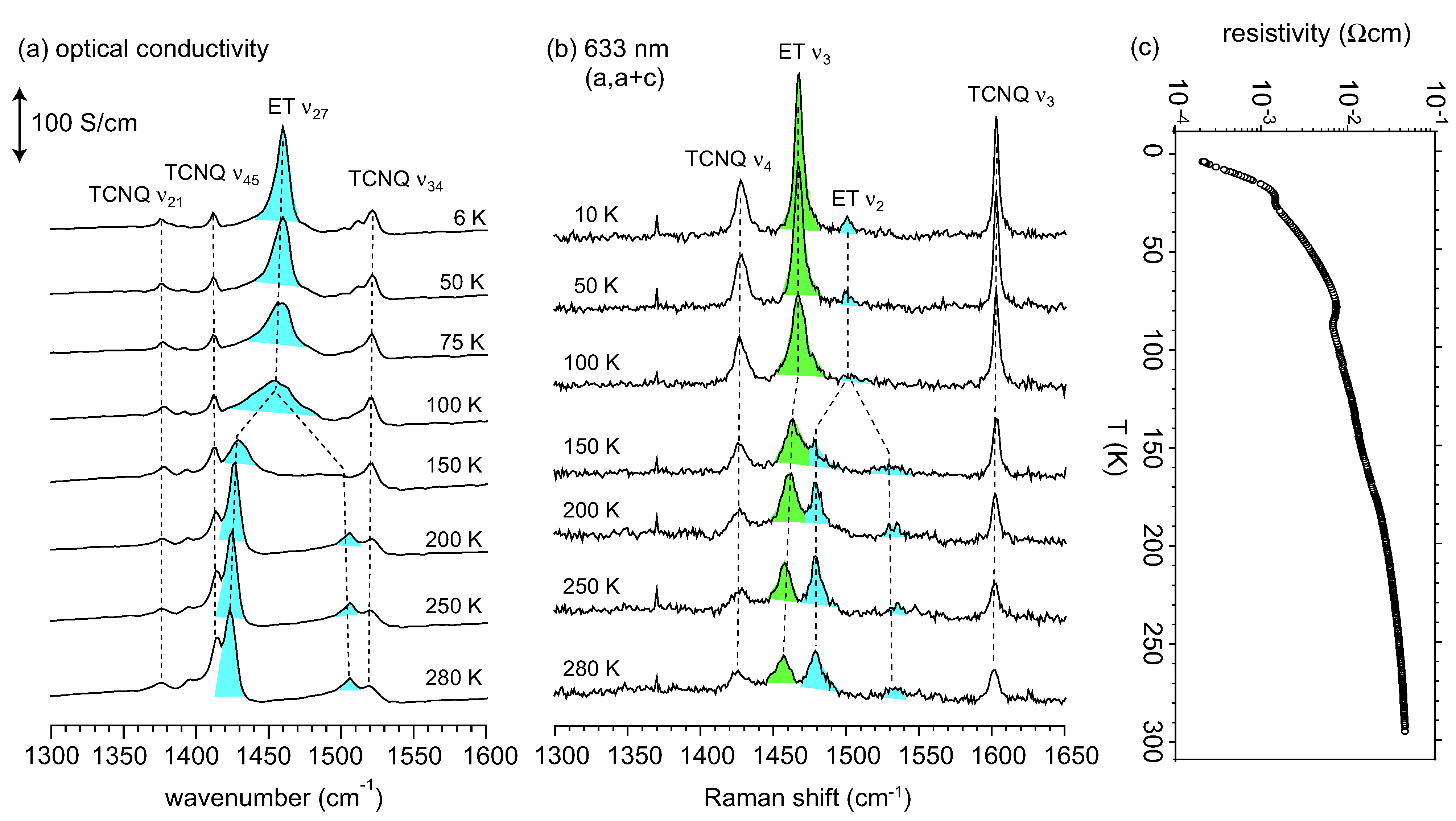
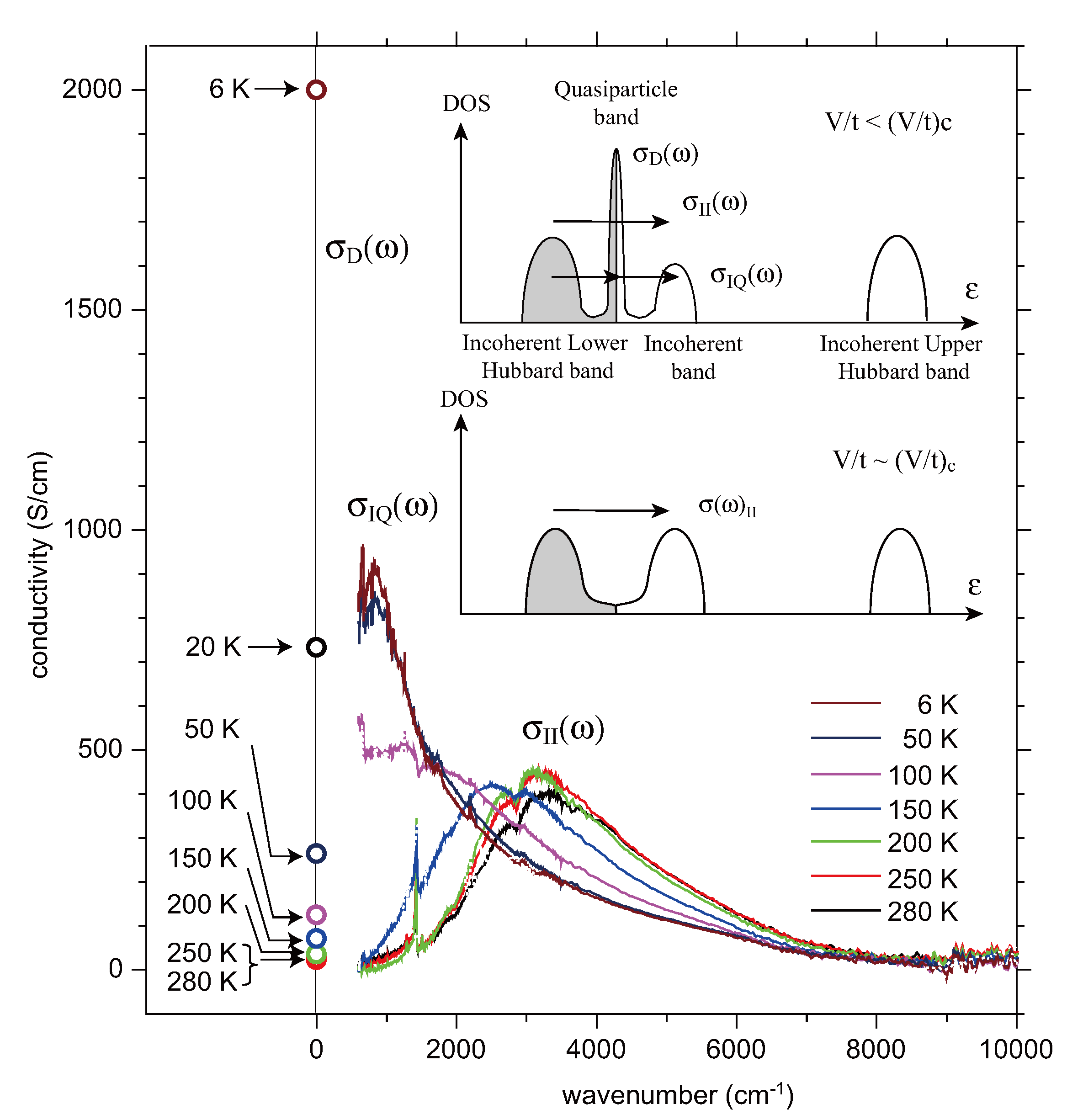
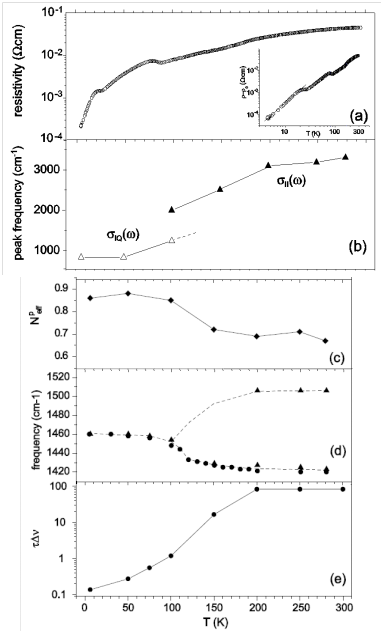
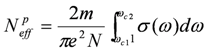
4. θ-(BEDT-TTF)2X
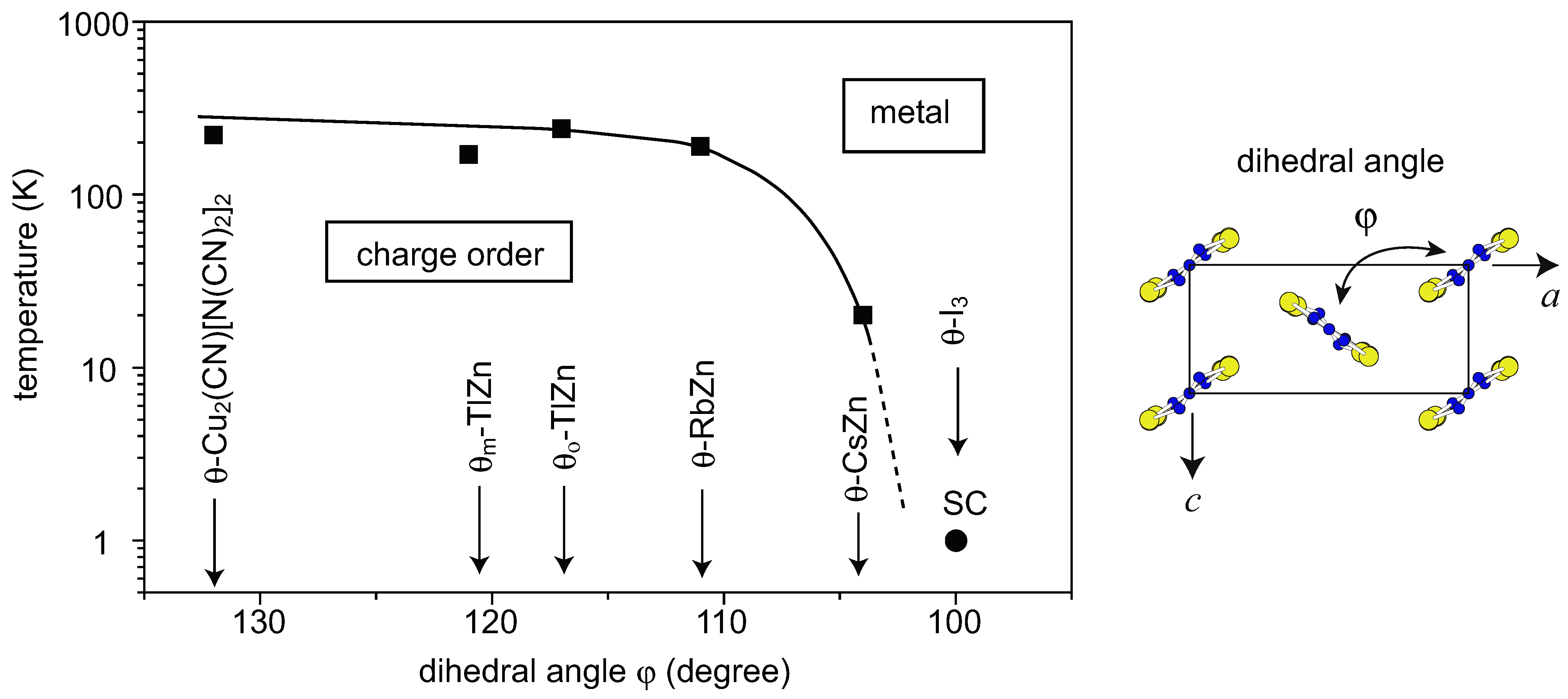
4.1. Charge-Ordered Phase of X = RbZn(SCN)4, TlZn(SCN)4, Cu2(CN)[N(CN)2]2
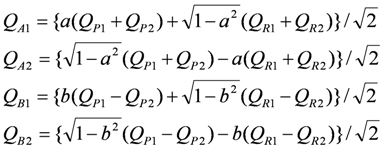
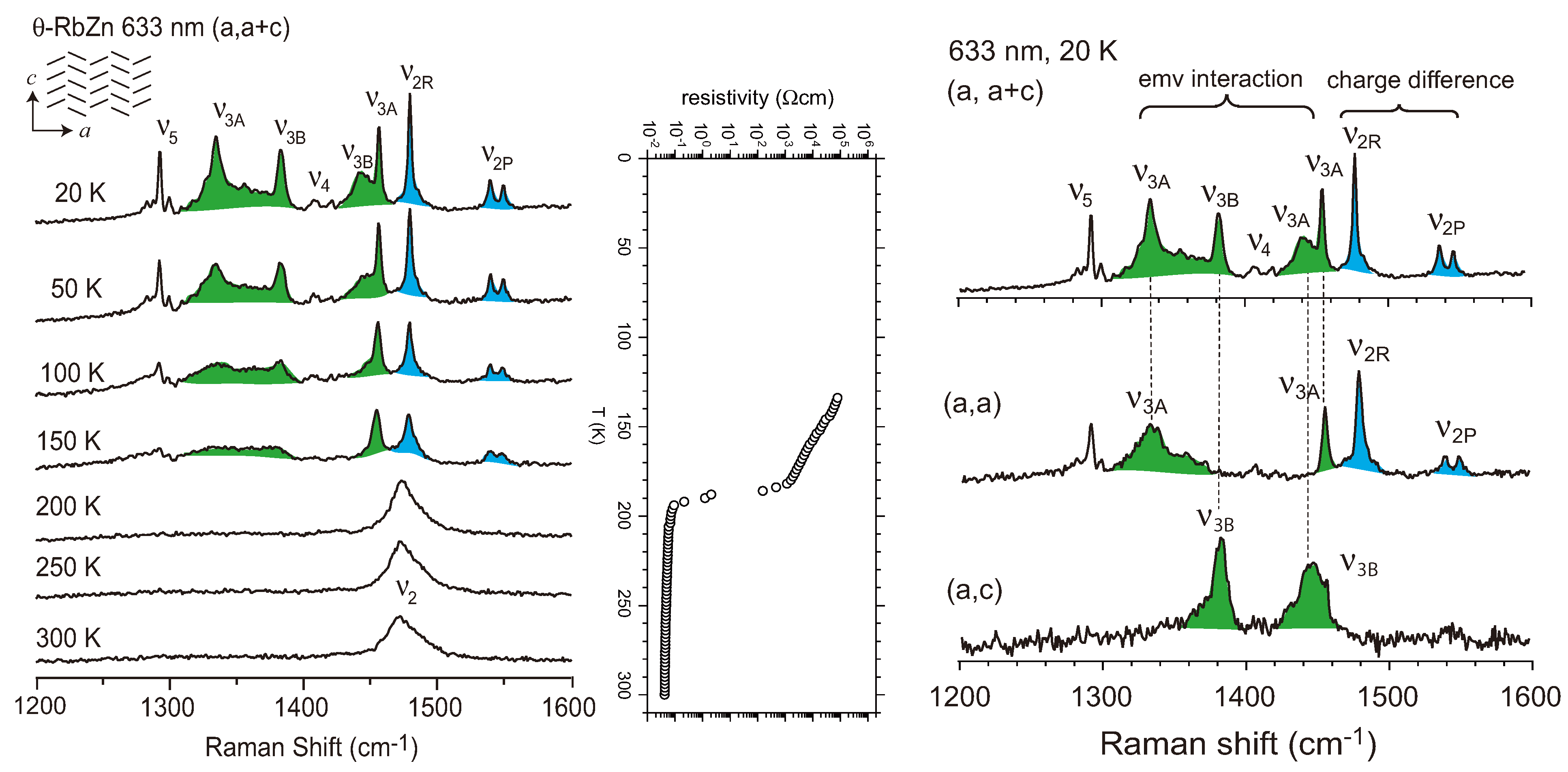
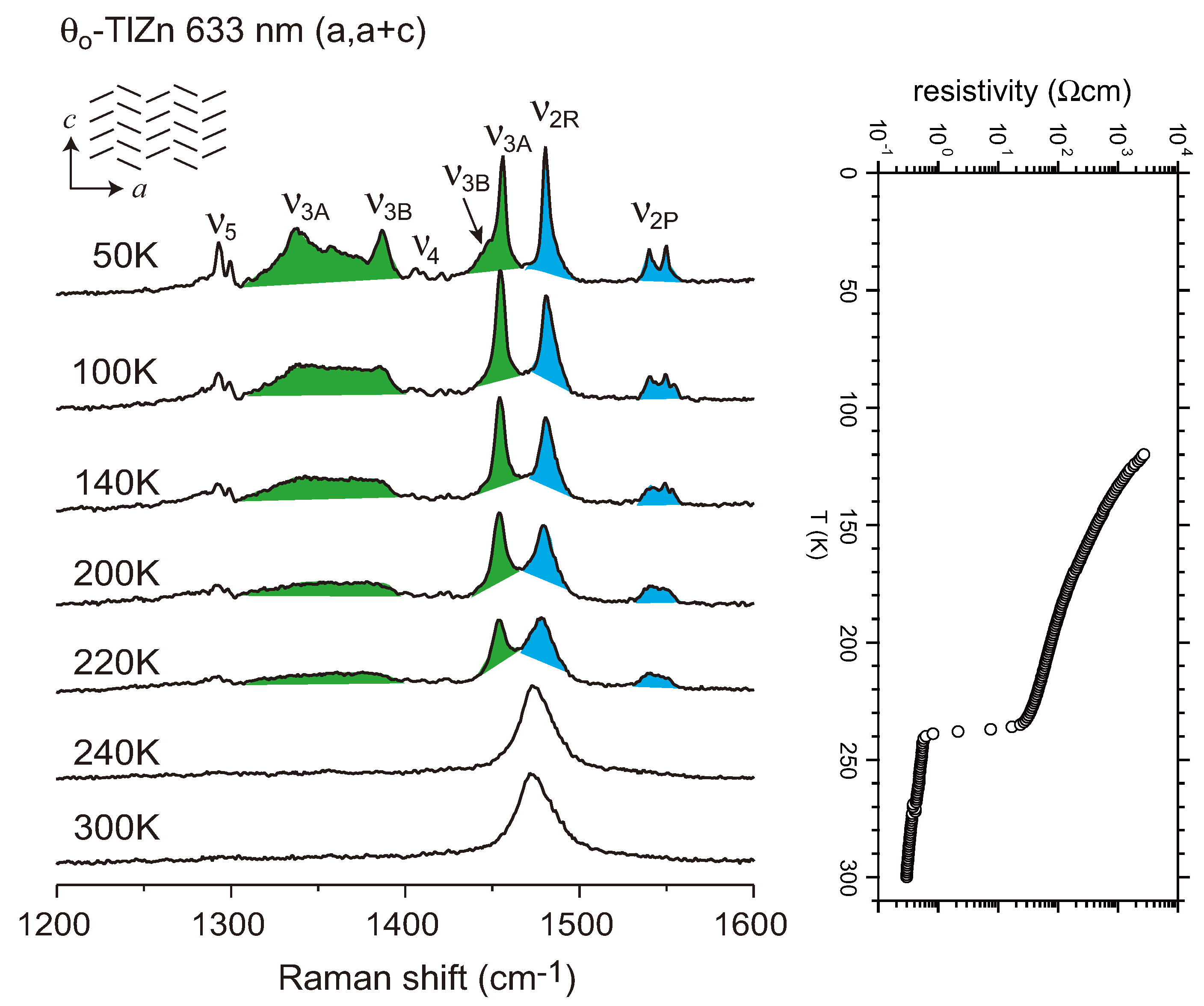
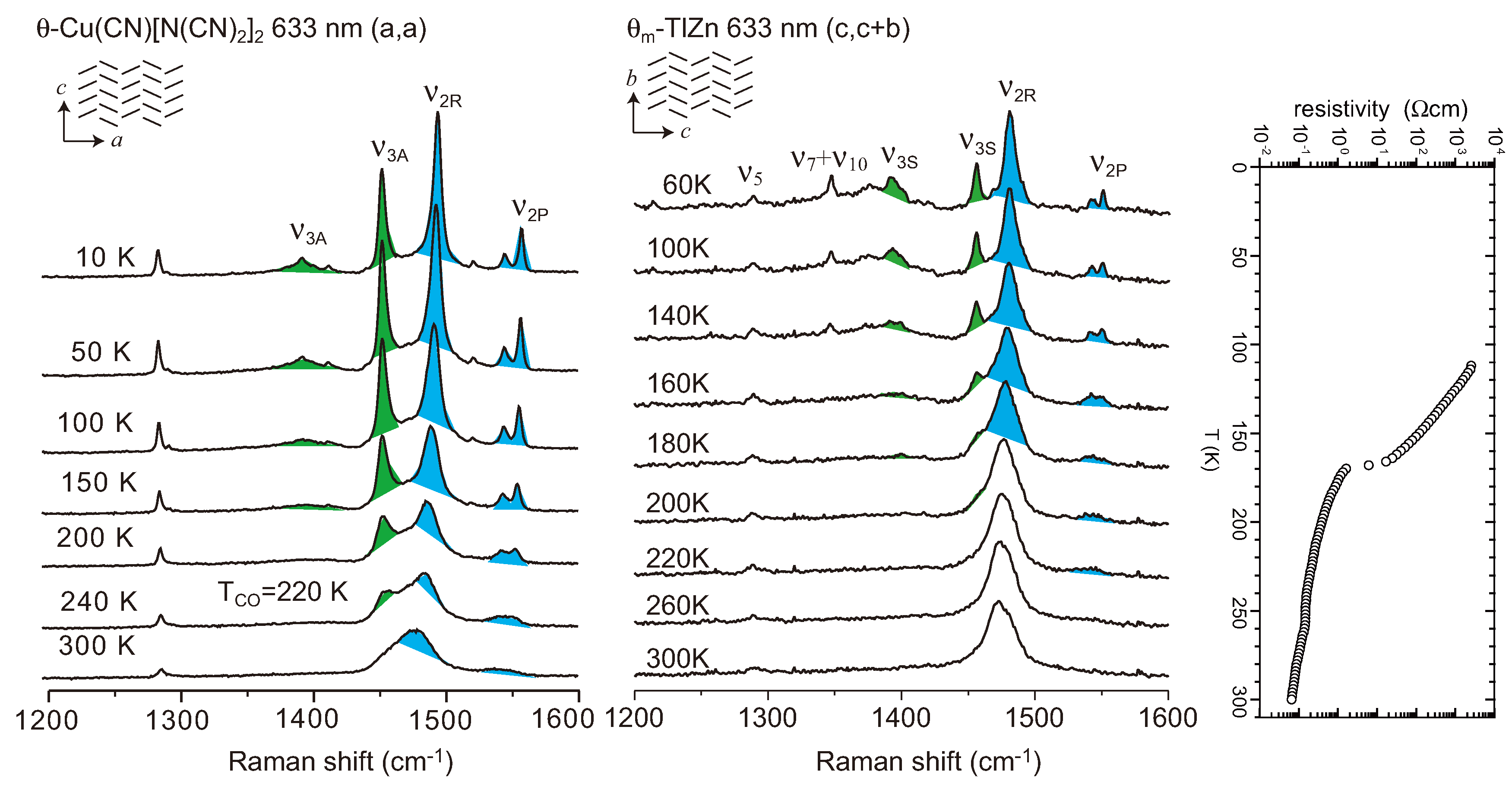
4.2. Metallic Phase of X = RbZn(SCN)4, TlZn(SCN)4, Cu2CN[N(CN)2]2
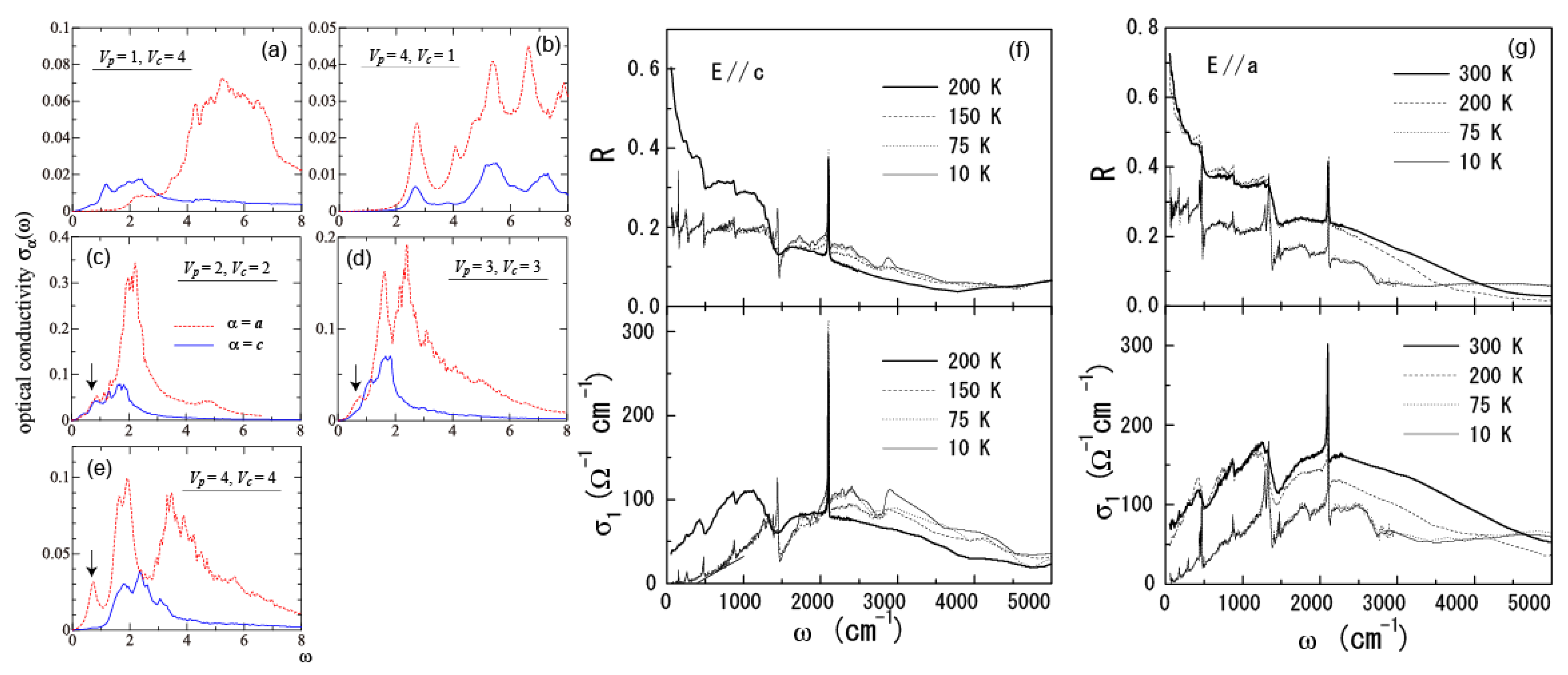
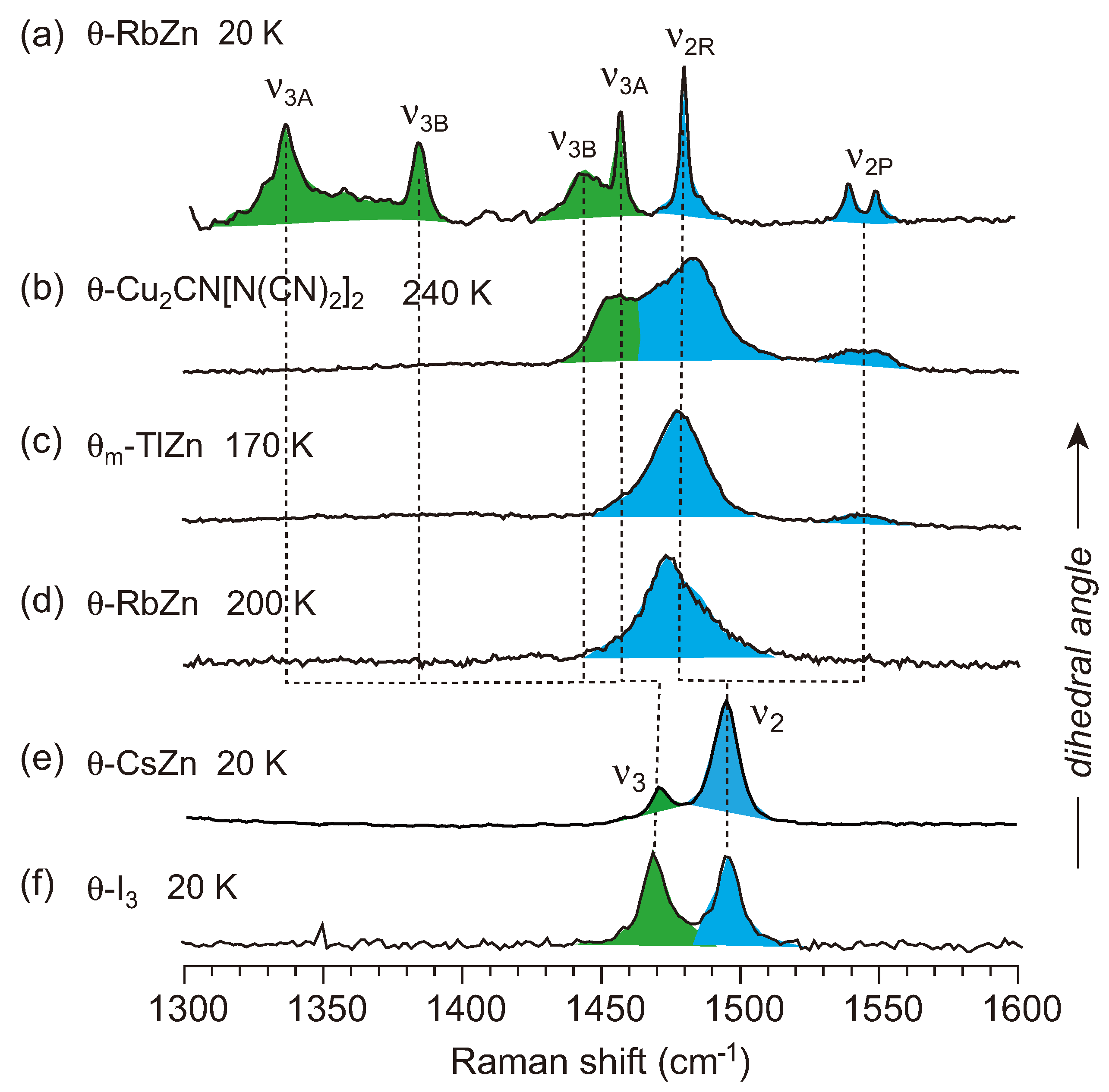
4.3. θ-(BEDT-TTF)2X (X = CsZn(SCN)4, I3)
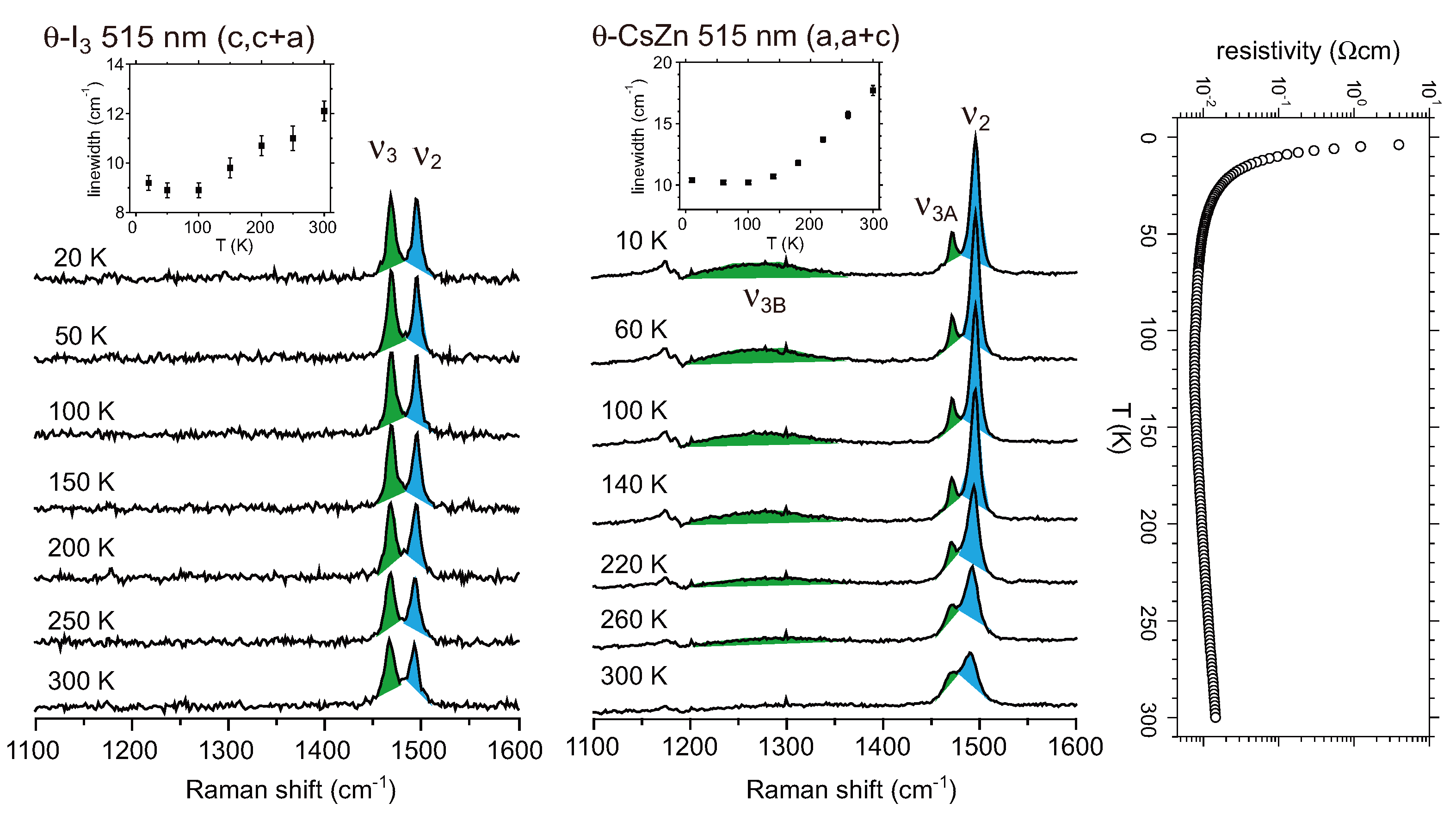
5. α-(BEDT-TTF)2I3 and Related Compounds
 , whereas the horizontal stripe requires P1. Raman spectroscopy was used to examine the selection rule of the charge-sensitive mode and the symmetry reduction from
, whereas the horizontal stripe requires P1. Raman spectroscopy was used to examine the selection rule of the charge-sensitive mode and the symmetry reduction from  to P1 below TMI was claimed [111]. An x-ray diffraction study supported P1, and showed a horizontal stripe structure [128]. Decisive evidence for the breaking of inversion symmetry was given by the experiment of second harmonic generation (SHG) [124]. Recently, Alemany et al., pointed out that the hydrogen bond between the ethylene groups of BEDT-TTF and I3− plays an essential role in the CO transition of α-I3 [129].
to P1 below TMI was claimed [111]. An x-ray diffraction study supported P1, and showed a horizontal stripe structure [128]. Decisive evidence for the breaking of inversion symmetry was given by the experiment of second harmonic generation (SHG) [124]. Recently, Alemany et al., pointed out that the hydrogen bond between the ethylene groups of BEDT-TTF and I3− plays an essential role in the CO transition of α-I3 [129].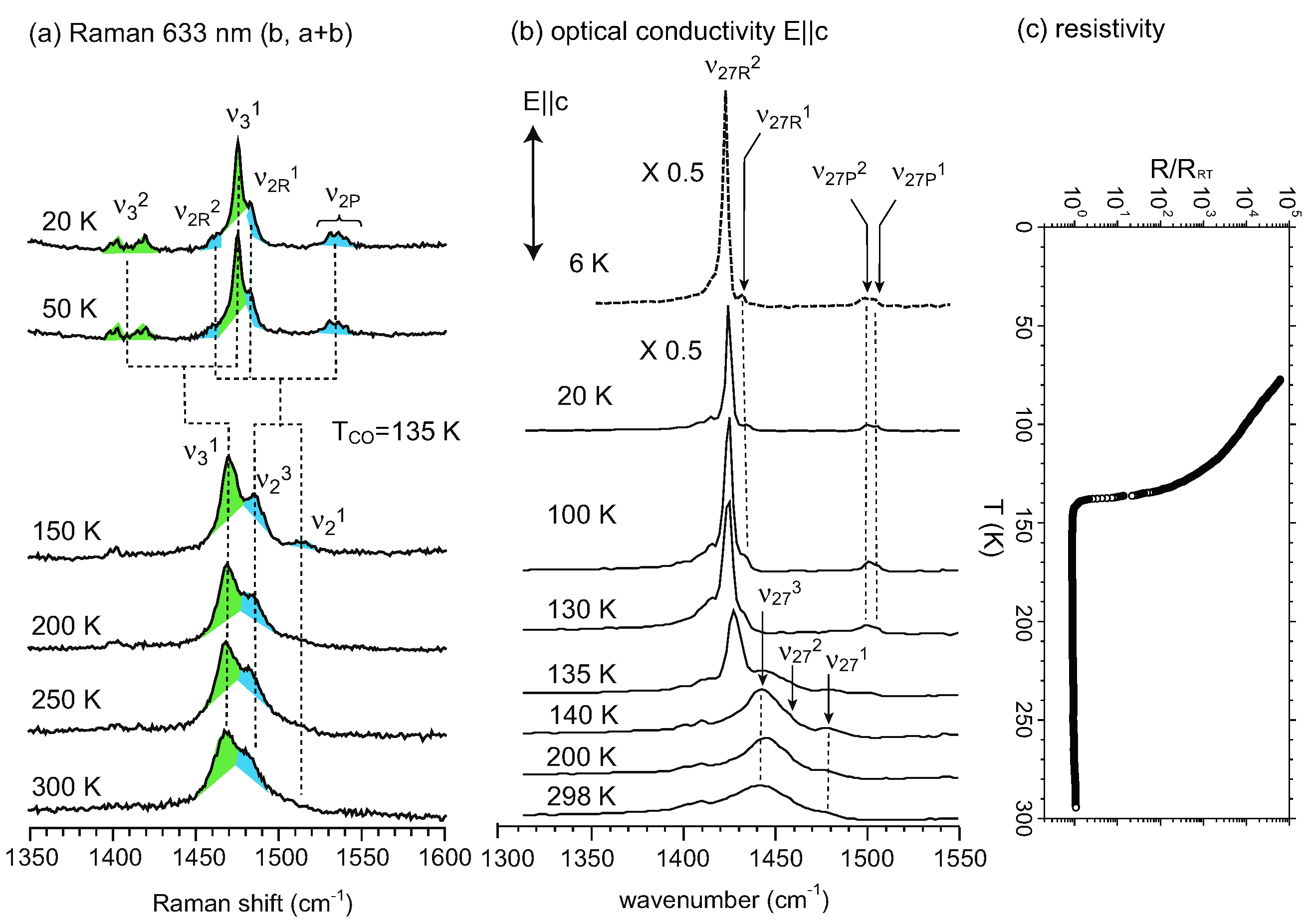
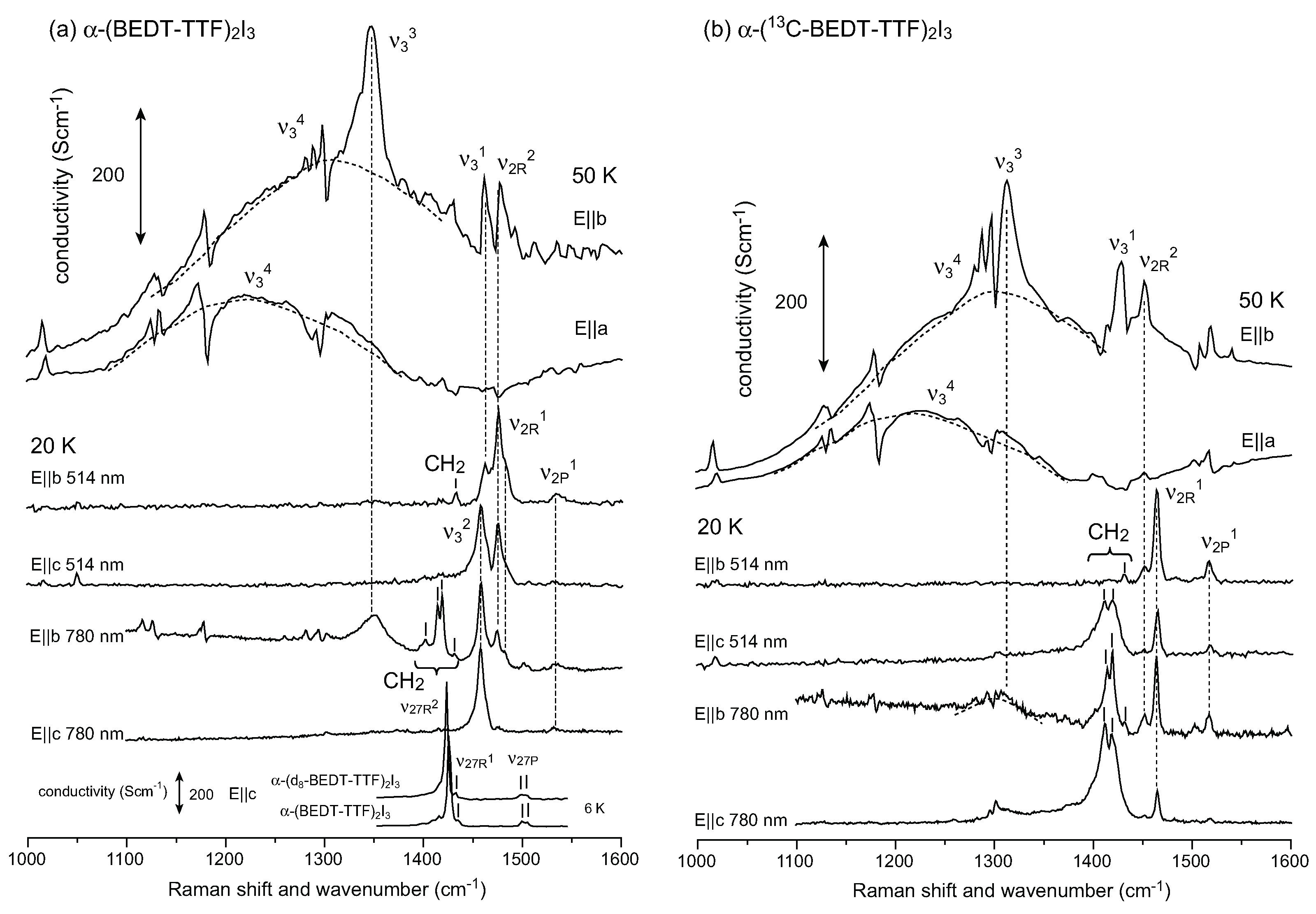
5.1. Charge-Ordered Phase of α-(BEDT-TTF)2I3
| Raman (20 K) | Infrared (50 K) | |||||
|---|---|---|---|---|---|---|
| α-I3 | α-(13C)2I3 | Δν | α-I3 | α-(13C)2I3 | Δν | |
| dip (2ν33) | - | - | - | 2688 | 2628 | 60 |
| ν2P1 | 1536 | 1517 | 19 | (1518?) | - | |
| ν2P2 | - | - | - | - | (1508?) | - |
| ν2R1 | 1483 | 1465 | 18 | - | - | - |
| ν2R2 | 1476 | 1452 | 24 | 1477 | 1454 | 23 |
| ν31 | 1462 | - | - | 1462 | 1431 | 31 |
| ν32 | 1458 | - | - | - | - | - |
| ν33 | 1349 | 1315 | 34 | 1346 | 1315 | 31 |
| ν34 | - | - | - | ~1300 (E|| b) ~1230 (E||a) | ~1300(E|| b) ~1230(E||a) | - |
 | 1431 | - | - | - | - | |
| CH2- | 1420 | - | - | - | - | |
| Bending | 1414 | - | - | - | - | |
| 1402 | - | - | - | - | ||
| ν27P1 | - | - | - | 1506 (E||c) | 1505 (E||c) | - |
| ν27P2 | - | - | - | 1501 (E||c) | 1500 (E||c) | - |
| ν27R1 | - | - | - | 1435 (E||c) | 1432 (E||c) | - |
| ν27R2 | - | - | - | 1425 (E||c) | 1423 (E||c) | - |
 to P1 [128]. Using the space group P1, they determined the molecular geometry of each site, and provided consistent result for the site charge distribution as ρA = 0.82(9), ρB = 0.73(9), ρA’ = 0.29(9), ρC = 0.26(9) at 20 K. Recently, Alemany et al., reported the site charges as ρA = 0.638, ρB = 0.577, ρA′ = 0.438, ρC = 0.359 using a numerical atomic orbital density functional theory (DFT) approach [129]. This CO amplitude ρmax = 0.28 is significantly smaller than the experimentally estimated value of ρmax = 0.56–0.70. The site charge distribution has been estimated from the 13C-NMR shift, which consists of Knight shift and chemical shift [15,134]. The chemical shift reflects the local charges, whereas the Knight shift is proportional to the local spin susceptibility which reflects the density of states at the Fermi level [135]. Therefore, the chemical shift should be analyzed to estimate the site charges. Kawai and Kawamoto conducted a 13C-NMR study using a single side 13C-enriched molecule [135]. To avoid the effect of the Knight shift and ring current within the molecule, they applied a magnetic field nearly parallel to the long axis of the molecule in the non-magnetic state (at 60 K). They determined the chemical shift tensor of the four sites, and estimated the site charge to be ρR~0.74 and ρP~0.19. If we simply apply the relation between the chemical shift and site charge which they present, site charge distribution is estimated as ρA = 0.74, ρB = 0.76, ρA’ = 0.18, and ρC = 0.20. All of these results studied by vibrational spectroscopy, x-ray diffraction, and 13C-NMR approximately consistent with each other.
to P1 [128]. Using the space group P1, they determined the molecular geometry of each site, and provided consistent result for the site charge distribution as ρA = 0.82(9), ρB = 0.73(9), ρA’ = 0.29(9), ρC = 0.26(9) at 20 K. Recently, Alemany et al., reported the site charges as ρA = 0.638, ρB = 0.577, ρA′ = 0.438, ρC = 0.359 using a numerical atomic orbital density functional theory (DFT) approach [129]. This CO amplitude ρmax = 0.28 is significantly smaller than the experimentally estimated value of ρmax = 0.56–0.70. The site charge distribution has been estimated from the 13C-NMR shift, which consists of Knight shift and chemical shift [15,134]. The chemical shift reflects the local charges, whereas the Knight shift is proportional to the local spin susceptibility which reflects the density of states at the Fermi level [135]. Therefore, the chemical shift should be analyzed to estimate the site charges. Kawai and Kawamoto conducted a 13C-NMR study using a single side 13C-enriched molecule [135]. To avoid the effect of the Knight shift and ring current within the molecule, they applied a magnetic field nearly parallel to the long axis of the molecule in the non-magnetic state (at 60 K). They determined the chemical shift tensor of the four sites, and estimated the site charge to be ρR~0.74 and ρP~0.19. If we simply apply the relation between the chemical shift and site charge which they present, site charge distribution is estimated as ρA = 0.74, ρB = 0.76, ρA’ = 0.18, and ρC = 0.20. All of these results studied by vibrational spectroscopy, x-ray diffraction, and 13C-NMR approximately consistent with each other.5.2. Metallic Phase of α-(BEDT-TTF)2I3 and Isostructural Metallic Compounds
5.2.1. Assignment in Metallic Phase
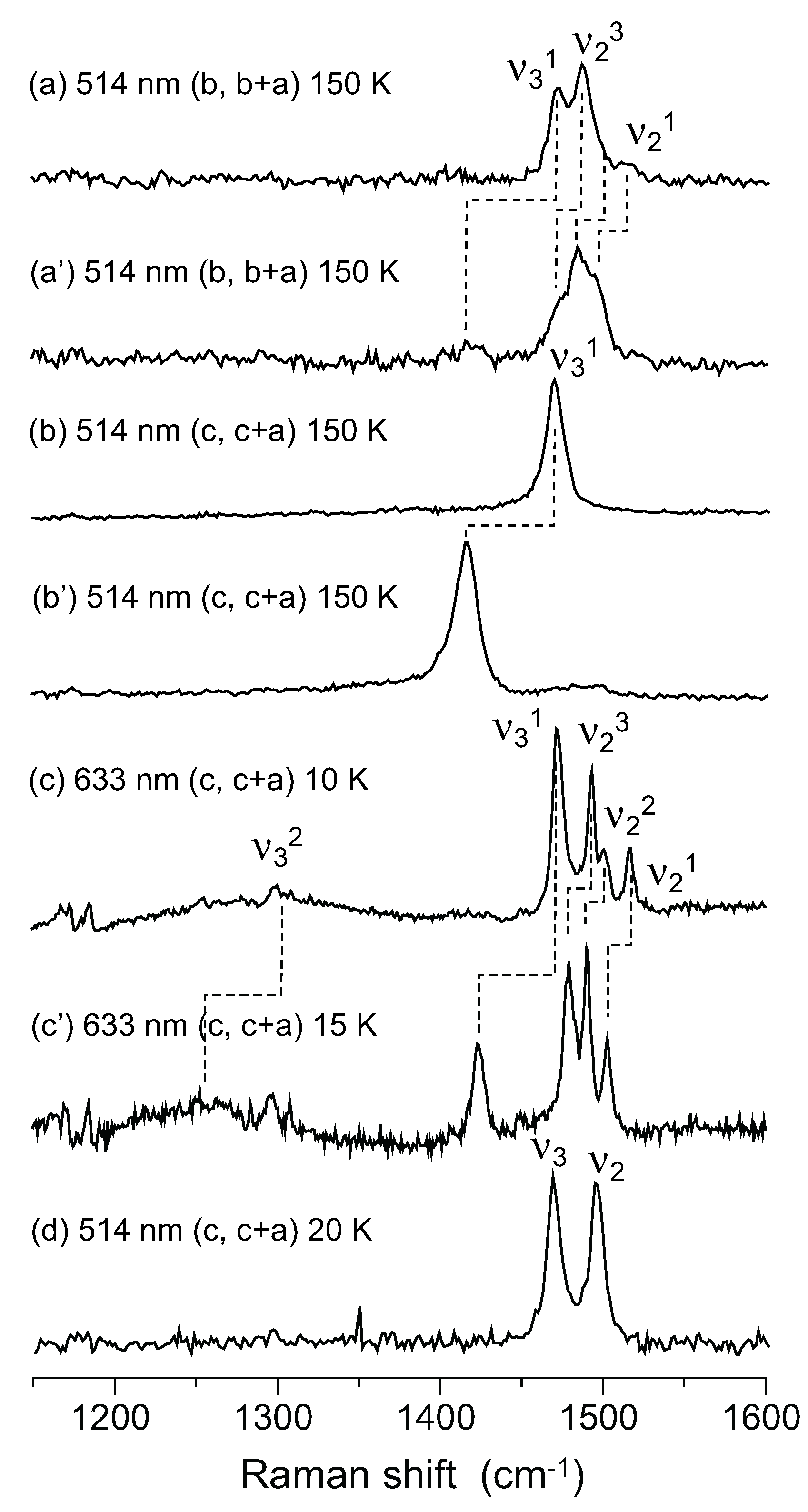
| α-(12C-ET)2I3 | α-(13C-ET)2I3 | α-(12C-ET)2 NH4Hg(SCN)4 | α-(13C-ET)2 NH4Hg(SCN)4 | θ-(ET)2I3 | |||
|---|---|---|---|---|---|---|---|
| Raman (150 K) | Raman (150 K) | Isotope shift ν12-ν13 | Raman (10 K) | Raman (15 K) | Isotopeshift ν12-ν13 | Raman (20 K) | |
| ν21 | 1516 | 1496 | ~20 | 1515 | 1503 | 13 | |
| ν22 | - | ~1484 | - | 1500 | 1490 | 10 | 1496 |
| ν23 | 1487 | 1470 | 17 | 1492 | 1479 | 14 | |
| ν31 | 1471 | ~1415 | ~56 | 1471 | 1423 | 48 | |
| ν32 | - | - | - | ~1300 | ~1250 | ~50 | 1469 |
5.2.2. Fluctuation of Charge Order in Metallic Phase
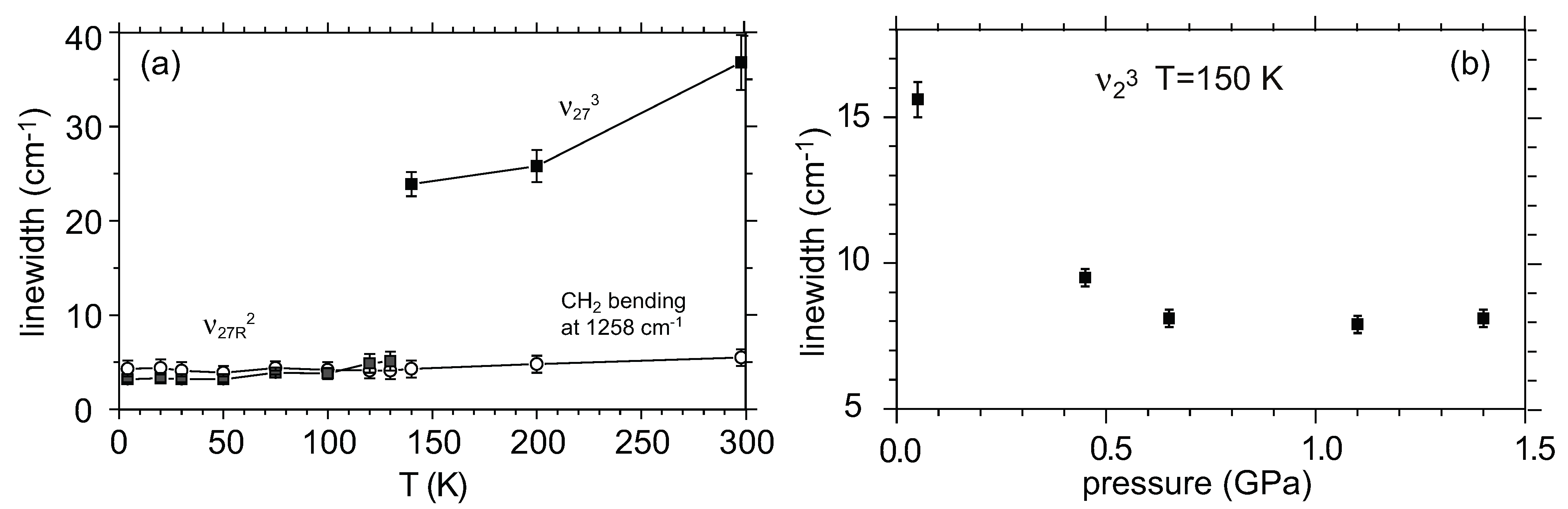
5.3. Non-Uniform Site-Charge Distribution in Metallic Phase
5.3.1. Relation between Frequency and Site Charge Near ρ = 0.5
 (ρ~0.5) is proposed, using ν2(0) = 1570 cm−1 for the calculated frequency of the flat neutral BEDT-TTF molecule, [46] ν2(0.5) = 1494 cm−1, 1494 cm−1, 1495 cm−1 respectively for β′-(BEDT-TTF)2ICl2, κ-(BEDT-TTF)2Cu2(CN)3, and κ-(BEDT-TTF)2Cu[N(CN)2]Cl at room temperature, and ν2(1) = 1447 cm−1 for (BEDT-TTF)ClO4 and (BEDT-TTF)AuBr2Cl2 at room temperature [153]. All of the compounds with ρ = 0.5 shows a frequency upshift by ~6 cm−1 on cooling from room temperature to 10 K due to hardening of the crystal lattice. The frequency shift due to lattice expansion is described by the equation,
(ρ~0.5) is proposed, using ν2(0) = 1570 cm−1 for the calculated frequency of the flat neutral BEDT-TTF molecule, [46] ν2(0.5) = 1494 cm−1, 1494 cm−1, 1495 cm−1 respectively for β′-(BEDT-TTF)2ICl2, κ-(BEDT-TTF)2Cu2(CN)3, and κ-(BEDT-TTF)2Cu[N(CN)2]Cl at room temperature, and ν2(1) = 1447 cm−1 for (BEDT-TTF)ClO4 and (BEDT-TTF)AuBr2Cl2 at room temperature [153]. All of the compounds with ρ = 0.5 shows a frequency upshift by ~6 cm−1 on cooling from room temperature to 10 K due to hardening of the crystal lattice. The frequency shift due to lattice expansion is described by the equation,  , where γ is the optical Gruneisen parameter and β(T) is the coefficient of volume thermal expansion. Therefore, this temperature dependence is given by the following equation,
, where γ is the optical Gruneisen parameter and β(T) is the coefficient of volume thermal expansion. Therefore, this temperature dependence is given by the following equation,  , if β(T) is approximated by the equation, β(T) = β0 + β1T [154]. The examples of for the ν2 modes of κ-Cu[N(CN)2]Cl and β′-ICl2 are shown in Figure 22. Although the function form of β(T) is too crude to express actual one, the frequency shift is well reproduced. If we assume that ν2(0) and ν2(1) also show the same temperature dependence, the quadratic expression can be corrected as
, if β(T) is approximated by the equation, β(T) = β0 + β1T [154]. The examples of for the ν2 modes of κ-Cu[N(CN)2]Cl and β′-ICl2 are shown in Figure 22. Although the function form of β(T) is too crude to express actual one, the frequency shift is well reproduced. If we assume that ν2(0) and ν2(1) also show the same temperature dependence, the quadratic expression can be corrected as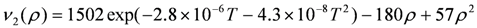
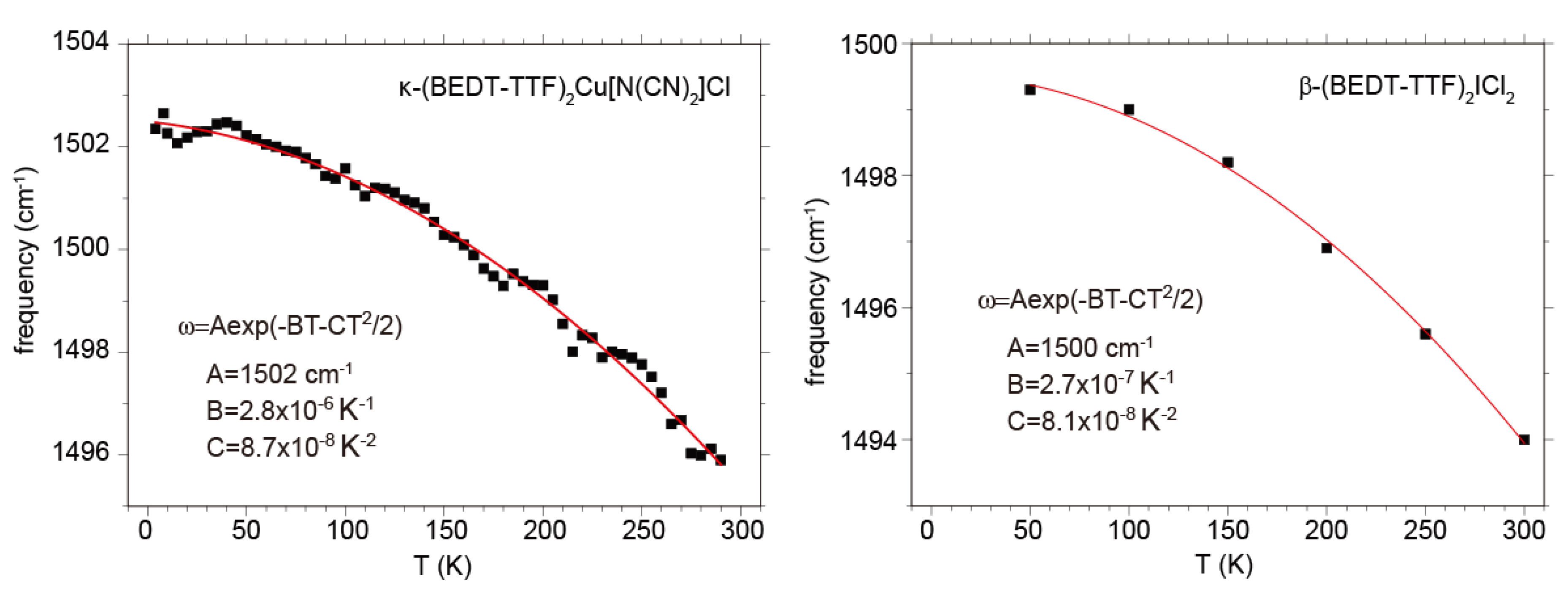
5.3.2. Site Charge Distribution in Metallic Phase at Ambient Pressure
| Raman (150 K) | Infrared [130] (140 K) | X-ray [128] (150 K) | MF [157] (150 K) | ab initio [158] | DFT [129] | ||
|---|---|---|---|---|---|---|---|
| (298 K) | (8 K) | (RT) | |||||
| ρA = ρA′ | (0.52(3)) | ~0.6 | 0.59(3) | 0.52 | 0.53 | 0.54 | 0.521 |
| ρB | 0.60(3) | 0.68 | 0.67(2) | 0.71 | 0.55 | 0.57 | 0.546 |
| ρC | 0.37(3) | 0.44 | 0.42(2) | 0.25 | 0.40 | 0.37 | 0.382 |
| α-NH4Hg | α-KHg | α-RbHg | α-TlHg | ||||
|---|---|---|---|---|---|---|---|
| Raman (10 K) | Infrared [130] (150 K) | MF (10 K) | Raman (10 K) | ab initio [147] (104 K) | Raman (10 K) | Raman (10 K) | |
| ρA = ρA’ | 0.39(3) | 0.40 | 0.51 | 0.42(3) | 0.520 | 0.42(3) | 0.42(3) |
| ρB |  |  | 0.47 |  | 0.424 |  |  |
| ρC | 0.50 | 0.527 | |||||
5.3.3. Site-Charge Distribution under Hydrostatic Pressure
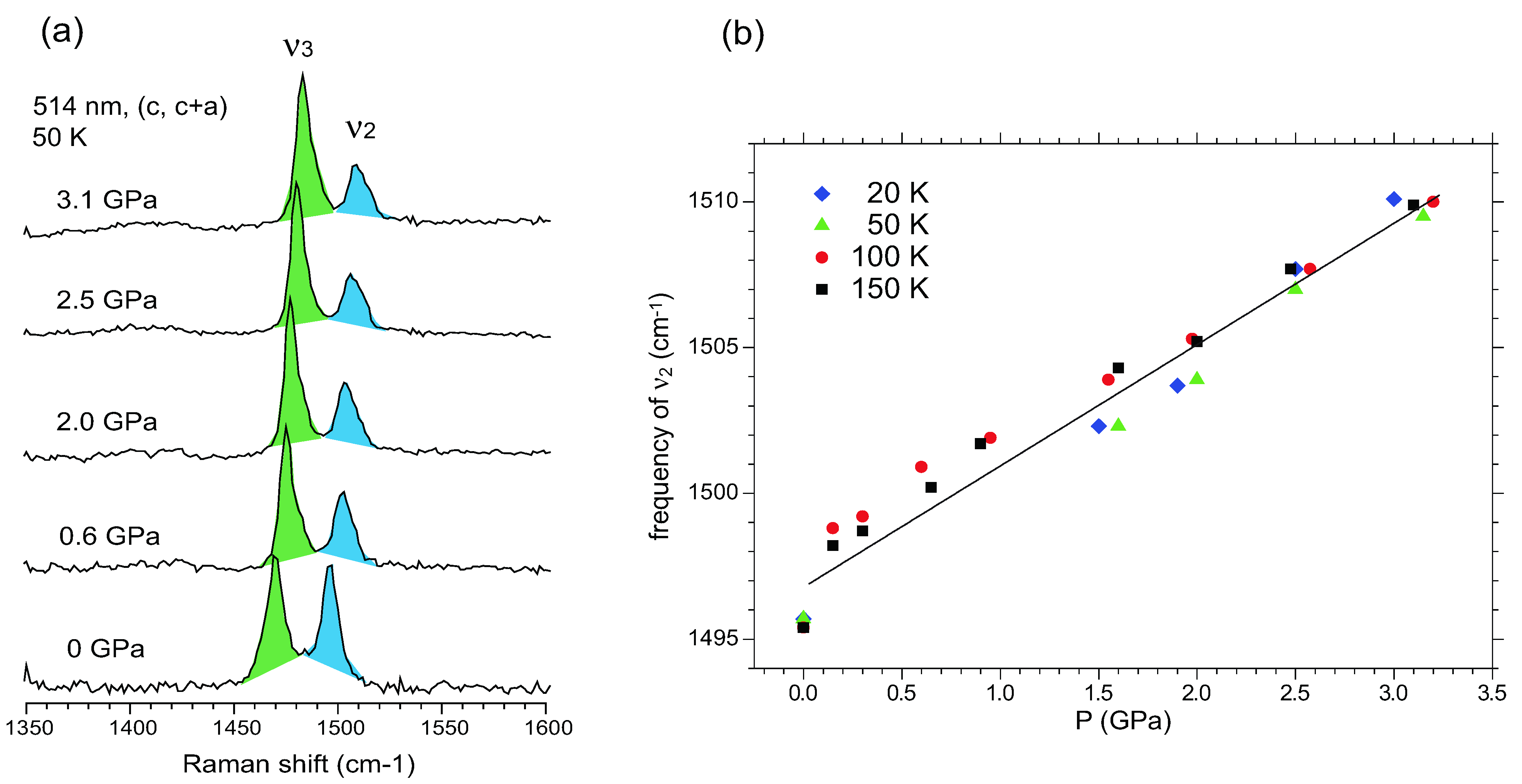
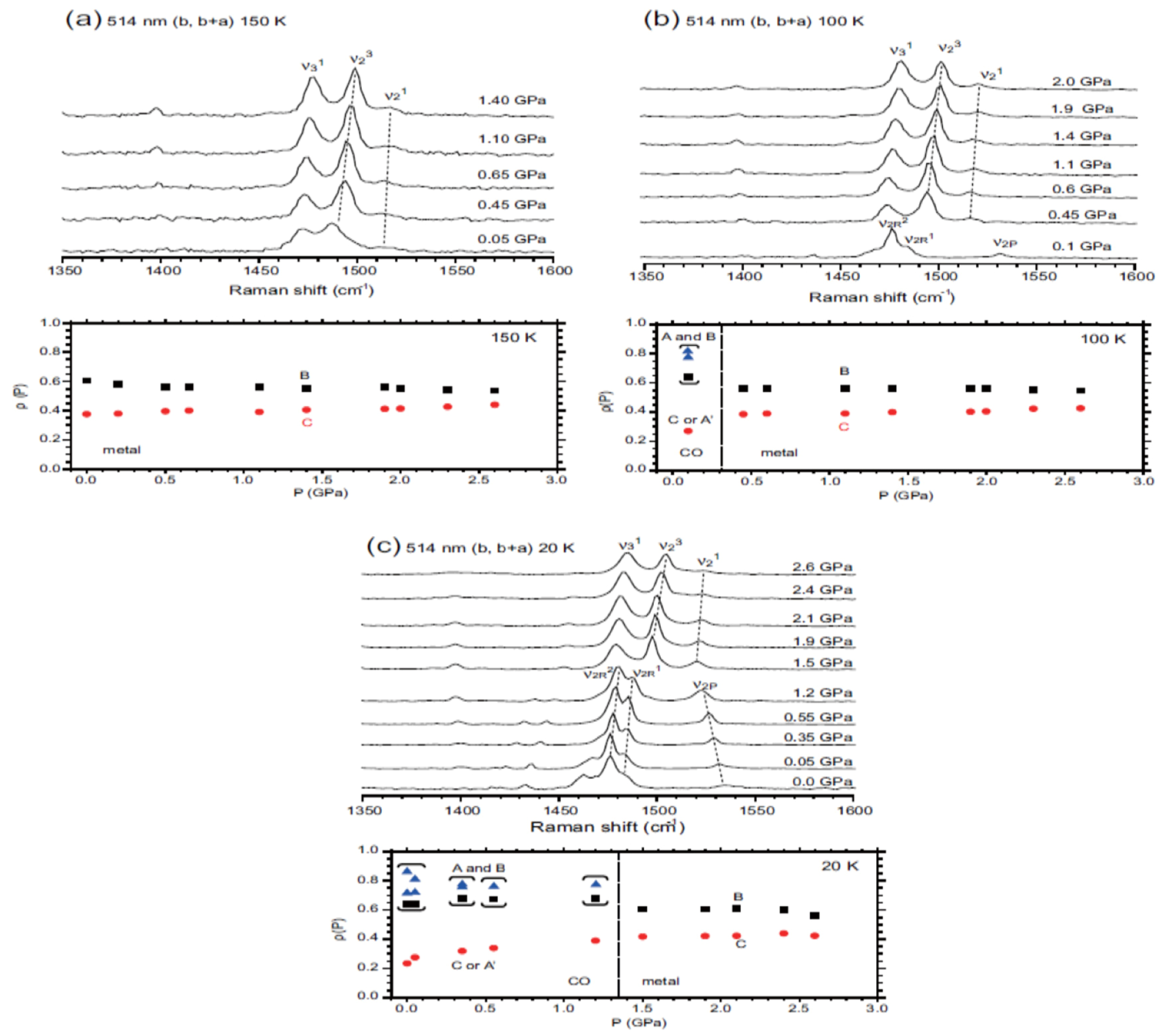
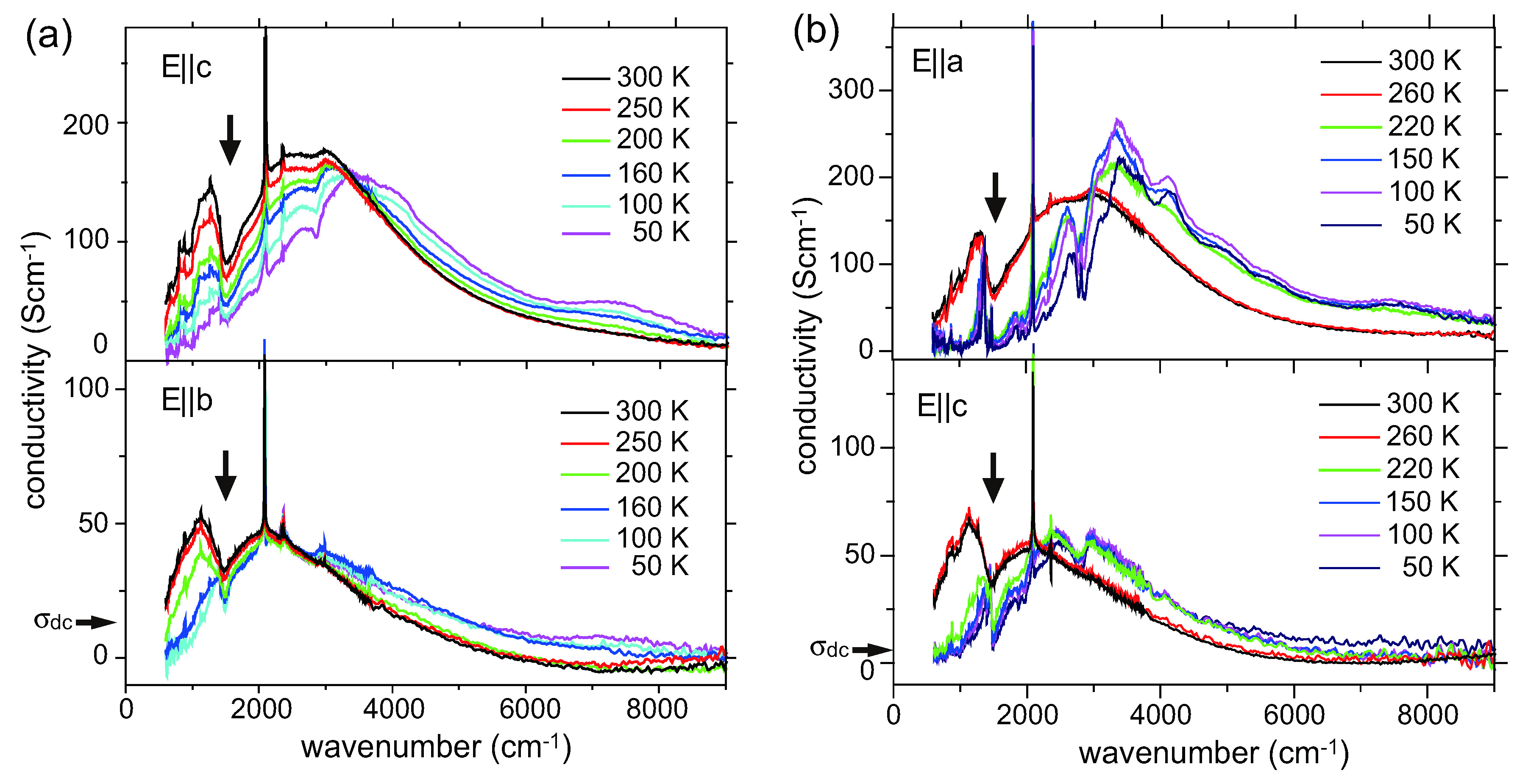
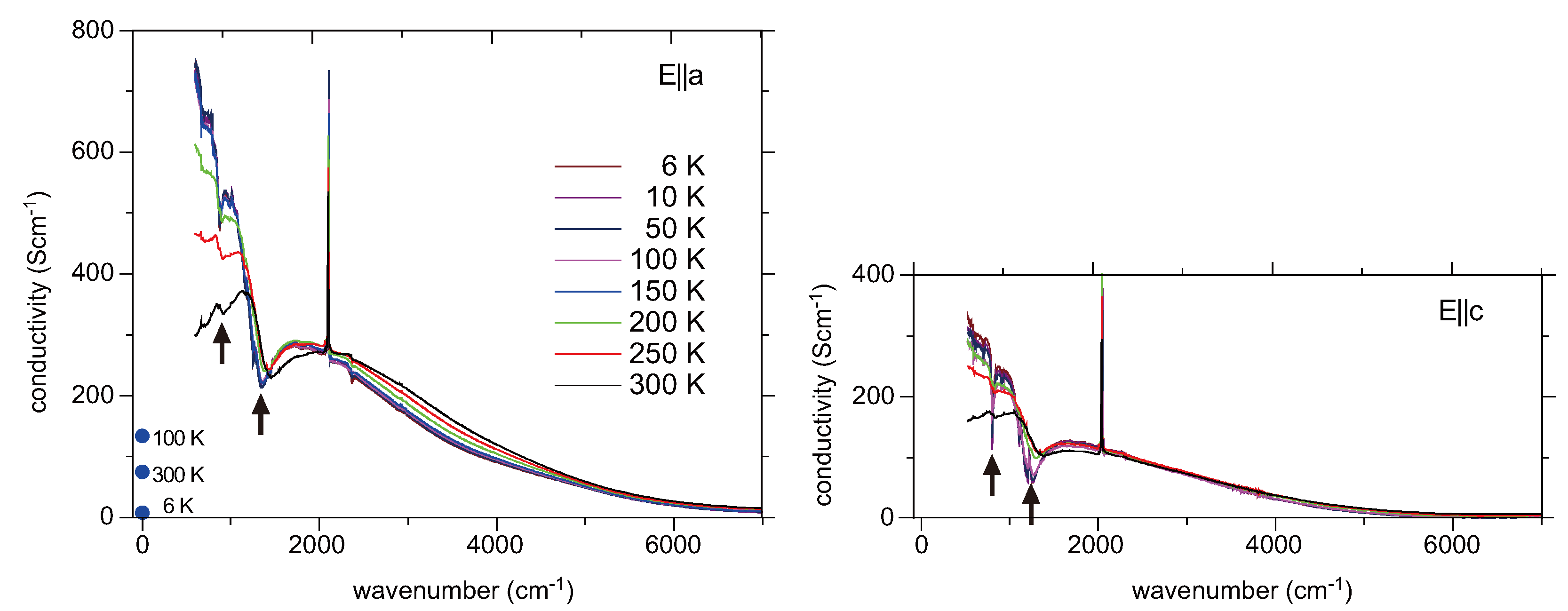
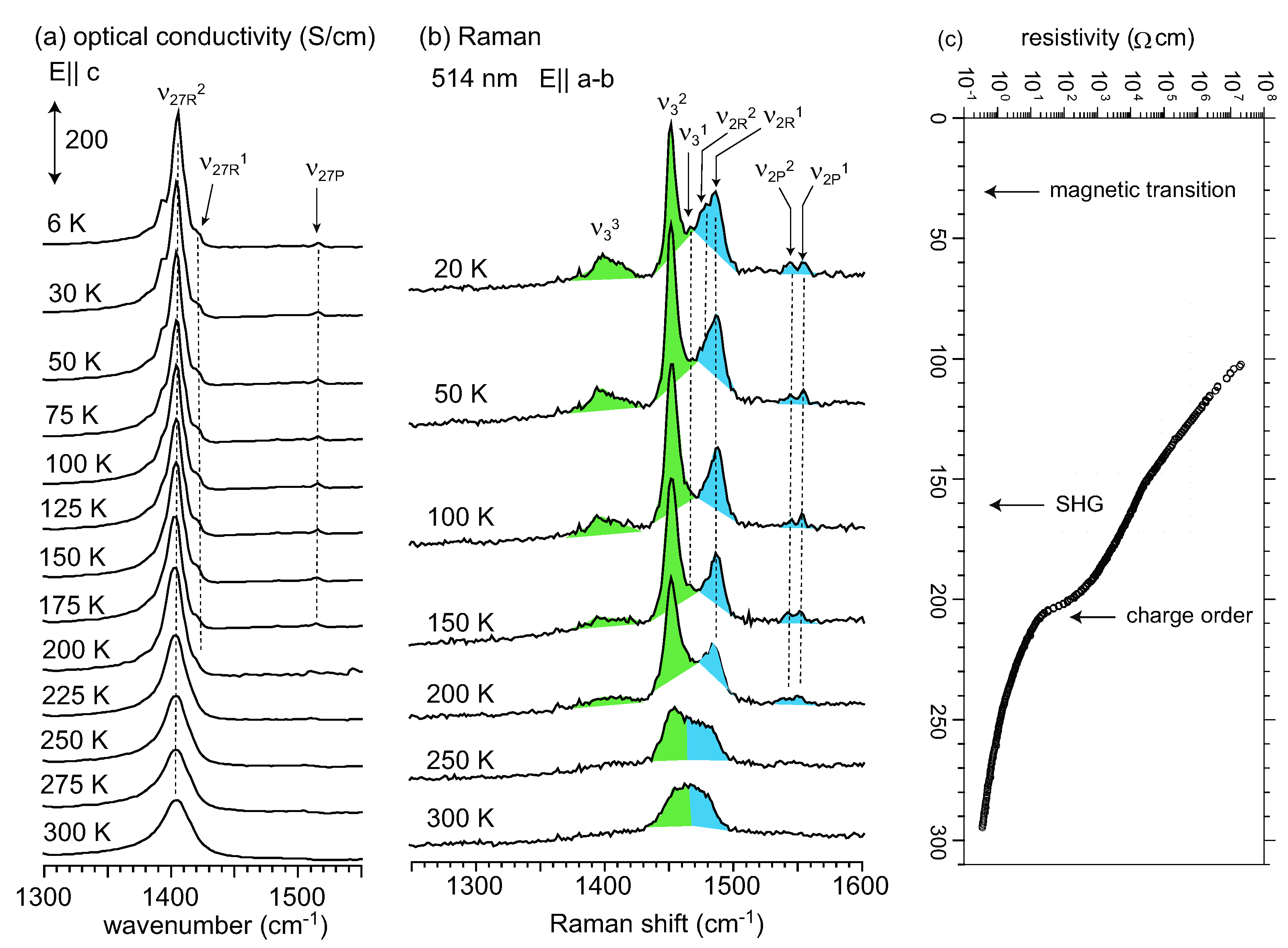
5.4. Optical Conductivity of α-(BEDT-TTF)2I3

5.5. α′-(BEDT-TTF)2IBr2
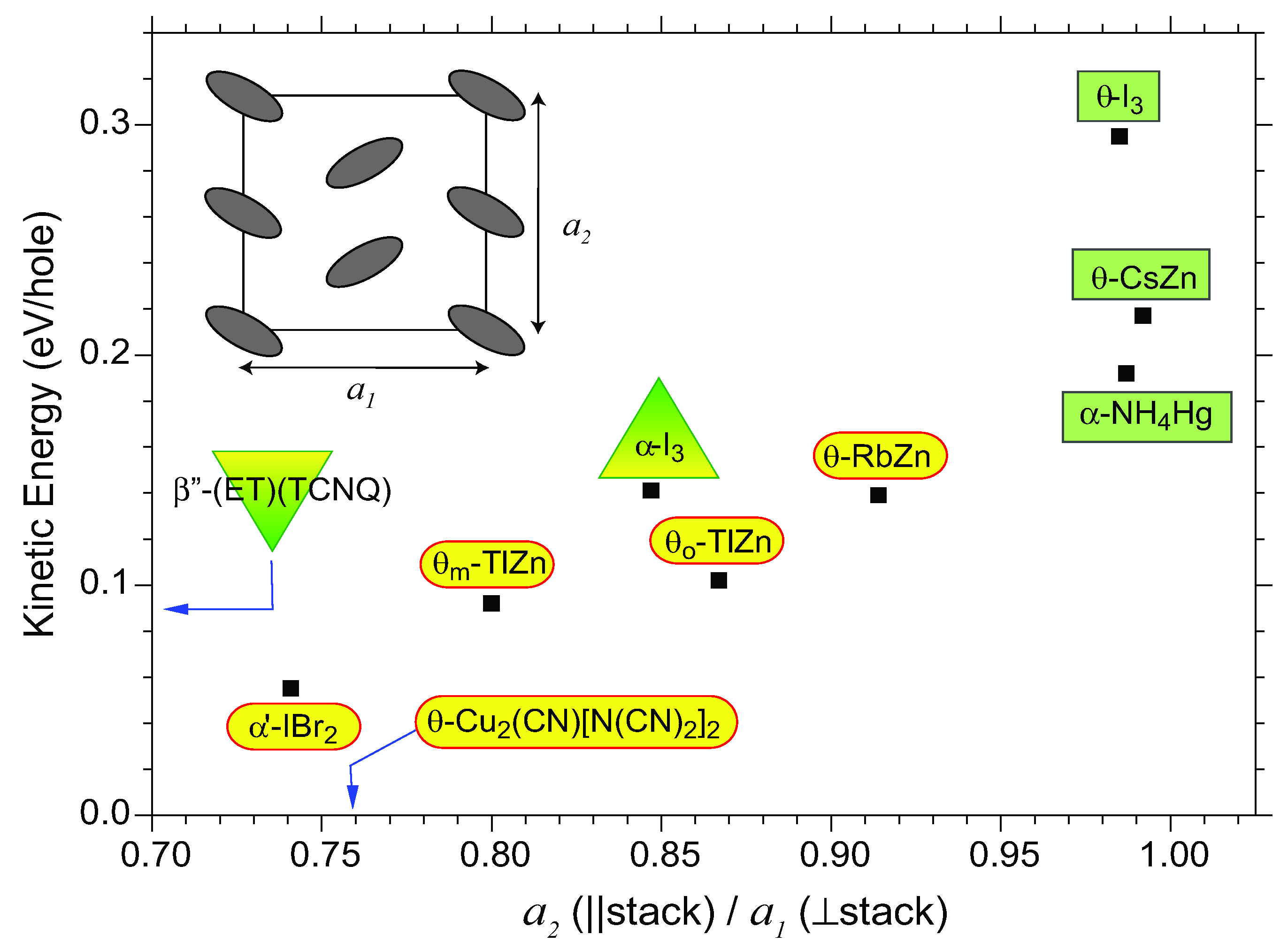
6. Summary
Acknowledgments
References and Notes
- Girlando, A.; Bozio, R.; Pecile, C. Infrared and Raman spectroscopic evidence of ground state charge densities at TCNQ sites in crystalline Cs2TCNQ3. Chem. Phys. Lett. 1974, 25, 409–412. [Google Scholar]
- Bozio, R.; Girlando, A.; Pecile, C. Vibrational analysis of spectra of quinoid molecular ions. J. Chem. Soc. Faraday Trans. 1975, 71, 1237–1254. [Google Scholar] [CrossRef]
- Matsuzaki, S.; Kuwata, R.; Toyoda, K. Raman spectra of conducting TCNQ salts; estimation of the degree of charge transfer from vibrational frequencies. Solid State Commun. 1980, 33, 403–405. [Google Scholar]
- Chappell, J.S.; Bloch, A.N.; Bryden, W.A.; Maxfield, M.; Poehler, T.O.; Cowan, D.O. Degree of charge transfer in organic conductors by infrared absorption spectroscopy. J. Am. Chem. Soc. 1980, 103, 2442–2443. [Google Scholar]
- Kagoshima, S.; Ishiguro, T.; Anzai, H. X-ray scattering study of phonon anomalies and superstructures in TTF-TCNQ. J. Phys. Soc. Jpn. 1976, 41, 2061–2071. [Google Scholar] [CrossRef]
- Kondo, J.; Yamaji, K. Density correlation of classical 1-d electron gas with reference to the 4κF anomaly in TTF-TCNQ. J. Phys. Soc. Jpn. 1977, 43, 424–436. [Google Scholar] [CrossRef]
- Torrance, J.B. Spin waves, scattering at 4κF, and spin-Peierls fluctuations in organic metal: Tetrathiafulvalene-Tetracyanoquinodimethane (TTF-TCNQ). Phys. Rev. 1978, 17, 3099–3103. [Google Scholar] [CrossRef]
- Hubbard, J. Generalized wigner lattices in one dimension and some applications to tetracyanoquinodimethane (TCNQ) salts. Phys. Rev. 1978, 17, 494–505. [Google Scholar] [CrossRef]
- Hiraki, K.; Kanoda, K. Wigner crystal type of charge ordring in an organic conductor with a quarter-filled band: (DI-DCNQI)2Ag. Phys. Rev. Lett. 1998, 80, 4737–4740. [Google Scholar] [CrossRef]
- Seo, H.; Fukuyama, H. Antiferromagntic phases of one-dimensional quarter-filled organic conductors. J. Phys. Soc. Jpn. 1997, 66, 1249–1252. [Google Scholar] [CrossRef]
- Chow, D.S.; Zamborszky, F.; Alavi, B.; Tantillo, D.J.; Baur, A.; Merlic, C.A.; Brown, S.E. Charge ordering in the TMTTF family of molecular conductors. Phys. Rev. Lett. 2000, 85, 1698–1701. [Google Scholar] [CrossRef]
- Moldenhauer, J.; Horn, C.; Pokhondnia, K.I.; Schweitzer, D.; Heinen, I.; Keller, H.J. FT-IR absorption spectroscopy of BEDT-TTF radical salts: Charge transfer and donor-anion interaction. Synth. Metal. 1993, 60, 31–38. [Google Scholar] [CrossRef]
- Kino, H.; Fukuyama, H. On the phase transition of α-(ET)2I3. J. Phys. Soc. Jpn. 1995, 64, 1877–1880. [Google Scholar] [CrossRef]
- Takano, Y.; Hiraki, K.; Yamamoto, H.M.; Nakamura, T.; Takahashi, T. Charge disproportionation in the organic conductor, α-(BEDT-TTF)2I3. J. Phys. Chem. Solid 2001, 62, 393–395. [Google Scholar] [CrossRef]
- Miyagawa, K.; Kawamoto, A.; Kanoda, K. Charge ordering in a quasi-two-dimensional organic conductor. Phys. Rev. 2000, 62, R7679–R7682. [Google Scholar] [CrossRef]
- Seo, H. Charge ordering in organic ET compounds. J. Phys. Soc. Jpn. 2000, 69, 805–820. [Google Scholar] [CrossRef]
- McKenzie, R.H.; Merino, J.; Marston, J.B.; Sushkov, O.P. Charge ordering and antiferromagnetic exchange in layered molecular crystals of the θ-type. Phys. Rev. 2001, 64, 085109:1–085109:11. [Google Scholar]
- Kuroki, K. Theoretical aspects of charge correlations in θ-(BEDT-TTF)2X. Sci. Technol. Adv. Mater. 2009, 10, 024312:1–024312:11. [Google Scholar]
- Mazumdar, S.; Clay, R.T.; Campbell, D.K. Bond-order and charge-density waves in the isotropic interacting two-dimensional quarter-filled band and the insulating state proximate to organic superconductivity. Phys. Rev. 2000, 62, 13400–13425. [Google Scholar] [CrossRef]
- Clay, R.T.; Mazumdar, S.; Campbell, D.K. Charge ordering in θ-(BEDT-TTF)2X materials. J. Phys. Soc. Jpn. 2002, 71, 1816–1819. [Google Scholar] [CrossRef]
- Dayal, S.; Clay, R.T.; Li, H.; Mazumdar, S. Paired-electron crystal: Order from frustration in the quarter-filled band. Phys. Rev. 2011, 83, 245106:1–245106:12. [Google Scholar]
- Merino, J.; McKenzie, R.H. Superconductivity mediated by charge fluctuations in layered molecular crystals. Phys. Rev. Lett. 2001, 87, 237002:1–237002:4. [Google Scholar]
- Cano-Cortes, L.; Merino, J.; Fratini, S. Quantum critical behavior of electrons at the edge of charge order. Phys. Rev. Lett. 2010, 105, 036405:1–036405:4. [Google Scholar]
- Takahashi, T.; Nogami, Y.; Yakushi, K. Charge ordering in organic conductors. J. Phys. Soc. Jpn. 2006, 75, 051008:1–051008:17. [Google Scholar]
- Seo, H.; Merino, J.; Yoshioka, H.; Ogata, M. Theoretical aspects of charge ordering in molecular conductors. J. Phys. Soc. Jpn. 2006, 75, 051009:1–051009:20. [Google Scholar]
- Dressel, M.; Drichko, N. Optical properties of two-dimensional organic conductors: Signatures of charge ordering and correlation effects. Chem. Rev. 2004, 104, 5689–5715. [Google Scholar] [CrossRef]
- Dressel, M. Quantum criticality in organic conductors? Fermi liquid versus non-Fermi-liquid behavior. J. Phys. Condens. Matter 2011, 23, 293201:1–293201:21. [Google Scholar]
- Nad, F.; Monceau, P. Dielectric response of the charge ordered state in the quasi-one-dimensional conductors. J. Phys. Soc. Jpn. 2006, 75, 051005:1–051005:12. [Google Scholar]
- Dressel, M.; Drichko, N.; Schlueter, J.; Merino, J. Proximity of the layered organic conductors α-(BEDT-TTF)2MHg(SCN)4 (M = K, NH4) to a charge-ordering transition. Phys. Rev. Lett. 2003, 90, 167002:1–167002:4. [Google Scholar]
- Drichko, N.; Dressel, M.; Kuntscher, C.A.; Pashkin, A.; Greco, A.; Merino, J.; Schlueter, J. Electronic properties of correlated metals in the vicinity of a charge-order transition: Optical spectroscopy of α-(BEDT-TTF)2MHg(SCN)4 (M = NH4, Rb, Tl). Phys. Rev. 2006, 74, 235121:1–235121:11. [Google Scholar]
- Kaiser, S.; Dressel, M.; Sun, Y.; Greco, A.; Schlueter, J.A.; Gard, G.L.; Drichko, N. Bandwidth tuning triggers interplay of charge order and superconductivity in two-dimensional organic materials. Phys. Rev. Lett. 2010, 105, 206402:1–206402:4. [Google Scholar]
- Tanaka, M.; Yamamoto, K.; Uruichi, M.; Yamamoto, T.; Yakushi, K.; Kimura, S.; Mori, H. Infrared and Raman study of the charge-ordered state in the vicinity of the superconducting state in the organic conductor β-(meso-DMBEDT-TTF)2PF6. J. Phys. Soc. Jpn. 2008, 77, 024714:1–024714:8. [Google Scholar]
- Morinaka, N.; Takahashi, K.; Chiba, R.; Yoshikane, F.; Niizeki, S.; Tanaka, M.; Yakushi, K.; Koeda, M.; Hedo, K.; Fujiwara, T.; et al. Superconductivity competitive with checkerboard-type charge ordering in the organic conductor β-(meso-DMBEDT-TTF)2PF6. Phys. Rev. 2009, 80, 092508:1–092508:4. [Google Scholar]
- Girlando, A.; Masino, M.; Kaiser, S.; Sun, Y.; Drichiko, N.; Dressel, M.; Mori, H. Spectroscopic characterization of charge order fluctuations in BEDT-TTF metals and superconductors. Phys. Status Solidi 2012, 249, 953–956. [Google Scholar] [CrossRef]
- Kobayashi, A.; Katayama, S.; Suzumura, Y. Superconductivity in charge ordered metal for quasi-two-dimensional organic conductor. J. Phys. Soc. Jpn. 2005, 74, 2897–2900. [Google Scholar] [CrossRef]
- Pouget, J.-P. Bond and charge ordering in low-dimensional organic conductors. Physica B 2012, 407, 1762–1770. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Foury-Leylekian, P.; Alemany, P.; Canadell, E. Charge ordering in low dimensional organic conductors: Structural aspects. Phys. Status Solidi 2012, 249, 937–942. [Google Scholar] [CrossRef]
- Ouyang, J.; Yakushi, K.; Misaki, Y.; Tanaka, K. Raman spectroscopic evidence for the charge disproportionation in a quasi-two-dimensional organic conductor θ-(BDT-TTP)2Cu(NCS)2. Phys. Rev. 2001, 63, 054301:1–054301:6. [Google Scholar]
- Yakushi, K.; Yamamoto, K.; Simonyan, M.; Ouyang, J.; Nakano, C.; Misaki, Y.; Tanaka, K. Charge-ordering and magnetic phase transitions in θ-(BDT-TTP)2Cu(NCS)2. Phys. Rev. 2002, 66, 235102:1–235102:5. [Google Scholar]
- Merino, J.; Greco, A.; McKenzie, R.H.; Calandra, M. Dynamical properties of a strongly correlated model for quarter-filled layered organic molecular crystals. Phys. Rev. 2003, 68, 245121:1–245121:15. [Google Scholar]
- Seo, H.; Tsutsumi, K.; Ogata, M.; Merino, J. Charge fluctuation in geometrically frustrated charge ordering system. J. Phys. Soc. Jpn. 2006, 75, 114707:1–114707:8. [Google Scholar]
- Kozlov, M.E.; Pokhondnia, K.I.; Yurchenko, A.A. The assignment of fundamental vibrations of BEDT-TTF and BEDT-TTF-d8. Spectrochim. Acta 1987, 43A, 323–329. [Google Scholar]
- Kozlov, M.E.; Pokhondnia, K.I.; Yurchenko, A.A. Electron molecular vibration coupling in vibrational spectra of BEDT-TTF based radical cation salts. Spectrochim. Acta 1989, 45A, 437–444. [Google Scholar]
- Eldridge, J.E.; Homes, C.C.; Williams, J.M.; Kini, A.M.; Wang, H.H. The assignment of the normal modes of the BEDT-TTF electron-donor molecule using the infrared and Raman spectra of several isotopic analogs. Spectrochim. Acta 1995, 51A, 947–960. [Google Scholar]
- Wang, H.H.; Ferraro, J.R.; Williams, J.M.; Geiser, U.; Schlueter, J.A. Rapid Raman spectroscopic determination of the stoichiometry of microscopic quantities of BEDT-TTF-based organic conducors and superconductors. J. Chem. Soc. Chem. Commun. 1994, 1893–1894. [Google Scholar]
- Yamamoto, T.; Uruichi, M.; Yamamoto, K.; Yakushi, K.; Kawamoto, A.; Taniguchi, H. Examination of the charge-sensitive vibrational modes in bis(ethylenedithio)tetrathiafulvalene. J. Phys. Chem. 2005, 109, 15226–15235. [Google Scholar]
- Although frequency is proportional to the square root of force constant, the frequency practically linearly depends upon the force constant in a narrow frequency range, Δω = ω(0) − ω(1)
- Rice, M.J.; Lipari, N.O.; Strassler, S. Dimerized organic linear-chain conductors and the unambiguous experimental determination of electron-molecular-vibration coupling constants. Phys. Rev. Lett. 1977, 21, 1357–1362. [Google Scholar]
- Rice, M.J. Towards the experimental determiation of the fundamental microscopic parameters of organic ion-radical compounds. Solid State Commun. 1979, 31, 93–98. [Google Scholar] [CrossRef]
- Girlando, A.; Bozio, R.; Pecile, C.; Torrance, J.B. Discovery of vibronic effects in the Raman spectra of mixed-stack charge-transfer crystals. Phys. Rev. 1982, 26, 2306–2309. [Google Scholar] [CrossRef]
- Painelli, A.; Girlando, A. Electron-molecular vibration (e-mv) coupling in charge-transfer compounds and its consequences on the optical spectra: A theoretical framework. J. Chem. Phys. 1986, 84, 5655–5671. [Google Scholar] [CrossRef]
- Yamamoto, K.; Yakushi, K. Electron-molecular vibration coupling effect on the Raman spectrum of organic charge transfer salts. J. Phys. (France) 2004, 114, 153–155. [Google Scholar] [CrossRef]
- Visentini, G.; Masino, M.; Bellitto, C.; Girlando, A. Experimental determination of BEDT-TTF+ electron-molecular vibration coupling constants through optical microreflectance. Phys. Rev. 1998, 58, 9460–9467. [Google Scholar] [CrossRef]
- Yartsev, V.M.; Graja, A. Electron-intramolecular vibration coupling in charge-transfer salts studied by infrared spectroscopy. Int. J. Mod. Phys. 1998, 12, 1643–1672. [Google Scholar] [CrossRef]
- Faltermeier, D.; Barz, J.; Dumm, M.; Dressel, M.; Drichko, N.; Petrov, B.; Semkin, V.; Vlasova, R.; Meziere, C.; Batil, P. Bandwidth-controlled Mott transition in κ-(BEDT-TTF)2Cu[N(CN)2]-BrxCl1−x: Optical studies of localized charge excitations. Phys. Rev. 2007, 76, 165113:1–165113:12. [Google Scholar]
- Girlando, A. Charge sensitive vibrations and electron-molecular vibration coupling in bis(ethylenethio)-thetrathiafulvalene (BEDT-TTF). J. Phys. Chem. 2011, 115, 19371–19378. [Google Scholar]
- Yamamoto, T.; Yakushi, K.; Shimizu, Y.; Saito, G. Infrared and Raman study of the charge-ordered state of θ-(ET)2Cu(CN)[N(CN)2]2. J. Phys. Soc. Jpn. 2004, 73, 2326–2332. [Google Scholar] [CrossRef]
- Yue, Y.; Nakano, C.; Yamamoto, K.; Uruichi, M.; Wojciechowski, R.; Inokuchi, M.; Yakushi, K.; Kawamoto, A. Charge order-disorder phase transition in α′-(Bis(ethylenedithio)tetrathiafulvalene)2 IBr2 [α′-(BEDT-TTF)2IBr2]. J. Phys. Soc. Jpn. 2009, 78, 044701:1–044701:10. [Google Scholar]
- Kubo, R. A stochastic theory of line shape. Adv. Chem. Phys. 1969, 15, 101–127. [Google Scholar] [CrossRef]
- Sue, J.; Yan, Y.J.; Mukamel, S. Raman excitation profiles of polyatomic molecules in condensed phases. A stochastic theory. J. Chem. Phys. 1986, 85, 462–474. [Google Scholar] [CrossRef]
- Uruichi, M.; Yakushi, K.; Yamamoto, H.M.; Kato, R. Infrared and Raman studies of the charge-ordering phase transition at ~170 K in the quarter-filled organic conductor, β″-(ET) (TCNQ). J. Phys. Soc. Jpn. 2006, 75, 074720:1–074720:10. [Google Scholar]
- Yamamoto, H.M.; Hagiwara, M.; Kato, R. New phase of (BEDT-TTF)(TCNQ). Synth. Metal. 2003, 133, 449–451. [Google Scholar] [CrossRef]
- Nogami, Y. Private communication. 2009. Okayama University. [Google Scholar]
- Yamamoto, H.M.; Tajima, N.; Hagiwara, M.; Kato, R.; Yamaura, J.I. Strange electric magnetic behaviour of new (BEDT-TTF)(TCNQ). Synth. Metal. 2003, 135, 623–624. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Terakura, C.; Terashima, T.; Yakabe, T.; Terai, Y.; Yamamoto, H.M.; Kato, R.; Uji, S. Fermi surface and resistance anomalies in ET-TCNQ. Synth. Metal. 2003, 135, 647–648. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Graf, D.; Choi, E.S.; Brooks, J.S.; Terashima, T.; Konoike, T.; Enomoto, K.; Nishimura, M.; Yamamoto, H.M.; Kato, R.; et al. Pressure-induced Fermi surface change in quasi-one-dimensional conductor β″-(ET)(TCNQ). J. Phys. IV Fr. 2004, 114, 157–158. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Uji, S.; Enomoto, K.; Konoike, T.; Nishimura, M.; Terashima, T.; Graf, D.; Choi, E.S.; Brooks, J.S.; Yamamoto, H.M.; et al. Pressure effect on fermi surface in β″-(ET)(TCNQ). Synth. Metal. 2005, 152, 437–440. [Google Scholar] [CrossRef]
- Kimata, M.; Ohta, H.; Koyama, K.; Oshima, Y.; Motokawa, M.; Yamamoto, H.M.; Kato, R. Development of the high field magneto-optical measurement system with a rotational cavity for the study of organic conductors. Int. J. Mod. Phys. 2004, 18, 3803–3806. [Google Scholar] [CrossRef]
- Kimata, M.; Oshima, Y.; Ohta, H.; Koyama, K.; Motokawa, M.; Yamamoto, H.M.; Kato, R. Magnetooptical measurements of β″-(BEDT-TTF)(TCNQ). Physica B 2004, 346, 382–386. [Google Scholar] [CrossRef]
- Yakushi, K.; Uruichi, M.; Yamamoto, H.M.; Kato, R. Dynamical fluctuation of the site-charge density in metallic β″-(BEDT-TTF)(TCNQ). J. Phys. IV Fr. 2004, 114, 149–151. [Google Scholar] [CrossRef]
- Drichko, N.; Kaiser, S.; Sun, Y.; Clauss, C.; Dressel, M.; Mori, H.; Schlueter, J.; Zhyliaeva, E.I.; Torunova, S.A.; Lyubovskaya, R.N. Evidence for charge order in organic superconductors obtained by vibrational spectroscopy. Physica B 2009, 404, 490–493. [Google Scholar]
- Yamamoto, K.; Yakushi, K.; Miyagawa, K.; Kanota, K.; Kawamoto, A. Charge ordering in θ-(BEDT-TTF)2RbZn(SCN)4 studied by vibrational spectroscopy. Phys. Rev. 2002, 65, 085110:1–085110:8. [Google Scholar]
- There is another incoherent optical excitation at ~U with very weak intensity, which corresponds to the optical transition from the lower Hubbard to the upper Hubbard band.
- Merino, J. Nonlocal Coulomb Correlation in metals close to a charge order insulator transition. Phys. Rev. Lett. 2007, 99, 036404:1–036404:4. [Google Scholar]
- Kondo, R.; Higa, M.; Kagoshima, S.; Hoshino, H.; Mori, T.; Mori, H. Electrical and structural properties of θ-type BEDT-TTF organic conductors under uniaxial strain. J. Phys. Soc. Jpn. 2006, 75, 044716:1–044716:7. [Google Scholar]
- Kuroki, K. The origin of the charge ordering and its relevance to superconductivity in θ-(BEDT-TTF)2X: The effect of the fermi surface nesting and the distant electron-electron interactions. J. Phys. Soc. Jpn. 2006, 75, 114716:1–114716:14. [Google Scholar]
- Hotta, C. Classification of quasi-two dimensional organic conductors based on a new minimal model. J. Phys. Soc. Jpn. 2003, 72, 840–853. [Google Scholar] [CrossRef]
- Watanabe, H.; Ogata, M. Novel charge order and superconductivity in two-dimensional frustrated lattice at quarter filling. J. Phys. Soc. Jpn. 2006, 75, 063702:1–063702:4. [Google Scholar]
- Mori, H.; Tanaka, S.; Mori, T. Systematic study of the electronic state of θ-type BEDT-TTF organic conductors by changing electronic correlation. Phys. Rev. 1998, 57, 12023–12029. [Google Scholar] [CrossRef]
- Kobayashi, H.; Kato, R.; Kobayashi, A.; Nishio, Y.; Kajita, K.; Sasaki, W. New molecular superconductor (BEDT-TTF)2(I3)x(AuI2)1−x (x < 0.02). Chem. Lett. 1986, 789–792. [Google Scholar]
- Mori, H.; Tanaka, S.; Mori, T.; Kobayashi, A.; Kobayashi, H. Crystal structure and physical properties of M = Rb and Tl salts of (BEDT-TTF)2MM′(SCN)4, [M′ = Co, Zn]. Bull. Chem. Soc. Jpn. 1998, 71, 797–806. [Google Scholar] [CrossRef]
- Komatsu, T.; Sato, H.; Nakamura, T.; Matsukawa, N.; Yamochi, H.; Saito, G.; Kusunoki, M.; Sakagushi, K.; Kagoshima, S. The electrical and magnetic properties of a novel two-dimensional antiferromagnet based on BEDT-TTF, θ-(BEDT-TTF)2Cu(CN)[N(CN)2]2. Bull Chem. Soc. Jpn. 1995, 68, 2233–2244. [Google Scholar] [CrossRef]
- The doublet of ν2P is interpreted as the Fermi resonance [72].
- Watanabe, M.; Noda, Y.; Nogami, Y.; Mori, H. Transfer integrals and spatial pattern of charge ordering in θ-(BEDT-TTF)2RbZn(SCN)4 at 90 K. J. Phys. Soc. Jpn. 2004, 73, 116–122. [Google Scholar] [CrossRef]
- Suzuki, K.; Yamamoto, K.; Yakushi, K. Charge-ordering transition in orthorhombic and monoclinic single crystals of θ-(BEDT-TTF)2TlZn(SCN)4 studied by vibrational spectroscopy. Phys. Rev. 2004, 69, 085114:1–085114:11. [Google Scholar]
- Tajima, H.; Kyoden, S.; Mori, H.; Tanaka, S. Estimation of charge-ordering patterns in θ-ET2MM′(SCN)4(MM′ = RbCo, RbZn, CsZn) by reflection spectroscopy. Phys. Rev. 2000, 62, 9378–9385. [Google Scholar] [CrossRef]
- Tanaka, Y.; Yonemitsu, K. Effects of electron-lattice coupling on charge order in θ-(ET)2X. J. Phys. Soc. Jpn. 2008, 77, 034708:1–034708:9. [Google Scholar]
- Chiba, R.; Hiraki, K.; Takahashi, T.; Yamamoto, H.M.; Nakamura, T. Extremely slow charge fluctuations in the metallic state of the two-dimensional molecular conductor θ-(BEDT-TTF)2RbZn(SCN)4. Phys. Rev. Lett. 2004, 93, 216405:1–216405:4. [Google Scholar]
- Nakamura, T.; Miyagawa, W.; Kinami, R.; Konishi, Y.; Takahashi, T. Low-temperature electronic states in θ-(BEDT-TTF)2RbZn(SCN)4: Competition of different ground states. Synth. Metal. 1999, 103, 1898–1899. [Google Scholar] [CrossRef]
- Kanoda, K.; Ohnou, K.; Kodama, M.; Miyagawa, K.; Itou, T.; Hiraki, K. Charge ordering and frustration in organic conductors. J. Phys. IV Fr. 2005, 131, 21–26. [Google Scholar] [CrossRef]
- Watanabe, M.; Noda, Y.; Nogami, Y.; Mori, H. Investigation of X-ray diffuse scattering in θ-(BEDT-TTF)2RbM′(SCN)4. Synth. Metal. 2003, 135, 665–666. [Google Scholar] [CrossRef]
- Nogami, Y.; Hanasaki, N.; Watanabe, M.; Yamamoto, K.; Ito, T.; Ikeda, N.; Ohsumi, H.; Tokawa, H.; Noda, Y.; Terasaki, I.; et al. Charge order competition leading to nonlinearity in organic thyristor family. J. Phys. Soc. Jpn. 2010, 79. [Google Scholar] [CrossRef]
- A weak broad ν3 band is probably involved in the low-frequency region of the broad ν2 band. The assignment of the broad ν2 band with the aid of isotope shift is given in ref. [94].
- Suzuki, K.; Yamamoto, K.; Yakushi, K.; Kawamoto, A. Infrared and Raman studies of θ-(BEDT-TTF)2CsZn(SCN)4: Comparison with the frozen state of θ-(BEDT-TTF)2RbZn(SCN)4. J. Phys. Soc. Jpn. 2005, 74, 2631–2639. [Google Scholar] [CrossRef]
- Wang, N.L.; Mori, H.; Tanaka, S.; Dong, J.; Clayman, B.P. Far infrared study of insulator-metal transition in θ-(BEDT-TTF)2RbZn(SCN)4. J. Phys. Condens. Matter 2001, 13, 5463–5470. [Google Scholar] [CrossRef]
- Nishimoto, S.; Shingai, M.; Ohta, Y. Coexistence of distinct charge fluctuations in θ-(BEDT-TTF)2X. Phys. Rev. 2008, 78, 035113:1–035113:9. [Google Scholar]
- The reason why the ν2 mode of metallic I3 salt is significantly deviated from the center of ν2P and ν2R is ascribed to the interaction between ν2R and the neighbor ν3A. [46].
- Mori, T. Non-Stripe charge order in the θ-phase organic conductors. J. Phys. Soc. Jpn. 2003, 72, 1469–1475. [Google Scholar] [CrossRef]
- Mori, T. Estimation of off-site coulomb integrals and phase diagrams of charge ordered states in the θ-phase organic conductor. Bull. Chem. Soc. Jpn. 2000, 73, 2243–2253. [Google Scholar] [CrossRef]
- Watanabe, M.; Nogami, Y.; Oshima, K.; Mori, H.; Tanaka, S. Novel pressure-induced 2κF CDW state in organic low-dimensional compound θ-(BEDT-TTF)2CsCo(SCN)4. J. Phys. Soc. Jpn. 1999, 68, 2654–2663. [Google Scholar] [CrossRef]
- Watanabe, M.; Yamamoto, K.; Ito, T.; Nakashima, Y.; Tanabe, M.; Hanasaki, N.; Ikeda, N.; Nogami, Y.; Ohsumi, H.; Toyokawa, H.; et al. Non-thermal evidence for current-induced melting of charge order in θ-(BEDT-TTF)2CsZn(SCN)4. J. Phys. Soc. Jpn. 2008, 77, 065004:1–065004:2. [Google Scholar]
- Inagaki, K.; Terasaki, I.; Mori, H.; Mori, T. Large dielectric constant and giant nonlinear conduction in organic conductor θ-(BEDT-TTF)2CsZn(SCN)4. J. Phys. Soc. Jpn. 2004, 73, 3364–3369. [Google Scholar] [CrossRef]
- Sawano, F.; Terasaki, I.; Mori, H.; Mori, T.; Watanabe, M.; Ikeda, N.; Nogami, Y.; Noda, Y. An organic thyristor. Nature 2005, 437, 522–524. [Google Scholar] [CrossRef]
- Chiba, R.; Hiraki, K.; Takahashi, T.; Yamamoto, H.M.; Nakamura, T. Charge disproportionation and dynamics in θ-(BEDT-TTF)2CsZn(SCN)4. Phys. Rev. 2008, 77, 115113:1–115113:10. [Google Scholar]
- Nad, F.; Monceau, P.; Yamamoto, H.M. A possible glass-like state in θ-(BEDT-TTF)2CsZn(SCN)4 at low temperature. J. Phys. Condens. Matter 2008, 20, 485211:1–485211:6. [Google Scholar]
- Udagawa, M.; Motome, Y. Charge ordering and coexistence of charge fluctuations in quasi-two-dimensional organic conductors θ-(BEDT-TTF)2X. Phys. Rev. Lett. 2007, 98, 206405:1–206405:4. [Google Scholar]
- Kajita, K.; Nishio, Y.; Moriyama, S.; Sasaki, W.; Kato, R.; Kobayashi, H.; Kobayashi, A. ew organic suprconductors κ- and θ-(BEDT-TTF)2I3; Transport property. Solid State Commun. 1987, 64, 1279–1284. [Google Scholar] [CrossRef]
- Salameh, B.; Nothardt, A.; Balthes, E.; Schmidt, W.; Schweitzer, D.; Strempfer, J.; Hinrichsen, B.; Jansen, M.; Maude, D.K. Electronic properties of the organic metals θ-(BEDT-TTF)2I3 and θT-(BEDT-TTF)2I3. Phys. Rev. 2007, 75, 054509:1–054509:13. [Google Scholar]
- The symmetry of 3a × 3c superlattice has not been clarified.
- Wang, N.L.; Feng, T.; Chen, Z.J.; Mori, H. Infrared properties of θ-type ET charge-transfer salts: θ-(ET)2RbZn(SCN)4 vs. θ-(ET)2CsZn(SCN)4. Synth. Metal. 2003, 135, 701–702. [Google Scholar] [CrossRef]
- Wojciechowski, R.; Yamamoto, K.; Yakushi, K.; Inokuchi, M.; Kawamoto, A. High-pressure Raman study of the charge ordering in α-(BEDT-TTF)2I3. Phys. Rev. 2003, 67, 224105:1–224105:11. [Google Scholar]
- Takenaka, K.; Tamura, M.; Tajima, N. Collapse of coherence quasiparticle states in θ-(bedt-ttf)2i3 observed by optical spectroscopy. Phys. Rev. Lett. 2005, 95, 227801:1–227801:4. [Google Scholar]
- Kobayashi, A.; Kato, R.; Kobayashi, H.; Moriyama, S.; Nishio, Y.; Kajita, K.; Sasaki, W. Anion arrangement in a new molecular superconductor, θ-(BEDT-TTF)2(I3)1−x(AuI2)x, (x < 0.02). Chem. Lett. 1986, 2017–2020. [Google Scholar]
- Tamura, M.; Yakushi, K.; Kuroda, H. Temperature dependence of the polarized reflectance spectra of the θ-Type of bis(ethylenedithio)tetrathiafulvalenium) triiodide θ-(BEDT-TTF)2I3: Estimation of band parameters. J. Phys. Soc. Jpn. 1988, 57, 3239–3247. [Google Scholar] [CrossRef]
- ACS, Molecular Conductors: Thematic Issue (Special issue); ACS Publication: Washington, DC, USA, 2004; pp. 4887–5781.
- Mori, T. Structural genealogy of BEDT-TTF-based organic conductors I. Parallel molecules: β and β″ phases. Bull. Chem. Soc. Jpn. 1998, 71, 2509–2526. [Google Scholar] [CrossRef]
- Mori, T. Structural genealogy of BEDT-TTF-based organic conductors II. Inclined molecules: θ- and α-, and κ-phases. Bull. Chem. Soc. Jpn. 1999, 72, 179–197. [Google Scholar] [CrossRef]
- Mori, T. Structural genealogy of BEDT-TTF-based organic conductors III. Twisted molecules: δ- and α’-phases. Bull. Chem. Soc. Jpn. 1998, 72, 2011–2027. [Google Scholar] [CrossRef]
- Takano, Y.; Hiraki, K.; Yamamoto, H.M.; Nakamura, T.; Takahashi, T. Charge ordering in α-(BEDT-TTF)2I3. Synth. Metal. 2001, 120, 1081–1082. [Google Scholar] [CrossRef]
- Tajima, N.; Ebina-Tajima, A.; Tamura, M.; Nishio, Y.; Kajita, K. Effects of uniaxial strain on transport properties of organic conductor α-(BEDT-TTF)2I3 and discovery of superconductivity. J. Phys. Soc. Jpn. 2002, 71, 1832–1835. [Google Scholar] [CrossRef]
- Tajima, N.; Kajita, K. Experimental study organic zero-gap conductor α-(BEDT-TTF)2I3. Sci. Technol. Adv. Mater. 2009, 10, 024308:1–024308:7. [Google Scholar]
- Kobayashi, A.; Katayama, S.; Suzumura, Y. Theoretical study of the zero-gap organic conductor α-(BEDT-TTF)2I3. Sci. Technol. Adv. Mater. 2009, 10, 024309:1–024309:15. [Google Scholar]
- Iwai, S.; Yamamoto, K.; Kashiwazaki, A.; Hiramatsu, F.; Nakaya, H.; Kawakami, Y.; Yakushi, K.; Okamoto, H.; Mori, H.; Nishio, Y. Photoinduced melting of a stripe-type charge-order and metallic domain formation in a layered BEDT-TTF-based organic salt. Phys. Rev. Lett. 2007, 98, 097402:1–097402:4. [Google Scholar]
- Yamamoto, K.; Iwai, S.; Boyko, S.; Kashiwazaki, A.; Hiramatsu, F.; Okabe, C.; Nishi, N.; Yakushi, K. Strong optical nonlinearity and its ultrafast response associated with electron ferroelectricity in an organic conductor. J. Phys. Soc. Jpn. 2008, 77, 074709:1–074709:6. [Google Scholar]
- Bender, K.; Henning, I.; Schweitzer, D.; Dietz, K.; Endres, H.; Keller, H.J. Synthesis, structure, and physical properties of a two-dimensional organic metal, di[bis(ethylenedithiolo)tetrathio-fulvalene] triiodide, (BEDT-TTF)2+I3-. Mol. Cryst. Liq. Cryst. 1984, 108, 359–371. [Google Scholar] [CrossRef]
- Kino, H.; Fukuyama, H. Phase diagram of two-dimensional organic conductors: (BEDT-TTF)2X. J. Phys. Soc. Jpn. 1996, 65, 2158–2169. [Google Scholar] [CrossRef]
- Takahashi, T.; Hiraki, K.; Moroto, S.; Tajima, N.; Takano, Y.; Kubo, Y.; Satsukawa, H.; Chiba, R.; Yamamoto, H.M.; Kato, R.; et al. Charge disproportionation, everywhere! J. Phys. IV Fr. 2004, 114, 3–8. [Google Scholar] [CrossRef]
- Kakiuchi, T.; Wakabayashi, Y.; Sawa, H.; Takahashi, T.; Nakamura, T. Charge ordering in α-(BEDT-TTF)2I3 by synchrotron x-ray diffraction. J. Phys. Soc. Jpn. 2007, 76, 113702:1–113702:10. [Google Scholar]
- Alemany, P.; Pouget, J.-P.; Canadell, E. Essential role of anions in the charge ordering transition of α-(BEDT-TTF)2I3. Phys. Rev. B 2012, 85, 195118:1–195118:10. [Google Scholar]
- Yue, Y.; Yamamoto, K.; Uruichi, M.; Nakano, C.; Yakushi, K.; Yamada, S.; Hiejima, T.; Kawamoto, A. Nonuniform site-charge distribution and fluctuations of charge order in the metallic state of α-(BEDT-TTF)2I3. Phys. Rev. 2010, 82, 075134:1–075134:8. [Google Scholar]
- Yamamoto, K.; Kowalska, A.A.; Yue, Y.; Yakushi, K. Vibronic activation of molecular vibrational overtones in the infrared spectra of charge-ordered organic conductors. Phys. Rev. 2011, 84, 064306:1–064306:13. [Google Scholar]
- Yamamoto, K.; Kowalska, A.A.; Yue, Y.; Yakushi, K. E-mv coupling of vibrational overtone in organic conductors: Relationship to optical nonlinearity and ferroelectricity. Physica B 2012, 407, 1775–1778. [Google Scholar] [CrossRef]
- Ivek, T.; Korin-Hamzic, N.; Milat, O.; Tomic, S.; Clauss, C.; Drichko, N.; Schweitzer, D.; Dressel, M. Electrodynamic response of the charge ordering phase: Dielectric and optical studies of α-(BEDT-TTF)2I3. Phys. Rev. 2011, 83, 165128:1–165128:13. [Google Scholar]
- Moroto, S.; Hiraki, K.-I.; Takano, Y.; Kubo, Y.; Takahashi, T.; Yamamoto, H.M.; Nakmura, T. Charge disproportionation in the metallic state of α-(BEDT-TTF)2I3. J. Phys. IV Fr. 2004, 114, 339–340. [Google Scholar]
- Kawai, T.; Kawamoto, A. 13C-NMR study of charge ordering state in the organic conductor, α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2009, 78, 074711:1–074711:6. [Google Scholar]
- Yamamoto, K.; Yakushi, K. Second-Harmonic Generation Study Of Ferroelectric Organic Conductors α-(BEDT-TTF)2X (X = I3 and I2Br). In Molecular Electronic and Related Materials—Control and Probe with Light; Naito, T., Ed.; Transworld Research Network: Kerala, Indian, 2010; pp. 185–201. [Google Scholar]
- Yamamoto, K.; Kowalska, A.A.; Yakushi, K. Direct observation of ferroelectric domains by Wigner crystallization of electrons in α-[bis(ethylenedithio)tetetrathiafulvalene]2I3. App. Phys. Lett. 2010, 96, 122901:1–122901:3. [Google Scholar]
- Ikeda, N.; Ohsumi, H.; Ohwada, K.; Ishii, K.; Inami, T.; Kakura, K.; Murakami, Y.; Yoshii, K.; Mori, S.; Horibe, Y.; et al. Ferroelectricity from iron valence ordering in the charge-frustrated system LuFe2O4. Nature 2005, 436, 1136–1138. [Google Scholar]
- Iwai, S.; Yamamoto, K.; Hiramatsu, F.; Nakaya, H.; Kawakami, Y.; Yakushi, K. Hydrostatic pressure effect on photoinduced insulator-to-metal transition in the layered organic salt α-(BEDT-TTF)2I3. Phys. Rev. 2008, 77, 125131:1–125131:5. [Google Scholar]
- Kawakami, Y.; Fukatsu, T.; Sakurai, Y.; Unno, H.; Itoh, H.; Iwai, S.; Sasaki, T.; Yamamoto, K.; Yakushi, K.; Yonemitsu, K. Early-State dynamics of light-matter interaction leading to the insulator-to-metal transition in a charge ordered organic crystal. Phys. Rev. Lett. 2010, 105, 246402:1–246402:4. [Google Scholar]
- Mori, H.; Tanaka, S.; Oshima, K.; Saito, G.; Mori, T.; Maruyama, Y.; Inokuchi, H. Electrical properties and crystal structure of mercury (II) thiocyanate salts based upon BEDT-TTF with Li+, K+, NH4+, Rb+, and Cs+. Synth. Metal. 1991, 42, 2013–2018. [Google Scholar] [CrossRef]
- Mori, H.; Tanaka, S.; Oshima, M.; Saito, G.; Mori, T.; Maruyama, Y.; Inokuchi, H. Crystal and electronic structures of (BEDT-TTF)2[MHg(SCN)4] (M = K and NH4). Bull. Chem. Soc. Jpn. 1990, 63, 2183–2190. [Google Scholar] [CrossRef]
- Kobayashi, H.; Kato, R.; Kobayashi, A.; Nishio, Y.; Kajita, K.; Sasaki, W. Crystal and electronic structures of layered molecular superconductor, θ-(BEDT-TTF)2(I3)x(AuI2)1−x (x < 0.02). Chem. Lett. 1986, 833–836. [Google Scholar]
- Tajima, N.; Tamura, M.; Nishio, Y.; Kajita, K.; Iye, Y. Transport property of an organic conductor α-(BEDT-TTF)2I3 under hydrostatic pressure—Discovery of a novel type of conductor. J. Phys. Soc. Jpn. 2000, 69, 543–551. [Google Scholar] [CrossRef]
- Hiejima, T.; Yamada, S.; Uruichi, M.; Yakushi, K. Infrared and Raman studies of α-(BEDT-TTF)2 MHg(SCN)4 with M = NH4 and K at low temperature: Breaking of inversion symmetry due to charge-ordering fluctuation. Physica B 2010, 405, 5153–5156. [Google Scholar]
- Foury-Leylekian, P.; Ravy, S.; Pouget, J.-P.; Muller, H. X-ray study of the density wave instability of α-(BEDT-TTF)2MHg(SCN)4 with M = K and Rb. Synth. Metal. 2003, 137, 1271–1272. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Pouget, J.-P.; Lee, Y.-J.; Nieminen, R.M.; Ordejon, P.; Canadell, E. Density-wave instability in α-(BEDT-TTF)2KHg(SCN)4 studied by x-ray diffuse scattering and by first-principle calculations. Phys. Rev. 2010, 82, 134116:1–134116:14. [Google Scholar]
- This value was estimated from the separation of ν27j mode, (~7 cm−1)/(140 cm−1/e).
- Yamamoto, T.; Yamamoto, H.M.; Kato, R.; Uruichi, M.; Yakushi, K.; Akutsu, H.; Sato-Akutsu, A.; Kawamoto, A.; Turner, S.S.; Day, P. Inhomogeneous site charges at the boundary between the insulating, superconducting, and metallic phases of β″-type bis-ethylenedithio-tetrathiafulvalene molecular charge-transfer salts. Phys. Rev. 2008, 77, 205120:1–205120:13. [Google Scholar]
- Bangura, A.F.; Coldea, A.I.; Singleton, J.; Ardavan, A.; Akutsu-Sato, A.; Akutsu, H.; Turner, S.S.; Day, P.; Yamamoto, T.; Yakushi, K. Robust superconducting state in the low-quasiparticle-density due to proximity to a charge-ordered state. Phys. Rev. 2005, 72, 014543:1–014543:13. [Google Scholar]
- See ref. [46] about the reason why this equation is applicable in the range of 0 ≤ ρ ≤ 0.8.
- Although frequency is proportional to the square root of force constant, the frequency practically linearly depends upon the force constant in a narrow frequency range, Δω = ω(0) – ω(1)
- The κ- and β′-ET salts with ρ = 0.5 have a dimer unit with large transfer integral. However, the blue shift of ν2 is not attributed to the emv (electron-molecular-vibration) coupling, because similar blue shift is found in non-dimeric θ-(ET)2I3 which will be shown in the next subsection.
- Hess, L.A.; Prasad, P.N. Vibrational dephasing in organic solids: Temperature dependence of Raman active internal mode of naphthalene. J. Phys. Chem. 1980, 72, 573–579. [Google Scholar] [CrossRef]
- The frequency of the infrared-active ν27 mode at ρ = 0.5 is also deviated from the linear relationship. The examination similar to ν2 is necessary including temperature dependence.
- Kayatama, S.; Kobayashi, A.; Suzumura, Y. Effect of anion potential on the zero-gap state in the two-dimensional organic conductor α-(BEDT-TTF)2I3. J. Phys. Conf. Ser. 2008, 132, 012003:1–012003:7. [Google Scholar]
- Kobayashi, A.; Katayama, S.; Suzumura, Y.; Fukuyama, H. Massless fermions in organic conductor. J. Phys. Soc. Jpn. 2007, 76, 034711:1–034711:6. [Google Scholar]
- Ishibashi, S.; Tamura, T.; Kohyama, M.; Terakura, K. Ab initio electronic-structure calculation. J. Phys. Soc. Jpn. 2006, 75, 015005:1–015005:2. [Google Scholar]
- Tamura, M.; Matsuzaki, F.; Tajima, N.; Nishio, Y.; Kajita, K. Transport study of an organic conductor, θ-(BEDT-TTF)2I3. Synth. Metal. 1997, 86, 2007–2008. [Google Scholar] [CrossRef]
- Tajima, N.; Tajima, A.; Tamura, M.; Kato, R.; Nishio, Y.; Kajita, K. Pressure control of transport property of organic conductors; α-, θ-(BEDT-TTF)2I3 and θ-(DIETS)2[Au(CN)4]. J. Phys. IV Fr. 2004, 114, 263–267. [Google Scholar] [CrossRef]
- Miyagawa, K.; Hirayama, M.; Tamura, M.; Kanoda, K. 13C NMR study on zero-gap state in the organic conductor θ-(BEDT-TTF)2I3 under pressure. J. Phys. Soc. Jpn. 2010, 79, 063703:1–063703:3. [Google Scholar]
- As ν2R is mixed with ν31, the hole numbers shown in the CO state shown in Figure 5b,c are inaccurate.
- Kondo, R.; Kagoshima, S.; Tajima, N.; Kato, R. Crystal and electronic structures of the quasi-two-dimensional organic conductor α-(BEDT-TTF)2I3 and its selenium analogue α-(BEDT-TSeF)2I3 under hydrostatic pressure at room temperature. J. Phys. Soc. Jpn. 2009, 78, 114714:1–114714:7. [Google Scholar]
- Yakushi, K.; Kanbara, H.; Tajima, H.; Kuroda, H.; Saito, G.; Mori, T. Temperature dependence of the reflectance spectra of the single crystals of bis(ethylenedithio)tetrathiafulvalene salts. α-(BEDT-TTF)3(ReO4)2 and α-(BEDT-TTF)2I3. Bull. Chem. Soc. Jpn. 1987, 60, 4251–4257. [Google Scholar] [CrossRef]
- Zelezny, V.; Petzelt, J.; Swietlik, R.; Gorshunov, B.P.; Volkov, A.A.; Kozlov, G.V.; Schweitzer, D.; Keller, H.J. Far infrared response of α- and αt-(BEDT-TTF)2I3. J. Phys. Fr. 1990, 51, 869–881. [Google Scholar] [CrossRef]
- Dressel, M.; Gruner, G.; Pouget, J.P.; Breining, A.; Schweitzer, D. Field and frequency dependent transport in the two-dimensional organic conductor α-(BEDT-TTF)2I3. J. Phys. I Fr. 1994, 4, 579–594. [Google Scholar] [CrossRef]
- Clauss, C.; Drichko, N.; Schweitzer, D.; Dressel, M. Charge-order gap in α-(BEDT-TTF)2I3. Physica B 2010, 405, S144–S146. [Google Scholar] [CrossRef]
- Tamura, K.; Ozawa, T.; Bando, Y.; Kawamoto, T.; Mori, T. Voltage oscillation associated with nonlinear conductivity in the organic conductor α-(BEDT-TTF)2I3. J. Appl. Phys. 2010, 107, 103716:1–103716:5. [Google Scholar]
- Ivek, T.; Korin-Hamzic, B.; Milat, O.; Tomic, S.; Clauss, C.; Drichko, N.; Schweitzer, D.; Dressel, M. Collective excitation in the charge-ordered phase of α-(BEDT-TTF)2I3. Phys. Rev. Lett. 2010, 104, 206406:1–206406:4. [Google Scholar]
- Dressel, M.; Drichko, N.; Kaiser, S. Collective charge-order excitations. Physica C 2010, 470, S589–S591. [Google Scholar] [CrossRef]
- Watanabe, M.; Nishikawa, M.; Nogami, Y.; Oshima, K.; Saito, G. Low temperature structure of the α′-(BEDT-TTF)2IBr2 organic magnetic semiconductor. J. Korean Phys. Soc. 1997, 31, 95–98. [Google Scholar]
- Tokumoto, M.; Anzai, H.; Ishiguro, T.; Saito, G.; Kobayashi, H.; Kato, R.; Kobayashi, A. Electrical and magnetic properties of organic semiconductors, (BEDT-TTF)2X (X = IBr2, IBrCl, and ICl2). Synth. Metal. 1987, 19, 215–220. [Google Scholar] [CrossRef]
- Maniwa, Y.; Takahashi, T.; Saito, G. 1H NMR in organic superconductor β-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 1986, 55, 47–50. [Google Scholar] [CrossRef]
- Nogami, Y.; Kagoshima, S.; Sugano, T.; Saito, G. X-ray evidence for structural changes in the organic conductors, α-(BEDT-TTF)2I3, α-(BEDT-TTF)2IBr2,and β-(BEDT-TTF)2I3. Synth. Metal. 1986, 16, 367–377. [Google Scholar] [CrossRef]
- Inokuchi, M.; Yakushi, K.; Kinoshita, M.; Saito, G. Optical properties of α′-(BEDT-TTF)2IBr2. Synth. Metal. 1992, 103, 2102–2103. [Google Scholar]
- Yue, Y.; Nakano, C.; Yamamoto, K.; Uruichi, M.; Yakushi, K.; Kawamoto, A. Charge-ordering phase transition in α′-(BEDT-TTF)2IBr2. J. Phys. Conf. Ser. 2008, 132, 012007:1–012007:7. [Google Scholar]
- Yue, Y.; Yamamoto, K.; Nakano, C.; Uruichi, M.; Yakushi, K.; Inokuchi, M.; Hiejima, T.; Kawamoto, A. Order-disorder type of charge-ordering phase transition in narrow-bandwidth compound, α′-(BEDT-TTF)2IBr2. Physica B 2010, 405, S232–S236. [Google Scholar]
- Kowalska, A.A.; Yamamoto, K.; Yakushi, K. Ferroelectric polarization in α′-(ET)2IBr2 studied by second-harmonic generation microscopy. J. Phys. Conf. Ser. 2008, 132, 012006:1–012006:5. [Google Scholar]
- Yamashita, A.; Watanabe, M.; Kobayashi, K.; Kumai, R.; Yamamoto, K.; Yakushi, K.; Noda, Y. SR-based study of successive phase transition of α′-(BEDT-TTF)2IBr2 II. Meeting Abstr. Phys. Soc. Jpn. 2012, 67, 907. [Google Scholar]
- Sugano, T.; Saito, G.; Kinoshita, M. Conduction-electron-spin resonance in organic conductors: A and b phases of di[bis(ethylenedithiolo)tetrathiafulvalene]triiodide [(BEDT-TTF)2I3]. Phys. Rev. 1986, 34, 117–125. [Google Scholar] [CrossRef]
- The optical conductivities from 50–6000 cm−1 of α′-IBr2, α-I3 and α-NH4Hg were obtained in our research group. The low-frequency region from 0–600 cm−1 of β″-(BEDT-TTF)(TCNQ), θm-RbZn, θo-RbZn, and θ-CsZn were extrapolated to the dc conductivity value by straight line. The optical conductivities of θ-RbZn and θ-I3 were taken from the papers reported by Wang [95] and Takenaka [112], respectively.
- Van der Marel, D. Optical Signatures of Electron Correlations in the Cuprates. In Strong Interactions in Low Dimensions; Baeriswyl, D., Degiorgi, L., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 237–276. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yakushi, K. Infrared and Raman Studies of Charge Ordering in Organic Conductors, BEDT-TTF Salts with Quarter-Filled Bands. Crystals 2012, 2, 1291-1346. https://doi.org/10.3390/cryst2031291
Yakushi K. Infrared and Raman Studies of Charge Ordering in Organic Conductors, BEDT-TTF Salts with Quarter-Filled Bands. Crystals. 2012; 2(3):1291-1346. https://doi.org/10.3390/cryst2031291
Chicago/Turabian StyleYakushi, Kyuya. 2012. "Infrared and Raman Studies of Charge Ordering in Organic Conductors, BEDT-TTF Salts with Quarter-Filled Bands" Crystals 2, no. 3: 1291-1346. https://doi.org/10.3390/cryst2031291
APA StyleYakushi, K. (2012). Infrared and Raman Studies of Charge Ordering in Organic Conductors, BEDT-TTF Salts with Quarter-Filled Bands. Crystals, 2(3), 1291-1346. https://doi.org/10.3390/cryst2031291




