Next Article in Journal
Structural and Optical Properties of Defected and Exotic Calcium Monochalcogenide Nanoparticles: Insights from DFT and TD-DFT Calculations
Previous Article in Journal
A Data-Driven Framework for Accelerated Modeling of Stacking Fault Energy from Density of States Spectra
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 15
Issue 5
10.3390/cryst15050391
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Single Crystal Growth and Structural Study of the New MCu2Zn20 (M = Nb, Hf) Compounds

by
Sarah M. Longworth
1,2,
Marium M. Mou
1,
Nusrat Yasmin
1,
Md Fahel Bin Noor
1,
Ridwan Sakidja
1 and
Tiglet Besara
1,*
1
Department of Physics, Astronomy, and Materials Science, Missouri State University, Springfield, MO 65897, USA
2
Department of Chemistry and Biochemistry, Missouri State University, Springfield, MO 65897, USA
*
Author to whom correspondence should be addressed.
Crystals 2025, 15(5), 391; https://doi.org/10.3390/cryst15050391
Submission received: 25 March 2025 / Revised: 17 April 2025 / Accepted: 21 April 2025 / Published: 23 April 2025
Browse Figures
Versions Notes

Abstract

:
Two new cage-structured compounds—NbCu2Zn20 and HfCu2Zn20—belonging to the MM’2X20 (M, M’ = transition or rare earth metals, and X = Al, Zn, or Cd) family of structures have been synthesized via the self-flux method. The new compounds crystallize in the space group F d 3 ¯ m with lattice parameter 13.9013(2) Å for NbCu2Zn20 and 13.9856(2) Å for HfCu2Zn20. The structures follow the expected metallic radii trend in MM’20Zn20 (M = Nb or Hf, M’ = Mn, Fe, Co, Ni, and Cu). While NbCu2Zn20 is stoichiometric, HfCu2Zn20 exhibits Cu/Zn site mixing and Hf-site underoccupancy, resulting in a final stoichiometry of Hf0.96Cu1.67Zn20.33 (Hf1–δCu2–xZn20+x, δ = 0.04, x = 0.33).

1. Introduction

The interest in the large family of isostructural ternary intermetallic compounds with chemical formula MM’2X20 (M, M’ = transition or rare earth metals and X = Al, Zn, Cd) has increased recently. These compounds crystallize in the CeCr2Al20-type structure [1] with space group F d 3 ¯ m (#227) and comprise “cages” formed by the X element and which contain the loosely-bound M and M’ elements [2,3,4,5,6,7,8].
The phase space of these ternaries has been explored extensively with—to our knowledge—92 compounds in the MM’2Zn20 family, 84 compounds in the MM’2Al20 family, and 26 compounds in the MM’2Cd20 family [7,9,10]. A review of their structure–property relationships was recently published [7]. Many of these compounds display disorder at the X atom positions, e.g., Al/Zn and In/Zn mixing [11,12,13], Sn/Zn mixing [14], and Mn/Zn mixing in ZrMn2Zn20 [15] and HfMn2Zn20 [9]. Recently, a new mixing was discovered: Al/Ga, thus, creating the first gallides in this structure [16]. With such a variety of compounds that crystallize in this structure across the rare earths and the transition metals, there is naturally a large spread in physical properties.
Many members of this family have been explored for their magnetic behavior. The magnetic properties cover the whole spectrum: paramagnetism [16,17,18], ferromagnetism [19,20,21,22,23], antiferromagnetism [22,24,25,26,27,28,29], itinerant magnetism [9,15,23], metamagnetic transitions [30], and double magnetic transitions [31]. Others structures have been explored for their electronic stability [32], crystalline electric fields [33,34,35], elastic constant [36], and their Fermi surface [37,38,39,40].
Their most recent attraction is due to their enhanced low-temperature thermoelectric properties and their exhibition of superconductivity. The thermoelectricity in these compounds is based on the so-called “phonon-glass, electron-crystal” concept [41,42,43]. The loosely bound M and M’ elements rattle in their cages and disperse phonons and, hence, decrease the lattice contribution to the thermal conductivity. This has been explored in the YbTM2Zn20 (TM = transition metals) compounds [44,45] and more recently in the mixed M-site REIr2Zn20 (RE = rare earth metals) compounds [46]. The superconductivity has been explored in terms of enhanced TC due to the rattling in the cages, mainly in X = Al compounds [47,48,49,50] but also in X = Zn [51] and X = Cd [52] compounds.
Of these 202 isostructural compounds, only one compound containing Cu has been synthesized: ZrCu2Zn20 [15] as part of a larger study of ZrM’2Zn20 compounds (M’ = Cr–Cu). In that study, it was suggested that site mixing increased with M’ size: largest mixing for Cr, smaller for Mn, and no mixing for Fe–Cu. Here, we present the single crystal synthesis and structure of two new members in this family containing Cu, NbCu2Zn20 and HfCu2Zn20. We compare their structures to other NbM’2Zn20 and HfM’2Zn20, where the M’ are first-period transition metals, and to ZrCu2Zn20, and look at lattice parameter trends and site mixing. Neither NbCu2Zn20 nor HfCu2Zn20 comprise magnetic atoms and are therefore not expected to exhibit any magnetic properties. They are, however, both candidates for low-temperature thermoelectricity, similar to YbTM2Zn20. NbCu2Zn20 is a possible superconductor due to the presence of Nb.

2. Methods

2.1. Synthesis

We grew single crystals of NbCu2Zn20 and HfCu2Zn20 by a self-flux method which is described in detail by M. Tachibana [53]: Polycrystalline amounts of 1 mmol of Nb (≈92.91 mg, 99.99%, Alfa Aesar) or Hf metal (≈178.5 mg, 99.6%, Alfa Aesar), 2 mmol of Cu (≈127.1 mg, 99.9%, Alfa Aesar), and 60 mmol of Zn (≈3.925 g, 99.9%, Alfa Aesar) were loaded into 2 mL alumina crucibles (13 mm diameter and 25 mm height). The starting ratios were chosen to maintain a Nb/Hf:Cu ratio of 1:2, while the amount of 60 mmol of Zn ensured that adequate Zn was present to act as the molten medium (the flux) in which crystallization takes place. The alumina crucibles were capped by upside-down alumina crucibles partly filled with quartz wool. The crucible ensembles were then sealed in fused silica ampoules under vacuum to hinder oxidation. The ampoules were put in a muffle furnace, heated to 800 °C at a rate of about 100 °C/h and kept at that temperature for 20 h, allowing the starting materials to soak well in the zinc flux. This was followed by slow-cooling at 5 °C/h until 550 °C—more than 100 degrees above the flux melting point. At that point, the ampoules were rapidly pulled out of the furnace, immediately flipped, and centrifuged, to ensure separation of solid crystals and still-molten flux. The quartz wool in the alumina caps served as the filter by letting through the molten flux while stopping crystals from going through. We harvested crystals after the ampoules cooled to ambient temperature. Some of the crystals had extra flux on their surface which was etched away with highly diluted HCl solution which attacked the elemental zinc at a higher rate than the crystals. The crystals are stable in the air.

2.2. Energy Dispersion Spectroscopy

We performed elemental analysis via energy-dispersive spectroscopy (EDS) using a FEI QUANTA 200 FEG scanning electron microscope (SEM) equipped with an Oxford Instruments Ultim Max EDS detector. All crystals were mounted on copper tape with a flat crystal face up, and the measurements were made at 20 kV. We measured several crystals of various sizes and shapes with EDS to confirm the stoichiometry of the compounds, with (Nb,Hf):Cu:Zn molar ratios of on average 4.5:8.5:87.0 to within a percent.

2.3. X-Ray Diffraction

We performed single-crystal X-ray diffraction with a Rigaku-Oxford Diffraction XtaLAB Synergy-S diffractometer equipped with a HyPix-6000HE Hybrid Photon Counting detector and dual PhotonJet-S Mo/Cu 50W Microfocus X-ray Sources. We collected data at room temperature with Mo Kα radiation (λ = 0.71073 Å) using ω scans with 0.5° frame widths to a resolution of 0.5 Å, equivalent to 2θ ≈ 90°. The reflections were recorded, indexed, and corrected for absorption using the Rigaku Oxford Diffraction CrysAlisPro software [54]. We performed the subsequent refinements with the X-ray structure refinement and analysis software CRYSTALS [55], where we employed the charge-flipping software SUPERFLIP [56] to solve the crystal structure. The data quality allowed for an unconstrained full matrix refinement against F2 with anisotropic displacement parameters for all atoms. We have deposited CIFs with the Cambridge Crystallographic Data Centre (CSD # 2201921 and 2201922) [57].

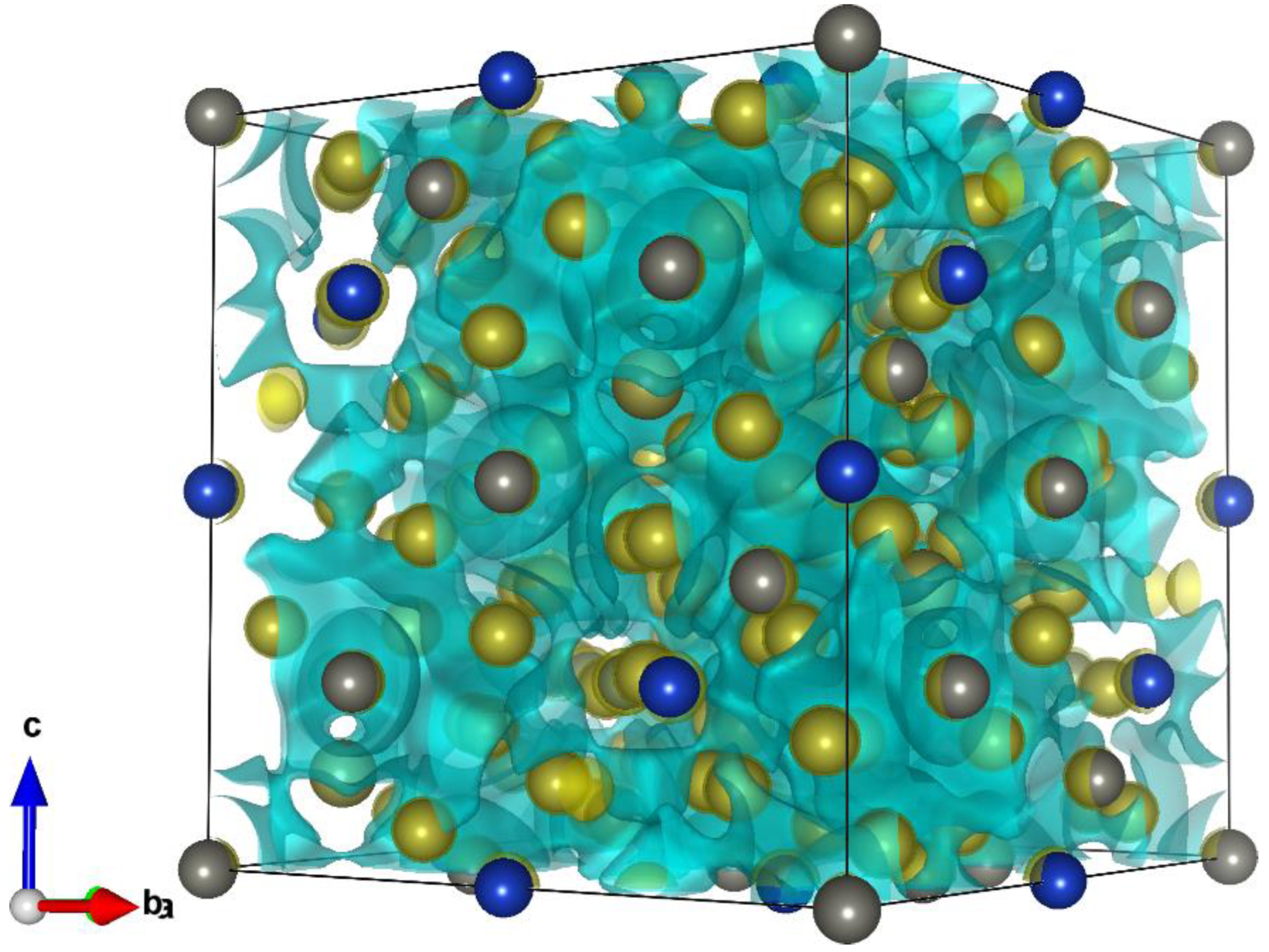
2.4. Density Functional Theory

We performed density-functional theory (DFT) calculations with VASP [58,59], employing spin-polarization with the PBE functional and with PAW pseudopotentials for Hf (Hf_pv with the valence electron configuration of 5p6 5d3 6s1), Cu (Cu_pv with the valence electron configuration of 3p6 3d10 4s1), and Zn (Zn with the valence electron configuration of 3d10 4s2). We used a plane-wave cutoff energy of 400 eV, ensuring a balance between accuracy and computational efficiency. The electronic relaxation is controlled by an SCF convergence criterion of 1.0∙10−5 eV. We employed an ionic relaxation following a quasi-Newton-Raphson scheme with a force convergence criterion of 1.0∙10−4 eV. We performed a full relaxation of both the atomic positions and the cell shape. Gaussian smearing is applied appropriately for the metallic behavior of the compound. Given the relatively large structure, the 1 × 1 × 1 Monkhorst-Pack k-point grid is appropriate, providing efficient sampling that prioritizes accurate relaxation of atomic positions and cell parameters.

3. Results and Discussion

The flux synthesis of MCu2Zn20 (M = Nb, Hf) resulted in high yields of small crystals (<1 mm on each side). The crystals display, in general, an octahedral morphology (see the insets in Figure 1 for SEM images) and crystallize in the cubic space group F d 3 ¯ m (Z = 8) as has been reported for all other members of this family. Crystal data and crystallographic parameters resulting from the single-crystal x-ray diffraction and subsequent refinement and structure solution are summarized in Table 1, while Table 2 lists the atomic coordinates of the two compounds. The Hf compound experiences mixing on the 16d site in addition to a not fully occupied 8a site (the Hf site), which will be discussed further down. Similar behavior was also reported in HfMn2Zn20 [9]. This compound, however, will still be referred to as HfCu2Zn20 for clarity. Figure 1 displays the unit cell of these compounds, viewed along [010] in Figure 1a and along [110] in Figure 1b. All structure figures were generated using CrystalMaker [60].
As has been reported earlier [2,3,7,44], these structures comprise large cages, or voids, of Zn (or Al or Cd) with M or M’ in the center of the cages. These cages are shown in Figure 1b. All cages are corner shared via the Zn1 atoms. The M atom is surrounded by 16 Zn atoms (12 Zn1 and four Zn3) forming a Frank–Kasper polyhedron (blue polyhedra in Figure 1b) while the Cu atom is surrounded by 12 Zn atoms (six Zn1 and six Zn2) forming an icosahedron (magenta polyhedra in Figure 1b) [44]. The cage structures are shown in Figure 2 with all atoms displaying anisotropic displacement ellipsoids of 95% probability. Only minute differences can be observed between the polyhedra of NbCu2Zn20 and HfCu2Zn20.
The unit cell of HfCu2Zn20 is, as expected, larger than the unit cell of NbCu2Zn20; however, the lattice parameter increases only by approximately 0.61% and the unit cell volume by approximately 1.83%, even though the metallic radii of Nb and Hf are 1.46 Å and 1.59 Å [61], respectively, which constitutes a difference of approximately 8.90% (see Table 3). Comparing the atom-to-atom distances making up the cages and other atomic distances in the structures, all distances increase but on the order of less than 1%. Interestingly, both polyhedra grow when changing from NbCu2Zn20 to HfCu2Zn20, i.e., not only does the Frank–Kasper polyhedra containing M grow but so does the icosahedron containing Cu. The Frank–Kasper polyhedron grows by approximately 2.58%, while the icosahedron by less than half of that, 1.25%. We surmise that the reason that the Cu-containing icosahedron also grows is because it is not completely surrounded by M-containing Frank–Kasper polyhedra: only 6 of its 12 atoms are corner shared with Frank–Kasper polyhedra, the rest are corner shared with other icosahedra. Had the icosahedron been fully surrounded by Frank–Kasper polyhedra, one would expect a compression of the icosahedron rather than an expansion since the Frank–Kasper polyhedra grows when the M atom in its center changes from Nb to Hf. Instead, some rearrangement of atoms takes place, resulting in all distances increasing. Comparing all this to the expansion in metallic radii, it is clear that the Frank–Kasper polyhedron has the capability of “absorbing” substantial expansions in atomic radii, therefore enlarging the full unit cell by a smaller percentage.
Gross et al. [3] compared structural parameters of several MM’20Zn20 compounds, including NbM’2Zn20 and HfM’2Zn20 with—among others—M’ = Fe, Co, and Ni, and showed a reduction in lattice parameter and unit cell volume from Fe to Co to Ni, consistent with the trend in the metallic radii of these transition metals [61]. We recently extended the HfM’2Zn20 series to also include Mn [9]. The structural trend is extended here with the addition of the two new compounds NbCu2Zn20 and HfCu2Zn20 and can be seen in Figure 3. The lattice parameter and unit cell volume increase for M’ = Cu, as expected, since the metallic radius of Cu is 1.28 Å, while that of the preceding element Ni is 1.24 Å (upper panel of Figure 3) [61], thereby explaining the observed expansions. Compared to the Ni metallic radius, the Cu metallic radius increases by approximately 4.96%. The lattice parameter expansion from MNi2Zn20 to MCu2Zn20, on the other hand, is only approximately 0.67% and 0.88% for M = Nb and Hf, respectively, while the unit cell volume growth is 2.00% and 2.67%, less than the relative expansion of the metallic radius. This shows that the icosahedron of M’—similar to the Frank–Kasper polyhedra of M—also has the capability of “absorbing” substantial expansions in atomic radii, therefore enlarging the full unit cell by a smaller percentage than the metallic radii increase.
If we look at the polyhedra volumes as M’ changes (Figure 4), the icosahedron volume containing the M’ atom follows the M’ metallic radius trend for both NbM’2Zn20 and HfM’2Zn20 (middle panel of Figure 4): the volumes shrink from M’ = Mn to Ni and then expand for M’ = Cu. The shrinking of the volume from Fe to Co to Ni is more pronounced for NbM’2Zn20 than for HfM’2Zn20: a change of 0.661 Å3 in the HfM’2Zn20 case and a change of 2.331 Å3 in the NbM’2Zn20.
The Frank–Kasper polyhedron containing the M atom, on the other hand, does not follow the full metallic radii trend (lower panel of Figure 4), which was already noted for Mn when it was added to the trend of HfM’2Zn20 [9]. In the HfM’2Zn20 case (green circles in Figure 4) from Fe to Co to Ni, the volume follows the metallic radius: decreasing metallic radius results in shrinking of volume. Instead of an expected increase, however, of the Frank–Kasper volume from Fe to Mn (since the metallic radius increases), the volume shrank. This was explained by the fact that a Frank–Kasper polyhedron is corner shared with 12 M’-containing icosahedra and only four other Frank–Kasper polyhedra and is therefore affected strongly by the expansion of the surrounding icosahedra. Since this volume shrinks as its center atom changes from Fe (metallic radius 1.26 Å) to Mn (metallic radius 1.27 Å), it should also shrink further as the center atom changes from Ni (metallic radius 1.24 Å) to Cu (metallic radius 1.28 Å). This is clearly observed.
In the NbM’2Zn20 case (orange squares in Figure 4), on the other hand, the trend is different. As the M’ metallic radius shrinks from Fe to Co to Ni, the Frank–Kasper polyhedra expands. This can be explained by the more excessive shrinking of the icosahedron, therefore, leaving space for the Frank–Kasper polyhedra to expand. From Ni to Cu, however, the volume shrinks. With a metallic radius change from 1.24 Å (Ni) to 1.28 Å (Cu), the expansion of the surrounding icosahedra (12 of them) overcomes any potential volume increase and instead the Frank–Kasper polyhedron shrinks.
As mentioned previously, of the 202 compounds grown in this family [7,10], only one other M’ = Cu compound has been synthesized: ZrCu2Zn20 [15]. Table 4 lists all the existing MM’2Zn20 compounds (filled circles) with NbCu2Zn20 and HfCu2Zn20 added (open circles).
Comparing the attributes of the new compounds to ZrCu2Zn20, the trends are as expected. The metallic radius of Zr is 1.60 Å, approximately 0.63% larger than that of Hf (1.59 Å) and approximately 9.59% larger than that of Nb (1.46 Å) [61]. All attributes—lattice parameter, unit cell volume, Frank–Kasper polyhedron volume, icosahedron volume—of ZrCu2Zn20 are larger than those of HfCu2Zn20 and NbCu2Zn20 (see Table 5).
Svanidze et al. [15] observed an M’/Zn mixing at the 16d position (the M’-site, labeled M in their manuscript [9]) for their ZrM’2Zn20 compounds (M’ = Cr–Cu). The mixing apparently increased with the M’ size, with the largest mixing for M’ = Cr, resulting in ZrCrZn21 (ZrCr2–xZn20+x, x = 1), followed by M’ = Mn, resulting in ZrMn1.78Zn20.22 (ZrMn2–xZn20+x, x = 0.22). For the remaining compounds of M’ = Fe, Co, Ni, and Cu, no mixing was observed, resulting in stoichiometric ZrM’2Zn20 compounds. We recently observed similar Mn/Zn mixing at the 16d site in HfMn2Zn20 [9]. This then raises the question of whether the mixing is M’-size dependent since the metallic radius of Cu is as large as that of Cr (1.28 Å). To check the composition of the two new compounds, the site occupancy factors were relaxed for the five sites in the structures. In addition, since there is only one electron difference between Cu and Zn, refinements were repeated with a mixed Cu/Zn 16d position. In the case of NbCu2Zn20, no mixing was observed (negative occupancy factor for Cu and increased residuals), and only negligible deviations from the ideal composition. Therefore, it can be concluded that NbCu2Zn20 is stoichiometric. In the case of HfCu2Zn20, on the other hand, mixing was observed, and the residuals improved to R1 = 0.160 and wR2 = 0.276 and the goodness-of-fit to 0.9989. In addition, the 8a site of Hf was slightly underoccupied. It is not clear why the Hf site is slightly underoccupied as there is no reason for Cu or Zn to occupy the same site as Hf. Such underoccupancy was also observed in HfMn2Zn20 [9]. The final composition of this compound is then Hf0.96Cu1.67Zn20.33 (Hf1–δCu2–xZn20+x, δ = 0.04, x = 0.33). While the ZrM’2Zn20 compounds (M’ = Cr–Cu) displayed the largest site mixing in the M’ = Cr case, followed by M’ = Mn, and no site mixing in M’ = Fe, Co, Ni, and Cu, the HfM’2Zn20 compounds exhibit site mixing in the M’ = Mn and Cu cases, as shown in Ref. [9] and this study, with a larger mixing in the M’ = Mn case (Hf0.93Mn1.63Zn20.37). Gross et al. [3] did not observe any site mixing in the M’ = Fe, Co, and Ni cases.
To further support the experimental observation and analyze the cohesive stability of the new compounds, we performed ground state calculations by employing spin-polarized DFT calculations. Figure 5 presents the 3D isosurfaces of the charge density for the compounds, mapped at different charge density threshold values (F), ranging from a minimum of 0.014 to a maximum of 5.89 e/Å3. The isosurfaces are visualized at three distinct levels: 0.5 e/Å3 (light yellow), 0.025 e/Å3 (light blue), and 0.0125 e/Å3 (not visible due to too low of electron concentration), only for clarification and to show the special deformation of the valence electron density.
Figure 6 illustrates the electron density distribution along the (111) planes, scanned in 0.5 Å increments from the origin. At the center of the structure, the Hf atom is covalently bonded to Zn atoms, with iso-surface slices extending up to 8 Å from the origin. Only selected iso-surface slices are shown: at the origin, at 2.5 Å, at 3 Å, at 3.5 Å, at 4 Å, and at 8 Å. A movie of all slices from origin to 8 Å can be found in the Supplementary Material. The deformation observed in the Hf valence electron density map suggests significant charge redistribution due to covalent bonding between Hf and the partially mixed Cu/Zn sites. This charge redistribution may enhance the cohesive stability of the newly synthesized compound relative to its Zr-based counterparts, which may translate into a larger tolerance towards some degree of off-stoichiometry. Notably, in conventional Laves phases [62], Hf-based structures exhibit a greater degree of off-stoichiometry compared to their Zr-based counterparts, which may further influence the observed charge density variations.

4. Conclusions

In summary, we have synthesized two new members of the MM’2Zn20 family of compounds—NbCu2Zn20 and HfCu2Zn20—in single crystalline form. Their structures and sizes follow the M’ metallic radius trend with the lattice successively shrinking from MFe2Zn20 to MCo2Zn20 to MNi2Zn20 and then expanding to MCu2Zn20. With these two new compounds, MCu2X20 (M = transition or rare earth metals and X = Al, Zn, Cd) has been expanded to three members since only ZrCu2Zn20 existed before. While NbCu2Zn20 crystallizes in the ideal composition, HfCu2Zn20 does not: it exhibits Cu/Zn site mixing at the Cu site and an underoccupied Hf site, rendering its final composition Hf0.96Cu1.67Zn20.33. The results were corroborated with DFT calculations by exploring the electron density distribution at different cross-sections. Similar site mixing was observed in HfMn2Zn20 [9]. Interestingly, no site mixing was observed in ZrCu2Zn20 [15] but it was observed in the ZrCr2Zn20 and ZrMn2Zn20 compounds which was attributed to M’ size differences. Since Hf and Zr have near identical metallic radii, it is interesting that mixing is observed in HfCu2Zn20, with Hf being a 5d element, but not in ZrCu2Zn20 and NbCu2Zn20, with Zr and Nb being 4d elements. To explore these trends further, we will attempt to synthesize the M = Ta (a 5d element but with a metallic radius identical to that of Nb) analog TaCu2Zn20.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15050391/s1, Video S1: HfCu2Zn20_movie.

Author Contributions

Conceptualization, T.B.; Methodology, S.M.L., N.Y., M.F.B.N., R.S. and T.B.; Software, M.M.M. and R.S.; Validation, T.B.; Formal analysis, R.S. and T.B.; Investigation, S.M.L., M.M.M., N.Y., M.F.B.N., R.S. and T.B.; Resources, T.B.; Data curation, T.B.; Writing—original draft, T.B.; Writing—review & editing, S.M.L., R.S. and T.B.; Supervision, T.B.; Project administration, T.B.; Funding acquisition, T.B. All authors have read and agreed to the published version of the manuscript.

Funding

A portion of this work was funded by the National Science Foundation grant number CHE-2117129. S.M.L. was funded by the NASA Missouri Space Grant Consortium.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

S.M.L. and T.B. acknowledge the NASA Missouri Space Grant Consortium for providing undergraduate internships. N.Y., M.F.B.N., and T.B. acknowledge financial support provided by Missouri State University’s new faculty startup fund. M.M.M. and R.S. acknowledge Missouri State University for the GPU workstation facility.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kripyakevich, P.I.; Zarechnyuk, O.S. RCr2Al20 Compounds in Systems of Rare Earth Metals and Calcium, and their Crystal Structures. Dopov. Akad. Nauk Ukr. RSR Ser. A 1968, 30, 364–367. [Google Scholar]
  2. Nasch, T.; Jeitschko, W.; Rodewald, U.C. Ternary Rare Earth Transition Metal Zinc Compounds RT2Zn20 with T = Fe, Ru, Co, Rh, and Ni. Z. Naturforsch. B 1997, 52, 1023–1030. [Google Scholar] [CrossRef]
  3. Gross, N.; Nasch, T.; Jeitschko, W. Ternary Intermetallics with High Zinc Content: TT′2Zn20 (T = Zr, Hf, Nb; T′ = Mn, Fe, Ru, Co, Rh, Ni) with CeCr2Al20-type Structure. J. Solid State Chem. 2001, 161, 288–293. [Google Scholar] [CrossRef]
  4. Niemann, S.; Jeitschko, W. Ternary Aluminides AT2Al20 (A = Rare Earth Elements and Uranium; T = Ti, Nb, Ta, Mo, and W) with CeCr2Al20-type Structure. J. Solid State Chem. 1995, 114, 337–341. [Google Scholar] [CrossRef]
  5. Canfield, P.C.; Jia, S.; Mun, E.D.; Bud’ko, S.L.; Samolyuk, G.D.; Torikachvili, M.S. Myriad of Correlated Electron Effects Found in the RT2Zn20 Family. Phys. B Condens. Matter 2008, 403, 844–846. [Google Scholar] [CrossRef]
  6. Thiede, V.M.T.; Jeitschko, W.; Niemann, S.; Ebel, T. EuTa2Al20, Ca6W4Al43 and Other Compounds with CeCr2Al20 and Ho6Mo4Al43 Type Structures and Some Magnetic Properties of These Compounds. J. Alloys Comp. 1998, 267, 23–31. [Google Scholar] [CrossRef]
  7. Pöttgen, R.; Janka, O. CeCr2Al20-type Intermetallics—Structure-property Relationships. Rev. Inorg. Chem. 2023, 43, 357–383. [Google Scholar] [CrossRef]
  8. Koldemir, A.; Klenner, S.; Pöttgen, R. Crystal Structure of Europium Dichromium Icosaaluminum, EuCr2Al20. Z. Für Kristallographie-New Cryst. Struct. 2023, 238, 507–509. [Google Scholar] [CrossRef]
  9. Yasmin, N.; Noor, M.F.B.; Besara, T. Structural Trends and Itinerant Magnetism of the New Cage-structured Compound HfMn2Zn20. J. Phys. Condens. Matter 2024, 36, 275801. [Google Scholar] [CrossRef]
  10. Zagorac, D.; Müller, H.; Ruehl, S.; Zagorac, J.; Rehme, S. Recent Developments in the Inorganic Crystal Structure Database: Theoretical Crystal Structure Data and Related Features. J. Appl. Crystallogr. 2019, 52, 918–925. [Google Scholar] [CrossRef]
  11. Okamoto, Y.; Shimizu, T.; Yamaura, J.; Hiroi, Z. Crystal Chemistry and Magnetic Properties of Manganese Zinc Alloy “YMn2Zn20” Comprising a Mn Pyrochlore Lattice. J. Solid State Chem. 2012, 191, 246–256. [Google Scholar] [CrossRef]
  12. Okamoto, Y.; Shimizu, T.; Yamaura, J.-i.; Kiuchi, Y.; Hiroi, Z. Itinerant-electron Magnet of the Pyrochlore Lattice: Indium-doped YMn2Zn20. J. Phys. Soc. Jpn. 2010, 79, 093712. [Google Scholar] [CrossRef]
  13. Benbow, E.M.; Latturner, S.E. Mixed-metal Flux Synthesis of Quaternary RMn2TrxZn20−x Compounds with Tr = Al, In. J. Solid State Chem. 2006, 179, 3989–3996. [Google Scholar] [CrossRef]
  14. Yogi, M.; Kubota, F.; Uehara, H.; Higa, N.; Sugiyama, Y.; Wakiya, K.; Umehara, I. NMR Studies of Structural Stabilization by Site-Selective Element Substitution in 1-2-20 System. JPS Conf. Proc. 2020, 29, 015004. [Google Scholar] [CrossRef]
  15. Svanidze, E.; Kindy II, M.; Georgen, C.; Fulfer, B.W.; Lapidus, S.H.; Chan, J.Y.; Morosan, E. Magnetic and Crystallographic Properties of ZrM2−dZn20+d (M = Cr−Cu). J. Magn. Magn. Mater. 2016, 416, 401–407. [Google Scholar] [CrossRef]
  16. Schumacher, L.; Kösters, J.; Hensmann, L.; Pöttgen, R. The Solid Solutions RETi2Al20−xGax (0 ≤ x ≤ 10) with RE = Eu, Gd, Tb, Dy and Yb−First Gallides with CeCr2Al20-type Structure. Z. Für Kristallographie-Cryst. Mater. 2024, 239, 367–376. [Google Scholar] [CrossRef]
  17. Swatek, P.; Kaczorowski, D. Magnetic and Electrical Properties of UCr2Al20 Single Crystals. J. Solid State Chem. 2012, 191, 191–194. [Google Scholar] [CrossRef]
  18. Schumacher, L.; Schreiner, F.; Koldemir, A.; Janka, O.; Hansen, M.R.; Pöttgen, R. Cadmium-rich Intermetallic Phases ARh2Cd20—Structure, Magnetic Behavior, 151Eu Mössbauer and 113Cd Solid-state NMR Spectroscopy. Dalton Trans. 2025. Advance Article. [Google Scholar] [CrossRef]
  19. Jia, S.; Bud’ko, S.L.; Samolyuk, G.D.; Canfield, P.C. Nearly Ferromagnetic Fermi-liquid Behaviour in YFe2Zn20 and High-temperature Ferromagnetism of GdFe2Zn20. Nat. Phys. 2007, 3, 334–338. [Google Scholar] [CrossRef]
  20. Jia, S.; Ni, N.; Bud’ko, S.L.; Canfield, P.C. Magnetic Properties of GdxY1−xFe2Zn20: Dilute, Large-S Moments in a Nearly Ferromagnetic Fermi Liquid. Phys. Rev. B 2007, 76, 184410. [Google Scholar] [CrossRef]
  21. Jia, S.; Ni, N.; Bud’ko, S.L.; Canfield, P.C. Magnetic Properties of RFe2Zn20 and RCo2Zn20 (R = Y, Nd, Sm, Gd-Lu). Phys. Rev. B 2009, 80, 104403. [Google Scholar] [CrossRef]
  22. Jia, S.; Ni, N.; Samolyuk, G.D.; Safa-Sefat, A.; Dennis, K.; Ko, H.; Miller, G.J.; Bud’ko, S.L.; Canfield, P.C. Variation of the Magnetic Ordering in GdT2Zn20 (T = Fe, Ru, Os, Co, Rh and Ir) and Its Correlation with the Electronic Structure of Isostructural YT2Zn20. Phys. Rev. B 2008, 77, 104408. [Google Scholar] [CrossRef]
  23. Wang, C.H.; Lawrence, J.M.; Bauer, E.D.; Kothapalli, K.; Gardner, J.S.; Ronning, F.; Gofryk, K.; Thompson, J.D.; Nakotte, H.; Trouw, F. Unusual Signatures of the Ferromagnetic Transition in the Heavy Fermion Compound UMn2Al20. Phys. Rev. B 2010, 82, 094406. [Google Scholar] [CrossRef]
  24. Kase, N.; Shimura, Y.; Kittaka, S.; Sakakibara, T.; Nakatsuji, S.; Nakano, T.; Takeda, N.; Akimitsu, J. Antiferromagnetic Transition of the Caged Compound TmTi2Al20. J. Phys. Conf. Ser. 2015, 592, 012052. [Google Scholar] [CrossRef]
  25. Hirose, Y.; Doto, H.; Honda, F.; Li, D.; Aoki, D.; Haga, Y.; Settai, R. New Heavy-fermion Antiferromagnet UPd2Cd20. J. Phys. Condens. Matter 2016, 28, 425601. [Google Scholar] [CrossRef] [PubMed]
  26. Torikachvili, M.S.; Jia, S.; Mun, E.D.; Hannahs, S.T.; Black, R.C.; Neils, W.K.; Martien, D.; Bud’ko, S.L.; Canfield, P.C. Six Closely Related YbT2Zn20 (T = Fe, Co, Ru, Rh, Os, Ir) Heavy Fermion Compounds with Large Local Moment Degeneracy. Proc. Natl. Acad. Sci. USA 2007, 104, 9960–9963. [Google Scholar] [CrossRef] [PubMed]
  27. Verbovytsky, Y.; Łątka, K.; Tomala, K. The Crystal Structure and Magnetic Properties of the GdV2Al20 and GdCr2Al20 Ternary Compounds. J. Alloys Comp. 2007, 442, 334–336. [Google Scholar] [CrossRef]
  28. Tian, W.; Christianson, A.D.; Zarestky, J.L.; Jia, S.; Bud’ko, S.L.; Canfield, P.C.; Piccoli, P.M.B.; Schultz, A.J. Magnetic Order in TbCo2Zn20 and TbFe2Zn20. Phys. Rev. B 2010, 81, 144409. [Google Scholar] [CrossRef]
  29. Yamamoto, R.; Onimaru, T.; Yamane, Y.; Shimura, Y.; Umeo, K.; Takabatake, T. Magnetic Properties of a Diluted Nd System Y1−xNdxCo2Zn20 for x = 0.20 with a Γ6 Doublet Ground State. JPS Conf. Proc. 2020, 29, 015006. [Google Scholar] [CrossRef]
  30. Hirose, Y.; Toda, M.; Yoshiuchi, S.; Yasui, S.; Sugiyama, K.; Honda, F.; Hagiwara, M.; Kindo, K.; Settai, R.; Ōnuki, Y. Metamagnetic Transition in Heavy Fermion Compounds YbT2Zn20 (T: Co, Rh, Ir). J. Phys. Conf. Ser. 2011, 273, 012003. [Google Scholar] [CrossRef]
  31. Ramesh Kumar, K.; Nair, H.S.; Christian, R.; Thamizhavel, A.; Strydom, A.M. Magnetic, Specific Heat and Electrical Transport Properties of Frank-Kasper Cage Compounds RTM2Al20 [R  =  Eu, Gd and La; TM = V, Ti]. J. Phys. Condens. Matter 2016, 28, 436002. [Google Scholar] [CrossRef]
  32. Yaniv, G.; Vidal, D.; Fuks, D.; Meshi, L. Bonding and Stability of Ternary Structures in the CeT2Al20 (T = Ta, W, Re) and YRe2Al20 Alloys. Metals 2020, 10, 422. [Google Scholar] [CrossRef]
  33. Yamamoto, R.; Le, M.D.; Adroja, D.T.; Shimura, Y.; Takabatake, T.; Onimaru, T. Inelastic Neutron Scattering Study of Crystalline Electric Field Excitations in the Caged Compounds NdT2Zn20 (T = Co, Rh, and Ir). Phys. Rev. B 2023, 107, 075114. [Google Scholar] [CrossRef]
  34. Yamane, Y.; Onimaru, T.; Shimura, Y.; Umeo, K.; Takabatake, T. Non-Kramers Γ3 Doublet Ground State in a Diluted Pr System Y1−xPrxCo2Zn20. JPS Conf. Proc. 2020, 29, 015001. [Google Scholar] [CrossRef]
  35. Kubo, T.; Tou, H.; Kotegawa, H.; Harima, H.; Higashinaka, R.; Nakamaka, A.; Aoki, Y.; Sato, H. Development of Short-range Correlations of 4f Electrons in the Non-Kramers Γ3 System PrNb2Al20 at Low Temperatures Investigated by NMR Measurements. JPS Conf. Proc. 2020, 29, 015003. [Google Scholar] [CrossRef]
  36. Yanagisawa, T.; Hidaka, H.; Amitsuka, H.; Zherlitsyn, S.; Wosnitza, J.; Yamane, Y.; Onimaru, T. Logarithmic Elastic Response in the Dilute Non-Kramers System Y1−xPrxIr2Zn20. JPS Conf. Proc. 2020, 29, 015002. [Google Scholar] [CrossRef]
  37. Afzal, M.A.; Ōnuki, Y.; Aoki, D.; Harima, H.; Higashinaka, R.; Aoki, Y.; Matsuda, T.D. Large Cyclotron Effective Masses in Antiferromagnet SmTi2Al20 Compared with Conventional Masses in Ferromagnet SmNi2Cd20 and Antiferromagnet SmPd2Cd20. J. Phys. Soc. Jpn. 2024, 93, 054710. [Google Scholar] [CrossRef]
  38. Omasa, K.; Matsuoka, E.; Aoki, D.; Sugawara, H. de Haas-van Alphen Effect in SmTi2Al20. JPS Conf. Proc. 2020, 29, 015007. [Google Scholar] [CrossRef]
  39. Kubo, T.; Matsuoka, E.; Kotegawa, H.; Tou, H.; Nakamura, A.; Aoki, D.; Harima, H.; Sugawara, H. Fermi Surface of the Heavy-fermion Superconductor PrTi2Al20. J. Phys. Soc. Jpn. 2020, 89, 084704. [Google Scholar] [CrossRef]
  40. Magishi, K.; Hisada, A.; Saito, T.; Koyama, K.; Namiki, T.; Nishimura, K. NMR Study of Caged Cubic Compound NdTr2Al20 (Tr = Ti and V). JPS Conf. Proc. 2020, 29, 015005. [Google Scholar] [CrossRef]
  41. Slack, G.A. New Materials and Performance Limits for Thermoelectric Cooling. In CRC Handbook of Thermoelectrics; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 1995; pp. 407–440. [Google Scholar]
  42. Sales, B.C. Novel Thermoelectric Materials. Curr. Opin. Solid State Mater. Sci. 1997, 2, 284–289. [Google Scholar] [CrossRef]
  43. Beekman, M.; Morelli, D.T.; Nolas, G.S. Better Thermoelectrics through Glass-like Crystals. Nat. Mater. 2015, 14, 1182–1185. [Google Scholar] [CrossRef]
  44. Wei, K.; Neu, J.N.; Lai, Y.; Chen, K.-W.; Hobbis, D.; Nolas, G.S.; Graf, D.E.; Siegrist, T.; Baumbach, R.E. Enhanced Thermoelectric Performance of Heavy-fermion Compounds YbTM2Zn20 (TM = Co, Rh, Ir) at Low Temperatures. Sci. Adv. 2019, 5, eaaw6183. [Google Scholar] [CrossRef] [PubMed]
  45. Mun, E.D.; Jia, S.; Bud’ko, S.L.; Canfield, P.C. Thermoelectric Power of the YbT2Zn20 (T = Fe, Ru, Os, Ir, Rh, and Co) Heavy Fermions. Phys. Rev. B 2012, 86, 115110. [Google Scholar] [CrossRef]
  46. Galeano-Cabral, J.R.; Karr, E.; Schundelmier, B.; Oladehin, O.; Choi, E.S.; Siegrist, T.; Ordonez, J.; Shastri, S.; Petkov, V.; Baumbach, R.E.; et al. Enhanced Thermoelectric Properties of Heavy-fermion Compounds YbxCeySmzIr2Zn20 (x + y + z = 1). Phys. Rev. Mater. 2023, 7, 025406. [Google Scholar] [CrossRef]
  47. Nakamura, N.; Higashinaka, R.; Aoki, Y.; Sato, H.; Matsuda, T.D. Superconducting Properties of Cage Compounds YbTr2Al20 with Tr = Mo and Ta. Solid State Commmun. 2023, 363, 115098. [Google Scholar] [CrossRef]
  48. Winiarski, M.J.; Wiendlocha, B.; Sternik, M.; Wiśniewski, P.; O’Brien, J.R.; Kaczorowski, D.; Klimczuk, T. Rattling-enhanced Superconductivity in MV2Al20 (M = Sc, Lu, Y) Intermetallic Cage Compounds. Phys. Rev. B 2016, 93, 134507. [Google Scholar] [CrossRef]
  49. Hiroi, Z.; Onosaka, A.; Okamoto, Y.; Yamaura, J.; Harima, H. Rattling and Superconducting Properties of the Cage Compound GaxV2Al20. J. Phys. Soc. Jpn. 2012, 81, 124707. [Google Scholar] [CrossRef]
  50. Onosaka, A.; Okamoto, Y.; Yamaura, J.-i.; Hiroi, Z. Superconductivity in the Einstein Solid AxV2Al20 (A = Al and Ga). J. Phys. Soc. Jpn. 2012, 81, 023703. [Google Scholar] [CrossRef]
  51. Onimaru, T.; Matsumoto, K.T.; Inoue, Y.F.; Umeo, K.; Saiga, Y.; Matsushita, Y.; Tamura, R.; Nishimoto, K.; Ishii, I.; Suzuki, T.; et al. Superconductivity and Structural Phase Transitions in Caged Compounds RT2Zn20 (R = La, Pr, T = Ru, Ir). J. Phys. Soc. Jpn. 2010, 79, 033704. [Google Scholar] [CrossRef]
  52. Panday, S.R.; Dzero, M. Superconductivity in Ce-based Cage Compounds. J. Phys. Condens. Matter 2023, 35, 335601. [Google Scholar] [CrossRef]
  53. Tachibana, M. Beginner’s Guide to Flux Crystal Growth; Springer: Tokyo, Japan, 2017. [Google Scholar] [CrossRef]
  54. Rigaku Oxford Diffraction CrysAlisPro, version 1.171.42.53a; Rigaku Corporation: Oxford, UK, 2022.
  55. Betteridge, P.W.; Carruthers, J.R.; Cooper, R.I.; Prout, K.; Watkin, D.J. CRYSTALS version 12: Software for Guided Crystal Structure Analysis. J. Appl. Crystallogr. 2003, 36, 1487. [Google Scholar] [CrossRef]
  56. Palatinus, L.; Chapuis, G. SUPERFLIP—A Computer Program for the Solution of Crystal Structures by Charge Flipping in Arbitrary Dimensions. J. Appl. Crystallogr. 2007, 40, 786–790. [Google Scholar] [CrossRef]
  57. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. B 2016, 72, 171–179. [Google Scholar] [CrossRef]
  58. Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
  59. Kresse, G.; Hafner, J. Ab Initio Molecular-dynamics Simulation of the Liquid-metal-amorphous-semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
  60. CrystalMaker, version 10.8.1; CrystalMaker Software Ltd.: Oxford, UK, 2023.
  61. Slater, J.C. Atomic Radii in Crystals. J. Chem. Phys. 1964, 41, 3199–3204. [Google Scholar] [CrossRef]
  62. Baker, H.; Henry, S.D.; Okamoto, H. ASM Handbook. Volume 3: Alloy Phase Diagrams; ASM International: Materials Park, OH, USA, 1992. [Google Scholar]
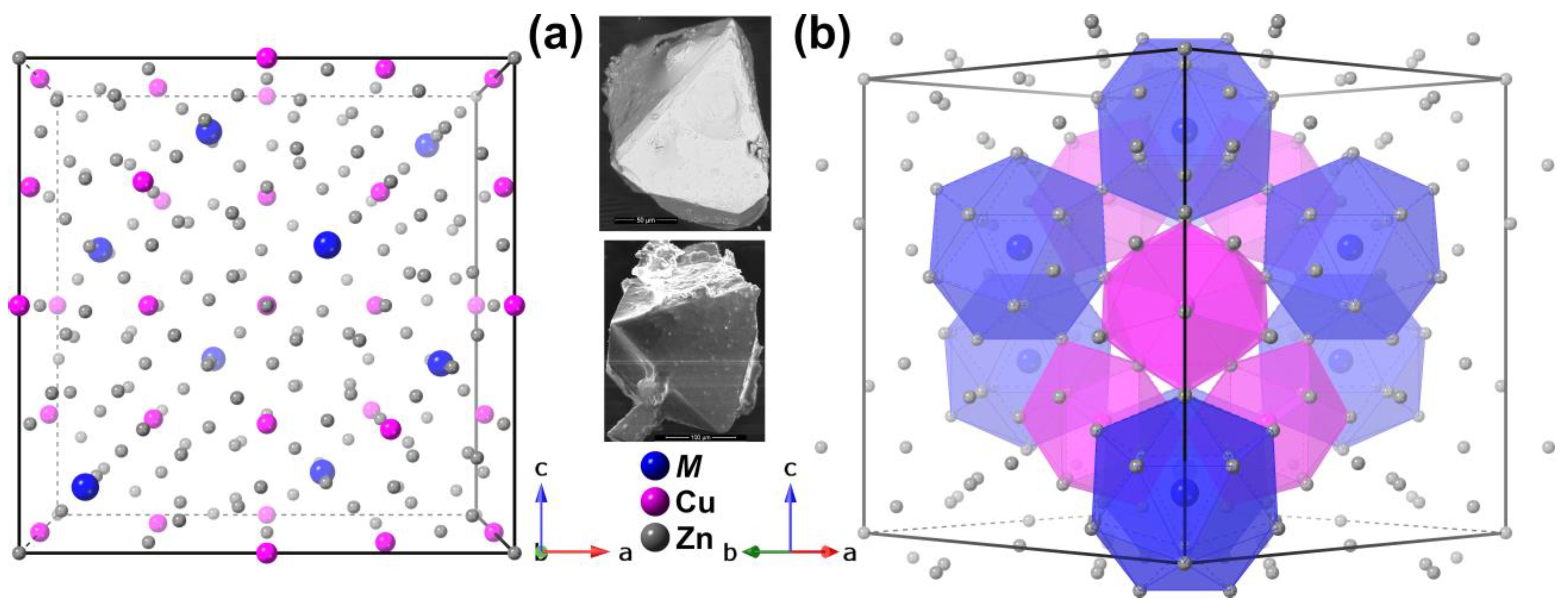
Crystals 15 00391 g001
Figure 1. Unit cell of MCu2Zn20 (M = Nb, Hf) shown in perspective mode (a) along [010] and (b) along [110], and also highlighting the cages formed by zinc atoms. The blue atoms are the transition metals Nb or Hf, the magenta atoms are Cu, and the gray atoms are Zn. The insets in the middle show SEM images of two crystals.
Figure 1. Unit cell of MCu2Zn20 (M = Nb, Hf) shown in perspective mode (a) along [010] and (b) along [110], and also highlighting the cages formed by zinc atoms. The blue atoms are the transition metals Nb or Hf, the magenta atoms are Cu, and the gray atoms are Zn. The insets in the middle show SEM images of two crystals.
Crystals 15 00391 g001
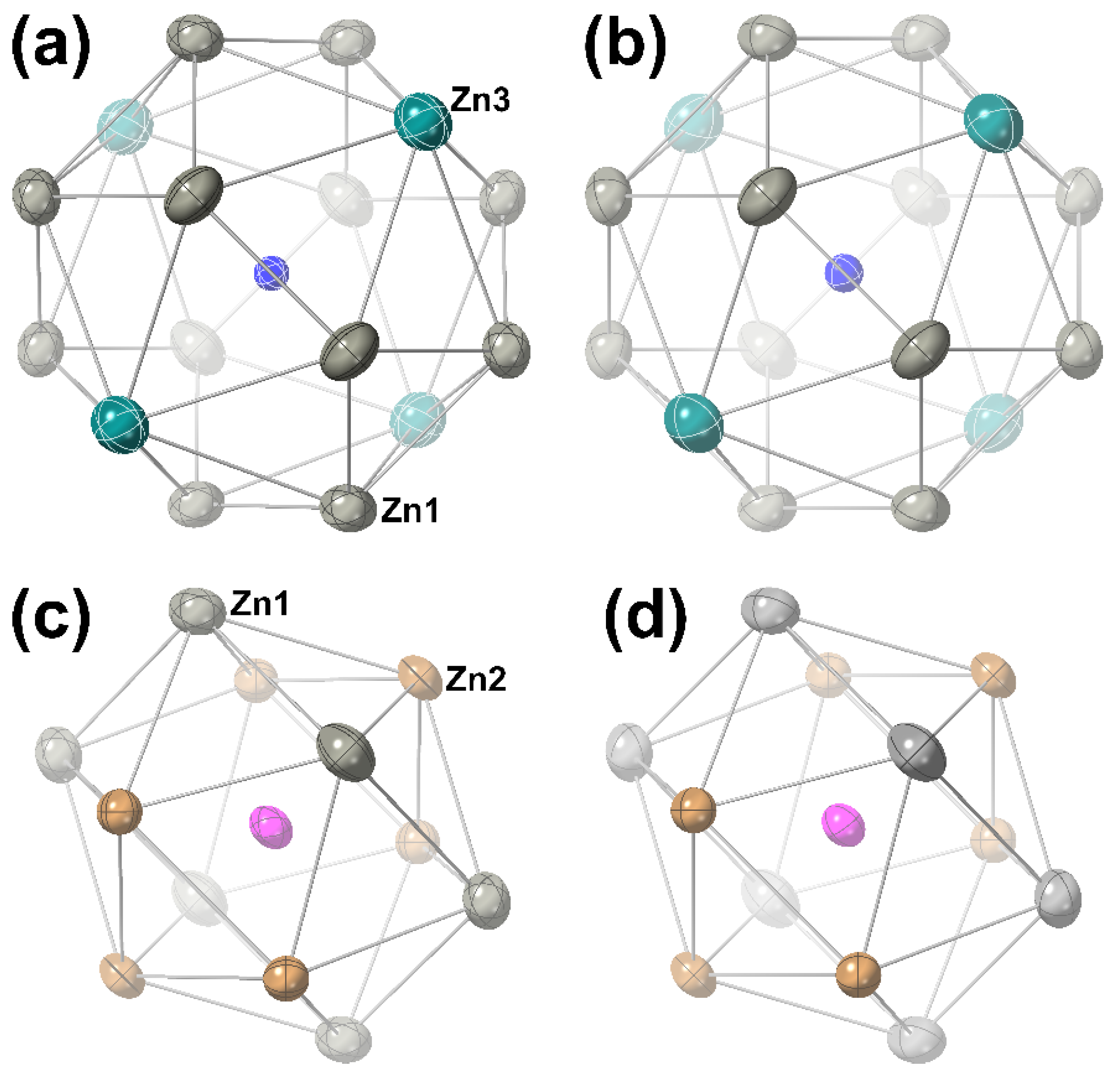
Crystals 15 00391 g002
Figure 2. The polyhedra/cages of MCu2Zn20 (M = Nb, Hf) displaying anisotropic displacement ellipsoids with 95% probability: (a,b) display the atomic environments of Nb and Hf (blue), respectively, comprising 12 Zn1 and four Zn3 atoms in a Frank–Kasper polyhedron, while (c,d) display the atomic environment of Cu (magenta) in NbCu2Zn20 and HfCu2Zn20, respectively, comprising six Zn1 and six Zn2 atoms in an icosahedron. The Zn1 atoms are gray, while the Zn2 atoms have been colored brown, and the Zn3 atoms teal for clarity.
Figure 2. The polyhedra/cages of MCu2Zn20 (M = Nb, Hf) displaying anisotropic displacement ellipsoids with 95% probability: (a,b) display the atomic environments of Nb and Hf (blue), respectively, comprising 12 Zn1 and four Zn3 atoms in a Frank–Kasper polyhedron, while (c,d) display the atomic environment of Cu (magenta) in NbCu2Zn20 and HfCu2Zn20, respectively, comprising six Zn1 and six Zn2 atoms in an icosahedron. The Zn1 atoms are gray, while the Zn2 atoms have been colored brown, and the Zn3 atoms teal for clarity.
Crystals 15 00391 g002
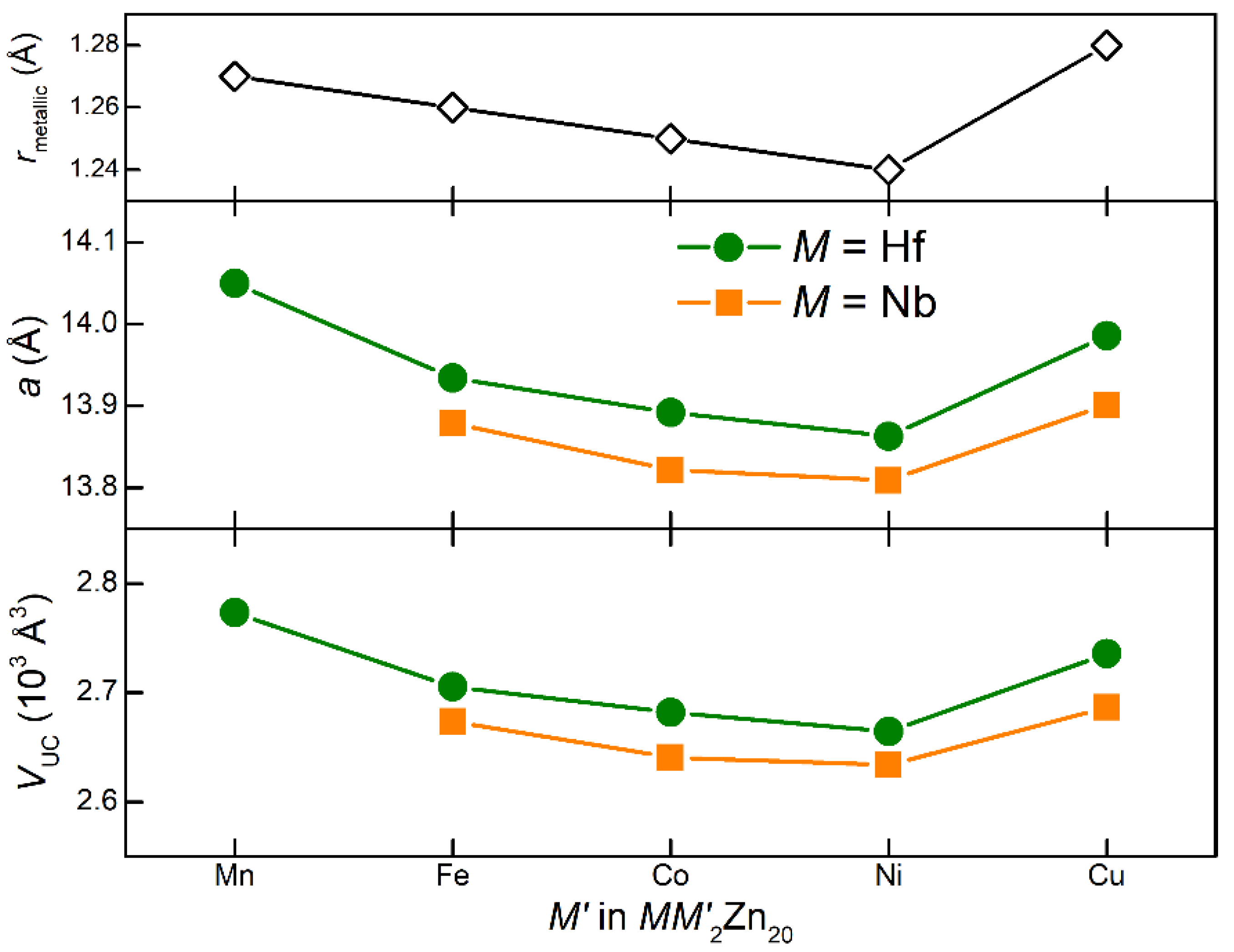
Crystals 15 00391 g003
Figure 3. Trend of lattice parameter (middle panel) and unit cell volume (lower panel) for NbM’2Zn20 (orange squares) and HfM’2Zn20 (green circles) across M’ = Mn, Fe, Co, Ni, and Cu. The metallic radius is shown in the (upper panel). The lattice parameter and unit cell volume expansions for the new M’ = Cu compounds follow the metallic radius trend. Data for the M’ = Mn compound are taken from Ref. [9], while data for the M’ = Fe, Co, and Ni compounds are taken from Ref. [3]. Metallic radii values are taken from Ref. [61]. Lines are guides to the eye. All error bars are within symbols.
Figure 3. Trend of lattice parameter (middle panel) and unit cell volume (lower panel) for NbM’2Zn20 (orange squares) and HfM’2Zn20 (green circles) across M’ = Mn, Fe, Co, Ni, and Cu. The metallic radius is shown in the (upper panel). The lattice parameter and unit cell volume expansions for the new M’ = Cu compounds follow the metallic radius trend. Data for the M’ = Mn compound are taken from Ref. [9], while data for the M’ = Fe, Co, and Ni compounds are taken from Ref. [3]. Metallic radii values are taken from Ref. [61]. Lines are guides to the eye. All error bars are within symbols.
Crystals 15 00391 g003
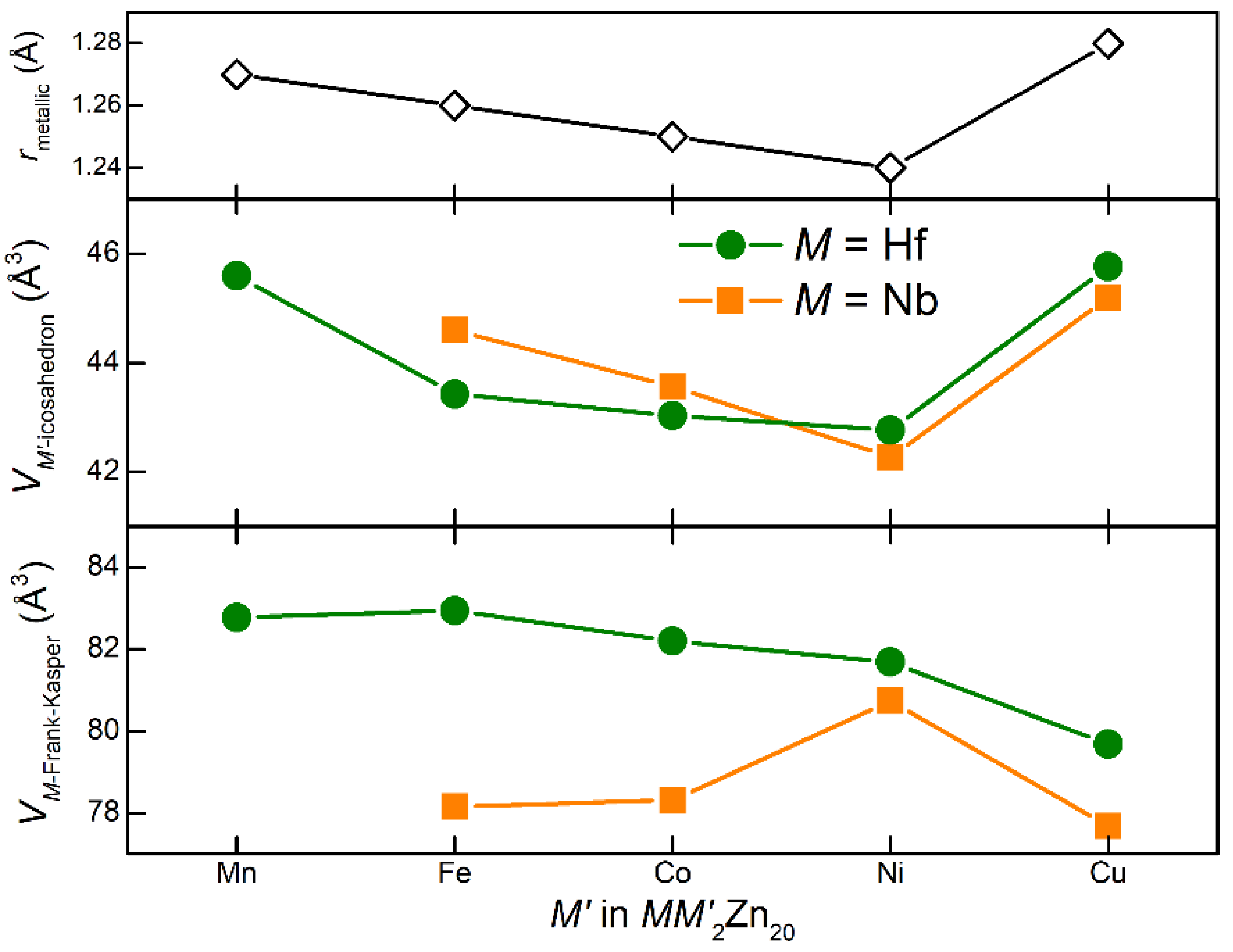
Crystals 15 00391 g004
Figure 4. Trend of M’-icosahedra volume (middle panel) and Frank–Kasper polyhedra volume (lower panel) for NbM’2Zn20 (orange squares) and HfM’2Zn20 (green circles) across M’ = Mn, Fe, Co, Ni, and Cu. The metallic radius trend is shown in the (upper panel). Data for the M’ = Mn compound is taken from Ref. [9], while data for the M’ = Fe, Co, and Ni compounds are taken from Ref. [3]. Metallic radii values are taken from Ref. [61]. Lines are guides to the eye. All error bars are within symbols.
Figure 4. Trend of M’-icosahedra volume (middle panel) and Frank–Kasper polyhedra volume (lower panel) for NbM’2Zn20 (orange squares) and HfM’2Zn20 (green circles) across M’ = Mn, Fe, Co, Ni, and Cu. The metallic radius trend is shown in the (upper panel). Data for the M’ = Mn compound is taken from Ref. [9], while data for the M’ = Fe, Co, and Ni compounds are taken from Ref. [3]. Metallic radii values are taken from Ref. [61]. Lines are guides to the eye. All error bars are within symbols.
Crystals 15 00391 g004
Crystals 15 00391 g005
Figure 5. Isosurface charge density 3D map, visualized at three distinct levels: 0.5 e/Å3 (light yellow), 0.025 e/Å3 (light blue), and 0.0125 e/Å3 (not visible due to too low of electron concentration). The dark yellow spheres are Hf, the dark blue spheres are Cu, and the gray spheres are Zn.
Figure 5. Isosurface charge density 3D map, visualized at three distinct levels: 0.5 e/Å3 (light yellow), 0.025 e/Å3 (light blue), and 0.0125 e/Å3 (not visible due to too low of electron concentration). The dark yellow spheres are Hf, the dark blue spheres are Cu, and the gray spheres are Zn.
Crystals 15 00391 g005
Crystals 15 00391 g006
Figure 6. Progression of selected charge slices normal to (111) planes: (a) at origin, (b) at 2.5 Å, (c) at 3 Å, (d) at 3.5 Å, (e) at 4 Å, and (f) at 8 Å. A movie of all slices from origin to 8 Å can be found in the Supplementary Material. The colors follow the same assignment as in Figure 5.
Figure 6. Progression of selected charge slices normal to (111) planes: (a) at origin, (b) at 2.5 Å, (c) at 3 Å, (d) at 3.5 Å, (e) at 4 Å, and (f) at 8 Å. A movie of all slices from origin to 8 Å can be found in the Supplementary Material. The colors follow the same assignment as in Figure 5.
Crystals 15 00391 g006
Table 1. Single crystal x-ray diffraction data and collection parameters for MCu2Zn20 (M = Nb, Hf), collected at room temperature. The data in square brackets in the M = Hf column refer to a refinement with fixed HfCu2Zn20 stoichiometry.
Table 1. Single crystal x-ray diffraction data and collection parameters for MCu2Zn20 (M = Nb, Hf), collected at room temperature. The data in square brackets in the M = Hf column refer to a refinement with fixed HfCu2Zn20 stoichiometry.
NbCu2Zn20Hf0.96Cu1.67Zn20.33
Molecular weight (g/mol)1527.601607.14 [1613.18]
Space group F d 3 ¯ m (#227) F d 3 ¯ m (#227)
a (Å)13.9013(2)13.9856(2)
V (Å3)2686.35(8)2735.52(7)
Z88
ρcalc (g/cm3)7.5547.804 [7.834]
Absorption coefficient µ (mm−1)38.80144.634 [44.850]
Absorption corrections Tmin, Tmax0.222, 0.3900.04, 0.12 [0.107, 0.280]
Crystal size (mm3)0.038 × 0.062 × 0.0680.048 × 0.076 × 0.094
Data collection range (°)2.54 < θ < 44.812.52 < θ < 44.76
h range−20 ≤ h ≤ 21−23 ≤ h ≤ 26
k range−27 ≤ k ≤ 26−27 ≤ k ≤ 27
l range−27 ≤ l ≤ 26−27 ≤ l ≤ 27
Reflections collected30496235
Independent reflections574577
Parameters refined1717
Restraints06 [0]
Δρmin, Δρmax (e/Å−3)−0.81, 0.71−3.51, 0.94 [−4.75, 1.32]
Rint0.0190.032
R1(F) for all data a0.01600.0160 [0.0198]
wR2(FO2) b0.03900.0276 [0.0473]
Goodness-of-fit on F20.99910.9989 [0.9872]
CSD #22019212201922
a R1 = Σ║FO│–│FC║/Σ│FO║. b wR2 = [Σw(FO2 − FC2)2/Σw(FO2)2]1/2, w = 1/[σ2(FO2) + (A·P)2 + B·P], P = [2FC2 + Max(FO2,0)]/3 where A = 0.02 and B = 16.54 for NbCu2Zn20, and A = 0.01 and B = 19.39 for Hf0.96Cu1.67Zn20.33 [A = 0.02 and B = 61.68 for HfCu2Zn20]].
Table 2. Atomic coordinates, site occupancy factors, and equivalent displacement parameters of MCu2Zn20 (M = Nb, Hf).
Table 2. Atomic coordinates, site occupancy factors, and equivalent displacement parameters of MCu2Zn20 (M = Nb, Hf).
MAtomSiteSOFxyzUeq (Å2)
NbNb8a11/81/81/80.0055(1)
Cu16d11/21/21/20.0084(1)
Zn196g10.06126(1)=x0.32041(2)0.0130(1)
Zn248f10.48739(2)1/81/80.0090(1)
Zn316c10000.0144(1)
HfHf8a0.963(2)1/81/81/80.0061(1)
Cu1116d0.837(2)1/21/21/20.0084(1)
Zn120.163(2)
Zn196g10.06101(2)=x0.32106(2)0.0139(1)
Zn248f10.48752(3)1/81/80.0096(1)
Zn316c10000.0162(1)
Table 3. Selected distances and volumes in MCu2Zn20 (M = Nb, Hf). Zn1 and Zn3 create the Frank–Kasper polyhedron containing M, while Zn1 and Zn2 create the icosahedron containing Cu (see also Figure 2). The last column displays the percent increase of each value from NbCu2Zn20 to HfCu2Zn20.
Table 3. Selected distances and volumes in MCu2Zn20 (M = Nb, Hf). Zn1 and Zn3 create the Frank–Kasper polyhedron containing M, while Zn1 and Zn2 create the icosahedron containing Cu (see also Figure 2). The last column displays the percent increase of each value from NbCu2Zn20 to HfCu2Zn20.
M = NbM = Hf% Change
Lattice parameter (Å)13.9013(2)13.9856(2)0.61
Unit cell volume (Å3)2686.35(8)2735.52(7)1.83
Frank–Kasper polyhedron of M
M—Zn1 (Å)2.992(1)3.020(1)0.94
M—Zn3 (Å)3.010(1)3.028(1)0.60
Volume (Å3)77.676(3)79.678(3)2.58
Icosahedron of Cu
Cu—Zn1 (Å)2.772(1)2.778(1)0.22
Cu—Zn2 (Å)2.464(1)2.478(1)0.57
Volume (Å3)45.197(3)45.764(3)1.25
Other measures
M—M (Å)6.019(1)6.056(1)0.62
Cu—Cu (Å)4.915(1)4.945(1)0.61
M—Cu (Å)5.763(1)5.798(1)0.61
M—Zn2 (Å) (not part of cage)5.038(1)5.070(1)0.64
Cu—Zn3 (Å) (not part of cage)4.915(1)4.945(1)0.61
Table 4. Existing compounds in the MM’2Zn20 family either in polycrystalline or single crystalline form. Note that only one MCu2Zn20 compound existed previously: ZrCu2Zn20. The open circles are the two compounds of the current work.
Table 4. Existing compounds in the MM’2Zn20 family either in polycrystalline or single crystalline form. Note that only one MCu2Zn20 compound existed previously: ZrCu2Zn20. The open circles are the two compounds of the current work.
M’
CrMnFeCoNiCuRuRhOsIr
MSc ● ●
Y ● b●● ●●●●
Zr● a● a●●●●●●
Nb ●●●o
Hf ● c●●●o●●
Ce ● b ●● ●
Pr ● b ●●
Nd ● b ● ●●
Sm ● b ● ●●
Gd ● b●● ●●●●
Tb ●● ●●
Dy ● b●●● ●●
Ho ●●● ●●
Er ● b●●● ●●
Tm ●●● ●●
Yb ● b●● ●●●●
Lu ●●● ●●
U ●● ●●●●
a Due to M’/Zn mixing at the 16d site, the stoichiometry for these compounds are ZrCrZn21 (ZrCr2–xZn20+x, x = 1) and ZrMn1.78Zn20.22 (ZrMn2–xZn20+x, x = 0.22) [15]. b These compounds exhibit In/Zn or Al/Zn mixing [11,12,13]. c Due to Mn/Zn mixing at the 16d site and underoccupancy at the Hf-site, the stoichiometry for this compound is Hf0.93Mn1.63Zn20.37 (Hf1–δMn2–xZn20+x, δ = 0.07, x = 0.37) [9].
Table 5. Lattice parameter, unit cell volume, Frank–Kasper polyhedron volume, and icosahedron volume of ZrCu2Zn20 [15] with the percent changes when compared to NbCu2Zn20 and HfCu2Zn20.
Table 5. Lattice parameter, unit cell volume, Frank–Kasper polyhedron volume, and icosahedron volume of ZrCu2Zn20 [15] with the percent changes when compared to NbCu2Zn20 and HfCu2Zn20.
ZrCu2Zn20% Larger than HfCu2Zn20% Larger than NbCu2Zn20
Lattice parameter (Å)14.01160.190.79
Unit cell volume (Å3)2750.830.562.40
M Frank–Kasper polyhedron (Å3)79.9790.382.96
Cu Icosahedron (Å3)46.0850.701.96
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Longworth, S.M.; Mou, M.M.; Yasmin, N.; Noor, M.F.B.; Sakidja, R.; Besara, T. Single Crystal Growth and Structural Study of the New MCu2Zn20 (M = Nb, Hf) Compounds. Crystals 2025, 15, 391. https://doi.org/10.3390/cryst15050391

AMA Style

Longworth SM, Mou MM, Yasmin N, Noor MFB, Sakidja R, Besara T. Single Crystal Growth and Structural Study of the New MCu2Zn20 (M = Nb, Hf) Compounds. Crystals. 2025; 15(5):391. https://doi.org/10.3390/cryst15050391

Chicago/Turabian Style

Longworth, Sarah M., Marium M. Mou, Nusrat Yasmin, Md Fahel Bin Noor, Ridwan Sakidja, and Tiglet Besara. 2025. "Single Crystal Growth and Structural Study of the New MCu2Zn20 (M = Nb, Hf) Compounds" Crystals 15, no. 5: 391. https://doi.org/10.3390/cryst15050391

APA Style

Longworth, S. M., Mou, M. M., Yasmin, N., Noor, M. F. B., Sakidja, R., & Besara, T. (2025). Single Crystal Growth and Structural Study of the New MCu2Zn20 (M = Nb, Hf) Compounds. Crystals, 15(5), 391. https://doi.org/10.3390/cryst15050391

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop