Germanium-Based Temperonic Crystal

Abstract

We propose a germanium-based temperonic crystal consisting of a two-layer unit cell designed to enable interference of thermal waves in the non-Fourier regime. Each layer features temperature-dependent properties, including thermal diffusivity $D\left(T\right)$, thermal conductivity $\kappa \left(T\right)$, and relaxation time $\tau \left(T\right)$. Utilizing the Cattaneo-Vernotte model, we predict band gaps in the temperature oscillation frequencies. Our analysis reveals that band gaps emerge when one layer is maintained at 110 K and the other at 50 K; however, these gaps close rapidly as the temperature contrast diminishes or the overall temperature increases. Drawing from the temperonic-crystal paradigm and inspired by recent experimental observations of thermal waves in germanium, this design offers a promising pathway for on-chip control of ultrafast thermal pulses and thermal-management devices in semiconductors.

1. Introduction

Fourier’s law provides the standard framework for heat diffusion and the conventional description of temperature propagation in many phenomena. However, the discovery of non-Fourier heat transport at the nanoscale has motivated theories that extend beyond classical diffusion [1]. The classical Fourier law assumes infinite propagation speed, leading to a paradox that fails to account for finite-speed thermal signals observed in nanoscale systems and under nonequilibrium conditions [2]. Among non-Fourier theories, the Cattaneo–Vernotte model accommodates wave-like temperature propagation by introducing only one additional parameter: the relaxation time, which sets a finite speed for heat waves. This simple yet powerful model is crucial for understanding heat transport in micro- and nano-devices, as well as biological systems, where wave-like temperature behavior becomes significant [3].

Recently, Beardo et al. observed thermal wave oscillations in germanium (Ge), offering a striking example of non-Fourier heat transport in semiconductors modeled by the Cattaneo-Vernotte (CV) theory [4]. By applying high-frequency oscillatory heating, heat propagates as waves rather than through diffusion. Historically, this wave-like propagation has been termed ‘second sound,’ in analogy to a mechanical wave transport found in superfluids and predicted for dielectric solids above a critical frequency [5]. This discovery suggests a new framework for heat transport in semiconductors, with implications for advanced thermal management in microelectronics.

A central idea in non-Fourier heat propagation is exploring structured materials that control thermal signals via interference, beyond homogeneous media. Thermal wave crystals (TWCs), originally proposed by Chen et al., extend band-gap concepts from electronic and photonic crystals to temperature oscillations [6]. In such structures, periodic media exhibit forbidden frequency band gaps, engineered by varying thermal parameters. Applying Bloch’s theorem reveals bands and gaps in the thermal oscillation frequencies, enabling heat transfer control analogous to photonic crystals [7].

The field of TWCs has evolved rapidly, paralleling advancements in photonic and phononic crystals [8]. For instance, TWCs have been proposed as thermal mirrors via Bragg interference in 1D crystals, with applications in biological and semiconductor systems [9,10,11]. Further developments include waveguides and heterostructures for guiding heat waves [12,13], as well as 2D crystals with defect-induced waveguiding and complex band structures [11].

A key motivation for this work is the temperonic-crystal concept introduced by Gandolfi et al. [14]. By incorporating temperature-dependent thermal parameters, this paradigm uses a unit cell of two layers at different temperatures (e.g., $T_a$ and $T_b$) to support thermal waves, yielding dispersion relations with bands and gaps. Temperonic crystals thus enable nanoscale filtering, guiding, and storage of thermal energy.

Building on this, our work presents a minimal realization of the temperonic-crystal concept in a germanium-based two-layer unit cell [14]. To our knowledge, this is the second such temperonic crystal proposed in the literature. We exploit temperature-dependent properties in each layer, coupled via interface conditions under periodic boundaries, using experimental data from germanium [4]. The objective is to demonstrate band gaps in a semiconductor-based temperonic crystal. Our results show band gaps when one layer is at 110 K and the other at 50 K, but these close rapidly as the temperature contrast diminishes or the overall temperature increases.

2. The Cattaneo-Vernotte Model

The CV heat-conduction model modifies Fourier’s law for the one-dimensional heat flux $q(x,t)$ as follows [6]:

$$q(x,t)+\tau {\displaystyle \frac{\partial q(x,t)}{\partial t}}=-\kappa {\displaystyle \frac{\partial T(x,t)}{\partial x}},$$

(1)

the energy conservation equation in the absence of heat sources is

$${\displaystyle \frac{\partial q(x,t)}{\partial x}}=-\rho c_p{\displaystyle \frac{\partial T(x,t)}{\partial t}},$$

(2)

where $c_p$ is the specific heat capacity, $\kappa$ is the thermal conductivity, $\tau$ is the relaxation time, and $\rho$ is the mass density. Combining (1) and (2) yields the hyperbolic wave equation

$$\tau {\displaystyle \frac{{\partial }^{2}T(x,t)}{\partial t^2}}+{\displaystyle \frac{\partial T(x,t)}{\partial t}}=D{\displaystyle \frac{{\partial }^{2}T(x,t)}{\partial x^2}},$$

(3)

where $D=\kappa /\left(\rho c_p\right)$ is the thermal diffusivity.

For harmonic thermal waves, we apply the Fourier transform to map the time-domain fields into the frequency domain, following the convention in Jackson [15]:

$$T(x,t)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{\infty }T(x,\omega )e^{-i\omega t}d\omega ,$$

(4)

$$q(x,t)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{\infty }q(x,\omega )e^{-i\omega t}d\omega .$$

(5)

We assume real frequencies, as is typical in photonic and phononic crystals for analyzing steady-state dispersion relations and band structures [7]. In the frequency domain, (1) and (2) become

$$q(x,\omega )=-{\displaystyle \frac{\kappa }{1-i\omega \tau }}{\displaystyle \frac{\partial T(x,\omega )}{\partial x}},$$

(6)

$$T(x,\omega )={\displaystyle \frac{1}{i\omega \rho c_p}}{\displaystyle \frac{\partial q(x,\omega )}{\partial x}}.$$

(7)

Substituting these expressions yields the complex Helmholtz equation

$${\displaystyle \frac{{\partial }^{2}T(x,\omega )}{\partial x^2}}=-{\gamma }^{2}T(x,\omega ),$$

(8)

with the wavevector

$${\gamma }^2={\displaystyle \frac{{\omega }^2}{v^2}}\left(1+{\displaystyle \frac{i}{\omega \tau }}\right),$$

(9)

where the thermal wave velocity is

$$v^2={\displaystyle \frac{D}{\tau }}.$$

(10)

The wavevector is complex, separated into real and imaginary parts as

$$\gamma ={\gamma }_r+i{\gamma }_i,$$

(11)

where

$${\gamma }_r={\displaystyle \frac{\omega }{v}}{\displaystyle \frac{1}{\sqrt{2}}}{\left[\sqrt{1+{\left({\displaystyle \frac{1}{\omega \tau }}\right)}^2}+1\right]}^{1/2}$$

(12)

and

$${\gamma }_i={\displaystyle \frac{\omega }{v}}{\displaystyle \frac{1}{\sqrt{2}}}{\left[\sqrt{1+{\left({\displaystyle \frac{1}{\omega \tau }}\right)}^2}-1\right]}^{1/2}.$$

(13)

The propagation of thermal waves in a periodic multilayer structure, composed of alternating layers a and b with thicknesses $d_a$ and $d_b$, can be analyzed using this hyperbolic model. In Ref. [10], a dispersion relation under the Cattaneo–Vernotte framework is derived via a Kronig–Penney-type formalism [16]. This relation takes the form

$$cosh\left(i{\gamma }_{B}d\right)=cosh\left(i{\gamma }_a{d}_a\right)cosh\left(i{\gamma }_b{d}_b\right)+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{\eta }_a{\gamma }_a}{{\eta }_b{\gamma }_b}}+{\displaystyle \frac{{\eta }_b{\gamma }_b}{{\eta }_a{\gamma }_a}}\right)sinh\left(i{\gamma }_a{d}_a\right)sinh\left(i{\gamma }_b{d}_b\right),$$

(14)

where ${\gamma }_B$ is the Bloch wavevector and $d=d_a+d_b$ is the unit cell period. The material-specific parameters are

$${\gamma }_a={\displaystyle \frac{\omega }{v_a}}\sqrt{1+{\displaystyle \frac{i}{\omega {\tau }_a}}},$$

(15)

$${\gamma }_b={\displaystyle \frac{\omega }{v_b}}\sqrt{1+{\displaystyle \frac{i}{\omega {\tau }_b}}},$$

(16)

$${\eta }_a={\displaystyle \frac{{\kappa }_a}{1-i\omega {\tau }_a}},$$

(17)

$${\eta }_b={\displaystyle \frac{{\kappa }_b}{1-i\omega {\tau }_b}}.$$

(18)

In the context of temperonic crystals, these parameters become temperature-dependent, as detailed in subsequent sections.

3. Temperature-Dependent Thermal Parameters of Germanium

In this section, we examine the temperature dependence of the thermophysical parameters of germanium (Ge).

Table 1. Thermal parameters of germanium extracted from the supplementary material of Ref. [4]. Values are for pure Ge and have been adjusted to experimental results.

T (K)	$\mathit{\kappa }$ (W m−1 K−1)	$\mathit{\tau }$ ($\times {10}^{-9}$ s)	D ($\times {10}^{-5}$ m2 s−1)
50	400	10.4	83.4
100	172	2.05	15.9
150	100	0.965	7.54
200	75	0.622	4.94
250	55	0.46	3.70
300	50	0.366	3.04

presents a tabulation of the thermal conductivity $\kappa$, relaxation time $\tau$, and thermal diffusivity D based on values found in the supplementary material of Ref. [4]. These values have been calculated for the case of pure Ge. For the thermal conductivity, it is reported that an ab initio calculation was performed. For the relaxation time and thermal diffusivity values, it is reported that Density Functional Theory (DFT) calculations were carried out. These values have been adjusted to match experimental results.

3.1. Discussion of Thermal Parameters

The values tabulated in Table 1 reveal clear temperature-dependent trends in the thermophysical properties of pure germanium, which are consistent with phonon transport theory in crystalline semiconductors. At low temperatures (e.g., 50 K), the thermal conductivity $\kappa$ is notably high (400 W m⁻¹ K⁻¹), reflecting reduced phonon-phonon scattering and longer mean free paths. As temperature increases, $\kappa$ decreases monotonically, reaching 50 W m⁻¹ K⁻¹ at 300 K.

Similarly, the relaxation time $\tau$ exhibits a decrease from 10.4 $\times {10}^{-9}$ s at 50 K to 3.04 $\times {10}^{-9}$ s at 300 K. The thermal diffusivity D follows a parallel decrease, from 83.4 $\times {10}^{-5}$ m² s⁻¹ at 50 K to 3.04 $\times {10}^{-5}$ m² s⁻¹ at 300 K, underscoring the reduction in heat propagation efficiency with rising temperature.

The data cover temperatures from 50 to 300 K in intervals of 50 K, totaling 6 data points. To obtain values across the entire range, we performed a numerical fit using an exponential decay form in all cases. In Figure 1a, the thermal conductivity is fitted using the relation

$$\kappa \left(T\right)=A_k{e}^{-B_{k}T}+C_k,$$

(19)

with the values $A_k=971$ W/(m K), $B_k=0.206$ K⁻¹, and $C_k=52.3$ W/(m K).

In Figure 1b, the relaxation time was fitted using the relation

$$\tau \left(T\right)=A_{\tau }{e}^{-B_{\tau }T}+C_{\tau },$$

(20)

where we used $A_{\tau }=6.07\times {10}^{-8}$ s, $B_{\tau }=0.0363$ K⁻¹, and $C_{\tau }=5.07\times {10}^{-10}$ s.

In Figure 1c, we fitted the thermal diffusivity using the relation

$$D\left(T\right)=A_D{e}^{-B_{D}T}+C_D,$$

(21)

where we used the values $A_D=5.1\times {10}^{-3}$ m²/s, $B_D=0.0373$ K⁻¹, and $C_D=4.13\times {10}^{-5}$ m²/s. In panels (a)–(c), the exponential fit is shown as a dashed line. In all cases, the curves and the points related to Table 1 match very well, as expected from a fit to a theoretical model, where there are no uncertainties related to experimental conditions.

Figure 1. Temperature dependence of thermophysical parameters for pure germanium (Ge) from 50 to 300 K. (a) Thermal conductivity, $\kappa \left(T\right)$, (b) relaxation time, $\tau \left(T\right)$, and (c) thermal diffusivity, $D\left(T\right)$. Data points are from Table 1; dashed lines represent exponential fits. (d) Calculated sound velocity $v\left(T\right)$, derived from the relation $v\left(T\right)=\sqrt{D\left(T\right)/\tau \left(T\right)}$.

Figure 1. Temperature dependence of thermophysical parameters for pure germanium (Ge) from 50 to 300 K. (a) Thermal conductivity, $\kappa \left(T\right)$, (b) relaxation time, $\tau \left(T\right)$, and (c) thermal diffusivity, $D\left(T\right)$. Data points are from Table 1; dashed lines represent exponential fits. (d) Calculated sound velocity $v\left(T\right)$, derived from the relation $v\left(T\right)=\sqrt{D\left(T\right)/\tau \left(T\right)}$.

These trends are well-captured by the exponential fits (e.g., (19)), which provide a smooth interpolation across the temperature range. For instance, the fitted $\kappa \left(T\right)$ decreases exponentially, matching the data points with high fidelity. The derived velocity function

$$v\left(T\right)=\sqrt{{\displaystyle \frac{D\left(T\right)}{\tau \left(T\right)}}},$$

(22)

presented in Figure 1d, further illustrates these dynamics. It is observed that the curve starts with a value v(50 K) = 283 m/s, has a minimum around 110 K with v(110 K) = 278.07 m/s, and then rises to 285 m/s at 300 K.

3.2. Wavevector Analysis

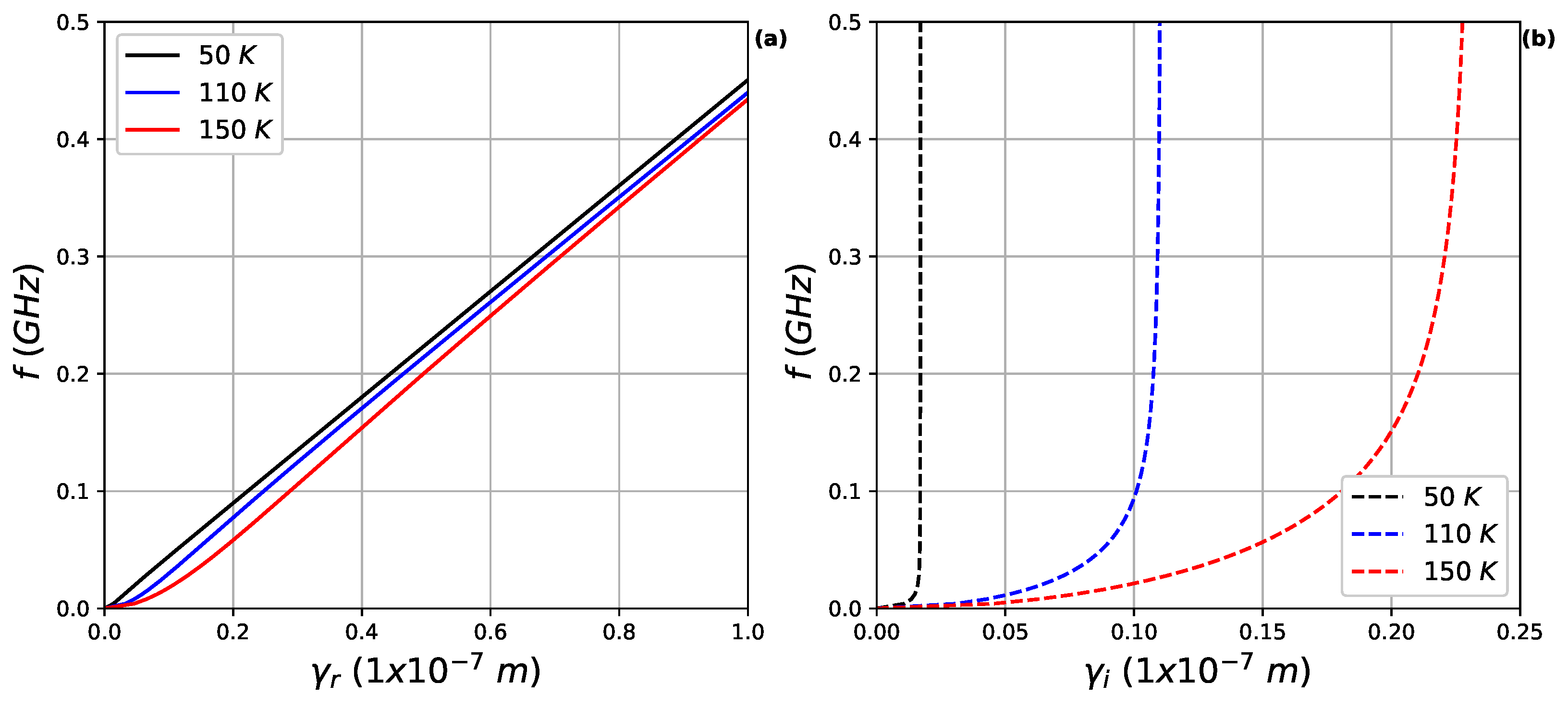
Building on the temperature-dependent thermal parameters discussed previously, we now analyze the complex wavevector $\gamma ={\gamma }_r+i{\gamma }_i$ (defined in (11)), which describes the propagation of thermal waves in pure germanium. Figure 2 presents the real and imaginary parts of $\gamma$ as a function of frequency f for selected temperatures: 50 K, 110 K, and 150 K.

In panel (a), the real part ${\gamma }_r$ (scaled by $\times {10}^{-7}$ m) is plotted against f (in GHz), showing a monotonic increase with frequency for each temperature. The curves are colored as follows: black for 50 K, blue for 110 K, and red for 150 K.

In panel (b), the imaginary part ${\gamma }_i$ (also scaled by $\times {10}^{-7}$ m) is shown with dashed lines in the same color scheme. Here, the x-axis is limited to 0 to 0.25 $\times {10}^{-7}$ m, highlighting the attenuation behavior. The imaginary part indicates damping, which increases with temperature due to enhanced scattering.

These plots were generated using numerical computations based on the fitted parameters from Table 1, demonstrating how temperature affects wave propagation in Ge. For instance, at lower temperatures like 50 K, the real part dominates, suggesting longer mean free paths, while at 150 K, damping (imaginary part) becomes more pronounced.

4. Band Structure of Temperonic Crystals

In this section, we analyze the band structure of a periodic temperonic crystal where each unit cell consists of two germanium layers, a and b, maintained at temperatures $T_a$ and $T_b$, respectively. For simplicity, we assume equal layer thicknesses, $d_a=d_b$.

To select an appropriate thickness $d_a$, we consider the Knudsen number, defined as $K_n=l/d_a$, where l is the phonon mean free path [17,18,19]. According to kinetic theory for solids, the phonon mean free path is approximated by $l=3D/v$, where D is the thermal diffusivity and v is the phonon group velocity (approximately the speed of sound) [20]. Using the experimental speed of sound in Ge, $v=4910$ m/s at room temperature [21], and $D\left(300\mathrm{K}\right)=3.04\times {10}^{-5}$ m²/s from Table 1, we obtain $l\approx 18.5$ nm. Selecting $d_a=100$ nm yields $K_n\approx 0.185$, which falls within the transitional regime ($K_n\sim 0.1$–1) where non-Fourier thermal wave propagation, as described by the Cattaneo-Vernotte model, is expected to dominate [19].

It is worth noting that our analysis focuses on pure crystalline germanium. In contrast, amorphous germanium (a-Ge) exhibits a longer mean free path, exceeding 100 nm, as reported in Ref. [22].

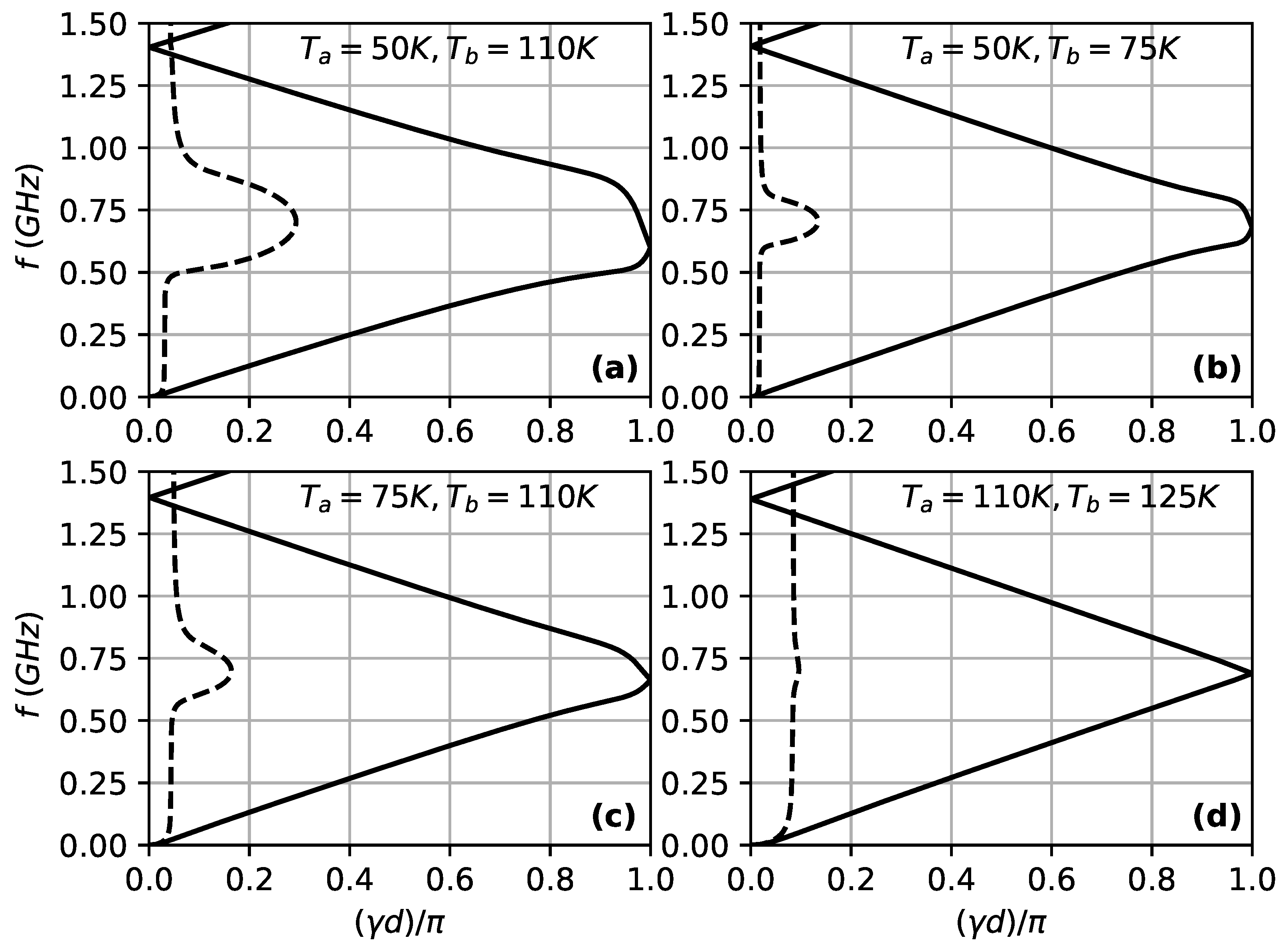
To investigate the impact of temperature gradients on thermal wave propagation, we compute the complex dispersion relations using Equation (14) and the fitted temperature-dependent parameters from Section 3. Figure 3 presents the real (${\gamma }_r$, solid lines) and imaginary (${\gamma }_i$, dashed lines) parts of the Bloch wavevector as a function of frequency $f=\omega /\left(2\pi \right)$ (in GHz) for a unit cell with total width $d=200$ nm ($d_a=d_b=100$ nm). The panels correspond to different temperature pairs $(T_a,T_b)$.

In panels (a), (b), and (c), band gaps are evident, corresponding to frequency ranges where the imaginary show an increasing (evanescent modes). The largest band gap occurs in panel (a) ($T_a=50$ K, $T_b=110$ K), spanning 50 GHz to 87.5 GHz. Panel (b) ($T_a=50$ K, $T_b=75$ K) shows a gap from 62.5 GHz to 80 GHz, while panel (c) ($T_a=75$ K, $T_b=110$ K) exhibits the smallest gap, centered around 70 GHz. In contrast, panel (d) ($T_a=110$ K, $T_b=125$ K) shows no band gap, as the temperature difference is insufficient to create significant parameter contrast. These results demonstrate that band gaps emerge and widen with larger temperature differences, particularly at lower temperatures.

5. Discussion

The results presented in this work provide compelling evidence for the feasibility of a germanium-based temperonic crystal, where temperature gradients alone induce periodic contrasts in thermal parameters, leading to tunable band gaps in thermal wave propagation. By leveraging the Cattaneo-Vernotte model and experimentally grounded fits to Ge’s properties (e.g., Equations (19)–(22)), we observe that band gaps emerge prominently when the temperature difference $\mathrm{\Delta }T=|T_a-T_b|$ is substantial, such as in the 50 K/110 K case (Figure 3, panel (a)), with a gap spanning 50–87.5 GHz. This arises from the enhanced mismatch in complex wavevectors ${\gamma }_a$ and ${\gamma }_b$ (Equations (15) and (16)) and effective conductivities ${\eta }_a$ and ${\eta }_b$ (Equations (17) and (18)), driven by the strong temperature dependence of $\kappa \left(T\right)$ and $\tau \left(T\right)$ at low temperatures. As $\mathrm{\Delta }T$ diminishes (e.g., 110 K/125 K in Figure 3d), the parameter contrast weakens, closing the gaps due to reduced interference effects—analogous to the vanishing photonic band gaps in low-index-contrast materials [7].

This design represents a minimal yet powerful realization of the temperonic-crystal concept introduced by Gandolfi et al. [14], extending it to a single-material semiconductor system informed by recent observations of second-sound-like waves in Ge [4]. Unlike heterogeneous thermal wave crystals [6,10], which rely on material interfaces, our approach exploits intrinsic temperature tunability, simplifying fabrication for on-chip applications. The transitional Knudsen regime ($K_n\approx 0.185$) ensures non-Fourier behavior dominates, aligning with predictions for nanoscale heat transport [19]. Notably, the damping revealed in the imaginary wavevector components (Figure 2) highlights how increased scattering at higher temperatures limits gap widths, underscoring the need for cryogenic operation to maximize functionality.

From an applied perspective, these tunable band gaps could enable novel thermal-management devices, such as frequency-selective filters for ultrafast heat pulses in microelectronics or sensors that switch states via localized cooling. For instance, integrating this structure with existing Ge-based optoelectronics could facilitate hybrid photonic-thermal devices, where temperature modulates both light and heat waves. However, limitations exist: our model assumes ideal temperature isolation between layers and neglects nonlinear effects or external perturbations, which could broaden gaps or introduce losses in real systems. Future work might incorporate finite-element simulations to account for realistic gradients, explore 2D/3D geometries for omnidirectional gaps [11], or experimentally validate using high-frequency thermoreflectance techniques [4]. Additionally, extending to doped or amorphous Ge [22] could yield wider operational temperature ranges, bridging the gap between theory and practical nanotechnology.

6. Conclusions

In summary, we have proposed and analyzed a germanium-based temperonic crystal that harnesses temperature-dependent thermal parameters to generate tunable band gaps in non-Fourier thermal waves. Through the Cattaneo-Vernotte framework and precise fits to experimental data, our calculations reveal robust gaps at low-temperature contrasts (e.g., 50–87.5 GHz for $\mathrm{\Delta }T=60$ K), which close rapidly as temperatures equilibrate, demonstrating exquisite thermal sensitivity. This single-material design advances the temperonic paradigm [14], offering a realistic pathway for semiconductor-integrated thermal control beyond classical diffusion.

Ultimately, this work not only validates wave-like heat propagation in Ge but also paves the way for innovative devices in ultrafast thermal management, potentially revolutionizing heat handling in next-generation electronics. By blending simplicity with tunability, it invites further exploration into hybrid thermal systems, where temperature becomes a dynamic knob for engineering energy flows at the nanoscale.