Incomplete Absorption Correction Results in an Increased Positive Mean Value of Weighted Residuals

Abstract

Incomplete absorption correction procedures in single-crystal diffraction experiments leave a characteristic trace—a “fingerprint”—in the residuals. Specifically, weak intensities are systematically overestimated, contributing disproportionately and sometimes even dominantly to the chi-square sum in least squares refinements. An analysis of six published crystal structures spanning a wide range of absorption coefficients reveals a consistent positive shift of the weighted residuals, which were significant for crystals with $>5.02$ mm⁻¹. This shift is all the stronger the greater the absorption coefficient and is accompanied by a proportionally increasing fraction of positive excess residuals. The simultaneous increase in the mean value of the residuals and the fraction of positive excess residuals proves that the shift is not caused by strong reflections or isolated outliers, but rather by the systematic overestimation of many weak intensities. Diagnostic plots and statistical metrics are presented for additional published data sets, supporting the generality of the findings. These findings can support the development of improved methods for absorption correction, which lead to physically meaningful thermal motion parameters even with strong absorption.

1. Introduction

In modern single-crystal X-ray diffraction experiments, the raw intensities $I_{raw}$ and corresponding standard uncertainties are obtained by integration of the diffraction images from area detectors. These are subjected in a second step to data correction and data reduction steps in order to obtain the Bragg intensity. Many things have to be considered in this second step, including possible changes in the irradiated crystal volume, Lorentz, polarization corrections, crystal decay, beam intensity changes, and absorption effects. The main basic methods for absorption correction procedures are (i) exact numerical corrections, like analytical [1] and Gaussian quadrature [2] methods or—as an example for new developments—those involving ray tracing [3] based on tomographic reconstructions (ii) and semi-empirical corrections like $\mathrm{\Psi }$ scans [4] or multiscan [5] methods. Semi empirical methods need additional intensity measurements. Traditional analytical methods may not be applicable when the crystal is irregularly shaped or too small to index the faces, a problem that may be solved with the method of tomographic reconstruction. Empirical methods do not require knowledge of the crystal geometry; they minimize the differences between incident and diffracted beams based on Fourier series [6,7] or spherical harmonics [8]. The latter is implemented also in SADABS [9] with the difference that [8] applied spherical harmonics to both the incident and the diffracted beam, whereas in SADABS, the spherical harmonics are only applied to the diffracted beam and the incident beam is modeled with the help of a scale factor $S\left(n\right)$ that changes with the frame number n:

$$I_{corrected}=I_{raw}S\left(n\right)P(u,v,w)Q(\mu r,2\theta ),$$

(1)

with corrected intensity $I_{corrected}$; raw intensity $I_{raw}$; incident beam scale factor $S\left(n\right)$ with the frame number n; diffracted beam factor $P(u,v,w)$ based on spherical harmonics, where u, v, and w are the direction cosines of the diffracted beam relative to crystal-fixed axes and a spherical crystal factor $Q(\mu r,2\theta )$, where r is the effective radius of the crystal and $\mu$ the linear absorption coefficient; and $Q(\mu r,2\theta )$ is a correction factor to take into account the $2\theta$ dependence, as equivalent reflections with different paths through the crystal still share the same $2\theta$ Bragg angle. The correction procedure implemented in SADABS is of great importance due to the wide distribution of this software.

Generally known consequences of insufficient absorption corrections are, for examplem non-positive definite anisotropic displacement parameters (ADPs), and cigar-shaped or oblate thermal motion ellipsoids, in short, non-physical thermal motion. But, accurate description of thermal motion plays a crucial role, for example, to clearly discriminate between disorder and thermal motion or when extracting physical properties like thermodynamic properties from the ADPs [10]. In macromolecular crystallography, insufficient absorption correction methods at long wavelengths limit sulfur SAD phasing experiments [3].

In the present work, error profiling is employed in order to characterize weaknesses of absorption correction procedures. The idea of error profiling in small molecule crystallography—where residuals usually do not receive much attention—is to relate the source of a systematic error with the appearance in the weighted residuals. In small molecule crystallography, application of a weighting scheme is very popular. Typically, a SHELXL [11]-like weighting scheme is applied with two parameters a and b. The weight is then defined as $w={\displaystyle \frac{1}{s.u{.}^2\left(I_{obs}\right)+{\left(aP\right)}^2+bP}}$, where $s.u.\left(I_{obs}\right)$ are the standard uncertainties of the observed intensities and P is a parameter that represents the intensity and is obtained from averaging observed and calculated intensities according to a procedure suggested by Wilson [12]. Please note that this type of weighting scheme is not able to handle the simple error of too small $s.u.\left(I_{obs}\right)$ for weak intensities [13]. Back to how the source of a systematic error is connected to the appearance in the weighted residuals for error profiling: This is achieved by using as many and as different descriptors of the residuals as possible to describe the appearance of the error in the residuals in such great detail that a highly specific and recognizable fingerprint of the systematic error under investigation is obtained. This approach hinges crucially on the availability of metrics describing the weighted residuals. Important recent metrics developed for this purpose like the mean value of the weighted residuals, $〈\zeta 〉$, the mean value of the weighted residuals separately for only positive ($〈{\zeta }_{+}〉$) and for only negative residuals ($〈|{\zeta }_{-}|〉$), and so forth are described in greater detail further down. The implicit reference in error profiling is always the error-free case in which the residuals are symmetrically distributed (with respect to zero) random variables that do not change with resolution, intensity, and other entities. For example, when systematic errors are absent is the weighted residuals distributed such that the mean value is close to zero, $〈\zeta 〉\approx 0$, and such that positive and negative fluctuations in the residuals appear equally often and with approximately equal amplitude. From this requirement follows then, for example, that the mean value from positive residuals and the absolute mean value from negative residuals are equal $〈{\zeta }_{+}〉\approx 〈|{\zeta }_{-}|〉$ within the limits given by stochastic fluctuations and that the integer number of positive residuals $\#{\zeta }_{+}$ is equal to the integer number of negative residuals $\#{\zeta }_{-}$ within the limits given by statistical fluctuations. The second important condition for successful error profiling is to obtain data sets with the error in question—but with no other severe errors. Other errors may distort, obstruct, or even reverse some or even all of the details of the fingerprint traces to the point where it is not specific or not even meaningful any more. This can be achieved either by using simulations or by using data from important “proof of principle” studies from well-known crystallographers with a reputation for high quality. The second approach will be used in this work, when analyzing published data that is intended to show that “the IUCr publication requirement that a numerical absorption correction must be applied for strongly absorbing crystals is in need of revision.” [9]. The weighted residuals are treated in the error profiling Ansatz like a very important and central entity that keeps all the relevant information about possible improvements in general and for absorption correction procedures in particular. Error profiling with the help of the weighted residuals has been used successfully earlier for developing new metrics for data sets contaminated by low energy radiation [14] and for characterizing a specific error which appears due to the ineptitude of a SHELXL-like weighting scheme to handle too small standard uncertainties for weak reflections [13]. Error profiling does not only give characteristic fingerprint traces for the identification of systematic errors in diffraction data, it also helps organize types of errors by providing the categories and metrics that are used or invented to describe systematic errors. As an example for such a new metric, the mean value of the weighted residuals will be discussed further down and applied in the context of absorption correction procedures. But, error profiling with the weighted residuals as central entity achieves even more: it facilitates the comprehension of the connection between the sources of systematic errors and the appearance of systematic errors in the weighted residuals. This is of great importance in order to make progress in the field of better understanding systematic errors. Existing tools like the normal probability plot (npp) are also very helpful in proving the existence of systematic errors in a given data set, but the npp alone does not give a clue to the origin of the error, which leaves the experimenter in the embarrassing situation of knowing about the existence of systematic errors but not about the cause or the steps necessary to remove it. A better comprehension of systematic errors may help close this gap. And finally, error profiling guides the way to methodological improvements—this is not limited to absorption correction procedures but includes all data reduction and data correction methods. For example, future protocols for improved absorption correction procedures may use the (missing) fingerprint traces developed in this work for proof of progress.

One additional and very important aspect of error profiling is that it necessarily leads to a critical review of the existing and accepted data quality evaluation protocols and associated metrics. Weaknesses and dangers of the existing protocols may be identified in this way. This is more important as it appears at first glance: We will see in this work that insufficient absorption correction procedures lead one-sidedly more often to the overestimation of observed intensities.

Overestimated intensities, in turn, lead to (i) artificially low agreement factors, which is a separate topic and cannot be discussed fully in the present work but is briefly touched upon. Furthermore, (ii) the anisotropic displacement parameters are also artificially low in the case of overestimated intensities, which result from underestimated absorption in combination with scaling. That underestimation of absorption leads to artificially low ADPs has been known for a long time; however, the question is whether this knowledge is considered in the state of the art of current absorption procedures. Low agreement factors and small thermal motion parameters are both often perceived as signs of high-quality structure refinement and, to a certain extent, they really are; however, certain errors may lead to unrealistic and artificially lowered values. In these cases, the results only appear to be of high quality but need not be of high quality in reality.

The present work aims to establish precise and specific traces of incomplete absorption in the residuals which are easy to recognize even for laymen. Moreover, experts can use these traces to develop even better absorption correction procedures. And finally, it is intended to raise awareness of applying metrics critically in diffraction experiments.

In Section 2, the methodology and the crystallographic structures from the literature are described. A minimal amount of background knowledge about how the mean value of the weighted residuals can be used for data evaluation is provided in Section 3.1 in the main part. How the mean value of the weighted residuals is connected to specific systematic errors is briefly discussed in Section 3.2. In Section 3.3, the mean value of the weighted residuals $〈\zeta 〉$ is shown to tend to increase with the linear absorption coefficient $\mu$ by analyzing the published data sets from a study with a set of structures covering an extremely large range of absorption coefficients and including highly absorbing structures. In Section 3.4, a rationale is developed to understand the systematic connection empirically found in the preceding paragraph. From this rationale, expected characteristic traces of incomplete absorption correction in the residuals are derived in Section 3.5. Precisely, these specific traces are found in the above mentioned published data sets in the case of strongly absorbing crystals but they are not found in the weakly absorbing crystal of the same study as shown in Section 3.6, which is taken as evidence for a correct assignment of specific traces of incomplete absorption correction. These specific traces are searched for and found in published data sets with significant absorption from other authors, in order to not be limited to a small number of data sets from a single study (Section 3.7). Section 3.8 focuses on aspects of quantification of these traces. The rationale developed in Section 3.4 is put to another test in Section 3.9. The results are discussed in Section 4. Finally, a summary follows in Section 5.

2. Methods

The main method is to apply error profiling methods to analyze published data sets with the help of residual descriptors in order to identify and quantify traces in the residuals and connect these to incomplete or insufficient absorption correction procedures, for example, by showing that these traces are more pronounced for strong absorbers and missing for weak absorbers. The most important descriptors used are the mean value of the weighted residuals $〈\zeta 〉$; the significance of the mean value of the weighted residuals $〈\zeta 〉/\sigma \left(〈\zeta 〉\right)$, which indicates whether a deviation $〈\zeta 〉\ne 0$ is within the limits of statistical fluctuations; the mean value of positive residuals $〈{\zeta }_{+}〉$ and the absolute mean value of negative residuals $〈|{\zeta }_{-}|〉$, with the comparison of these latter two indicating the (missing) existence of the symmetry of the distribution of residuals with respect to zero; and the fraction of positive excess residuals $(\#{\zeta }_{+}-\#{\zeta }_{-})/N_{obs}$ and its significance $(\#{\zeta }_{+}-\#{\zeta }_{-})/\sqrt{N_{obs}}$. When the fraction of positive excess residuals and $〈\zeta 〉$ simultaneously show a large positive or a large negative value, this indicates a shift in the distribution of the residuals from zero rather than individual large outliers, causing $〈\zeta 〉\ne 0$. This may be confirmed by $〈{\zeta }_{+}〉\ne 〈|{\zeta }_{-}|〉$. These descriptors are introduced in greater detail in the main part. They are applied to six crystals with a large range of absorption coefficients taken from one publication [9], where the data were collected on Bruker Smart Apex II systems (Tokyo, Japan) with a D8 three-circle goniometer at 100 K. Data reduction was accomplished with SAINT (version 7.68A, [15]) from the APEX2 software (version 2.2012.2-0; [15], with refined box sizes for data integration. Data scaling and absorption correction were achieved with SADABS (version 2014/04). The importance of [9] lies in applying multiscan absorption methods to strongly absorbing crystals, where data were collected with microfocus technology, which is known for having a anisotropic beam profile that makes a uniform homogeneous sample illumination impossible. The claim is that multiscan methods work generally well with microfocus technology even in the case of crystals being too large for the highly focused beam. The six crystals used were (1) scandium platinate (spacegroup $Pbam$), (2) murdochite ($Fm\overline{3}m$), (3) sodium tungstate ($Pbca$), (4) scandium cobalt carbide ($Immm$), (5) a dibromoacridine derivative ($P{2}_1/n$), and (6) an inorganic cobalt complex ($P{2}_1/n$) (

Table 1. Description of crystals from the literature used in this work. Crystals 1–6 from study [9], listed in decreasing order of absorption coefficient for $\mathrm{Mo}$ K_α and $\mathrm{Ag}$ K_α radiation, respectively. Crystals 7–13 from various other authors. Column one: crystal number; column two: compound type; column three: anode material; column four: absorption coefficient in [mm⁻¹]; column five: reflections in the least square refinement; column six: reference.

	Compound Type	Anode	$\mathit{\mu }$ [mm−1]	${\mathit{N}}_{\mathbf{obs}}$	Original Publication
Crystal 1	Scandium platinate	Mo Ag	121.02 65.26	2976 † 6207	[22]
Crystal 2	Murdochite	Mo Ag	38.25 20.48	313 770	[23]
Crystal 3	Sodium tungstate	Mo Ag	18.84 10.16	7584 ‡ 10047	[24]
Crystal 4	Scandium cobalt carbide	Mo Ag	9.78 5.02	704 1590	[25]
Crystal 5	Dibromoacridine derivative	Mo Ag	5.90 3.16	2918 * 2948	—
Crystal 6	Inorganic cobalt complex	Mo Ag	2.87 1.53	7847 + 7811	[26]
Crystal 7	Sodium tungstate	Mo	18.66	1811	[24]
Crystal 8	Cu(II) paratungstate B • ${\mathrm{Na}}_4{\mathrm{Cu}}_3\left[{\mathrm{W}}_{12}{\mathrm{O}}_{40}{\left(\mathrm{OH}\right)}_2\right]28{\mathrm{H}}_2\mathrm{O}$	Mo	24.53	4720	[27]
Crystal 9	Iron (II) paratungstate B • ${\mathrm{Na}}_5{\mathrm{Fe}}_{2.5}\left[{\mathrm{W}}_{12}{\mathrm{O}}_{40}{\left(\mathrm{OH}\right)}_2\right]36{\mathrm{H}}_2\mathrm{O}$	Mo	21.02	10876	[27]
Crystal 10	Bismuth compound $\mathrm{Bi}{\left({\mathrm{C}}_9{\mathrm{H}}_6{\mathrm{NS}}_2\right)}_3$	Cu	17.34	5322	[28]
Crystal 11	Osmium compound $\left[{\left\{{\mathrm{Os}}_2{\left(\mathrm{CO}\right)}_4{\left({\mathrm{C}}_{21}{\mathrm{H}}_{21}\mathrm{P}\right)}_2\right\}}_2{\left({\mathrm{C}}_{12}{\mathrm{H}}_{14}{\mathrm{O}}_4\right)}_2\right]$	Cu	9.33	9674	[29]
Crystal 12	Djurleite ${\mathrm{Cu}}_{61.39}{\mathrm{S}}_{32}$	Mo	23.54	7077	[30]
Crystal 13	Anticancer gold agent STG-2	Cu	8.42	8803	[31]

^† Numbers given in [9]: 3183; ^‡ 8341; * 3130; ⁺ 8338. ^• Paratungstate B, ${\left[{\mathrm{W}}_{12}{\mathrm{O}}_{40}{\left(\mathrm{OH}\right)}_2\right]}^{10-}$.

). The traces of insufficient absorption correction in the weighted residuals are established with these six crystals and searched for in other published structures (Crystal 7–13) with $\mu >6$ mm⁻¹. From those, Crystal 7 is the same structure as Crystal 3, but in contrast to Crystal 3, absorption correction was performed with face indexing methods in Crystal 7. In Crystals 8, 9, 12, and 13, multiscan methods were used with SADABS; in Crystal 10, Gaussian absorption correction methods were used with Agilent Software Crysalis PRO [16]; and in Crystal 11, multiscan methods were used with Rigaku Software Crysalis PRO [17]. For the critical reader, diagnostic plots are shown for some additional structures [18,19,20,21] with small absorption coefficients $\mu <0.16$ mm⁻¹ to demonstrate absence of the typical signs of insufficient absorption correction like in Crystal 6. These examples show that even face indexing absorption correction methods are affected by signs of insufficient absorption correction and that signs of insufficient absorption correction appear with different software.

3. Main Part

3.1. The Mean Value of Residuals Is Generally Connected to Systematic Errors

The mean value of the weighted residuals, $〈\zeta 〉={\displaystyle \frac{1}{N_{obs}}}{\sum }_{i=1}^{N_{obs}}{\zeta }_i$, is centered around zero when the weighted residuals ${\zeta }_i={\displaystyle \frac{I_{obs,i}-I_{calc,i}}{\sigma \left(I_{obs,i}\right)}}$, where $i=hkl$ abbreviates the Miller triples, are unbiased random variables. $\sigma \left(I_{obs}\right)$ is the assigned weight. The summation is over the $N_{obs}$ reflections participating in the least squares refinement. The angle brackets thus just indicate the arithmetic mean. The distribution of the weighted residuals is often associated with a Gaussian distribution. However, statistical fluctuations lead naturally to deviations of the mean value of the residuals from zero. Whether or not such a deviation is still in accordance with the assumption of random errors can easily be quantified by the significance of the deviation of the mean value of the residuals from zero:

$${\displaystyle \frac{〈\zeta 〉}{\sigma \left(〈\zeta 〉\right)}}={\displaystyle \frac{\frac{1}{N_{obs}}{\displaystyle \sum _{i=1}^{Nobs}}{\zeta }_i}{\sqrt{var\left(\zeta \right)/N_{obs}}}}$$

(2)

$$var\left(\zeta \right)={\displaystyle \frac{1}{N_{obs}-1}}\sum _{i=1}^{N_{obs}}{\left({\zeta }_i-〈\zeta 〉\right)}^2$$

(3)

which is obtained by dividing the mean value of the residuals $〈\zeta 〉$ by the square root of the population variance $var\left(\zeta \right)$ of the residuals over $N_{obs}$ [14,32].

Significant deviations of the mean value of the residuals ($\left|{\displaystyle \frac{〈\zeta 〉}{\sigma \left(〈\zeta 〉\right)}}\right|>3$) are widespread: from 127 highlighted data sets published with IUCrData, 52% did show significant deviations. The mean significance was 4.30 [32]. Significant positive values of the mean values of the residuals were found to appear more often then negative ones. These results give an overriding importance to the mean value of the weighted residuals as a data quality metric as it has the following pleasing characteristics: it is relevant, easy to understand, easy to apply, and easy to interpret. Significant deviations from zero indicate the presence of systematic errors—regardless of the results from $GoF$, $wR\left(F^2\right)$, or other metrics. The present work shows how the mean value of the weighted residuals is connected to absorption correction procedures and which specific traces in the residuals characterize incomplete absorption correction.

3.2. More Specific Relationship Between the Mean Value of Residuals and Systematic Errors

It has been demonstrated earlier that, e.g., modeling of disorder and of twinning may reduce the significance of the shift in the mean value of the residuals, ${\displaystyle \frac{〈\zeta 〉}{\sigma \left(〈\zeta 〉\right)}}$, and associated metrics like the significance of the number of positive excess residuals as given by ${\displaystyle \frac{\#{\zeta }_{+}-\#{\zeta }_{-}}{\sqrt{N_{obs}}}}$, where $\#{\zeta }_{+}$ denotes the integer number of residuals with positive signs and $\#{\zeta }_{-}$ denotes the integer number of residuals with negative signs in a set of $N_{obs}=\#{\zeta }_{+}+\#{\zeta }_{-}$ residuals [14].

Factors that increase the mean value of the residuals were found to be not modeled disorder, missed twinning, low energy contamination [14], application of a significance or an intensity cut off, as well as missing electrons (missing scattering mass). Factors that decrease the mean value of the residuals may occur self evidently from missed extinction, beam shadowing, and detector saturation. Not so evidently, underestimated $s.u.\left(I_{obs}\right)$ for weak intensities in combination with the SHELX default “OMIT -2” command can lead to distinct negative shifts [13] as well as excess scattering mass. (The results regarding significance and intensity cut offs, and missing and excess scattering mass are not yet published. The manuscript is still in preparation.)

The strategy in previous publications was to develop specific criteria, describing how exactly certain systematic errors affect the weighted residuals (fingerprint and “smoking gun”) and to quantify these expected traces by corresponding metrics or at least to visualize these in appropriately chosen graphics. In the present work, the same strategy is adopted to investigate absorption correction procedures.

3.3. Absorption Correction: Application to Strongly and Weakly Absorbing Crystals from the Literature

In [9], six crystals of different sizes and with absorption coefficients varying between 1.53 and 121.02 mm⁻¹ were measured at 100 K on a Bruker Apex II diffractometer with microfocus X-ray source and mirror optics. Data sets were taken with $\mathrm{Ag}$ K_α and $\mathrm{Mo}$ K_α radiation for the same crystals and processed with the same software. Some of the crystals were slightly or even clearly (Crystal 5) too big for being fully immersed in the highly focused microsource beam. The beam diameter at the focal point is given in [9] as 110 $\mathsf{\mu }$m for the $\mathrm{Mo}$ K_α and 90 $\mathsf{\mu }$m for $\mathrm{Ag}$ K_α. These values are taken from the literature [33]. The aim of the work was obviously to demonstrate the applicability and validity of an empirical absorption correction with microsource technology. The empirical correction procedure works by refining an incident beam scale factor and spherical harmonic coefficients in one step of the process. In another separate step, a spherical crystal term $Q(\mu r,2\theta )$ with absorption coefficient $\mu$ and effective radius r is refined to take the $\theta$ dependence of the absorption process into account. The empirical absorption correction is much easier to apply compared to methods that require face indexing like analytical methods [1] and Gaussian quadrature [34]. Crystal 1 has the largest and Crystal 6 the lowest absorption coefficients. The absorption coefficients are given for $\mathrm{Ag}$ K_α and $\mathrm{Mo}$ K_α radiation in Table 1.

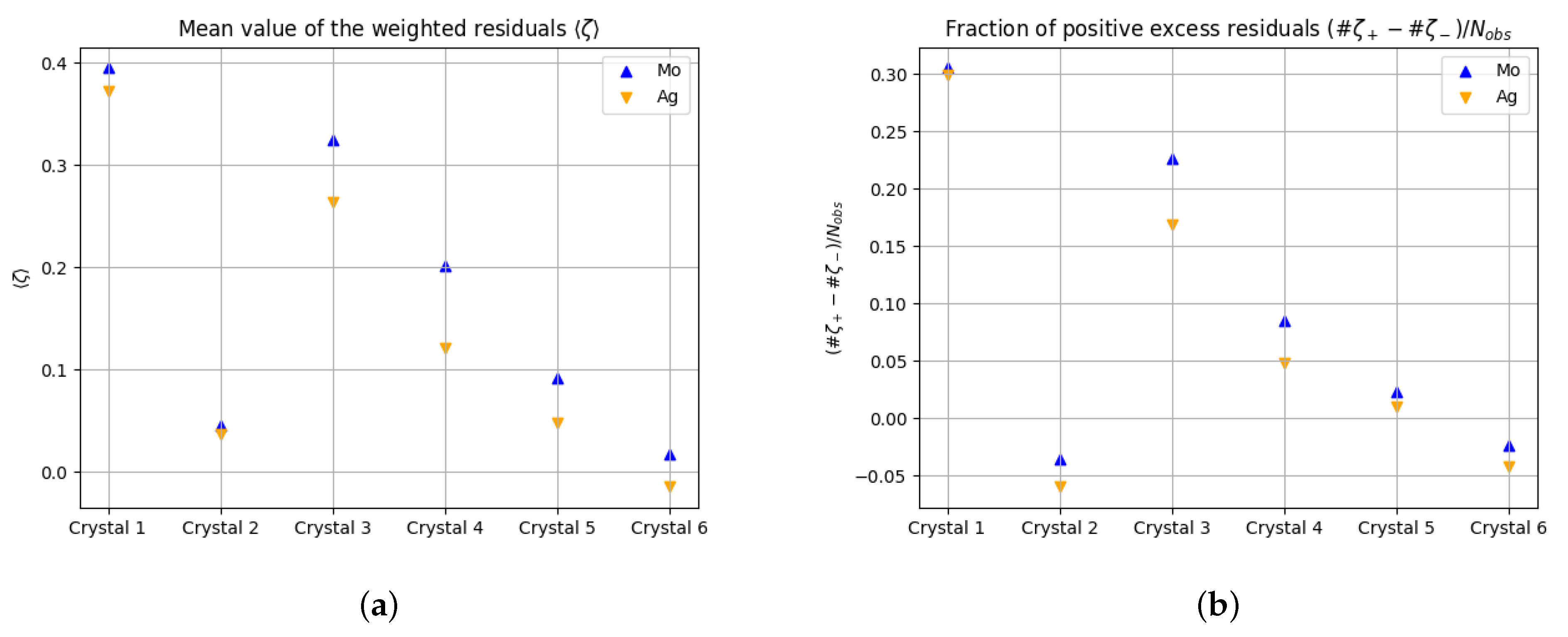
Figure 1 shows that (i) the mean value of the residuals is positive in almost all cases $〈\zeta 〉>0$; (ii) the larger the absorption coefficient, the larger the mean value of the residuals, $〈\zeta 〉\propto \mu$; and (iii) $〈\zeta 〉\propto {\displaystyle \frac{(\#{\zeta }_{+}-\#{\zeta }_{-})}{N_{obs}}}$, where (iii) holds in all cases, and (i) and (ii) only with the exception of Crystal 2. $〈\zeta 〉$ scatters stochastically around zero with positive and negative deviations in data sets without systematic errors.

Table 2. Residual descriptors of Crystals 1–13. Column two: anode material; column three: fraction of positive excess residuals (FOPERs) with $\#{\zeta }_{+}$ indicating the integer number of positive residuals and $\#{\zeta }_{-}$ indicating the integer number of negative residuals, negative numbers indicating that negative residuals appear more often than positive ones, and data sets without systematic errors showing positive and negative values with the same probability; column four: significance of FOPER as given by a random walk approach with equal probabilities for positive and for negative steps; columns five and six: weighting scheme parameters a and b; column seven: total mean value of weighted residuals, with data sets without systematic errors showing insignificant small positive and negative values with the same probability; column eight: significance of deviation of mean value of weighted residuals from zero; column nine: bin scale factor $K={\displaystyle \frac{〈I_{obs}〉}{〈I_{calc}〉}}$ for bin 1 (lowest 10%) from in total 10 bins of intensity sorted reflections similar to, but not identical with, the numbers given in SHELXL output files due to differing bin widths; column ten: mean value of only positive residuals; column eleven: standard deviation of mean value of only positive residuals; column twelve: absolute mean value of only negative residuals; column eleven: standard deviation of absolute mean value of only negative residuals. For more information about the metrics ${\displaystyle \frac{(\#{\zeta }_{+}-\#{\zeta }_{-})}{N_{obs}}}$, ${\displaystyle \frac{(\#{\zeta }_{+}-\#{\zeta }_{-})}{\sqrt{N_{obs}}}}$, $〈\zeta 〉$, ${\displaystyle \frac{〈\zeta 〉}{\sigma \left(〈\zeta 〉\right)}}$, $〈{\zeta }_{+}〉$, $\sigma \left(〈{\zeta }_{+}〉\right)$, $〈|{\zeta }_{-}|〉$, and $\sigma \left(〈|{\zeta }_{-}|〉\right)$, see also [14,32].

Data Set	Anode	$\frac{(\#{\mathit{\zeta }}_{+}-\#{\mathit{\zeta }}_{-})}{{\mathit{N}}_{\mathbf{obs}}}$	$\frac{(\#{\mathit{\zeta }}_{+}-\#{\mathit{\zeta }}_{-})}{\sqrt{{\mathit{N}}_{\mathbf{obs}}}}$	a	b	$〈\mathit{\zeta }〉$	$\frac{〈\mathit{\zeta }〉}{\mathit{\sigma }\left(〈\mathit{\zeta }〉\right)}$	${\mathit{K}}_1\left[{\mathit{I}}_{\mathit{calc}}\right]$	$〈{\mathit{\zeta }}_{+}〉$	$\mathit{\sigma }\left(〈{\mathit{\zeta }}_{+}〉\right)$	$〈|{\mathit{\zeta }}_{-}|〉$	$\mathit{\sigma }\left(〈|{\mathit{\zeta }}_{-}|〉\right)$
Crystal 1	Mo	0.3051	16.6444	0.0265	6.5030	0.3951	17.75	2.47	1.0368	0.0193	0.8101	0.0253
Crystal 2	Mo	−0.0351	−0.6218	0.0319	1.8322	0.0457	0.54	1.05	1.1788	0.0922	1.0104	0.0706
Crystal 3	Mo	0.2265	19.7276	0.0103	1.1388	0.3247	25.13	1.88	0.9885	0.0124	0.7279	0.0106
Crystal 4	Mo	0.0852	2.2613	0.0174	0.0528	0.2019	4.31	1.24	0.9825	0.0542	0.7241	0.0384
Crystal 5	Mo	0.0233	1.2588	0.0260	1.6275	0.0923	4.78	1.37	0.8206	0.0220	0.6707	0.0154
Crystal 6	Mo	−0.0238	−2.1110	0.0270	2.4392	0.0173	1.43	1.03	0.8063	0.0142	0.7350	0.0094
Crystal 1	Ag	0.2985	23.5198	0.0096	0.9879	0.3727	24.87	6.14	0.9551	0.0150	0.7052	0.0154
Crystal 2	Ag	−0.0597	−1.6577	0.0381	0.0000	0.0369	0.77	1.06	1.0582	0.0546	0.8693	0.0395
Crystal 3	Ag	0.1691	16.9502	0.0046	0.8512	0.2633	23.68	1.40	0.9781	0.0104	0.7423	0.0093
Crystal 4	Ag	0.0478	1.9060	0.0156	0.0264	0.1216	4.48	1.02	0.8694	0.0288	0.7013	0.0232
Crystal 5	Ag	0.0102	0.5525	0.0233	1.4071	0.0475	2.49	1.11	0.8048	0.0195	0.7254	0.0166
Crystal 6	Ag	−0.0424	−3.7452	0.0225	1.9900	−0.0147	−1.32	0.64	0.7720	0.0111	0.7375	0.0093
Crystal 7	Mo	0.1176	5.0052	0.0230	2.0063	0.1925	6.79	1.49	0.9258	0.0312	0.7363	0.0253
Crystal 8	Mo	0.0930	6.7860	0.0463	6.2838	0.1120	8.19	1.90	0.7908	0.0133	0.7060	0.0120
Crystal 9	Mo	0.0925	10.2715	0.0176	7.2977	0.1344	14.39	2.28	0.8411	0.0090	0.7164	0.0082
Crystal 10	Cu	0.1482	10.8123	0.0178	1.2762	0.1657	11.46	1.25	0.8545	0.0127	0.7627	0.0141
Crystal 11	Cu	0.1254	12.5730	0.0375	7.1306	0.1542	15.31	1.52	0.8434	0.0089	0.7325	0.0091
Crystal 12	Mo	0.3232	32.4812	0.0431	226.7933	0.3466	41.42	11.15	0.8021	0.0072	0.5440	0.0079
Crystal 13	Cu	0.2421	22.7127	0.0000	84.1555	0.3535	30.08	4.00	0.9624	0.0116	0.6444	0.0110

Table 2. Residual descriptors of Crystals 1–13. Column two: anode material; column three: fraction of positive excess residuals (FOPERs) with $\#{\zeta }_{+}$ indicating the integer number of positive residuals and $\#{\zeta }_{-}$ indicating the integer number of negative residuals, negative numbers indicating that negative residuals appear more often than positive ones, and data sets without systematic errors showing positive and negative values with the same probability; column four: significance of FOPER as given by a random walk approach with equal probabilities for positive and for negative steps; columns five and six: weighting scheme parameters a and b; column seven: total mean value of weighted residuals, with data sets without systematic errors showing insignificant small positive and negative values with the same probability; column eight: significance of deviation of mean value of weighted residuals from zero; column nine: bin scale factor $K={\displaystyle \frac{〈I_{obs}〉}{〈I_{calc}〉}}$ for bin 1 (lowest 10%) from in total 10 bins of intensity sorted reflections similar to, but not identical with, the numbers given in SHELXL output files due to differing bin widths; column ten: mean value of only positive residuals; column eleven: standard deviation of mean value of only positive residuals; column twelve: absolute mean value of only negative residuals; column eleven: standard deviation of absolute mean value of only negative residuals. For more information about the metrics ${\displaystyle \frac{(\#{\zeta }_{+}-\#{\zeta }_{-})}{N_{obs}}}$, ${\displaystyle \frac{(\#{\zeta }_{+}-\#{\zeta }_{-})}{\sqrt{N_{obs}}}}$, $〈\zeta 〉$, ${\displaystyle \frac{〈\zeta 〉}{\sigma \left(〈\zeta 〉\right)}}$, $〈{\zeta }_{+}〉$, $\sigma \left(〈{\zeta }_{+}〉\right)$, $〈|{\zeta }_{-}|〉$, and $\sigma \left(〈|{\zeta }_{-}|〉\right)$, see also [14,32].

Data Set	Anode	$\frac{(\#{\mathit{\zeta }}_{+}-\#{\mathit{\zeta }}_{-})}{{\mathit{N}}_{\mathbf{obs}}}$	$\frac{(\#{\mathit{\zeta }}_{+}-\#{\mathit{\zeta }}_{-})}{\sqrt{{\mathit{N}}_{\mathbf{obs}}}}$	a	b	$〈\mathit{\zeta }〉$	$\frac{〈\mathit{\zeta }〉}{\mathit{\sigma }\left(〈\mathit{\zeta }〉\right)}$	${\mathit{K}}_1\left[{\mathit{I}}_{\mathit{calc}}\right]$	$〈{\mathit{\zeta }}_{+}〉$	$\mathit{\sigma }\left(〈{\mathit{\zeta }}_{+}〉\right)$	$〈|{\mathit{\zeta }}_{-}|〉$	$\mathit{\sigma }\left(〈|{\mathit{\zeta }}_{-}|〉\right)$
Crystal 1	Mo	0.3051	16.6444	0.0265	6.5030	0.3951	17.75	2.47	1.0368	0.0193	0.8101	0.0253
Crystal 2	Mo	−0.0351	−0.6218	0.0319	1.8322	0.0457	0.54	1.05	1.1788	0.0922	1.0104	0.0706
Crystal 3	Mo	0.2265	19.7276	0.0103	1.1388	0.3247	25.13	1.88	0.9885	0.0124	0.7279	0.0106
Crystal 4	Mo	0.0852	2.2613	0.0174	0.0528	0.2019	4.31	1.24	0.9825	0.0542	0.7241	0.0384
Crystal 5	Mo	0.0233	1.2588	0.0260	1.6275	0.0923	4.78	1.37	0.8206	0.0220	0.6707	0.0154
Crystal 6	Mo	−0.0238	−2.1110	0.0270	2.4392	0.0173	1.43	1.03	0.8063	0.0142	0.7350	0.0094
Crystal 1	Ag	0.2985	23.5198	0.0096	0.9879	0.3727	24.87	6.14	0.9551	0.0150	0.7052	0.0154
Crystal 2	Ag	−0.0597	−1.6577	0.0381	0.0000	0.0369	0.77	1.06	1.0582	0.0546	0.8693	0.0395
Crystal 3	Ag	0.1691	16.9502	0.0046	0.8512	0.2633	23.68	1.40	0.9781	0.0104	0.7423	0.0093
Crystal 4	Ag	0.0478	1.9060	0.0156	0.0264	0.1216	4.48	1.02	0.8694	0.0288	0.7013	0.0232
Crystal 5	Ag	0.0102	0.5525	0.0233	1.4071	0.0475	2.49	1.11	0.8048	0.0195	0.7254	0.0166
Crystal 6	Ag	−0.0424	−3.7452	0.0225	1.9900	−0.0147	−1.32	0.64	0.7720	0.0111	0.7375	0.0093
Crystal 7	Mo	0.1176	5.0052	0.0230	2.0063	0.1925	6.79	1.49	0.9258	0.0312	0.7363	0.0253
Crystal 8	Mo	0.0930	6.7860	0.0463	6.2838	0.1120	8.19	1.90	0.7908	0.0133	0.7060	0.0120
Crystal 9	Mo	0.0925	10.2715	0.0176	7.2977	0.1344	14.39	2.28	0.8411	0.0090	0.7164	0.0082
Crystal 10	Cu	0.1482	10.8123	0.0178	1.2762	0.1657	11.46	1.25	0.8545	0.0127	0.7627	0.0141
Crystal 11	Cu	0.1254	12.5730	0.0375	7.1306	0.1542	15.31	1.52	0.8434	0.0089	0.7325	0.0091
Crystal 12	Mo	0.3232	32.4812	0.0431	226.7933	0.3466	41.42	11.15	0.8021	0.0072	0.5440	0.0079
Crystal 13	Cu	0.2421	22.7127	0.0000	84.1555	0.3535	30.08	4.00	0.9624	0.0116	0.6444	0.0110

3.4. An Attempt to Rationalize $〈\zeta 〉>0$ for Absorbing Crystals

The diffracted beams are weakened by absorption in proportion to the absorption coefficient $\mu$ and the path length $x_{hkl}$ of the diffracted beam through the crystal

$$I_{measured}=I_{Bragg}{\exp }^{-\mu x_{hkl}}.$$

(4)

In order to obtain a “Bragg” intensity not affected by absorption, the individual diffracted beams need to be multiplied by an individual factor ${\exp }^{\mu x_{hkl}}>1$:

$$I_{Bragg}=I_{measured}{\exp }^{+\mu x_{hkl}}.$$

(5)

Absorption correction procedures therefore increase the measured intensities. The difficulty is that every individual diffracted beam may have another path length and that these path lengths may be very different for example for crystals with plate or needle shapes. When the path length is underestimated, $x_{hkl}<x_{true}$, the assumed factor ${\exp }^{-\mu x_{hkl}}>{\exp }^{-\mu x_{true}}$ is too large (as the reduction from one is too low), and therefore, the correction factor ${\exp }^{+\mu x_{hkl}}>1$ is too small. The Bragg intensity is therefore too small. When the path length is overestimated, the Bragg intensity is correspondingly too large.

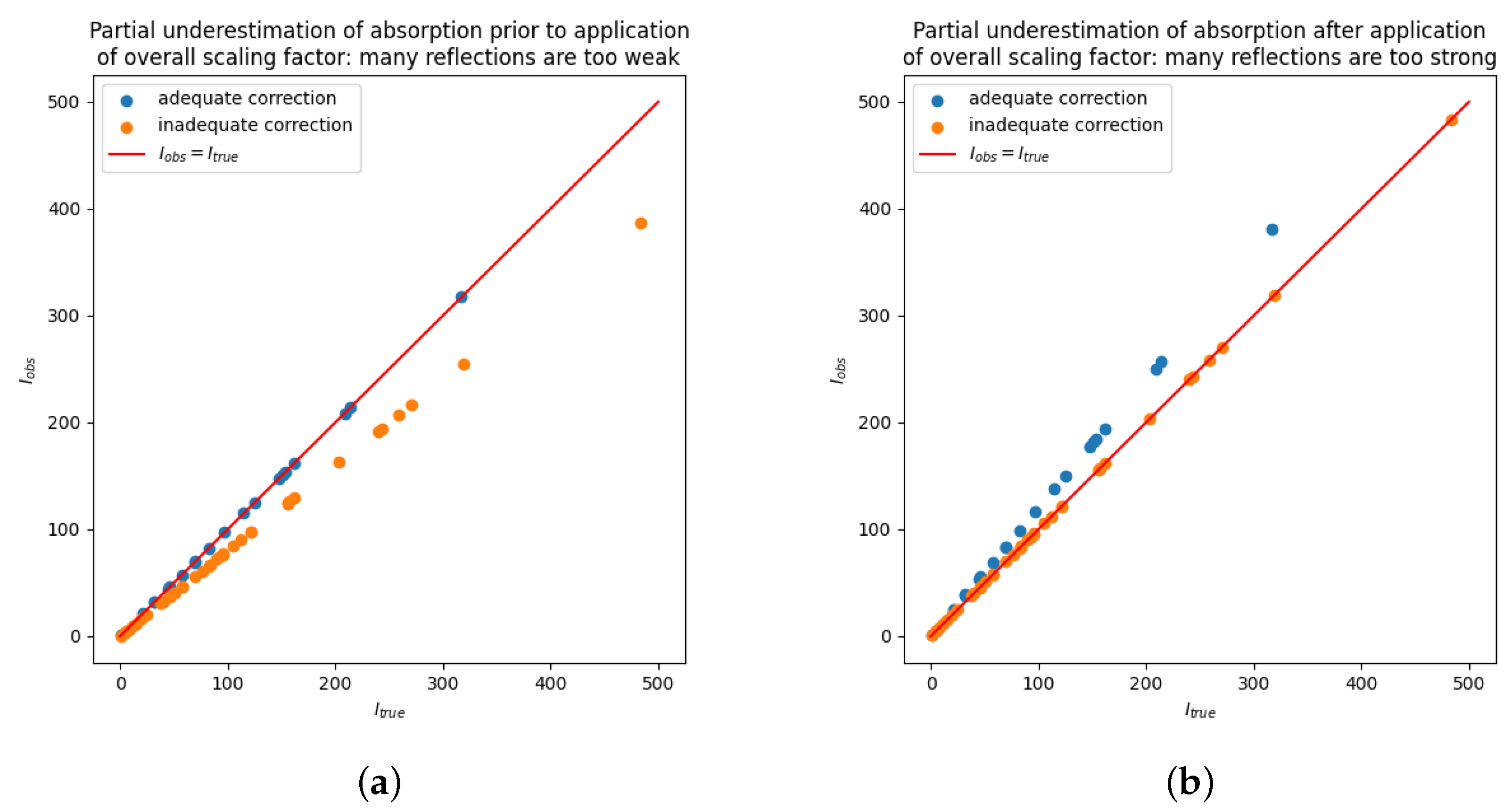
Now suppose, for a slightly elongated crystal with dimensions, say, $d_{min}=d_{mid}\approx 0.75d_{max}$, a sphere is assigned with radius $r_{eff}=0.5d_{min}$ for absorption correction. The absorption correction would work well for a part of the diffracted beams, namely those that do not propagate along the extended direction. This subset of reflections is called the subset with adequate absorption correction. For the majority of reflections with a component propagating along the extended direction, the path length would be underestimated by assigning an effective radius $r_{eff}=0.5d_{min}$. For these, the Bragg intensity is underestimated, as discussed above, when only Equation (5) is taken into account and scaling procedures are ignored. This subset of reflections is called the subset, with inadequate absorption correction leading to underestimated $I_{obs}$. As a result, a part of the Bragg intensities are adequate and a part is underestimated. The situation is sketched schematically in Figure 2a. The overall scale factor would compensate for the loss by the inadequate correction by magnifying all observed intensities. Let us assume that the reflections with adequate correction are the minority. From the many reflections with inadequate correction, which are all too small, multiplication with the overall scale factor will on average restore larger values that are closer to the unbiased, true value as in Figure 2b. However, the reflections with adequate correction will all tend to have slightly too large observed intensities.

3.5. Characteristic Traces of Incomplete/Insufficient Absorption Correction

The above thoughts result in the expectation of overestimated intensities in the case of incomplete absorption correction. The individual overestimation of $I_{obs}$ may well be much smaller than the corresponding individual standard uncertainties in many or even all cases; however, it will be systematic and will, therefore, in particular, manifest as $K={\displaystyle \frac{〈I_{obs}〉}{〈I_{calc}〉}}>1$ in the lowest bin of the intensity dependent scale factor K. In other words, partial underestimation of absorption may lead via the overall scale factor to the following characteristic traces, which together may be used as a fingerprint of traces in the data characteristic of this specific error:

• Many weak observed intensities, that are too large, which may, in turn, lead to invoking the weighting scheme parameter $b>0$;
• More positive residuals than negative residuals, $\#{\zeta }_{+}>\#{\zeta }_{-}$, in particular for weak reflections, that are relatively the most affected by overestimation;
• The mean value of the positive residuals will tend to be larger than the absolute mean value of the negative residuals, $〈{\zeta }_{+}〉>〈\left|{\zeta }_{-}\right|〉$;
• Connected to all of the aforementioned effects, the weighted residuals will in total tend toward positive values, $〈\zeta 〉\ge 0$;
• And, the intensity-dependent scale factor $K={\displaystyle \frac{〈I_{obs}〉}{〈I_{calc}〉}}>1$ tends toward values larger than one in particular for the weakest intensities.

By analogy, partial overestimation of absorption leads more often to negative residuals, absolute larger negative residuals, and a shift in the weighted residuals to negative values and to a small value in $K<1$ for the lowest intensity bin. If the absorption correction error is the dominant systematic error, the list can be completed by the following

6.

Low-intensity reflections contribute most to the sum of squared residuals (chi-square sum);

Point (6) is particular convincing, as usually the strong reflections are expected to contribute most to the chi square sum, but here, the weak intensities are the main contributors. Additional traces in the data could be

7.

A broad scatter plot $I_{obs}$ vs. $I_{calc}$, as sketched in Figure 2b

The most important observation is that (partial) underestimation of absorption leads to increased observed intensities. As a consequence, a systematic shift in the weighted residuals to positive values may indicate underestimation of absorption and a systematic shift of the weighted residuals to negative values may indicate overestimation of absorption.

The list (1)–(7) gives a fingerprint of expected effects on the fit data for the case that the anisotropy of the crystal has not been compensated for by other means, like frame scale factors and spherical harmonics.

But, before we report on the application to real data, a general note on systematic errors that lead to overestimated observed intensities is appropriate here, as it might be objected that this error reveals itself by increasing the agreement factors. But, that is—withing certain limits—not the case; it is quite the opposite: overestimation of observed intensities can even lead to artificially reduced agreement factors. This is shown and discussed elsewhere in greater detail, but some arguments are briefly discussed in Appendix A to give the reader at least some evidence for this assertion. Errors that lead to seemingly better results are unlikely to be found easily as good results are less often and less hard-questioned compared to results that are disappointing. This effect is known in the literature as ”confirmation bias”. A confirmation bias may result in methodological errors that are not found for a long time.

3.6. Application to a Strongly and a Weakly Absorbing Crystal from the Literature

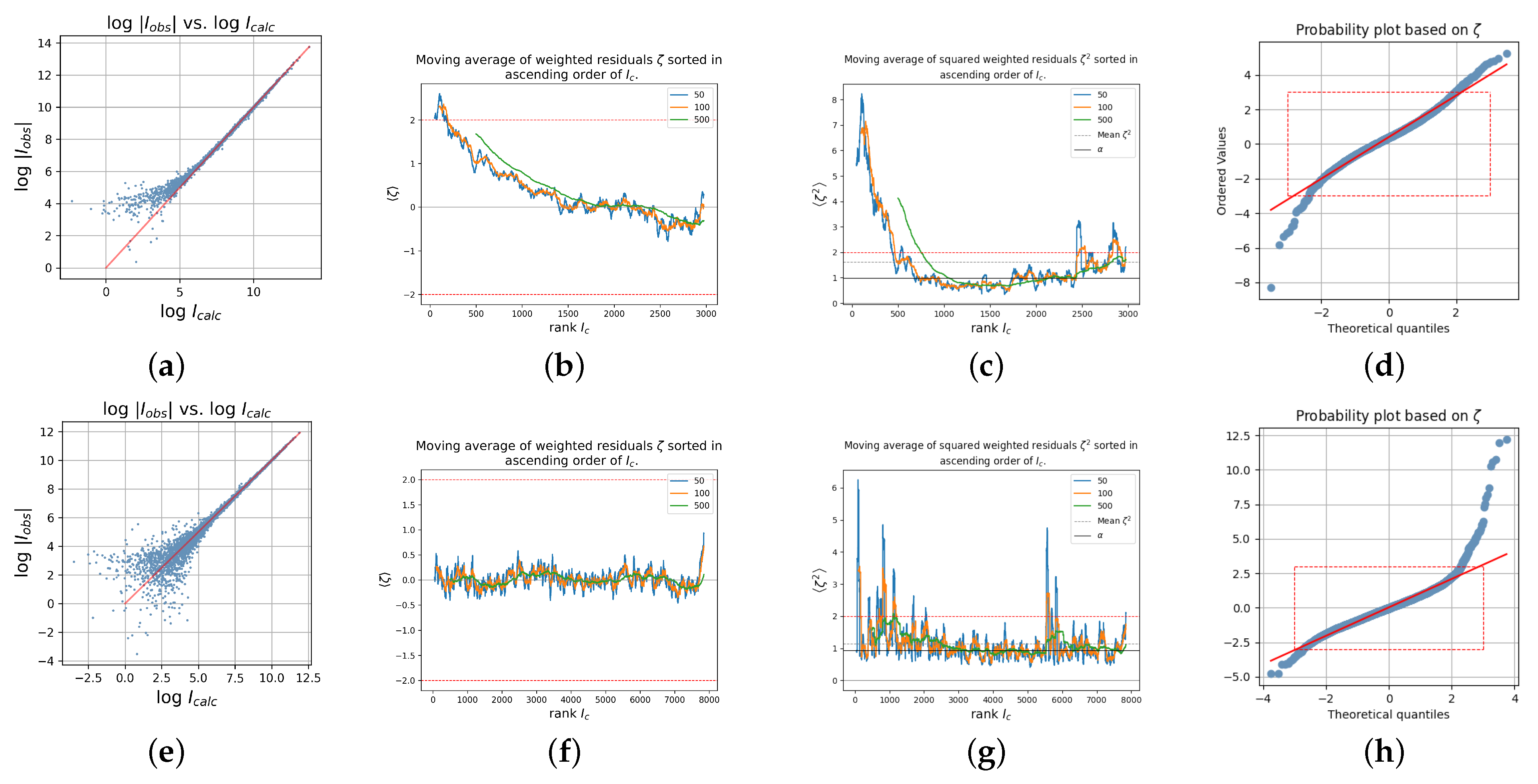
Coming back to the study discussed in Section 3.3, it is reasonable to expect visible traces of absorption correction for the strongly absorbing Crystal 1, but not for the weak absorber Crystal 6. Figure 3 shows a variety of diagnostic plots, which were chosen in order to visualize some of the fingerprint criteria 1–7 from the above list, for the $\mathrm{Mo}$ data sets of the strongly absorbing Crystal 1 (first row) and of the weakly absorbing Crystal 6 (second row).

A tendency toward larger observed weak intensities as compared to the corresponding calculated intensities, $I_{obs}>I_{calc}$, is particularly good, illustrated by plotting the observed versus calculated intensities on a logarithmic scale. Figure 3a does show a systematic difference for weak observed and calculated intensities for Crystal 1, whereas Figure 3e does not show this feature for Crystal 6.

More positive than negative residuals particularly for the weak intensities (point (1) from the above list), stronger positive residuals than absolute negative residuals for the weak intensities ((2) and (3)), an overall shift to positive residuals (4), and $K>1$ for the weakest intensities (5) is illustrated by Figure 3b, which displays a moving average of the weighted residuals for the data sorted by increasing $I_{calc}$. Different windows of size 50 (blue), 100 (orange), and 500 (green), respectively, were used for the calculation of the moving average. For a data set with no systematic errors, all of these curves fluctuate around zero, similar to Figure 3f for Crystal 6; however, the residuals are, on average larger than two for the lowest intensities of Crystal 1 (Figure 3b). This is an impressive deviation on average from zero.

Figure 3c,g show the moving averages of the squared weighted residuals—the entities constituting the chi-square sum that is minimized in the least squares model refinement—sorted in increasing order of the calculated intensities for Crystal 1, Figure 3c, and Crystal 6, Figure 3g. It is seen that the chi-square sum is clearly dominated by contributions from weak intensities for Crystal 1. Finally, the bent normal probability plots in Figure 3d,h confirm the existence of systematic errors in both data sets [35].

The normal probability plot with one-sidedly large positive residuals like in Figure 3h is a typical sign for contamination with low energy photons, which may occur in micro-sources with a mirror monochromator [14,36,37].

The plots in the top row of Figure 3 for the strongly absorbing Crystal 1 clearly display the expected signs of insufficient absorption correction, while those in the bottom row for the weakly absorbing Crystal 6 from the same study do not exhibit these typical features. This is taken as evidence for the validity of the rationale discussed in Section 3.4 and the characteristic traces derived from it as discussed in Section 3.5.

3.7. Application to Other Data

In order to further substantiate these findings, additional published data sets were analyzed from other authors. The structures of Crystal 8—Crystal 13 were published in the time period 2018–2024 and comprise $\mathrm{Cu}$ and $\mathrm{Mo}$ radiation sources; absorption coefficients between 8.42 mm⁻¹ (Crystal 13) and 24.53 mm⁻¹ (Crystal 8); and different diffractometer and detector types, including hybrid pixel detectors (Crystal 11). Mirror optics were used in most cases, and all structures were taken at 100 K, but Crystal 12, which was measured at 296 K and is the only one without a mirror monochromator. Crystal 12 is in many ways exceptional as it was also refined as a two-component twin and shows an extremely large weighting scheme parameter $b=226.7933$.

The additional structures are Crystal 7, sodium tungsate again [24], the same structure as Crystal 3; two further tungstate compounds with paratungstate B decorated by iron (II) or copper (II) from [27] (Crystals 8 and 9); a Bismuth compound, taken with copper radiation, Crystal 10 [28]; an Osmium compound again taken with copper radiation, Crystal 11 [29]; the somewhat exotic Djurleite Crystal 12 [30]; and an anti-cancer agent gold compound taken again with copper radiation, Crystal 13 [31]. More information to these data sets is also found in Table 1 and Table 2. 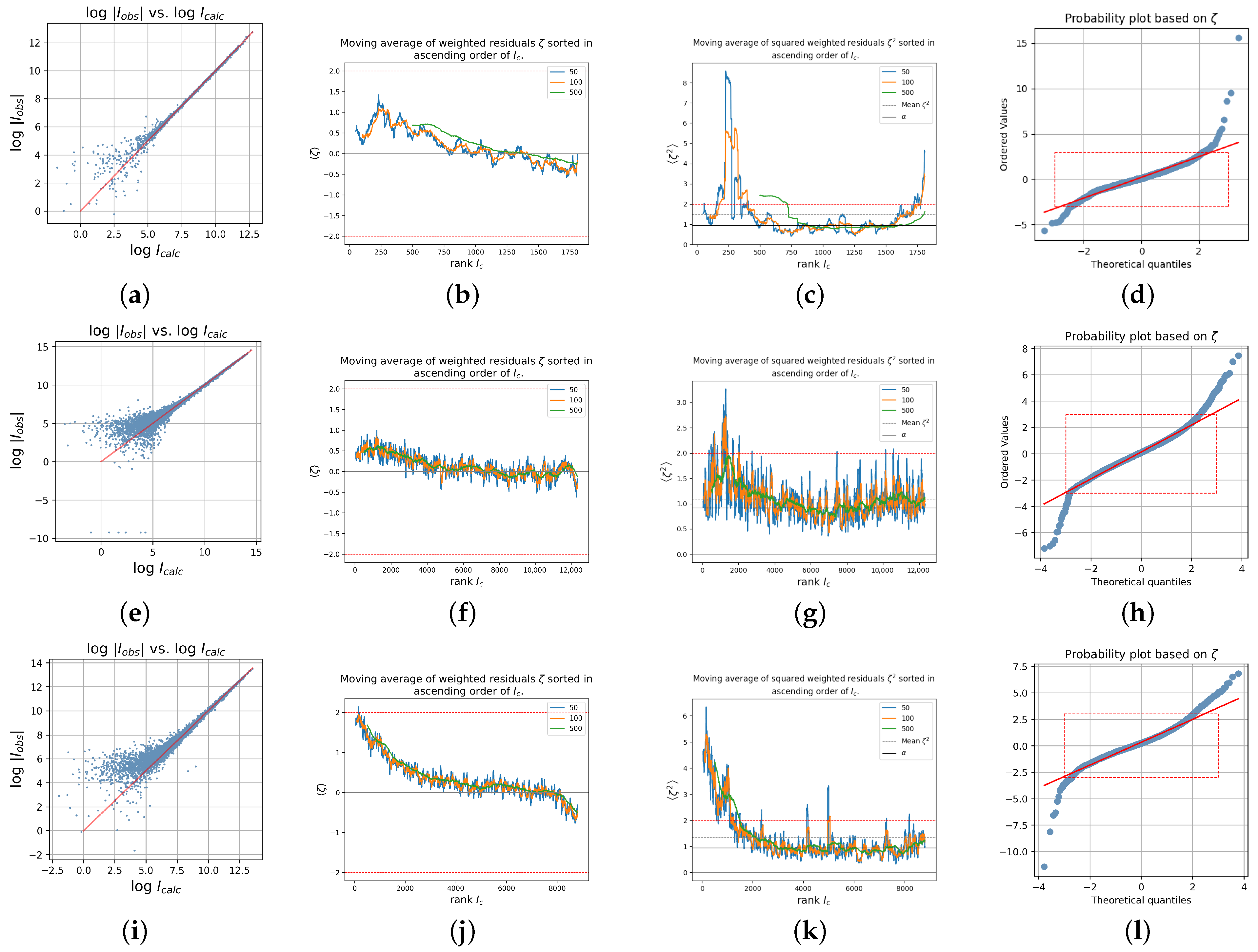The diagnostic plots for all these crystals are found in the Supplementary Materials. In this section, only three of the crystals are very briefly discussed: The diagnostic plots for Crystal 7 (sodium tungstate); Crystal 9, iron (II) paratungstate B; and Crystal 13, the anticancer gold agent STG-2, are shown in Figure 4. Crystal 7 is the same structure as Crystal 3 and was also taken with Mo radiation but with the more traditional analytical absorption correction that requires indexing of the crystal faces. The structure with the chemical formula ${\mathrm{Na}}_2{\mathrm{WO}}_4·2{\mathrm{H}}_2\mathrm{O}$ crystallizes in the orthorhombic space group $Pbca$ and was measured on an Enraf Nonius diffractometer with graphite monochromator at 291 K and with Mo K_α radiation up to ${\theta }_{max}=30.0^{\circ }$.

A direct comparison with Crystal 3 is not possible as several variables are different, like temperature and resolution (Crystal 3: T = 100 K, ${\theta }_{max}=54.1^{\circ }$); however, it is interesting to see that Crystal 7 also shows traces of insufficient absorption correction but to a smaller degree than Crystal 3. The mean value of the weighted residuals is with ${〈\zeta 〉}_{Crystal7}=0.1925$ less than two thirds of ${〈\zeta 〉}_{Crystal3}=0.3247$, and ${{\displaystyle \frac{(\#{\zeta }_{+}-\#{\zeta }_{-})}{N_{obs}}}}_{\mathrm{Crystal}7}=0.1176$ is approximately only one half ${{\displaystyle \frac{(\#{\zeta }_{+}-\#{\zeta }_{-})}{N_{obs}}}}_{\mathrm{Crystal}3}=0.2265$ according to Table 2; both values are highly significant in both cases. Crystal 3 was measured up to ${\theta }_{max}=54.1^{\circ }$ and Crystal 7 only to ${\theta }_{max}=30.0^{\circ }$; however, when only data up to ${\theta }_{max}=30.0^{\circ }$ are used in a refinement of Crystal 3, the mean of the weighted residuals increases from the previous 0.3247 (Crystal 3, ${\theta }_{max}=54.1^{\circ }$) to 0.3996 (Crystal 3, ${\theta }_{max}=30.0^{\circ }$)! This increase may surprisingly indicate that specifically the weak data from low-resolution batches contribute particularly strong to a positive shift of the residuals. This is in line with the results by [38], who found that weak data tend to be overestimated for short exposure times.

Crystal 9, the new paratungstate B compound decorated with iron (II), chemical formula ${\mathrm{Na}}_5{\mathrm{Fe}}_{2.5}\left[{\mathrm{W}}_{12}{\mathrm{O}}_{40}{\left(\mathrm{OH}\right)}_2\right]·36{\mathrm{H}}_2\mathrm{O}$, crystallizes in space group $P\overline{1}$. Measurements were carried out according to the literature with Mo K_α radiation at 100 K with a Bruker diffractometer equipped with a sealed X-ray tube and Incoatec $I\mu S$ mirror optics. Disordered water molecules in the coordination sphere of atoms $\mathrm{Na}4$ and $\mathrm{Na}5$ were modeled. The ${\left[{\mathrm{W}}_{12}{\mathrm{O}}_{40}{\left(\mathrm{OH}\right)}_2\right]}^{10-}$ anion links transition metal and sodium cations.

Crystal 13, a new bisphosphine gold (I) complex with anticancer activity, chemical formula ${\mathrm{C}}_{48}{\mathrm{H}}_{38}{\mathrm{AuCl}}_2{\mathrm{NOP}}_2$, crystallizes in space group $C2/c$ and was measured at 100 K with a Bruker diffractometer equipped with a microsource and Cu K_α radiation. The absorption coefficient is with $\mu =8.42$ mm⁻¹ smaller than those of Crystal 7 ($\mu =18.66$ mm⁻¹) and 9 ($\mu =21.09$ mm⁻¹). The data are used in an excellent tutorial at the wepage https://xray.uky.edu/Tutorials/shelxl-wght/4-WGHT-example (accessed on 6 October 2025) where they can be downloaded from, too. The SQUEEZE [39] procedure was used. Despite the comparably small absorption coefficient, distinct signs of insufficient absorption correction are visible as seen from the plots in Figure 4i–l.

3.8. Discussion of Table 2

The fingerprint traces 1–5 are found in Table 2:

• Weak observed intensities too strong. This is reflected in the overall shift to positive residuals as given by $〈\zeta 〉>0$, which applies to all cases but to $\mathrm{Ag}$ data of the weakly absorbing Crystal 6. The mean value of the weighted residuals is significantly different from zero for all of the $\mathrm{Mo}$ data sets, with the exception of Crystal 2 and Crystal 6. Even for Crystal 5 with a comparatively low absorption coefficient of $\mu =5.90$, mm⁻¹ is the shift $〈\zeta 〉=0.0923$ with ${\displaystyle \frac{〈\zeta 〉}{\sigma \left(〈\zeta 〉\right)}}=4.78$ still significant. The mean value of the residuals tends to be positive and significant approximately for crystals with $\mu \ge 5$ mm⁻¹
• More positive residuals than negative residuals in particular for weak reflections, which are relatively the most affected by overestimation: $\#{\zeta }_{+}>\#{\zeta }_{-}$. This is seen in the fraction of positive excess residuals, which is positive for all data sets but again the $\mathrm{Ag}$ data of the weakly absorbing Crystal 6 and additionally the $\mathrm{Ag}$ and $\mathrm{Mo}$ data of the outlier Crystal 2. The number of positive excess residuals is significant for all data sets with approximately $\mu \ge 10$ mm⁻¹
• The mean value of the positive residuals tends to be larger than the absolute mean value of the negative residuals, $〈{\zeta }_{+}〉>〈\left|{\zeta }_{-}\right|〉$; this applies to all data sets in the table.
• A shift in the weighted residuals to slightly positive regions in particular for the weak intensities, $〈\zeta 〉\ge 0$. This is more visible from the diagnostic plots, but it is also reflected in the next point (5):
• The intensity-dependent scale factor tends toward values larger than one, $K={\displaystyle \frac{〈I_{obs}〉}{〈I_{calc}〉}}>1$. K ranges between 0.64 ($\mathrm{Ag}$-data of Crystal 6)—the only case with $K<1$— and stunning 11.15 (Crystal 12, $N_{obs}=7077$), followed by still large $K=6.14$ ($\mathrm{Ag}$-data of Crystal 1, $N_{obs}=2976$) and $K=4.00$ (Crystal 13, $N_{obs}=8803$). To verbalize this for Crystal 12 as an example, for the weakest 707 reflections (in order of $I_{calc}$), the observed intensity is on average 11.15 times as large as the calculated intensity: $〈I_{obs}〉=11.15〈I_{calc}〉$. The affected number of reflections is in all cases much too large to be accidental. Moreover, for data sets not affected by systematic errors, one would expect numbers of K above and below one to appear approximately equally often. This is evidently not the case here.

All data sets but the Ag data set of Crystal 2 show a weighting scheme parameter $b>0$. This parameter indicates problems in the analysis of variance with weak reflections.

3.9. Testing the Hypothesis $〈\zeta 〉\propto \exp (-d_{max}\mu )$

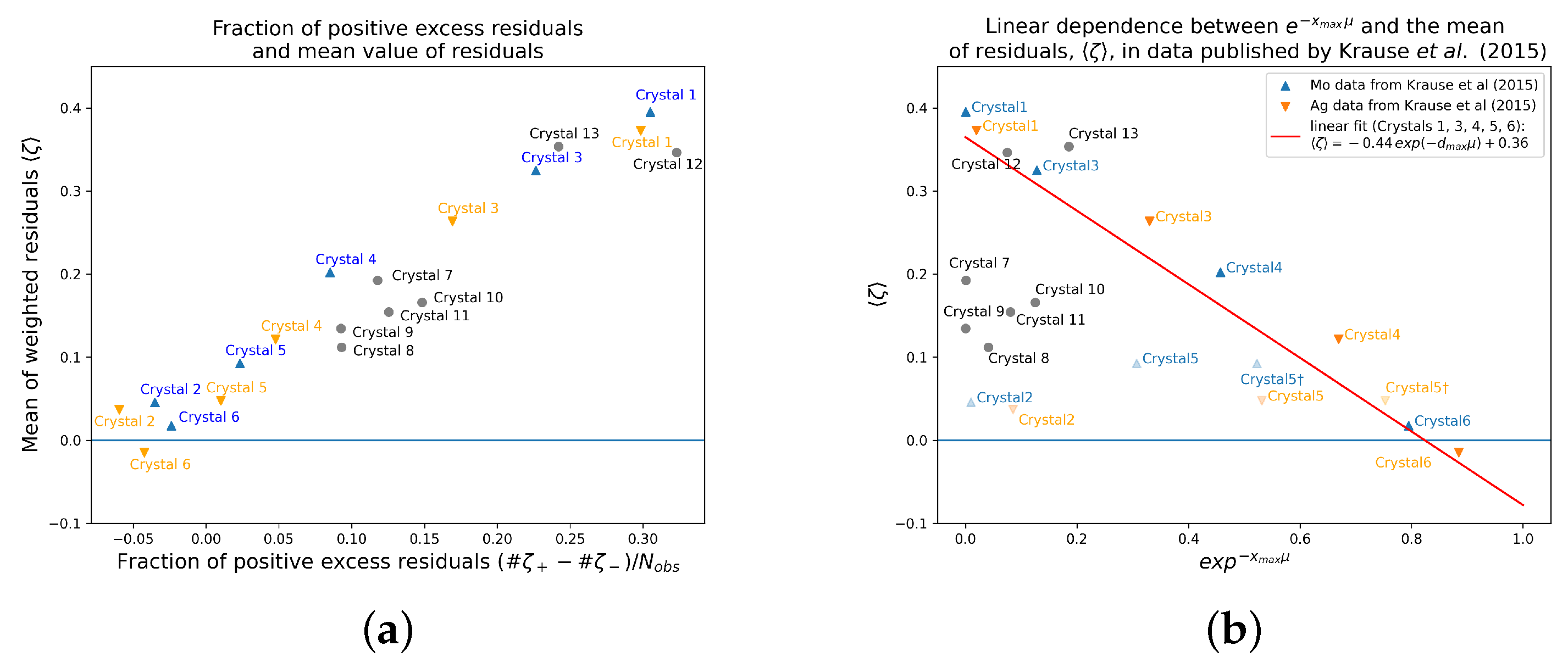
In Section 3.4, it was discussed that the crystal dimensions play a role in the absorption procedure: The effective radius is chosen to be close to half of the smallest crystal dimension. As a consequence, when the fraction of the subset with incomplete correction is more pronounced, the larger the absorption for the maximum crystal dimension. In short, $〈\zeta 〉\propto \exp (-d_{max}\mu )$. Figure 4b displays $〈\zeta 〉$ vs. $\exp (-d_{max}\mu )$ for all discussed data sets. A fit of the Mo and Ag data sets for Crystals 1, 3, 4, 5, and 6 (Crystal 2 was the outlier and was therefore omitted) results in the equation

$$〈\zeta 〉=-0.4429\exp (-d_{max}\mu )+0.3649$$

(6)

with $R^2=0.8370$ and standard errors for the parameter estimates $\pm 0.069$ (for the parameter value, −0.4429) and $\pm 0.035$ for the parameter value 0.3649. Thus, for a hypothetically not absorbing crystal with $d_{max}\mu =0$, the mean value results at ${〈\zeta 〉}_{min}=0.078$, which is only slightly larger than the expected ideal value zero and for increasing values of $d_{max}\mu$, $〈\zeta 〉$ becomes increasingly larger with a maximum value of about ${〈\zeta 〉}_{max}=0.3649$. In short, the stronger the absorption, the larger the mean value of the weighted residuals. Figure 5 shows that Crystal 2 is a clear outlier and that Crystal 5 also tends toward too small values on the x-axis (the absorption along the maximum dimension). From Crystals 1 to 6, Crystal 5 was the one with by far the largest maximum dimension, that is with $d_{max}=0.2$ mm much larger than the diameter of the focused X-ray beam that is given in the literature with 110 and 90 $\mathsf{\mu }$m for $\mathrm{Mo}$ K_α and Ag K_α, respectively [33]. Taking these diameters of the beam focus as $d_{max}$ in the respective equation leads to the positions marked with a dagger, “†”, for Crystal 5—very close to the fit line. This might be taken again as additional evidence for the validity of the fit. The remaining data sets from other authors, however, do not fit in. But, what is very consistent across all data sets is that the mean value of the weighted residuals and the fraction of positive excess residuals increase together, as depicted in Figure 5a. This is evidence for a shift in (a part of) the residual distribution (mainly for the weak intensities) in all cases, rather than large positive outliers being responsible for $〈\zeta 〉>0$. This is an important point as it conforms to the fingerprint criteria from above and it excludes the possibility that other systematic errors with very large positive outliers, e.g., from strong intensities, are the main driving force behind large positive values of $〈\zeta 〉$.

4. Discussion

The results show that for Crystals 1–6, the residuals of structures with notable absorption coefficient (i) tend to show positive mean values accompanied by (ii) positive excess residuals. The larger the mean value of the residuals, the larger the absorption coefficient. Positive residuals origin mainly from weak intensities, which contribute most to the ${\chi }^2$ sum of the least squares refinement. The results also show that other factors are important, too, as only the set of structures Crystals 1–6 measured on the same diffractometers to similar resolution with the same temperature fit to Equation (6), whereas Crystal 7–13 do not fit in. However, what almost all data sets have in common is (i) a positive mean value of the residuals (exception: $\mathrm{Ag}$-data of the weakest absorbing Crystal 6) and (ii) an increase in the number of positive excess residuals for increasing mean values of the residuals (no exception, not even for Crystal 2). The rate of increase is similar for Crystals 1–6 (see Figure 5a). Note that Crystals 1–6 were measured to higher resolution compared to Crystals 7–13.

4.1. Other Errors Found in the Data Sets for Crystals 1–6

There seems to be an additional slight contamination with low energy radiation, which also increases the mean value of the residuals [14]. The application of the python script described in [37] yields correction factors $k_{3\lambda }=0.0010, 0.0015, 0.0011, 0.0004, 0.0038, 0.0067$ for the $\mathrm{Mo}$ data sets of Crystals 1–6, respectively, some of which are comparable to the correction factors $k_{3\lambda }=0.0123, 0.0086, 0.0080, 0.0061, 0.0016$ for compounds 1– 5 reported in [37]. This leads to another important open question: how does an insufficient absorption correction affect those low-energy contamination signals and corresponding correction factors and vice versa? Would a more accurate absorption correction increase or decrease $k_{3\lambda }$ and similar metrics? At least it is known that low-energy contamination affects the mean value of the residuals likely only by a little: the significances of the deviation of the mean value of the weighted residuals from zero reported in [14] about those five data sets, each in three “flavors” ((i) contaminated by low-energy radiation; (ii) not contaminated as a thin foil was used to physically block the low-energy radiation; and (iii) the corrected data set, where a correction procedure was applied to the data set contaminated by low-energy radiation), from [37] and all with low absorption coefficients ($0.081\le \mu \le 0.111$ mm⁻¹) are in the range of $1.10\le {\displaystyle \frac{〈\zeta 〉}{\sigma \left(〈\zeta 〉\right)}}\le 5.74$. The absolute values (these are not given in the cited literature but were extracted from the personal archive of the author) are in the range of $0.0296\le 〈\zeta 〉\le 0.0996$ for the 15 data sets from five structures. So, the absolute values are much smaller compared to most of those from the present study (see Table 2). This rules out low-energy contamination as a strong contributor to the large mean values of the residuals and leaves the larger resolution and stronger absorption as the likely main cause. The results found by [38] may give a clue in combination with the observation from above that cutting high-resolution data down to standard resolution increases the mean value of the residuals: maybe it is not the high resolution per se but an indirect result caused by those low-intensity reflections from low-resolution batches taken with shorter exposure times which are particularly strong overestimated according to [38]. The very large $〈\zeta 〉$ values for Crystals 12 and 13 are most likely not explained by an insufficient absorption correction alone, but additional sources of error, but these were not yet identified. It was found earlier that not modeled twinning and not modeled disorder may increase the mean value of the weighted residuals [14]. It is, however, an open question of how procedures modeling (or squeezing out) solvent affect the mean value of the residuals, if at all.

4.2. A Remark on Elecron Density Peaks and Holes

It is often seen that the largest residual electron density peaks and holes are close to the heaviest atom(s) of the structure. Sometimes, these peaks and holes are really connected to the heavy atom, like in the case of anharmonic nuclear motion, which may be visible in high-resolution experiments (see, for example, [40]). But, sometimes, errors that may originate elsewhere tend to “condensate” in the residual density at the heaviest atoms in the structure. Insufficient absorption correction with $I_{obs}>I_{calc}$ for many weak reflections would result one-sidedly in a pronounced contribution to the residual electron density peaks, contributing in this way to an often observed imbalance in the residual electron density, where the residual density peaks tend to be larger than the modulus of the residual density holes.

4.3. A Remark on Anisotropic Displacement Parameters, ADPs

When it comes to ADPs and strongly absorbing crystals, one may first think about non positive-definite ADPs, cigar-shaped and oblate thermal motion ellipsoids which are known to indicate problems with absorption correction. However, before thermal motion ellipsoids look pronouncedly misshaped and raise alerts, they may appear first only slightly elongated or flattened, oriented in non-physical ways, strangely aligned or just unusual strong or weak. Although this is of course still part of the progression to cigar-shaped and oblate thermal motion ellipsoids, it is clear that the next important step would be to obtain physically meaningful ADPs that are only affected by absorption corrections and other sources of systematic error by a little and that are similar for same-temperature data sets of identical crystals measured with different radiation. A basic step forward to this goal would be to obtain similar $U_{eq}$ values for same-temperature data of same crystals. For Crystals 1–4, however, the values $U_{eq}$ from $\mathrm{Mo}$ data are often several standard deviations larger compared to those from $\mathrm{Ag}$ data. Does this mean that $U_{eq}$ from $\mathrm{Ag}$ data are more accurate? Not necessarily; it may as well indicate that there are correction performance discrepancies for the $\mathrm{Mo}$ and $\mathrm{Ag}$ data sets and both may underestimate the physical ADPs, although to different degrees. If the correction procedure itself is affected by systematic errors—which appears to be likely in this case in view of the results of the present work—the inherent main assumption that the absorption correction procedure is equally effective across the data sets breaks down. The information given about “Absorption correction in WinGX” (https://www.chem.gla.ac.uk/~louis/software/wingx/absorb.html (accessed on 6 Octeber 2025)), indicates, in view of the numerical results from Table 2 on that site, that

“The accepted wisdom is that absorption errors cause the adp’s to be somewhat smaller and more anisotropic than the “true” values (in this context the “true” value is assumed to be that obtained from the analytical correction.). Examination of the values obtained with no absorption correction bear this out”.

This could be rephrased as follows: underestimation of absorption effects leads to too small ADPs—which might even be the case for the results from [24] (see again Figure 4a–d). Signs of underestimated absorption are apparent in almost all data sets discussed here. In the present study, the focus was, however, on the traces of absorption correction in the residuals. Identifying these traces might help to reach the next milestone in obtaining even better absorption correction procedures: these would show consistent ADPs among data sets from different radiation sources collected at the same temperature and from the same crystal. Consistent does not mean that they are identical, but they would be similar within just a few standard deviations. The step after this milestone is having ADPs physically meaningful and describing mainly and realistically thermal motion even in strongly absorbing crystals.

5. Summary

In total, it was convincingly shown that absorption correction leads to specific traces in the residuals. If absorption correction procedures were complete, these specific traces were not observable. They can be rationalized and are described by the fingerprint criteria 1–7 as discussed above. Furthermore, they are consistent for all crystals analyzed in this work (apart from Crystal 2) and are even found for crystals with comparatively low absorption coefficients like Crystal 4 (Mo data, $\mu =9.78$ mm⁻¹), Crystal 11 ($\mu =9.33$ mm⁻¹), and Crystal 13 ($\mu =8.42$ mm⁻¹). Other sources of systematic errors like low energy contamination and an unknown systematic error in Crystal 2 with an error compensation effect on the mean value of the weighted residuals are present in the analyzed data sets as well. These results could help guide the way to improving absorption correction procedures in the future.