Multiscale Theory of Dislocation Plasticity

Abstract

Motion of dislocations is a common mechanism of plasticity in many materials. Dislocation-mediated deformation is essentially an inhomogeneous process, which is manifest in the formation of slip lines and complicated cell wall structures. An adequate description of these processes is an important goal of Materials Theory, which aims to describe the mechanical properties of materials and their reliability in service. This publication advances the thermodynamically consistent theory of dislocation-mediated plasticity to include the spatial gradients of the independent variables. We conducted the renormalization group scaling analysis of deformation and obtained the low-energy dislocation structures as ordinary solutions of the equilibrium equations without any arbitrary assumptions. We matched the emerging theoretical structures with the experimentally observed and made several predictions regarding possible experiments.

1. Dislocation-Mediated Bifurcation Theory of Plasticity

Over the years, a number of dislocation density-based theories of plasticity have been developed. To describe the strain hardening of soft metals, Kocks, Mecking, and Estrin [1,2,3] developed phenomenological models, which made it possible to analyze the plastic behavior of materials both under dynamic loading and creep. The treatment is based on the notion of a kinetic equation relating the equivalent plastic strain rate to the equivalent stress. The model must be supplemented with a structure parameter expressed by the dislocation density that determines the state of the material. To solve the same problem, Langer et al. [4,5] considered dislocation lines in the framework of “Cottrell’s birds’ nest” and developed a qualitative thermodynamic theory based on the concept of an effective temperature. For the motion of dislocations, they conceived of a linearized equation, which satisfies the principle of detailed balance. To simulate the development of the dislocation structures in single crystals, Ortiz and Koslowski et al. [6,7] developed a phase-field model of dislocations where an integer valued field accounts for the number of dislocations which have crossed over a point. The dislocation density in the model is proportional to the gradient of the field. To describe the evolution of dislocation arrangements the authors invoke a principle of energy minimization at discrete moments when the assumed dissipative nature of short-range interactions between the dislocations gives rise to irreversibility and hysteretic behavior. Although these theories were able to match a few experimental results, their physical bases remain in question.

The density-based theories of dislocation plasticity rely on the knowledge of dislocation energy and internal stress. Gavazza and Barnett [8] considered the elastic energy stored in the material outside a tube region surrounding the dislocation line. They calculated the self-force on a planar dislocation loop by computing the first variation of the loop self-energy during an arbitrary virtual planar change in the loop configuration. By allowing the dislocation core to spread, Cai et al. [9] presented non-singular analytic expressions for energy, stress, and forces on the dislocations, which retain most of the analytic structure of the classical expressions for these quantities but without the singularities. Berdichevsky [10] obtained an expression for the energy of a random set of dislocation lines using its scalar density as the state variable with the intention of using this expression to determine characteristics of dislocation networks.

1.1. Free Energy

It is known that plasticity is an essentially irreversible process, even when it is quasistatic, which puts in question the possibility of developing a thermodynamic theory of plasticity [11,12,13,14]. One can introduce a principle of thermodynamic alternative according to which a quasistatic thermodynamic process must be either reversible or hysteretic. Then, plastic deformation becomes an example of a hysteretic thermodynamic process while a phase transition of a reversible one. In [15], the author developed a thermodynamically consistent theory of plasticity, the most important assumption of which is the existence of the free energy. The theory describes equilibrium states and deformation processes of a specimen by varying the free energy as a function of strain and damage parameter. In [16], the author extended the concept of damage [17] to the cases of dislocation-mediated plasticity. A more detailed description of rate-independent plasticity may be developed based on the Preisach model of hysteresis [18].

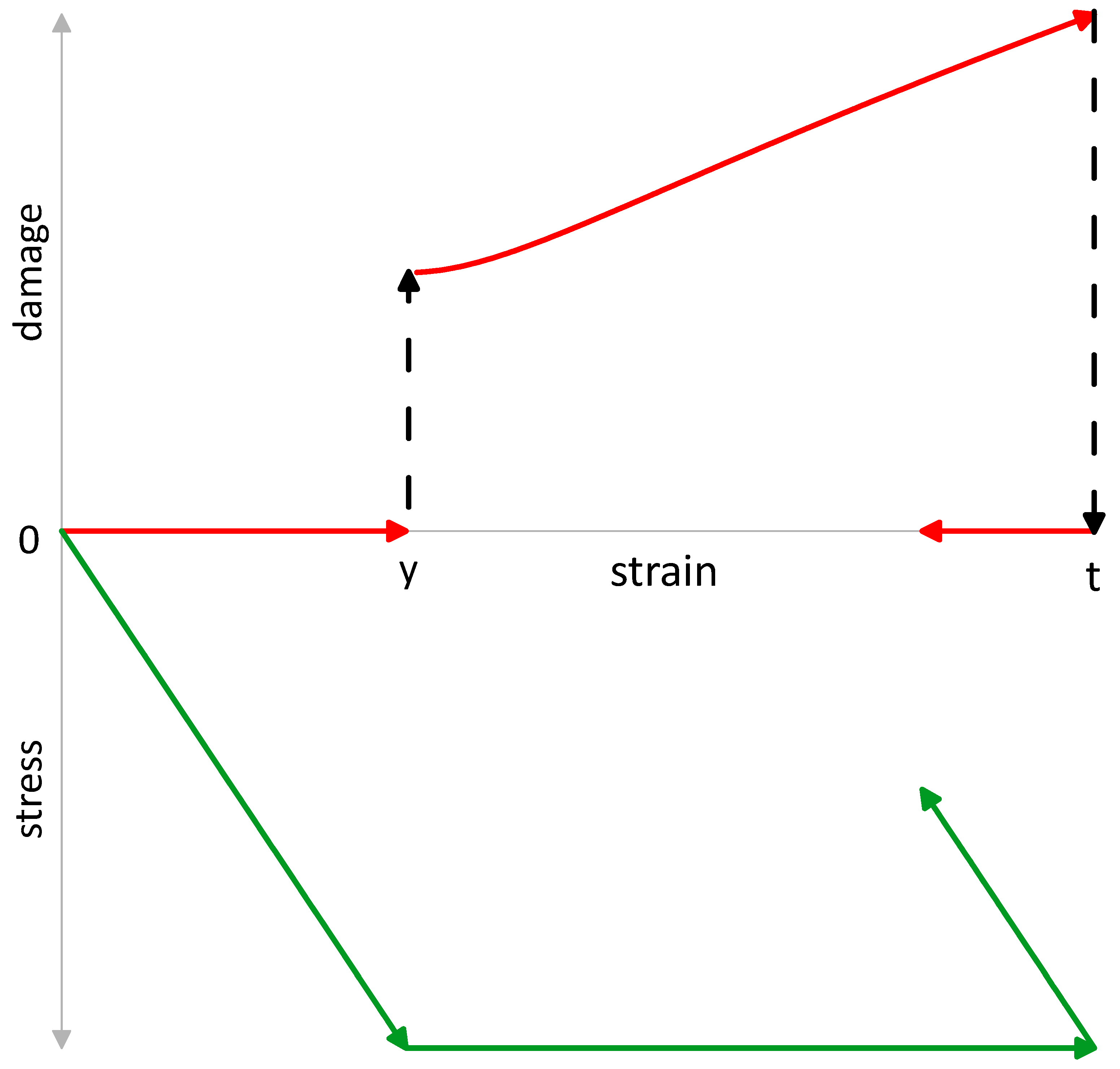
The main points of thermodynamic theory of plasticity are as follows: (1) The state of uniaxial tension or compression of a homogeneously (uniformly) deformed virgin specimen may be described by the Helmholtz free energy density f as a function of the total strain ε and damage parameter ω, where f is a sum of the elastic f^e and plastic f^p contributions. (2) Initiation of plasticity (or termination of elasticity), that is, yielding, is described as a bifurcation in the phase space of the total strain and damage parameter (ε, ω), so that ω = 0 corresponds to the elastic (or quasi-elastic) state of the material and ω > 0—to its equilibrium plastic state with damaged crystalline lattice. (3) The stress/strain reversal (unloading) in the plastic state is described as a turning point where the material returns to the quasi-elastic state with ω = 0 (or nearly zero), and two parameters of the deformation reflecting the history of loading, called back and residual strains (ε^b, ε^r), change their values. (4) The failure of the specimen is characterized by the accumulation of a certain value of damage ${\omega }^f$.

After several stages of loading, unloading, and reloading, the state of uniaxial tension or compression of a deformed specimen is described by the Helmholtz free energy density:

$$f\left(\epsilon ,{\epsilon }^r,{\epsilon }^b,\omega ,T\right)=f^e\left(\epsilon -{\epsilon }^r,T\right)+f^p\left(\omega ,\phi \right)$$

(1)

The elastic free energy f^e is a function of temperature T and the difference (ε − ε^r) of the total and residual strains, where the latter is the accumulation of the plastic strains. The plastic free energy f^p is a function of the damage parameter ω and the loading function:

$$\phi =\phi \left(\left|\epsilon -{\epsilon }^b\right|,{\epsilon }_y;T\right)$$

(2)

which depends on temperature T, the difference (ε − ε^b) of the total and back strains, where the latter is related to the hardening properties of the material, and yield strain ${\epsilon }_y\ge 0$, which may be zero. The constitutive relation in the theory is as follows:

$$\sigma \left(\epsilon ,\omega \right)\equiv {\displaystyle \frac{\partial f}{\partial \epsilon }}={\displaystyle \frac{\partial f^e}{\partial \epsilon }}+{\displaystyle \frac{\partial f^p}{\partial \epsilon }}$$

(3)

In the present model, we consider only materials with linear (Hookean) elasticity:

$$f^e={\displaystyle \frac{1}{2}}\mu {\left(\epsilon -{\epsilon }^r\right)}^2$$

(4)

where μ > 0 is the shear modulus. The strain partitioning into elastic, plastic, and residual parts takes the following form:

$$\epsilon ={\epsilon }^e+{\epsilon }^p+{\epsilon }^r={\displaystyle \frac{\sigma }{\mu }}-{\displaystyle \frac{1}{\mu }}{\displaystyle \frac{\partial f^p}{\partial \epsilon }}+{\epsilon }^r$$

(5a)

where the jump of the residual strain at the turning point $\left({\sigma }_t,{\epsilon }_t\right)$ is as follows:

$$⟦{\epsilon }^r⟧={\epsilon }_t-{\displaystyle \frac{{\sigma }_t}{\mu }}$$

(5b)

In the theory, we use the hardening rule according to which, after unloading, the representative point of the specimen finds itself on the yield surface. Then,

$${\epsilon }^b={\epsilon }_t+{\epsilon }_y\mathit{sign}{\displaystyle \frac{\partial \phi }{\partial \epsilon }}$$

(6)

At the turning point, the free energy experiences a drop in the amount of plastic work:

$$⟦f⟧=-W_t^p<0$$

(7)

even if the deformation proceeds quasi-statically. This is a manifestation of the rate independence in plasticity.

The quasistatic processes of loading of a virgin specimen and its subsequent unloading are shown in Figure 1. Material yielding represents a bifurcation, which is continuous by the free energy but may be continuous or discontinuous by the damage. The unloading, a turning point of loading, is characterized by the discontinuous drops (emission) of damage and free energy. Strain and stress remain continuous in both transitions. In the case of discontinuous-by-damage yielding the damage gap may be overcome by fluctuations.

1.2. Dislocation-Mediated Plasticity

As is known [8,9,10], a 3D network Γ of mobile dislocation can be described by the density of its lines:

$$\rho \equiv {\displaystyle \frac{{\sum }_{\Gamma }\mathcal{L}}{V}}$$

(8)

where ${\sum }_{\Gamma }\mathcal{L}$ is the total length of its lines and V is the volume of the network. The entire body of the dislocation theory motivated the author to introduce a damage parameter in the form:

$$\omega \equiv b\sqrt{\rho }$$

(9)

where b is the magnitude of the Burgers vector [16]. Using this definition of the damage parameter, the plastic (microstructure) free energy density can be described by the following expression:

$$f^p=u^p-T{s}^p=\mu {\omega }^2\left(\phi +\mathit{ln}{\displaystyle \frac{1}{\omega }}+{\displaystyle \frac{\omega }{{\omega }_{\ast }}}\right)$$

(10a)

where $u^p$ is the internal energy density, $s^p$ is the entropy density, and

$${\omega }_{\ast }\equiv {\displaystyle \frac{\mu }{T\psi }}$$

(10b)

is a typical scale of damage in the specimen and ψ is an entropy factor, which may depend on temperature. The damage parameter in Equations (9) and (10) accounts for the incipient and mobile dislocations and $\omega \approx b/l$ where $l$ is the average distance between them, while the immobile (forest) dislocations—geometrically necessary and statistically stored—are accounted for, respectively, by the residual ε^r, Equations (4) and (5), and back ε^b, Equations (2) and (6), strains. In other words, the unloading process immobilizes the mobile dislocations and makes them a part of the elastic continuum. The discontinuous reduction in the damage parameter to zero (or nearly zero) at the turning point describes absorption of the dislocations by the elastic continuum, not the healing of the material. The back strain in Equation (6) is determined by the forest (stored) dislocations and expresses the forest hardening, while the residual strain in Equation (5) is a measure of plastic deformation determined by the geometrically necessary dislocations. Notice that although the total strain is not a state variable, that is, it depends on the deformation path, the differences of the total and residual (ε − ε^r) and the total and back (ε − ε^b) strains are the state variables, that is, they do not depend on the deformation path. In the dislocation theory, the former is the elastic strain, and the latter is polarization. 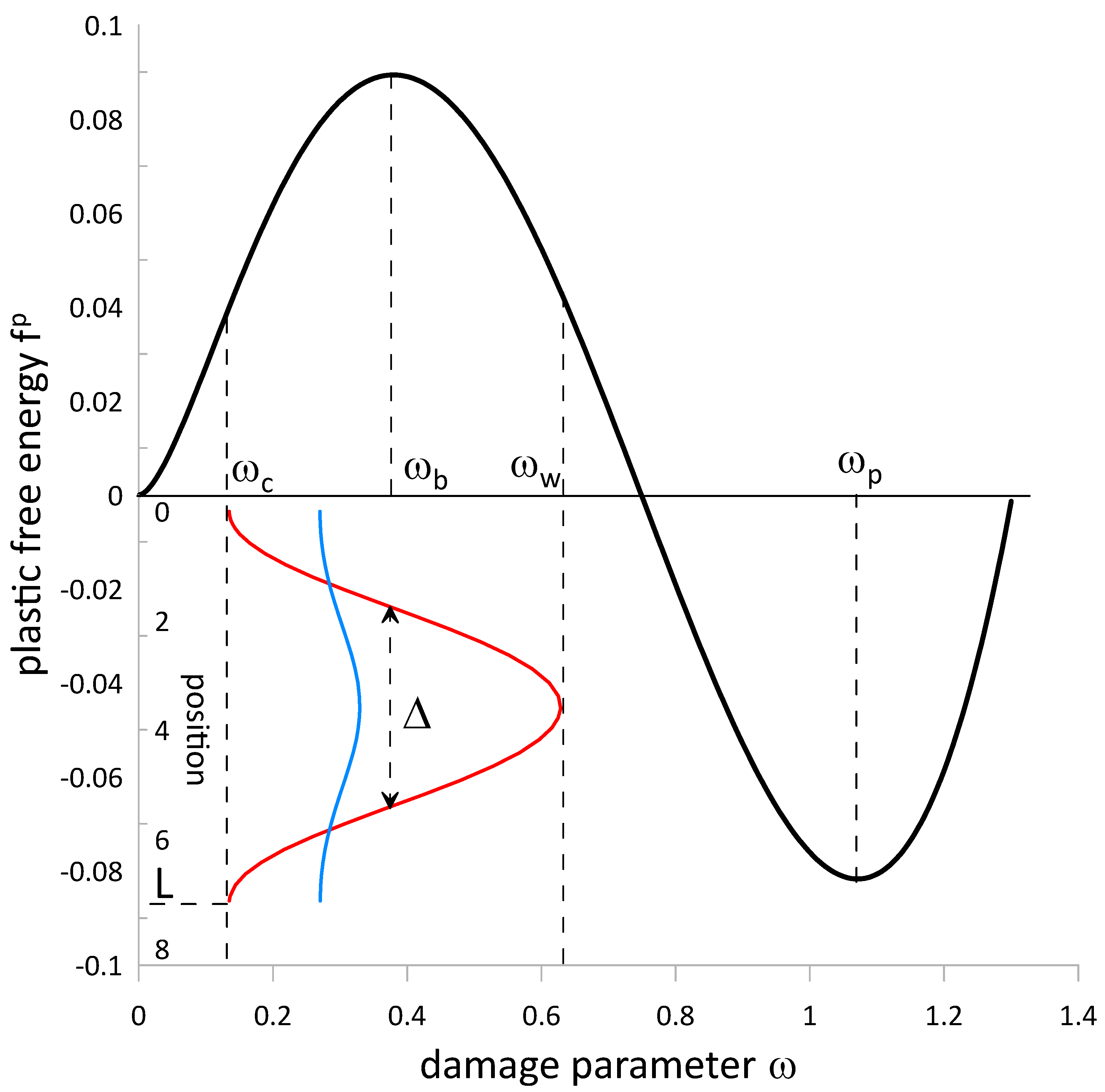The plastic free energy density, Equation (10a) is plotted in Figure 2; here and below, all quantities are presented in dimensionless units.

The damage parameter of an equilibrium state is determined by the following equation:

$${{\partial }_{\omega }f}^p=0$$

(11a)

where

$${{\partial }_{\omega }f}^p=2\mu \omega \left(\phi -{\displaystyle \frac{1}{2}}+\mathit{ln}{\displaystyle \frac{1}{\omega }}+{\displaystyle \frac{3\omega }{2{\omega }_{\ast }}}\right)$$

(11b)

For the elastic state ${\omega }_e=0$. The damage parameter of the equilibrium plastic state must be found from:

$$\phi -{\displaystyle \frac{1}{2}}+\mathit{ln}{\displaystyle \frac{1}{{\omega }_p}}+{\displaystyle \frac{3{\omega }_p}{2{\omega }_{\ast }}}=0$$

(12)

Another solution of this equation is a barrier state with ${\omega }_e<{\omega }_b<{\omega }_p\left(T, \epsilon \right)$.

The local stability of the equilibrium states is determined by the sign of the second derivative:

$${{\partial }_{\omega }^{2}f}^p=2\mu \left(\phi -{\displaystyle \frac{3}{2}}+\mathit{ln}{\displaystyle \frac{1}{\omega }}+3{\displaystyle \frac{\omega }{{\omega }_{\ast }}}\right)$$

(13)

The elastic state is always stable because ${\partial }_{\omega }^2{f}_e^p\to +\infty$ while for the plastic state we have:

$${\partial }_{\omega }^2{f}_p^p=\mu \left(3{\displaystyle \frac{{\omega }_p}{{\omega }_{\ast }}}-2\right)$$

(14)

Hence, the plastic state is also locally stable because

$${\omega }_p>{\omega }_r={\displaystyle \frac{2}{3}}{\omega }_{\ast }$$

(15a)

while the barrier state is locally unstable because ${\omega }_b<{\omega }_r$. At the critical point of the plastic-state stability:

$${\phi }_r=-\mathit{ln}{\displaystyle \frac{3}{2{\omega }_{\ast }}}-{\displaystyle \frac{1}{2}}$$

(15b)

The global stability analysis of the equilibrium states is based on the calculations of their plastic free energy densities. For the elastic state, it is $f_e^p=0$, while for the plastic state:

$$f_p^p={\displaystyle \frac{\mu }{2}}{\omega }_p^2\left(1-{\displaystyle \frac{{\omega }_p}{{\omega }_{\ast }}}\right)$$

(16)

Hence, the plastic state is globally stable for

$${\omega }_p\ge {\omega }_y={\omega }_{\ast }$$

(17a)

$$\phi \le {\phi }_y=-\mathit{ln}{\displaystyle \frac{1}{{\omega }_{\ast }}}-1$$

(17b)

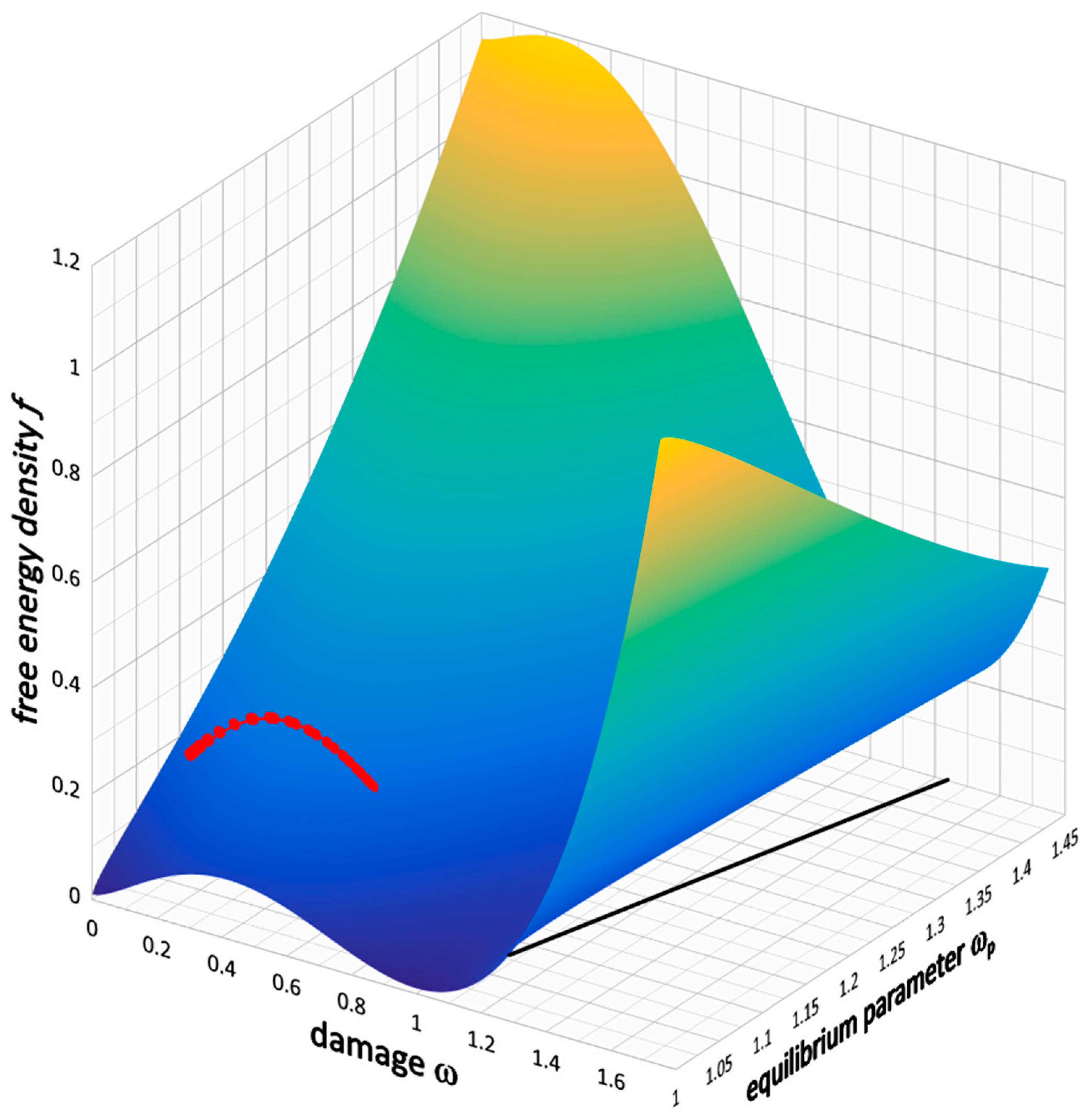
Not surprisingly, the barrier state is globally unstable because $f_b^p>0$, which also follows from its local instability. The right-hand sides of the inequalities in Equation (17) are the damage parameter and the loading function of the yield point of the specimen, that is, the point of transition from elastic to the plastic state. The Helmholtz free energy density, Equations (1), (4), and (10), is plotted in Figure 3 as a function of damage ω and equilibrium plastic damage ω_p, which replaces the loading function φ by Equation (12).

The dislocation-mediated plasticity described by free energy (10) is an example of discontinuous-by-damage yielding, that is, activated plasticity, which has the following distinct features. First, at the yield point, there is a jump in the damage parameter of magnitude ${\omega }_{\ast }$. Second, the elastic-plastic yielding has a small free energy barrier separating the elastic and plastic states:

$${\omega }_b^y=0.417{\omega }_{\ast }$$

(18a)

$$f_b^p=0.0507\mu {\omega }_{\ast }^2$$

(18b)

which can be expressed as a barrier per unit dislocation length:

$$W_P\equiv {\displaystyle \frac{{\mathcal{F} }^p\left(\rho \right)}{b^2{\sum }_{\Gamma }\mathcal{L}}}={\displaystyle \frac{f_b^p}{{\left({\omega }_b^y\right)}^2}}=0.292\mu$$

(18c)

Third, there is a domain of coexistence of the elastic and plastic states. The domain of stability of the elastic state $\left[0,\right.\left.{\omega }^b\right)$ shrinks with the decrease in the loading function φ.

In Equation (10), the dependence of the plastic free energy on strain and temperature is set by the loading function $\phi \left(\left|\epsilon -{\epsilon }^b\right|,{\epsilon }_y;T\right)$ which can be derived from a microscopic model of deformation of the dislocation network where the strain is represented by the network’s polarization. If bottom-up derivation is not an option, there is a top-down way to find the function $\phi \left(\left|\epsilon -{\epsilon }^b\right|,{\epsilon }_y;T\right)$ based on the analysis of the quasistatic unidirectional stress–strain curve of the specimen. First, using the constitutive relation (3), we present the flow stress as follows:

$$\sigma \left(\epsilon ,\omega \right)=\mu \epsilon +\mu {\omega }^2{\displaystyle \frac{\partial \phi }{\partial \epsilon }}$$

(19)

Then, using the equilibrium Equation (12) we obtain:

$$\sigma \left(\epsilon ,{\omega }_p\right)=\mu \epsilon +\mu {\omega }_p\left(1-{\displaystyle \frac{3{\omega }_p}{2{\omega }_{\ast }}}\right){\displaystyle \frac{\partial {\omega }_p}{\partial \epsilon }}$$

(20)

If stress is set as a function of the strain, variables of this equation separate, and it is readily integrable. If stress is a function of the damage parameter also, Equation (20) can be integrated numerically. In both cases, Equation (12) and the solution of Equation (20) provide a parametric expression for $\phi \left(\left|\epsilon -{\epsilon }^b\right|,{\epsilon }_y;T\right)$. Notice that if the state of a specimen is set by the applied stress, the barrier and plastic states are strained differently and, hence, the loading function has different values at these states.

Furthermore, using the partitioning of the total strain, Equation (5), one can find an expression for the plastic strain in the form:

$${\epsilon }^p=-{\omega }^2{\displaystyle \frac{\partial \phi }{\partial \epsilon }}$$

(21)

Applying Equation (9), we find Equation (21) to be the Orowan expression with the dislocation mean-free path $\left(-b{\partial }_{\epsilon }\phi \right)$ which may depend on strain and temperature.

A popular model of plasticity for many metals and alloys, called ideal or perfect, describes a quasistatic, homogeneous, monotonic, and unidirectional deformation by the following stress–strain relation [19]:

$$\sigma \left(\epsilon \right)=\left\{\begin{array}{c}\mu \epsilon , \left|\epsilon -{\epsilon }^b\right|<{\epsilon }_y\\ \mu {\epsilon }_y, \left|\epsilon -{\epsilon }^b\right|\ge {\epsilon }_y\end{array}\right.$$

(22)

It allows one to resolve Equations (12), (19) and (21) as follows:

$${\displaystyle \frac{\partial \phi }{\partial \epsilon }}=-{\displaystyle \frac{z}{{\omega }_p^2}}\mathit{sign}\left(\epsilon -{\epsilon }^b\right)$$

(23a)

$${\omega }_p^2\left({\displaystyle \frac{{\omega }_p}{{\omega }_{\ast }}}-1\right)=z^2$$

(23b)

$${\epsilon }^p=z{\left({\displaystyle \frac{\omega }{{\omega }_p}}\right)}^2\mathit{sign}\left(\epsilon -{\epsilon }^b\right)$$

(23c)

where a new quantity, called plasticity, is introduced:

$$z\equiv \left|\epsilon -{\epsilon }^b\right|-{\epsilon }_y$$

(23d)

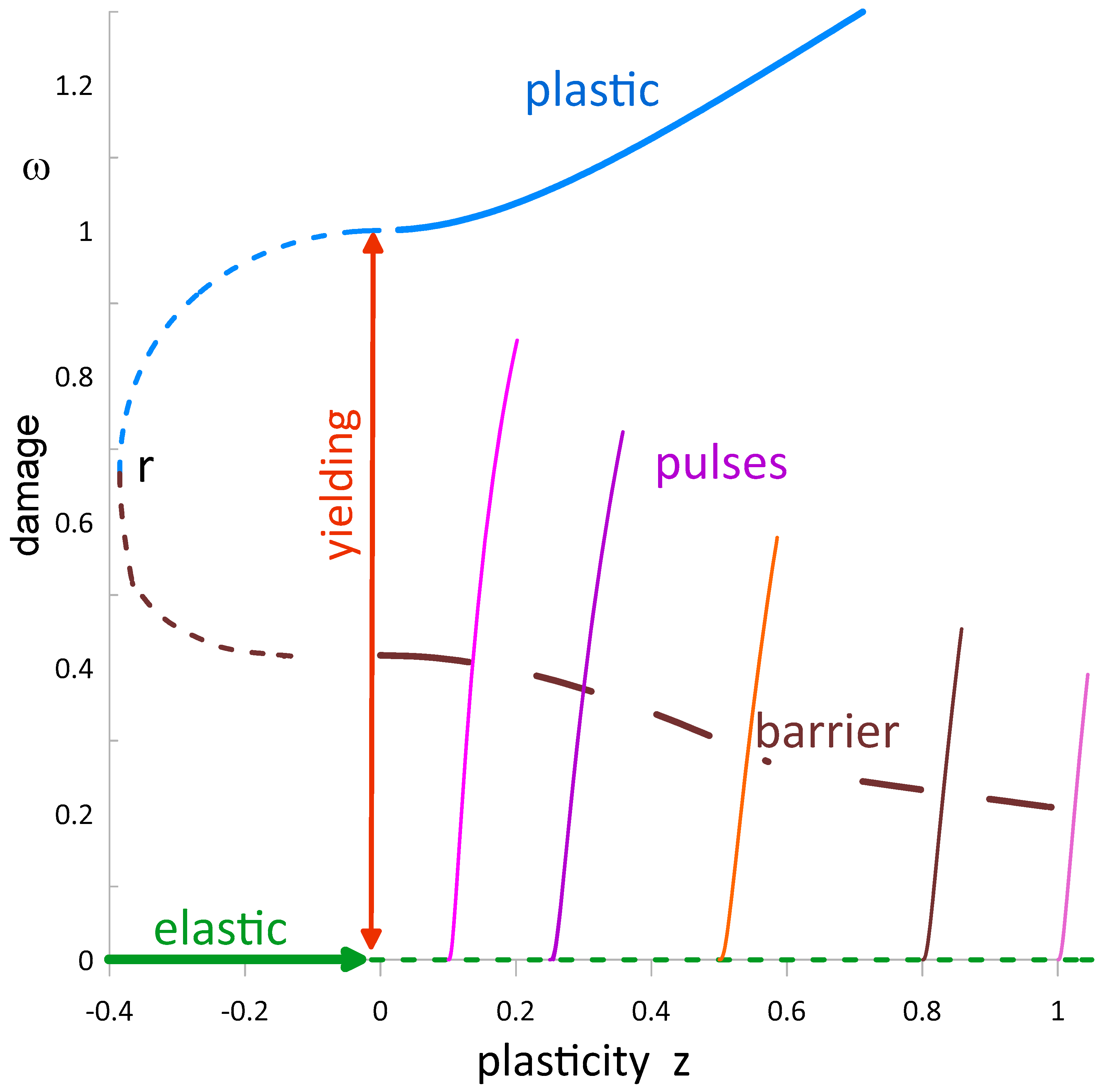
Notice from Equations (5), (6), and (23) that for the quasistatic ideal deformation ${\epsilon }^r={\epsilon }^b$ and ${\epsilon }_p^p=z$. In Figure 4, the equilibrium state diagram of an ideal plastic specimen with free energy density (10) is expressed in the phase space (z, ω).

1.3. Gradient-Flow Dynamic Equation

For the evolution of the damage parameter in a homogeneously deformed specimen in [16] was derived the gradient-flow equation:

$${\displaystyle \frac{d\omega }{dt}}=-{\gamma }_n\left(\omega \right) {\displaystyle \frac{\partial f^p}{\partial \omega }}$$

(24a)

with the relaxation coefficient:

$${\gamma }_n\left(\omega \right)={\displaystyle \frac{{\alpha }_n}{4D}}{\left({\displaystyle \frac{V^{1/3}}{b}}\right)}^{2\left(n-2\right)}{\omega }^{2\left(n-1\right)}>0$$

(24b)

where D is the dislocation drag coefficient, n is an integer, and ${\alpha }_n>0$ is an order-of-one positive dimensionless coefficient. (The comment above Equation (26) in [16] that “dependence of the mobility on volume V constitutes the dynamic size effect” appeared in error).

Equation (24) has a general solution:

$$t=-{\int }^{\omega }{\displaystyle \frac{d\omega }{ {\gamma }_n\left(\omega \right){\partial }_{\omega }{f}^p\left(\omega ,\phi \right)}}=-{\displaystyle \frac{1}{2\mu }}{\int }^{\omega }{\displaystyle \frac{d\omega }{ {\gamma }_n\left(\omega \right)\omega \left(\phi +\mathit{ln}\frac{1}{\omega }+\frac{3\omega }{2{\omega }_{\ast }}-\frac{1}{2}\right)}}$$

(25)

where the last expression is for the free energy, Equation (10). The characteristic time of damage evolution is as follows:

$$\tau ={\left[{\gamma }_n\left(\overline{\omega }\right){{\partial }_{\omega }^{2}f}^p\left(\overline{\omega }, \overline{\phi }\right)\right]}^{-1}$$

(26)

where $\left(\overline{\omega }, \overline{\phi }\right)$ are average values of damage and loading function.

As the gradient ${\partial }_{\omega }{f}^p\left(\omega ,\phi \right)$ changes sign at the barrier state, see Figure 2, the domain of the damage parameter evolution ${\omega }_e<{\omega }_p$ breaks down into two subdomains: ${\omega }_e<{\omega }_b$ and ${\omega }_b<{\omega }_p$ such that the damage is driven to increase in the latter and decrease in the former. For the domain of damage increase, one can define the characteristic time as follows:

$${\tau }_p\equiv {\displaystyle \frac{{\omega }_p-{\omega }_b}{\underset{t}{\mathit{max}}\left|{\partial }_t\omega \right|}}={\displaystyle \frac{1}{\mu {\gamma }_n\left({\omega }_m\right)}}{\displaystyle \frac{{\omega }_p-{\omega }_b}{{\omega }_m\left(3\frac{{\omega }_m}{{\omega }_{\ast }}-2\right)}}\approx {\displaystyle \frac{4.43}{\mu {\gamma }_n\left({\omega }_m\right)}}$$

(27a)

where ${\omega }_m$ is the solution of the following equation:

$$\phi -{\displaystyle \frac{3}{2}}+\mathit{ln}{\displaystyle \frac{1}{{\omega }_m}}+3{\displaystyle \frac{{\omega }_m}{{\omega }_{\ast }}}=0$$

(27b)

For the domain of damage decrease, the characteristic time is ${\tau }_e\approx 2.17/\mu {\gamma }_n\left({\omega }_m\right)$.

2. Inhomogeneous Deformation

Deformation is fundamentally a localized process, which comes about as a result of its inhomogeneity. The structural examples of that are persistent slip bands and dislocation cell wall structures, which appear both in compression and tension experiments. Other manifestations of inhomogeneity of deformation processes are their multiple size effects. Toupin [20] and Mindlin et al. [21] developed a continuum theory of linear elasticity with higher-order gradients of displacements, which, however, did not receive experimental corroboration. To describe the role of dislocations in localization effects of deformation, Aifantis [22,23] used analogy with “generalized chemical reactions” and introduced spatial gradients of densities of mobile and immobile dislocations. He also suggested, although with little justification, equations of evolution where the effects of inhomogeneity are expressed by the second derivatives of the densities. Gurtin and Anand [19,24] expanded the Aifantis formulation on the cases of not small strains. Fleck and Hutchinson [25,26] assumed that “the strain free energy density function depends upon a single scalar strain measure which consists of the elastic strain energy and square strain-gradient contribution” and used that relationship to explain the strain gradient hardening effect. Combining various approaches to inhomogeneous deformation, Estrin et al. [27,28] expanded their theory of plasticity by introducing first- and second-order spatial gradients of plastic strain and applied the theory to the high-pressure torsion process of deformation with the intention to study structure formation in plasticity.

2.1. Gradient Expansion

Inhomogeneity of deformation of a specimen gives rise to several distinct changes in our theory. (Effects of inhomogeneous temperature distribution are not considered here). First, the density of the dislocation lines is averaged in Equation (8) not over the entire volume of the specimen V but over the characteristic volume of the network where the density remains practically homogeneous, that is, the correlation volume Ω. Second, the total free energy of an inhomogeneously deformed specimen depends on the inhomogeneous measures of the independent variables of the representative volumes of the specimen, that is, strain and damage. Hence, it becomes a functional:

$$\mathcal{F}\left\{\epsilon ,\omega \right\}={\int }_V\widehat{f}\left(\epsilon ,\omega ,{\partial }_{x_i}\epsilon ,{\partial }_{x_i}\omega \right) {dx}^3$$

(28a)

where the integrand is the free energy density. Third, expansion of the free energy density in powers of the gradients of strain and damage shows that it can be separated into homogeneous and inhomogeneous contributions:

$$\widehat{f}=f^e+f^p+f^g$$

(28b)

where the latter is a quadratic form of the spatial gradients of the strain and damage:

$$f^g={\displaystyle \frac{1}{2}}{\kappa }_{\epsilon }{\left[\nabla \left(\epsilon -{\epsilon }^r\right)\right]}^2+{\displaystyle \frac{1}{2}}{\kappa }_{\omega }{\left(\nabla \omega \right)}^2$$

(28c)

because it is the lowest-order, non-singular, scalar form of such an expansion. Here, ${\kappa }_{\epsilon }$ and ${\kappa }_{\omega }$ are the gradient energy coefficients, which are material properties. Notice that the terms ${\nabla }^2\epsilon$ and ${\nabla }^2\omega$ are not included because with the help of Gauss’s theorem, they can be transformed into the square-gradient terms plus the surface contributions, which may be disregarded for large specimens (but not the small ones).

The constitutive relation (3) transforms now to the functional derivative of the free energy:

$$\sigma \left\{\epsilon ,\omega \right\}\equiv {\displaystyle \frac{\delta \mathcal{F}}{\delta \epsilon }}=\mu \left(\epsilon -{\epsilon }^r\right)-{\kappa }_{\epsilon }{\nabla }^2\left(\epsilon -{\epsilon }^r\right)+\mu {\omega }^2{\displaystyle \frac{\partial \phi }{\partial \epsilon }}$$

(29)

The second term in the r.h.s. of Equation (29) is the long-range stress component, which is a function of the difference in the total and residual strains. Notice that the term $\nabla \sigma \nabla \epsilon$ has the same spatial properties as the first term in Equation (28c), that is, is apart of it. However, the flow stress has another long-range contribution due to spatial variation of the damage parameter in the r.h.s. of Equation (29). Hence, Equation (28c) presents a complete form of the expansion of the free energy density up to the second order of the spatial gradients.

If an inhomogeneously deformed state of a specimen is set by external loading conditions, its equilibrium state, instead of Equation (11a), must obey a system of Euler–Lagrange equations:

$${\displaystyle \frac{\delta \mathcal{F}}{\delta \omega }}\equiv {\partial }_{\omega }{f}^p-{\kappa }_{\omega }{\nabla }^2\omega =0$$

(30a)

$${\displaystyle \frac{\delta \mathcal{F}}{\delta \epsilon }}\equiv {\partial }_{\epsilon }{f}^e+{\partial }_{\epsilon }{f}^p-{\kappa }_{\epsilon }{\nabla }^2\epsilon =\sigma$$

(30b)

where σ is the applied resolved stress. Variations of damage subjected to Equation (30) have a correlation volume Ω = R^d with the following correlation radius:

$$R=\sqrt{{\displaystyle \frac{{\kappa }_{\omega }}{{{\partial }_{\omega }^{2}f}^p\left(\overline{\omega }, \phi \left(\overline{\epsilon }\right)\right)}}}$$

(31)

where $\left(\overline{\epsilon }, \overline{\omega }\right)$ are the average strain and damage in the volume, and d is its dimensionality.

2.2. Evolution of Damage

Evolution of an inhomogeneously deformed specimen, instead of Equation (24), obeys the inhomogeneous gradient-flow equation:

$${\displaystyle \frac{d\omega }{dt}}=-{\gamma }_n\left(\omega \right) {\displaystyle \frac{\delta \mathcal{F}}{\delta \omega }}$$

(32a)

$${\gamma }_n\left(\omega \right)={\displaystyle \frac{{\alpha }_n}{4D}}{\left({\displaystyle \frac{{\kappa }_{\omega }}{b^2{{\partial }_{\omega }^{2}f}^p}}\right)}^{\left(n-2\right)}{\omega }^{2\left(n-1\right)}>0$$

(32b)

As we discussed above, the domain of the damage parameter evolution in the phase space breaks down into two subdomains such that the damage is driven to increase in one and decrease in the other one, see Figure 2. The presence of the spatial gradients of strain and damage changes the ‘driving force’ to ${\delta }_{\omega }\mathcal{F} \left\{\omega ,\phi \right\}$, but does not change the overall conclusion. Because of that, the growth of damage in the subdomain ${\omega }_e<{\omega }_b$ cannot be described by the homogeneous gradient-flow equation alone. Hence, inhomogeneous plastic deformation of a specimen must be accompanied by fluctuations of damage.

Let us assume that under conditions of thermodynamic equilibrium, the elastic state contains a fluctuating network of mobile dislocations described by the average density ${\rho }_f>0$, damage parameter ${\omega }_f=b\sqrt{{\rho }_f}$, and variance ${\omega }_f^2/3$ (do not confuse ${\rho }_f$ with forest dislocations). The fluctuations are caused by the operation of various sources of dislocation nucleation and annihilation, where nucleation prevails. The value ${\omega }_f$ is much smaller than the equilibrium value of the damage parameter in the plastic state ${\omega }_{\ast }$, Equation (10b), and may depend on temperature and state of strain. (The sources of fluctuations in the specimen will be considered elsewhere). Evolution of such a network may be described by the following Langevin-type equation:

$${\displaystyle \frac{d\omega }{dt}}=-{\gamma }_n\left(\omega \right) {\displaystyle \frac{\delta \mathcal{F}}{\delta \omega }}+\varpi \left(x,t\right)$$

(33)

where the Langevin force (noise) $\varpi \left(x,t\right)$ has the following correlation properties:

$$〈\varpi \left(x,t\right)〉={\gamma }_n\left({\omega }_f\right){\omega }_f{{\partial }_{\omega }^{2}f}^p\left({\omega }_f, \phi \right)$$

(34a)

$$〈\varpi \left(x_1,t_1\right)\varpi \left(x_2,t_2\right)〉={\displaystyle \frac{8}{3}}{\gamma }_n\left({\omega }_f\right)\mathsf{\Omega }{\omega }_f^2{{\partial }_{\omega }^{2}f}^p\left({\omega }_f, \phi \right)\delta \left(x_2-x_1\right)\delta \left(t_2-t_1\right)$$

(34b)

where the angle brackets mean statistical averaging. The correlation radius and time of such fluctuation are described, respectively, by Equations (26) and (31) with $\overline{\omega }={\omega }_f$. Such Langevin force can be reproduced by the following function:

$$\varpi \left(x,t\right)=2{\gamma }_n\left({\omega }_f\right){\omega }_f{{\partial }_{\omega }^{2}f}^p\left({\omega }_f,\phi \right)\xi \left(\Delta x, \Delta t;d\right)$$

(34c)

where ξ is a random variable uniformly distributed on the interval $\left[0, 1\right]$, Δx and Δt are the representative size and time inside which the noise ξ is strongly correlated. For the correlation function of the Langevin force expressed by Equation (34c) to be equal to expression (34b), Δx and Δt must be equal to the correlation radius, Equation (31), and time, Equation (26). For the fluctuational growth in the subdomain ${\omega }_e<{\omega }_b$ one may introduce the characteristic time as follows:

$${\tau }_f\equiv {\displaystyle \frac{{\omega }_b}{〈\varpi \left(x,t\right)〉}}\approx {\displaystyle \frac{1}{\gamma \mu }}{\displaystyle \frac{{\omega }_b}{2{\omega }_f\mathit{ln}\frac{{\omega }_{\ast }}{{\omega }_f}}}$$

(35a)

The derivatives of the free energy in Equation (34) may be taken at the point of yielding:

$${\partial }_{\omega }{f}^p\left({\omega }_f, {\phi }_y\right)=\mu {\omega }_f\left[2\mathit{ln}{\displaystyle \frac{{\omega }_{\ast }}{{\omega }_f}}+3\left({\displaystyle \frac{{\omega }_f}{{\omega }_{\ast }}}-1\right)\right]\approx 2\mu {\omega }_f\mathit{ln}{\displaystyle \frac{{\omega }_{\ast }}{{\omega }_f}}$$

(35b)

$${\partial }_{\omega }^2{f}^p\left({\omega }_f, {\phi }_y\right)=2\mu \left(\mathit{ln}{\displaystyle \frac{{\omega }_{\ast }}{{\omega }_f}}+3{\displaystyle \frac{{\omega }_f}{{\omega }_{\ast }}}-{\displaystyle \frac{5}{2}}\right)\approx 2\mu \mathit{ln}{\displaystyle \frac{{\omega }_{\ast }}{{\omega }_f}}$$

(35c)

Notice that the Langevin force, Equation (34), has a nonvanishing correlation with the driving force of Equation (32a). Indeed

$$〈{\displaystyle \frac{\delta \mathcal{F}}{\delta \omega }}\left(x_1,t_1\right)\varpi \left(x_2,t_2\right)〉={\gamma }_n\left({\omega }_f\right){\omega }_f{{\partial }_{\omega }f}^p\left({\omega }_f, {\phi }_y\right){{\partial }_{\omega }^{2}f}^p\left({\omega }_f, {\phi }_y\right)\approx 4{\gamma }_n\left({\omega }_f\right){\left(\mu {\omega }_f\mathit{ln}{\displaystyle \frac{{\omega }_{\ast }}{{\omega }_f}}\right)}^2$$

(36)

3. Scaling Properties of Dislocation Structures

Under practically all conditions of plastic deformation and in a wide range of materials, the microstructures are found to form, which include micron-sized, comparatively free of dislocations cells/subgrains separated by well-defined densely populated dislocation walls/boundaries [29,30,31,32,33,34,35]. The walls/boundaries may undergo internal, structural changes of their own, transforming from narrow packets of tangles to thin-layered networks. Three spatial characteristics of the dislocation structures, which are most often measured in the experiments, are the dislocation densities in the walls and cells and the cell/subgrain size L. These parameters change depending on the applied stress or plastic strain. For the size dependence of the dislocation cells on applied stress, almost all studies return a power–law relationship:

$${\displaystyle \frac{L}{b}}\approx K{\displaystyle \frac{\mu }{{\sigma }_{int}}}$$

(37a)

where σ_int is the internal stress, and the coefficient of proportionality K is found to be close to 10 and vary non-critically with temperature. The size of the cells was also found to be proportional to the average distance between the dislocations:

$$L\approx gl$$

(37b)

where the coefficient of proportionality g is scattered between 10 and 100 [29,30,31,32,33,34,35]. Combining (37a) and (37b), one obtains that ${\sigma }_{int}~1/l$. Based on these findings, Kuhlmann-Wilsdorf [31,34] introduced a “principle of similitude”, according to which cells and walls are low-energy dislocation structures (LEDS), which shrink in scale as the applied stress is increased. Dislocation structures in stressed metallic materials demonstrate another prominent feature, namely slip lines or bands of localized plastic deformation [30,36,37]. They arise from dislocations gliding on a particular slip plane, in a particular slip direction, under an external load. These structures are critical because the concentrated shear of slip bands can nucleate cracks in the slip plane. The slip lines formed under cyclic conditions are usually called persistent slip bands [38,39,40].

Scaling is an important tool of theoretical analysis as it can help find a particular regime of evolution by hinting at the existence of a particular solution of a problem, its property of self-similarity or “intermediate asymptotes” [41]. Two major tracks of scaling are dimensional analysis and stretching transformation; their main findings are the π-theorem and renormalization group invariance, respectively [41,42]. Expanding the principle of similitude, Zaiser and Sandfeld [43] conducted scaling analysis of the dislocation structure and found that the static dislocation networks emerging in plastic deformation are often invariant under the stretching transformation:

$$x\to x, r\to \lambda r$$

(38a)

$${\sigma }_{int}\to {\lambda }^{-1}{\sigma }_{int}$$

(38b)

where x’s are the Eulerian coordinates of the specimen, r’s are the dislocation coordinates of the network, and λ is the stretching factor. Unsurprisingly, the scaling (38) satisfies Equation (37a). Importantly, the properties of the background crystal, which carries the dislocation network, are not subjected to the stretching transformation, Equation (38), that is, the Burgers vectors of the dislocations and the shear modulus of the crystal remain untransformed: b→b, μ→μ. Then, the dislocation density and network interaction energy transform as follows:

$$\rho \to {\lambda }^{-2}\rho$$

(39a)

$$E_{int}\to \lambda E_{int}$$

(39b)

Later, Berdichevsky [44] expanded the transformation (37)–(39) on the case of varying temperature:

$$T\to \lambda T$$

(40a)

which clarifies the structural relations between characteristic parameters of the networks, the temperature, and internal stress:

$$L~T~{\sigma }_{int}^{-1}$$

(40b)

$$l~T$$

(40c)

As far as the time evolution of the network is concerned, multiple options were found. First, Zaiser and Sandfeld [43] found that if the dislocation velocity is proportional to the resolved shear stress at the dislocation position, then the stretching transformation must include the following transformation of time:

$$t\to {\lambda }^{2}t$$

(41a)

However, if the dislocation motion is thermally activated, that is, its velocity depends on the interaction energy change, the time remains untransformed:

$$t\to t$$

(41b)

In addition, Berdichevsky [44] found that if the dislocation drag coefficient is linearly proportional to temperature, then the time transforms as follows:

$$t\to {\lambda }^{3}t$$

(41c)

Applying the π-theorem, he also found the following dependence of the dislocation internal stress on the control parameters, like strain rate $\dot{\epsilon }$ and temperature T:

$${\sigma }_{int}=F\left(T{\dot{\epsilon }}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}\right)$$

(41d)

where F denotes an unspecified functional dependence.

As an extension of the work [43], the authors identified the limits of the self-similarity imposed by the scaling (38), (39), and (41) on the 3D dislocation networks. Beyond the obvious omissions of the cross-slip and dislocation annihilation, they notice that the internal stress field becomes singular on the dislocation lines themselves, which makes the self-energy logarithmically divergent, violating the scaling (39b).

Let us now analyze the scaling of the theory presented in Section 1 and Section 2, taking into account that the properties of the background crystal, like the shear modulus and gradient-energy and dislocation-drag coefficients in Equations (4), (24b) and (28c), do not transform by the stretching, although they may depend on the Burgers vector b—the microscopic property of the crystal. First, notice that along with the plastic free energy density we consider the elastic free energy density contribution (4), which is a function of the elastic strain, that is, the gradient of displacement u: $\epsilon =\partial u/\partial x$. Second, to subject a crystal with a dislocation network to the stretching transformation (38a) is equivalent to subjecting it to another transformation:

$$r\to r, u\to {\lambda }^{-1}u,$$

(42a)

that is, to decrease the displacements by λ times. Hence,

$$\epsilon \to {\lambda }^{-1}\epsilon$$

(42b)

The elastic free energy density (4) is essentially a quadratic function of its strain; hence,

$$f^e\to {\lambda }^{-2}{f}^e$$

(42c)

Second, using Equations (8), (9), and (39) we obtain the following:

$$\omega \to {\lambda }^{-1}\omega$$

(43a)

which establishes a structural relation between damage and internal stress:

$$\omega ~{\sigma }_{int}$$

(43b)

The plastic free energy density is a sum of the self-energy, energy of interactions, and the entropic contribution. Then, taking into account the logarithmic divergence of self-energy in Equation (10) we obtain:

$$u_{int}^p\to {\lambda }^{-2}{u}_{int}^p, u_{self}^p~\to {\lambda }^{-2}{u}_{self}^p, s^p\to {\lambda }^{-3}{s}^p$$

(44a)

Finally, taking into account the transformations of temperature (40a) and strain (42b), we obtain from (10b) that $\psi /\mu =\mathit{const}\left(\lambda \right)$, hence,

$${\displaystyle \frac{\psi }{\mu }}=F\left(T\epsilon \right)$$

(44b)

and from (10a) that

$$f^p\to {\lambda }^{-2}{f}^p$$

(44c)

Furthermore, using (38a), (42b), and (43a) we obtain the stretching transformation for the gradient energy density in the form:

$$f^g\to {\lambda }^{-2}{f}^g$$

(45)

Finally, to calculate the total free energy of a specimen (28a), we add up all components of the density, Equations (44a), (44c), and (45), and integrate them over the volume of the specimen, not the network. Hence,

$$\mathcal{F}\to {\lambda }^{-2}\mathcal{F}$$

(46)

Moreover, taking into account that in a thermally activated process time remains untransformed, see Equation (41b), we obtain that the gradient-flow dynamic Equation (32a) is invariant with respect to the stretching transformation of (38) if the relaxation coefficient is independent of the damage parameter:

$$\gamma =\mathit{const}\left(\omega \right).$$

(47)

Then, taking into account that ${\partial }_{\omega }^2{f}^p~\mu$, we obtain that in Equation (32b) $n=1$. For a growing network of dislocations, it means that its mean square curvature is preserved [16]. For the Langevin force, Equation (34c), it means that it is represented by an additive-noise function with the scaling: $\varpi \to {\lambda }^{-1}\varpi$. For the properties of the background crystal, it means that

$$\gamma ~{\displaystyle \frac{{\mu b}^2}{D{\kappa }_{\omega }}}=\mathit{const}\left(b\right)$$

(48)

This concludes the renormalization group invariance analysis of the dislocation network evolution, and we can look at its dimensional analysis. The free energy (10) motivates the following scaling of strain, damage, stress, and energy density:

$$\left[\epsilon \right]=\left[\omega \right]={\omega }_{\ast };\left[\sigma \right]=\mu {\omega }_{\ast };\left[ f\right]={\displaystyle \frac{1}{2}}\mu {\omega }_{\ast }^2$$

(49)

while the dynamic Equation (33) motivates the following scaling of the Eulerian space-time:

$$\left[x\right]=\sqrt{{\displaystyle \frac{{\kappa }_{\omega }}{\mu }}}; \left[t\right]={\displaystyle \frac{1}{\gamma \mu }}$$

(50)

4. Equilibrium and Evolution of Dislocation Structures

The evolution equations derived above can be used to study dislocation structures that appear under various conditions of loading. In real-world situations, the deformation state of a specimen may be set by two different loading strategies: by applying force/stress or by setting the displacement/strain. In this article, we are considering the former; the latter is a more complicated case and will be considered in future publications. Let us consider the case of uniaxial, unidirectional deformation of a long, thin rod subjected to external loading described by the applied stress σ. Then, ${\epsilon }^r={\epsilon }^b=0$, $f^g={\displaystyle \frac{1}{2}}{\kappa }_{\epsilon }{\left({\partial }_x\epsilon \right)}^2+{\displaystyle \frac{1}{2}}{\kappa }_{\omega }{\left({\partial }_x\omega \right)}^2$ and the equilibrium state Equation (30) take the form:

$${\kappa }_{\omega }{\displaystyle \frac{d^2\omega }{{dx}^2}}={\partial }_{\omega }{f}^p\left(\omega ,\phi \right)$$

(51)

$${\kappa }_{\epsilon }{\displaystyle \frac{d^2\epsilon }{{dx}^2}}={\partial }_{\epsilon }{f}^e\left(\epsilon \right)+{\partial }_{\epsilon }{f}^p\left(\omega ,\epsilon ,T\right)-\sigma$$

(52)

This system of equations has a homogeneous solution $\overline{\omega }\left(T, \epsilon \right)$, which consists of the elastic ${\omega }_e=0$ and plastic ${\omega }_p\left(T, \epsilon \right)$ states (see Equation (12) and Figure 4) and a first integral:

$$\chi \equiv f^e\left(\epsilon ,T\right)-\sigma \epsilon +f^p\left(\omega ,\phi \right)-f^g\left({\partial }_x\epsilon ,{\partial }_x\omega \right)=const\left(x\right),$$

(53)

which represents various heterogeneous states and will be called here the mechanical potential. The total free energy of a heterogeneously deformed rod of initial length $X_0$ is as follows:

$$\mathcal{F}\equiv {\int }_0^{X_0}\widehat{f} dx=\sigma \Delta X+\chi X_0+{\int }_{-\infty }^{+\infty }2f^{g}dx$$

(54)

where $\Delta X={\int }_0^{X_0}\epsilon dx$ is the total displacement of the specimen, integration in the last expression was expanded from −∞ to +∞, and Equation (28b) was used. The first term in the r.h.s. is the work of the external forces, the second term—is the bulk free energy of the rod, and the third term—is the excess energy due to the heterogeneous layer connecting the elastic and plastic states:

$$\Gamma \equiv {\int }_{-\infty }^{+\infty }2f^{g}dx={\int }_{-\infty }^{+\infty }\left[{\kappa }_{\epsilon }{\left({\displaystyle \frac{d\epsilon }{dx}}\right)}^2+{\kappa }_{\omega }{\left({\displaystyle \frac{d\omega }{dx}}\right)}^2\right]dx$$

(55)

This layer is also characterized by its thickness, which may be defined as follows:

$$\mathsf{\Lambda }\equiv {\displaystyle \frac{\underset{x,x^{\prime }}{\mathit{max}}\left|\omega \left(x\right)-\omega \left(x^{\prime }\right)\right|}{\underset{x}{\mathit{max}}\left|{\partial }_x\omega \right|}}$$

(56)

4.1. Heterogeneous Yielding State

One of the heterogeneous equilibrium states described by Equations (51) and (52), $\omega =\stackrel{⃡}{\omega }\left(x\right)$, connects the domains of undamaged elastic and damaged plastic states:

$$x=\sqrt{{\displaystyle \frac{{\kappa }_{\omega }}{2}}}{\int }_{{\omega }_b^y}^{\stackrel{⃡}{\omega }}{\displaystyle \frac{d\omega }{\sqrt{f^p\left(\omega ,{\phi }_y\right)}}}$$

(57a)

at the yielding strain and stress:

$$\epsilon =const\left(x\right)={\epsilon }_y, \sigma =\mu {\epsilon }_y.$$

(57b)

This state may be called heterogeneous yielding, that is, the state of coexistence of large domains of dislocation network and undamaged elastic state. The domains are connected by a layer whose thickness and excess energy are as follows:

$${\mathsf{\Lambda }}_y={\displaystyle \frac{\Delta \stackrel{⃡}{\omega }}{\underset{x}{\mathit{max}}\left|{\partial }_x\stackrel{⃡}{\omega }\right|}}={\omega }_{\ast }\sqrt{{\displaystyle \frac{{\kappa }_{\omega }}{2f_b^p}}}=3.14\sqrt{{\displaystyle \frac{{\kappa }_{\omega }}{\mu }}}$$

(58)

$${\Gamma }_y={\int }_{-\infty }^{+\infty }{\kappa }_{\omega }{\left({\displaystyle \frac{d\stackrel{⃡}{\omega }}{dx}}\right)}^{2}dx=\sqrt{2{\kappa }_{\omega }}{\int }_0^{{\omega }_{\ast }}\sqrt{f^p\left(\stackrel{⃡}{\omega },{\phi }_y\right)}d\omega =0.217\sqrt{\mu {\kappa }_{\omega }}{\omega }_{\ast }^2=0.069\mu {\omega }_{\ast }^2{\mathsf{\Lambda }}_y.$$

(59)

A heterogeneous yielding state $\omega =\stackrel{⃡}{\omega }\left(x\right)$ is shown schematically in the equilibrium state diagrams of Figure 4 and calculated by Equation (57) in Figure 5.

4.2. Dislocation Structures

In the ideal plastic material, Equations (22) and (23), the heterogeneous yielding is the only state of equilibrium coexistence of large domains of dislocation networks with undamaged elastic states. However, heterogeneity of deformation breaks the parity of ideal plasticity, and other heterogeneous equilibrium states may appear in a specimen at the applied stress above the yield stress. In the case of tensile deformation, Equations (10), (22), (23), and (52) transform as follows:

$${\kappa }_{\omega }{\displaystyle \frac{d^2\omega }{{dx}^2}}=\mu \omega \left(2\mathit{ln}{\displaystyle \frac{{\omega }_p}{\omega }}+3{\displaystyle \frac{\omega -{\omega }_p}{{\omega }_{\ast }}}\right)$$

(60a)

$${\kappa }_{\epsilon }{\displaystyle \frac{d^{2}z}{{dx}^2}}=\mu z\left(1-{\displaystyle \frac{{\omega }^2}{{\omega }_p^2}}\right)-\Delta \sigma$$

(60b)

$$\chi +{\displaystyle \frac{1}{2}}\mu {\epsilon }_y^2+\Delta \sigma {\epsilon }_y={\displaystyle \frac{1}{2}}\mu z^2-\Delta \sigma z+{\displaystyle \frac{1}{2}}\mu {\omega }^2\left(2\mathit{ln}{\displaystyle \frac{{\omega }_p}{\omega }}+{\displaystyle \frac{2\omega -3{\omega }_p}{{\omega }_{\ast }}}+1\right)-{\displaystyle \frac{1}{2}}{\kappa }_{\epsilon }{\left({\displaystyle \frac{dz}{dx}}\right)}^2+{\displaystyle \frac{1}{2}}{\kappa }_{\omega }{\left({\displaystyle \frac{d\omega }{dx}}\right)}^2=const\left(x\right)$$

(60c)

where

$$\Delta \sigma =\sigma -\mu {\epsilon }_y$$

(60d)

is applied stress in excess of the yield stress. There are two types of solutions to these equations, which are of great interest in this theory. Their characteristics depend on the values of stress excess (60d) and the mechanical potential (60c). First, there are solutions which represent solitary pulses of plasticity in the sea of elasticity $\omega =\widehat{\omega }\left(x\right)$. In mathematical terms, they correspond to the lowest acceptable value of the mechanical potential χ for a given value of the stress excess $\Delta \sigma$ and are called homoclinic orbits. In mechanical terms, these solutions represent the slip lines surrounded by undamaged material. These solutions differ from the heterogeneous yielding by the presence of the turning point, where the states of damage and strain reach maximum. The turning point introduces a characteristic thickness of the pulse Δ as twice the distance between the turning and barrier state points of the orbit. The pulse states $\omega =\widehat{\omega }\left(x\right)$ were numerically computed using the shooting method. These states are shown for various $\Delta \sigma$ on the equilibrium state diagram of Figure 4, and one of these states is depicted in Figure 5 as a function of position. In Figure 6, the excess energy Γ, Equation (55), pulse thickness Δ, and the sum of the maximum values of damage ${\omega }_m$ and plasticity z_m are plotted as functions of the applied stress $\Delta \sigma$.

The second type are periodic solutions of Equation (60) $\omega =\tilde{\omega }\left(x\right)$; one of them is shown in Figure 2. These solutions present a more complicated set than the solitary pulses because the periodic solutions are not unique for the same stress excess $\Delta \sigma$ while there is a unique pulse in this case. The periodic solutions differ by the value of the mechanical potential χ, while the pulse corresponds to its lowest possible value. In mechanical terms, these solutions represent the cell-wall dislocation structures, which are characterized by the size, that is, the length of the spatial period L, the thickness of the wall Δ, and the maximum (wall) ${\omega }_w$ and minimum (cell) ${\omega }_c$ damage, and the average energy density $\overline{f}$ of the structure. In Figure 7, the cell wall structural characteristics: period L, wall thickness Δ, and the sum of the wall damage ${\omega }_w$ and plasticity z_w are plotted as functions of the applied stress $\Delta \sigma$. Importantly, the theory shows that multiple cell sizes are possible at the same value of stress.

Another important features of the cell wall structures may be uncovered if the wall damage amplitude ${\omega }_w$ is replotted as a function of the structural period L for a fixed value of the stress $\Delta \sigma$, see Figure 8. On the one hand, as the period grows, the wall amplitude quickly reaches the value of the pulse at the same stress. On the other hand, for any stress level, there exists a minimal size of the structural period $\tilde{L}$ below which a periodic cell wall structure is not possible, and the specimen must remain homogeneously damaged. Analysis of Equation (60) shows that the specimen remains homogeneously damaged at

$${\omega }_c={\omega }_w={\omega }_b\left(\Delta \sigma \right)$$

(61a)

for $L<\tilde{L}$ where the minimal size is as follows:

$$\tilde{L}=\pi \sqrt{{\displaystyle \frac{{\kappa }_{\omega }}{-{{\partial }_{\omega }^{2}f}^p\left({\omega }_b, \Delta \sigma \right)}}}={\displaystyle \frac{\pi }{\sqrt{-2\left(\mathit{ln}\frac{{\omega }_p}{{\omega }_b}+3\frac{2{\omega }_b-{\omega }_p}{2{\omega }_{\ast }}-1\right)}}}\sqrt{{\displaystyle \frac{{\kappa }_{\omega }}{\mu }}}$$

(61b)

It is said that at point $\left(\tilde{L}, {\omega }_b\right)$, the structure undergoes a size-amplitude bifurcation (SABi). The equilibrium Equation (60a,b) and the ideal plasticity relation (23b) help find the dependence of the bifurcation parameters on the excess stress $\Delta \sigma$:

$$2\mathit{ln}{\displaystyle \frac{{\omega }_p}{{\omega }_b}}+3{\displaystyle \frac{{\omega }_b-{\omega }_p}{{\omega }_{\ast }}}=0$$

(62a)

$$\mu z\left(1-{\displaystyle \frac{{\omega }_b^2}{{\omega }_p^2}}\right)=\Delta \sigma$$

(62b)

$${\omega }_p^2\left({\displaystyle \frac{{\omega }_p}{{\omega }_{\ast }}}-1\right)=z^2$$

(62c)

This relation is also shown in Figure 8.

4.3. Stationary Motion of Dislocation Domains

As we found in Section 4.1, an undamaged elastic state and damaged plastic state may coexist, being connected by a layer of finite thickness. The heterogeneous yielding $\omega =\stackrel{⃡}{\omega }\left(x\right)$ is such a state at $\sigma =\mu {\epsilon }_y$. For $\sigma >\mu {\epsilon }_y$ the slip lines (pulses) or dislocation cells and walls (periodic) equilibrium structures appear. However, another scenario of the evolution of deformation for $\sigma >\mu {\epsilon }_y$ is possible: the dislocation domains start moving such that the undamaged state is replaced by the damaged one—the slip band motion. Assuming that relaxation of strain proceeds much faster than motion of dislocations, evolution of the dislocation structure in this case is described by Equations (32a) and (47), which, for an unidirectionally deformed long thin rod, take the form:

$${\displaystyle \frac{1}{\gamma }}{\partial }_t\omega ={\kappa }_{\omega }{\partial }_x^2\omega -{\partial }_{\omega }{f}^p\left(\omega ,\phi \right).$$

(63)

Stationary motion of the dislocation domain from +∞ to −∞ is described by functions $\omega \left(x,t\right)=\omega \left(y\right)$, $\epsilon \left(x,t\right)=\mathit{const}\left(y\right)>{\epsilon }_y$, which obey the following equation:

$${\kappa }_{\omega }{\displaystyle \frac{d^2\omega }{{dy}^2}}-{\displaystyle \frac{v}{\gamma }}{\displaystyle \frac{d\omega }{dy}}-{\partial }_{\omega }{f}^p\left(\omega ,\phi \right)=0$$

(64)

where $y=x+vt$ and $v$ is an unknown speed of the slip band motion. This is a velocity selection problem. Its dimensional analysis shows that

$$v=\gamma \sqrt{\mu {\kappa }_{\omega }}\vartheta \left(\phi \right)$$

(65)

where $\vartheta \left(\phi \right)$ is a dimensionless function of loading. For small plasticity z, Equation (64), can be resolved perturbatively. Indeed, introducing the new variables:

$$w\left(y\right)=\omega \left(y\right)-\stackrel{⃡}{\omega }\left(y\right)$$

(66a)

$$\Delta \phi =\phi \left(\epsilon \right)-{\phi }_y$$

(66b)

which are of the same order of smallness as $v$, and disregarding terms of the order of smallness higher than one, we obtain:

$${\kappa }_{\omega }{\displaystyle \frac{d^{2}w}{{dy}^2}}-{\partial }_{\omega }^2{f}^p\left(\stackrel{⃡}{\omega },{\phi }_y\right)w={\displaystyle \frac{v}{\gamma }}{\displaystyle \frac{d\stackrel{⃡}{\omega }}{dy}}+{\partial }_{\omega \phi }{f}^p\left(\stackrel{⃡}{\omega },{\phi }_y\right)\Delta \phi .$$

(67)

where $\stackrel{⃡}{\omega }\left(x\right)$ is the heterogeneous yielding state. The left-hand side of this equation depends on the perturbation w(y), while the right-hand side is independent of it but depends on $v$ and $\Delta \phi$. This allows us to conclude that both left- and right-hand sides vanish. Then the left-hand side yields an equation:

$${\kappa }_{\omega }{\displaystyle \frac{d^{2}w}{{dy}^2}}-{\partial }_{\omega }^2{f}^p\left(\stackrel{⃡}{\omega },{\phi }_y\right)w=0$$

(68a)

whose solution is known:

$$w=A{\displaystyle \frac{d\stackrel{⃡}{\omega }}{dy}}.$$

(68b)

To find amplitude A, the higher-order terms of Equation (64) must be analyzed with the help of the first integral, Equation (60c). The right-hand side of Equation (67) may be estimated at the barrier point ${\omega }_b^y$ to yield:

$$v=-\gamma \sqrt{{\displaystyle \frac{{\kappa }_{\omega }}{2}}}{\displaystyle \frac{{\partial }_{\omega \phi }{f}^p\left({\omega }_b^y,{\phi }_y\right)}{\sqrt{f^p\left({\omega }_b^y,{\phi }_y\right)}}}\Delta \phi$$

(69)

For plastic free energy, Equation (10), the speed of motion is as follows:

$$v=-\gamma \sqrt{{\displaystyle \frac{2\mu {\kappa }_{\omega }}{\mathit{ln}\frac{{\omega }_{\ast }}{{\omega }_b^y}+\frac{{\omega }_b^y}{{\omega }_{\ast }}-1}}}\Delta \phi \approx -2.62\gamma \sqrt{\mu {\kappa }_{\omega }}\Delta \phi$$

(70)

Applying Equation (23a) near the point of yielding of ideal plasticity, that is, for small z, one can estimate the loading function:

$$\Delta \phi \approx -{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{z}{{\omega }_{\ast }}}\right)}^2$$

(71)

and obtain a formula for the slip band speed:

$$v\approx 1.31\gamma \sqrt{\mu {\kappa }_{\omega }}{\left({\displaystyle \frac{z}{{\omega }_{\ast }}}\right)}^2$$

(72)

Importantly, this is not the speed of motion of a dislocation, but the speed of propagation of a slip band. Notice that the ideal plasticity of the material does not allow us to relate plasticity z to the stress excess $\Delta \sigma$. For not small z, one cannot disregard variations of strain in the moving layer described by Equation (64).

4.4. Comparative Analysis of Equilibrium Structures

In this article we are considering deformation states of a specimen set by applying external stress. The low-energy dislocation structures (LEDS) emerge in this theory as solutions of the scale invariant equilibrium equations whose scaling properties suggest a few relations between structural characteristics and internal stress, Equations (37), (43b) and (61). The total damage must be measured by the sum of the maximum damage and plasticity of the structural units. The internal stress at equilibrium is equal to the applied stress and, according to Equation (60d) and scaling (49), it is ${\sigma }_{int}=1+\Delta \sigma$. Then, Figure 6b and Figure 7b manifest relation (43b) while Figure 7a—relation (37a). Also, recalling that $\omega \approx b/l$, we obtain that $L\approx 10l$ in accordance with (37b). Another prediction of the theory is that in specimens of sizes smaller than the minimal size $X_0<\tilde{L}$ the cell wall structures are not possible, and the specimen must either be homogeneously damaged to the level of the barrier state or remain dislocation-free.

Although LEDS emerging in the current work reproduce many of the experimentally observed features, a quantitative verification of the relations is desirable. For that, we use copper as the most popular metal in dislocation structure studies. In Figure 7a, the experimentally measured sizes of the cell structures in phosphorus alloyed copper [45] are plotted together with the theoretical results. In the process of matching, we used the values of yield stress ${\sigma }_y=70 \mathrm{M}\mathrm{P}\mathrm{a}$, shear modulus $\mu =35.209 \mathrm{G}\mathrm{P}\mathrm{a}$, and Burgers vector b = 0.256 nm obtained from [46] and two adjustable parameters: ${\kappa }_{\omega }=0.2 \mathrm{m}\mathrm{J}/\mathrm{m}$ and ${\omega }_{\ast }=0.005$. The adjustable parameters return the values of the typical dislocation density of ${\rho }_{\ast }=3.8\times {10}^{14} {\mathrm{m}}^{-2}$ and length scale $\left[x\right]=75 \mathrm{n}\mathrm{m}$ for the dislocation structures in copper. Although the experimental measurements of the cell sizes fall well within the range of calculations, their sharper dependence on the applied stress is noticeable. In [45], the dislocation cell sizes were also compared with the plastic deformation of the structures. In Figure 9, the experimentally observed relation is matched with that of the theoretical structures. To calculate the plastic deformation of the structure, the local plastic strain, Equation (23c), was integrated over the cell period L. The experimental and theoretical results are of the same order of magnitude; however, experimental sizes decrease with the increase in plastic deformation, while the theoretical relation is opposite. Overall, we do not consider the plastic deformation a reliable control parameter of the dislocation cell wall structure.

The present theory revealed an important feature of the dislocation structure formation: a possibility of multiple dislocation cell wall equilibrium structures for the same level of applied stress or plastic deformation, see Figure 7a and Figure 9. In fact, that feature had been observed experimentally without clear realization of its physical meaning [45]. Multiplicity of the structures for the same level of applied stress raises a few interesting questions. First, how does a specimen ‘select’ the proper dislocation structure? The answer to this question depends on the total energy of the structure. Indeed, the structures differ by the value of the mechanical potential χ, which is the main contributor to the total free energy, see Equation (54). The potential is not a control parameter and cannot be set externally, like stress or strain. Hence, the specimen ‘selects’ a particular LEDS by setting the potential internally.

In Figure 10, the average energy density $\overline{f}$ and maximum (wall) damage ${\omega }_w$ of the dislocation cell wall structures are plotted as functions of the potential χ for the stress excess $\Delta \sigma =0.25$. It shows that the solitary pulse $\omega =\widehat{\omega }\left(x\right)$ has less energy density than any of the periodic cell wall structures $\omega =\tilde{\omega }\left(x\right)$. Moreover, the heterogeneous structures have more energy than the homogeneously deformed plastic state, the global optimizer of the system. This raises another question: why do we observe the dislocated cell wall structures in real experiments, although there are structures which have less energy? The answer to this question may be found in Figure 2, Figure 3 and Figure 4. Ideally, deformation of an elastic state (${\omega }_e=0$) must end up with the formation of the homogeneous plastic state (${\omega }_p=1$). However, the ‘long distance’ between the two homogeneous states is intersected by the intermediate heterogeneous equilibrium states, pulses, and periodic structures, which, although having more energy, are ‘closer’ to the initial state—the so-called Ostwald’s conjecture. Third question: Why do we observe slip lines and dislocation cell wall structures in real experiments? The problem is that the pulses and periodic structures are known to be thermodynamically unstable, that is, with respect to small perturbation. The answer to this question deals with a number of factors, among which the defective structure of the material, e.g., grain structure, is one of the most important.

5. Concluding Remarks

In this publication, we advanced the thermodynamically consistent theory of dislocation-mediated plasticity, which was started in [15,16]. The main assumption of the theory is the existence of free energy. This assumption allowed us, first, to limit the number of independent variables to temperature, total strain, damage, and residual and back strains as the history variables, and second, to expand the free energy in the spatial gradients of strain and damage, Equation (28). The gradient-flow dynamic equation for damage was expanded on the case of inhomogeneous deformation, including processes of dislocation multiplication and annihilation, Equation (33). This equation does not include specific sources of dislocation, and to describe the deformation process, we include dislocation fluctuations in the specimen. In Section 3, the renormalization group scaling was applied to the equilibrium and dynamic equations of the theory. It shed light on the characteristic features of the network. The low-energy dislocation structures (LEDS) emerge in the theory as ordinary solutions of the equilibrium Equations (51)–(53) without any arbitrary assumptions, Section 4. They include the state of heterogeneous yielding, slip lines, cell wall structures, and dislocation-free small particles. The emerging theoretical structures can be matched by the dislocation slip-line and cell wall structures observed experimentally, Section 5. 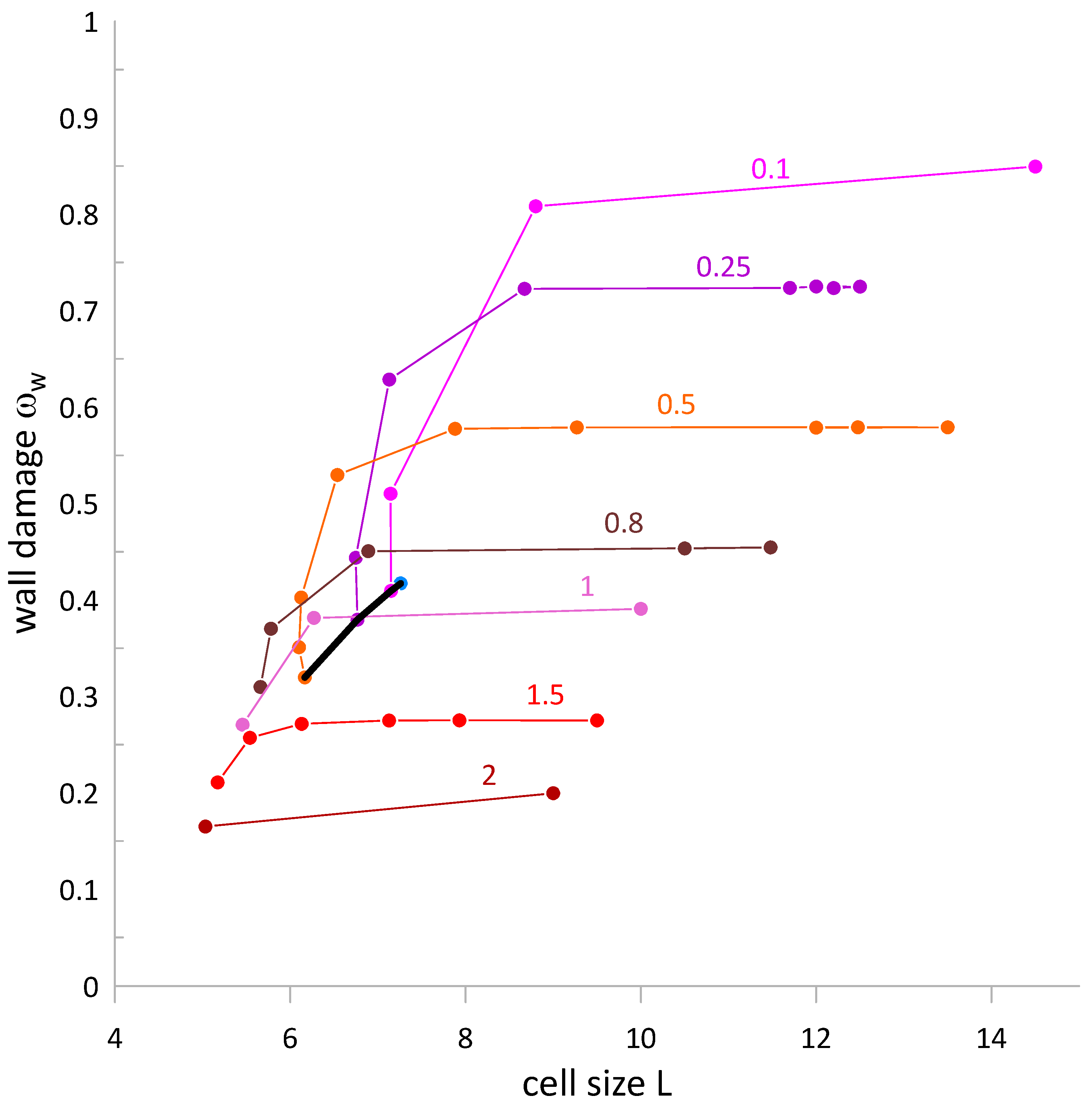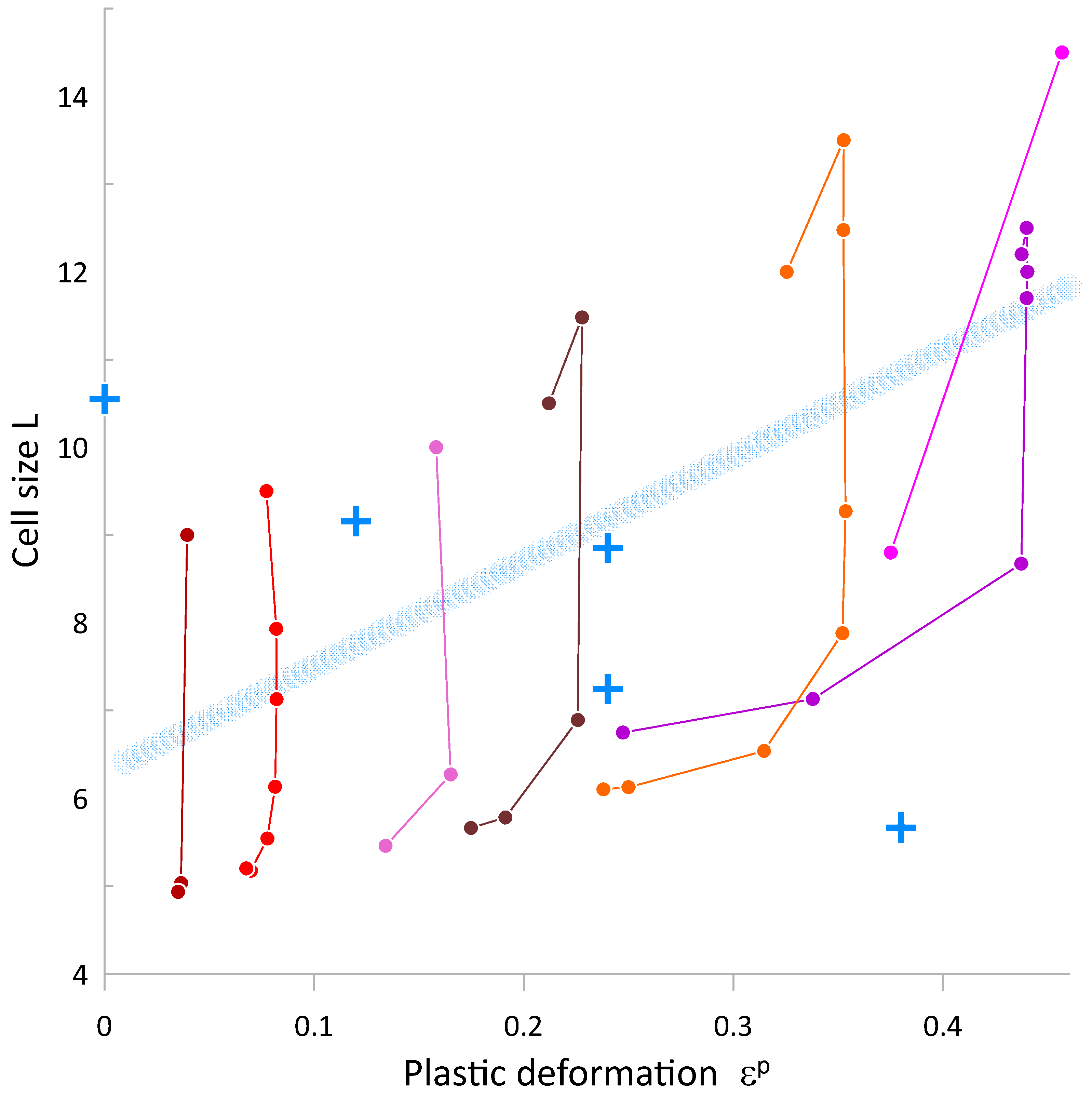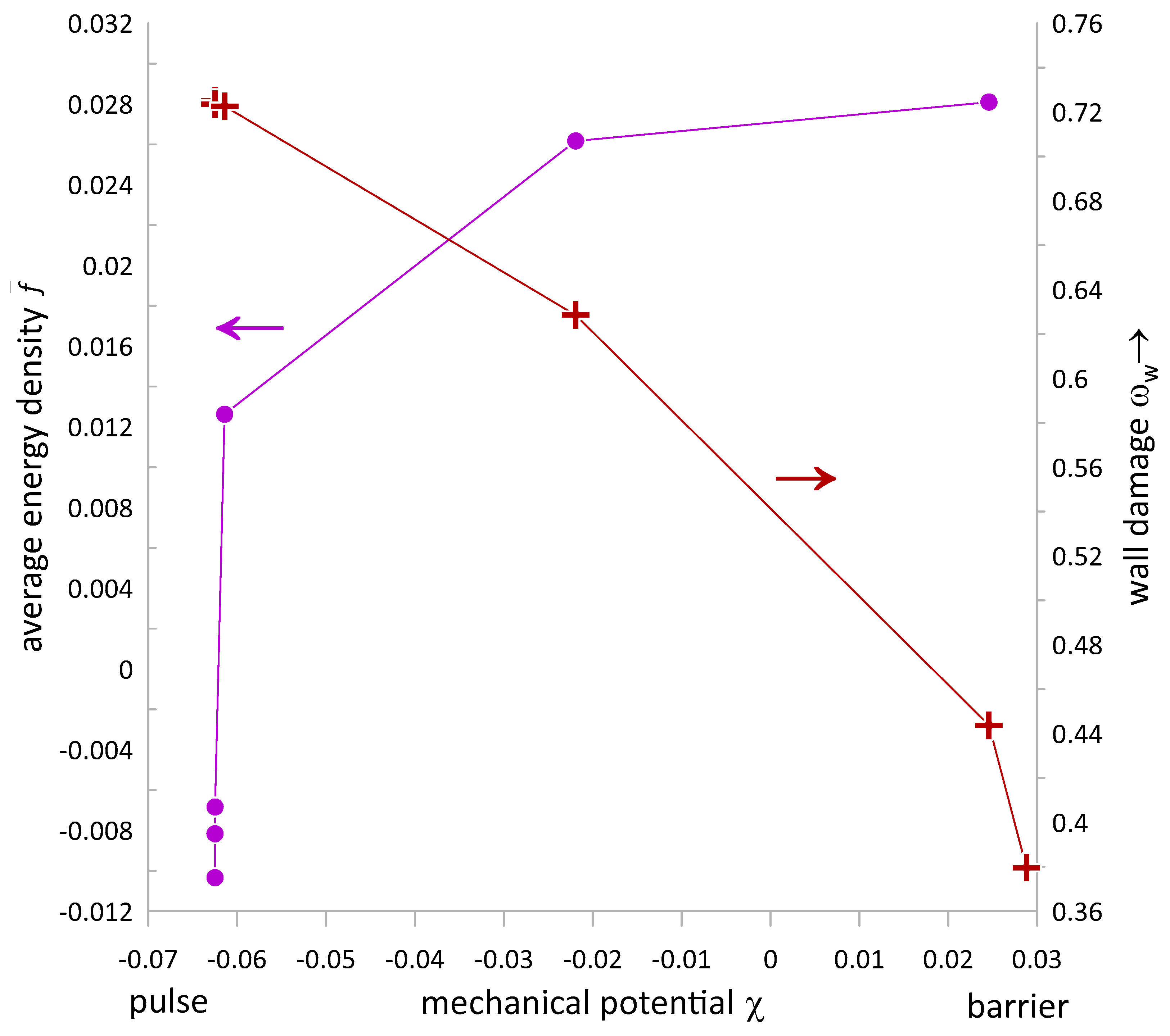The scaling properties of the theoretical structures, Equations (37) and (43b), and Figure 6, Figure 7, and Figure 9 match the properties of the experimental counterparts. The present theory revealed an important feature of the dislocation structure formation: a possibility of multiple dislocation cell wall equilibrium structures for the same level of applied stress or plastic deformation, Figure 7a and Figure 9. That feature had been observed experimentally without clear realization of its physical meaning [45]. Some of the discrepancies between the theoretical and experimental results may be explained as an artifact of the ideal plasticity of the studied material.

The conducted analysis raised a few questions about the emergent dislocation structures. For instance, why do we observe them in materials although a homogeneously deformed plastic state has less energy as the global optimizer of the system? The answer to this question can be found in Ostwald’s conjecture, according to which the ‘long distance’ between the two homogeneous states is intersected by the intermediate heterogeneous equilibrium states, pulses, and periodic structures, which, although unstable, are ‘closer’ to the initial state. Moreover, the heterogeneous dislocation structures are known to be unstable with respect to small perturbations. Then, how can we observe them in the first place? The answer to this question deals with the defective (e.g., grain) structure of the material.

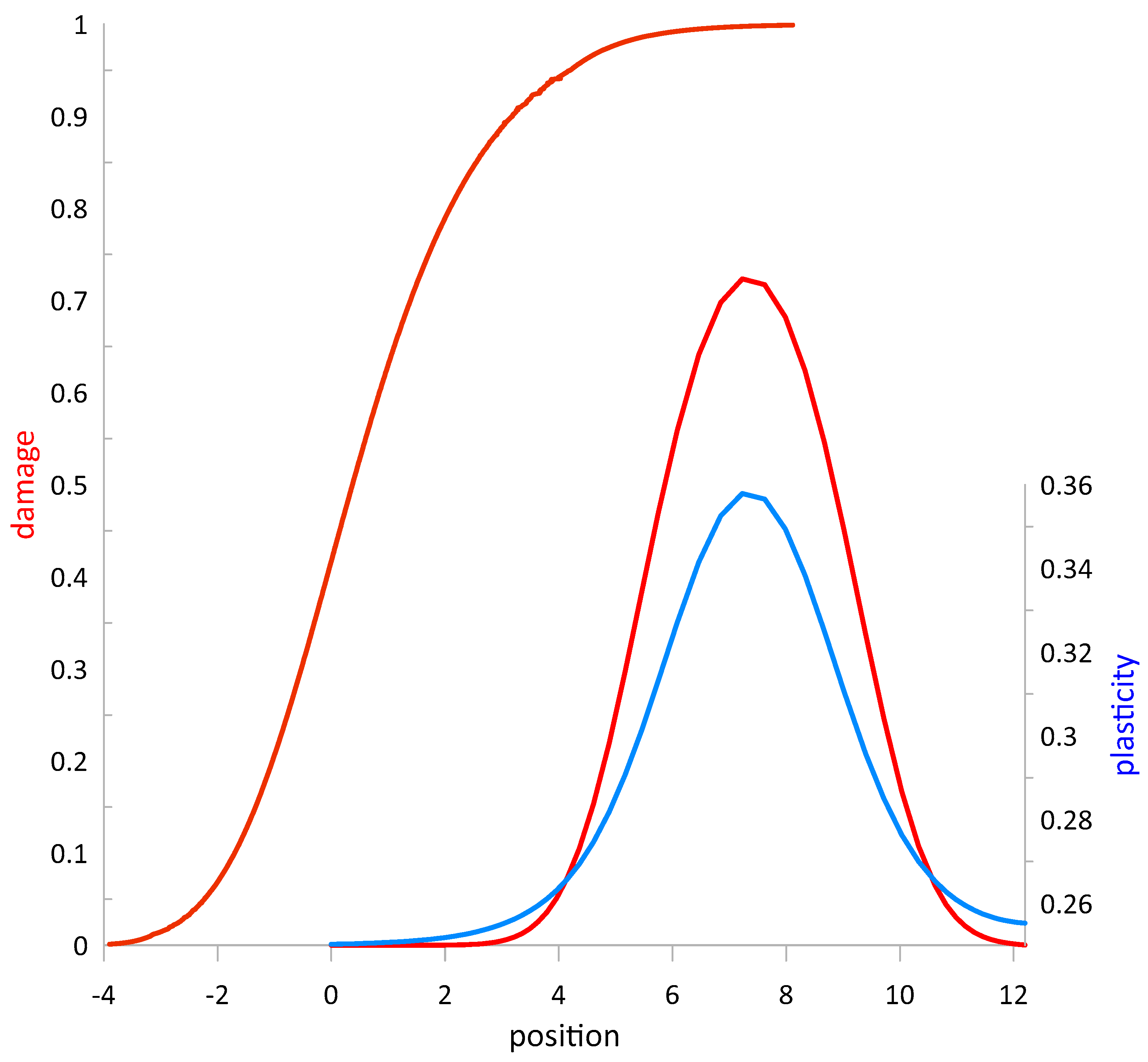
The conducted theoretical analysis allows us to make several predictions regarding experimental observations of the dislocation structures. First, the theory predicts elevation of strain distribution in the high-density regions of dislocation walls or slip lines, as shown in Figure 2 and Figure 5. Such strain elevation may be visualized with the help of one of the atomic-resolution electron microscopy techniques. Second, small particles are known to remain dislocation free under various conditions of loading. 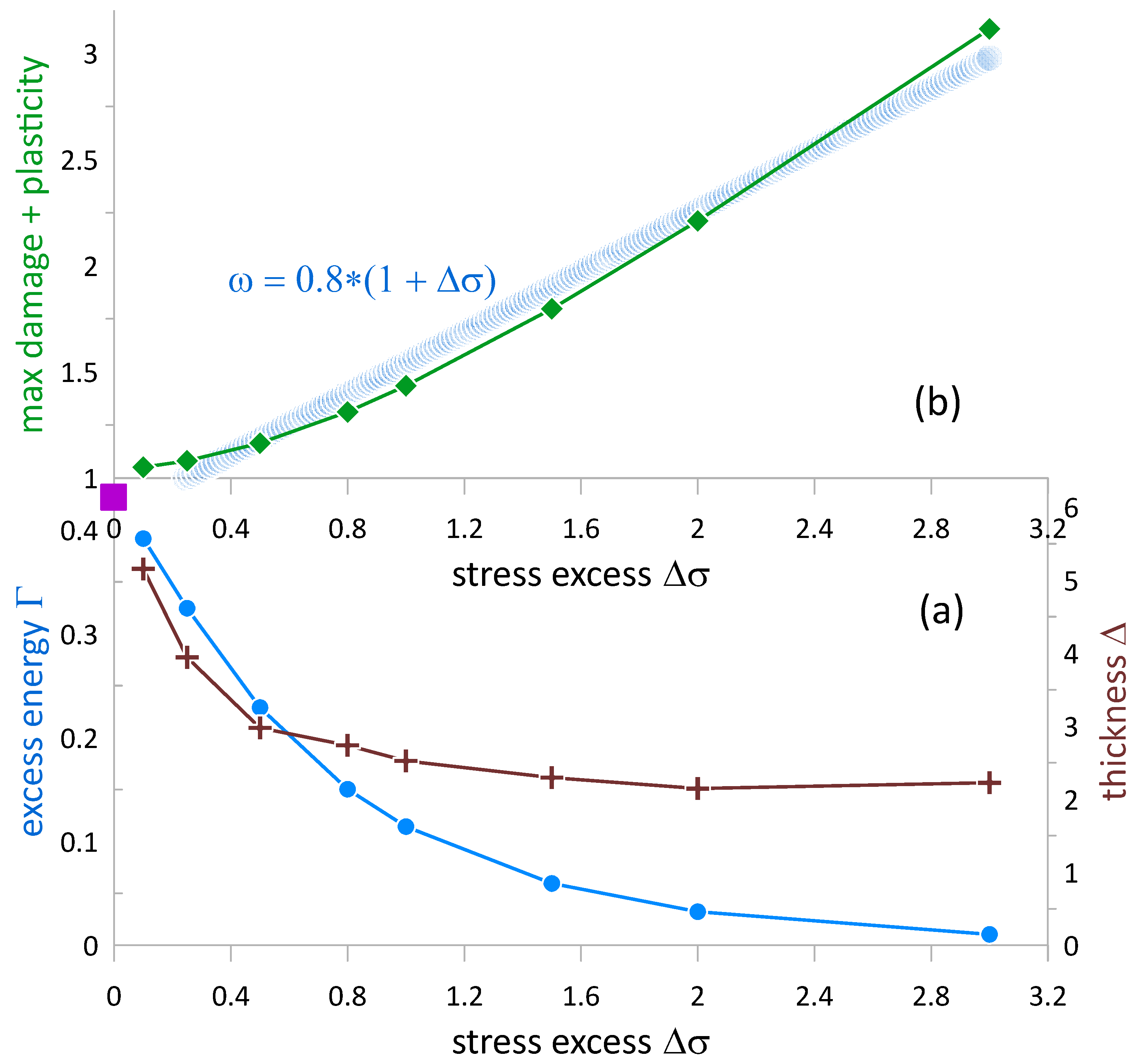The minimal size $\tilde{L}$ of these particles is predicted to decrease slightly with stress, as shown in Figure 8, and be inversely proportional to the square root of the shear modulus, as described in Equation (61b). In addition, the microstructural analysis of small particles should allow us to evaluate the gradient energy coefficients, ${\kappa }_{\epsilon }$ and ${\kappa }_{\omega }$, which are critical for the theory. Third, recalling that $\omega \approx b/l$ and that the edge component of a dislocation network contributes to misorientation between the neighboring subgrains, the theory predicts that misorientation may be estimated as 50% of the total damage in the network.

In the future we plan to include thermal properties and multiaxial deformation into the consideration of non-ideal materials like steel and titanium and aluminum alloys.