Abstract
We herein investigate the scattering of orthogonal counterpropagating waves and one-way propagating bulk waves in discrete acoustic superlattices subjected to a scattering potential applied to one of the superlattice unit cells. We demonstrate theoretically that the orthogonality of counterpropagating modes does not provide robust protection against backscattering. By contrast, the one-way propagating modes do satisfy a no-reflection condition, i.e., they exhibit immunity to backscattering, for a wide range of applied scattering potentials, which represent defects and disorder.
1. Introduction
Broken symmetries such as time-reversal or inversion symmetry is at the heart of the extraordinary properties of acoustic topological insulators, such as the topological protection of acoustic waves against backscattering. For a review of the field of topological acoustics, please see reference [1]. Here, we explore attributes of topological acoustic waves that may lead to immunity to backscattering. Acoustic topological insulators are bulk mechanical systems possessing gapped acoustic band structures whose vectorial representations of the acoustic wave field amplitude exhibits unusual topologies as the field parametrically spans the representation space.
The topological protection of acoustic waves to overcome backscattering in two-dimensions can be achieved in gapped mechanical systems with broken time-reversal symmetry. This approach emulates the quantum Hall effect (QHE) of solid-state physics. These two-dimensional systems support, inside their gap, unidirectionally propagating edge modes at their one-dimensional boundaries (edges), thereby making backscattering impossible. The edge modes are chiral, i.e., they have handedness, considering a system with two parallel surfaces, with edge modes propagating in opposite directions that are not located on the same edge but on opposite edges. Chirality results from the mirror symmetry that relates modes propagating in opposite directions on opposite surfaces. Exciting only one surface produces a unidirectionally propagating wave. A scatterer on that surface cannot convert the mode propagating into the counterpropagating mode since it is not supported there. However, if the two surfaces are close enough for the evanescent component of the acoustic (or any other) field perpendicular to the surfaces to overlap, then scattering can transfer energy to the counterpropagating mode. Currently, such robust immunity to backscattering in these systems is achieved using active devices that break time-reversal symmetry, making their practical implementation difficult.
A second approach to attain topological properties in two dimensions exploits a mechanism analogous to the quantum spin Hall effect (QSHE) in systems satisfying time-reversal symmetry, but with broken spatial symmetry, e.g., inversion symmetry in the case of a valley Hall type of systems. Here, a two-dimensional gapped mechanical system may support—inside its gap—degenerate edge modes at its boundaries. However, because time-reversal symmetry is satisfied, edge modes propagating in opposite directions coexist on the same boundary. The acoustic fields associated with this counterpropagating pair of edge modes are orthogonal to each other and may be treated as possessing an intrinsic degree of freedom analogous to the spin of fermionic quantum particles, and therefore are sometimes referred to as pseudospins. The orthogonality of these pseudospins for edge modes propagating in opposite directions and connected by the time reversal endows them with helical symmetry. An arbitrary (non-pseudospin selective) excitation at only one boundary produces two waves propagating in opposite directions. A perturbation on that surface may or may not scatter an incident mode depending on its ability to flip the pseudospin, thus converting the impinging mode into its orthogonal counterpart, i.e., into a reflected wave. Therefore, the orthogonality of pseudospins of co-located acoustic waves may not be a strong enough condition for immunity to backscattering by any type of scatterer. No backscattering can only occur for perturbations without a mechanism for pseudospin flip.
Topological immunity to backscattering for bulk acoustic waves can be realized in several ways. Modulation in space and time of the physical properties of acoustic media introduces a bias which breaks time-reversal symmetry and, additionally, inversion symmetry, leading to a one-way propagation of bulk acoustic waves [2,3,4,5]. In these systems, the time-dependence of the modulation leads to a frequency splitting that resembles Brillouin scattering. The frequency of the Brillouin modes, resembling Stokes and anti-Stokes bands, corresponds to harmonics of the frequency associated with the temporal modulation. A Brillouin mode which hybridizes with the folded bands due to the spatial periodicity of the modulation (i.e., Bloch waves) forms a band gap on one side of the Brillouin zone and not the other. This asymmetry in band structure ensures that a physical perturbation cannot scatter an incident traveling wave, with frequency within the hybridization band gap, into a traveling reflected wave. However, other Brillouin modes span the gap frequency range, providing channels for wave propagation and, therefore, scattering. In spite of these channels, spatiotemporal modulations have been shown to provide high-level protection against backscattering by mass defects [2]. In addition, the challenge in achieving spatiotemporal modulations of the medium’s physical properties makes the experimental practical implementation difficult [6].
More recently, Deymier et al. have shown that continuous and/or discrete acoustic superlattices can support waves that do not satisfy the translational invariance of Bloch waves over the entire Brillouin zone, unless their amplitude vanishes for some wave number [7]. In honor of Paul Dirac, these modes will be subsequently denoted as DRAK (pronounced as “DeeRAK”) modes. DRAK modes are characterized by a pseudospin and occur only on one side of the first Brillouin zone, leading to one-way propagation. In these superlattices, time-reversal symmetry is satisfied but inversion symmetry is not. The existence of DRAK modes results from the interplay of translational invariance of Bloch waves, pseudospin, and a Fabry–Pérot resonance condition [8] in the superlattice unit cell.
In the current paper, we investigate the interaction between acoustic waves in discrete superlattices and scattering potentials with the aim of revealing the conditions which lead to immunity to backscattering. For the sake of analytical simplicity, we limit our study of scattering in topological acoustic superlattices to (1) the elastic analog of the Su–Schrieffer–Heeger (SSH) model [9] and (2) the simplest binary superlattice, which possesses a Fabry–Pérot resonance. The SSH system does not exhibit DRAK modes but, as it will be shown, it possesses one mode for which the forward and backward propagating waves are orthogonal to each other. We show that in this case, the orthogonality of counterpropagating modes does not provide protection against backscattering. By contrast, the superlattice with a Fabry–Pérot resonance supporting a DRAK mode can be topologically protected against backscattering.
2. Model System
In a previous publication [7], we investigated discrete binary superlattices (Figure 1a) and the Bloch waves they could support. The binary superlattice systems were formed by periodically repeating unit cells composed of two segments of different one-dimensional mass–spring harmonic chains. The masses were identical and denoted by M. The stiffness of the springs in the two segments, 1 and 2, were defined as and . The spacing between adjacent masses was defined as . The lengths of segments 1 and 2 in a general superlattice were and , where and are integers. As shown in Figure 1b, when and , the system becomes the Su–Schrieffer–Heeger (SSH) model [10]. Here, we also consider the model of Figure 1c, which is the simplest binary superlattice that supports a Fabry–Pérot resonance in segment 2, and consequently a DRAK mode with zero amplitude in one direction of propagation and non-zero amplitude in the opposite direction.
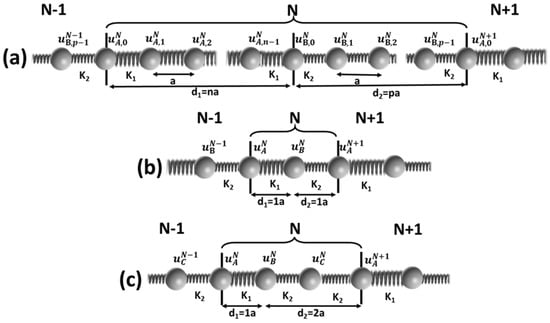
Figure 1.
(a) Schematic representation of a general one-dimensional discrete superlattice. A periodically repeating unit cell N is composed of equally spaced identical masses M coupled through linear springs with stiffnesses and . The extent of segment 1 with stiffness is . The length of segment 2 is . (b) Su–Schrieffer–Heeger (SSH) model for . (c) Simplest superlattice with one Fabry–Pérot resonance in segment 2 with and . In the SSH system (b), we also refer to the masses in the unit cell by A and B. In system (c), we refer to the masses in a unit cell as A, B, and C.
2.1. General Binary Superlattice
Using the transfer matrix method, we sought plane wave solutions for the general binary superlattice in the following forms:
The wave numbers with j = 1,2 are related to the angular frequency via the well-known dispersion relation of infinite harmonic chains:
Since the superlattice is periodic with period , we look for Bloch wave solutions by choosing and , where q is the wave number. The transfer matrix method enables us [7] to obtain analytical expressions for the band structure of the superlattice as well as the amplitudes and . The dispersion relation is given by
where . We note that when the absolute value of the right-hand side of Equation (3) exceeds 1, the frequency lies within band gaps of the system corresponding to evanescent modes.
The amplitudes in segment 1 are expressed as
In Equation (4a,b), we define with j = 1,2. The amplitudes in segment 2 are given by the relation
with .
The DRAK mode occurs when a Fabry–Pérot resonance exists in segment (2), i.e., when , i.e., at circular frequencies , such that is an even or odd multiple of π, which corresponds to DRAK modes inside the first Brillouin zone where wave number q takes values in the range . In the case of being an odd multiple of π, the dispersion relation reduces to or . With these conditions, clearly from Equation (4a), . Equation (4b) reduces to . when . Since , the reduced wave number is located inside the negative side of the first Brillouin zone. is the corresponding wave number inside the second Brillouin zone (where ). for , which is located symmetrically on the positive side of the Brillouin zone. By virtue of Equation (5), when = 0. The DRAK mode has zero amplitude on one side of the Brillouin zone but a non-zero amplitude on the symmetric opposite side. In Figure 2, we illustrate the DRAK mode in the band structure of a superlattice with and . The Fabry–Pérot resonance occurs for , which, using Equation (2) for medium 2 gives for unit mass M. Two band structures are calculated from Equation (3) for the two cases , and , . The corresponding is also shown as horizontal lines. When , the resonance frequency intersects the associated second band only at zero wave number. When , the resonance frequency intersects the second band at two locations . As discussed above, the amplitude of the mode with a negative wave number is 0, while the amplitude of the mode with the symmetric positive wave number is non-zero. To find the location of these wave numbers, we use Equation (2) for the mass of type 1 with and find , that is, , which gives .
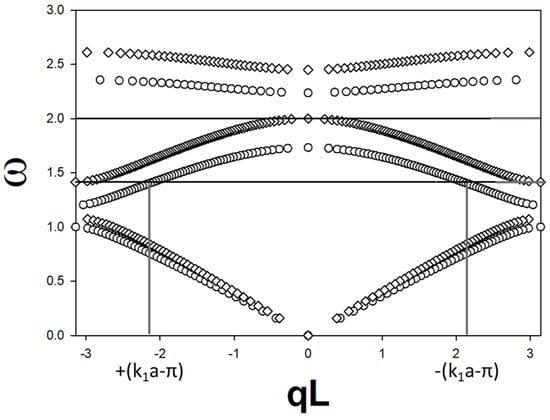
Figure 2.
Band structure of superlattice with d1 = a and d2 = 2a with M = 1 kg. (a) Open circles correspond to K1 = 2 N/m and K2 = 1 N/m and (b) open diamonds correspond to K1 = 1 N/m and K2 = 2 N/m. The two horizontal lines identify the frequencies of Fabry–Pérot resonances . See text for more details.
In the case of being an even multiple of π, the dispersion relation reduces to or . In that case, If , then , but if , then .
2.2. SSH System and Scattering
We recall that the SSH system is obtained when and . The dispersion relation is given by
The motion of the two masses in a unit cell N is described by Bloch waves, and . The amplitudes are given by Equation (1a,b): and with
Here, the “*” denotes complex conjugation. The refers to the bands in Equation (6). We note that these amplitudes cannot be zero for any value of the wave number q. The Bloch wave amplitudes given by Equation (7) form a vector in a two-dimensional complex space with the basis of the masses A and B of a unit cell. This representation of the displacement field within a cell spans the complex space by parametrically varying the wave number q. We therefore seek wave numbers +q and −q, such that the corresponding vector representations are orthogonal to each other. Considering two waves propagating in opposite directions, and , the condition of orthogonality between these two modes can be written as
This condition reduces to = 2 or
Orthogonal counter propagating modes only exist when , which corresponds to the topologically nontrivial phase of the elastic SSH system [11].
We now explore the scattering of waves in the SSH model. We consider a general frequency-dependent scattering potential , acting on the mass of type A of the unit cell N = 0. For example, if we consider that this potential arises from a perturbation of the mass of A in the N = 0 unit cell, such that its mass is now , we have . The scattering potential may take many other functional forms depending on the type and origin of the perturbation such as, for instance, resonant perturbations.
The dynamical equations in the vicinity of the defected unit cell take the following forms:
The amplitudes of and are supposed to be unknown and written as
We also consider that the semi-infinite medium to the left of the defected unit cell supports an incident “i” and a reflected “r” wave:
The medium to the right of the defected cell supports a transmitted “t” wave:
The scattering problem solved here is illustrated in Figure 3.
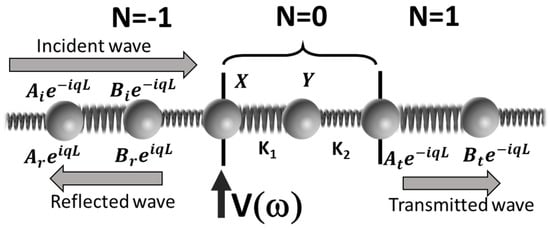
Figure 3.
Schematic illustration of the SSH system subjected to a scattering potential . The amplitudes of the incident; reflected and transmitted waves are shown as well as the amplitude of the two masses in the cell N = 0. The black arrow indicates the location of the applied scattering potential.
Using Equation (7), we have
where .
Furthermore, we define the reflection coefficient and with and the transmission coefficient and with .
We now have four equations (10a,b,c,d) and four independent unknowns . Eliminating from the equations, after algebraic manipulations, we extract expressions for the reflection and transmission coefficients in terms of the scattering potential, namely
We easily verify that when , and If , then and . It is also easy to verify that a mode satisfying the condition of orthogonality between counterpropagating waves (Equation (9)) does not restrict Equations (15) and (16). Indeed, the condition of orthogonality states that , that is, . In this case, and . Orthogonality in the direction of propagation for the topologically unconventional phase of the SSH system does not protect against backscattering.
2.3. Scattering of DRAK Mode
We consider, now, the system of Figure 1c and apply a scattering potential V on the mass A in the N = 0 cell. We focus on the scattering of the DRAK mode for which there is a zero amplitude for one direction of propagation and a non-zero amplitude in the opposite direction. In this case, and in contrast to the SSH system discussed in the previous subsection, analytical expressions of reflexion and transmission coefficients cannot be derived and one cannot analyze mathematically the scattering of a DRAK mode by considering an incident wave and a reflected wave on one side of the scatterer and a transmitted wave on the other side. Here, since the DRAK mode could be reflectionless [12], we address the scattering problem by considering that an incident wave is not reflected and, therefore, it is totally transmitted. We therefore seek the existence of localized modes in the vicinity of the scattering potential which are compatible with a reflectionless incident wave. The scattering potential may then be associated with an evanescent or localized field around the defected cell [13]. Since the DRAK mode corresponds to frequencies which lie within a band and in the one-dimensional binary superlattice, the evanescent modes live within the band gaps, and the localized mode we seek cannot be evanescent. We only look for the existence of a localized mode in the perturbed cell compatible with the DRAK reflectionless character and the applied scattering potential.
First, we write the equations of motion for the masses A, B, and C in the perturbed cell:
Similarly to the previous section, we assume that the scattering potential acts on the mass A in the unit cell N = 0. We further assume that and are given as
where is the wave number of the DRAK mode that has non-zero amplitude. Equation (1a,b) state that , , and because , so A = B = C = 0 when for the DRAK mode on one side of the Brillouin zone (e.g., for a reflected wave).
We now assume that
are the unknown amplitudes of masses A, B, and C in the defected N = 0 cell, which enable the zero reflection of the DRAK mode by the scattering potential (see Figure 4). The existence of a nontrivial solution for is a necessary condition for immunity to backscattering by the potential .
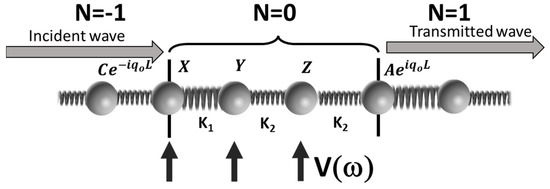
Figure 4.
Schematic illustration of the scattering of a reflectionless DRAK mode by a potential . The amplitudes of the incident and transmitted waves are shown as well as the amplitude of the three masses in the cell, N = 0. The black arrows indicate the three locations of the applied scattering potential investigated here.
The three Equation (17a,b,c) to solve are rewritten as
For illustrative purposes, we consider a DRAK mode with non-zero amplitude corresponding to with ; we can rewrite this set of equations in the form
where the matrix W is given by with and . Since the DRAK mode corresponds to , the dispersion relation of the homogeneous medium of type 2 given by Equation (2) is , that is, and . With this, we have
After inverting the matrix W, we obtain the amplitudes
We have verified that when , the amplitudes become those of the unperturbed superlattice, that is, . Furthermore, we can verify that when , the amplitudes of the perturbed cell converge to a nontrivial solution . Let us consider an infinitely large scattering potential for all frequencies, for instance, in the case of a potential, , resulting from a mass defect with very large mass, . In that case, mass A does not move but masses B and C are able to transfer the incident wave to a transmitted wave as if the scatterer were not affecting the system. Note that this is reminiscent of an anti-resonance, whereby one mass remains static but transfers some driving force to other masses it is interacting with. The existence of nontrivial amplitudes suggests that the DRAK mode resulting from the nontrivial topology of the superlattice is immune to backscattering when the scattering potential is applied to mass A.
We now ask the question about immunity to backscattering when the scattering potential acts on mass B in the cell N = 0. In this case, the matrix W becomes
Solving Equation (21) yields the amplitudes
In the limit , the amplitudes become those of the unperturbed system, . We note that X and Y are independent of the potential. In the limit , the amplitude Z diverges. When the scattering potential applies to the mass B, there is no finite physical solution for amplitude . The no-reflection assumption breaks down for an infinite potential applied to mass B. For finite scattering potentials, Equation (23a,b,c) offer solutions for that are compatible with the assumption of no reflection. The DRAK mode appears to be immune to backscattering but for infinite potentials applied to mass B.
In the case of a scattering potential applied to the mass C in cell N = 0, the matrix W is
Its inverse takes the form
For finite scattering potentials, there exist amplitudes of the mass in the perturbed cell which are compatible with the no-reflection assumption. In the limit , the inverse matrix simplifies to
which leads to the following amplitudes:
An infinite scattering potential on the mass C in the perturbed cell is accommodated by a zero amplitude of that mass. Again, this behavior is reminiscent of an anti-resonance, which enables the incident wave to be transmitted through the perturbed cell even for very large scattering potentials.
Apart from an infinite potential on mass B, the no-reflection assumption for a DRAK mode is compatible with any scattering potential applied to the masses A, B, and C in cell N = 0.
Hence, single-frequency DRAK modes appear to possess a strong immunity to backscattering.
3. Conclusions
We have investigated the scattering of acoustic waves in topologically non-conventional discrete superlattices. We have considered the case of a two-mass-per-unit-cell superlattice analogous to the SSH model as well as the case of the simplest binary superlattice, with three masses per unit cell, which possesses a Fabry–Pérot resonance. The latter system supports a one-way propagating mode (denoted DRAK mode) which has zero amplitude on one side of the Brillouin zone but has a finite amplitude on the other side. The SSH analog system does not exhibit DRAK modes but possesses one mode for which the forward and backward propagating waves are orthogonal to each other. We investigated the scattering of orthogonal and DRAK modes in their respective superlattice when masses in one cell are selectively subjected to a general scattering potential. We demonstrate theoretically that the orthogonality of counterpropagating modes does not provide robust protection against backscattering. In contrast, the DRAK mode does satisfy a no-reflection condition (i.e., shows immunity to backscattering) for a wide range of scattering potentials applied to all three masses constituting the perturbed cell. Future work will include the study of scattering in more general topological acoustic superlattices such as continuous superlattices in addition to discrete ones. Additionally, here, we have considered scattering potentials applied to individual masses within a unit cell; topological protection against more complex scattering potentials will need to be studied.
Recently, the robustness of topological protection against backscattering in electronic and photonic topological interface modes has been questioned [14,15,16]. The demonstration of robust immunity to backscattering for bulk acoustic waves in topologically non-conventional superlattices, without breaking time-reversal symmetry, may have implications for the practical application of topological protection to engineered acoustic devices and systems. The narrow-frequency DRAK modes in superlattice immune to backscattering could offer low-cost and industry-compatible solutions to reducing insertion loss (e.g., reflection loss due to defects) in next-generation acoustic wave filters and devices for telecommunications and sensing. Experimental verification of the findings reported in this paper for micro-acoustic wave devices, such as thin-film-based superlattices, as well as one-dimensional acoustic waveguide superlattices is underway.
Author Contributions
Conceptualization, P.A.D., K.R. and J.O.V.; methodology, J.O.V. and P.A.D.; validation, J.O.V.; formal analysis, P.A.D., J.O.V., K.R., A.A. and A.K.; writing—original draft preparation, P.A.D.; writing—review and editing, J.O.V., K.R., A.A., and A.K.; supervision, P.A.D.; project administration, P.A.D.; funding acquisition, P.A.D., A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the US National Science Foundation (NSF) grant #2242925 through the Science and Technology Center New Frontiers of Sound (NewFoS).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xue, H.; Yang, Y.; Zhang, B. Topological acoustics. Nat. Rev. Mater. 2022, 7, 975. [Google Scholar] [CrossRef]
- Swinteck, N.; Matsuo, S.; Runge, K.; Vasseur, J.O.; Lucas, P.; Deymier, P.A. Bulk elastic waves with unidirectional backscattering-immune topological states in a time-dependent superlattice. J. Appl. Phys. 2015, 118, 063103. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Fleury, R.; Mousavi, H.; Alù, A. Topologically Robust Sound Propagation in an Angular-Momentum-Biased Graphene-Like Resonator Lattice. Nat. Commun. 2015, 6, 8260. [Google Scholar] [CrossRef] [PubMed]
- Trainiti, G.; Ruzzene, M. Non-reciprocal elastic wave propagation in spatiotemporal periodic structures. New J. Phys. 2016, 18, 083047. [Google Scholar] [CrossRef]
- Nassar, H.; Chen, H.; Norris, A.N.; Haberman, M.R.; Huang, G.L. Non-reciprocal wave propagation in modulated elastic metamaterials. Proc. R. Soc. 2017, 473, 20170188. [Google Scholar] [CrossRef] [PubMed]
- Tessier Brothelande, S.; Croënne, C.; Allein, F.; Vasseur, J.O.; Amberg, M.; Giraud, F.; Dubus, B. Experimental evidence of nonreciprocal propagation in space-time modulated piezoelectric phononic crystals. Appl. Phys. Lett. 2023, 123, 201701. [Google Scholar] [CrossRef]
- Deymier, P.A.; Runge, K.; Khanikaev, A.; Alù, A. Pseudo-Spin Polarized One-Way Elastic Wave Eigenstates in One-Dimensional Phononic Superlattices. Crystals 2024, 14, 92. [Google Scholar] [CrossRef]
- Pérot, A.; Fabry, C. On the application of interference phenomena to the solution of various problems of spectroscopy and metrology. Astrophys. J. 1899, 9, 87. [Google Scholar] [CrossRef]
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698. [Google Scholar] [CrossRef]
- Huang, H.; Chen, J.; Huo, S. Recent advances in topological elastic metamaterials. J. Phys. Condens. Matter. 2021, 33, 503002. [Google Scholar] [CrossRef]
- Hasan, M.A.; Calderın, L.; Runge, K.; Deymier, P.A. Spectral Analysis of Amplitudes and Phases of Lattice Vibrations: Topological Applications. J. Acoust. Soc. Am. 2019, 146, 748. [Google Scholar] [CrossRef]
- Sweeney, W.R.; Hsu, C.W.; Stone, A.D. Theory of reflectionless scattering modes. Phys. Rev. A 2020, 102, 063511. [Google Scholar] [CrossRef]
- Bonnet-Ben Dhia, A.S.; Chesnel, L.; Pagneux, V. Trapped modes and reflectionless modes as eigenfunctions of the same spectral problem. Proc. R. Soc. A 2018, 474, 20180050. [Google Scholar] [CrossRef]
- Karimi, M.; Amini, M.; Soltani, M.; Sadeghizadeh, M. Backscattering of topologically protected helical edge states by line defects. Phys. Rev. B 2024, 109, 024108. [Google Scholar] [CrossRef]
- Rosiek, C.A.; Arregui, G.; Vladimirova, A.; Albrechtsen, M.; Lahijani, B.V.; Christiansen, R.E.; Stobbe, S. Observation of strong backscattering in valley-Hall photonic topological interface modes. Nat. Photonics 2023, 17, 386. [Google Scholar] [CrossRef]
- Rechtsman, M.C. Reciprocal topological photonic crystals allow backscattering. Nat. Photonics 2023, 17, 383. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).