The Thermophysical Properties of TcO2
Abstract
1. Introduction
2. Methods
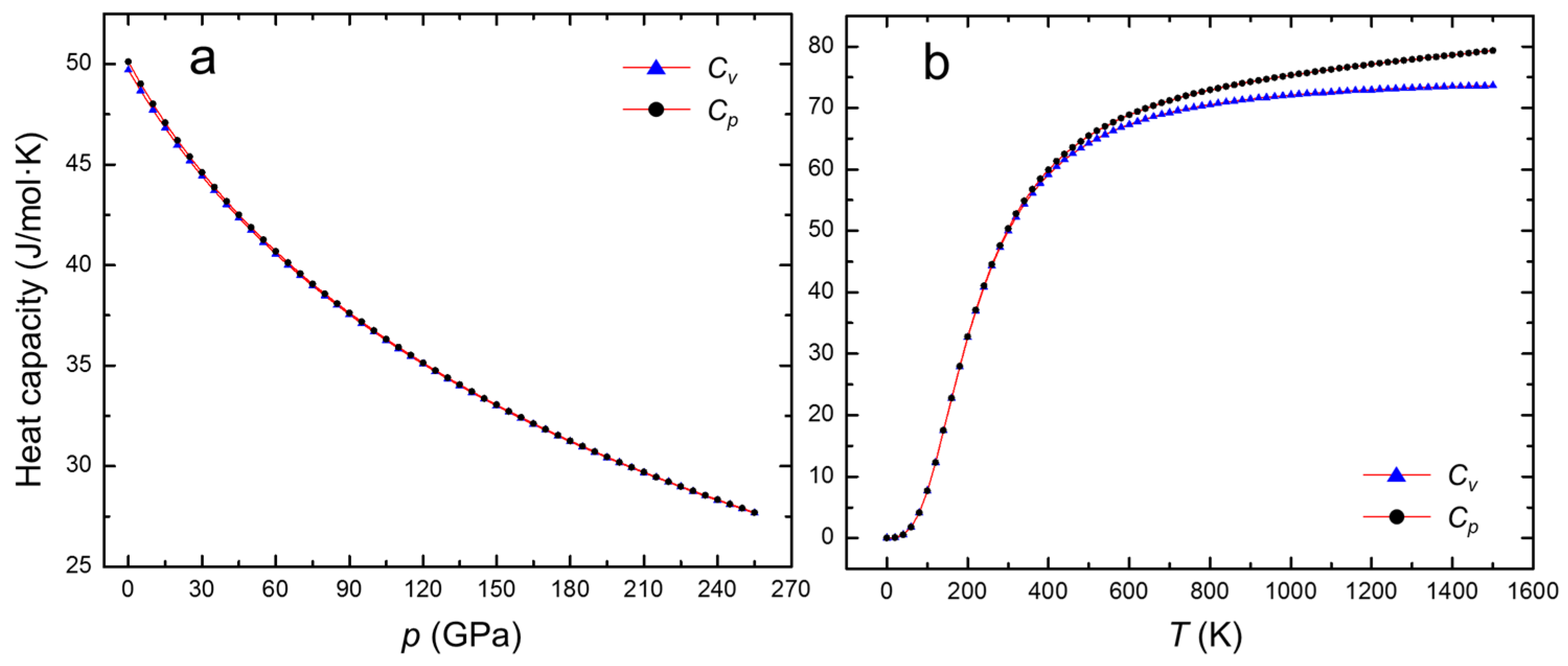
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Childs, B.C.; Braband, H.; Lawler, K.; Mast, D.S.; Bigler, L.; Stalder, U.; Forster, P.M.; Czerwinski, K.R.; Alberto, R.; Sattelberger, A.P.; et al. Ditechnetium heptoxide revisited: Solid-state, gas-phase, and theoretical studies. Inorg. Chem. 2016, 55, 10445–10452. [Google Scholar] [CrossRef] [PubMed]
- Chotkowski, M.; Wrzosek, B.; Grden, M. Intermediate oxidation states of technetium in concentrated sulfuric acid solutions. J. Electroanal. Chem. 2018, 814, 83–90. [Google Scholar] [CrossRef]
- Lawler, K.V.; Childs, B.; Czerwinski, K.R.; Sattelberger, A.P.; Poineau, F.; Forster, P.M. Unraveling the mystery of “tech red”—A volatile technetium oxide. Chem. Commun. 2018, 54, 1261–1264. [Google Scholar] [CrossRef] [PubMed]
- Lawler, K.V.; Childs, B.C.; Mast, D.S.; Czerwinski, K.R.; Sattelberger, A.P.; Poineau, F.; Forster, P.M. Molecular and electronic structures of M2O7(M = Mn, Tc, Re). Inorg. Chem. 2017, 56, 2448–2458. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, E.E.; Poineau, F.; Llobet, A.; Sattelberger, A.P.; Bhattacharjee, J.; Waghmare, U.V.; Hartmann, T.; Cheetham, A.K. Structural studies of TcO2 by neutron powder diffraction and first-principles calculations. J. Am. Chem. Soc. 2007, 129, 10244–10248. [Google Scholar] [CrossRef]
- Schwochau, K. Technetium: Chemistry and Radiopharmaceutical Applications; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2000. [Google Scholar]
- Kim, D.; Kruger, A.A. Volatile species of technetium and rhenium during waste vitrification. J. Non-Cryst. Solids 2018, 481, 41–50. [Google Scholar] [CrossRef]
- Darab, J.G.; Smith, P.A. Chemistry of technetium and rhenium species during low-level radioactive waste vitrification. Chem. Mater. 1996, 8, 1004–1021. [Google Scholar] [CrossRef]
- Kim, D.S.; Bagaasen, L.M.; Crum, J.V.; Fluegel, A.; Gallegos, A.; Martinez, B.; Matyas, J.; Meyer, P.A.; Paulsen, D.; Riley, B.J.; et al. Investigation of Tc Migration Mechanism during Bulk Vitrification Process Using Re Surrogate; PNNL-16267; Pacific Northwest National Laboratory: Richland, WA, USA, 2006. [Google Scholar]
- Langowski, M.H.; Darab, J.G.; Smith, P.A. Volatility Literature of Chlorine, Iodine, Cesium, Strontium, Technetium, and Rhenium; Technetium and Rhenium Volatility Testing; PNNL-11052; Pacific Northwest National Laboratory: Richland, WA, USA, 1996. [Google Scholar]
- Soderquist, C.Z.; Schweiger, M.J.; Kim, D.-S.; Lukens, W.W.; McCloy, J.S. Redox-dependent solubility of technetium in low activity waste glass. J. Nucl. Mater. 2014, 449, 173–180. [Google Scholar] [CrossRef]
- Pegg, I.L. Behavior of technetium in nuclear waste vitrification processes. J. Radioanal. Nucl. Chem. 2015, 305, 287–292. [Google Scholar] [CrossRef]
- Soderquist, C.Z.; Buck, E.C.; McCloy, J.S.; Schweiger, M.J.; Kruger, A.A. Formation of technetium salts in Hanford low-activity waste glass. J. Am. Ceram. Soc. 2016, 99, 3924–3931. [Google Scholar] [CrossRef]
- Reynolds, E.; Zhang, Z.; Avdeev, M.; Thorogood, G.J.; Poineau, F.; Czerwinski, K.R.; Kimpton, J.A.; Kennedy, B.J. Thermal expansion behavior in TcO2. Toward breaking the Tc−Tc bond. Inorg. Chem. 2017, 56, 9219–9224. [Google Scholar] [CrossRef]
- Weaver, J.; Soderquist, C.Z.; Washton, N.M.; Lipton, A.S.; Gassman, P.L.; Lukens, W.W.; Kruger, A.A.; Wall, N.A.; McCloy, J.S. Chemical trends in solid alkali pertechnetates. Inorg. Chem. 2017, 56, 2533–2544. [Google Scholar] [CrossRef]
- Sa, B.; Miao, N.; Sun, Z.; Wu, B. Polyhedral transformation and phase transition in TcO2. RSC Adv. 2015, 5, 1690–1696. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Cond. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kucukbenli, E.; Monni, M.; Adetunji, B.I.; Ge, X.; Adebayo, G.A.; Marzari, N.; De Gironcoli, S.; Dal Corso, A. Projector augmented-wave and all-electron calculations across the periodic table: A comparison of structural and energetic properties. arXiv 2014, arXiv:1404.3015v1. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Nakayama, M.; Ohshima, H.; Nogami, M.; Martin, M. A concerted migration mechanism of mixed oxide ion and electron conduction in reduced ceria studied by first-principles density functional theory. Phys. Chem. Chem. Phys. 2012, 14, 6079–6084. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Abbasi-Pérez, D.; Luaña, V. Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comp. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Luaña, V. Gibbs2: A new version of the quasi-harmonic model code. I. Robust treatment of the static data. Comp. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
- Debye, P. Zur Theorie der spezifischen Wärmen. Ann. Phys. 1912, 344, 789–839. [Google Scholar] [CrossRef]
- Slater, J.C. Introduction to Chemical Physics; McGraw-Hill: New York, NY, USA, 1939. [Google Scholar]
- Moruzzi, V.L.; Janak, J.F.; Schwarz, K. Calculated thermal properties of metals. Phys. Rev. B 1988, 37, 790–799. [Google Scholar] [CrossRef] [PubMed]
- Otero-de-la-Roza, A.; Luaña, V. Treatment of first-principles data for predictive quasiharmonic thermodynamics of solids: The case of MgO. Phys. Rev. B 2011, 84, 024109. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Li, Y.-L.; Zeng, Z. Structural, elastic and electronic properties of ReO2. Chin. Phys. Lett. 2008, 25, 4086–4089. [Google Scholar] [CrossRef]
- Caravaca, M.A.; Miño, J.C.; Pérez, V.J.; Casali, R.A.; Ponce, C.A. Ab initio study of the elastic properties of single and polycrystal TiO2, ZrO2 and HfO2 in the cotunnite structure. J. Phys. Condens. Matter 2008, 21, 015501. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.Y.; Sladek, R.J. Elastic Debye temperatures in tetragonal crystals: Their determination and use. Phys. Rev. B 1982, 25, 5230–5233. [Google Scholar] [CrossRef]
- Langenberg, E.; Ferreiro-Vila, E.; Leborán, V.; Fumega, A.O.; Pardo, V.; Rivadulla, F. Analysis of the temperature dependence of the thermal conductivity of insulating single crystal oxides. APL Mater. 2016, 4, 104815. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Wang, W.; Fu, Z. A simple bulk modulus model for crystal materials based on the bond valence model. Phys. Chem. Chem. Phys. 2017, 19, 22177–22189. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Wang, Q.; Tian, Y. Bulk modulus for polar covalent crystals. Sci. Rep. 2013, 3, 3068. [Google Scholar] [CrossRef] [PubMed]
- Hermet, P.; Lignie, A.; Fraysse, G.; Armand, P.; Papet, P. Thermodynamic properties of the α-quartz-type and rutile-type GeO2 from first-principles calculations. Phys. Chem. Chem. Phys. 2013, 15, 15943–15948. [Google Scholar] [CrossRef] [PubMed]
- Kirchner, H.P. Thermal expansion anisotropy of oxides and oxide solid solutions. J. Am. Ceram. Soc. 1969, 52, 379–386. [Google Scholar] [CrossRef]
- Rao, K.V.K.; Naidu, S.V.N.; Iyengar, L. Precision lattice parameters and the coefficients of thermal expansion of hexagonal germanium dioxide. J. Appl. Cryst. 1973, 6, 136–138. [Google Scholar] [CrossRef]
- Leitner, J.; Chuchvalec, P.; Sedmidubský, D.; Strejc, A.; Abrman, P. Estimation of heat capacities of solid mixed oxides. Thermochim. Acta 2003, 395, 27–46. [Google Scholar] [CrossRef]
- Leitner, J.; Sedmidubský, D.; Chuchvalec, P. Prediction of heat capacities of solid binary oxides from group contribution method. Ceram.-Silikáty 2002, 46, 29–32. [Google Scholar]
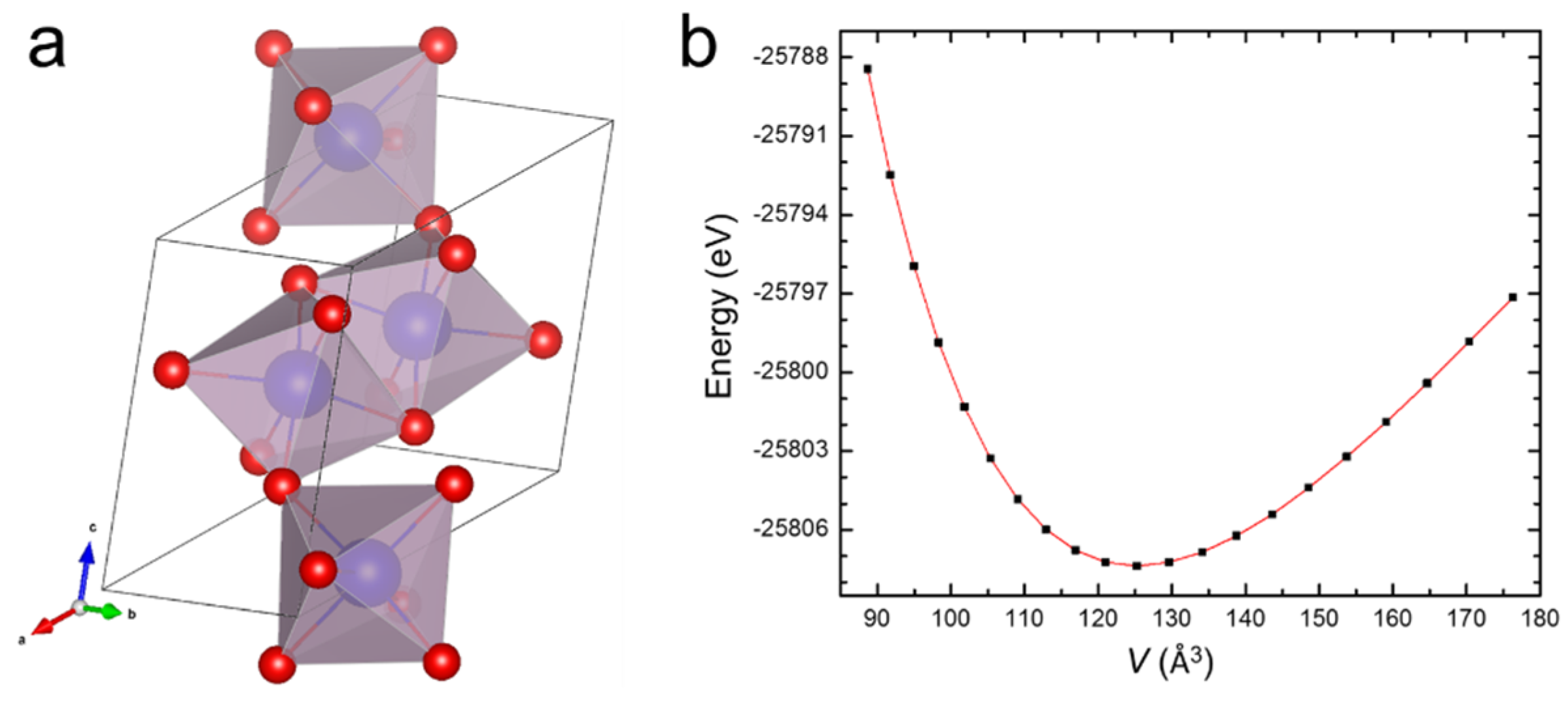
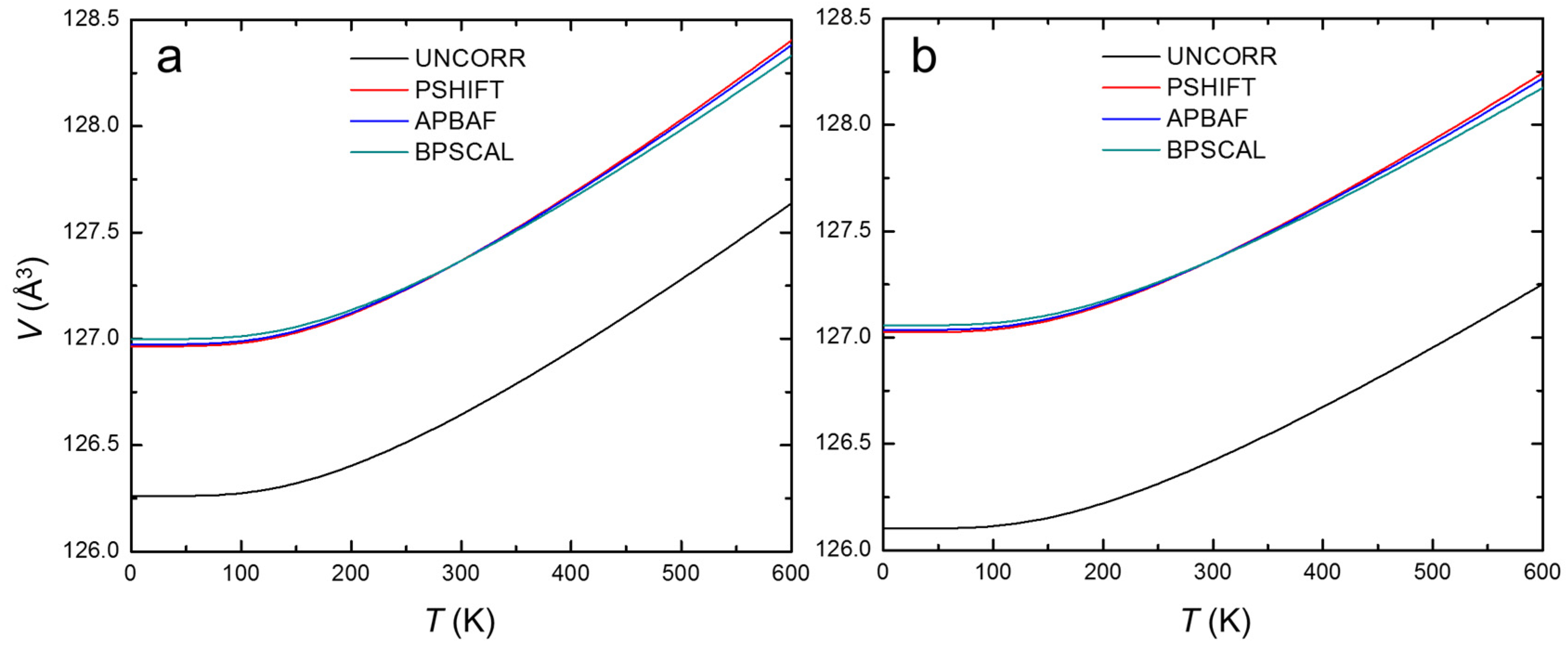
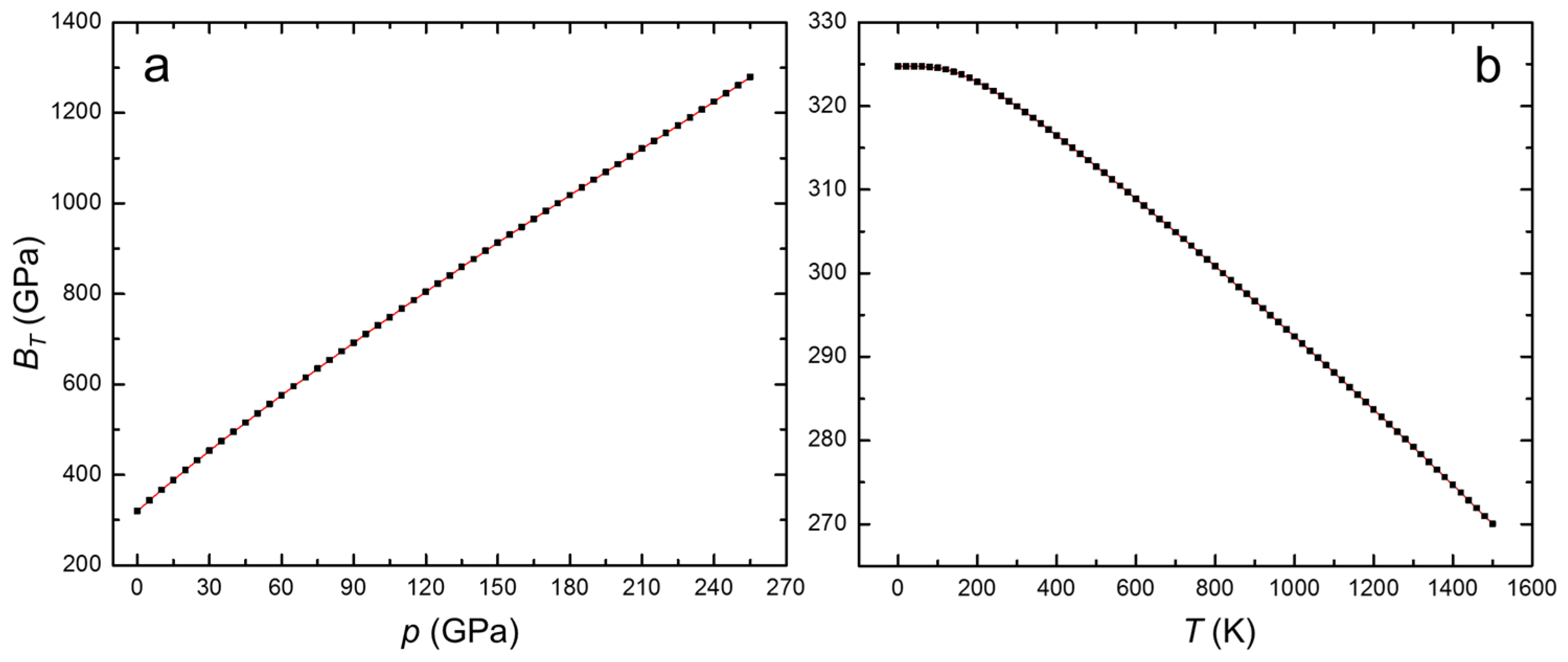
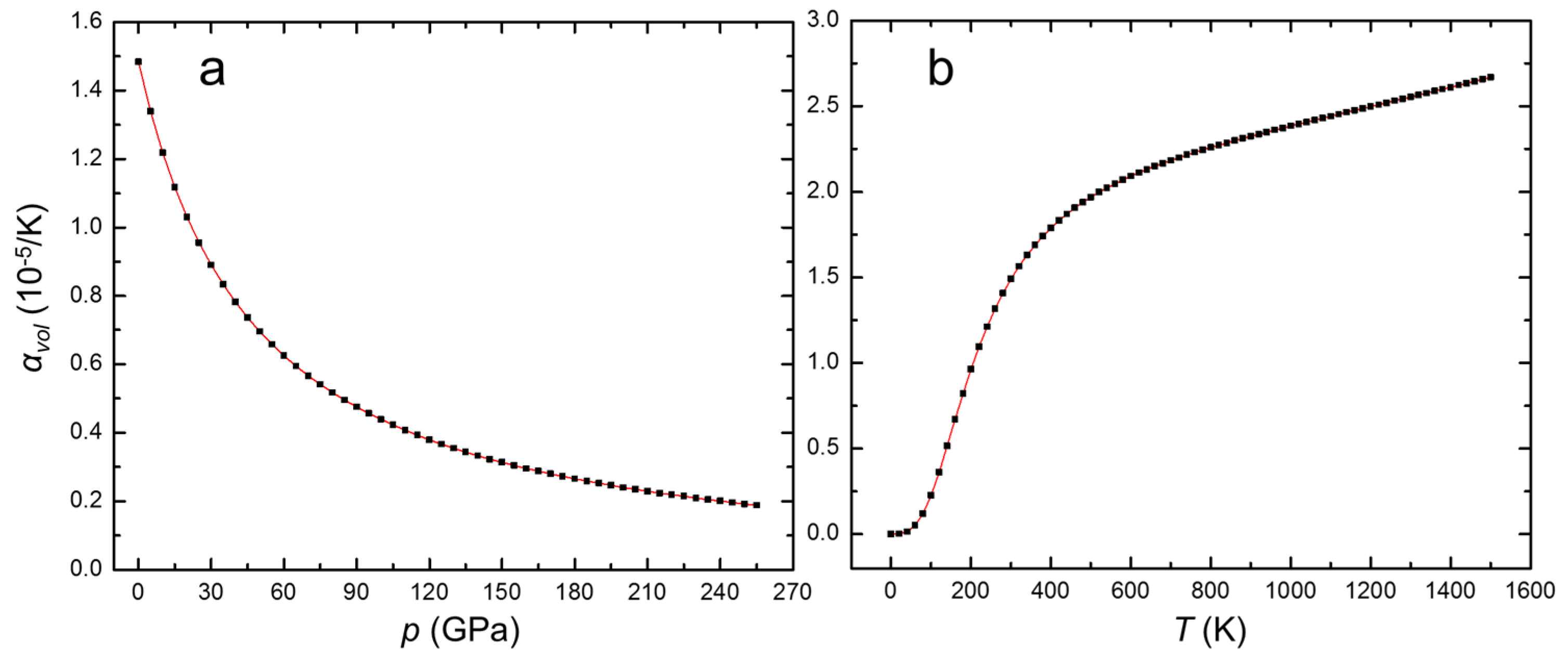
| Crystal Parameter | |||
|---|---|---|---|
| a1 | 5.591 | 0.000 | 0.000 |
| a2 | 0.000 | 4.761 | 0.000 |
| a3 | −2.858 | 0.000 | 4.706 |
| Tc | 0.26535 | 0.00459 | 0.98489 |
| O1 | 0.10706 | 0.19253 | 0.19506 |
| O2 | 0.39102 | 0.71259 | 0.26659 |
| Debye–Slater | Debye–Grüneisen | Literature [5] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| UNCORR | PSHIFT | APBAF | BPSCAL | UNCORR | PSHIFT | APBAF | BPSCAL | ||
| 15 K | 126.261 | 126.965 | 126.975 | 126.999 | 126.102 | 127.025 | 127.036 | 127.057 | 127.124 |
| 298.15 K | 126.639 | 127.362 | 127.362 | 127.362 | 126.418 | 127.362 | 127.362 | 127.362 | 127.362 |
| 280 | 285 | 290 | 295 | 300 | 305 | 310 | 315 | 320 | |
|---|---|---|---|---|---|---|---|---|---|
| 0.20 | 127.068 | 127.077 | 127.085 | 127.092 | 127.100 | 127.107 | 127.113 | 127.120 | 127.126 |
| 0.21 | 127.061 | 127.070 | 127.078 | 127.085 | 127.093 | 127.100 | 127.107 | 127.114 | 127.120 |
| 0.22 | 127.054 | 127.062 | 127.070 | 127.078 | 127.086 | 127.093 | 127.100 | 127.107 | 127.113 |
| 0.23 | 127.046 | 127.055 | 127.063 | 127.071 | 127.079 | 127.086 | 127.093 | 127.100 | 127.107 |
| 0.24 | 127.038 | 127.047 | 127.055 | 127.063 | 127.071 | 127.079 | 127.086 | 127.093 | 127.100 |
| 0.25 | 127.030 | 127.039 | 127.047 | 127.056 | 127.064 | 127.071 | 127.079 | 127.086 | 127.093 |
| 0.26 | 127.021 | 127.030 | 127.039 | 127.048 | 127.056 | 127.063 | 127.0709 | 127.078 | 127.085 |
| 0.27 | 127.012 | 127.022 | 127.031 | 127.039 | 127.047 | 127.055 | 127.063 | 127.070 | 127.077 |
| 0.28 | 127.003 | 127.013 | 127.022 | 127.031 | 127.039 | 127.047 | 127.055 | 127.062 | 127.069 |
| 0.29 | 126.994 | 127.003 | 127.013 | 127.021 | 127.030 | 127.038 | 127.046 | 127.054 | 127.061 |
| 0.30 | 126.984 | 126.994 | 127.003 | 127.012 | 127.021 | 127.029 | 127.037 | 127.045 | 127.052 |
| Thermophysical Properties, Symbol, Unit | Value |
|---|---|
| Gibbs free energy, G, kJ/mol | −6.225 × 105 |
| Debye temperature, ΘD, K | 891.91 |
| Volumetric thermal expansion coefficient, αvol, 10−5/K | 1.484 |
| Isothermal bulk modulus, BT, GPa | 320 |
| Adiabatic bulk modulus, BS, GPa | 322.59 |
| Grüneisen parameter, γ | 1.832 |
| Constant pressure heat capacity, Cp, J/mol·K | 50.103 |
| Constant volume heat capacity, Cv, J/mol·K | 49.700 |
| Thermal pressure, pth, GPa | 2.991 |
| Vibrational contribution to the Helmholtz free energy, Fvib, KJ/mol | 21.762 |
| Entropy, S, J/mol·K | 32.256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, H.; Lonergan, J.; McCloy, J.S.; Beckman, S.P. The Thermophysical Properties of TcO2. Crystals 2024, 14, 228. https://doi.org/10.3390/cryst14030228
Zhong H, Lonergan J, McCloy JS, Beckman SP. The Thermophysical Properties of TcO2. Crystals. 2024; 14(3):228. https://doi.org/10.3390/cryst14030228
Chicago/Turabian StyleZhong, Hong, Jason Lonergan, John S. McCloy, and Scott P. Beckman. 2024. "The Thermophysical Properties of TcO2" Crystals 14, no. 3: 228. https://doi.org/10.3390/cryst14030228
APA StyleZhong, H., Lonergan, J., McCloy, J. S., & Beckman, S. P. (2024). The Thermophysical Properties of TcO2. Crystals, 14(3), 228. https://doi.org/10.3390/cryst14030228







