Mechanical Analysis of Functionally Graded Multilayered Two-Dimensional Decagonal Piezoelectric Quasicrystal Laminates with Imperfect Interfaces
Abstract
1. Introduction
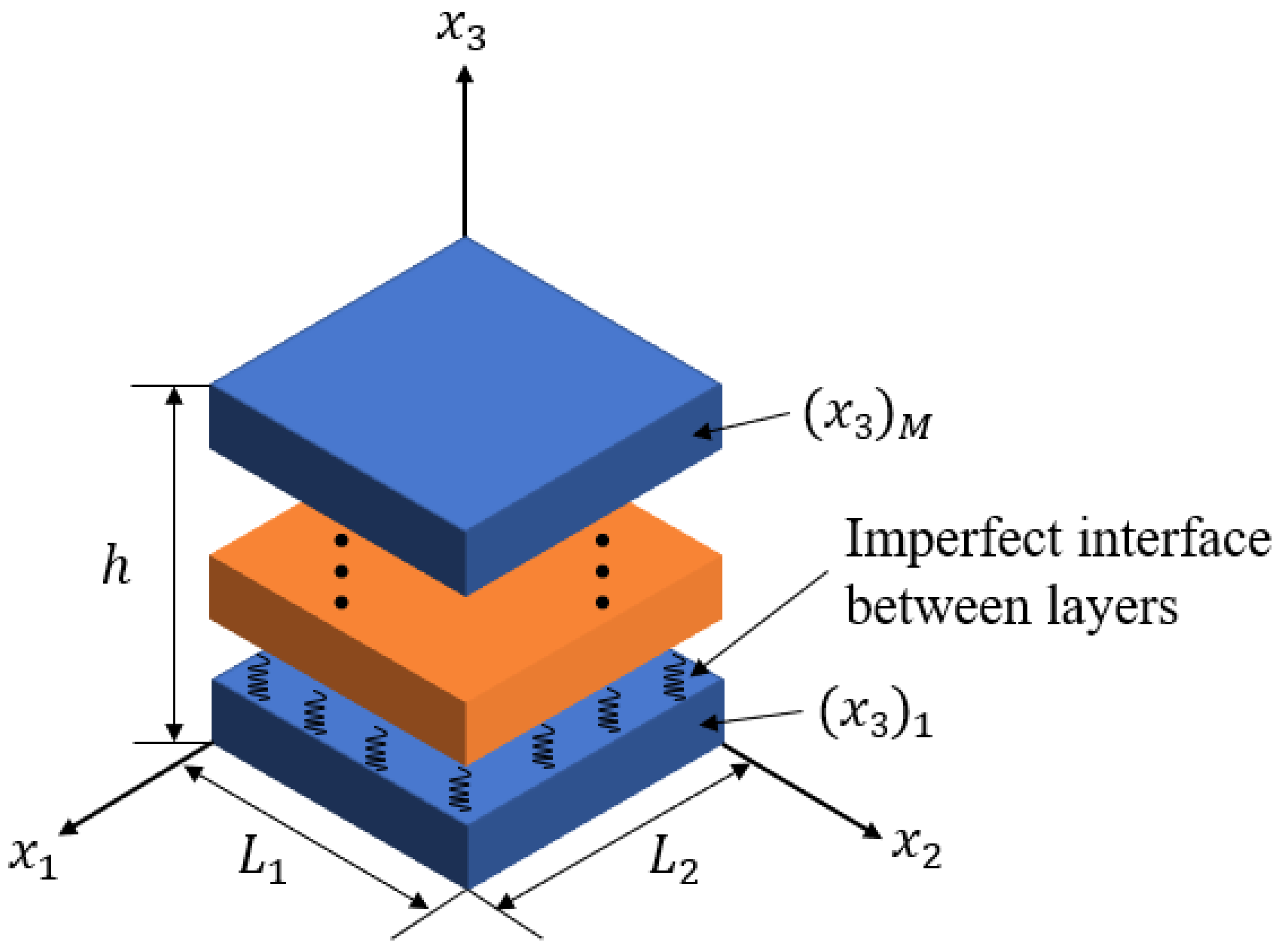
2. Description and Formulation of the Problem
2.1. Basic Equations
2.2. State Equations of a Homogeneous QC Laminate Layer
3. General Solutions for a 2D QC Laminate
4. Imperfect Conductive Interface Analysis
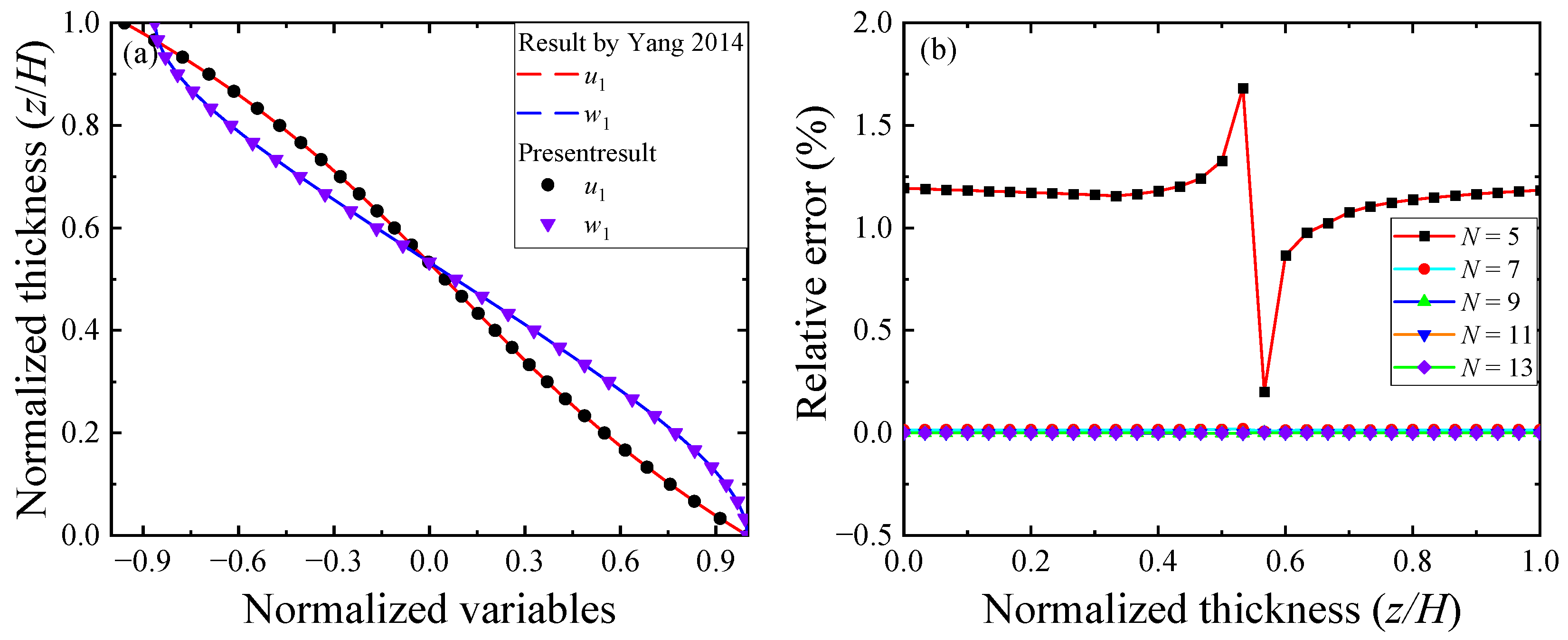
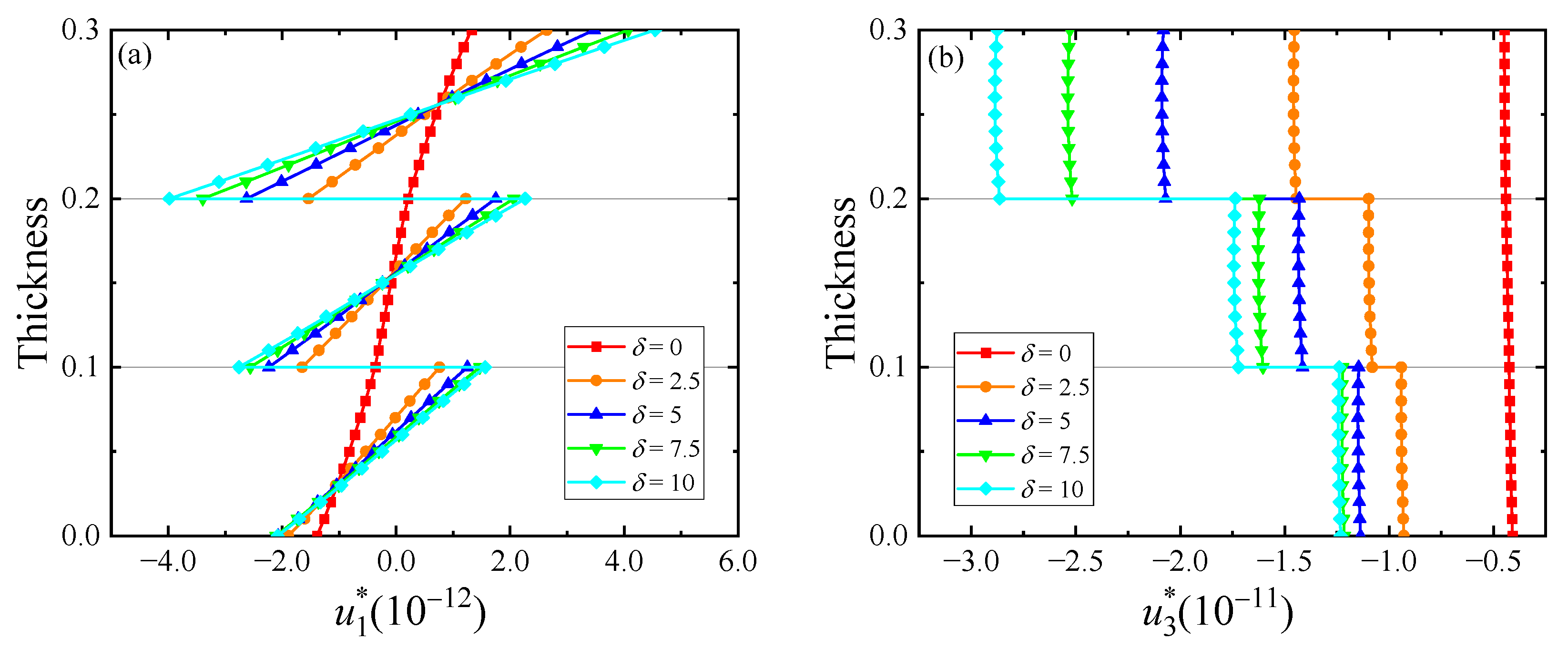
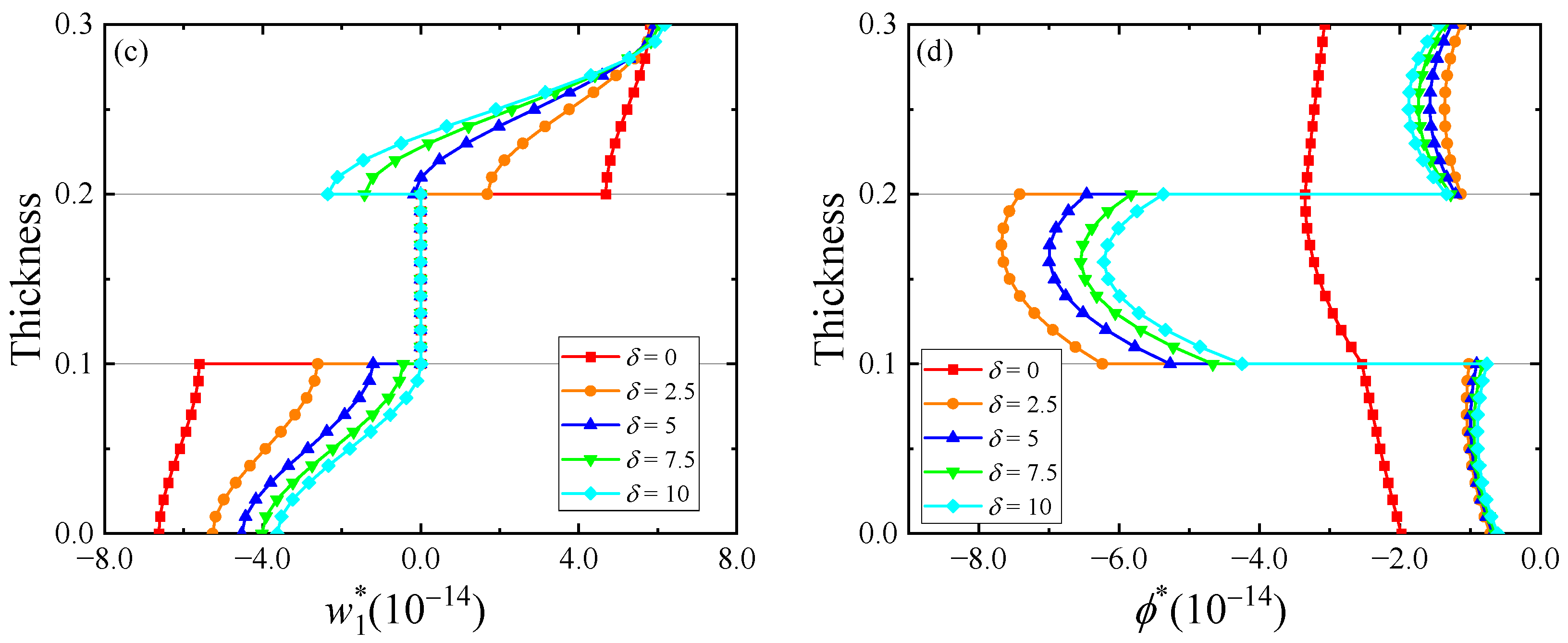
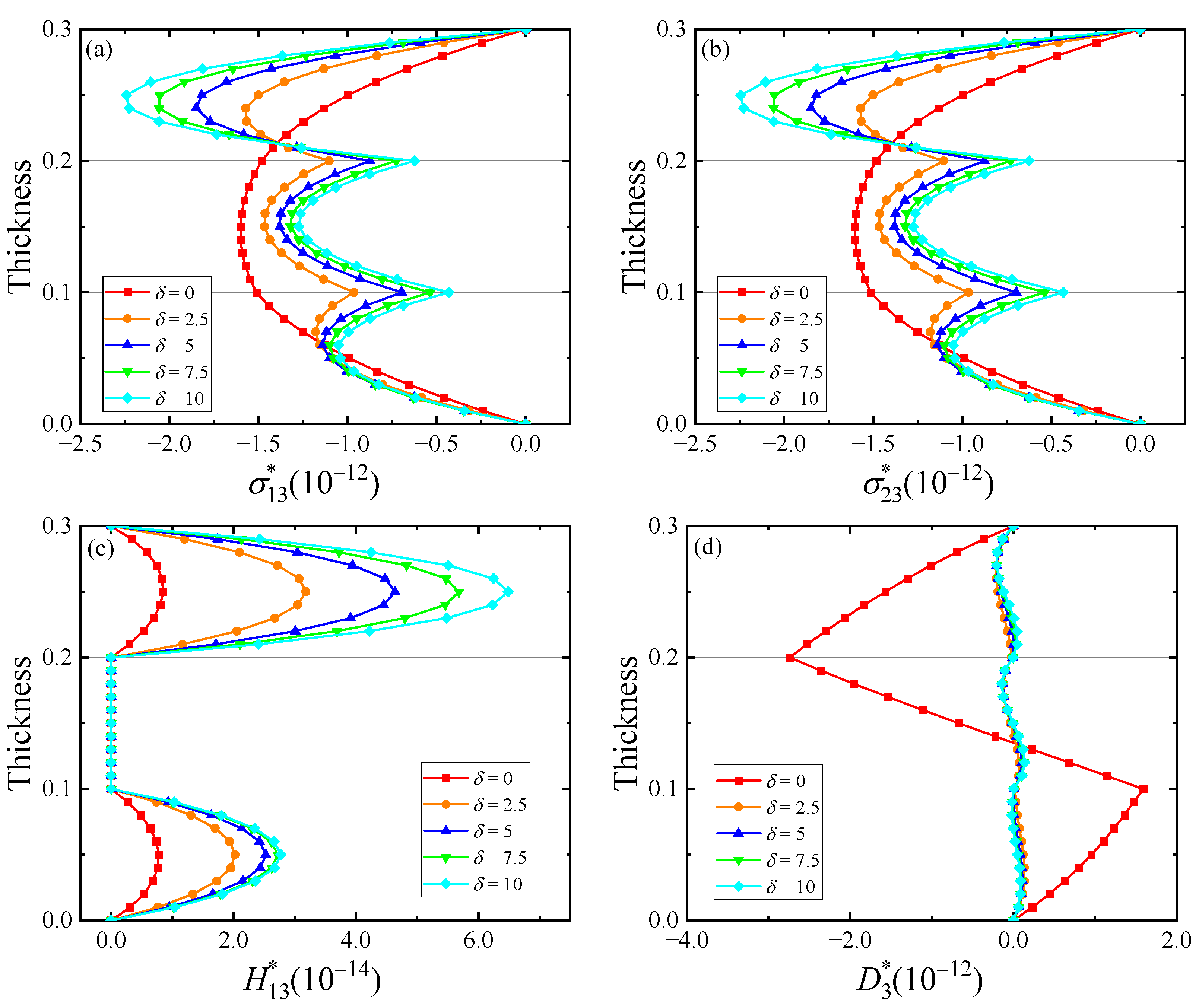
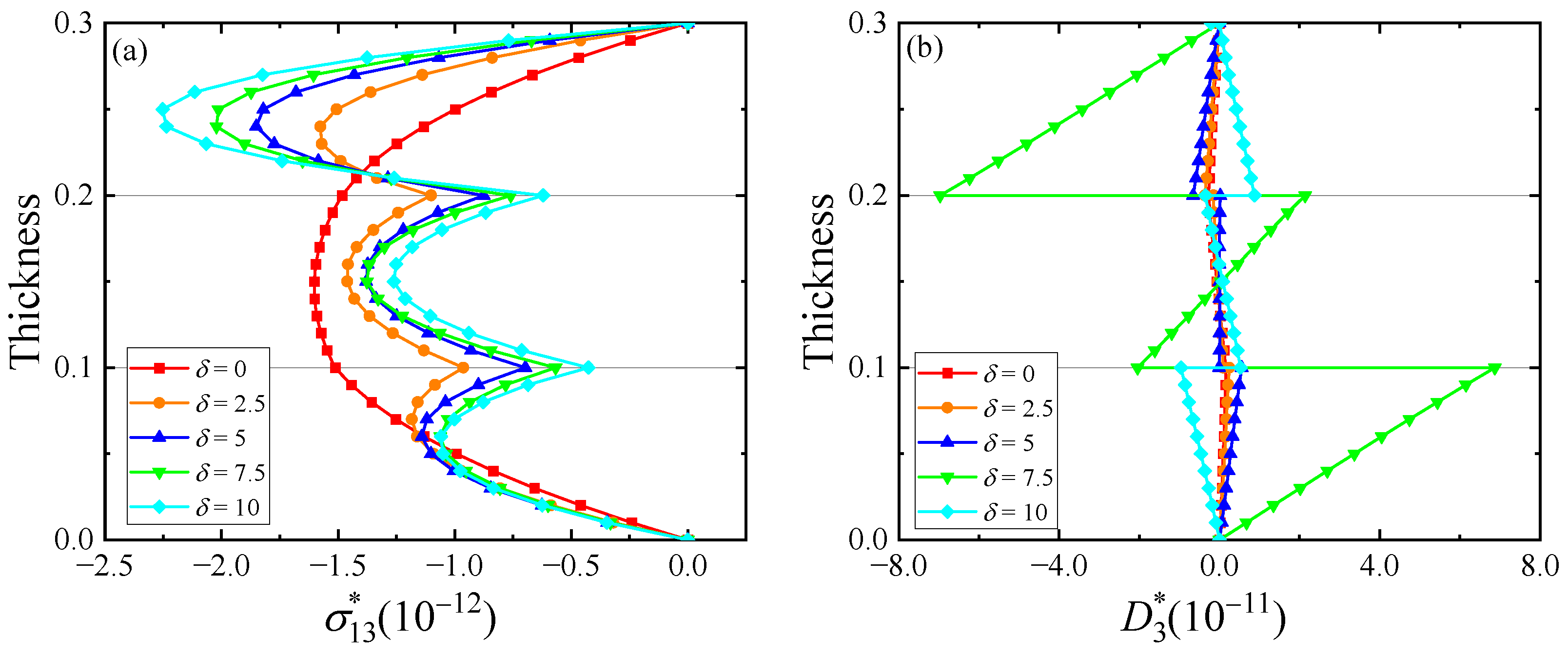
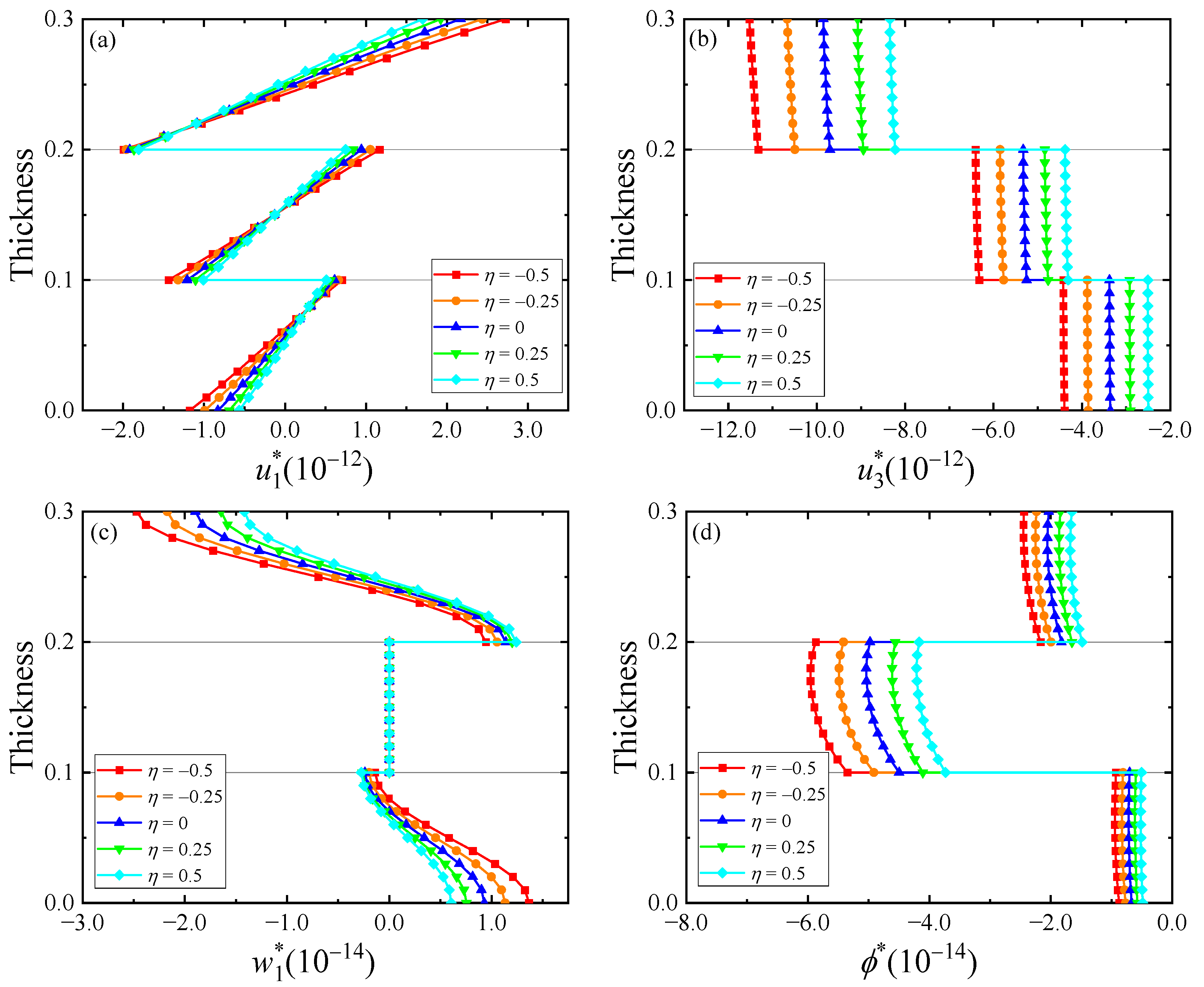
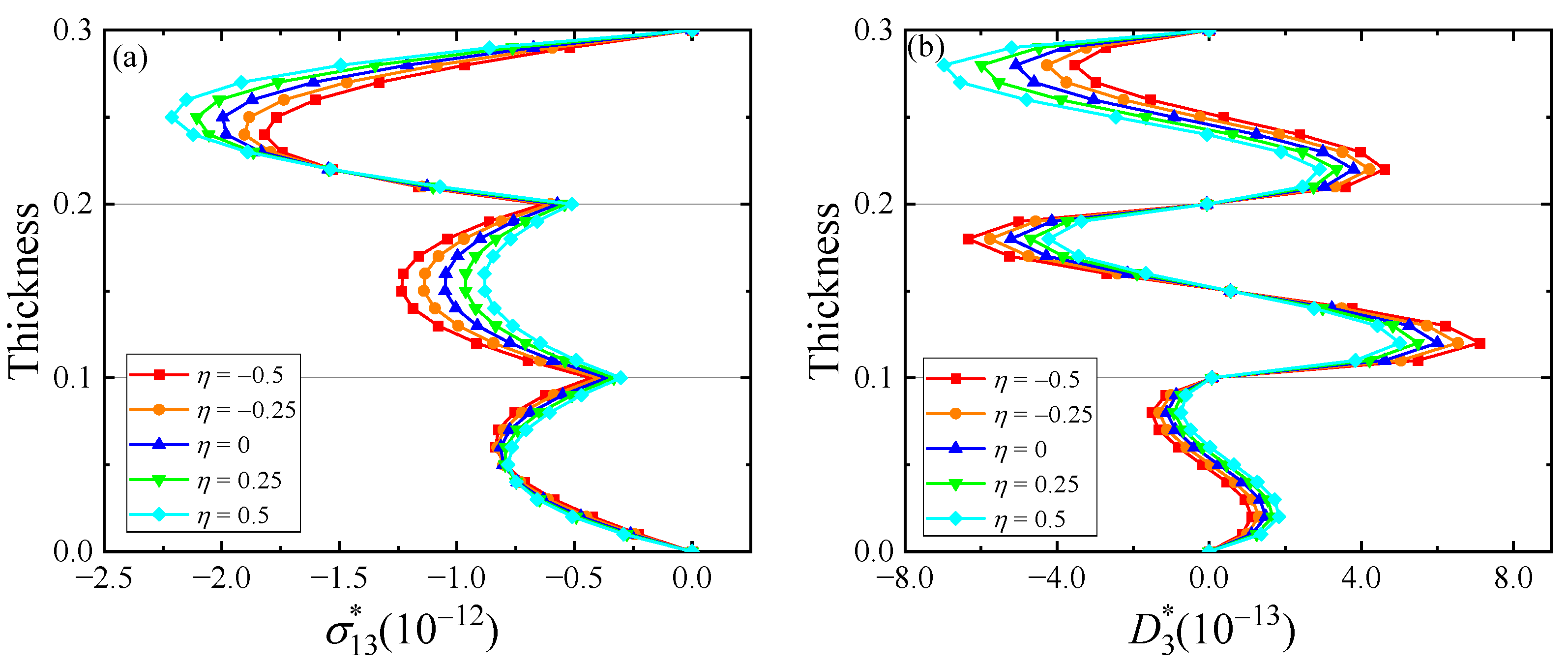
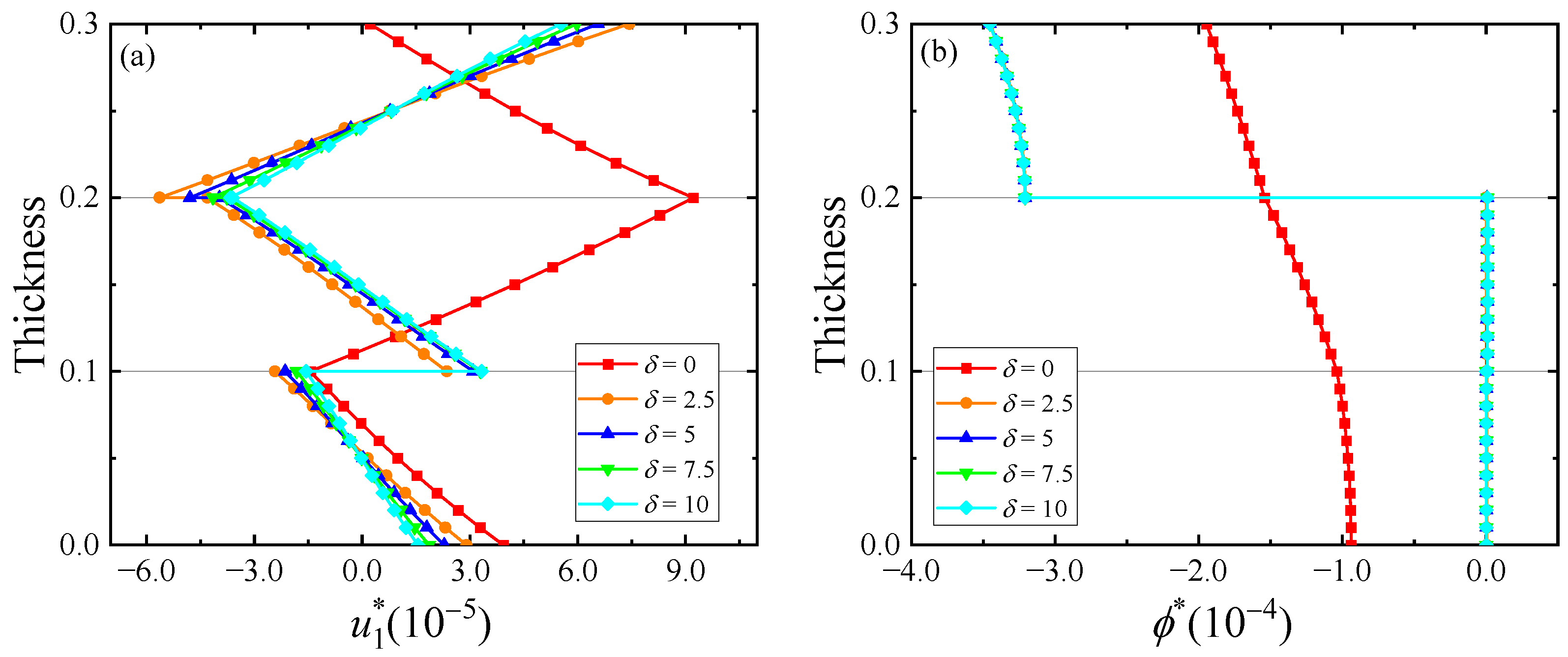
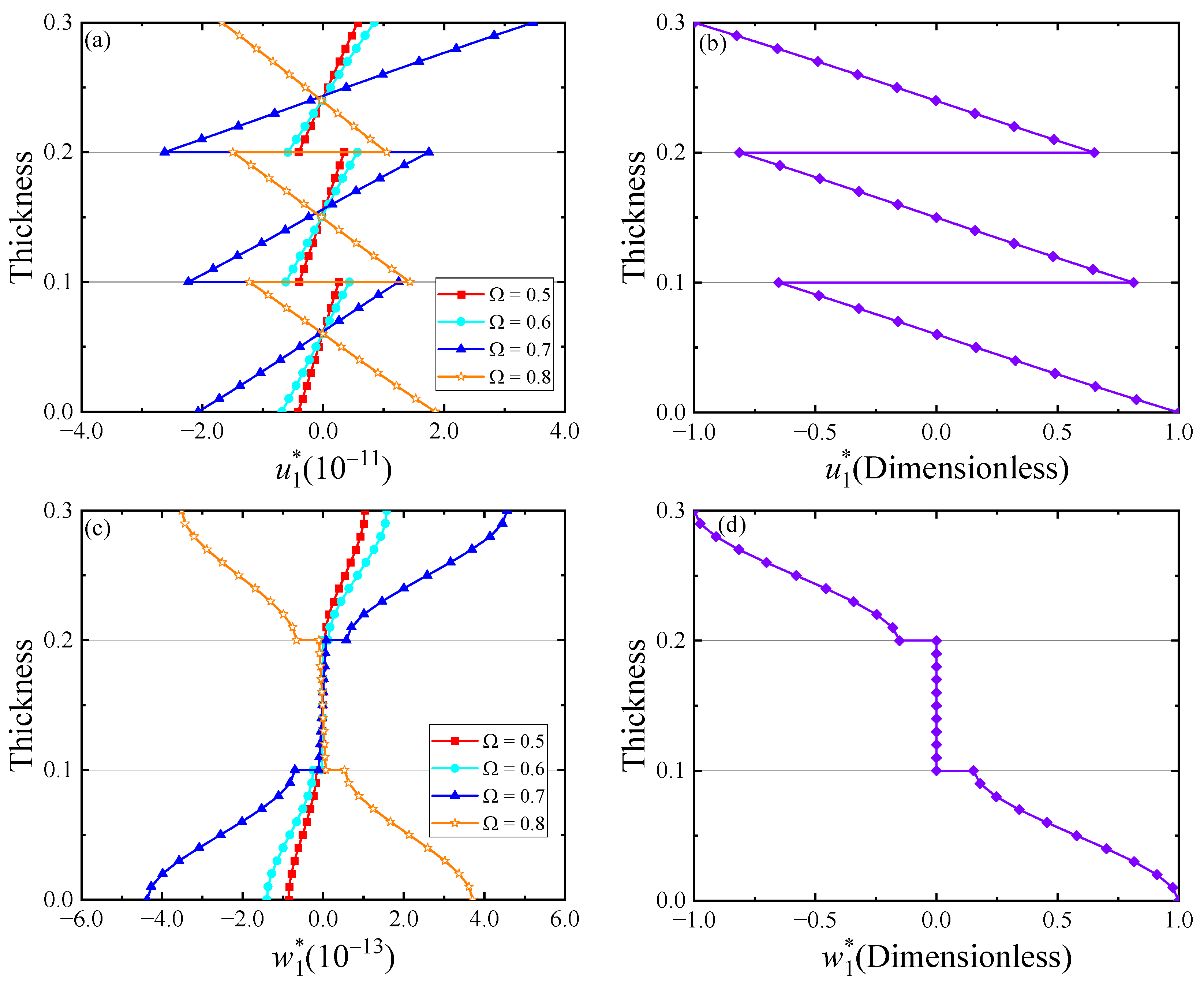
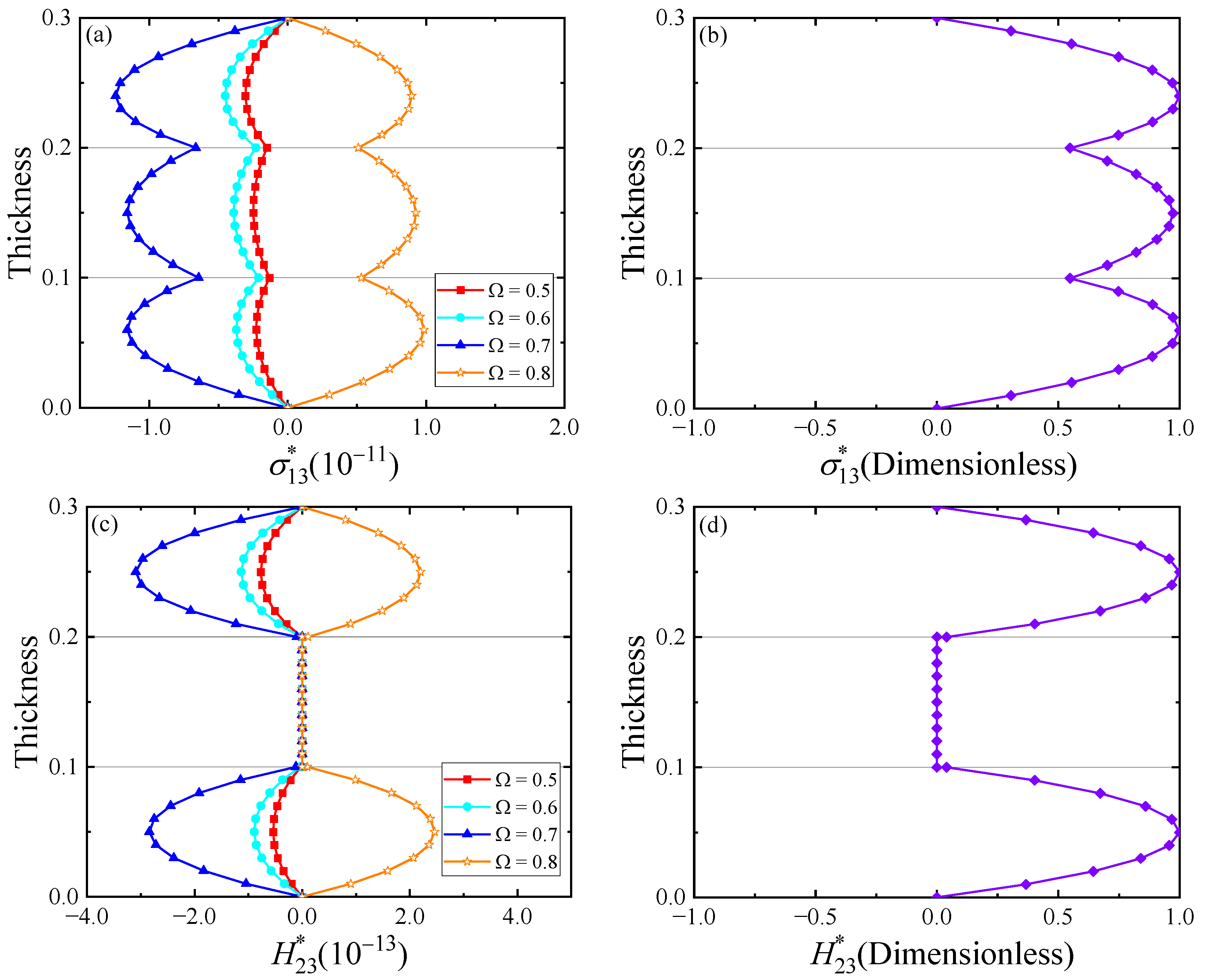
5. Numerical Examples
6. Conclusions
- As the degree of imperfect connection at the interface increases, some physical quantities become discontinuous at the interface, such as displacements.
- As the functional gradient factor changes, each physical quantity only changes its numerical magnitude while keeping its variation trend.
- An increase in the interface compliance would reduce the overall stiffness of the laminates while an increase in functional gradient factor would enhance the stiffness. The free vibration frequency will gradually increase as the interface compliance decreases and the functional gradient factor increases.
- The variation trends of the field quantities under different loading frequencies are similar to that of the eigenmode shape at the natural frequency, which is near the loading frequency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. The State Equations in the Partial Differential Form Are
Appendix A.2. The State Equations for the Dynamic Problem
Appendix A.3. The Exported Components and the Coefficients in Equations (A1) and (A2)
Appendix A.4. The State Equations in the Partial Differential Form
Appendix A.5. The State Equations under SSSS Boundary Conditions with Opposite Edge Discretization
Appendix A.6. The State Equations under CCCC Boundary Conditions with Opposite Edge Discretization
Appendix A.7. The Coefficients in Equations (A5) and (A6)
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Bindi, L.; Steinhardt, P.J.; Yao, N.; Lu, P.J. Natural Quasicrystals. Science 2009, 324, 1306–1309. [Google Scholar] [CrossRef]
- Bindi, L.; Yao, N.; Lin, C.; Hollister, L.S.; Andronicos, C.L.; Distler, V.V.; Eddy, M.P.; Kostin, A.; Kryachko, V.; MacPherson, G.J.; et al. Natural quasicrystal with decagonal symmetry. Sci. Rep. 2015, 5, 9111. [Google Scholar] [CrossRef]
- Jaric, M.V.; Nelson, D.R. Introduction to quasicrystals. Phys. Today 1990, 43, 77–79. [Google Scholar] [CrossRef]
- Fan, T.Y. Mathematical Theory of Elasticity of Quasicrystals and Its Applications; Springer: Heidelberg, Germany, 2011. [Google Scholar]
- Huang, Y.Z.; Chen, J.; Zhao, M.; Feng, M. Electromechanical coupling characteristics of double-layer piezoelectric quasicrystal actuators. Int. J. Mech. Sci. 2021, 196, 106293. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhang, H.L.; Li, Y.; Wang, J.; Lu, C. Static Electro-Mechanical Response of Axisymmetric One-Dimensional Piezoelectric Quasicrystal Circular Actuator. Materials 2022, 15, 3157. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.S.; Xiao, T. Free vibration of the one-dimensional piezoelectric quasicrystal microb eams base d on modifie d couple stress theory. Appl. Math. Model. 2021, 96, 733–750. [Google Scholar] [CrossRef]
- Loboda, V.; Komarov, O.; Bilyi, D.; Lapusta, Y. An analytical approach to the analysis of an electrically permeable interface crack in a 1D piezoelectric quasicrystal. Acta Mech. 2020, 231, 3419–3433. [Google Scholar] [CrossRef]
- Zhu, S.B.; Tong, Z.Z.; Li, Y.Q.; Sun, J.; Zhou, Z.; Xu, X. Post-buckling of two-dimensional decagonal piezoelectric quasicrystal cylindrical shells under compression. Int. J. Mech. Sci. 2022, 235, 107720. [Google Scholar] [CrossRef]
- Zhou, Y.B.; Liu, G.T.; Li, L.H. Effect of T-stress on the fracture in an infinite one-dimensional hexagonal piezoelectric quasicrystal with a Griffith crack. Eur. J. Mech. A/Solids 2021, 86, 104184. [Google Scholar] [CrossRef]
- Yang, L.Z.; Gao, Y.; Pan, E.; Waksmanski, N. An exact solution for a multilayered two-dimensional decagonal quasicrystal plate. Int. J. Solids Struct. 2014, 51, 1737–1749. [Google Scholar] [CrossRef]
- Guo, J.H.; Zhang, M.; Chen, W.Q.; Zhang, X.Y. Free and forced vibration of layered one-dimensional quasicrystal nanoplates with modified couple-stress effect. Sci. China 2020, 63, 124–125. [Google Scholar] [CrossRef]
- Huang, Y.Z.; Li, Y.; Zhang, L.L.; Zhang, H.; Gao, Y. Dynamic analysis of a multilayered piezoelectric two-dimensional quasicrystal cylindrical shell filled with compressible fluid using the state-space approach. Acta Mech. 2020, 231, 2351–2368. [Google Scholar] [CrossRef]
- Huang, B.; Kim, H.S. Free-edge interlaminar stress analysis of piezo-bonded composite laminates under symmetric electric excitation. Int. J. Solids Struct. 2014, 51, 1246–1252. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, J.H.; Xing, Y.M. Nonlocal analytical solution of functionally graded multilayered one-dimensional hexagonal piezoelectric quasicrystal nanoplates. Acta Mech. 2019, 230, 1781–1810. [Google Scholar] [CrossRef]
- Vel, S.S.; Batra, R.C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates. J. Sound Vib. 2004, 272, 703–730. [Google Scholar] [CrossRef]
- Phung-Van, P.; Tran, L.V.; Ferreira, A.J.M.; Nguyen-Xuan, H.; Abdel-Wahab, M. Nonlinear transient isogeometric analysis of smart piezoelectric functionally graded material plates based on generalized shear deformation theory under thermo-electro-mechanical loads. Nonlinear Dyn. 2017, 87, 879–894. [Google Scholar] [CrossRef]
- Guo, J.H.; Chen, J.Y.; Pan, E. A three-dimensional size-dependent layered model for simply-supported and functionally graded magnetoelectroelastic plates. Acta Mech. Solida Sin. 2018, 31, 652–671. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, L.L.; Wang, Y.X.; Zhang, J.M.; Zhang, H.; Gao, Y. Static response of functionally graded multilayered two-dimensional quasicrystal plates with mixed boundary conditions. Appl. Math. Mech. 2021, 42, 1599–1618. [Google Scholar] [CrossRef]
- Ma, W.S.; Liu, F.H.; Li, D.X.; Zhang, J.Y.; Lü, S.F. Global dynamics of a special symmetrically laid composite laminated rectangular plate. J. Inn. Mong. Univ. Technol. 2023, 42, 109–115. [Google Scholar]
- Benveniste, Y. The effective mechanical behaviour of composite materials with imperfect contact between the constituents. Mech. Mater. 1985, 4, 197–208. [Google Scholar] [CrossRef]
- Cheng, Z.Q.; Jemah, A.K.; Williams, F.W. Theory for multilayered anisotropic plates with weakened interfaces. J. Appl. Mech. 1996, 63, 1019–1026. [Google Scholar] [CrossRef]
- Qu, J.M. The effect of slightly weakened interfaces on the overall elastic properties of composite-materials. Mech. Mater. 1993, 14, 269–281. [Google Scholar] [CrossRef]
- Shariyat, M. A generalized high-order global-local plate theory for nonlinear bending and buckling analyses of imperfect sandwich plates subjected to thermo-mechanical loads. Compos. Struct. 2010, 92, 130–143. [Google Scholar] [CrossRef]
- Chen, W.Q.; Cai, J.B.; Ye, G.R.; Wang, Y.F. Exact three-dimensional solutions of laminated orthotropic piezoelectric rectangular plates featuring interlaminar bonding imperfections modeled by a general spring layer. Int. J. Solids Struct. 2004, 41, 5247–5263. [Google Scholar] [CrossRef]
- Bellman, R.; Kashef, B.G.; Casti, J. Differential quadrature: A technique for the rapid solution of nonlinear partial differential equations. J. Comput. Phys. 1972, 10, 40–52. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature: A powerful new technique for analysis of composite structures. Compos. Struct. 1997, 39, 179–189. [Google Scholar] [CrossRef]
- Chen, W.Q.; Lv, C.F.; Bian, Z.G. Free vibration analysis of generally laminated beams via state-space-based differential quadrature. Compos. Struct. 2004, 63, 417–425. [Google Scholar] [CrossRef]
- Lü, C.F.; Chen, W.Q.; Shao, J.W. Semi-analytical three-dimensional elasticity solutions for generally laminated composite plates. Eur. J. Mech. A/Solids 2008, 27, 899–917. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Chen, W.Q.; Lü, C.F. Semi-analytical solution for orthotropic piezoelectric laminates in cylindrical bending with interfacial imperfections. Compos. Struct. 2010, 92, 1009–1018. [Google Scholar] [CrossRef]
- Lü, C.F.; Lee, Y.Y.; Lim, C.W.; Chen, W.Q. Free vibration of long-span continuous rectangular Kirchhoff plates with internal rigid line supports. J. Sound Vib. 2006, 297, 351–364. [Google Scholar] [CrossRef]
- Agiasofitou, E.; Lazar, M. On the Constitutive Modelling of Piezoelectric Quasicrystals. Crystals 2023, 13, 1652. [Google Scholar] [CrossRef]
- Bak, P. Phenomenological theory of icosahedral incommensurate (quasiperiodic) order in Mn-Al alloys. Phys. Rev. Lett. 1985, 54, 1517–1519. [Google Scholar] [CrossRef]
- Bak, P. Symmetry, stability, and elastic properties of icosahedral incommensurate crystals. Phys. Rev. B 1985, 32, 5764–5772. [Google Scholar] [CrossRef]
- Lubensky, T.; Ramaswamy, S.; Toner, J. Hydrodynamics of icosahedral quasicrystals. Phys. Rev. B 1985, 32, 7444. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.H.; Yang, W.G.; Hu, C.Z.; Wang, R.H. Generalized elasticity theory of quasicrystals. Phys. Rev. B Condens. Matter 1993, 48, 7003–7010. [Google Scholar] [CrossRef] [PubMed]
- Agiasofitou, E.; Lazar, M. On the equations of motion of dislocations in quasicrystals. Mech. Res. Commun. 2014, 57, 27–33. [Google Scholar] [CrossRef]
- Liu, C.; Feng, X.; Li, Y.; Zhang, L.L.; Gao, Y. Static solution of two-dimensional decagonal piezoelectric quasicrystal laminates with mixed boundary conditions. Mech. Adv. Mater. Struct. 2022, 1–17. [Google Scholar] [CrossRef]




| C11 | C12 | C13 | C33 | C44 | K1 | K2 | K4 | |
| QC1 | 234.33 | 57.41 | 66.63 | 232.22 | 70.19 | 122 | 24 | 12 |
| QC2 | 166 | 77 | 78 | 162 | 43 | 0 | 0 | 0 |
| e15 | e31 | e33 | ρ | R1 | ||||
| QC1 | 5.8 | −2.2 | 9.3 | 22.4 | 22.4 | 25.2 | 4186 | 8.846 |
| QC2 | 11.6 | −4.4 | 18.6 | 11.2 | 11.2 | 12.6 | 5800 | 0 |
| δ* = 0 | δ* = 2.5 | δ* = 5 | δ* = 7.5 | δ* = 10 | |
|---|---|---|---|---|---|
| η = −0.5 | 1.3510 | 0.8549 | 0.7392 | 0.6865 | 0.6560 |
| η = −0.25 | 1.3563 | 0.8564 | 0.7408 | 0.6883 | 0.6580 |
| η = 0 | 1.3616 | 0.8580 | 0.7425 | 0.6902 | 0.6599 |
| η = 0.25 | 1.3670 | 0.8596 | 0.7442 | 0.6920 | 0.6619 |
| η = 0.5 | 1.3723 | 0.8612 | 0.7460 | 0.6940 | 0.6639 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, C.; Zhang, L.; Pan, E.; Gao, Y. Mechanical Analysis of Functionally Graded Multilayered Two-Dimensional Decagonal Piezoelectric Quasicrystal Laminates with Imperfect Interfaces. Crystals 2024, 14, 170. https://doi.org/10.3390/cryst14020170
Wang Y, Liu C, Zhang L, Pan E, Gao Y. Mechanical Analysis of Functionally Graded Multilayered Two-Dimensional Decagonal Piezoelectric Quasicrystal Laminates with Imperfect Interfaces. Crystals. 2024; 14(2):170. https://doi.org/10.3390/cryst14020170
Chicago/Turabian StyleWang, Yuxuan, Chao Liu, Liangliang Zhang, Ernian Pan, and Yang Gao. 2024. "Mechanical Analysis of Functionally Graded Multilayered Two-Dimensional Decagonal Piezoelectric Quasicrystal Laminates with Imperfect Interfaces" Crystals 14, no. 2: 170. https://doi.org/10.3390/cryst14020170
APA StyleWang, Y., Liu, C., Zhang, L., Pan, E., & Gao, Y. (2024). Mechanical Analysis of Functionally Graded Multilayered Two-Dimensional Decagonal Piezoelectric Quasicrystal Laminates with Imperfect Interfaces. Crystals, 14(2), 170. https://doi.org/10.3390/cryst14020170







