Size and Temperature Effects on Band Gap Analysis of a Defective Phononic Crystal Beam

Abstract

In this paper, a new defective phononic crystal (PC) microbeam model in a thermal environment is developed with the application of modified couple stress theory (MCST). By using Hamilton’s principle, the wave equation and complete boundary conditions of a heated Bernoulli–Euler microbeam are obtained. The band structures of the perfect and defective heated PC microbeams are solved by employing the transfer matrix method and supercell technology. The accuracy of the new model is validated using the finite element model, and the parametric analysis is conducted to examine the influences of size and temperature effects, as well as defect segment length, on the band structures of current microbeams. The results indicate that the size effect induces microstructure hardening, while the increase in temperature has a softening impact, decreasing the band gap frequencies. The inclusion of defect cells leads to the localization of elastic waves. These findings have significant implications for the design of microdevices, including applications in micro-energy harvesters, energy absorbers, and micro-electro-mechanical systems (MEMS).

1. Introduction

Phononic crystal (PC) [1,2,3,4] is an artificial composite structure characterized by periodic variations in material parameters or geometric shapes. One significant attribute of PC is the ability to create band gaps in the propagation of elastic waves, which means that elastic waves in certain or all directions within a specified frequency range cannot freely propagate in the structure [5,6,7,8]. If the periodicity of PC is disrupted, one or more dispersion curves, referred to as defect bands, will appear within that gap [9,10,11,12]. Consequently, elastic waves with defect frequencies are localized at these defects, which means that the vibration energy concentrates at specific locations. Although the presence of defect bands does not entirely prevent the propagation of elastic waves within the PC, it allows for the concentration and harvesting of vibrational energy at specific locations. By employing the numerical method, Sigalas [11] revealed for the first time the generation mechanism of defect bands in two-dimensional PCs with geometric defects. Li et al. [13] introduced material defects by replacing materials at different positions of the PC and studied the impact of material properties on the waveguiding and acoustic confinement of the defect PC plate. Yao et al. [14] investigated the impacts of defect configurations, encompassing geometric size and filling fraction, on defect bands within PC plates. Jo et al. [15] discussed the principles of defect band formation and splitting based on PC models with single or double defects.

As the engineering environment grows increasingly complex, traditional PCs face challenges in adapting to changes in external conditions and autonomously adjusting the bandgap frequency and bandwidth post-manufacturing. Currently, researchers have developed various PC models that control the band gap through multi-physics coupling, incorporating mechanisms such as electro-elastic coupling [16,17,18], magneto-elastic coupling [19], and thermo-elastic coupling [20]. Likewise, the defect bands can be actively regulated by controlling the magnetic field [21,22] or electric field [23]. Typically, the environment temperature can significantly influence the performance of the device [24,25]. Temperature variations not only alter the physical properties of materials but also impact the structural stress state through thermal effects, consequently influencing the dynamic behavior of PC. Hu et al. [26] numerically studied the influence of temperature changes on the defect state of two-dimensional PC. Geng et al. investigated the band structure and energy harvesting behavior of PC Timoshenko beams with single [27] or double [28] defects under thermal load.

With the advancement of manufacturing technology, devices are progressively moving towards micronization. However, numerous static [29,30,31,32] and dynamic experiments [33,34] have demonstrated that the prediction of the mechanical behavior of microstructures based on classical continuum mechanics theory significantly deviates from experimental results. The size effect induces distinct mechanical properties in microstructures compared to macrostructures. Currently, many high-order theories are proposed to describe the size effect [35,36,37,38,39,40,41,42,43,44], such as the couple stress theory [45], strain gradient theory [46], non-local elasticity theory [47], surface elasticity theory [48], and reformulated strain gradient elasticity theory [49,50,51]. Utilizing the couple stress theory, Yang et al. established the modified couple stress theory (MCST), which specifically accounts for the symmetric curvature tensor with one additional material parameter for isotropic material. Based on the simplified non-classical theory, the mechanical behaviors of numerous microstructures have been investigated [52,53,54]. However, there is currently no research on one-dimensional defective PC micromodels with temperature effects based on non-classical theory. This paper fills this gap.

This paper studies the band gap characteristics of defective PC microbeams incorporating temperature effects. In Section 2, the wave equation and boundary conditions are obtained based on the MCST. In Section 3, the dispersion curves of perfect and defective heated PC microbeams are solved by using the transfer matrix method (TMM) and supercell technology. In Section 4, the accuracy of the current model is verified with the help of the finite element method. The influence of size effect, thermal effect, and defect segment length on the band gap of the current and classic models is discussed. The mode shapes of the defective heated PC microbeam at the defect frequency are also exhibited to discuss the feasibility of the structure for energy harvesting. The conclusion is given in Section 5.

2. Model and Formulation

As depicted in Figure 1, an Euler microbeam subjected to axial thermal load F_T with length L, height h, and width b in the Cartesian coordinate system is considered. Because of the temperature variation and boundary conditions, an axial load is generated at both ends of the beam.

According to the Bernoulli–Euler beam theory, the displacements are given as follows [39,55]:

$$u_1=-\frac{\partial w\left(x, t\right)}{\partial z}, u_2=0, u_3=w\left(x, t\right).$$

(1)

where u₁, u₂, and u₃ are the displacements of a point (x, y, z) in the microbeam at time t, respectively. And w denotes the deflection.

Based on the MCST [56,57], the components of the strain and symmetric curvature tensors are defined as

$$\begin{array}{l}{\epsilon }_{ij}=\frac{1}{2}\left(u_{i,j}+u_{j,i}\right), \\ {\chi }_{ij}=\frac{1}{4}\left(e_{ipq}{u}_{q,pj}+e_{jpq}{u}_{q,pi}\right),\end{array}$$

(2)

where e_ijk represents the Levi-Civita symbol; u_i,j is the derivative of u_i with respect to j; u_q,pj is the second derivative of u_q with respect to p and j; and i, j, p, q = x − z. ε_ij and χ_ij are both second-order tensors.

Substituting Equation (1) into Equation (2) yields

$${\epsilon }_{xx}=-z\frac{{\partial }^{2}w}{\partial x^2}, {\chi }_{xy}=-\frac{1}{2}\frac{{\partial }^{2}w}{\partial x^2}.$$

(3)

The constitutive relations of the heated microbeam composed of isotropic material are written as

$$\begin{array}{l}{\sigma }_{ij}=\lambda {\epsilon }_{kk}{\delta }_{ij}+2\mu {\epsilon }_{ij}-\alpha \Delta T, \\ m_{ij}=2l^2\mu {\chi }_{ij}.\end{array}$$

(4)

where σ_ij and m_ij are, respectively, the Cauchy stress and deviatoric couple stresses, λ and μ are the lame constants, δ_ij is the Kronecker symbol, α is the material thermal expansion coefficient, and ΔT represents the temperature rise of the environment. l is the material length scale parameter.

According to Equation (3), Equation (4) can be written as

$${\sigma }_{xx}=-\frac{E\left(1-v\right)}{\left(1+v\right)\left(1-2v\right)}z\frac{{\partial }^{2}w}{\partial x^2}-\alpha \Delta T, m_{xy}=-l^2\mu \frac{{\partial }^{2}w}{\partial x^2}.$$

(5)

where E is the Young’s modulus and v is the Poisson’s ratio.

It is worth noticing that the stress in Equation (5) includes Poisson’s effect on the microbeam. Because only the axial stress σ_xx is considered in the equilibrium of the microbeam, the strain component ε_xx is only related to σ_xx, so that (1 − v)/((1 + v)(1 − 2v)) is equal to 1 in Equation (5).

According to Equations (3) and (5), the strain energy is described by

$${\displaystyle {\int }_{T}U}\mathrm{d}t={\displaystyle {\int }_T{\displaystyle {\int }_{\mathsf{\Omega }}\left({\sigma }_{xx}{\epsilon }_{xx}+2m_{xy}{\chi }_{xy}\right)}\mathrm{d}V\mathrm{d}t,}$$

(6)

with Ω being the beam volume.

The kinetic energy of the microbeam can be written as [58]

$${\displaystyle {\int }_{T}K}\mathrm{d}t=\frac{1}{2}{\displaystyle {\int }_T{\displaystyle {\int }_{\mathsf{\Omega }}\rho \left(\frac{\partial u_i}{\partial t}\frac{\partial u_i}{\partial t}\right)\mathrm{d}V\mathrm{d}t,}}$$

(7)

where ρ denotes the mass density.

The work carried out by the thermal load of the microbeam without any other external force is given as follows

$${\displaystyle {\int }_{T}W}\mathrm{d}t=\frac{1}{2}{\displaystyle {\int }_T{\displaystyle {\int }_L{F}_T{\left(\frac{\partial w}{\partial x}\right)}^2\mathrm{d}x\mathrm{d}t.}}$$

(8)

where F_T is the axial load produced by temperature rise.

With the application of Hamilton’s principle [58], the relationship of the first variation of the strain energy, kinetic energy, and external work must meet the following balance requirement

$$\delta {\displaystyle {\int }_T\left[K-\left(U-W\right)\right]}\mathrm{d}t=0.$$

(9)

And the first variation of strain and kinetic energy, and virtual work are expressed as

$$\begin{array}{l}\delta {\displaystyle {\int }_{T}U\mathrm{d}t}={{\displaystyle {\int }_T{M}_{xx}\left(-\frac{\partial w}{\partial x}\right)|}}_0^L\mathrm{d}t+{{\displaystyle {\int }_T\frac{\partial M_{xx}}{\partial x}\delta w|}}_0^L\mathrm{d}t-{\displaystyle {\int }_T{\displaystyle {\int }_L\frac{{\partial }^2{M}_{xx}}{\partial x^2}\delta w\mathrm{d}x\mathrm{d}t}}\\ \hfill +{{\displaystyle {\int }_T\frac{\partial Y_{xy}}{\partial x}\delta w|}}_0^L\mathrm{d}t-{{\displaystyle {\int }_T{Y}_{xy}\frac{\partial w}{\partial x}|}}_0^L\mathrm{d}t-{\displaystyle {\int }_T{\displaystyle {\int }_L\frac{{\partial }^2{Y}_{xy}}{\partial x^2}\delta w\mathrm{d}x\mathrm{d}t,}}\hfill \end{array}$$

(10)

$$\delta {\displaystyle {\int }_{T}K\mathrm{d}t}=-{\displaystyle {\int }_T{\displaystyle {\int }_L\left(\rho A\frac{{\partial }^{2}w}{\partial t^2}-\rho I\frac{{\partial }^{4}w}{\partial x^2\partial t^2}\right)}\delta w\mathrm{d}x\mathrm{d}t,}$$

(11)

$$\delta {\displaystyle {\int }_{T}W}\mathrm{d}t=-{\displaystyle {\int }_T{\displaystyle {\int }_L{F}_T\frac{{\partial }^{2}w}{\partial x^2}\delta w\mathrm{d}x\mathrm{d}t+{\displaystyle {\int }_T{F}_T}{\frac{\partial w}{\partial x}\delta w|}_0^L\mathrm{d}t,}}$$

(12)

where

$$M_{xx}={\displaystyle {\int }_{A}z{\sigma }_{xx}\mathrm{d}A=-EI}\frac{{\partial }^{2}w}{\partial x^2}, Y_{xy}={\displaystyle {\int }_A{m}_{xy}\mathrm{d}A=-GA{l}^2}\frac{{\partial }^{2}w}{\partial x^2}.$$

(13)

And A = bh is the section area, and I = bh³/12 is the inertia moment.

Substituting Equations (10)–(12) into Equation (9), applying the fundamental lemma of the variation calculus, the governing equation is obtained as

$$-\left(EI+l^{2}GA\right)\frac{{\partial }^{4}w}{\partial x^4}+F_T\frac{{\partial }^{2}w}{\partial x^2}=\rho A\frac{{\partial }^{2}w}{\partial t^2}-\rho I\frac{{\partial }^{4}w}{\partial x^2\partial t^2}.$$

(14)

And the boundary conditions are expressed as

$$-\left(EI+l^{2}GA\right)\frac{{\partial }^{3}w}{\partial x^3}+F_T\frac{\partial w}{\partial x}=0 \mathrm{or} w=\overline{w} \mathrm{at} x=0 \mathrm{and} x=L,$$

(15)

$$\left(EI+l^{2}GA\right)\frac{{\partial }^{2}w}{\partial x^2}=0 \mathrm{or} \frac{\partial w}{\partial x}=\overline{\frac{\partial w}{\partial x}} \mathrm{at} x=0 \mathrm{and} x=L.$$

(16)

When l = 0, Equations (14)–(16) will degenerate into the governing equation and boundary conditions of a classical model without the couple stress effect.

3. Solution Methodology for Band Gap

Consider a PC microbeam as shown in Figure 2, which is composed of serval unit cells consisting of two different segments. The lengths of segments Ⅰ and II are a₁ and a₂, respectively. The lattice constant a of a unit cell is a₁ + a₂.

For one unit cell of the microbeam in a thermal environment, the length variation caused by ΔT can be given by

$$\Delta x_T=\left({\alpha }_1{a}_1+{\alpha }_2{a}_2\right)\Delta T,$$

(17)

where α₁ and α₂ are the thermal expansion coefficients of segments Ⅰ and II, respectively. And the length variation resulting from axial thermal load F_T is expressed as

$$\Delta x_F=-\left(\frac{F_T{a}_1}{E_1{A}_1}+\frac{F_T{a}_2}{E_2{A}_2}\right).$$

(18)

Due to the periodic boundary conditions of the two ends of a unit cell, adjacent unit cells constrain the axial expansion deformation. Therefore, the sum of the length variations caused by both ΔT and F_T is 0, and then the axial thermal load F_T can be expressed as

$$F_T=-\left(\frac{{\alpha }_1{a}_1+{\alpha }_2{a}_2}{E_2{A}_2{a}_1+E_1{A}_1{a}_2}\right)E_1{E}_2{A}_1{A}_2\Delta T.$$

(19)

With the application of TMM, the dispersion relation of the current heated PC microbeam can be solved.

3.1. TMM for Perfect Heated PC Microbeam

In the case of steady-state vibration, the transverse displacement is written as

$$w_i\left(x,t\right)=W_i\left(x\right)e^{i\omega t},$$

(20)

where i is the unit cell number and i² = −1 is the imaginary unit.

Substituting Equation (20) into Equation (14), the motion equation can be rewritten as

$$W_i^{(\mathrm{IV})}-{\gamma }_i{W}_i^{″}-{\beta }_i{W}_i=0,$$

(21)

where

$${\gamma }_i=\frac{F_T-{\rho }_i{I}_i{\omega }^2}{E_i{I}_i+l_i^2{G}_i{A}_i}, {\beta }_i=\frac{{\rho }_i{A}_i{\omega }^2}{E_i{I}_i+l_i^2{G}_i{A}_i}.$$

(22)

The roots of the characteristic equation of Equation (21) can be obtained as

$${\lambda }_i^{\left(1\right)}=\sqrt{\sqrt{{\beta }_i+\frac{{\gamma }_i^2}{4}}-\frac{{\gamma }_i}{2}}, {\lambda }_i^{\left(2\right)}=\sqrt{\sqrt{{\beta }_i+\frac{{\gamma }_i^2}{4}}+\frac{{\gamma }_i}{2}}.$$

(23)

And then, the general solution of Equation (21) is expressed as

$$W_i\left(x\right)=A_i\cos \left({\lambda }_i^{\left(1\right)}x\right)+B_i\sin \left({\lambda }_i^{\left(1\right)}x\right)+C_i\cosh \left({\lambda }_i^{\left(2\right)}x\right)+D_i\sinh \left({\lambda }_i^{\left(2\right)}x\right).$$

(24)

According to the continuity requirements, it is expected that within each unit cell, the deflection, rotation angle, bending moment and shear force on the interface between the end of segment Ⅰ and the beginning of segment II should remain consistent. For the nth unit cell, the continuity conditions within the unit cell can be expressed as

$$\begin{array}{c}{\phi }_{n2}\left(0\right)={\phi }_{n1}\left(a_1\right),\\ {\phi }_{n2}^{\prime }\left(0\right)={\phi }_{n1}^{\prime }\left(a_1\right),\\ \left(E_2{I}_2-G_2{A}_2{l}_2^2\right){\phi }_{n2}^{″}\left(0\right)=\left(E_1{I}_1-G_1{A}_1{l}_1^2\right){\phi }_{n1}^{″}\left(a_1\right),\\ \left(E_2{I}_2-G_2{A}_2{l}_2^2\right){\phi }_{n2}^{‴}\left(0\right)=\left(E_1{I}_1-G_1{A}_1{l}_1^2\right){\phi }_{n1}^{‴}\left(a_1\right),\end{array}$$

(25)

which can be rewritten as a matrix form

$$K_2{\psi }_{n2}=H_1{\psi }_{n1}$$

(26)

where 1 and 2 represent segments Ⅰ and II, respectively, and

$${\psi }_{ni}={\left[A_{ni} B_{ni} C_{ni} D_{ni}\right]}^{\mathrm{T}}.$$

(27)

In the same way, the continuity conditions of the interface between the nth unit cell and the (n + 1)th unit cell can be written as

$$K_2{\psi }_{n2}=H_1{\psi }_{n1},$$

(28)

where

$$K_i=\left[\begin{array}{cccc}1& 0& 1& 0\\ 0& {\lambda }_i^{\left(1\right)}& 0& {\lambda }_i^{\left(2\right)}\\ -E_i{\left({\lambda }_i^{\left(1\right)}\right)}^2& 0& E_i{\left({\lambda }_i^{\left(2\right)}\right)}^2& 0\\ 0& -E_i{\left({\lambda }_i^{\left(1\right)}\right)}^3& 0& E_i{\left({\lambda }_i^{\left(2\right)}\right)}^3\end{array}\right],$$

(29)

$$\begin{array}{l}{H}_i=[\begin{array}{cc}\cos \left({\lambda }_i^{\left(1\right)}{a}_i\right)& \sin \left({\lambda }_i^{\left(1\right)}{a}_i\right)\\ -{\lambda }_i^{\left(1\right)}\sin \left({\lambda }_i^{\left(1\right)}{a}_i\right)& {\lambda }_i^{\left(1\right)}\cos \left({\lambda }_i^{\left(1\right)}{a}_i\right)\\ -\left(E_i{I}_i-G_i{A}_i{l}_i^2\right){\left({\lambda }_i^{\left(1\right)}\right)}^2\cos \left({\lambda }_i^{\left(1\right)}{a}_i\right)& -\left(E_i{I}_i-G_i{A}_i{l}_i^2\right){\left({\lambda }_i^{\left(1\right)}\right)}^2\sin \left({\lambda }_i^{\left(1\right)}{a}_i\right)\\ \left(E_i{I}_i-G_i{A}_i{l}_i^2\right){\left({\lambda }_i^{\left(1\right)}\right)}^3\sin \left({\lambda }_i^{\left(1\right)}{a}_i\right)& -\left(E_i{I}_i-G_i{A}_i{l}_i^2\right){\left({\lambda }_i^{\left(1\right)}\right)}^3\cos \left({\lambda }_i^{\left(1\right)}{a}_i\right)\end{array}\\ \hspace{1em}\hspace{1em}\begin{array}{cc}\cosh \left({\lambda }_i^{\left(2\right)}{a}_i\right)& \sinh \left({\lambda }_i^{\left(2\right)}{a}_i\right)\\ {\lambda }_i^{\left(2\right)}\sinh \left({\lambda }_i^{\left(1\right)}{a}_i\right)& {\lambda }_i^{\left(2\right)}\cosh \left({\lambda }_i^{\left(2\right)}{a}_i\right)\\ \left(E_i{I}_i-G_i{A}_i{l}_i^2\right){\left({\lambda }_i^{\left(2\right)}\right)}^2\cosh \left({\lambda }_i^{\left(2\right)}{a}_i\right)& \left(E_i{I}_i-G_i{A}_i{l}_i^2\right){\left({\lambda }_i^{\left(2\right)}\right)}^2\sinh \left({\lambda }_i^{\left(2\right)}{a}_i\right)\\ \left(E_i{I}_i-G_i{A}_i{l}_i^2\right){\left({\lambda }_i^{\left(1\right)}\right)}^3\sinh \left({\lambda }_i^{\left(2\right)}{a}_i\right)& \left(E_i{I}_i-G_i{A}_i{l}_i^2\right){\left({\lambda }_i^{\left(2\right)}\right)}^3\cosh \left({\lambda }_i^{\left(2\right)}{a}_i\right)\end{array}].\end{array}$$

(30)

Combining Equations (26) and (28), it can be written as

$${\psi }_{\left(n+1\right)1}=T_c{\psi }_{n1},$$

(31)

where T_c = $K_1^{-1}$ H₂$K_2^{-1}$ H₁ is the transfer matrix.

For the periodic structure, with the application of Bloch theorem, it is obtained as

$${\psi }_{\left(n+1\right)1}={\psi }_{n1}{e}^{\mathrm{i}ka},$$

(32)

where k is the Bloch wave number of the PC microbeam.

Substituting Equation (31) into Equation (32), the eigenvalue equation is expressed as

$$\left(T_c-e^{\mathrm{i}ka}\mathrm{I}\right){\psi }_{n1}=0,$$

(33)

In order for Equation (33) to have non-trivial solutions, it needs to satisfy

$$\left|T_c-\lambda \mathrm{I}\right|=0.$$

(34)

where I is a 4 × 4 unit element, and solving Equation (33) with a specified angular frequency yields four eigenvalues, corresponding to four wave numbers k, and then the dispersion relation of the perfect PC microbeam is obtained. For the case where the k values are all non-real numbers, the elastic wave of the corresponding frequency rapidly attenuates in the PC beam and cannot propagate. This frequency range is the band gap.

3.2. TMM for Defect Heated PC Microbeam

As shown in Figure 3, the periodicity of the perfect heated PC microbeam is destroyed by the introduction of a defect cell. For calculating the dispersion relation of the defect-heated PC microbeam, the supercell technique is applied.

Based on the transfer matrix derived in Section 3.1, the transfer matrix for the supercell which consists of serval unit cells is calculated by [27,59]

$$T_{sc}=T_{cm}{T}_{c\left(m-1\right)}\dots T_d\dots T_{c2}{T}_{c1.}$$

(35)

where T_ci and T_d represent the transfer matrices of the ith normal unit cell and the defect cell, respectively.

And for the supercell, the periodic conditions at both ends are expressed as

$${\psi }_{\left(n+1\right)1}={\psi }_{n1}{e}^{\mathrm{i}kL},$$

(36)

where L represents the supercell length.

Therefore, the eigenvalue equation of the supercell is written as

$$\left(T_{sc}-e^{\mathrm{i}kL}\mathrm{I}\right){\psi }_{n1}=0.$$

(37)

By solving Equation (37), the band structure of the defect-heated PC microbeam including the size effect and thermal effect can be obtained.

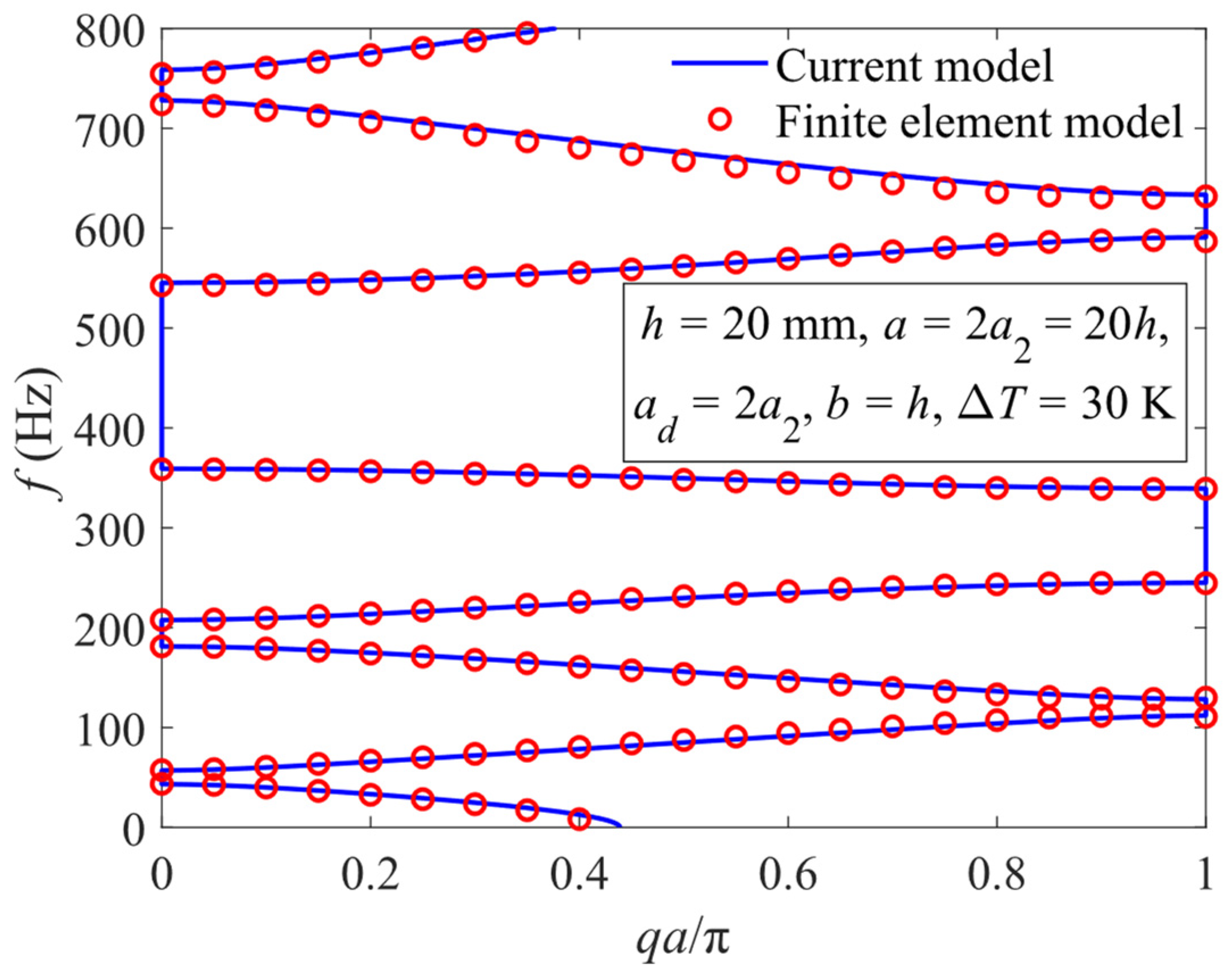
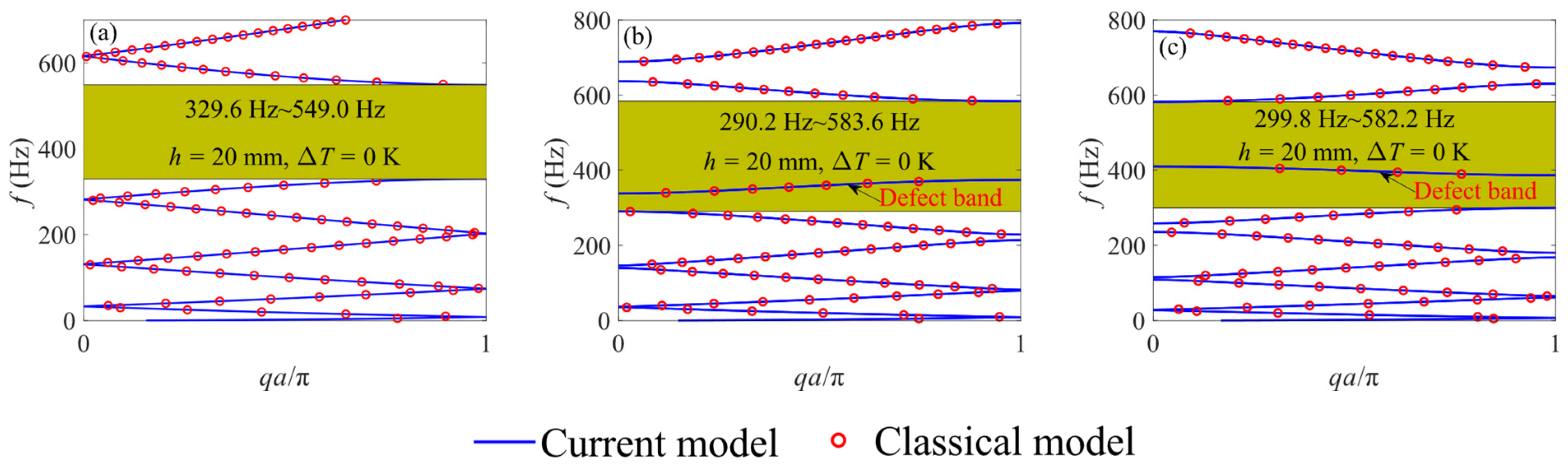
4. Band Gap Analysis

In Section 4, a parametric analysis of the band structure of the heated PC microbeam is performed, and the influence of the size and temperature effects on the band gap and defect band is discussed. The supercell model consists of six normal unit cells and one defect cell which is located at the center of the PC microbeam. For the purpose of obtaining wider band gaps and flatter defect bands to display the results more clearly, the material of segment I is selected to be B₄C, and segment II is made of aluminum. The material properties are listed in

Table 1. Material properties of B₄C [60,61] and aluminum [62].

Material	Young’s Modulus (GPa)	Poisson’s Ratio	Mass Density (kg/m3)	Thermal Expansion Coefficient (10−6/K)	Material Length Scale Parameter (μm)
B4C	460	0.17	2500	5.73	6.34
Aluminum	77.56	0.23	2730	23	6.58

. For a normal unit, a₁ = a₂ = 0.5a, a = 20h, and the beam cross-section is square with width b equal to height h.

To validate the accuracy of the current model, a finite element model of a defective heated PC microbeam is constructed using the thermal stress interface in COMSOL Multiphysics. As COMSOL Multiphysics lacks the capability to capture the size effect of microstructures, both the current model and the finite element model are at a macro scale. The beam height h is specified as 20 mm. The supercell contains seven unit cells, with a defective unit cell in the center and the others are normal unit cells. While the current model incorporates size effects, the finite element model does not account for the effect. Other material properties remain consistent with those in Table 1, and the temperature rise ΔT is set at 30 K.

It is evident from Figure 4 that the dispersion curves of the current model and the finite element model agree well, albeit with some discrepancies at higher frequencies attributed to the inherent high-order stability issue of TMM. Through comparison with the finite element model, the validity of the proposed model has been confirmed. Furthermore, the noticeable consistency in the results of the two defective PC macro-beams, as depicted in Figure 4, underscores that the size effect has a minimal impact on the band structure of the macrostructure.

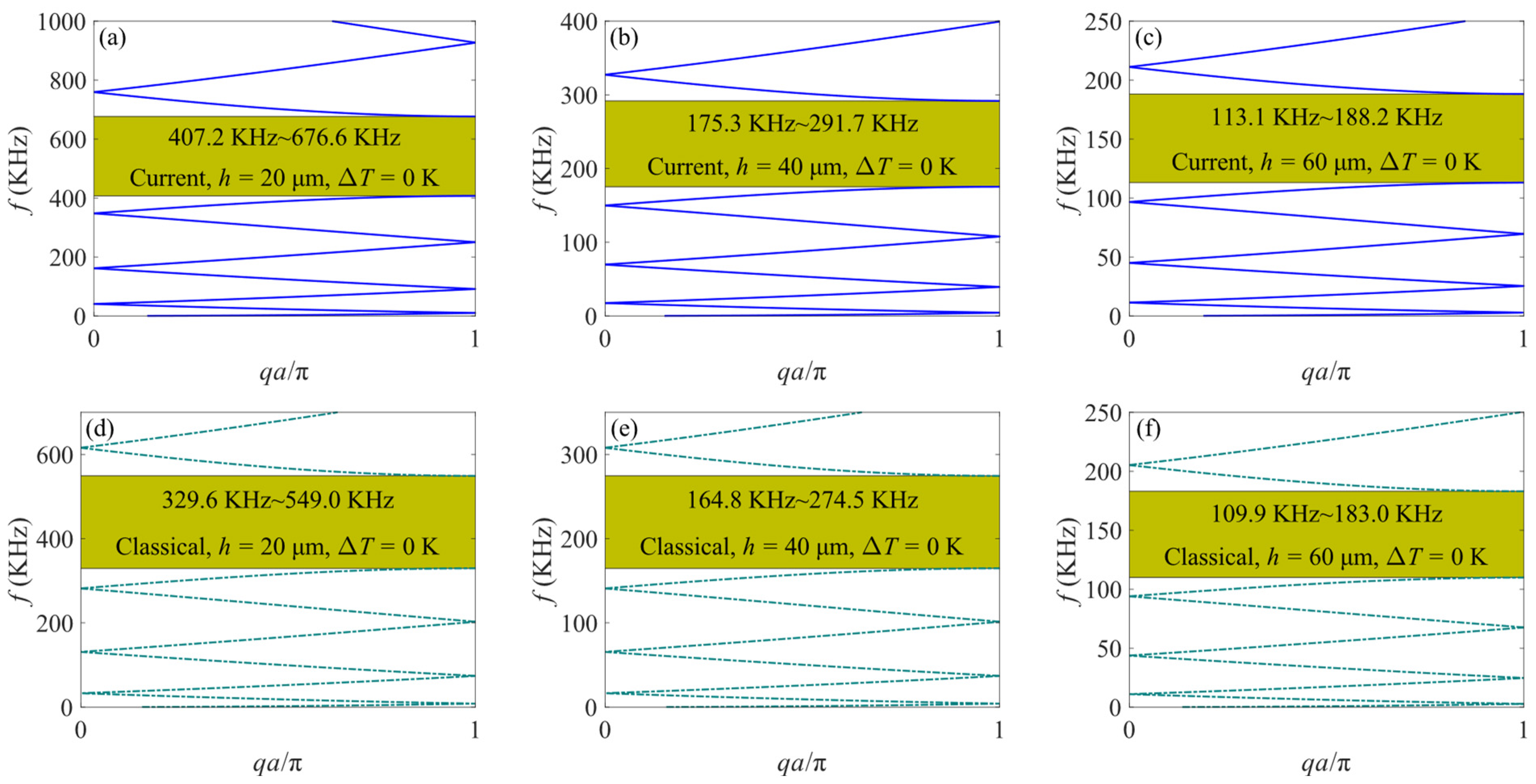
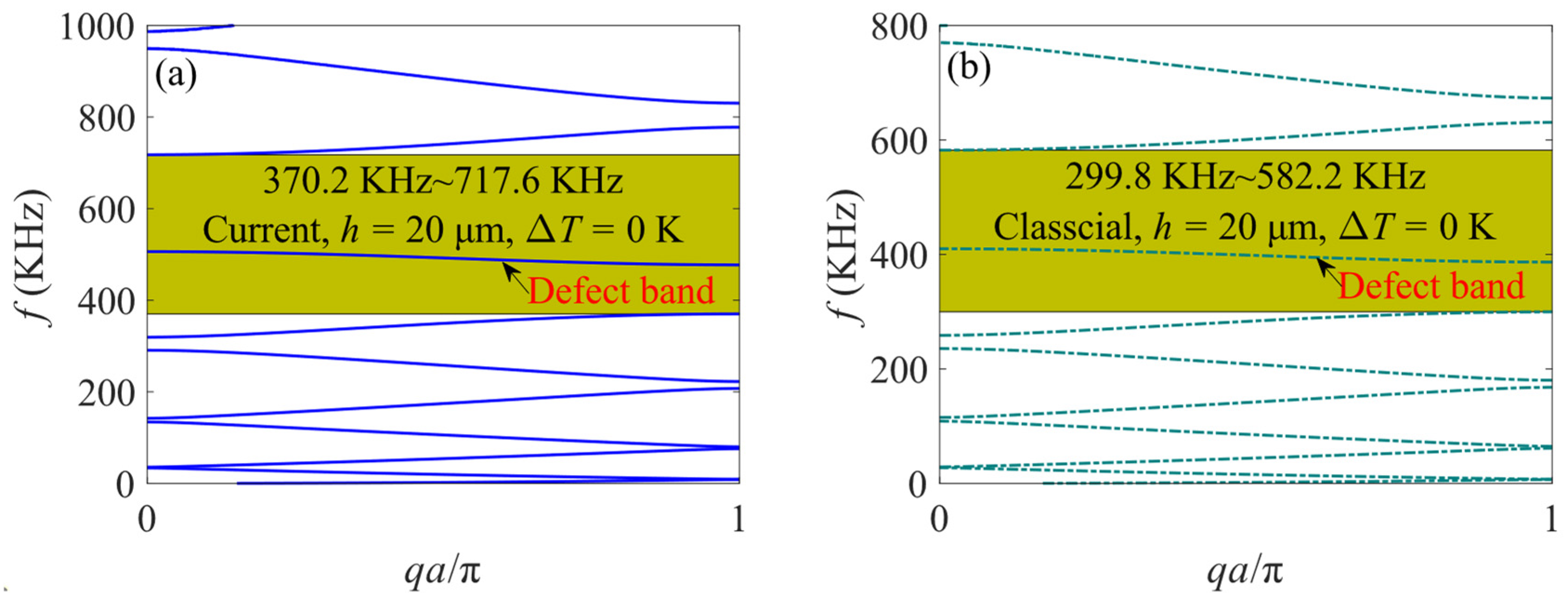
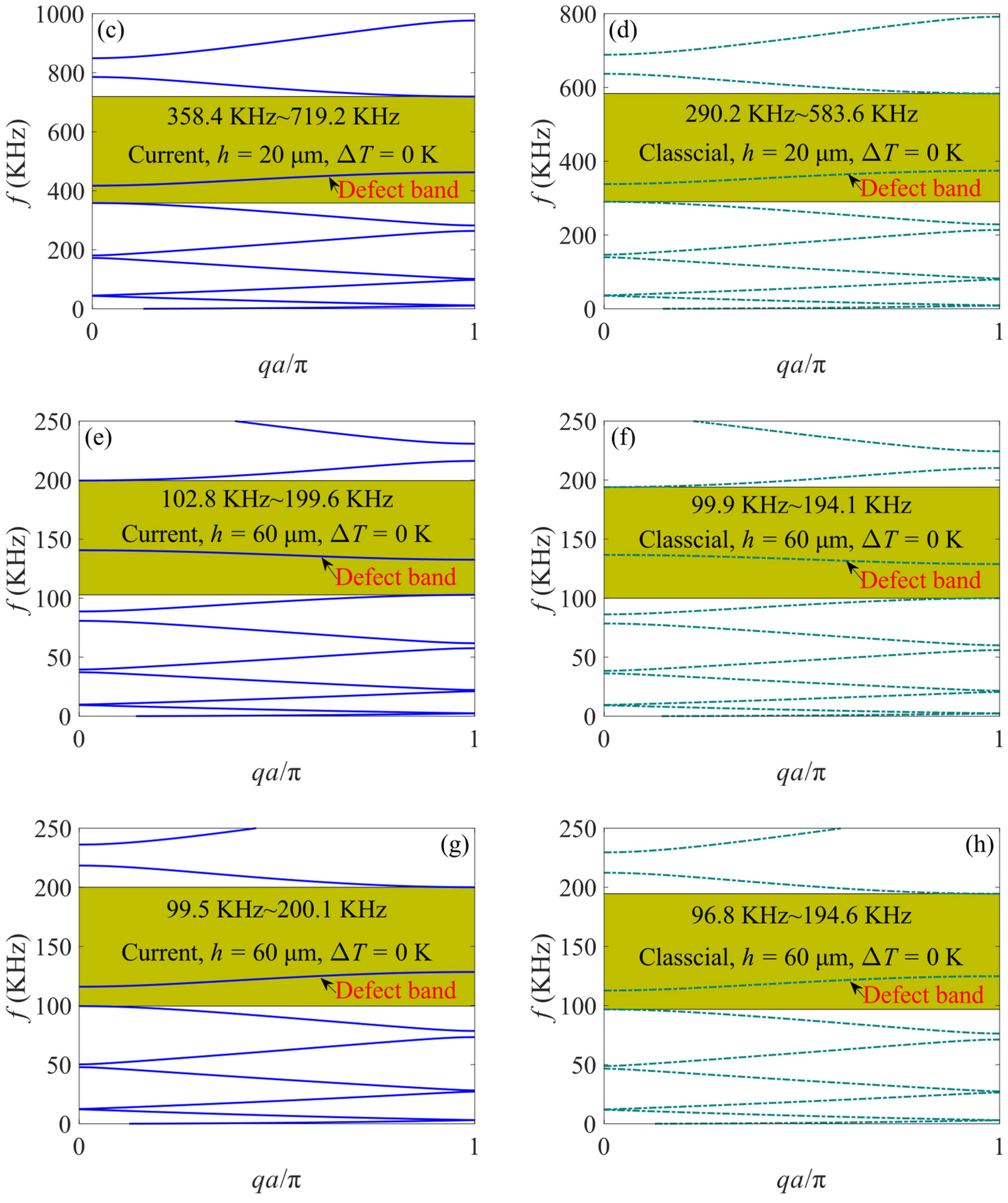
4.1. The Influence of Size Effect

For the purpose of studying the influence of size effect on the band structures of the perfect heated PC microbeam, Figure 5 illustrates the band structure of both the current and classical perfect PC microbeam without any temperature elevation.

From Figure 5, it is obvious that the band gaps appear in both the current and classical models due to the difference in material properties between segments I and II. And the frequencies of dispersion curves predicted by the current PC microbeam are higher than those of the classical one, which means that the size effect increases the stiffness of microstructures. In addition, for B₄C and aluminum adopted in this section, the size effect leads to an increase in the stiffness difference between the two materials, so that the bandwidths of the current model are larger than the classical model. With the increase in beam height, the frequencies of the dispersion curves predicted by the current model progressively converge with those of the classical model, and the disparity in band gaps also diminishes. This phenomenon indicates that the size effect induces a stiffening influence solely on PC beams with a microscopic scale while having almost no effect on the macrostructures.

Disrupting the periodicity of the PC microbeam leads to variations in the band structure. A defective cell can be generated in the perfect PC microbeam by changing the length of segment II in this section. Figure 6 displays the band structure of the defective PC microbeam with different beam heights and defect segment lengths in the case of ΔT = 0 K.

In Figure 6a,b, it can be seen that the band gap ranges of current and classical models are both broadened when the periodicity of the perfect PC microbeam is destroyed. For the case where a_d > a₂, the frequencies of the eighth dispersion curve decrease and appear alone in the band gap, which is called the defect band, while the ninth dispersion curve becomes the upper boundary of the band gap. Similarly, in Figure 6c,d, when a_d < a₂, the bandwidths of the current and classical models are also expanded, and a defect band appears within the band gap, which is the seventh dispersion curve with increasing frequencies, and the sixth dispersion curve becomes the lower boundary of the band gap. In addition, the band structures of the defective PC microbeams also open some narrow band gaps at low frequencies. By comparing Figure 6a–d with Figure 6e–h, it is found that for any length of a defective segment, the size effect affects the frequencies of the band gap and defect band of the defective PC microbeam. Furthermore, it is noted that the impact of the size effect becomes more pronounced as the size of the beam decreases, which aligns with the trend observed in Figure 5.

Figure 7 plots the band structures of the perfect PC beam and defective PC beam at the macroscale. It can be found that the dispersion curves of the classical and current models are almost completely consistent, which once again proves that the size effect has almost no impact on the dynamic response of the macrostructure.

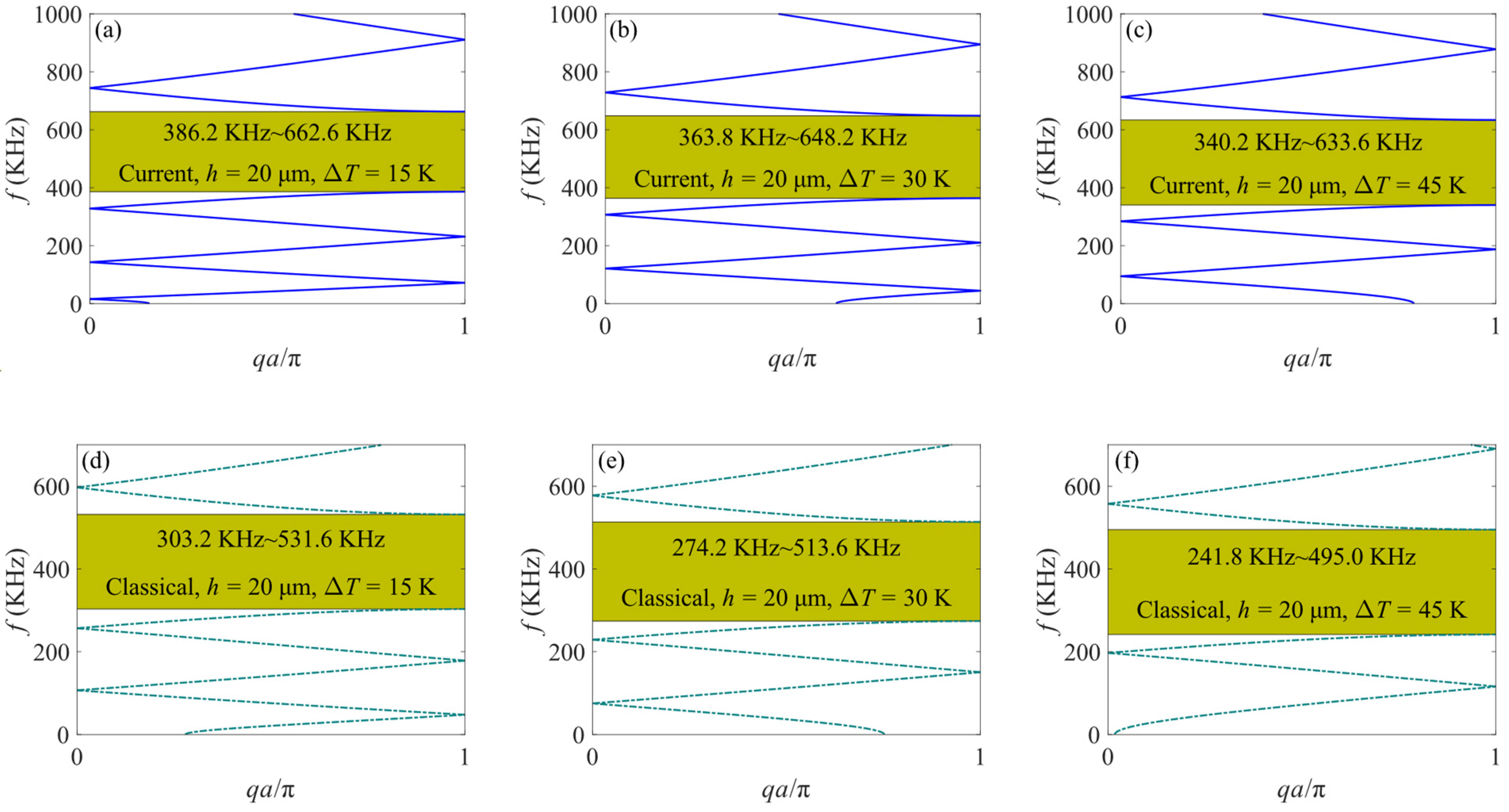
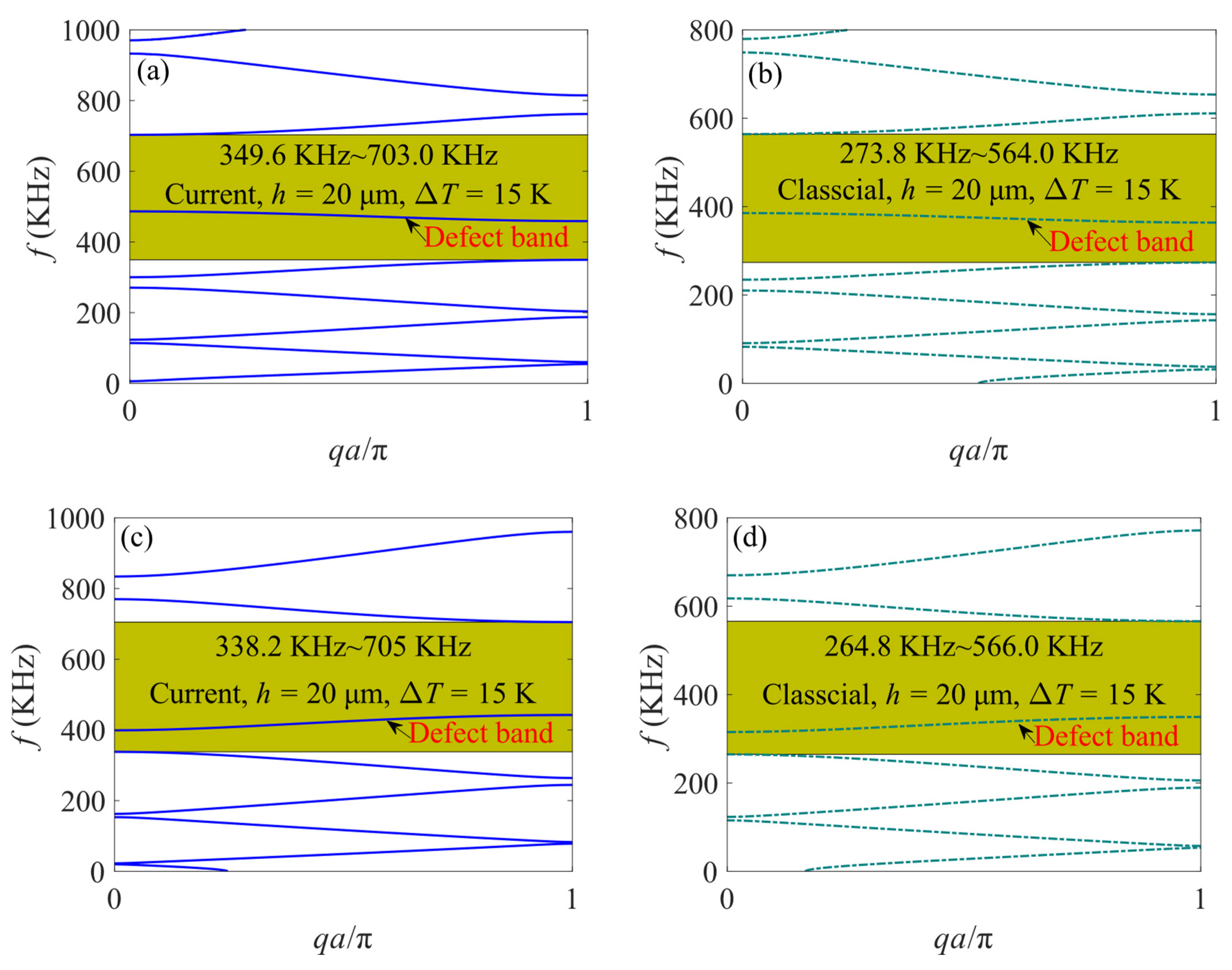
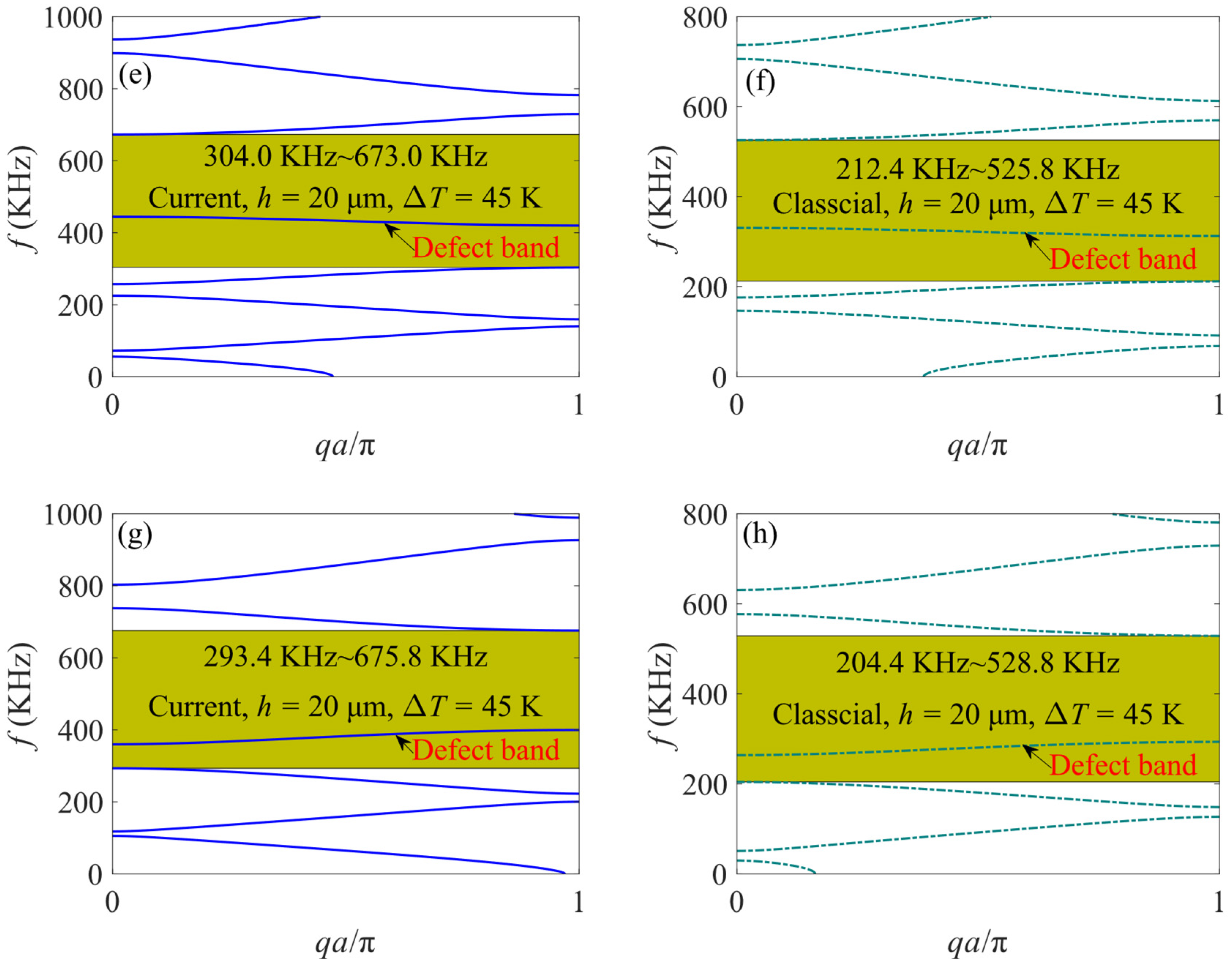
4.2. The Influence of Temperature Effect

The dispersion curves obtained from Equations (33) and (37) include the influence of temperature rise. In order to explore the impact of the thermal effect on the band gap of a perfect PC microbeam, Figure 8 exhibits the band structures of the perfect PC microbeam with various temperature rises.

Figure 8 reveals that with increasing temperature, the upper and lower frequency bounds of the band gap for both the current and classical models decrease. This phenomenon is attributed to the axial thermal force generated by the temperature rise, leading to the softening effect of the microbeam. Furthermore, elevated temperatures contribute to an expanded bandwidth in both the current and classical models. This is a consequence of the higher thermal expansion coefficient of aluminum compared to B₄C, so that under the same temperature rise conditions, the axial thermal force in aluminum with lower stiffness is greater, accentuating the material stiffness disparity. Consistent with the trend observed in Figure 5, the frequencies of dispersion curves predicted by the current microbeam model consistently surpass those of the classical model, which underscores that the size effect cannot be disregarded when calculating the band structure of microstructures.

To investigate the impact of temperature effects on the band structure of a heated defective supercell, Figure 9 illustrates the band structure of a heated defective PC microbeam with varying defect segment lengths under different temperature rise conditions. As observed in Figure 9, the introduction of the defective cell results in expanded bandwidths, and the length of the defect segment significantly influences the frequencies of both the band gap and the defect band. With increasing temperature, the frequency of the defect band undergoes a downward shift, aligning with the trend seen in the dispersion curve changes depicted in Figure 8. Furthermore, under arbitrary defect segment length and temperature rise conditions, there are obvious differences between the band structures of the current model and the classical model with the same conditions. This finding once again underscores the significance of the size effect in accurately predicting the mechanical response of microstructures.

When segment II, characterized by lower stiffness, undergoes elongation in the defective unit cell, as depicted in Figure 10a,c, the mode shape of the defective PC microbeam model at the frequency of the defect band exhibits an antisymmetric shape with the midpoint of segment II in the defect segment as the center. This results in the most pronounced bending at the two ends of the defect segment. And when the defect segment is shortened, as shown in Figure 10b,d, the mode shape of the defect PC microbeam becomes symmetrical, with the midpoint of the defective segment serving as the center. The curvature of the microbeam reaches its maximum at the midpoint of the defect segment. Figure 10 illustrates that the flexural wave energy is concentrated predominantly near the defect segment. For various defect modes, piezoelectric materials could be strategically attached at specific positions to capture and convert the vibrational energy into electrical energy. Moreover, through a comparison of Figure 10a,b and Figure 10c,d, it becomes apparent that temperature variations have almost no impact on the mode shape of the heated defective PC microbeam.

For the purpose of further analyzing the localization effect of the defective PC microbeam, the quantified method of energy localization can be found in [63]. The localization rate τ is defined by the following equation:

$$\tau (\%)=100\left|\frac{w_i}{w_{\max }}\right|$$

(38)

where w_i is the deflection of ith point on the centroidal axis, and w_max is the maximum deflection.

Since temperature variation has no effect on the mode shape of the current defective PC microbeam, Figure 11 only displays the phenomenon of displacement localization of the defective PC microbeam with different defect cell lengths under the condition of ΔT = 15 K. As shown in Figure 11, under different lengths of the segment II of defect cell, the localization rate reaches the maximum value near the defect cell. This phenomenon fully demonstrates that the defective PC microbeam has a localization effect and can achieve energy harvesting at a specific location.

5. Conclusions

This paper establishes a theoretical model for a heated defective PC microbeam considering both size and thermal effects based on the MCST. Utilizing TMM and supercell technology, the band structures of heated perfect and defective microbeams are solved. The accuracy of the presented model is verified by comparing the results with a finite element model developed by COMSOL Multiphysics. Using parametric analysis, the influence of size effect, defect segment length, and temperature rise on the band structures and mode shapes of the current and classical models is discussed. The prediction results show the following:

• Size effects significantly impact the band structure of the PC microbeam, leading to increased stiffness and higher band gap frequencies. However, the size effect is negligible on the macrostructure.
• The introduction of defect cells widens the band gap of the defective PC microbeam, revealing a smooth dispersion curve within the band gap known as the defect band.
• Temperature rises will cause thermal axial forces to appear at both ends of unit cells, leading to a decrease in band gaps and defect band frequencies for both current and classical models.
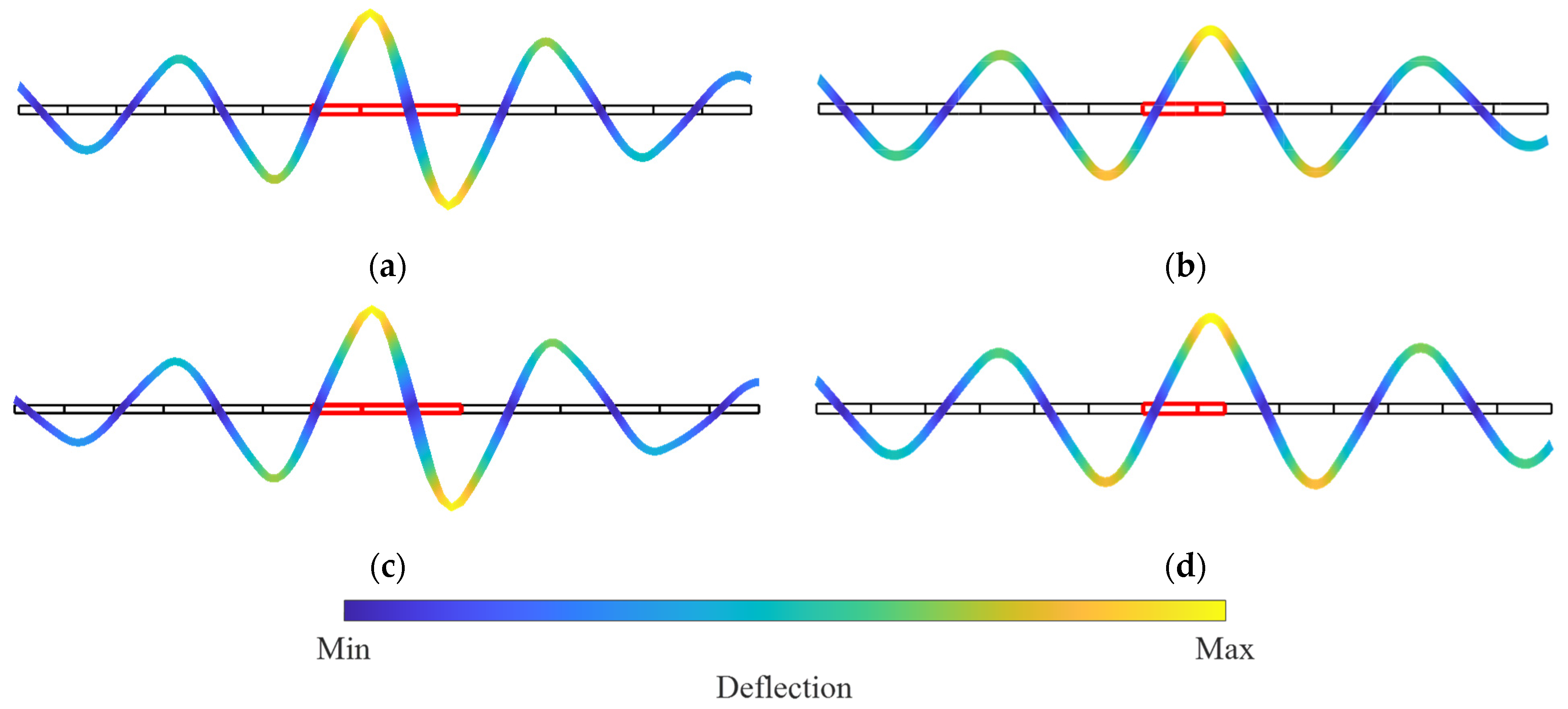
• Different defect modes result in a distinct mode shape of the defective PC microbeam at the frequency of the defect band. Elongation of the defect segment with lower stiffness produces an antisymmetric mode shape while shortening the defect segment corresponds to a symmetric mode shape. The mode shape of the heated defective PC microbeam remains largely unaffected by temperature.
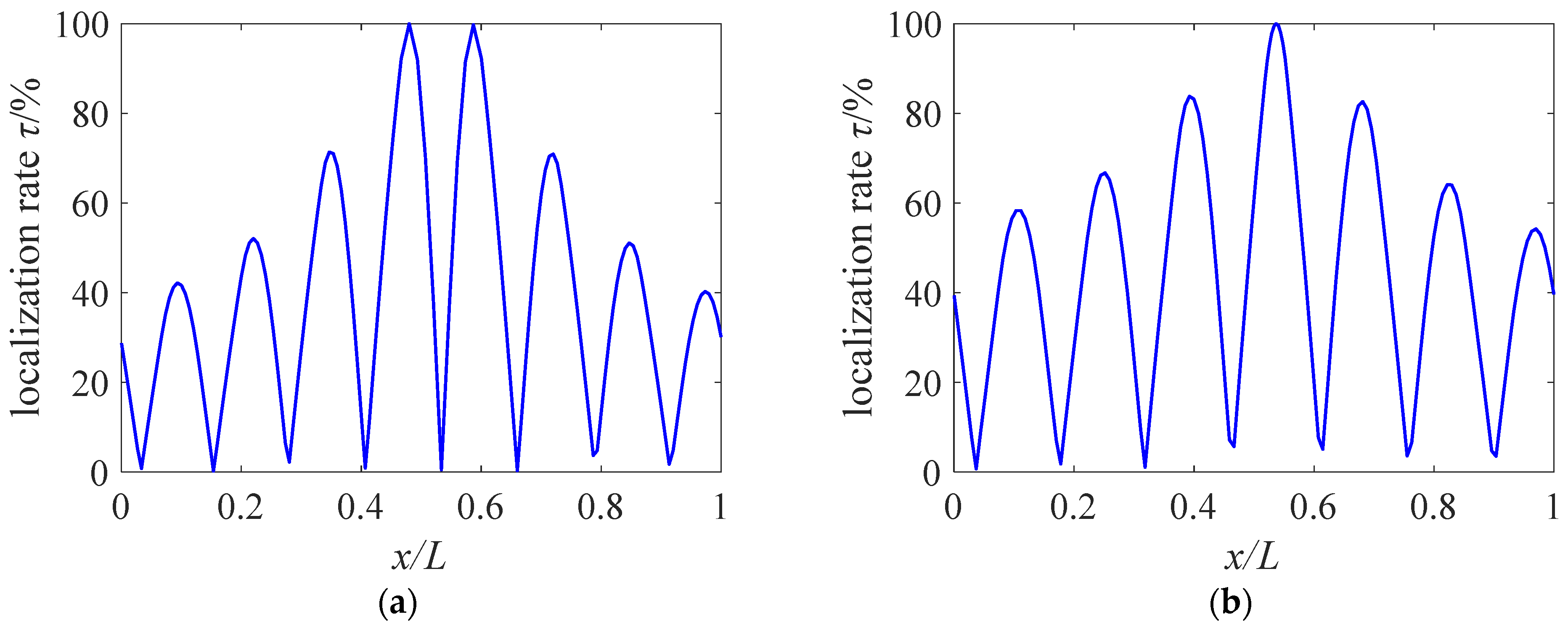
• The vibration energy will be concentrated near the defective unit cells, which is conducive to energy collection or absorption at specific locations.

The results presented in this paper establish a valuable theoretical foundation with potential implications for the design and engineering applications of various micro-devices, including energy harvesters, micro-sensors, and micro-electro-mechanical systems. The findings contribute to the broader field of micro-scale mechanics and may guide future advancements in the development and application of micro-scale technologies.