Self-Organization of Micro- and Nanosystems in the Form of Patterns
Abstract
1. Introduction
2. Materials and Methods
2.1. Nucleation Processes Under Near-Equilibrium Conditions and Simultaneous Action of an Active Medium
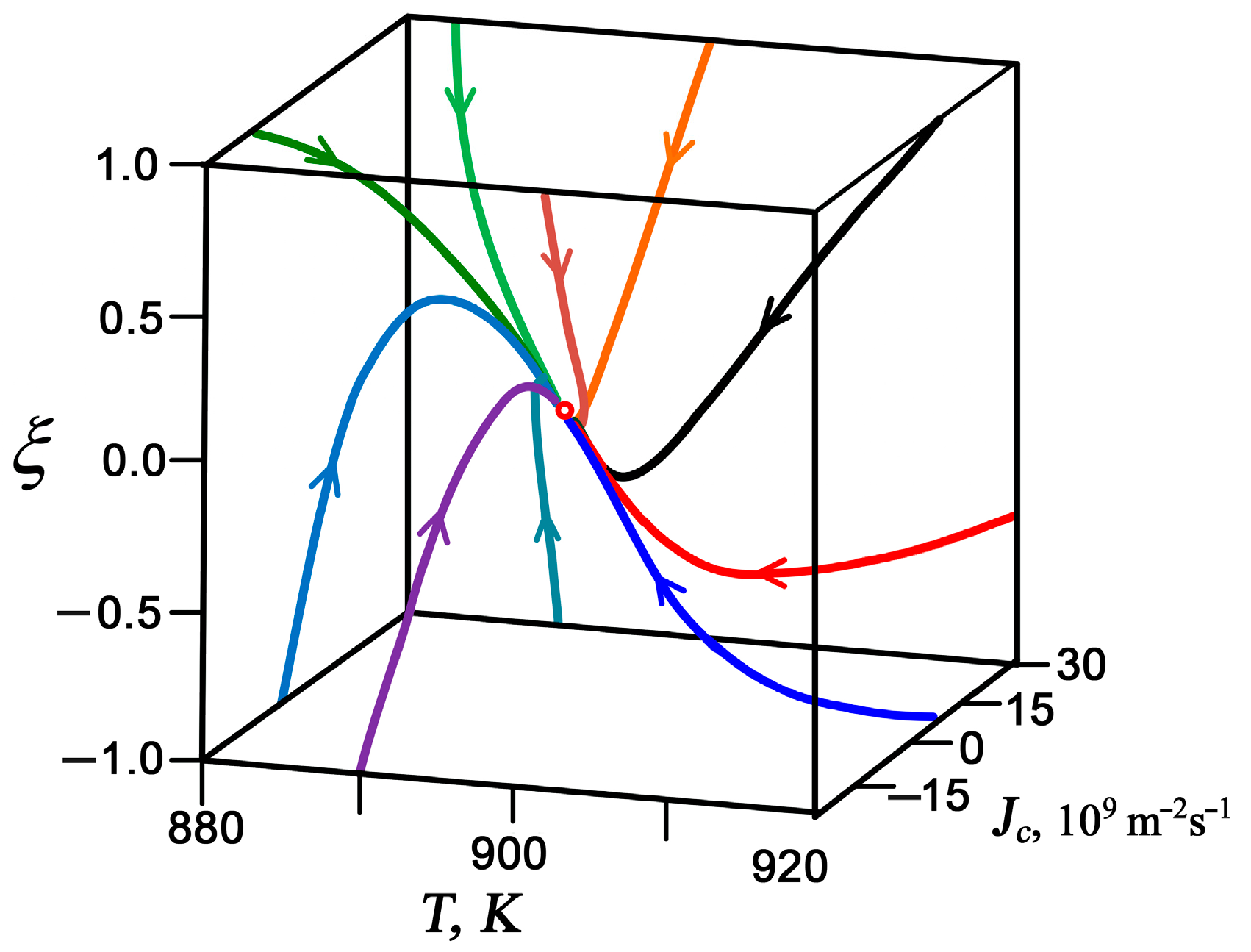
2.2. Criterion of Stationarity of Near-Equilibrium Condensation
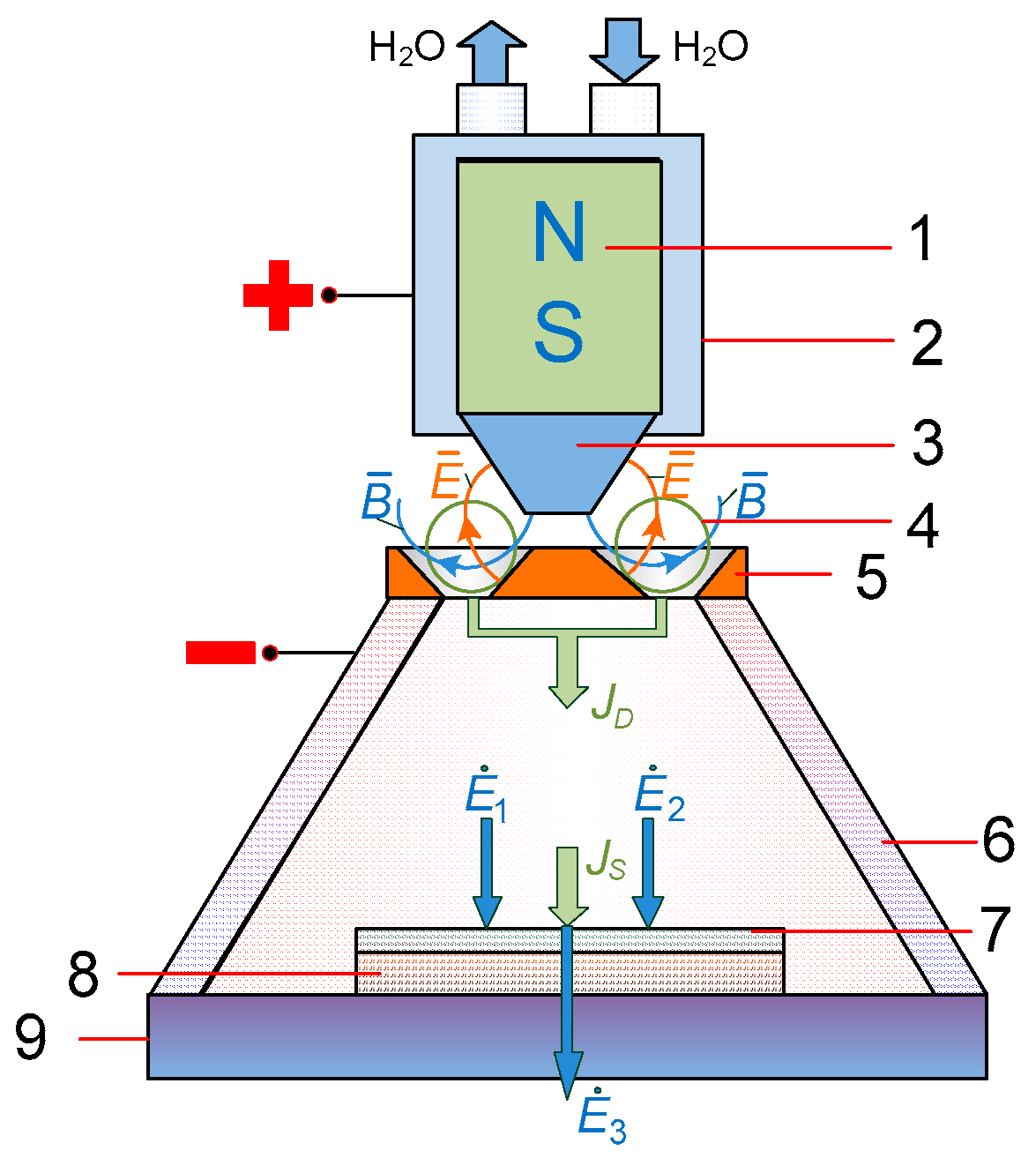
2.3. Experimental Setup
3. Results and Discussion
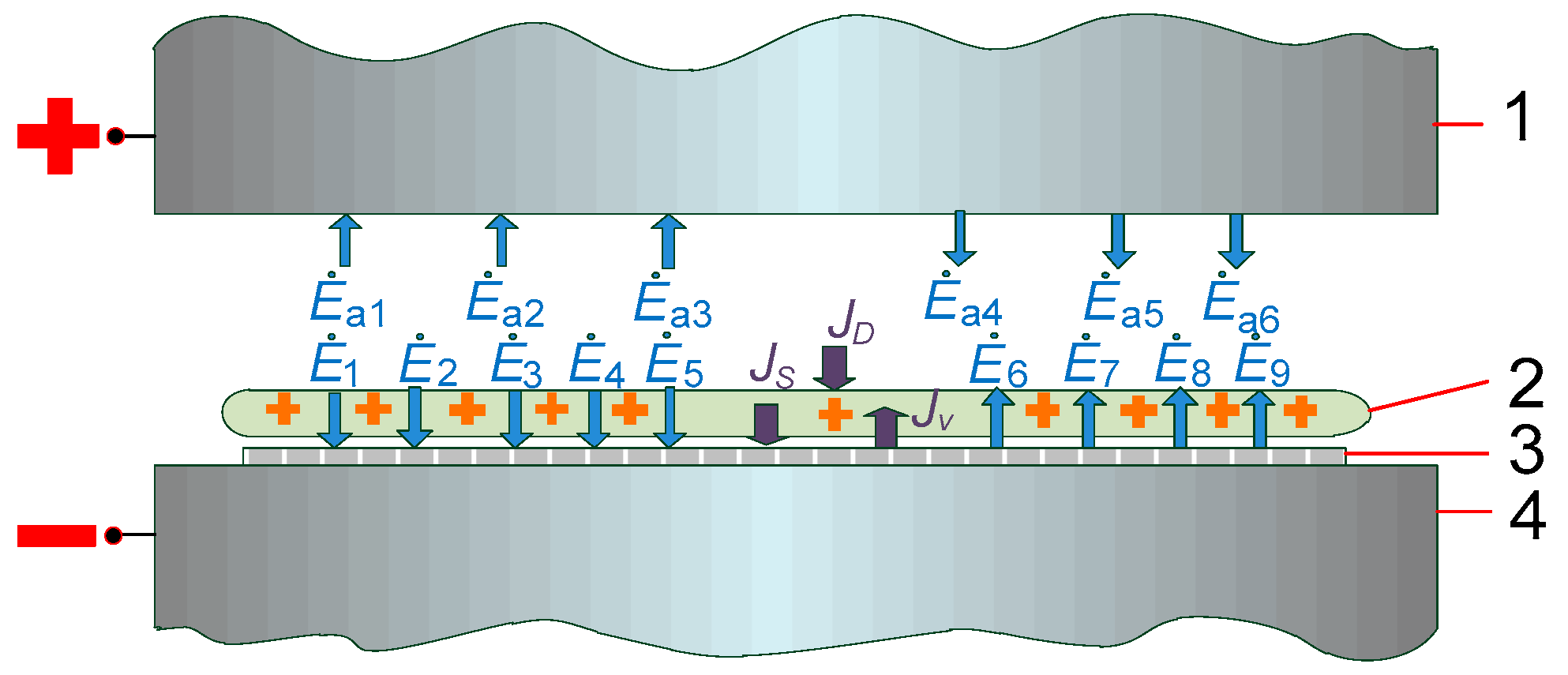
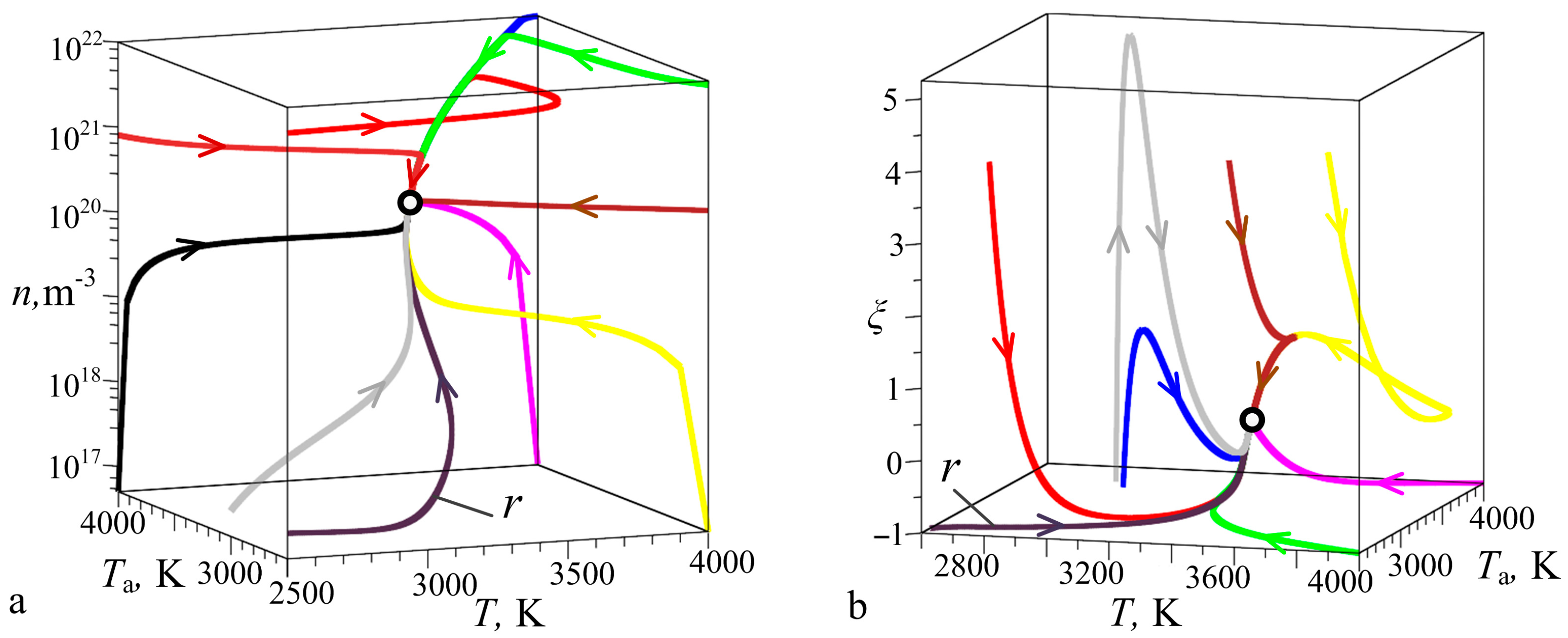
3.1. Interrelationships Between Local Growth Kinetics and Local Technological Parameters as a Basis for Pattern Self-Organization
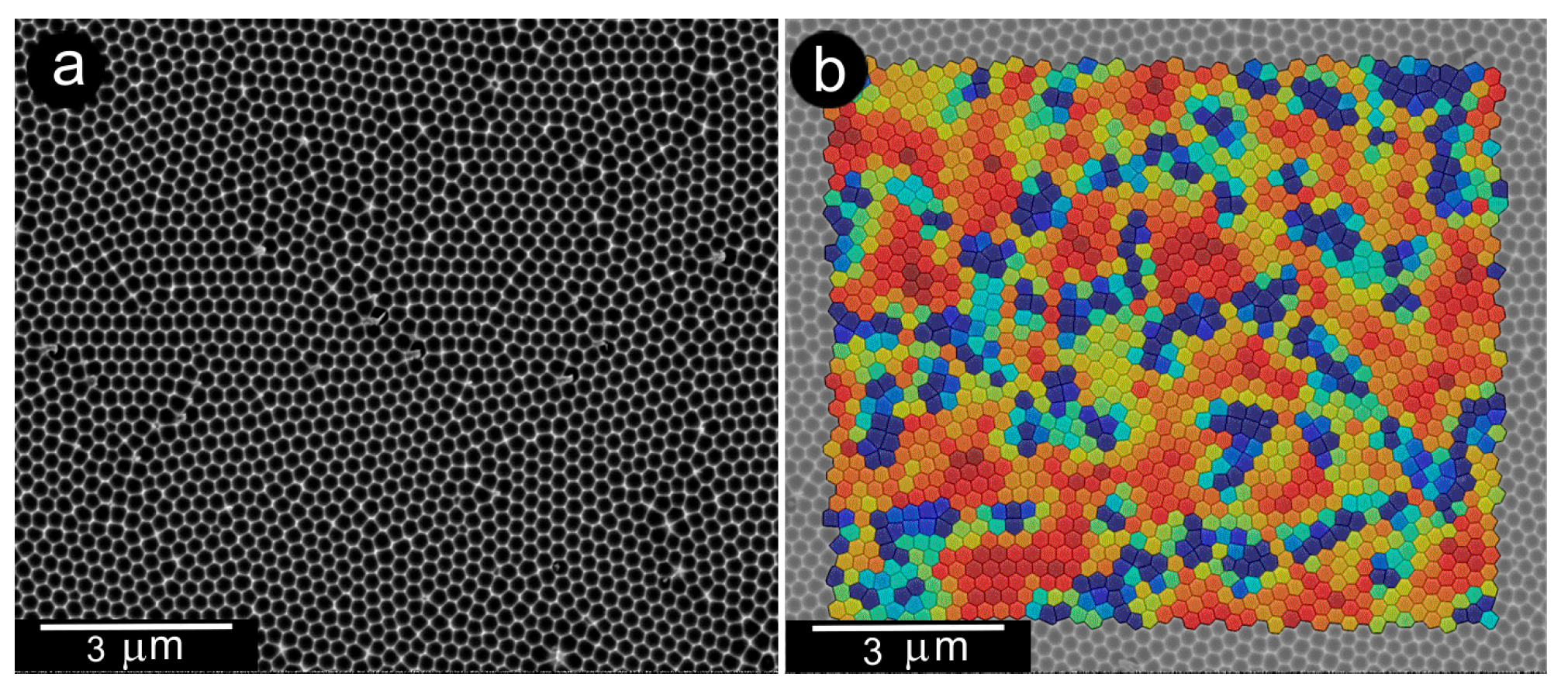
3.2. Low Supersaturations Dissipative Self-Organization of as a Basis for Nanosystems in the Form of Patterns Formation
4. Conclusions
- Self-organization of micro- and nanosystems in the form of patterns at condensate formation from a vapor phase could be realized under the condition of small supersaturation and the presence of a limited number of active centers on the growing surface. Along with this, the influence of the plasma onto the condensate surface reduced the desorption energy of adatoms to an effective value, which made it possible to increase the vapor flow of the condensed substance, keeping the value of the relative supersaturations small and steady.
- The reproducible formation of patterned micro- and nanosystems was possible under the condition of stationary quasi-equilibrium condensation. The criterion of stationarity was defined by the time-invariant critical desorption energy value or its constant position in the spectrum of all possible desorption energies.
- When the condensation conditions approached thermodynamic equilibrium, the local condensate growth kinetics and the corresponding local deposition parameters became interdependent. This interdependence was a precondition for self-organization of patterned micro- and nanosystems in different structural and morphological forms. Moreover, the processes of the condensates self-organization could be also affected by the fluctuations in the electrical voltages above the growth surface.
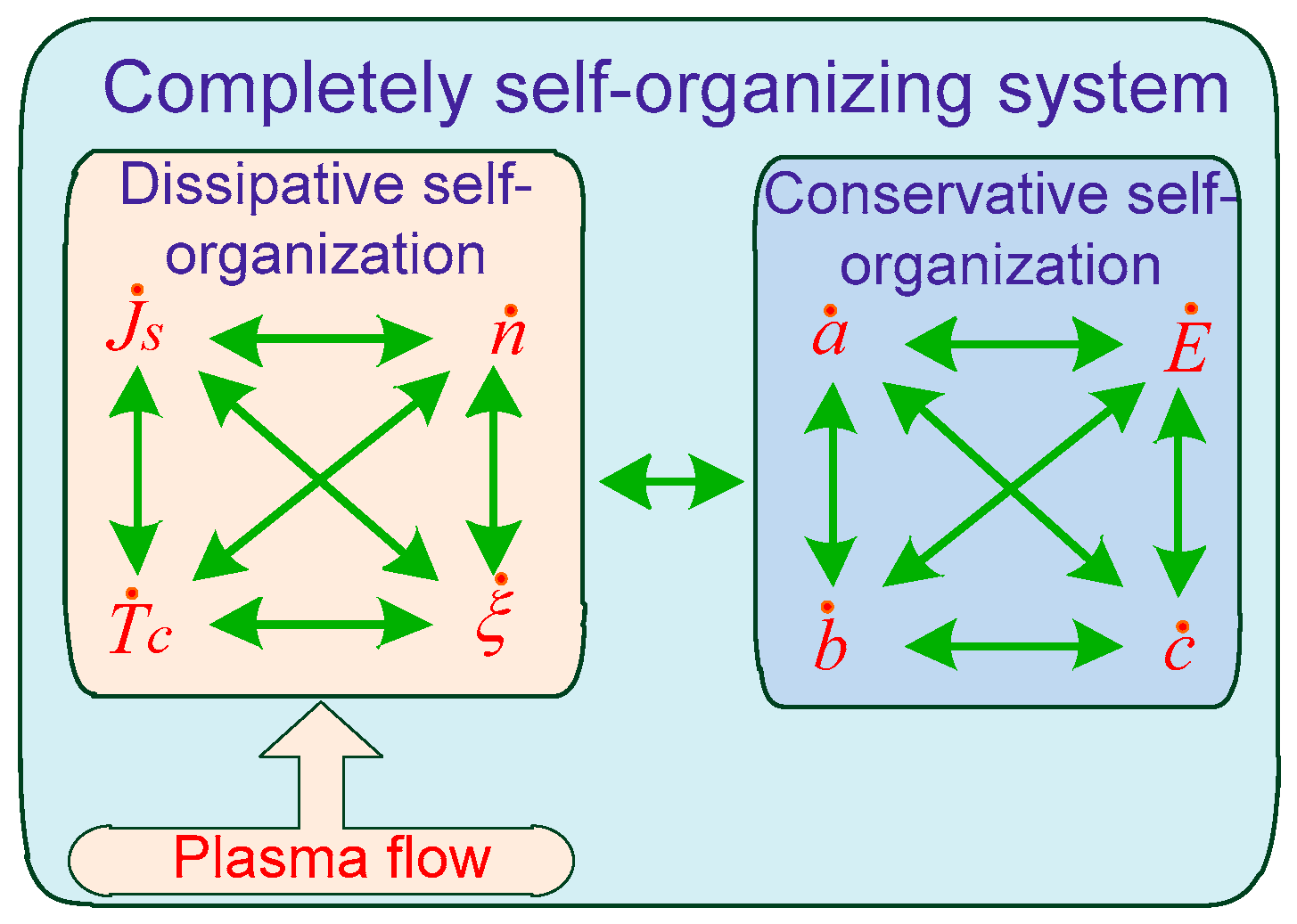
- The self-organization of patterns occurred according to the principles of conservative self-organization, i.e., at extremely low relative supersaturations in the vapor accumulation volume due to relatively weak diffusion flows. Thus, the combination of dissipative self-organization of small supersaturations with a conservative self-organization of patterned micro- and nanosystem in different structural and morphological forms represents a system of complete self-organization.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kwon, H.; Alarcón-Correa, M.; Schärf, I.; Fischer, P. Ultrathin nanoporous metallic films and their integration in sensors. Mater. Adv. 2024, 5, 3973–3980. [Google Scholar] [CrossRef]
- Chu, Y.; Zhou, H.; Wang, X.; Zhang, H.; Zhao, L.; Xu, T.; Yan, H.; Zhao, F. A flexible and self-supported nanoporous gold wire electrode with a seamless structure for electrochemical ascorbic acid sensor. Microchem. J. 2023, 186, 108259. [Google Scholar] [CrossRef]
- Si, L.; Yu, P.; Huang, J.; Zhao, Z.; Huang, M.; He, S.; Liu, H.; Wang, X.; Liu, W. Advances in gas-sensitive materials based on polyurethane film, foam, and fiber. Mater. Today Commun. 2024, 38, 108528. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, J.H.; Jeon, J.G.; Shin, G.; So, B.J.; Choi, Y.; Lee, H.; Kim, J.H.; Kang, T.J. Overpotential-controlled deposition of porous platinum for non-enzymatic glucose detection. Microchem. J. 2024, 204, 111113. [Google Scholar] [CrossRef]
- Zhang, J.; Xiong, Q.; Xu, J. Research progress in non-precious metal oxide/compound-based electrodes for non-enzymatic electrochemical glucose sensor applications. Mat. Sci. Semicon. Proc. 2024, 181, 108643. [Google Scholar] [CrossRef]
- Mushahary, N.; Sarkar, A.; Basumatary, F.; Brahma, S.; Das, B.; Basumatary, S. Recent developments on graphene oxide and its composite materials: From fundamentals to applications in biodiesel synthesis, adsorption, photocatalysis, supercapacitors, sensors, and antimicrobial activity. Results Surf. Interfaces 2024, 15, 100225. [Google Scholar] [CrossRef]
- Ambi, R.R.; Mane, A.A.; Patil, V.B.; Mane, R.D. Highly porous hierarchical NiO coated ZnO pn heterostructure for NO2 detection. MSEB 2024, 300, 117066. [Google Scholar] [CrossRef]
- Kadja, G.T.; Ilmi, M.M.; Azhari, N.J.; Khalil, M.; Fajar, A.T.; Makertihartha, I.G.B.N.; Gunawan, M.L.; Rasrendra, C.B.; Wenten, I.G. Recent advances on the nanoporous catalysts for the generation of renewable fuels. J. Mater. Res. Technol. 2022, 17, 3277–3336. [Google Scholar] [CrossRef]
- Tran, D.T.; Van, H.T.; Nguyen, L.H.; Van Quang, N.; Tsai, Y.C.; Lin, K.Y.A.; Tuan, D.D. Hierarchical porous cobalt nanoparticles encapsulated in heteroatom-doped hollow carbon as an enhancing multifunctional catalyst for hydrolysis of sodium borohydride and hydrogenation of bromate in water. J. Surf. Interfaces 2024, 48, 104329. [Google Scholar] [CrossRef]
- Kadja, G.T.; Mardiana, S.; Culsum, N.T.; Saputera, W.H.; Azhari, N.J.; Krisnandi, Y.K.; Khatrin, I.; Pamungkas, A.Z.; Larasati, L.; Lestari, W.W.; et al. Recent advances in the synthesis of hierarchically porous catalysts for the generation of renewable fuels. In Comprehensive Materials Processing, 2nd ed.; Hashmi, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2024; Volume 2, pp. 249–263. [Google Scholar] [CrossRef]
- Mondal, K.; Malode, S.J.; Shetti, N.P.; Alqarni, S.A.; Pandiaraj, S.; Alodhayb, A. Porous nanostructures for hydrogen generation and storage. J. Energy Storage 2024, 76, 109719. [Google Scholar] [CrossRef]
- Goc, K.; Prendota, W.; Przewoźnik, J.; Gondek, Ł.; Kapusta, C.; Radziszewska, A.; Mineo, K.; Takasaki, A. Magnetron sputtering as a method for introducing catalytic elements to magnesium hydride. Int. J. Hydrogen Energy 2018, 43, 20836–20842. [Google Scholar] [CrossRef]
- Li, L.; Deng, Y.; Hu, K.; Xu, B.; Wang, N.; Bai, Z.; Xu, X.; Yang, J. Nanostructure designing and hybridizing of high-capacity silicon-based anodes for lithium-ion batteries. Prog. Nat. Sci.-Mater. 2023, 33, 16–36. [Google Scholar] [CrossRef]
- Darjazi, H.; Madinabeitia, I.; Zarrabeitia, M.; Gonzalo, E.; Acebedo, B.; Javad Rezvani, S.; Fernández-Carretero, F.J.; Nobili, F.; García-Luis, A.; Muñoz-Márquez, M.Á. LiNi0.5Mn1.5O4 thin films grown by magnetron sputtering under inert gas flow mixtures as high-voltage cathode materials for lithium-ion batteries. Chem. Electro. Chem. 2023, 10, e202201004. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Q.; Meng, Q.; Lei, S.; Song, F.; Ma, J. Synergy of a hierarchical porous morphology and anionic defects of nanosized Li4Ti5O12 toward a high-rate and large-capacity lithium-ion battery. J. Energy Chem. 2021, 54, 699–711. [Google Scholar] [CrossRef]
- Cao, Z.; Yang, Y.; Qin, J.; Su, J. A core-shell porous MnO2/Carbon nanosphere composite as the anode of lithium-ion batteries. J. Power Sources 2021, 491, 229577. [Google Scholar] [CrossRef]
- Li, Y.; Yan, Y.; Yao, M.S.; Wang, F.; Li, Y.; Collins, S.M.; Du, S. Porous electrodes from self-assembled 3D jointed Pd polyhedra for direct formic acid fuel cells. Chem. Eng. J. 2023, 462, 142244. [Google Scholar] [CrossRef]
- Zhang, Y.; Tao, Y.; Shao, J. Application of porous materials for the flow field in polymer electrolyte membrane fuel cells. J. Power Sources 2021, 492, 229664. [Google Scholar] [CrossRef]
- Wiame, F. Strategies for the growth of large-scale self-organized structures. Thin Solid Film. 2017, 642, 258–275. [Google Scholar] [CrossRef]
- Desai, R.C.; Kapral, R. Dynamics of Self-Organized and Self-Assembled Structures; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Haken, H. Information and Self-Organization; Springer: Berlin, Germany, 2000. [Google Scholar]
- Haken, H. Synergetics. In Introduction and Advanced Topics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004. [Google Scholar]
- Eessaa, A.K.; El-Shamy, A.M. Review on fabrication, characterization, and applications of porous anodic aluminum oxide films with tunable pore sizes for emerging technologies. Microelectron. Eng. 2023, 279, 112061. [Google Scholar] [CrossRef]
- Prigogine, I.; Nicolis, G. Self-Organization in Non-Equilibrium Systems; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Al-Shamery, K.; Parisi, J. (Eds.) Self-Organized Morphology in Nanostructured Materials; Springer: Berlin, Germany, 2007. [Google Scholar]
- Müller, I.; Weiss, W. Thermodynamics of irreversible processes—Past and present. Eur. Phys. J. H 2012, 37, 139–236. [Google Scholar] [CrossRef]
- Ivanova, V.S.; Balankin, A.S.; Bunin, I.Z.; Oksogoev, A.A. Synergetics and Fractals in Materials Science; Nauka: Moscow, Russia, 1994. [Google Scholar]
- Ivanova, V.S.; Bunin, I.J.; Nosenko, V.I. Fractal material science: A new direction in materials science. JOM 1998, 50, 52–54. [Google Scholar] [CrossRef]
- Olemskoi, A.I.; Khomenko, A.V. Synergetics of Condensed Matter: A Textbook for University Students; Sumy State University: Sumy, Ukraine, 2002. (In Russian) [Google Scholar]
- Müller, A.; Reuter, H.; Dillinger, S. Supramolecular Inorganic Chemistry: Small Guests in Small and Large Hosts. Angew. Chem. Int. Ed. Engl. 1995, 34, 2328–2361. [Google Scholar] [CrossRef]
- Adachi, M.; Lockwood, D.J. Self-Organized Nanoscale Materials; Springer: Berlin, Germany, 2006. [Google Scholar]
- Lehn, J.M.; Sanders, J.K.M. Supramolecular Chemistry: Concepts and Perspectives. Angew. Chem. Int. Ed. Engl. 1995, 34, 2563. [Google Scholar] [CrossRef]
- Pearce, N.; Champness, N.R. Metal Complexes in Supramolecular Chemistry and Self-Assembly. Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Müller, S.C.; Parisi, J. Bottom-Up Self-Organization in Supramolecular Soft Matter; Springer: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Perekrestov, V.I.; Kornyushchenko, A.S.; Kosminskaya, Y.A. Formation of nanosystems under near-equilibrium copper condensation in an ultrapure inert medium. JETP Lett. 2008, 86, 767–771. [Google Scholar] [CrossRef]
- Perekrestov, V.I.; Kosminska, Y.O.; Kornyushchenko, A.S.; Mokrenko, A.A. Impact of selective processes on Al porous structures formation during self-organized quasi-equilibrium steady-state condensation. J. Porous Mater. 2013, 20, 967–974. [Google Scholar] [CrossRef]
- Halley, J.D.; Winkler, D.A. Consistent concepts of self-organization and self-assembly. Complexity 2008, 14, 10–17. [Google Scholar] [CrossRef]
- Chernov, A.A. Modern Crystallography III: Crystal Growth; Springer: Berlin, Germany, 2012. [Google Scholar]
- Martin, P.M. Handbook of Deposition Technologies for Films and Coatings: Science, Applications and Technology; William Andrew: Oxford, UK, 2009. [Google Scholar]
- Perekrestov, V.I.; Kosminska, Y.O.; Mokrenko, A.A.; Kononenko, I.N.; Kornyushchenko, A.S. Structure formation mechanisms of low-dimensional porous titanium systems condensed under quasi-equilibrium steady-state conditions. Vacuum 2011, 86, 111–118. [Google Scholar] [CrossRef]
- Perekrestov, V.I.; Olemskoi, A.I.; Kosminska, Y.O.; Mokrenko, A.A. Self-organization of quasi-equilibrium steady-state condensation in accumulative ion-plasma devices. Phys. Lett. A 2009, 373, 3386–3391. [Google Scholar] [CrossRef]
- Kosminska, Y.O.; Perekrestov, V.I. Regularities of self-organization of technological conditions during plasma-arc synthesis of carbon nanotubes. Diam. Relat. Mater. 2018, 85, 37–48. [Google Scholar] [CrossRef]
- Harsha, K.S. Principles of Physical Vapor Deposition of Thin Films; Elsevier: Oxford, UK, 2006. [Google Scholar]
- Kelly, P.J.; Arnell, R.D. Magnetron sputtering: A review of recent developments and applications. Vacuum 2000, 56, 159–172. [Google Scholar] [CrossRef]
- Greene, J.E. Tracing the recorded history of thin-film sputter deposition: From the 1800s to 2017. J. Vac. Sci. Technol. A 2017, 35, 05C204. [Google Scholar] [CrossRef]
- Konuma, M. Film Deposition by Plasma Techniques; Springer: Berlin, Germany, 2012. [Google Scholar]
- Randhawa, H. Review of plasma-assisted deposition processes. Thin Solid Film. 1991, 196, 329–349. [Google Scholar] [CrossRef]
- Rollings, E.; Gweon, G.-H.; Zhou, S.Y.; Mun, B.S.; McChesney, J.L.; Hussain, B.S.; Fedorov, A.V.; First, P.N.; de Heer, W.A.; Lanzara, A. Synthesis and characterization of atomically thin graphite films on a silicon carbide substrate. J. Phys. Chem. Solids 2006, 67, 2172–2177. [Google Scholar] [CrossRef]
- Hass, J.; Feng, R.; Li, T.; Li, X.; Zong, Z.; de Heer, W.A.; First, P.N.; Conrad, E.H.; Jeffrey, C.A.; Berger, C. Highly ordered graphene for two dimensional electronics. Appl. Phys. Lett. 2006, 89, 143106. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. Thin-film condensation processes. Phys. Usp. 1998, 41, 983. [Google Scholar] [CrossRef]
- Birney, R. Special Issue: Current Research in Thin Film Deposition: Applications, Theory, Processing, and Characterization. Coatings 2020, 10, 1228. [Google Scholar] [CrossRef]
- Walgraef, D. Nanostructure evolution during thin film deposition. Phys. E Low-Dimens. Syst. Nanostruct. 2003, 18, 393–401. [Google Scholar] [CrossRef]
- Du, D.; Srolovitz, D.J. Crystal morphology evolution in film growth: A general approach. J. Cryst. Growth 2006, 96, 86–96. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. New phase formation on solid surfaces and thin film condensation. Prog. Surf. Sci. 1996, 51, 1–107. [Google Scholar] [CrossRef]
- Osipov, A.V. Kinetic model of vapour-deposited thin film condensation: Nucleation stage. Thin Solid Film. 1993, 227, 111–118. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Cirlin, G.E. Growth kinetics of thin films formed by nucleation during layer formation. Semiconductors 2005, 39, 1267–1274. [Google Scholar] [CrossRef]
- Kuni, F.M.; Shchekin, A.K.; Grinin, F.P. Theory of heterogeneous nucleation under conditions of gradual formation of a metastable state. Usp. Fiz. Nauk 2001, 171, 345–385. [Google Scholar] [CrossRef]
- Pedersen, H.; Elliott, S.D. Studying chemical vapor deposition processes with theoretical chemistry. Theor. Chem. Acc. 2014, 133, 1476. [Google Scholar] [CrossRef]
- Perekrestov, V.I.; Kornyushchenko, A.S.; Kosminska, Y.A.; Shevchenko, S.T.; Natalich, V.V. Systems of complete self-organization of the nanotechnological process. In Proceedings of the 2021 IEEE 11th International Conference Nanomaterials: Applications & Properties (NAP), Odessa, Ukraine, 5–11 September 2021; pp. NSS09-1–NSS09-4. [Google Scholar] [CrossRef]
- Perekrestov, V.I.; Mokrenko, A.A.; Kosminskaya, Y.A.; Rubets, D.I. Formation of Nickel Extended Surface upon Quasi-Equilibrium Steady-State Condensation. J. Surf. Investig. Synchrotron Neutron Tech. 2011, 5, 667–671. [Google Scholar] [CrossRef]
- Dubrovsky, V.G. Criterion for the onset of the Ostwald ripening stage, taking into account fluctuations in the number of particles in the bud. Tech. Phys. Lett. 2010, 36, 219–223. [Google Scholar] [CrossRef]
- Galdikas, A. Study of nanoclusters growth at initial stages of ultrathin film deposition by kinetic modeling. Appl. Surf. Sci. 2008, 254, 3964–3970. [Google Scholar] [CrossRef]
- Bunshah, R. Handbook of Deposition Technologies for Films and Coatings: Science, Technology and Applications; Noyes Publications: New York, NY, USA, 1994. [Google Scholar]
- Perekrestov, V.I.; Kosminska, Y.O.; Kornyushchenko, A.S.; Latyshev, V.M. Self-assembly of porous Cu structures during steady-state condensation of weakly supersaturated vapors. J. Porous Mater. 2014, 21, 1159–1167. [Google Scholar] [CrossRef]
- Kornyushchenko, A.S.; Natalich, V.V.; Perekrestov, V.I. Formation of copper porous structures under near-equilibrium chemical vapor deposition. J. Cryst. Growth 2016, 442, 68–74. [Google Scholar] [CrossRef]
- Perekrestov, V.I.; Kosminska, Y.O.; Mokrenko, A.A.; Davydenko, T. Self-assembly of condensates with advanced surface by means of the competing field selectivity and Gibbs–Thomson effect. Appl. Surf. Sci. 2014, 298, 171–175. [Google Scholar] [CrossRef]
- Kornyushchenko, A.S.; Natalich, V.V.; Shevchenko, S.T. Selective processes during formation of porous carbon nanosystems. In Proceedings of the 2019 IEEE 9th International Conference Nanomaterials: Applications & Properties (NAP), Odessa, Ukraine, 15–20 September 2019; pp. 01SSAN20-1–01SSAN20-4. [Google Scholar] [CrossRef]
- Ostendorp, S. Anodic Aluminum Oxide for Surface Nano-Structuring Purposes. Ph.D. Thesis, Muenster University, Münster, Germany, 2017. [Google Scholar]
- Granitzer, P.; Rumpf, K. Porous silicon—A versatile host material. Materials 2010, 3, 943–998. [Google Scholar] [CrossRef]
- Levchenko, I.; Keidar, M.; Xu, S.; Kersten, H.; Ostrikov, K. Low-temperature plasmas in carbon nanostructure synthesis. J. Vac. Sci. Technol. B 2013, 31, 050801. [Google Scholar] [CrossRef]
- Prasek, J.; Drbohlavova, J.; Chomoucka, J.; Hubalek, J.; Jasek, O.; Adam, V.; Kizek, R. Methods for carbon nanotubes synthesis—A review. J. Mater. Chem. 2011, 21, 15872–15884. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Gershman, S.; Raitses, Y. Unstable behavior of anodic arc discharge for synthesis of nanomaterials. J. Phys. D Appl. Phys. 2016, 49, 345201. [Google Scholar] [CrossRef]
- Yeh, Y.W.; Raitses, Y.; Yao, N. Structural variations of the cathode deposit in the carbon arc. Carbon 2016, 105, 490–495. [Google Scholar] [CrossRef]
- Ng, J.; Raitses, Y. Self-organization processes in the carbon arc for nanosynthesis. J. Appl. Phys. 2015, 117, 063303. [Google Scholar] [CrossRef]
- Shashurin, A.; Keidar, M. Factors affecting the size and deposition rate of the cathode deposit in an anodic arc used to produce carbon nanotubes. Carbon 2008, 46, 1826–1828. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perekrestov, V.; Kornyushchenko, A.; Kosminska, Y.; Kubakh, M.; Wilde, G. Self-Organization of Micro- and Nanosystems in the Form of Patterns. Crystals 2024, 14, 953. https://doi.org/10.3390/cryst14110953
Perekrestov V, Kornyushchenko A, Kosminska Y, Kubakh M, Wilde G. Self-Organization of Micro- and Nanosystems in the Form of Patterns. Crystals. 2024; 14(11):953. https://doi.org/10.3390/cryst14110953
Chicago/Turabian StylePerekrestov, Vyacheslav, Anna Kornyushchenko, Yuliia Kosminska, Maksym Kubakh, and Gerhard Wilde. 2024. "Self-Organization of Micro- and Nanosystems in the Form of Patterns" Crystals 14, no. 11: 953. https://doi.org/10.3390/cryst14110953
APA StylePerekrestov, V., Kornyushchenko, A., Kosminska, Y., Kubakh, M., & Wilde, G. (2024). Self-Organization of Micro- and Nanosystems in the Form of Patterns. Crystals, 14(11), 953. https://doi.org/10.3390/cryst14110953





