Directional Crystallization in the Presence of a Mushy Layer with Applications to the Earth’s Inner Core Boundary

Abstract

We formulate the mathematical model of directional crystallization of a binary melt with a mushy layer (region) between purely solid and liquid phases. This model is complicated by melt convection and pressure-dependent phase transition temperature. Approximate analytical solutions to this nonlinear moving-boundary problem are constructed. Namely, the concentration of impurity, fraction of solid phase, mushy region thickness, average fluid velocity, primary interdendritic spacing, mean radius of a chimney, and a characteristic distance between chimneys in a mushy region are found. Using this analytical solution, we describe the mushy region structure near the inner core boundary of the Earth, which is consistent with computer simulations and estimates existing in recent literature. A scheme illustrating the mushy region arrangement with chimneys at the inner core boundary of the Earth is presented. This arrangement based on the developed theory represents the novelty and importance of our study.

1. Introduction

The Earth’s core is the deepest central region of the planet; it has inner and outer parts. Presumably, the core consists of an alloy of iron and nickel with an admixture of various elements (sulfur, oxygen, silicon, chromium, phosphorus, and others). The core’s temperature is estimated to be around 5000–6000 degrees Celsius. Since for the most part the core consists of iron, it weighs about 1/3 of the planet’s mass. The inner part of the core, with a radius of about 1300 km, is in a solid state. The temperature on the outer part of the core is about 6000 degrees Celsius. The inner part of the core has a high density and is under tremendous pressure. The outer part of the core is in a liquid state, enveloping the inner core and circulating around it. Between these two parts of the Earth’s core, there is a transitional two-phase region filled with solid and liquid phases and possessing the properties of the inner and outer parts of the core.

The theory of two-phase (mushy and/or slurry) regions filled with solid and liquid phases at the Earth’s inner core originates from classical works [1,2]. This theory is still being actively explored [3,4,5,6]. The existence of such a region may be a consequence of constitutional supercooling, which is the driving force of crystal formation and dendrite growth [7]. The growing solid phase elements release the latent heat of crystallization and, thus, compensate for the supercooling. As a result, by analogy with classical processes of directional and bulk crystallization in terrestrial conditions, a slurry, mushy, or mixed-type region can be developed at the Earth’s inner core boundary. The morphological stability analysis of the interfacial boundary can elucidate which of the aforementioned types of liquid–solid regions are present at the Earth’s inner core. It is vital to note that the crystallization of the Earth’s core occurs under conditions that are very different from those on the Earth’s surface. Namely, the key differences are (i) extremely slow crystallization velocity, (ii) strong pressure dependence of the phase transformation temperature, (iii) higher temperature of the solidified core as compared to the surrounding liquid, and (iv) the significant impact of convection on the solidification process. These factors suggest that the use of the classical morphological stability theory developed by Mullins and Sekerka [8,9] is incorrect under the solidification conditions of Earth’s inner core. Therefore, the classical stability theory has been modified to take the above-mentioned factors into account in several recently published works [10,11,12,13]. For example, the stability analysis is made without taking the convective melt flow into account in [10], and convection is only considered in part in [11]. A more general analysis of morphological stability with convection was made in [12,13]. The criteria for morphological stability and constitutional supercooling derived in this paper showed the possibility of stable and unstable crystallization scenarios in the region of constitutional supercooling. These scenarios are consistent with the crystallization processes of the Earth’s inner core, which involve slurry and mushy regions, respectively (for details, see the crystallization model developed in [12]). Supporting the existence of a mushy region near the Earth’s inner core is the theory presented in [10]. Here, the authors show that the existence of a slurry region is less likely because of the need to provide sufficient nuclei to sustain such a region. The authors of [14] also favor the existence of a mushy region that extends from the Earth’s inner core surface to the center of the fluid’s outer core. It is significant that this conclusion is proved by the seismological data of [15,16].

An important circumstance of the Earth’s core crystallization is that it is accompanied by the emission of light elements [17]. This impurity maintains the constitutional supercooling near the interphase boundary, which acts as the catalyst for the growth of the solid phase and the evolution of the mushy region. Hydrodynamic currents and pressure gradients at the Earth’s inner core also play important roles in this process. On the one hand, fluid currents dilute the impurity concentration and attenuate the constitutional supercooling. On the other hand, the pressure gradient supported by convective currents enters the criterion of constitutional supercooling under conditions of the Earth’s core crystallization and enhances the supercooling. As a result, the supercooled region becomes larger, which promotes the growth of the solid phase and the development of morphological perturbations. This paper focuses on the impact of convection and the mushy region on crystallization under the conditions of the Earth’s inner core.

2. Governing Equations and Analytical Solutions

The local conservation of heat and solutes in the mushy region $u_s\tau <{\zeta }_1<h+u_s\tau$ can be represented as follows, referencing [18] ($u_s$ is the solidification velocity, $\tau$ is the time, ${\zeta }_1$ is the spatial coordinate of the solidification direction, and h is the mushy region thickness):

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \rho \left(\varphi \right)c\left(\varphi \right)\frac{\partial \theta }{\partial \tau }+\rho \left(\varphi \right)c\left(\varphi \right)\mathbf{V}·\nabla \theta \\ \hfill =\nabla \left({\lambda }_{sl}\left(\varphi \right)\nabla \theta \right)+Q_V\left(\frac{\partial \varphi }{\partial \tau }+\mathbf{V}·\nabla \varphi \right),\end{array}\end{array}$$

(1)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill (1-\varphi )\frac{\partial \sigma }{\partial \tau }+(1-\varphi )\mathbf{V}·\nabla \sigma \\ \hfill =\nabla \left(D\left(\varphi \right)\nabla \sigma \right)+(1-k_0)\sigma \left(\frac{\partial \varphi }{\partial \tau }+\mathbf{V}·\nabla \varphi \right),\end{array}\end{array}$$

(2)

where

$$\rho \left(\varphi \right)c\left(\varphi \right)={\rho }_s{c}_s\varphi +{\rho }_l{c}_l(1-\varphi ),$$

$${\lambda }_{sl}\left(\varphi \right)={\lambda }_s\varphi +{\lambda }_l(1-\varphi ),$$

$$D\left(\varphi \right)=D_l(1-\varphi ).$$

Parameter $\rho$ is the density, $\varphi$ is the solid fraction in the mushy region, c is the thermal (heat) capacity, $\theta$ is the temperature, $\tau$ is the time, $\mathbf{V}$ is the fluid velocity, ${\lambda }_s$ and ${\lambda }_l$ are the thermal conductivities in solid and liquid phases, respectively, $Q_V$ is the latent heat of solidification, $\sigma$ is the impurity concentration, D is the chemical diffusivity in the mush, $D_l$ is the chemical diffusivity in the liquid, and $k_0$ is the partition coefficient. Note that parameters $\rho$, c, ${\lambda }_{sl}$, and D are chosen via the properties of solid and liquid phases [18,19].

Let us consider the mushy region as a porous substance and use Darcy’s equation [18,20] to model the flow

$$\eta (1-\varphi )\mathbf{V}=\Pi \left(\varphi \right)\left[({\rho }_l-{\rho }_h)\mathbf{g}-\nabla p\right],$$

(3)

where the fluid velocity satisfies the continuity equation, and the permeability $\Pi$ is dependent of the solid fraction $\varphi$

$$\nabla \left[{\rho }_l(1-\varphi )\mathbf{V}\right]=0.$$

(4)

Parameter $\eta$ represents the dynamic viscosity, ${\rho }_h$ is the density of the liquid phase, and $\mathbf{g}$ and p are the acceleration of the gravity and pressure, respectively.

Further, we use the equation for the permeability in the form of

$$\Pi \left(\varphi \right)={\Pi }_0{(1-\varphi )}^3,$$

where ${\Pi }_0$ is the permeability constant. This expression represents a slightly simplified version of the Kozeny–Carmen law [21,22]. Note that this formula has no singularity at the mushy region/liquid interface, where $\varphi \to 0$, in comparison with the Kozeny–Carmen equation.

In order to define the buoyancy forcing (3), the fluid density must be a function of the state equation. The density ${\rho }_l$ can be expressed as a function of $\sigma$ [23,24] in the case of intense convective motions near the inner core. We approximate this dependence with a linear function and, by analogy with [18], we obtain the following expression:

$${\rho }_l={\rho }_h\left[1+\kappa (\sigma -{\sigma }_h)\right],$$

(5)

where ${\sigma }_h$ is the solute concentration at ${\zeta }_1=h$, and $\kappa$ is a positive constant. This parameter can be evaluated from density variations in the fluid’s outer core. The density of the Earth’s core changes from the core-mantle boundary to the inner core boundary by about 20% [25].

We assume that the latent heat of dendritic growth in the mushy region completely compensates for the constitutional supercooling. This leads us to the quasi-equilibrium mushy layer model [18,26,27], where it is possible for various dendrite-like structures to evolve. In addition, this model assumes that crystal nucleation does not occur in the two-phase region, which greatly simplifies the heat and mass transfer model. In this case, the temperature gradient in a mush is equal to the phase transition temperature gradient, which depends on the pressure and impurity concentrations. Introducing this relationship by a linear expression, we obtain [11,12]

$$\nabla \theta =m_{\sigma }\nabla \sigma +m_p\nabla p,$$

(6)

where $m_{\sigma }$ is the liquidus slope and $m_p$ is the Clapeyron slope.

Strictly speaking, the buoyancy forcing (treated as a local linear function of the convective impurity concentration near the inner core) cannot describe the whole outer core density variation (by about 20%) in Equation (5) because there is a large compressional component to the density variation across the whole outer core. It is not a function of just the impurity concentration. Furthermore, integrating this local derivative across the whole mushy layer precludes any of the very interesting effects discovered in high-pressure liquidus phase diagrams, showing that the melting points of binary systems can be quite complex, nonlinear, and pressure-dependent. For example, the effect of “snowing” of solid crystals at the bottom, middle, or top of the core during convection, depending on the system, impurity, and pressure [28], is precluded in the present treatment. This leads to a non-linear form of Equation (6). Here, for the sake of simplicity, we ignore the real complex possibilities that the phase equilibrium determinations of high-pressure liquids likely make.

To solve the problem, we should use the boundary conditions at the inner core surface, where ${\zeta }_1=u_s\tau$, in the form of

$${\lambda }_s\mathbf{n}{\left(\nabla \theta \right)}_{{\zeta }_1=u_s\tau -0}-{\lambda }_{sl}\mathbf{n}{\left(\nabla \theta \right)}_{{\zeta }_1=u_s\tau +0}=\left(1-{\varphi }_{*}\right)u_s{Q}_V,$$

(7)

where ${\varphi }_{*}$ represents the boundary fraction of the solid, $\mathbf{n}$ is the unit normal vector pointing toward the liquid, and $\mathbf{n}{\left(\nabla \theta \right)}_{{\zeta }_1=u_s\tau -0}=G_s$ is the temperature gradient in the solid inner core at the phase transition boundary, where ${\zeta }_1=u_s\tau$.

At the mushy region–liquid boundary, the density, concentration, and fraction of the solid will be assumed to be known as

$$\sigma ={\sigma }_h,{\rho }_l={\rho }_h,\varphi =0,{\zeta }_1=u_s\tau +h.$$

(8)

Thus, the model of equations and boundary conditions (1)–(8) defines the main characteristics and arrangements of the mushy region near the inner core.

Note that the Earth’s inner core becomes cooled by transporting heat to the liquid mantle, which is further moved to the Earth’s surface by convection within the Earth’s mantle [29]. This cooling of the Earth’s core is the driving force for its crystallization. As this takes place, the denser melt components crystallize to become the Earth’s inner core, while the lighter components float to the Earth’s outer core. These light components stir in the molten core by convection, leading to different chemical compositions of its parts [30]. In addition, the compositional convection is responsible for the geodynamo mechanism. To save space, we refer the interested reader to the literature review of this problem [31], which discusses the mutual influence of the Earth’s core crystallization, melt convection, and the planet’s magnetic field. Note that an important feature of melt flows in the Earth’s liquid core is the fact that the buoyancy, Lorentz, and Coriolis mechanisms partially compensate for melt turbulization [32]. This allows us to consider the melt flows in the outer core as non-turbulent flows. The fluid currents are likely to be represented by thin upward melt channels (chimneys) and thick downward melt channels that lie between them [32,33]. This mushy region at the Earth’s solid core is confirmed by several laboratory experiments [34,35]. Below, we use the convective theory developed in [36] to describe the mushy region near the Earth’s inner core.

We describe the mass transfer in a mush using the Scheil approximation, neglecting the diffusion term in Formula (2), since in the case of convective motions, diffusion is not effective at redistributing the impurity material. This approach is often used by researchers (see [37,38]). In addition, we consider Equation (2) in the region where the fluid is sinking. So, if $v_{\zeta }$ represents the $\zeta$-component of fluid velocity, convective terms corresponding to the perpendicular directions are significantly smaller than the convective term $v_{\zeta }(1-\varphi )\partial \sigma /\partial {\zeta }_1$. Thus, after the transition to the moving coordinate system $\zeta ={\zeta }_1-u_s\tau$, we obtain $\left(1-\varphi \right)d\sigma /d\zeta =(1-k_0)\sigma d\varphi /d\zeta$. Now we can find the concentration of impurity as a function of $\varphi$ in the mushy region, where $0<\zeta <h$, by integrating this equation and taking into account the boundary condition (8), i.e.,

$$\sigma \left(\varphi \right)={\sigma }_h{\left(1-\varphi \right)}^{k_0-1}.$$

(9)

Taking into account expressions (3) and (5), substituting the temperature derivative $d\theta /d\zeta$ from (6) into (1) in the moving frame of the reference and denoting $\psi \left(\varphi \right)=d\varphi /d\zeta$, we arrive at

$$\frac{d\psi }{d\varphi }=\frac{y_1(\varphi ,\psi )+y_2(\varphi ,\psi )+y_3(\varphi ,\psi )}{{\lambda }_{sl}\left(\varphi \right)m_{\sigma }{\sigma }_h(k_0-1){(1-\varphi )}^{k_0-2}\psi },$$

(10)

where

$$\begin{array}{c}{y}_1=\rho \left(\varphi \right)c\left(\varphi \right)(v_{\zeta }-u_s)\\ \times \left[m_{\sigma }{\sigma }_h(k_0-1){(1-\varphi )}^{k_0-2}\psi +{\rho }_h\kappa {\sigma }_h\left({(1-\varphi )}^{k_0-1}-1\right)g{m}_p-\eta (1-\varphi )v_{\zeta }{m}_p{\Pi }^{-1}\left(\varphi \right)\right],\end{array}$$

$$\begin{array}{c}{y}_2=m_{\sigma }{\sigma }_h(k_0-1){(1-\varphi )}^{k_0-3}{\psi }^2\\ \times \left[{\lambda }_{sl}\left(\varphi \right)(k_0-2)-({\lambda }_s-{\lambda }_l)(1-\varphi )\right]-({\lambda }_s-{\lambda }_l)({\rho }_l-{\rho }_h)g{m}_p\psi ,\end{array}$$

$$\begin{array}{c}{y}_3={\lambda }_{sl}\left(\varphi \right)\kappa {\rho }_h{\sigma }_h(k_0-1){(1-\varphi )}^{k_0-2}g{m}_p\psi \\ +Q_V(v_{\zeta }-u_s)\psi +\frac{d}{d\varphi }\left[\frac{{\lambda }_{sl}\left(\varphi \right)\eta (1-\varphi )v_{\zeta }{m}_p}{\Pi \left(\varphi \right)}\right]\psi .\end{array}$$

By integrating Equation (4), we obtain the velocity component as follows:

$$v_{\zeta }\left(\varphi \right)=\frac{B}{(1-\varphi ){\rho }_l\left(\varphi \right)},$$

(11)

where parameter B is defined in terms of the average velocity $\overline{V}$, i.e.,

$$B=\frac{\overline{V}{\varphi }_{*}}{\underset{0}{\overset{{\varphi }_{*}}{\int }}\frac{d\varphi }{(1-\varphi ){\rho }_l\left(\varphi \right)}},$$

$$\overline{V}=\frac{1}{{\varphi }_{*}}\underset{0}{\overset{{\varphi }_{*}}{\int }}{v}_{\zeta }\left(\varphi \right)d\varphi .$$

The solid fraction ${\varphi }_{*}$ on the inner core’s surface may be expressed from the boundary condition (7) in terms of temperature gradients on the left $g_s$ and right $g_l$ sides of the boundary

$${\varphi }_{*}=\frac{{\lambda }_s{g}_s-{\lambda }_l{g}_l-Q_V{u}_s}{g_l({\lambda }_s-{\lambda }_l)-u_s{Q}_V}.$$

(12)

The boundary condition to Equation (10) now follows from expressions (3) and (6) at the inner core surface (where $\varphi ={\varphi }_{*}$):

$$\psi =\frac{\eta (1-{\varphi }_{*})v_{\zeta }\left({\varphi }_{*}\right)m_p/\Pi \left({\varphi }_{*}\right)-g_l-({\rho }_l-{\rho }_h)g{m}_p}{m_{\sigma }{\sigma }_h(k_0-1){(1-{\varphi }_{*})}^{k_0-2}}.$$

(13)

Equations (10) and (13) present the standard Cauchy problem, whose solution determines the function $\psi \left(\varphi \right)$.

Next, the thickness of the mushy region and the fraction of the solid phase can be found using the following integrals:

$$h=\underset{{\varphi }_{*}}{\overset{0}{\int }}{\psi }^{-1}\left(\varphi \right)d\varphi ,\zeta \left(\varphi \right)=h+\underset{0}{\overset{\varphi }{\int }}{\psi }^{-1}\left(\varphi \right)d\varphi .$$

(14)

3. Discussion

Analytical solutions obtained in accordance with expressions (9)–(14) for various physical constants, which are typical for the Earth’s core (

Table 1. Physical parameters characterizing the solidification conditions of the Earth’s core [12].

Parameter	Symbol	Value	Units
Chemical diffusivity in the liquid phase	$D_l$	10${}^{-9}$	m2/s
Thermal diffusivity in the liquid phase	${\lambda }_l/\left({\rho }_h{c}_l\right)$	$6·{10}^{-6}$	m2/s
Thermal diffusivity in the solid phase	${\lambda }_s/\left({\rho }_s{c}_s\right)$	$7·{10}^{-6}$	m2/s
Thermal conductivity in the liquid phase	${\lambda }_l$	63	J/(m s K)
Thermal conductivity in the solid phase	${\lambda }_s$	79	J/(m s K)
Solute partition coefficient	$k_0$	0.25	-
Latent heat of solidification	$Q_V$	$6.84·{10}^9$	J/m3
Thermal (heat) capacity in the liquid phase	$c_l$	860	J/(kg K)
Acceleration of gravity	g	4.4	m/s2
Clapeyron slope	$m_p$	$9·{10}^{-9}$	K/Pa
Permeability constant	${\Pi }_0$	10	m2
Capillary constant	$d_0$	${10}^{-9}$	m

), are presented in Figure 1 and Figure 2. The viscosity of the inner core is known to vary over a wide range from ${10}^{13}$ to ${10}^{21}$ Pa-s [39], ${10}^7$ Pa-s [40,41], and ${10}^{-2}$ Pa-s [42,43]. Our calculations demonstrate that an increase in viscosity leads to a decrease in the thickness of the mushy region. Small viscosities, when $\eta$ is less than or of the order of ${10}^{10}$ Pa-s, correspond to extremely large thicknesses of the mushy region h exceeding the radius of the outer core. This gives a lower bound estimate of the dynamical viscosity of ${10}^{11}$ Pa-s.

However, if $\eta$ is of the order of or greater than ${10}^{19}$ Pa-s, the thickness of the mushy region vanishes. This presents an upper-bound estimate of the dynamic viscosity of ∼10${}^{18}$ Pa-s. Hence, the existence of a mushy region in the vicinity of the inner core boundary based on the analysis of the morphological instability of the inner core boundary in the presence of convection [12] yields a viscosity range of ${10}^{11}$–${10}^{18}$ Pa-s. But this relatively wide range of viscosities can be narrowed, based on narrowing the characteristic intervals of fluid velocities. Assuming an average fluid velocity of $\overline{V}$∼${10}^{-8}$–${10}^{-6}$ m/s [44], the gradient of temperature on the upper side of the inner core boundary $g_l$∼$-3.7·{10}^{-4}$ K/m [10], and solidification velocity $u_s$∼$6·{10}^{-12}$ m/s [11], we arrive at a viscosity estimate of $\eta$∼${10}^{14}$–${10}^{16}$ Pa-s. 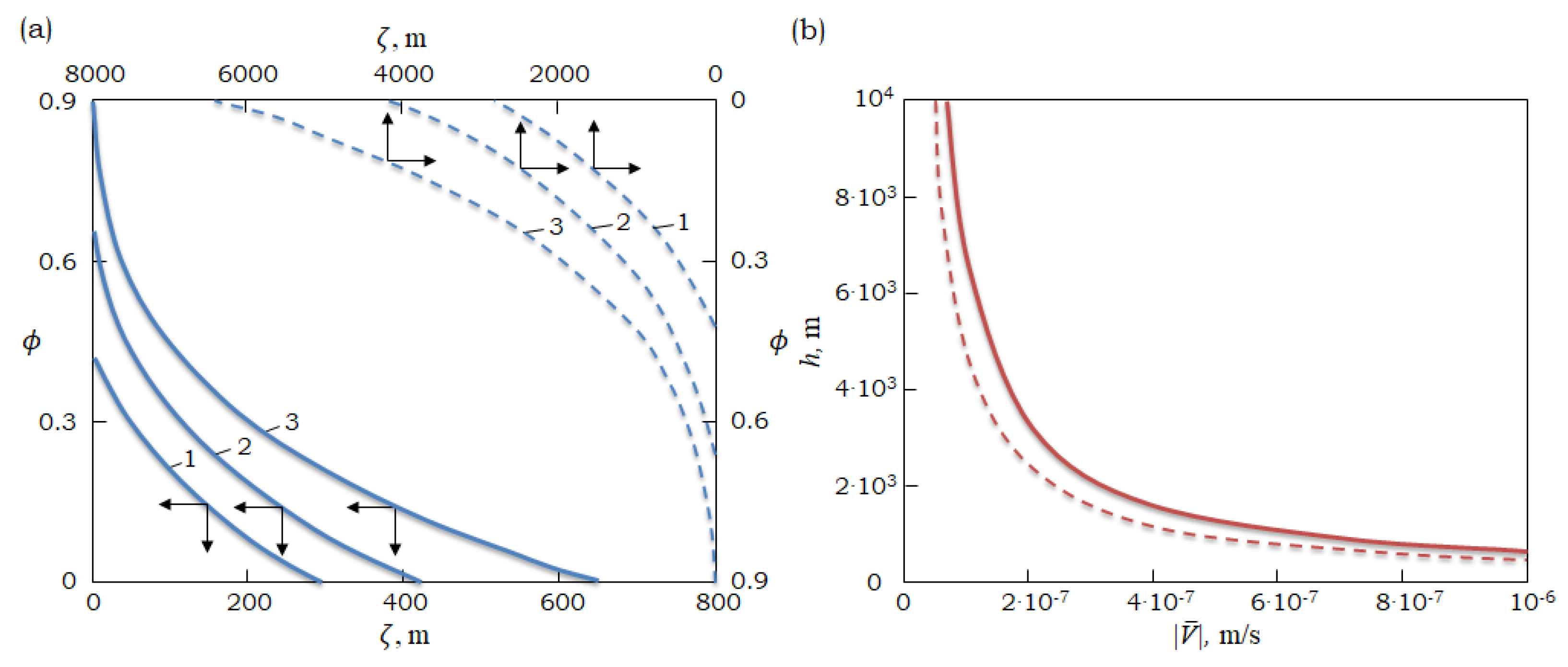Figure 1 shows that small possible variations of $g_l$ and $u_s$ may expand this interval to ${10}^{13}$–${10}^{17}$ Pa-s. This estimate agrees well with the selection theory of dendritic growth at the inner core boundary [7].

Figure 1 and Figure 2 demonstrate that the width of the mushy region increases with the growth of the solid fraction ${\varphi }_{*}$ at the inner core boundary, temperature gradient $g_l$, and solidification velocity $u_s$ at the inner core boundary, and with the decrease in the average fluid velocity $|\overline{V}|$ oriented from the inner core boundary to the fluid’s outer core. However, at certain physical parameters, sufficiently small average velocities $\left|\overline{V}\right|<\left|{\overline{V}}_c\right|$ (see Figure 1) do not cause the formation of a mushy region due to the absence of convective cooling. Notably, an increase in $|\overline{V}|$ leads to an increase in the solid fraction ${\varphi }_{*}$ and solidification rate $u_s$ for a fixed value of the mushy region thickness h (see Figure 1).

Now, we will evaluate the effect of the liquidus slope $m_{\sigma }$ on the width of the mushy region as this parameter also changes in a wide range from $-{10}^2$ to $-1.1·{10}^4$ K [10,11]. The thickness of the mushy region can extend to the center of the inner core if $|m_{\sigma }|$ is larger than $1.3·{10}^3$ K, as noted by Degen et al. [11]. Conversely, the thermodynamic estimates give that h∼$3·{10}^5$ m if $|m_{\sigma }|$∼${10}^2$ K. Several estimates, which are based on a collapsing mushy region, result in a width of ∼10–10⁵ m due to uncertainties in $\eta$. It is shown in Figure 2 that an increase in the absolute value of the liquidus slope causes an increase in the thickness. At the same time, smaller velocities $|\overline{V}|$ give larger differences in the two curves in Figure 2.

The primary interdendritic spacing ${\lambda }_1$ represents one of the important physical parameters of the mushy region structure. This average distance separating two dendritic tips characterizes the hydrodynamics of the mushy region and the size of the crystal. For a stationary solidification and the case of an axisymmetric dendritic tip, the interdendritic spacing at the inner core surface can be formulated as [11]

$${\lambda }_1=\sqrt{\frac{2\pi r}{b_1\left(\frac{d\varphi }{d\zeta }\right)}}.$$

(15)

Here, $\left(\frac{d\varphi }{d\zeta }\right)=\psi$ is defined from the boundary condition (13), and parameters $b_1=1$ and $b_1=0.86$ for cubic and hexagonal dendritic lattices, respectively.

Let us briefly formulate the main predictions following the stable dendrite growth theories: (a) we assume that the dendritic shape remains parabolic near the tip; (b) $r^2{u}_s$ is constant; (c) $r^2{u}_s$ is independent of the transverse flow component and grows linearly with the increasing longitudinal flow component $|\overline{V}|$ (see [45]) for various impurity concentrations of the order of ${10}^{-2}$, characteristic of the inner core surface conditions, i.e.,

$$r^2{u}_s=\frac{2d_0{D}_l}{{\sigma }_0}\left(1+\frac{\varpi d_0|\overline{V}|}{D_l}\right).$$

(16)

Here, $d_0$ represents the capillary constant, and numerical constants are estimated as ${\sigma }_0=0.032$ and $\varpi =5300$ [45]. Note that dendrite vertices reach stationary velocity very quickly in terrestrial and microgravity conditions [46]. Considering this circumstance, we estimate the growth rate of their vertices to be of the order of the rate of motion of the solid inner core surface. Further, eliminating the radius of the dendrite tip r from Equations (15) and (16), we arrive at the interdendritic spacing ${\lambda }_1$.

Figure 3 illustrates how the parameter ${\lambda }_1$ depends on the potential differences in the main parameters of the mushy region of the Earth’s core. An increase in fluid velocity $|\overline{V}|$, solidification velocity, and dynamic viscosity results in a decrease in interdendritic spacing. Our findings incorporate previous estimates for ${\lambda }_1$ as presented by Bergman [47], where ${\lambda }_1$∼${10}^2$ m, and by Deguen et al. [11], where ${\lambda }_1$∼10 m, showing that the interdendritic interval strongly depends on the solidification conditions at the inner core surface. Notice that the dendrite tip radius r ranges from 2 mm to 6 mm for all curves shown in Figure 3. This agrees well with the estimates previously reported in [11], where r varies from ∼1 mm to ∼1 cm.

The laboratory experiments on the crystallization of binary liquids are well known to be the main instruments for investigating the structure of the mushy region. Similar experiments carried out with various mixtures (water solutions [48] and metal alloys [49]) show the chimney formation development. The mushy region is an area of descending liquid, except in narrow areas (plumes), where buoyant liquid rises from each chimney. This kind of mushy region structure probably exists at the inner core surface [44]. To evaluate its characteristic horizontal dimension $\Xi$ (average chimney spacing), we integrate the temperature conductivity expression (1) in the vicinity of the inner core surface, where the fluid flows mainly along the perpendicular direction $\xi$. Taking the small variations of $\varphi$, we obtain the following formula near the inner core surface:

$$\rho \left(\varphi \right)c\left(\varphi \right)v_{\xi }\theta \approx {\lambda }_{sl}\left(\varphi \right)\frac{d\theta }{d\xi }+Q_V{v}_{\xi }\varphi ,$$

(17)

where $v_{\xi }$ is the $\xi$ component of the fluid velocity. The integration constant is selected, such that $d\theta /d\xi \approx 0$, $v_{\xi }\approx 0$ at $\xi =0$. Determining $\varphi \approx {\varphi }_{*}$ and $v_{\xi }\approx \mathrm{const}$ in the vicinity of the inner core surface, integrating this equation, and taking into account that $\theta ={\theta }_0$ at $\xi =0$, we obtain

$$\xi \approx \frac{{\lambda }_{sl}\left({\varphi }_{*}\right)}{\rho \left({\varphi }_{*}\right)c\left({\varphi }_{*}\right)v_{\xi }}ln\frac{\theta -{\theta }_v}{{\theta }_0-{\theta }_v},{\theta }_v=\frac{Q_V{\varphi }_{*}}{\rho \left({\varphi }_{*}\right)c\left({\varphi }_{*}\right)}.$$

(18)

Substituting $\theta ={\theta }_{\Xi }$ at $\xi =\Xi$ in Equation (18) and equating the upward and downward fluid flows in the mushy region, we arrive at the horizontal dimension $\Xi$ of the mushy region’s convective mesh and the radius of the chimney $\alpha$ in the form of

$$\Xi \approx \frac{{\lambda }_{sl}\left({\varphi }_{*}\right)}{\rho \left({\varphi }_{*}\right)c\left({\varphi }_{*}\right)v_{\xi }}ln\frac{{\theta }_{\Xi }-{\theta }_v}{{\theta }_0-{\theta }_v},\alpha \approx \Xi \sqrt{|\overline{V}/\overline{v}|}.$$

(19)

It is possible to estimate here ${\theta }_{\Xi }$ and ${\theta }_0$ as the maximum and minimum temperatures at the inner core surface (for example, ${\theta }_{\Xi }\approx 6000$ K and ${\theta }_0\approx 5000$ K [11]), and $|\overline{V}|$ and $|\overline{v}|$ denote the average velocities of downward and upward fluid flows.

The average radius of the chimney $\alpha$ and the average distance between the chimneys ∼$2\Xi$ are shown in Figure 3. As can easily be seen, the $\alpha$ radius grows as the average velocity of the fluid $|\overline{V}|$ (directed toward the inner core surface) builds up. It is worth noting that our estimate for $\alpha$, less than or of the order of ${10}^{-1}\Xi$, is in agreement with the numerical simulation of the chimney formation in a Hele–Shaw cell, as noted by Katz and Worster [22].

4. Conclusions

A schematic arrangement of the mushy region with narrow chimneys of convective fluid at the Earth’s inner core is shown in Figure 4. Namely, the chimneys are relatively narrow regions of upward melt flows from the solid inner core to the outer core (their characteristic size is of the order of $2\alpha$). Broader regions of downward melt flows lie between them, whose characteristic sizes are of the order of $2\Xi$. As this takes place, a mushy region consisting of dendrite-like elements is located between two neighboring chimneys (the characteristic sizes of dendritic tips and their stable growth rate selection are presented in [7]). It is important to note that the mushy region width (dashed curve connecting dendritic tips in Figure 4) grows up from the central region ($\xi \approx 0$) to the place lying near a chimney ($\xi \approx \Xi$). This can be attributed to the fact that as the melt velocity decreases, constitutional supercooling increases. In other words, relatively low flow velocities $|\overline{V}|$∼$|{\overline{V}}_c|$ lead to a larger width of the mushy region. Also, it is significant that the mushy region vanishes near the channel filled with incoming hot melt (where $|\overline{V}|$ is less than $|{\overline{V}}_c|$).

In summary, let us formulate the most important conclusions of the developed theory. (1) A schematic arrangement of the mushy region near the Earth’s inner core is similar to crystallization processes in terrestrial conditions [22,34]. Namely, the mushy region width changes along the solid inner core boundary (with a spatial axis of $\xi$) because of different melt velocities at different points $\xi$. In addition, this width increases with the growth of the solid phase near the inner core, its crystallization velocity, and as the melt velocity slows down while moving from the fluid outer core to the solid inner core. (2) A typical dynamic viscosity of the inner core melt is estimated as ${10}^{13}$–${10}^{17}$ Pa-s (which is consistent with [7,50]) while the characteristic size of dendritic tips is in the range of ∼${10}^{-3}$–${10}^{-2}$ m (which is consistent with [7]). As this takes place, the characteristic spacing $2\Xi$ between chimneys is of the order of ∼${10}^1$–${10}^3$ m while a typical size $2\alpha$ of a chimney is of the order of ${10}^{-1}\Xi$. Note that these parameters have been found based on their orders of magnitude using analytical solutions that took into account characteristic physical parameters related to the Earth’s inner core solidification. (3) A typical interdendritic spacing ${\lambda }_1$ between the primary stems of dendrites in a mush is of the order of 10–10² m. It is significant that the primary interdendritic spacing reduces when the crystallization and melt velocities increase, as well as when the dynamic viscosity of the melt is estimated to be larger.