Designing an Efficient Lead-Free Perovskite Solar Cell through a Computational Method
Abstract
1. Introduction
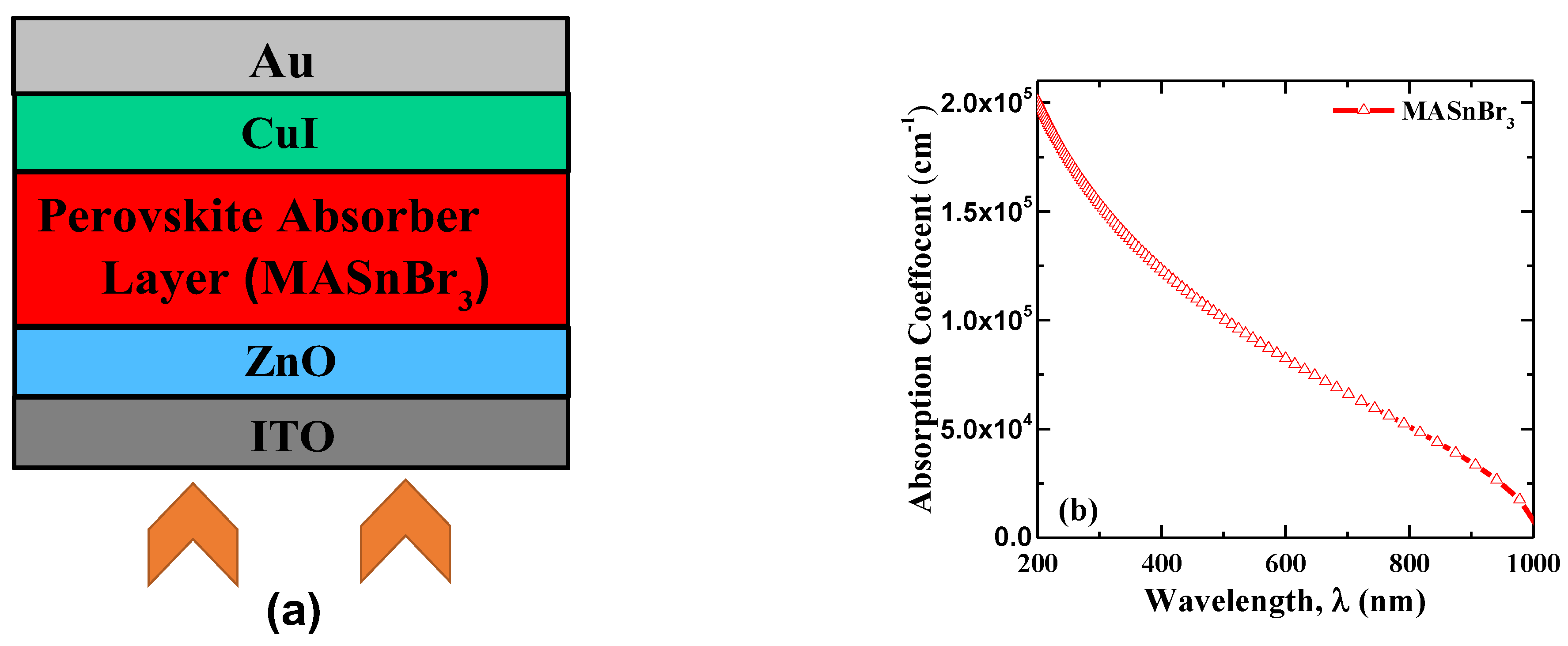
2. Simulated Device Structures
3. Computational Modeling
4. Results and Discussions
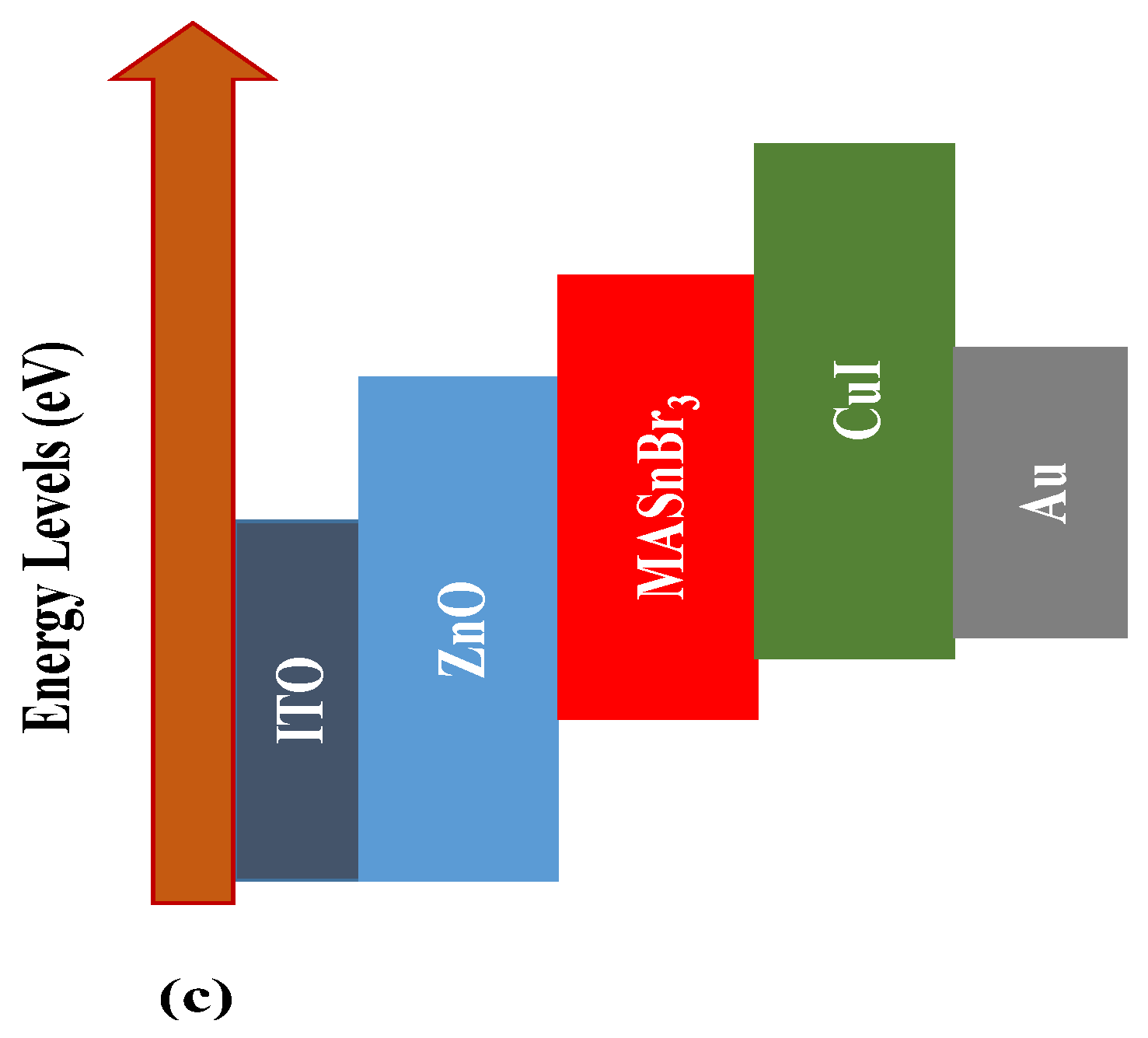
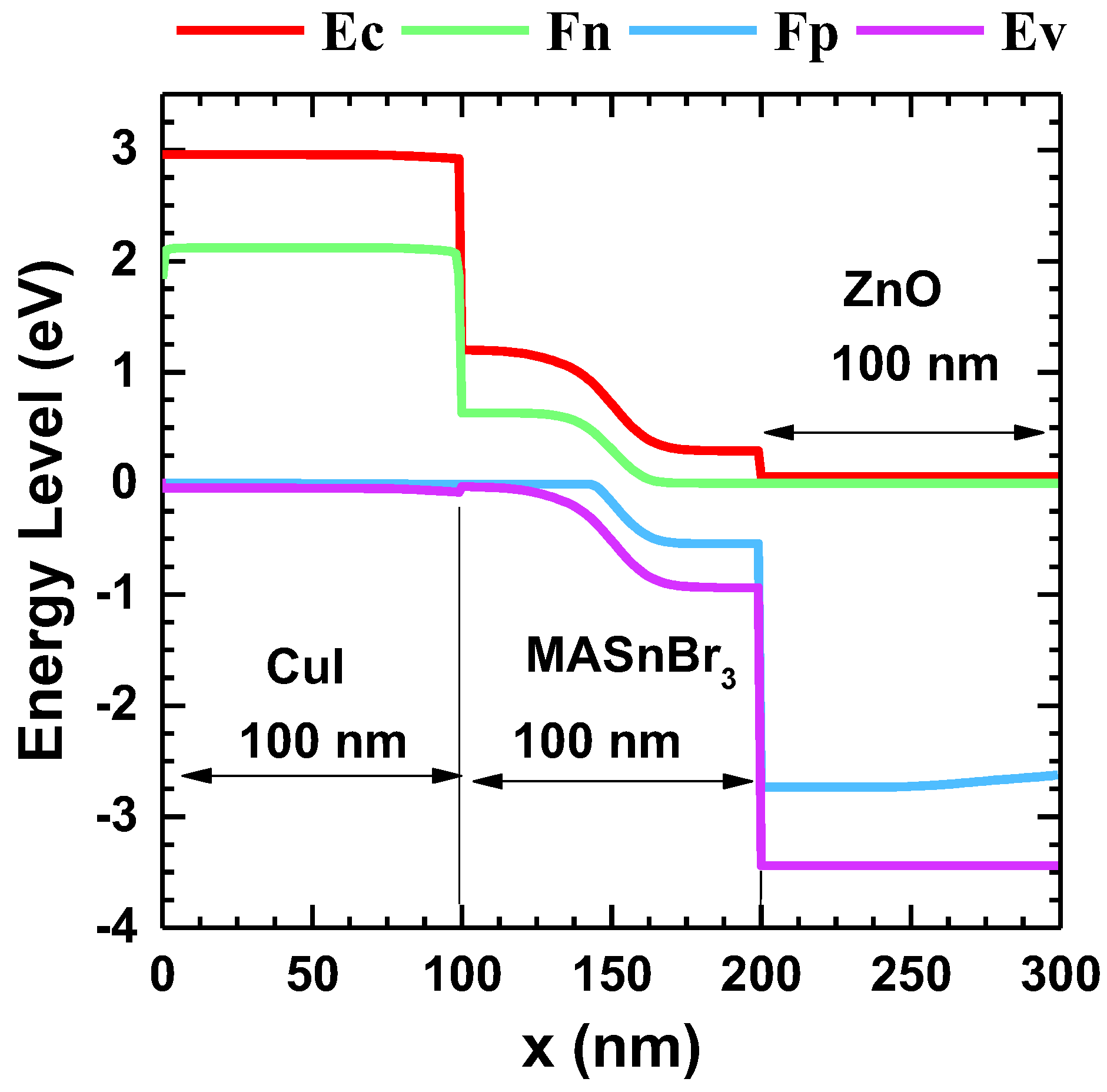
4.1. The Alignment of the Bandgap of PSC
4.2. Effect of Active Layer Thickness
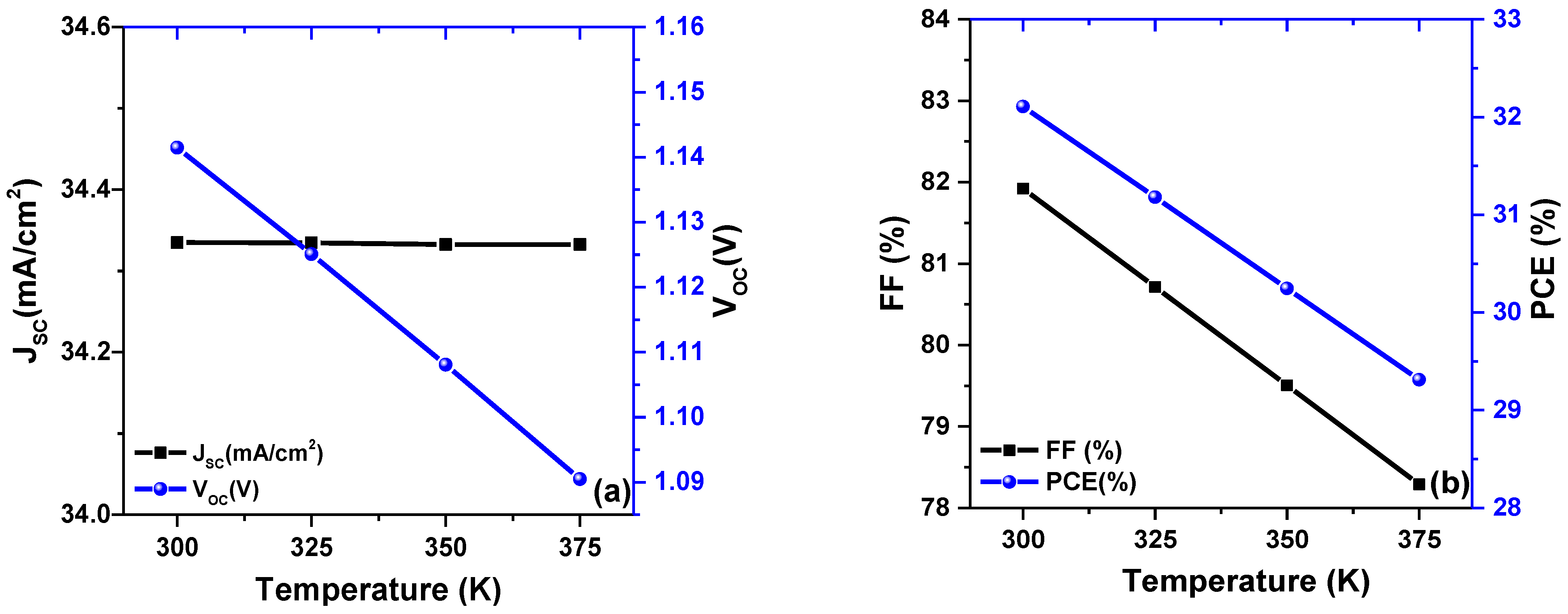
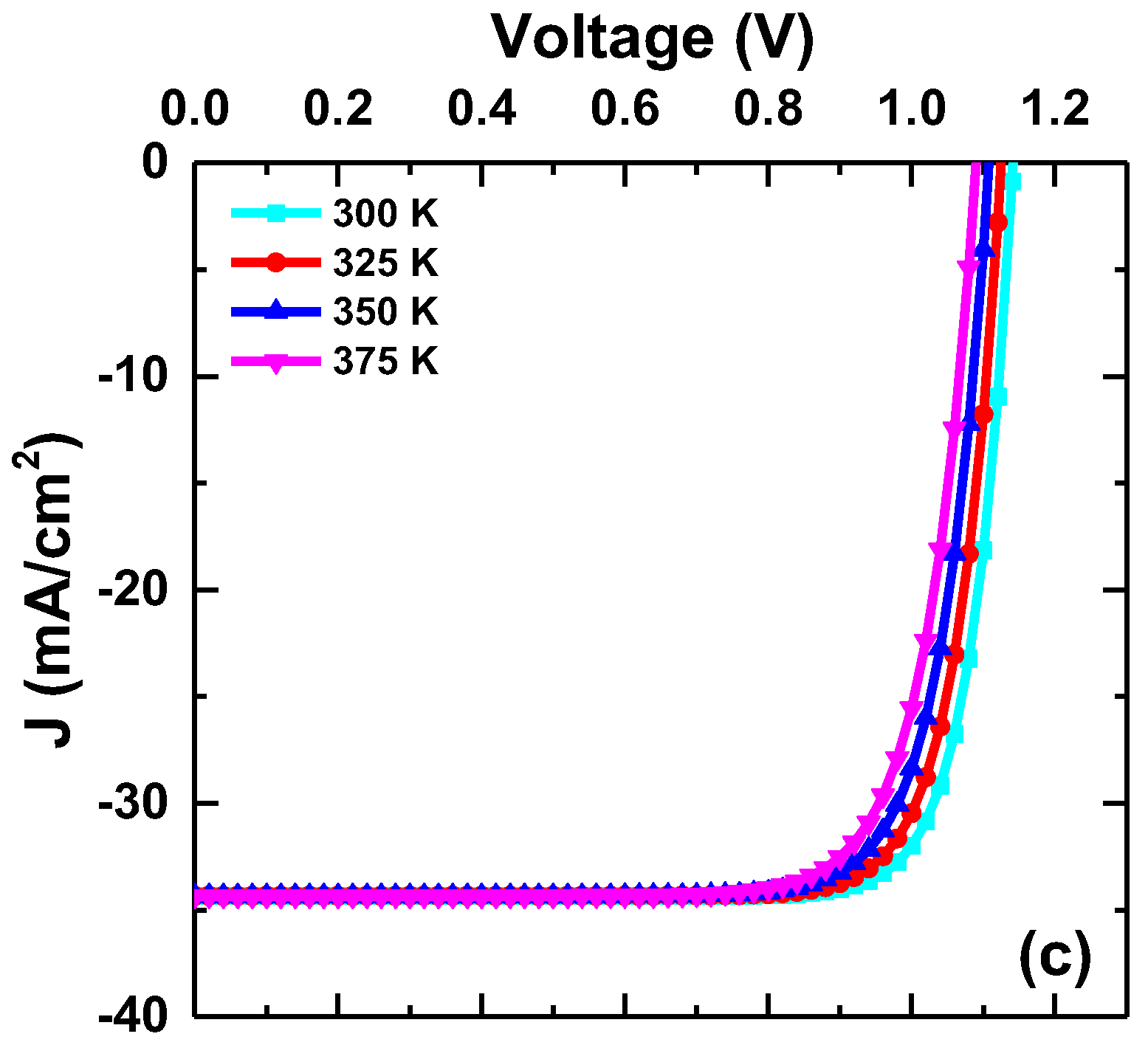
4.3. Effect of Temperature
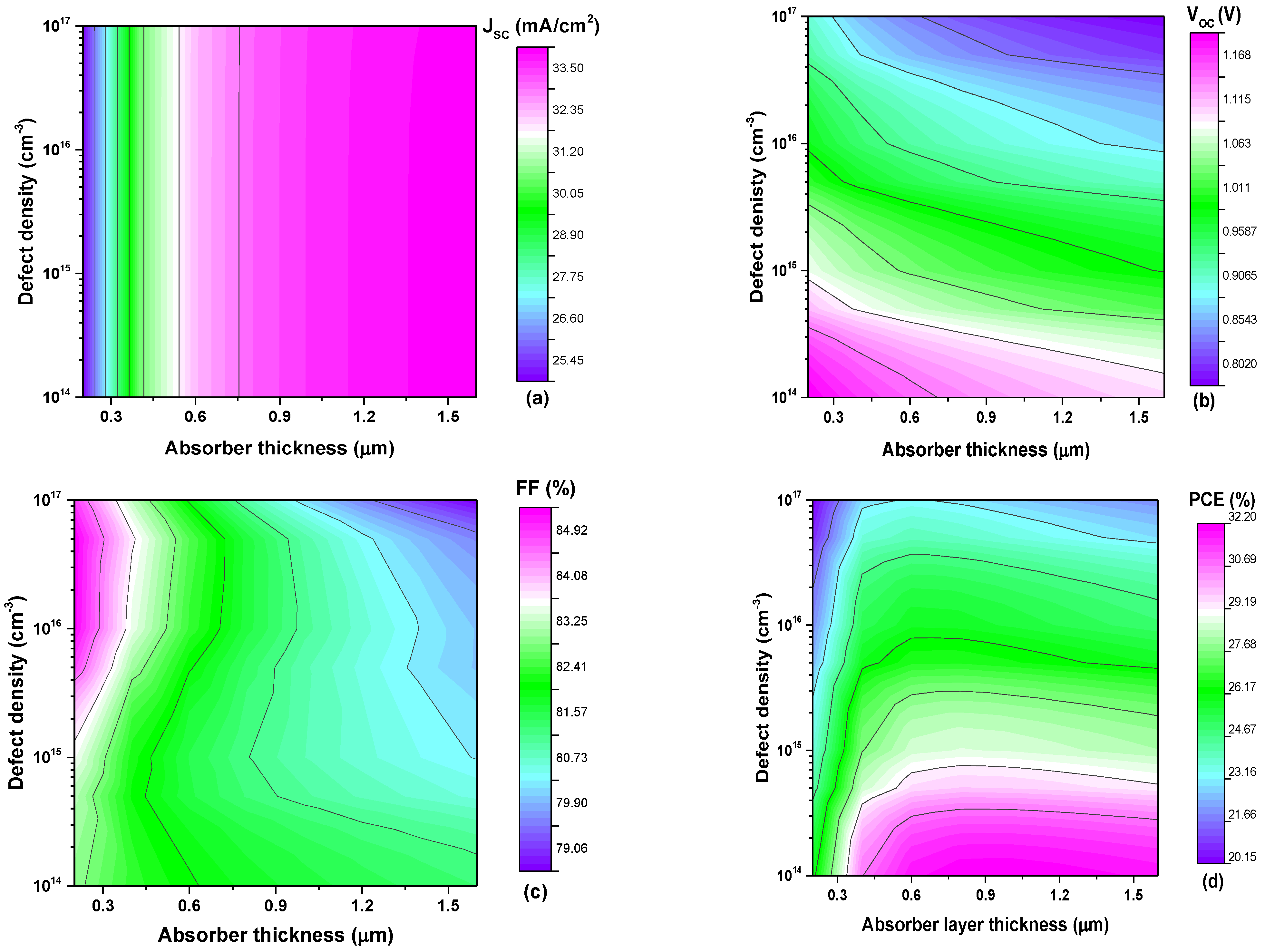
4.4. Effect of the Bulk Defect—Density of the Active Layers
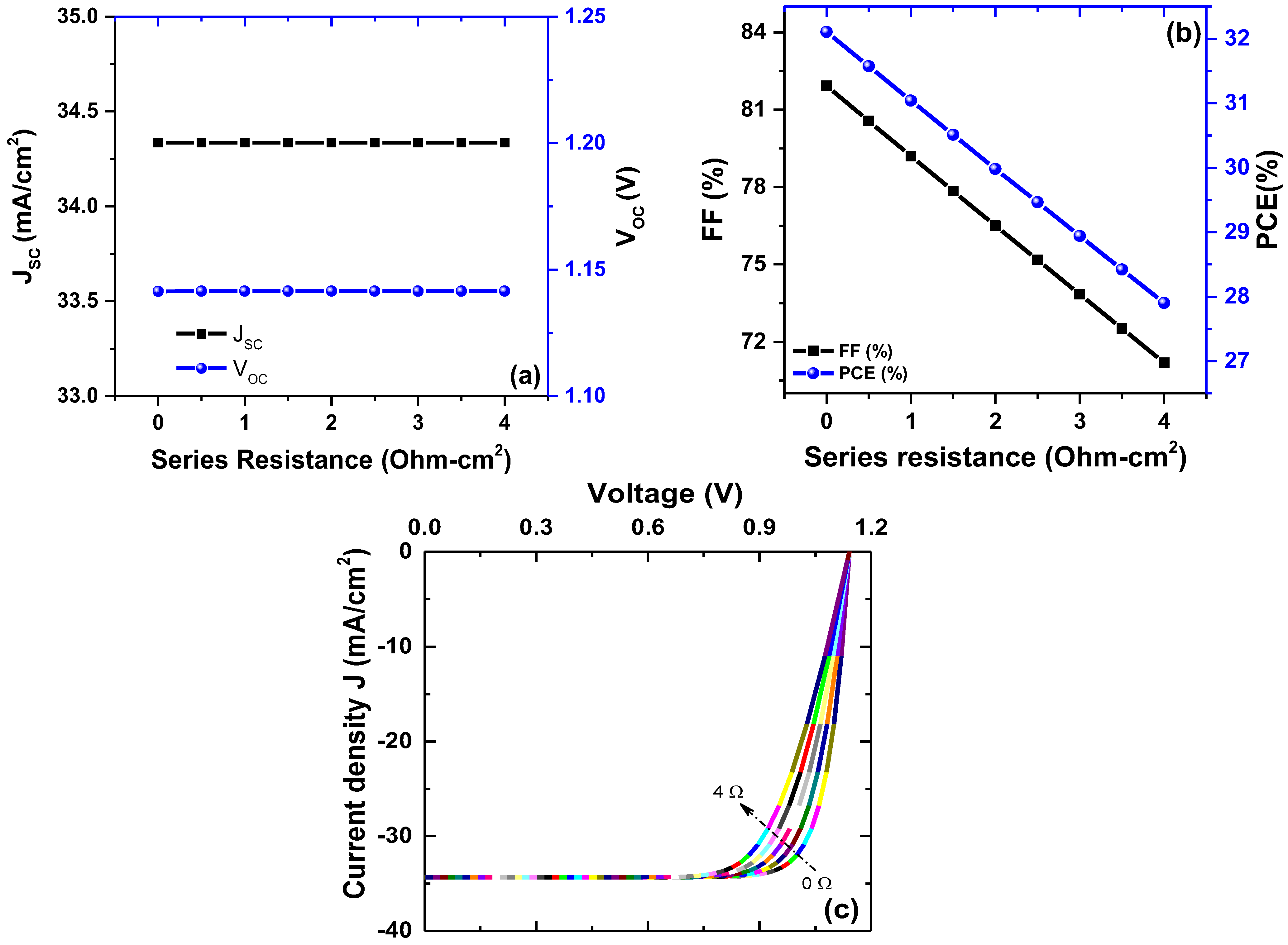
4.5. Impact of Series Resistance on Outputs of the PSC
4.6. The Collective Impact of Total Defect Density and Thickness
4.7. The Quantum Efficiency (QE) and Current vs. Voltage (JV) Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hima, A.; Lakhdar, N.; Benhaoua, B.; Saadoune, A.; Kemerchou, I.; Rogti, F. An optimized perovskite solar cell designs for high conversion efficiency. Superlattices Microstruct. 2019, 129, 240–246. [Google Scholar] [CrossRef]
- Bhattarai, S.; Mhamdi, A.; Hossain, I.; Raoui, Y.; Pandey, R.; Madan, J.; Bouazizi, A.; Maiti, M.; Gogoi, D.; Sharma, A. A detailed review of perovskite solar cells: Introduction, working principle, modelling, fabrication techniques, future challenges. Micro Nanostructur. 2022, 172, 207450. [Google Scholar] [CrossRef]
- Raoui, Y.; Ez-Zahraouy, H.; Kazim, S.; Ahmad, S. Energy level engineering of charge selective contact and halide perovskite by modulating band offset: Mechanistic insights. J. Energy Chem. 2021, 54, 822–829. [Google Scholar] [CrossRef]
- Snaith, H.J.; Hacke, P.J.N.E. Enabling reliability assessments of pre-commercial perovskite photovoltaics with lessons learned from industrial standards. Nat. Energy 2018, 3, 459–465. [Google Scholar] [CrossRef]
- Bhattarai, S.; Das, T.D. Optimization of carrier transport materials for the performance enhancement of the MAGeI3 based perovskite solar cell. Sol. Energy 2021, 217, 200–207. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Muchahary, D.; Ram, L.S.; Narzary, R.; Sahu, P.P.; Bhattarai, S.; Tayal, V. Heterojunction between crystalline silicon and nanocomposite coupled ZnO·SnO2 and optimization of its photovoltaic performance. Curr. Appl. Phys. 2022, 38, 15–21. [Google Scholar] [CrossRef]
- Bhattarai, S.; Pandey, R.; Madan, J.; Ahmed, F.; Shabnam, S. Performance improvement approach of all inorganic perovskite solar cell with numerical simulation. Mater. Today Commun. 2022, 33, 104364. [Google Scholar] [CrossRef]
- Devi, C.; Mehra, R. Device simulation of lead-free MASnI3 solar cell with CuSbS2 (copper antimony sulfide). J. Mater. Sci. 2019, 54, 5615–5624. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.; Pandey, R. Computational Modelling and Optimization of a Methylammonium-free Perovskite and Ga-free Chalcogenide Tandem Solar Cell with an Efficiency above 25 %. ChemistrySelect 2022, 7, e202200667. [Google Scholar] [CrossRef]
- Im, J.-H.; Lee, C.-R.; Lee, J.-W.; Park, S.-W.; Park, N.-G. 6.5% efficient perovskite quantum-dot-sensitized solar cell. Nanoscale 2011, 3, 4088–4093. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-S.; Lee, C.-R.; Im, J.-H.; Lee, K.-B.; Moehl, T.; Marchioro, A.; Moon, S.-J.; Humphry-Baker, R.; Yum, J.-H.; Moser, J.E.; et al. Lead Iodide Perovskite Sensitized All-Solid-State Submicron Thin Film Mesoscopic Solar Cell with Efficiency Exceeding 9%. Sci. Rep. 2012, 2, 591. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Johnston, M.B.; Snaith, H.J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef]
- Xi, J.Y.; Jia, R.; Li, W.; Wang, J.; Bai, F.Q.; Eglitis, R.I.; Zhang, H.X. How does graphene enhance the photoelectric conversion efficiency of dye sensitized solar cells? An insight from a theoretical perspective. J. Mater. Chem. A 2019, 7, 2730–2740. [Google Scholar] [CrossRef]
- Bhattarai, S.; Das, T.D. Optimization of the perovskite solar cell design to achieve a highly improved efficiency. Opt. Mater. 2021, 111, 110661. [Google Scholar] [CrossRef]
- Bhattarai, S.; Sharma, A.; Muchahary, D.; Gogoi, D.; Das, T.D. Numerical simulation study for efficiency enhancement of doubly graded perovskite solar cell. Opt. Mater. 2021, 118, 111285. [Google Scholar] [CrossRef]
- Ahmed, M.I.; Habib, A.; Javaid, S.S. Perovskite Solar Cells: Potentials, Challenges, and Opportunities. Int. J. Photoenergy 2015, 205, 592308. [Google Scholar] [CrossRef]
- Lakhdar, N.; Hima, A.J.O.M. Electron transport material effect on performance of perovskite solar cells based on CH3NH3GeI3. Opt. Mater. 2020, 99, 109517. [Google Scholar]
- Bhattarai, S.; Pandey, R.; Madan, J.; Mhamdi, A.; Bouazizi, A.; Muchahary, D.; Gogoi, D.; Sharma, A.; Das, T.D. Investigation of Carrier Transport Materials for Performance Assessment of Lead-Free Perovskite Solar Cells. IEEE Trans. Electron Devices 2022, 69, 3217–3224. [Google Scholar] [CrossRef]
- Huang, P.-H.; Wang, Y.-H.; Ke, J.-C.; Huang, C.-J. The Effect of Solvents on the Performance of CH3NH3PbI3 Perovskite Solar Cells. Energies 2017, 10, 599. [Google Scholar] [CrossRef]
- Du, H.-J.; Wang, W.-C.; Zhu, J.-Z. Device simulation of lead-free CH3NH3SnI3 perovskite solar cells with high efficiency. Chin. Phys. B 2016, 25, 108802. [Google Scholar] [CrossRef]
- Noel, N.K.; Stranks, S.D.; Abate, A.; Wehrenfennig, C.; Guarnera, S.; Haghighirad, A.-A.; Sadhanala, A.; Eperon, G.E.; Pathak, S.K.; Johnston, M.B.; et al. Lead-free organic–inorganic tin halide perovskites for photovoltaic applications. Energy Environ. Sci. 2014, 7, 3061–3068. [Google Scholar] [CrossRef]
- Umari, P.; Mosconi, E.; Angelis, F.D. Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 Perovskites for Solar Cell Applications. Sci. Rep. 2014, 4, 4467. [Google Scholar] [CrossRef]
- Bhattarai, S.; Pandey, R.; Madan, J.; Muchahary, D.; Gogoi, D. A novel graded approach for improving the efficiency of Lead-Free perovskite solar cells. Sol. Energy 2022, 244, 255–263. [Google Scholar] [CrossRef]
- Mottakin, M.; Sobayel, K.; Sarkar, D.; Alkhammash, H.; Alharthi, S.; Techato, K.; Shahiduzzaman, M.; Amin, N.; Sopian, K.; Akhtaruzzaman, M. Design and Modelling of Eco-Friendly CH3NH3SnI3-Based Perovskite Solar Cells with Suitable Transport Layers. Energies 2021, 14, 7200. [Google Scholar] [CrossRef]
- Jeon, I.; Kim, K.; Jokar, E.; Park, M.; Lee, H.-W.; Diau, E.W. Environmentally Compatible Lead-Free Perovskite Solar Cells and Their Potential as Light Harvesters in Energy Storage Systems. Nanomaterials 2021, 11, 2066. [Google Scholar] [CrossRef]
- Burgelman, M.; Verschraegen, J.; Degrave, S.; Nollet, P. Modeling thin-film PV devices. Prog. Photovolt. 2004, 12, 143–153. [Google Scholar] [CrossRef]
- Burgelman, M.; Marlein, J. Analysis of graded band gap solar cells with SCAPS. In Proceedings of the 23rd European Photovoltaic Conference, Valencia, Spain, 1–5 September 2008. [Google Scholar]
- Bhattarai, S.; Sharma, A.; Das, T.D. Factor affecting the performance of perovskite solar cell for distinct MAPI layer thickness. AIP Conf. Proc. 2020, 2269, 030071. [Google Scholar]
- Elumalai, N.K.; Mahmud, M.A.; Wang, D.; Uddin, A. Perovskite Solar Cells: Progress and Advancements. Energies 2016, 9, 861. [Google Scholar] [CrossRef]
- Karthick, S.; Velumani, S.; Bouclé, J. Experimental and SCAPS simulated formamidinium perovskite solar cells: A comparison of device performance. Sol. Energy 2020, 205, 349–357. [Google Scholar] [CrossRef]
- Rai, S.; Pandey, B.K.; Dwivedi, D.K. Modeling of highly efficient and low cost CH3NH3Pb(I1-xClx)3 based perovskite solar cell by numerical simulation. Opt. Mater. 2020, 100, 109631. [Google Scholar] [CrossRef]
- Al-Mousoi, A.K.; Mohammed, M.K.A.; Pandey, R.; Madan, J.; Dastan, D.; Ravi, G.; Sakthivel, P.; Anandha babu, G. Simulation and analysis of lead-free perovskite solar cells incorporating cerium oxide as electron transporting layer. RSC Adv. 2022, 12, 32365–32373. [Google Scholar] [CrossRef] [PubMed]
- Samiul Islam, M.; Sobayel, K.; Al-Kahtani, A.; Islam, M.A.; Muhammad, G.; Amin, N.; Shahiduzzaman, M.; Akhtaruzzaman, M. Defect Study and Modelling of SnX3-Based Perovskite Solar Cells with SCAPS-1D. Nanomaterials 2021, 11, 1218. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Kelly, T.L. Perovskite solar cells with a planar heterojunction structure prepared using room-temperature solution processing techniques. Nat. Photonics 2014, 8, 133–138. [Google Scholar] [CrossRef]
- Ebner, M.; Marone, F.; Stampanoni, M.; Wood, V.J.S. Visualization and quantification of electrochemical and mechanical degradation in Li ion batteries. Science 2013, 342, 716–720. [Google Scholar] [CrossRef]
- Fossum, J.G. Computer-aided numerical analysis of silicon solar cells. Solid State Electron. 1976, 19, 269–277. [Google Scholar] [CrossRef]
- Bhattarai, S.; Sharma, A.; Muchahary, D.; Gogoi, M.; Das, T.D. Carrier transport layer free perovskite solar cell for enhancing the efficiency: A simulation study. Optik 2021, 243, 167492. [Google Scholar] [CrossRef]
- Singh, A.K.; Srivastava, S.; Mahapatra, A.; Baral, J.K.; Pradhan, B. Performance optimization of lead free-MASnI3 based solar cell with 27% efficiency by numerical simulation. Opt. Mater. 2021, 117, 111193. [Google Scholar] [CrossRef]



| Parameters | ETM (ZnO) | PVK (MASnBr3) | HTM (CuI) |
|---|---|---|---|
| t (µm) | 0.1 | 0.2–1.6 | 0.1 |
| Eg (eV) | 3.3 | 1.3 | 3.5 |
| εr | 9 | 10 | 6.5 |
| χ (eV) | 4.1 | 4.17 | 2.1 |
| Nc (1/cm3) | 4 × 1018 | 2.2 × 1018 | 2.8 × 1019 |
| NV (1/cm3) | 1 × 1019 | 1.8 × 1019 | 1 × 1019 |
| µn (cm2/Vs) | 100 | 1.6 | 1.7 × 10−4 |
| µp (cm2/Vs) | 50 | 1.6 | 2 × 10−4 |
| NA (1/cm3) | 1 × 105 | 1 × 1013 | 1 × 1018 |
| ND (1/cm3) | 1 × 1018 | 1 × 1013 | 0 |
| Nt (1/cm3) | 1 × 1015 | 1 × 1015 | 1 × 1015 |
| Parameters | CuI/ PALs | PALs/ZnO |
|---|---|---|
| Defect type | Neutral | Neutral |
| Capture cross section electrons (cm2) | 1 × 10−19 | 1 × 10−19 |
| Capture cross section holes (cm2) | 1 × 10−19 | 1 × 10−19 |
| Energy distributions | single | single |
| Reference for defect energy level | Above the highest EV | Above the highest EV |
| Energy with respect to reference (eV) | 0.6 | 0.6 |
| Total density (integrated over all energies) (cm−2) | 1 × 109 | 1 × 109 |
| Device Architectures | JSC (mA/cm2) | VOC (V) | FF (%) | PCE (%) |
|---|---|---|---|---|
| Optimized Device (Present work) | 34.09 | 1.145 | 82.06 | 32.19 |
| Bhattarai et al. [19] | 33.19 | 0.876 | 76.19 | 22.16 |
| Du et al. [21] | 23.36 | 0.92 | 79.99 | 23.36 |
| Singh et al. [39] | 25.97 | 1.203 | 87.79 | 27.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattarai, S.; Kalita, P.K.; Hossain, I.; Alsubaie, A.S.; Mahmoud, K.H.; Ansari, M.Z.; Janicek, P. Designing an Efficient Lead-Free Perovskite Solar Cell through a Computational Method. Crystals 2023, 13, 1175. https://doi.org/10.3390/cryst13081175
Bhattarai S, Kalita PK, Hossain I, Alsubaie AS, Mahmoud KH, Ansari MZ, Janicek P. Designing an Efficient Lead-Free Perovskite Solar Cell through a Computational Method. Crystals. 2023; 13(8):1175. https://doi.org/10.3390/cryst13081175
Chicago/Turabian StyleBhattarai, Sagar, P. K. Kalita, Ismail Hossain, Abdullah Saad Alsubaie, Khaled Hussein Mahmoud, Mohd Zahid Ansari, and Petr Janicek. 2023. "Designing an Efficient Lead-Free Perovskite Solar Cell through a Computational Method" Crystals 13, no. 8: 1175. https://doi.org/10.3390/cryst13081175
APA StyleBhattarai, S., Kalita, P. K., Hossain, I., Alsubaie, A. S., Mahmoud, K. H., Ansari, M. Z., & Janicek, P. (2023). Designing an Efficient Lead-Free Perovskite Solar Cell through a Computational Method. Crystals, 13(8), 1175. https://doi.org/10.3390/cryst13081175







