Interface-Dominated Plasticity and Kink Bands in Metallic Nanolaminates
Abstract
1. Introduction
2. Review of MFDM Theory
2.1. Boundary Conditions
- The evolution equation (shown in Equation (4a)) has a convective boundary condition of the form , where is a second order tensor valued function of position and time on the boundary, characterizing the flux of dislocations at the surface satisfying the constraint . Here, n is the outward unit normal field on the boundary.The boundary condition is specified in two ways: (a) Plastically constrained: is specified at a point x on the boundary for all times, which ensures that there is no outflow of dislocations at that point of the boundary, and only parallel motion along the boundary is allowed. (b) Plastically unconstrained: A less restrictive boundary condition where is simply evaluated at the boundary (akin to an outflow condition), along with the specification of dislocation flux on the inflow part of the boundary. Additionally, for all calculations presented in this paper is imposed, a particular specification of a boundary condition that arises from simple mathematical modeling of the manifestation of dislocation core energy at the mesoscale.
- For the incompatibility equation, is applied on the outer boundary of the domain, which along with the system (4b) ensures that vanishes when is zero in the entire domain.
- The evolution equation requires a Neumann boundary condition, i.e., on the outer boundary of the domain.
- The material velocity boundary conditions are applied based on the loading type, which is discussed later in Section 4.
2.2. Initial Conditions
- The initial condition is assumed for all simulations here.
- In general, the initial condition for is obtained by solving for from the incompatibility equation and solving for from the equilibrium equation, for prescribed on the given initial configuration. We refer to this scheme as the elastic theory of continuously distributed dislocations (ECDD). For the initial conditions on considered above, this step is trivial, with , where X is the position field on the initial configuration.
- The model admits an arbitrary specification of at a point to uniquely evolve f using (4c) in time, and this rate is prescribed to vanish.
2.3. Constitutive Relations
3. Review of Results from MFDM
- It is difficult to deduce a physical connection between the plastic strain/distortion in classical plasticity theory to the mechanics of dislocation, beyond modeling in 1-D. The MFDM framework brings out an explicit connection between the plastic strain rate and the motion and geometry of an evolving microscopic array of dislocations. Obviously, this has many benefits, even for a phenomenological specification of the macroscopic plastic strain rate. Moreover, the MFDM framework has allowed for a first unification between phenomenological and crystal plasticity theories and quantitative dislocation mechanics.
- With a single extra material fitting parameter beyond a classical plasticity model (and two in the finite deformation setting), the MFDM framework has enabled a significant variety of phenomena to be modeled, in qualitative and quantitative accord with experimental results.
4. Results and Discussion
- at the bottom boundary of the domain.
- at the top boundary of the domain, where L is the length of the laminate in the (undeformed) initial configuration at .
- The applied traction in the horizontal direction is zero on both the top and the bottom boundary of the domain.
- at a single node of the bottom boundary. This along with the above conditions suffices to constrain rigid motion.
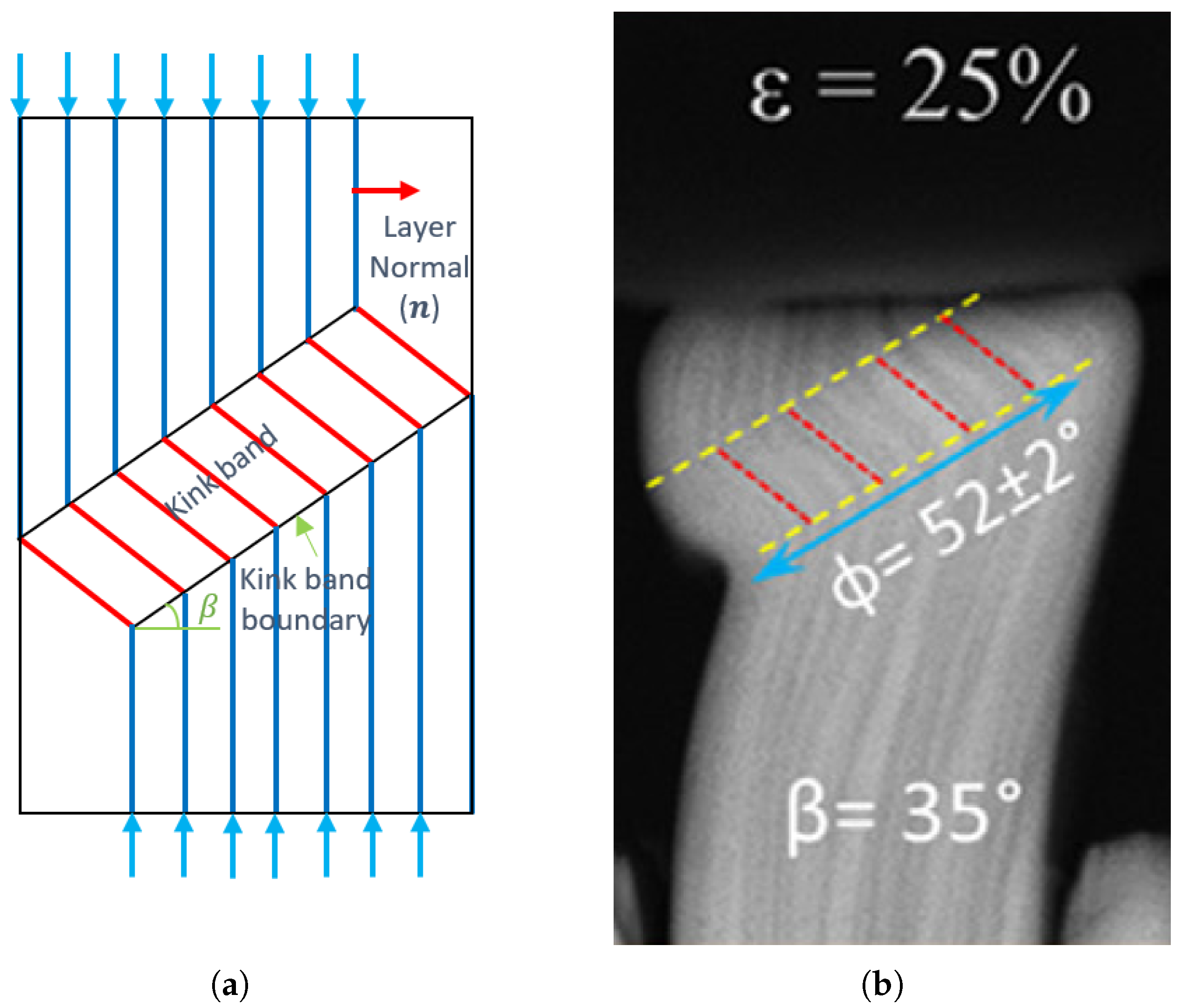
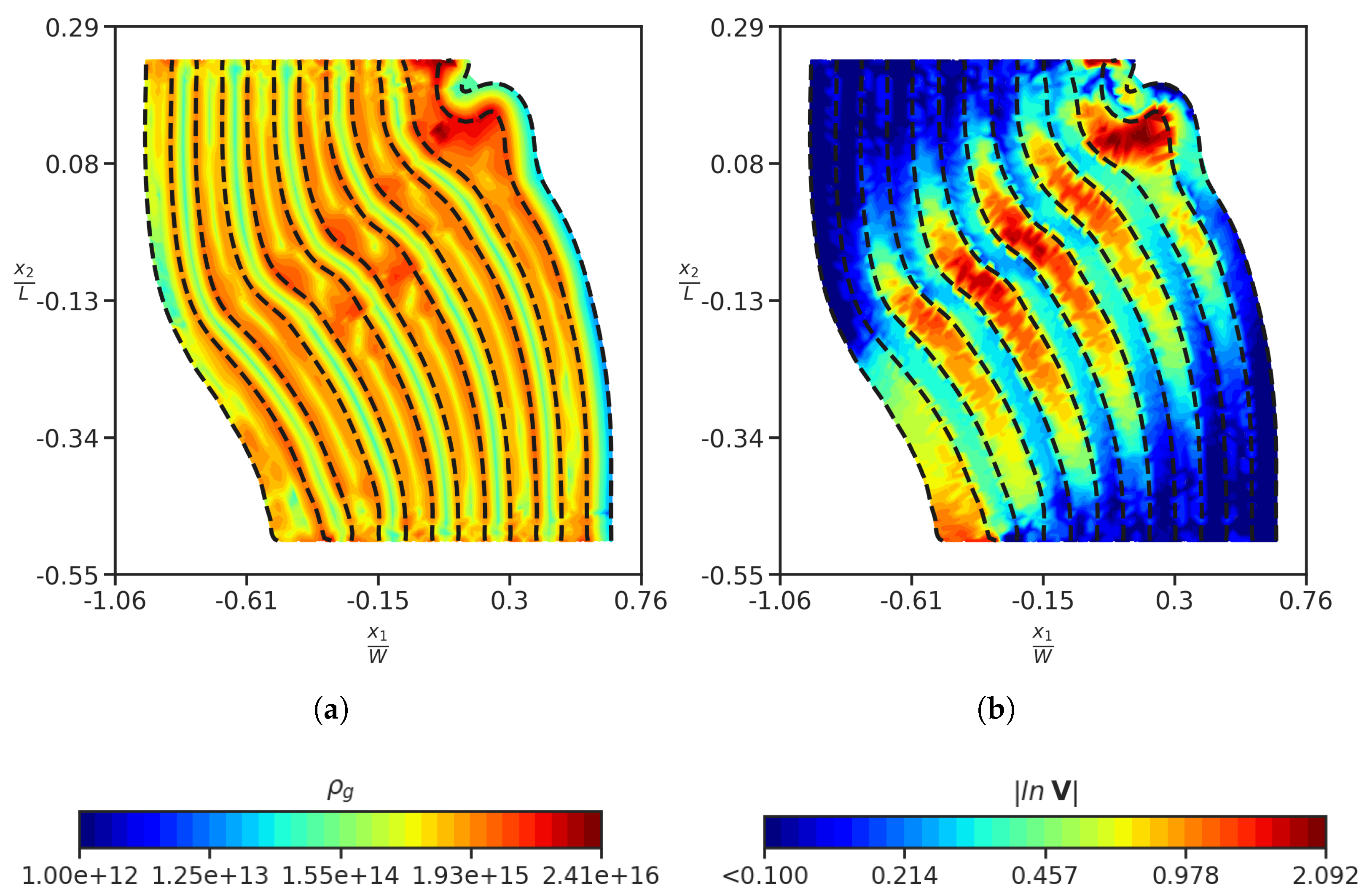
4.1. Kink Band Formation
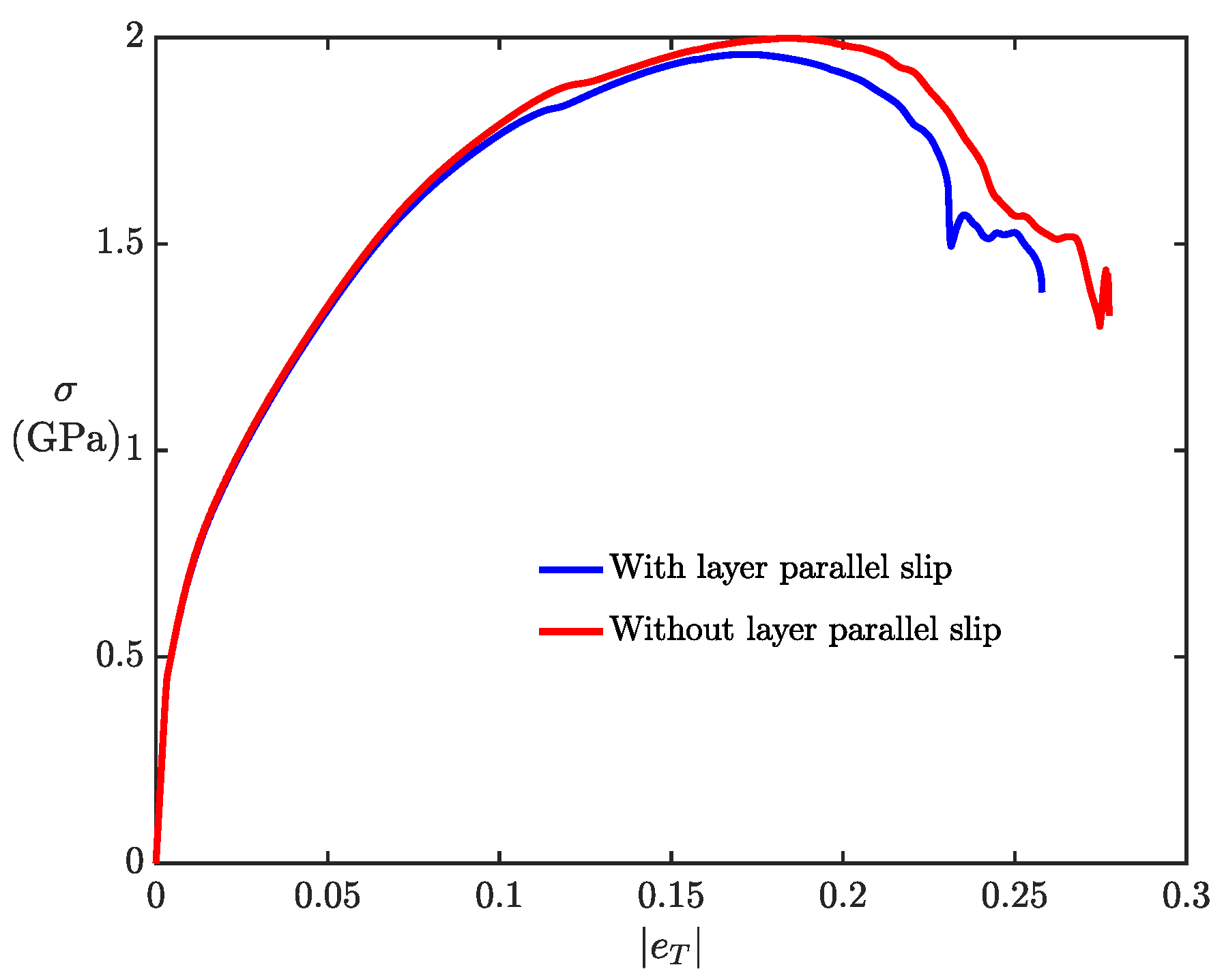
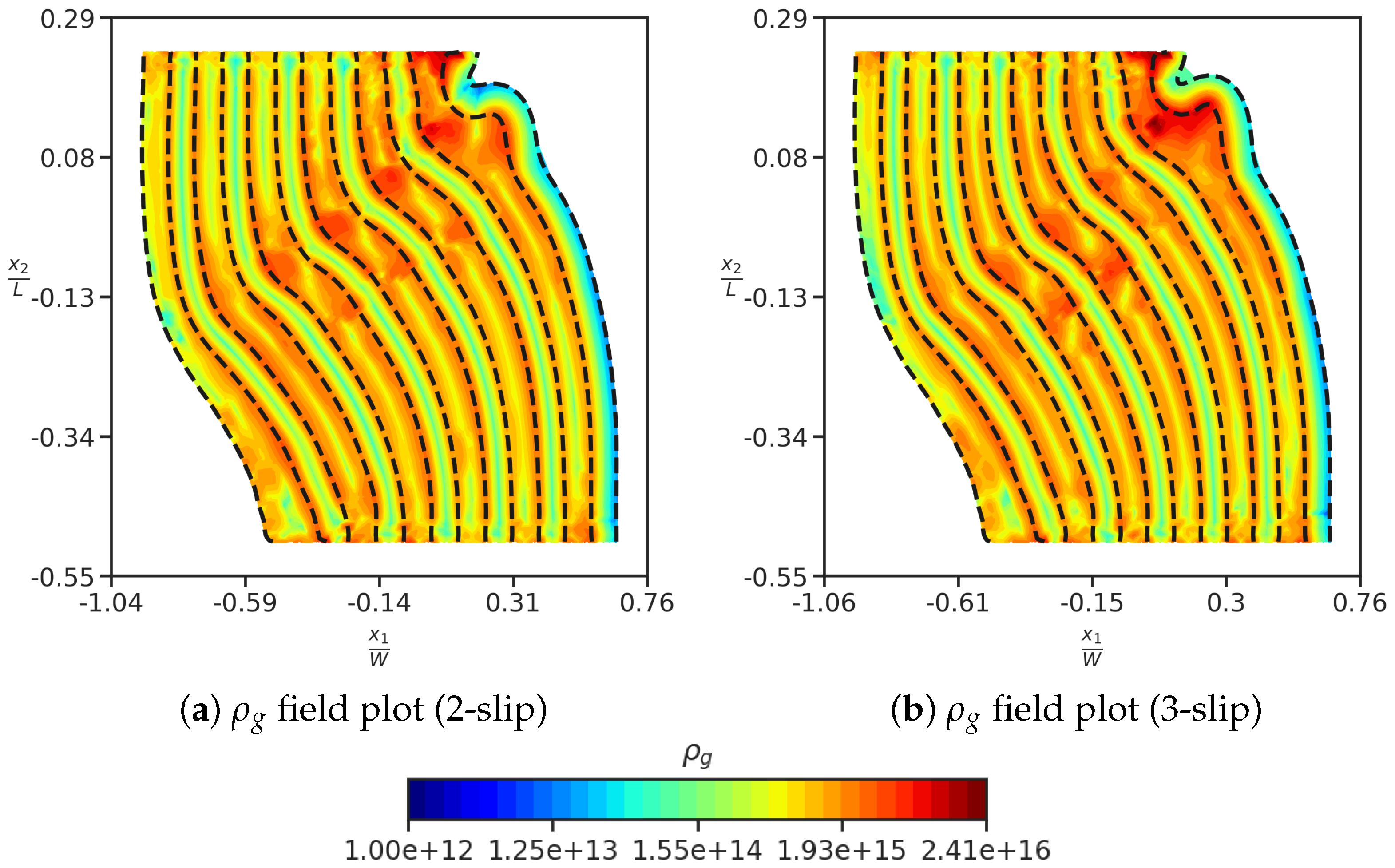
4.2. Effect of Different Slip Systems, Ordering of Metallic Layers, and Slip Systems Orientations
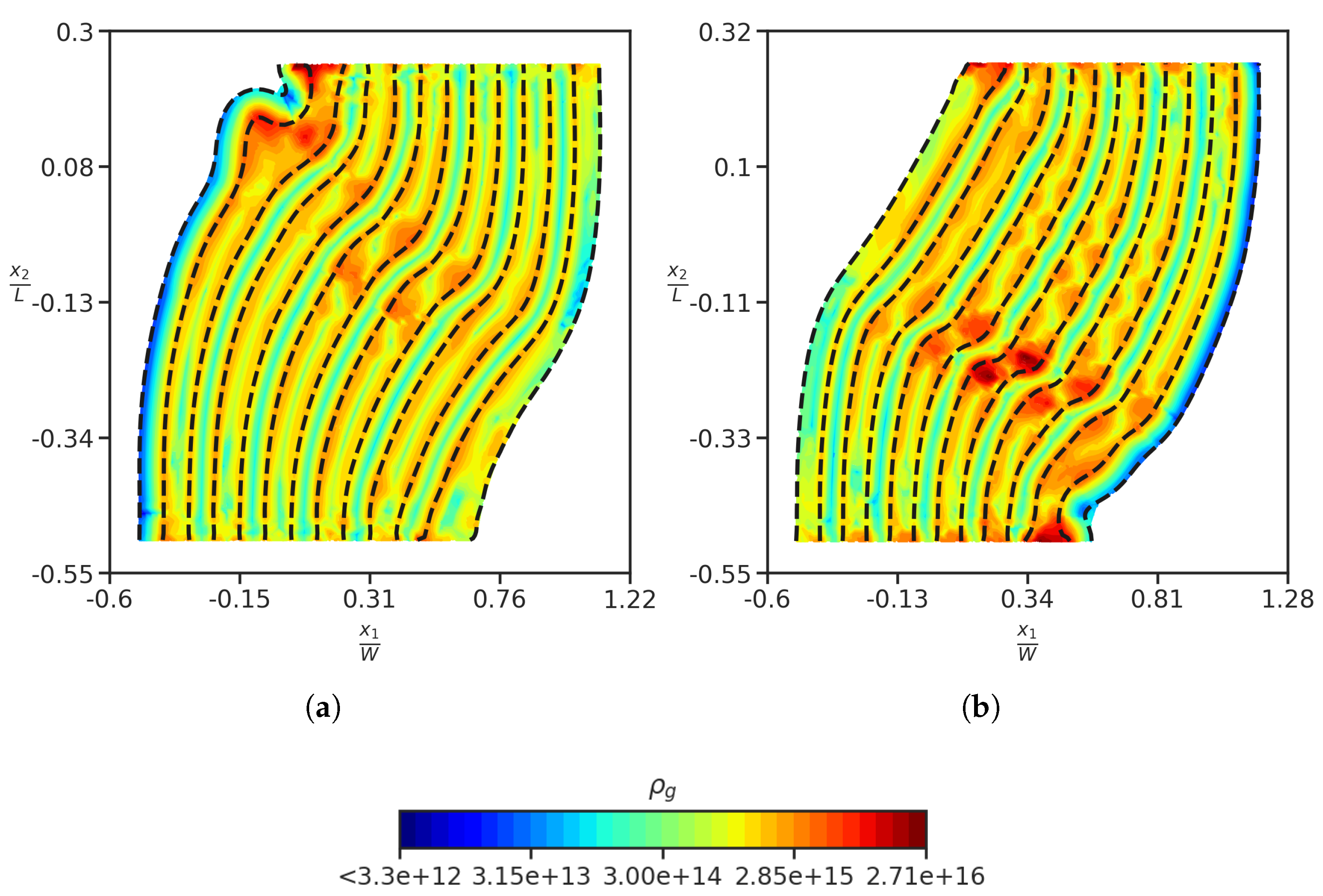
- Flipping the order of Cu and Nb layers in the nano-laminate structure resulted in a change in the orientation of the band as shown in Figure 6a, due to a geometrical asymmetry in the initial configuration.
- Removal of inclined slip system, and just considering layer parallel slip system and inclined slip system, resulted in the orientation of the band as shown in Figure 6b.
- Removal of the oriented slip plane did not change the orientation of the kink band formed, and it is similar to as shown in Figure 3.
- We consider different orientations of slip vectors () from to for Cu, and keep the slip vector orientation for Nb to be the same i.e., . Kink bands form for slip vector orientations from to , but for to kink bands do not form, and NMLs undergo more uniform compression.
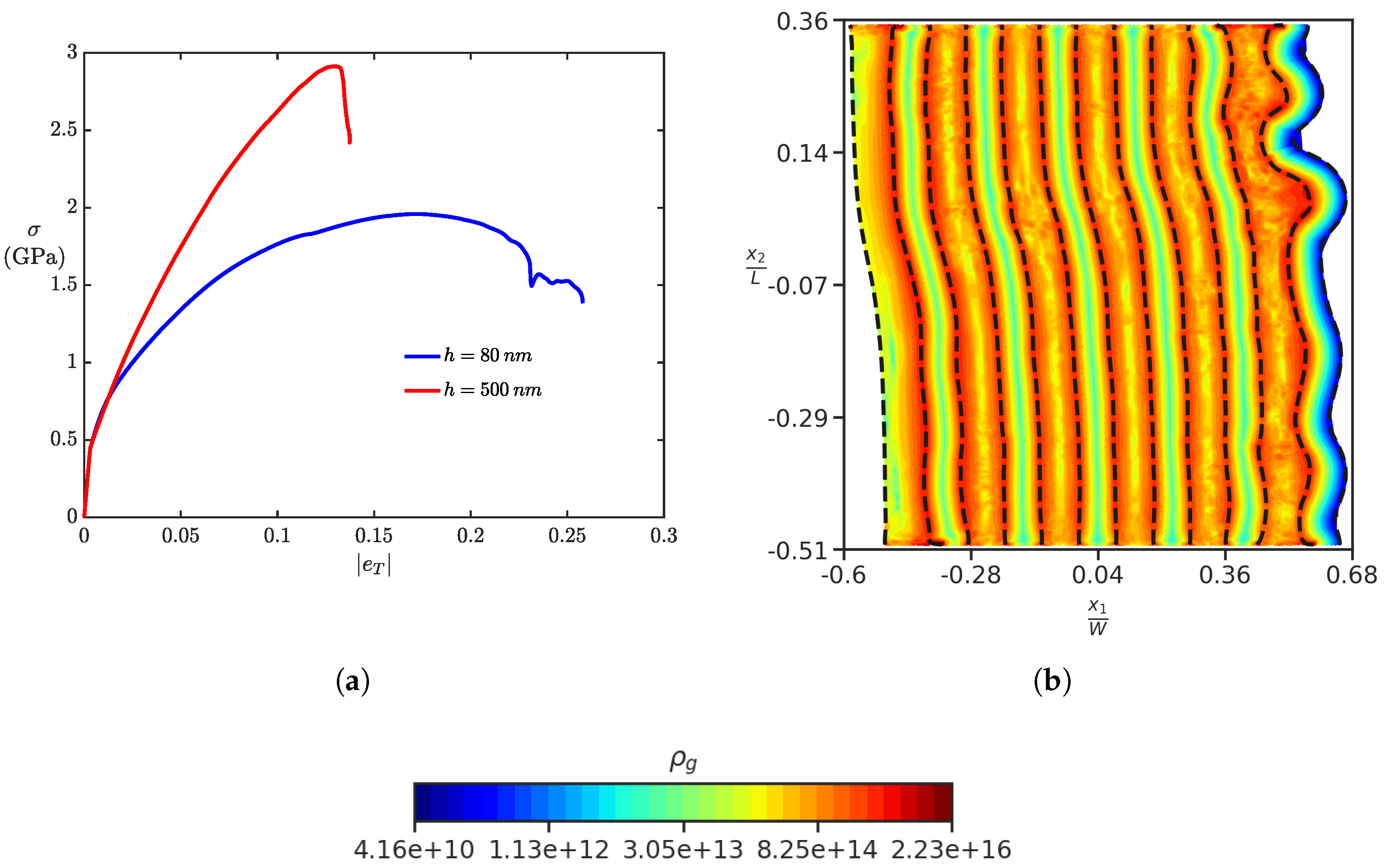
4.3. Effect of Layer Thickness Length Scale on the Formation of Kink Band
4.4. Conventional Plasticity within Our Model
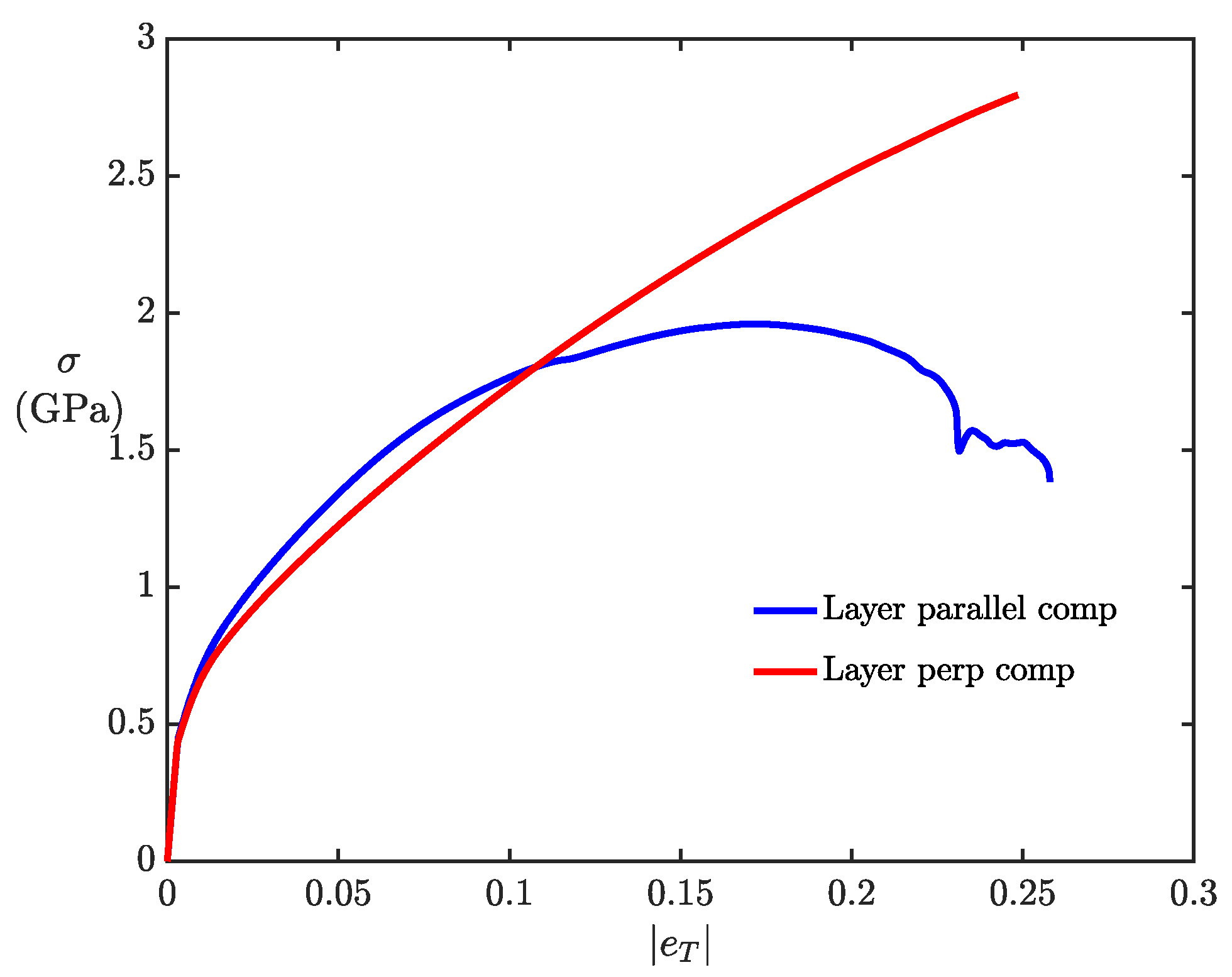
4.5. NML Subjected to Layer-Perpendicular Compression
4.6. Comparison of Strain Gradient Plasticity (SGP) Models and MFDM
- The numerical results that we have obtained are with continuous plastic flow across the interfaces, imposing continuity of certain components of plastic strain rate across the interface. Moreover, we see the accumulation of GND density across the interface (refer to Figure 3a), without having to do constrained plastic flow across the interface, which models the impenetrable interfaces in MFDM framework, as discussed in [25]. This is unlike the recent work by Zecevic et al. [5], where ‘micro-hard’ boundary conditions are implemented on the interfaces for their numerical study. From the current state-of-the-art of SGP models [5,40] there appears to be a high degree of indeterminacy in the nature of boundary/interface conditions to be imposed, with a significant impact on model predictions.Using ‘micro-hard’ boundary conditions within SGP models would make it difficult to reproduce drastically different scalings in the micropillar compression experiments for two different configurations ( and oriented metal thin film with respect to compression loading axis), as experimentally observed in [41]. In the work of Kuroda et al. [40], the plastic constraints on the metal-ceramic interface are relaxed beyond a certain level of plastic strain gradient on the interface/boundary, in order to obtain the same scalings as experimentally observed. However, our model is able to reproduce similar scalings as compared to experimental ones, without any ad-hoc modifications to the boundary conditions, as shown in [23]. Moreover, our model also predicts the formation of kink bands in the compression of NMLs, as shown in this current (first) simplified study, again with no special fitting of material parameters or changes to the structure of the theory (which, of course, includes the nature of boundary and interface conditions). The jump conditions of our model have also been shown to be successful in studies of texture evolution and recrystallization, among others [27,42,43].
- Our model is not able to reproduce size dependence on the initial yield strength, as observed in the micropillar compression experiments of single crystal pure Ni [44]; to our knowledge, SGP-based theories have not modeled these experiments either. Most SGP theories are able to predict a significant size effect at initial yield in the presence of boundary constraints or in the presence of inhomogeneous deformation, without being able to fundamentally distinguish boundary constraints arising from the kinematics of dislocation slip [16,23].
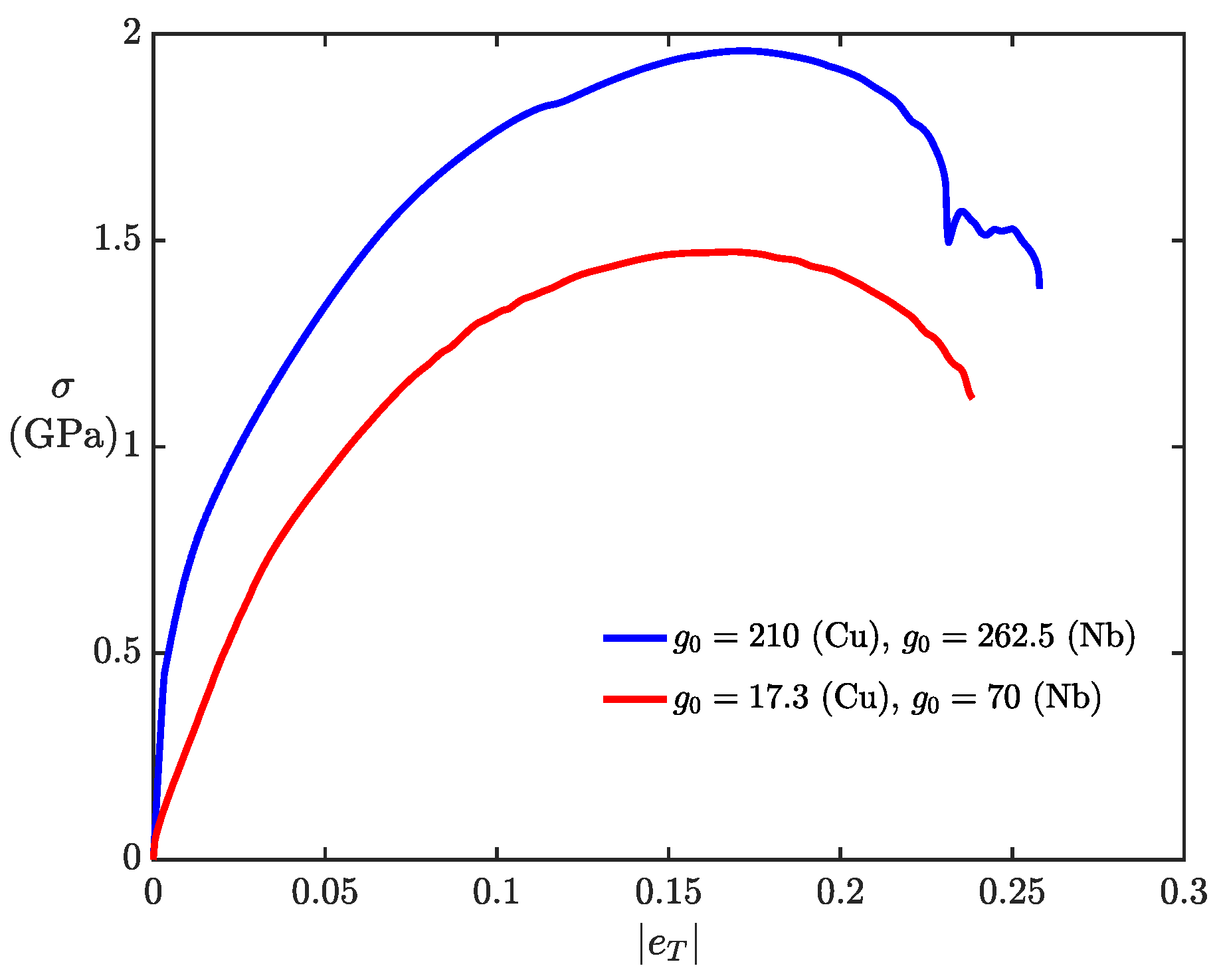
- SGP studies of micropillar confined thin film plasticity and kink banding [5,40,45], usually employ a value of work hardening to reproduce experimental behavior, raising the question of accurate representation of macroscopic behavior by the models. Moreover, the SGP studies of [5,46] employ several variants of the core energy function and show a sensitive and significant dependence on stress-strain response to such a choice. In our work, no such choices are required, and the work hardening rates we use in our strength evolution ensure, at least in the confined thin film problem and for modeling macroscopic response, that a physically appropriate mechanical response is obtained. For the present kink-band problem, the obtained stress-strain response (without any fitting) is unsatisfactory compared to the experiment (but no worse than the SGP result of [5]), and this is an issue that requires further work.
5. Conclusions
- dependence of kink-band formation on the layer thickness.
- kink bands do not form when the layer direction is aligned perpendicular to the compression loading direction, and there is shear-driven deformation within the layers of NML.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Beyerlein, I.J.; Li, Z.; Mara, N.A. Mechanical Properties of Metal Nanolaminates. Annu. Rev. Mater. Res. 2022, 52, 281–304. [Google Scholar] [CrossRef]
- Mara, N.A.; Bhattacharyya, D.; Dickerson, P.; Hoagland, R.G.; Misra, A. Deformability of ultrahigh strength 5 nm Cu/Nb nanolayered composites. Appl. Phys. Lett. 2008, 92, 231901. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Mara, N.A.; Carpenter, J.S.; Nizolek, T.; Mook, W.M.; Wynn, T.A.; McCabe, R.J.; Mayeur, J.R.; Kang, K.; Zheng, S.; et al. Interface-driven microstructure development and ultra high strength of bulk nanostructured Cu-Nb multilayers fabricated by severe plastic deformation. J. Mater. Res. 2013, 28, 1799–1812. [Google Scholar] [CrossRef]
- Nizolek, T.; Mara, N.A.; Beyerlein, I.J.; Avallone, J.T.; Pollock, T.M. Enhanced plasticity via kinking in cubic metallic nanolaminates. Adv. Eng. Mater. 2015, 17, 781–785. [Google Scholar] [CrossRef]
- Zecevic, M.; Lebensohn, R.A.; Capolungo, L. Non-local large-strain FFT-based formulation and its application to interface-dominated plasticity of nano-metallic laminates. J. Mech. Phys. Solids 2023, 173, 105187. [Google Scholar] [CrossRef]
- Jia, D.; Ramesh, K.T.; Ma, E. Effects of nanocrystalline and ultrafine grain sizes on constitutive behavior and shear bands in iron. Acta Mater. 2003, 51, 3495–3509. [Google Scholar] [CrossRef]
- Narayanan, S.; Schadler, L.S. Mechanisms of kink-band formation in graphite/epoxy composites: A micromechanical experimental study. Compos. Sci. Technol. 1999, 59, 2201–2213. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, N.; Schneider, M.M.; Nizolek, T.J.; Capolungo, L.; McCabe, R.J. Kink mechanism in Cu/Nb nanolaminates explored by in situ pillar compression. Acta Mater. 2022, 237, 118150. [Google Scholar] [CrossRef]
- Cahn, R.W. Slip and Polygonization in Aluminum. J. Inst. Met. 1951, 79, 129–158. [Google Scholar]
- Gurtin, M.E. A gradient theory of single-crystal viscoplasticity that accounts for geometrically necessary dislocations. J. Mech. Phys. Solids 2002, 50, 5–32. [Google Scholar] [CrossRef]
- Arora, R.; Acharya, A. Dislocation pattern formation in finite deformation crystal plasticity. Int. J. Solids Struct. 2020, 184, 114–135. [Google Scholar] [CrossRef]
- Ueta, R.; Shizawa, K. A Dislocation-based Crystal Plasticity Simulation on Kink Band Formation and Evolution in Polycrystalline Mg Alloy with LPSO Phase. In Advances in Engineering Plasticity XII; Key Engineering Materials; Trans Tech Publications: Stafa-Zurich, Switzerland, 2015; Volume 626, pp. 281–286. [Google Scholar]
- Asaro, R.J.; Rice, J.R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef]
- Forest, S. Modeling slip, kink, and shear banding in classical and generalized single crystal plasticity. Acta Mater. 1998, 46, 3265–3281. [Google Scholar] [CrossRef]
- Arora, R.; Zhang, X.; Acharya, A. Finite element approximation of finite deformation dislocation mechanics. Comput. Methods Appl. Mech. Eng. 2020, 367, 113076. [Google Scholar] [CrossRef]
- Arora, R.; Acharya, A. A unification of finite deformation J2 Von-Mises plasticity and quantitative dislocation mechanics. J. Mech. Phys. Solids 2020, 143, 104050. [Google Scholar] [CrossRef]
- Arora, R. Computational Approximation of Mesoscale Field Dislocation Mechanics at Finite Deformation. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2019. [Google Scholar]
- Acharya, A. Microcanonical entropy and mesoscale dislocation mechanics and plasticity. J. Elast. 2011, 104, 23–44. [Google Scholar] [CrossRef]
- Acharya, A. Jump condition for GND evolution as a constraint on slip transmission at grain boundaries. Philos. Mag. 2007, 87, 1349–1359. [Google Scholar] [CrossRef]
- Acharya, A.; Roy, A. Size effects and idealized dislocation microstructure at small scales: Predictions of a phenomenological model of mesoscopic field dislocation mechanics: Part I. J. Mech. Phys. Solids 2006, 54, 1687–1710. [Google Scholar] [CrossRef]
- Acharya, A.; Chapman, S.J. Elementary observations on the averaging of dislocation mechanics: Dislocation origin of aspects of anisotropic yield and plastic spin. Procedia IUTAM 2012, 3, 301–313. [Google Scholar] [CrossRef]
- Acharya, A.; Beaudoin, A.J. Grain-size effect in viscoplastic polycrystals at moderate strains. J. Mech. Phys. Solids 2000, 48, 2213–2230. [Google Scholar] [CrossRef]
- Arora, A.; Arora, R.; Acharya, A. Mechanics of micropillar confined thin film plasticity. Acta Mater. 2022, 238, 118192. [Google Scholar] [CrossRef]
- Puri, S.; Acharya, A.; Rollett, A.D. Controlling plastic flow across grain boundaries in a continuum model. Metall. Mater. Trans. A 2011, 42, 669–675. [Google Scholar] [CrossRef]
- Puri, S.; Das, A.; Acharya, A. Mechanical response of multicrystalline thin films in mesoscale field dislocation mechanics. J. Mech. Phys. Solids 2011, 59, 2400–2417. [Google Scholar] [CrossRef]
- Puri, S.; Roy, A.; Acharya, A.; Dimiduk, D. Modeling dislocation sources and size effects at initial yield in continuum plasticity. J. Mech. Mater. Struct. 2010, 4, 1603–1618. [Google Scholar] [CrossRef]
- Mach, J.C.; Beaudoin, A.J.; Acharya, A. Continuity in the plastic strain rate and its influence on texture evolution. J. Mech. Phys. Solids 2010, 58, 105–128. [Google Scholar] [CrossRef]
- Fressengeas, C.; Acharya, A.; Beaudoin, A.J. Dislocation mediated continuum plasticity: Case studies on modeling scale dependence, scale-invariance, and directionality of sharp yield-point. In Computational Methods for Microstructure-Property Relationships; Springer: Berlin, Germany, 2010; pp. 277–309. [Google Scholar]
- Das, A.; Acharya, A.; Suquet, P. Microstructure in plasticity without nonconvexity. Comput. Mech. 2016, 57, 387–403. [Google Scholar] [CrossRef]
- Fressengeas, C.; Beaudoin, A.J.; Entemeyer, D.; Lebedkina, T.; Lebyodkin, M.; Taupin, V. Dislocation transport and intermittency in the plasticity of crystalline solids. Phys. Rev. B 2009, 79, 014108. [Google Scholar] [CrossRef]
- Taupin, V.; Varadhan, S.; Chevy, J.; Fressengeas, C.; Beaudoin, A.J.; Montagnat, M.; Duval, P. Effects of size on the dynamics of dislocations in ice single crystals. Phys. Rev. Lett. 2007, 99, 155507. [Google Scholar] [CrossRef]
- Taupin, V.; Berbenni, S.; Fressengeas, C.; Bouaziz, O. On particle size effects: An internal length mean field approach using field dislocation mechanics. Acta Mater. 2010, 58, 5532–5544. [Google Scholar] [CrossRef]
- Richeton, T.; Wang, G.F.; Fressengeas, C. Continuity constraints at interfaces and their consequences on the work hardening of metal–matrix composites. J. Mech. Phys. Solids 2011, 59, 2023–2043. [Google Scholar] [CrossRef]
- Taupin, V.; Varadhan, S.; Fressengeas, C.; Beaudoin, A.J. Directionality of yield point in strain-aged steels: The role of polar dislocations. Acta Mater. 2008, 56, 3002–3010. [Google Scholar] [CrossRef]
- Djaka, K.S.; Taupin, V.; Berbenni, S.; Fressengeas, C. A numerical spectral approach to solve the dislocation density transport equation. Model. Simul. Mater. Sci. Eng. 2015, 23, 065008. [Google Scholar] [CrossRef]
- Varadhan, S.; Beaudoin, A.J.; Fressengeas, C. Lattice incompatibility and strain-aging in single crystals. J. Mech. Phys. Solids 2009, 57, 1733–1748. [Google Scholar] [CrossRef]
- Djaka, K.S.; Berbenni, S.; Taupin, V.; Lebensohn, R.A. A FFT-based numerical implementation of mesoscale field dislocation mechanics: Application to two-phase laminates. Int. J. Solids Struct. 2020, 184, 136–152. [Google Scholar] [CrossRef]
- Berbenni, S.; Taupin, V.; Lebensohn, R.A. A fast Fourier transform-based mesoscale field dislocation mechanics study of grain size effects and reversible plasticity in polycrystals. J. Mech. Phys. Solids 2020, 135, 103808. [Google Scholar] [CrossRef]
- Genee, J.; Berbenni, S.; Gey, N.; Lebensohn, R.A.; Bonnet, F. Particle interspacing effects on the mechanical behavior of a Fe–TiB2 metal matrix composite using FFT-based mesoscopic field dislocation mechanics. Adv. Model. Simul. Eng. Sci. 2020, 7, 6. [Google Scholar] [CrossRef]
- Kuroda, M.; Tvergaard, V.; Needleman, A. Constraint and size effects in confined layer plasticity. J. Mech. Phys. Solids 2021, 149, 104328. [Google Scholar] [CrossRef]
- Mu, Y.; Zhang, X.; Hutchinson, J.W.; Meng, W.J. Dependence of confined plastic flow of polycrystalline Cu thin films on microstructure. MRS Commun. 2016, 6, 289–294. [Google Scholar] [CrossRef]
- Fressengeas, C.; Upadhyay, M.V. A continuum model for slip transfer at grain boundaries. Adv. Model. Simul. Eng. Sci. 2020, 7, 12. [Google Scholar] [CrossRef]
- Su, Y.; Han, S.; Eisenlohr, P.; Crimp, M.A. Predicting shear transmission across grain boundaries with an iterative stress relief model. Acta Mater. 2021, 215, 116992. [Google Scholar] [CrossRef]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample dimensions influence strength and crystal plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Kuroda, M.; Needleman, A. A simple model for size effects in constrained shear. Extrem. Mech. Lett. 2019, 33, 100581. [Google Scholar] [CrossRef]
- Nicola, L.; Van der Giessen, E.; Gurtin, M.E. Effect of defect energy on strain-gradient predictions of confined single-crystal plasticity. J. Mech. Phys. Solids 2005, 53, 1280–1294. [Google Scholar] [CrossRef]
- Mu, Y.; Chen, K.; Meng, W.J. Thickness dependence of flow stress of Cu thin films in confined shear plastic flow. MRS Commun. 2014, 4, 129–133. [Google Scholar] [CrossRef]




| Saint-Venant-Kirchhoff Material | |
| Core energy density |
| Crystal plasticity | |
| ; | ||
| Parameter | m | b | l | E | |||||||
| () | (Å) | (MPa) | (MPa) | (MPa) | (m) | (GPa) | |||||
| Cu | 0.001 | 0.03 | 2.556 | 210 | 1890 | 273 | 20 | 144.58 | 0.324 | ||
| Nb | 0.001 | 0.03 | 2.86 | 262.5 | 2362.5 | 198 | 20 | 110.25 | 0.392 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arora, A.; Arora, R.; Acharya, A. Interface-Dominated Plasticity and Kink Bands in Metallic Nanolaminates. Crystals 2023, 13, 828. https://doi.org/10.3390/cryst13050828
Arora A, Arora R, Acharya A. Interface-Dominated Plasticity and Kink Bands in Metallic Nanolaminates. Crystals. 2023; 13(5):828. https://doi.org/10.3390/cryst13050828
Chicago/Turabian StyleArora, Abhishek, Rajat Arora, and Amit Acharya. 2023. "Interface-Dominated Plasticity and Kink Bands in Metallic Nanolaminates" Crystals 13, no. 5: 828. https://doi.org/10.3390/cryst13050828
APA StyleArora, A., Arora, R., & Acharya, A. (2023). Interface-Dominated Plasticity and Kink Bands in Metallic Nanolaminates. Crystals, 13(5), 828. https://doi.org/10.3390/cryst13050828





